Permutation-Based Trellis Optimization for a Large-Kernel Polar Code Decoding Algorithm

Abstract

Compared to Arikan’s $G_2$ kernel, large-kernel polar codes exhibit higher polarization rates and superior error correction performance. The critical steps of exact successive cancellation (SC) decoding for such codes can be implemented via trellis-based computations to reduce complexity. However, the complexity remains high for large kernels. This paper proposes a permutation-based trellis optimization scheme. The approach builds on the Massey minimal trellis and reorders its time axis to find a permutation that minimizes the number of trellis edges, thereby further reducing the exact SC decoding complexity. For smaller kernels ($G_3$–$G_{12}$), an exhaustive search is conducted to identify the optimal trellis. For larger kernels ($G_{13}$–$G_{16}$), where an exhaustive search becomes infeasible due to the factorial growth of the permutation space, an ant colony optimization (ACO)-based method is employed to find a near-optimal permutation. Simulation results show that the permutation-optimized trellis lowers the direct SC decoding complexity drastically. Furthermore, compared to the $l$-expression, the $W$-formula and original Massey trellis methods, it achieves multiplication operation reductions of up to 99.2%, 58.1%, and 56.5%, respectively. The improvement is particularly beneficial for large kernels, where traditional decoding methods become computationally prohibitive.

1. Introduction

Polar codes are the first class of error-correction codes mathematically proven to achieve the Shannon limit over binary-input discrete memoryless channels (B-DMCs) with low encoding and decoding complexity [1]. This theoretical breakthrough led to their adoption in the 5G New Radio (NR) standard, where polar codes are specified for control channels while low-density parity-check (LDPC) codes serve data channels [2]. The binary LDPC codes adopted for 5G data channels provide a compelling balance of high throughput and feasible complexity. Non-binary LDPC codes, despite potential performance gains in some scenarios, incur substantially higher decoding complexity [3], which aligns with the system considerations that favored polar codes for control channels. In contrast, polar codes are well-suited for control signalling primarily due to their deterministic construction, which facilitates standardization and implementation, and their provable capacity-achieving property, which provides a solid theoretical foundation for high reliability.

The original polar code construction employs the small 2 × 2 kernel $G_2=\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]$. In 5G NR, polar codes are implemented through recursive application of this kernel using the Kronecker product. However, theoretical work by Korada et al. established that a polarizing transformation based on a larger kernel matrix (e.g., 16 × 16) can achieve a higher polarization exponent than the recursive (Kronecker) construction based solely on $G_2$ [4]. This implies that for a fixed code length, large-kernel polar codes could potentially offer better error-correction performance. Furthermore, techniques have been developed to estimate the capacities and Bhattacharyya parameters of the bit subchannels induced by large kernels, which are essential for their practical construction [5]. However, directly adopting such large kernels introduces a fundamental challenge: the computational load of the successive cancellation (SC) decoding scales exponentially with the kernel size $n$, quickly becoming prohibitive.

Research on large-kernel polar codes has thus evolved along two complementary directions: one focused on code construction and kernel optimization [5], and the other—which this paper addresses—concentrating on decoding efficiency. We specifically investigate exact SC decoding, which maintains accuracy without approximation and preserves the code’s theoretical guarantees. Our work is confined to binary kernels $G_n$ with 3 ≤ n ≤ 16 as defined in [6].

To address SC decoding complexity, several approaches have emerged. The successive cancellation list (SCL) decoder improves error-correction performance but significantly increases computational load [7]. Alternatively, sequential decoding methods such as the Fano algorithm and the more recent SC-Creeper decoder—which incorporates a cost metric threshold—offer different complexity–performance trade-offs through dynamic tree search [8]. Our work takes an alternative path by focusing on accelerating the exact SC decoder through computational optimization of its kernel operations, preserving the algorithm’s original structure and exactness.

Trellis-based implementations represent one promising direction for this kind of optimization [9]. Although early trellis-based SC decoders relied on approximations [10,11], the development of exact SC decoding led to formulations in the likelihood ($l$-) domain [1], and later, to more efficient probability-pair ($W$-formula) methods [12]. Zhang et al. made significant progress by showing that exact SC decoding could be implemented without approximation using the Viterbi algorithm on a Massey minimal trellis [13]. However, their work was limited to a kernel of size three, and the complexity remains high for larger kernels.

This paper aims to make exact SC decoding practical for larger kernels. We propose a permutation-based trellis optimization scheme built on the Massey minimal trellis. The core idea is to reorder the trellis time axis to minimize the number of edges, thereby directly reducing computational load. We apply this optimization to binary kernels from $G_3$ to $G_{16}$. For smaller kernels ($G_3$–$G_{12}$), an exhaustive search is used to find the optimal permutation. For larger kernels ($G_{13}$–$G_{16}$), where an exhaustive search is infeasible, we employ an ant colony optimization (ACO) metaheuristic to efficiently find near-optimal permutations [14]. Simulations show that our approach achieves substantial complexity reductions compared to all existing exact SC decoding methods, making large-kernel polar codes more amenable to practical implementation.

2. Background

This section provides the necessary background for the proposed trellis optimization scheme. It first reviews the mathematical formulation of large-kernel polar codes. Then, it details the time axis of a trellis, which serves as the foundation for the subsequent optimization problem. Finally, it establishes the fundamental connection between the SC decoding algorithm and trellis-based computation.

2.1. Large-Kernel Polar Code

Let $W:\{0,1\}\to Y$ denote a B-DMC, where the input set is $\{0,1\}$, the output set is $Y$ and the transition probability is $W(y|x),x\in \{0,1\},y\in Y$. Let $a_1^n$ denote the row vector $(a_1,\dots ,a_n)$.

For a given kernel $G_n$, the channel $W_{G_n}:{\{0,1\}}^n\to Y^n$ can be defined as

$$W_{G_n}(y_1^n|u_1^n)\triangleq {\displaystyle \prod _{i=1}^{n}W(y_i|{(u_1^n{G}_n)}_i)}.$$

(1)

The transition probability of the $i$th subchannel $W_{G_n}^{(i)}:\{0,1\}\to Y^n,1\le i\le n$ is defined as

$$W_{G_n}^{(i)}(y_1^n,u_1^{i-1}|u_i)={\displaystyle \frac{1}{2^{n-1}}}{\displaystyle \sum _{u_{i+1}^n}{\displaystyle \prod _{j=1}^{n}W(y_j|{(u_1^n{G}_n)}_j)}}.$$

(2)

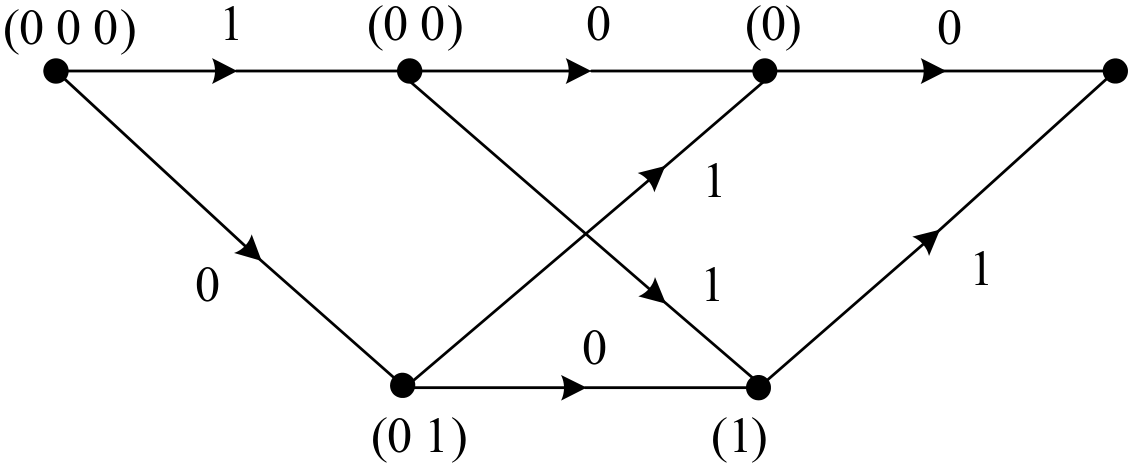
2.2. Time Axis of a Trellis

The transition probability calculation in Equation (2) is the kernel internal operation of SC decoding, which can be simplified via a trellis diagram. A trellis diagram is a time-layered directed graph with edge labels, typically represented as a triple $(V,E,A)$, where $V$ is the vertex set, $E$ is the edge set, and $A$ is the edge label set.

Each edge in the trellis diagram can be denoted as $(v,v^{\prime },a)$, indicating a directed connection from vertex $v$ to $v^{\prime }$ ($v,v^{\prime }\in V$) with edge label $a\in A$. For every vertex $v\in V$, there exists at least one directed path from the source point to $v$. If such a path contains $i$ edges, the depth of the vertex $v$ is defined as $i$. Let $V_i$ denote the vertex set with depth $i$. For a trellis of depth $n$, its vertex set can be partitioned into $n+1$ disjoint subsets $V_0,V_1,\cdots ,V_n$, and its edge set corresponds to $n$ disjoint subsets $E_0,E_1,\cdots ,E_{n-1}$. The ordered set $(0,1,\cdots ,n)$ resulting from this partition is called the time axis of the trellis.

2.3. Connecting SC Decoding to Trellis Computation

Direct evaluation of Equation (2) requires summing over $2^{n-i}$ terms, leading to exponential complexity in $n$. This summation can be computed exactly on a trellis representing the linear code defined by $G_n$. For a fixed decoding step $i$ and given past bits $u_1^{i-1}$, each complete path from $V_0$ to $V_n$ in the trellis corresponds to one specific assignment of the future bits $\left(u_{i+1},\cdots ,u_n\right)$ in (2). The edge label at depth $j$ equals the channel transition probability $W\left(y_j\left|x_j\right.\right)$, where the code bit $x_j$ is determined by the path and the kernel $G_n$. Thus, the product of labels along any path equals one term in the product ${\displaystyle \prod _{j=1}^{n}W(\cdot )}$ of (2).

The forward sum-product algorithm on the trellis computes the total probability mass at $V_n$ by merging paths at shared vertices. This merging exploits the distributive law, reducing the number of multiplications compared to direct expansion of the sum.

Consider decoding the first bit $u_1$ with the ternary kernel $G_3=\left[\begin{array}{l}1 0 0\\ 1 1 0\\ 1 0 1\end{array}\right]$ as an example, and assume $u_1=0$. Equation (2) reduces to

$${W_{G_3}}^{\left(1\right)}\left(y_1^3\left|u_1=0\right.\right)={\displaystyle \frac{1}{4}}{\displaystyle \sum _{u_2,u_3\in \left\{0,1\right\}}W\left(y_1\left|u_2\oplus u_3\right.\right)W\left(y_2\left|u_2\right.\right)W\left(y_3\left|u_3\right.\right)}.$$

(3)

According to the method in [13], trellis T1 is built for this computation and is shown in Figure 1. It can be seen that T1 has four paths, each corresponding to one of the four ($u_2,u_3$) pairs. Computing the total flow to the terminal vertex yields the same result as (3). As shown in [13], this trellis-based method uses only 6 multiplications, compared to 8 for the direct sum—the reduction is a result of merging paths at the central vertex.

Critically, the number of multiplications in the forward pass is proportional to the number of edges in the trellis. Different trellis representations of the same $G_n$ code can have different edge counts while maintaining identical decoding performance. Therefore, minimizing the trellis edge count is equivalent to minimizing the kernel computation complexity. This observation directs us to find the trellis with the minimal edge count for a given kernel, which we address in Section 3 through time-axis permutation.

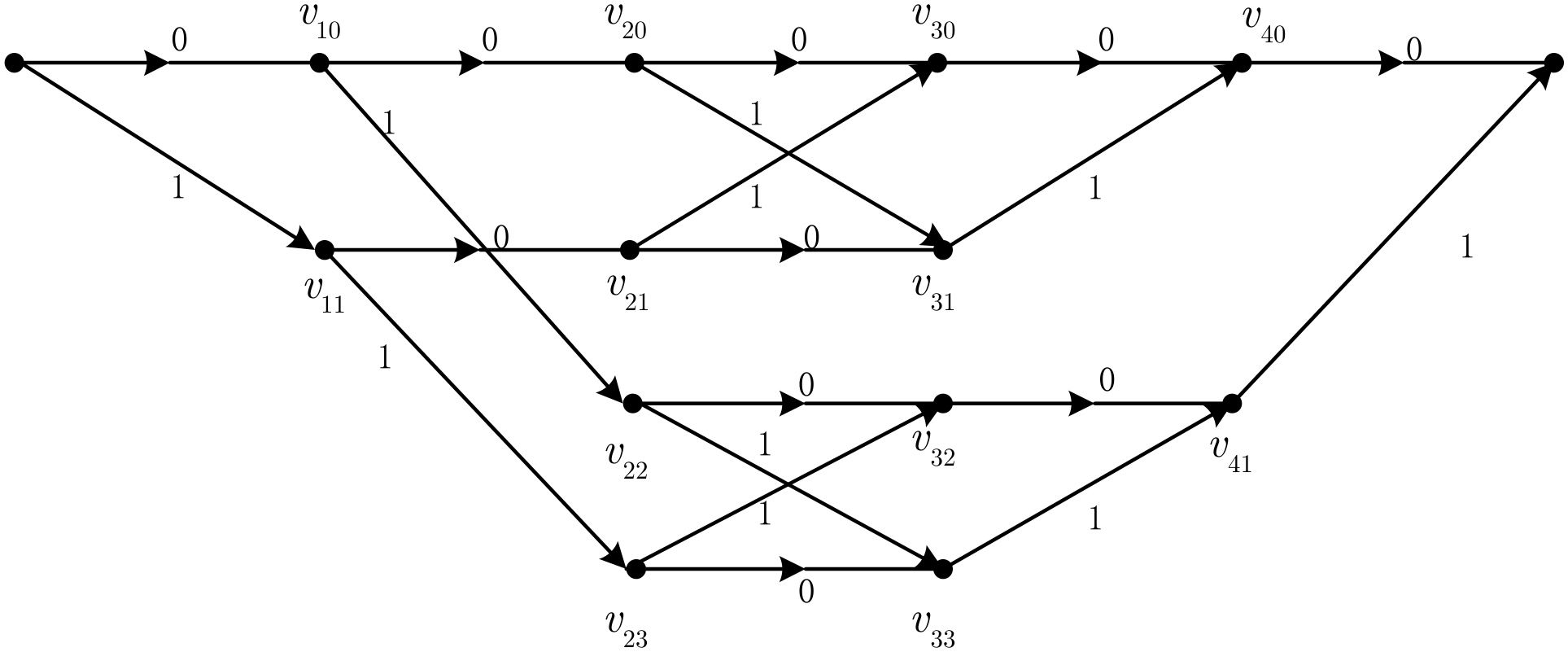
3. Permutation-Based Trellis Optimization

The computational cost of trellis-based exact SC decoding is primarily determined by the number of edges in the trellis. Therefore, minimizing the number of edges is crucial for reducing decoding complexity. For a fixed time axis, the best trellis is the minimal trellis. In this paper, the work is based on the Massey minimal trellis.

Figure 2 depicts the Massey minimal trellis generated from the generator matrix $\left[\begin{array}{ccccc}1& 0& 1& 0& 0\\ 1& 0& 0& 1& 0\\ 1& 1& 1& 0& 1\end{array}\right]$, which corresponds to the time axis $I_1=\{0,1,2,3,4\}$. Then, map this time axis to $I_2=\{0,3,2,1,4\}$ and its corresponding Massey trellis is as shown in Figure 3. Figure 2 and Figure 3 were obtained by using the methods in [13].

As can be observed, Figure 2 contains 14 vertices and 20 edges, whereas Figure 3 comprises only 9 and 12, respectively, demonstrating a significantly simpler structure. Hence, exact SC decoding on the trellis in Figure 3 is more efficient than that in Figure 2. Importantly, the generator matrices corresponding to Figure 2 and Figure 3 exhibit a one-to-one mapping, meaning that they represent the same code. Thus, exact SC decoding on the trellis in Figure 2 and Figure 3 will have the same decoding performance, which guarantees that the error-correction capability is preserved under the proposed permutation-based optimization. This indicates that the computational cost can be further reduced by reordering the time axis without any performance sacrifice.

The search for the trellis with the lowest computational cost involves generating Massey trellises from all possible time-axis permutations of the generator matrix and then selecting the one with the fewest edges. The resultant structure is termed the permutation-optimized trellis.

The above method is performed to identify the permutation-optimized trellis for smaller kernels ($G_3$–$G_{12}$). Once the permutation-optimized trellis is determined, exact SC decoding proceeds on this trellis, following the method in [13].

It should be noted that for kernels up to $G_{12}$, the permutation space (e.g., 12! ≈ 4.79 × 10⁸ for $G_{12}$) permits an exhaustive search in an offline setting. This is feasible because evaluating a single permutation’s trellis complexity is computationally trivial (microsecond-scale), and the process is perfectly parallelizable. In our experiments, the search for $G_{12}$ completed in hours on a multi-core machine.

For larger kernels ($G_{13}$–$G_{16}$), the factorial growth of the permutation space makes an exhaustive search intractable. We therefore employ the ACO-based heuristic method described next.

4. ACO-Based Time-Axis Permutation Optimization for Larger Kernels

The ACO algorithm is modeled on ant foraging behavior. Its core mechanism is the use of pheromones. As ants move, they lay down pheromone trails, and the strength of this scent influences the path choices of other ants. They essentially collectively reinforce favorable paths. Through this iterative process, the colony progressively identifies optimal or near-optimal solutions.

In this section, we apply ACO to the time-axis permutation optimization for larger kernels ($G_{13}$–$G_{16}$). We first detail the foundational concepts and steps of the ACO algorithm for this task. We then present the procedure for identifying the optimal or near-optimal permutation using ACO.

4.1. Concepts and Basic Steps of the ACO Algorithm

The application of an ACO algorithm to the time-axis permutation problem involves some fundamental concepts such as “ants”, “pheromone”, and “path selection”.

4.1.1. Ants

For a kernel $G_n$, there are $n$ points at time $\{0,1,\cdots ,n-1\}$. As shown in Figure 4, $t_i$($i=0,1,\cdots ,n-1$) represent $n$ time-axis nodes, $r_{i,k}\left(k=0,1,\cdots ,n-1-i\right)$ represent the branch numbers. $t_0\in \{0,1,\cdots ,n-1\}$ is the first time node of the time-axis permutation. There are $n$ lines from the starting point $O$ to $t_0$, representing the $n$ branches searching for $t_0$. Given $t_0$, $n-1$ lines from $t_0$ to $t_1$ represent the subsequent branches for $t_1$.

The ants are hypothetical path choosers. They start from $O$ and choose a branch to arrive at $t_0$. Then, they choose a branch from $t_0$ to arrive at $t_1$. Finally, they choose a branch from $t_{n-2}$ to arrive at $t_{n-1}$. In this way, path selection is completed, thereby obtaining a time-axis permutation scheme.

4.1.2. Time-Axis Permutation Scheme

Let the path chosen by the ant be $\{r_{0,0},r_{1,0},\cdots ,r_{n-2,0},r_{n-1,0}\}$, denoted as

$$p=[r_{0,0},r_{1,0},\cdots ,r_{n-2,0},r_{n-1,0}].$$

(4)

$p$ represents a time-axis permutation scheme. Define the trellis complexity of $p$ as the number of edges in its corresponding Massey trellis, denoted as $S(p)$.

There are $Na$ ants whose initial paths are randomly selected and labeled $p_0^{(0)},p_1^{(0)},\cdots ,p_{Na-1}^{(0)}$. The ants update their paths according to a specific “update rule” iteratively, and the paths generated after the $m$th iteration are denoted as $p_0^{(m)},p_1^{(m)},\cdots ,p_{Na-1}^{(m)}$.

4.1.3. Pheromone

Pheromone guides the ants’ path selection. Paths with higher pheromone concentrations are more likely to be chosen by the ants. To ensure unbiased exploration at the start of the search, the initial pheromone level on every branch is set to a constant, ${\tau }_0$, giving all paths an equal selection probability.

4.1.4. Iterative Optimal and Global Optimal

Denote the trellis complexities of $p_0^{(m)},p_1^{(m)},\cdots ,p_{Na-1}^{(m)}$ as $S(p_0^{(m)}),S(p_1^{(m)}),\cdots ,S(p_{Na-1}^{(m)})$. The iterative optimal scheme, denoted as $p_d^{(m)}$, is the one with the minimum trellis complexity among this iteration’s time-axis permutations. The global optimal scheme, denoted as $p_g^{(m)}$, is the one with the smallest complexity among all currently generated permutations.

4.1.5. Pheromone Update Rules

Let $L$ represent the set of all branches, and $\Gamma$ represent the pheromone space, specifically the following:

$$L=\left\{r_{i,k}\right|i=0,1,\dots ,n-1;k=0,1,\cdots ,n-1-i\},$$

(5)

$$\Gamma =\left\{{\tau }_{ik}\right|i=0,1,\dots ,n-1;k=0,1,\cdots ,n-1-i\}.$$

(6)

The pheromone value of branch $r_{i,k}$ after the $m$th iteration is ${\tau }_{ik}^{(m)}$. As mentioned earlier, for $m=0$, all the pheromone values are initially set to a constant ${\tau }_0$, that is, ${\tau }_{ik}^{(0)}={\tau }_0,i=0,1,\dots ,n-1;$$k=0,1,\cdots ,n-1-i$. The pheromone update formula is as follows [14]:

$${\tau }_{ik}^{(m+1)}=(1-\rho ){\tau }_{ik}^{(m)}+k△{\tau }_{ik}^{(m+1)}.$$

(7)

In Equation (7), $\rho$ represents the pheromone evaporation coefficient, and $\Delta {\tau }_{ik}^{(m+1)}$ is defined as follows [14]:

$$\Delta {\tau }_{ik}^{(m+1)}=\left\{\begin{array}{l}{\displaystyle \frac{Q}{S(p_g^{(m)})}}, (r_{i-1,k},r_{i,k}) \mathrm{in} p_g^{(m)} \\ {\displaystyle \frac{Q}{S(p_d^{(m)})}}, (r_{i-1,k},r_{i,k}) \mathrm{in} p_d^{(m)}\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \mathrm{otherwise}\end{array}\right.,$$

(8)

where $Q$ is the pheromone intensity, which refers to the amount of pheromone released by each ant after completing a full path search.

To prevent the ACO algorithm from converging prematurely to a local optimum and to enhance its global search ability, the following constraints are imposed on ${\tau }_{ik}^{(m+1)}$:

$${\tau }_{ik}^{(m+1)}=\left\{\begin{array}{l}{\tau }_{\max }, {\tau }_{ik}^{(m+1)}>{\tau }_{\max }\\ {\tau }_{\min }, {\tau }_{ik}^{(m+1)}<{\tau }_{\min }\end{array}\right..$$

(9)

And the values of ${\tau }_{\max }$ and ${\tau }_{\min }$ are given by the following formula:

$${\tau }_{\max }={\displaystyle \frac{1}{(1-\rho )S(p_d^{(m)})}},{\tau }_{\min }=0.05{\tau }_{\max }.$$

(10)

4.1.6. Convergence Factor

The formula for the convergence factor $cg$ is defined as follows [14]:

$$c{g}^{(m+1)}=2\left(\left({\displaystyle \frac{{\displaystyle \sum _{{\tau }_{ik}^{(m+1)}\in L}\max \{{\tau }_{\max }-{\tau }_{ik}^{(m+1)},{\tau }_{ik}^{(m+1)}-{\tau }_{\min }\}}}{\left|L\right|({\tau }_{\max }-{\tau }_{\min })}}\right)-0.5\right),$$

(11)

where $\left|L\right|$ is the cardinality of $L$.

4.1.7. Roulette Wheel Selection

Suppose that an ant can choose branch $r_0,r_1,\cdots ,r_{s-1}$ at some time point with corresponding probabilities $p_0,p_1,\cdots ,p_{s-1}$ and $p_0+p_1+\cdots +p_{s-1}=1$.

The ant chooses the branch as follows:

(1)

Generate a uniformly distributed random number $b$ in [0, 1].

(2)

Determine an index $i$ such that

$${\displaystyle \sum _{j=0}^{i-1}{p}_j}\le b\le {\displaystyle \sum _{j=0}^i{p}_j}.$$

(12)

(3)

Choose $r_i$ as the branch for this ant at that time point.

4.1.8. Generate Time-Axis Permutation Scheme

For time point $t_i$, the probability of each branch is calculated according to the pheromone space as follows:

$$p_{ik}^{(m)}={\displaystyle \frac{{\tau }_{ik}^{(m)}}{{\displaystyle \sum _{l=0}^{n-1-i}{\tau }_{il}^{(m)}}}},$$

(13)

where $k=0,1,\cdots ,n-1-i$.

For the kernel $G_n$, ants generate a time-axis permutation scheme as follows:

(1)

Start from the starting point $O$, and set $i=0$.

(2)

Calculate the probability of each branch for time point $t_i$ according to Equation (13). Then, choose the branch for time point $t_i$ according to the “roulette wheel selection”.

(3)

Increment $i$ by 1. Repeat (2) until $i=n-1$.

In this way, an ant chooses a path in Figure 4; that is, a time-axis permutation scheme is generated.

4.2. Algorithm Design

Based on the foundational concepts and operations outlined in Section 4.1, the procedure for identifying the optimal permutation using the ACO algorithm is as follows:

Step 1: Initialization. Set the initial parameters, such as the number of ants ($Na$), the initial pheromone evaporation coefficient (${\rho }_0$), the pheromone intensity ($Q$) and the initial pheromone value ${\tau }_0$.

Step 2: Solution construction and evaluation. Each ant generates a time-axis permutation scheme following the procedure in Section 4.1.8. The trellis complexity for each generated scheme is then computed. Subsequently, both the current iterative optimal scheme and the global optimal scheme are updated.

Step 3: Pheromone update and convergence assessment. The whole pheromone space is updated as per Section 4.1.5. Following this, the convergence factor for the current pheromone space is calculated according to Section 4.1.6.

Step 4: Termination check. The algorithm flow branches based on the value of the convergence factor $cg$:

(1)

If $cg<0.9999$ or the maximum number of iterations has not been reached, the algorithm returns to Step 2 to commence the next iteration.

(2)

Otherwise, the algorithm terminates and outputs the final result.

5. Simulation Results and Analysis for Polar Codes with $G_3$ – $G_{12}$ Kernels

This section presents the simulation results for polar codes with $G_3$–$G_{12}$ kernels.

Table 1. Average number of multiplication operations required for kernel computations ($G_3$–$G_{12}$): (a) direct SC decoding; (b) $l$-expression method [1]; (c) $W$-formula method [12]; (d) Massey trellis [13]; (e) permutation-optimized trellis.

Kernel Size $\mathit{n}$	(a)	(b)	(c)	(d)	(e)
3	9.3	3.7	8.7	10.6	10.0
4	22.5	2.0	4.0	17.5	15.5
5	49.6	7.8	19.2	26.4	21.2
6	105.0	11.3	25.3	35.6	27.6
7	217.7	21.9	33.7	52.5	37.7
8	446.3	42.8	44.8	71.7	46.7
9	908.4	52.1	56.7	91.1	58
10	1841.4	83.8	67.4	123.0	64.2
11	3721.8	246.0	118.5	159.6	91.2
12	7505.5	673.8	171.0	217.8	115.8

provides the precise average number of multiplication operations required for kernel computations in direct SC decoding, the $l$-expression, the $W$-formula, the Massey trellis, and the proposed permutation-optimized trellis. Because the proposed optimization reduces the number of trellis edges, the reported reduction in multiplications proportionally reflects the reduction in overall computational complexity.

As shown in Table 1, for $n\ge 4$, it significantly outperforms direct SC decoding, with the average number of multiplication operations decreasing progressively as $n$ increases. For $n\ge 10$, the optimized trellis reduces operations by 23.4%, 63%, and 82.8% relative to the $l$-expression-based SC decoding, and by 4.7%, 23%, and 32.3% compared to the $W$-formula-based approach. Furthermore, for $n\ge 3$, it achieves operation reductions of 5.7% to 46.8% compared to SC decoding on the Massey trellis.

Consequently, the simulation results demonstrate that the permutation-optimized trellis offers a lower computational cost than benchmark methods for $n\ge 10$, establishing it as a more efficient decoding method for large-kernel polar codes.

6. Simulation Results and Analysis for Polar Codes with $G_{13}$ – $G_{16}$ Kernels

This section presents the simulation results for polar codes with $G_{13}$–$G_{16}$ kernels using the ACO algorithm for permutation optimization. First, the parameter settings for the ACO algorithm are analyzed. Subsequently, the simulation results and their analysis are presented.

6.1. Parameter Settings

In ACO, parameter settings are highly sensitive to the overall algorithm performance. Because parameters are interdependent, adjusting one may affect others. Thus, no universally optimal parameter combination suits all scenarios. We finalized the parameters through repeated experiments to observe their individual impacts. The following analysis examines the ACO parameters using the time-axis permutation of the $G_{16}$ kernel matrix as an example.

6.1.1. Analysis of the Number of Ants

The number of ants, $Na$, requires careful consideration in ACO design. Although more ants allow for broader exploration of possible solutions, too many ants lead to repeated searches along similar paths. This repetition increases computation time while providing diminishing returns in solution quality. Therefore, $Na$ should be determined according to the specific problem’s requirements and constraints.

For each ant number $Na$, we conducted 10 independent experiments and selected the best result. For this best result, we recorded both the total number of edges in the trellis corresponding to the optimal time-axis permutation (i.e., the optimal trellis edges) and the corresponding number of iterations to convergence.

As shown in

Table 2. Impact of number of ants on ACO performance.

Number of Ants	Total Number of Optimal Trellis Edges	Number of Iterations to Convergence
30	220	57
40	220	61
50	220	49
60	220	41
70	220	33
80	220	23
90	220	20
100	220	20
110	220	22
120	220	21

, across different values of $Na$, the total number of optimal trellis edges remained unchanged at 220, whereas the number of iterations to convergence varied. The convergence iteration count stabilized at $Na=90$, which was consequently adopted for all subsequent simulations in this work.

6.1.2. Analysis of the Pheromone Evaporation Coefficient

The pheromone evaporation coefficient, $\rho$, controls the pheromone update rate. The value of $\rho$ influences the balance between exploration and exploitation: a smaller $\rho$ favors global exploration at the cost of slower convergence, while a larger $\rho$ accelerates convergence but increases the risk of local optima. To address this, our study dynamically adjusts $\rho$ based on the convergence factor $cg$, setting it low initially to promote exploration and increasing it later to enhance convergence speed.

We tested each initial value of ${\rho }_0$ with 10 independent runs, selecting the best result, and recorded the total number of optimal trellis edges and the number of iterations to convergence.

Table 3. Impact of initial evaporation coefficient on ACO performance.

Initial Evaporation Coefficient	Total Number of Optimal Trellis Edges	Number of Iterations to Convergence
0.1	220	35
0.2	220	17
0.3	220	13
0.4	220	14
0.5	220	19
0.6	220	20
0.7	220	23
0.8	236	24
0.9	236	22
1.0	252	27

shows that ${\rho }_0=0.3$ achieves the optimal time-axis permutation with minimal iterations. Decreasing ${\rho }_0$ increases the number of iterations to convergence, while increasing it prevents the algorithm from finding the optimal permutation. Therefore, ${\rho }_0$ was set to 0.3 for all subsequent simulations.

6.1.3. Analysis of the Pheromone Intensity

The pheromone intensity, $Q$, plays a key role in ACO. If $Q$ is too low, pheromone differences between paths become too small to guide the search effectively, slowing convergence. Excessively high $Q$ values, however, allocate a disproportionately large share of pheromone to paths found early on. This can cause the search to prematurely lock into these initially promising but potentially suboptimal regions. For each value of $Q$, we conducted 10 independent runs, selecting the best result, and recorded the total number of optimal trellis edges and the number of iterations to convergence.

As shown in

Table 4. Impact of evaporation coefficient on ACO performance.

Pheromone Intensity	Total Number of Optimal Trellis Edges	Number of Iterations to Convergence
10	220	23
20	220	16
30	220	16
40	220	13
50	220	12
60	220	17
70	220	23
80	220	27
90	220	29
100	220	27

, across 10 experiments with different $Q$ values, the total number of optimal trellis edges remained constant at 220, while the number of iterations to convergence varied. The convergence iteration count reached its minimum when $Q$ was set to 50. Any deviation from this value—whether an increase or decrease—resulted in a higher number of iterations to convergence. Therefore, a pheromone intensity of $Q=50$ was adopted for subsequent simulations in this work.

6.2. Simulation Results and Analysis

This subsection presents the simulation results from the application of the ACO algorithm to the $G_{13}$–$G_{16}$ kernels. The ACO parameters are configured as follows:

Number of ants: $Na=90$,

Maximum iterations: $NcMax=100$,

Initial pheromone evaporation coefficient: ${\rho }_0=0.3$,

Pheromone intensity: $Q=50$,

Initial pheromone value: ${\tau }_0=0.0625$.

The weights of the global optimum $k_g$ and iterative optimum $k_d$, and the dynamically changing pheromone evaporation coefficient $\rho$ are related to the convergence factor $cg$. They are set as follows:

$$\left\{\begin{array}{c}0\le cg<0.5:k_g=0.0,k_d=1.0,\rho =0.3\\ 0.5\le cg<0.7:k_g=0.382,k_d=0.618,\rho =0.32\\ 0.7\le cg<0.9:k_g=0.5,k_d=0.5,\rho =0.34\\ 0.9\le cg<0.999:k_g=0.618,k_d=0.382,\rho =0.36\\ cg\ge 0.999:k_g=0.8,k_d=0.2,\rho =0.38\end{array}\right..$$

Table 5. Average number of multiplication operations required for kernel computations ($G_{13}$–$G_{16}$): (a) direct SC decoding; (b) $l$-expression method; (c) $W$-formula method; (d) Massey trellis; (e) permutation-optimized trellis.

Kernel Size $\mathit{n}$	(a)	(b)	(c)	(d)	(e)
13	15,121.8	1271.5	240.2	297.2	130.3
14	30,425.6	3790.6	372.0	355.3	160.7
15	61,165.1	10,736.6	481.3	446.9	205.1
16	122,878.1	34,145.0	630.1	606.8	263.8

provides the precise average number of multiplication operations required for kernel computations in direct SC decoding, the $l$-expression, the $W$-formula, the Massey trellis, and the proposed permutation-optimized trellis. Because our trellis optimization reduces the total number of edges, the number of required multiplications scales proportionally with the overall number of all operations (additions, multiplications, etc.).

As shown in Table 5, for kernel sizes from 13 to 16, the proposed optimized trellis significantly outperforms direct SC decoding, reducing the average number of multiplication operations by more than 99%. And compared to the $l$-expression, the $W$-formula, and the Massey trellis, the reductions in multiplication count are (89.8%, 95.8%, 98.1%, 99.2%), (45.8%, 56.8%, 57.4%, 58.1%), (56.2%, 54.8%, 54.1%, 56.5%), respectively, for $n=13 \mathrm{to} 16$.

The above results indicate that for $n\ge 13$, the proposed optimized trellis significantly outperforms all benchmark methods. As decisively shown in Table 5, the substantial complexity reduction achieved is robust and persists even when the ACO parameters employed for the trellis discovery are not finely tuned to their theoretical optimum. This establishes the permutation-optimized trellis as a more efficient approach for large-kernel exact SC decoding.

7. Conclusions

This paper proposed a permutation-based trellis optimization scheme to reduce the computational complexity of exact SC decoding. Based on the Massey minimal trellis, our approach reordered the time axis to further minimize the number of edges, yielding a more computationally efficient structure.

We first introduced the fundamental permutation problem and illustrated the structural improvements achieved through optimization. Then, depending on the kernel size, we applied two distinct methods—an exhaustive search and ACO—to find the optimal or near-optimal time-axis permutation. Specifically, (1) for smaller kernels ($G_3$–$G_{12}$), a full permutation search was performed to identify the optimal time-axis permutation by exhaustively evaluating all possible configurations. (2) For larger kernels ($G_{13}$–$G_{16}$), the ACO algorithm was employed to efficiently determine a near-optimal permutation, thereby lowering computational overhead.

Simulation results indicated that our approach significantly outperformed existing methods, including the direct SC decoding, $l$-expression and $W$-formula methods, and the original Massey trellis, especially for large kernels. This improvement was particularly crucial as it made the practical adoption of large-kernel polar codes possible.