Opinion Formation at Ising Social Networks

Abstract

We study the process of opinion formation in an Ising social network of scientific collaborations. The network is undirected. An Ising spin is associated with each network node being oriented up (red) or down (blue). Certain nodes carry fixed, opposite opinions whose influence propagates over the other spins, which are flipped according to the majority-influence opinion of neighbors of a given spin during the asynchronous Monte Carlo process. The amplitude influence of each spin is self-consistently adapted, and a flip occurs only if this majority influence exceeds a certain conviction threshold. All non-fixed spins are initially randomly distributed, with half of them oriented up and half down. Such a system can be viewed as a model of elite influence, coming from the fixed spins, on the opinions of the crowd of non-fixed spins. We show that a phase transition occurs as the amplitude influence of the crowd spins increases: the dominant opinion shifts from that of the elite nodes to a phase in which the crowd spins’ opinion becomes dominant and the elite can no longer impose their views.

1. Introduction

Social networks now exert a significant influence on human society, and, as a result, their properties are being actively investigated by the scientific community (see, e.g., [1,2,3]). Recently, their impact has been argued to extend specifically to opinion formation and even to affect political elections [4,5]. This very problem of opinion formation in a group of electors is being actively investigated in the field of sociophysics, using diverse models and methods (see, e.g., [6,7,8,9,10,11,12]). Usually, in these studies, there are two competing opinions of electors, often modeled as network nodes, governed by a local majority rule whereby an elector’s opinion is determined by the majority opinion of its linked neighbors. Thus, each node has a red or blue color (or an Ising spin up or down), and the system represents an Ising network of spin halves with N nodes and a huge space of $N_{conf}=2^N$ configuration states (see, e.g., [11]). The opinion, or spin polarization, of nodes is determined by an asynchronous Monte Carlo process in a system of spins described by an Ising Hamiltonian on a network. A similar Monte Carlo process is used in models of associative memory [13,14], and a similar process is also considered in Boolean networks [15,16].

Recently, it was proposed that such an opinion formation process can also describe a country’s preference to trade in one currency or another (e.g., USD or hypothetical BRICS currency) [17]. An important new element, introduced in [17] and then extended in [18], is that the opinion of certain network nodes is considered to be fixed (spin always up or down) and not affected by the opinions of other nodes. In addition, in such an Ising Network of Opinion Formation (INOF) model [18], it is assumed that, at the initial stage, only fixed nodes have a given fixed spin polarization, while all other nodes are white (zero spin), thus producing no influence on the opinions (spins) of other nodes. However, these white nodes exhibit spin polarization up or down during the asynchronous Monte Carlo process of opinion formation on the Ising network. All the above studies have been conducted on directed networks with the INOF approach of fixed and white nodes applied to Wikipedia Ising Networks (WIN) considering contests between different social concepts, companies, political leaders and countries [18]. When we consider a contest between two political leaders, like Trump and Putin, in WIN, it is rather natural to assume that all other nodes (Wikipedia articles) have no specific opinion on these two figures at the initial stage of the Monte Carlo process of INOF, so that they are considered white nodes. However, it may be important to understand the influence of the initial random opinions of non-fixed nodes on the contest results. Beyond this, the INOF approach can be applied to social networks, which, in many cases, are undirected, such as Facebook. We note that the properties of the Ising model of complex networks have been studied previously (see, e.g., [19,20]), but the opinion formation process has not.

To this end, in this work, we apply the INOF approach to a social network of scientists studied by Newman [21,22] with data sets from his database [23,24]. On the basis of this undirected network, we study the process and features of opinion formation and analyze the effects of the randomized opinions of non-fixed nodes on this process.

The paper is organized as follows. In Section 2, we describe the data sets and the Generalized INOF (GINOF) model; Section 3 presents the results, starting with the original INOF model and then analyzing the phase transition in the GINOF model; a discussion of the results and conclusions is provided in Section 4. Certain data sets are also available at https://www.quantware.ups-tlse.fr/QWLIB/GINOF4socialnets/ (accessed on 16 November 2025), marked below as the GINOF web page.

2. Data Sets and Model Description

For our studies, we choose the social collaborative network of $N=379$ scientists (nodes), analyzed in [21,22], taken from [23]. The network image is available in Figure 8 in [22] and in [24], where the network nodes are given with the names of scientists. This is an undirected network with weighted symmetric adjacency matrix $A_{ij}=A_{ji}$, with the number of links $N_{\ell }=1828$; the weights of links change from a minimal $a_{min}=A_{ij}=0.125$ to a maximal $a_{max}=4.225$ value; there are no isolated communities in this network. The average number of links per node is $\kappa =N_{\ell }/N\approx 4.8$. The effects of non-linear perturbation and dynamical thermalization in this network were recently studied in [25]. The full list of network links and node names is available in [23,24] and on the GINOF web page.

As in [25], we construct the Google matrix of the network defined in a standard way [25,26] as $G_{ij}=\alpha S_{ij}+(1-\alpha )/N$, where $S_{ij}$ is the matrix of Markov transitions obtained from $A_{ij}$ by normalizing to unity all matrix elements in each column. We use here the standard value of damping factor $\alpha =0.85$. There are no dangling nodes in this network. The PageRank vector $P_i$ is the solution of the equation $GP=\lambda P$ at $\lambda =1$; its elements are positive and give a probability of finding a random surfer on a node i [26]. By ordering all nodes by a decreasing order of $P_i$, we obtain the PageRank index K changing from $K=1$ at the maximal $P\left(K\right)$ to $K=379$ at the minimal $P\left(K\right)$. The top 10 PageRank nodes from $K=1$ to 10 are Barabasi, Newman, Sole, Jeong, Pastorsatorras, Boccaletti, Vespignani, Moreno, Kurths, and Stauffer [25]. All links $A_{ij}$ and PageRank indexes with names are available at the GINOF web page given above.

The INOF procedure of opinion formation on Ising networks is described in detail in [18]. It assumes that there is a group of fixed red nodes (spin ${\sigma }_i=1$) and another group of fixed blue nodes (spin ${\sigma }_i=-1$); all other nodes are white (${\sigma }_i=0$) at the initial state but can change their spins to $\pm 1$ during an asynchronous Monte Carlo process. Compared to the INOF model [18], here, we extend the condition of spin flip and the initial states of white nodes. Thus, to all originally white nodes, we attribute vote power, or amplitude influence, determined by coefficients $W_i$, which characterize the level of an elector’s conviction regarding the importance of the election and/or his interest in elections. Initially, all white nodes have the same $W_i=W<1$. For fixed nodes, we always have $W_i=1$. Moreover, all previously white nodes are randomly assigned spins ${\sigma }_i=1$ or ${\sigma }_i=-1$. Thus, for our network, we have 188 red and 188 blue nodes with a random distribution of colors (1 node remains white due to the odd number of nodes), and there are also 2 fixed nodes with opposite spins $\sigma =\pm 1$. With this initial configuration of all node spins, the spin i flip condition is determined by the accumulated influence of the opinions of linked nodes j:

$$Z_i=\sum _{j\ne i}{\sigma }_j{W}_j{A}_{ij}$$

(1)

Here, the sum runs over all j nodes linked to i with the contribution of $A_{ij}$ links and vote power $W_j$. The flip condition of spin i is defined as follows: for $Z_i>Z_c$, its ${\sigma }_i=1$ and its $W_i=1$; for $Z_i<-Z_c$, its ${\sigma }_i=-1$ and its $W_i=1$; for $|Z_i|\le Z_c$, its spin ${\sigma }_i$ and coefficient $W_i$ remain unchanged. Thus, the parameter $Z_c$ denotes the opinion conviction threshold (OCT), so that, if the module of influence of friends $|Z_i|$ is less than $Z_c$, then the elector i does not take into account their opinions. Moreover, if $|Z_i|>Z_c$, then this elector i becomes convinced of the importance of this election and it reaches $W_i=1$ for all future evolutions.

This asynchronous Monte Carlo procedure of spin flips is applied for all spins (except fixed ones) without repetitions. When the run over all spins is complete, we arrive at the Monte Carlo time $\tau =1$, after which the procedure goes to $\tau =2$ with another random pathway order of spin flips and so on till $\tau =20$, when the process has converged to a steady state. This corresponds to a one-pathway realization for a specific order of spin flips; then, the process is repeated for another pathway realization of spin flip order, and an average fraction of red $f_r$ and blue $f_b$ nodes (up/down spins) is determined, averaging over all pathway realizations and all nodes, which gives the total red fraction $f_r$ (by construction $f_r+f_b=1$ since there are no white nodes in this network at the steady state). Several examples of the $\tau —$evolution of red fraction $f_r$ are shown in Figure 1. We also determine the average fraction of red nodes $f_r\left(i\right)$ for each node i by averaging over $N_r$ pathway realizations. We use $N_r={10}^4$ and ${10}^5$ in this work.

We refer to the INOF model described above as the Generalized INOF model (GINOF). The main new elements of GINOF are the following: there now no white nodes at the initial state but all non-fixed nodes now have spins up or down, chosen as a random spin configuration with half up and half down spins. However, now, each spin of this configuration has an amplitude of influence $W_i<1$, entering the influence score $Z_i$ at (1); initially, all non-fixed nodes have $W_i=W<1$. A flip of spin i takes place only if its influence score exceeds the opinion conviction threshold $Z_c$ with $|Z_i|>Z_c$, and, if $|Z_i|>Z_c$, then its amplitude of influence becomes $W_i=1$ for all further iterations. Of course, the fixed nodes always have their $W=1$ and their opinions remain fixed.

In a certain sense, in the GINOF model, the fixed nodes can be viewed as two competing elite groups with opposite opinions that try to convince other society electors (people crowd) with random opinions (half red and half blue). Moreover, these crowd electors at the initial state of the election process have a weak amplitude influence on the scores of other electors ($W<1$). During the election campaign, modeled as a Monte Carlo process, the crowd nodes, with influence scores above the opinion conviction threshold $Z_c$, become active in the election process, achieving the maximal amplitude influence $W_i=1$. For the case with $W_i=W=0$, the GINOF model is reduced to the original INOF model studied in [18].

At first glance, it seems that the network with $N=379$ nodes considered here is much smaller compared to those in INOF studies with $N\sim {10}^6$ reported in [18]. However, we point out that, even with $N=379$, the number of configuration states of the Ising network is huge, being $N_{conf}=2^N$. Moreover, in studies of other spin systems with an asynchronous Monte Carlo process, a similar number of nodes has been considered, with $N\approx$ 400–1000 in [14] and $N\approx 100$ in [27,28].

The results for the GINOF model are presented in the next section. They show that there is a transition between two phases: from a phase where the elite is able to impose its opinion to a phase where the opinion of the elector crowd is dominant over the elite opinion.

3. Results

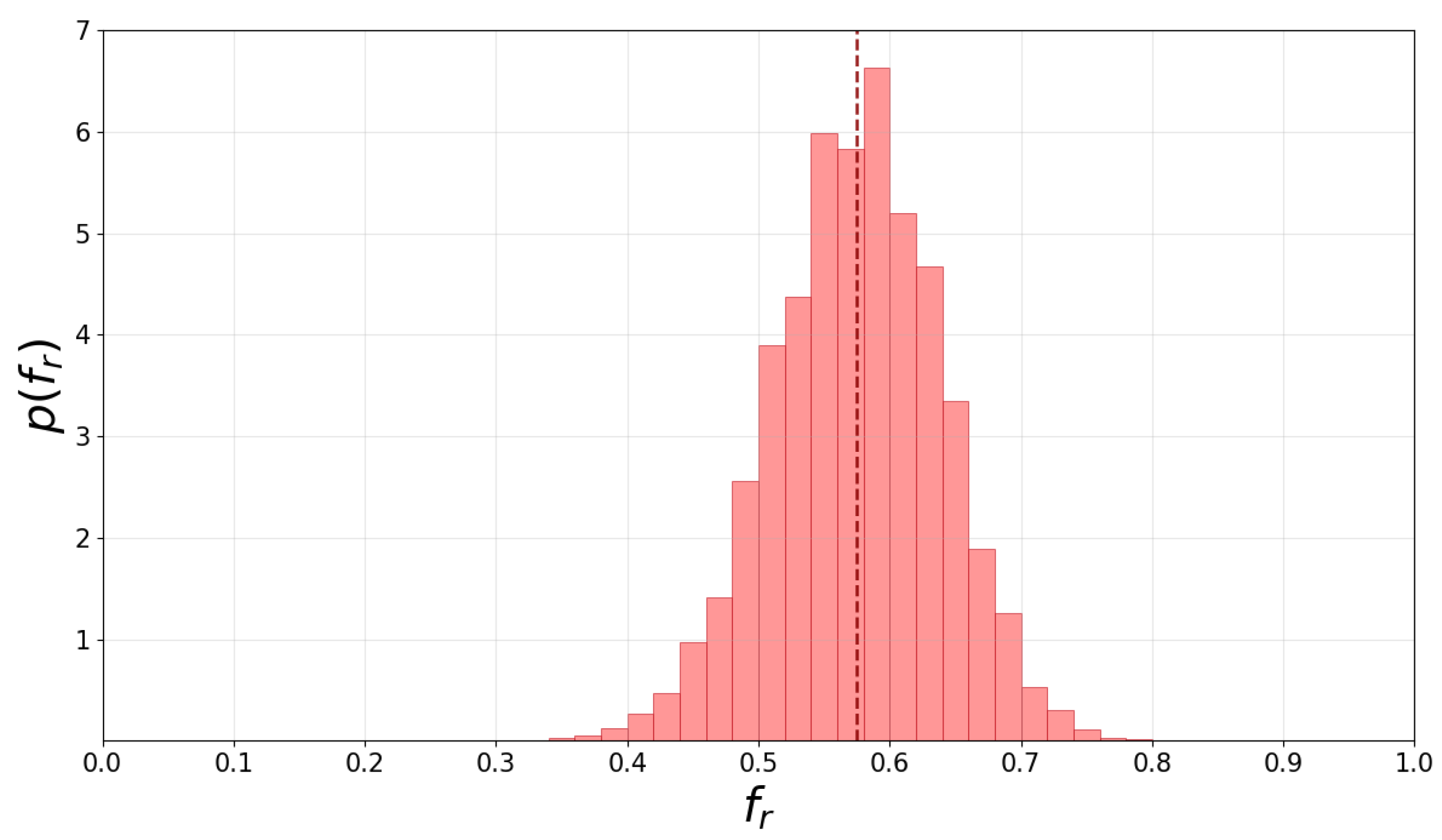
3.1. INOF Results with White Notes

We first present the results for the INOF model [18] with an initial state where non-fixed nodes are white. As nodes with fixed opinions, we choose the node of Newman (red, spin up) and the node of Barabasi (blue, spin down) (see the network with the names of scientists in [22,24]). We use these two fixed nodes for all other network results in this work. We point out that such an initial condition of spin polarization also corresponds to the GINOF model at $Z_c=0,W_i=W=0$, as described in the previous section.

The histogram of the probability distribution $p\left(f_r\right)$ of red fractions $f_r$, obtained in the steady state (at $\tau =20$), is shown in Figure 2. It is obtained by averaging over $N_r={10}^5$ pathway realizations and all $N=379$ nodes. The total average fraction of red nodes is $<f_r>=0.637$, being in favor of Newman. The average polarization of all spins is ${\mu }_0=<f_r>-<f_b>=2<f_r>-1=0.276$.

It is interesting to note that the distribution $p\left(f_r\right)$ can be significantly affected if, in the initial state, one replaces a certain white node with an initial node with spin up or down (red or blue), which, however, is not fixed and can be flipped during the Monte Carlo process. We show an example of such a striking influence in Figure 3, where the initial white node Sole (see network with names in [24]) is replaced by a blue node (all other nodes are the same as in Figure 2). We see that such a one-node change causes the complete modification of the distribution $p\left(f_r\right)$ with the total average probability $<f_r>=0.325$, favoring Barabasi. The reason for such a strong effect is the fact that the Erdös number $N_E$ [2] of Sole with respect to Newman is $N_E=1$ (direct link between them) and also that the right part of the whole network (see [24]) is linked with Newman, mainly via the Sole node. In a certain sense, such specific placement of a blue node in the initial configuration of colored nodes represents the Erdös barrage, which was also shown to be very efficient in the case of fibrosis disease propagation in the MetaCore network of protein–protein interactions [29].

We note that from the perspective of certain network characteristics, the node Sole is not very specific, e.g., it has a PageRank probability $P\left(Sole\right)=0.01263$ and $K=3$, being not significantly different from, e.g., those of node Kurth at $K=9$ with $P\left(9\right)=0.01006$. However, the node Sole effectively (but approximately) separates the network into two parts, and this is why the initial blue color of this node strongly affects the opinion balance, as shown in Figure 3. Various computer science algorithms have been developed to determine weakly connected parts of a given network with the determination of crucial nodes linking such parts (see, e.g., [30,31]). However, it is also possible to use the approach applied in [29], which we also apply here: we consider a fixed node and determine all its nodes with the Erdös number $N_E=1$; then, we check the influence of a non-fixed opposite color placed on one of these Erdös nodes with $N_E=1$. This approach determines the most efficient node of the Erdös barrage that affects the opinion in the strongest way. This procedure is rather efficient and works well for our network with $N=379$ and also for a rather large MetaCore network of protein–protein interactions at $N\approx 4\times {10}^4$, as was shown in [29].

In the framework of the GINOF model, we obtain not only the average value of the red opinion $<f_r>$ but also the average red opinion for each node $f_r\left(K\right)$ with K being the PageRank index. The dependence $f_r\left(K\right)$ is shown in Figure 4 for the top 40 PageRank nodes with $K=1,\dots ,40$ (all $f_r\left(K\right)$ values are available at the GINOF web page). For the top 10 PageRank nodes, we have $f_r\left(K\right)$ values: 0.000, 1.000, 0.991, 0.000, 0.913, 0.913, 0.913, 0.913, 0.913, 0.954 for $K=1,\dots ,10$ (see the corresponding 10 names above). Usually, the nodes with Erdös number $N_E=1$ with respect to Newman have a $f_r=1$ value or those very close to 1, being similar for nodes at $N_E=1$ from Barabasi with $f_r\approx 0$. However, there are cases with $N_E=5$ and $f_r(K=9)=0.913$ (Kurths), indicating that the competition of colors in this social network has a rather complex structure. It is also clear that there is no simple correlation between the top PageRank index and the top values of the probabilities of red or blue colors.

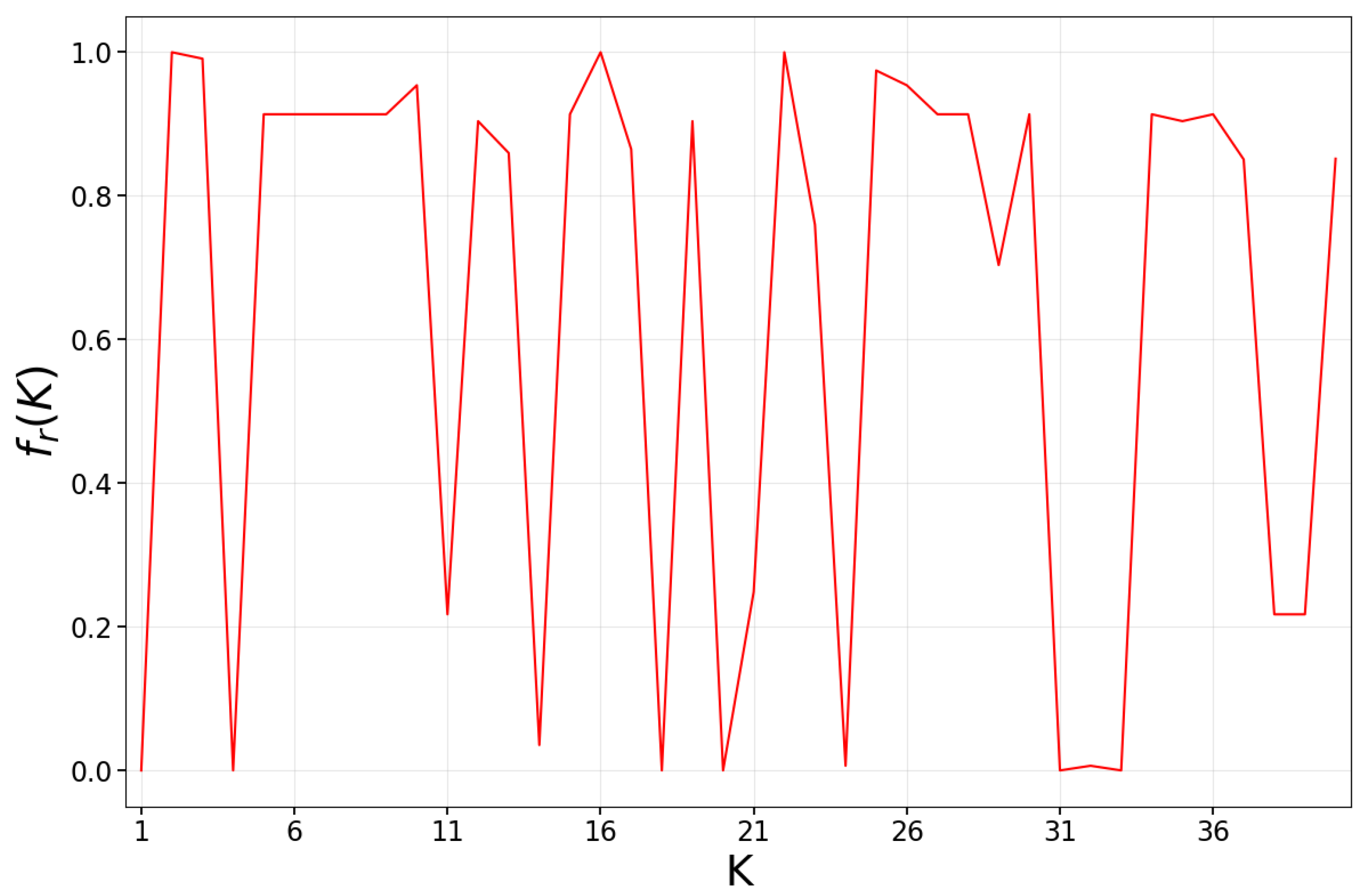
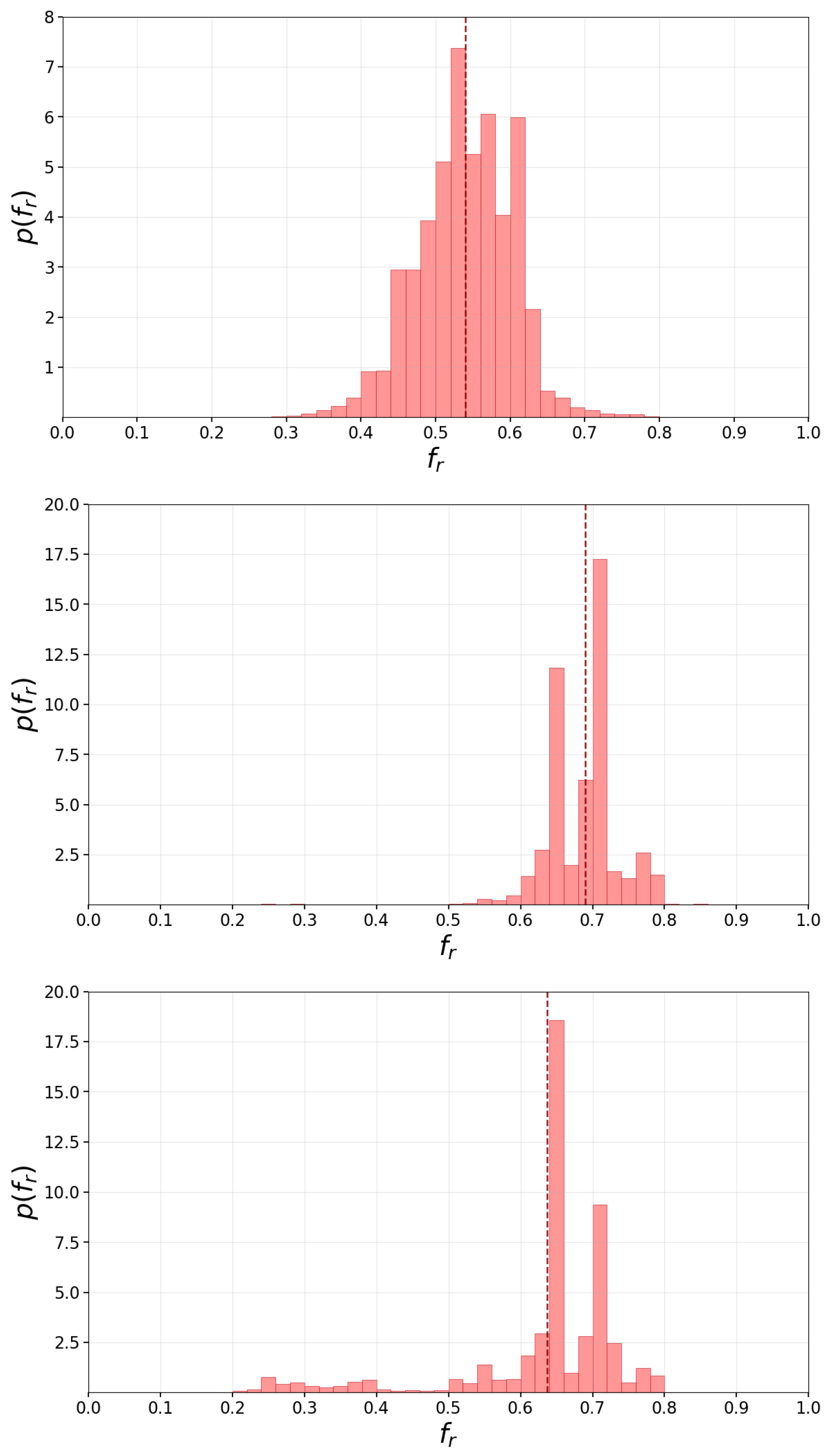
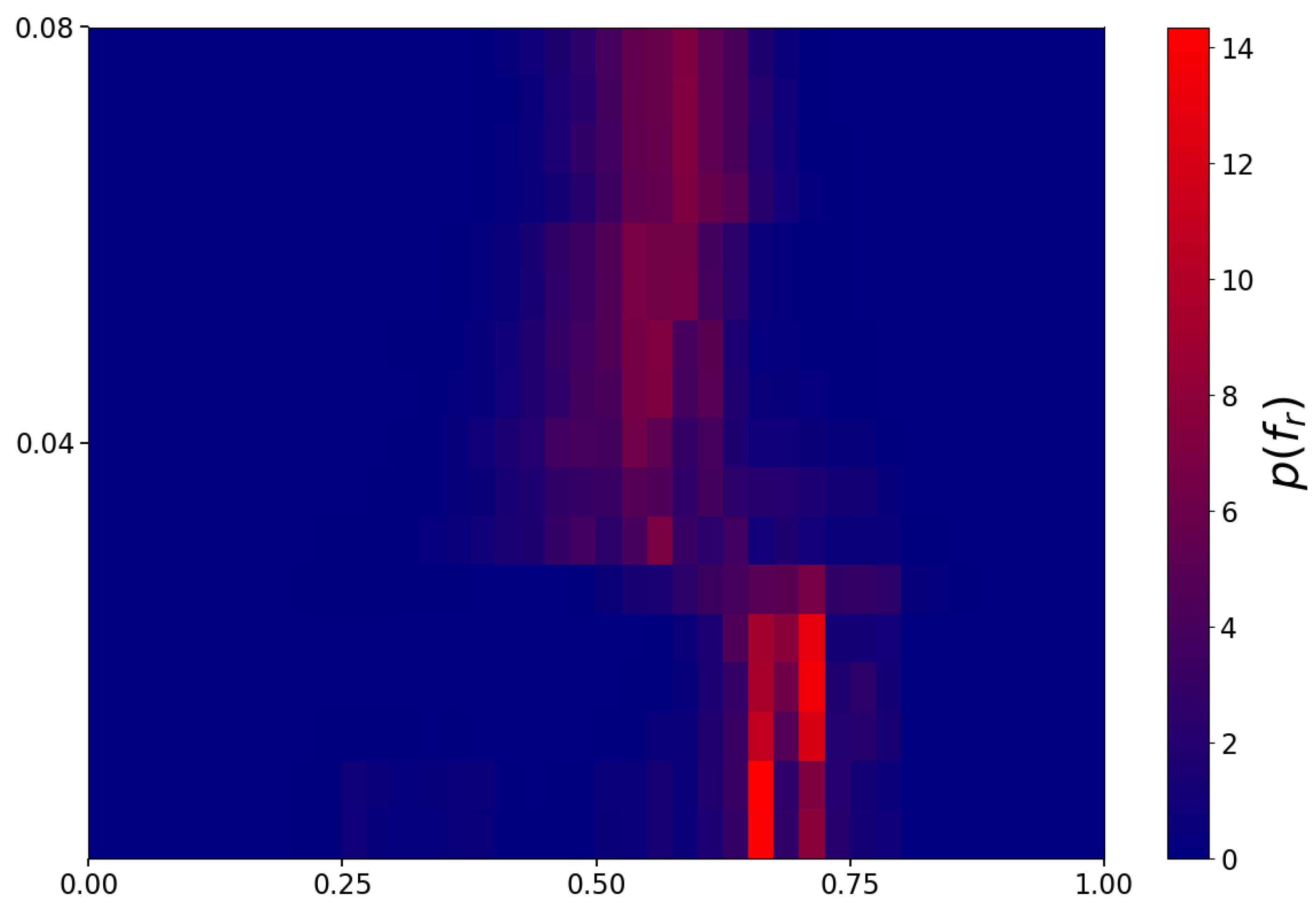
3.2. Effects of Opinion Conviction Threshold in GINOF

One of the most important elements of the INOF model is the presence of white nodes at the initial state. This can be considered a natural choice for Wikipedia and some other directed networks [18,29]. However, for models of election votes in social networks, it may be more appropriate to assume that elite members of society have fixed opposite opinions on the leaders of two parties, while the crowd of common people or electors has some random red and blue opinions with low initial interest in elections and hence a low amplitude influence among their votes $W<1$ (e.g., because only a small fraction of such electors participate in an election). Thus, we posit that the GINOF model is more suitable for the situation of elections in social networks.

At first glance, it seems that it is sufficient to consider the GINOF model with the opinion conviction threshold $Z_c=0$, taking a certain moderate value of vote amplitude influence W. However, in the framework of GINOF at $Z_c=0$, even a very small value $W=0.005$ produces a complete change in the probability distribution $p\left(f_r\right)$ compared to the INOF case with white nodes or the GINOF case at $Z_c=0,W=0$ (see Figure 2 and Figure 5). The reason for this drastic change in distributions is that, at $Z_c=0$, even a very small value of $W\ll 1$ leads to a process whereby the crowd electors easily convince their friends to have a red or blue opinion, which rapidly increases their vote amplitude influence to $W=1$, and then the elite influence becomes weak and the $f_r$ values are distributed around $f_r\approx 0.5$, corresponding to the initial fractions of red and blue opinions of non-fixed nodes (see Figure 5). In this situation, as seen in Figure 5, the elite influence is still present with $<f_r>=0.575$, but we can see that even such a small value as $W=0.005$ causes a qualitative change in the probability distribution $p\left(f_r\right)$ in Figure 2.

Thus, it is more appropriate to introduce the opinion conviction threshold $Z_c>0$ as described in Section 2. We choose $Z_c=0.1$ so that it is close to the minimum value $a_{min}=0.125$ of the matrix elements of the weighted adjacency matrix $A_{ij}$ (excluding zero elements). The evolution of the probability distribution with an increase in the vote amplitude influence W is shown in Figure 6. For small $W\le 0.005$, the initial distribution $p\left(f_r\right)$ in Figure 2 remains practically unchanged; then, with an increase to $W=0.015$, it starts to be modified, and, at $W=0.05$, the initial structure of Figure 2 is completely washed out, with $p\left(f_r\right)$ being close to that of Figure 5.

The results in Figure 6 are obtained for one specific initial random configuration of up–down spins of non-fixed nodes, but we have verified that the same results hold for other random configurations. In [18], it was shown that the statistical error $\delta$ of $p\left(f_r\right)$ values scales approximately as $1/\sqrt{N_r}$, which, for $N_r={10}^5$, gives $\delta =0.003$. For our model, we find the same statistical accuracy.

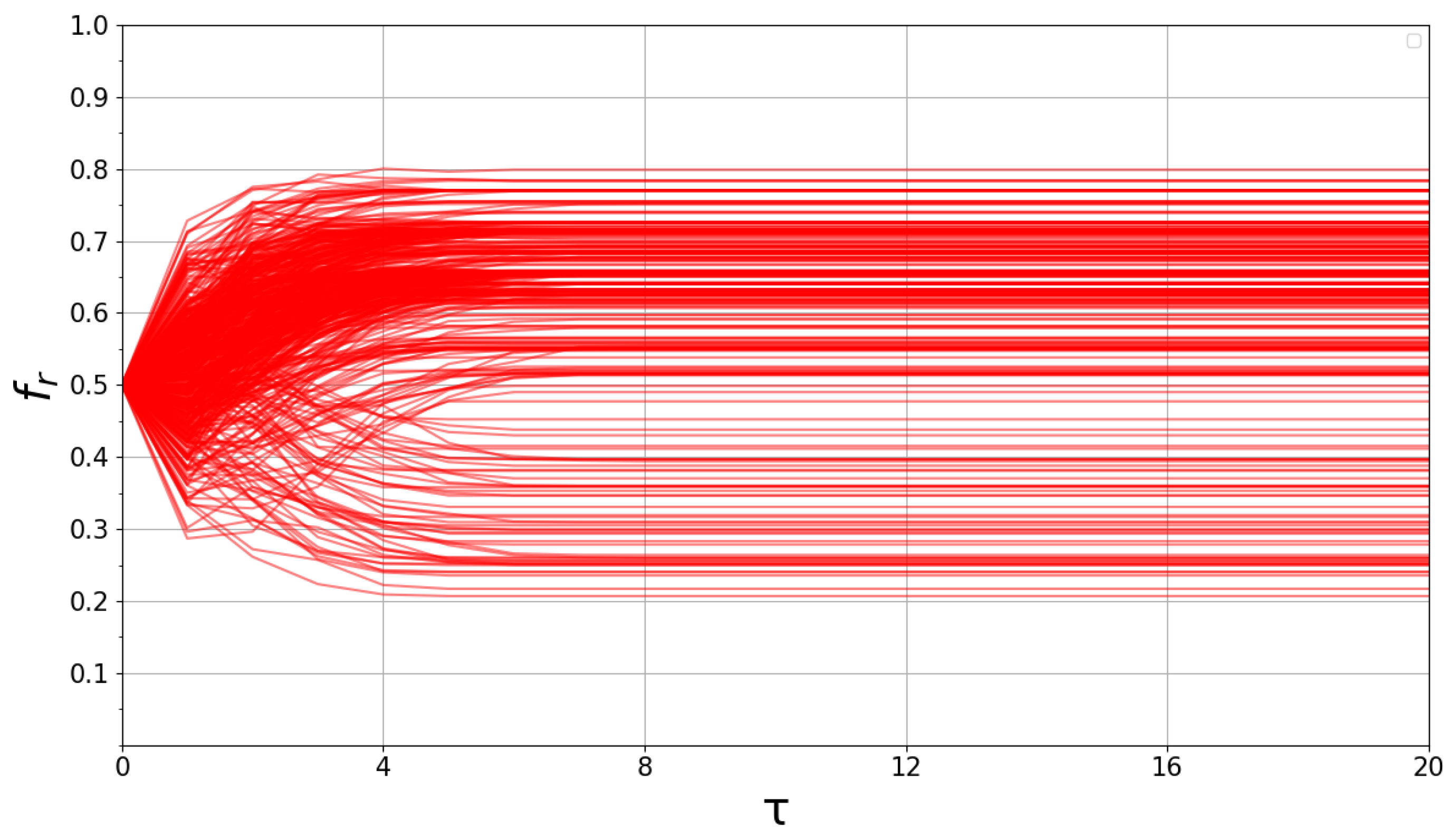
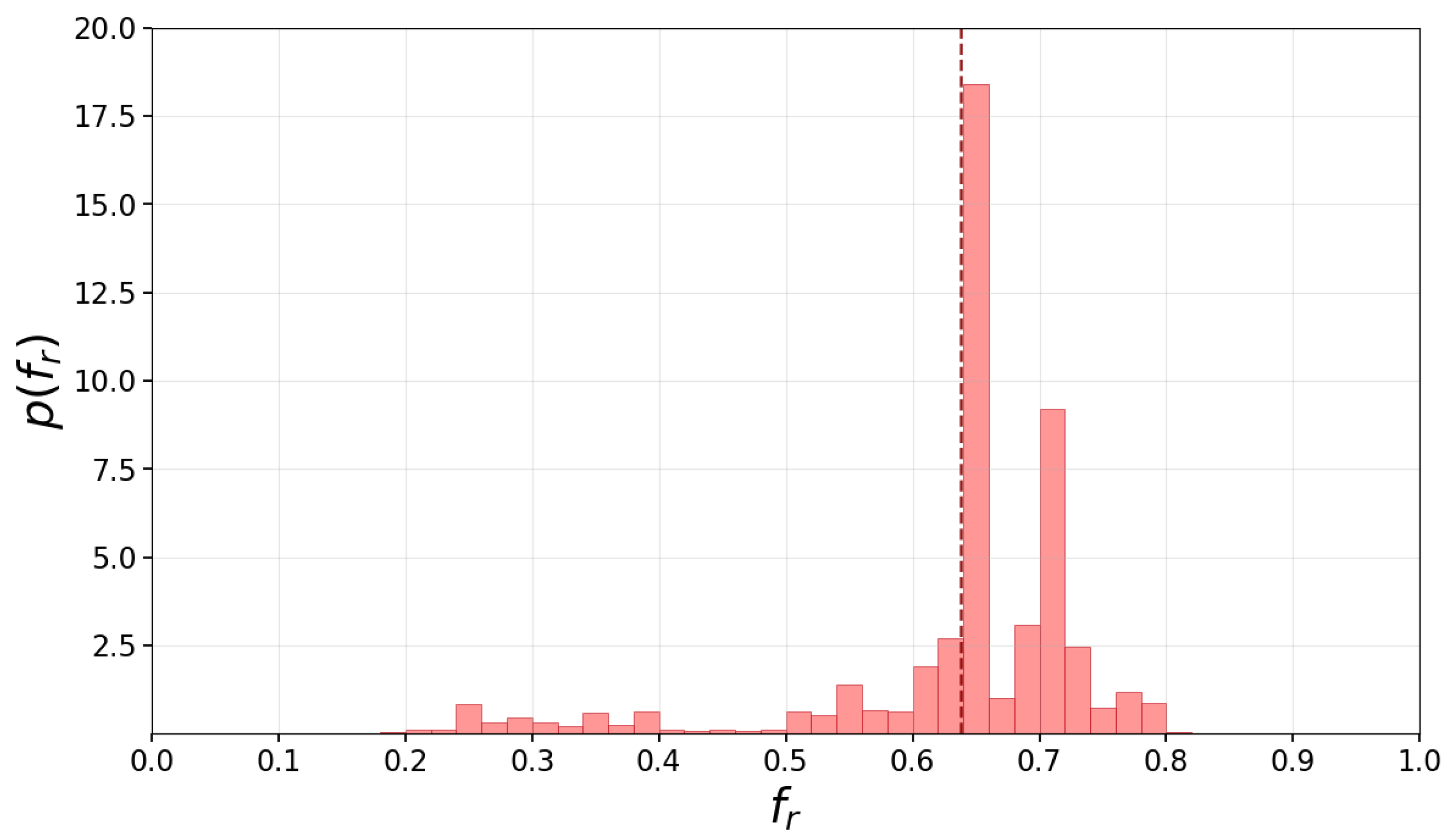
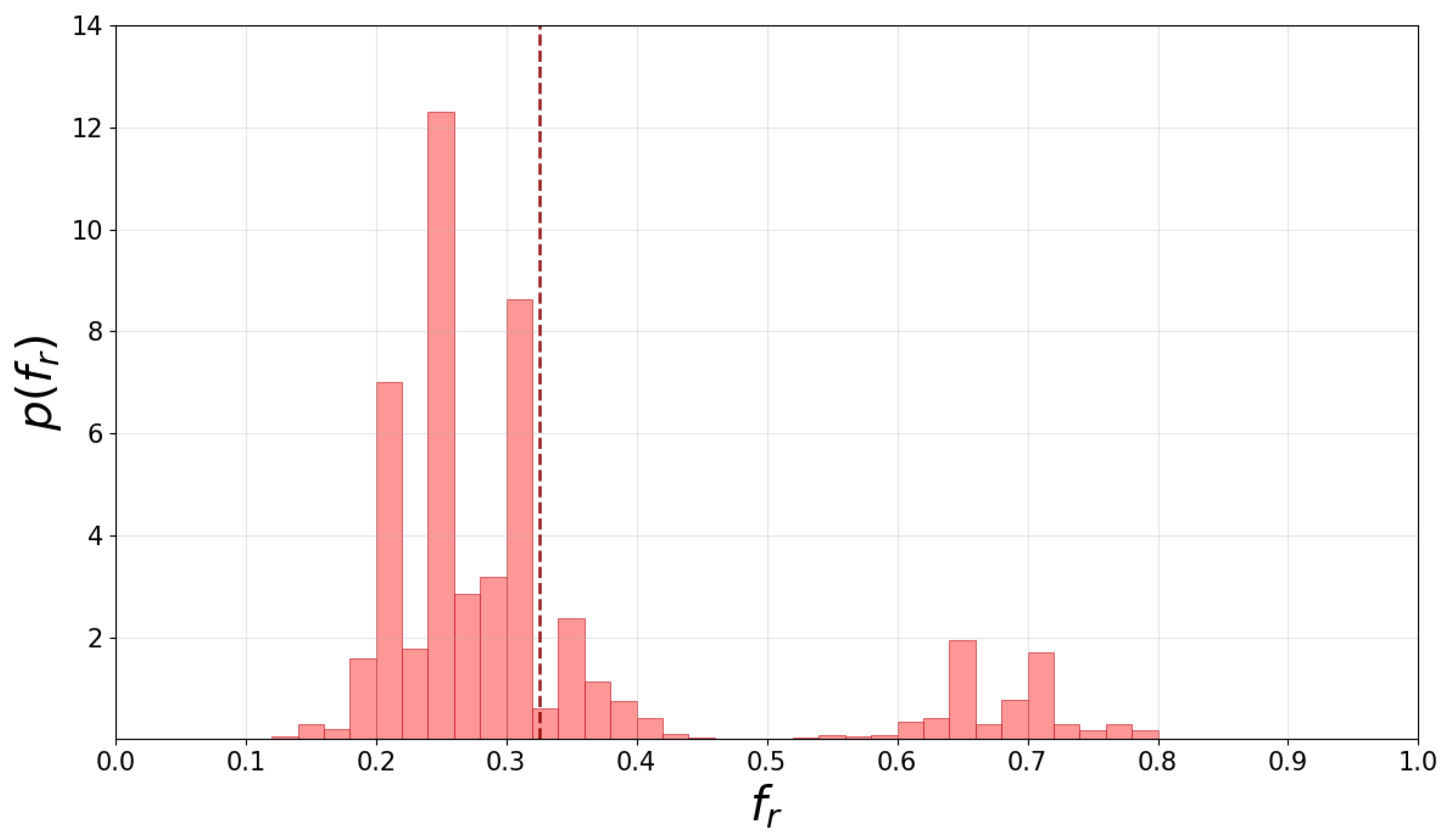
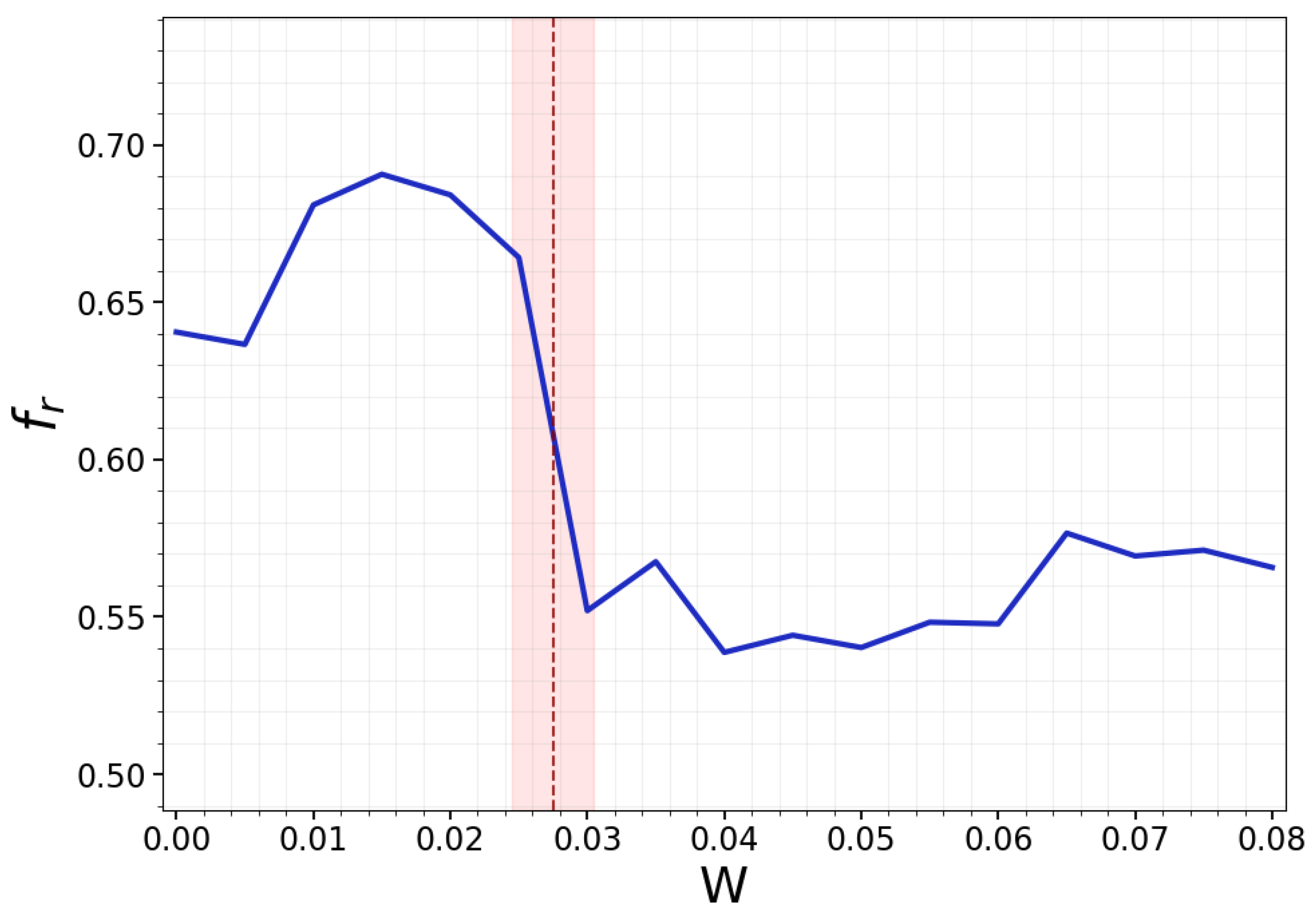
3.3. Phase Transition of Opinion Formation

The results in Figure 6 indicate that there is a phase transition from the regime at $W<W_{cr}$, where the elite imposes its opinion, to a regime at $W>W_{cr}$, where the elite influence is weak and elections are mainly affected by votes from crowd electors. This transition is illustrated in Figure 7 and in a more detailed manner in Figure 8. Indeed, in the transition band (marked in red in Figure 8), the probability $p\left(f_r\right)$ is changed by approximately 20% of its value, while, on the left and right sides of this range, the variations in $p\left(f_r\right)$ are about four to five times smaller ($|\Delta p\left(f_r\right)|/p\left(f_p\right)\approx 0.04$). The critical vote amplitude influence is approximately $W_{cr}\approx 0.027$.

We argue that this critical $W_{cr}$ value is determined by the condition that the votes of all neighbors can exceed the opinion conviction threshold so that

$$W_{cr}\approx Z_c/\kappa .$$

(2)

In our case, the average number of neighbors is $\kappa =N_{\ell }/N\approx 4.8$, so that, for $Z_c=0.1$, $W_{cr}\approx 0.021$. This value is close to the above numerical values in Figure 7 and Figure 8. The estimate (2) assumes that the majority of $\kappa$ neighbors have the same opinion, which allows them to overcome the opinion conviction threshold $Z_c$. It is possible that, for networks with a high number of links per node $\kappa \gg 1$, a more accurate estimate may be required.

Of course, it is desirable to have a developed theory for the above transition. It is possible that a mean field approach, used, e.g., in [32], will allow us to achieve progress in this direction. However, this task requires further investigations of the GINOF model, since this model has certain features that are not standard for the mean field approach. Indeed, at the initial stage, non-fixed nodes have amplitudes of vote influence $W<1$ and they achieve its maximal value $W=1$ only during multiple steps of the Monte Carlo process. This represents a kind of non-equilibrium stage during the Monte Carlo process, and we suppose that this intermediate stage would require certain additional extensions for the mean field approach, which will be of interest for future studies.

Thus, the obtained results for the GINOF model demonstrate that, in the presence of an opinion conviction threshold, elections in social networks are characterized by a transition from a phase where elections are dominated by the elite opinion to a phase dominated by the votes of crowd electors. This transition takes place when the vote amplitude influence W exceeds the critical value $W_{cr}$ given by the relation (2).

We should note that there are many studies of social networks (see, e.g., [2,3]), including a network of scientists from all their publications in Physical Review journals [33]. The network considered here is relatively small, but it is useful for investigating new elements of the GINOF approach. Its new elements are that each node has an Ising spin associated with it and the opinion formation of all nodes is determined by the majority opinion of neighbors, with the introduction of the opinion conviction threshold and amplitude of vote influence. These new elements lead to a phase transition between two phases, as discussed above. A somewhat similar approach has been studied for models of consensus processes for interacting agents, as discussed in [34,35,36,37]. However, these studies were not performed for Ising spin complex social networks with an opinion conviction threshold linked to the amplitude of vote influence.

4. Discussion

In this work, we have generalized the model of opinion formation on directed Ising networks (INOF) introduced in [18]. This generalized GINOF model is applied to an undirected social network of scientific collaboration studied by Newman in [21,22,23,24]. The new elements of the GINOF model compared to the INOF one are as follows: in addition to fixed-opinion nodes, considered as the society’s elite, all non-fixed nodes are initialized with random opinions—half red and half blue. Furthermore, these non-fixed nodes initially have a weak amplitude influence ($W\ll 1$), which self-consistently increases during the asynchronous Monte Carlo process that simulates an election campaign. In addition, any change in opinion of a given spin node (a spin flip) takes place only if the modulus of the majority score of a given node’s neighbors’ opinions is above a certain opinion conviction threshold.

We show that, for the GINOF model of elections in undirected social networks, there is a phase transition from elections dominated by the elite opinion to a phase where the elite cannot affect the election and the vote results are determined by the opinions of electors. We also demonstrate that the Erdös barrage can significantly affect the probability distribution of red and blue nodes.

At present, there are numerous undirected networks functioning in human society and various scientific fields, such as Facebook [38], VK [39], and the protein–protein interaction network STRING [40]. Thus, in the work [30], the developed algorithm allowed a network of politicians to be extracted from Facebook with about 6000 nodes, which can be analyzed in the framework of the GINOF approach. It is possible also to model fibrosis progression in the huge STRING network [40] using GINOF analysis following the strategy described here and in [29]. In the same way, the treatment of other diseases can be studied with GINOF methods within the STRING database. We hope that the GINOF model will find useful applications in these domains.