Hardware Validation for Semi-Coherent Transmission Security †
Abstract
1. Introduction
2. System Overview
2.1. Spread Spectrum Modulation
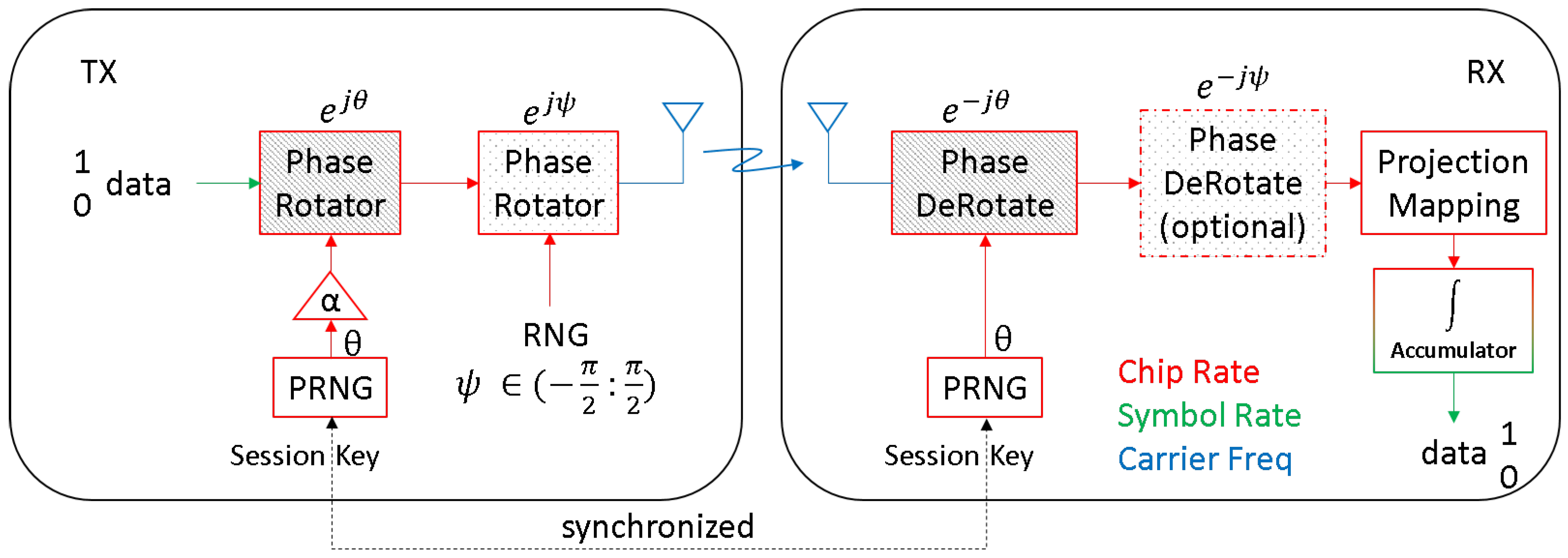
2.2. Semi-Coherent TRANSEC
2.3. Session Key Protection
3. System Design
3.1. Perturbation Types
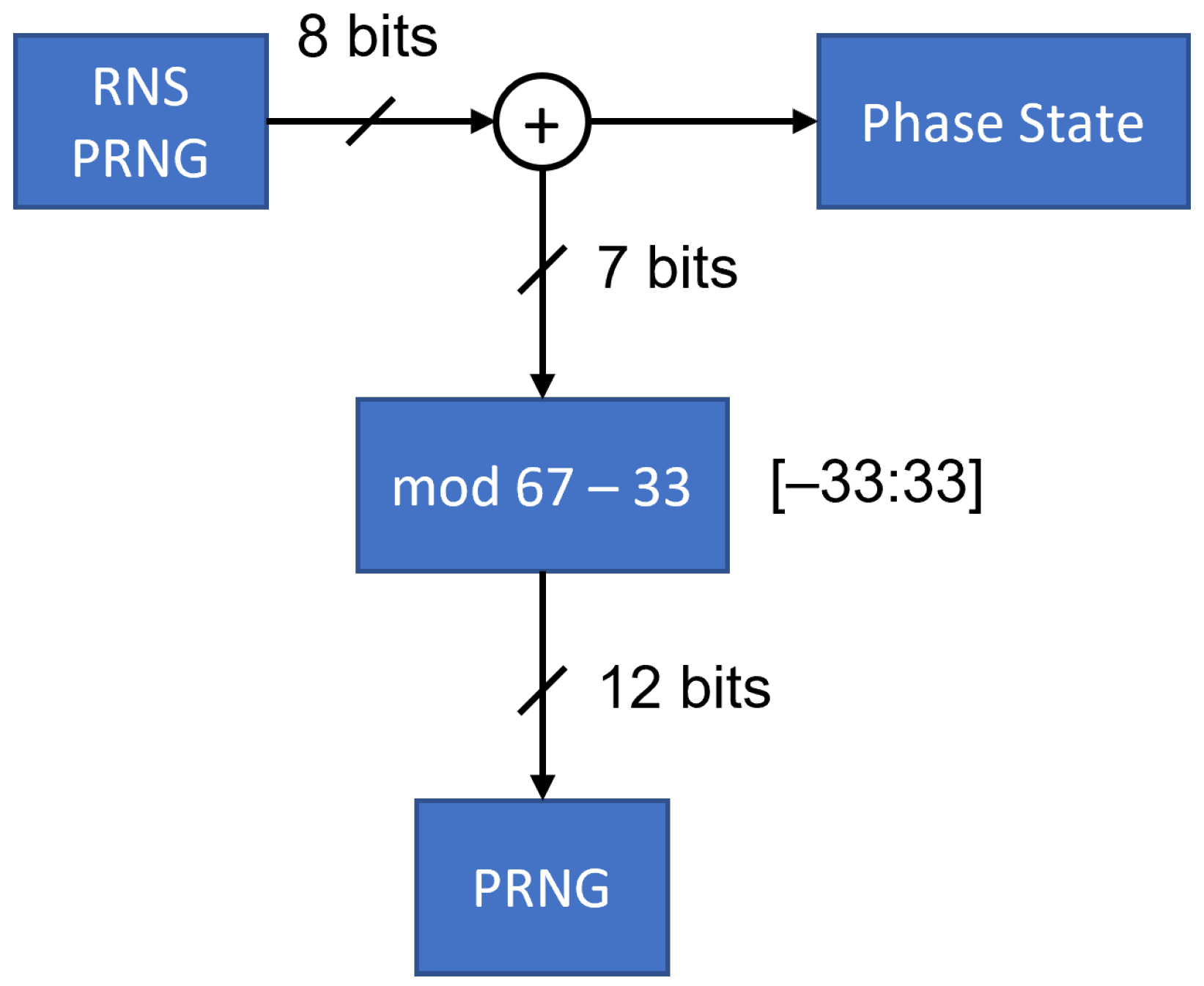
3.1.1. Truly Random Number
3.1.2. Unsynchronized Psuedorandom Number
3.1.3. Synchronized Psuedorandom Number
3.1.4. Markovian Process
3.2. Phase Modulation
3.2.1. Continuous Phase
3.2.2. Discrete Phase State Mapping
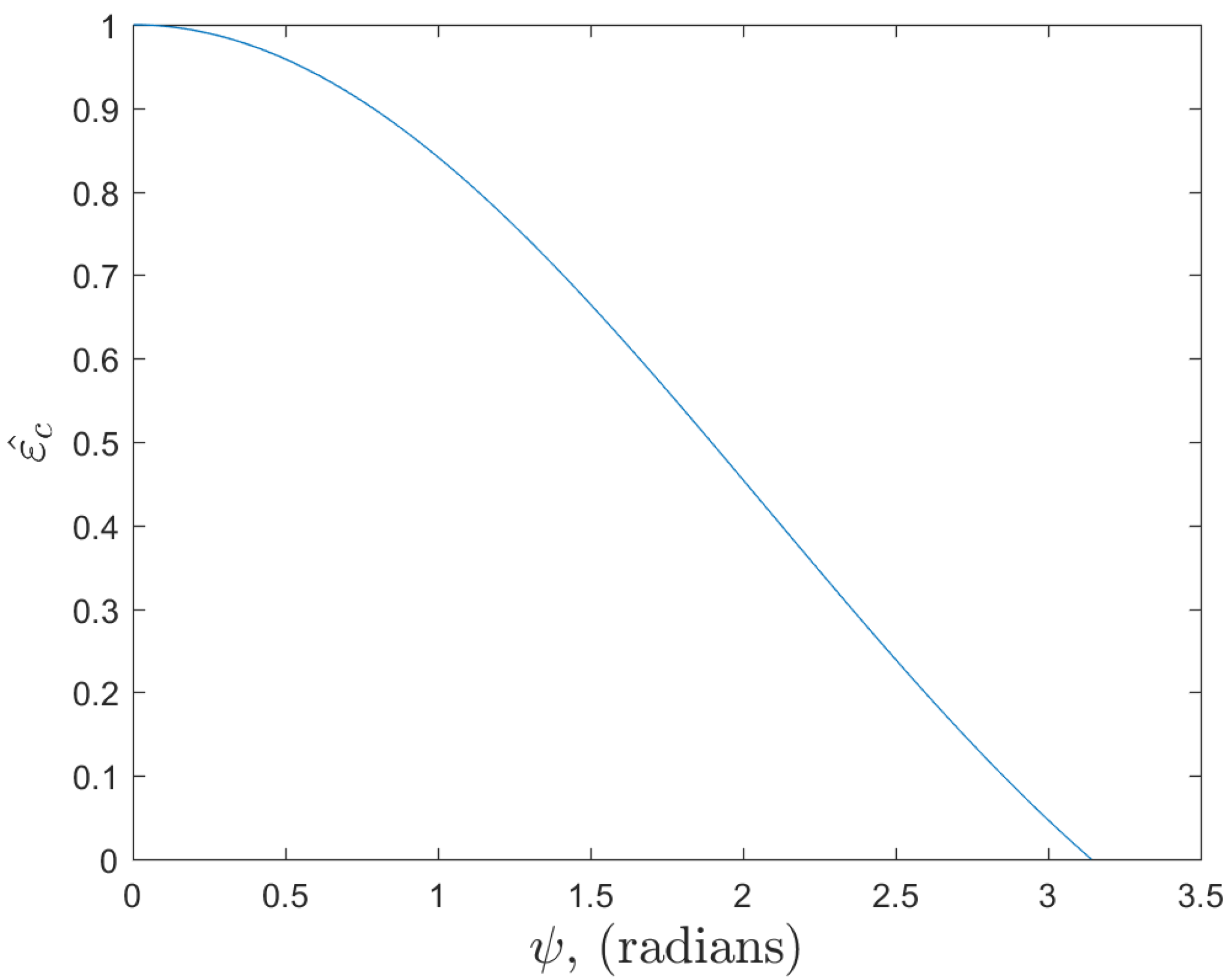
3.3. Energy per Symbol Calculations
4. Exemplary Design and Simulation Basis
4.1. Proof-of-Concept Model
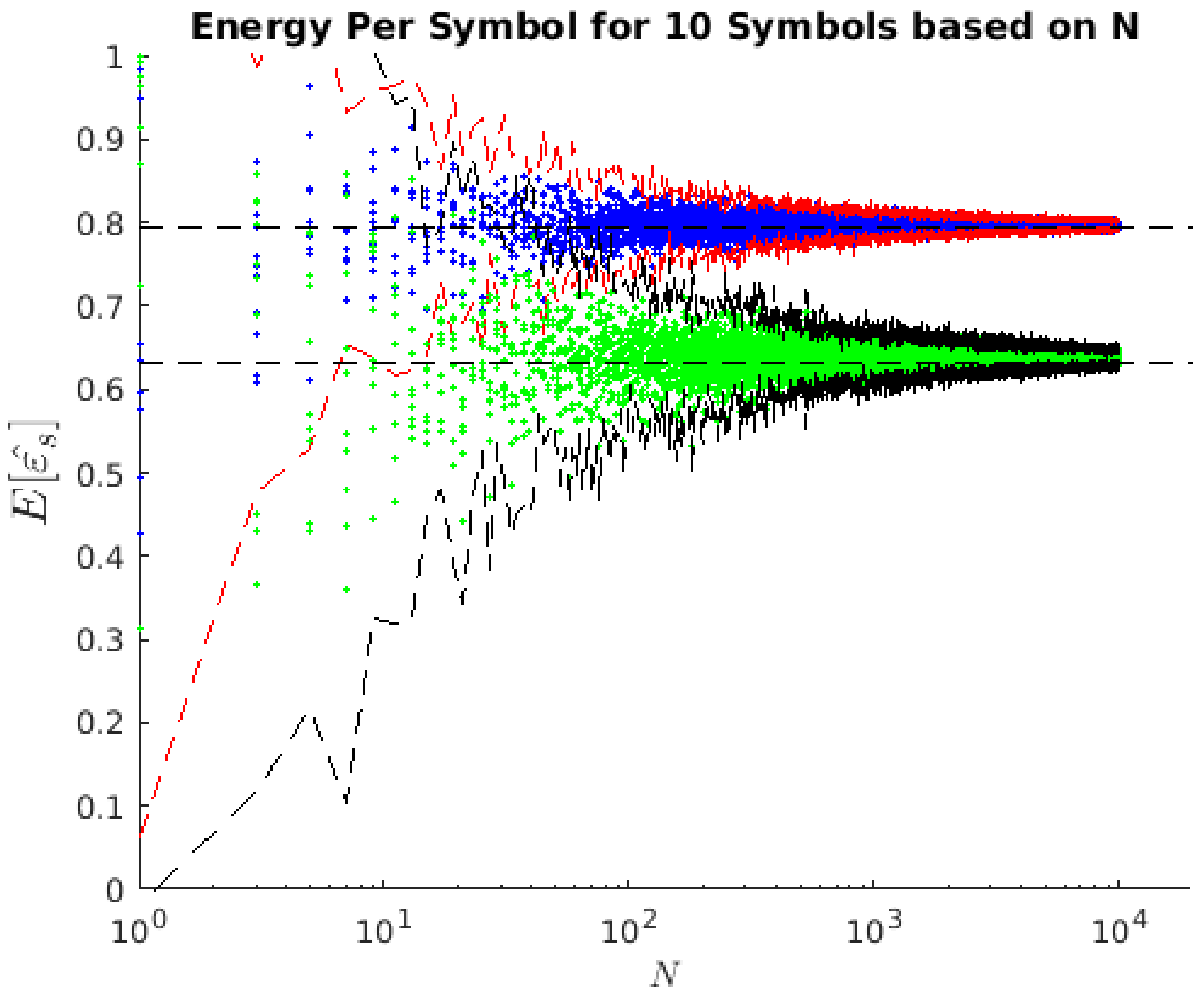
4.2. Simulation Results
4.3. Symbol Energy Calculations
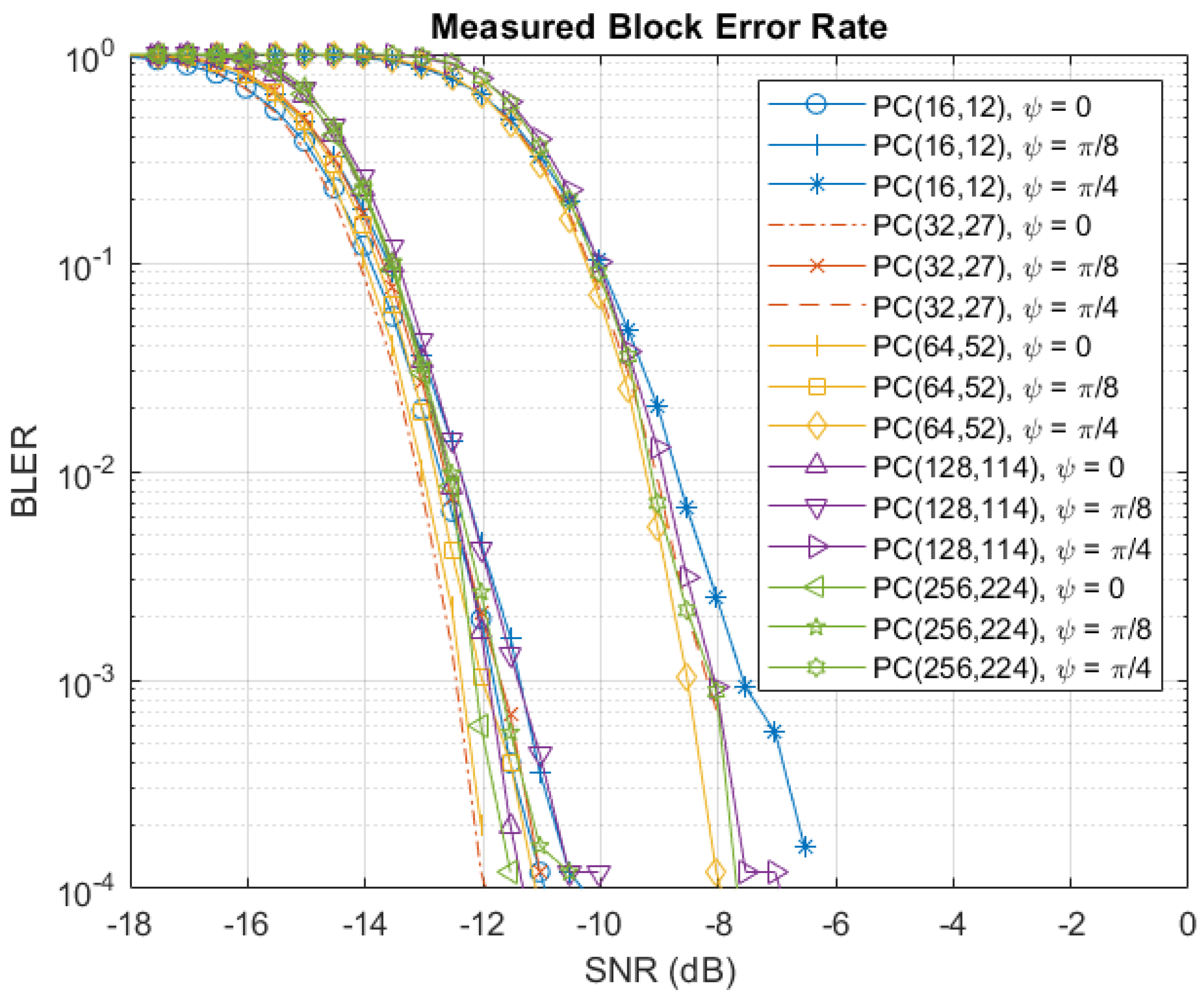
5. Implementation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vasseur, J.P.; Dunkels, A. Interconnecting Smart Objects with IP: The Next Internet; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2010. [Google Scholar]
- Shannon, C.E. Communication theory of secrecy systems. Bell Labs Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Kenyeres, M.; Kenyeres, J.; Hassankhani Dolatabadi, S. Distributed Consensus Gossip-Based Data Fusion for Suppressing Incorrect Sensor Readings in Wireless Sensor Networks. J. Low Power Electron. Appl. 2025, 15, 6. [Google Scholar] [CrossRef]
- Su, X.; Wang, Z.; Liu, X.; Choi, C.; Choi, D. Study to Improve Security for IoT Smart Device Controller: Drawbacks and Countermeasures. Secur. Commun. Netw. 2018, 2018, 4296934. [Google Scholar] [CrossRef]
- Soto-Cruz, J.; Ruiz-Ibarra, E.; Vázquez-Castillo, J.; Espinoza-Ruiz, A.; Castillo-Atoche, A.; Mass-Sanchez, J. A Survey of Efficient Lightweight Cryptography for Power-Constrained Microcontrollers. Technologies 2025, 13, 3. [Google Scholar] [CrossRef]
- Gazziro, M.; Carmo, J.P. Power Consumption Efficiency of Encryption Schemes for RFID. Chips 2024, 3, 216–228. [Google Scholar] [CrossRef]
- Sabbry, N.H.; Levina, A.B. An Optimized Point Multiplication Strategy in Elliptic Curve Cryptography for Resource-Constrained Devices. Mathematics 2024, 12, 881. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Wang, F.; Shi, C. An LPI design for secure burst communication systems. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xian, China, 9–13 July 2014; pp. 631–635. [Google Scholar] [CrossRef]
- Shi, C.; Wang, F.; Salous, S.; Zhou, J. Optimal Power Allocation Strategy in a Joint Bistatic Radar and Communication System Based on Low Probability of Intercept. Sensors 2017, 17, 2731. [Google Scholar] [CrossRef]
- Li, L.; Lv, J.; Ma, X.; Han, Y.; Feng, J. Design of Low Probability Detection Signal with Application to Physical Layer Security. Electronics 2023, 12, 1075. [Google Scholar] [CrossRef]
- Pickholtz, R.; Schilling, D.; Milstein, L. Theory of Spread-Spectrum Communications—A Tutorial. IEEE Trans. Commun. 1982, 30, 855–884. [Google Scholar] [CrossRef]
- Di Benedetto, M.G.; Vojcic, B.R. Ultra wide band wireless communications: A tutorial. J. Commun. Netw. 2003, 5, 290–302. [Google Scholar] [CrossRef]
- Harvey, B.; Howard, D.; Barnhart, E.; Loso, F.; Staba, J. An analysis of MMW wireless LANs for LPI/AJ command post communications. In Proceedings of the MILCOM’93—IEEE Military Communications Conference, Boston, MA, USA, 11–14 October 1993; Volume 2, pp. 580–584. [Google Scholar] [CrossRef]
- Yip, L. Performance Assessment of LPD/LPI Satellite Communication Systems. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MO, USA, 4–11 March 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Winarno, A.; Sari, R.F. A Novel Secure End-to-End IoT Communication Scheme Using Lightweight Cryptography Based on Block Cipher. Appl. Sci. 2022, 12, 8817. [Google Scholar] [CrossRef]
- Rodriguez Bejarano, J.M.; Yun, A.; De La Cuesta, B. Security in IP satellite networks: COMSEC and TRANSEC integration aspects. In Proceedings of the 2012 6th Advanced Satellite Multimedia Systems Conference (ASMS) and 12th Signal Processing for Space Communications Workshop (SPSC), Vigo, Spain, 5–7 September 2012; pp. 281–288. [Google Scholar] [CrossRef]
- Wyner, A.D. The Wire-Tap Channel. Bell Syst. Tech. J. 1975, 54, 1355–1387. [Google Scholar] [CrossRef]
- Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory 1993, 39, 733–742. [Google Scholar] [CrossRef]
- Hero, A.O. Secure space-time communication. IEEE Trans. Inf. Theory 2003, 49, 3235–3249. [Google Scholar] [CrossRef]
- Thangaraj, A.; Dihidar, S.; Calderbank, A.R.; McLaughlin, S.; Merolla, J.M. Capacity achieving codes for the wiretap channel with applications to quantum key distribution. arXiv 2004, arXiv:0411003. [Google Scholar]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless Information-Theoretic Security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Alhamarneh, R.A.; Mahinderjit Singh, M. Strengthening Internet of Things Security: Surveying Physical Unclonable Functions for Authentication, Communication Protocols, Challenges, and Applications. Appl. Sci. 2024, 14, 1700. [Google Scholar] [CrossRef]
- Wu, T.Y.; Kong, F.; Wang, L.; Chen, Y.C.; Kumari, S.; Pan, J.S. Toward Smart Home Authentication Using PUF and Edge-Computing Paradigm. Sensors 2022, 22, 9174. [Google Scholar] [CrossRef]
- Zou, Y.; Zhu, J.; Wang, X.; Leung, V.C.M. Improving physical-layer security in wireless communications using diversity techniques. IEEE Netw. 2015, 29, 42–48. [Google Scholar] [CrossRef]
- Efstathiou, D.; Papadopoulos, G.D.; Tsipouridou, D.; Pavlidou, F.N. Enhancement of transmission security for OFDM based systems. In Proceedings of the 2017 IEEE Symposium on Computers and Communications (ISCC), Heraklion, Greece, 3–6 July 2017; pp. 546–551. [Google Scholar] [CrossRef]
- Elmasry, G.; Corwin, P. Hiding the RF Signal Signature in Tactical 5G. In Proceedings of the MILCOM 2021—2021 IEEE Military Communications Conference (MILCOM), San Diego, CA, USA, 29 November–2 December 2021; pp. 733–738. [Google Scholar] [CrossRef]
- Sperandio, C.; Flikkema, P.G. Wireless physical-layer security via transmit precoding over dispersive channels: Optimum linear eavesdropping. In Proceedings of the MILCOM 2002, Anaheim, CA, USA, 7–10 October 2002; Volume 2, pp. 1113–1117. [Google Scholar] [CrossRef]
- Peng, H.; Xie, K.; Zou, W. Research on an Enhanced Multimodal Network for Specific Emitter Identification. Electronics 2024, 13, 651. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, F.; Huang, Y.; Meng, X. Adaptive Detection of Direct-Sequence Spread-Spectrum Signals Based on Knowledge-Enhanced Compressive Measurements and Artificial Neural Networks. Sensors 2021, 21, 2538. [Google Scholar] [CrossRef] [PubMed]
- McGinthy, J.M.; Michaels, A.J. Semi-Coherent Transmission Security for Low Power IoT Devices. In Proceedings of the 2018 IEEE International Conference on Internet of Things (iThings-2018), Halifax, NS, Canada, 30 July–3 August 2018. [Google Scholar]
- Xu, L.; Liu, X.; Zhang, Y. Blind Estimation of Spreading Code Sequence of QPSK-DSSS Signal Based on Fast-ICA. Information 2023, 14, 112. [Google Scholar] [CrossRef]
- Grzesiak, K.; Piotrowski, Z. From Constellation Dithering to NOMA Multiple Access: Security in Wireless Systems. Sensors 2021, 21, 2752. [Google Scholar] [CrossRef] [PubMed]
- Stallings, W. Cryptography and Network Security: Principles and Practice, 7th ed.; Pearson Education: London, UK, 2017. [Google Scholar]
- Nguyen, H.; Hoang, T.; Tran, L. Efficient Hardware Implementation of Elliptic-Curve Diffie–Hellman Ephemeral on Curve25519. Electronics 2023, 12, 4480. [Google Scholar] [CrossRef]
- Zeghid, M.; Sghaier, A.; Ahmed, H.Y.; Abdalla, O.A. Power/Area-Efficient ECC Processor Implementation for Resource-Constrained Devices. Electronics 2023, 12, 4110. [Google Scholar] [CrossRef]
- Miller, F.P.; Vandome, A.F.; McBrewster, J. Advanced Encryption Standard; Alpha Press: Halifax, UK, 2009. [Google Scholar]
- Sklar, B. Digital Communications; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
- Viterbi, A.J. CDMA: Principles of Spread Spectrum Communication; Addison-Wesley: Boston, MA, USA, 1995; Volume 122. [Google Scholar]
- Braasch, M.S.; van Dierendonck, A.J. GPS receiver architectures and measurements. Proc. IEEE 1999, 87, 48–64. [Google Scholar] [CrossRef]
- Kaddoum, G.; Gagnon, G.; Gagnon, F. Spread spectrum communication system with sequence synchronization unit using chaotic symbolic dynamics modulation. Int. J. Bifurc. Chaos 2013, 23, 1350019. [Google Scholar] [CrossRef]
- IEEE Std 802.11-2012 (Revision of IEEE Std 802.11-2007); IEEE Standard for Information Technology–Telecommunications and Information Exchange Between Systems Local and Metropolitan Area Networks–Specific Requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. IEEE Standards Association: New York, NY, USA, 2012; pp. 1–2793. [CrossRef]
- Garg, V.K. IS-95 CDMA and CDMA2000: Cellular/PCS Systems Implementation; Pearson Education: London, UK, 1999. [Google Scholar]
- Michaels, A.J. High-Order PSK Signaling (HOPS) Techniques for Low-Power Spread Spectrum Communications. In Proceedings of the 2018 IEEE 19th International Symposium on “A World of Wireless, Mobile and Multimedia Networks” (WoWMoM), Chania, Greece, 12–15 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Karimov, T.; Rybin, V.; Kolev, G.; Rodionova, E.; Butusov, D. Chaotic Communication System with Symmetry-Based Modulation. Appl. Sci. 2021, 11, 3698. [Google Scholar] [CrossRef]
- Vennos, A.; George, K.; Michaels, A. Attacks and Defenses for Single-Stage Residue Number System PRNGs. IoT 2021, 2, 375–400. [Google Scholar] [CrossRef]
- Liu, C.; Ding, L.; Ding, Q. Research about the Characteristics of Chaotic Systems Based on Multi-Scale Entropy. Entropy 2019, 21, 663. [Google Scholar] [CrossRef]
- Spread Spectrum Satcom Hacking: Attacking the Globalstar Simplex Data Service. 2015. Available online: https://www.blackhat.com/docs/us-15/materials/us-15-Moore-Spread-Spectrum-Satcom-Hacking-Attacking-The-GlobalStar-Simplex-Data-Service.pdf (accessed on 19 March 2025).
- Bras-Amorós, M.; O’Sullivan, M.E. The Symmetric Key Equation for Reed–Solomon Codes and a New Perspective on the Berlekamp–Massey Algorithm. Symmetry 2019, 11, 1357. [Google Scholar] [CrossRef]
- Lee, D.H.; Lee, I.Y. A Lightweight Authentication and Key Agreement Schemes for IoT Environments. Sensors 2020, 20, 5350. [Google Scholar] [CrossRef]
- Alshammari, F.; Ong, L.; Tan, J.Y. An Optimal Secure Key Distribution Scheme for Internet of Things Devices in Multi-Session Network Communications. Electronics 2024, 13, 4951. [Google Scholar] [CrossRef]
- Wold, K.; Petrovic, S. Optimizing Speed of a True Random Number Generator in FPGA by Spectral Analysis. In Proceedings of the 2009 Fourth International Conference on Computer Sciences and Convergence Information Technology, Seoul, Republic of Korea, 24–26 November 2009; pp. 1105–1110. [Google Scholar] [CrossRef]
- Wanna, P.; Wongthanavasu, S. An Efficient Cellular Automata-Based Classifier with Variance Decision Table. Appl. Sci. 2023, 13, 4346. [Google Scholar] [CrossRef]
- Stoller, S.; Campbell, K.A. Demonstration of Three True Random Number Generator Circuits Using Memristor Created Entropy and Commercial Off-the-Shelf Components. Entropy 2021, 23, 371. [Google Scholar] [CrossRef] [PubMed]
- Michaels, A.J. A maximal entropy digital chaotic circuit. In Proceedings of the Circuits and Systems (ISCAS), 2011 IEEE International Symposium, Rio de Janeiro, Brazil, 15–18 May 2011; pp. 717–720. [Google Scholar]
- Zeng, K.; Yang, C.H.; Wei, D.Y.; Rao, T.R.N. Pseudorandom bit generators in stream-cipher cryptography. Computer 1991, 24, 8–17. [Google Scholar] [CrossRef]
- Blum, L.; Blum, M.; Shub, M. A Simple Unpredictable Pseudo-Random Number Generator. SIAM J. Comput. 1986, 15, 364–383. [Google Scholar] [CrossRef]
- Barker, E.B.; Kelsey, J.M. SP 800-90A Rev. 1. Recommendation for Random Number Generation Using Deterministic Random Bit Generators; Technical report; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2012. [Google Scholar]
- Fletcher, M.; Paulz, E.; Ridge, D.; Michaels, A.J. Low-Latency Wireless Network Extension for Industrial Internet of Things. Sensors 2024, 24, 2113. [Google Scholar] [CrossRef]
- McGinthy, J.M.; Michaels, A.J. Session Key Derivation for Low Power IoT Devices. In Proceedings of the 2018 IEEE 4th International Conference on Big Data Security on Cloud (bigdatasecurity), IEEE International Conference on High Performance and Smart Computing (HPSC), and IEEE International Conference on Intelligent Data and Security (IDS), Omaha, NE, USA, 3–5 May 2018. [Google Scholar]
- Hamamreh, J.M.; Furqan, H.M.; Arslan, H. Classifications and Applications of Physical Layer Security Techniques for Confidentiality: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2019, 21, 1773–1828. [Google Scholar] [CrossRef]
- Shiu, Y.S.; Chang, S.Y.; Wu, H.C.; Huang, S.C.H.; Chen, H.H. Physical layer security in wireless networks: A tutorial. IEEE Wirel. Commun. 2011, 18, 66–74. [Google Scholar] [CrossRef]
- Fletcher, M. Enhanced Implementations for Arbitrary-Phase Spread Spectrum Waveforms. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2019. [Google Scholar]
- Michaels, A.J.; Palukuru, V.S.S.; Fletcher, M.J.; Henshaw, C.; Williams, S.; Krauss, T.; Lawlis, J.; Moore, J.J. CAN Bus Message Authentication via Co-Channel RF Watermark. IEEE Trans. Veh. Technol. 2022, 71, 3670–3686. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhou, N.; Zheng, H.; Qin, P.; Yi, L. Security Enhancement for Noise Aggregation in DVB-S2 Systems. In Proceedings of the Signal and Information Processing, Networking and Computers, Ji’nan, China, 13–17 September 2021; Sun, J., Wang, Y., Huo, M., Xu, L., Eds.; Springer Nature: Singapore, 2023; pp. 326–334. [Google Scholar]
- Himanshi; Garg, A. Comparative Study of Physical Layer Secure Key Generation for Wireless Networks. In Proceedings of the 2024 IEEE Region 10 Symposium (TENSYMP), New Delhi, India, 27–29 September 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Jeung, J.; Jeong, S.; Lim, J. Adaptive rapid channel-hopping scheme mitigating smart jammer attacks in secure WLAN. In Proceedings of the 2011—MILCOM 2011 Military Communications Conference, Baltimore, MD, USA, 7–10 November 2011; pp. 1231–1236. [Google Scholar] [CrossRef]
- Fraga-Lamas, P.; Castedo-Ribas, L.; Morales-Méndez, A.; Camas-Albar, J.M. Evolving military broadband wireless communication systems: WiMAX, LTE and WLAN. In Proceedings of the 2016 International Conference on Military Communications and Information Systems (ICMCIS), Brussels, Belgium, 23–24 May 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Shahriar, C.; La Pan, M.; Lichtman, M.; Clancy, T.C.; McGwier, R.; Tandon, R.; Sodagari, S.; Reed, J.H. PHY-Layer Resiliency in OFDM Communications: A Tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 292–314. [Google Scholar] [CrossRef]
- Mcginthy, J.M.; Michaels, A.J. Secure Industrial Internet of Things Critical Infrastructure Node Design. IEEE Internet Things J. 2019, 6, 8021–8037. [Google Scholar] [CrossRef]







| Loss (dB) | (radians) |
|---|---|
| 0.1 | |
| 0.25 | |
| 0.5 | |
| 1 | |
| 2 | |
| 3 |
| Loss (dB) | ||||
|---|---|---|---|---|
| 0.1 | 0.398 | 0.378 | 0.373 | 0.371 |
| 0.25 | 0.752 | 0.609 | 0.589 | 0.5855 |
| 0.5 | - | 0.891 | 0.83 | 0.82 |
| 1 | - | 1.48 | 1.197 | 1.156 |
| 2 | - | - | 1.733 | 1.591 |
| 3 | - | - | 2.207 | 1.899 |
| M-Ary Phase Mapping | |||||
|---|---|---|---|---|---|
| Loss (dB) | 8 | 16 | 64 | 256 | 216 |
| 0.1 | 1 | 1 | 7 | 31 | 7745 |
| 0.25 | 1 | 3 | 11 | 47 | 12,189 |
| 0.5 | 3 | 5 | 17 | 67 | 17,137 |
| 1 | 3 | 5 | 23 | 93 | 23,949 |
| 2 | 5 | 9 | 33 | 129 | 33,063 |
| 3 | 5 | 9 | 39 | 155 | 39,541 |
| m | Expected Average Loss | Calculated Average Loss |
|---|---|---|
| 31 | 0.1 dB | 0.1053 dB |
| 47 | 0.25 dB | 0.2440 dB |
| 67 | 0.5 dB | 0.5021 dB |
| 93 | 1 dB | 0.9888 dB |
| 129 | 2 dB | 1.9797 dB |
| 155 | 3 dB | 3.0493 dB |
| m | Expected Average Loss | Calculated Average Loss |
|---|---|---|
| 31 | 0.1 dB | 0.0922 dB |
| 47 | 0.25 dB | 0.2207 dB |
| 67 | 0.5 dB | 0.4568 dB |
| 97 | 1 dB | 0.9565 dB |
| 141 | 2 dB | 1.9525 dB |
| 179 | 3 dB | 2.9468 dB |
| ALMs | ALUTs | Registers | Memory Bits | M20Ks | |
|---|---|---|---|---|---|
| Design A | 91,418.6 | 128,180 | 133,608 | 1,324,208 | 108 |
| Design B | 92,899.7 | 129,301 | 133,818 | 1,373,360 | 124 |
| Change (B-A) | 1481.1 (1.6%) | 1121 (0.9%) | 210 (0.2%) | 49,152 (3.7%) | 16 (14.8%) |
| Approach | Key Techniques | Advantages | Challenges | Representative Papers |
|---|---|---|---|---|
| Spread Spectrum (FHSS, DSSS) | Frequency Hopping (FH), Direct Sequence Spread Spectrum (DSSS) | Robust to jamming; low detectability | Spectrum inefficiency; synchronization issues | Shiu et al., 2011 [61] |
| Waveform Agility | Arbitrary-phase spread spectrum | High TRANSEC robustness; PHY-layer watermarking | Implementation complexity | Fletcher, 2019 [62] |
| Co-Channel Watermarking | Embedding authentication signals in RF | Real-time message verification | Susceptible to advanced jammers | Michaels et al., 2022 [63] |
| Noise Aggregation | Masking signal in thermal noise | High confidentiality | Reduced SNR and capacity | Zhao et al., 2022 [64] |
| PHY-Layer Key Generation | Channel reciprocity and randomness | No key exchange needed | Low entropy in static environments | Garg, 2024 [65] |
| Adaptive Frequency Hopping | Jamming-resilient hopping with ML | Resilience to smart jammers | Latency in rapid adaptation | Lim et al., 2011 [66] |
| Channel-Aware Signal Modulation | Leveraging channel state information (CSI) | Higher secrecy capacity | Requires accurate CSI estimation | Hamamreh et al., 2018 [60] |
| Scenario-Based Military TRANSEC | WiMAX, LTE, WLAN comparison | Application-specific design | Limited commercial relevance | Fraga-Lamas et al., 2016 [67] |
| OFDM vs. SC-FDMA Resilience | PHY resilience to jamming in multi-carrier systems | Suitable for 5G | High computational cost | Shahriar et al., 2014 [68] |
| Secure PHY for IIoT Nodes | Embedded TRANSEC engines for IIoT | Hardware efficiency | Rigid hardware constraints | McGinthy & Michaels, 2019 [69] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fletcher, M.; McGinthy, J.; Michaels, A.J. Hardware Validation for Semi-Coherent Transmission Security. Information 2025, 16, 773. https://doi.org/10.3390/info16090773
Fletcher M, McGinthy J, Michaels AJ. Hardware Validation for Semi-Coherent Transmission Security. Information. 2025; 16(9):773. https://doi.org/10.3390/info16090773
Chicago/Turabian StyleFletcher, Michael, Jason McGinthy, and Alan J. Michaels. 2025. "Hardware Validation for Semi-Coherent Transmission Security" Information 16, no. 9: 773. https://doi.org/10.3390/info16090773
APA StyleFletcher, M., McGinthy, J., & Michaels, A. J. (2025). Hardware Validation for Semi-Coherent Transmission Security. Information, 16(9), 773. https://doi.org/10.3390/info16090773







