The Role of Mutual Information Estimator Choice in Feature Selection: An Empirical Study on mRMR

Abstract

Maximum Relevance Minimum Redundancy (mRMR) is a widely used feature selection method that is applied in a wide range of applications in various fields. mRMR adds to the optimal subset the features that have high relevance to the target variable while having minimum redundancy with each other. Mutual information is a key component of mRMR as it measures the degree of dependence between two variables. However, the real value of mutual information is not known and needs to be estimated. The aim of this study is to examine whether the choice of mutual information estimator affects the performance of mRMR. To this end, three variations of mRMR are compared. The first one uses Parzen window estimation to assess mutual information between continuous variables. The second is based on equidistant partitioning using the cells method, while the third incorporates a bias-corrected version of the same estimator. All methods are tested with and without a regularization term in the mRMR denominator, introduced to improve numerical stability. The evaluation is conducted on synthetic datasets where the target variable is defined as a combination of continuous features, simulating both linear and nonlinear dependencies. To demonstrate the applicability of the proposed methods, we also include a case study in real-world classification tasks. The study carried out showed that the choice of mutual information estimator can affect the performance of mRMR and it must be carefully selected depending on the dataset and the parameters of the examined problem. The application of the corrected mutual information estimator improves the performance of mRMR in the examined setup.

1. Introduction

Nowadays, there has been an explosive increase in the amount of data. The widespread use of digital technologies and the internet, the growth of social media, mobile devices, and the Internet of Things (IoT) have all contributed to the explosion of the available data [1]. The availability of these data has made possible the development and the improvement of machine learning algorithms [2]. Large datasets are necessary for machine learning algorithms, which can learn from the available data and consequently train effectively [3]. In addition, with big data, deep learning models, which are a subset of machine learning models, are becoming capable of recognizing and learning patterns in images, speech, text and other types of unstructured data [4,5,6,7]. Therefore, it becomes easier to create and develop reliable algorithms for handling diverse and complex problems and datasets [8,9,10].

Nevertheless, on several occasions, having an excessive amount of data might be detrimental and it could reduce the efficiency and therefore the reliability of the algorithms [11]. Specifically, this may occur when the dataset contains noise or irrelevant and redundant features. This can result in overfitting and decrease the model’s performance in terms of accuracy and generalization [12]. Additionally, it could also lead to computational challenges and scalability issues, especially when the analysis concerns deep learning algorithms, which demand significant computational resources to execute [13]. In order to avoid such issues, various techniques have been developed and used. One such technique is feature selection [14].

Feature selection plays an especially critical role in domains such as natural language processing (NLP), where datasets often involve high-dimensional, sparse representations like term frequency-inverse document frequency (TF-IDF), n-grams or word embeddings [15]. In such settings, a large proportion of the features may be irrelevant or redundant, contributing little to the prediction task and increasing the risk of overfitting [16]. Filter-based feature selection methods, such as mRMR [17], are well suited for these contexts because they evaluate features based on intrinsic statistical properties rather than relying on specific classifiers [18]. This allows for dimensionality reduction before model training, improving computational efficiency and enabling better generalization, especially when only a limited number of labeled instances are available [19,20].

Compared to wrapper and embedded methods, which can be computationally expensive or tightly coupled with specific models, mRMR offers a lightweight and model-agnostic solution [21]. While modern deep learning models often include built-in mechanisms for feature weighting or selection, such approaches require large amounts of data and resources and may still suffer from interpretability challenges [22]. Furthermore, post hoc explainability techniques such as SHAP or LRP are useful for model interpretation, but they cannot replace the role of robust feature filtering before training [23]. The mRMR method remains valuable in this preprocessing stage [24], particularly when enhanced with effective estimators of mutual information that better capture complex, potentially nonlinear dependencies between variables [25,26].

The process of feature selection is frequently employed as a preparatory stage or in conjunction with machine learning [27]. The aim of feature selection algorithms is to construct a subset of features from the initial one, by selecting the most relevant features to the class variable and by removing irrelevant and redundant features. This procedure may produce a substantially smaller dataset that only includes the most relevant features [28]. Feature selection methods are classified into three main categories. Various methods have been proposed and used in several research for both wrapper methods [29,30,31,32], filter methods [33,34], and embedded methods [35,36,37]. In this paper, a filter method for feature selection known as mRMR will be studied [17].

The minimum Redundancy Maximum Relevance (mRMR) feature selection method aims to create a subset that contains features that have maximum relevance to the target variable, while having minimum redundancy with each other [17]. Until a predefined number of features is reached, mRMR iteratively adds features to the optimal subset of features, selecting the features with the highest dependency with the class variable and the lowest dependency between the feature and the previously selected features. In order to quantify the dependency between the variables and consequently relevance and redundancy, various statistical measures can be used. A widespread statistical measure that is also an important component of mRMR is mutual information. Mutual information measures the amount of information that one feature contains about another specific feature and it can be applied to quantify relevance and redundancy [38]. This measure has the advantage of being able to detect both linear and nonlinear dependencies, contrary to other statistical measures such as Pearson’s correlation.

Nevertheless, despite the advantages of mutual information, its reliable estimation is considered challenging for real-world datasets, as most of them involve continuous variables. In such cases, the joint probability distribution is not directly known and must be approximated from finite samples, which often introduces bias or instability in the estimates. To confront with this problem and to achieve a reliable assessment of mutual information, in many research various methods have been proposed, some non-parametric ones for density estimation such as k-nearest neighbors [39] and B-splines [40], but also discretization techniques such as equidistant binning, equiprobable binning and adaptive partitioning [41], that generally give worse assessment of mutual information compared to the non-parametric ones [42,43].

Generally, numerous recent studies have focused on improving feature selection techniques, addressing different aspects of the process. One line of work has proposed approaches that enhance mutual information–based feature selection by incorporating unique relevance criteria [44]. Other contributions have introduced conditional mutual information strategies for dynamic feature selection [45], as well as ensemble evaluation functions that combine linear measures, such as the Pearson correlation coefficient, with nonlinear measures like normalized mutual information, in order to capture complex feature–class relationships while maintaining low redundancy [46]. Further research has emphasized the benchmarking and evaluation of mutual information estimators in high-dimensional and complex settings [47]. Additionally, methods have been proposed to address the numerical instability of k-nearest-neighbor-based normalized mutual information estimators in high-dimensional spaces [48]. Feature reduction has also been investigated in the context of IoT intrusion detection, where efficient selection methods are essential for real-time attack classification [49].

Although these approaches highlight significant advances in the broader field of feature selection, it remains the case that the choice of mutual information estimator, despite being a central component of many methods, often receives comparatively less attention. As a result, distinguishing the impact of the estimator from that of the selection strategy itself continues to be a challenge in the literature.

In fact, numerous well-known and widely applied mutual information estimators exist, yet in many studies the emphasis is placed primarily on the choice of the feature selection method itself, while the choice of the mutual information estimator, despite being universally acknowledged as a critical component, often receives comparatively less attention [50,51,52,53,54]. It is not uncommon to find comparisons between feature selection methods that rely on different mutual information estimators, which makes it difficult to disentangle the effect of the selection strategy from that of the estimator [33].

The goal of the present work is not to propose the most advanced or bias-free estimator, since more sophisticated and reliable methods already exist, but rather to demonstrate how even a very small correction to a widely used discretization-based estimator, under otherwise identical conditions, can lead to noticeably different outcomes. This correction is derived directly from the same estimator itself, by subtracting the average mutual information obtained from surrogate samples from the original estimate, which ensures that the estimator is not fundamentally altered but is adjusted in a simple and controlled way. By doing so, we aim to draw further attention within the research community to the importance of carefully considering the choice of mutual information estimator, in addition to the choice of the feature selection method.

To accomplish this, we evaluate the impact of different mutual information estimators on the performance of the mRMR feature selection method. To this end, three variations of mRMR are compared. The first uses the Parzen window estimation of mutual information, the second is based on equidistant binning using the cells method, and the third incorporates a bias-corrected version of the same discretization-based estimator. A regularization term is optionally added to the mRMR denominator to enhance numerical stability. The comparison is performed through an extensive simulation study involving synthetic datasets with both linear and nonlinear dependencies. In addition, a case study using real-world datasets is included to assess the applicability of the methods in practice. The rest of this paper is organized as follows. In Section 2, the methodology and the materials used are presented. In Section 3, a simulation study is carried out in different systems and the results are presented. Additionally, in Section 4, a case study using real-world datasets is included to evaluate the practical applicability of the proposed methods. In Section 5 the results are discussed, and in Section 6 the conclusions are drawn.

2. Materials and Methods

In this section, the tools and methods that were used are described. Initially, some theoretical background on mutual information and surrogates is described. Next, the mutual information estimators and the mRMR feature selection method are presented.

2.1. Mutual Information

Mutual information is an entropy-based measure that detects linear and nonlinear dependencies. It measures the amount of information that two random variables share and, specifically, how much uncertainty about a variable is reduced when the other variable is known. In terms of Shannon entropies, it is calculated as follows:

$$I(X;Y)=H\left(X\right)+H\left(Y\right)-H(X,Y)$$

where $H\left(X\right)$ and $H\left(Y\right)$ are the marginal entropies of the random variables X and Y, respectively, and $H(X,Y)$ is their joint one.

Mutual information is a measure of the interdependence between two random variables X and Y. It is a bidirectional relationship, meaning that it measures how much information X provides about Y, and vice versa. For discrete variables it can be measured as follows:

$$I(X;Y)=\sum _{y\in Y}\sum _{x\in X}{p}_{X,Y}(x,y)log({\displaystyle \frac{p_{X,Y}(x,y)}{p_X\left(x\right)p_Y\left(y\right)}})$$

where $p_{X,Y}(x,y)$ is the joint probability mass function of the variables X, Y and $p_X\left(x\right)$, $p_Y\left(y\right)$ are the probability mass functions of the variables X, Y, respectively. The domain of mutual information is defined as

$$0⩽I(X;Y)⩽min\left[H\right(X),H(Y\left)\right]$$

2.2. Surrogates

Shifted Surrogates

The time-shifted technique for creating surrogate samples, is a method for eradicating the relationship between two time series while preserving their original properties. Let us consider two random variables X, Y and their corresponding time series $\{x_1,\dots ,x_n\}$ and $\{y_1,\dots ,y_n\}$. In this method a random integer d is chosen and then the values of one of the time series, e.g., $\{x_1,\dots ,x_n\}$ are shifted by d time steps. In particular, the original time series is replaced with the time series $x_t=\{x_{d+1},\dots ,x_n,x_1,\dots ,x_d\}$, which is created by shifting the first d values to the end. Although the time-shifted surrogate method is typically used in time series analysis to destroy temporal correlations, in this study, we draw inspiration from this approach and apply a similar idea to multivariate data, aiming to disrupt dependencies between feature variables. Specifically, we perform a shift on individual feature vectors in order to disrupt their dependency with other variables, while preserving their marginal distributions. This approach is used to generate surrogate datasets that allow for the estimation of the bias introduced by the mutual information estimator. By comparing the mutual information computed on the original data to that obtained from the surrogates, we obtain a reference value that reflects the mutual information expected when no statistical dependency is present.

2.3. Mutual Information Estimators

In this subsection, the three mutual information estimators that were employed in this study are presented. Each estimator follows a different strategy for estimating mutual information between variables. Specifically, the estimators include a binning-based approach, a bias-corrected version of it and a kernel-based estimator that utilizes Parzen windows. Their structure and computational process are described in the following.

2.3.1. Original Estimator of Mutual Information

As aforementioned, the mutual information estimator that has been chosen in this study (from now on original estimator), uses an equidistant binning technique for discretization and specifically the cells method. This estimator is applied to continuous variables, which are discretized beforehand in order to allow the computation of mutual information using frequency-based probability estimates. The process for estimating mutual information using the original estimator is presented below in algorithmic form.

• Consider two continuous variables of sample size n, denoted as $x_1={\left\{x_{1,i}\right\}}_{i=1}^n$ and $x_2={\left\{x_{2,i}\right\}}_{i=1}^n$.
• Set the number of bins as $m=\mathrm{round}\left(\sqrt{n/5}\right)$, which defines the resolution of the discretization and the size of the cell grids $C_{1,m}$ and $C_{2,m}$.
• Normalize each variable to the interval $[0,1]$ using min–max scaling:

  $$x_{k,i}^{\mathrm{norm}}={\displaystyle \frac{x_{k,i}-min\left(x_k\right)}{max\left(x_k\right)-min\left(x_k\right)}}\mathrm{for}k=1,2$$
• For each $i=1,\dots ,n$, compute:

  $$c_{k,i}=x_{k,i}^{\mathrm{norm}}·m\mathrm{and}\mathrm{update}\mathrm{the}\mathrm{corresponding}\mathrm{bin}:C_{k,\lfloor c_{k,i}\rfloor }=C_{k,\lfloor c_{k,i}\rfloor }+1$$

  where $\lfloor c_{k,i}\rfloor$ is the integer part of $c_{k,i}$.
• Based on the bin counts $C_{1,m}$ and $C_{2,m}$, estimate the joint and marginal probability distributions for $x_1$ and $x_2$.
• Finally, compute mutual information using the standard definition:

  $$I(x_1;x_2)=\sum _j\sum _i{p}_{x_1,x_2}(i,j)log\left({\displaystyle \frac{p_{x_1,x_2}(i,j)}{p_{x_1}\left(i\right)·p_{x_2}\left(j\right)}}\right)$$

2.3.2. The Proposed Correction

The second mutual information estimator employed in this study is a correction of the original one, based on the methodology proposed by [55]. This correction addresses the bias that is often introduced in mutual information estimation when discretization is applied to continuous variables.

Generally, the corrected mutual information estimator does not differ significantly to the original one. The idea is to divide the data into progressively smaller segments, compute mutual information for each and use linear regression to extrapolate the mutual information corresponding to a larger target sample size. Additionally, surrogate data are used to remove spurious effects. Specifically, for each input variable, mutual information is computed for different subdivisions of the data and then linearly regressed against the logarithm of the corresponding sample sizes. This process is applied both to the original data and to randomized surrogates.

The corrected mutual information is obtained as the difference between the extrapolated mutual information of the real data and the average extrapolated mutual information of the surrogates. The algorithmic procedure is summarized as follows:

• Let $x={\left\{x_i\right\}}_{i=1}^n$ and $y={\left\{y_i\right\}}_{i=1}^n$ be two variables with n samples.
• Choose a number of subdivisions d. For each $r=1,\dots ,d$, set $p=2^{r-1}$.
• For each p, divide both x and y into p equal-length parts. Estimate the mutual information in each part and compute the average:

  $$I_{{\displaystyle \frac{n}{p}}}(x;y)={\displaystyle \frac{1}{p}}\sum _{j=1}^{p}I(x^{\left[j\right]};y^{\left[j\right]})$$

  where $x^{\left[j\right]}$ and $y^{\left[j\right]}$ denote the j-th segment.
• Fit a linear model $I=\alpha ln\left(n\right)+\beta$ based on the values $I_{{\displaystyle \frac{n}{p}}}$ and $ln(n/p)$ to estimate the mutual information for a larger target sample size $n_{\mathrm{target}}$. In this study, the original sample size was $n=1024$ and the target size was set to $n_{\mathrm{target}}=2048$.
• Repeat the above steps using M surrogate versions of x (via circular time shifting) and compute the average surrogate mutual information ${\widehat{I}}_{\mathrm{surrogate}}$.
• The final corrected mutual information is:

  $$I_{\mathrm{corrected}}={\widehat{I}}_{\mathrm{original}}-{\widehat{I}}_{\mathrm{surrogate}}$$

For clarity, the bias correction procedure is also illustrated in a flowchart in Figure 1.

The initial idea for the proposed correction arose from the observation that the estimated mutual information values obtained with the original discretization-based estimator tend to vary with the length of the dataset [55]. In particular, for sufficiently large sample sizes the estimates appear to converge to a stable value, yet still show a systematic bias when compared with the theoretical expectation. It was further noted that subtracting the mutual information computed on surrogate datasets from the original estimates consistently reduced this bias, yielding values closer to the theoretical reference. This motivated the design of the correction procedure, which combines extrapolation based on subdivisions with surrogate adjustment, while keeping the underlying estimator essentially unchanged.

Following the rationale proposed in [55], the number of subdivisions d was chosen according to the size of the examined dataset. Specifically, when the sample size was $n=1024$, we set $d=5$, which yielded partitions of 64, 128, 256, 512 and 1024 samples, with the regression extrapolated to 2048. For $n=512$, we used $d=4$, resulting in partitions of 64, 128, 256 and 512, again with extrapolation to 2048. Similarly, for $n=256$, $d=4$ was selected, giving partitions of 32, 64, 128 and 256, with regression to 1024. For larger sample sizes such as those equal to or greater than 2048, we observed that convergence of the estimates had already occurred, so extrapolation was no longer necessary and only the surrogate correction (subtraction step) was applied.

2.3.3. Parzen-Window-Based Estimation for Continuous Variables

This estimator corresponds to the mutual information computation method used for continuous variables in the original mRMR feature selection framework, as introduced by [17]. It is based on the Parzen window (kernel density estimation, KDE) technique and is particularly suitable when at least one of the variables involved is continuous. In the original work, this estimator was adopted as a practical alternative to discretization, especially in cases involving continuous or mixed-type variables. The method avoids discretization by directly estimating the probability density functions using Gaussian kernels centered at the observed data points.

Given two real-valued random variables X and Y with n observations $\{(x_1,y_1),\dots ,(x_n,y_n)\}$, the procedure is as follows:

• Estimate the marginal densities $\widehat{p}\left(x_i\right)$ and $\widehat{p}\left(y_i\right)$ using Parzen window estimation:

  $$\widehat{p}\left(x_i\right)={\displaystyle \frac{1}{n}}\sum _{j=1}^n\phi (x_i-x_j;h),\widehat{p}\left(y_i\right)={\displaystyle \frac{1}{n}}\sum _{j=1}^n\phi (y_i-y_j;h)$$

  where $\phi (·;h)$ denotes the Gaussian kernel with bandwidth h.
• Estimate the joint density $\widehat{p}(x_i,y_i)$ using bivariate kernel density estimation with full covariance matrix $\Omega$:

  $$\widehat{p}(x_i,y_i)={\displaystyle \frac{1}{n}}\sum _{j=1}^n\phi \left(\left[\begin{array}{c}{x}_i\\ y_i\end{array}\right]-\left[\begin{array}{c}{x}_j\\ y_j\end{array}\right];h,\Omega \right)$$
• Approximate the mutual information as:

  $$I(X;Y)\approx {\displaystyle \frac{1}{n}}\sum _{i=1}^{n}log\left({\displaystyle \frac{\widehat{p}(x_i,y_i)}{\widehat{p}\left(x_i\right)\widehat{p}\left(y_i\right)}}\right)$$
• For discrete target variables, the conditional entropy $H(X\mid Y)$ is estimated separately for each class. The mutual information is then computed using the following identity:

  $$I(X;Y)=H\left(X\right)-H(X\mid Y)$$

2.4. mRMR

mRMR is a filter method for feature selection that uses mutual information to measure the dependencies between the features and the class variable, but also between the features themselves in order to find the features that are most relevant to the class variable and less redundant with each other, ultimately to create an optimal subset of features, which will eventually include as much information as possible about the initial dataset by including only a few features of it. The optimal feature subset S is filled in progressively, starting with just one feature that has the maximum mutual information with the class variable C${max}_{f_i\in F}I(f_i,C)$. Until a predefined number of features is reached, mRMR iteratively adds features to the optimal subset. Particularly, in each search cycle, mRMR adds to the optimal subset the feature that satisfies the following equation:

$$\underset{f_i\in F-S}{max}\left[{\displaystyle \frac{I(f_i;C)}{\frac{1}{\left|S\right|}{\sum }_{f_j\in S}I(f_i;f_j)}}\right]$$

(1)

It has to be noted that in this study, instead of using the classical mRMR as seen in Equation (1), we use a variant of it, as presented in Equation (2). The only difference between the two, is that we added one unit to the denominator, because during the study, we observed that for features that had minimal correlation or theoretically zero correlation, the estimation of mutual information through the proposed correction gave values slightly smaller than zero. This is partly logical as the estimation of mutual information through the proposed correction involves subtraction, as we previously saw. In addition to this, other variations were examined, such as setting the negative values to zero, but this often led the fraction to tend to infinity. Another idea was to convert the denominator to an absolute intersection, but then the property of redundancy was completely lost, as we could equate a pair of features that had correlation with one that had none. However, because it gave a negative value, its absolute value made it appear as if there was a dependency. We believe that the chosen method affects the whole process of mRMR less, because although it makes mRMR more sensitive to relevance, the redundancy still contributes to the final outcome, albeit to a lesser extent. We decided to add 1 to the denominator instead of, e.g., 0, $0.05$, $0.1$, $0.2$, $0.3$, $0.5$, $0.7$ and $0.8$, since after various attempts in different systems, it appeared to perform better compared to the other values tested (see Figure 2 and Figure 3 for details). For the original estimator, we also used Equation (2) although it was not necessary, so that the comparison could be made on equal terms, as the primary goal was to evaluate how the choice of mutual information estimator affects the reliability and efficiency of mRMR and in order to examine this, all the other parameters have to be the same.

$$\underset{f_i\in F-S}{max}\left[{\displaystyle \frac{I(f_i;C)}{1+\frac{1}{\left|S\right|}{\sum }_{f_j\in S}I(f_i;f_j)}}\right]$$

(2)

3. Simulation Study

In this section, a simulation study is conducted to evaluate the performance of the mRMR feature selection algorithm. Simulated datasets are constructed such that the features relevant to the class variable are known in advance. This allows for a direct assessment of the algorithm’s ability to identify informative features. The systems have been selected progressively from very simple ones to more complex, in order to examine the performance of mRMR in different scenarios. In the following examples, the variable y gives the classes after discretization and the features $f_i$ are random normal variables, some of which are predictors of the class variable y, while some of them are functionally related to the predictors. Beyond the features that are related to the class variable either directly or indirectly, we also added random variables, until each dataset consists of a total of thirty features.

For discretization, the number of classes k is chosen to satisfy the relation $k=\mathrm{round}\left(\sqrt{n/5}\right)$, where n is the number of samples. This setting follows the same rationale as in the study where the corrected mutual information estimator was originally introduced. Each system was simulated by generating 20 datasets of 1024 samples. However, for the corrected mutual information estimator, which requires extrapolation to a larger sample size, the estimation was performed by projecting to a length of 2048, following the procedure described in Section 2.3.2. The results reported in Section 3.2 correspond to the average performance across these 20 datasets.

To assess the effect of the mutual information estimator and the mRMR configuration, five variations of the mRMR algorithm were compared:

• Original-mRMR (s = 0): Uses the original mutual information estimator and applies Equation (1), without modification to the denominator.
• Original-mRMR (s = 1): Same estimator, but with one unit added to the denominator (Equation (2)).
• Corr-mRMR (s = 1): Uses the proposed correction of mutual information with one unit added to the denominator.
• Parzen-mRMR (s = 0): Uses the Parzen (KDE-based) estimator without adjustment in the denominator.
• Parzen-mRMR (s = 1): Uses the Parzen estimator with one unit added to the denominator.

In addition to the original and corrected mutual information estimators, we also included the original Parzen-based estimator, as proposed by [17], in order to gain a more complete picture of the mRMR framework’s performance under different estimation strategies. This setup allows us to systematically compare how the choice of mutual information estimator, as well as the presence or absence of a stabilizing constant in the denominator, affects the reliability and effectiveness of mRMR across diverse systems.

3.1. Systems

• $y=0.5f_1+0.5f_2+e$,
• $y=0.5f_1+0.5f_2+e$, with additional features correlated to $f_1$ and $f_2$,
• $y=0.5f_1+0.5f_2+0.5f_3+e$, where $f_3=f_1·f_2$,
• $y=0.5f_1+0.5f_2+0.5f_3+e$, where $f_3=f_1·f_2·z_3$,
• $y=f_1+f_2+0.2f_3+0.3f_4+e$, where $f_3=0.2f_1+0.3f_2+2z_3$ and $f_4=0.1f_1^2+0.1f_2^2$,
• $y={\sum }_{i=1}^6{\beta }_i{f}_i+e$, where $f_1=z_1$, $f_2=z_2$, $f_3=z_1·z_2$, $f_4=z_3$, $f_5=z_4^2$, and $f_6=z_1·z_5·z_6$.

System 1 is the simplest of all, as there are only two functionally related features to the class variable y, the features $f_1$ and $f_2$, which are moderately correlated with the class variable (both coefficients = 0.5). e is a standard normal random variable. As aforementioned, for all cases the dataset consists of a total of 30 features, of which the remaining 28 are irrelevant features generated from a standard normal distribution.

System 2 is identical to System 1 in terms of the functionally related features to the class variable. In addition to these two features, there are two groups of two features each. The features in the first group are strongly correlated with $f_1$ ($coefficient=0.8$), while the features in the second group are weakly correlated with $f_2$ ($coefficient=0.4$). Similar to System 1, the remaining 24 features are irrelevant features generated from a standard normal distribution.

In System 3 there are three functionally related features to the class variable y, particularly the features $f_1$, $f_2$ and $f_3$. In this case, feature 3 is correlated with the first two selected features. The remaining 27 features are irrelevant. Here, the optimal subset should contain any two of the three functionally related features. In mRMR, the number of features that the optimal subset should contain before the algorithm stops is arbitrarily defined. In this case, we set the algorithm to stop when the optimal subset contains 3 features, in order to examine whether the feature selection algorithm selects the features, $f_1$, $f_2$ and $f_3$, or prefers to add in an irrelevant feature to the optimal subset, when it has already selected two of the functionally related features.

System 4 also has three functionally related features to the class variable, specifically the features, $f_1$, $f_2$ and $f_3$. However, unlike in System 3, feature $f_3$ in System 4 contains information about another random variable, $z_3$, in addition to being correlated with $f_1$ and $f_2$. The remaining 27 features are irrelevant random variables. In this case, the optimal subset should contain all three functionally related features and the objective is to investigate whether the feature selection algorithm chooses them or another irrelevant feature, given that $f_3$ contains information about the predictors of y, namely $f_1$ and $f_2$.

System 5 has four functionally related features to the class variable, namely $f_1$, $f_2$, $f_3$ and $f_4$. In this case the functionally related features do not equally affect the class variable, since their coefficients differ. Specifically, $f_1$ and $f_2$ are strongly correlated with the class variable y (coefficients = 1), while $f_3$ and $f_4$ are weakly correlated, since their coefficients are equal to 0.2 and 0.3, respectively. In this case, the number of features contained in the optimal subset is set as four, because we consider it more appropriate for the feature selection algorithm to select a feature that contains the same information as other selected predictors e.g., $f_4$, rather than select an irrelevant feature (standard random variable).

In System 6, there is a group of six predictors of the class variable y, namely $f_1$,…,$f_6$, that are functionally related to the random independent standard variables $z_i$, $i=1,\dots ,6$. The ${\beta }_i$ are set as ${\displaystyle \frac{1}{{\sigma }_i}}$, i = 1,…,6, where ${\sigma }_i$ is the standard deviation of $f_i$, so that all features contribute the same to y. The number of the features that contained in the optimal subset was set as six, for the same reason aforementioned in the description of System 5. In addition to these six features, there are also two groups of six features each. The features of one of these groups are strongly correlated to the corresponding features of the first group ($coefficient=0.8$), while the six features of the other group are weakly correlated to the corresponding features of the first group ($coefficient=0.4$). The remaining 12 features are irrelevant.

To provide a concise overview of the experimental setup, we summarize the main characteristics of all six systems in

Table 1. Summary of the systems used in the simulation study.

System	Functional Relationship (y)	Relevant/Redundant Features	Irrelevant Features
$S_1$	$0.5f_1+0.5f_2+e$	$f_1,f_2$	28
$S_2$	$0.5f_1+0.5f_2+e$	$f_1,f_2$ + 4 correlated features	24
$S_3$	$0.5f_1+0.5f_2+0.5f_3+e$; $f_3=f_1{f}_2$	$f_1,f_2,f_3$ (redundant)	27
$S_4$	$0.5f_1+0.5f_2+0.5f_3+e$; $f_3=f_1{f}_2{z}_3$	$f_1,f_2,f_3$	27
$S_5$	$f_1+f_2+0.2f_3+0.3f_4+e$; $f_3,f_4$ functions of $f_1,f_2$	$f_1,f_2,f_3,f_4$	26
$S_6$	${\sum }_{i=1}^6{\beta }_i{f}_i+e$; $f_1,\dots ,f_6$ depend on $z_1,\dots ,z_6$	6 relevant ($f_1,\dots ,f_6$), + 12 correlated (0.8/0.4)	12

. This table highlights the functional relationships, the relevant and redundant features, as well as the number of irrelevant features in each case, allowing the reader to more easily interpret and compare the different scenarios.

3.2. Results

In this section, the results are presented. We set the feature selection algorithm to stop when the optimal subset contains the same number of features with the functionally related features, as described in Section 3.1. If the optimal subset contains all of the features that are functionally related to the class variable, then it is considered as correct (from now on success rate). The results refer to the average accuracy obtained by the 20 generated datasets of each system.

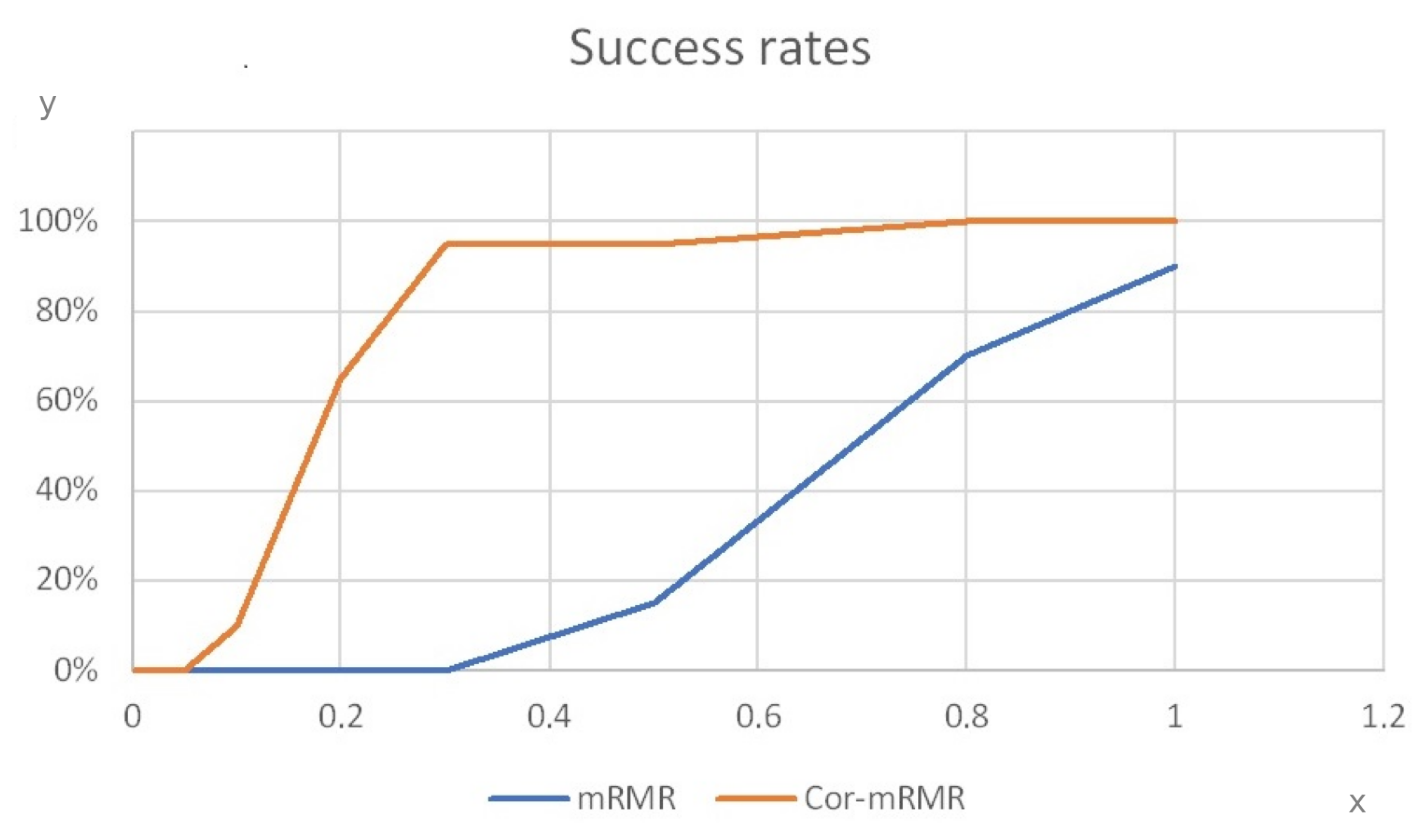
First, the Figure 2 and Figure 3 for Systems 5 and 6, respectively, are presented. These figures depict the success rate of mRMR using two different mutual information estimators across various values of s, where s is the number added to the denominator of mRMR to prevent negative values. The algorithm that uses the original estimator is referred to as mRMR, while the one that uses the proposed mutual information correction is referred to as Corr-mRMR.

Figure 2 shows that both of the examined feature selection methods achieve the highest success rate when the number 1 is added to the denominator of mRMR. Corr-mRMR achieves a success rate of above 80% when s is equal to 0.3 or higher, while simple mRMR only does so when s is equal to 1. Additionally, it is observed that for this system, the success rate of the Corr-mRMR method is always equal to or better than that of simple mRMR, regardless of the choice of s.

Figure 3 differs slightly from Figure 2. When the values of s are equal to 0, 0.05 and 0.1, the Original-mRMR method appears to be more efficient than the corrected one. However, when the value of s is equal to 0.2, the success rate of Corr-mRMR increases rapidly to 65%, while the corresponding success rate of the Original-mRMR is only 40%. The same trend seems to apply for values of s greater than 0.2, where Corr-mRMR performs better. For the selected value of s, which in this study is $s=1$, both of the examined methods appear to have a success rate smaller than the maximum achievable. Nevertheless, the differences between these success rates and the optimal ones are small compared to other systems, where choosing $s=1$ was found to be the optimal choice.

The results presented in

Table 2. Success rate (%) of the examined mRMR variations across different systems. The success rate refers to the correct identification of all functionally related features. Reported values represent averages over 20 generated datasets.

System	Original (s = 0)	Original (s = 1)	Corr (s = 1)	Parzen (s = 0)	Parzen (s = 1)
$S_1$	100	100	100	100	100
$S_2$	80	90	100	100	100
$S_3$	0	95	95	100	100
$S_4$	0	80	95	100	100
$S_5$	0	85	95	100	100
$S_6$	0	55	70	100	100

indicate that in general, mRMR performs better when the corrected mutual information estimator is used.

In System 1, both of the predictors are moderately correlated to the class variable y (coefficients = 0.5). For this system, all the variations of mRMR performed equally well without making a mistake, since all included in the optimal subset the features $f_1$ and $f_2$, which are the only features that are functionally related to the class variable, while the remaining 28features are irrelevant.

In System 2, while both Parzen variations and the corrected mRMR method achieve 100% success, the original estimator gives only 80% for $s=0$ and 90% for $s=1$. On the other hand, the corrected and KDE-based estimators demonstrate better resilience to redundancy. The performance of Corr-mRMR was slightly better, since its success rate is 100%, while the Original-mRMR ($s=1$), using the original estimator of mutual information, achieved a success rate of 90%. Systems 1 and 2 are similar, except that beyond the two functionally related features to the class variable, System 2 has four additional features that are correlated with the predictors of y, while in System 1, the remaining 28 features are irrelevant. It is observed that Corr-mRMR does not confront difficulties in identifying the actual relevant features, while Original-mRMR ($s=0$) and Original-mRMR ($s=1$) make a few mistakes.

System 3 introduces nonlinearity through the feature $f_3=f_1·f_2$, creating a higher-order dependency. In this case, the Parzen-based methods again achieve perfect performance (100%), while both the Original-mRMR ($s=0$) and Corr-mRMR ($s=1$) fail to fully recover the true subset. On the contrary, the Original-mRMR ($s=0$) method without correction completely fails (0%). It is worth noting, however, that the 0% success rate of the Original-mRMR with $s=0$ reflects only the strict definition of success—namely, recovering all three relevant features. If we were to restrict the optimal subset to only the two strongest predictors ($f_1$ and $f_2$), its performance would be nearly equivalent to that of the $s=1$ variant. The failure occurs in the final selection step: instead of selecting the third relevant (though redundant) feature $f_3$, Original-mRMR ($s=0$) tends to include a completely unrelated feature, ignoring the partial redundancy advantage of $f_3$ over irrelevant variables. The corrected mRMR (Corr-mRMR), which uses the adjusted mutual information estimator and $s=1$, performs similarly to the Original-mRMR ($s=1$) in this example, also achieving 95%.

System 4 is similar to System 3, except that in System 3, the three features were functions of only two independent predictors, contrary to the System 4, where $f_1$, $f_2$ and $f_3$ are functions of three independent predictors, since $f_3=f_1\ast f_2\ast z_3$. In this system the optimal subset should contain all three features ($f_1$, $f_2$ and $f_3$). The increased complexity affects the classical estimators more severely. The Original-mRMR with $s=0$ fails completely (0%) as it strongly penalizes redundancy and fails to recognize the added informational contribution of $f_3$. Increasing the denominator to $s=1$ improves the performance to 80%, indicating a more balanced treatment between relevance and redundancy. However, some misranking still occurs. The corrected version (Corr-mRMR), which incorporates the proposed mutual information adjustment and also uses $s=1$, achieves a success rate of 95%. This performance comes very close to the Parzen-based methods (both at 100%), highlighting that the correction significantly improves reliability in more complex scenarios where redundancy and relevance coexist.

In System 5 there are four functionally related features to the class variable but only three independent predictors. The Parzen-mRMR methods still succeed in identifying all relevant features. In contrast, the Original-mRMR fails completely for $s=0$ (0%) and performs better with $s=1$ (85%), while the corrected estimator improves further to 95%. The difference lies in the selection of $f_4$, since for all the generated datasets, both of them selected correctly the features $f_1$, $f_2$ and $f_3$, but the simple mRMR in a couple of times added an irrelevant feature to the optimal subset, instead of adding $f_4$, which, however, is a function of the features $f_1$ and $f_2$. Contrary to System 4, for this system the complete failure of mRMR for $s=0$ stems from the addition of a completely irrelevant feature instead of the weakly informative $f_4$, which is a nonlinear function of $f_1$ and $f_2$. If the selected subset had been limited to three features—namely $f_1$, $f_2$ and $f_3$—the performance of Original-mRMR with $s=0$ would have been comparable to that with $s=1$. Both $s=1$ and Corr-mRMR handle the balance between relevance and redundancy more effectively, with the latter approaching the Parzen benchmark.

System 6 is considered the most complex of all the examined systems. In this system there are six functionally related features to the class variable, five of which are independent predictors, while the sixth ($f_3$) is the product of $f_1$ and $f_2$. Once again, the Original-mRMR fails when $s=0$ (0%) and performs modestly when $s=1$ (55%). The Corr-mRMR performs better (70%), but only the Parzen-based methods were able to identify all the relevant features (100%). Notably, even when the stopping criterion is set to five features instead of six, Corr-mRMR fails to recover the complete set of relevant features in only 5% of the cases, whereas the Original-mRMR does so in 15%.

4. Case Study

To assess the practical applicability of the examined mRMR variations, we conducted a case study in real-world classification tasks. Specifically, we employed a diverse set of benchmark datasets widely used in feature selection and classification research. The collection includes financial datasets (bankrupt, credit), bioinformatics datasets (qsar), software defect prediction datasets (kc1, pc1) and text or signal classification datasets (spambase, magic).

To ensure consistency with the experimental design used in the simulation study, we randomly selected a subset of 1140 instances from the full datasets. This choice allows training to be conducted on 1026 observations, aligning with the sample size used for the corrected mutual information estimation in previous sections.

Each method was configured to select the top 5 features. Using these subsets, we then trained and evaluated four standard classifiers: Logistic Regression, Decision Tree, Random Forest and K-Nearest Neighbors (KNN). Classification performance was assessed using 10-fold cross-validation and we report the mean accuracy and standard deviation across folds.

The following tables (

Table 3. Classification accuracies (mean ± std) using logistic regression across seven benchmark datasets. Columns correspond to different mRMR variations: Original ($\mathbf{s}=\mathbf{0}$) uses the original mutual information estimator without modification to the denominator; Original ($\mathbf{s}=\mathbf{1}$) adds a regularization term of one unit to the denominator; Corr ($\mathbf{s}=\mathbf{1}$) employs the bias-corrected mutual information estimator with the same regularization; Parzen ($\mathbf{s}=\mathbf{0}$) and Parzen ($\mathbf{s}=\mathbf{1}$) rely on Parzen window (KDE-based) estimation without and with the $s=1$ regularization, respectively. The parameter s denotes the regularization constant added to the denominator of the mRMR criterion. The best-performing method for each dataset is highlighted in bold.

Dataset	Original (s = 1)	Original (s = 0)	Corr (s = 1)	Parzen (s = 1)	Parzen (s = 0)
bankrupt	0.9588 ± 0.0124	0.9570 ± 0.0083	0.9649 ± 0.0147	0.9544 ± 0.0053	0.9491 ± 0.0066
qsar	0.7469 ± 0.0332	0.7726 ± 0.0329	0.8010 ± 0.0200	0.7631 ± 0.0199	0.7270 ± 0.0223
spambase	0.6833 ± 0.0138	0.8000 ± 0.0265	0.8482 ± 0.0398	0.7588 ± 0.0375	0.6667 ± 0.0245
magic	0.8044 ± 0.0340	0.8044 ± 0.0331	0.8009 ± 0.0344	0.7702 ± 0.0355	0.7702 ± 0.0355
kc1	0.8500 ± 0.0249	0.8482 ± 0.0245	0.8518 ± 0.0262	0.8509 ± 0.0294	0.8456 ± 0.0212
pc1	0.8851 ± 0.0073	0.8860 ± 0.0118	0.8851 ± 0.0114	0.8842 ± 0.0110	0.8860 ± 0.0124
credit	0.8000 ± 0.0225	0.7991 ± 0.0194	0.8018 ± 0.0229	0.8000 ± 0.0225	0.8026 ± 0.0177

,

Table 4. Classification accuracies (mean ± std) using Decision Tree across seven benchmark datasets. Column descriptions as in Table 3. The best-performing method for each dataset is highlighted in bold.

Dataset	Original (s = 1)	Original (s = 0)	Corr (s = 1)	Parzen (s = 1)	Parzen (s = 0)
bankrupt	0.9307 ± 0.0159	0.9412 ± 0.0104	0.9325 ± 0.0239	0.9061 ± 0.0222	0.9386 ± 0.0277
qsar	0.7242 ± 0.0342	0.7262 ± 0.0319	0.7514 ± 0.0242	0.7210 ± 0.0218	0.7120 ± 0.0256
spambase	0.7211 ± 0.0188	0.7460 ± 0.0256	0.7671 ± 0.0321	0.7254 ± 0.0216	0.7167 ± 0.0278
magic	0.7825 ± 0.0310	0.7939 ± 0.0328	0.7904 ± 0.0297	0.7693 ± 0.0285	0.7719 ± 0.0301
kc1	0.8105 ± 0.0275	0.8123 ± 0.0260	0.8228 ± 0.0302	0.8053 ± 0.0291	0.7991 ± 0.0272
pc1	0.8421 ± 0.0178	0.8456 ± 0.0210	0.8518 ± 0.0204	0.8412 ± 0.0197	0.8465 ± 0.0213
credit	0.7658 ± 0.0202	0.7623 ± 0.0199	0.7684 ± 0.0221	0.7614 ± 0.0187	0.7702 ± 0.0194

,

Table 5. Classification accuracies (mean ± std) using Random Forest across seven benchmark datasets. Column descriptions as in Table 3. The best-performing method for each dataset is highlighted in bold.

Dataset	Original (s = 1)	Original (s = 0)	Corr (s = 1)	Parzen (s = 1)	Parzen (s = 0)
bankrupt	0.9544 ± 0.0116	0.9596 ± 0.0105	0.9526 ± 0.0153	0.9070 ± 0.0208	0.9588 ± 0.0152
qsar	0.8158 ± 0.0289	0.8104 ± 0.0314	0.8351 ± 0.0261	0.8184 ± 0.0256	0.8096 ± 0.0298
spambase	0.8254 ± 0.0302	0.7991 ± 0.0198	0.8395 ± 0.0487	0.8237 ± 0.0279	0.8158 ± 0.0332
magic	0.8302 ± 0.0341	0.8447 ± 0.0347	0.8298 ± 0.0389	0.8193 ± 0.0328	0.8272 ± 0.0356
kc1	0.8465 ± 0.0299	0.8412 ± 0.0310	0.8333 ± 0.0301	0.8526 ± 0.0280	0.8561 ± 0.0277
pc1	0.8719 ± 0.0192	0.8746 ± 0.0196	0.8904 ± 0.0212	0.8789 ± 0.0189	0.8728 ± 0.0203
credit	0.8026 ± 0.0214	0.7974 ± 0.0198	0.8018 ± 0.0209	0.8061 ± 0.0287	0.8088 ± 0.0220

and

Table 6. Classification accuracies (mean ± std) using K-Nearest Neighbors across seven benchmark datasets. Column descriptions as in Table 3. The best-performing method for each dataset is highlighted in bold.

Dataset	Original (s = 1)	Original (s = 0)	Corr (s = 1)	Parzen (s = 1)	Parzen (s = 0)
bankrupt	0.9500 ± 0.0196	0.9570 ± 0.0149	0.9500 ± 0.0196	0.9482 ± 0.0073	0.9544 ± 0.0140
qsar	0.7588 ± 0.0291	0.7658 ± 0.0288	0.7816 ± 0.0267	0.7623 ± 0.0275	0.7544 ± 0.0299
spambase	0.7702 ± 0.0310	0.7825 ± 0.0294	0.7930 ± 0.0345	0.7719 ± 0.0302	0.7667 ± 0.0328
magic	0.8026 ± 0.0335	0.8167 ± 0.0327	0.8096 ± 0.0352	0.8018 ± 0.0340	0.8070 ± 0.0331
kc1	0.8351 ± 0.0286	0.8386 ± 0.0271	0.8421 ± 0.0294	0.8342 ± 0.0279	0.8368 ± 0.0263
pc1	0.8649 ± 0.0208	0.8675 ± 0.0211	0.8728 ± 0.0224	0.8684 ± 0.0207	0.8667 ± 0.0218
credit	0.7912 ± 0.0197	0.7939 ± 0.0189	0.7956 ± 0.0202	0.7921 ± 0.0190	0.7982 ± 0.0187

) summarize the classification accuracies for each classifier across all datasets. For each dataset, the best-performing method is highlighted in bold to emphasize its relative performance.

The results presented in Table 3 demonstrate how different mutual information estimators and regularization settings influence the performance of the mRMR feature selection algorithm when combined with Logistic Regression. Across the seven benchmark datasets, Corr-mRMR achieved the highest accuracy in four cases, while the Original-mRMR (s = 1), the Original-mRMR (s = 0) and Parzen-mRMR (s = 0) methods performed best in one dataset each. These results indicate that Corr-mRMR provided a measurable advantage over both the uncorrected mRMR variants and the Parzen-based estimators in the majority of cases.

In several datasets, such as bankrupt, magic, kc1, pc1 and credit, the differences between Corr-mRMR and Original-mRMR (s = 1) were minimal, with accuracies differing by less than 0.01. For instance, in bankrupt, Corr-mRMR achieved 0.9649, compared with 0.9588 obtained by Original-mRMR (s = 1). In kc1, the corresponding values were 0.8518 and 0.8500, while in pc1, all three methods, including the Parzen variants, produced nearly identical results in the range 0.8851–0.8860. Similarly, in credit, the performance of the examined methods was nearly identical, with only marginal differences between them.

By contrast, notable performance differences were observed in the qsar and spambase datasets. In qsar, Corr-mRMR achieved an accuracy of 0.8010, clearly higher than Original-mRMR (s = 1) (0.7469) and the best Parzen-based result (0.7631). An even larger improvement was observed in spambase, where Corr-mRMR reached 0.8482, substantially outperforming Original-mRMR (s = 1) (0.6833) as well as the Parzen methods, the best of which achieved 0.7588. It is worth noting that in these two datasets, the direct comparison between Corr-mRMR and Original-mRMR (s = 1) (which differ only in the use of the bias-corrected mutual information estimator while all other parameters remain identical) shows that even a seemingly minor adjustment, which leads to the corrected estimator of mutual information, can result in a substantial performance gain.

Overall, the choice of mutual information estimator appears to have a substantial impact on the performance of feature selection methods in certain cases. Among the examined approaches, the mRMR variant that employs the corrected mutual information estimator (Corr-mRMR) exhibited the most stable performance across all datasets, achieving results that were either nearly identical to or better than those of the alternative methods.

The results presented in Table 4 show the performance of the examined mRMR variations combined with Decision Tree classifiers across seven benchmark datasets. In this setting, Corr-mRMR achieved the highest accuracy in four datasets (qsar, spambase, kc1 and pc1), while Original-mRMR (s = 0) performed best in bankrupt and magic and Parzen-mRMR (s = 0) slightly outperformed the others in credit.

In most datasets, the performance differences between methods were modest, typically within a range of 0.01–0.02. For example, in pc1, Corr-mRMR achieved 0.8518, closely followed by Original-mRMR (s = 0) with 0.8456 and Parzen-mRMR (s = 0) with 0.8465. Similarly, in credit, Parzen (s = 0) achieved the highest accuracy (0.7702), differing by less than 0.01 from Corr-mRMR (0.7684) and Original-mRMR (s = 1) (0.7658).

However, clearer advantages for Corr-mRMR were observed in the qsar and spambase datasets, where it outperformed the other examined methods by approximately 0.025 and 0.021, respectively.

Notably, when compared directly with the mRMR variant employing the Parzen estimator (Parzen-mRMR (s = 0)), which is the configuration used in the study where mRMR was originally introduced, the Corr-mRMR showed clear advantages in most of the datasets. In qsar, Corr-mRMR achieved 0.7514, compared with 0.7120 of Parzen-mRMR (s = 0), while in spambase the respective values were 0.7671 and 0.7167. Similarly, in magic, the corrected variant reached 0.7904, outperforming Parzen-mRMR (s = 0) at 0.7719 and in kc1 it obtained 0.8228 compared with 0.7991.

The results in Table 5 summarize the performance of the examined mRMR variants with Random Forest classifiers. Overall, the differences between methods are relatively modest, with accuracies generally within a 0.01–0.03 range. Corr-mRMR achieved the best performance in qsar, spambase and pc1, reaching 0.8351, 0.8395 and 0.8904, respectively, each representing an improvement of about 0.02 compared with the best performing of the other examined methods. In contrast, Original-mRMR (s = 0) was slightly superior in bankrupt (0.9596) and magic (0.8447), while Parzen-mRMR (s = 0) was the most accurate in kc1 (0.8561) and credit (0.8088) datasets.

These findings suggest that no single method dominates across all datasets, though Corr-mRMR provided some measurable gains, particularly in qsar and spambase.

It is worth noting that in this setting, all the examined methods performed particularly well, as nearly all achieved accuracies equal to or above 0.80 across the benchmark datasets, with only minimal deviations observed for Original-mRMR (s = 0).

The results presented in Table 6 summarize the performance of the examined mRMR variations combined with K-Nearest Neighbors classifiers. Corr-mRMR attained the highest accuracy in four datasets (qsar, spambase, kc1 and pc1), while Original-mRMR (s = 0) performed best in bankrupt and magic, and Parzen-mRMR (s = 0) achieved the highest accuracy in credit.

Across most datasets, the observed differences were modest, typically below 0.01–0.015 in absolute accuracy. For example, in pc1, Corr-mRMR reached 0.8728, only slightly higher than Original-mRMR (s = 0) (0.8675), Parzen (s = 1) (0.8684) and Original-mRMR (s = 1), which with 0.8649 yielded the lowest accuracy among the examined methods. Similarly, in kc1, Corr-mRMR obtained 0.8421 compared with 0.8342 for Parzen-mRMR (s = 1).

More pronounced differences appeared in qsar and spambase. Specifically, Corr-mRMR achieved 0.7816 in qsar, compared with 0.7544 for Parzen-mRMR (s = 0) and 0.7930 in spambase, compared with 0.7667. These results highlight that adopting the corrected mutual information estimator can yield measurable gains even when the improvements appear numerically moderate.

Overall, these findings confirm that incorporating the corrected mutual information estimator into the mRMR framework is effective not only in controlled synthetic settings, but also across a broad range of real-world applications. The results demonstrate that the observed benefits are generalizable and not restricted to a specific domain or dataset.

4.1. Comparison with State-of-the-Art Feature Selection Methods

To further evaluate the Corr-MRMR method, we compared it against two well-established mutual information-based feature selection algorithms, CONMI_FS [46], and MIFS-ND [51].

All three methods were applied to the same benchmark datasets described in Section 4. In this case, the number of selected features was not fixed a priori. Instead, we adopted the intrinsic stopping criterion of CONMI_FS, as defined in its original description. Because CONMI_FS is the only method among the three that specifies a stopping criterion, we used its selected cardinality $k^{★}$ on each dataset as the target subset size. MIFS-ND and Corr-mRMR were then constrained to return exactly $k^{★}$ features. This approach ensured that the comparison was performed using feature subsets of equal cardinality across all methods.

For CONMI_FS and MIFS-ND, algorithm parameters were set according to the values reported in their respective original studies, corresponding to configurations that achieved the best empirical performance. In particular, for CONMI_FS, the hyperparameter $\lambda$ was fixed at $0.9$, as this value yielded the best classification results in preliminary testing.

Classification performance was assessed using four classifiers: Logistic Regression (LR), Decision Tree (DT), Random Forest (RF) and K-Nearest Neighbors (KNN), each evaluated with 10-fold cross-validation.

The classification results obtained for all datasets and classifiers are summarized in

Table 7. Mean classification accuracy (± standard deviation) with Logistic Regression after feature selection using CONMI_FS, MIFS-ND and Corr-mRMR. The “# Features” column indicates the subset size $k^{★}$ given by the CONMI_FS stopping criterion and applied to all methods. Bold values denote the highest accuracy for each dataset.

Dataset	# Features	CONMI_FS	MIFS-ND	Corr-MRMR
bankrupt	4	0.9509 ± 0.0105	0.9588 ± 0.0088	0.9640 ± 0.0144
qsar	4	0.8113 ± 0.0329	0.8076 ± 0.0355	0.7754 ± 0.0258
spambase	16	0.9123 ± 0.0245	0.9088 ± 0.0326	0.8807 ± 0.0333
magic	2	0.7658 ± 0.0400	0.7658 ± 0.0400	0.7991 ± 0.0373

,

Table 8. Mean classification accuracy (± standard deviation) with Decision Tree after feature selection using CONMI_FS, MIFS-ND and Corr-mRMR. The “# Features” column indicates the subset size $k^{★}$ given by the CONMI_FS stopping criterion and applied to all methods. Bold values denote the highest accuracy for each dataset.

Dataset	# Features	CONMI_FS	MIFS-ND	Corr-mRMR
bankrupt	4	0.9456 ± 0.0183	0.9421 ± 0.0112	0.9316 ± 0.0110
qsar	4	0.7735 ± 0.0498	0.7574 ± 0.0405	0.7308 ± 0.0306
spambase	16	0.8904 ± 0.0319	0.8798 ± 0.0222	0.8561 ± 0.0478
magic	2	0.7246 ± 0.0336	0.7298 ± 0.0344	0.7553 ± 0.0375

,

Table 9. Mean classification accuracy (± standard deviation) with Random Forest after feature selection using CONMI_FS, MIFS-ND and Corr-mRMR. The “# Features” column indicates the subset size $k^{★}$ given by the CONMI_FS stopping criterion and applied to all methods. Bold values denote the highest accuracy for each dataset.

Dataset	# Features	CONMI_FS	MIFS-ND	Corr-mRMR
bankrupt	4	0.9561 ± 0.0088	0.9570 ± 0.0107	0.9491 ± 0.0140
qsar	4	0.7838 ± 0.0345	0.8179 ± 0.0307	0.7536 ± 0.0154
spambase	16	0.9246 ± 0.0242	0.9193 ± 0.0303	0.9053 ± 0.0280
magic	2	0.7570 ± 0.0328	0.7509 ± 0.0356	0.8070 ± 0.0423

and

Table 10. Mean classification accuracy (± standard deviation) with K-nearest neighbors after feature selection using CONMI_FS, MIFS-ND and Corr-mRMR. The “# Features” column indicates the subset size $k^{★}$ given by the CONMI_FS stopping criterion and applied to all methods. Bold values denote the highest accuracy for each dataset.

Dataset	# Features	CONMI_FS	MIFS-ND	Corr-mRMR
bankrupt	4	0.9526 ± 0.0080	0.9561 ± 0.0141	0.9570 ± 0.0121
qsar	4	0.8218 ± 0.0340	0.8113 ± 0.0366	0.7612 ± 0.0232
spambase	16	0.8912 ± 0.0252	0.8886 ± 0.0340	0.8711 ± 0.0311
magic	2	0.7667 ± 0.0329	0.7667 ± 0.0329	0.8500 ± 0.0397

. For each dataset, the mean accuracy and standard deviation are reported, with the highest value in each row highlighted in bold.

Only four out of the seven datasets examined in the case study are reported here. In the remaining three datasets (kc1, pc1 and credit), the stopping criterion of CONMI_FS halted the feature selection process when the subset contained a single feature. In these cases, all three methods selected the same feature, resulting in identical classification performance. Therefore, the corresponding results are omitted for brevity.

The results in Table 7 present the classification performance of CONMI_FS, MIFS-ND, and Corr-mRMR when combined with Logistic Regression. Among the four datasets considered, Corr-mRMR achieved the highest accuracy in two cases (bankrupt and magic), CONMI_FS in two cases (qsar and spambase), while MIFS-ND did not achieve the highest accuracy in any dataset.

In bankrupt, Corr-mRMR obtained an accuracy of 0.9640, slightly higher than MIFS-ND (0.9588) and CONMI_FS (0.9509). In magic, Corr-mRMR again outperformed the other two methods, achieving 0.7991 compared with 0.7658 for both CONMI_FS and MIFS-ND. In qsar, CONMI_FS led with 0.8113, marginally surpassing MIFS-ND (0.8076) and showing a clearer advantage over Corr-mRMR (0.7754). For spambase, all three methods achieved relatively high performance, with CONMI_FS obtaining the highest accuracy (0.9123), exceeding MIFS-ND (0.9088) by 0.0035 and Corr-mRMR (0.8807) by 0.0316.

The results in Table 8 show the classification performance of CONMI_FS, MIFS-ND and Corr-mRMR when combined with a Decision Tree classifier. Compared with the Logistic Regression results, the differences between methods are generally smaller, with relatively close performance across all datasets.

CONMI_FS achieved the highest accuracy in three out of the four datasets (bankrupt, qsar and spambase), while Corr-mRMR led in one case (magic). In bankrupt, CONMI_FS obtained 0.9456, exceeding MIFS-ND (0.9421) by 0.0035 and Corr-mRMR (0.9316) by 0.0140. In qsar, CONMI_FS reached 0.7735, which was 0.0161 higher than MIFS-ND and 0.0427 higher than Corr-mRMR. In spambase, CONMI_FS scored 0.8904, ahead of MIFS-ND (0.8798) and Corr-mRMR (0.8561). The magic dataset was the only case where Corr-mRMR achieved the highest performance (0.7553), outperforming CONMI_FS (0.7246) by 0.0307 and MIFS-ND (0.7298) by 0.0255.

The results in Table 9 show the classification performance of CONMI_FS, MIFS-ND and Corr-mRMR when combined with a Random Forest classifier. In bankrupt, all three methods achieved very similar performance, with MIFS-ND obtaining the highest accuracy (0.9570), marginally surpassing CONMI_FS (0.9561) by 0.0009 and Corr-mRMR (0.9491) by 0.0079.A similar pattern was observed in spambase, where Corr-mRMR reached 0.9053, compared with 0.9193 for MIFS-ND and 0.9246 for CONMI_FS. The maximum difference between methods in this dataset was 0.0193.

In contrast, more pronounced differences were observed in qsar and magic. In qsar, MIFS-ND achieved 0.8179, outperforming CONMI_FS (0.7838) by 0.0341 and Corr-mRMR (0.7536) by 0.0643. In magic, Corr-mRMR obtained the highest accuracy (0.8070), exceeding CONMI_FS (0.7570) by 0.0500 and MIFS-ND (0.7509) by 0.0561.

The results in Table 10 indicate that, for the K-nearest neighbors classifier, Corr-mRMR achieved the highest accuracy in two out of the four examined datasets (bankrupt and magic), while CONMI_FS led in the remaining two (qsar and spambase). In bankrupt, the differences among the three methods were minimal, with all accuracies within 0.005 of each other. Similarly, in spambase, CONMI_FS outperformed the other two methods by small margins, with deviations of less than 0.021. More pronounced differences occurred in qsar and magic. In qsar, CONMI_FS reached 0.8218, outperforming MIFS-ND and Corr-mRMR by 0.0105 and 0.0606, respectively. The magic dataset presented the most substantial difference observed across all experiments in this study, with Corr-mRMR achieving 0.8500 and surpassing both CONMI_FS and MIFS-ND (0.7667) by 0.0833.

Overall, no single feature selection method managed to achieve the highest accuracy across all classifiers and datasets. In some cases, the differences were minimal, such as in bankrupt, where depending on the classifier, each of the examined methods achieved the best performance. A similar pattern was observed in spambase, where CONMI_FS consistently achieved the highest accuracy, but with only small margins over the other methods. For qsar, the best-performing method varied between MIFS-ND and CONMI_FS depending on the classifier, while in magic, Corr-mRMR consistently produced the highest accuracy, with the largest observed margins in the study. These findings indicate that the proposed correction to the mutual information estimator enables Corr-MRMR to match or exceed the performance of other strong, well-established feature selection approaches.

4.2. Impact of the Corrected Mutual Information Estimator on CONMI_FS

In order to further evaluate the impact of the mutual information estimator on feature selection performance, we extended our analysis to the CONMI_FS algorithm. Given that CONMI_FS employs the same mutual information estimator as the one originally used in mRMR, this provided an opportunity to examine whether substituting it with the bias-corrected version would yield any notable changes in results. In CONMI_FS, the data discretization process is performed prior to feature selection because the normalized mutual information in the integration requires a discrete data format. Specifically, the Equal-Width discretization method is used to divide each continuous feature into equal intervals, as described in the original study.

Although CONMI_FS integrates Pearson’s correlation coefficient with mutual information in its criterion, which may limit the influence of the mutual information estimator, we considered it relevant to assess whether the corrected estimator could still have a measurable effect. For this comparison, we evaluated the original CONMI_FS alongside a variant (CONMI_Cormut) in which the corrected estimator of mutual information was applied, using the same datasets as in the previous experiments. In this case, however, both methods were allowed to operate with their intrinsic stopping criteria, determining the number of selected features independently. Since the CONMI_FS scoring formula subtracts redundancy from relevance and relies on normalized rather than unnormalized mutual information, the expected impact of estimation bias is somewhat smaller than in the mRMR setting.

Table 11. Random Forest classification accuracy (mean ± std) and number of selected features for each dataset. For each method, the feature count is shown in the column immediately preceding its accuracy column: the first pair corresponds to CONMI_FS and the second to its corrected variant (CONMI_Cormut). Bold values indicate the highest accuracy for each dataset.

Dataset	# Features	CONMI_FS	# Features	CONMI_Cormut
bankrupt	4	0.9561 ± 0.0088	9	0.9579 ± 0.0146
qsar	4	0.7838 ± 0.0345	6	0.7678 ± 0.0389
spambase	16	0.9246 ± 0.0242	23	0.9219 ± 0.0273
magic	2	0.7570 ± 0.0328	2	0.7614 ± 0.0400
kc1	1	0.8289 ± 0.0189	1	0.8518 ± 0.0164
pc1	1	0.8886 ± 0.0251	1	0.8860 ± 0.0248
credit	1	0.8184 ± 0.0226	6	0.8053 ± 0.0265

summarises, for each dataset, the number of features selected by CONMI_FS and CONMI_Cormut, together with the corresponding classification accuracy obtained using the Random Forest classifier.

The results in Table 11 indicate that the bias-corrected variant of CONMI_FS achieved higher accuracy in bankrupt, magic and kc1, with the largest improvement observed for kc1 despite both methods selecting a single feature. In contrast, the original method performed better in qsar, spambase, pc1 and credit, with the largest difference occurring in credit, where CONMI_Cormut selected six features compared to a single feature for CONMI_FS.

Differences in the number of selected features varied considerably across datasets. For example, in bankrupt and spambase the CONMI_Cormut selected more than twice as many features as the CONMI_FS, without a proportional accuracy gain, whereas in magic and kc1 the subset size was identical between methods, suggesting that the observed accuracy differences in these cases were most likely attributable to the estimator change.

As noted earlier, the smaller influence of mutual information in the CONMI_FS formulation resulting from the use of normalized mutual information, its combination with Pearson correlation and the subtraction of redundancy from relevance, reduces the expected effect of replacing the estimator. The present results are consistent with this expectation, while also illustrating that such modifications can still yield measurable changes in certain scenarios.

Since CONMI_FS also relies primarily on the same mutual information estimator used in our mRMR variants, we found it worthwhile to investigate whether the bias-corrected version could lead to different outcomes in this context. This additional analysis was intended not only to assess its effect here, but also to encourage further examination of such adjustments in other feature selection methods, where the impact might be more pronounced.

5. Discussion

The primary objective of this study was not to identify the most accurate version of the mRMR algorithm, but rather to investigate how the choice of mutual information estimator affects the performance of this widely used feature selection method. To this end, we evaluated five mRMR variations, based on two different estimators (a discretization-based estimator and a Parzen KDE-based estimator), with or without a denominator correction ($s=0$ or $s=1$), as well as a corrected mutual information version (Corr-mRMR), across both synthetic and real data.

Although the original mutual information estimator used in this study is not considered optimal compared to certain non-parametric alternatives such as k-nearest neighbors or B-spline-based approaches (see Introduction, Section 1), it was chosen due to observed biases in prior work and the existence of a proposed correction. The corrected estimator was integrated into the mRMR framework to evaluate whether mitigating this bias improves selection outcomes.

Overall, the results from the simulation study indicate that the correction has a clear positive effect, especially in more complex systems involving nonlinear dependencies or redundant features. In simpler systems, where the functionally related features were strongly or moderately correlated with the class variable, all methods achieved near-perfect performance. These results were also supported by the use of a slightly modified mRMR formulation (Equation (2)) that places more emphasis on relevance than redundancy (see Section 2.4).

For systems such as System 3, we deliberately set the size of the optimal feature subset to include all functionally related features—despite the fact that only two were sufficient to capture the underlying information—so as to test whether the methods would prioritize redundant-but-relevant features over completely irrelevant ones. This decision aligns with practical use cases, where the user predefines the number of features, and thus selection behavior, in such important contexts.

An interesting observation is that the Parzen-based variants performed consistently well across all systems, even in the presence of redundancy and nonlinearity. This suggests that density-based mutual information estimation may offer improved robustness over discretization-based techniques, particularly in more realistic data scenarios. Corr-mRMR, which employs the corrected estimator and $s=1$ in the denominator, approached the performance of the Parzen-based methods in most cases—often surpassing both the uncorrected versions ($s=0$ and $s=1$) and offering a strong compromise between computational simplicity and selection accuracy.

It also should be noted that during simulations with the aforementioned setup, for systems where some of the predictors were weakly correlated to the class variable e.g., $y=0.8f_1+0.3f_2$, but also when the coefficients of the functionally related features did not all have the same signs and their sum tended to zero, the simple mRMR appeared to be more accurate compared to the corrected one.

In addition to these observations, it should also be noted that the corrected estimator is substantially slower than the original discretization-based version, since it requires computing the mutual information once on the original data and repeatedly (in our case 100 times) on surrogate datasets. This leads to a significantly higher runtime compared to the original method. However, the main aim of this study was not to propose the fastest estimator, but rather to highlight how even a small correction to the mutual information estimation process can lead to markedly different outcomes in mRMR. Therefore, the computational overhead of the corrected estimator should be viewed as secondary to the conceptual point being made.

In addition to the effect of sample size, which was discussed in Section 2.3.2, dimensionality is another important factor that may influence the performance of mutual information estimators. In very high-dimensional feature spaces, sparsity can reduce the reliability of probability estimates, potentially affecting the stability of mRMR outcomes. A more systematic investigation of this aspect could be pursued in future work.

Finally, the results from the case study further support the simulation findings, showing that the mRMR variant employing the corrected mutual information estimator consistently provided competitive and often superior classification performance across diverse real-world datasets. While Parzen-based and Original-mRMR methods also performed strongly, the corrected-estimator variant (Corr-mRMR) frequently achieved the highest accuracies, particularly in datasets such as qsar and spambase, where the gains were substantial. These results reinforce the conclusion that the choice of mutual information estimator, and even relatively small adjustments to its formulation, can have a measurable impact on feature selection outcomes, especially in scenarios involving complex feature dependencies.

From a practical perspective, the findings of this study highlight that the choice of mutual information estimator can substantially influence the outcome of mRMR-based feature selection, even when all other parameters are kept constant. It is therefore important to consider not only the feature selection framework itself but also the underlying estimator used to quantify dependencies.

Overall, the results suggest that aligning the choice of estimator with the characteristics of the dataset and the resource constraints of the task can lead to more effective and reliable feature selection in practice.

6. Conclusions

This study investigated the impact of a mutual information estimator choice on the performance of the mRMR feature selection algorithm. Specifically, we evaluated five variants: two using a discretization-based mutual information estimator (with and without a regularization constant in the denominator), two based on a Parzen window approach and one employing a bias-corrected discretization-based mutual information estimator.

The evaluation included both synthetic systems, ranging from simple linear structures to more complex nonlinear and redundant systems and real-world classification tasks. The results revealed that the choice of mutual information estimator can substantially affect feature selection outcomes, particularly in settings with nonlinear dependencies or feature redundancy. In such cases, the examined Parzen-based and bias-corrected estimators demonstrated clear advantages over the original discretization-based version.

The results also highlight the importance of carefully tuning the redundancy term in mRMR’s denominator. Although switching from $s=0$ to $s=1$ often led to more stable outcomes, the effect was not uniform across all scenarios.

It is also emphasized how crucial it is to select the appropriate settings based on the requirements of each problem, because different setups yield dramatically different results.

Further research would involve a comparison between state-of-the-art mutual information estimators in several systems and setups in order to clarify which one is considered as the most appropriate in different problems.