Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem
Abstract
1. Introduction
- Development of dedicated combinatorial operators: We design adaptive operators for permutation-based optimization, capable of reacting to stochastic changes in travel conditions and road gradients.
- Integration into an adaptive metaheuristic framework: The proposed operators are embedded into the OCO metaheuristic, enabling efficient and scalable dynamic optimization.
- Rigorous empirical validation: Through dynamic benchmarks, real-world case studies, and comprehensive statistical testing, we demonstrate the superiority of our method over GA, PSO, GWO, and ACO.
- Formulation of the DG-TSP: We formalize a novel problem definition that integrates dynamic service conditions and environmental sustainability into the classical TSP model.
2. Green Logistics
- Mathematical Formulation of the Green Traveling Salesman Problem (Green TSP):For completeness and consistency with the classical mathematical literature on the TSP, we also provide the standard integer programming formulation.Let a complete graph , where
- -
- denotes the set of cities (with 1 as the start/return city);
- -
- E denotes the set of arcs between the cities.
The parameters and decision variables are defined as follows:- -
- : Environmental cost (e.g., CO2 consumption) associated with traveling from city i to city j;
- -
- : Binary variable equal to 1 if the tour travels from i to j, and 0 otherwise;
- -
- : Auxiliary variable used to eliminate subtours (Miller–Tucker–Zemlin formulation).
- Objective function:
- Constraints:
- Variable domains:
- Principle of the MTZ Method:In the TSP, the objective is to find a tour that visits each city exactly once and returns to the starting point. However, some solutions that satisfy degree constraints may contain subtours, i.e., smaller cycles not covering all cities. These are invalid for the TSP. The Miller–Tucker–Zemlin (MTZ) method is a classical technique for eliminating such subtours in integer linear programming formulations. An auxiliary continuous variable is introduced for each city (excluding city 0, the depot). This variable estimates the visit order of city i in the tour. Linear constraints are then imposed to enforce a logical progression in the tour, thereby preventing subtours. Let
- -
- be a binary variable indicating whether arc is used;
- -
- be the order of visiting city i.
- -
- If , the constraint becomes , hence : city j is visited after i.
- -
- If , the constraint is trivially satisfied: always holds.
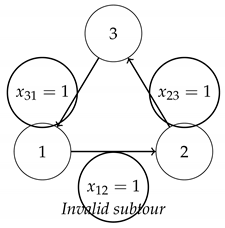
This ensures a consistent visit order among cities and prevents the formation of closed cycles (subtours) among subsets of cities. - Illustration of a forbidden subtour:In this subtour, cities 1, 2, and 3 form a closed cycle without visiting all cities (e.g., city 0 is excluded). The MTZ constraints prevent such configurations, as they would imply , which is contradictory.
3. Dynamic Green Logistics
- Dynamic Green TSP (DG-TSP) with Traffic FactorsIn this paper, we generate Dynamic Green TSPs (DG-TSPs) by incorporating the traffic factor, which directly affects CO2 emissions. We assume that the cost of the link between cities i and j is given by , where represents the normal travel distance and denotes the traffic factor. Every f iteration of running an algorithm, a random number is generated to simulate potential traffic congestion, where and are the lower and upper bounds of the traffic factor , respectively, [29]. It is needless to say that traffic congestion significantly exacerbates air pollution.Each link between cities i and j has a probability m of being affected by traffic, wherein a distinct R value is generated to represent low, normal, or high levels of traffic congestion on different roads. Meanwhile, the remaining links are assigned , indicating an absence of traffic.For instance, high-traffic roads are generated by assigning a higher probability to R values closer to , whereas low-traffic roads are generated with a higher probability of assigning R values closer to . This class of DG-TSP is referred to as random DG-TSP in this paper, since previously visited environments are not guaranteed to reappear [30].
- Cyclic Dynamic Green TSPAnother variation of the DG-TSP with traffic factors is the Cyclic DG-TSP, in which dynamic changes follow a cyclic pattern. In other words, previous environments are guaranteed to reoccur in the future. Such environments are more realistic than purely random ones, as they can, for instance, model the 24-h traffic dynamics of a typical day [31].A cyclic environment can be constructed by generating different dynamic scenarios with traffic factors as the base states, representing DG-TSP environments with low, normal, or high levels of traffic. The environment then transitions cyclically among these base states in a fixed logical sequence. Depending on the time of day, environments with varying traffic conditions can be generated. For example, during rush hours or on roads with steep slopes, there is a higher probability of generating R values closer to , whereas during off-peak evening hours, a higher probability is assigned to R values closer to .
3.1. Formulation of the DTSP
- denotes the optimization problem;
- is the search space at time t;
- is the set of constraints at time t;
- is the objective function at time t, which assigns an objective value to each solution , with all components being time-dependent;
- T is the set of time values.
- Definitions and Notations:Let a dynamic graph be defined as for each time step where H is the time horizon.
- -
- : Set of available cities at time t;
- -
- : Set of valid arcs at time t;
- -
- : Equal to 1 if the route from city i to j is taken at time t;
- -
- : Ecological cost (e.g., CO2 emissions, energy) for the route at time t;
- -
- : Distance or travel time between i and j at time t;
- -
- : Equal to 1 if city i is available at time t, 0 otherwise;
- -
- : Position of city i in the tour (for subtour elimination);
- -
- : Total number of cities to be visited (fixed).
- Objective Function:Minimize the cumulative environmental cost (CO2 emissions) of the dynamic tour:
- Constraints:
- Each city is visited exactly once over the horizon:
- Temporal availability of cities and routes:
- Subtour elimination (MTZ formulation)
- Departure from and return to the initial city (city 0):
- Domain of the decision variables:
- Remarks:
- -
- The graph may evolve over time: certain cities may become available or unavailable, and the costs may vary.
- -
- The cost incorporates CO2 emissions.
- -
- This model can be used in real-time or predictive environments (smart logistics, electric vehicles, etc.).
3.2. Integrating Real-World Constraints into DG-TSP for Green Logistics
- Time-dependent service requests: These add a layer of complexity because the problem needs to adapt in real time. Research has explored ways to handle this uncertainty, using methods like scenario-based planning and reinforcement learning [32]. The focus is on creating algorithms that can efficiently manage these changing requests.
- Slopes with different inclinations: Factoring in actual road conditions is essential for accurately estimating fuel consumption. Studies show that using detailed road gradient data can significantly improve fuel consumption and overall efficiency [33].
- Fuel consumption optimization: This is a core aspect of making logistics sustainable. Studies demonstrate that incorporating fuel consumption models into routing algorithms can lead to major reductions in greenhouse gas emissions [34]. Smart technologies also play a role in optimizing routes to lower costs and environmental impact [34].
- Sustainable logistics and smart technologies: Using smart technologies in logistics is becoming increasingly common for sustainability. This includes decision support systems and key performance indicators that rely on data to optimize operations. Digital twin technology can also make public transport systems more efficient through simulations and real-time insights.
4. Open Competency Optimization
- Each student formulates their unique educational trajectory predicated upon their specific skill sets;
- Each student engaged in the learning process collaborates with the most immediate cohort, whether this is defined by geographical closeness or intellectual competencies. It is important to highlight that the size of this group is limited to a maximum of five participants;
- Students have the opportunity to interact with each other via deliberations or by embracing advanced recommendations (i.e., optimal resolutions) from their colleagues.

| Algorithm 1 OCO algorithm: principal steps |
|
- Algorithm 3 generates solutions through a neighborhood-based approach leveraging local information for guided exploration.
- Algorithm 4 constructs solutions randomly to enhance exploration capabilities.
4.1. Self-Learning
| Algorithm 2 Self-learning conditions |
|
4.2. Neighbor Learner Groups
| Algorithm 3 Strategy for the student group within a limited neighborhood |
|
| Algorithm 4 Strategy of the randomly chosen learner group |
|
4.3. Leadership Interaction
- Each student assimilates or responds to the concept of optimality. Either the optimal solution is retained or alternative avenues for the optimal solution are exploited. The competency-based paradigm is inadequately encapsulated by the notion of the middle class. Within conventional educational frameworks, students are predominantly influenced by their peers who perform at an average level. Those who excel or struggle significantly are often excluded from the benefits of such pedagogical methodologies. The entirety of learning within this paradigm tends to prioritize certain means while disregarding alternative approaches. To mitigate this predicament, each student engages with the average in accordance with their individual capabilities, as they cultivate their own competencies. This dynamic enhances the exploratory essence of the algorithm, and consequently, facilitates the enrichment of diverse ideas (solutions to the problem).
5. Operators for the TSP
5.1. Addition ⊕
- = [1, 2, 3, 4, 5, 6, 7, 8]
- = [4, 3, 2, 1, 6, 7, 8, 5]
5.2. Multiplication ⊗
- = [1, 2, 3, 4, 5, 6, 7, 8]
- = [5, 6, 7, 8, 1, 2, 3, 4]
- [1, 6, 3, 4, 5, 2, 7, 8]
- [5, 2, 7, 8, 1, 6, 3, 4]
5.3. Subtraction ⊖
- = [1, 2, 3, 4, 5, 6, 7, 8]
- = [5, 6, 7, 8, 1, 2, 3, 4] reverse() = [4, 3, 2, 1, 8, 7, 6, 5]
- = reverse() = [1, 3, 2, 4, 5, 7, 6, 8]
5.4. Scalar Multiplication ⊙
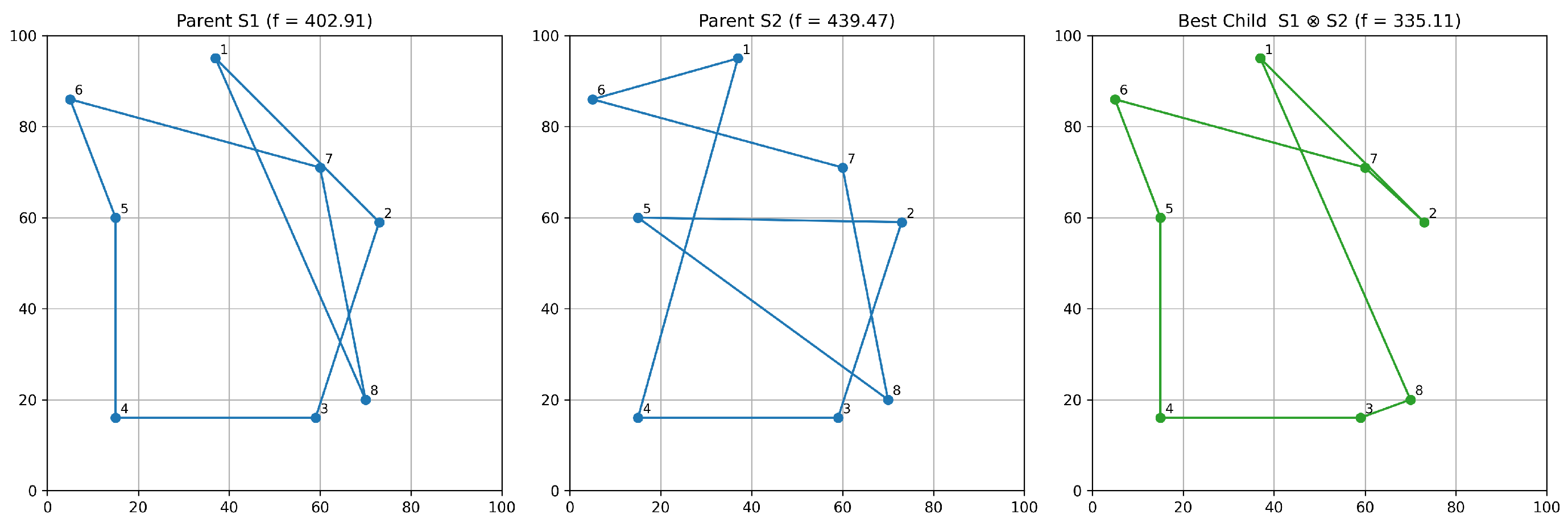
- Initially, the scalar undergoes an initial transformation via one of the nine predefined transformation functions proposed in this study, converting it into an integer value within the set , where N denotes the population size. Following this conversion, the population is systematically ranked based on the fitness function. The swap mutation operator selects two random positions within the solution and exchanges their elements. This simple yet effective operation helps to maintain the permutation structure of the solution, which is crucial for routing problems. For example, if the solution is [1, 3, 2, 4], swapping positions 2 and 3 results in [1, 2, 3, 4].A swap mutation is then applied to the tour , where denotes the index of the solution within the population. The outcome of this mutation is a tour, which we shall designate as (). Subsequently, we apply the multiplication operation, as defined in this study, with ().
- Additionally, a heuristic mutation is applied. This mutation employs a problem-specific improvement strategy, such as 2-opt, to refine the tour further and enhance its quality.
- = [1, 2, 3, 4, 5, 6, 7, 8]
- k = 0.25
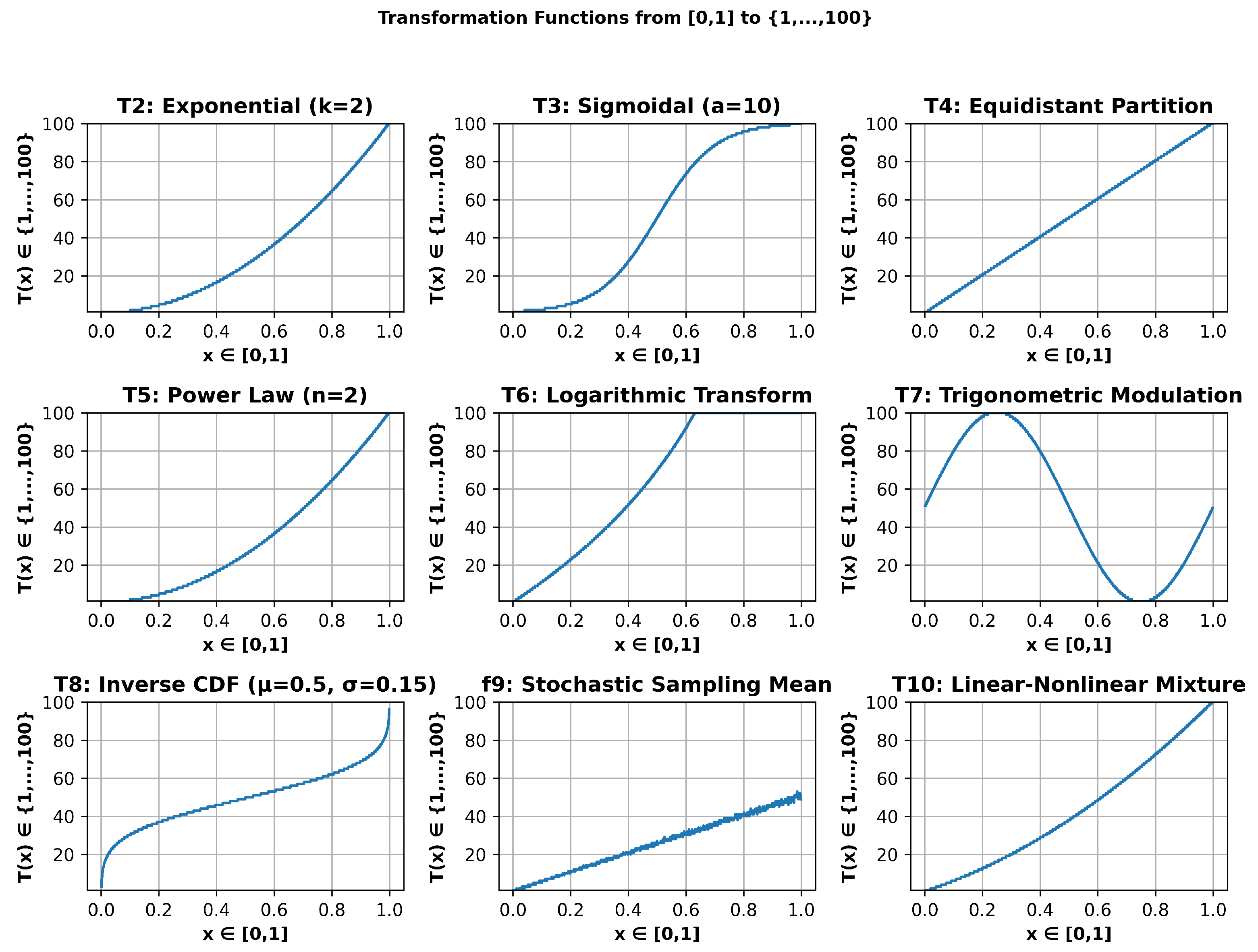
- Exponential transformation (parametric control):For , smaller integers are favored (with an enhanced threshold effect).
- Sigmoidal function (central concentration):Parameter a controls the transition slope (typically ).
- Equidistant partition (indicator function):Exact implementation of a discrete uniform CDF.
- Power law (controlled bias):For , .
- Logarithmic transform (long tail):Requires special handling of (to avoid ).
- Trigonometric modulation (periodicity):Produces a bimodal distribution (favors extreme values).
- CDF inverse (distributional adaptation):Allows the imposition of any arbitrary discrete distribution.
- Stochastic method (secondary randomization):Introduces additional variance controlled by x.
- Linear–nonlinear mixture (compromise):Interpolation between linear (x) and quadratic () behaviors.
- For all functions , we have and , except
- -
- (logarithmic transform) requires to avoid the divergence of at ;
- -
- (trigonometric modulation) reaches its maximum value (101) at and , but not at ;
- -
- (stochastic method) requires to ensure the upper bound of the uniform distribution is at least 1.
- All functions are piecewise continuous except for (equidistant partition), which is purely discrete.
- Functions (uniform partition) and (CDF inverse) preserve important theoretical properties:
- -
- ensures fairness via uniform discretization;
- -
- is inherently invertible if the target CDF is strictly increasing.
- Functions (exponential), (power law), and (linear–quadratic mixture) allow the explicit parametric control or structural modulation of the output distribution.
- is the only non-deterministic transformation, introducing randomness via a uniform integer sampling based on x.
- All functions require explicit boundary treatment to ensure well-defined behavior over the domain .
5.5. Rationale and Advantages
- Feasibility preservation: Each operator ensures that the resulting tours remain valid permutations of cities, avoiding infeasible solutions;
- Diversity promotion: The integration of crossover and mutation mechanisms enhances exploration of the search space;
- Heuristic integration: The inclusion of heuristic mutation in scalar multiplication balances exploration and exploitation, thereby improving solution quality;
- Scalability: The modular design of the operators allows for adaptation to other combinatorial problems beyond TSP.
6. Experimental Studies
6.1. Comparison with Other Metaheuristics
- Tour Length Performance:OCO consistently achieves superior performance with lower distances, maintaining stability even under high dynamics (e.g., magnitude = 0.75; frequency = 100; OCO = 26,786 vs. RI-GA = 64,870, as shown in Table 8).
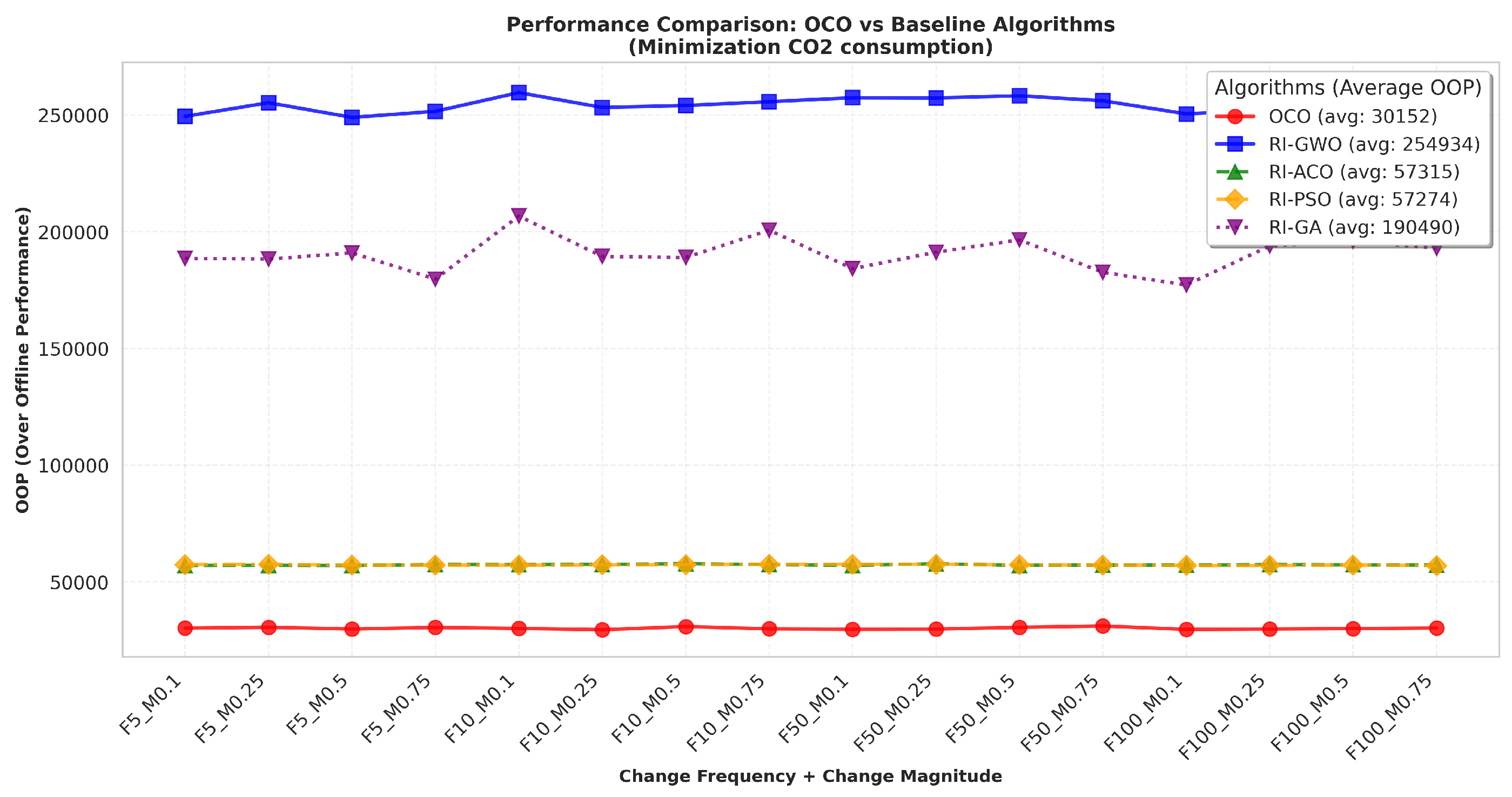
- Overall offline performance (OOP):For instance, at a change magnitude of 0.1, OCO achieves a tour length of 29,347 and an OOP of 29,654.7, significantly better than those of RI-GWO (OOP: 250,479.01), RI-ACO (OOP: 57,187.85), RI-PSO (OOP: 57,009.21), and RI-GA (OOP: 177,192.2) as shown in Table 12. This trend remains stable across increasing dynamic intensities, highlighting OCO’s robustness and adaptability to dynamic environments with both low and high degrees of change.
- Computational efficiency (expressed in seconds):With respect to computational time, OCO incurs a higher computational cost than RI-ACO, RI-PSO, and RI-GA, yet remains substantially more efficient than RI-GWO. For example, at a change magnitude of 0.5, OCO’s execution time is approximately 333 s, whereas RI-GWO requires over 3000 s. While RI-ACO, RI-PSO, and RI-GA achieve faster runtimes (between 9 and 35 s), these are accompanied by significantly poorer solution quality in both tour length and OOP metrics.This trade-off suggests that OCO achieves a superior balance between dynamic performance and computational efficiency, making it particularly suitable for scenarios where solution accuracy and adaptability to environmental changes are critical, such as in green and sustainable logistics contexts.
- OCO achieves superior performance (OOP = 30,152), outperforming all baseline methods;
- RI-GWO shows the weakest results (OOP = 254,934);
- RI-ACO and RI-PSO demonstrate intermediate performance (57,000);
- RI-GA performs better than RI-GWO but worse than OCO (OOP = 190,490).
- Superiority of OCO: The algorithm demonstrates remarkable efficiency, achieving an 88% reduction in offline performance (OOP) compared to RI-GWO (30,152 vs. 254,934) and an 84% improvement over RI-GA. This significant margin suggests OCO’s enhanced capability to handle dynamic optimization constraints.
- Intermediate Performers: RI-ACO and RI-PSO show comparable results, both being approximately 47% less efficient than OCO. Their similar performance profiles (57,000 OOP) indicate comparable limitations in adapting to environmental changes.
- Relative underperformance: The substantial gap between OCO and RI-GWO (254,934 OOP) highlights fundamental limitations in the latter’s exploration–exploitation balance, particularly when addressing CO2 minimization in dynamic scenarios.
- Dynamic parameter adaptation;
- Robustness against environmental variability;
- Sustainable optimization capability.
- OCO’s adaptive learning mechanism effectively handles dynamic environmental changes;
- Traditional metaheuristics (RI-GWO, RI-GA) struggle with frequency and magnitude changes;
- Population-based methods (RI-ACO, RI-PSO) show moderate adaptability.
6.2. Statistical Tests
6.2.1. Wilcoxon Signed-Rank Test
- : The two algorithms have equivalent performance distributions (median of differences is zero).
- : The performance distributions differ significantly (median of differences is non-zero).
6.2.2. Friedman Test
6.2.3. Nemenyi Post Hoc Test
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Osaba, E.; Yang, X.S.; Del Ser, J. Traveling salesman problem: A perspective review of recent research and new results with bio-inspired metaheuristics. In Nature-Inspired Computation and Swarm Intelligence; Elsevier: Amsterdam, The Netherlands, 2020; pp. 135–164. [Google Scholar]
- Gao, W.; Luo, Z.; Shen, H. A branch-and-price-and-cut algorithm for time-dependent pollution routing problem. Transp. Res. Part C Emerg. Technol. 2023, 156, 104339. [Google Scholar] [CrossRef]
- Ben Jelloun, R.; Jebari, K.; El Moujahid, A. Open Competency Optimization: A Human-Inspired Optimizer for the Dynamic Vehicle-Routing Problem. Algorithms 2024, 17, 449. [Google Scholar] [CrossRef]
- Nicoletti, B.; Appolloni, A. Green Logistics 5.0: A review of sustainability-oriented innovation with foundation models in logistics. Eur. J. Innov. Manag. 2024, 27, 542–561. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, S.; Zhen, L.; Laporte, G. Integrating operations research into green logistics: A review. Front. Eng. Manag. 2023, 10, 517–533. [Google Scholar] [CrossRef]
- Blanco, E.E.; Sheffi, Y. Green logistics. In Sustainable Supply Chains: A Research-Based Textbook on Operations and Strategy; Springer: Berlin/Heidelberg, Germany, 2024; pp. 101–141. [Google Scholar]
- Zhang, M.; Sun, M.; Bi, D.; Liu, T. Green logistics development decision-making: Factor identification and hierarchical framework construction. IEEE Access 2020, 8, 127897–127912. [Google Scholar] [CrossRef]
- Greco, F. Travelling Salesman Problem; In-teh: London, UK, 2002; pp. 75–115. [Google Scholar]
- Halim, A.H.; Ismail, I. Combinatorial optimization: Comparison of heuristic algorithms in travelling salesman problem. Arch. Comput. Methods Eng. 2019, 26, 367–380. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K.; Demir, E.; Benyettou, A. The green vehicle routing problem: A systematic literature review. J. Clean. Prod. 2021, 279, 123691. [Google Scholar] [CrossRef]
- Küçükoğlu, İ.; Ene, S.; Aksoy, A.; Öztürk, N. A memory structure adapted simulated annealing algorithm for a green vehicle routing problem. Environ. Sci. Pollut. Res. 2015, 22, 3279–3297. [Google Scholar] [CrossRef]
- Úbeda, S.; Faulin, J.; Serrano, A.; Arcelus, F.J. Solving the green capacitated vehicle routing problem using a tabu search algorithm. Lect. Notes Manag. Sci. 2014, 6, 141–149. [Google Scholar]
- Zhang, C.; Zhao, Y.; Leng, L. A hyper-heuristic algorithm for time-dependent green location routing problem with time windows. IEEE Access 2020, 8, 83092–83104. [Google Scholar] [CrossRef]
- Rodríguez-Esparza, E.; Masegosa, A.D.; Oliva, D.; Onieva, E. A new hyper-heuristic based on adaptive simulated annealing and reinforcement learning for the capacitated electric vehicle routing problem. Expert Syst. Appl. 2024, 252, 124197. [Google Scholar] [CrossRef]
- Zhang, S.; Gajpal, Y.; Appadoo, S. A meta-heuristic for capacitated green vehicle routing problem. Ann. Oper. Res. 2018, 269, 753–771. [Google Scholar] [CrossRef]
- Andelmin, J.; Bartolini, E. A multi-start local search heuristic for the green vehicle routing problem based on a multigraph reformulation. Comput. Oper. Res. 2019, 109, 43–63. [Google Scholar] [CrossRef]
- Zhao, W.; Bian, X.; Mei, X. An Adaptive Multi-Objective Genetic Algorithm for Solving Heterogeneous Green City Vehicle Routing Problem. Appl. Sci. 2024, 14, 6594. [Google Scholar] [CrossRef]
- Micale, R.; Marannano, G.; Giallanza, A.; Miglietta, P.; Agnusdei, G.; La Scalia, G. Sustainable vehicle routing based on firefly algorithm and TOPSIS methodology. Sustain. Futur. 2019, 1, 100001. [Google Scholar] [CrossRef]
- Bektaş, T.; Laporte, G. The pollution-routing problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Guntsch, M.; Middendorf, M.; Schmeck, H. An ant colony optimization approach to dynamic TSP. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, Málaga, Spain, 14–18 July 2025; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 2001; pp. 860–867. [Google Scholar]
- Guntsch, M.; Middendorf, M. Pheromone modification strategies for ant algorithms applied to dynamic TSP. In Proceedings of the Applications of Evolutionary Computing, Como, Italy, 18–20 April 2001; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Psaraftis, H.N. Dynamic vehicle routing: Status and prospects. Ann. Oper. Res. 1995, 61, 143–164. [Google Scholar] [CrossRef]
- Stodola, P.; Michenka, K.; Nohel, J.; Rybanskỳ, M. Hybrid algorithm based on ant colony optimization and simulated annealing applied to the dynamic traveling salesman problem. Entropy 2020, 22, 884. [Google Scholar] [CrossRef]
- Kang, L.; Zhou, A.; McKay, B.; Li, Y.; Kang, Z. Benchmarking algorithms for dynamic travelling salesman problems. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1286–1292. [Google Scholar]
- Younes, A.; Basir, O.; Calamai, P. Adaptive control of genetic parameters for dynamic combinatorial problems. In Metaheuristics: Progress in Complex Systems Optimization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 205–223. [Google Scholar]
- Mavrovouniotis, M.; Yang, S.; Yao, X. A benchmark generator for dynamic permutation-encoded problems. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Taormina, Italy, 1–5 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 508–517. [Google Scholar]
- Mavrovouniotis, M.; Yang, S. Ant algorithms with immigrants schemes for the dynamic vehicle routing problem. Inf. Sci. 2015, 294, 456–477. [Google Scholar] [CrossRef]
- Touzout, F.A.; Ladier, A.L.; Hadj-Hamou, K. An assign-and-route matheuristic for the time-dependent inventory routing problem. Eur. J. Oper. Res. 2022, 300, 1081–1097. [Google Scholar] [CrossRef]
- Asghari, M.; Mirzapour Al-e-hashem, S.M.J. Green vehicle routing problem: A state-of-the-art review. Int. J. Prod. Econ. 2021, 231, 107899. [Google Scholar] [CrossRef]
- Daşcıoğlu, B.G.; Yazgan, H.R. Dynamic green location and routing problem for service points. Int. J. Procure. Manag. 2020, 13, 112–133. [Google Scholar] [CrossRef]
- Gao, Z.; Xu, X.; Hu, Y.; Wang, H.; Zhou, C.; Zhang, H. Based on improved NSGA-II algorithm for solving time-dependent green vehicle routing problem of urban waste removal with the consideration of traffic congestion: A case study in China. Systems 2023, 11, 173. [Google Scholar] [CrossRef]
- Çimen, M.; Soysal, M. Time-dependent green vehicle routing problem with stochastic vehicle speeds: An approximate dynamic programming algorithm. Transp. Res. Part Transp. Environ. 2017, 54, 82–98. [Google Scholar] [CrossRef]
- Dündar, H.; Soysal, M.; Ömürgönülşen, M.; Kanellopoulos, A. A green dynamic TSP with detailed road gradient dependent fuel consumption estimation. Comput. Ind. Eng. 2022, 168, 108024. [Google Scholar] [CrossRef]
- Lu, Y.; Yuan, Y.; Yasenjiang, J.; Sitahong, A.; Chao, Y.; Wang, Y. An Optimized Method for Solving the Green Permutation Flow Shop Scheduling Problem Using a Combination of Deep Reinforcement Learning and Improved Genetic Algorithm. Mathematics 2025, 13, 545. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Tian, Z.; Sun, S.; Li, J.; Yang, J. A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem. Appl. Soft Comput. 2022, 127, 109339. [Google Scholar] [CrossRef]
- TSPLIB95. 2025. Available online: http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/ (accessed on 10 April 2025).
- Jin, Y.; Branke, J. Evolutionary optimization in uncertain environments-a survey. IEEE Trans. Evol. Comput. 2005, 9, 303–317. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]

| Algorithms | Change_Magnitude | Length | OOP | Computational_Time |
|---|---|---|---|---|
| OCO | 0.1 | 21,059 | 21,290.9 | 22.3921022415161 |
| RI-GWO | 0.1 | 21,949 | 122,881.04 | 127.165235280991 |
| RI-ACO | 0.1 | 32,994 | 36,957.6 | 8.11824822425842 |
| RI-PSO | 0.1 | 21,701 | 36,744.29 | 9.33303236961365 |
| RI-GA | 0.1 | 21,251 | 59,296.5 | 15.7245984077454 |
| OCO | 0.25 | 21,535 | 21,911.1 | 23.079371213913 |
| RI-GWO | 0.25 | 23,035 | 123,244.58 | 128.834784030914 |
| RI-ACO | 0.25 | 31,928 | 36,809.04 | 8.31470632553101 |
| RI-PSO | 0.25 | 23,224 | 37,126.01 | 9.31120896339417 |
| RI-GA | 0.25 | 20,802 | 60,145.1 | 17.3999660015106 |
| OCO | 0.5 | 20,492 | 20,775.9 | 25.1404733657837 |
| RI-GWO | 0.5 | 21,298 | 126,085.52 | 132.616602420807 |
| RI-ACO | 0.5 | 32,951 | 36,863.78 | 8.51267838478088 |
| RI-PSO | 0.5 | 23,116 | 36,728.87 | 9.72644925117493 |
| RI-GA | 0.5 | 21,795 | 54,423.2 | 16.6300027370453 |
| OCO | 0.75 | 20,677 | 20,677 | 24.9908838272095 |
| RI-GWO | 0.75 | 21,709 | 125,660.76 | 121.951491594315 |
| RI-ACO | 0.75 | 32,767 | 36,773.7 | 9.96449542045593 |
| RI-PSO | 0.75 | 21,595 | 37,064.6 | 10.0018041133881 |
| RI-GA | 0.75 | 21,853 | 57,858.2 | 12.9152412414551 |
| Algorithms | Change_Magnitude | Length | OOP | Computational_Time |
|---|---|---|---|---|
| OCO | 0.1 | 21,213 | 21,755.4 | 20.9276142120361 |
| RI-GWO | 0.1 | 22,415 | 123,082 | 141.25444483757 |
| RI-ACO | 0.1 | 32,642 | 36,868.92 | 8.4200701713562 |
| RI-PSO | 0.1 | 23,366 | 36,433.43 | 9.23282861709595 |
| RI-GA | 0.1 | 22,261 | 54,110.1 | 12.2368183135986 |
| OCO | 0.25 | 20,941 | 21,319.1 | 19.2564599514008 |
| RI-GWO | 0.25 | 22,445 | 121,673.9 | 135.933153390884 |
| RI-ACO | 0.25 | 32,025 | 37,099.71 | 8.23803329467773 |
| RI-PSO | 0.25 | 21,938 | 36,932.47 | 9.66085481643677 |
| RI-GA | 0.25 | 21,944 | 60,938.4 | 17.2285289764404 |
| OCO | 0.5 | 21,113 | 21,733.4 | 17.0954973697662 |
| RI-GWO | 0.5 | 22,685 | 124,461.43 | 125.362582683563 |
| RI-ACO | 0.5 | 32,468 | 37,053.77 | 8.51956224441528 |
| RI-PSO | 0.5 | 22,375 | 36,750.32 | 9.71863651275635 |
| RI-GA | 0.5 | 21,272 | 65,360 | 16.1961874961853 |
| OCO | 0.75 | 21,600 | 21,698.6 | 20.8990180492401 |
| RI-GWO | 0.75 | 22,810 | 122,989.42 | 128.998858451843 |
| RI-ACO | 0.75 | 31,587 | 37,074.31 | 8.57306122779846 |
| RI-PSO | 0.75 | 22,787 | 37,073.63 | 9.89743041992188 |
| RI-GA | 0.75 | 21,332 | 55,110 | 11.2393550872803 |
| Algorithms | Change_Magnitude | Length | OOP | Computational_Time |
|---|---|---|---|---|
| OCO | 0.1 | 21,381 | 21,719.8 | 13.9666087627411 |
| RI-GWO | 0.1 | 22,508 | 125,408.07 | 131.110047101975 |
| RI-ACO | 0.1 | 32,384 | 37,043.3 | 8.42682528495789 |
| RI-PSO | 0.1 | 22,703 | 36,992.84 | 9.46939182281494 |
| RI-GA | 0.1 | 22,297 | 57,462.1 | 13.7826321125031 |
| OCO | 0.25 | 21,123 | 21,356.2 | 21.1810195446014 |
| RI-GWO | 0.25 | 22,165 | 124,025.48 | 134.562022924423 |
| RI-ACO | 0.25 | 33,515 | 36,917.27 | 8.55448985099793 |
| RI-PSO | 0.25 | 22,197 | 37,195.98 | 10.2855339050293 |
| RI-GA | 0.25 | 21,237 | 59,372.9 | 11.4311144351959 |
| OCO | 0.5 | 20,996 | 21,833.3 | 24.4424633979797 |
| RI-GWO | 0.5 | 21,806 | 123,893.6 | 127.856323480606 |
| RI-ACO | 0.5 | 32,071 | 36,921.34 | 8.39604187011719 |
| RI-PSO | 0.5 | 23,580 | 36,845.21 | 10.1386339664459 |
| RI-GA | 0.5 | 20,826 | 60,281.1 | 13.3048303127289 |
| OCO | 0.75 | 21,498 | 21,900 | 25.3512442111969 |
| RI-GWO | 0.75 | 22,563 | 125,067.34 | 121.043132781982 |
| RI-ACO | 0.75 | 33,274 | 37,134.15 | 8.59075498580933 |
| RI-PSO | 0.75 | 21,980 | 36,792.84 | 9.66982936859131 |
| RI-GA | 0.75 | 21,072 | 51,068.4 | 12.845165014267 |
| Algorithms | Change_Magnitude | Length | OOP | Computational_Time |
|---|---|---|---|---|
| OCO | 0.1 | 21,432 | 21,640.4 | 24.6619594097138 |
| RI-GWO | 0.1 | 21,847 | 125,376.59 | 122.259998083115 |
| RI-ACO | 0.1 | 32,999 | 37,034.76 | 8.71673130989075 |
| RI-PSO | 0.1 | 22,890 | 36,705.15 | 9.7340042591095 |
| RI-GA | 0.1 | 21,204 | 58,763 | 15.9396677017212 |
| OCO | 0.25 | 20,933 | 21,222.7 | 18.1225333213806 |
| RI-GWO | 0.25 | 22,386 | 120,743.46 | 132.594746589661 |
| RI-ACO | 0.25 | 32,153 | 36,821.59 | 8.32460141181946 |
| RI-PSO | 0.25 | 22,932 | 37,105.08 | 9.6085958480835 |
| RI-GA | 0.25 | 20,694 | 56,726.3 | 13.8298809528351 |
| OCO | 0.5 | 20,738 | 21,019.8 | 21.4589228630066 |
| RI-GWO | 0.5 | 22,282 | 124,836.81 | 130.818113327026 |
| RI-ACO | 0.5 | 31,304 | 36,751.17 | 8.78234338760376 |
| RI-PSO | 0.5 | 21,863 | 36,829.68 | 10.0047512054443 |
| RI-GA | 0.5 | 20,917 | 61,604.2 | 14.5410196781158 |
| OCO | 0.75 | 20,827 | 21,206.8 | 23.4733896255493 |
| RI-GWO | 0.75 | 21,874 | 123,096.34 | 128.855330705643 |
| RI-ACO | 0.75 | 32,790 | 36,805.24 | 9.08334875106812 |
| RI-PSO | 0.75 | 22,173 | 36,951.24 | 10.3831281661987 |
| RI-GA | 0.75 | 21,746 | 58,370.4 | 24.3120296001434 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 27,514 | 27,537.4 | 97.709445476532 |
| RI-GWO | 0.1 | 27,691 | 192,926.74 | 808.249512910843 |
| RI-ACO | 0.1 | 44,471 | 48,827.62 | 14.8391666412354 |
| RI-PSO | 0.1 | 27,883 | 48,902.14 | 18.997878074646 |
| RI-GA | 0.1 | 51,134 | 115,868.41 | 24.0980129241943 |
| OCO | 0.25 | 27,539 | 28,145.8 | 100.827348232269 |
| RI-GWO | 0.25 | 28,224 | 198,925.63 | 761.52139878273 |
| RI-ACO | 0.25 | 44,691 | 49,477.85 | 15.3931782245636 |
| RI-PSO | 0.25 | 27,485 | 49,082 | 20.4046738147736 |
| RI-GA | 0.25 | 63,970 | 119,283.8 | 18.8867592811585 |
| OCO | 0.5 | 26,385 | 27,051 | 107.441903352737 |
| RI-GWO | 0.5 | 27,061 | 183,743.64 | 685.366256713867 |
| RI-ACO | 0.5 | 43,174 | 48,899.89 | 15.3056991100311 |
| RI-PSO | 0.5 | 29,019 | 49,057.83 | 18.8881287574768 |
| RI-GA | 0.5 | 66,929 | 125,583.8 | 21.7121329307556 |
| OCO | 0.75 | 27,079 | 27,404.5 | 123.916888237 |
| RI-GWO | 0.75 | 28,196 | 193,147.6 | 763.206788778305 |
| RI-ACO | 0.75 | 41,112 | 49,126.15 | 15.0603370666504 |
| RI-PSO | 0.75 | 27,187 | 49,133.53 | 20.5533874034882 |
| RI-GA | 0.75 | 64,776 | 122,469.6 | 48.262743473053 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 26,379 | 26,659.9 | 97.8753378391266 |
| RI-GWO | 0.1 | 27,858 | 193,429.5 | 714.04919552803 |
| RI-ACO | 0.1 | 44,118 | 48,824.16 | 14.9826173782349 |
| RI-PSO | 0.1 | 28,386 | 48,637.3 | 20.6628074645996 |
| RI-GA | 0.1 | 57,195 | 117,651 | 14.7551081180573 |
| OCO | 0.25 | 26,842 | 27,165.5 | 126.872204780579 |
| RI-GWO | 0.25 | 27,508 | 189,454.85 | 1025.27630829811 |
| RI-ACO | 0.25 | 44,301 | 48,997.67 | 17.3445875644684 |
| RI-PSO | 0.25 | 27,794 | 49,175.62 | 22.2102901935577 |
| RI-GA | 0.25 | 58,335 | 112,912.1 | 34.976592540741 |
| OCO | 0.5 | 26,542 | 26,662.7 | 134.05682182312 |
| RI-GWO | 0.5 | 27,838 | 190,610.73 | 1075.06168675423 |
| RI-ACO | 0.5 | 42,873 | 48,877.36 | 18.8859694004059 |
| RI-PSO | 0.5 | 28,643 | 49,179.19 | 22.0664458274841 |
| RI-GA | 0.5 | 79,180 | 124,260.7 | 46.1346783638001 |
| OCO | 0.75 | 27,818 | 27,818 | 152.461178541184 |
| RI-GWO | 0.75 | 28,778 | 190,314.64 | 884.227702140808 |
| RI-ACO | 0.75 | 43,797 | 49,108.45 | 18.1741693019867 |
| RI-PSO | 0.75 | 28,550 | 49,162.81 | 22.0895233154297 |
| RI-GA | 0.75 | 64,176 | 121,569.8 | 20.1959164142609 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 27,526 | 27,762 | 121.465321063995 |
| RI-GWO | 0.1 | 28,414 | 190,501.7 | 830.968395471573 |
| RI-ACO | 0.1 | 44,371 | 49,287.28 | 17.7421343326569 |
| RI-PSO | 0.1 | 28,011 | 48,972.69 | 21.2658190727234 |
| RI-GA | 0.1 | 54,251 | 122,030.8 | 38.3366434574127 |
| OCO | 0.25 | 26,849 | 27,048.1 | 160.889377355576 |
| RI-GWO | 0.25 | 27,152 | 187,012.87 | 852.514069080353 |
| RI-ACO | 0.25 | 42,296 | 49,089.16 | 17.8825562000275 |
| RI-PSO | 0.25 | 28,028 | 49,131.98 | 22.7740960121155 |
| RI-GA | 0.25 | 57,388 | 120,709.2 | 23.9269785881043 |
| OCO | 0.5 | 26,495 | 26,973.5 | 113.92518901825 |
| RI-GWO | 0.5 | 27,340 | 187,346.31 | 734.989396572113 |
| RI-ACO | 0.5 | 43,177 | 49,190.58 | 19.0754761695862 |
| RI-PSO | 0.5 | 29,017 | 49,260.82 | 24.9999492168427 |
| RI-GA | 0.5 | 51,720 | 125,504.5 | 12.8652136325836 |
| OCO | 0.75 | 26,691 | 27,890.9 | 124.87078166008 |
| RI-GWO | 0.75 | 27,430 | 187,354.89 | 872.875902891159 |
| RI-ACO | 0.75 | 44,236 | 49,154.95 | 17.7652485370636 |
| RI-PSO | 0.75 | 28,569 | 49,329.81 | 22.5915353298187 |
| RI-GA | 0.75 | 60,577 | 121,889.3 | 22.4923396110535 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 26,483 | 26,967.1 | 151.894057273865 |
| RI-GWO | 0.1 | 27,697 | 180,809.23 | 901.101784229279 |
| RI-ACO | 0.1 | 44,994 | 49,155.87 | 17.162840127945 |
| RI-PSO | 0.1 | 28,527 | 49,025.66 | 21.9899196624756 |
| RI-GA | 0.1 | 60,838 | 120,722 | 32.3962223529816 |
| OCO | 0.25 | 27,618 | 27,912.8 | 158.637745141983 |
| RI-GWO | 0.25 | 27,085 | 186,486.95 | 821.483963251114 |
| RI-ACO | 0.25 | 44,502 | 49,334.34 | 17.9162790775299 |
| RI-PSO | 0.25 | 28,052 | 49,130.45 | 22.5717957019806 |
| RI-GA | 0.25 | 68,551 | 136,928 | 33.0491642951965 |
| OCO | 0.5 | 26,634 | 26,822.1 | 106.701067209244 |
| RI-GWO | 0.5 | 27,528 | 188,537.37 | 842.777728319168 |
| RI-ACO | 0.5 | 44,130 | 49,125.67 | 17.9808030128479 |
| RI-PSO | 0.5 | 27,307 | 49,025.28 | 21.8809659481049 |
| RI-GA | 0.5 | 58,353 | 117,597.2 | 30.5044939517975 |
| OCO | 0.75 | 26,786 | 26,896.5 | 142.47221159935 |
| RI-GWO | 0.75 | 27,566 | 189,727.8 | 914.117618083954 |
| RI-ACO | 0.75 | 42,768 | 49,019.32 | 18.6860890388489 |
| RI-PSO | 0.75 | 28,928 | 49,119.65 | 21.5470142364502 |
| RI-GA | 0.75 | 64,870 | 127,442 | 27.0094890594482 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 29,944 | 30,206.1 | 359.626891613007 |
| RI-GWO | 0.1 | 30,594 | 249,415.27 | 2679.29984951019 |
| RI-ACO | 0.1 | 52,040 | 57,023.46 | 21.3514449596405 |
| RI-PSO | 0.1 | 31,233 | 57,408.64 | 29.1911859512329 |
| RI-GA | 0.1 | 127,401 | 188,598.4 | 20.3655452728272 |
| OCO | 0.25 | 30,348 | 30,588 | 297.62440609932 |
| RI-GWO | 0.25 | 30,245 | 255,258.47 | 2495.94751191139 |
| RI-ACO | 0.25 | 51,166 | 57,067.17 | 21.998370885849 |
| RI-PSO | 0.25 | 31,537 | 57,454.16 | 31.5070748329163 |
| RI-GA | 0.25 | 120,371 | 188,276.66 | 13.6076040267944 |
| OCO | 0.5 | 29,506 | 29,820.4 | 353.145201206207 |
| RI-GWO | 0.5 | 30,662 | 248,967.74 | 2924.53922724724 |
| RI-ACO | 0.5 | 51,043 | 56,992.95 | 21.9690067768097 |
| RI-PSO | 0.5 | 31,309 | 57,256.14 | 31.3970522880554 |
| RI-GA | 0.5 | 108,760 | 190,927.5 | 8.91393232345581 |
| OCO | 0.75 | 29,971 | 30,516.5 | 410.367824316025 |
| RI-GWO | 0.75 | 29,946 | 251,574.78 | 2558.51860165596 |
| RI-ACO | 0.75 | 52,456 | 57,456.91 | 22.2017307281494 |
| RI-PSO | 0.75 | 31,088 | 57,208.24 | 31.7390558719635 |
| RI-GA | 0.75 | 104,103 | 179,700.8 | 10.56822681427 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 29,713 | 30,080 | 319.550868988037 |
| RI-GWO | 0.1 | 30,343 | 259,596.23 | 2727.19788074493 |
| RI-ACO | 0.1 | 52,371 | 57,396.37 | 22.1682703495026 |
| RI-PSO | 0.1 | 31,336 | 57,121.05 | 33.6118106842041 |
| RI-GA | 0.1 | 147,503 | 206,709.31 | 40.0141541957855 |
| OCO | 0.25 | 29,328 | 29,523 | 362.919169902802 |
| RI-GWO | 0.25 | 30,347 | 253,222.11 | 2659.1444709301 |
| RI-ACO | 0.25 | 52,314 | 57,486.26 | 21.7984554767609 |
| RI-PSO | 0.25 | 32,082 | 57,334.82 | 29.6725142002106 |
| RI-GA | 0.25 | 120,751 | 189,406.3 | 8.541428565979 |
| OCO | 0.5 | 30,681 | 30,876 | 305.512933254242 |
| RI-GWO | 0.5 | 30,888 | 254,072.17 | 2496.83245229721 |
| RI-ACO | 0.5 | 53,070 | 57,826.88 | 22.5814046859741 |
| RI-PSO | 0.5 | 31,825 | 57,389.25 | 30.6847245693207 |
| RI-GA | 0.5 | 115,006 | 188,956.3 | 17.9437294006348 |
| OCO | 0.75 | 29,516 | 29,894.3 | 415.858951568604 |
| RI-GWO | 0.75 | 30,352 | 255,688.22 | 2832.66897535324 |
| RI-ACO | 0.75 | 50,243 | 57,443.92 | 22.2953035831451 |
| RI-PSO | 0.75 | 31,063 | 57,491.21 | 30.4808707237244 |
| RI-GA | 0.75 | 131,803 | 200,674.7 | 18.042248249054 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 29,210 | 29,729.5 | 451.447427988052 |
| RI-GWO | 0.1 | 30,854 | 257,405.18 | 2592.22149825096 |
| RI-ACO | 0.1 | 50,964 | 57,112.58 | 21.6153562068939 |
| RI-PSO | 0.1 | 30,811 | 57,450.28 | 32.6675596237183 |
| RI-GA | 0.1 | 104,405 | 184,189.1 | 19.2394804954529 |
| OCO | 0.25 | 29,042 | 29,800.8 | 415.193927288055 |
| RI-GWO | 0.25 | 31,585 | 257,293.01 | 2587.61305117607 |
| RI-ACO | 0.25 | 52,744 | 57,805.21 | 22.3461935520172 |
| RI-PSO | 0.25 | 31,216 | 57,549.1 | 30.3804461956024 |
| RI-GA | 0.25 | 118,791 | 191,227.6 | 10.8311760425568 |
| OCO | 0.5 | 30,159 | 30,541.2 | 338.287764072418 |
| RI-GWO | 0.5 | 31,024 | 258,235.32 | 3005.51641082764 |
| RI-ACO | 0.5 | 51,174 | 57,097.42 | 23.0797967910767 |
| RI-PSO | 0.5 | 30,733 | 57,288.76 | 32.4898002147675 |
| RI-GA | 0.5 | 139,844 | 196,514.9 | 29.3715693950653 |
| OCO | 0.75 | 30,773 | 31,107.1 | 353.920367956162 |
| RI-GWO | 0.75 | 30,745 | 256,092.13 | 2695.67001247406 |
| RI-ACO | 0.75 | 49,638 | 57,178.93 | 23.6201846599579 |
| RI-PSO | 0.75 | 31,856 | 57,250.21 | 31.6116788387299 |
| RI-GA | 0.75 | 103,571 | 182,581.4 | 12.4816913604736 |
| Algorithms | Change_Magnitude | Length | OOP | Computation_Time |
|---|---|---|---|---|
| OCO | 0.1 | 29,347 | 29,654.7 | 459.092036247253 |
| RI-GWO | 0.1 | 30,037 | 250,479.01 | 3030.58809566498 |
| RI-ACO | 0.1 | 50,683 | 57,187.85 | 23.9921379089356 |
| RI-PSO | 0.1 | 31,676 | 57,009.21 | 35.8889374732971 |
| RI-GA | 0.1 | 103,736 | 177,192.2 | 19.6413018703461 |
| OCO | 0.25 | 29,219 | 29,821.6 | 499.806445360184 |
| RI-GWO | 0.25 | 30,100 | 252,264.76 | 2929.30351305008 |
| RI-ACO | 0.25 | 53,362 | 57,415.55 | 23.0371935367584 |
| RI-PSO | 0.25 | 32,896 | 57,003.6 | 30.6185252666473 |
| RI-GA | 0.25 | 121,289 | 193,924.8 | 24.688747882843 |
| OCO | 0.5 | 29,367 | 30,011.7 | 333.434591770172 |
| RI-GWO | 0.5 | 30,207 | 261,022.39 | 3064.4821677208 |
| RI-ACO | 0.5 | 51,705 | 57,332.88 | 23.3675134181976 |
| RI-PSO | 0.5 | 31,396 | 57,218.29 | 34.7962794303894 |
| RI-GA | 0.5 | 110,632 | 195,980.8 | 9.07850098609924 |
| OCO | 0.75 | 29,658 | 30,261.6 | 478.82949590683 |
| RI-GWO | 0.75 | 31,108 | 258,356.64 | 2811.53076457977 |
| RI-ACO | 0.75 | 52,296 | 57,220.32 | 23.4361596107483 |
| RI-PSO | 0.75 | 30,644 | 56,953.96 | 33.5193908214569 |
| RI-GA | 0.75 | 132,413 | 192,981.3 | 24.235230922699 |
| Metric | Comparison | p-Value | Significant |
|---|---|---|---|
| Tour length | OCO vs. RI-GWO | 0.00015 | Yes |
| Tour length | OCO vs. RI-ACO | 0.00003 | Yes |
| Tour length | OCO vs. RI-PSO | 0.00006 | Yes |
| Tour length | OCO vs. RI-GA | 0.00003 | Yes |
| Offline performance | OCO vs. RI-GWO | 0.00003 | Yes |
| Offline performance | OCO vs. RI-ACO | 0.00003 | Yes |
| Offline performance | OCO vs. RI-PSO | 0.00003 | Yes |
| Offline performance | OCO vs. RI-GA | 0.00003 | Yes |
| Computation time | OCO vs. RI-GWO | 0.00003 | Yes |
| Computation time | OCO vs. RI-ACO | 0.00003 | Yes |
| Computation time | OCO vs. RI-PSO | 0.00003 | Yes |
| Computation time | OCO vs. RI-GA | 0.00003 | Yes |
| Metric | p-Value | Significant | |
|---|---|---|---|
| Tour length | 59 | Yes | |
| Offline performance | 61 | Yes | |
| Computation time | 58.75 | Yes |
| Metric | Comparison | p-Value |
|---|---|---|
| Tour length | OCO vs. RI-ACO | |
| Tour length | OCO vs. RI-GA | |
| Tour length | OCO vs. RI-GWO | 0.259 |
| Tour length | OCO vs. RI-PSO | 0.056 |
| Offline performance | OCO vs. RI-ACO | |
| Offline performance | OCO vs. RI-GA | 0.030 |
| Offline performance | OCO vs. RI-GWO | 0.10 |
| Offline performance | OCO vs. RI-PSO | |
| Computation time | OCO vs. RI-ACO | 0.076 |
| Computation time | OCO vs. RI-GA | 0.021 |
| Computation time | OCO vs. RI-GWO | |
| Computation time | OCO vs. RI-PSO | 0.380 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benjelloun, R.; Tarik, M.; Jebari, K. Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem. Information 2025, 16, 675. https://doi.org/10.3390/info16080675
Benjelloun R, Tarik M, Jebari K. Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem. Information. 2025; 16(8):675. https://doi.org/10.3390/info16080675
Chicago/Turabian StyleBenjelloun, Rim, Mouna Tarik, and Khalid Jebari. 2025. "Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem" Information 16, no. 8: 675. https://doi.org/10.3390/info16080675
APA StyleBenjelloun, R., Tarik, M., & Jebari, K. (2025). Open Competency Optimization with Combinatorial Operators for the Dynamic Green Traveling Salesman Problem. Information, 16(8), 675. https://doi.org/10.3390/info16080675