Automated Grading Method of Python Code Submissions Using Large Language Models and Machine Learning

Abstract

Assessment is fundamental to programming education; however, it is a labour-intensive and complicated process, especially in extensive learning contexts where it relies significantly on human teachers. This paper presents an automated grading methodology designed to assess Python programming exercises, producing both continuous and discrete grades. The methodology incorporates GPT-4-Turbo, a robust large language model, and machine learning models selected by PyCaret’s automated process. The Extra Trees Regressor demonstrated superior performance in continuous grade prediction, with a Mean Absolute Error (MAE) of 4.43 out of 100 and an R² score of 0.83. The Random Forest Classifier attained the highest scores for discrete grade classification, achieving an accuracy of 91% and a Quadratic Weighted Kappa of 0.84, indicating substantial concordance with human-assigned categories. These findings underscore the promise of integrating LLMs and automated model selection to facilitate scalable, consistent, and equitable assessment in programming education, while substantially alleviating the workload on human evaluators.

1. Introduction

Learning programming is becoming increasingly common, as it is a fundamental skill in many areas [1]. However, this increasing availability remains limited by a continual scarcity of skilled instructors. Educators are required to assess students’ code contributions, which necessitates significant time and mental work, frequently compromising the overall efficacy of the teaching process [2]. Besides being resource-intensive, hand grading is prone to discrepancies and subjective evaluations, thus undermining the fairness and reliability of assessments [3,4]. These limitations underscore the pressing necessity to develop an automated evaluation method. This approach would substantially alleviate teachers’ burden and provide pupils with expedited feedback. We present an automated evaluation method for Python programming tasks that integrates GPT-4-Turbo, an advanced variant of OpenAI’s large language model, with a Random Forest machine learning algorithm. This collaboration between generative artificial intelligence and supervised learning aims to assign continuous and discrete grades with an accuracy level comparable to that of a human assessor. The aim is to significantly decrease grading duration while guaranteeing more objective, consistent, and reproducible evaluations.

Our main contribution, compared to existing approaches, lies in the ability of our system to evaluate all student submissions, including those that do not compile. In contrast, some methods discard such cases outright or systematically assign them a default failing grade [2]. Furthermore, among the approaches that leverage Large Language Models (LLMs), many rely solely on the model’s generative reasoning without executing the code, which can compromise the reliability of the evaluation. In contrast, our approach utilises LLMs for code correction and analysis, without placing blind trust in their output; every submission is systematically subjected to controlled execution through unit testing. This supervision mechanism enhances the robustness of the evaluation, enables the detection of faulty behaviours, and ensures pedagogically meaningful feedback even for incomplete or non-runnable code. As such, our system promotes a more inclusive, rigorous, and explainable assessment process. Accordingly, we pose the following research questions:

• RQ1: Can the proposed system detect and correct syntactic and logical errors in student code submissions, including non-compilable ones?
• RQ2: Which supervised learning model, automatically selected and evaluated using PyCaret, best replicates human grading in terms of accuracy, reliability, and consistency across both continuous and discrete scoring tasks?
• RQ3: How does the performance of the proposed system compare to recent automated grading approaches, particularly in terms of accuracy, robustness, and generalisation across diverse evaluation metrics?

The rest of this paper is organised as follows. In Section 2, relevant studies on automated code assessment are reviewed, including methods based on large language models, machine learning, and static and dynamic analysis. Section 3 defines the fundamental technologies employed in our system, followed by the research paradigm and methodological framework that support our proposed evaluation strategy. The following Section 4, Section 5 and Section 6 describe the results of the research, discuss their consequences, and conclude the study.

2. Related Works

Over the past decade, the automatic grading of programming exercises has attracted growing interest within the scientific community. The objective is to reduce instructors’ grading burden and provide learners with timely, consistent, and formative feedback [5]. Several systems have been developed to address a variety of tasks, such as multiple-choice questions (MCQs) [6], short answers [7,8], Parson’s puzzles [9], and code-writing exercises, which present a particular challenge due to the variability of possible implementations, the need to verify functional behaviour, and the qualitative assessment of code structure and logic [10].

Several systematic reviews have been conducted to organise existing approaches to the automatic grading and assessment of programming exercises. Messer, Brown et al. [2] review is considered a key reference, classifying existing systems into three main methodological categories: static analysis, dynamic analysis, and machine learning-based approaches.

In our review of related work, we build on this classification by extending it with a fourth, more recent category, focused on LLMs, which are rapidly gaining traction. Our analysis is limited to studies addressing the automatic grading of code-writing exercises.

2.1. Approaches Based on Static and/or Dynamic Analysis

Among the works based on syntactic analysis of code, Verma et al. [11] introduce the SSM (Source-code Similarity Measurement) system, which automatically evaluates student submissions by comparing their structure to a reference solution. The method transforms the code into abstract syntax trees (ASTs), followed by identifier standardisation and the generation of syntactic fingerprints using a winnowing-inspired fingerprinting algorithm. These fingerprints are then compared using a Support Vector Machine (SVM) to produce a continuous score, normalised on a scale from 0 to 1. The authors report mean absolute errors (MAE) of less than 0.06, indicating a deviation of approximately 6% from human annotations.

Čepelis [12], on the other hand, proposes a hybrid approach that combines static analysis (via AST) and dynamic analysis (through unit testing). This approach is structured around a grading rubric in which a specific test verifies each criterion. This method enables continuous partial scoring by considering the presence and correct usage of expected structures and adherence to the intended functional behaviour. The results show a strong correlation with human evaluation, with a Pearson coefficient of 0.81, demonstrating the reliability of this automated approach for formative assessment in programming.

Both systems share a foundation in structural code analysis and generate continuous scores validated against human annotations. However, they also share a key limitation: they exclude non-compilable submissions, as AST-based analysis requires syntactically valid code.

Our method overcomes this constraint by incorporating a preliminary automated correction step using an LLM, which enables syntactic analysis even for initially erroneous code. It further distinguishes itself through the actual execution of code, the extraction of explainable metrics, and the use of a supervised learning model, resulting in a more robust, inclusive, and interpretable evaluation process.

2.2. Approaches Based on Supervised Machine Learning

Classical machine learning approaches have also been explored. In this context, Souza, Assis Zampirolli et al. [13] propose an automatic grading method for Java programming assignments, based on vector representations of code. After a normalisation phase, student submissions are transformed into vectors using a skip-gram model that captures lexical context and then processed by a convolutional neural network (CNN) to predict a discrete grade. This approach, which focuses exclusively on lexical semantics, does not incorporate code execution or structural analysis, thereby limiting its applicability for functional evaluation. Nevertheless, the authors report an average accuracy of 74.9%, demonstrating the viability of this strategy in a constrained context.

2.3. Approaches Based on Large Language Models

The use of LLMs for the automated grading of programming exercises is attracting growing interest. Several studies have proposed diverse approaches, combining supervised learning, advanced prompting strategies, or model aggregation techniques.

BeGrading, developed by Yousef et al. [14], relies on a specialised model trained on annotated and synthetic data. It achieves an MAE of ±0.95 on a 0–5 scale, corresponding to a relative error of 19%.

For their part, Akyash et al. [15] introduce StepGrade, which leverages chain-of-thought (CoT) prompting with GPT-4 to generate test cases, assess functionality, code quality, and algorithmic efficiency, and produce graded feedback. While this system achieves an MAE between 4.4% and 5.6% for the functionality criterion.

In a generation-based approach, Tseng et al. [16] developed CodEv, a framework built on multiple LLMs (GPT-4, LLaMA, Gemma), whose various evaluations are combined using majority voting, averaging, or median aggregation. Despite this complexity, the lowest MAE achieved is 6.30%.

The study by Mendonça et al. [17], conducted within the introEduAI platform, confirms this trend. The evaluations generated by LLMs, whether open-source or premium, show average deviations ranging from ±3 to ±9 points out of 100 compared to human grades, suggesting an estimated MAE between 5% and 6%. Once again, no code execution is performed, limiting the verifiability of the assessments.

Jukiewicz [18] proposes a minimalist approach using a structured prompt to generate discrete scores (0, 0.5, 1) without training or execution. The system assesses grading consistency through multiple passes. While using the modal grade improves stability against hallucinations, the absence of formal evaluation criteria or functional validation limits the generalisability of this method. Our approach addresses these shortcomings by combining semantic analysis with systematic verification of program behaviour.

None of the five systems analysed incorporates functional validation based on the actual execution of student-submitted code. This omission represents a significant limitation in terms of reliability, particularly for detecting runtime errors, unexpected outputs, or model hallucinations. In contrast, our approach stands out by combining the generative capabilities of LLMs with systematic validation through unit testing, enabling a framework for the automated assessment of code submissions.

2.4. Evaluation Techniques Comparison

To better situate our contribution within existing research,

Table 1. Comparison of evaluation techniques used in an Automatic grading system.

Reference	Scoring Type	Static Analysis	Dynamic Analysis	Machine Learning	LLM
Verma et al. [11]	Continuous	AST	No	SVM	No
Čepelis [12]	Continuous	AST	Unit-test	No	No
Souza et al. [13]	Discrete	No	No	CNN	No
Yousef et al. [14]	Continuous	No	No	Fine-tuned model	Yes
Akyash et al. [15]	Continuous	No	No	No	GPT-4
Tseng et al. [16]	Continuous	No	No	No	GPT-4o, LLaMA, Gemma
Mendonça et al. [17]	Continuous	No	No	No	GPT-4, and open-source models
Jukiewicz [18]	Discrete	No	No	No	Chat GPT
Our System	Discrete	AST	Unit-test	Random Forest	GPT-4-Turbo
	Continuous			Extra Trees Regressor

presents a comparative overview of key automated grading systems, highlighting their scoring types (continuous or discrete), the use of static and dynamic analysis, machine learning, and large language model (LLM) techniques.

The comparative study in the table above underscores the unique advantages of our methodology compared to existing solutions. Our approach combines supervised learning, automatic correction through LLMs, and static and dynamic analysis in a new way. This combination facilitates a comprehensive and inclusive review procedure, adept at addressing non-compilable inputs that are sometimes overlooked in previous studies, while meticulously validating LLM-generated outputs to ensure a reliable assessment.

3. Materials and Methods

3.1. GPT-4-Turbo

GPT-4-Turbo [19] is a robust multimodal language model created by OpenAI, founded on the Generative Pre-trained Transformer architecture. It has robust proficiency in reasoning, comprehending intricate instructions, and executing programming jobs across various languages, including Python. This study utilises GPT-4-Turbo through the gpt-4 endpoint of the OpenAI API, facilitating automated engagement with the model. The system utilises the temperature parameter (from 0 to 2) to regulate response variability, with lower values producing more deterministic outputs and higher values resulting in greater diversity of completions. These attributes make GPT-4-Turbo very proficient for tasks such as code rectification, feedback generation, and automated assessment in programming education.

3.2. Automated Model Selection Using PyCaret

PyCaret is an open-source, low-code Python toolkit for machine learning that simplifies the automation of comprehensive machine learning tasks. It has components for classification, regression, clustering, anomaly detection, and natural language processing, rendering it exceptionally suitable for efficient experimentation across diverse models [20]. This study employed PyCaret’s classification and regression modules to assess a wide array of supervised learning methods for forecasting student grades based on code analysis criteria. The models compared include Random Forest [21], Extreme Gradient Boosting [22], Extra Trees, LightGBM, AdaBoost [23], Ridge Regression, Decision Tree, K-Nearest Neighbours, Bayesian Ridge, and others.

PyCaret methodically executes cross-validation, implements automatic hyperparameter optimisation, and evaluates models based on diverse performance measures. For regression tasks, the evaluation included Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and R² score; for classification, metrics such as accuracy, F1-score, precision, and recall were assessed. This framework enables the current study to adopt a thorough, data-driven, and reproducible methodology for selecting the optimal models for continuous and discrete grade prediction.

3.3. Research Paradigm and Approach

The present study adopts a positivist approach, seeking to quantify and mimic human grading behaviour using objective, observable characteristics derived from evaluated code. The study employs a quantitative and experimental methodology, including automated input through large language models and predictive modelling via machine learning. We implement and test our evaluation approach utilising real student data to guarantee reproducibility and empirical validity.

3.4. General Process of Programming Code Correction

Programming code correction presents several challenges, as students may employ different strategies to address the same issue. Variations may occur in logic implementation, control structures, data types, function utilisation, naming standards, and general code organisation. The differences make the rectification process difficult and non-linear.

To remedy this, students’ solutions are typically corrected using a methodical process.

• Understanding the intent of the code: It is essential to understand the purpose of the code that needs to be fixed and what it is intended to do.
• Error identification: This step involves identifying the different types of errors in the student’s answer, such as syntax errors, execution errors, and logical errors.
• Correcting and modifying the code: This step involves changing the original code (student answer) by rewriting parts, inserting new lines, or deleting parts.
• Validate the new solution: after making the necessary changes, ensure that the new code works correctly and that the recent changes do not introduce new problems.
• Rate the code: This crucial step allows grades to be awarded based on the accuracy of the answers. These scores distinguish between students who have mastered the material and those who need additional support or intervention.

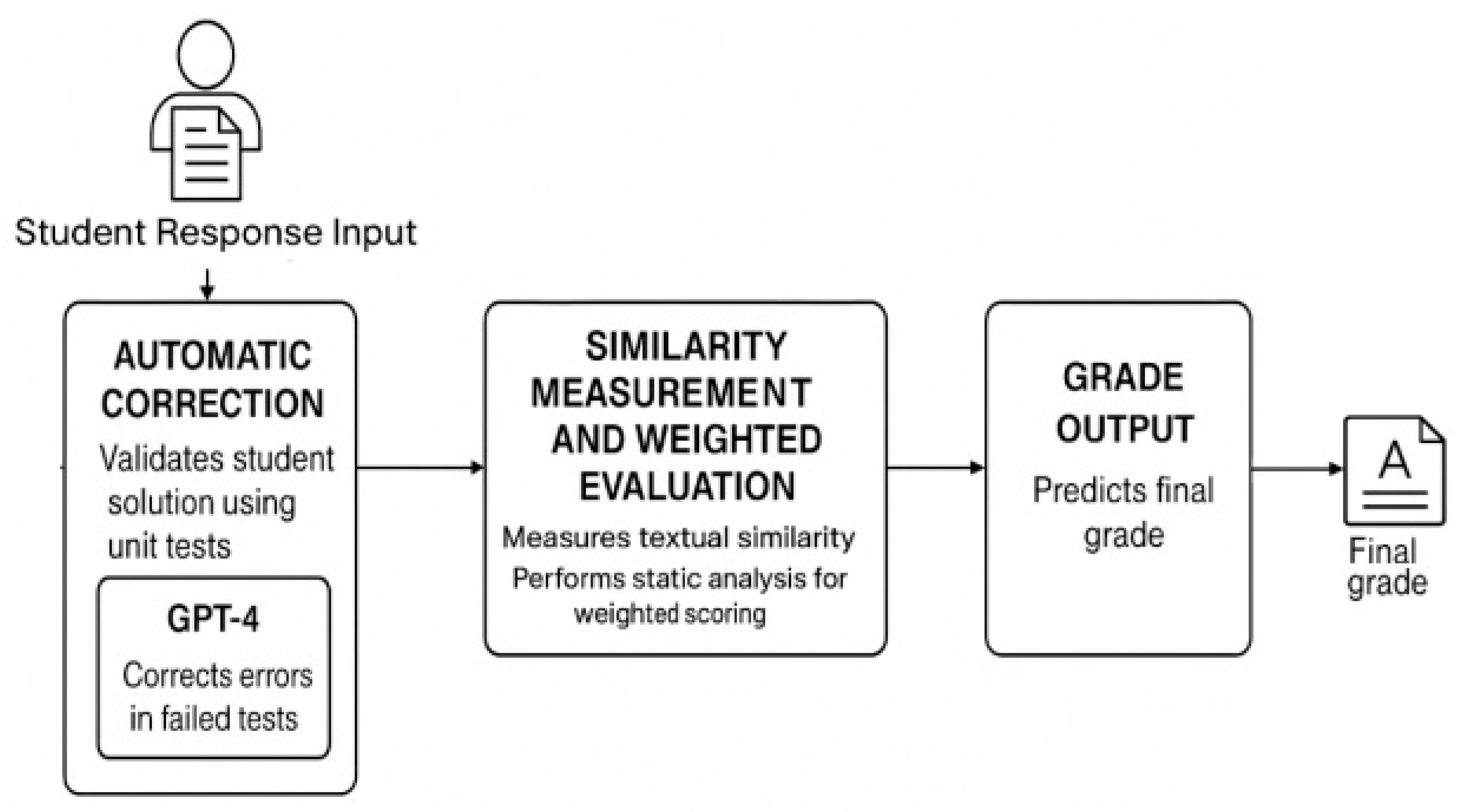
3.5. Grading Workflow Review of the Proposed Model

The grading workflow is fully integrated into a unified platform called the Semi Code Writing Intelligent Tutoring System (SCW-ITS) [9], designed to support both students and instructors in learning Python.

Students interact with the system through a user-friendly interface that presents programming exercises. Once they submit their code, the platform automatically processes each response. The resulting submissions are then evaluated manually by a human instructor using a continuous grading scale from 0 to 100, which serves as a benchmark for training the predictive models.

The Automatic Correction Module begins by executing predefined unit tests. If the code fails or does not compile, GPT-4-Turbo is invoked to attempt a correction, making minimal modifications to preserve the original student logic. The corrected version is then re-evaluated with the same tests to ensure it produces valid outputs.

Next, the Similarity and Evaluation Module compares the corrected code with the student’s original submission. It performs both textual similarity analysis and static analysis, emphasising key programming constructs such as control flow and logic over superficial elements like I/O operations. This process yields a set of interpretable metrics, including the test pass rate and the ratio of preserved, modified, inserted, and deleted lines.

The Grade Output Module uses these metrics to predict a final grade using a machine learning model. For classification tasks, a Random Forest Classifier is employed; for continuous score prediction, the Extra Trees Regressor is used.

The collected data, encompassing student submissions, correction metrics, and instructor-assigned grades, constitutes the training and test datasets used in our experiments with PyCaret (version 3.3.2) for automated model selection and tuning.

All code executions, including both system-generated corrections and students’ original Python submissions, were performed using Python 3.10.12 to ensure consistency across the evaluation workflow.

Figure 1 below illustrates the interaction among the three primary modules of our methodology.

3.5.1. The Automatic Correction Module

The Automatic Correction module takes as input the student’s response, the corresponding unit tests, and the exercise statement. Each student submission, written in Python, is evaluated by executing the unit tests. If all tests pass, the solution is considered correct. Otherwise, GPT-4 Turbo is used to generate a corrected version of the erroneous code. The prompt instructs the model to apply minimal changes, aiming to keep the correction as close as possible to the student’s original submission. The correction provided by the LLM is then re-evaluated using the same unit tests. If the corrected solution still fails, GPT-4-Turbo is prompted again to refine its response. This iterative correction process is limited to five attempts. If, after five iterations, GPT-4-Turbo is still unable to produce a valid solution, the response is marked as invalid, highlighting the model’s limitations in resolving the issue. Regarding the generation settings, the temperature and top-p are both set to 1, which reduces diversity and promotes consistency in the responses. The presence penalty and frequency penalty are both set to 0, allowing the model to repeat tokens without restriction. Figure 2 illustrates the correction workflow using GPT-4-Turbo.

3.5.2. The Similarity Measurement and Weighted Evaluation Module

The Similarity Measurement and Weighted Evaluation module uses a customised version of Python’s SequenceMatcher library to compare the student’s original code with the corrected version generated by GPT-4-Turbo. The modified implementation identifies four distinct categories of lines:

• Correct lines: unchanged lines that are syntactically and semantically correct.
• Updated lines: modified lines that reflect corrections made to existing code.
• Added lines: new lines introduced in the corrected version to complete or fix the solution.
• Removed lines: lines present only in the original submission that were eliminated during correction.

After categorising the changes, we apply a weighted evaluation based on Abstract Syntax Tree (AST) analysis. Each line is classified by its role (input, output, or logic) and assigned a corresponding weight to reflect its significance. Input lines are given a weight of 2, logic and function lines receive the highest weight of 3, and output lines are assigned a weight of 1. This weighting ensures that more critical components, such as core logic and functional structures, have a greater impact on the final evaluation.

After applying the weight analysis to each line category, we compute the final ratios for each type of change. This ensures that complex or critical lines, especially those involving logic and functions, carry greater weight in the final grade. For modified lines, we first calculate a similarity score using an edit distance function, which measures the degree to which each modified line matches the original. This score is then integrated into a weighted similarity ratio, adjusted according to the functional importance of each line.

The resulting metrics include:

• Weighted ratio of correct lines: Proportion of unchanged, correct lines, adjusted by their functional significance.
• Weighted ratio of deleted lines: Reflects the impact of removed lines on the overall solution.
• Weighted ratio of inserted lines: Evaluates the contribution of added lines in completing the correct solution.
• Weighted similarity ratio of modified lines: Combines edit distance similarity and line importance, giving more credit to accurate, minimally invasive changes in key code segments.

3.5.3. The Grade Output Module

The Grade Output Module represents the final stage of our automated evaluation system. It leverages a machine learning model selected using PyCaret’s automated regression and classification workflows to predict the final grade based on the feature set generated by the previous module. Among the models tested, the Extra Trees Regressor achieved the best results for continuous score prediction, while the Random Forest Classifier consistently attained the highest performance across all metrics in the classification task, confirming their respective effectiveness for each grading type.

3.5.4. Model Training and Dataset Preparation

We trained our model using a dataset of 350 student submissions collected from the Semi Code Writing Intelligent Tutoring System (SCW-ITS) [9], a platform designed to support Python learning and graded manually by a human evaluator on a continuous scale from 0 to 100. Each assignment is paired with input test data and expected output values, enabling functional validation through unit tests. The dataset includes solutions to various programming assignments covering fundamental topics such as input/output operations, nested loops, functions, and sorting algorithms.

To create the model, we automatically divided the dataset into training and testing sets using PyCaret’s built-in setup, which included preprocessing operations such as scaling, encoding, and imputation. The standard division employed was 70% for training and 30% for testing, accompanied by 10-fold cross-validation on the training dataset. This design allowed for uniform assessment across all models, enabling automated cross-validation, hyperparameter optimisation, and metric comparison without necessitating manual input.

3.5.5. Human Grading

To guarantee a reliable and replicable grading of programming tasks, we implement an approach based on Instruction-Weighted Evaluation (IWE). This method combines functional assessment through unit tests with a qualitative analysis of each code instruction, assigning a specific weight depending on its role in the program (logic, input, or output). Grading is performed using a penalty-based system, where deductions are made from a baseline score of 100 according to the type and severity of the errors. IWE draws on the findings of Keuning et al. [24], who emphasise the importance teachers place on algorithmic structure, and Ihantola et al. [25], who demonstrate that multiple dimensions—such as functionality, structure, and style—are considered in human grading.

Building on this framework, each instruction is analysed in terms of its functional role in the expected solution, logic, input, or output. Penalties are then assigned accordingly: minor issues like syntax errors or naming inaccuracies typically result in a 5–10% deduction, while more severe faults, such as incorrect or missing logic, may be penalised by up to 20%, depending on their importance and the total number of expected instructions. Additional lines that compromise the program’s coherence are also subject to penalties, ensuring that the final score reflects both the accuracy and the structural soundness of the submission.

To illustrate the practical implementation of the Instruction-Weighted Evaluation (IWE) technique and its penalty-based scoring system, we provide a representative example of a student’s erroneous submission for a factorial function assignment.

Table 2. Penalties for faulty code instructions in a factorial function assignment.

Line	Role	Error Type	Penalty
2	Logic	Incorrect initialization	−10%
3	Logic	Off-by-one error in range	−10%
4	Logic	Incorrect operation	−10%
5	Output	Uses print() instead of return	−5%

details the penalties applied to each faulty instruction based on its role and the severity of the error, highlighting how the final score is derived through weighted deductions.

Exercise statement:

Write a Python function that takes a positive integer n as input and returns its factorial.

Correct Solution:

• def factorial(n):
•   result = 1
•   for i in range(1, n + 1):
•     result *= i
• return result

Student submission (with errors):

• def factorial(n):       # correct
•   result = 0        # logic (incorrect initialization)
•   for i in range(n):    # logic (off-by-one error)
•     result = result + i  # logic (incorrect operation)
•   print(result)       # output (misused: should return)

Final Score Calculation: 100%—(10% + 10% + 10% + 5%) = 65%

4. Results

4.1. Correction of the Student Code

We observed that the GPT-4-Turbo model successfully corrected 88% of the erroneous codes submitted by students in our dataset. This performance results from an iterative prompting technique, wherein the prompt is adjusted at each iteration to enhance output. This approach improved the correction rate by 11%, increasing from 77% to 88%. Additionally, 12% of the model’s responses were classified as invalid, either due to failed corrections or outputs that did not pass the unit tests.

Table 3. GPT-4-Turbo repair success rate across k iterations.

Number of Iterations	Successful Repair
1	77%
2	87%
3	87.5%
4	87.5%
5	88%

represents the repair coverage of GPT-4-Turbo as a function of the number of prompt iterations (k).

While GPT-4-Turbo successfully corrected the majority of students’ submissions, 12% remained uncorrected. Upon initial inspection, these failures were not primarily due to logical errors but rather output mismatches or structural issues. A deeper analysis of these cases is presented in Section 5.

4.2. Predicting Scores of the Student Code Using PyCaret

We employed PyCaret’s regression and classification modules to evaluate a variety of machine learning models for predicting both continuous scores and discrete grades from features extracted from student code. Regression models were evaluated using standard metrics such as MAE, RMSE, and R², while classification models were assessed using accuracy, F1-score, recall, and Quadratic Weighted Kappa (QWK). The following subsections provide a detailed comparison of model performance across both tasks.

4.2.1. Regression Results

We utilised PyCaret’s regression module, which automatically trained and analysed a range of machine learning models using cross-validation, to evaluate the prediction of continuous scores. The models were evaluated using three primary metrics: Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), and the R² Score.

Table 4. Performance metrics for Regression models evaluated by PyCaret.

	Model	MAE	RMSE	R2 Score
1	Extra Trees Regressor	4.43	8.36	0.83
2	Random Forest Regressor	5.32	9.14	0.79
3	Extreme Gradient Boosting	4.90	9.03	0.78
4	Gradient Boosting Regressor	5.56	9.15	0.76
5	AdaBoost Regressor	6.27	10.26	0.74
6	K Neighbours Regressor	6.62	10.96	0.73
7	Decision Tree Regressor	5.55	10.29	0.73
8	Elastic Net	6.89	10.84	0.71
9	Lasso Least Angle Regression	7.23	11.33	0.70
10	Lass Regression	7.24	11.33	0.69

displays the ten highest-performing regression models, sorted by their predictive efficacy. The Extra Trees Regressor achieved the most favourable outcomes, exhibiting the lowest MAE (4.43) and RMSE (8.36), alongside the highest R² score (0.83), indicating robust predictive precision and minimal error. The Random Forest Regressor (MAE = 5.32, RMSE = 9.14, R² = 0.79) and Extreme Gradient Boosting (MAE = 4.90, RMSE = 9.03, R² = 0.78) closely followed. These models exhibited robust generalisation abilities and accurately reflected the variability in instructor-assigned scores. In general, ensemble-based models—especially those based on trees—performed better than linear models, which produced lower explanatory power and greater error rates (e.g., Lasso Regression with MAE = 7.24 and R² = 0.69). These findings validate the efficacy of ensemble approaches in forecasting student success in programming assignments utilising structured code metrics.

To evaluate the prediction accuracy of the regression model, particularly its correspondence with human-assigned grades across the entire scoring spectrum, we incorporated a scatterplot representation, as shown in Figure 2.

The scatterplot in Figure 2 shows a visual comparison of the Extra Trees Regressor’s projected scores and the human-assigned values, both of which are on a scale of 0 to 100. Each blue dot represents a student submission. The green dashed line denotes the optimal prediction line (y = x), signifying complete concordance with human evaluation. The red solid line represents the fitted regression line (y = 0.89x + 8.48) with a coefficient of determination R² = 0.94, signifying a robust linear correlation between model predictions and instructor-assigned grades.

The grey shaded region and the dashed lines denote a ±10-point tolerance interval, encompassing the range within which discrepancies between two human evaluators are typically deemed acceptable. The majority of projected scores reside within this interval, particularly in the mid-to-high range (scores over 50), indicating the model’s reliability for practical application.

Nevertheless, for very low scores (below 20), the model tends to slightly overestimate student performance, while for high scores (above 90), it tends to slightly underestimate. Despite these minor discrepancies, the model’s predictions remain within an educationally acceptable margin and rarely exhibit substantial deviations, making it suitable even for borderline or underperforming submissions.

4.2.2. Classification Results

We utilised PyCaret’s classification module to evaluate various supervised learning methods for predicting discrete grades. The numerical scores given by human evaluators were initially converted into three categorical grade levels—”Poor” (0–39), “Moderate” (40–79), and “Good” (80–100)—to conform to conventional grading standards. The “Good” range reflects exemplary performance, while the “Moderate” range indicates acceptable but not exemplary performance, and the “Poor” range signifies a need for improvement.

Several classification measures were used to evaluate the models in order to provide a thorough evaluation of their performance. Accuracy quantifies the ratio of correct predictions to the total forecasts produced. Even though it makes sense, it can be deceptive when working with unbalanced datasets. Recall evaluates the model’s ability to recognise all pertinent instances, while the F1-score provides a balanced metric by integrating precision and recall, making it particularly advantageous in scenarios of class imbalance.

The Quadratic Weighted Kappa (QWK) metric, especially pertinent in educational evaluation, measures the degree of concordance between the model’s predictions and human-assigned labels. In contrast to basic accuracy, QWK considers the ordinal characteristics of the target classes and imposes penalties on predictions that diverge significantly from the actual class. The values vary from −1 to 1, with scores interpreted as follows: slight (<0.20), fair (<0.40), moderate (<0.60), significant (<0.80), and almost perfect (≥0.80) agreement [26].

Table 5. Performance metrics for classification models evaluated by PyCaret.

	Model	Accuracy	Recall	F1	Kappa
1	Random Forest Classifier	0.91	0.91	0.91	0.84
2	Gradient Boosting Classifier	0.90	0.90	0.90	0.82
3	Extra Trees Classifier	0.90	0.90	0.89	0.81
4	Light Gradient Boosting Machine	0.87	0.87	0.87	0.76
5	K Neighbours Classifier	0.86	0.86	0.85	0.73
6	Decision Tree Classifier	0.86	0.86	0.86	0.74
7	AdaBoost Classifier	0.81	0.81	0.81	0.67
8	Logistic Regression	0.80	0.80	0.78	0.61
9	Linear Discriminant Analysis	0.79	0.79	0.77	0.61
10	Ridge Classifier	0.74	0.74	0.68	0.58

presents the ten most effective models ranked by their prediction performance. The Random Forest Classifier consistently achieved the highest scores across all evaluation metrics, with an accuracy of 0.91, an F1-score of 0.91, and a QWK of 0.84, signifying a near-perfect concordance with human-graded categories. The Gradient Boosting and Extra Trees classifiers demonstrated robust performance, attaining an accuracy of 0.90 and QWK scores exceeding 0.80. These findings support the applicability of ensemble approaches for educational evaluation problems, including both regression and classification.

5. Discussion

The findings validate the efficacy of the suggested methodology, which integrates GPT-4-Turbo for automatic code rectification with machine learning models for grade forecasting. The Extra Trees Regressor attained superior performance in continuous score prediction, whilst the Random Forest Classifier had the highest accuracy in discrete grade classification. The 88% correction success rate underscores GPT-4-Turbo’s dependability in rectifying diverse student coding errors. The implementation of iterative prompting markedly enhanced the correction rate by 11%.

GPT-4-Turbo exhibited the capability to rectify various categories of erroneous student replies, including: Incomplete solutions, characterised by the absence of critical components of the reasoning; Incomplete solutions, combining accurate and erroneous code segments; and incoherent comments that were structurally or logically incorrect.

The ability to manage numerous error kinds validates the model’s promise to facilitate formative assessment by autonomously rectifying different student misconceptions and errors.

Nevertheless, 12% of the entries remained unedited. Our investigation revealed that many failures were caused by output format discrepancies rather than logical errors. For example, when the anticipated output was a return value (e.g., return 25), the model occasionally generated a print() statement or incorporated the result into a string (e.g., “The result is 25”), resulting in unit test failures. These complications arose despite the prompt explicitly outlining the anticipated format. Subsequent analysis revealed that the phrasing of the exercise statement significantly impacted the model’s performance, underscoring the vulnerability of large language models to prompt construction and task definition.

Additionally, we investigated the effect of the temperature parameter on the quality of GPT-4-Turbo’s code corrections. Tests were conducted with values of 0.5, 1, 1.5, and 2. Across all settings, the model consistently produced accurate and coherent feedback, with no hallucinations observed, even at higher temperature levels. These findings suggest that GPT-4-Turbo maintains a stable level of reliability and precision irrespective of temperature fluctuations. Consequently, we opted for a temperature value of 1 in our experiments, as it strikes an effective balance between response diversity and correction consistency.

In evaluating the performance of our regression models, the Extra Trees Regressor emerged as the most effective for predicting continuous grades, achieving the lowest Mean Absolute Error (MAE = 4.43) and the highest R² score (0.83). These results indicate that the model successfully captures the key factors influencing student performance and closely approximates instructor-assigned scores. The Root Mean Squared Error (RMSE) of 8.66 reflects the typical deviation between predicted and actual scores, which remains acceptable within the 0–100 grading scale. This margin of error is consistent with the natural variability observed among human graders, where subjectivity can lead to similar discrepancies. As such, the model demonstrates strong predictive reliability and offers a credible alternative to manual assessment.

The examination of the scatterplot (Figure 2) indicates that, although the Extra Trees Regressor demonstrates commendable performance overall, it exhibits minor biases at the extremes of the score spectrum. The model generally overestimates low scores (below 20) and underestimates high scores (above 90). The inconsistencies may result from the comparatively reduced incidence of severe occurrences in the training data, which can diminish model sensitivity in such areas. Nonetheless, these variations are minimal and within pedagogically acceptable parameters, indicating that the model retains its resilience even for marginal contributions. From a formative assessment standpoint, this behaviour is acceptable, as it mitigates severe penalties for inferior submissions and curtails grade inflation at the upper echelon. Future efforts may rectify this by rebalancing the training dataset or implementing post-processing calibration to enhance predictions at the boundary.

The Random Forest Classifier emerged as the top-performing model across all key evaluation metrics, confirming its robustness and adaptability in classification tasks. It achieved an accuracy of 91%, indicating a high rate of correct predictions, and an F1-score of 0.91, reflecting a strong balance between precision and recall. Notably, its QWK score reached 0.84, highlighting excellent agreement with the actual labels and demonstrating the model’s strength in preserving the ordinal relationships among grade categories.

While accuracy measures exact matches, QWK accounts for the degree of error, rewarding predictions that are close to the true class. This is particularly relevant in educational contexts where slight misclassifications may still reflect a fair understanding of student performance. Even if the model does not always assign the exact correct class, for example, classifying a “Good” score as “Moderate”, its predictions tend to be close to the ground truth, rather than drastically incorrect. Moreover, the model often respects the logical progression of categories (from “Poor” to “Good”), which is precisely what the QWK metric captures. Together, these metrics demonstrate that Random Forest is reliable in ranking student performance and managing different types of classification errors, even when the predicted class is not strictly accurate.

After analysing these classification errors, we observed that many discrepancies occurred near the boundaries of grade intervals. This can be attributed to the way discrete grade categories were automatically assigned by mapping continuous scores into predefined ranges, rather than being manually labelled by human evaluators. For instance, a score of 79 is classified as “Moderate” by the model, while a human teacher might consider it “Good.” This rigid binning approach introduces borderline misclassifications that may unfairly penalise the model’s apparent performance. To address this, future work could involve incorporating human-assigned discrete grades to better reflect expert judgement and pedagogical nuance, particularly in cases where the grading is on the edge.

Although a direct comparison of performance metrics with prior studies is limited by differences in datasets and evaluation contexts, a qualitative analysis suggests that our results are comparable to, or even surpass, those reported in the literature. Prior works on automated programming assessment typically report MAE values ranging from 5 to 10 [11,14,15,16,17] and classification accuracies between 80% and 90% [12,13,18], depending on the nature of the dataset and task complexity. In our case, the Extra Trees Regressor achieved a low MAE of 4.43 and an R² of 0.83 in continuous score prediction, while the Random Forest Classifier reached an accuracy of 91% and a QWK score of 0.84 in discrete classification. These results fall within—or exceed—the performance range observed in existing approaches, reinforcing the effectiveness of our method.

Moreover, our method differs from recent LLM-based grading approaches [14,15,16,17,18], as we utilise the LLM not to grade directly, but to repair student code so that it can be executed. This enables traditional unit tests to be applied to the corrected code, combining the strengths of LLM reasoning with behaviour-based validation. Unlike systems that discard non-compilable submissions [11,12], our approach uses GPT-4-Turbo to make these codes executable before applying validation, ensuring full coverage of all student outputs. This increases both robustness and fairness by preventing the exclusion of weaker or partially correct submissions.

6. Conclusions

This study introduces an innovative methodology for the automatic evaluation of Python code submissions, capable of yielding both continuous and discrete grades. The system demonstrates reliable performance that closely aligns with human evaluations by integrating syntactic descriptor extraction, functional validation through unit testing, GPT-4-Turbo for code correction, and machine learning models, specifically the Extra Trees Regressor for continuous score prediction and the Random Forest Classifier for discrete grade classification, both trained on human annotations. It is distinguished by its capacity to manage non-compilable contributions and provide comprehensive, interpretable evaluations. Our model achieves mean absolute error (MAE) values that are equivalent to or better than those produced by contemporary automated grading systems, underscoring its robust performance and dependability. The results illustrate the model’s ability to address significant shortcomings in current methodologies, particularly in relation to non-compilable code management and evaluation transparency. A primary constraint of our methodology is the reliance on a single goal grade for each submission, typically assigned by a single instructor. To enhance equity and accurately represent varied grading viewpoints, we intend to integrate assessments from various instructors by calculating a weighted average as the learning objective. Furthermore, we intend to manually allocate distinct grade categories instead of obtaining them through automated mapping from continuous scores. These enhancements would more precisely reflect the diversity and intricacies of actual grading methods.

Moreover, although the existing approach emphasises functional correctness, a significant enhancement would be to expand the evaluation criteria to include elements such as code quality (e.g., readability, style, modularity) and algorithmic complexity. This would facilitate more thorough and educationally significant comments.

In the future, we intend to expand the system beyond Python, evaluating its adaptability and performance on code submissions in several programming languages with differing syntactic and semantic attributes.

As LLMs enhance their proficiency in producing accurate solutions for fundamental programming tasks, conventional evaluations could decline in their ability to evaluate real student comprehension. This transition requires a reevaluation of programming education, prioritising competencies that LLMs cannot readily duplicate, such as debugging, problem framing, and critical reasoning. As a result, future curricula may transition to more open-ended, interpretive, or contentious assignments that promote greater involvement and genuine learning.