1. Introduction
The continuing growth of
data science has highlighted the importance of
statistics in data-driven decisions [
1]. Statistics is a core knowledge in data science that is broadly taught in universities around the world. Practical knowledge and skills of statistics have an essential role in the implementation of data science regarding analyzing data and gaining valuable insights from it [
2].
However, conventional statistics learning in universities often lacks practices in real-world data science applications using computer programs. The current situation can cause a separation between the understanding of the fundamental statistics concept involving statistics equations and their practical hands-on skills. In real-world applications, data processing, calculations, and visualizations are often performed using
Python programming [
3,
4,
5]. Therefore, an integrated learning method of combining fundamental statistics with
Python programming should be offered to bridge the gap and give a solution for students to improve their practical skills in data science implementations.
Python programming has become an essential tool in data science implementations due to its extensive and versatile libraries for statistics, such as
NumPy,
Pandas, and
SciPy [
6,
7]. It supports a simple and readable syntax that makes it easy to understand and write codes in statistics. The integration of statistics with
Python programming allows students to practice computational procedures and understand logic behind syntax.
Many studies highlight the growing trend of implementing
Python to enhance practical statistics learning. Guler et al. demonstrated that the implementation of
Python in
Jupyter Notebooks as digital formative assessment tools significantly improved the self-efficacy of teachers in digital assessment activities [
8]. Avila-Garzon & Bacca-Acosta, through a bibliometric analysis, identified active learning strategies, such as project-based learning driven by
Python programming exercises, as dominant trends in data science curricula [
9]. Tufino et al. successfully integrated
Python modules for data analysis into a first-year laboratory course, reporting a 30% increase in students’ data handling proficiency [
10]. Moreover, Branko et al. found that the collaborative development of modular interactive
Jupyter Notebooks enhances undergraduate mastery of statistical concepts by providing immediate coding feedback within learning platforms [
11]. Conversely, recent pedagogical trends emphasize the integration focus on incorporating interactive computational tools like
Python within
Jupyter Notebooks to encourage active learning. These approaches leverage Python’s readability, extensive ecosystem, and community support to bridge the gap between theory and practice.
Previously, we have studied a system for assisting in learning basic statistics topics with
Python programming [
12]. This preliminary system integrates the
element fill-in-blank (EFP), the
grammar concept understanding problem (GUP), and the
value trace problem (VTP) in the
Programming Learning Assistant System (PLAS) that has been developed as a self-learning platform for various programming languages. The
EFP asks one to fill in the blanks for missing elements in the source code provided, the
GUP asks for answers regarding grammar and libraries, and the
VTP asks for answers regarding the values of important variables or the outputs while running the given code. The application results for students demonstrated that the system supports the practical learning of basic statistics topics effectively. Unfortunately, this system does not cover some required fundamental statistics topics in data science implementations.
In this paper, we present a self-learning method through Python programming that covers fundamental statistics topics for data science implementations. This study proposes the integration of the EFP, GUP, and VTP in the PLAS to assist students in improving their skills of Python programming for data science implementations. To assist students in learning statistics efficiently, reference documents on the statistics topics are also provided. This combination allows students to write codes, understand fundamental statistics concepts, and track execution flows while obtaining instant feedback, which will improve retention, understanding, and practical skills in learning statistics using Python programming.
For evaluations, we generated 22 instances using Python source codes for fundamental statistics topics and assigned them to 40 first-year undergraduate students in the two-session evaluation at UPN Veteran Jawa Timur, Indonesia. The application results of the number of submissions and the correct answer rate were analyzed using statistics analytical methods to assess the difficulty of instances and student learning performances. In addition, the final grades were compared between the students who used the proposed method and those who did not use it.
The structure of this paper is organized as follows.
Section 2 presents a literature review.
Section 3 describes an overview of the
programming assistant learning system (PLAS) in previous studies.
Section 4 presents the fundamental statistics self-learning method with
Python programming.
Section 5 shows the evaluation results of the proposal. Finally,
Section 6 provides the conclusion and future works.
2. Literature Review
In this section, we briefly review related works in the literature. These works mainly present statistics learning with programming tools. However, many of these approaches lack comprehensive coverage of fundamental statistics topics using Python programming or do not sufficiently support self-learning with interactive exercises and immediate feedback. Our proposed method aims to fill these gaps.
In ref. [
13], Holman & Hachler examine the use of
Python to teach
Monte Carlo simulation, focusing on a teaching strategy where the teacher asks students to complete simulation exercises in
Google Spreadsheets before transitioning to
Python. This approach aims to enhance the comprehension of students who are comfortable with spreadsheets but new to statistical computing. The method could enhance student learning and the transition from spreadsheets to
Python proved to be effective. However, this method does not cover fundamental statistics topics using
Python programming, which limits its applicability for broader data science education.
In ref. [
14], Burckhardt et al. proposed a platform that utilizes
R programming for learning statistics and data analysis. They emphasized fundamental concepts and introduced various types of data early on, without requiring programming prerequisites. The platform, known as the
Integrated Statistics Learning Environment (ISLE), is a web-based e-learning and lesson authoring framework for teaching statistics. Nevertheless, the platform has not been evaluated regarding student feedback and learning outcomes, leaving its educational effectiveness unclear.
In ref. [
15], Al-Haddad et al. explored challenges of teaching statistics courses and emphasized the importance of using technology to engage students in learning. They implemented a
technology-enhanced supportive instruction (TSI) model using
Microsoft Excel as a tool to teach statistics, helping students to stay engaged in both face-to-face and distance learning environments. The findings show that both teaching techniques did not differ significantly, supporting the potential usefulness of this model. Unfortunately, this system does not facilitate self-directed learning, as it requires the presence of a teacher for effective implementation.
In ref. [
16], Lu demonstrated that
web-based applets are usable for teaching statistics. The applets were designed for a traditional
introductory statistics course, focusing on two specific areas:
real-time response data and
dataset generation for assignments. However, the lack of formal assessment of the applets’ effectiveness led to confusion among students on using the system and understanding core statistics concepts.
In ref. [
17], Gerbing used
R programming in introductory statistics courses to help students to practice applying statistical concepts in data analysis. An
R package-4.1.2 was developed based on feedback from hundreds of introductory statistics students over multiple years, providing a set of functions to apply basic statistical principles using
command-line R. The findings indicate that the implementation was successful in teaching and homework assignments. However, students faced challenges in obtaining timely feedback during practice, highlighting the need for immediate guidance in programming-based learning.
In ref. [
18], Schawrz explored the implementation of
ChatGPT 4.0 for statistical data analysis and its application in statistics education at universities. They used
ChatGPT to perform statistical analyses and evaluate its capabilities and limitations. The results indicate that while
ChatGPT can generate appropriate codes, it emphasizes minimal knowledge of statistics. Consequently, students still require instructor support when using this approach for learning statistics.
In ref. [
19], Munthe investigated implementations of programming in mathematics classes and the types of difficulties that students experienced when working on programming tasks. A student’s main problem was converting a mathematical procedure into a programming code. The teacher mitigated this issue by simplifying the equation and converting complex mathematical symbols into programming elements that were easier to understand. This was achieved by simplifying variables and utilizing functions in programming, specifically using
Python programming. This pedagogical strategy informs our method to reduce errors in student implementations.
In ref. [
20], Quinones et al. demonstrated an innovative statistics tool, namely “
EastApp”. This application is designed for teaching and learning descriptive statistics in university courses. It enhances the understanding of (1) statistical models through interactive graphs and data visualizers; (2) probability concepts via a probability calculator; and (3) descriptive statistics through real-time data generation and visualizers. However, the evaluation focused mainly on usability, while the educational effectiveness and learning outcomes remained underexplored.
In summary, various tools and methods have been developed to integrate programming with statistics learning, and we found that most of them have several limitations. Many focus on specific statistical topics or tools like Monte Carlo simulation, R programming, and Excel, lack comprehensive coverage of fundamental statistics using Python programming, or do not support fully self-directed learning environments. Additionally, there is often an insufficient evaluation of learning outcomes, limited immediate feedback mechanisms, and reliance on instructor presence, which constrain scalability and effectiveness.
Our proposed method provides a comprehensive self-learning framework that integrates fundamental statistics topics with Python programming through hands-on exercises on the PLAS platform. This approach supports conceptual understanding, coding skills, and timely feedback, enabling effective and autonomous learning for data science implementation.
Author Contributions
Conceptualization, P.A.R. and N.F.; methodology, P.A.R. and N.F.; application tools, P.A.R. and M.M.; visualization, K.C.B. and M.M.; implementation, P.A.R., D.A.P. and A.T.D.; writing—original draft, P.A.R.; writing—review and editing, N.F.; supervision, N.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was conducted following the ethical guidelines of UPN Veteran Jawa Timur. Formal approval from the Institutional Review Board was not required because the research involved normal educational practices and anonymized academic performance data, posing no risks to participants.
Informed Consent Statement
Informed consent was implied through voluntary participation in the programming exercises. All participants were informed that their anonymized performance data would be used for research purposes.
Data Availability Statement
Acknowledgments
We would like to thank all the colleagues in the Distributing System Laboratory at Okayama University and the Department of Data Science at the Universitas Pembangunan National Veteran Jawa Timur who participated in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Weihs, C.; Ickstadt, K. Data Science: The impact of statistics. Int. J. Data Sci. Anal. 2018, 6, 189–194. [Google Scholar] [CrossRef]
- Pallavi, G.; Nitin, V.T. The Impact and Importance of Statistics in Data Science. Int. J. Comput. Appl. 2020, 176, 10–14. [Google Scholar] [CrossRef]
- Ranjan, M.; Barot, K.; Khairnar, V.; Rawal, V.; Pimpalgaonkar, A.; Saxena, S.; Sattar, A. Python: Empowering Data Science Applications and Research. J. Oper. Syst. Dev. Trends 2023, 10, 27–33. [Google Scholar] [CrossRef]
- Siva, P.; Yamaganti, D.; Rohita, D.; Sikharam, U. A Review on Python for Data Science, Machine Learning and IOT. Int. J. Sci. Eng. Res. 2023, 10, 851–858. [Google Scholar] [CrossRef]
- Yadav, N.; DeBello, J.E. Recommended Practices for Python Pedagogy in Graduate Data Science Courses. In Proceedings of the 2019 IEEE Frontiers in Education Conference (FIE), Covington, KY, USA, 16–19 October 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Kabir, M.A.; Ahmed, F.; Islam, M.M.; Ahmed, M.R. Python For Data Analytics: A Systematic Literature Review Of Tools, Techniques, And Applications. Acad. J. Sci. Technol. Eng. Math. Educ. 2024, 4, 134–154. [Google Scholar] [CrossRef]
- Donald, A.; Aditya, T.; Srinivas, T.A. A Short Review of Python Libraries and Data Science Tools. South Asian Res. J. Eng. Technol. 2022, 5, 1–5. [Google Scholar] [CrossRef]
- Yavuz Temel, G.; Barenthien, J.; Padubrin, T. Using Jupyter Notebooks as digital assessment tools: An empirical examination of student teachers’ attitudes and skills towards digital assessment. Educ. Inf. Technol. 2025, 30, 1–30. [Google Scholar] [CrossRef]
- Avila-Garzon, C.; Bacca-Acosta, J. Curriculum, Pedagogy, and Teaching/Learning Strategies in Data Science Education. Educ. Sci. 2025, 15, 186. [Google Scholar] [CrossRef]
- Tufino, E.; Oss, S.; Alemani, M. Integrating Python data analysis in an existing introductory laboratory course. Eur. J. Phys. 2024, 45, 045707. [Google Scholar] [CrossRef]
- Duda, M.; Sovacool, K.; Farzaneh, N.; Nguyen, V.; Haynes, S.; Falk, H.; Furman, K.; Walker, L.; Diao, R.; Oneka, M.; et al. Teaching Python for Data Science: Collaborative development of a modular interactive curriculum. J. Open Source Educ. 2021, 4, 138. [Google Scholar] [CrossRef]
- Riyantoko, P.; Funabiki, N.; Wai, K.; Aung, S.; Muhaimin, A.; Trimono. A Proposal of Python Programming Exercise Problems for Basic Statistics Learning. In Proceedings of the 2024 Seventh International Conference on Vocational Education and Electrical Engineering (ICVEE), Malang, Indonesia, 30–31 October 2024; pp. 289–295. [Google Scholar] [CrossRef]
- Holman, J.O.; Hacherl, A. Teaching Monte Carlo Simulation with Python. J. Stat. Data Sci. Educ. 2023, 31, 33–44. [Google Scholar] [CrossRef]
- Burckhardt, P.; Nugent, R.; Genovese, C.R. Teaching Statistical Concepts and Modern Data Analysis with a Computing-Integrated Learning Environment. J. Stat. Data Sci. Educ. 2021, 29, S61–S73. [Google Scholar] [CrossRef]
- Al-Haddad, S.; Chick, N.; Safi, F. Teaching Statistics: A Technology-Enhanced Supportive Instruction (TSI) Model During the Covid-19 Pandemic and Beyond. J. Stat. Data Sci. Educ. 2024, 32, 129–142. [Google Scholar] [CrossRef]
- Lu, Y. Web-Based Applets for Facilitating Simulations and Generating Randomized Datasets for Teaching Statistics. J. Stat. Data Sci. Educ. 2023, 31, 264–272. [Google Scholar] [CrossRef]
- Gerbing, W.D. Enhancement of the Command-Line Environment for use in the Introductory Statistics Course and Beyond. J. Stat. Data Sci. Educ. 2021, 29, 251–266. [Google Scholar] [CrossRef]
- Schwarz, J. The use of generative AI in statistical data analysis and its impact on teaching statistics at universities of applied sciences. Teach. Stat. 2025, 47, 118–128. [Google Scholar] [CrossRef]
- Munthe, M. Programming in the mathematics classroom—Adversities students encounter. Acta Didact. Nord. 2022, 16, 22 sider. [Google Scholar] [CrossRef]
- Quiñones, D.; Ruz, F.; Díaz-Arancibia, J.; Paz, F.; Osega, J.; Rojas, L.F. Innovating Statistics Education: The Design of a Novel App Using Design Thinking. Appl. Sci. 2024, 14, 8515. [Google Scholar] [CrossRef]
- Hnin, H.W.; Zaw, K.K. Element Fill-in-Blank Problems in Python Programming Learning Assistant System. In Proceedings of the 2020 International Conference on Advanced Information Technologies (ICAIT), Yangon, Myanmar, 4–5 November 2020; pp. 88–93. [Google Scholar] [CrossRef]
- Htet, E.E.; Shwe, S.H.; Aung, S.T.; Funabiki, N.; Fajrianti, E.D.; Sukaridhoto, S. A Study of Grammar-Concept Understanding Problem for Python Programming Learning. In Proceedings of the 2022 IEEE 4th Global Conference on Life Sciences and Technologies (LifeTech), Osaka, Japan, 7–9 March 2022; pp. 241–242. [Google Scholar] [CrossRef]
- Shwe, S.; Funabiki, N.; Syaifudin, Y.; Tar, P.; Kyaw, H.H.; Hnin Aye, T.; Kao, W.C.; Min, N.; Myint, T.; Htet, E. Value trace problems with assisting references for Python programming self-study. Int. J. Web Inf. Syst. 2021; ahead-of-print. [Google Scholar] [CrossRef]
- Muhammed, S.; Eltahir, O.; Khan, Z.; Ebert, J. Mastering Statistics: A Journey from Data Science to Doctoral Excellence. Int. J. Innov. Sci. Res. Rev. 2025, 7, 7613–7621. [Google Scholar]
- Sial, M.; Abid, A. Measurement of Central Tendencies. J. Res. Appl. Sci. Biotechnol. 2023, 2, 212–214. [Google Scholar] [CrossRef]
- Rakrak, M. Exploring Variability in Data: The Role of Range, Variance, and Standard Deviation. Int. J. Multidiscip. Res. Anal. 2025, 8, 1327–1331. [Google Scholar] [CrossRef]
- Viti, A.; Terzi, A.; Bertolaccini, L. A practical overview on probability distributions. J. Thorac. Dis. 2015, 7, E03–E07. [Google Scholar] [CrossRef]
- Munthe, M.; Naalsund, M. Designing Mathematical Programming Problems. Digit. Exp. Math. Educ. 2024, 10, 260–286. [Google Scholar] [CrossRef]
- Ross, M.; Church, K.; Rolon-Mérette, D. Tutorial 3: Introduction to Functions and Libraries in Python. Quant. Methods Psychol. 2021, 17, S13–S20. [Google Scholar] [CrossRef]
- Yadav, V. An Introduction to Cognitive Load Theory; ABS Book: Delhi, India, 2023; pp. 30–45. [Google Scholar]
- Mayer, R. The Past, Present, and Future of the Cognitive Theory of Multimedia Learning. Educ. Psychol. Rev. 2024, 36, 8. [Google Scholar] [CrossRef]
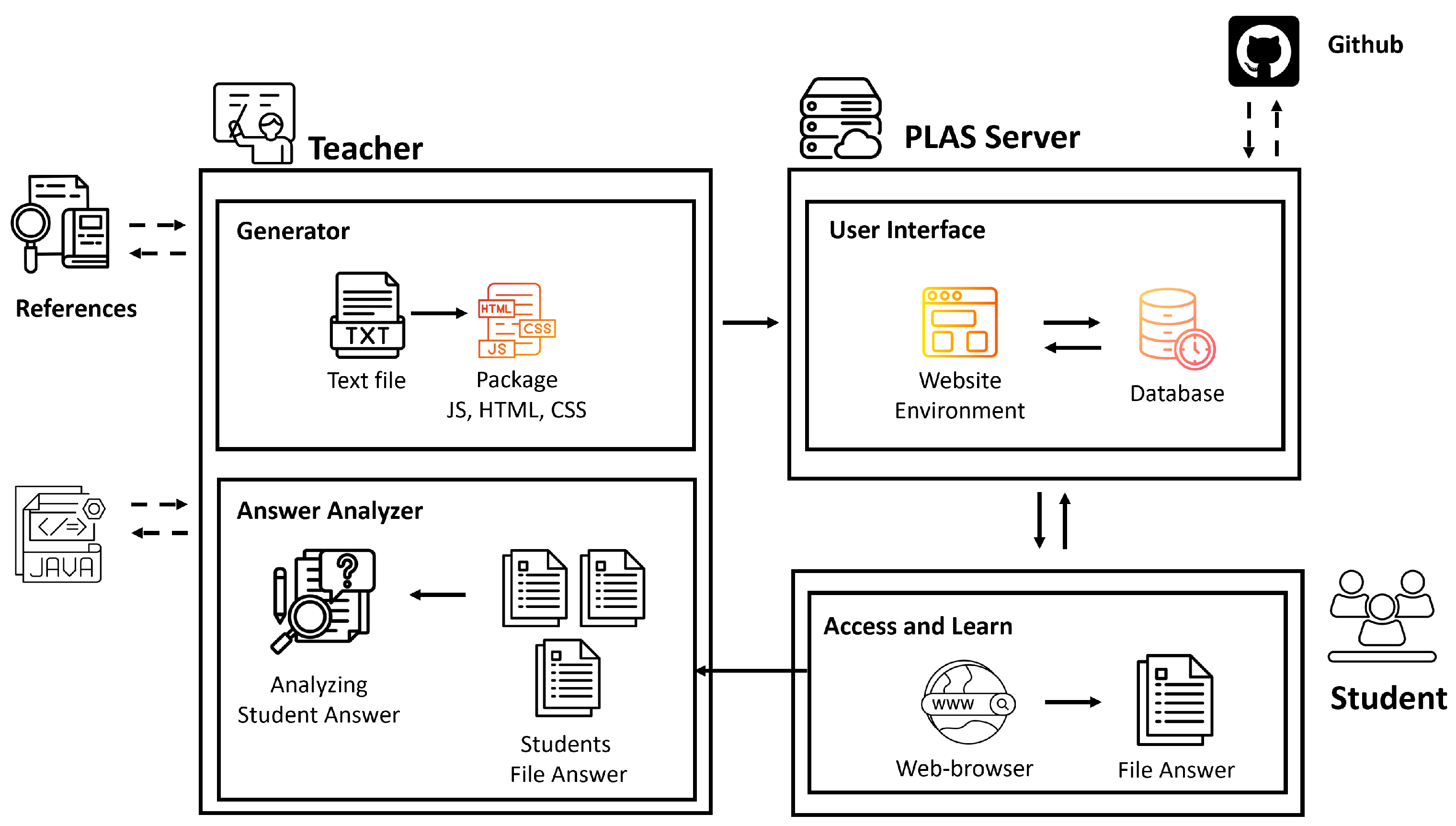
Figure 1.
Overview of PLAS.
Figure 2.
Answer interface.
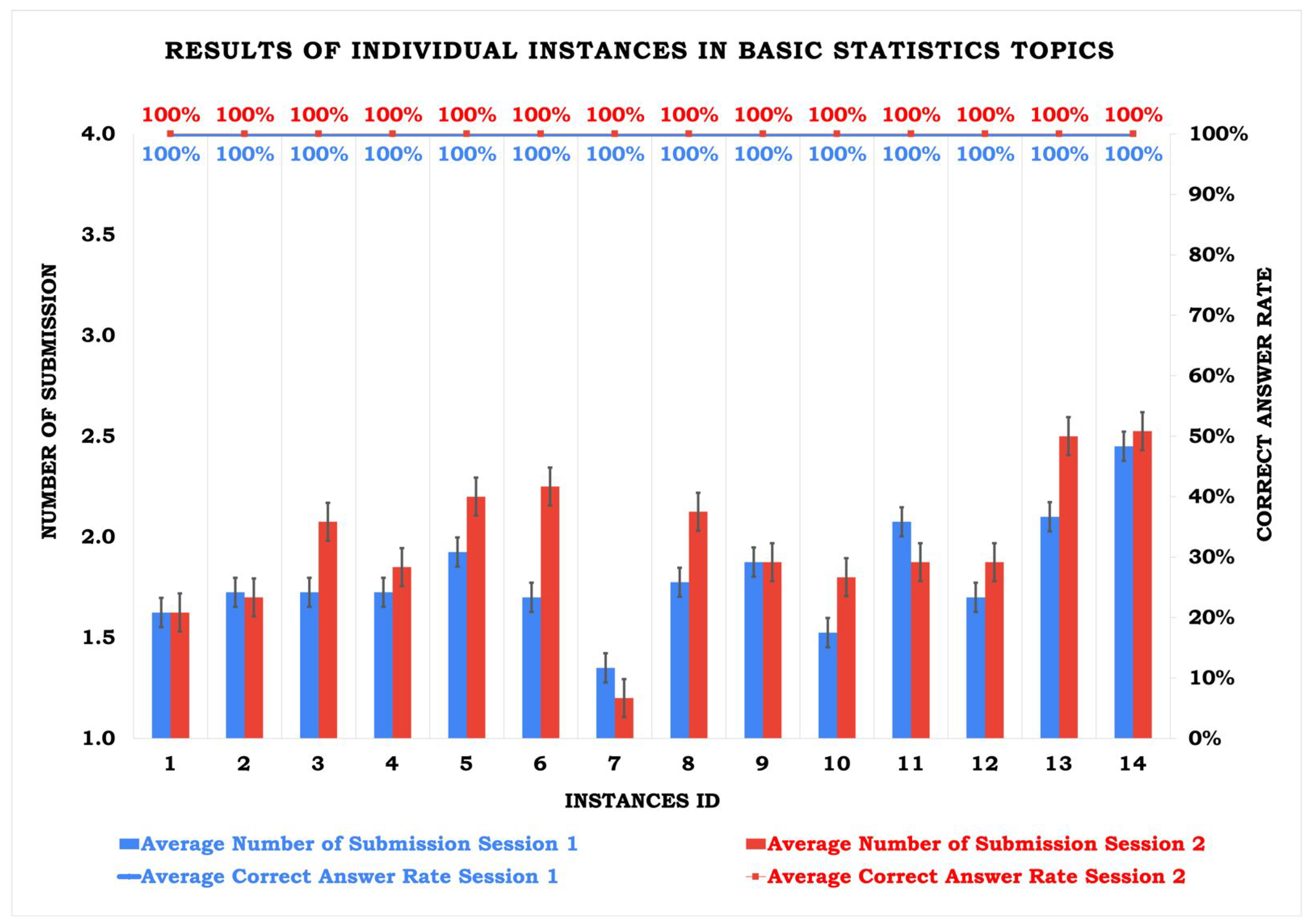
Figure 3.
Results of individual instances in basic statistics topics.
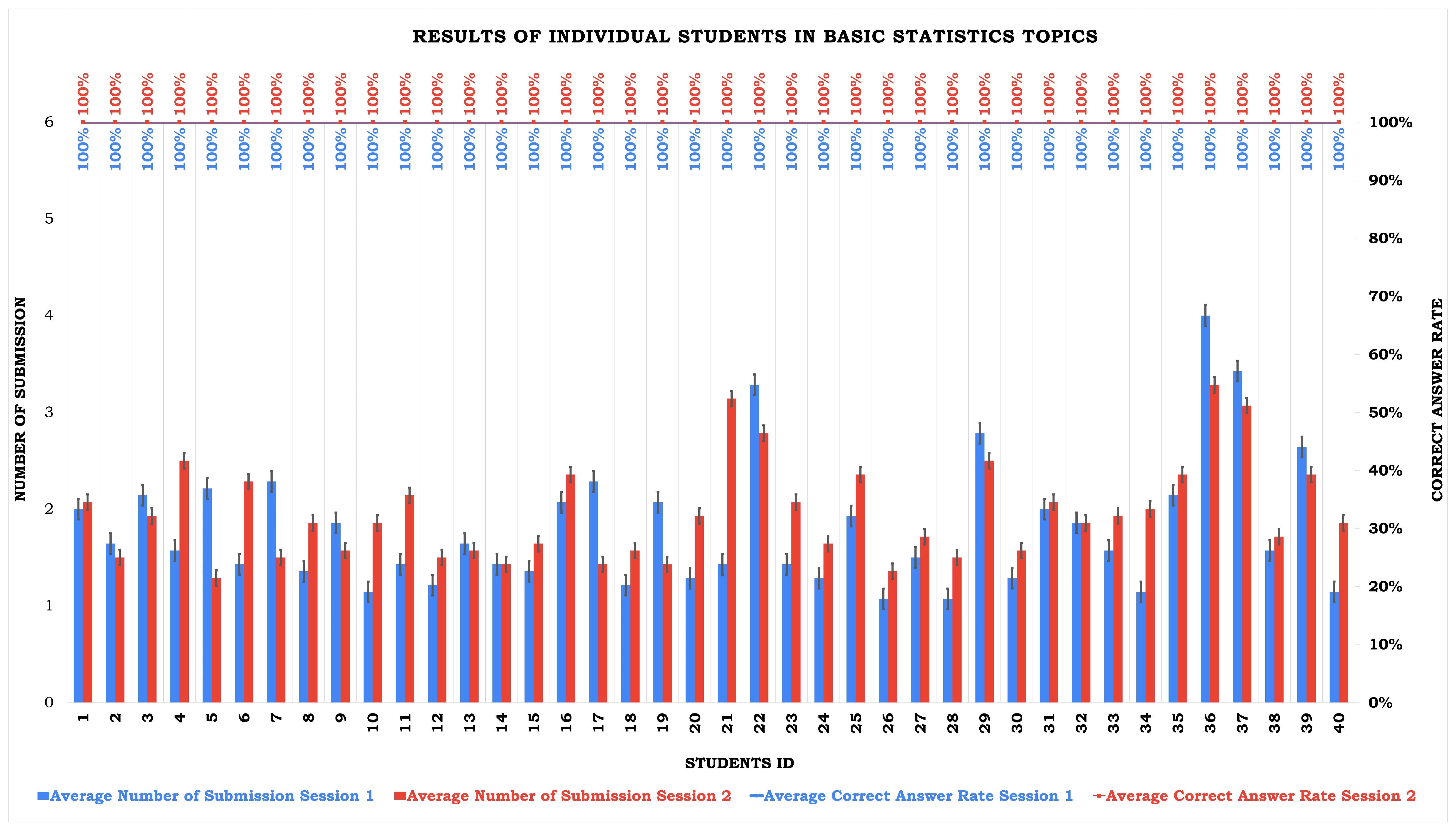
Figure 4.
Results of individual students in basic statistics topics.
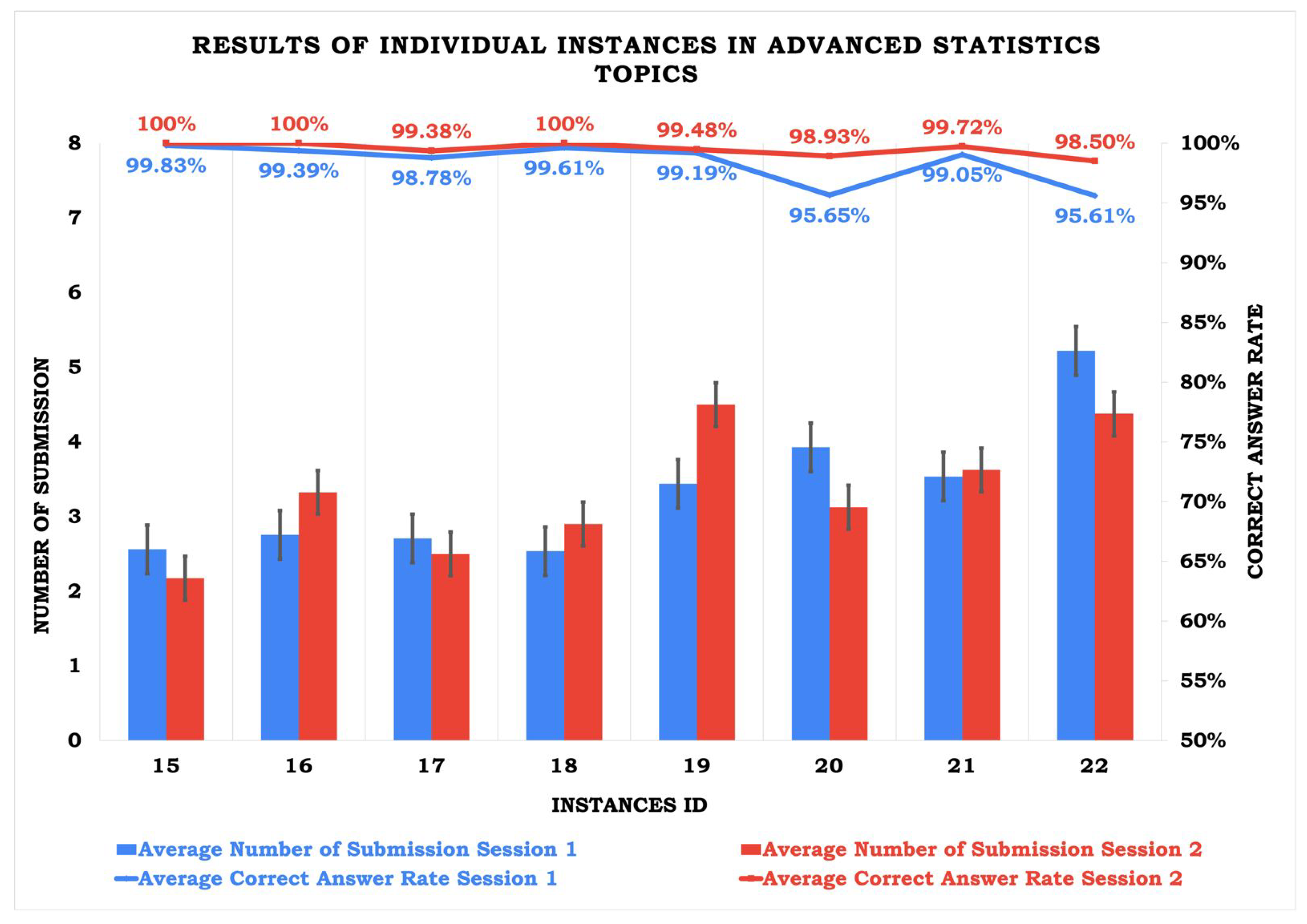
Figure 5.
Results of individual instances in advanced statistics topics.
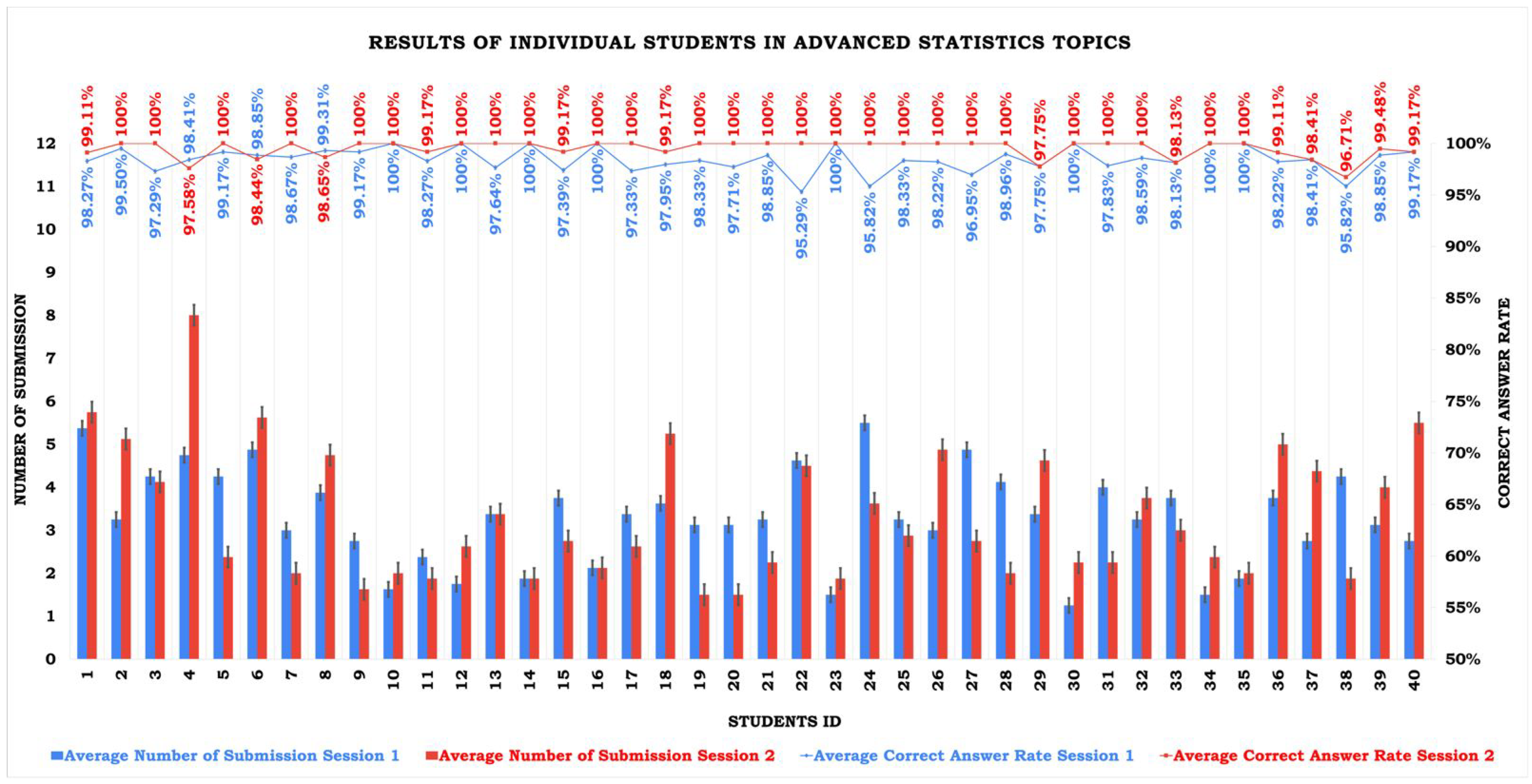
Figure 6.
Results of individual students in advanced statistics topics.
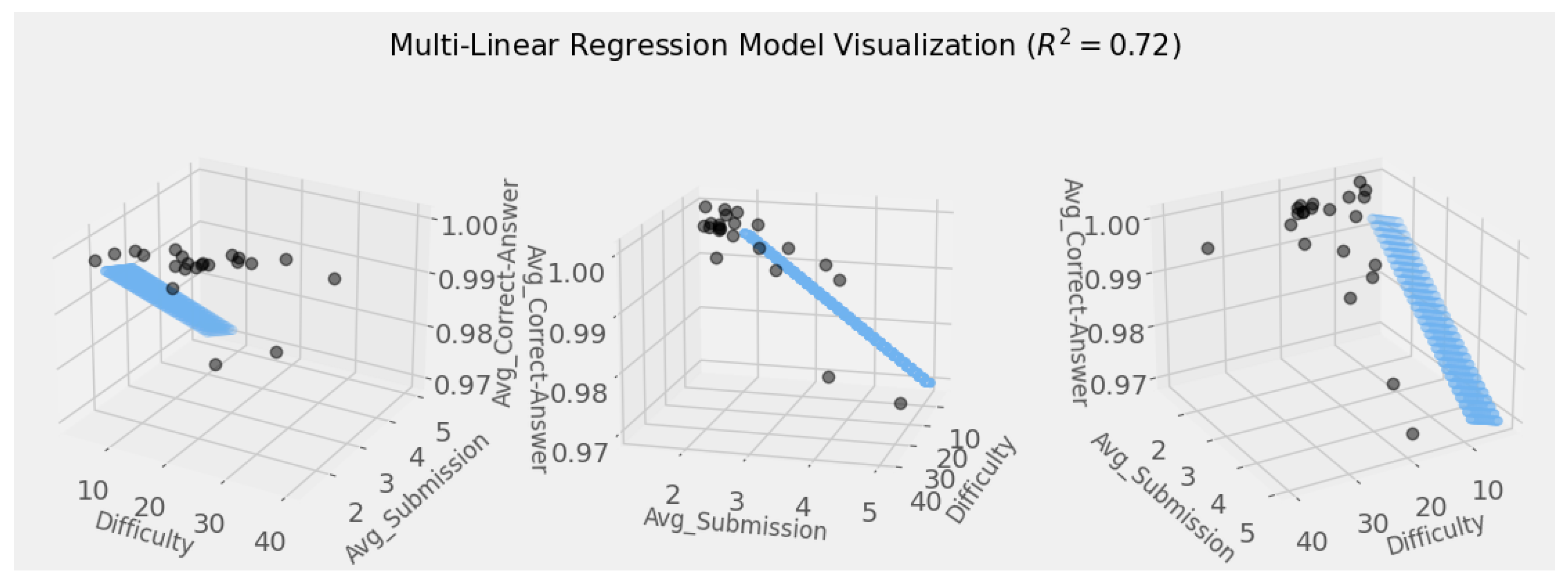
Figure 7.
Three-dimensional visualizations of multiple linear regression models.
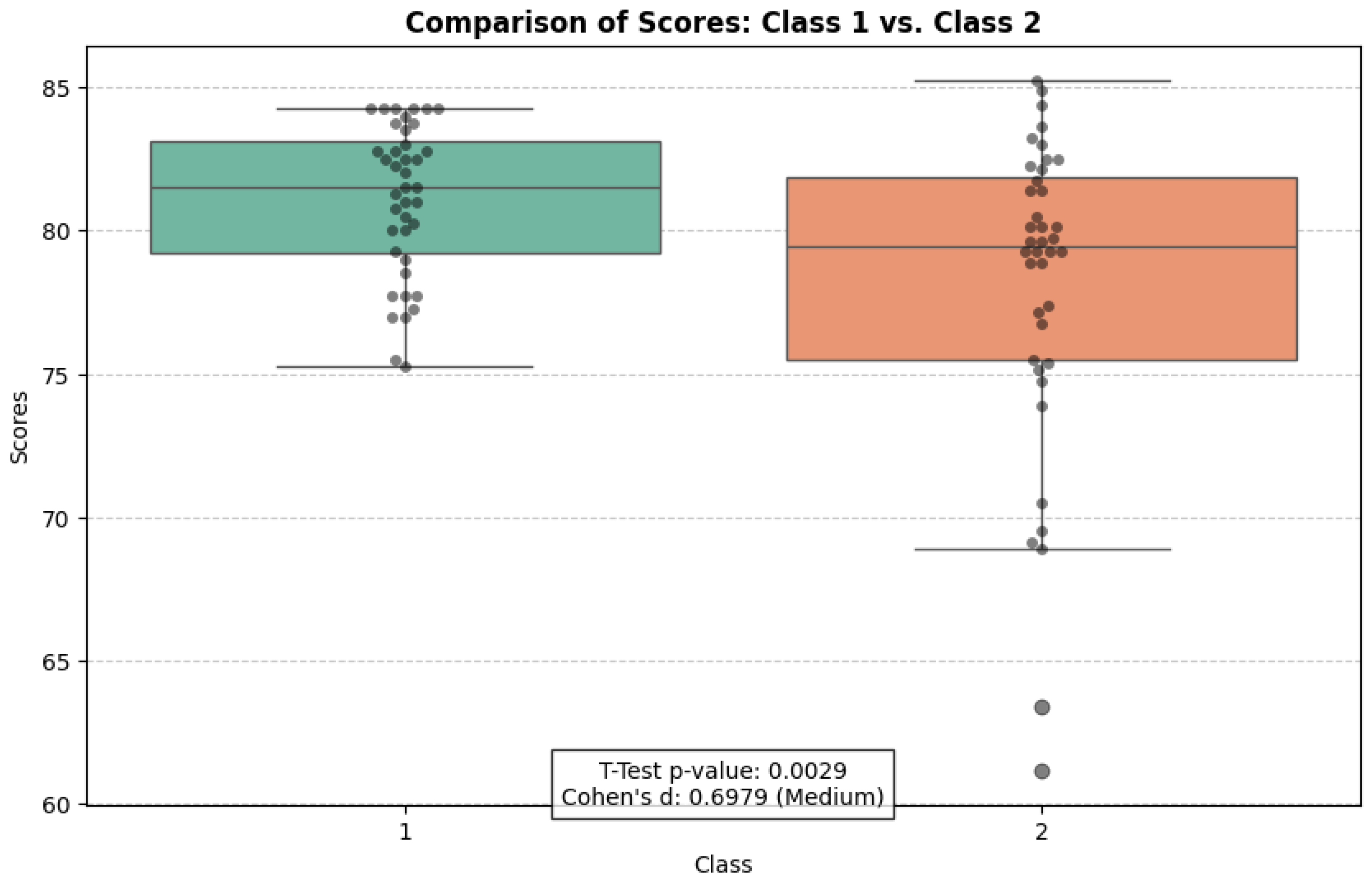
Figure 8.
Comparison of scores between Class 1 and Class 2 to provide the effect size using Cohen’s d score.
Table 1.
Selected statistics topics.
| No | Category | Topics | Instance IDs |
|---|
| 1 | basic | mean, median, mode | 1, 2, 3 |
| 2 | basic | variance, standard deviation, coefficient of variation, range | 4, 5, 6, 7 |
| 3 | basic | quartile 1, quartile 2, quartile 3, decile, percentile | 8, 9, 10, 11, 12 |
| 4 | basic | skewness, kurtosis | 13, 14 |
| 5 | advanced | binomial distribution, multinomial distribution, geometric distribution, Poisson distribution | 15, 16, 17, 18 |
| 6 | advanced | normal distribution, t-distribution, exponential distribution, chi-square distribution | 19, 20, 21, 22 |
Table 2.
Possible blank elements for EFPs.
| No | Category | Elements |
|---|
| 1 | Variable | , , n, x, , , |
| 2 | Operator | /, −, |
| 3 | Constant | 2, 1 |
| 4 | Function | , , |
Table 3.
Elements and questions for GUPs.
| No | Category | Elements | Questions |
|---|
| 1 | Keywords | | Which keyword is used to determine the initial data? |
| 2 | Keywords | n | Which keyword is used to count the amount of data? |
| 3 | Keywords | | Which keyword is used to determine data summarization? |
| 4 | Keywords | | Which keyword is used to calculate the average value? |
| 5 | Keywords | | Which keyword is used to calculate the squared differences between the data and mean value? |
| 6 | Keywords | | Which keyword is used to calculate the variance value? |
| 7 | Keywords | | Which keyword is used to calculate the standard deviation value? |
| 8 | Library | | Which library is used in the standard deviation calculation? |
| 9 | Function | | Which function is used to count the amount of data? |
| 10 | Function | | Which function is used to summarize the data? |
| 11 | Function | | Which function is used to return the square root of a number? |
Table 4.
Variables, values, and questions in VTPs.
| No | Value Description | Results | Questions |
|---|
| 1 | Length of data | 10 | What is the value from the length of data? |
| 2 | Summation of data | 110 | What is the value from the summation of data? |
| 3 | Mean | 11 | What is the average value of the given dataset? |
| 4 | Variance | | What is the value of variance? |
| 5 | Standard deviation | | What is the value of standard deviation? |
Table 5.
Instances in basic statistics topics.
| ID | Topic | Number of Questions |
|---|
| EFP | GUP | VTP | Total |
|---|
| 1 | Mean | 4 | 2 | 2 | 8 |
| 2 | Median | 16 | 1 | 1 | 18 |
| 3 | Mode | 5 | 4 | 1 | 10 |
| 4 | Variance | 11 | 0 | 1 | 12 |
| 5 | Standard Deviation | 12 | 3 | 2 | 17 |
| 6 | Coefficient of Variation | 16 | 4 | 2 | 22 |
| 7 | Range | 4 | 2 | 1 | 7 |
| 8 | Quartile 1 | 18 | 1 | 2 | 21 |
| 9 | Quartile 2 | 16 | 1 | 2 | 19 |
| 10 | Quartile 3 | 16 | 2 | 2 | 20 |
| 11 | Decile | 16 | 3 | 2 | 21 |
| 12 | Percentile | 16 | 3 | 2 | 21 |
| 13 | Skewness | 21 | 2 | 2 | 25 |
| 14 | Kurtosis | 36 | 2 | 2 | 40 |
Table 6.
Instances in advanced statistics topics.
| ID | Topic | Number of Questions |
|---|
| EFP | GUP | VTP | Total |
|---|
| 15 | Binomial Distribution | 10 | 3 | 1 | 14 |
| 16 | Multinomial Distribution | 14 | 5 | 1 | 20 |
| 17 | Geometric Distribution | 10 | 1 | 1 | 12 |
| 18 | Poisson Distribution | 20 | 4 | 1 | 25 |
| 19 | Normal Distribution | 18 | 5 | 1 | 24 |
| 20 | t-Distribution | 7 | 5 | 2 | 14 |
| 21 | Exponential Distribution | 16 | 1 | 1 | 18 |
| 22 | Chi-Square Distribution | 11 | 5 | 2 | 18 |
Table 7.
Summary of solution results in basic and advanced statistics topics.
| Statistics Topics | Variables | Parameters | Number of Submission | Correct Answer Rate |
|---|
| Session 1 | Session 2 | Session 1 | Session 2 |
|---|
| Basic Statistics | Instances | Mean | 1.81 | 1.96 | 100% | 100% |
| Std Dev | 0.26 | 0.34 | 0% | 0% |
| Students | Mean | 1.81 | 1.96 | 100% | 100% |
| Std Dev | 0.67 | 0.50 | 0% | 0% |
| Advanced Statistics | Instances | Mean | 3.34 | 3.32 | 98.39% | 99.50% |
| Std Dev | 0.86 | 0.77 | 1.62% | 0.52% |
| Students | Mean | 3.31 | 3.32 | 98.46% | 99.50% |
| Std Dev | 1.08 | 1.51 | 1.18% | 0.82% |
Table 8.
Data of average number of submissions and number of questions for determining instances difficulty analysis.
| Instance IDs | Average # of Submissions | Number of Questions |
|---|
| 1 | 1.63 | 8 |
| 2 | 1.71 | 18 |
| 3 | 1.90 | 10 |
| 4 | 1.79 | 12 |
| 5 | 2.06 | 17 |
| 6 | 1.98 | 22 |
| 7 | 1.28 | 7 |
| 8 | 1.95 | 21 |
| 9 | 1.88 | 19 |
| 10 | 1.66 | 20 |
| 11 | 1.98 | 21 |
| 12 | 1.79 | 21 |
| 13 | 2.30 | 25 |
| 14 | 2.49 | 40 |
| 15 | 2.37 | 14 |
| 16 | 3.04 | 20 |
| 17 | 2.60 | 12 |
| 18 | 2.72 | 25 |
| 19 | 3.97 | 24 |
| 20 | 3.53 | 14 |
| 21 | 3.58 | 18 |
| 22 | 4.80 | 18 |
Table 9.
Average of correct answer rate and pre-test score data for student ability analysis.
| Student IDs | Average Correct Answer Rate | Pre-Test Score |
|---|
| 1 | 99.35 | 85 |
| 2 | 99.88 | 85 |
| 3 | 99.32 | 100 |
| 4 | 99.00 | 100 |
| 5 | 99.79 | 85 |
| 6 | 99.32 | 85 |
| 7 | 99.67 | 85 |
| 8 | 99.49 | 85 |
| 9 | 99.79 | 100 |
| 10 | 100 | 85 |
| 11 | 99.36 | 100 |
| 12 | 100 | 75 |
| 13 | 99.41 | 100 |
| 14 | 100 | 95 |
| 15 | 99.14 | 85 |
| 16 | 100 | 85 |
| 17 | 99.33 | 85 |
| 18 | 99.28 | 85 |
| 19 | 99.58 | 100 |
| 20 | 99.43 | 100 |
| 21 | 99.71 | 75 |
| 22 | 98.82 | 100 |
| 23 | 100 | 85 |
| 24 | 98.96 | 100 |
| 25 | 99.58 | 100 |
| 26 | 99.55 | 100 |
| 27 | 99.24 | 100 |
| 28 | 99.74 | 100 |
| 29 | 98.88 | 75 |
| 30 | 100 | 100 |
| 31 | 99.46 | 100 |
| 32 | 99.65 | 100 |
| 33 | 99.06 | 75 |
| 34 | 100 | 100 |
| 35 | 100 | 85 |
| 36 | 99.33 | 75 |
| 37 | 99.21 | 100 |
| 38 | 98.13 | 85 |
| 39 | 99.58 | 85 |
| 40 | 99.58 | 100 |
Table 10.
Summary of data for use of statistics in correlation analysis and multiple linear regression analysis.
| Instance ID | Number of Questions (Difficulty) | Avg. Submission | Avg. Correct Answer Rate (%) |
|---|
| 1 | 8 | 1.63 | 100 |
| 2 | 18 | 1.71 | 100 |
| 3 | 10 | 1.90 | 100 |
| 4 | 12 | 1.79 | 100 |
| 5 | 17 | 2.06 | 100 |
| 6 | 22 | 1.98 | 100 |
| 7 | 7 | 1.28 | 100 |
| 8 | 21 | 1.95 | 100 |
| 9 | 19 | 1.88 | 100 |
| 10 | 20 | 1.66 | 100 |
| 11 | 21 | 1.98 | 100 |
| 12 | 21 | 1.79 | 100 |
| 13 | 25 | 2.30 | 100 |
| 14 | 40 | 2.49 | 100 |
| 15 | 14 | 2.37 | 99.91 |
| 16 | 20 | 3.04 | 99.70 |
| 17 | 12 | 2.60 | 99.08 |
| 18 | 25 | 2.72 | 99.80 |
| 19 | 24 | 3.97 | 99.33 |
| 20 | 14 | 3.53 | 97.29 |
| 21 | 18 | 3.58 | 99.39 |
| 22 | 18 | 4.80 | 97.05 |
Table 11.
Correlation analysis between three factors for each instance.
| | Number of Questions | Avg. Submission | Avg. Correct Answer Rates |
|---|
| Number of Questions | 1.000 | 0.217 | 0.117 |
| Avg. Submission | 0.217 | 1.000 | |
| Avg. Correct Answer Rates | 0.117 | | 1.000 |
Table 12.
Student final grades in the fundamental statistics course.
| Class | Number of Students | Mean | Std. Dev |
|---|
| Class 1 | 40 | 81.08 | 2.65 |
| Class 2 | 40 | 78.04 | 5.58 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).