Mitigating Selection Bias in Local Optima: A Meta-Analysis of Niching Methods in Continuous Optimization
Abstract
1. Introduction
2. Background
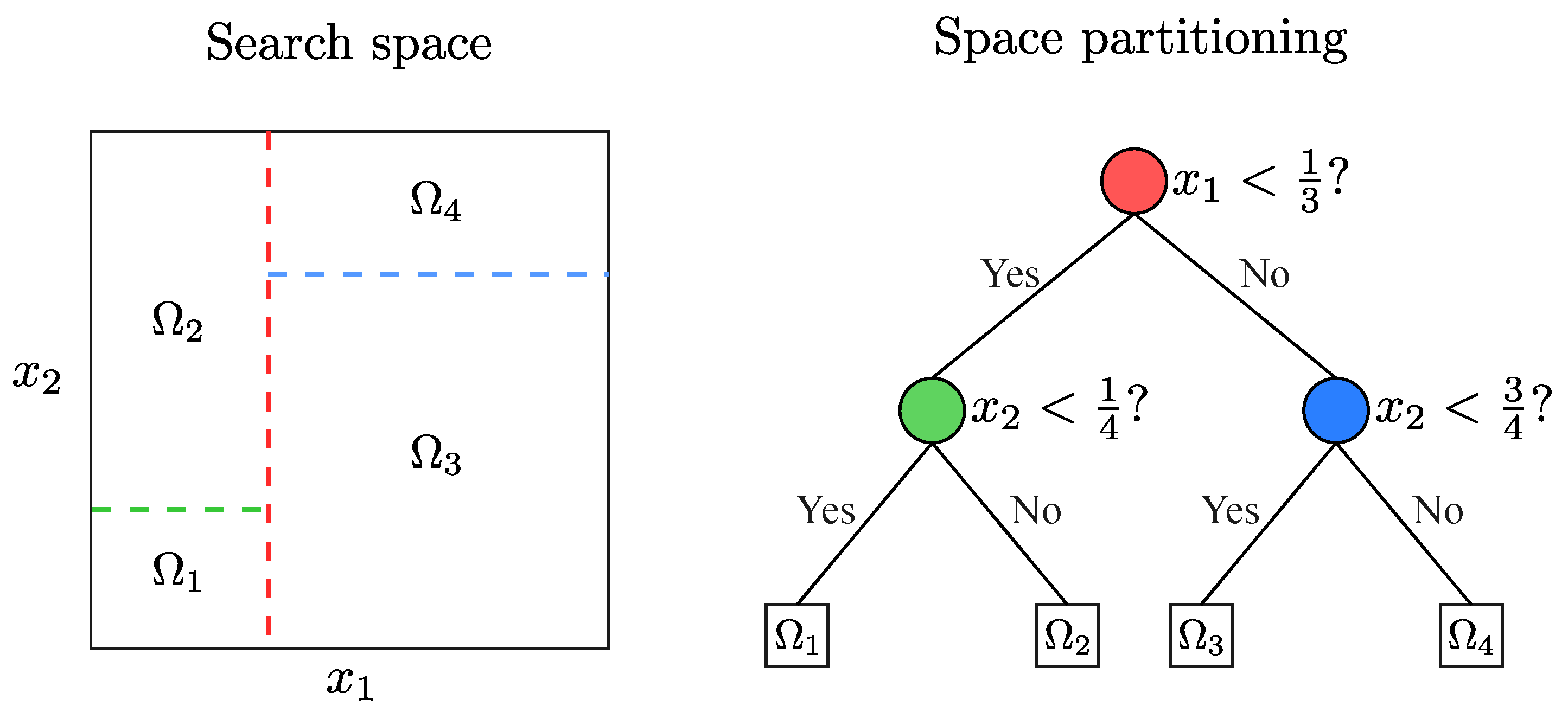
2.1. Basin of Attraction
2.2. Free Peaks
2.3. Niching Methods
3. Benchmark Scenarios
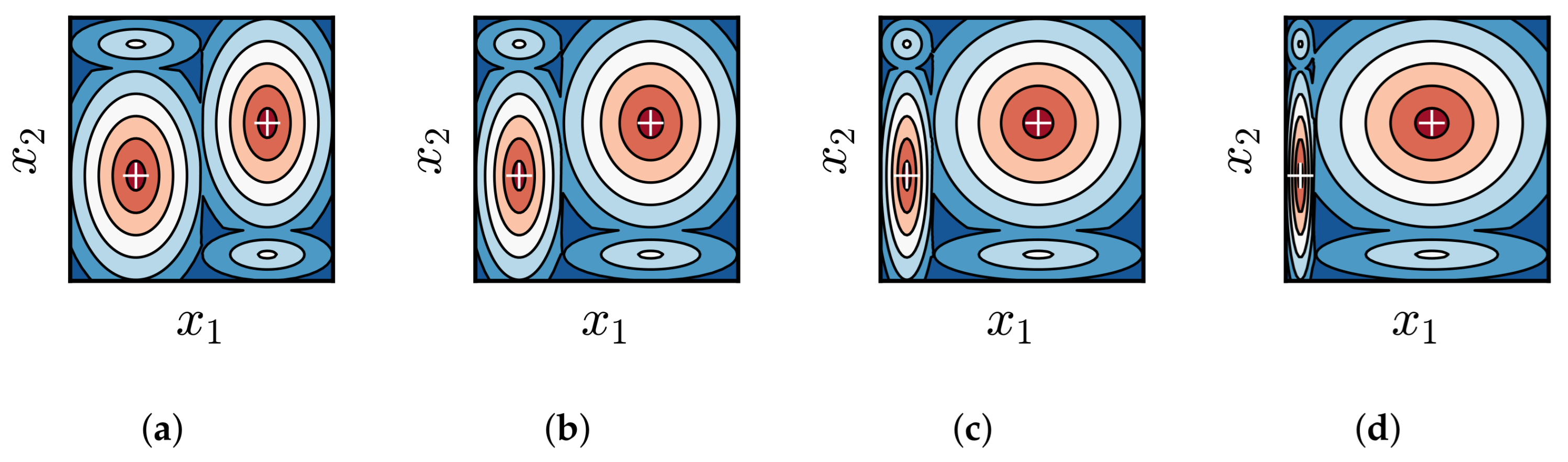
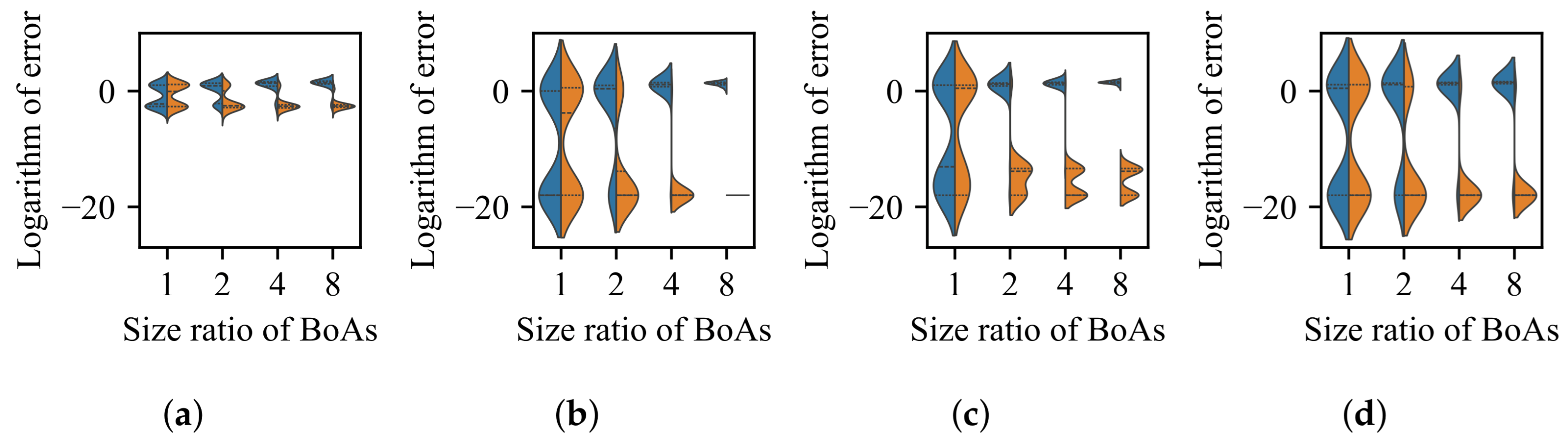
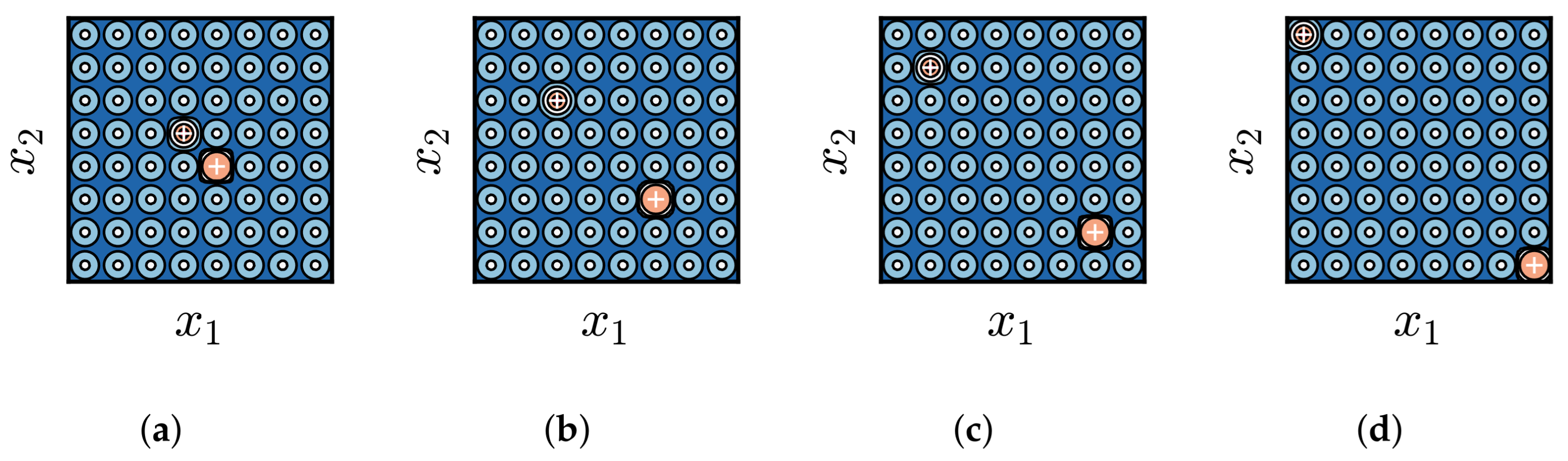
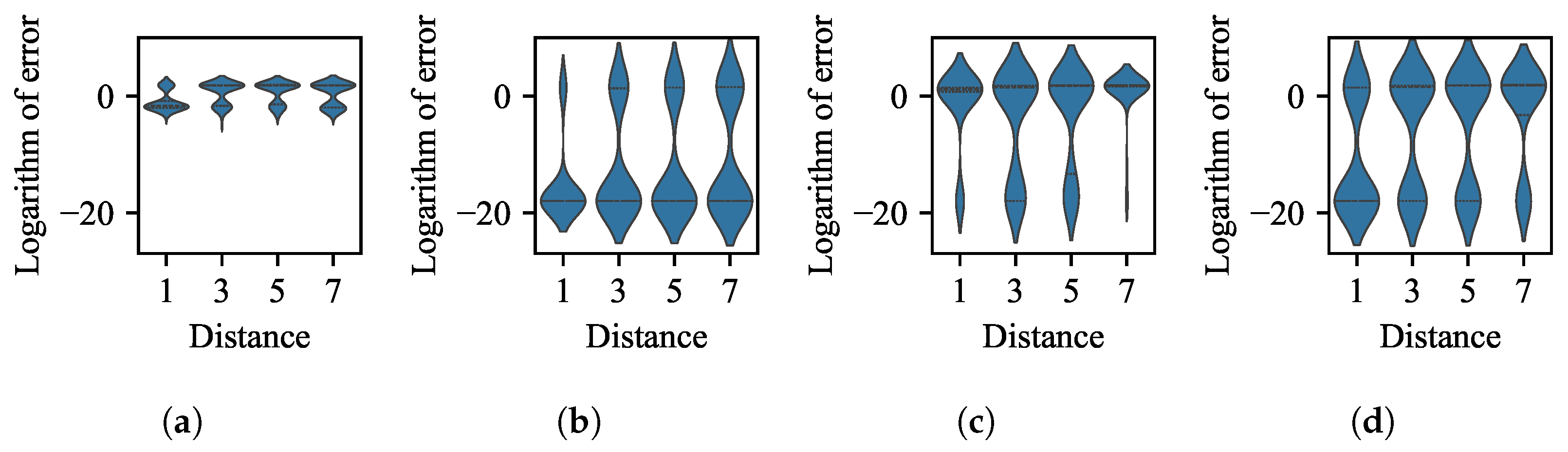
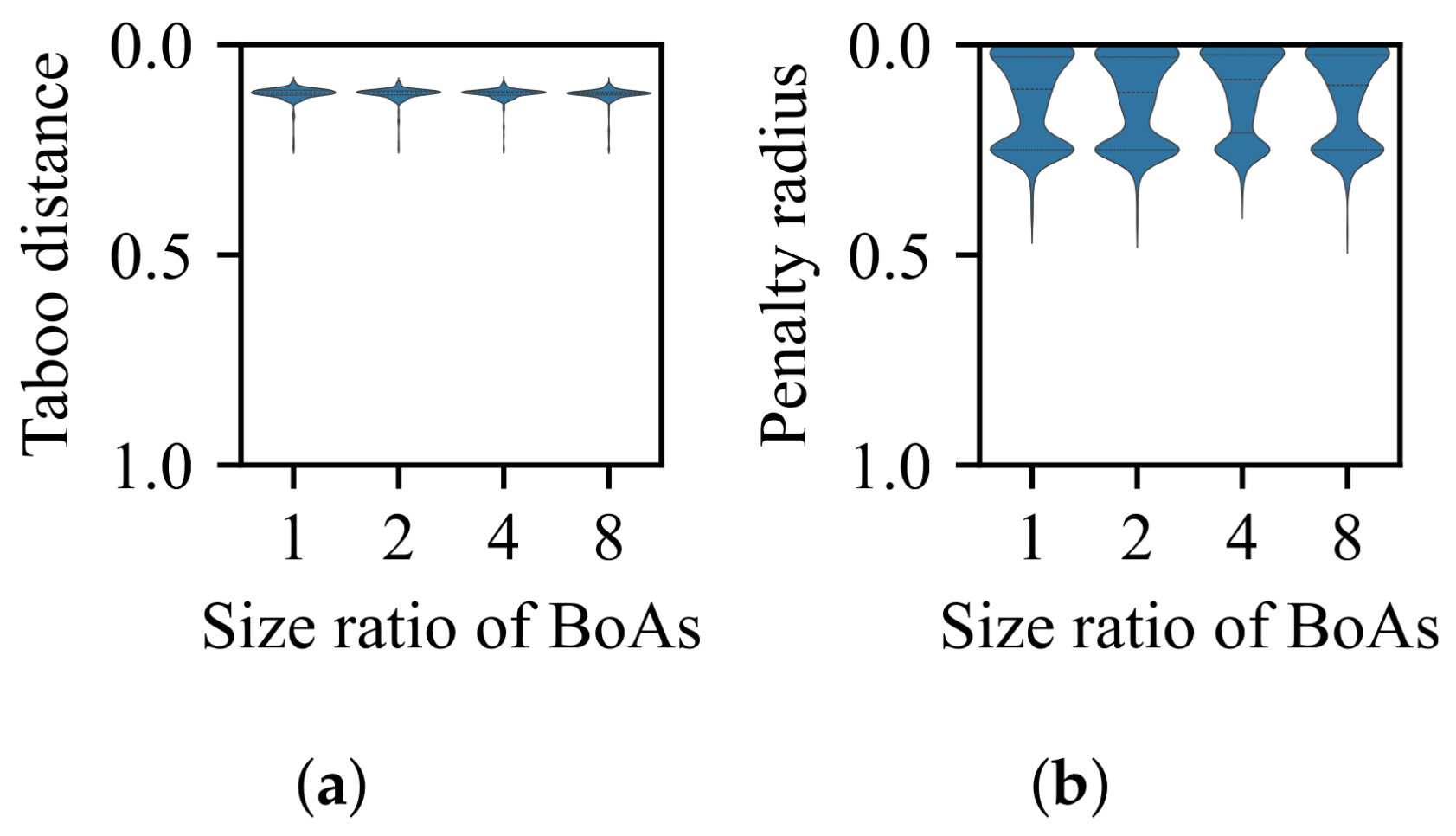
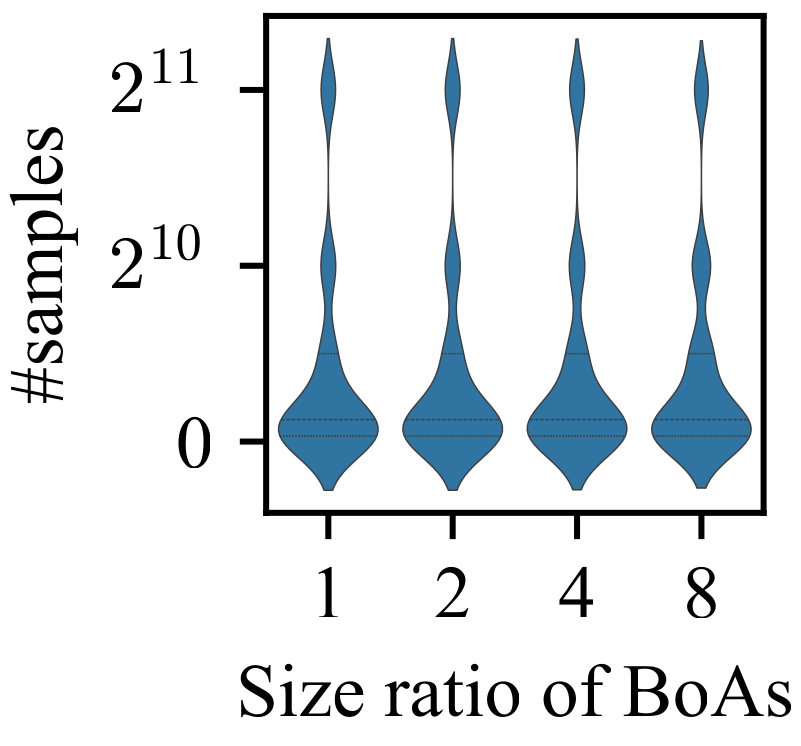
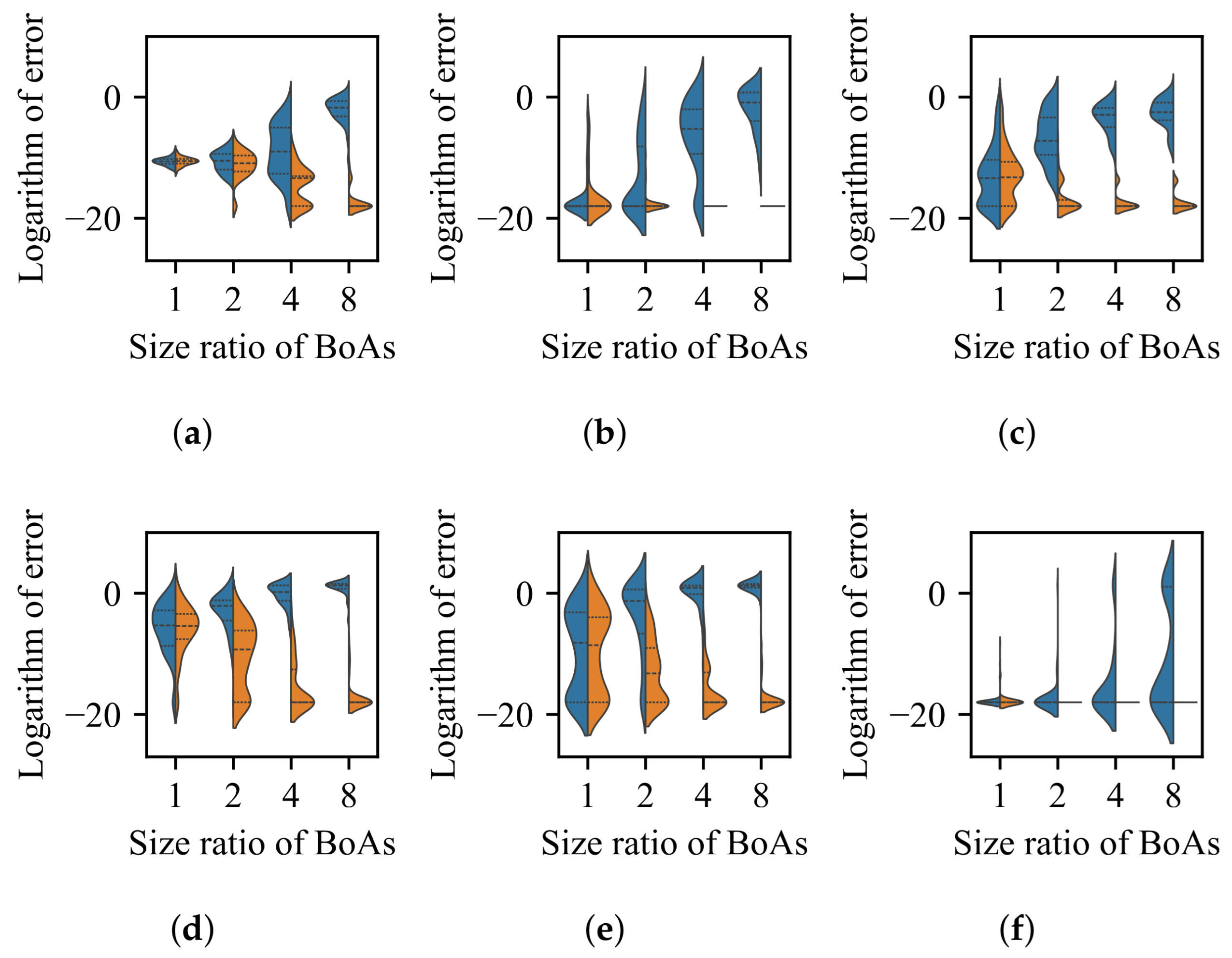
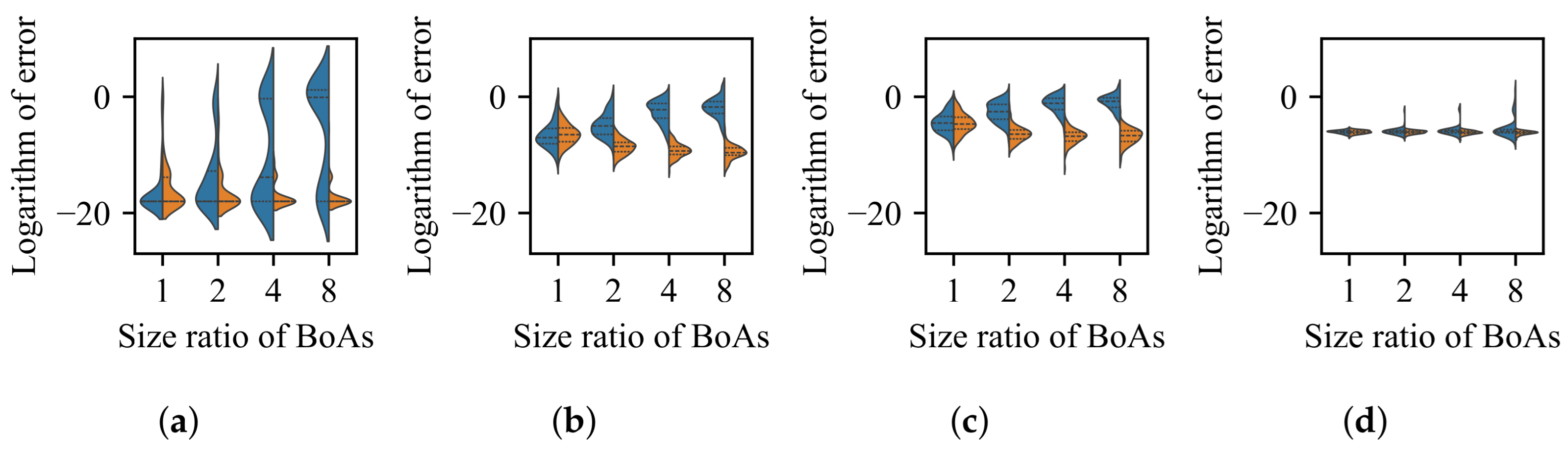
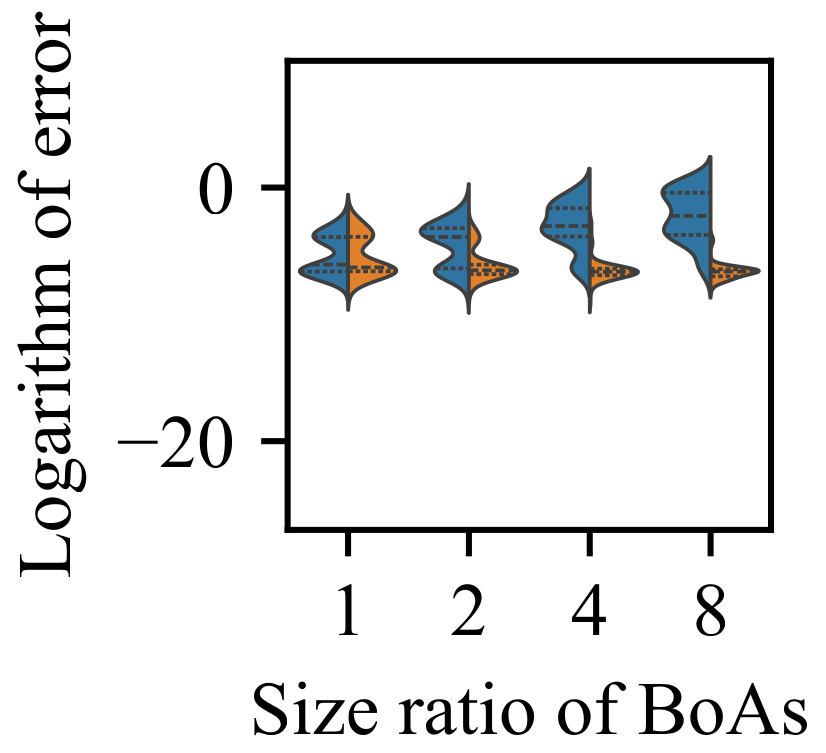
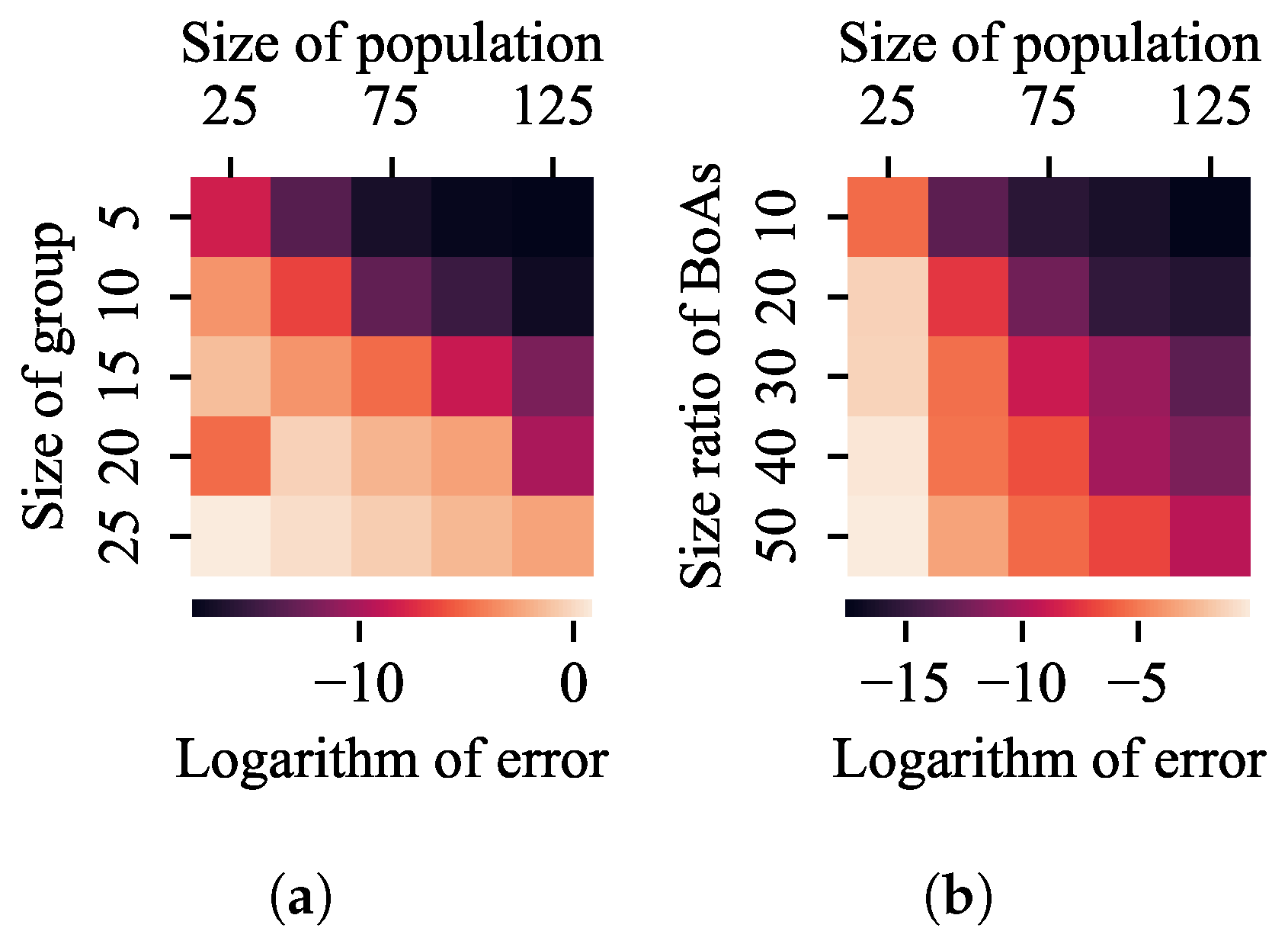
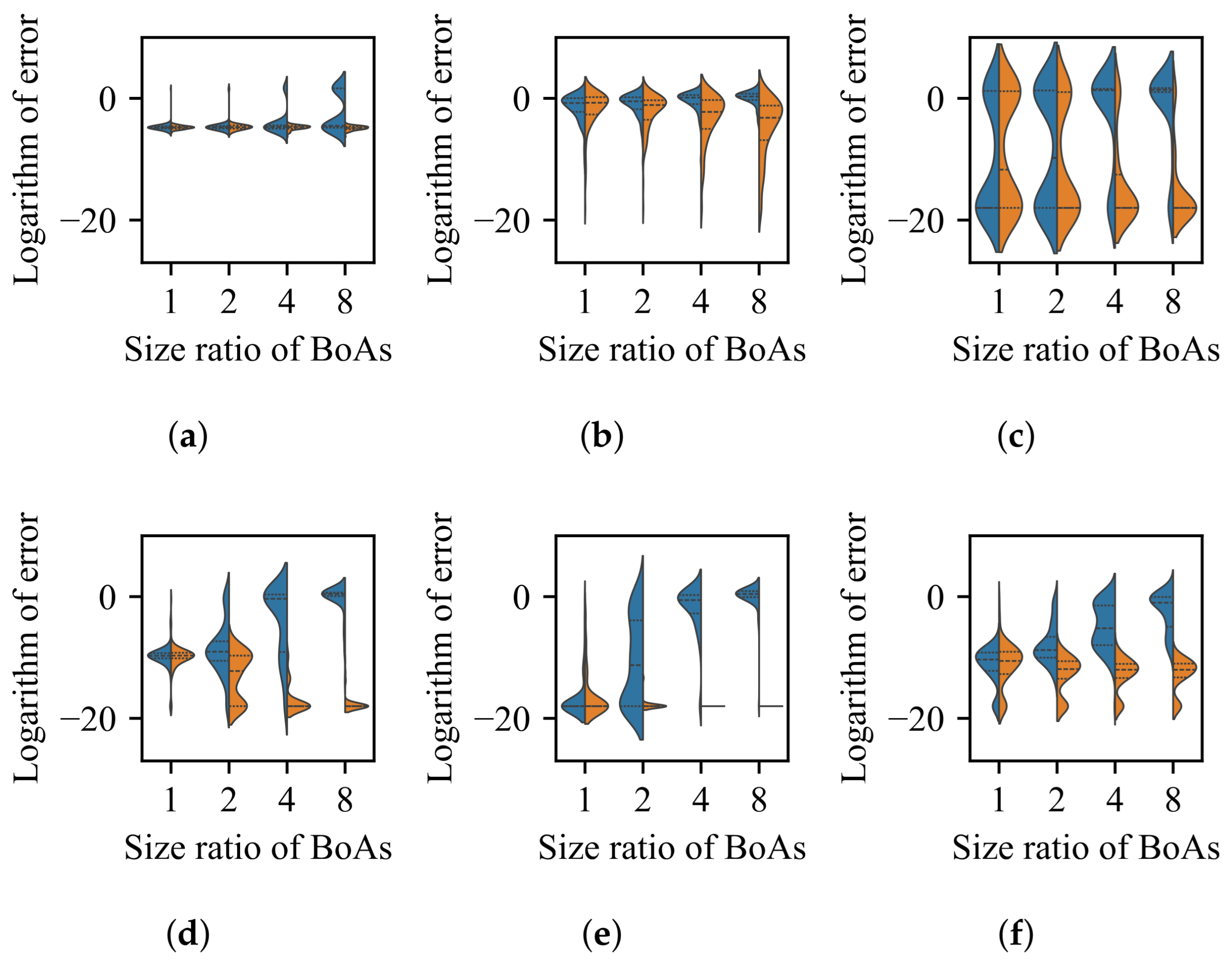
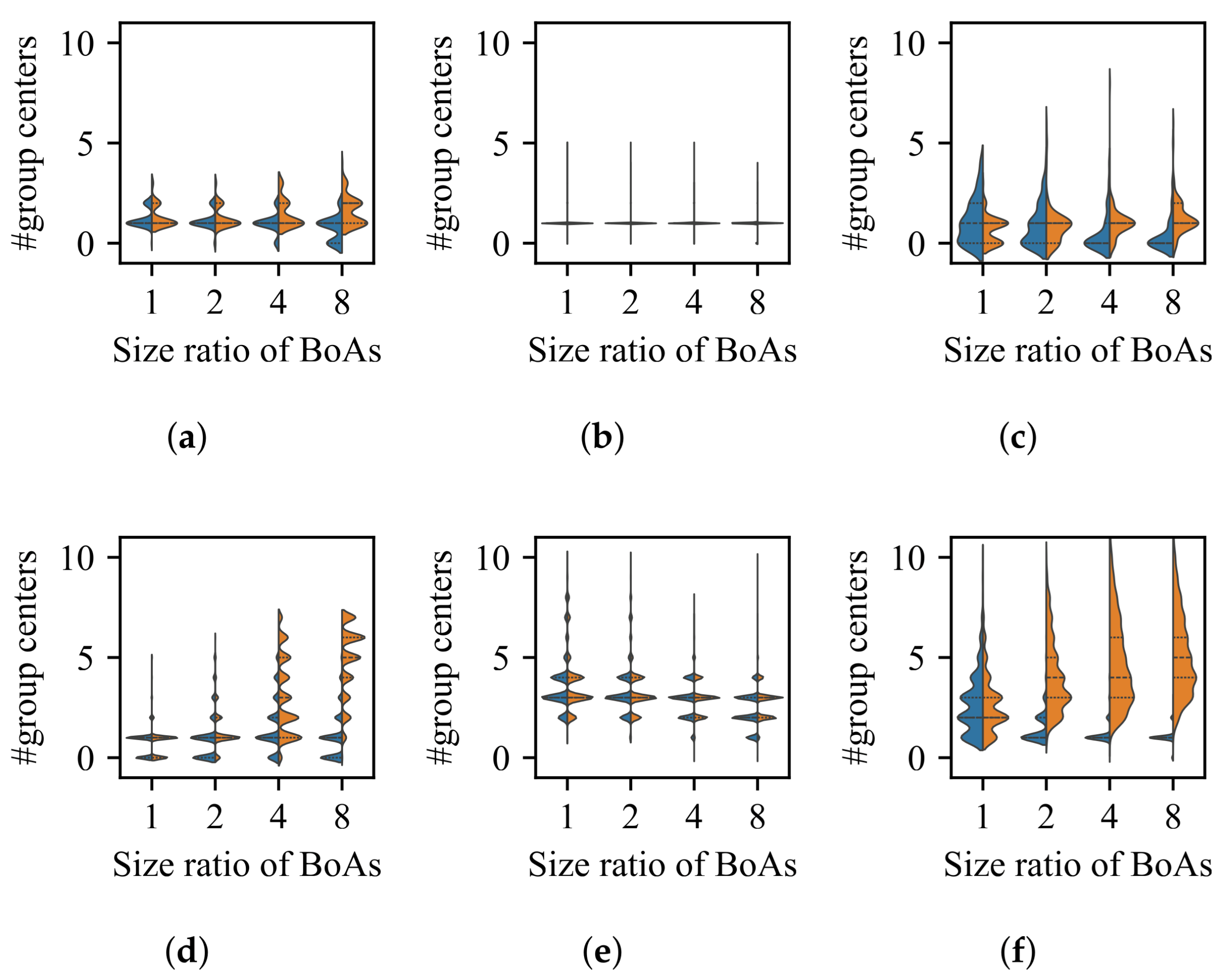
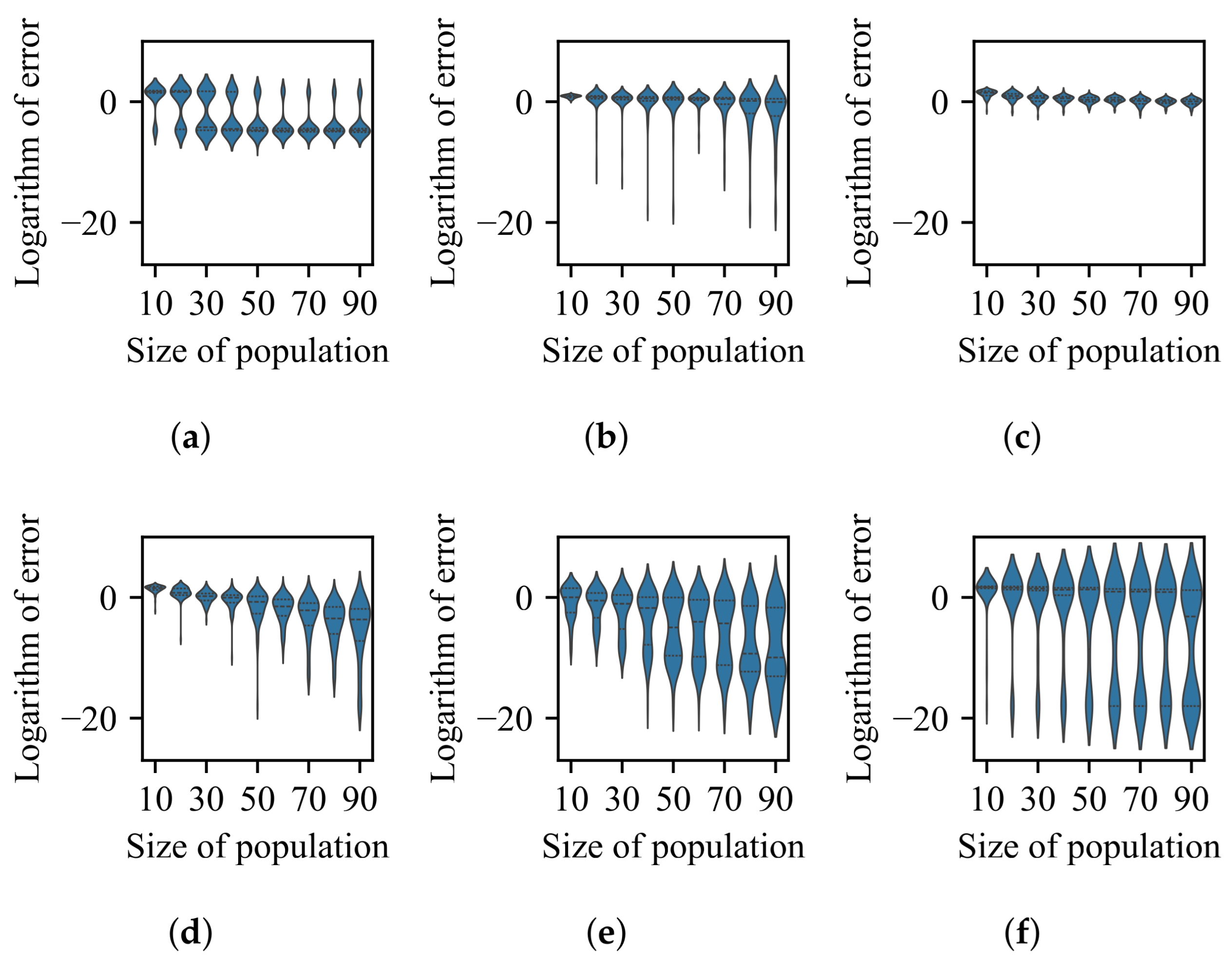
3.1. Impact of Difference in Size Between BoAs
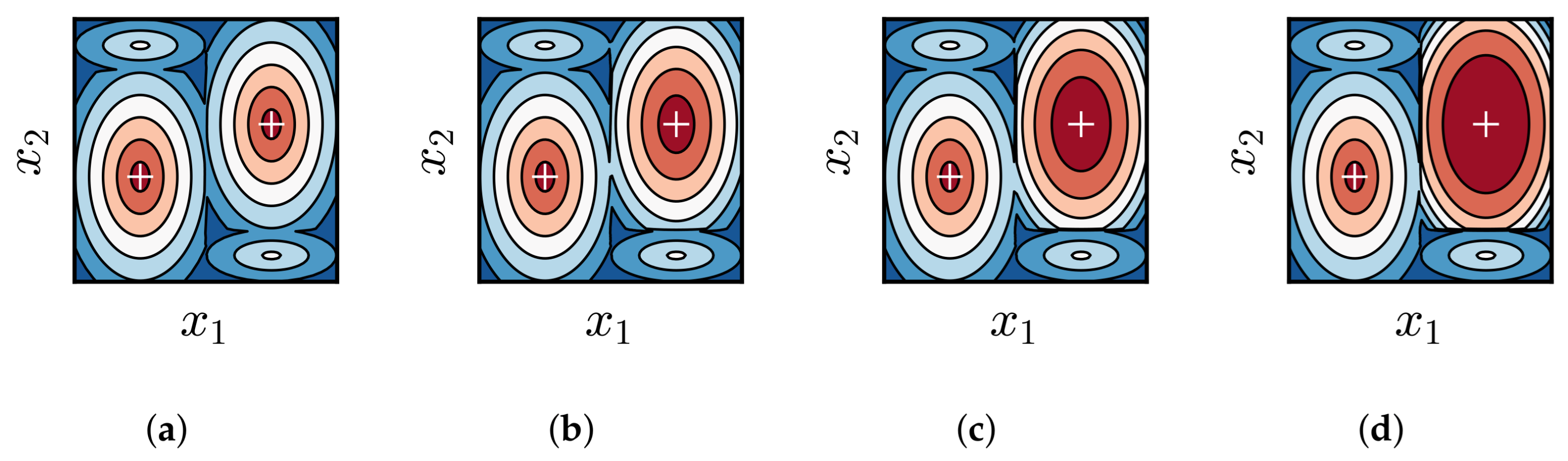
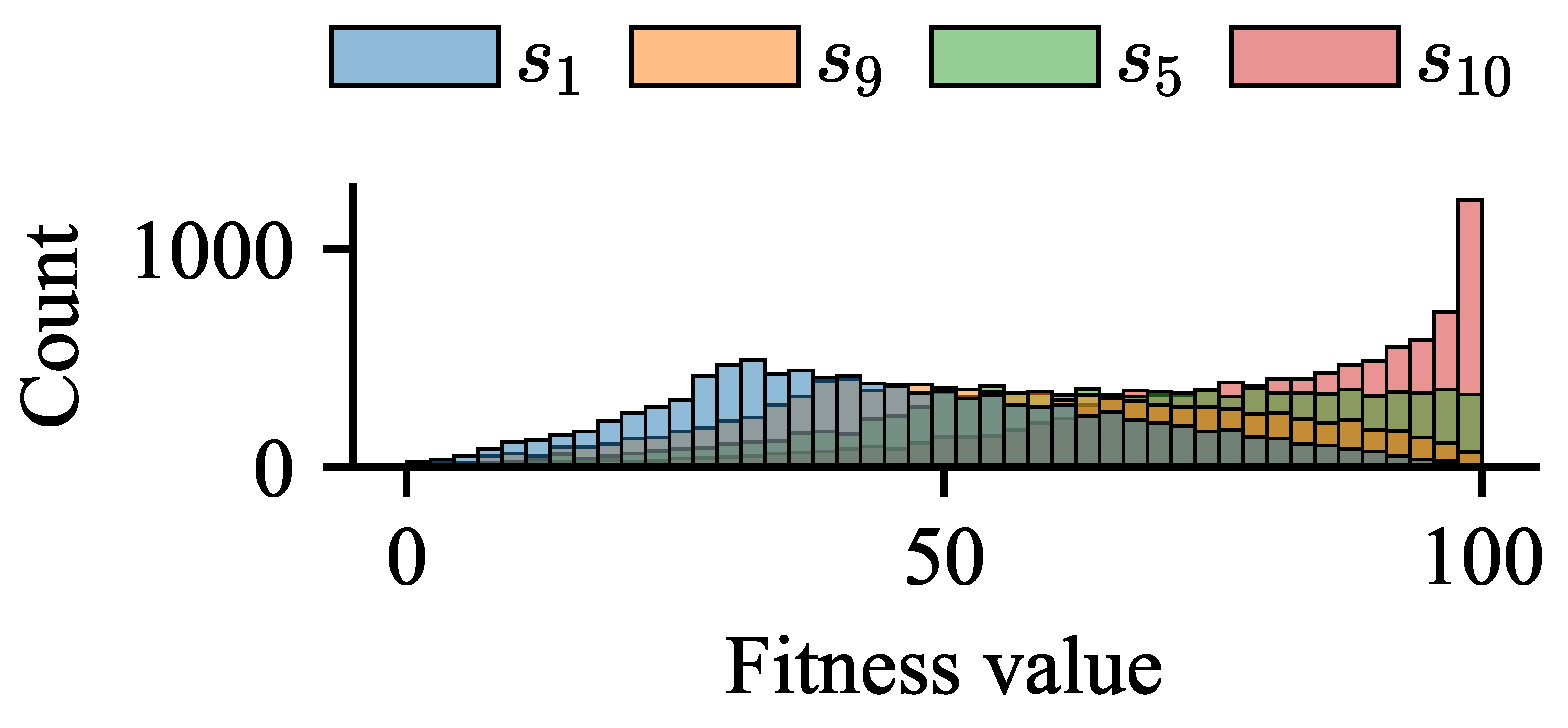
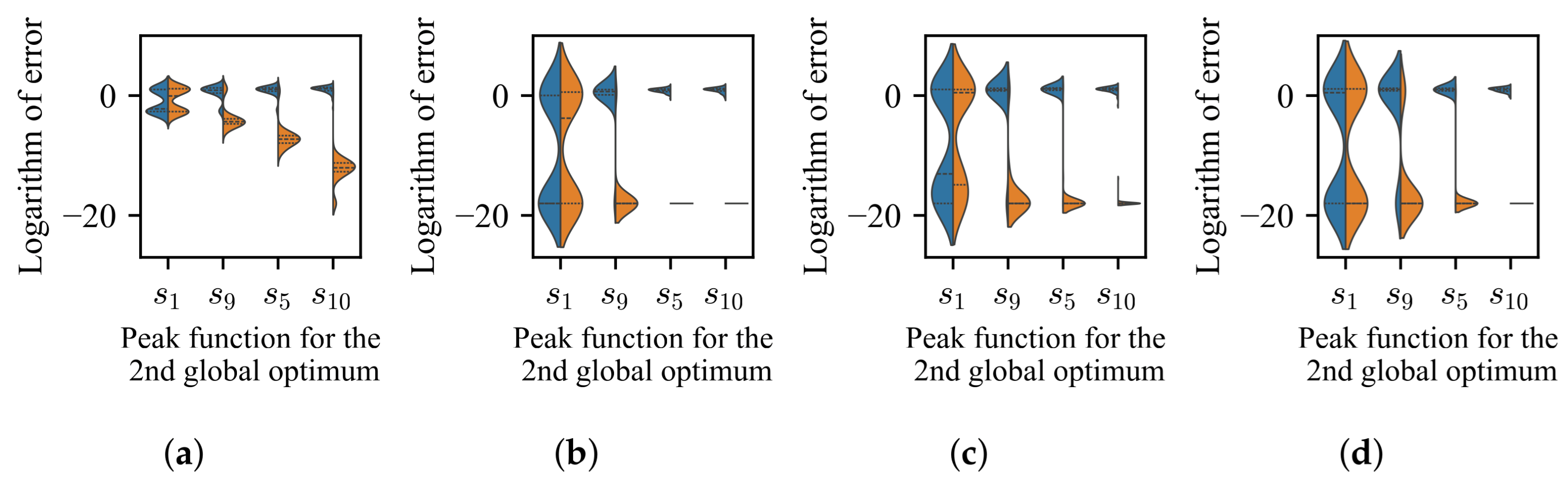
3.2. Impact of Difference in Average Fitness Between BoAs
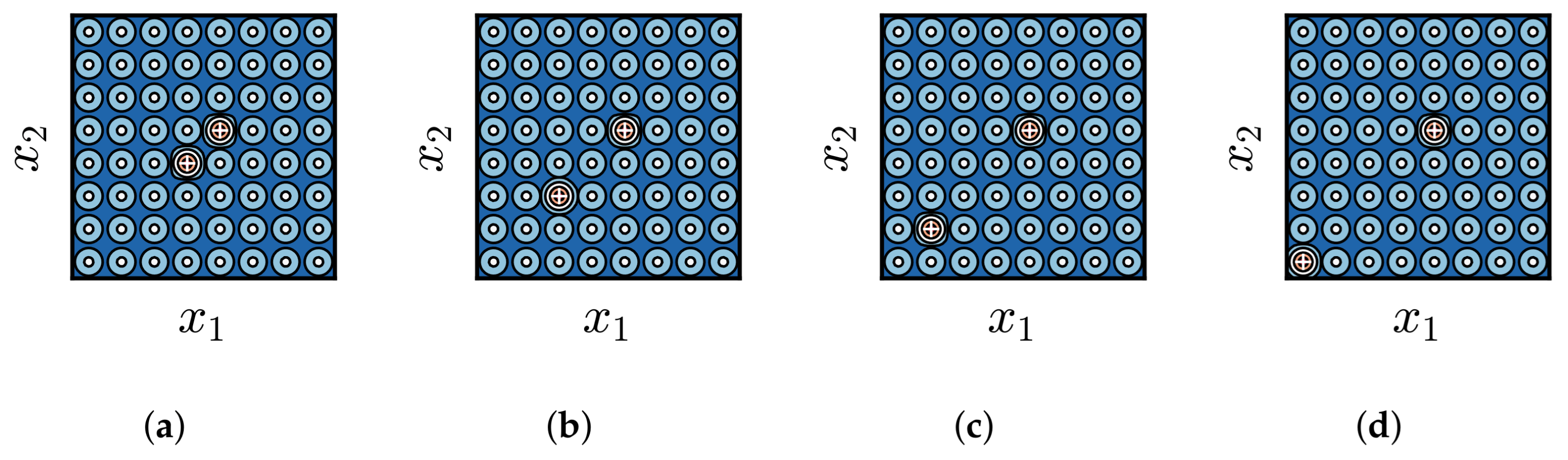
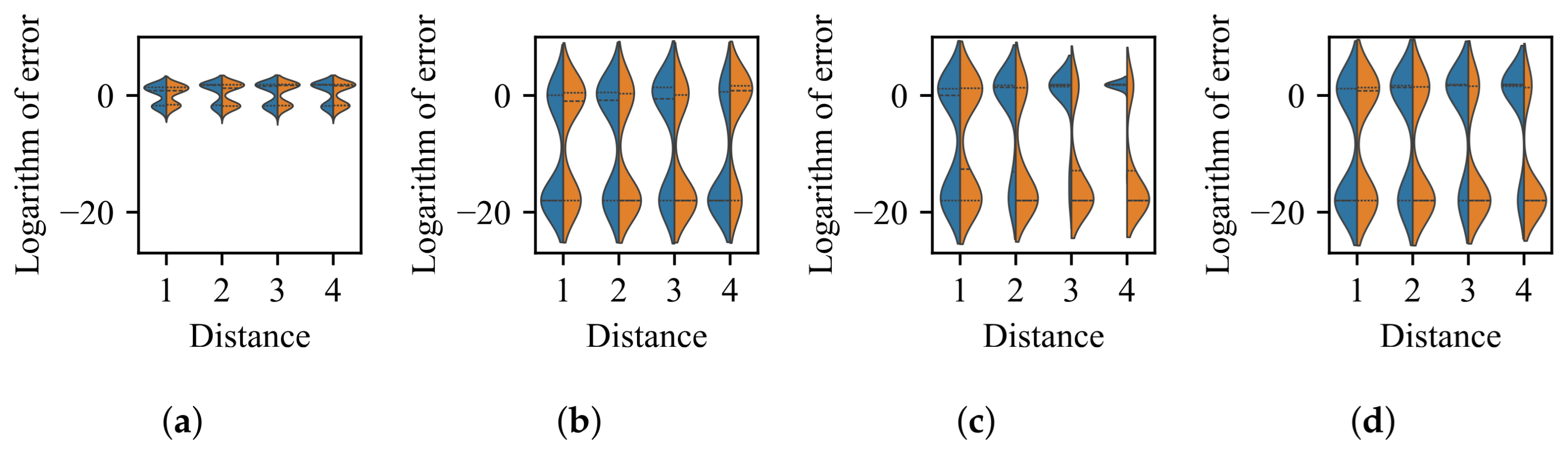
3.3. Impact of Difference in Distribution Between BoAs
3.4. Discussion
4. Niching Techniques
- Radial repulsion: If an individual is deemed to be sufficiently close to a local optimum, then all other individuals that are at a distance greater than a given threshold from this individual cannot be replaced by this individual or any other individuals that are at a distance less than the given threshold from this individual.
- Valley detection: An individual cannot be replaced by another individual if there exists a worse individual between them. The method to determine whether such a worse individual exists involves sampling and evaluating a specified number of gradation points at equal intervals along the line segment connecting the two individuals.
- k-nearest neighbors: An individual can only be replaced by a given number of individuals that are closest to it.
- Clustering with a specified number of groups: Individuals are divided into a specified number of equally sized groups, with the aim of ensuring that the centers of these groups are as optimal and as far apart from one another as possible. Competition is confined within each group.
- Clustering with an adaptive number of groups: Individuals are divided into a dynamically adjusted number of groups based on their density in the search space or dominance relationships. Competition is confined within each group.
- Techniques that appeared decades ago, namely radial repulsion and valley detection, are still adopted in some state-of-the-art niching methods;
- In the niching methods of the past decade, the k-nearest neighbors technique and two clustering-based techniques have gained significant popularity;
- The k-nearest neighbors technique is frequently used in conjunction with other techniques.
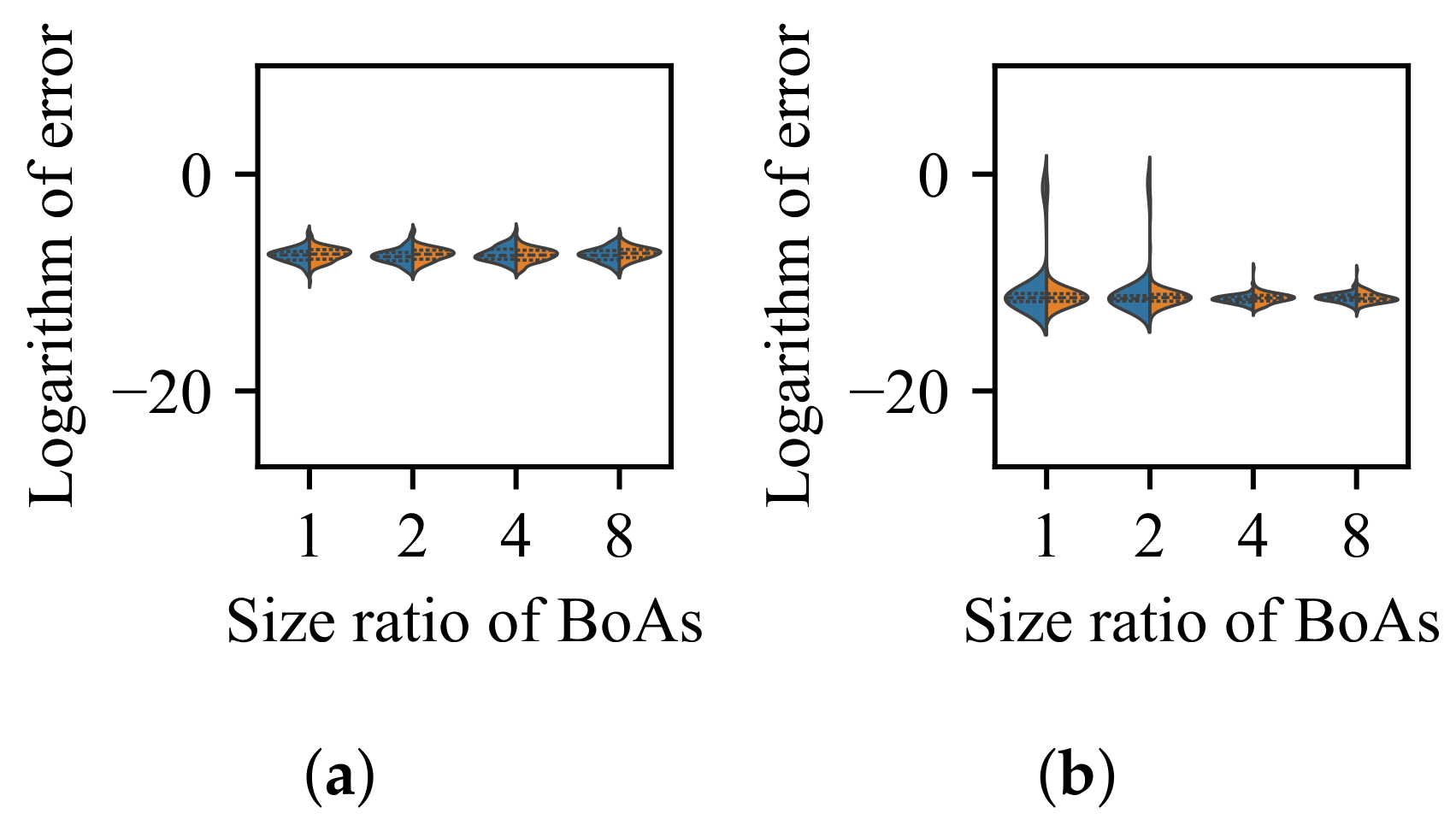
4.1. Radial Repulsion
| Algorithm 1: LRDE |
 |
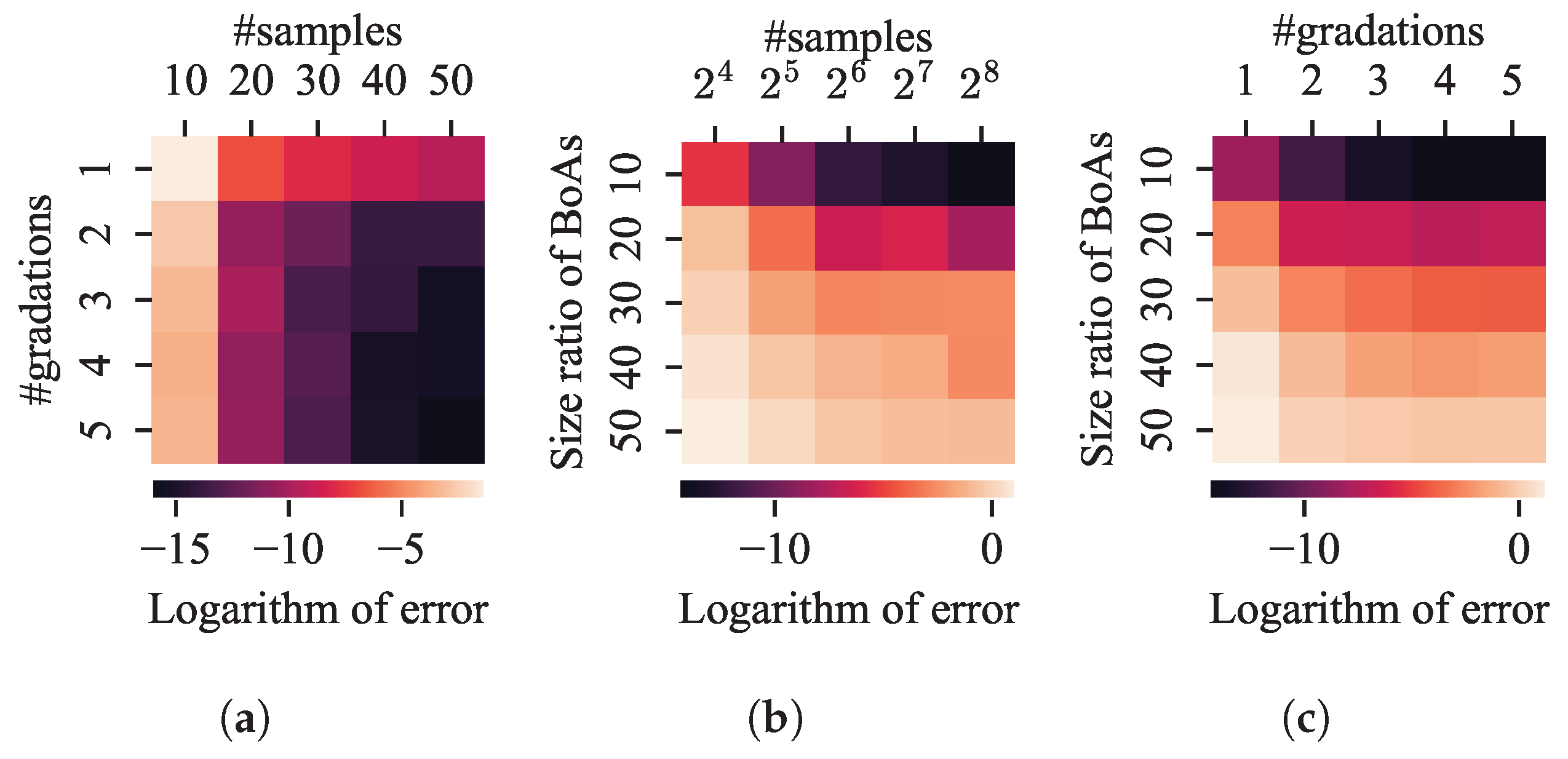
Valley Detection
| Algorithm 2: HVES |
 |
| Algorithm 3: valley Detect |
 |
4.2. k-Nearest Neighbors
| Algorithm 4: kNPSO |
 |
4.3. Clustering with a Specified Number of Groups
4.4. Clustering with an Adaptive Number of Groups
5. Conclusions
- The difference in size of the superior region between BoAs represents a common obstacle for most EC methods, whereas the differential distribution of local optima primarily hinders EC methods with less uniform reproduction operators, such as CMA-ES.
- After classifying the niching techniques into five categories, each characterized by a unique set of key parameters, the potential of each category obtained through parameter tuning is as follows:
- –
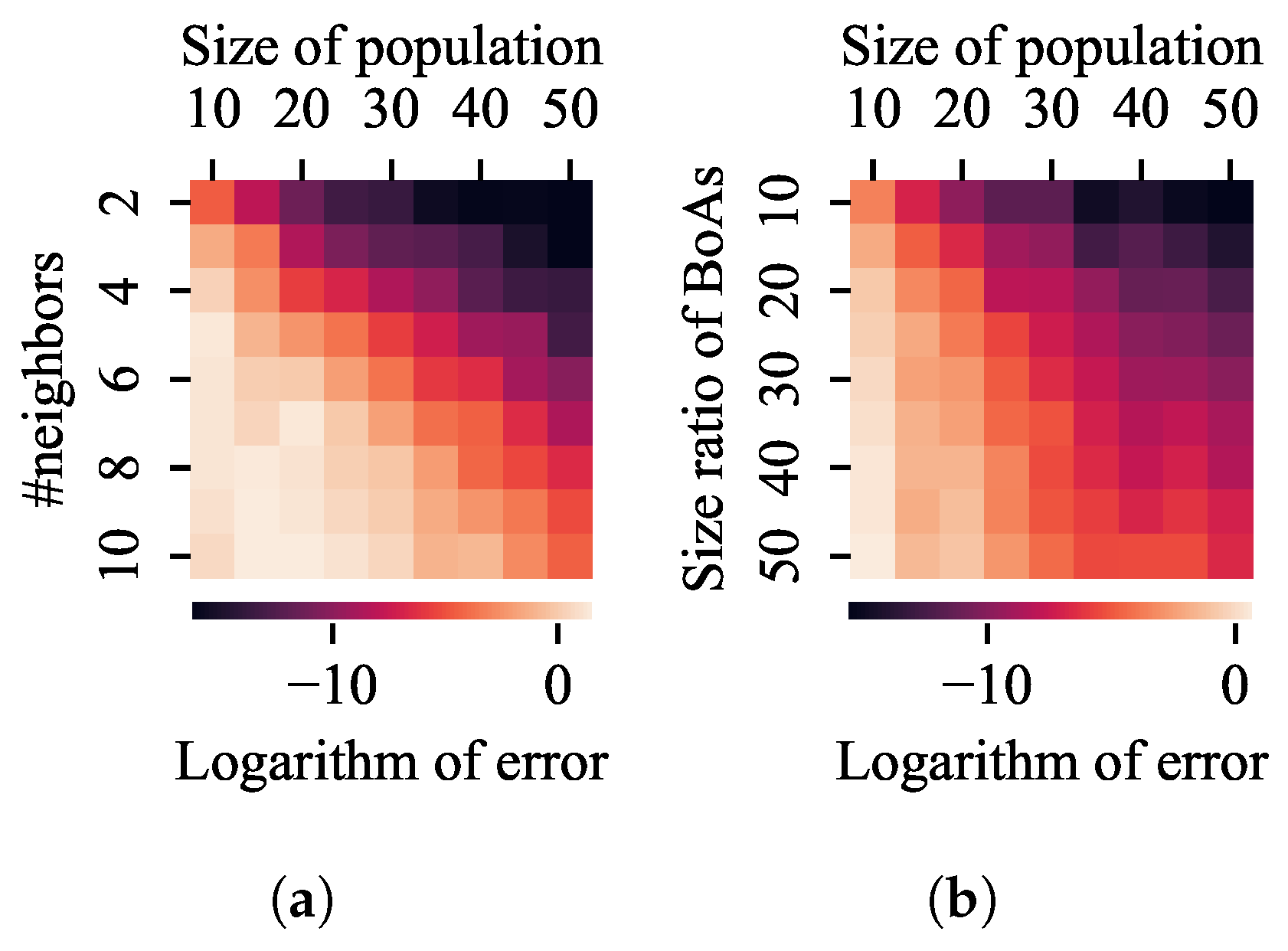
- The radial repulsion technique can be enhanced by setting the repulsion radius within a narrower and more suitable range; however, determining the optimal range remains challenging.
- –
- The performance of the valley detection can be improved by increasing the population size or the number of gradations. Nevertheless, an exponential increase in population size is necessary to counteract the challenge posed by a linear increase in the difference between BoA sizes.
- –
- Both the k-nearest neighbors and clustering with a specified number of groups techniques can be improved by reducing the number of neighbors or the group size while increasing the population size. Despite a minimum threshold for the number of neighbors or group size, a linear increase in population size can overcome the challenge presented by a linear growth in the difference between BoA sizes.
- –
- The capability of the clustering with an adaptive number of groups technique can be enhanced by increasing the population size. While it is relatively straightforward for the adaptive clustering methods employed in current EC methods that use this technique to identify the presence of more challenging optima, there is a need for more balanced strategies to distribute function evaluations between these and other easily discoverable optima.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bu, C.; Luo, W.; Yue, L. Continuous dynamic constrained optimization with ensemble of locating and tracking feasible regions strategies. IEEE Trans. Evol. Comput. 2016, 21, 14–33. [Google Scholar] [CrossRef]
- Liang, J.J.; Yue, C.; Qu, B.Y. Multimodal multi-objective optimization: A preliminary study. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 2454–2461. [Google Scholar]
- Weise, T.; Chiong, R.; Tang, K. Evolutionary optimization: Pitfalls and booby traps. J. Comput. Sci. Technol. 2012, 27, 907–936. [Google Scholar] [CrossRef]
- Baketarić, M.; Mernik, M.; Kosar, T. Attraction basins in metaheuristics: A systematic mapping study. Mathematics 2021, 9, 3036. [Google Scholar] [CrossRef]
- Li, X.; Engelbrecht, A.; Epitropakis, M.G. Benchmark Functions for CEC’2013 Special Session and Competition on Niching Methods for Multimodal Function Optimization; Technical Report; Evolutionary Computation and Machine Learning Group, RMIT University: Melbourne, VIC, Australia, 2013. [Google Scholar]
- Qu, B.; Liang, J.J.; Wang, Z.; Chen, Q.; Suganthan, P.N. Novel benchmark functions for continuous multimodal optimization with comparative results. Swarm Evol. Comput. 2016, 26, 23–34. [Google Scholar] [CrossRef]
- Ahrari, A.; Deb, K.; Preuss, M. Multimodal optimization by covariance matrix self-adaptation evolution strategy with repelling subpopulations. Evol. Comput. 2017, 25, 439–471. [Google Scholar] [CrossRef]
- Ahrari, A.; Deb, K. A novel class of test problems for performance evaluation of niching methods. IEEE Trans. Evol. Comput. 2017, 22, 909–919. [Google Scholar] [CrossRef]
- Li, C.; Nguyen, T.T.; Zeng, S.; Yang, M.; Wu, M. An open framework for constructing continuous optimization problems. IEEE Trans. Cybern. 2018, 49, 2316–2330. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Richardson, J. Genetic algorithms with sharing for multimodal function optimization. In Genetic Algorithms and Their Applications, Proceedings of the Second International Conference on Genetic Algorithms, Cambridge, MA, USA, 28–31 July 1987; Lawrence Erlbaum: Hillsdale, NJ, USA, 1987; Volume 4149. [Google Scholar]
- Pétrowski, A. A clearing procedure as a niching method for genetic algorithms. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 798–803. [Google Scholar]
- Tsutsui, S.; Fujimoto, Y.; Ghosh, A. Forking genetic algorithms: GAs with search space division schemes. Evol. Comput. 1997, 5, 61–80. [Google Scholar] [CrossRef]
- Li, J.P.; Balazs, M.E.; Parks, G.T.; Clarkson, P.J. A species conserving genetic algorithm for multimodal function optimization. Evol. Comput. 2002, 10, 207–234. [Google Scholar] [CrossRef]
- Wei, Z.; Gao, W.; Li, G.; Zhang, Q. A penalty-based differential evolution for multimodal optimization. IEEE Trans. Cybern. 2021, 52, 6024–6033. [Google Scholar] [CrossRef]
- Ursem, R.K. Multinational evolutionary algorithms. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99, Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1633–1640. [Google Scholar]
- Yao, J.; Kharma, N.; Zhu, Y.Q. On clustering in evolutionary computation. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1752–1759. [Google Scholar]
- Stoean, C.; Preuss, M.; Stoean, R.; Dumitrescu, D. Multimodal optimization by means of a topological species conservation algorithm. IEEE Trans. Evol. Comput. 2010, 14, 842–864. [Google Scholar] [CrossRef]
- Maree, S.C.; Alderliesten, T.; Thierens, D.; Bosman, P.A.N. Real-valued evolutionary multi-modal optimization driven by hill-valley clustering. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO’18, Kyoto, Japan, 15–19 July 2018; Association for Computing Machinery: New York, NY, USA, 2018; pp. 857–864. [Google Scholar]
- Thomsen, R. Multimodal optimization using crowding-based differential evolution. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1382–1389. [Google Scholar]
- Epitropakis, M.G.; Plagianakos, V.P.; Vrahatis, M.N. Finding multiple global optima exploiting differential evolution’s niching capability. In Proceedings of the 2011 IEEE Symposium on Differential Evolution (SDE), Paris, France, 11–15 April 2011; pp. 1–8. [Google Scholar]
- Li, X. Niching without niching parameters: Particle swarm optimization using a ring topology. IEEE Trans. Evol. Comput. 2009, 14, 150–169. [Google Scholar]
- Qu, B.Y.; Suganthan, P.N.; Das, S. A distance-based locally informed particle swarm model for multimodal optimization. IEEE Trans. Evol. Comput. 2012, 17, 387–402. [Google Scholar] [CrossRef]
- Qu, B.Y.; Suganthan, P.N.; Liang, J.J. Differential evolution with neighborhood mutation for multimodal optimization. IEEE Trans. Evol. Comput. 2012, 16, 601–614. [Google Scholar] [CrossRef]
- Gao, W.; Yen, G.G.; Liu, S. A cluster-based differential evolution with self-adaptive strategy for multimodal optimization. IEEE Trans. Cybern. 2014, 44, 1314–1327. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Gong, W.; Deng, L.; Wang, L. Multimodal optimization via dynamically hybrid niching differential evolution. Knowl.-Based Syst. 2022, 238, 107972. [Google Scholar] [CrossRef]
- Preuss, M. Niching the CMA-ES via nearest-better clustering. In Proceedings of the 12th Annual Conference Companion on Genetic and Evolutionary Computation, Portland, OR, USA, 7–11 July 2010; pp. 1711–1718. [Google Scholar]
- Li, L.; Tang, K. History-based topological speciation for multimodal optimization. IEEE Trans. Evol. Comput. 2015, 19, 136–150. [Google Scholar] [CrossRef]
- Li, C.; Nguyen, T.T.; Yang, M.; Mavrovouniotis, M.; Yang, S. An adaptive multi-population framework for locating and tracking multiple optima. IEEE Trans. Evol. Comput. 2016, 4, 590–605. [Google Scholar] [CrossRef]
- Cheng, R.; Li, M.; Li, K.; Yao, X. Evolutionary multiobjective optimization-based multimodal optimization: Fitness landscape approximation and peak detection. IEEE Trans. Evol. Comput. 2017, 22, 692–706. [Google Scholar] [CrossRef]
- Wang, Z.J.; Zhan, Z.H.; Lin, Y.; Yu, W.J.; Wang, H.; Kwong, S.; Zhang, J. Automatic niching differential evolution with contour prediction approach for multimodal optimization problems. IEEE Trans. Evol. Comput. 2019, 24, 114–128. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhan, Z.; Tan, K.C.; Zhang, J. Optimizing niche center for multimodal optimization problems. IEEE Trans. Cybern. 2023, 53, 2544–2557. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Huang, L.; Gao, W.; Wei, Z.; Huang, T.; Xu, J.; Gong, M. History information-based hill-valley technique for multimodal optimization problems. Inf. Sci. 2023, 631, 15–30. [Google Scholar] [CrossRef]
- Wang, J.; Li, C.; Zeng, S.; Yang, S. History-guided hill exploration for evolutionary computation. IEEE Trans. Evol. Comput. 2023, 27, 1962–1975. [Google Scholar] [CrossRef]
- De Jong, K.A. An Analysis of the Behavior of a Class of Genetic Adaptive Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001, 9, 159–195. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Clerc, M.; Rojas, R. Standard particle swarm optimisation 2011 at CEC-2013: A baseline for future PSO improvements. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2337–2344. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization; Technical Report 2005005; Kanpur Genetic Algorithms Laboratory, IIT Kanpur: Kanpur, India, 2005. [Google Scholar]
- Beyer, H.G.; Sendhoff, B. Covariance matrix adaptation revisited—The CMSA evolution strategy–. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Dortmund, Germany, 13–17 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 123–132. [Google Scholar]
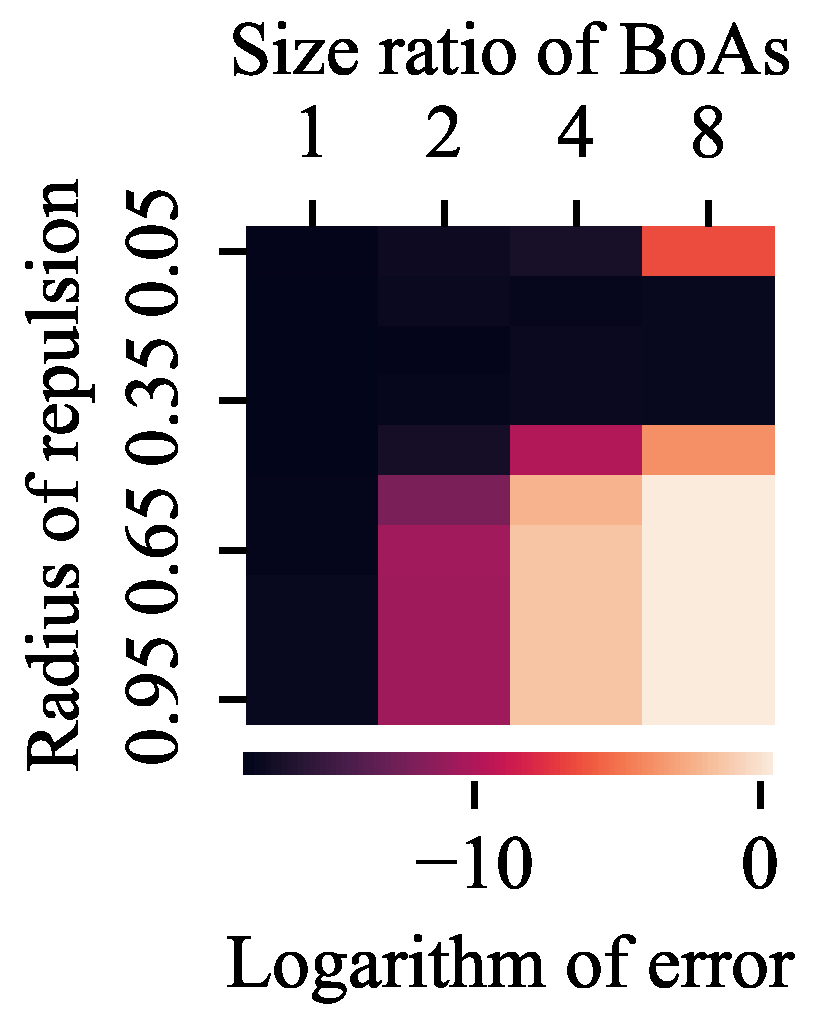
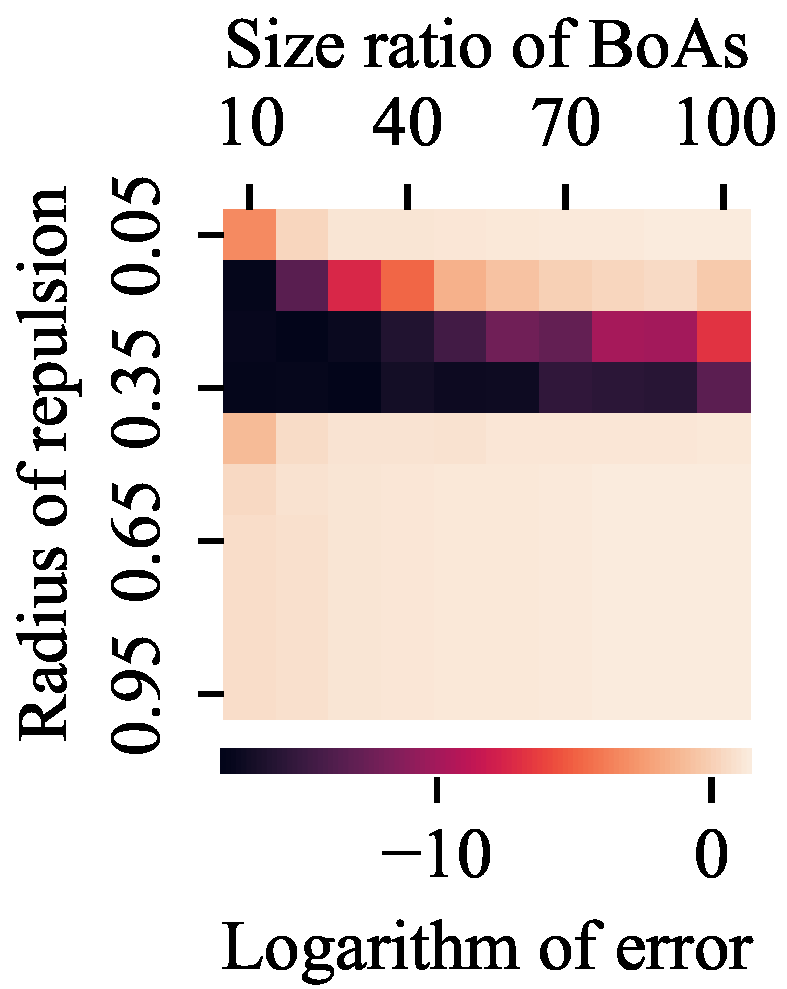



| Niching Method | Niching Technique | ||||
|---|---|---|---|---|---|
| Radial Repulsion | Valley Detection | -Nearest Neighbors | Clustering with a Specified # of Groups | Clustering with an Adaptive # of Groups | |
| Sharing [10] | ✓ | ||||
| Clearing [11] | ✓ | ||||
| Forking-GA [12] | ✓ | ||||
| Speciation [13] | ✓ | ||||
| PMODE [14] | ✓ | ||||
| RS-CMSA [7] | ✓ | ✓ | |||
| Multinationl EA [15] | ✓ | ||||
| DNC-RM [16] | ✓ | ||||
| TSC2 [17] | ✓ | ||||
| HillVallEA [18] | ✓ | ||||
| CDE [19] | ✓ | ||||
| DE/nrand/1 [20] | ✓ | ||||
| Ring-PSO [21] | ✓ | ||||
| LIPS [22] | ✓ | ||||
| NCDE [23] | ✓ | ||||
| NSDE [23] | ✓ | ||||
| Self-CCDE [24] | ✓ | ✓ | |||
| Self-CSDE [24] | ✓ | ✓ | |||
| DHNDE [25] | ✓ | ||||
| NEA2 [26] | ✓ | ||||
| HTS-CDE [27] | ✓ | ✓ | |||
| AMP-DE [28] | ✓ | ||||
| EMO-MMO [29] | ✓ | ||||
| ANDE [30] | ✓ | ✓ | |||
| NCD-DE [31] | ✓ | ✓ | |||
| ESPDE [32] | ✓ | ✓ | |||
| HGHE-DE [33] | ✓ | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, C.; Diao, Y. Mitigating Selection Bias in Local Optima: A Meta-Analysis of Niching Methods in Continuous Optimization. Information 2025, 16, 583. https://doi.org/10.3390/info16070583
Wang J, Li C, Diao Y. Mitigating Selection Bias in Local Optima: A Meta-Analysis of Niching Methods in Continuous Optimization. Information. 2025; 16(7):583. https://doi.org/10.3390/info16070583
Chicago/Turabian StyleWang, Junchen, Changhe Li, and Yiya Diao. 2025. "Mitigating Selection Bias in Local Optima: A Meta-Analysis of Niching Methods in Continuous Optimization" Information 16, no. 7: 583. https://doi.org/10.3390/info16070583
APA StyleWang, J., Li, C., & Diao, Y. (2025). Mitigating Selection Bias in Local Optima: A Meta-Analysis of Niching Methods in Continuous Optimization. Information, 16(7), 583. https://doi.org/10.3390/info16070583






