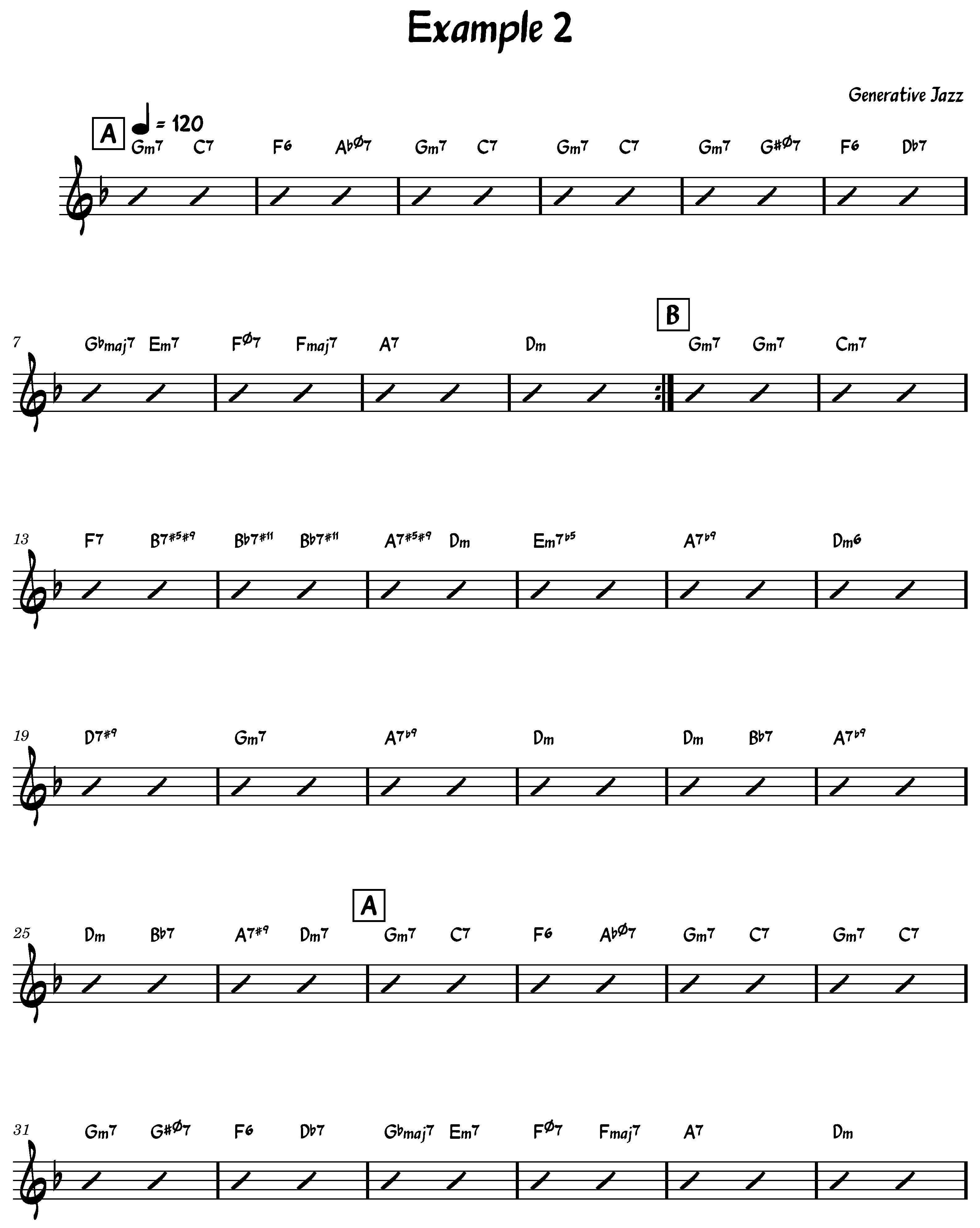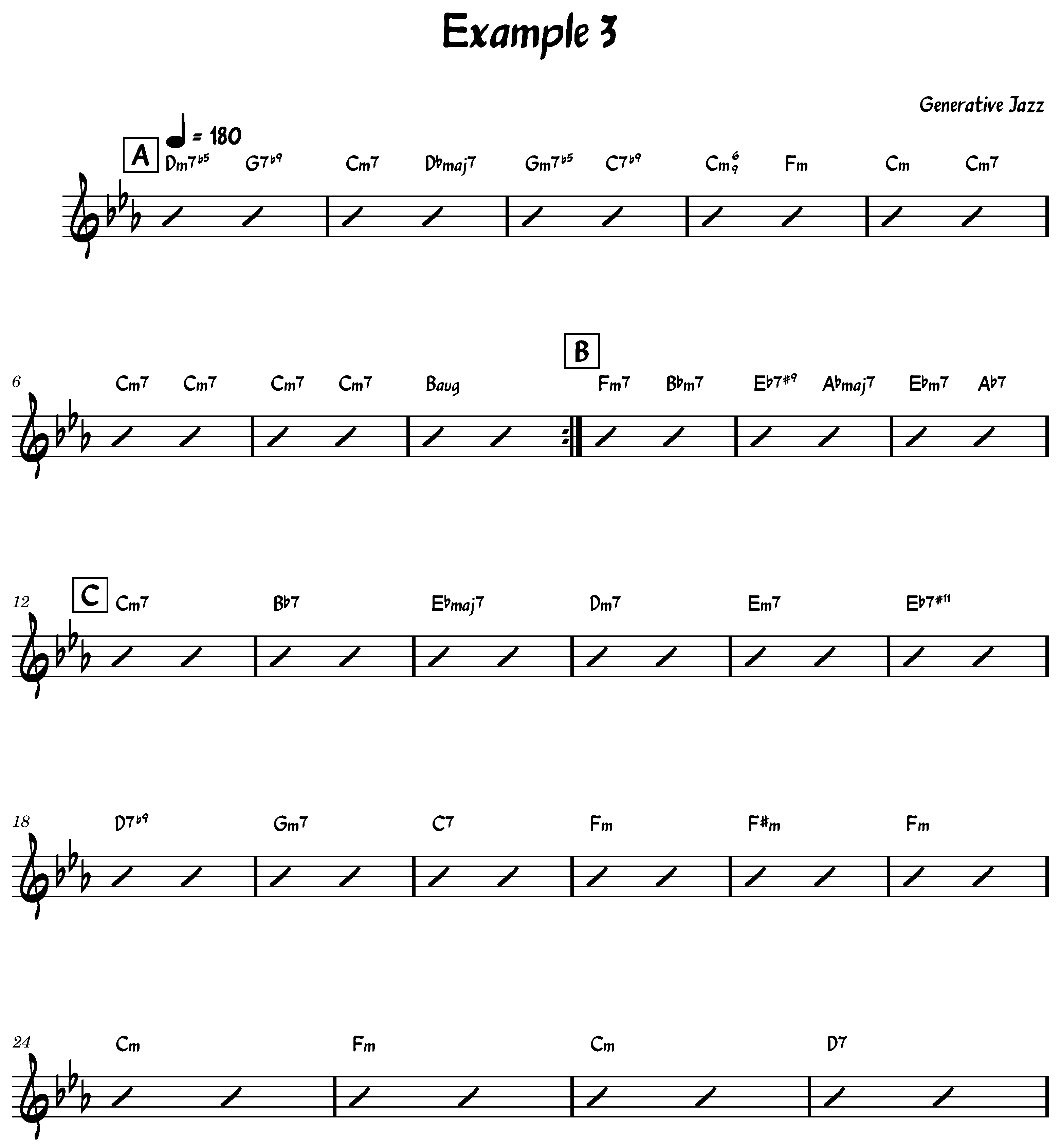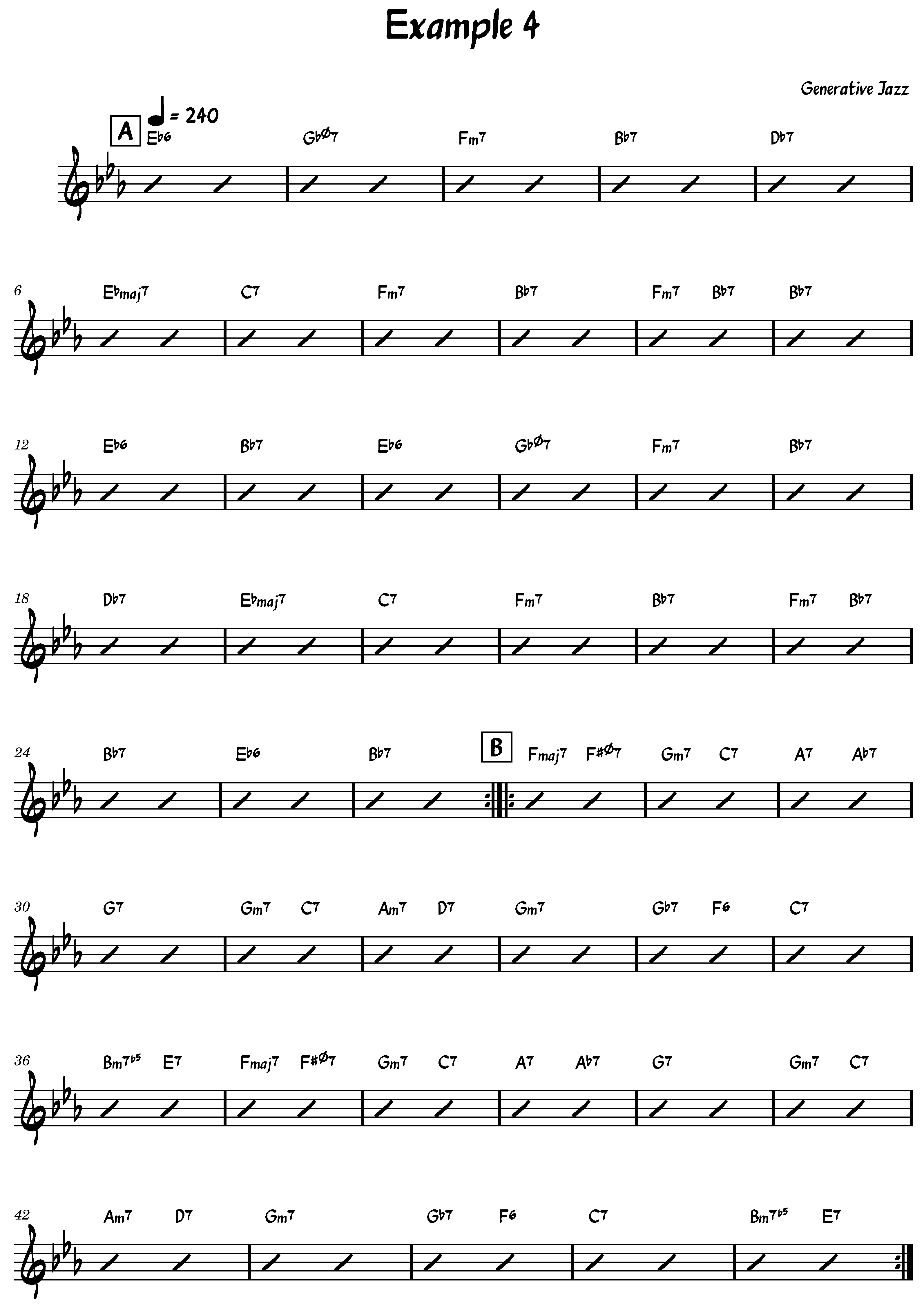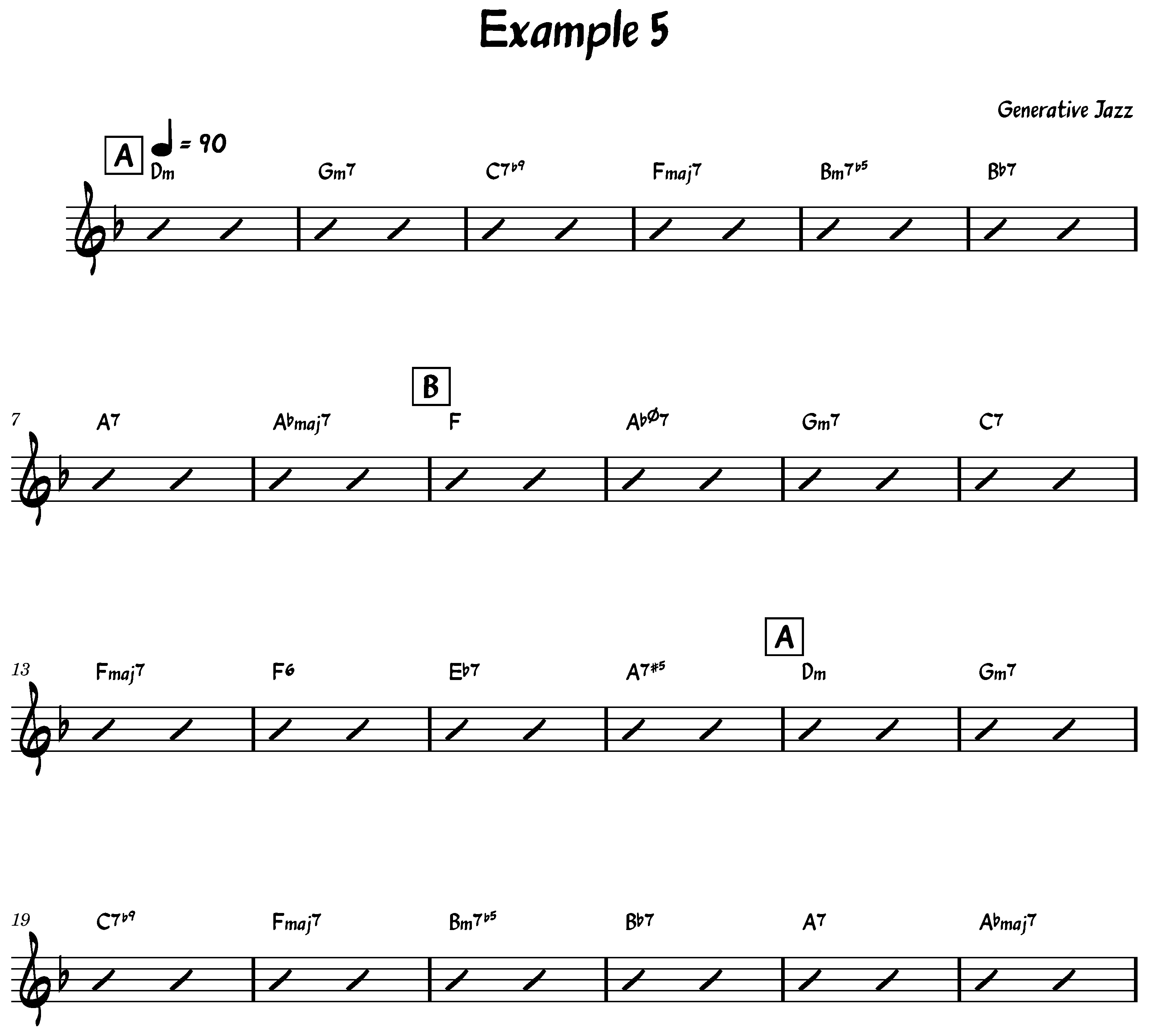Generative Jazz Chord Progressions: A Statistical Approach to Harmonic Creativity

Abstract

Jazz music has long been a subject of interest in the field of generative music. Traditional jazz chord progressions follow established patterns that contribute to the genre’s distinct sound. However, the demand for more innovative and diverse harmonic structures has led to the exploration of alternative approaches in music generation. This paper addresses the challenge of generating novel and engaging jazz chord sequences that go beyond traditional chord progressions. It proposes an unconventional statistical approach, leveraging a corpus of 1382 jazz standards, which includes key information, song structure, and chord sequences by section. The proposed method generates chord sequences based on statistical patterns extracted from the corpus, considering a tonal context while introducing a degree of unpredictability that enhances the results with elements of surprise and interest. The goal is to move beyond conventional and well-known jazz chord progressions, exploring new and inspiring harmonic possibilities. The evaluation of the generated dataset, which matches the size of the learning corpus, demonstrates a strong statistical alignment between distributions across multiple analysis parameters while also revealing opportunities for further exploration of novel harmonic pathways.

1. Introduction

1.1. Background

In general, music can be divided into three main constituent elements: melody, harmony, and rhythm. Rhythm serves as the backbone, dictating the temporal organization and pulse of a piece through patterns of beats and accents. Melody embodies the sequence of notes that form a recognizable and memorable tune. Harmony, on the other hand, consists of the simultaneous combination of different musical notes to create chords that provide a musical background for the melody or, as is often the case in jazz, for improvisation. Thus, some authors argue that chord sequences are essential building blocks in tonal music [1]. Sequences of chords, traditionally referred to as chord progressions, can be created with two different goals: (1) to harmonize existing melodies [2]; or (2) to serve as a harmonic basis for melody composition or improvisation.

In the jazz genre, it is common for musicians to improvise melodic lines over the harmonic structures of well-known songs, usually referred to as “standards.” Most of these jazz standards were composed many decades ago and generally adhere to established rules concerning chord progressions. For instance, given the seven chords in a major key, it is common to use the fifth-degree chord after a second-degree chord in a progression known as a II-V progression. Other common chord progressions include the popular II-V-I-I progression and the I-VI-II-V progression, among others, which are considered traditional progressions. However, we propose that, in order to create new and fresh chord progressions, it is sometimes necessary to break these established rules.

The task of generating jazz chord progressions without an accompanying melody is a non-trivial, musically meaningful, and independently valuable problem. Several studies have treated this as a standalone domain, focusing on the structural and stylistic modeling of harmonic sequences [3,4,5,6]. This complements the broader goals of jazz improvisation, where the harmonic framework serves as a central guide for melodic invention.

1.2. Literature Review

The automatic generation of chord progressions remains a challenging task due to factors such as musical context, aesthetic choices, and individual preferences, as noted by Navarro et al. [7]. Various methodologies have been explored to address these challenges, ranging from formal rule-based systems to probabilistic and machine-learning approaches.

Generative grammar approaches have historically been foundational in chord sequence generation. Steedman [3] developed formal grammatical rules for jazz chord progressions, focusing on the 12-bar blues structure. Chemillier extended this work to enable the incremental generation of chord sequences, emphasizing cadential structures and precompilation techniques for real-time improvisation [4]. Later, Terrat advocated for pregroup grammars to recognize and classify chord sequences, highlighting the need for robust formal characterizations of musical structures [5,6]. Our method differs from these grammar-based approaches by relying not on symbolic rules but on probabilistic modeling learned from real musical corpora, enabling the generation of stylistically grounded yet novel chord sequences. Ogura et al. [8] further contributed with an incremental parser using context-free grammar rules and chart-parsing techniques to analyze jazz standards. These approaches underscore the significant role of formal descriptions in capturing the structural complexity of music. Functional grammars can be used to create a set of rules that define how chords interact in a jazz progression, capturing concepts like preparation, prolongation, and embedded modulation, similar to how they are applied in language to structure sentences. Functional grammar-based systems provide interpretability and adherence to rules, making them particularly well-suited for style-constrained jazz chord modeling. These systems can also generate new jazz melodies and chord progressions, exploring a range of possibilities within the defined framework [9].

Evolutionary algorithms have also been applied to the generation of harmonic sequences. Eigenfeldt’s PAT system generates full musical compositions, including harmony, by analyzing corpora to guide evolutionary processes [10]. Similarly, Backman’s Evolutionary Jazz Improvisation (EJI) system creates jazz harmonies and solos, leveraging evolutionary techniques informed by the characteristics of master improvisers [11]. These approaches emphasize adaptive mechanisms for generating musically coherent outputs.

Probabilistic models, particularly those based on Markov chains, have been widely used for generating chord progressions. Eigenfeldt [12] employed a variable-order Markov model to balance harmonic tension and user influence, prioritizing creative practice. Roig et al. [13] extended Markov models with temporal layers to address mid- and long-term dependencies in harmonic progressions. Kaliakatsos-Papakostas et al. [2] proposed an HMM-based system for harmonizing jazz standards, incorporating harmonic constraints and a structured harmonic space. Building on these ideas, Wang introduced the Variable Markov Oracle (VMO-HMM) model to capture long-term dependencies in jazz harmony generation [14]. HMM-based approaches offer a probabilistic and interpretable framework well-suited for modeling the sequential and functional nature of jazz harmony.

Beyond Markov-based approaches, statistical methods such as Bayesian models have also been explored. Katz [15] utilized Bayesian model selection to analyze harmonic structures in blues forms, demonstrating the potential of statistical techniques for understanding complex musical phenomena.

A variety of other computational techniques have been proposed for chord sequence generation. Bernardes et al. developed Conchord, a real-time harmony generator leveraging Tonal Interval Spaces [16], as well as D’accord, which generates harmonically compatible accompaniments based on tonal pitch relatedness and consonance [17]. Shukla and Banka [18] introduced reinforcement learning (RL) for automatic chord progression generation, while Zeng and Lau [19] applied RL to melody harmonization. Wilk and Sagayama [20] proposed a user-driven approach to music completion, avoiding probabilistic harmony models to allow for more creative and less conventional outputs. Other real-time rule-based systems, such as GenJam [21] and Impro-Visor [22], highlight the utility of explicitly defined musical heuristics for interactive or improvisational applications.

The musical and creative value of generating chord progressions without melodic conditioning has continued to be explored through a variety of machine-learning approaches. For example, Hutchings and McCormack employed autonomous agents to generate harmonic structures in real-time improvisation systems [23]. Li used LSTM-based neural networks to model chord-based music generation, demonstrating the effectiveness of purely harmonic representations [24]. Similarly, Dalmazzo et al. introduced a Transformer-based harmony model that operates solely on chord tokens, emphasizing the relevance and expressivity of progression modeling without melodic context [25].

More recently, various approaches have been explored for melody harmonization. Sun et al. proposed a method leveraging orderless NADE, chord balancing, and blocked Gibbs sampling to improve harmonic coherence [26]. In a related study, the same group introduced the concept of a melodic skeleton as a key feature for harmonization, highlighting its effectiveness in capturing musical structures [27]. Rhyu et al. employed a Transformer-based model for structured and flexible melody-to-chord translation, demonstrating improved adaptability in harmonization tasks [28]. Ji and Yang explored emotion-conditioned melody harmonization using a hierarchical variational autoencoder, enabling emotion-driven harmonic generation [29]. Wu et al. investigated chord-conditioned melody harmonization with controllable harmonicity, allowing greater flexibility in harmonic generation [30]. Similarly, Li et al. introduced a Transformer-based chord generation model incorporating color harmony theory to enhance chord progression coherence [31]. Wu et al. further refined melody-to-chord generation by incorporating flexible harmonic rhythm and controllable harmonic density, providing increased expressiveness in generated chord progressions [32]. Additionally, Ji et al. presented RL-Chord, a deep reinforcement learning-based approach for melody harmonization, effectively capturing long-term harmonic dependencies [33]. Lastly, Bora proposed a heuristic model for selecting optimal chords from scales based on adjustable musical criteria, offering a rule-based perspective on harmony generation [34]. These Transformer-based approaches have shown impressive capabilities in modeling long-term harmonic structure and stylistic coherence, particularly in melody harmonization and chord generation. However, they often require large datasets and may lack interpretability compared to rule-based or probabilistic methods.

Our approach complements these paradigms by integrating statistical analysis with musically informed symbolic representations, balancing interpretability, flexibility, and corpus-based grounding without relying on large-scale deep learning or predefined rule sets.

1.3. Research Gap and Motivation

Despite extensive research, there remains a need for probabilistic models tailored to chord progression generation, as highlighted by Paiement et al. [1]. The present paper addresses this gap by proposing a probabilistic analysis of a large corpus of 1382 jazz standards, offering a comprehensive resource for researchers and practitioners. Unlike earlier studies, such as Mauch et al.’s analysis of four-chord sequences in jazz [35], this work extends beyond common progressions, introducing novel sequences. The resulting stochastic data will be freely available, enabling further exploration in musical composition and analysis.

The motivation behind this research stems from the desire to push the boundaries of conventional jazz chord progressions, which have remained largely unchanged for decades. Despite their effectiveness, these traditional progressions can limit the creativity and uniqueness of musical compositions. The need for more diverse, unpredictable harmonic structures is crucial not only for generating new musical experiences but also for enriching the creative process for musicians and composers. This paper addresses the problem of generating new and innovative chord progressions, combined into full song-length chord sequences in the jazz genre. While contextualized in jazz, the proposed methodology can be easily adapted to other genres, such as pop or rock music, simply by replacing the jazz standards corpus with one suited to the target genre.

1.4. Challenge

Notably, symbolic generative methods for jazz chord progressions have seen limited advancement in recent years. This paper aims to bridge this gap by integrating probabilistic modeling with symbolic analysis to advance the state of the art in jazz harmony generation.

One of the key challenges in generating jazz chord progressions is striking a balance between novelty and harmonic coherence. Traditional jazz progressions adhere to well-established harmonic conventions, but strictly following these patterns can stifle innovation. Conversely, introducing excessive randomness may lead to progressions that lack musical structure and coherence. The challenge, therefore, is to generate chord sequences that feel fresh and unique while maintaining a logical harmonic flow that aligns with jazz idioms. Achieving this requires a structured approach to probabilistic modeling, ensuring that transitions between chords remain musically valid even when diverging from conventional jazz harmony.

1.5. Contributions

This paper makes some novel contributions to the field of generative AI music, particularly in symbolic jazz harmony generation. Our approach introduces a novel probabilistic framework that enhances the generation of dynamic and inspiring chord sequences, addressing limitations in traditional rule-based and deep learning methods.

We present a probabilistic transition-based model for generating jazz chord progressions, leveraging statistical techniques to estimate transition probabilities between chords within a given key. Unlike purely rule-based approaches, which strictly adhere to predefined harmonic principles, our model allows for controlled deviations, balancing stylistic adherence with creative exploration. This enables the generation of chord sequences that are both musically coherent and structurally diverse, closely mimicking the harmonic evolution found in real jazz compositions.

While deep learning models for symbolic music generation often require large-scale training datasets and significant computational resources, our approach is computationally lightweight and well-suited for real-time applications. This makes it particularly useful for interactive music systems that require real-time harmony generation, AI-assisted composition tools that provide musicians with chord suggestions, and educational applications that help students explore jazz harmony through generative examples. By ensuring low-latency generation, our method can be integrated into real-time music production environments such as DAWs, live performance tools, or generative improvisation assistants.

These contributions advance the state of the art in symbolic music generation, offering a scalable, flexible, and musically meaningful approach to jazz harmony modeling.

1.6. Paper Organization

The remainder of the paper is organized as follows. Section 2 presents the key components of our methodology, beginning with an introduction to the jazz standards corpus used for training, followed by a detailed explanation of the probabilistic analysis. Section 2.1 provides an overview of the dataset, while Section 2.2 outlines the probabilistic calculations performed, including key distributions. In Section 3, we evaluate the performance of our generative method by comparing the statistical properties of synthesized chord sequences with those of real jazz standards. Finally, Section 4 summarizes our findings and discusses potential extensions and improvements to the methodology.

2. Materials and Methods

As mentioned earlier, this paper presents a new methodology for generating jazz chord sequences using a statistical approach. This section is divided into three main parts: (1) the first part introduces the corpus used to train our model, a comprehensive dataset containing the harmonic structures of over one thousand jazz standards; (2) the second part presents the statistical calculations; and (3) the third and final part presents a detailed explanation of the new method for generating chord sequences.

2.1. The Jazz Standards Corpus

Next to classical music, jazz is perhaps one of the most prolific music genres. Born from the confluence of African rhythms, European harmonies, and American blues, jazz emerged in the late 19th and early 20th centuries as a musical form unlike any other.

At its inception, jazz was an oral tradition, passed down through generations of musicians via jam sessions, performances, and late-night collaborations. However, as jazz became increasingly complex and sophisticated, a need arose for a standardized method of sharing its repertoire.

A lead sheet is a simplified musical score commonly used in jazz. It typically consists of two main elements: melody notation and chord symbols, which indicate the underlying harmonic structure of the music. Lead sheets are prized for their simplicity and versatility, making them ideal for improvisation and spontaneous collaboration among musicians.

In the early 1970s, a group of musicians in Boston compiled a collection of lead sheets of jazz standards and originals. These clandestine collections, often referred to as “fake books,” became essential tools for jazz musicians, providing a common language through which to interpret and perform the vast repertoire of the genre. The Real Book was first published in 1975 and became an indispensable companion for jazz musicians around the world.

More recently, iReal Pro (version 2025.2), a mobile app and software program designed for musicians, particularly those who play jazz and other improvisational styles, was launched. The app and its associated forums serve as a collaborative platform for musicians to publicly share, among other things, the harmonic structure of jazz standards in a format similar to a lead sheet. The corpus of 1382 standards used in this work can be found at iReal (https://irealb.com/forums/ (accessed on 14 June 2025)).

2.1.1. Terminology

Throughout this paper, we refer to “chords” as they appear in lead sheets and datasets such as iReal Pro. Unless otherwise stated, the term “chord” refers specifically to the chord symbol—a notated label (e.g., Dm7, G7, Cmaj7) representing a harmonic structure—rather than a specific voicing or performed sonority. In contrast, harmonic function refers to the role a chord plays within a tonal key (e.g., G7 functioning as the dominant, or V7, in C major). While chord symbols often imply function, jazz practice allows for flexible interpretation, meaning the same chord symbol may serve different harmonic functions depending on context. This distinction is important in both our corpus analysis and generation methodology.

2.1.2. Song Structure and Section Chord Patterns

The song structure in jazz standards encompasses the organization and progression of musical elements within a composition, providing a framework for performers to navigate and interpret the piece while allowing for creative expression and improvisation within established boundaries. For example, many song structures in jazz standards typically follow a format known as the AABA form, where the A section (also known as the verse) is played twice, the B section (or chorus) is played once, and the song ends with a repetition of the A section (known as the return). However, the corpus used in this study contains many other song structures. All of these structures are covered by the probabilistic analysis presented in the next section of this paper.

Another important concept to introduce at this point is the section chord pattern used in this paper. As mentioned earlier, in a jazz standard, each section contains a sequence of bars (or measures). Each bar may contain none, one, or more than one chord. In the context of the methodology presented in this paper, a section chord pattern is a sequence of numbers where the length of the sequence corresponds to the number of bars in the section, and each number corresponds to the number of chords in a particular bar.

2.2. Probabilistic Analysis: Training the Model

The probabilistic analysis and training of our model constitute a fundamental aspect of our generative approach to chord sequence generation. This section presents in detail all the aspects that have been the subject of analysis, namely,

• The probabilities of the 24 possible central tonal keys of the song (12 major keys and 12 minor keys).
• The probabilities of all existing section structure forms in the corpus.
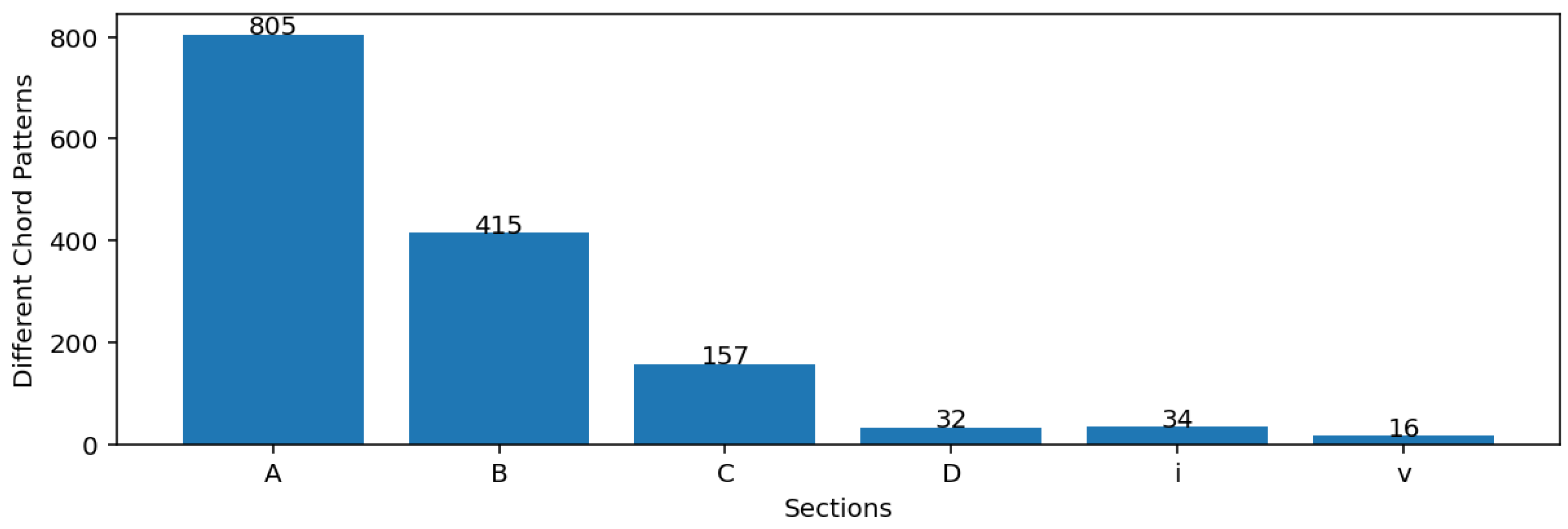
• The probabilities of all existing section chord patterns in the corpus.
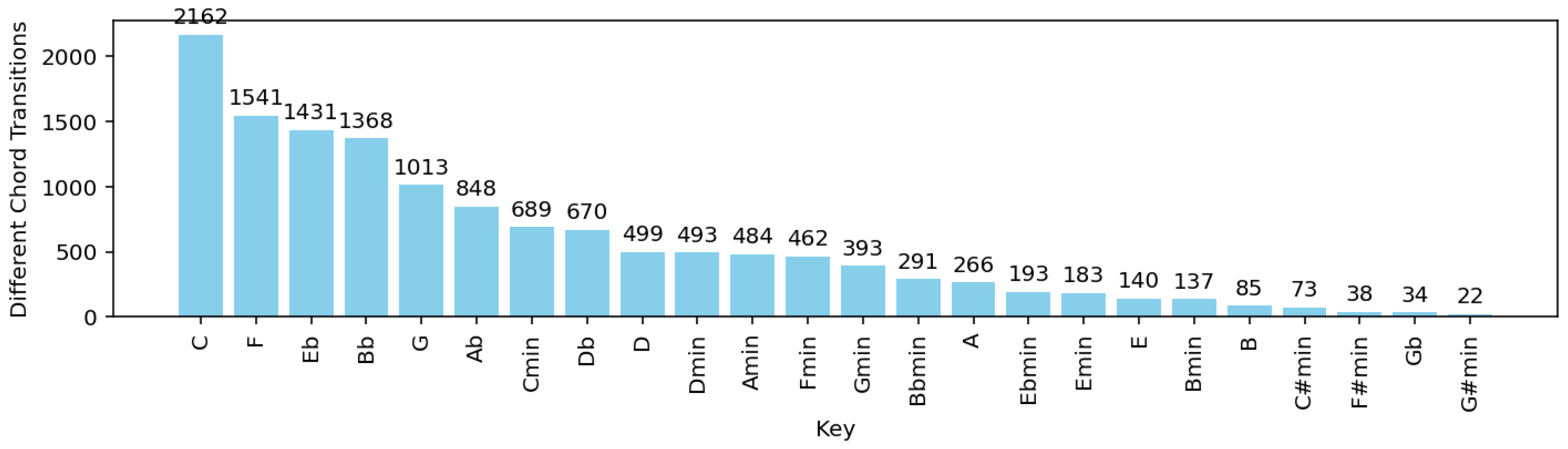
• The probabilities of all chord transitions in each of the 24 tonal keys.

The data resulting from this probabilistic analysis will be instrumental for the implementation of the core chord sequence generation method.

2.2.1. Probabilistic Analysis of the Keys

After analyzing the corpus concerning the central tonality probabilities, we observed that F (18.4%), C (16.9%), Eb (15.1%), and Bb (12.4%) are the most common keys in jazz, while Gb (0.1%), F#min (0.1%), and G#min (0.1%) are the least used keys (see

Table 1. Probabilities of all the keys in the jazz corpus.

Major Keys				Minor Keys
Key	Prob.	Key	Prob.	Key	Prob.	Key	Prob.
F	0.184	Db	0.027	Cmin	0.040	Ebmin	0.008
C	0.169	D	0.017	Dmin	0.029	Bmin	0.005
Eb	0.151	A	0.008	Fmin	0.026	F#min	0.001
Bb	0.124	B	0.004	Amin	0.020	G#min	0.001
G	0.085	E	0.003	Gmin	0.020	C#min	0.003
Ab	0.056	Gb	0.001	Bbmin	0.013	Emin	0.009
$\Sigma$ 0.826				$\Sigma$ 0.174

). Furthermore, 82.6% of the jazz standards in the corpus have a major central tonality, while only 17.4% have a minor key.

As an empirical conclusion, this means that we can obtain much more variability in chord sequences for the keys of F, C, Eb, and Bb because we have larger learning datasets for each of these keys compared to less common keys. Nevertheless, as we will further show, our method allows key changes between sections to increase variability.

2.2.2. Probabilistic Analysis of the Structure

Regarding the structure (or form) of the songs in the corpus, the probabilistic analysis yielded the data presented in

Table 2. Probabilities of the most common structures (forms) in the jazz corpus.

Structure	Prob.	Structure	Prob.	Structure	Prob.	…
AABA	31.5%	AAB	4.2%	ABCD	1.7%	…
A	10.7%	AABC	2.7%	AABAA	1.7%	…
ABAC	8.5%	BBAA	2.6%	ABB	1.5%	…
AB	6.6%	ABA	2.5%	ABCA	1.2%	…
AA	4.8%	ABC	1.9%	…	…	…

. As expected, and as previously mentioned, the AABA form is by far the most prevalent structure in jazz standards, with a probability of occurrence of 31.5%, followed by the single-section form A at 10.7%, and the ABAC form at 8.5%.

In our method, the user can explicitly choose to generate a chord sequence that follows a predetermined structure or generate the structure using these probabilities.

2.2.3. Probabilistic Analysis of Chord Patterns

The concept of chord pattern was already defined in Section 2.1.2. Regarding chord patterns, the probabilistic analysis adopted a section-oriented approach, i.e., we decided to separate the probabilistic calculations for each type of section. This decision was made empirically because, for example, an i section (intro) is usually shorter and has more chords per bar than, for instance, an A section (verse). As shown in Figure 1, there is a significant difference in the number of different patterns between the types of sections. As expected, there is much more variability in the patterns for the A Section (805 different chord patterns) and much less variability for i Sections (34 different patterns).

Regarding probabilities, as shown in

Table 3. Top 5 most common chord pattern probabilities by section type.

Section A		Section D
Pattern	Prob.	Pattern	Prob.
11111111	0.097	11111111	0.174
22222222	0.043	11111112	0.087
1111111111111111	0.038	111111111111	0.043
222222	0.025	11111211	0.043
11111112	0.023	1111111111111111	0.043
…	…	…	…
Section B		Section i
Pattern	Prob.	Pattern	Prob.
11111111	0.170	1111	0.361
1111111111111111	0.046	11111111	0.108
11111112	0.045	2222	0.072
11111122	0.035	11111112	0.036
22222222	0.034	1112	0.036
…	…	…	…
Section C		Section v
Pattern	Prob.	Pattern	Prob.
11111111	0.132	111111111111	0.063
11111122	0.039	2222121222122212	0.063
11111112	0.035	4441	0.063
22222222	0.032	1111111121222222	0.063
1111111111111111	0.029	222422	0.063
…	…	…	…

, the pattern 11111111 (8 bars with 1 chord per bar) is the most used pattern in the most common sections, except in the i sections, where the most popular chord pattern is 1111 (4 bars with 1 chord per bar). This confirms our initial empirical hypothesis that i sections are usually shorter. Notably, the 16-bar pattern with 1 chord per bar is also one of the most common chord patterns, ranking in the top 5 for all the different section types, with a probability of 4% to 5%. In general, except for i and C sections, the 8-bar chord patterns are by far the most used form, usually consisting of different combinations of 1 and 2 chords per bar.

Nevertheless, even with a higher prevalence of some chord patterns, and because there is such great variability, especially in A and B sections, our methodology generates truly interesting, uncommon, and unexpected chord patterns. This phenomenon is easily explained because, taking an A section as an example, from the 6th to the 805th patterns, all have approximately the same probability of occurrence. As a matter of fact, it is not uncommon for our method to generate bars with 4 chords, despite the corpus containing only one pattern with 4 chords per bar.

2.2.4. The First Chord Probabilistic Analysis

At this point, it is also important to introduce and analyze the concept of the first chord in a sequence. This is instrumental for the method because, for every new chord sequence, it is necessary to decide which chord the sequence should start with. Since this feature depends on the tonal key of the song or section, a key-oriented probabilistic analysis was performed. It is expected that the probabilities of the chords used to begin a sequence in one key will differ from the probabilities of the chords used to begin a sequence in another key.

Table 4. Top 5 most probable first chords for major keys.

C	Db	D	Eb	E	F	Gb	G	Ab	A	Bb	B
Cmaj7	Dbmaj7	Dmaj7	Ebmaj7	Emaj7	Fmaj7	Gbmaj7	Gmaj7	Abmaj7	Amaj7	Bbmaj7	Bmaj7
(0.39)	(0.32)	(0.26)	(0.50)	(0.50)	(0.43)	(1.00)	(0.47)	(0.22)	(0.45)	(0.39)	(0.20)
C6	B7#11	D6	Eb6	G#m9	F6		Am7	Bbm7	A7	Bb6	B7sus
(0.15)	(0.05)	(0.17)	(0.16)	(0.25)	(0.12)		(0.11)	(0.16)	(0.18)	(0.15)	(0.20)
Dm7	Db7	F7#11	Fm7	F#maj7	Gm7		G6	Fm7	E7	Bb7	C#m7
(0.06)	(0.05)	(0.04)	(0.11)	(0.25)	(0.12)		(0.09)	(0.10)	(0.09)	(0.14)	(0.20)
C	Db6	D	Eb		F7		G7	Ab	E	Bb	B7#5
(0.06)	(0.05)	(0.04)	(0.04)		(0.07)		(0.05)	(0.08)	(0.09)	(0.06)	(0.20)
C7	Gm7b5	D9sus	Eb7		F		G	Bb7	Bbmaj7#11	Cm7	B7/A
(0.04)	(0.05)	(0.04)	(0.02)		(0.07)		(0.04)	(0.08)	(0.09)	(0.05)	(0.20)
…	…	…	…		…		…	…	…	…	…

presents the probabilities of all first chords found in the corpus for every major key, and 

Table 5. Top 5 most probable first chords for minor keys.

Cm	C#m	Dm	Ebm	Em	Fm	F#m	Gm	G#m	Am	Bbm	Bm
Cm7	C#m7	Dm	Ebm7	Em7	Fm7	F#m	Gm7	Abm7	Am	Bbm7	Bm7
(0.45)	(0.25)	(0.33)	(0.27)	(0.58)	(0.28)	(1.00)	(0.44)	(0.50)	(0.41)	(0.39)	(0.29)
Cm	C#m9	Dm7	Ebm	Em9	Fm		Gm	Abm	Am7	Bbm	Bm9
(0.18)	(0.25)	(0.28)	(0.09)	(0.08)	(0.25)		(0.19)	(0.50)	(0.30)	(0.11)	(0.29)
Cm6	E	Dm6	Am7b5	C#m7	Fm6		Gm6		Am6	Bbm6	Em9
(0.11)	(0.25)	(0.10)	(0.09)	(0.08)	(0.22)		(0.11)		(0.07)	(0.11)	(0.14)
Cm11	C#m11	Dm11	Em11	Em	Fm11		Bbm7		Cmaj7	Bb7	Gmaj7#11
(0.04)	(0.25)	(0.08)	(0.09)	(0.08)	(0.08)		(0.04)		(0.04)	(0.06)	(0.14)
Dm7b5		Gm7	Eb7#9	F#7sus	Fm9		D7b9		Bm7b5	Fm7	G/D
(0.04)		(0.05)	(0.09)	(0.08)	(0.06)		(0.04)		(0.04)	(0.06)	(0.14)
…	…	…	…		…	…	…	…	…	…	…

shows the probabilities for every minor key. As observed in the scatter plots, for each central tonal key, only a few chords appear as the first chord of the progression. As expected, the most probable first chord for major keys is the corresponding I degree maj7 chord, while for minor keys, it is the I degree min7 chord. However, other chords can also occur as the first chord in the progression.

In summary, it is expected that the generative method will exhibit a higher degree of variability and unpredictability in the most commonly used central tonal keys. Additionally, if a chord is never used in the corpus as the first chord of a sequence for a given central tonal key, the chord sequences generated by our method will never begin with that chord, as its probability of occurrence will be 0.

2.2.5. The Chord Transition Probabilistic Analysis

Keeping in mind that the generation of chord sequences is central to the generative method presented in this paper, it is worth mentioning that a sequence consists of at least two chords, and every chord transition can be seen as a state change from one chord to the next. Inspired by the concepts of Markov chains, we define chord transition probability as the probability of transitioning from one chord to another. A chord transition can be represented as a pair of chords (bigram): (1) the origin chord and (2) the destination chord (follower). We also adopt the following notation to represent a chord transition: $c_o\to c_d$, where $c_o$ represents the origin chord and $c_d$ represents the destination chord. Figure 2 shows the number of different chord transitions by central tonal key.

To calculate the probability of a given chord transition in a given key k, let us define the variables used in the equations:

• k—a musical key in which chord transitions are analyzed.
• $T_k$—the set of all distinct chord transitions in key k that originate from a specific chord $c_o$.
• $c_o$—the origin chord in a transition.
• $c_{d_i}$—a possible destination chord in key k, where i indexes the different destination chords.
• ${\sigma }_k={\sum }_{i=1}^n{\sigma }_i$—the total number of chord transition occurrences (including repetitions) in key k that have $c_o$ as the origin chord.
• ${\sigma }_i$—the number of times the specific transition $c_o\to c_{d_i}$ occurs in key k.
• $p_k(c_o\to c_{d_i})={\displaystyle \frac{{\sigma }_i}{{\sigma }_k}}$—the probability of the transition from $c_o$ to $c_{d_i}$ occurring in key k.
• n—the total number of unique destination chords reachable from $c_o$ in key k.

With these definitions in place, we can express the set $T_k$ as follows [36]:

$$T_k=\{c_o\to c_{d_1},c_o\to c_{d_2},\dots ,c_o\to c_{d_n}\}$$

(1)

To compute the transition probabilities, we count occurrences of each transition type. The probability of a given transition $c_o\to c_{d_i}$ in key k is given by

$$p_k(c_o\to c_{d_i})={\displaystyle \frac{{\sigma }_i}{{\sigma }_k}}$$

(2)

Since all transition probabilities for a given origin chord $c_o$ must sum to 1, we verify this property with

$$\sum _{i=1}^n{p}_k(c_o\to c_{d_i})=1$$

(3)

To complete the probabilistic analysis, this process is repeated for all different origin chords $c_o$ in key k, and then across all keys in the corpus [36].

As an example, Figure 3 illustrates the transition probabilities between chords in the context of the G#min key. This key was chosen as an example because it has the fewest different chord transitions, as shown in Figure 2, making visualization easier. Notice that the sum of the probabilities in each row equals 1, confirming Equation (3).

In our model, we used 24 matrices, one for each key in the corpus, as shown in Figure 3. These matrices are not included in this paper to save space. It is also important to mention that chord transitions not present in the corpus were not generated because their probability is 0. However, to avoid sparse matrices, we did not use a full probability matrix. Instead, we used a map of existing chord transitions in the desired key, along with their probabilities.

2.2.6. Modulation Between Sections

The corpus we worked with provides only the global key of each song, without any annotation of the key used in individual sections. This limitation prevented us from adopting a corpus-informed statistical approach to model key modulations between sections, such as estimating transition probabilities from observed section-level modulations.

Knowing that modulations to the dominant, subdominant, or relative key are common in tonal music due to their closeness to the original key in the circle of fifths, we adopted a key proximity-based approach, assigning higher modulation probabilities to keys that are closer to the original key. While this approach is not directly derived from corpus data, it provides a realistic and musically grounded strategy for generating plausible modulations.

Let $\varphi \left(k\right)\in \{0,1,\dots ,11\}$ be a mapping of each of the 12 major and 12 minor keys to consecutive positions around the circle of fifths as presented in

Table 6. Mapping of each of the 12 major and 12 minor key positions around the circle of fifths.

k	C	G	D	A	E	B	Gb	Db	Ab	Eb	Bb	F
	Amin	Emin	Bmin	F#min	C#min	G#min	Ebmin	Bbmin	Fmin	Cmin	Gmin	Dmin
$\varphi \left(k\right)$	0	1	2	3	4	5	6	7	8	9	10	11

.

We define the distance between a candidate key k and the current key $k_{\mathrm{ref}}$ as follows:

$$D\left(k\right)=min\left(\left|\varphi \left(k\right)-\varphi \left(k_{\mathrm{ref}}\right)\right|,12-\left|\varphi \left(k\right)-\varphi \left(k_{\mathrm{ref}}\right)\right|\right)$$

(4)

This ensures that $D\left(k\right)\in \{0,1,\dots ,6\}$ always reflects the minimal number of steps between two keys on the circle of fifths, regardless of direction (clockwise or counterclockwise).

Based on this distance, we model the probability of modulating to key k using an exponential decay function:

$$P\left(k\right)=e^{-\lambda D\left(k\right)}\mathrm{where}\lambda \mathrm{is}\mathrm{the}\mathrm{decay}\mathrm{constant}$$

(5)

To ensure a valid probability distribution over all candidate keys, we normalize the function:

$$P_{\mathrm{norm}}\left(k\right)={\displaystyle \frac{P\left(k\right)}{{\sum }_{k^{\prime }}P\left(k^{\prime }\right)}}$$

(6)

where the sum is taken over all possible modulation targets $k^{\prime }$. This formulation gives higher probabilities to modulations toward keys closer to the current key, effectively favoring common modulations like to the dominant, subdominant, or relative, while still allowing for rarer modulations with lower probability, leaving room for exploratory compositions.

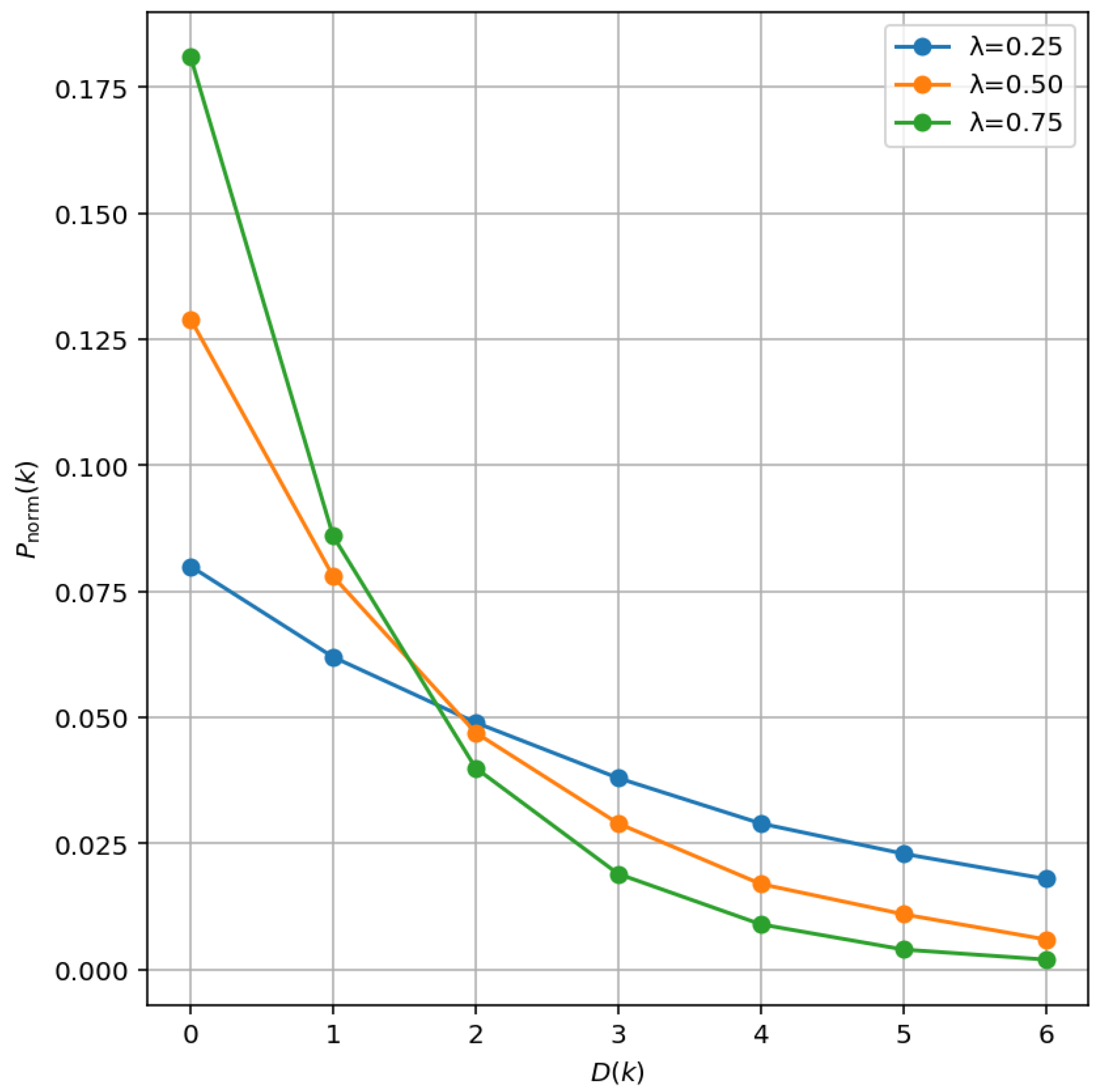
Figure 4 illustrates how the decay function behaves for different values of $\lambda$, while Figure 5 presents an example centered on C major as the current key. In this example, the model appropriately favors modulation to Amin (the relative minor), G (the dominant), and F (the subdominant). The same pattern applies to any other key, with the modulation probabilities centered accordingly.

Selecting a value of $\lambda$ between 0.25 and 0.75 effectively emphasizes the most harmonically plausible modulations, while still allowing for transitions to more distant keys—even those at the maximal circle-of-fifths distance $D=6$. This balance enables the system to prioritize musically related modulations without being overly restrictive, thereby preserving modulation diversity.

2.3. Generate the Chord Progression

While it is entirely possible to generate independent chord sequences outside the context of a song, this section introduces a straightforward methodology for generating chord sequences for a structured, full-length song. After training our generative model as described in Section 2.2, we present the core algorithm of our generative methodology in Algorithm 1.

It is important to distinguish between chord transitions (i.e., bigrams) and chord progressions (i.e., full sequences). Our generative method employs a first-order Markov model to sample chord-to-chord transitions based on empirical probabilities derived from the dataset. While these bigrams are observed in the training corpus, the complete chord sequences generated by our model are not directly sampled from the data. Instead, they are constructed by stochastically chaining transitions, enabling the system to explore novel combinations of known elements. With this approach, even though all transitions are grounded in the dataset, it is both possible—and very likely—for chord progressions to emerge that do not exist in the original corpus, which is precisely our goal. This effect is not limited to short sequences; if it occurs with shorter progressions, it naturally propagates and becomes increasingly likely in longer progressions, where the combinatorial possibilities expand significantly.

The algorithm works equally well for both randomly chosen and explicitly chosen keys and song structures (see lines 1 to 6 of Algorithm 1). After that, the algorithm begins by iterating over S, which represents the song structure, and for each section label section in S, it generates a chord pattern P and the first chord of the section using the key k. The first chord of the section is then added to the array of chords C. Subsequently, the algorithm iterates over the string representing the chord pattern P and, taking into account the origin chords and the key, generates new chords that are added to the final array of chords C.

Algorithm 1 was developed to generate the entire harmony for a full song with several sections, including potential key changes between sections. However, the algorithm can be adapted and simplified to generate a single chord sequence in a given key (random or not). To achieve this, the section processing can be omitted, following only lines 9 to 19 of the algorithm.

The time complexity of Algorithm 1 can be analyzed as $O\left(\right|S|·|P|·N)$, where $\left|S\right|$ represents the number of sections in the structure S, $\left|P\right|$ is the average size of the patterns generated for each section, and N is the average number of iterations in the innermost loop, determined by the pattern values. The algorithm iterates through $\left|S\right|$ sections, and for each section, it processes a pattern of size $\left|P\right|$. For each element in the pattern, the innermost loop iterates N times to generate chords. Thus, the overall time complexity reflects the combined contribution of these nested iterations.

The space complexity is dominated by the storage requirements for the chord progression array C, which grows proportionally to the total number of chords generated. This depends on $\left|S\right|$, $\left|P\right|$, and N, leading to a space complexity of $O\left(\right|S|·|P|·N)$. Temporary variables and probabilistic data structures used for chord generation contribute only a constant $O\left(1\right)$ space overhead. As a result, both the time and space complexities are proportional to the total number of chords generated by the algorithm.

Algorithm 1 Generating the chord progression of a structured song

Require:  A key k and a structure S Ensure:  An array of chords C   1: if k is null then   2:    $k\leftarrow randomKe{y}^1\left(\right)$   3: end if   4: if S is null then   5:    $S\leftarrow randomStructur{e}^2\left(\right)$   6: end if   7: for $i=1$ to $sizeOf\left(S\right)$ do   8:    $section\leftarrow S\left[i\right]$   9:    $P\leftarrow randomPatter{n}^3\left(section\right)$ 10:    $originChord\leftarrow randomFirstChor{d}^4\left(k\right)$ 11:    Add $originChord$ to C 12:    for $j\leftarrow 1$ to $sizeOf\left(P\right)$ do 13:      $n\leftarrow P\left[j\right]$ 14:      for $k=1$ to n do 15:         $destinyChord\leftarrow randomDestinyChor{d}^5(k,originChord)$ 16:         Add $destinyChord$ to C 17:         $originChord\leftarrow destinyChord$ 18:      end for 19:    end for 20:    $k\leftarrow keyModulatio{n}^6\left(\right)$ 21: end for 22: return C

¹ 

The starting key is stochastically picked following the probabilities presented in Table 1.

² 

The section structure of the song is generated based on the probabilities presented in Table 2.

³ 

The chord patterns can be randomly generated using the probabilistic analysis in Table 3.

⁴ 

The first chord of each section is chosen randomly based on the probabilistic analysis presented in Section 2.2.4.

⁵ 

The destination chord is chosen randomly based on the probabilities presented in Section 2.2.5.

⁶ 

The stochastic key modulation between sections is presented in Section 2.2.6.

2.4. Prototype Implementation

To validate the proposed generative method, we developed a prototype implementation in Java. The implementation consists of (a) a generator library that serves as the core engine, implementing the generative algorithm; and (b) a graphical user interface (GUI) designed to facilitate interaction with the generator library and provide a user-friendly experience.

The generator library loads training data from a JSON corpus, processes it, and generates chord progressions based on probabilistic patterns. Generated harmonies can be exported to the MusicXML format for use in external music software such as MuseScore.

A GUI was developed to provide an intuitive interface for users to interact with the generator library (Figure 6). The GUI displays the generated chord sequences and allows real-time playback via an integrated MIDI player. Users can select MIDI outputs, enabling playback through virtual or physical synthesizers, and adjust tempo settings as needed.

The complete prototype, including the training data, generator library, and GUI, will be publicly available as open-source software.

Appendix A provides examples of harmonies generated by our prototype using the method described in this manuscript, presented in the form of lead sheets. These examples illustrate the output in a musically interpretable format and are intended to support both analytical and practical evaluation. For listening purposes, the same examples are also available at https://musescore.com/user/101346721 (accessed on 14 June 2025). Audio examples demonstrating the generated outputs are also available in the Supplementary Materials.

3. Results and Discussion

Evaluating a generative method is a critical step in validating its ability to replicate or innovate within the constraints of the domain it seeks to emulate. In the context of music, and particularly generative music systems, this evaluation becomes even more essential due to the inherently subjective nature of artistic and aesthetic judgments. Unlike purely objective domains, the quality of music is often assessed through individual or cultural preferences, making it difficult to establish universal benchmarks for evaluation. To mitigate this subjectivity, statistical evaluation provides a robust, quantitative framework for comparing generated outputs to known datasets, enabling a more rigorous and replicable assessment of a model’s performance.

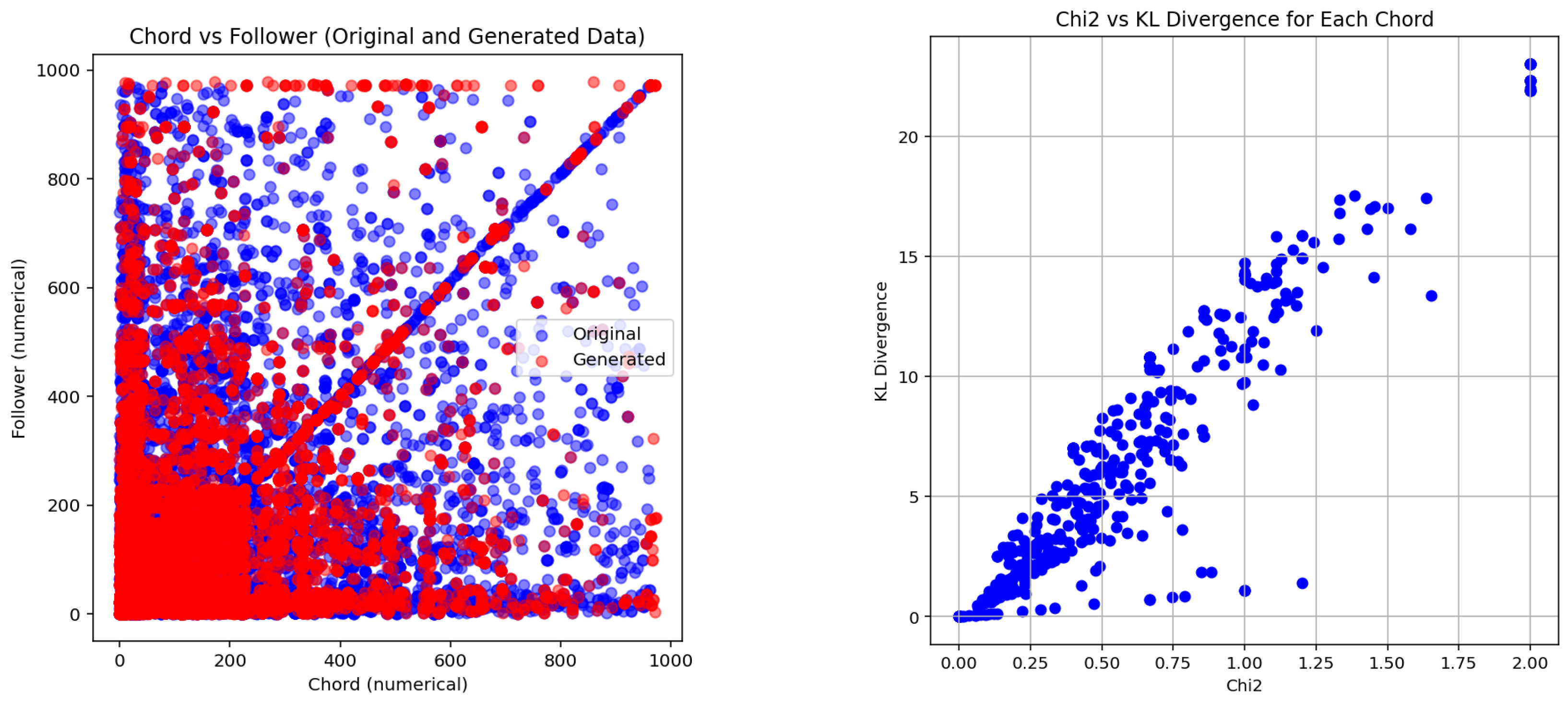
In this study, the generative method was evaluated using a dataset comprising 1382 harmonies from jazz standards, serving as the “original” dataset. This was compared against a corresponding “generated” dataset containing 1382 harmonies synthesized by our model. The synthesized dataset took less than 7 s to generate on an Intel i7 consumer laptop.

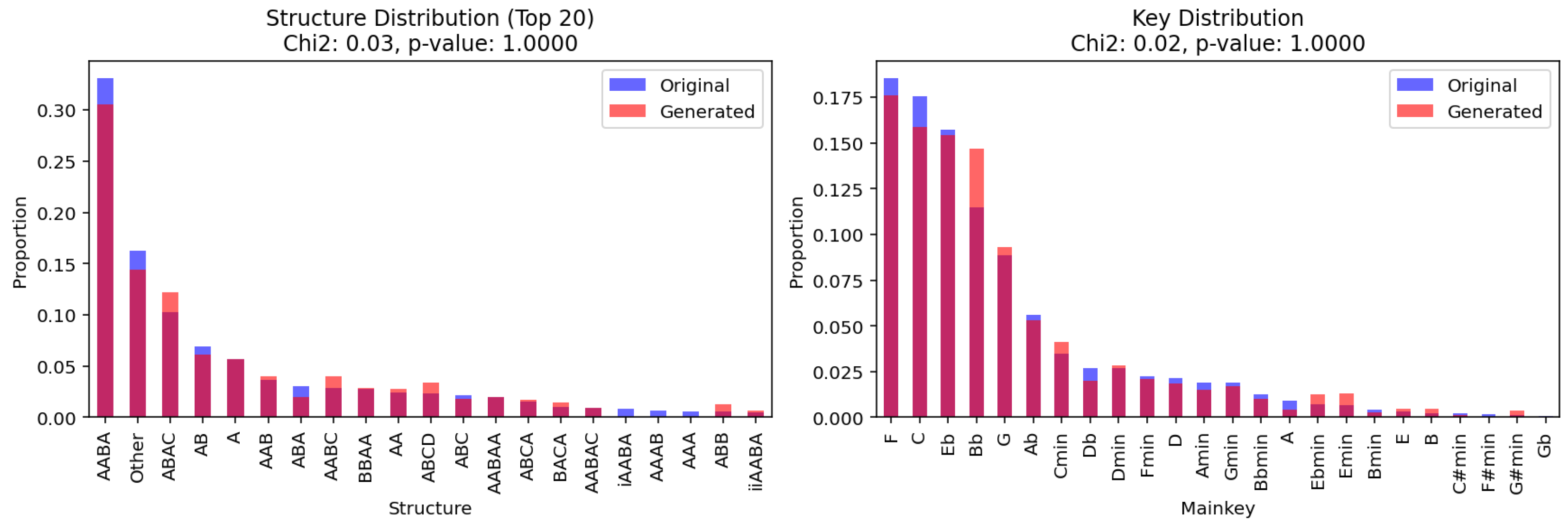
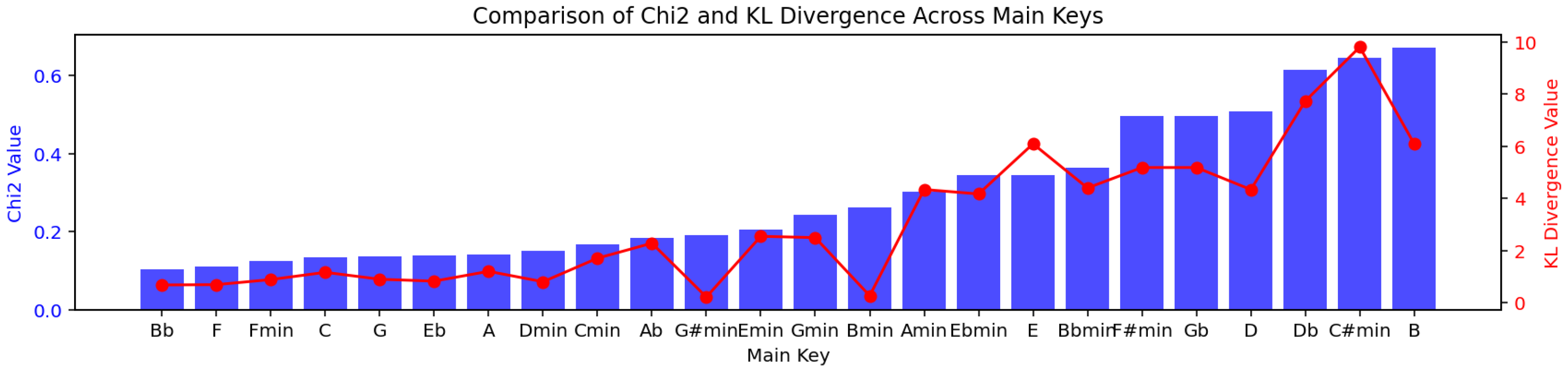
To facilitate a meaningful comparison, both datasets were decomposed into bigrams of chord–follower pairs, capturing the fundamental transitions between chords. These bigrams allowed for a granular analysis of the relationships and dependencies between chords, providing insights into the model’s ability to replicate the structure and stylistic nuances of the original dataset. The statistical evaluation, performed through metrics such as Chi-squared and Kullback–Leibler divergence, ensured that the generative method was assessed not only for surface-level similarity but also for its deeper alignment with the probabilistic and structural patterns of the original data. This approach bridges the gap between the subjective appreciation of generated music and the objective criteria needed for scientific validation.

One of the key challenges in evaluating our proposed method is the lack of directly comparable existing work. To the best of our knowledge, previous studies on harmony generation primarily focus on melody harmonization, where a given melody is harmonized with appropriate chord progressions. In contrast, our approach generates chord progressions independently, without requiring a predefined melody, making it particularly suitable for applications such as improvisation and exploratory composition. Due to this fundamental difference, there is no established benchmark or prior work that directly addresses the same problem formulation. As a result, we propose our method as a first benchmark for this specific task, paving the way for future research in this direction.

3.1. “Structure” and “Key” Statistical Distributions

The bar chart in Figure 7 (left) compares the distribution of musical structures between the original dataset and the sequences generated by the proposed generative method. The top 20 most frequent structures are displayed, along with their proportions in both datasets. The Chi-squared statistic is 0.03, with a p-value of 1.000. This suggests no statistically significant difference between the distributions of the original and generated structures. A high p-value (greater than 0.05) implies that the null hypothesis cannot be rejected. In this case, the null hypothesis posits that the two distributions are the same.

In our model, the user can choose a specific main key, but if not, the model stochastically generates a key. To assess how the algorithm performs in doing so, Figure 7 (right) illustrates the key distribution between the original dataset (blue) and the generated dataset (red). The similarity in the frequency distribution across the keys highlights the generative method’s ability to replicate the overall statistical properties of the original dataset in terms of key usage. The Chi-squared test results (Chi-squared: 0.02, p-value: 1.0000) indicate no statistically significant difference between the two distributions, suggesting that the generative model accurately captures the key distribution of the original jazz standards. Despite this strong agreement, further analysis may consider potential deviations in less frequent keys, as these can indicate nuanced areas for improvement in the model’s representation of rare tonal keys.

3.2. Evaluation of the “First Chord” Generation

The chart in Figure 8 compares the distributions of the original and generated datasets in terms of the first chord in the context of each tonal key within a section. For tonal keys where the Chi-squared values are low and the bar heights align closely, the generative model can be validated as effective in reproducing the original dataset’s chord distributions. This indicates that the model has successfully learned the contextual relationship between the tonal key and the choice of the first chord.

Discrepancies in tonal keys with high Chi-squared values point to areas where the model requires further training or refinement. For instance, if specific chords are underrepresented in the generated dataset (e.g., uncommon keys in jazz), it suggests that the model has not fully captured the probabilistic structure of the original data. Overall, the alignment between the original and generated distributions across most tonal keys validates the generative model’s ability to produce realistic first chord distributions in the context of each tonal key.

3.3. Evaluation of the “Chord–Follower” Bigram Generation

To validate the sequence of chords composed by the “chord, follower” bigrams, the goal is to assess how well the generative method replicates the relationship between chords and their followers in a sequence. This can be done by comparing the original data (real sequences) with the generated data (model-generated sequences) and analyzing the similarity between the two datasets.

The scatter plot in Figure 9 (left) compares the original and generated datasets by mapping chord (numerical index) on the x-axis and follower (numerical index) on the y-axis. Both original (blue) and generated (red) data are overlaid to assess how well the generative model reproduces the chord-follow relationships. The overall scatter of points in the original (blue) and generated (red) data largely overlaps, suggesting that the generative model captures the broader structure of chord–follower relationships. A visible diagonal line of points (where chord = follower) exists in both datasets, indicating transitions where chords follow themselves (e.g., repeated chords). The generative model successfully reproduces this pattern, evident by the alignment of red points with the blue. In some less densely populated regions of the scatter plot, red points (generated) do not align perfectly with blue points (original). This may indicate areas where the model struggles to generate certain rare transitions or overestimates others. Dense clusters in the lower-left corner and other sections of the plot are similarly represented in both datasets. These clusters represent common chord transitions, and the alignment suggests that the model effectively captures frequently occurring patterns.

We also compared the bigram distributions of the original and generated datasets using the Chi-squared test to see if the distributions of bigrams differ significantly. Additionally, we used the Kullback–Leibler divergence to measure how one distribution diverges from the other. This provides additional insights into the similarity between the two datasets. Figure 9 (right) compares the Chi-squared statistic and the Kullback–Leibler (KL) divergence for individual chords, measuring how well the generative model replicates the bigram distribution of chords (chord and follower) observed in the original dataset.

There is a clear positive correlation between Chi-squared and KL divergence. Chords with higher Chi-squared values also tend to exhibit higher KL divergence. This suggests that deviations in the frequency distribution between the original and generated datasets (measured by Chi-squared) are often accompanied by greater dissimilarity in probability distributions (measured by KL). A significant number of chords are clustered near the lower-left corner of the plot, with low Chi-squared and KL divergence values. This indicates that the generative model reproduces these chords and their followers accurately, showing minimal statistical deviation. A few chords (e.g., in the top-right area) exhibit significantly higher Chi-squared and KL divergence values. These outliers suggest that the generative model struggles to reproduce less common chords. For the majority of chords, the generative model performs well, with Chi-squared and KL values indicating close alignment between the original and generated distributions. The plots in Figure 9 provide evidence that the generative method is generally effective at replicating the chord–follower distributions.

3.4. Implications, Limitations, and Future Directions

The use of a first-order Markov model in our method represents both a limitation and an intentional design choice. By relying only on the immediately preceding state, the model does not capture longer-term dependencies that might contribute to more structured or conventional harmonic sequences. However, this lack of higher-order memory also introduces greater freedom in the generation process, increasing the chances of producing novel and less predictable chord progressions. This aligns with our objective of enabling exploratory harmony generation beyond traditional formulas. An important direction for future work is the incorporation of higher-order Markov or Variable Order Markov (VOM) models. These could allow the system to better balance local coherence with longer-term harmonic consistency, potentially enhancing both musical relevance and structural variety in the generated sequences.

A notable limitation of our current approach lies in the modulation strategy between sections. Due to the lack of section-level key annotations in the corpus, we cannot directly extract or model transitions from data. As a realistic compromise, we adopt a key proximity-based probabilistic model, where the likelihood of modulating to a new key is determined by the exponential decay of its key signature distance from the current key. This favors common modulations such as to the dominant, subdominant, or relative keys, which are harmonically close and prevalent in jazz practice—while still leaving room for rarer, exploratory key changes. While this strategy introduces stylistically grounded harmonic variation, it does not yet capture the full complexity of tonal logic observed in actual jazz compositions. As future work, we plan to develop a corpus-informed modulation mechanism based on observed section-level key transitions.

Concerning musicological implications, the novel generated chord progressions produced by our method offer significant contrasts to typical, rule-based sequences. Traditional chord progressions are foundational to the harmonic language of jazz, providing a familiar structure that improvisers and composers rely on. However, our approach generates progressions that deviate from these conventions, offering new harmonic possibilities that challenge the established framework. This shift could have profound effects on improvisation, as musicians may no longer follow the traditional progression-based resolutions that shape their approach to performance. Instead, they may need to adapt to unexpected harmonic landscapes, which could encourage the development of novel improvisational techniques and creative exploration.

4. Conclusions

This paper presents a novel statistical approach to generating jazz chord sequences that extends beyond traditional jazz progressions. By leveraging a comprehensive corpus of 1382 jazz standards, the proposed method integrates key information, song structure, and chord sequences to produce harmonically rich and contextually coherent progressions. This approach not only ensures alignment with the stylistic essence of jazz but also introduces a degree of unpredictability, fostering the creation of innovative and inspiring harmonic pathways.

The primary advantages of this method include its ability to generate stylistically authentic yet novel harmonic progressions, striking a balance between adherence to established jazz conventions and creative exploration. The approach offers a systematic and scalable means of analyzing and synthesizing jazz harmony, making it a valuable tool for both music analysis and generative composition. Additionally, it facilitates the discovery of new harmonic structures that could inspire composers, improvisers, and educators alike.

While our method incorporates well-known statistical tools such as first-order Markov models, we emphasize that the overall generative framework introduced in this work is novel. This includes not only the use of a section chord pattern—a structural representation that defines the number of chords per bar over a fixed-length segment—but also the combination of structural modeling, harmonic transition probabilities, and stylistic constraints to guide the generation of full chord progressions. To the best of our knowledge, this probabilistic integrated approach to jazz chord progression generation has not been previously proposed.

The evaluation of the generated dataset highlights the method’s ability to closely align with the statistical characteristics of the original corpus across multiple analytical parameters. This suggests that the approach successfully balances adherence to established jazz conventions while enabling the exploration of novel harmonic possibilities. While the generated results demonstrate significant promise, the findings also reveal opportunities for further refinement, particularly in enhancing the diversity and complexity of harmonic structures.

Despite these advantages, the proposed method has certain limitations. While the statistical framework ensures coherence with established jazz conventions, it does not explicitly model voice leading, instrumentation, or phrasing—crucial elements of jazz performance. Thus, while quantitative evaluation confirms statistical alignment with the corpus, a more comprehensive qualitative assessment involving expert musicians is needed to fully understand the aesthetic and practical implications of the generated progressions.

Future work could focus on expanding the generative framework to incorporate temporal dynamics, inter-sectional relationships, and real-time adaptability, further enriching the creative potential of the system. Additionally, qualitative evaluations involving expert musicians and listeners could provide deeper insights into the aesthetic and practical applications of the generated progressions in modern jazz compositions. This research lays the groundwork for a broader exploration of statistical methods in music generation, opening new avenues for creativity in jazz and beyond.