Enhancing Quantum Information Distribution Through Noisy Channels Using Quantum Communication Architectures
Abstract
1. Introduction
2. Architectures to Enhance Quantum Communication Quality
2.1. Fidelity of a Transmission Qubit Chain Going Through an Imperfect Communication Channel
2.2. Three-Qubit Correction Code as Classical Complementary Procedure
- (1)
- The 3-qubit correction code is applied following a primary quantum-based correction procedure that successfully ensures as a basis.
- (2)
- The generation of three identical input qubits must be achievable with low temporal and computational overhead.
- (3)
- The triplet of qubits must be reliably and quickly distinguishable as individual entities on the channel output.
- (4)
- In scenarios where the QEC procedure yields stochastic outcomes, its success probability should be close to unity, minimizing failures or enabling supplementary repetition mechanisms.
2.3. A Couple of Quantum Architectures with Imperfect Channels
2.4. Composed Pauli Channels Architectures and Kraus Operators
2.5. Fidelity and Success Probabilities
3. Average Fidelities by Tracing the Control System in Quantum Communication
3.1. Path Superposition Scheme
3.2. Indefinite Causal Order Scheme
4. Average Fidelities with Measuring the Control System in Quantum Communication
4.1. Path Superposition Scheme
4.2. Indefinite Causal Order Scheme
4.3. Improved Fidelity with ICO Architecture for Emblematic Channels
5. Eavesdropping Under the Communication Schemes for QKD
5.1. Single Eavesdropping Attack Through Measurement and Replacement
5.2. Analysis of the Eavesdropper Success Probability
5.3. Analysis of Quantum Bit Error Rate
6. Discussion and Future Work
6.1. Extension to More General Channels
6.2. Feasibility of Complementary Methods for Error Correction to the Current Architectures
6.3. Expectations for Multiple or Coherent Eavesdropping
6.4. Integration of PS and ICO in Current Commercial QKD Systems in the NISQ Era
6.5. Further Applicability for Information Enhancement and Future Work
7. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ch | Single channel |
| ICO | Indefinite Causal Order |
| ICO | Indefinite Causal Order plus 3-qubit correction code |
| LDPC | Low-Density Parity Check |
| M | Measuring |
| NISQ | Noise Intermediate-Scale Quantum |
| PS | Path Superposition |
| PS + 3-QC | Path Superposition plus 3-qubit correction code |
| QBER | Quantum Bit Error Rate |
| QC | Quantum Commuication |
| QEC | Quantum Error Correction |
| QEM | Quantum Error Mitigation |
| QKD | Quantum Key Distribution |
| Sch | Scheme |
| T | Tracing |
References
- Rozenman, G.; Kundu, N.K.; Liu, R.; Zhang, L.; Maslennikov, A.; Reches, Y.; Youm, H. The quantum internet: A synergy of quantum information technologies and 6G networks. IET Quantum Commun. 2023, 4, 147–166. [Google Scholar] [CrossRef]
- Khan, M.; Ghafoor, S.; Zaidi, S.; Khan, H.; Ahmad, A. From quantum communication fundamentals to decoherence mitigation strategies: Addressing global quantum network challenges and projected applications. Heliyon 2024, 10, 2405–8440. [Google Scholar] [CrossRef]
- Illiano, J.; Caleffi, M.; Manzalini, A.; Cacciapuoti, A.S. Quantum Internet Protocol Stack: A Comprehensive Survey. Comput. Netw. 2022, 213, 109092. [Google Scholar] [CrossRef]
- Cacciapuoti, A.S.; Illiano, J.; Koudia, S.; Simonov, K.; Caleffi, M. The Quantum Internet: Enhancing Classical Internet Services One Qubit at a Time. IEEE Netw. 2022, 36, 6–12. [Google Scholar] [CrossRef]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Xia, Y.; Li, W.; Zhuang, Q.; Zhang, Z. Quantum-Enhanced Data Classification with a Variational Entangled Sensor Network. Phys. Rev. X 2021, 11, 021047. [Google Scholar] [CrossRef]
- Castelvecchi, D. IBM releases first-ever 1,000-qubit quantum chip. Nature 2023, 624, 238. [Google Scholar] [CrossRef]
- Devitt, S.J.; Munro, W.J.; Nemoto, K. Quantum error correction for beginners. Rep. Prog. Phys. 2013, 76, 7–9. [Google Scholar] [CrossRef]
- Lau, J.; Lim, K.; Shrotriya, H.; Kwek, L. NISQ computing: Where are we and where do we go? AAPPS Bull. 2022, 32, 27. [Google Scholar] [CrossRef]
- Ekert, A.; Suominen, K.; Plenio, M.; Knight, P.; Macchiavello, C.; Palma, G.; Steane, A.; Huelga, S. Decoherence and Quantum Error Correction. In The Physics of Quantum Information; Springer-Verlag Berlin: Heidelberg, Germany, 2020; pp. 221–259. [Google Scholar]
- Hong, K.W.; Foong, O.M.; Low, T.J. Challenges in Quantum Key Distribution: A Review. In ICINS ’16: Proceedings of the 4th International Conference on Information and Network Security; Association for Computing Machinery: New York, NY, USA, 2016; pp. 29–33. [Google Scholar]
- Diamanti, E.; Lo, H.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. Npj Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef]
- Ezzell, N.; Pokharel, B.; Tewala, L.; Quiroz, G.; Lidar, D. Dynamical decoupling for superconducting qubits: A performance survey. Phys. Rev. Appl. 2023, 20, 064027. [Google Scholar] [CrossRef]
- Sun, J.; Yuan, X.; Tsunoda, T.; Vedral, V.; Benjamin, S.; Endo, S. Mitigating Realistic Noise in Practical Noisy Intermediate-Scale Quantum Devices. Phys. Rev. Appl. 2021, 15, 034026. [Google Scholar] [CrossRef]
- Ortega, V.; Majumder, S.; Pooser, R. Quantum error mitigation by hidden inverses protocol in superconducting quantum devices. Quantum Sci. Technol. 2023, 8, 014008. [Google Scholar] [CrossRef]
- Wallman, J.; Emerson, J. Noise tailoring for scalable quantum computation via randomized compiling. Phys. Rev. A 2016, 94, 052325. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P. Quantum circuit architecture. Phys. Rev. Lett. 2008, 101, 060401. [Google Scholar] [CrossRef]
- Abbott, A.; Wechs, J.; Horsman, D.; Mhalla, M.; Branciard, C. Communication through coherent control of quantum channels. Quantum 2020, 4, 333. [Google Scholar] [CrossRef]
- Ebler, D.; Salek, S.; Chiribella, G. Enhanced Communication with the Assistance of Indefinite Causal Order. Phys. Rev. Lett. 2017, 120, 120502. [Google Scholar] [CrossRef]
- Delgado, F.; Cardoso-Isidoro, C. Performance characterization of Pauli channels assisted by indefinite causal order and post-measurement. Quantum Inf. Comput. 2020, 20, 1261–1280. [Google Scholar] [CrossRef]
- Katarzyna, S. Geometry of Pauli maps and Pauli channels. Phys. Rev. A 2019, 100, 062331. [Google Scholar]
- Kraus, K. States, Effects and Operations: Fundamental Notions of Quantum Theory; Springer: Berlin, Germany, 1983. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Chiribella, G.; D’Ariano, G.M.; Perinotti, P.; Valiron, B. Quantum computations without definite causal structure. Phys. Rev. A 2013, 88, 022318. [Google Scholar] [CrossRef]
- Morales-Alvarado, C.; Morazán-Luz, J.R.; Navarro-Carrillo, M.; Pabon-Barbery, M.; Delgado, F. Effect on a QKD Chain Going Through a Generic Pauli Channel Together with a Correction Based on the 3-qubit Code. J. Phys. Conf. Ser. 2024, 2701, 012112. [Google Scholar] [CrossRef]
- Reed, M.; DiCarlo, L.; Nigg, S.; Sun, L.; Frunzio, L.; Girvin, S.M.; Schoelkopf, R.J. Realization of three-qubit quantum error correction with superconducting circuits. Nature 2012, 482, 382–385. [Google Scholar] [CrossRef]
- Procopio, L.M.; Delgado, F.; Enríquez, M.; Belabas, N.; Levenson, J.A. Sending classical information via three noisy channels in superposition of causal orders. Phys. Rev. A 2020, 101, 012346. [Google Scholar] [CrossRef]
- Ji, Y.; Chung, Y.; Sprinzak, D.; Heiblum, M.; Mahalu, D.; Shtrikman, H. An Electronic Mach–Zehnder Interferometer. Nature 2003, 422, 415–418. [Google Scholar] [CrossRef]
- Rubino, G.; Rozema, L.A.; Feix, A.; Araújo, M.; Zeuner, J.M.; Procopio, L.M.; Brukner, Č.; Walther, P. Experimental Verification of an Indefinite Causal Order. Sci. Adv. 2017, 3, e1602589. [Google Scholar] [CrossRef]
- Delgado, F. Parametric symmetries in architectures involving Indefinite Causal Order and Path Superposition for Quantum parameter estimation of Pauli channels. Symmetry 2023, 15, 1097. [Google Scholar] [CrossRef]
- Makarov, V.; Hjelme, D. Faked states attack on quantum cryptosystems. J. Mod. Opt. 2005, 52, 691–705. [Google Scholar] [CrossRef]
- Cardoso-Isidoro, C.; Delgado, F. Shared Quantum Key Distribution Based on Asymmetric Double Quantum Teleportation. Symmetry 2022, 14, 713. [Google Scholar] [CrossRef]
- Bennett, C.H. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 1992, 68, 3121. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, A.; Jassem, Y. Enhancement of Quantum Key Distribution Protocol BB84. J. Comput. Theor. Nanosci. 2019, 16, 1138–1154. [Google Scholar] [CrossRef]
- Agarwal, A.; Lindoy, L.P.; Lall, D.; Jamet, F.; Rungger, I. Modelling Non-Markovian Noise in Driven Superconducting Qubits. Quantum Sci. Technol. 2024, 9, 035017. [Google Scholar] [CrossRef]
- Ritter, W.G. Quantum Channels and Representation Theory. J. Math. Phys. 2005, 46, 082103. [Google Scholar] [CrossRef]
- Delgado, F. Symmetries of Quantum Fisher Information as Parameter Estimator for Pauli Channels under Indefinite Causal Order. Symmetry 2022, 14, 1813. [Google Scholar] [CrossRef]
- Krenn, M.; Landgraf, J.; Foesel, T.; Marquardt, F. Artificial Intelligence and Machine Learning for Quantum Technologies. Phys. Rev. A 2023, 107, 010101. [Google Scholar] [CrossRef]
- Cimini, V.; Valeri, M.; Polino, E.; Piacentini, S.; Ceccarelli, F.; Corrielli, G.; Spagnolo, N.; Osellame, R.; Sciarrino, F. Deep Reinforcement Learning for Quantum Multiparameter Estimation. Adv. Photon. 2023, 5, 016005. [Google Scholar] [CrossRef]
- Fowler, A.G.; Mariantoni, M.; Martinis, J.M.; Cleland, A.N. Surface Codes: Towards Practical Large-Scale Quantum Computation. Phys. Rev. A 2012, 86, 032324. [Google Scholar] [CrossRef]
- Yoshida, S.; Tamiya, S.; Yamasaki, H. Concatenate Codes, Save Qubits. arXiv 2025, arXiv:2402.09606. Available online: https://arxiv.org/abs/2402.09606 (accessed on 1 June 2025). [CrossRef]
- Soleymani, M.R.; Gao, Y.; Vilaipornsawai, U. Low Density Parity Check Codes. In Communications and Coding; Springer: Boston, MA, USA, 2002. [Google Scholar] [CrossRef]
- Wath, Y.; Hariprasad, M.; Shah, F.; Gupta, S. Eavesdropping a Quantum Key Distribution Network Using Sequential Quantum Unsharp Measurement Attacks. Eur. Phys. J. Plus 2023, 138, 54. [Google Scholar] [CrossRef]
- Hernández, C.; Portillo, M.; Sánchez-Gaitán, E.; Delgado, F.; Anaya, A. Quantum Key Distribution Shared Protocol Using Teleportation and Delayed Measurement. J. Phys. Conf. Ser. 2024, 2701, 012111. [Google Scholar] [CrossRef]
- Cirac, J.I.; Gisin, N. Coherent Eavesdropping Strategies for the Four State Quantum Cryptography Protocol. Phys. Lett. A 1997, 229, 1–7. [Google Scholar] [CrossRef]
- Rozema, L.A.; Strömberg, T.; Cao, H.; Guo, Y.; Liu, B.-H.; Walther, P. Experimental Aspects of Indefinite Causal Order in Quantum Mechanics. Nat. Rev. Phys. 2024, 6, 483–499. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, Z.; Yuan, H.; Yang, Y. Strict Hierarchy of Strategies for Non-asymptotic Quantum Metrology. arXiv 2023, arXiv:2203.09758. [Google Scholar]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum Secret Sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Johnson, S.; Rarity, J.; Padgett, M. Transmission of Quantum-Secured Images. Sci. Rep. 2024, 14, 11579. [Google Scholar] [CrossRef]
- Cardoso-Isidoro, C.; Delgado, F. Symmetries in Teleportation Assisted by N-Channels under Indefinite Causal Order and Post-Measurement. Symmetry 2020, 12, 1904. [Google Scholar] [CrossRef]
- Pan, D.; Lin, Z.; Wu, J.; Sun, Z.; Ruan, D.; Yin, L.; Long, G. Experimental Free-Space Quantum Secure Direct Communication and Its Security Analysis. Photonics Res. 2020, 8, 1522–1531. [Google Scholar] [CrossRef]
- Limar, I.; Vasiliu, Y.; Kumysh, V. Classification of the Methods of Eavesdropping and Data Corruption in Quantum Cryptosystems. preprint 2018. [CrossRef]

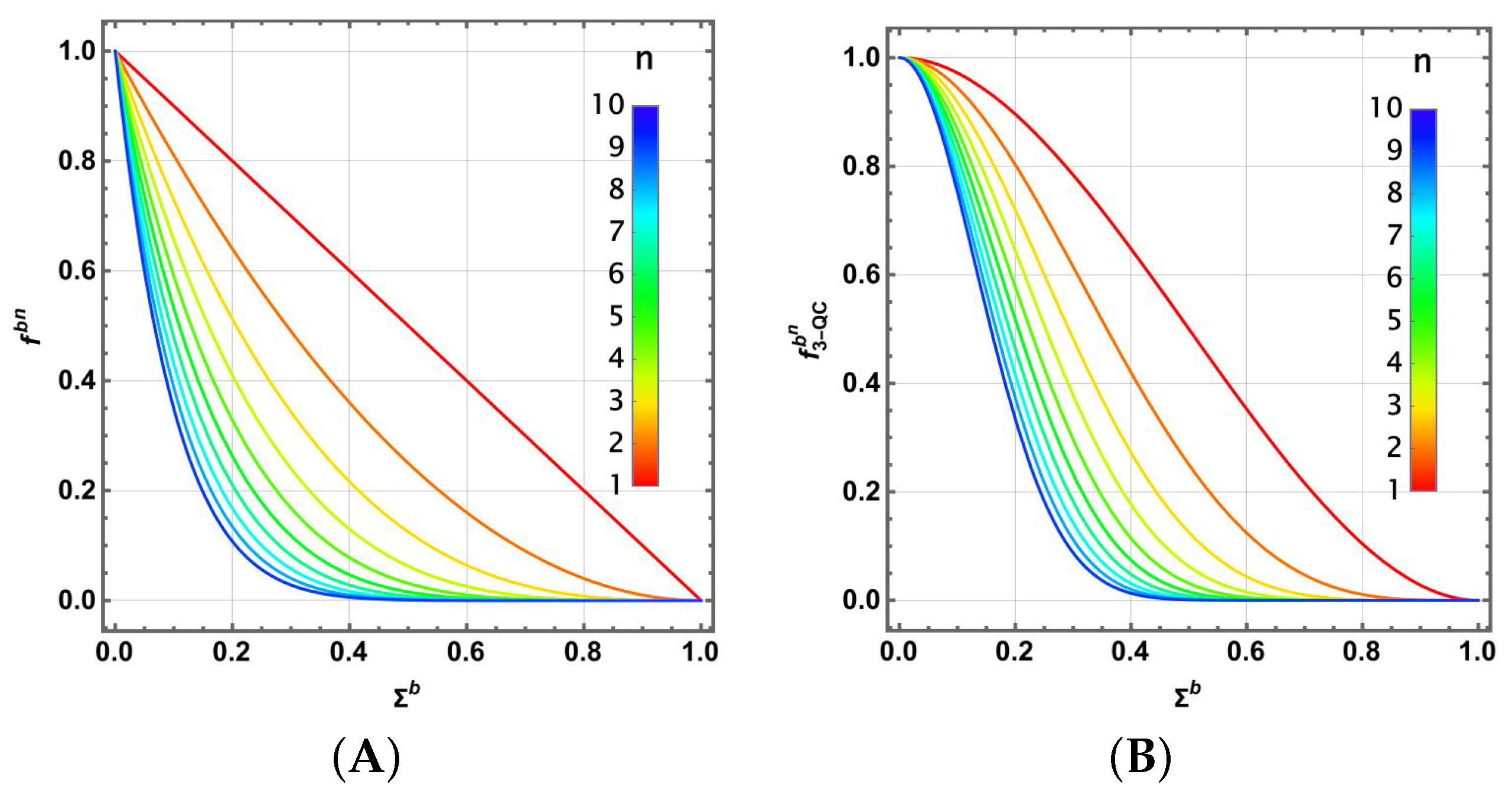

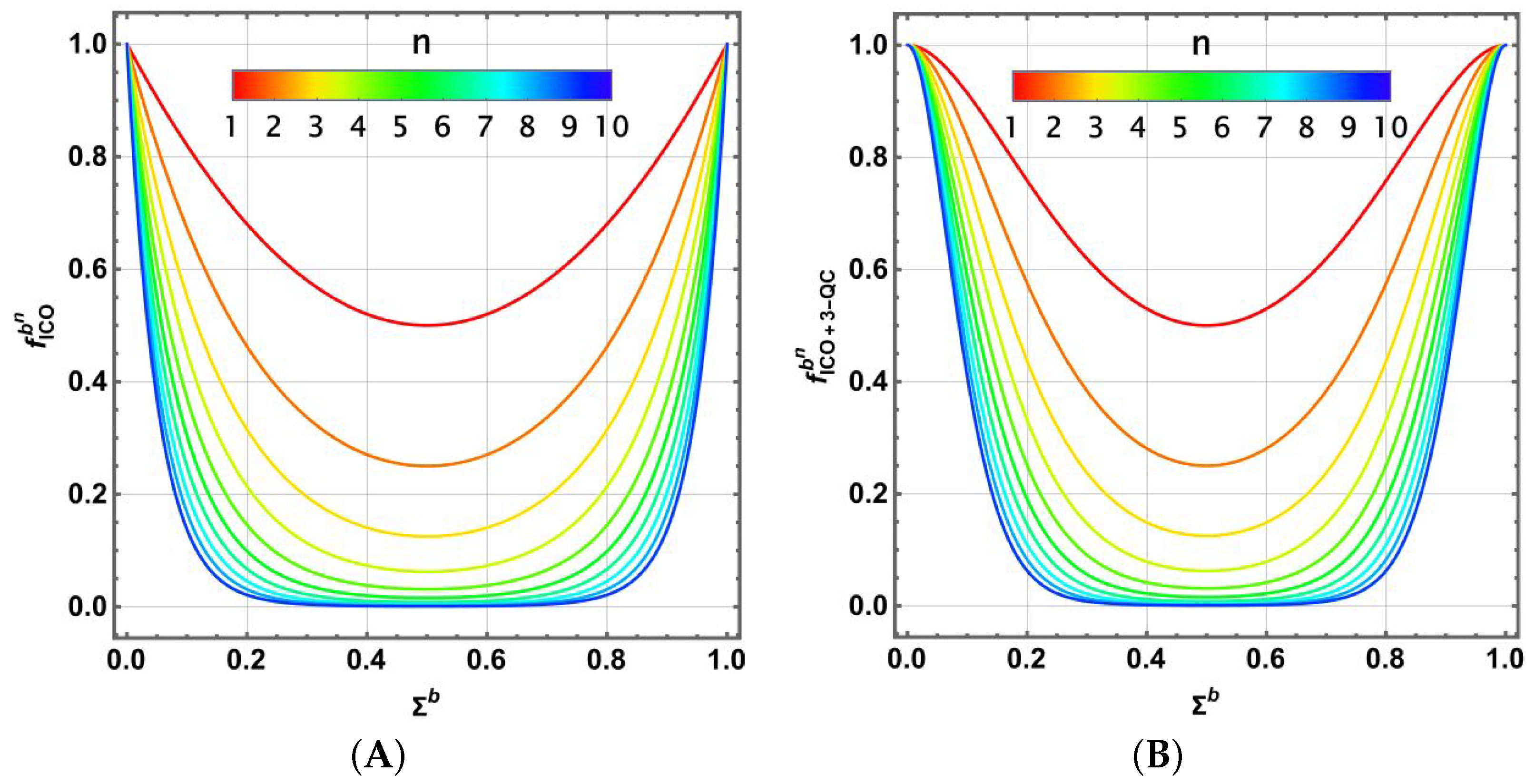
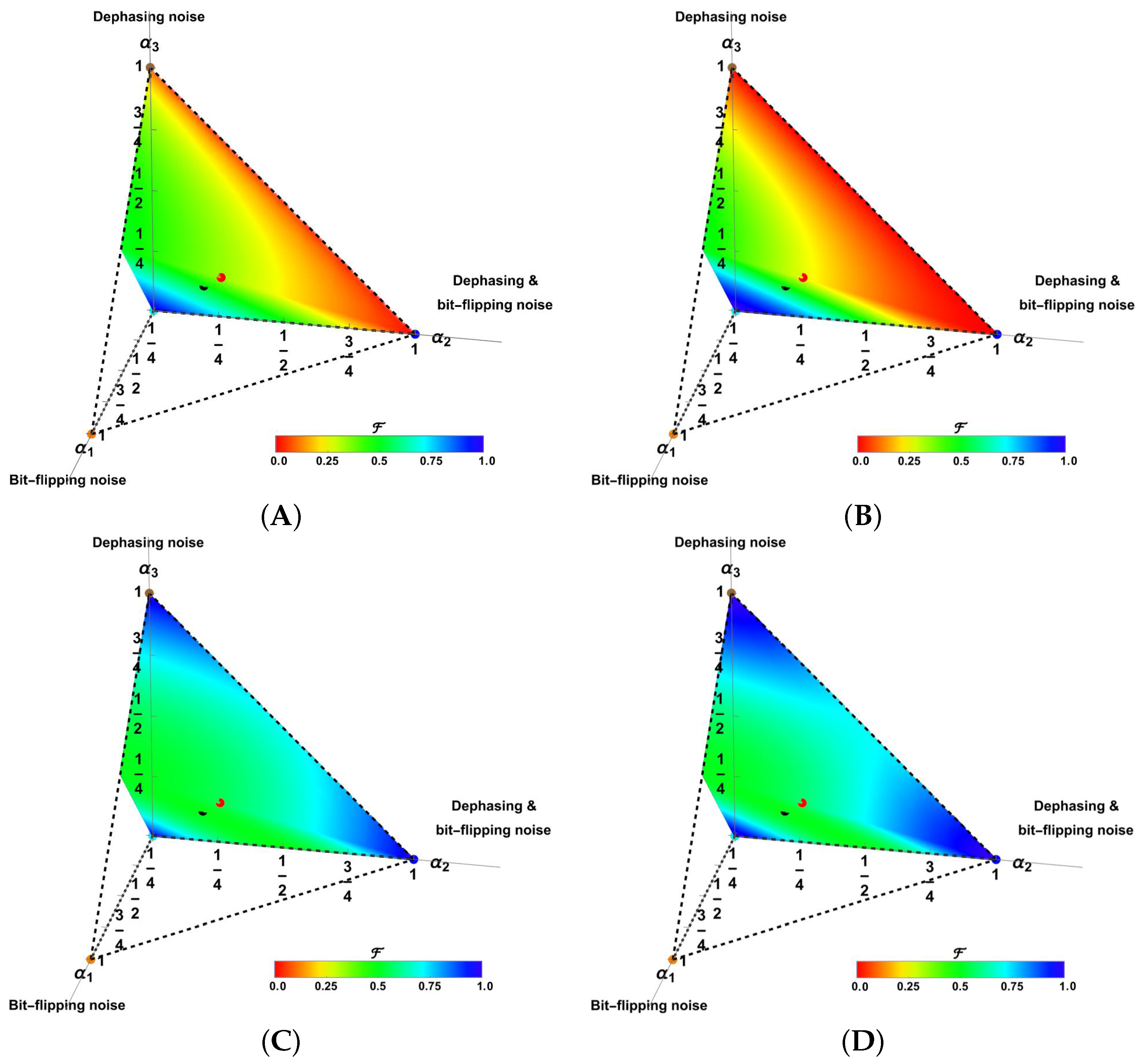
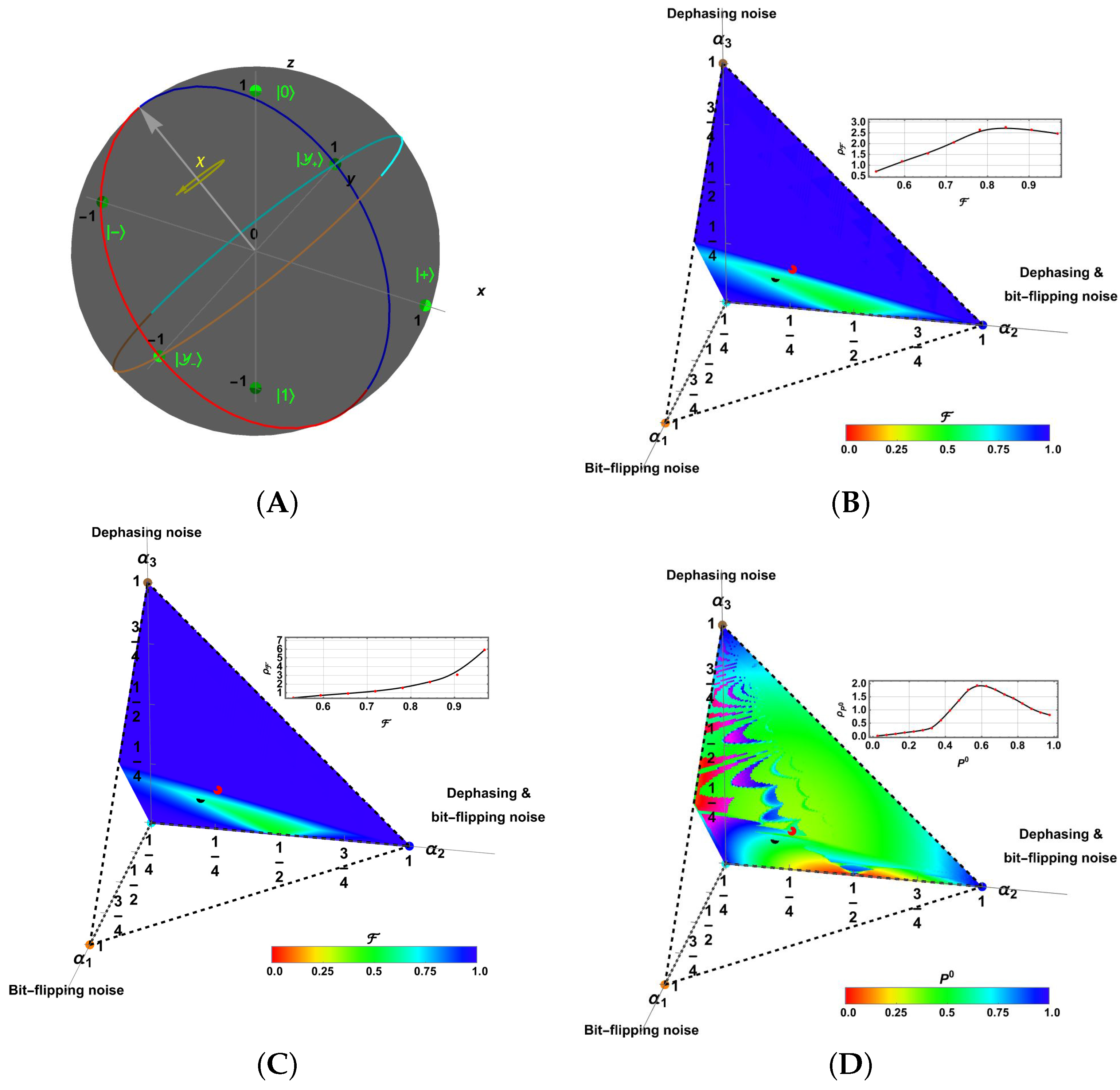
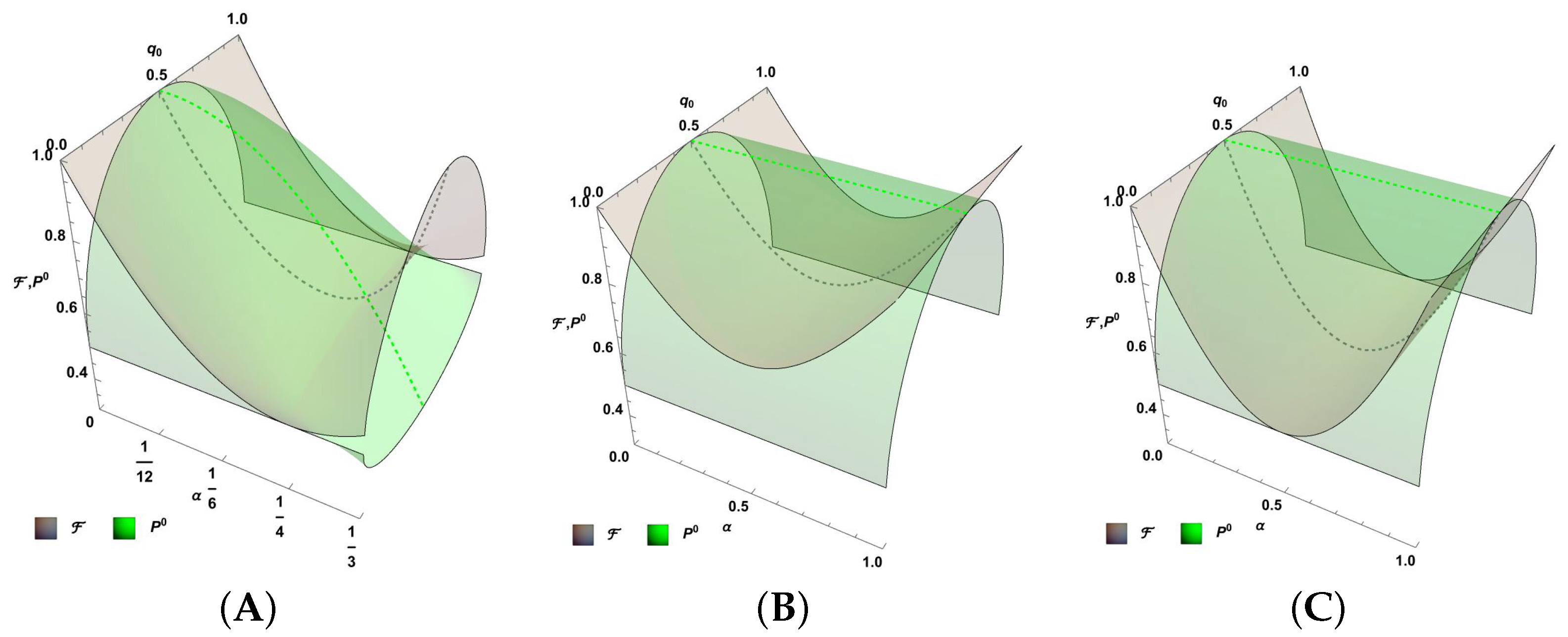
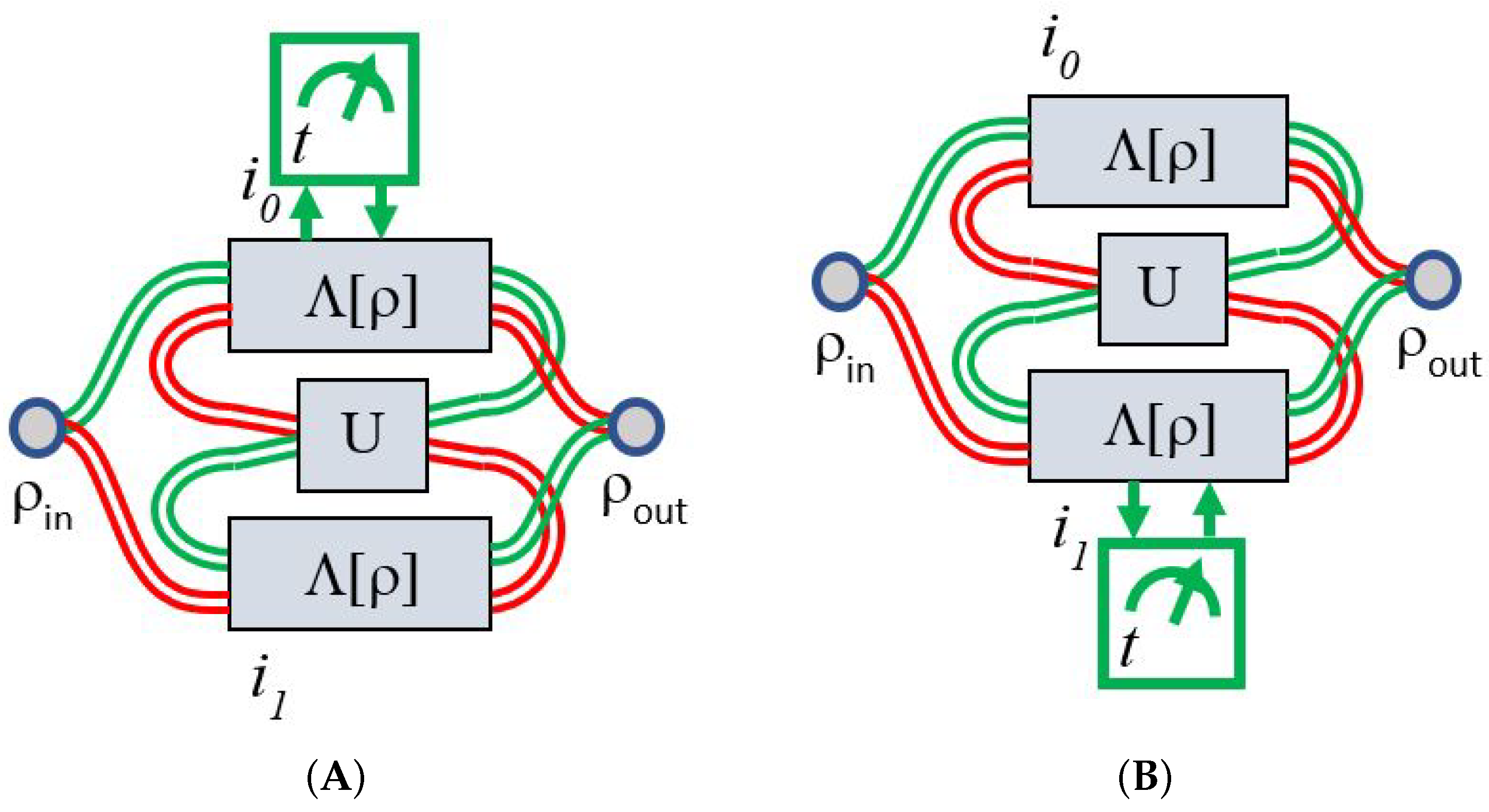
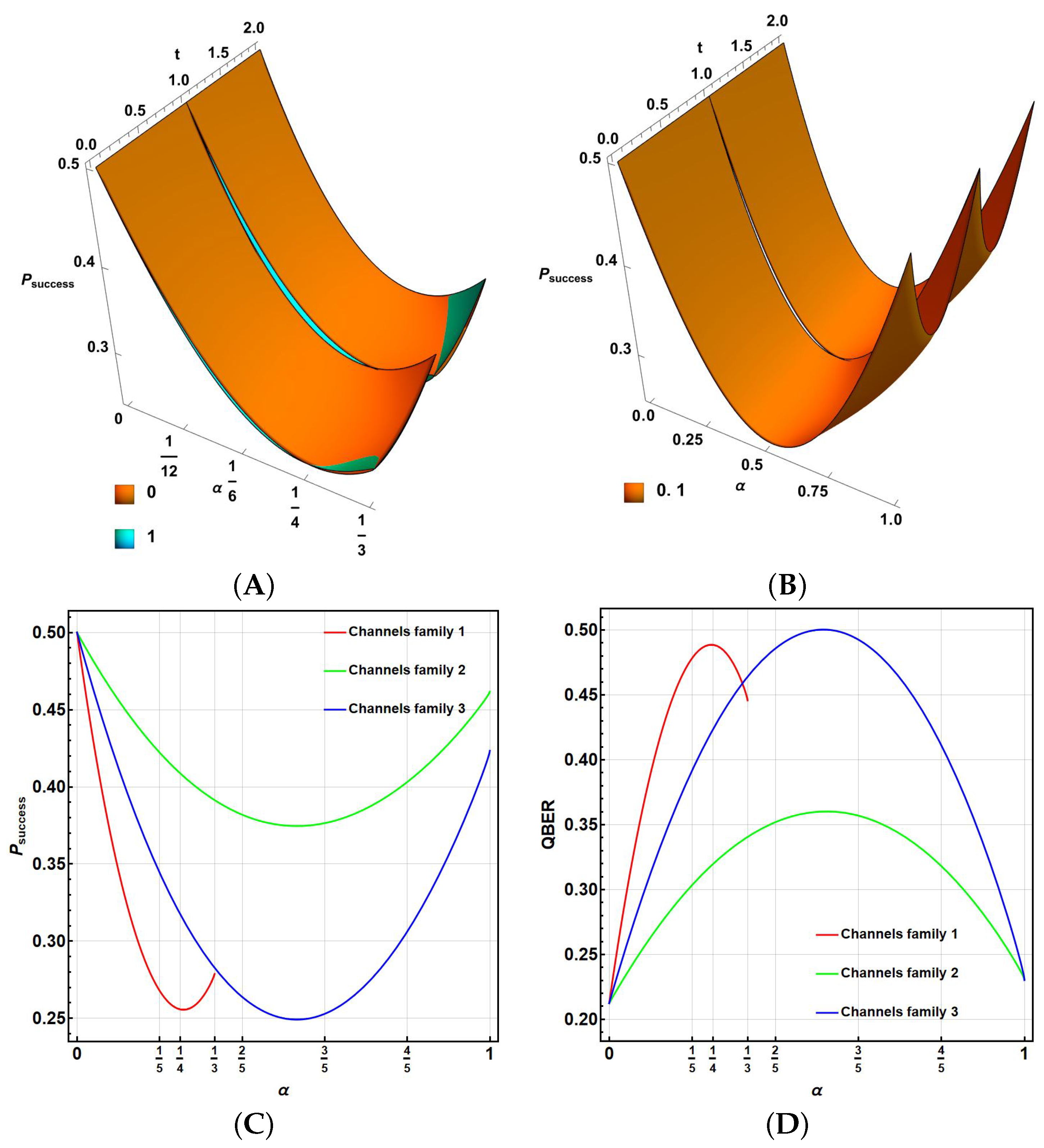
| Sch | b | |||
|---|---|---|---|---|
| PS | 0 | |||
| PS | 1 | |||
| ICO | 0 | |||
| ICO | 1 |
| Sch | Ch | 3-QC | ICOT | ICO + 3-QCT | ICOM | ICO + 3-QCM |
|---|---|---|---|---|---|---|
| 0.471 | 0.445 | 0.598 | 0.634 | 0.725 | 0.861 | |
| 0.172 | 0.230 | 0.080 | 0.103 | 0.125 | 0.127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, F. Enhancing Quantum Information Distribution Through Noisy Channels Using Quantum Communication Architectures. Information 2025, 16, 485. https://doi.org/10.3390/info16060485
Delgado F. Enhancing Quantum Information Distribution Through Noisy Channels Using Quantum Communication Architectures. Information. 2025; 16(6):485. https://doi.org/10.3390/info16060485
Chicago/Turabian StyleDelgado, Francisco. 2025. "Enhancing Quantum Information Distribution Through Noisy Channels Using Quantum Communication Architectures" Information 16, no. 6: 485. https://doi.org/10.3390/info16060485
APA StyleDelgado, F. (2025). Enhancing Quantum Information Distribution Through Noisy Channels Using Quantum Communication Architectures. Information, 16(6), 485. https://doi.org/10.3390/info16060485






