Towards MR-Only Radiotherapy in Head and Neck: Generation of Synthetic CT from Zero-TE MRI Using Deep Learning
Abstract
1. Introduction
- -
- Utilization of ZTE MRI: ZTE was employed for its unique ability to capture signals from short-T2 tissues such as cortical bone—overcoming limitations of conventional MRI sequences—while also providing silent acquisition and reduced artifact sensitivity [22].
- -
- Development of a novel synthetic CT (sCT) generation framework: A 2D attention deep residual U-Net (ADR-Unet) that extends the standard U-Net by incorporating attention gates and deep residual units was proposed. The attention mechanisms enable the model to focus on anatomically relevant regions and suppress irrelevant features, while the residual blocks improve training stability by mitigating vanishing gradient issues.
- -
- Comprehensive benchmarking and validation: ADR-Unet was evaluated under both adversarial and non-adversarial training schemes and compared with baseline architectures (U-Net [23] and Unet++ [24]) adapted from image segmentation to sCT generation. The benefits of the architectural enhancements were validated through both geometric and dosimetric evaluations, demonstrating the superior performance of ADR-Unet for MR-only radiotherapy planning.
2. Materials and Methods
2.1. Data Description
2.1.1. Data Collection
2.1.2. Data Preprocessing
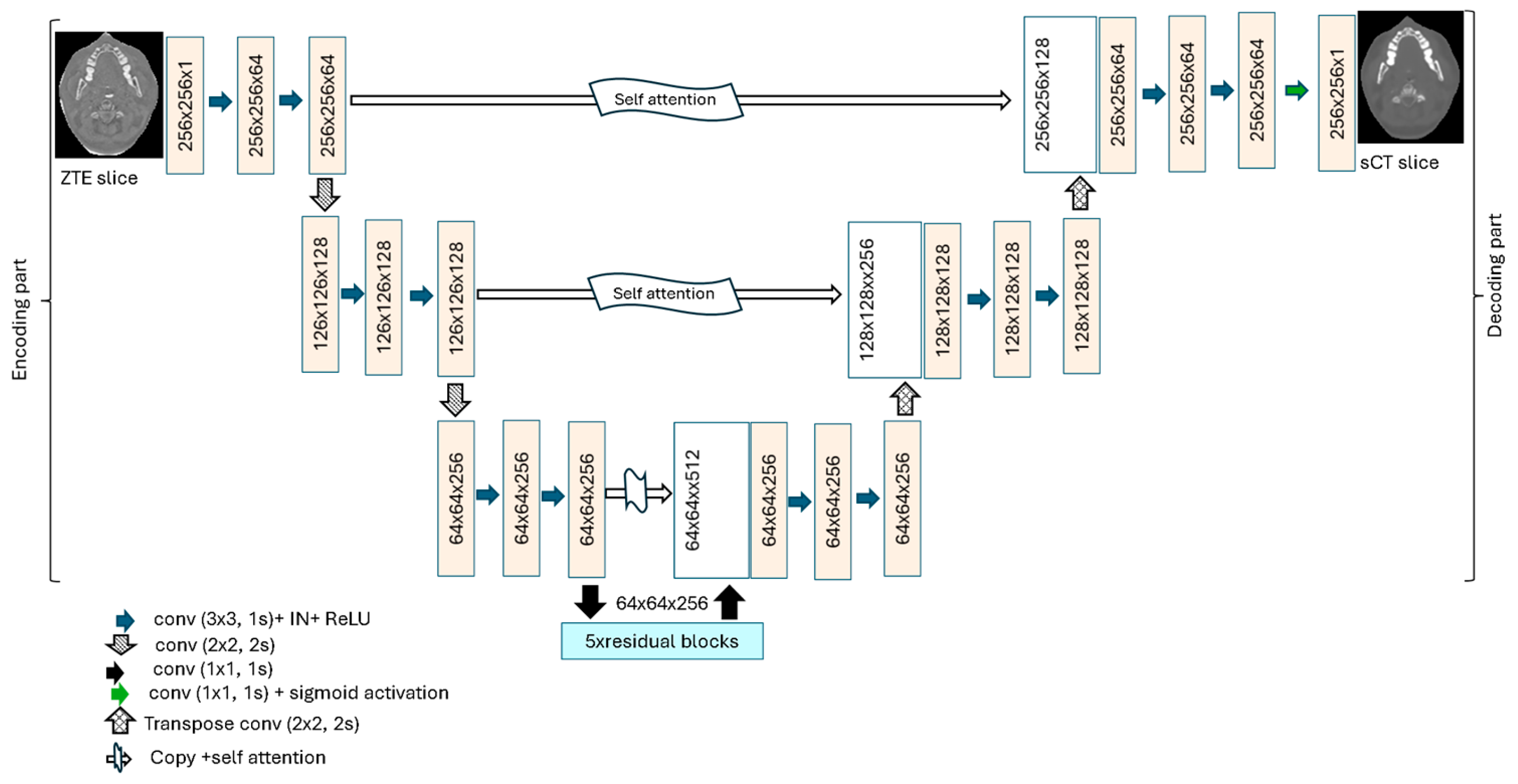
2.2. Attention Deep Residual U-Net for sCT Generation
2.2.1. ADR-Unet Architecture
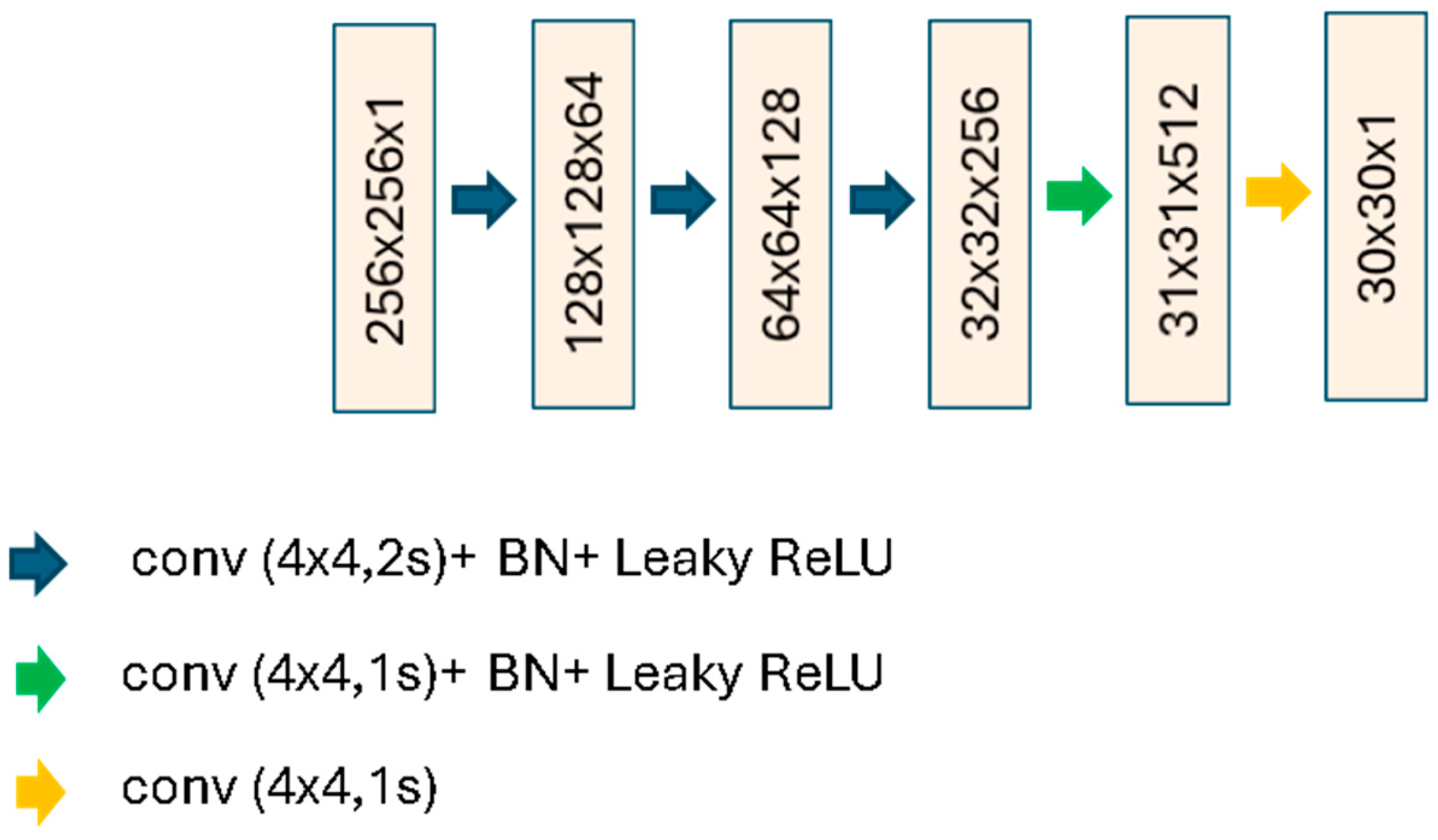
2.2.2. Conditional Generative Adversarial Network for sCT Generation
2.3. Comparison Networks
2.3.1. Unet++
2.3.2. U-Net
2.4. Implementation Details
2.5. Quantitative Evaluation of Synthetic CT and DRRs
2.6. Dosimetric Evaluation Approach
3. Results
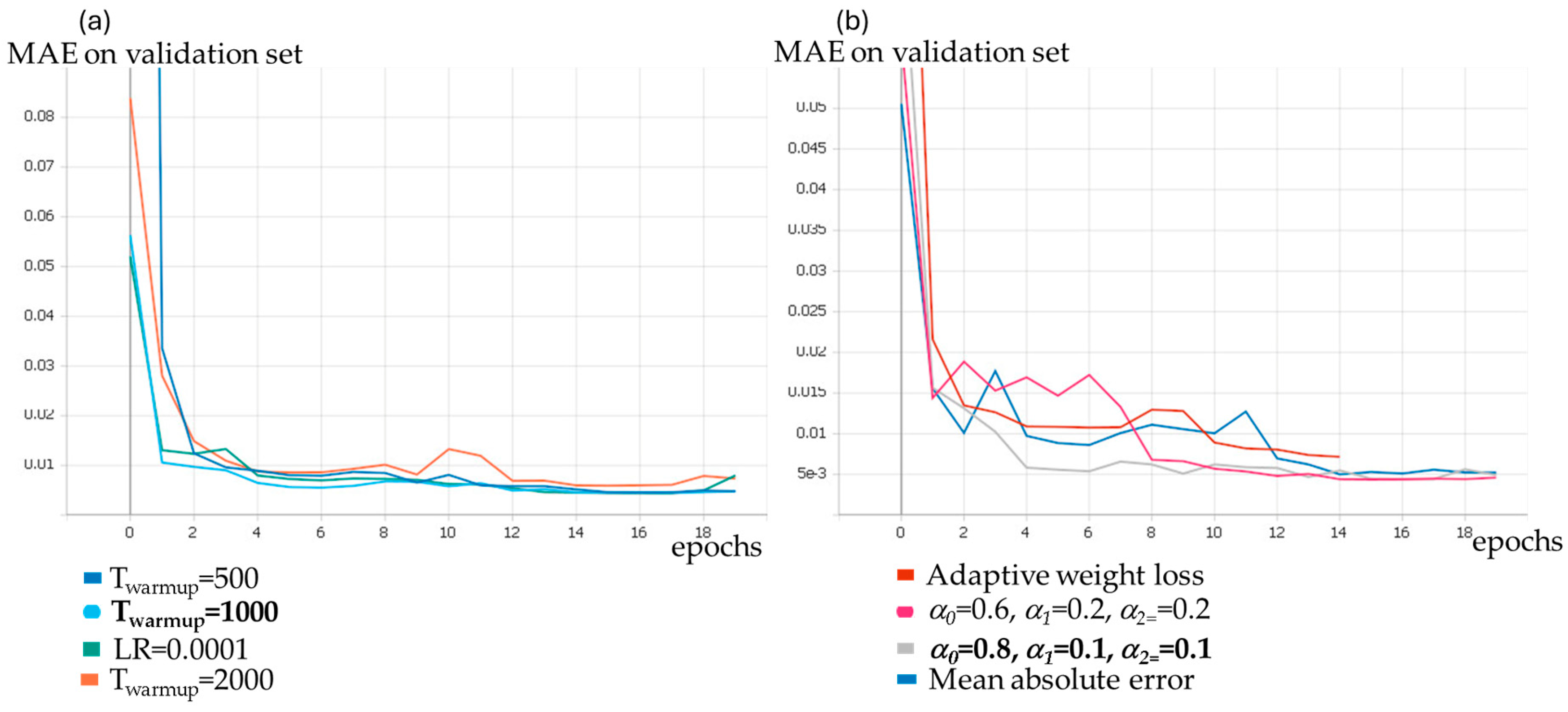
3.1. Parameters Selection
3.2. Validation of Image Registration
3.3. Image Quality Assessment of Attention Deep Residual U-Net
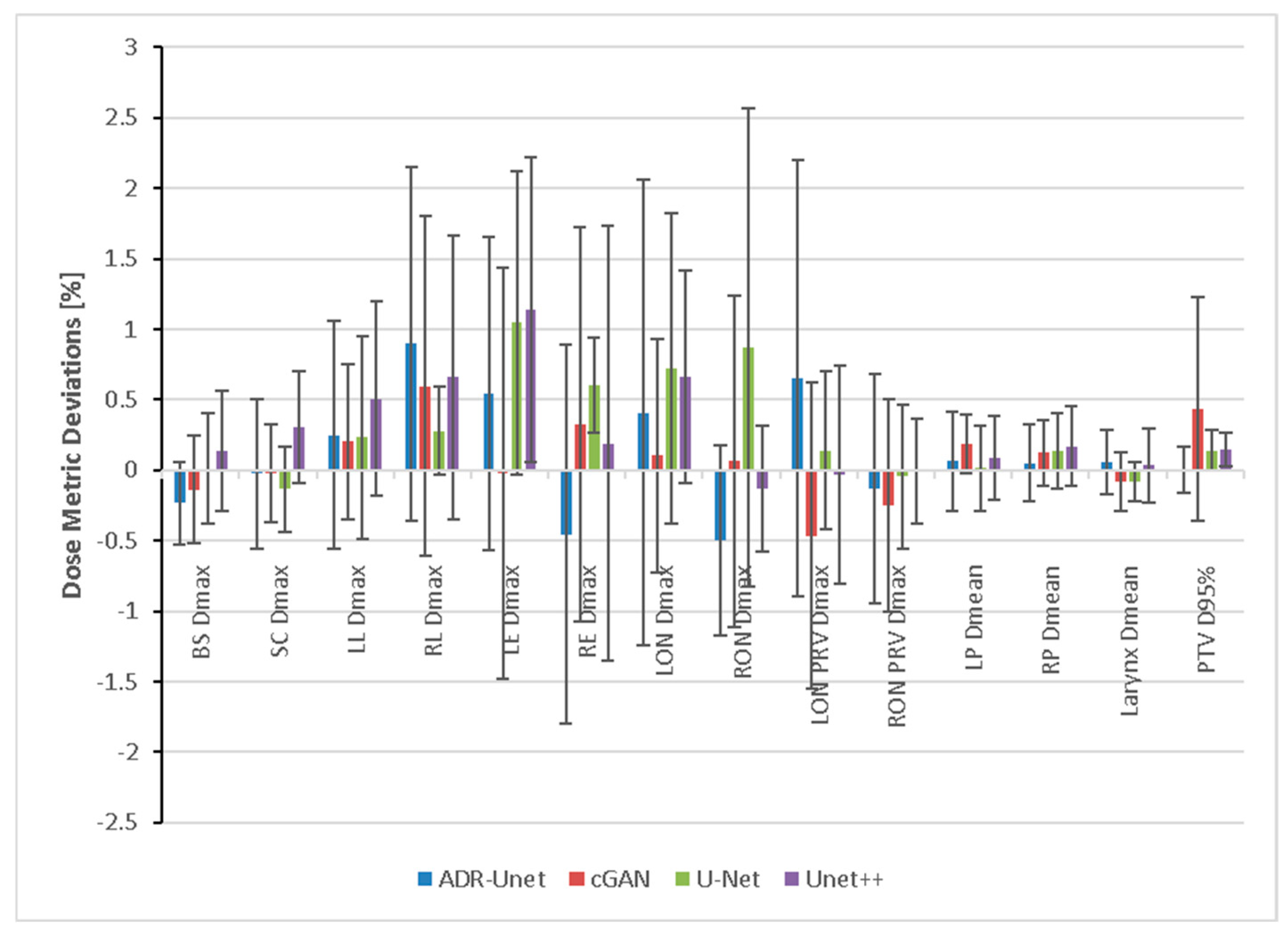
3.4. Dosimetric Evaluation
4. Discussion
| Authors and Year | Number of Patients | MRI Sequence Type | Method | MAE (HU) |
|---|---|---|---|---|
| Current study, 2025 | 17 | ZTE/1.5 T GE MR450w/ | ADR-Unet | 55.49 ± 7.79 |
| cGAN | 57.66 ± 10.44 | |||
| U-Net | 60.06 ± 10.94 | |||
| Unet++ | 59.32 ± 7.09 | |||
| Lauwers et al., 2025 [36] | 127 | ZTE/1.5 T GE MR450w/ | multi-task 2D U-Net | 94 ± 11 |
| Ang et al., 2022 [41] | 51 | T2 Dixon | 2D cGAN with hybrid loss | 68.22 ± 35.63 |
| Dinkla et al., 2019 [42] | 34 | T2 Dixon/3 T Philips | U-Net/DR/3D | 75 ± 9 |
| Palmér et al., 2021 [43] | 44 | T1 Dixon Vibe/1.5 T Siemens | DCNN/RR + DR/2D | 67 ± 14 |
| Klages et al., 2019 [38] | 20 | T1 Dixon Fast Field Echo (FFE)/3 T Philips | cGAN (Pix2Pix)/DR/2D | 92.4 ± 13.5 |
| cycle-GAN/DR/2D | 100.7 ± 14.6 | |||
| Largent et al., 2020 [44] | 8 | 3D T2/1.5 T GE | GAN/RR and DR/2D | 82.8 ± 48.6 |
| Wang et al., 2019 [45] | 33 | T2 TSE/1.5 T Siemens | U-Net/RR and DR/2D | 131 ± 24 |
| Li et al., 2023 [37] | 78 | T1/3 T Philips | 2D DCNN + transformers | 53.88± 3.33 |
| Peng et al., 2020 [46] | 173 | T1/3 T Philips | cGAN/DR/2D | 69.7 ± 9.3 |
| cycle-GAN (unregistered pairs)/-/2D | 100.6 ± 7.7 | |||
| Thummerer et al., 2020 [47] | 27 | 3D spoiled gradient recalled echo/3 T Siemens | DCNN/DR/2.5D | 65.4 ± 3.6 |
| Tie et al., 2020 [48] | 32 | T1,T1c, T2/1.5 T Siemens | cGAN (Pix2Pix)/RR/2D | 75.7 ± 14.6 |
| Qi et al., 2020 [21] | 45 | T1, T2, T1c, T1Dixonc | cGAN/RR/2D | T1 = 75.2 ± 11.5 |
| T2 = 87.0 ± 10.8 | ||||
| T1C = 80.0 ± 10.9 | ||||
| T1Dixonc = 86.3 ± 10.8 | ||||
| Multiseq. = 70.0 ± 12.0 | ||||
| U-Net/RR/2D | 71.3 ± 12.4 |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADR-Unet | Attention deep residual U-Net |
| AG | Self-attention gate |
| cGAN | Conditional generative adversarial network |
| DL | Deep learning |
| DRR | Digitally reconstructed radiograph |
| DRU | Deep residual unit |
| DVH | Dose–volume histogram |
| EBRT | External beam radiotherapy |
| GELU | Gaussian error linear unit |
| HN | Head and neck |
| LOOCV | Leave-one-out cross-validation |
| OAR | Organ at risk |
| PDMD | Percentage of dose metric deviation |
| PTV | Planning target volume |
| PRV | Planning organ at risk volume |
| ReLU | Rectified linear unit |
| sCT | Synthetic CT |
| TPS | Treatment planning system |
| UTE | Ultrashort time echo |
| VMAT | Volumetric modulated arc therapy |
| ZTE | Zero time echo |
References
- Ingle, M.; Lalondrelle, S. Current Status of Anatomical Magnetic Resonance Imaging in Brachytherapy and External Beam Radiotherapy Planning and Delivery. Clin. Oncol. 2020, 32, 817–827. [Google Scholar] [CrossRef] [PubMed]
- Chandarana, H.; Wang, H.; Tijssen, R.H.N.; Das, I.J. Emerging Role of MRI in Radiation Therapy. J. Magn. Reson. Imaging 2018, 48, 1468–1478. [Google Scholar] [CrossRef]
- Daisne, J.-F.; Sibomana, M.; Bol, A.; Cosnard, G.; Lonneux, M.; Grégoire, V. Evaluation of a Multimodality Image (CT, MRI and PET) Coregistration Procedure on Phantom and Head and Neck Cancer Patients: Accuracy, Reproducibility and Consistency. Radiother. Oncol. 2003, 69, 237–245. [Google Scholar] [CrossRef]
- Kim, J.; Glide-Hurst, C.; Doemer, A.; Wen, N.; Movsas, B.; Chetty, I.J. Implementation of a Novel Algorithm For Generating Synthetic CT Images from Magnetic Resonance Imaging Data Sets for Prostate Cancer Radiation Therapy. Int. J. Radiat. Oncol. 2015, 91, 39–47. [Google Scholar] [CrossRef]
- Korhonen, J.; Kapanen, M.; Keyriläinen, J.; Seppälä, T.; Tenhunen, M. A Dual Model HU Conversion from MRI Intensity Values within and Outside of Bone Segment for MRI-Based Radiotherapy Treatment Planning of Prostate Cancer. Med. Phys. 2013, 41, 011704. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Caldwell, C.; Balogh, J.; Mah, K. Toward Magnetic Resonance-Only Simulation: Segmentation of Bone in MR for Radiation Therapy Verification of the Head. Int. J. Radiat. Oncol. Biol. Phys. 2014, 89, 649–657. [Google Scholar] [CrossRef]
- Holmes, J.E.; Bydder, G.M. MR Imaging with Ultrashort TE (UTE) Pulse Sequences: Basic Principles. Radiography 2005, 11, 163–174. [Google Scholar] [CrossRef]
- Berker, Y.; Franke, J.; Salomon, A.; Palmowski, M.; Donker, H.C.W.; Temur, Y.; Mottaghy, F.M.; Kuhl, C.; Izquierdo-Garcia, D.; Fayad, Z.A.; et al. MRI-Based Attenuation Correction for Hybrid PET/MRI Systems: A 4-Class Tissue Segmentation Technique Using a Combined Ultrashort-Echo-Time/Dixon MRI Sequence. J. Nucl. Med. 2012, 53, 796–804. [Google Scholar] [CrossRef] [PubMed]
- Kapanen, M.; Tenhunen, M. T1/T2*-Weighted MRI Provides Clinically Relevant Pseudo-CT Density Data for the Pelvic Bones in MRI-Only Based Radiotherapy Treatment Planning. Acta Oncol. 2013, 52, 612–618. [Google Scholar] [CrossRef]
- Sjölund, J.; Forsberg, D.; Andersson, M.; Knutsson, H. Generating Patient Specific Pseudo-CT of the Head from MR Using Atlas-Based Regression. Phys. Med. Biol. 2015, 60, 825–839. [Google Scholar] [CrossRef]
- Uh, J.; Merchant, T.E.; Li, Y.; Li, X.; Hua, C. MRI-Based Treatment Planning with Pseudo CT Generated through Atlas Registration. Med. Phys. 2014, 41, 051711. [Google Scholar] [CrossRef]
- Aouadi, S.; Vasic, A.; Paloor, S.; Torfeh, T.; McGarry, M.; Petric, P.; Riyas, M.; Hammoud, R.; Al-Hammadi, N. Generation of Synthetic CT Using Multi-Scale and Dual-Contrast Patches for Brain MRI-Only External Beam Radiotherapy. Phys. Medica 2017, 42, 174–184. [Google Scholar] [CrossRef] [PubMed]
- Boulanger, M.; Nunes, J.-C.; Chourak, H.; Largent, A.; Tahri, S.; Acosta, O.; De Crevoisier, R.; Lafond, C.; Barateau, A. Deep Learning Methods to Generate Synthetic CT from MRI in Radiotherapy: A Literature Review. Phys. Medica 2021, 89, 265–281. [Google Scholar] [CrossRef] [PubMed]
- Aouadi, S.; Torfeh, T.; Bouhali, O.; Yoganathan, S.; Paloor, S.; Chandramouli, S.; Hammoud, R.; Al-Hammadi, N. Prediction of Cervix Cancer Stage and Grade from Diffusion Weighted Imaging Using EfficientNet. Biomed. Phys. Eng. Express 2024, 10, 045042. [Google Scholar] [CrossRef]
- Aouadi, S.; Torfeh, T.; Yoganathan, S.; Paloor, S.; Riyas, M.; Hammoud, R.; Al-Hammadi, N. Investigation of Radiomics and Deep Convolutional Neural Networks Approaches for Glioma Grading. Biomed. Phys. Eng. Express 2023, 9, 35020. [Google Scholar] [CrossRef]
- Sahiner, B.; Pezeshk, A.; Hadjiiski, L.M.; Wang, X.; Drukker, K.; Cha, K.H.; Summers, R.M.; Giger, M.L. Deep Learning in Medical Imaging and Radiation Therapy. Med. Phys. 2019, 46, e1–e36. [Google Scholar] [CrossRef]
- Sherwani, M.K.; Gopalakrishnan, S. A Systematic Literature Review: Deep Learning Techniques for Synthetic Medical Image Generation and Their Applications in Radiotherapy. Front. Radiol. 2024, 4, 1385742. [Google Scholar] [CrossRef] [PubMed]
- Lastrucci, A.; Wandael, Y.; Ricci, R.; Maccioni, G.; Giansanti, D. The Integration of Deep Learning in Radiotherapy: Exploring Challenges, Opportunities, and Future Directions through an Umbrella Review. Diagnostics 2024, 14, 939. [Google Scholar] [CrossRef]
- Aouadi, S.; Mohamed, N.; Aloudeh, J.; Zeid, M.; Bouhali, O.; Hammoud, R.; Al-Hammadi, N.; Torfeh, T. Review of Cervix Cancer Classification Using Radiomics on Diffusion-Weighted Imaging. In IntechOpen Bioinformatics and Medical Informatics; IntechOpen: London, UK, 2022; p. 13. [Google Scholar]
- Lauritzen, A.D.; Papademetris, X.; Turovets, S.; Onofrey, J.A. Evaluation of CT Image Synthesis Methods:From Atlas-Based Registration to Deep Learning. arXiv 2019, arXiv:1906.04467. [Google Scholar]
- Qi, M.; Li, Y.; Wu, A.; Jia, Q.; Li, B.; Sun, W.; Dai, Z.; Lu, X.; Zhou, L.; Deng, X.; et al. Multi-sequence MR Image-based Synthetic CT Generation Using a Generative Adversarial Network for Head and Neck MRI-only Radiotherapy. Med. Phys. 2020, 47, 1880–1894. [Google Scholar] [CrossRef]
- Wiesinger, F.; Ho, M.L. Zero-TE MRI: Principles and Applications in the Head and Neck. Br. J. Radiol. 2022, 95, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11045, pp. 3–11. [Google Scholar] [CrossRef]
- Lawson, J.D.; Schreibmann, E.; Jani, A.B.; Fox, T. Quantitative Evaluation of a Cone-beam Computed Tomography–Planning Computed Tomography Deformable Image Registration Method for Adaptive Radiation Therapy. J. Appl. Clin. Med. Phys. 2007, 8, 96–113. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.-Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar]
- Taigman, Y.; Polyak, A.; Wolf, L. Unsupervised Cross-Domain Image Generation. arXiv 2016, arXiv:1611.02200. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, Banff, AB, Canada, 22 December 2014; pp. 1–13. [Google Scholar]
- Peli, E. Contrast in Complex Images. J. Opt. Soc. Am. A 1990, 7, 2032–2040. [Google Scholar] [CrossRef] [PubMed]
- Vassiliev, O.N.; Wareing, T.A.; McGhee, J.; Failla, G.; Salehpour, M.R.; Mourtada, F. Validation of a New Grid-Based Boltzmann Equation Solver for Dose Calculation in Radiotherapy with Photon Beams. Phys. Med. Biol. 2010, 55, 581–598. [Google Scholar] [CrossRef]
- Grégoire, V.; Mackie, T.R. State of the Art on Dose Prescription, Reporting and Recording in Intensity-Modulated Radiation Therapy (ICRU Report No. 83). Cancer Radiother. 2011, 15, 555–559. [Google Scholar] [CrossRef]
- Bentzen, S.M.; Constine, L.S.; Deasy, J.O.; Eisbruch, A.; Jackson, A.; Marks, L.B.; Ten Haken, R.K.; Yorke, E.D. Quantitative Analyses of Normal Tissue Effects in the Clinic (QUANTEC): An Introduction to the Scientific Issues. Int. J. Radiat. Oncol. 2010, 76, S3–S9. [Google Scholar] [CrossRef]
- Huq, A.; Pervin, M.T. Adaptive Weight Assignment Scheme for Multi-Task Learning. IAES Int. J. Artif. Intell. 2022, 11, 173. [Google Scholar] [CrossRef]
- Varadhan, R.; Karangelis, G.; Krishnan, K.; Hui, S. A Framework for Deformable Image Registration Validation in Radiotherapy Clinical Applications. J. Appl. Clin. Med. Phys. 2013, 14, 192–213. [Google Scholar] [CrossRef]
- Lauwers, I.; Capala, M.; Kaushik, S.; Ruskó, L.; Cozzini, C.; Kleijnen, J.P.; Wyatt, J.; McCallum, H.; Verduijn, G.; Wiesinger, F.; et al. Synthetic CT Generation Using Zero TE MR for Head-and-Neck Radiotherapy. Radiother. Oncol. 2025, 205, 110762. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Xu, S.; Lu, Y.; Qi, Z. CT Synthesis from MRI with an Improved Multi-Scale Learning Network. Front. Phys. 2023, 11, 1–11. [Google Scholar] [CrossRef]
- Klages, P.; Benslimane, I.; Riyahi, S.; Jiang, J.; Hunt, M.; Deasy, J.; Veeraraghavan, H.; Tyagi, N. Comparison of Patch-Based Conditional Generative Adversarial Neural Net Models with Emphasis on Model Robustness for Use in Head and Neck Cases for MR-Only Planning. arXiv 2019, arXiv:1902.00536. [Google Scholar]
- Papanikolaou, N.; Battista, J.J.; Boyer, A.L.; Kappas, C.; Klein, E.; Mackie, T.R.; Sharpe, M.; Dyk, J. Van Tissue Inhomogeneity Corrections for Megavoltage Photon Beams; American Association of Physicists in Medicine: College Park, MD, USA, 2004. [Google Scholar]
- Kondo, S.; Kasai, S.; Hirasawa, K. Synthesizing 3D Computed Tomography from MRI or CBCT Using 2.5D Deep Neural Networks. arXiv 2023, arXiv:2308.13553. [Google Scholar]
- Ang, S.P.; Lam Phung, S.; Field, M.; Schira, M.M. An Improved Deep Learning Framework for MR-to-CT Image Synthesis with a New Hybrid Objective Function. In Proceedings of the IEEE International Symposium on Biomedical Imaging (ISBI) 2022, Kolkata, India, 28–31 March 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Dinkla, A.M.; Florkow, M.C.; Maspero, M.; Savenije, M.H.F.; Zijlstra, F.; Doornaert, P.A.H.; van Stralen, M.; Philippens, M.E.P.; van den Berg, C.A.T.; Seevinck, P.R. Dosimetric Evaluation of Synthetic CT for Head and Neck Radiotherapy Generated by a Patch-based Three-dimensional Convolutional Neural Network. Med. Phys. 2019, 46, 4095–4104. [Google Scholar] [CrossRef]
- Palmér, E.; Karlsson, A.; Nordström, F.; Petruson, K.; Siversson, C.; Ljungberg, M.; Sohlin, M. Synthetic Computed Tomography Data Allows for Accurate Absorbed Dose Calculations in a Magnetic Resonance Imaging Only Workflow for Head and Neck Radiotherapy. Phys. Imaging Radiat. Oncol. 2021, 17, 36–42. [Google Scholar] [CrossRef]
- Largent, A.; Marage, L.; Gicquiau, I.; Nunes, J.-C.; Reynaert, N.; Castelli, J.; Chajon, E.; Acosta, O.; Gambarota, G.; de Crevoisier, R.; et al. Head-and-Neck MRI-Only Radiotherapy Treatment Planning: From Acquisition in Treatment Position to Pseudo-CT Generation. Cancer/Radiothérapie 2020, 24, 288–297. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Zhang, X.; Deng, W. Synthetic CT Generation Based on T2 Weighted MRI of Nasopharyngeal Carcinoma (NPC) Using a Deep Convolutional Neural Network (DCNN). Front. Oncol. 2019, 9, 1333. [Google Scholar] [CrossRef]
- Peng, Y.; Chen, S.; Qin, A.; Chen, M.; Gao, X.; Liu, Y.; Miao, J.; Gu, H.; Zhao, C.; Deng, X.; et al. Magnetic Resonance-Based Synthetic Computed Tomography Images Generated Using Generative Adversarial Networks for Nasopharyngeal Carcinoma Radiotherapy Treatment Planning. Radiother. Oncol. 2020, 150, 217–224. [Google Scholar] [CrossRef]
- Thummerer, A.; de Jong, B.A.; Zaffino, P.; Meijers, A.; Marmitt, G.G.; Seco, J.; Steenbakkers, R.J.H.M.; Langendijk, J.A.; Both, S.; Spadea, M.F.; et al. Comparison of the Suitability of CBCT- and MR-Based Synthetic CTs for Daily Adaptive Proton Therapy in Head and Neck Patients. Phys. Med. Biol. 2020, 65, 235036. [Google Scholar] [CrossRef]
- Tie, X.; Lam, S.; Zhang, Y.; Lee, K.; Au, K.; Cai, J. Pseudo-CT Generation from Multi-parametric MRI Using a Novel Multi-channel Multi-path Conditional Generative Adversarial Network for Nasopharyngeal Carcinoma Patients. Med. Phys. 2020, 47, 1750–1762. [Google Scholar] [CrossRef] [PubMed]
- Fortunati, V.; Verhaart, R.F.; Angeloni, F.; van der Lugt, A.; Niessen, W.J.; Veenland, J.F.; Paulides, M.M.; van Walsum, T. Feasibility of Multimodal Deformable Registration for Head and Neck Tumor Treatment Planning. Int. J. Radiat. Oncol. 2014, 90, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, N.; Fontenla, S.; Zelefsky, M.; Chong-Ton, M.; Ostergren, K.; Shah, N.; Warner, L.; Kadbi, M.; Mechalakos, J.; Hunt, M. Clinical Workflow for MR-Only Simulation and Planning in Prostate. Radiat. Oncol. 2017, 12, 119. [Google Scholar] [CrossRef]
- Karlsson, M.; Karlsson, M.G.; Nyholm, T.; Amies, C.; Zackrisson, B. Dedicated Magnetic Resonance Imaging in the Radiotherapy Clinic. Int. J. Radiat. Oncol. 2009, 74, 644–651. [Google Scholar] [CrossRef] [PubMed]



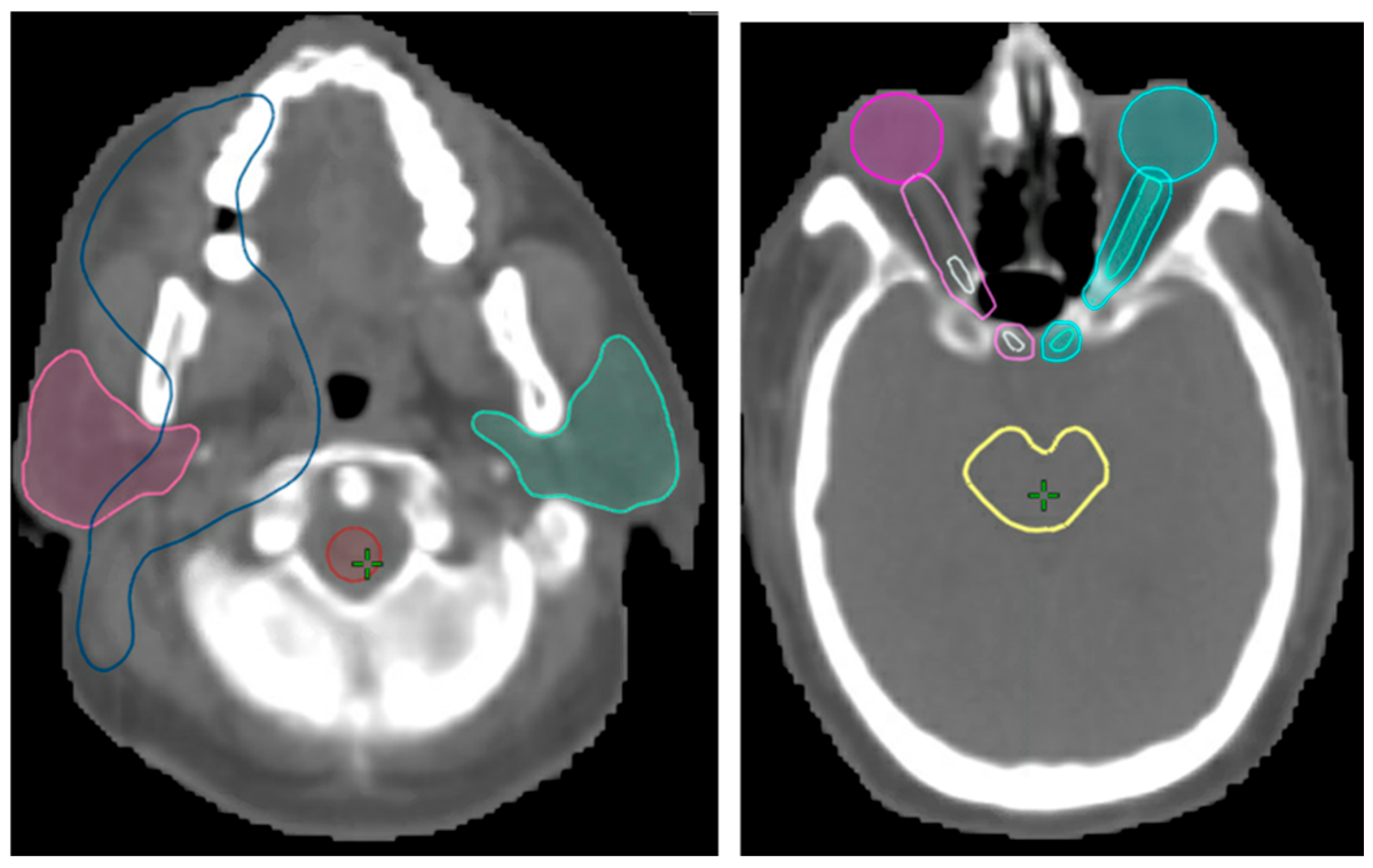
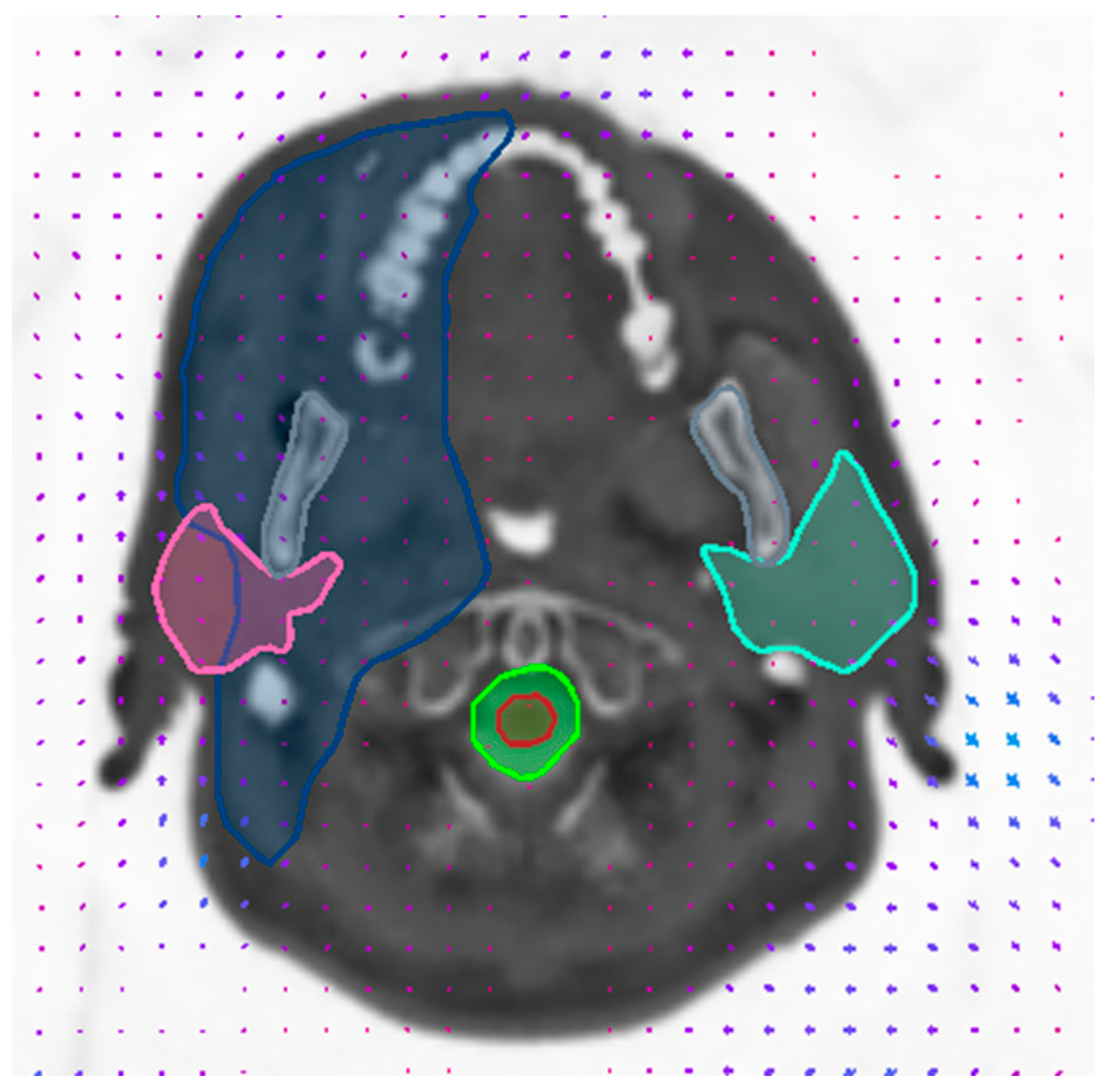
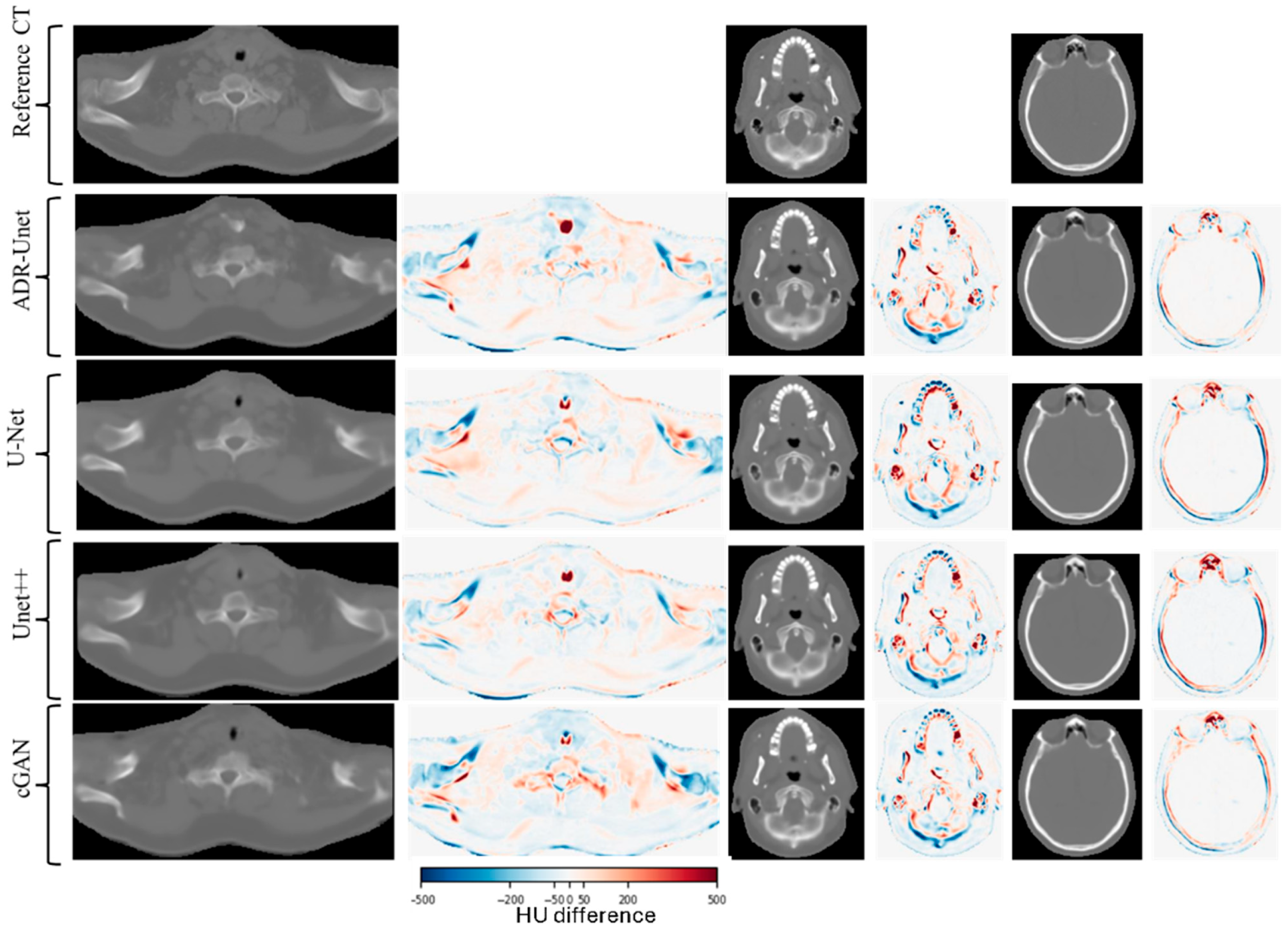
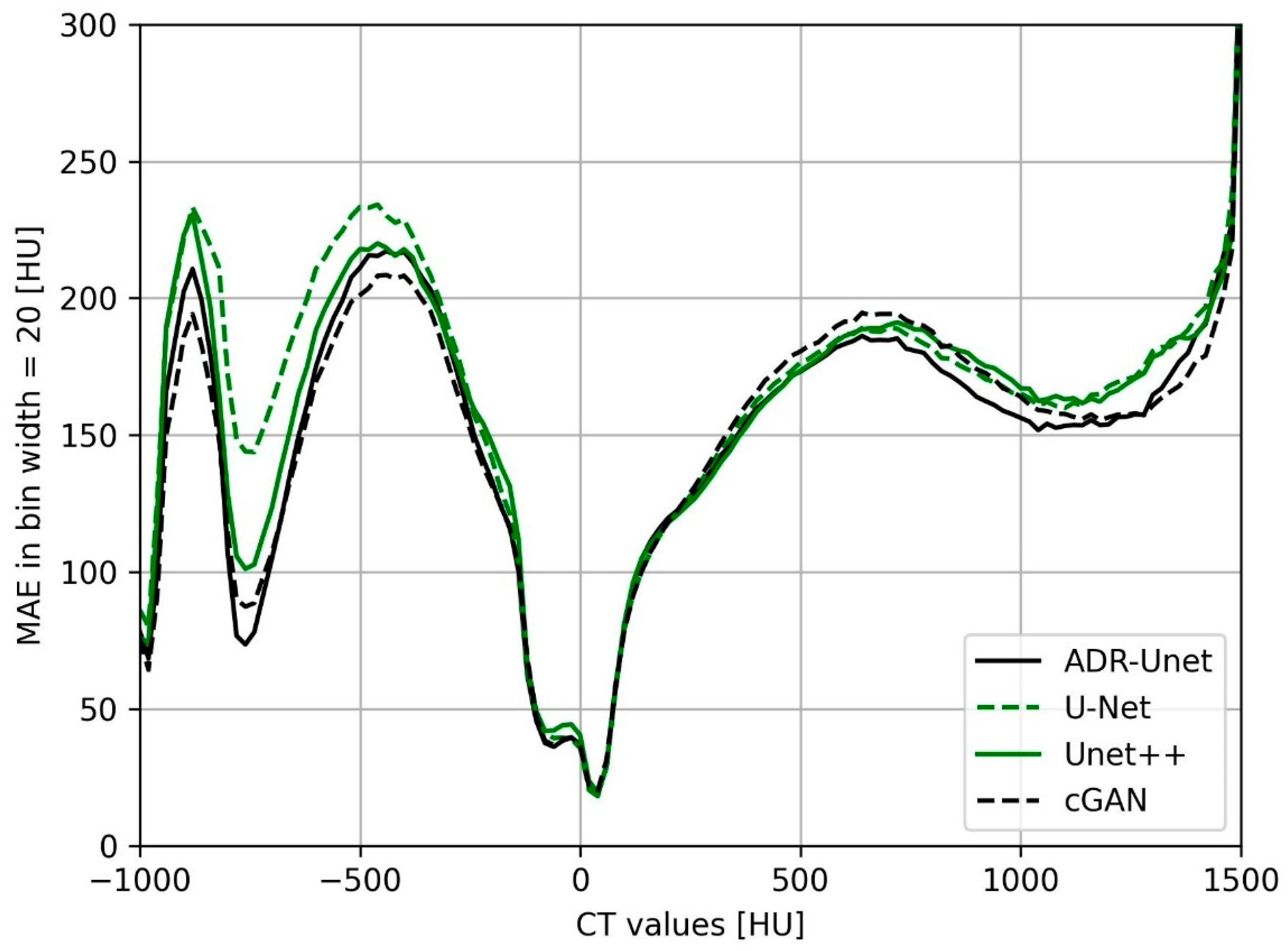
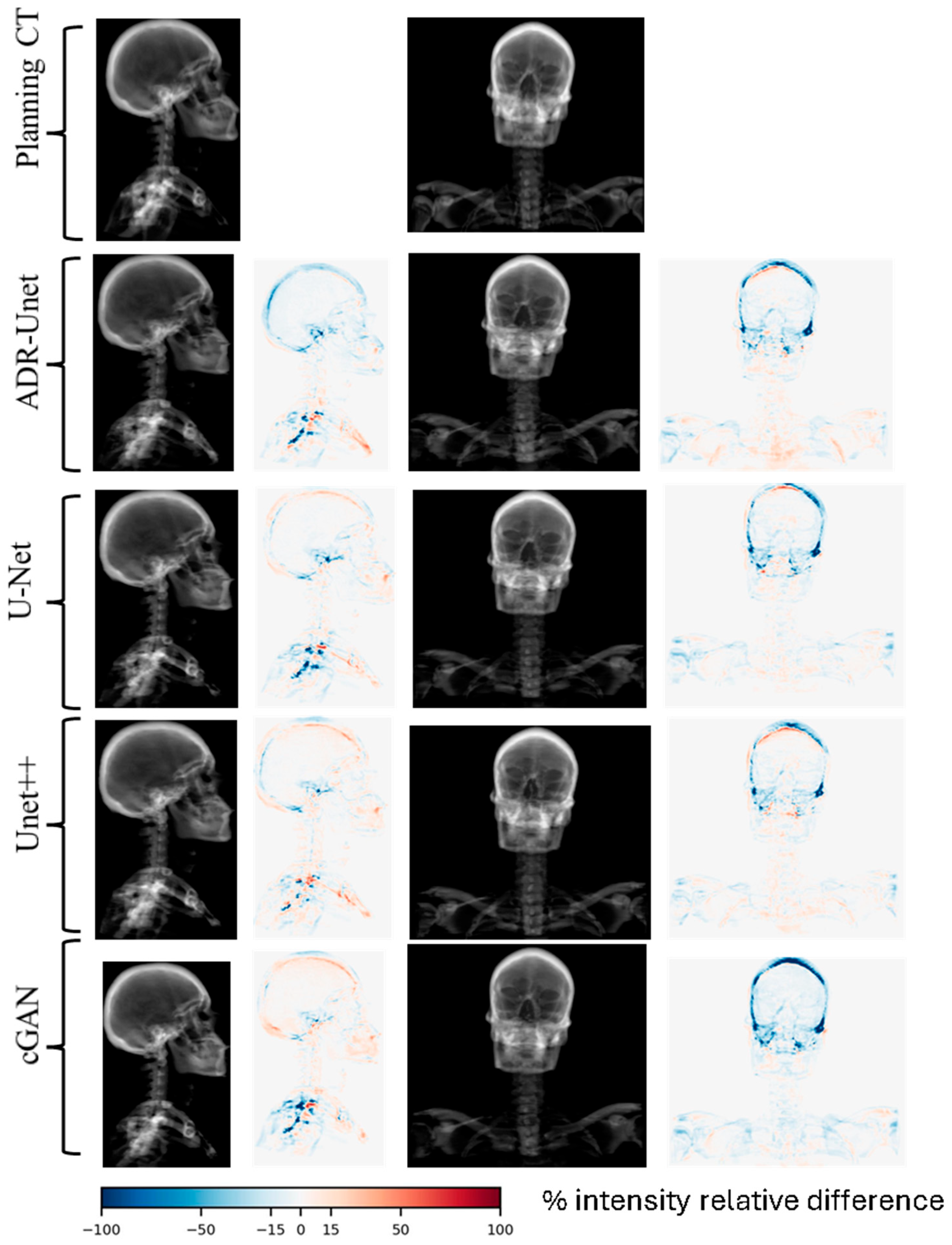

| Structure | Mean Warp Magnitude (mm) | Max Warp Magnitude (mm) | Mean Jacobian Determinant | Min Jacobian | Max Jacobian |
|---|---|---|---|---|---|
| Spinal cord | 1.24 | 2.69 | 1.02 | 0.96 | 1.14 |
| Parotid L | 0.76 | 1.59 | 1.07 | 0.99 | 1.16 |
| Parotid R | 1.09 | 1.52 | 0.98 | 0.9 | 1.06 |
| Larynx | 1.66 | 2.51 | 0.97 | 0.9 | 1.04 |
| Brainstem | 0.76 | 1.07 | 0.98 | 0.94 | 1.02 |
| Eye R | 0.51 | 1.07 | 1.03 | 0.97 | 1.07 |
| Eye L | 0.82 | 1.1 | 1.02 | 0.99 | 1.05 |
| Lens R | 0.38 | 0.52 | 1.04 | 1.02 | 1.05 |
| Lens L | 0.86 | 0.96 | 1.03 | 1.03 | 1.04 |
| PTV | 1.05 | 2.56 | 1.01 | 0.88 | 1.18 |
| Error Type | ADR-Unet | cGAN | Unet | Unet++ |
|---|---|---|---|---|
| MAE [HU] | 55.49 ± 7.79 | 57.66 ± 10.44 | 60.06 ± 10.94 | 59.32 ± 7.09 |
| ME [HU] | −1.75 ± 7.62 | −4.57 ± 17.59 | 2.77 ± 13.31 | 0.25 ± 10.40 |
| PSNR [dB] | 56.07 ± 0.87 | 55.95 ± 1.51 | 55.77 ± 1.45 | 55.89 ± 0.72 |
| SSIM | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99 ± 0.00 | 0.99± 0.00 |
| Gamma pass rate [%] | 99.4 ± 0.26 | 99.6 ± 0.18 | 99.5 ± 1.85 | 99.4± 1.63 |
| Method | Structures | DI | SE | SP |
|---|---|---|---|---|
| ADR-Unet | BONE | 0.86 ± 0.02 | 0.85 ± 0.03 | 0.99 ± 0.0 |
| AIR | 0.78 ± 0.06 | 0.74 ± 0.07 | 0.99 ± 0.0 | |
| SOFT | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.99 ± 0.00 | |
| cGAN | BONE | 0.84 ± 0.02 | 0.81 ± 0.02 | 0.99 ± 0.00 |
| AIR | 0.77 ± 0.10 | 0.74 ± 0.15 | 0.99 ± 0.00 | |
| SOFT | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.99 ± 0.00 | |
| U-Net | BONE | 0.84 ± 0.03 | 0.82 ± 0.03 | 0.99 ± 0.00 |
| AIR | 0.76 ± 0.12 | 0.69 ± 0.13 | 0.99 ± 0.00 | |
| SOFT | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.99 ± 0.00 | |
| Unet++ | BONE | 0.84 ± 0.01 | 0.84 ± 0.01 | 0.99 ± 0.00 |
| AIR | 0.78 ± 0.09 | 0.72 ± 0.11 | 0.99 ± 0.00 | |
| SOFT | 0.97 ± 0.00 | 0.97 ± 0.00 | 0.99 ± 0.00 |
| Type | DRRpCT | DRRADR-Unet | DRRcGAN | DRRU-Net | DRRUnet++ |
|---|---|---|---|---|---|
| LaR [db] | 45.09 ± 1.64 | 42.2 ± 1.92 | 42.15 ± 1.34 | 41.48 ±1.54 | 41.68 ± 2.53 |
| AP [db] | 46.44 ± 1.91 | 45.31 ± 0.73 | 45.04 ± 1.3 | 45.17 ± 0.56 | 44.97± 1.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aouadi, S.; Barzegar, M.; Al-Sabahi, A.; Torfeh, T.; Paloor, S.; Riyas, M.; Caparrotti, P.; Hammoud, R.; Al-Hammadi, N. Towards MR-Only Radiotherapy in Head and Neck: Generation of Synthetic CT from Zero-TE MRI Using Deep Learning. Information 2025, 16, 477. https://doi.org/10.3390/info16060477
Aouadi S, Barzegar M, Al-Sabahi A, Torfeh T, Paloor S, Riyas M, Caparrotti P, Hammoud R, Al-Hammadi N. Towards MR-Only Radiotherapy in Head and Neck: Generation of Synthetic CT from Zero-TE MRI Using Deep Learning. Information. 2025; 16(6):477. https://doi.org/10.3390/info16060477
Chicago/Turabian StyleAouadi, Souha, Mojtaba Barzegar, Alla Al-Sabahi, Tarraf Torfeh, Satheesh Paloor, Mohamed Riyas, Palmira Caparrotti, Rabih Hammoud, and Noora Al-Hammadi. 2025. "Towards MR-Only Radiotherapy in Head and Neck: Generation of Synthetic CT from Zero-TE MRI Using Deep Learning" Information 16, no. 6: 477. https://doi.org/10.3390/info16060477
APA StyleAouadi, S., Barzegar, M., Al-Sabahi, A., Torfeh, T., Paloor, S., Riyas, M., Caparrotti, P., Hammoud, R., & Al-Hammadi, N. (2025). Towards MR-Only Radiotherapy in Head and Neck: Generation of Synthetic CT from Zero-TE MRI Using Deep Learning. Information, 16(6), 477. https://doi.org/10.3390/info16060477






