Abstract
During natural disasters, social media platforms, such as X (formerly Twitter), become a valuable source of real-time information, with eyewitnesses and affected individuals posting messages about the produced damage and the victims. Although this information can be used to streamline the intervention process of local authorities and to achieve a better distribution of available resources, manually annotating these messages is often infeasible due to time and cost constraints. To address this challenge, we explore the use of semi-supervised learning, a technique that leverages both labeled and unlabeled data, to enhance neural models for disaster tweet classification. Specifically, we investigate state-of-the-art semi-supervised learning models and focus on co-training, a less-explored approach in recent years. Moreover, we propose a novel hybrid co-training architecture, Multihead Average Pseudo-Margin, which obtains state-of-the-art results on several classification tasks. Our approach extends the advantages of the voting mechanism from Multihead Co-Training by using the Average Pseudo-Margin (APM) score to improve the quality of the pseudo-labels and self-adaptive confidence thresholds for improving imbalanced classification. Our method achieves up to 7.98% accuracy improvement in low-data scenarios and 2.84% improvement when using the entire labeled dataset, reaching 89.55% accuracy on the Humanitarian task and 91.23% on the Informative task. These results demonstrate the potential of our approach in addressing the critical need for automated disaster tweet classification. We made our code publicly available for future research.
1. Introduction
According to the Centre for Research on the Epidemiology of Disasters (CRED), 399 natural hazards were recorded worldwide in 2023, resulting in 86473 fatalities, affecting million people, and causing a total economic loss of billion USD. In 2023, the United States alone was hit by 28 disasters with a billion-dollar damage magnitude, exceeding the previous record of 22 events set in 2020 [1]. In such situations, the lack of information represents a serious obstacle that local authorities face when distributing resources and managing intervention processes. Furthermore, the time-critical constraints associated with the nature of disasters amplify these problems and place additional pressure on the intervention teams.
The most straightforward way to assess damage levels and streamline resource distribution is to gather information from eyewitnesses and victims. However, entering into contact and centralizing large volumes of data are both difficult and time-consuming. An alternative is to use the extensive messages uploaded on X (formerly Twitter) and other social media platforms available for analysis during natural disasters. This method can provide valuable situational awareness while reducing the overhead of data collection and eliminating the need for centralization. In this idea, recent studies collected disaster data from social media and manually annotated them to identify situational awareness categories. Then, they trained machine learning models for these supervised classification tasks [2,3]. However, the manual annotation required for training machine learning models can be expensive and slow. To address this problem, recent studies have explored semi-supervised learning (SSL) approaches to harness the abundance of unlabeled user-generated data while minimizing the reliance on labeled data. While most of the research has focused on single-modality data [4,5], Sirbu et al. [6] introduced the first multimodal unlabeled corpus and an SSL method specifically designed for multimodal disaster tweet classification. Although the work of Sirbu et al. [6] represents a significant milestone, it does not compare multiple SSL methods, potentially overlooking algorithms better suited for this task. Such a comparison is essential not only to identify the most effective methods but also to deepen the understanding of what approaches are best suited for specific scenarios and why.
To respond to this need, we first adapt and explore a variety of SSL methods for the task of multimodal disaster tweet classification. Apart from the two methods from Sirbu et al. [6] that rely on the techniques of pseudo-labeling and consistency regularization (FixMatch [7] and FixMatch LS), we also experiment with two enhancements that solve the global thresholding problem of FixMatch (FlexMatch [8] and FreeMatch [9]), one method that uses a different paradigm for creating pseudo-labels, based on the history of predictions instead of the current logits (MarginMatch [10]), and an approach relying on a different SSL technique, co-training (Multihead Co-Training [11]).
As each SSL paradigm analyzed has its own strengths and weaknesses, we recognize the need for a unified framework that leverages their advantages while addressing their limitations.To this end, we introduce a semi-supervised method that combines the strengths of the other approaches to create a hybrid framework that we call Multihead Average Pseudo-Margin (Multihead APM). Specifically, we extend the Multihead Co-Training algorithm [11]. While the original algorithm uses the agreement between two classification heads to generate pseudo-labels for the third, we argue that hard examples—instances where the two heads fail to agree—carry critical information. To incorporate these cases into the training process, we introduce a method inspired by MarginMatch [10], employing the APM score to effectively handle such examples, as it is less sensitive to noisy predictions. Additionally, building on the insights from FlexMatch [8] and FreeMatch [9], which highlighted the limitations of global thresholding, we propose a self-adaptive thresholding mechanism tailored to our algorithm. The technical background and a detailed explanation of how Multihead APM fits into this context are provided in Section 3.
We analyze the performance of our approach in comparison to the other semi-supervised learning methods on the CrisisMMD [2] tasks, the largest publicly available disaster-related multimodal dataset. Since SSL requires domain-specific unlabeled data, we use the unlabeled corpus introduced by Sirbu et al. [6], containing 122k tweets with text and image in the same domain. The experimental results confirm that our proposed algorithm, leveraging a co-training architecture, achieves state-of-the-art performance on both the Humanitarian and Informative classification tasks in the CrisisMMD dataset [2]. Notably, compared to the supervised baseline, Multihead APM delivers up to 7.98% improvement with only 50 labeled examples per class and a 2.84% gain when utilizing the entire dataset. At the same time, it delivers important improvements compared to all the other SSL methods we have explored.
Our contributions are summarized as follows:
- 1.
- We are the first to adapt and compare multiple semi-supervised learning methods on multimodal disaster tweet classification tasks.
- 2.
- We introduce a new SSL method by extending the Multihead Co-Training framework with self-adaptive thresholds based on the Average Pseudo-Margins score.
- 3.
- We achieve state-of-the-art results on both the Humanitarian as well as the Informative CrisisMMD [2] classification tasks, and we prove the feasibility of our approach in low-resource settings.
- 4.
- We provide an in-depth analysis of the training process and failure cases for the baseline SSL methods in the context of highly imbalanced classes.
This paper continues with a section on related work, establishing the context and foundation for this study. This is followed by a detailed description of the methods employed in the proposed approach. The fourth section outlines the experimental setup, providing the necessary details for reproducibility. The results are then presented and discussed in the fifth section, highlighting the key findings. The sixth section delves deeper into the analysis of confidence thresholds, offering insights into their unexpected behavior. Finally, this paper concludes with a summary of the findings.
2. Related Work
2.1. Semi-Supervised Learning
Semi-supervised learning is a machine learning technique that utilizes labeled data together with large amounts of unlabeled data to train models. This approach is particularly useful when the labeled data are either scarce or difficult to obtain (i.e., high annotation costs, lack of time or skilled annotators, etc.).
According to Yang et al. [12], SSL algorithms can be grouped into several categories, based on loss function and model design. Their taxonomy includes categories for model types such as generative methods and graph-based approaches, as well as categories reflecting the SSL techniques employed, such as consistency regularization [13,14] or pseudo-labeling [15]. The core principle of consistency regularization is that realistic perturbations applied to data points should not alter the predictions of the model. Meanwhile, pseudo-labeling methods utilize high-confidence predictions as pseudo-labels, which are incorporated into the training dataset as labeled examples. Finally, hybrid methods form a category that integrates multiple SSL techniques to leverage their combined strengths.
A key representative of this category is FixMatch [7], one of the most successful SSL algorithms, which combines consistency regularization and pseudo-labeling. In this approach, the model first generates pseudo-labels for weakly augmented unlabeled images. Then, consistency regularization minimizes the cross-entropy loss between the predicted pseudo-labels and the output of the model on strongly augmented images. Given its effectiveness across a wide range of tasks [16,17,18], recent years have seen a surge in methods building upon FixMatch, with the research community increasingly focused on improving the two key concepts—consistency regularization and efficient pseudo-labeling.
For example, FlexMatch [8] uses the same concepts as FixMatch but additionally tries to solve the problem of imbalanced class distributions in the dataset. While FixMatch uses a static confidence threshold to filter out the unlabeled samples that should not be included in the unlabeled loss, FlexMatch proposes the use of an individual threshold for each class and adjusts the thresholds at each time step.
FreeMatch [9] further improves the adaptive threshold used in FlexMatch by splitting it into two components: a local and a global threshold. The local threshold is computed for each class independently, whereas the global threshold is common for all classes. Both are adaptive, and the final class threshold is computed by combining the local and global class thresholds.
MarginMatch [10] extends FlexMatch by introducing a new indicator to filter out the “untrustworthy” unlabeled samples: Average Pseudo-Margin (APM). Inspired by the Area Under the Margin [19], the APM score is a value calculated per sample, which keeps track of the model’s historical predictions on that particular sample. As opposed to the class threshold filters used in FlexMatch and FreeMatch that rely solely on the model’s prediction for the current iteration, the APM score incorporates information from all past epochs.
Another classical SSL technique is co-training [20], a disagreement-based method where multiple models are trained in parallel using different views of the data. Deep Co-Training [21] adapts the method to deep learning by using only one data source and relies on adversarial examples to ensure that models use different views of the data, which is necessary to avoid individual classifiers from collapsing into each other. JointMatch [22] extends the classical co-training framework by incorporating additional techniques: the consistency regularization introduced by FixMatch is employed using cross-labels instead of pseudo-labels and adaptive local thresholds are used similarly to FreeMatch. Additionally, the algorithm introduces a weighting mechanism for disagreement examples in the loss function, as these examples are shown to be more informative and keep the two networks diverged.
Multihead Co-Training [11] solves the drawback of having to train multiple classifiers by proposing a multihead architecture where each head uses the remaining ones to predict the pseudo-labels for a given data sample. If the heads reach an agreement, the sample is included in the unlabeled loss; otherwise, it is excluded.
Building on the strengths of these methods, we propose Multihead Average Pseudo-Margin (APM), a novel approach that combines the multihead architecture of Multihead Co-Training with the APM-based filtering mechanism introduced by MarginMatch and a self-adaptive thresholding strategy inspired by FreeMatch. This combination enables Multihead APM to address challenges such as class imbalance and unreliable pseudo-labels more effectively.
2.2. Disaster Tweet Classification
The relationship between deep learning and disaster tweets is not new. In fact, several studies have researched the ability to use the vast amounts of data generated by victims and eyewitnesses on social media platforms to streamline the intervention process of local authorities. Some of these studies focused on the information within text messages [23,24,25,26], whereas others tried to make use of the uploaded images [27,28,29,30,31]. More recently, with the observation that unimodal approaches lose sight of valuable information—since many disaster tweets contain both text and images—the attention has shifted toward multimodal models that aim to integrate information across both modalities [32,33,34,35,36,37,38]. These models typically utilize parallel architectures, such as combining a CNN-based image encoder with an RNN or transformer-based text encoder, followed by a fusion mechanism to integrate the two modalities. For example, Agarwal et al. [34] introduced a gated multimodal model that utilizes a Recurrent Convolutional Neural Network (RCNN) to process textual data [39] and an Inception-v3 network [40] for image features. These were integrated using an attention mechanism [41] to enhance the fusion of features and applied to multiple damage-related tasks defined by Alam et al. [2]. Abavisani et al. [35] proposed a framework that pairs DenseNet [42] for image encoding with BERT [43] for textual representation, incorporating a cross-attention module to suppress irrelevant information from either modality. Khattar and Quadri [44] proposed the Cross-Attention Multimodal (CAMM) framework, designed to leverage complementary information from the tweet text and images. The cross-attention mechanism is applied to text features extracted using a Bi-LSTM [45] and image features extracted using a VGG-16 network [46]. Koshy and Elango [47] introduced a transformer-based multimodal deep learning framework aimed at classifying informative tweets during disasters. Their approach employs a Vision Transformer [48] to extract visual features and a fine-tuned RoBERTa model [49] to extract word embeddings, followed by a Bi-directional LSTM [45] to capture contextual dependencies. A multimodal fusion module is then used to obtain the joint representation of the extracted features.
However, all of these methods rely on a relatively small number of manually labeled examples rather than taking advantage of the huge amounts of unlabeled data generated by social media users during natural disasters. Some studies [5,50] have applied semi-supervised learning to disaster tweets, but their focus was limited to textual data. Sirbu et al. [6] were the first to demonstrate the significant improvements that SSL algorithms can achieve over the supervised counterparts for this task when integrated with multimodal architectures for disaster tweet classification. They adapted FixMatch to a multimodal setup and introduced FixMatch LS, an enhancement that uses soft pseudo-labels and a linear schedule for the unlabeled loss coefficient. Although their work showed the feasibility of FixMatch and its enhancement for disaster tweet classification, it lacked a comparison to other semi-supervised algorithms and techniques. As a result, we are the first to adapt and compare several semi-supervised algorithms for this multimodal task, as well as the first to introduce a co-training approach in the context of disaster tweet classification.
3. Methods
In this section, we first describe the baselines we have employed—both supervised and semi-supervised. Then, we introduce Multihead APM, our proposed method built upon the Multihead Co-Training framework, which leverages the APM score to generate high-confidence pseudo-labels and introduces self-adaptive thresholds to address the class imbalance. The semi-supervised baselines also provide the theoretical background and justification for creating Multihead APM.
3.1. Baseline Supervised Models
Following Sirbu et al. [6], we adopt the Multimodal Bitransformer (MMBT) [51] as our base architecture, given its ability to simultaneously leverage text and image modalities for disaster tweet classification. This model has demonstrated strong performance on this task in both fully supervised [37] and semi-supervised setups [6].
To establish a stronger supervised baseline, we integrate weak text augmentation using EDA [52] and refer to the resulting model as MMBT Supervised Aug. While other multimodal models could have been investigated as potential baselines, doing so would have incurred additional GPU costs and falls beyond the scope of this work. Our primary focus is on analyzing semi-supervised approaches rather than benchmarking various multimodal architectures.
3.2. Baseline Semi-Supervised Methods
3.2.1. FixMatch for Multimodal Data
In order to make use of a large number of unlabeled data samples, FixMatch [7] heavily relies on two important principles in SSL: pseudo-labeling and consistency regularization [13,14]. Similar to Sirbu et al. [6], we adapt FixMatch to the multimodal setup by introducing two new augmentation functions: (used for weak text augmentations) and (used for strong text augmentations). As a result, the multimodal supervised loss is defined as follows:
while the multimodal unsupervised loss is the following:
where B is the batch size; is the labeled-to-unlabeled data ratio; H is the cross-entropy loss; (, ) is an (image, text) pair from the labeled dataset; (, ) is an (image, text) pair from the unlabeled dataset; is the model’s prediction (probability distribution over all classes) for a given input; ; ; is the weak image augmentation function; is the weak text augmentation function; is the strong image augmentation function; and is the strong text augmentation function. is the one-hot encoding of the target vector, while is the hard pseudo-label of the weakly augmented input sample and is the filtering function using the static threshold .
The final loss is , where is a fixed scalar denoting the weight of the unlabeled loss.
3.2.2. FixMatch LS
Sirbu et al. [6] provides two enhancements that improved the classification performance of FixMatch on the CrisisMMD tasks. The first change replaces hard pseudo-labels with soft ones to incorporate information about the entire probability distribution in the pseudo-labels. This enhancement proves to be useful for tweets with a strong semantic overlap between multiple classes. The second change uses a linear unlabeled loss weight, instead of a fixed one, which should decrease the unlabeled loss during the first iterations of the algorithm, when the model’s predictions are still not qualitative. The updated unlabeled and total loss formulas are as follows:
where , and t is the epoch number.
3.2.3. FlexMatch
FlexMatch [8] addresses the drawbacks encountered by FixMatch due to using a static threshold by replacing it with an adaptive one.
In order to achieve this goal, FlexMatch analyzes the correlation between the learning difficulty of a class and the count of its pseudo-labels that exceed the static threshold. A class with a large number of samples that exceed the threshold is considered to have a small learning difficulty, hence the need to use a high threshold for it. On the other hand, a class having a reduced number of samples above the threshold is difficult to learn and requires lowering the filtering threshold.
To this end, FlexMatch calculates a threshold for each individual class and dynamically changes it after each training iteration. To define the adaptive class thresholds, it first computes the number of pseudo-labels for each class that exceeds the static threshold:
Therefore, the adaptive class threshold can be expressed as follows:
where is a hyperparameter denoting the static confidence threshold. is used to normalize the pseudo-label count distribution and ensures that each adaptive class threshold is in the range .
During the first iterations, FlexMatch introduces the concept of threshold warm-up to decrease the confirmation bias. Thus, the samples that have not exceeded the confidence threshold for any class are introduced into a new virtual class, and the new normalization formula becomes the following:
Finally, FlexMatch employs a non-linear mapping function , which has a higher sensitivity for large values and vice versa. This is used to reduce threshold fluctuations during early training iterations when the model is still unstable. The final threshold formula is . While several convex functions can be used for , we employ the one proposed in the FlexMatch paper: .
By adapting FlexMatch to the multimodal setup, we obtain the multimodal loss formulas used in this work:
3.2.4. FreeMatch
FreeMatch [9] aims to improve the adaptive threshold used in FlexMatch by introducing a new technique called self-adaptive thresholding. According to Wang et al. [9], the thresholding scheme used in FlexMatch heavily relies on a fixed global threshold to compute the adaptive class thresholds and may struggle to adjust to the model’s learning progress. This happens especially when the labeled data are scarce and provides limited supervision for the model. To solve this problem, FreeMatch splits the threshold into two components: a global part and a local one.
The self-adaptive global threshold reflects the confidence of the model on the whole unlabeled dataset. Ideally, it should increase over time to exclude low-quality pseudo-labels in late training iterations:
where C is the number of classes and is the momentum decay of the exponential moving average (EMA).
The self-adaptive local threshold reflects the confidence of the model on the unlabeled dataset for a specific class:
By combining the global and local thresholds, the final self-adaptive class thresholds are obtained:
Using the new class thresholds, the unlabeled loss formula adapted for the multimodal setup becomes the following:
Additionally, FreeMatch introduces a new loss member called Self-Adaptive Fairness (SAF), which helps the model converge faster and make more diverse predictions:
where is the histogram distribution function, , and . Adding SAF, the final loss formula is defined as follows:
3.2.5. MarginMatch
MarginMatch [10] uses the same adaptive threshold presented in FlexMatch but additionally claims that the confidence checks performed on the pseudo-labels offer a limited amount of information, as they rely solely on the current model’s predictions. In order to gain full insight into the predictions from previous iterations, MarginMatch introduces an additional filter based on the Area Under the Margin (AUM) [19].
MarginMatch adapts the AUM score to unlabeled data, calling this new score the Average Pseudo-Margin (APM). Similar to the margin, the pseudo-margin (PM) proposed by MarginMatch is calculated per data sample after each epoch t. For a particular class c, the pseudo-margin is defined as the difference between the logit of class c and the greatest logit of a different class:
The APM for a particular sample is defined as the average of the previously computed pseudo-margins across all epochs up to the current one:
Judging by the above formula, it is straightforward that the APM score incorporates information from all past epochs. Furthermore, some important properties of the APM need to be mentioned. A negative APM score for a class c indicates that the predictions for this sample have fluctuated between different classes in the past and the historical confidence for class c is low. On the other hand, a positive score showcases a higher level of confidence and guarantees that class c has been selected as a pseudo-label in previous epochs.
MarginMatch further adapts the APM formula to an exponential moving average (EMA) setting similar to FreeMatch:
where is the smoothing factor.
MarginMatch uses the APM score as an additional filter to the one already used by FlexMatch before introducing a data sample in the unlabeled loss. The unlabeled loss formula, after adapting the model to a multimodal setting, becomes the following:
where , and is the APM threshold for the current iteration computed by introducing a virtual class of erroneous examples that mimics the training dynamics of incorrect pseudo-labels and .
3.2.6. Multihead Co-Training
Multihead Co-Training [11] adapts the Deep Co-Training [21] framework to use a single model with multiple classification heads on top. Pseudo-labels are calculated independently for each classification head using the weakly augmented version of the data (similar to FixMatch). Afterwards, each individual classification head uses the remaining ones to predict its pseudo-labels, based on head agreement. If a majority element is found among the pseudo-labels predicted by the remaining heads, an agreement is reached and this pseudo-label is included in the unsupervised loss for the current head. In particular, for three heads, an agreement is reached if and only if the remaining two heads will both predict the same pseudo-label. The decision process employed for selecting a pseudo-label is shown in Figure 1, when the two skip paths are active. The unsupervised loss is calculated for each head independently as the cross-entropy loss between the head’s pseudolabel—determined using the head agreement strategy—and the strongly augmented version of the sample. The final unsupervised loss is computed as the average of the individual unsupervised losses from all heads.
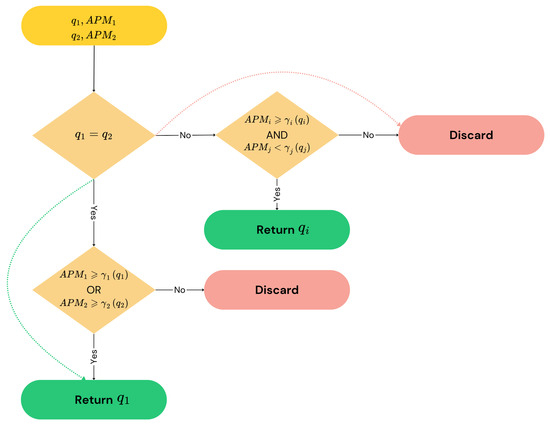
Figure 1.
The decision process of Multihead APM Agree. Multihead Co-Training follows the dotted red and green skip paths, so only one condition is checked for reaching a decision. Multihead APM No Agree follows only the green skip path, so it uses an additional condition only in case of disagreement. and are the pseudo-labels of the two heads involved in the decision process. and are their corresponding Average Pseudo-Margin (APM) scores. The use of denotes that any combination of indices respecting the condition is valid.
We adapt Multihead Co-Training to a multimodal setup by defining the multimodal losses for a three-headed model:
where is the head classifier with index m; marks if the remaining two heads have reached an agreement; and is the pseudo-label generated by one of the other heads. The supervised loss is computed as the sum of cross-entropy losses for each individual classification head, and the unsupervised loss is very similar to the one used in FixMatch, the main differences being that the confidence threshold was replaced with the head agreement technique and the cross-entropy loss is applied only on the samples that have reached an agreement.
3.3. Multihead Average Pseudo-Margin
Our main contribution is that we introduce a new semi-supervised learning method called Multihead Average Pseudo-Margin (Multihead APM) that combines co-training with MarginMatch [10]. For this, we draw inspiration and the best takeaways from the other approaches while using the Multihead Co-Training [11] framework as our backbone. This allows us to combine benefits from all three SSL techniques analyzed: co-training, pseudo-labeling, and consistency regularization. At the same time, we identify and fix a couple of shortcomings of the original approach. In addition, we perform a rigorous comparison of Multihead APM to several state-of-the-art semi-supervised learning algorithms for disaster tweet classification tasks, showing the benefits of our proposed method.
First, we notice that in the late-stage training process of Multihead Co-Training, the heads reach a very high degree of agreement, resulting in ineffective filtering of the unlabeled examples, with almost all of them being used in the loss computation. As this is a result of relying only on the agreement of the heads for filtering the samples, this can be solved by introducing adaptive thresholding techniques, similar to FlexMatch [8] or FreeMatch [9]. However, MarginMatch [10] has demonstrated the importance of historical predictions in filtering out untrustworthy data, so we decide to use the APM indicator. To exclude some of the samples where the heads have reached an agreement, we propose the following heuristic. If at least one head has the APM score for the selected pseudo-label above the current threshold, we keep the sample inside the unsupervised loss; otherwise, we drop it.
Second, Jointmatch [22] has shown that head disagreements should not be ignored, since they provide challenging examples that could improve the model’s performance, and they prevent the heads from converging or becoming indistinguishable. To incorporate the above idea into our architecture, we also use the APM score. If exactly one of the two remaining heads has an APM score above the threshold, the sample is included in the unsupervised loss using the pseudo-label of that head. Despite the disagreement, we use the APM score as a tiebreaker for selecting the pseudo-label. If both heads exceed the threshold or neither of them does, we cannot choose between the two pseudo-labels, and the sample is ignored.
Finally, we define a new method for selecting the APM thresholds. While we could use a virtual class of erroneous examples similar to MarginMatch, we prefer to take advantage of our three-headed co-training architecture and simply define the samples for which agreement is reached between the heads as the correctly classified examples that can be used for computing the self-adaptive thresholds. Moreover, as there can be large differences between the APM values belonging to different classes, we also draw inspiration from FreeMatch [9] and define our self-adaptive thresholds for each class and update them after each training epoch:
where f is a hyperparameter denoting the percentile and m and c are the current classification head and class. The APM thresholds are calculated individually for each pair as the bottom percentile of the reunion of APM scores for all remaining classification heads, where an agreement is reached and the selected pseudo-label is equal to the current class.
In the next section, we present the experiments conducted with different versions of the currently proposed approach:
- APM is used only for disagreements, and we set an additional threshold lower bound of 0 (Multihead APM No Agree).
- APM is used for both agreements and disagreements, and we set an additional threshold lower bound of 0 (Multihead APM Agree).
- APM is used only for disagreements without a lower bound (Multihead APM No Agree No Low).
- APM is used for both agreements and disagreements with no lower bound (Multihead APM Agree No Low).
The decision process employed for selecting a pseudo-label is shown in Figure 1. For Multihead APM Agree, no skip path is active, while for Multihead APM No Agree, the green skip path is followed. All the variants described above yield strong results. However, as expected, the versions that use the APM for both agreements and disagreements outperform the other ones, since they reduce the number of unlabeled samples that are used in the final iterations of the training process. In the next section, we will perform a detailed analysis of our setup and present our experimental results.
4. Experiments
4.1. Datasets
4.1.1. Labeled Data
CrisisMMD [2] is a multimodal dataset consisting of approximately 18,000 manually annotated tweets containing both text and images, collected from 7 natural disasters that occurred during the year 2017: Hurricane Irma, Hurricane Harvey, Hurricane Maria, the California wildfires, the Mexico earthquake, the Iraq–Iran earthquake, and the Sri Lanka floods. The dataset was designed for three distinct classification tasks, Informativeness, Humanitarian Categories, and Damage Severity, each offering a different perspective on the current state of the disaster.
The first task is to divide the tweets into two different categories, Informative and Not Informative, which distinguish useful tweets that should be analyzed by the intervention teams from those that do not convey important information. The second task aims to categorize the relevant tweets into eight distinct humanitarian categories. However, for the multimodal setup, the tweets were grouped by Ofli et al. [53] into only five categories that we also use: Affected individuals; Infrastructure and utility damage; Rescue, volunteering, or donation effort; Other relevant information; and Not humanitarian. The third task is to assess the severity of the damage as Little or no damage, Mild damage, or Severe damage. However, this task is annotated only based on the images, so it is not available for the multimodal setup. Therefore, we exclude it from our experiments.
The official train–validation–test splits for the multimodal setup were later released by Ofli et al. [53], so we use this version of the dataset in our study.
4.1.2. Unlabeled Data
To maintain consistency in our choices and simplify the comparison of our results with previous work, we use the same unlabeled dataset introduced by Sirbu et al. [6], which consists of 122K text and image pairs sampled using the Twitter streaming API during disasters that occurred in 2017. The tweets have been filtered in advance to avoid duplicates, retweets, and posts with multiple attached images. This dataset is further denoted as the unlabeled corpus and has been used in all our semi-supervised algorithm benchmarks.
4.2. Augmentation
As consistency regularization is the technique of training the model to predict similar outputs for augmented versions of the same input, it is clear that augmentation is an important part of the studied semi-supervised approaches. Moreover, most of them use pseudo-labeling in a manner similar to FixMatch [7], where the pseudo-label is computed on a weakly augmented version of the input and then used as a target for the strongly augmented version of the input. This underlines the importance of using not just one but two augmentation functions of different strengths.
As the baseline semi-supervised approaches have been introduced for images, it is easy for us to follow them and use RandAugment [54] for strong image augmentation and as weak image augmentation a standard flip-and-shift strategy with horizontal flip probability and up to horizontal or vertical translation.
For text augmentation, previous work [6] explored two different approaches: Easy Data Augmentation [52] (EDA) and back-translation [55]. EDA is a simple augmentation technique that randomly applies 4 possible operators to a text: synonym replacement, random insertion of a word, random swap of two words, and random deletion of a word. On the other hand, back-translation follows a more complex strategy: it translates the sentence to an intermediate language and then back to the original one. Thus, a different version of the sentence is obtained while preserving the underlying message. While both augmentation strategies showed comparable performance in Sirbu et al. [6], EDA offers the critical advantage of being run on a CPU without the need for a pre-trained generative model for machine translation that additionally requires GPU time. As a result, we employ EDA as our text augmentation strategy. For weak augmentation, we apply EDA to of the words in the sentence, whereas for strong augmentation, we apply it to of the words.
4.3. Low-Data Regimes
Low-data regimes refer to settings where training data are scarce or hard to obtain. For example, during natural disasters, only a small number of user-generated messages can be annotated due to time-critical constraints. This setup is compatible with a low-data setting, where labeled data are very limited, even though unlabeled data are widely available.
Previous work [6] proposed to mimic a low-data setting by considering that only a smaller portion of the labeled dataset is available at the time of training a model. Similar to them, we evaluate our algorithms on the Humanitarian and Informative tasks using only 50 labeled samples per class, which would better mimic the resources available during an active crisis event.
This final step in our experiments would help us understand the performance improvements that can be achieved in settings close to the real world. As the experiments show that the Multihead APM Agree No Low configuration performs the best among the Multihead APM variations presented in Section 3.3, we additionally test this version of the Multihead APM in low-data regimes to quantify the performance boost generated by unlabeled data in such settings.
4.4. Experimental Setup
To ensure that our experimental results are not influenced by non-deterministic factors, we run each experiment three times and report the average results.
We evaluate all the algorithms described in Section 3 on both the Humanitarian and the Informative tasks (as the Damage Severity task does not provide a multimodal setup). Each training process, using the entire labeled dataset, has an average execution time of 4h30m for 20 training epochs. Considering the total training time for the 11 proposed algorithms, we obtain 297 GPU hours or approximately 12 days. Including all the experimental settings—used for hyperparameter tuning, statistics accumulation, or other purposes—that have been omitted from this paper, the total execution time would be about double. All of our experiments were conducted in PyTorch, on a Linux system with an NVIDIA A100 GPU with 80 GB VRAM.
4.5. Hyperparameters
USB [56] is a benchmark for evaluating SSL algorithms across vision, language, and audio tasks. Building on this, we extend the USB codebase by implementing our Multihead APM approach, incorporating the multimodal tasks from CrisisMMD, and adapting the evaluated methods to the multimodal setup.
Each of the simulated algorithms has a distinct set of hyperparameters and configuration properties. We experiment with several values and choose the ones that generate the best F1 scores on the validation set while also keeping in mind the required computational power and the hardware limitations. The hyperparameters used are presented in Table 1. For the shared ones, we use the same values to ensure a fair comparison.

Table 1.
Hyperparameters used in all experiments.
4.6. Efficiency Considerations
While SSL algorithms may bring a substantial performance boost to a supervised model by utilizing additional unlabeled data, this usually results in slower training, as more data need to be passed through the model. Specifically, for a supervised model, the total training time is directly proportional to the number of epochs and the number of labeled examples (i.e., ). However, for an SSL approach, as the total data passed through the model each epoch are , the total training time becomes . This is valid for all the SSL algorithms used in this work.
Furthermore, some of the design choices may bring additional performance overhead. For example, a traditional co-training method requires double the time and memory, as it trains two models in parallel. While Multihead Co-Training addresses this by using a shared backbone, the use of three heads still implies passing data through two additional classification layers. However, the classification heads are usually small, and the impact on performance varies relative to the backbone used. In our experiments, with MMBT as a shared backbone, the performance overhead of Multihead Co-Training and Multihead APM is consistently less than in terms of additional training time compared to FixMatch. Similarly, computing the APM score or the adaptive thresholds introduces a slight overhead, but based on our experiments, it is negligible relative to the forward and backward passes through the model. Multihead APM, while incorporating these techniques, has a similar training time.
During inference, a model trained with SSL behaves similarly to the same model trained in a supervised manner, as the same amount of data are passed through the model, and the adaptive thresholds are no longer updated. However, the overhead associated with using a multihead architecture still remains. In our experiments, the prediction during inference was computed by averaging the logits from all three heads. This results in preserving a slight overhead (∼1%) compared to single-headed architectures, which may be relevant for real-world applications. However, the overhead may be eliminated post-training by using a single head during inference. This comes at a performance cost of ∼0.1% on our tasks, as the three heads reach a very high agreement during the final training stages.
5. Results
In this section, we present the results for the Humanitarian and Informative classification tasks, analyzing the key factors that contributed to the success or limitations of the various algorithms. We focus on the performance of our proposed method, Multihead APM, comparing the four variations and providing an explanation for the best-performing results. The comprehensive results for all the methods, using the full labeled dataset, are summarized in Table 2.

Table 2.
Classification results for the Humanitarian and Informative CrisisMMD tasks.
Our model achieves an accuracy improvement of and on the Humanitarian and Informative tasks, respectively, compared to the supervised baseline. Furthermore, it surpasses the previous state of the art (SOTA) established by the semi-supervised approach of Sirbu et al. [6], delivering at least a improvement for both tasks. In low-data scenarios, our approach demonstrates even greater effectiveness, achieving up to a accuracy increase over the supervised baseline with only 50 labeled examples per class, as shown in Table 3.

Table 3.
Classification results for the Humanitarian and Informative CrisisMMD tasks using 50 labeled samples per class.
Given the distinct characteristics of the Humanitarian and Informative tasks, we next analyze the results for each task in detail.
5.1. Humanitarian Task
As expected, the fully supervised baseline (MMBT Supervised Aug) is ranked among the lowest places in our list, since it does not use any unlabeled data. The obtained results are similar to Sirbu et al. [6]; however, our algorithm seems to have a slightly better precision, recall, and F1 score. Most likely, these changes arise from the fact that we use a weak augmentation strategy when computing the labeled loss.
The results obtained by FixMatch and FixMatch LS are again very similar to those reported by Sirbu et al. [6]. This was expected as we followed their experimental setup as closely as possible. The increase in performance of FixMatch LS over FixMatch demonstrates again the effectiveness of the enhancements proposed by Sirbu et al. [6] for the original FixMatch algorithm: the usage of soft pseudo-labels and the linear unlabeled loss coefficient.
For FlexMatch and FreeMatch the presented results look surprisingly low. In fact, these two algorithms rank in the lowest places in our benchmarks, both in terms of accuracy and F1 score, being outperformed not only by FixMatch and FixMatch LS but also by MMBT Supervised Aug. This outcome is quite the opposite of our initial expectations, especially as we decided to use these algorithms because the Humanitarian class distribution is highly unbalanced and the fixed cutoff threshold proposed by FixMatch was unable to account for the different learning difficulties of the classes. However, by analyzing the evolution of the pseudo-labels and confidence thresholds during the training process, as well as comparing the confusion matrices of different algorithms, we gain insight into the causes of this poor performance. FlexMatch and FreeMatch, which use adaptive confidence thresholds, end up using very low thresholds for the underrepresented classes—especially for Affected individuals, which accounts for less than of the labeled data. This makes the model consider any pseudo-label of an underrepresented class as accurate and includes it in the loss computation, thus affecting performance, as the model learns to predict the infrequent classes way too often. A more in-depth analysis is provided in Section 6.
Although MarginMatch shows an improvement over the supervised baseline, it still obtains worse results than FixMatch LS and FixMatch. A similar in-depth analysis is provided in Section 6.
The Multihead Co-Training approach obtains better results than MarginMatch but still underperforms compared to FixMatch. The main problem with this approach is that during training, as the heads make more confident predictions, they collapse into each other and more than of the unlabeled data are included in the unsupervised loss.
Analyzing the results of our proposed method, we see that all four Multihead APM variants stand at the top of the ranking. In particular, Multihead APM Agree and Multihead APM Agree No Low obtain the most promising results, with the latter performing slightly better. The dominance of the methods using the APM for both agreements and disagreements over those that use it just for disagreements can be easily explained. The problem with the classical Multihead Co-Training approach was the excessive usage of unlabeled data (i.e., the failure to filter out irrelevant samples). Adding an additional check on the APM threshold for the agreements limits the number of pseudo-labeled samples that the model will use. In particular, our proposed quantile value of uses approximately of the unlabeled dataset in the late-stage training process.
For comparison, Multihead APM Agree No Low achieves some impressive results, improving the accuracy of MMBT Supervised Aug by and the weighted F1 score by . Compared to FixMatch, we managed to increase the accuracy by and the weighted F1 score by . If we compare our results with those of Sirbu et al. [6], we can see that our algorithm has improved the accuracy of the best proposed model by and the F1 score by . This is particularly impressive since all of our experiments have used a labeled-to-unlabeled ratio of , whereas Sirbu et al. [6] used . A lower means that fewer unlabeled data are passed through the model during each iteration, resulting in faster training and more efficient memory usage. However, this may hinder the model from achieving its full potential, as demonstrated by Sirbu et al. [6].
5.2. Informative Task
For the Informative task, the relative rankings of MMBT Supervised Aug, FixMatch, and FixMatch LS are the same as for the Humanitarian task, with FixMatch LS outperforming FixMatch and both surpassing MMBT Supervised Aug.
For FlexMatch and FreeMatch, we can see that the results relative to other approaches are much better compared to the Humanitarian task. The more balanced class distribution of the Informative dataset played an important role in obtaining these results. While FlexMatch ranks between FixMatch and FixMatch LS, FreeMatch manages to slightly outrank FixMatch LS judging by the F1 score. Meanwhile, MarginMatch provides a relatively low improvement over the supervised baseline, as it performs comparably to FixMatch.
The Multihead Co-Training approach ranks above all previously analyzed algorithms in both accuracy and F1 score. We believe that the usage of a two-class dataset with a more uniform distribution compared to the Humanitarian task helps the model achieve better performance. Even though the head collapsing problem is still present toward the end of the training process, the model can distinguish more clearly between unlabeled samples belonging to different classes and predict the pseudo-labels with higher confidence.
As expected, the Multihead APM algorithms achieve some of the best results in our benchmarks. In particular, Multihead APM Agree No Low obtains the best accuracy, precision, recall, and F1 score from all the algorithms analyzed. Compared to MMBT Supervised Aug, Multihead APM Agree No Low improves the accuracy by and the F1 score by . If we use FixMatch LS as a baseline, our algorithm enhances the accuracy by and the F1 score by .
Comparing Multihead APM Agree No Low with the results from Sirbu et al. [6], we observe that our algorithm outperforms their best model in both accuracy and F1 score. This result is particularly impressive considering that Sirbu et al. [6] uses twice as much unlabeled data per batch, which helps improve performance at the cost of higher computational resources and slower training. Furthermore, their model employs back-translation for strong text augmentation, which has shown better results than EDA for this task.
5.3. Low-Data Regimes
We employ four methods for our low-regime benchmark: MMBT Supervised Aug, FixMatch, FixMatch LS, and our proposed model that achieved the best results on the CrisisMMD classification tasks—Multihead APM Agree No Low.
The results presented in Table 3 demonstrate the dominance of semi-supervised algorithms. This is expected as only a small number of labeled samples are used during the training process. Both FixMatch and FixMatch LS outperform MMBT Supervised Aug on both the Humanitarian and Informative classification tasks. However, our custom model ranks first by a significant margin in both accuracy and F1 score. This shows that Multihead APM is even more robust in the low regime compared to the currently best solution for these tasks (FixMatch LS).
Compared to the fully supervised algorithm, Multihead APM Agree No Low improves the accuracy and F1 score by and on the Humanitarian task and by and on the Informative task. Using FixMatch LS as the baseline, considered the best model introduced by Sirbu et al. [6], our method achieves an increase in accuracy and F1 score of and on the Humanitarian task and of and on the Informative one.
6. Confidence Thresholds Analysis
In Section 5, we noticed a few discrepancies between the obtained results and our initial expectations. More precisely, for the Humanitarian task consisting of highly imbalanced classes, the SSL methods FlexMatch and FreeMatch performed even worse than the supervised model MMBT Supervised Aug. This is surprising especially because they use adaptive confidence thresholds that aim to independently filter pseudo-labels for each class, favoring the underrepresented classes. To understand this phenomenon, we analyze the training process of SSL algorithms, focusing on confidence thresholds and their impact on the model’s performance. As the findings are similar for both the FlexMatch and FreeMatch algorithms, we present details only for one of them (FlexMatch). Then, we also analyze the thresholds based on the APM scores and explain why our method performs better than MarginMatch and why the variant Multihead APM Agree No Low outperforms the others.
The Affected Individuals class is particularly underpopulated in the Humanitarian dataset, having around of the labeled samples. On the other hand, the Not Humanitarian class consists of of the labeled dataset. In Table 4, we present the pseudo-label distribution and adaptive class thresholds for FlexMatch at the beginning of the training process, while Table 5 shows the same information at the end of the training process. In the beginning, the confidence threshold is less than for the most frequent class and for the bottom three classes. In the end, we observe some major changes. The confidence thresholds for the two most frequent classes are above and higher than for the top four. However, the last class still has a confidence threshold of , which is 10 times smaller than the threshold of the next smallest class.

Table 4.
FlexMatch adaptive class thresholds at the end of the first training epoch.

Table 5.
FlexMatch adaptive class thresholds at the end of the last training epoch.
The use of 0 thresholds during the first epochs of the training process will automatically incline the model to include more samples in these classes. This is especially true for the last class, which has a very small threshold even at the end of the training. The above idea can be observed in Figure 2, which showcases the confusion matrices from FixMatch and FlexMatch. We can clearly see that FlexMatch has a higher accuracy for the Affected Individuals class, but this comes at a great cost. The accuracy for the first three classes has decreased and the model started to include a larger number of mislabeled samples in the last two classes.
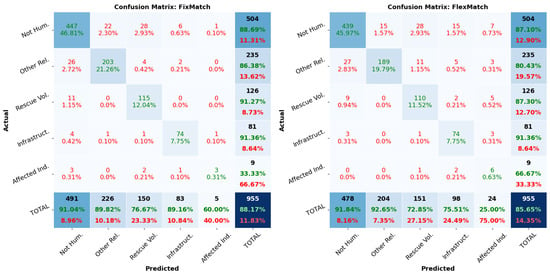
Figure 2.
Confusion matrices for FixMatch (left) and FlexMatch (right). Rows represent the actual class labels, and columns represent the predicted ones. The values corresponding to correct/incorrect labels are colored in green/red.
Looking at the confusion matrices, the values started to shift from the first three columns to the right. The number of samples from the last two classes that were incorrectly labeled by FixMatch as belonging to the first three classes (the first three columns under the main diagonal) has decreased. Meanwhile, the number of samples from the first three classes incorrectly labeled as the last two classes (the last two columns above the main diagonal) has increased. This shows the bias that FlexMatch introduces when making predictions, which affects the overall performance of the algorithm. Since the first three classes have a cumulative weight of of the entire labeled dataset, the performance drop for them will quickly affect the overall accuracy and weighted F1 score of the model. The same is also true for FreeMatch since both methods rely on adaptive thresholding techniques based on the current confidence of the model, which allow for the use of low-precision pseudo-labels. Multihead APM addresses this by incorporating APM-based thresholding combined with a voting mechanism, which increases the quality of the pseudo-labels.
In Table 6, we can see the average APM scores of MarginMatch for all the samples belonging to a certain pseudo-label at the end of the training process. The important values are located on the main diagonal, representing the average APM thresholds used for each class during the filtering process. It is easy to observe that all these values are quite different; hence, the use of a common threshold for all the classes, as proposed by MarginMatch, would not be suitable. However, the introduction of class-wise APM-based thresholds proposed by Multihead APM addresses this drawback by allowing a proportional number of pseudo-labels to be selected for each class. Furthermore, we can see that the Affected Individuals class has a negative average APM score. Since all our experiments used 0 as a fixed APM cutoff, we expect that our model will have difficulties predicting this class. The above fact is supported by Figure 3 in which we see the confusion matrix from MarginMatch. The last column is almost completely filled with zeros, and the accuracy of the Affected Individuals class is just .

Table 6.
Average APM scores for all the samples grouped by the same pseudo-label.
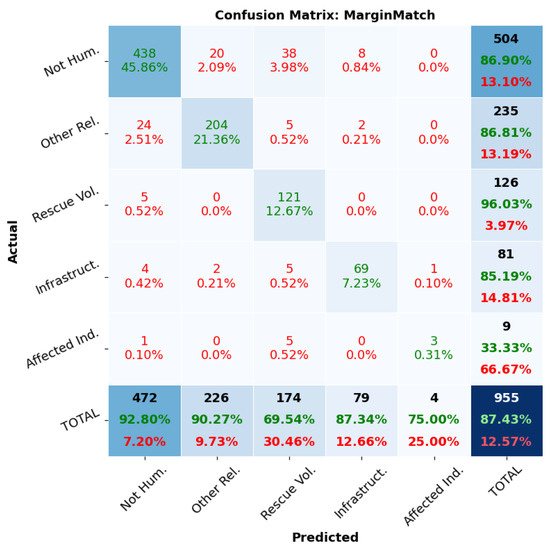
Figure 3.
Confusion matrix for MarginMatch. Rows represent the actual labels, and columns represent the predicted ones. The values corresponding to correct/incorrect labels are colored in green/red.
Additionally, in Table 6, we can see that the average APM score for the Affected Individuals class was negative. This is the main reason why Multihead APM Agree No Low performs better than Multihead APM Agree since the latter uses 0 as a lower bound for the APM threshold. Hence, it struggles to predict this class. This fact can be observed in Figure 4, where the last column of Multihead APM Agree is almost completely filled with zeros. In contrast, the confusion matrix for Multihead APM Agree No Low has a better accuracy for the Affected Individuals class and multiple non-zero values on the last column.
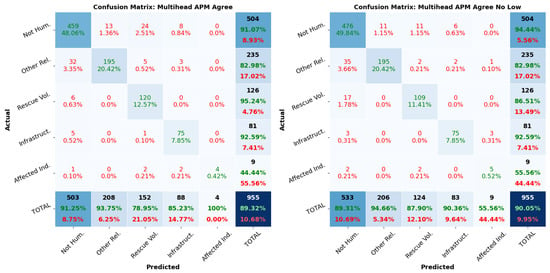
Figure 4.
Confusion matrices for Multihead APM Agree (left) and Multihead APM Agree No Low (right). Rows represent the actual labels, and columns represent the predicted ones. The values corresponding to correct/incorrect labels are colored in green/red.
7. Conclusions
As part of our research, we analyzed several state-of-the-art semi-supervised algorithms and adapted them to a multimodal setting. We created a centralized benchmark for the Humanitarian and Informative classification tasks from the CrisisMMD dataset [2] and performed a detailed analysis of the key factors that influenced the performance of each solution. Furthermore, we introduced a new semi-supervised learning method called Multihead APM by integrating the APM scores [19] proposed by MarginMatch [10] into our custom Multihead Co-Training [11] approach. We then demonstrated that it outperforms all the other analyzed algorithms and achieves state-of-the-art results on the CrisisMMD dataset with additional unlabeled data. As a final step in our research, we investigated the performance boost that semi-supervised methods can achieve compared to fully supervised ones by running our models in low-data regimes.
Our work has demonstrated that semi-supervised algorithms significantly improve the accuracy for both the Humanitarian and Informative classification tasks. Notably, our proposed Multihead APM method sets a new state of the art over strong SSL baselines, achieving substantial improvements for both tasks and showcasing its effectiveness in leveraging the extensive user-generated messages posted on X (Twitter) and other social media platforms. This progress directly supports our primary goal of enhancing the intervention process of local authorities during natural disasters.
For future work, we aim to evaluate the robustness and generalizability of Multihead APM on a broader range of datasets and modalities to explore its potential applications in other disaster-related contexts and beyond this domain. Experimenting with Multihead APM on other disaster-related datasets involves collecting relevant unlabeled data or researching domain-adaptation techniques that would allow for the use of an unlabeled corpus from a different domain. For example, the DisasterMM [57] dataset would require relevant tweets in the Italian language, which need to be collected or translated from an existing English corpus. This is beyond the scope of this work, but it is definitely a promising direction to further assess the generalizability of our approach. Additionally, we plan to integrate Multihead APM as part of the USB benchmark [56], making it easily accessible for comparison with more SSL approaches and diverse datasets.
Author Contributions
Conceptualization, I.S., R.-A.P., T.R. and Ș.T.-M.; methodology, I.S., R.-A.P. and T.R.; software, I.S. and R.-A.P.; validation, R.-A.P.; formal analysis, I.S. and R.-A.P.; investigation, I.S. and R.-A.P.; writing—original draft, I.S. and R.-A.P.; writing—review and editing, I.S., T.R. and Ș.T.-M.; visualization, I.S. and R.-A.P.; supervision, T.R. and Ș.T.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available as follows: the labeled dataset (CrisisMMD) is available at https://crisisnlp.qcri.org/crisismmd (accessed on 20 February 2024), the unlabeled corpus is available on GitHub at https://github.com/iustinsirbu13/multimodal-ssl-for-disaster-tweet-classification (accessed on 20 February 2024), and the code is available on GitHub at https://github.com/popovicirobert/Semi-supervised-learning/tree/feature-multihead-apm (accessed on 28 January 2025).
Conflicts of Interest
Author Traian Rebedea was employed by the company NVIDIA. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| APM | Average Pseudo-Margin |
| AUM | Area Under the Margin |
| EDA | Easy Data Augmentation |
| SSL | Semi-Supervised Learning |
References
- Centre for Research on the Epidemiology of Disasters (CRED). 2023 Disasters in Numbers: A Significant Year of Disaster Impact; Technical Report; Institute Health and Society—UCLouvain: Brussels, Belgium, 2024. [Google Scholar]
- Alam, F.; Ofli, F.; Imran, M. CrisisMMD: Multimodal Twitter Datasets from Natural Disasters. In Proceedings of the 12th International AAAI Conference on Web and Social Media (ICWSM), Palo Alto, CA, USA, 25–28 June 2018. [Google Scholar]
- Ashktorab, Z.; Brown, C.; Nandi, M.; Culotta, A. Tweedr: Mining twitter to inform disaster response. In Proceedings of the 11th International ISCRAM Conference, University Park, PA, USA, 18–21 May 2014; pp. 269–272. [Google Scholar]
- Zou, H.P.; Zhou, Y.; Zhang, W.; Caragea, C. Decrisismb: Debiased semi-supervised learning for crisis tweet classification via memory bank. arXiv 2023, arXiv:2310.14577. [Google Scholar]
- Zou, H.P.; Caragea, C.; Zhou, Y.; Caragea, D. Semi-supervised few-shot learning for fine-grained disaster tweet classification. In Proceedings of the 20th International ISCRAM Conference, ISCRAM 2023, Omaha, NE, USA, 28–31 May 2023. [Google Scholar]
- Sirbu, I.; Sosea, T.; Caragea, C.; Caragea, D.; Rebedea, T. Multimodal Semi-supervised Learning for Disaster Tweet Classification. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; International Committee on Computational Linguistics: Stroudsburg, PA, USA, 2022; pp. 2711–2723. [Google Scholar]
- Sohn, K.; Berthelot, D.; Li, C.L.; Zhang, Z.; Carlini, N.; Cubuk, E.D.; Kurakin, A.; Zhang, H.; Raffel, C. Fixmatch: Simplifying semi-supervised learning with consistency and confidence. arXiv 2020, arXiv:2001.07685. [Google Scholar]
- Zhang, B.; Wang, Y.; Hou, W.; Wu, H.; Wang, J.; Okumura, M.; Shinozaki, T. FlexMatch: Boosting Semi-Supervised Learning with Curriculum Pseudo Labeling. Adv. Neural Inf. Process. Syst. 2021, 34, 18408–18419. [Google Scholar]
- Wang, Y.; Chen, H.; Heng, Q.; Hou, W.; Fan, Y.; Wu, Z.; Wang, J.; Savvides, M.; Shinozaki, T.; Raj, B.; et al. FreeMatch: Self-adaptive Thresholding for Semi-supervised Learning. arXiv 2023, arXiv:2205.07246. [Google Scholar]
- Sosea, T.; Caragea, C. MarginMatch: Improving Semi-Supervised Learning with Pseudo-Margins. arXiv 2023, arXiv:2308.09037. [Google Scholar]
- Chen, M.; Du, Y.; Zhang, Y.; Qian, S.; Wang, C. Semi-Supervised Learning with Multi-Head Co-Training. arXiv 2021, arXiv:2107.04795. [Google Scholar] [CrossRef]
- Yang, X.; Song, Z.; King, I.; Xu, Z. A Survey on Deep Semi-supervised Learning. IEEE Trans. Knowl. Data Eng. 2021, 35, 8934–8954. [Google Scholar] [CrossRef]
- Sajjadi, M.; Javanmardi, M.; Tasdizen, T. Regularization with stochastic transformations and perturbations for deep semi-supervised learning. Adv. Neural Inf. Process. Syst. 2016, 29, 1163–1171. [Google Scholar]
- Laine, S.; Aila, T. Temporal ensembling for semi-supervised learning. arXiv 2016, arXiv:1610.02242. [Google Scholar]
- McLachlan, G.J. Iterative reclassification procedure for constructing an asymptotically optimal rule of allocation in discriminant analysis. J. Am. Stat. Assoc. 1975, 70, 365–369. [Google Scholar] [CrossRef]
- Zhou, S.; Tian, S.; Yu, L.; Wu, W.; Zhang, D.; Peng, Z.; Zhou, Z.; Wang, J. FixMatch-LS: Semi-supervised skin lesion classification with label smoothing. Biomed. Signal Process. Control 2023, 84, 104709. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, F.; Wang, C.; Han, B. Pixelfixmatch: A Semi-Supervised Image Segmentation Method Based on Fixmatch with Pixel Attention. In Proceedings of the 2024 IEEE International Symposium on Biomedical Imaging (ISBI), Athens, Greece, 27–30 May 2024; pp. 1–5. [Google Scholar]
- Ihler, S.; Kuhnke, F.; Kuhlgatz, T.; Seel, T. Distribution-Aware Multi-Label FixMatch for Semi-Supervised Learning on CheXpert. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2295–2304. [Google Scholar]
- Pleiss, G.; Zhang, T.; Elenberg, E.R.; Weinberger, K.Q. Identifying Mislabeled Data using the Area Under the Margin Ranking. Adv. Neural Inf. Process. Syst. 2020, 33, 17044–17056. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; pp. 92–100. [Google Scholar]
- Qiao, S.; Shen, W.; Zhang, Z.; Wang, B.; Yuille, A. Deep Co-Training for Semi-Supervised Image Recognition. arXiv 2018, arXiv:1803.05984. [Google Scholar]
- Zou, H.P.; Caragea, C. JointMatch: A Unified Approach for Diverse and Collaborative Pseudo-Labeling to Semi-Supervised Text Classification. arXiv 2023, arXiv:2310.14583. [Google Scholar]
- Yin, J.; Lampert, A.; Cameron, M.; Robinson, B.; Power, R. Using social media to enhance emergency situation awareness. IEEE Intell. Syst. 2012, 27, 52–59. [Google Scholar] [CrossRef]
- Guan, X.; Chen, C. Using social media data to understand and assess disasters. Nat. Hazards 2014, 74, 837–850. [Google Scholar] [CrossRef]
- Kryvasheyeu, Y.; Chen, H.; Obradovich, N.; Moro, E.; Van Hentenryck, P.; Fowler, J.; Cebrian, M. Rapid assessment of disaster damage using social media activity. Sci. Adv. 2016, 2, e1500779. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Caragea, D.; Caragea, C.; Herndon, N. Disaster response aided by tweet classification with a domain adaptation approach. J. Contingencies Crisis Manag. 2018, 26, 16–27. [Google Scholar] [CrossRef]
- Lagerstrom, R.; Arzhaeva, Y.; Szul, P.; Obst, O.; Power, R.; Robinson, B.; Bednarz, T. Image Classification to Support Emergency Situation Awareness. Front. Robot. AI 2016, 3, 54. [Google Scholar] [CrossRef]
- Alam, F.; Imran, M.; Ofli, F. Image4act: Online social media image processing for disaster response. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, Sydney, Australia, 31 July–3 August 2017; pp. 601–604. [Google Scholar]
- Nguyen, D.T.; Ofli, F.; Imran, M.; Mitra, P. Damage assessment from social media imagery data during disasters. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, Sydney, Australia, 31 July–3 August 2017; pp. 569–576. [Google Scholar]
- Li, X.; Caragea, D.; Zhang, H.; Imran, M. Localizing and quantifying infrastructure damage using class activation mapping approaches. Soc. Netw. Anal. Min. 2019, 9, 44. [Google Scholar] [CrossRef]
- Li, X.; Caragea, D.; Caragea, C.; Imran, M.; Ofli, F. Identifying Disaster Damage Images Using a Domain Adaptation Approach. In Proceedings of the 16th International Conference on Information Systems for Crisis Response and Management (ISCRAM 2019), Valencia, Spain, 19–22 May 2019. [Google Scholar]
- Gautam, A.K.; Misra, L.; Kumar, A.; Misra, K.; Aggarwal, S.; Shah, R.R. Multimodal analysis of disaster tweets. In Proceedings of the 2019 IEEE Fifth International Conference on Multimedia Big Data (BigMM), Singapore, 11–13 September 2019; pp. 94–103. [Google Scholar]
- Nalluru, G.; Pandey, R.; Purohit, H. Relevancy classification of multimodal social media streams for emergency services. In Proceedings of the 2019 IEEE International Conference on Smart Computing (SMARTCOMP), Washington, DC, USA, 12–15 June 2019; pp. 121–125. [Google Scholar]
- Agarwal, M.; Leekha, M.; Sawhney, R.; Shah, R.R. Crisis-DIAS: Towards Multimodal Damage Analysis-Deployment, Challenges and Assessment. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 346–353. [Google Scholar]
- Abavisani, M.; Wu, L.; Hu, S.; Tetreault, J.; Jaimes, A. Multimodal Categorization of Crisis Events in Social Media. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 14679–14689. [Google Scholar]
- Hao, H.; Wang, Y. Leveraging Multimodal Social Media Data for Rapid Disaster Damage Assessment. Int. J. Disaster Risk Reduct. 2020, 51, 101760. [Google Scholar] [CrossRef]
- Sosea, T.; Sirbu, I.; Caragea, C.; Caragea, D.; Rebedea, T. Using the Image-Text Relationship to Improve Multimodal Disaster Tweet Classification. In Proceedings of the 18th International Conference on Information Systems for Crisis Response and Management (ISCRAM 2021), Blacksburg, VA, USA, 23–26 May 2021. [Google Scholar]
- Dinani, S.T.; Caragea, D. Disaster Image Classification Using Capsule Networks. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Lai, S.; Xu, L.; Liu, K.; Zhao, J. Recurrent convolutional neural networks for text classification. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Hua, X.S.; Zhang, H.J. An attention-based decision fusion scheme for multimedia information retrieval. In Proceedings of the Pacific-Rim Conference on Multimedia, Tokyo, Japan, 30 November–3 December 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1001–1010. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Khattar, A.; Quadri, S. CAMM: Cross-attention multimodal classification of disaster-related tweets. IEEE Access 2022, 10, 92889–92902. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Koshy, R.; Elango, S. Multimodal tweet classification in disaster response systems using transformer-based bidirectional attention model. Neural Comput. Appl. 2023, 35, 1607–1627. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Y.; Ott, M.; Goyal, N.; Du, J.; Joshi, M.; Chen, D.; Levy, O.; Lewis, M.; Zettlemoyer, L.; Stoyanov, V. Roberta: A robustly optimized bert pretraining approach. arXiv 2019, arXiv:1907.11692. [Google Scholar]
- Alam, F.; Joty, S.; Imran, M. Graph based semi-supervised learning with convolution neural networks to classify crisis related tweets. In Proceedings of the International AAAI Conference on Web and Social Media, Palo Alto, CA, USA, 25–28 June 2018; Volume 12. [Google Scholar]
- Kiela, D.; Bhooshan, S.; Firooz, H.; Testuggine, D. Supervised multimodal bitransformers for classifying images and text. arXiv 2019, arXiv:1909.02950. [Google Scholar]
- Wei, J.; Zou, K. EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification Tasks. arXiv 2019, arXiv:1901.11196. [Google Scholar]
- Ofli, F.; Alam, F.; Imran, M. Analysis of Social Media Data using Multimodal Deep Learning for Disaster Response. arXiv 2020, arXiv:2004.11838. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. RandAugment: Practical automated data augmentation with a reduced search space. arXiv 2019, arXiv:1909.13719. [Google Scholar]
- Edunov, S.; Ott, M.; Auli, M.; Grangier, D. Understanding Back-Translation at Scale. arXiv 2018, arXiv:1808.09381. [Google Scholar]
- Wang, Y.; Chen, H.; Fan, Y.; Sun, W.; Tao, R.; Hou, W.; Wang, R.; Yang, L.; Zhou, Z.; Guo, L.Z.; et al. USB: A Unified Semi-supervised Learning Benchmark for Classification. arXiv 2022, arXiv:2208.07204. [Google Scholar]
- Andreadis, S.; Bozas, A.; Gialampoukidis, I.; Moumtzidou, A.; Fiorin, R.; Lombardo, F.; Mavropoulos, T.; Norbiato, D.; Vrochidis, S.; Ferri, M.; et al. DisasterMM: Multimedia Analysis of Disaster-Related Social Media Data Task at MediaEval 2022. In Proceedings of the MediaEval, Bergen, Norway, 13–15 January 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).