Abstract
A new multi-robot path planning (MRPP) algorithm for 2D static environments was developed and evaluated. It combines a roadmap method, utilising the visibility graph (VG), with the algebraic connectivity (second smallest eigenvalue (λ2)) of the graph’s Laplacian and Dijkstra’s algorithm. The paths depend on the planning order, i.e., they are in sequence path-by-path, based on the measured values of algebraic connectivity of the graph’s Laplacian and the determined weight functions. Algebraic connectivity maintains robust communication between the robots during their navigation while avoiding collisions. The algorithm efficiently balances connectivity maintenance and path length minimisation, thus improving the performance of path finding. It produced solutions with optimal paths, i.e., the shortest and safest route. The devised MRPP algorithm significantly improved path length efficiency across different configurations. The results demonstrated highly efficient and robust solutions for multi-robot systems requiring both optimal path planning and reliable connectivity, making it well-suited in scenarios where communication between robots is necessary. Simulation results demonstrated the performance of the proposed algorithm in balancing the path optimality and network connectivity across multiple static environments with varying complexities. The algorithm is suitable for identifying optimal and complete collision-free paths. The results illustrate the algorithm’s effectiveness, computational efficiency, and adaptability.
1. Introduction
Motion planning is commonly encountered in environments where several robots operate simultaneously and with multiple obstacles. Collision-free motion planning is an important field of robotics, enabling coordinated and efficient operations in various real-world applications [1]. It is also widely used in industrial automation and search and rescue operations such as exploration, object transport, and target tracking [2,3]. Signal processing techniques can also enhance multi-robot communication reliability in cluttered environments. High-resolution and wide-swath imaging is a fundamental capability of future spaceborne synthetic aperture radar systems [4]. A key challenge in motion planning problems is determining an efficient path from the initial location of each robot to the required destination while maintaining connectivity by balancing path optimality and computational efficiency [3,5]. Motion planning is a requirement for ensuring safe and efficient movement of robots to complete their allotted tasks [6]. Motion planning considers the obstacles in the operational environment and the movements of robots in the environment. Several approaches exist for the navigation of robots; however, path planning for multiple robots introduces several challenges, e.g., avoidance of collisions and maintaining communication [7,8]. The existing methods, such as potential fields, cell decomposition, and roadmap techniques, often do not address these challenges simultaneously. The choice of motion planning depends on the environment and the capabilities of the robots. Graph models are more appropriate for robot path and motion planning problems as they provide an intuitive, computationally effective approach to map and navigate the environment. The environment is a configuration space where robots and obstacles are located [9,10].
Graph models are foundational in multi-robot motion planning, where the vertices represent specific locations or points of interest in the operational environment and the edges represent the paths or connections between these locations. This graph structure allows the planners to use algorithms to determine the shortest or most efficient route between feasible points for the robots to navigate [9,10]. Different roadmaps were suggested to achieve this operation, e.g., visibility graphs (VGs) and Voronoi diagrams (VDs) [11,12,13,14]. A more popular method used in motion planning problems comprises Voronoi cells, each associated with a specific site. The edges are equidistant from two or more sites, forming cell boundaries. The cells are entirely convex polygons in 2D and partition space, with no gaps. Voronoi edges are not necessarily straight paths but represent boundaries of the regions based on proximity. In addition, VD paths are as far away as possible from the obstacles [11,14]. Although VDs generate long paths that are far from the obstacles (making them relatively safe, i.e., ensuring collision avoidance due to an increased distance between obstacles and robots), the paths are not optimal [11,13]. VG is also a popular method for robot path planning in environments with obstacles. It comprises vertices and edges representing direct lines of sight between the points. The nodes typically include the obstacles’ vertices, start and end points of the robots’ paths. The edges are straight lines connecting visible nodes, with associated weights often representing the Euclidean distances. An advantage of using a VG for motion planning is its well-understood and straightforward method that produces optimal paths in a two or three-dimensional workspace [9]. It is also computationally effective and guarantees an optimal path when one exists [11,12]. In contrast to Voronoi diagrams, VGs guarantee an optimal path; therefore, this study focused on VGs in 2D environments [11,13]. This work proposes and evaluates a hybrid approach to solving the multi-robot motion planning problem. It combines VGs for path planning, Dijkstra’s algorithm for optimal path finding, and algebraic connectivity to address path optimisation and maintain robust communication. The approach is highly suitable for static 2D environments as the layout is predefined, and robots need to coordinate their navigation to avoid collisions and stay connected. The traditional path-planning methods often focus on optimising path lengths but neglect the significance of maintaining communication that is critical for cooperative missions.
Dijkstra’s and A* algorithms have been widely used to find the shortest path; however, they differ in how they approach the problem and their efficiency in various scenarios [15,16]. In a weighted graph, the A* algorithm aims to find the shortest path between a starting node and a target node with heuristics, especially in environments where a goal is defined. The choice of the heuristic function is crucial. It must be admissible, meaning it never overestimates the actual cost to reach the goal, ensuring that A* finds an optimal path. However, its data storage requirement can be high, as it stores details of all generated nodes, which can be a limitation for large-scale problems. A heuristic method uses assumptions to minimise the complexity of pathfinding. This can be a limitation as it requires multiple variables and coefficients, which the algorithm designer must select. In addition, a well-defined manner for determining these variables has not been previously reported. As a result, heuristic methods do not provide general solutions. In other cases, the variables of a heuristic algorithm might need modification [17]. The A* search algorithm was not considered in this study because when it is combined with the VG method, the resultant path might not be optimal. It is challenging to compute the heuristic of A*, where the heuristic value is typically a computation of what the straight-line distance to the target would be if there were no obstacles. Therefore, there is no method to measure the cost of the straight lines that connect the vertices to the goals in an environment where the lines pass through obstacles. In addition, if the heuristic cost is not acceptable, i.e., higher than the actual cost, the identified path may not be optimal regarding the path length [4,11,12]. Therefore, the VG and Dijkstra’s algorithm are chosen for path planning in this study. Accordingly, a multi-robot motion planning problem becomes the problem of finding the optimal (i.e., the safest and shortest) paths. Furthermore, the VG method can help the robots in the system to move to the desired goal (g) location while avoiding collisions [11]. To integrate algebraic connectivity into this method for multi-robot motion planning, cooperation among robots is optimised by considering the graph’s connectivity that represents their paths. Algebraic connectivity is the second-smallest eigenvalue (λ2) of the Laplacian matrix of a graph that reflects the extent of a graph’s connectivity. A large value for λ2 implies a more robust and well-connected graph that benefits coordination in multi-robot systems [10].
In this study, the operating environment was a 2D space with polygonal obstacles accommodating multiple robots, each with a start location and a goal position. The aim was to find collision-free paths for the robots as they moved to their respective goals while maintaining a high level of connectivity. This goal was achieved by considering the algebraic connectivity of each robot’s communication graph. The paths in the vector environment model can be represented by the VG [6,9], which has been effective in many applications because of its simplicity, visualisation, and completeness [9]. The VG method used for multi-robot path planning is described as an undirected weighted graph , where V is the set of vertices representing the configurations of the robots, the starting and the endpoints of the robots’ movements, is a set of edges representing the paths between the vertices. In the expression , the symbol denotes the Cartesian product of the set with itself. The Cartesian product V V is defined as the set of all ordered pairs (), where both and are elements of V. Formally, this is expressed as . In graph theory, this indicates that E, the set of edges, is a subset of all possible ordered pairs of vertices from V. Each edge () in E represents a connection from vertex to vertex . This framework is fundamental in defining the structure of directed graphs, where the direction of the edge is significant. is a function that assigns the weights (i.e., the path length) to each edge in E. Depending on the context, these weights can represent various attributes, such as distances. The edges denote the physical distance between two points, essential in applications such as GPS navigation and logistics. The weights may represent the cost or resource requirements associated with traversing an edge, aiding in optimising routes to minimise cost. Capacities indicate the maximum flow between the nodes, which is crucial in network design and traffic management. This notation is valuable in problems involving weighted graphs, such as finding the shortest path [7,9,18,19]. Edges join all pairs of mutually visible nodes and the edges of the obstacles [19]. Edges exist between two vertices when there is a direct line of sight between them, meaning that the line connecting the vertices does not intersect any obstacle. VGs provide a representation of the environment that helps identify robots’ obstacle-free paths [20]. The weights of an edge represent the Euclidean distances between the vertices [21]. Hence, based on the problem’s requirements, it is essential that the VG covers connectivity effectively to avoid a collision and calculates the best path (i.e., the shortest and safest) for the robots [13,22]. Connectivity is critical for a multi-robot team to coordinate and execute complex missions efficiently [10]. Algebraic connectivity ensures that the multi-robot system remains well-connected during motions, facilitating communication and coordination. Dijkstra’s algorithm finds each robot’s shortest path while adhering to the connectivity constraints. This optimisation balances between minimising the path lengths and maintaining robust communication among robots [10].
This study’s contributions include a novel integration of the VG and algebraic connectivity, a communication–path optimisation strategy using Dijkstra’s algorithm, and an evaluation of the proposed methods in static 2D environments. The contributions also include a new path adjustment method based on algebraic connectivity for maintaining strong communication while optimising path lengths (i.e., an optimisation framework that balances path length and network robustness), which addresses the limitations of earlier approaches in connectivity maintenance and path efficiency. Combining the VG with algebraic connectivity enhances multi-robot systems by ensuring robust communication and efficient path planning throughout the mission. Our method simultaneously optimises path length and communication robustness. This has made it more effective where communication between robots is critical, especially in cooperative tasks. Connectivity indicates a more resilient network capable of withstanding individual robot failures without losing overall connectivity. Therefore, enhancing algebraic connectivity strengthens the communication network, ensuring the robots remain connected during operations. In the following sections, the related theory is explained, the study’s methodology is described, and the results are discussed.
2. Related Theory
In this section, the theoretical concepts related to the study are explained.
2.1. Overview of Multirobot Path Planning Algorithms
Considering a multi-robot environment, which has a limited, finite communication range (R) and is modelled as an undirected weighted graph the following is defined:
- is the set of vertices representing the n robots.
- is the set of edges representing paths between the vertices, where , , exists between the vertices if robot n (Rn) interacts with robot m (Rm); this means the two robots can communicate only if they are within the communication distance of each other; in addition, the presence of the edge refers to the presence of the edge . Therefore, = signifies that the edge is mutual and directionless. This characteristic is fundamental to undirected graphs, where edges do not have a specific direction.
- is a function that assigns the weight (length path) to each edge in E. is a set of weights, such that , and otherwise.
If we consider a team of n robots, the set of neighbours of the ith robot can be defined as , all the robots that can communicate with it. Hence, each robot is assumed to be able to interchange data with its neighbours [10,23]. A method to represent such an undirected weighted graph is using the Laplacian graph and its algebraic connectivity as an indicator of the system’s connectivity. Algebraic connectivity is defined as the second smallest eigenvalue ) of the graph Laplacian. Let the graph Laplacian be the weighted matrix which combines the adjacency (A) and the degree matrix (D). Here is the weight function, which can be seen as a function of the distance between robots i and j. is called the algebraic connectivity value of the system. The value of the algebraic connectivity is zero ( = 0) if the graph has disconnected components, i.e., no paths between the vertices or two disconnected components [24,25]. If is very small, it means the graph is nearly disconnected. Non-zero connectivity refers to a path between every pair of vertices (robots in the system) in the graph. A higher algebraic connectivity signifies a more robust and well-connected graph with many edges, i.e., the value of ranges between 0 and the number of vertices (N). In addition, connectivity refers to the number of vertices in the graph if the graph is completely connected. Thus, the maximum value of , and it is obtained when the entries of the adjacency matrix are all equal to 1, which means all possible edges are present in it [10,23].
2.2. Algebraic Connectivity for Communication of Multi-Robot Systems
The second smallest eigenvalue ( is indicated as a constraint to maintain communication during the motion. It ensures the robots remain well-connected for communication or coordination during their tasks. This is critical in scenarios where the robots need to share information or collaborate to perform tasks. The term is a function of the whole system’s state. It is an important parameter that affects the performance and robustness properties of dynamical systems working over an information network [23]. Algebraic connectivity maintains connectivity and enables them to execute tasks while maintaining connectivity within the system. Connectivity is managed by strategically adding edges that optimise the network’s structure to maintain robust communication within the system. This involves measuring the second smallest eigenvalue of the Laplacian matrix, known as the algebraic connectivity, and iteratively adjusting path calculations to ensure remains high. A higher algebraic connectivity signifies a more resilient network capable of withstanding individual node failures without losing overall connectivity. By focusing on this metric, the system enhances communication robustness while minimising path lengths [23,24,25]. Hence, this enables the robots to obtain complete information about the surroundings of the workspace environment to avoid collision and find the best safe paths. The weights of the edges control the motion time of robots, where the edges’ weights are functions of the inter-robot distances. Consequently, these weights can directly influence the time taken for a robot to move along a particular path. In robotics, motion time refers to the time for a robot to traverse from one location to another within the network. For example, edge weights are determined by inter-robot distances; a greater distance (and thus a higher edge weight) would typically correspond to a longer motion time for robots. This relationship is crucial in optimising robots’ trajectories to ensure efficient movement and coordination within the system, and it is essential for effective motion planning and coordination in multi-robot systems [10].
We assumed that the obstacles in the workspace environment were convex and static and that the distance between any two obstacles was greater than the size of the robots. The MRPP algorithm for 2D static environments has broad applications. One of the main contributions of this work is leveraging algebraic connectivity to maintain robust communication during motion planning. Establishing robustness under static environments is necessary before dealing with dynamic environments. Static environments provide a controlled framework to validate the principles of the concepts, especially path optimality and algebraic connectivity. However, the discussion section outlines techniques to incorporate dynamic obstacles into the algorithm.
We considered two types of collisions: (i) collisions between an obstacle and a robot and (ii) inter-robot collisions (i.e., collisions between two robots). Each robot could determine the presence of an obstacle and measure its relative location and the distance from its boundary within the communication range. Therefore, the aim was to solve the problem of a team of multi-robots, which began from the first configuration where the team was connected ( > 0), maintaining connectivity whilst being controlled to avoid collisions until reaching the target configuration. A collision avoidance mechanism was executed that prevented robots from colliding with each other. Their communication was defined based on the weights of the edges (which determined the quality of the communication links between the robots), and when was non-zero, whilst every robot tracked its paths to reach its goal location [10,23]. In addition, during the path planning, the weights () of the vertices changed and became equal to the moments at which the robot () passed through these vertices [9]. Therefore,
where is the vertex weight, and is the edge weight (i.e., the distance between vertex and vertex ).
2.3. Collision Avoidance
To provide collision avoidance, the weights of the edges can be modified during path planning, either by path correction, where a robot is not allowed to move on the edge that is occupied by another robot, or through controlling the robot’s motion time on some edges by controlling the distances between the vertices to free up the paths for other robots, the paths of which are planned earlier [9]. This means the increased time for the robots to traverse the graph edge from vertex . Thus, we have two principal conditions that need consideration for path correction and controlling robot motion time to avoid a collision. First, two robots cannot cross paths simultaneously on the same vertex of a graph. Thus, if this happens, to prevent collisions, let be the arrival time (i.e., the time when the robot passes through vertex ) and be nth robots (n = 1, 2, …, p, where p represents the number of robots). is expressed as follows:
The travel time between vertices and is represented by This formulation is commonly used in multi-robot path planning and scheduling to ensure coordinated movements and avoid collisions.
We assumed that is the minimum value of safe distance to ensure collision-free motions. Then, must provide a safe passage for the robots when crossing the crossroads through increased weight edge (distance) on the graph from vertex to vertex to increase the motion time of the robot on a graph edge by time units, corresponding to its motion time change. By other means, ϵ is a small increment, the unit of which is typically meters, or the relevant unit of distance measurement used within the system. By incorporating ϵ into the edge weights of the graph, the weights are iteratively adjusted to avoid collisions between the robots by incrementing ϵ to obtain optimal weights that improve their performance on the given tasks. This adjustment effectively increases the perceived distance between vertices and , discouraging the robots from occupying the same intersection simultaneously and thereby reducing the risk of collisions. Therefore, is a safety value from which two robots will not collide, and the weight of vertex is calculated according to Equation (1). It is not permissible for any two robots to move together on the same edge in opposite directions. Therefore, if any two robots are moving in opposite directions on the graph edge (straight paths) at the same time, then the following is true:
The operation of Equation (3) is elaborated next. Given mth robot () and nth robot (), the part in Equation (3) implies that two conditions need to be simultaneously satisfied (the symbol ^ denotes the “AND” operation). Equation (3) defines a safety condition for motion planning between two robots that might attempt to traverse the same edge, possibly in opposite directions, but do not collide.
The implication > confirms that arrives after , and thus no collision occurs. Because the motion is already safe, no adjustment to edge weight is needed. Since the path remains valid, the vertex cost can be calculated according to Equation (1). depends on the distance = between the edges of the graph. If this means the distance travelled by is more than the distance travelled by , hence the arrival time of is greater than the arrival time of [8]. Note that this is not an obstacle edge. It is a traversable edge in the graph that another robot may temporarily occupy. Obstacle edges are permanently blocked, whereas this edge is available based on timing.
On the other hand, Equation (4) detects a potential collision between two robots and that may use the same edge of the graph in sequence:
In this scenario, a collision occurs because , whose path is being planned, follows on the edge and collides with it due to the distance travelled by it being too short. To avoid a collision, it is essential to modify the edge weight of the current robot (i.e., reduce the movement of the robot whose path is being calculated). This means increasing its arrival time by increasing the distance in this edge as follows:
This shifts ’s trajectory to maintain safe temporal separation from . Then, the vertex weight is defined as in Equation (1). In addition, if
This occurs when two robots move in opposite directions, and , whose path is being planned, crosses through the edge before ; no collision will occur. Thus. the weight of the edge does not need to change. The weight of the next vertex is calculated as in Equation (1). In contrast, if:
a collision is possible when robot follows robot , whose path is being planned, and collides with it on the edge [9]. To avoid a collision, it is essential to modify the edge weight of the current robot (i.e., change the arrival time through increasing the distance) according to Equation (5), and then the vertex weight is defined as in Equation (1). In addition, if:
A collision is possible when follows and collides with , whose path is being planned, before the crossroads [9]. To avoid a collision, the arrival time of the current robot must be increased. So, the edge weight must be changed based on Equation (5), and then the vertex weight is calculated as in Equation (1).
3. Materials and Methods
In this section, the procedures followed to obtain the results are described.
3.1. Operation of a Mult-Robot Path Planning Algorithm
To address the motion planning problem for a multi-robot system and find a collision-free optimal path, the algorithm based on the VG method is proposed. The algorithm consists of the main tasks (i)–(vi):
- Establish a free workspace map.
- The algorithm defines each robot’s starting position () and goal positions () and the number and locations of obstacles.
- All obstacles in the map are modelled as polygons to facilitate efficient and accurate pathfinding. A polygon also allows the creation of visibility graphs where the vertices represent the obstacle corners, and the edges denote direct lines of sight between them. This framework is essential for determining the shortest collision-free paths. Polygonal obstacle modelling aids in expanding the obstacles appropriately to account for the robot’s size. This process ensures that path planning algorithms consider the robot’s physical footprint, preventing collisions. In addition, robotic systems can effectively navigate complex environments, ensuring accurate and efficient movement, while avoiding collisions. The algorithm analyses the position of each obstacle’s vertices. The robots’ start and goal positions are known relative to the obstacles in the surrounding environment. Each robot is considered a dynamic obstacle.
- Using the constructed free space and VG algorithm, the robots can navigate without colliding with obstacles.
- The workspace environment is divided into two disconnected components of undirected weighted graphs. Then, the best edges are chosen to add between these two graph components to find the paths for each robot, based on the measured values of algebraic connectivity of the graph Laplacian, which controls the inter-robot connectivity when it is unequal to zero.
- When planning a path for a robot, its vertex weight is changed just as in the single-robot path planning algorithm. The weights of the vertices of the graph are initialised with the maximum possible value, i.e., infinity (∞), whilst the start time value initialises the start vertex ( = ). According to the known edge weights, Dijkstra’s algorithm is applied to find the shortest path based on the cost corresponding to each edge (distance between the vertices), where the shortest path is the path with the minimum length. Therefore, it is required to find a vertex sequence (series waypoints), which denotes the shortest path from the starting point to the goal point. If Dijkstra’s algorithm finds the shortest paths, the robot’s path can be changed based on the distance, corresponding to the environment model correction. The MRPP algorithm is described as follows:
Inputs: start positions (), goal positions (), polygonal obstacles ().
Outputs: visibility graph (VG), optimal paths from to .
- Establish a free workspace map.
- Determine each robot’s and positions and the number of obstacles and their locations.
- Divide the workspace environment into two disconnected components of undirected weighted graphs .
- Select the best edges (, where i and j represent the edges between two vertices) to add between these two components of the graph based on the measured value of the algebraic connectivity of the graph Laplacian ().
- Create the VG.
- Find a vertex sequence (series waypoints) from to by using Dijkstra’s algorithm, which denotes the shortest paths.
- End: path is calculated, where = start point and = goal point.
The operations of the MRPP algorithm are also illustrated in Figure 1.
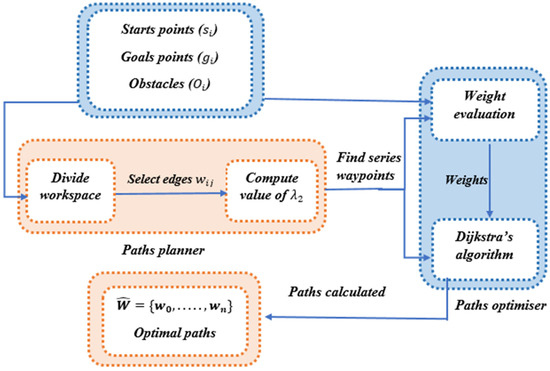
Figure 1.
The operation of the MRPP algorithm.
The key objective of the MRPP algorithm is to find optimal paths for all robots by minimising the path length. It maintains λ2 of the communication graph at a high level to ensure the multi-robot system remains connected during the motion and provides collision avoidance.
3.2. Procedure to Implement the MRPP Algorithm
The MRPP algorithm was implemented using the following steps:
- Create a VG for the environment, including all the start and goal positions of the robots. Each robot can be represented as a vertex, and edges exist between the robots. The edges (connections) between these vertices refer to the corresponding robots, are within a certain communication range, and can directly exchange information.
- Evaluate connectivity by calculating and define the communication or interaction graph between the robots. The Laplacian matrix L of this graph is constructed, and its eigenvalues are determined (). Higher algebraic connectivity implies that the robots are well-connected, meaning the communication graph is robust to disconnection for coordinated motion.
- Carry out an initial path planning by using Dijkstra’s algorithm to find each robot’s shortest path from start to finish.
3.3. Description of the Optimisation Process
During a motion planning process, the algorithm selects paths for the robots that minimise their travel distance and ensures that each robot network’s algebraic connectivity is improved and maintained [24]. The optimisation process involves calculating the paths and connectivity at each step as outlined by the steps below.
- If is small, indicating a weaker network connectivity, the paths can be adjusted to improve connectivity. Robots’ paths can be altered to keep them within the communication range of others. This may involve adding edges to maximise or maintain a high level of algebraic connectivity, thereby strengthening the network’s resilience to disconnections. The objective of adding edges is to increase robot proximity, increase , improve connectivity, and ensure the communication graph remains connected.
- Run Dijkstra’s algorithm on the VG for each robot to find the shortest initial paths.
- Repeat the above operations until optimal path lengths are obtained for all the robots to reach their targets while maintaining communication.
4. Results
The key aim of optimisation is minimising the path length (the total distance travelled by the robots) while maintaining a minimum level of connectivity in the communication graph. To illustrate how the algorithm operated, a scenario comprising six obstacles was considered as shown in Figure 2. The robots are R1–R3, and the associated goals are g1–g3.
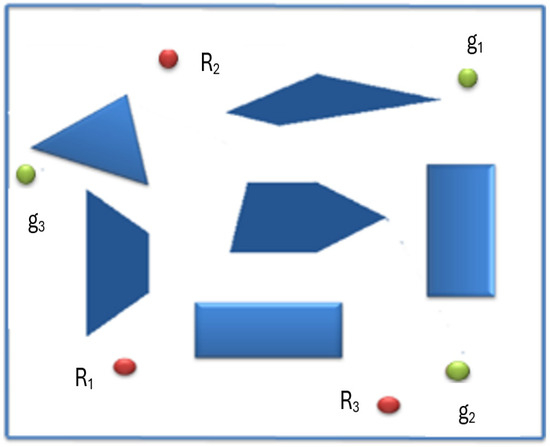
Figure 2.
Scenario of a workspace: R1, R2, and R3 are robots (shown in red); g1, g2 and g3 are the corresponding goals (shown in green), and the polygons are the obstacles (shown in blue).
The workspace scenario depicted in Figure 2 is represented as an undirected weighted graph in Figure 3. In this figure, the vertices correspond to specific locations or points within the workspace, and the edges represent the possible paths connecting these points. The weights assigned to each edge indicate the cost or distance associated with traversing that path, facilitating the analysis and optimisation of movements within the workspace.
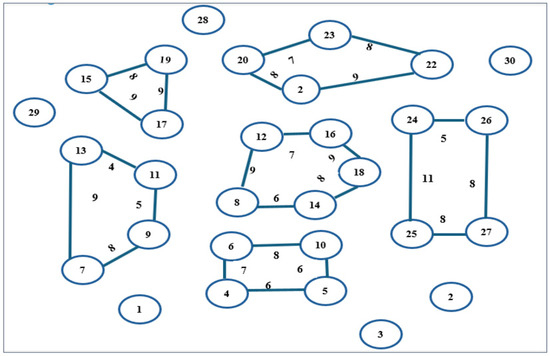
Figure 3.
Workspace represented as a weighted graph. The weights of the edges indicate the distance associated with traversing the paths. Vertices 1, 3 and 28 are the positions of robots. The positions of the goals are 2, 29 and 30. The remaining vertices are vertices of obstacles.
In this scenario, there are three robots and three goals. The workspace is divided into two disconnected components of an undirected weighted graph using a VG, such as in Figure 4.
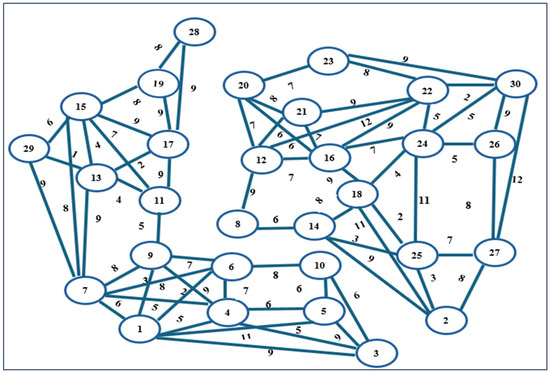
Figure 4.
Example of two disconnected components of an undirected weighted graph.
The graph in Figure 3 consists of vertices marked from = to and E = {}. There are six polygonal obstacles (, ). Each robot has an initial position () and the goal position Here, there are three goals for the three robots. The second smallest eigenvalue of the graph in Figure 2 has zero value, i.e., ( which means the graph is disconnected. The robots (, exist in the first component that contains vertices , where vertex is a goal for . Subsequently, can find a way to reach its target , but and do not have paths to reach their targets. The second component contains vertices vertices are goals for and respectively. When an edge was added between the vertices and increased to 0.087, and this enabled = to find a path to reach its target ), whereas if two edges were added, and ), increased to 0.181, which allowed ( to find the most suitable path to reach its target Furthermore, when the three edges were together {} increased to 0.347, and R2 found a path to reach its goal ). When all possible paths were added between the vertices of the graph, the second smallest eigenvalue increased, and robust connectivity was created in the graph, where 6.380. The shortest safe paths were found using Dijkstra’s algorithm, as shown in Figure 5. The shortest paths for the three robots using Dijkstra’s algorithm are shown in Figure 6.
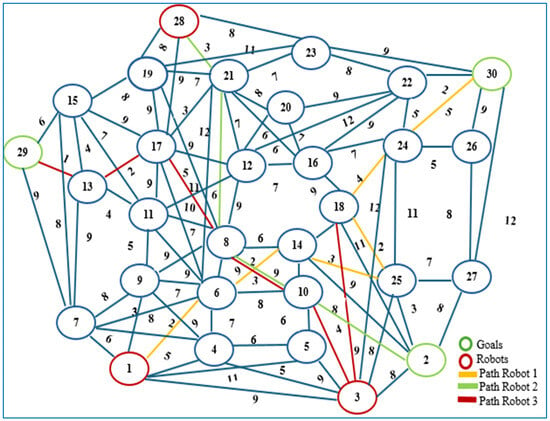
Figure 5.
The shortest paths for the three robots using Dijkstra’s algorithm. The numbers next to the links are the weights. The blue circles are the vertices of the obstacles.
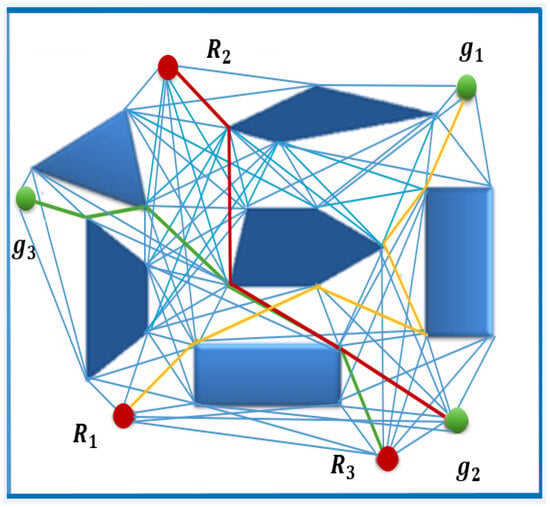
Figure 6.
The shortest paths of the three robots shown in Figure 5 determined using Dijkstra’s algorithm. The paths for robots 1, 2 and 3 are shown in yellow, red and green respectively. The red and green circles are robots and their goals respectively.
The MRPP algorithm planned the path for each robot based on a specific sequence or priority, i.e., the first path for , the second path for , and the third (last) path for . There was an intersection (crossroad) between the paths of and and opposite directions on the graph edges (straight roads) between the paths of and . However, no collision occurred as the algorithm planned a path for each robot sequentially (one by one). Hence, when planning the following path, it considers all the paths that have already been scheduled to prevent collisions and keep . There was a crossroad when passed the edge and passed the edge , but no collision occurred as passed before . The arrival time of when passing the vertex ( was ; once passing the vertex (, it was ; whereas the arrival time of when passing the vertex ( was ; when passing the vertex ( Consequently, that the arrival time of to the vertex was shorter than the arrival time of to the vertex because the distance (edge weight) that travelled to pass the vertex was less than the distance (edge weight) that travelled to pass the vertex ; thus, when arrived at the vertex , arrived at the vertex ; for this reason, no collision occurred, and a change of the edge weight was not necessary. If , then a collision would be possible (i.e., if the arrival time of on the vertex , then the change of the edge weight is necessary to avoid a collision). In addition, there were opposite directions (straight paths) on the edge between and . passed the edge earlier than the , where and . Thus, the arrival time of once it passed the edge was shorter than the arrival time of as the distance that had passed to arrive at the vertex was less than the distance that travelled to pass the vertex . Thus, . In addition, there was a crossroad on the vertex , where , and ; hence, , i.e., the arrival time of to the vertex was before . Accordingly, there was no need to change the edge weight since no collision occurred. If , then the collision happens, so the change of the edge weight is necessary to avoid a collision.
4.1. MRPP Algorithm-Based Prioritisation Sequence
MRPP algorithm determines the path for each robot based on a defined prioritisation sequence that considers performance criteria: path length, computation time, and connectivity robustness. Robots are prioritised according to the λ2 value and the weights of pre-defined edges, reflecting structural importance and potential communication links. This sequence ensures that connectivity is maintained and enhanced, reliable inter-robot communication is maintained, and collisions are avoided during coordinated navigation.
4.2. Comparative Analysis of Multiple Planning Sequences
This study compared distinct path planning sequences to evaluate how different robot prioritisation sequences affect performance in the MRPP algorithm. The analysis included total path length and the impact of λ2 on connectivity, reflecting the inter-robot communication robustness. In the scenario shown in Figure 4 and Table 1, found a path to its target , with a total distance of m, but , indicating the graph was disconnected. If we added a bridge (edge) between , the new path for would be ), with a total distance of 31 m. This would improve graph connectivity to , simultaneously forming a weak link graph. Additionally, adding a bridge between () would allow to reach its goal via (), with 32 m and , meaning the graph would be nearly disconnected. This clearly shows the planning order , and how each robot’s path and graph connectivity evolved sequentially.

Table 1.
Path planning sequence and connectivity analysis.
4.3. Multiple Planning Sequences Using the MRPP Algorithm
As shown in Table 2, the MRPP algorithm recalculated the paths for optimisation, examined the best edges to add, and chose vertices , with an increase of λ2 to 0.087. This created a robust link between the components because vertices had more connections in their respective components, enabling to find a path to reach its target: , with a total distance of 18 m. Then, it chose to add edges between vertices {(), ()} to find an optimal path for instead of the first path, while maintaining the communication graph at a high level. For , the new path was . With a total distance of 15 m, λ2 increased to 0.181. When the three edges were added together, { increased to 0.347. Then, found a path to reach its goal: with the total distance of 20 m. The MRPP algorithm chose the first path for R1, the second for R3, and the third (last) path for R2 (i.e., R1 → R3 → R2) based on a specific sequence or priority.

Table 2.
Path planning sequence and connectivity analysis using the MRPP algorithm.
The comparative results show that the path planning order using the MRPP algorithm impacted the total path length, distance, and robust connectivity, as evidenced by higher λ2 values and their impact on enhancing the robust connectivity. Although there was an intersection (crossroad) between the robots’ planned paths and opposite directions on the graph edges (straight roads), no collision occurred because the algorithm planned the paths based on the planning order. Choosing the correct sequence for robot path planning significantly impacted the team’s performance. This type of evaluation strengthens the reproducibility and robustness of the MRPP algorithm implementations in communication-sensitive multi-robot environments.
4.4. Impact of Connectivity (λ2) on the Task Completion Time in the MRPP Algorithm
In the MRPP algorithm framework, λ2 is a key indicator of the robustness and cohesiveness of the robots’ communication network. A higher λ2 means a stronger connectivity, which can significantly reduce delays caused by communication breakdowns, coordination conflicts, and replanning due to robot disconnections. In the earlier scenario (Figure 4), it was shown how improvements in λ2 affect the task completion time under the MRPP algorithm. Task completion time without connectivity optimisation resulted in λ2 = 0, with optimisation—in λ2 > 0. As an illustration, two cases (for both cases, velocity = 1 m/s) were compared:
Case 1: without connectivity optimisation (λ2 = 0). Path: . Distance: 5 + 6 + 9 = 20 m. Time = 20 s.
Improved edges , (λ2 = 0.04). Path: R2: . Distance: 11 + 4 + 7 + 6 + 3 = 31 m. Time = 31 s.
Improved edges , (λ2 = 0.038). Path: R1: . Distance: 11 + 9 + 12 = 32 m. Time = 32 s.
Total system task time = maximum (R1,R2,R3) = 32 s, λ2 = 0.038 ⇒ weak connectivity → less coordination, longer paths.
Case 2: with connectivity optimisation. Improved edges , (λ2 = 0.87). Path: R1: . Distance: 2 + 2 + 3 + 2 + 4 + 5 = 18 m. Time = 18 s.
Improved edges {() and (}, (λ2 = 0.181). Path: R3: v3 → v10 → v8 → v17 → v13 → v29. Distance: 4 + 3 + 5 + 2 + 1 = 15 m. Time = 15 s.
Improved edges: {}, (λ2 = 0.347). Path: R2: . Distance: 3 + 6 + 3 + 8 = 20 m. Time = 20 s.
Total system task time = maximum (R1,R2,R3) = 20 s. λ2 = 0.347 ⇒ stronger connectivity, shorter and more efficient paths.
The percentage reduction in the navigation time was as follows:
With a robust algebraic connectivity, path lengths reduced, and task completion time dropped significantly by about 37.5%. Communication improved, enabling coordinated, collision-free paths. This example demonstrates that the MRPP algorithm plans improved paths and leveraged λ2 to coordinate robots efficiently.
To further illustrate the process, the workspace environment was changed (see Figure 7).
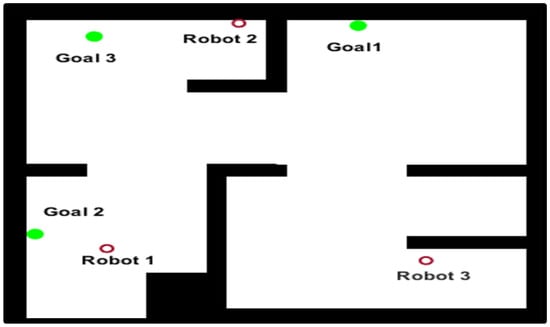
Figure 7.
A workspace environment containing three robots shown as red circles and three goals shown as green circles.
To apply the MRPP algorithm, the workspace is represented as an undirected weighted graph, then divided into two disconnected components of an undirected weighted graph using a VG such as Figure 8.
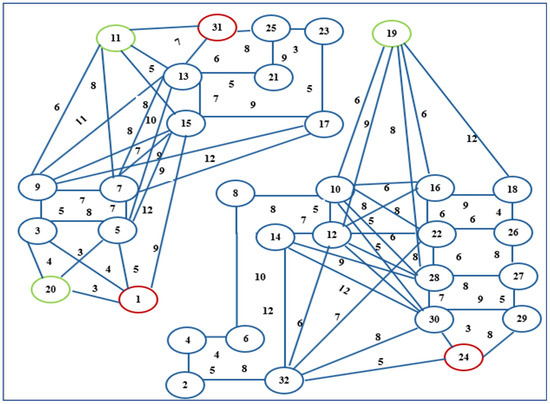
Figure 8.
Two disconnected components of undirected weighted graphs consisting of the three robots marked as red vertices and the three goals marked as green vertices.
The graph in Figure 8 consists of vertices , where the vertices represent the initial robot positions = that are marked with red, while the vertices represent the goal positions that are shown as green; E = {}; there are five polygonal obstacles (). The second smallest eigenvalue of the graph has a zero value ( because the graph has two disconnected components. has a path to reach its target, whilst and have their targets in the second component of the undirected weighted graph. If an edge is added between vertex and vertex , then can find a path to reach its target , and increases to 0.521. In addition, if we add edges , ), and , this enables to find a path to reach its target , and increases to 1.275. Additionally, when adding all the possible edges between the vertices of the graph, we created robust connectivity in the graph, and increased to 2.855. The shortest paths were found using Dijkstra’s algorithm, as shown in Figure 9 and Figure 10.
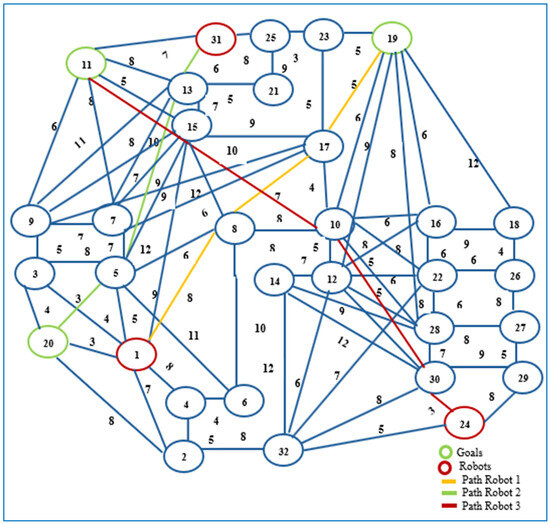
Figure 9.
The shortest paths for robot 1 highlighted in yellow, for robot 2—in green, and for robot 3—in red (Dijkstra’s algorithm).
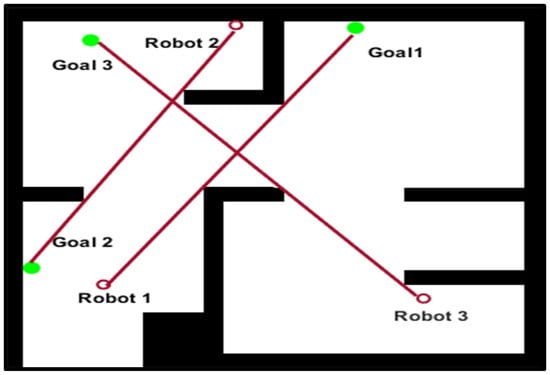
Figure 10.
The shortest paths for the three robots according to Dijkstra’s algorithm. The red lines are the robots’ paths to reach their targets.
Table 3 shows the calculated paths planned for each robot in Figure 9 and Figure 10. The MRPP algorithm planned the first path for R3, the second path for R1, and the third path for R2. No collision occurred because the algorithm controlled the arrival time of each robot by holding the weight of the edge (distance) and keeping > 0.
4.5. Simulation Procedure
This section introduces the simulation setup, parameters, and results of implementing the MRPP algorithm. This algorithm leverages a VG for obstacle avoidance, algebraic connectivity to maintain communication cohesion, and Dijkstra’s algorithm for optimal pathfinding.
Simulation environment: the path planning software simulations were conducted in a MATLAB/Simulink environment, version 2024 [26], leveraging custom VG generation and pathfinding scripts. All the required inputs were supplied to perform and complete the path planning process and followed a specific logical order. A 2D environment with static polygonal obstacles was devised, representing a workspace with dimensions of 18 × 12 units, where each unit represented one square metre. The obstacles were defined as geometric shapes such as triangles, rectangles, squares, zigzag lines, etc., and the robots were modelled as points.
Parameters: three robots (R1, R2, R3) appearing as three red points were selected. Three goals (g1, g2, g3) were represented by green points. The six randomly generated polygonal obstacles () of varying sizes were highlighted in blue with different labels. Each robot was initialised at random start points and assigned unique goal positions. The algorithm’s effectiveness was evaluated in different scenarios with varying obstacles and numbers of robots. The performance metrics included path optimality and connectivity maintenance.
Motion planning approach: each robot computed a visibility graph to represent possible paths around obstacles, connecting vertices (obstacles’ vertices and start and goal points) with edges representing collision-free paths. Dijkstra’s algorithm was applied to find the shortest route to the goal for each robot. Algebraic connectivity was constantly measured, ensuring all robots remained within the communication range. Adjustments were made to the paths when the connectivity = 0 or very small.
4.6. Results for the Simulation Scenarios
Scenario 1: six obstacles, three robots marked red, and three goals marked green are shown in Figure 11 and Figure 12.
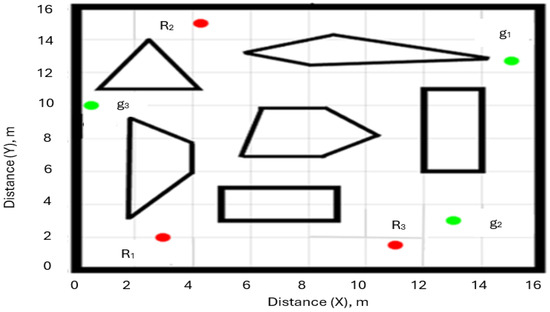
Figure 11.
The workspace: R1, R2, and R3 (shown in red) are the robots; g1, g2, and g3 (shown in green) are the goals. The polygons are the obstacles (shown black).
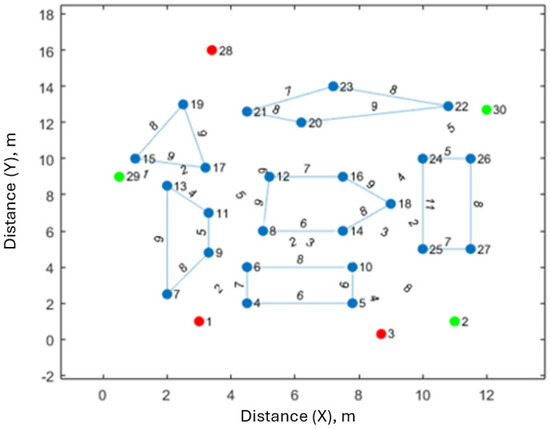
Figure 12.
Workspace represented as a graph containing three robots represented as red vertices and three goals represented as green vertices.
In the first scenario, three robots were deployed, with the density of the six obstacles marked as blue. A VG was established, and each robot’s path was computed using Dijkstra’s algorithm. Connectivity was maintained throughout the simulation. All the robots successfully reached their goals as illustrated in Figure 13.
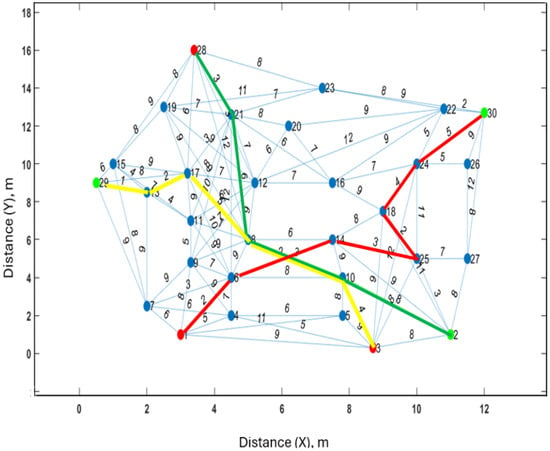
Figure 13.
Paths planned by the MRPP algorithm (red for R1, green for R2, and yellow for R3). Path 1 for R1 = 1, 6, 14, 25, 18, 24, 30 (distance = 18 m), path 2 for R2 = 3, 10, 8, 17, 13, 29 (distance = 15 m), path 3 for R3 = 28, 21, 8, 10, 2 (distance = 20 m).
The simulation results using MATLAB show that the robots reached their targets; the path of R1 is highlighted as yellow, the path of R2 is highlighted as green, and the path of R3 is highlighted as red, as shown in Figure 14.
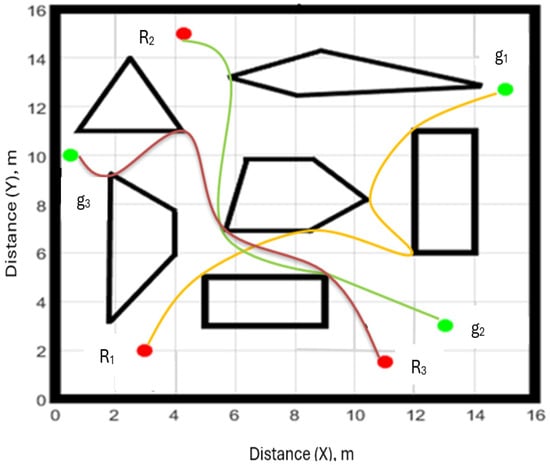
Figure 14.
Simulation for scenario 1, illustrating the robots reaching the goal points. The paths for robots R1, R2 and R3 are shown in yellow, green and red respectively. The red and green circles are robots and their goals respectively.
Scenario 2: five obstacles, three robots highlighted as blue, and three goals highlighted as green, see Figure 15 and Figure 16.
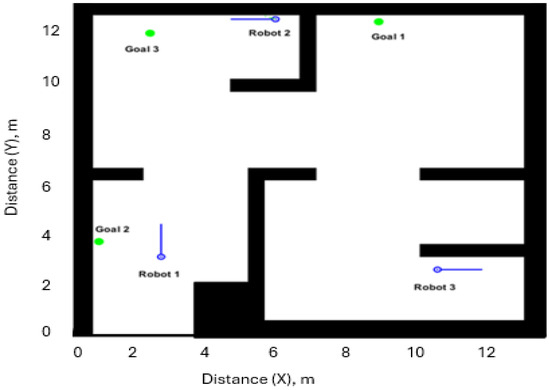
Figure 15.
Scenario 2 workspace environment consisting of three robots highlighted in blue and three goals highlighted as green, represented as a graph in Figure 16.
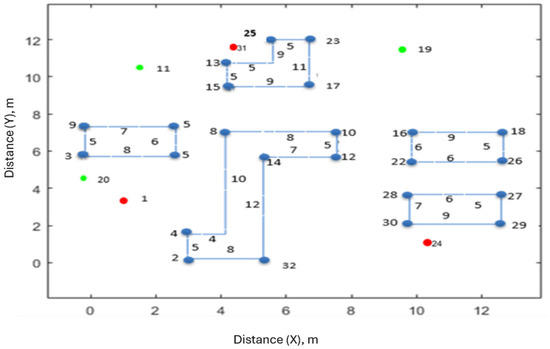
Figure 16.
Workspace represented as a graph consisting of three robots represented as red vertices and three goals represented as green vertices.
In scenario 2, three robots highlighted in blue navigated an environment with obstacles to reach three goals highlighted in green. A VG was generated for each robot. Dijkstra’s algorithm was used to measure the distance for each robot. All the robots reached their targets while maintaining connectivity, as shown in Figure 17.
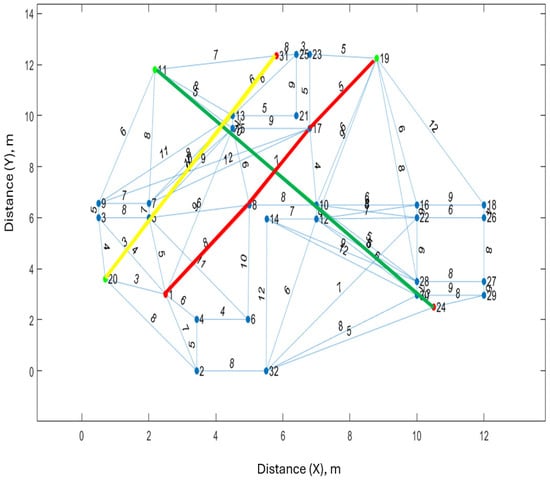
Figure 17.
Scenario 2: paths planned by the MRPP algorithm, highlighted as red, yellow, and green for each robot. Path 1 for R1 = 1, 8, 17, 19 (red, distance = 20 m), path 2 for R2 = 31, 13, 5, 20 (yellow, distance = 19 m), path 3 for R3 = 24, 30, 10, 11 (green, distance = 18 m).
The simulation results (Figure 18) shows that each robot reached its target without a collision.
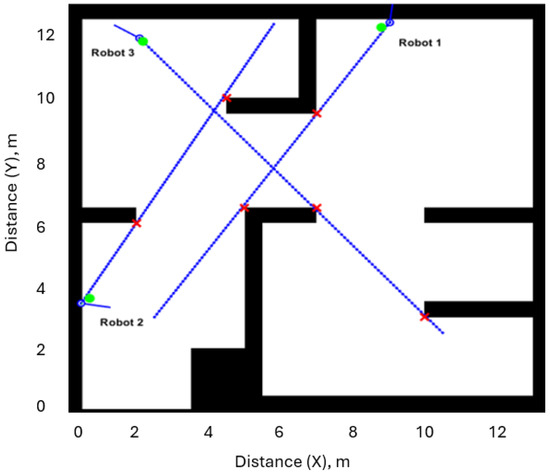
Figure 18.
Simulation results for scenario 2. The green dots are the goals for the robots, and the red crosses are the waypoints.
5. Discussion
The proposed multi-robot motion planning approach was evaluated through experiments using different environments with randomly placed obstacles and different robot configurations. The robots were assigned random start and goal locations, navigating through environments with varying obstacles. For each configuration, performance metrics included path length and the total distance that each robot travelled:
- computation of path: calculating paths while maintaining connectivity;
- algebraic connectivity: a measure of communication robustness among the robots;
- success rate: robots reaching their targets without collisions or connectivity loss.
These metrics align with previous studies such as [27], which emphasised path efficiency, robustness, and connectivity in multi-robot systems. The proposed paths contained two main components: a global planner and path optimisation. The global planner gathered information about the surrounding environment, such as the robot’s positions, targets, and obstacles. Depending on the path analysis, finding the path with minimum cost is necessary. When the optimal path was found with prior knowledge of the environment and static obstacles, a collision-free optimal path was created before the robots moved. A finding is that the proposed algorithm significantly improved the generation of efficient paths due to connectivity robustness, and the robots reached their goals reliably without collisions.
In tests with three robots for connectivity maintenance, the MRPP algorithm effectively determined paths by analysing all the possible routes and selecting the most suitable one based on the algebraic connectivity measure and the predefined weight evaluation function, indicating adaptability. The algorithm planned a sequential path for each robot one by one (i.e., path by path), considering all the already planned paths to avoid collisions. The MRPP algorithm provided each robot’s optimal (i.e., short-distance and safe) paths. The lengths and motion times of the paths were based on the planning order. The choice of the correct sequence for the path planning of the robots had a significant impact on the performance of the robot team. In the first workspace scenario, had a path to reach its target ), and the total distance was (20 m) (see Figure 4). However, this path was not optimal and = 0, meaning the graph was disconnected. Thus, for optimisation, the MRPP algorithm re-calculated the path and examined the two best edges and ) to add between the graph components and measured algebraic connectivity. The algorithm found an optimal path for R3 instead of the first path while maintaining of the communication graph at a high level (for R3, . The total distance was 15 m, and increased to 0.181; see Figure 5. Accordingly, the MRPP algorithm chose a path for each robot to ensure that the robots remained connected while performing their tasks and avoid collisions. Ensuring connectivity among the robots throughout their paths proved effective with algebraic connectivity. The system maintained an average algebraic connectivity value of 6.380 in Figure 4, indicating robust and consistent communication links due to recalculations that adaptively modified paths. This result is consistent with an earlier study [21], which demonstrated that multi-robot systems incorporating recalculation can effectively respond to real-time changes in their environment. This supports prior work by [28], highlighting algebraic connectivity’s effectiveness in maintaining communication in multi-robot networks and where connectivity is essential for coordinated robot actions [29].
The results demonstrated the visibility graph’s ability to avoid obstacles effectively while ensuring direct paths. This aligns with an earlier finding that reported similar results when comparing visibility-based methods with grid-based path planning in cluttered environments [30]. The VG method considers obstacles’ vertices in the map to be the vertices through which robots can reach their required positions. It links the visible vertices with each other, where the visible vertices are vertices with the property that a straight line (edge, path) connecting them does not intersect with any obstacles. Therefore, the calculated paths contain a set of waypoints () with the shortest length. These waypoints are determined as a series of consecutive points that begin from the lowest number of the first point to the goal; the waypoints are given by where is the starting point, and is the goal point. Hence, waypoints are a set of vertices of obstacles. For this reason, the paths have the least distances because they contain a set of waypoints, which are a set of vertices found by using VG with a combination of Dijkstra’s algorithm. These waypoints do not include the start points and the goal points, so they are always at specific vertices of obstacles. Thus, they can produce the shortest paths in terms of the Euclidean distance, where the essential condition is for a path to have a lower Euclidean distance from the starting point to the goal point in C-space, where each waypoint is a vertex of an obstacle. In robotics, the configuration space (often abbreviated as C-space) is a conceptual framework that represents all possible positions and orientations of a robot within its environment.
The proposed algorithm provided an efficient and robust solution for multi-robot motion planning. The work showcased notable benefits in path optimality and connectivity, providing reliable routes. This makes it well-suited for environments where efficient path planning and dependable connectivity are essential [31]. Consequently, this method is more effective for applications that require continuous communication, such as collaborative robotics and autonomous logistics [32]. The simulation results also indicated that the proposed approach is practical for multi-robot motion planning in different environments. In comparison, the VG method with Dijkstra’s algorithm generates pathfinding and provides efficient optimal paths in pathfinding applications. This approach allows for the computation of the shortest paths that navigate around obstacles effectively [33]. In addition, the connectivity constraints provided by algebraic connectivity enable a more resilient, robust communication framework, and it serves as an indicator of a network’s overall connectedness, facilitating better synchronisation and coordination among robots. This improvement in connectivity is valuable for applications requiring continuous communication, such as coordinated robotic systems in automated warehouses [34,35]. Our approach exhibited clear advantages in optimal path efficiency and robust connectivity, potentially enabling faster, safer, and more efficient operations in real-world applications [36].
It is possible to extend the MRPP algorithm to function in environments with dynamic obstacles. This would involve regenerating the obstacles’ edges to ensure robots avoid their positions [37,38]. The edge weights based on precomputed static paths could be dynamically adjusted to reflect the dynamic environment. This would include increasing edge weights in regions with high dynamic obstacle density and temporarily removing or reducing connectivity in areas that become impassable. Adjusting edge weights or restructuring the graph in response to environmental changes ensures the robot network remains connected and functional. In the MRPP algorithm, λ2 can still be employed in a dynamic environment; however, it should be recomputed periodically or maintained using distributed estimation techniques to adapt to the changes such as obstacle movements or communication disruptions [38]. The MRPP algorithm could include real-time replanning capabilities, where robot paths are recalculated as dynamic obstacles move. Algorithms such as D Lite or RRT (rapidly-exploring random trees) with replanning could be integrated to adapt trajectories while preserving global goals [39]. A future extension could incorporate spatiotemporal graphs and introduce time as an explicit dimension in path planning to predict and avoid dynamic obstacles, optimising both spatial and temporal aspects of robot motion (e.g., crossing an area only when it is expected to be clear) [38].
In this study, the MRPP algorithm was designed for uniform-sized robots using visibility graphs, assuming the obstacle spacings were sufficient for the navigation of the robots. In some environments, however, the size of robots can vary. Incorporating these variations requires modifications in the MRPP algorithm to ensure collision-free navigation. These include (i) the MRPP algorithm inflating obstacles in the configuration space based on the size of each robot to account for robot dimensions [40], (ii) the MRPP algorithm implementing priority adjustments where larger robots are prioritised in wider regions while smaller robots are provided greater flexibility, which improves collision avoidance and execution time [41], and (iii) considering the developments in Foodiebot that include advanced obstacle avoidance mechanisms to facilitate navigation in dynamic environments. The MRPP algorithm can benefit from such adaptability, allowing robots to adjust their paths in response to unforeseen environmental obstacles or changes [42,43].
As the number of robots grows, the MRPP algorithm faces increased graph complexities, which affect computation time, path conflict resolution, and communication demands. Maintaining path optimality and algebraic connectivity (λ2) becomes more computationally intensive. However, there could be a number of adaptions to improve scalability. These include (i) decentralised subgroup planning, whereby the robot team is partitioned into smaller groups, the navigation plan for each robot is undertaken locally, and updates are shared with nearby peers, thus reducing global computation [44]; (ii) adapting region-based graph construction, whereby visibility graphs are replaced with region-restricted graphs to constrain edge growth and simplify λ2 calculations [42]; and (iii) incorporating efficient connectivity estimation, whereby incremental or approximate methods (e.g., distributed spectral estimation) are used to update λ2 without full precomputation during each planning cycle [45].
The MRPP algorithm’s performance is influenced by obstacle density and workspace configuration. A higher obstacle density increases the complexity of the visibility graph. This affects both path optimality and inter-robot coordination. To maintain efficiency, the MRPP algorithm can incorporate adaptations that scale visibility analysis and maintain robust connectivity under spatial constraints. These include (i) application of an adaptive graph pruning to limit unnecessary edge evaluations in cluttered environments [42], (ii) adaptation of dynamic workspace segmentation to enable local planning in subdivided regions, thus improving responsiveness and reducing global complexity [46], (iii) inclusion of connectivity-aware edge evaluation to adjust edge weights based on the local obstacle density to preserve communication and minimise replanning [46], (iv) and integration of techniques such as particle swarm optimisation and beetle antennae search algorithm to further improve the MRPP algorithm. Precise control over robot trajectories reduces the likelihood of collisions, especially in environments with high obstacle density or scenarios involving varying-sized robots [42].
6. Conclusions
This article presents a novel path-planning (MRPP) algorithm in a 2D static environment. Our algorithm successfully balanced path length optimisation with the maintenance of communication between robots. It provided efficient and coordinated navigation in environments with obstacles while avoiding collisions. Simulation results demonstrated the effectiveness of the proposed algorithm, which efficiently navigated multiple robots in environments while ensuring robust communication. The MRPP algorithm has generated promising results in different scenarios and experiments. Future work could involve extending this approach to dynamic environments (i.e., moving obstacles) and varying robot sizes. It could also explore computation time reduction by optimising the VG construction or implementing parallel processing.
Author Contributions
Conceptualisation, F.A.S.A., X.X., L.A. and R.S.; methodology, F.A.S.A., X.X., L.A. and R.S.; software, F.A.S.A., X.X., L.A. and R.S.; validation, F.A.S.A., X.X., L.A. and R.S.; formal analysis, F.A.S.A., X.X., L.A. and R.S.; investigation, F.A.S.A., X.X., R.S. and L.A.; resources, F.A.S.A., X.X., R.S. and L.A.; data curation F.A.S.A., X.X., R.S. and L.A.; writing—original draft preparation, F.A.S.A., X.X., R.S. and L.A.; writing—review and editing, F.A.S.A., X.X., R.S. and L.A.; visualisation, F.A.S.A., X.X., R.S. and L.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, H. Graph-Based Multi-Robot Path Finding and Planning. Curr. Robot. Rep. 2022, 3, 77–84. [Google Scholar] [CrossRef]
- Chitikena, H.; Sanfilippo, F.; Ma, S. Robotics in Search and Rescue (SAR). Oper. Ethical Des. Perspect. Framew. Response Phase. Appl. Sci. 2023, 13, 1800. [Google Scholar]
- Bui, H.D. A Survey of Multi-Robot Motion Planning. arXiv 2023, arXiv:2310.08599. [Google Scholar]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Al-Kamil, S.J.; Szabolcsi, R. Optimizing Path Planning in Mobile Robot Systems Using Motion Capture Technology. Results Eng. 2024, 22, 102043. [Google Scholar] [CrossRef]
- Solis, I.; Motes, J.; Sandström, R.; Amato, N.M. Representation-Optimal Multi-Robot Motion Planning Using Conflict-Based Search. IEEE Robot. Autom. Lett. 2021, 6, 4608–4615. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar] [CrossRef]
- Hvězda, J. Comparison of Path Planning Methods for a Multi-Robot Team. Master’s Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2017. Available online: https://dspace.cvut.cz/bitstream/handle/10467/69497/F3-DP-2017-Hvezda-Jakub-Comparison_of_path_planning_methods_for_a_multi-robot_team.pdf (accessed on 9 May 2025).
- Kolushev, F.A.; Bogdanov, A.A. Multi-Agent Optimal Path Planning for Mobile Robots in Environment with Obstacles. In Perspectives of System Informatics 1999; Lecture Notes in Computer Science, 1755, Bjøner, D., Broy, M., Zamulin, A., Eds.; Springer: Berlin, Heidelberg, 2000; pp. 503–510. [Google Scholar] [CrossRef]
- Capelli, B.; Fouad, H.; Beltrame, G.; Sabattini, L. Decentralised Connectivity Maintenance With Time Delays Using Control Barrier Functions. In Proceedings of the International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1–7. [Google Scholar]
- Omar, R.B. Path Planning for Unmanned Aerial Vehicles Using Visibility Line-Based Methods. Ph.D. Thesis, University of Leicester, Leicester, UK, 2012. Available online: https://figshare.le.ac.uk/articles/thesis/Path_Planning_for_Unmanned_Aerial_Vehicles_Using_Visibility_Line-Based_Methods/10107965 (accessed on 10 April 2025).
- Giesbrecht, J. Global Path Planning For Unmanned Ground Vehicles. Technical Memorandum DRDC Suffield TM 2004-272 December, Defence R&D Canada—Suffield 2004, 1–59. Available online: https://apps.dtic.mil/sti/tr/pdf/ADA436274.pdf (accessed on 9 May 2025).
- Elbanhawi, M.; Simic, M.; Jazar, R. Autonomous Robots Path Planning: An Adaptive Roadmap Approach. Appl. Mech. Mater. 2013, 373–375, 246–254. [Google Scholar] [CrossRef]
- Omar, N. Path Planning Algorithm for a Car-Like Robot Based on Cell Decomposition Method. Ph.D. Thesis, Universiti Tun Hussein Onn Malaysia, Parit Raja, Malaysia, 2013. Available online: http://eprints.uthm.edu.my/2051/ (accessed on 10 April 2025).
- Banik, S.; Banik, S.C.; Mahmud, S.S. Path Planning Approaches in Multi-Robot System: A Review. Eng. Rep. 2025, 7, e13035. [Google Scholar] [CrossRef]
- Milos, S. Roadmap Methods vs. Cell Decomposition in Robot Motion Planning. In Proceedings of the 6th WSEAS International Conference on Signal processing, Robotics and Automation, Corfu, Greece, 16–19 February 2007; World Scientific and Engineering Academy and Society (WSEAS): Zografou, Greece. Available online: https://www.researchgate.net/publication/262215647_Roadmap_methods_vs_cell_decomposition_in_robot_motion_planning (accessed on 9 May 2025).
- Moldagalieva, A.; Ortiz-Haro, J.; Hönig, W. db-CBS: Discontinuity-Bounded Conflict-Based Search For Multi-Robot Kinodynamic Motion Planning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar]
- Wooden, D.T. Graph-Based Path Planning For Mobile Robots. Ph.D. Thesis, School of Electrical and Computer Engineering Georgia Institute of Technology, Atlanta, GA, USA, December 2006. Available online: http://mcs.csueastbay.edu/~grewe/CS3240/Mat/Graph/wooden_david_t_200611_phd.pdf (accessed on 9 May 2025).
- Kavraki, L.E.; Svestka, P.; Latombe, J.-C.; Overmars, M.H. Probabilistic Roadmaps For Path Planning in High-Dimensional Configuration Spaces. IEEE Trans. Robot. Autom. 1996, 12, 566–580. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems In Connection with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Toan, T.Q.; Sorokin, A.A.; Trang, V.T.H. Using Modification Of Visibility-Graph In Solving The Problem Of Finding Shortest Path For Robot. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Saad, A.F.A. Social Graphs And Their Applications To Robotics. Ph.D. Thesis, Sheffield Hallam University, Sheffield, UK, 2022. Available online: https://shura.shu.ac.uk/31906/ (accessed on 9 May 2025).
- Capelli, B.; Sabattini, L. Connectivity Maintenance: Global and Optimised Approach Through Control Barrier Functions. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 5590–5596. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic Connectivity of Graphs. Czechoslov. Math. J. 1973, 23, 298–305. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R.M. Consensus Problems in Networks of Agents with Switching Topology and Time-Delays. IEEE Trans. Autom. Control. 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- MathWorks. Mobile Robotics Simulation Toolbox; MathWorks: Natick, MA, USA, 2024; Available online: https://uk.mathworks.com/ (accessed on 9 May 2025).
- Zhao, D.; Zhang, S.; Shao, F.; Yang, L.; Liu, Q.; Zhang, H.; Zhang, Z. Path Planning for the Rapid Reconfiguration of a Multi-Robot Formation Using an Integrated Algorithm. Electronics 2023, 12, 3483. [Google Scholar] [CrossRef]
- Griparic, K. Algebraic Connectivity Control in Distributed Networks by Using Multiple Communication Channels. Sensors 2021, 21, 5014. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Deplano, D.; Li, Z.; Giua, A.; Franceschelli, M. Algebraic Connectivity Control and Maintenance in Multi-Agent NetWorks Under Attack. arXiv 2024, arXiv:2406.18467. [Google Scholar]
- Defoort, M.; Veluvolu, K.C. A Motion Planning Framework with Connectivity Management for Multiple Cooperative Robots. J. Intell. Robot. Syst. 2013, 75, 343–357. [Google Scholar] [CrossRef]
- Woosley, B.; Dasgupta, P.; Rogers, J.G.; Twigg, J. Multi-Robot Information Driven Path Planning Under Communication Constraints. Auton. Robot. 2020, 44, 721–737. [Google Scholar] [CrossRef]
- Alt, H.; Welzl, E. Visibility Graphs and Obstacle-Avoiding Shortest Paths. Z. Für Oper. Res. 1988, 32, 145–164. [Google Scholar] [CrossRef]
- Lee, W.; Choi, G.H.; Kim, T.W. Visibility Graph-based Path-Planning Algorithm with Quadtree Representation. Appl. Ocean. Res. 2021, 117, 102887. [Google Scholar] [CrossRef]
- Murayama, T. Distributed Control for Bi-Connectivity of Multi-Robot Network. SICE J. Control. Meas. Syst. Integr. 2023, 16, 1–10. [Google Scholar] [CrossRef]
- Matos, D.M.; Costa, P.; Sobreira, H.; Valente, A.; Lima, J. Efficient Multi-Robot Path Planning in Real Environments: A Centralized Coordination System. Int. J. Intell. Robot. Appl. 2025, 9, 217–244. [Google Scholar] [CrossRef]
- Zhou, C.; Li, J.; Shi, M.; Wu, T. Multi-Robot Path Planning Algorithm for Collaborative Mapping under Communication Constraints. Drones 2024, 8, 493. [Google Scholar] [CrossRef]
- Karaman, S.; Frazzoli, E. Sampling-Based Algorithms for Optimal Motion Planning. Int. J. Robot. Res. 2011, 30, 846–894. [Google Scholar] [CrossRef]
- Nordström, S.; Bai, Y.; Lindqvist, B.; Nikolakopoulos, G. A Time-Dependent Risk-Aware Distributed Multi-Agent Path Finder Based on A*. arXiv 2025, arXiv:2504.19593. [Google Scholar]
- Shen, Z.; Wilson, J.P.; Harvey, R.; Gupta, S. Online Multi-Robot Planning in Dynamic Environments Using Hybrid RRT and D Lite approaches. Sensors 2021, 21, 4938.2021. [Google Scholar]
- Sim, J.; Kim, J.; Nam, C. Safe Interval RRT∗ for Scalable Multi-Robot Path Planning in Continuous Space. arXiv 2025, arXiv:2404.01752. [Google Scholar]
- Huo, J.; Zheng, R.; Zhang, S.; Liu, M. Dual-Layer Multi-Robot Path Planning in Narrow-Lane Environments Under Specific Traffic Policies. Intell. Serv. Robot. 2022, 15, 537–555. [Google Scholar] [CrossRef]
- Moshayedi, A.J.; Roy, A.S.; Liao, L.; Khan, A.S.; Kolahdooz, A.; Eftekhari, A. Design and Development of Foodiebot Robot: From Simulation to Design. IEEE Access 2024, 12, 36148–36172. [Google Scholar] [CrossRef]
- Moshayedi, A.J.; Li, J.; Sina, N.; Chen, X.; Liao, L.; Gheisari, M.; Xie, X. Simulation and Validation of Optimized PID Controller in AGV (Automated Guided Vehicles) Model Using PSO and BAS Algorithms. Comput. Intell. Neurosci. 2022, 2022, 7799654. [Google Scholar] [CrossRef]
- Xu, W.-B.; Chen, X.-B.; Zhao, J.; Hung, T.Y. A Decentralized Method using Artificial Moments for Multi-Robot Path-Planning. Int. J. Adv. Robot. Syst. 2013, 10, 24. [Google Scholar] [CrossRef]
- Liu, W.; Fu, Y.; Guo, Y.; Wang, F.L.; Sun, W.; Zhang, Y. Two-Timescale Synchronization and Migration for Digital Twin Networks: A Multi-Agent Deep Reinforcement Learning Approach. arXiv 2024, arXiv:2409.01092. [Google Scholar] [CrossRef]
- Shetty, A.; Hussain, T.; Gao, G. Decentralized Connectivity Maintenance for Multi-robot Systems Under Motion and Sensing Uncertainties. J. Inst. Navig. 2023, 70, navi.552. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).