1. Introduction
In recent years, with the rapid development of e-commerce, social media and other Internet platforms, the challenge of mining content that users are most likely to be interested in from massive information has become a focal point for major companies.
Traditional recommendation systems usually extract embedding vectors from user–item interaction data, and then use the inner product of the embedding vectors of the user and the item to predict the interaction probability [
1,
2,
3]. While this approach provides decision-making assistance, a key limitation is data sparsity. Insufficient user–item interaction data may degrade the system’s representation capability [
4].
To address this challenge, several studies have begun to explore how auxiliary information can be utilized to enrich the representational capabilities of recommendation systems. It has been found [
5] that an individual’s preferences are often influenced by the friends in their social circles. This suggests that social relationships can be used as useful auxiliary information in recommendation systems [
6] to enhance the representation of users and items and alleviate the data sparsity problem.
Having alleviated the key problem of data sparsity, the researchers then focused on how to improve the performance of the recommendation system. The essence of a recommendation system is to maximize the difference in ratings between positive and negative samples as a way of distinguishing between items that users like (positive samples) and those that they dislike (negative samples). So the researchers focused on how to improve the quality of the negative samples and optimize the recommendation system in this way.
Although transformer-based approaches (e.g., [
7]) and large language models (LLMs) have achieved promising results in sequential recommendation tasks, they face inherent limitations in social recommendation scenarios. In particular, the quadratic complexity of self-attention mechanisms becomes prohibitive when modeling large-scale social graphs with sparse connectivity. LLM-based recommenders [
8] require dense textual metadata that are often unavailable to cold-start users with limited interaction history behavior. Our graph-based approach addresses these limitations by directly manipulating sparse social topologies.
Traditionally, a uniformly distributed negative sampling strategy is used [
9,
10,
11]. A study in 2022 [
12] designed two sampling strategies: positive-assisted sampling and exposure-enhanced sampling. Instead of extracting existing negative items from the graph data, they merged these two strategies in the embedding space to generate negative item embeddings, which greatly improved the accuracy of recommendations. Another study in 2024 [
13] proposed the idea of noise-free Negative Sampling (NNS) to select stable negative samples, which enhances the quality of negative samples and improves the recommendation performance.
However, the above methods only try to focus on improving negative sampling in discrete graph space, ignoring the structural information of Graph Neural Network (GNN) in embedding space and its unique neighbor aggregation process.
To address these shortcomings, we propose a social recommendation system based on negative sampling (HS-SocialRec). Due to the relative sparsity of social data, the method directly extracts the user’s social information from the user–item bipartite graph and constructs a new social graph to enrich the social data. High-quality hard negative samples are synthesized by introducing structural information and exploiting neighbor node information on the graph. Finally, the social graph and user–item bipartite graph are integrated into one model through the graph fusion mechanism, which not only improves the performance of the model but also simplifies the model in terms of temporal and spatial complexity.
The synthesis of hard negative samples is one of our highlights. First, the users who have no interaction with the users are selected as the original negative samples, and vice versa for the positive samples. Specifically, it can be divided into two steps: positive mixing and hop mixing. In positive mixing, an interpolation mixing method is introduced. By embedding positive sample information in the original negative samples of each layer of the social graph, augmented negative samples that do not interact with users but have the same characteristics in the real world are simulated. Hop mixing first extracts the overpowered negative samples with the highest inner product score with the positive samples from the augmented negative samples in each layer according to the theory in graph representation learning (MCNS) [
14], and then generates the hard negative samples through a pooling operation. The hard negative samples generated by this negative sampling strategy are extremely similar to the positive samples in the original data, and the gap with the normal negative samples is even larger, which improves the accuracy of the model recommendation.
In summary, our method has made the following contributions:
We construct a new social graph by extracting users’ social information from existing user–item interaction data. This enriches the semantic information of the recommendation system and alleviates the data sparsity problem.
The idea of synthesizing hard negative samples is introduced instead of extracting them directly from the data. This not only overcomes the limitation of sparse social data in traditional social recommendation systems, but also enhances the model’s ability to differentiate at the fine-grained level, thus improving the accuracy of recommendations.
We use a new graph fusion mechanism to integrate the social graph and user–item bipartite graph into a unified model. It not only improves the performance of the model, but also simplifies the complexity of the model in time and space.
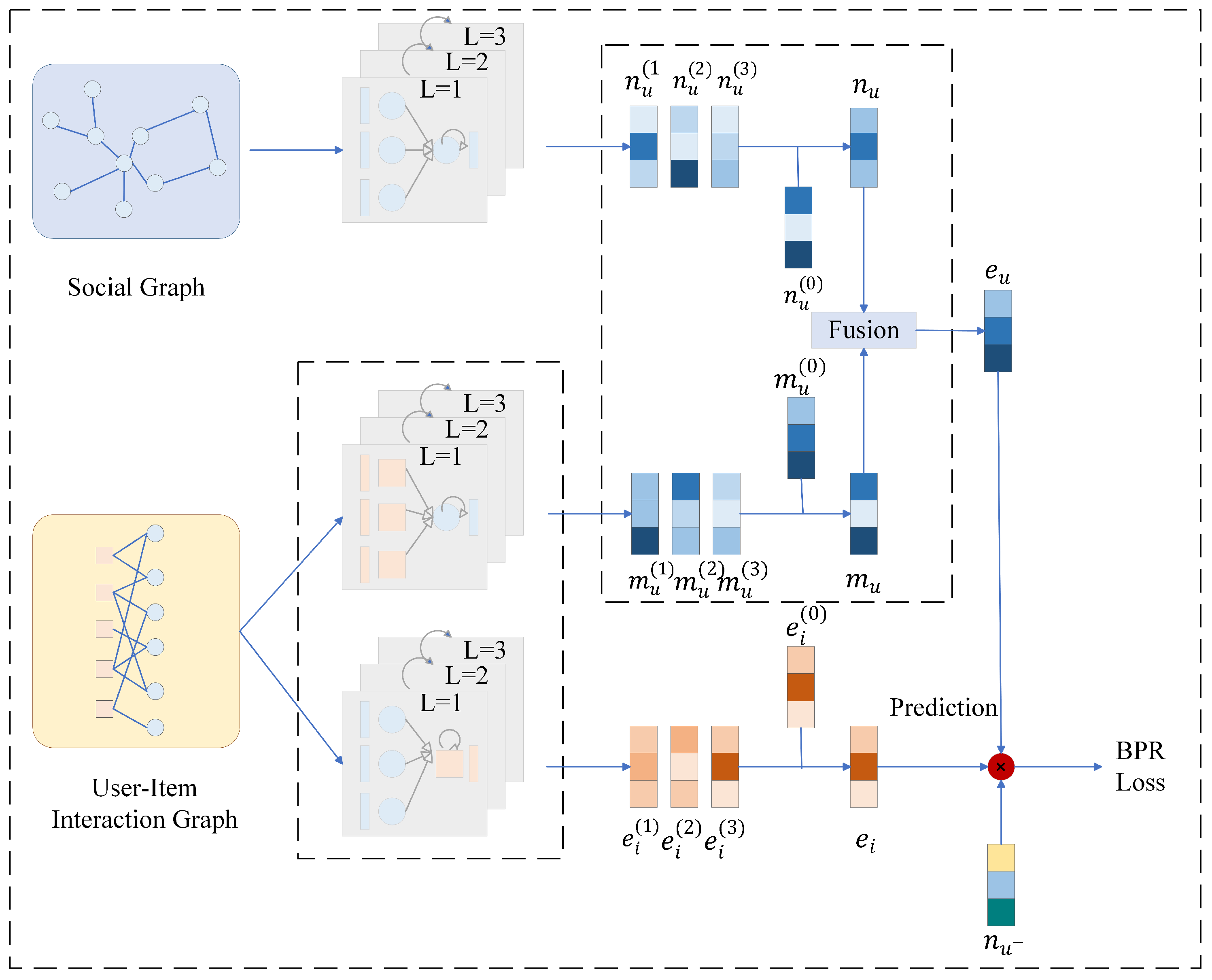
3. Method
Considering that personal preferences are often influenced by friends in the social circle, we mine user social information from existing user–item interaction data. As shown in
Figure 1, we use user social information to construct social graph as well as learn the social graph and user–item bipartite graph individually.
Due to the highly sparse nature of social data, we pay more attention to the quality of the data. Therefore, we mine implicit feedback by introducing hard negative sampling in the social graph. We describe the above method in detail below.
4. Experimental Results and Analysis
4.1. Experimental Settings
All experiments were run on devices equipped with RTX 3090 GPUs and implemented based on the PyTorch 1.7.1 framework. To validate the performance of the model, we chose four datasets, LastFM, Ciao, Delicious and Douban. These two datasets are significantly different in terms of data sparsity, which helps to evaluate the effect of different sparsity on recommendation effectiveness.
LastFM is an important dataset in the music domain, and after data cleaning and other preprocessing steps, we obtained the interaction records of 1892 users on the music platform. This dataset shows users’ music preferences and social connections in detail.
The Ciao dataset covers user behavior in the online shopping domain; it contains 7375 users’ ratings and purchase records for a wide range of products, revealing users’ consumption preferences and social connections.
Delicious is a social bookmarking platform dataset containing 104,799 annotated records of 69,226 web resources by 1867 users, which is suitable for tag recommendation and user interest modeling studies.
Duban is a cross-domain cultural social platform dataset covering 840,828 ratings of 17,902 book/movie/music items by 6739 users, with an interaction density of 0.697%. The rich social relationships support cross-domain recommendation and social enhancement algorithm research.
Table 1 lists the specific statistics of these four datasets used for the experiments, which facilitate further analysis of their characteristics and their impact on the recommendation model.
We use Precision, Recall and Normalized Discounted Cumulative Gain (NDCG) to evaluate the recommendation effectiveness of the HS-SocialRec model and the ten benchmark models. Precision and Recall are calculated in Equations (13) and (14), respectively:
where
,
, and
denote the number of true positive, false positive, and false negative samples, respectively.
where
indicates whether there is an interaction relationship between the user and the recommended item. When
is 1, it means there is interaction; when it is 0, it means no interaction.
is the sum of the scores of the top
N recommendation items in descending order of interaction scores.
Metric values where 1 indicates optimal performance. Five independent trials were conducted with mean results reported.
In the social recommendation scenario under study, we divide the dataset into training, validation and testing sets, considering that low-interaction users usually lack rich historical behavioral data, which leads to increased recommendation difficulty. In particular, we define the cold-start set, i.e., the set in which users have less than 10 interactions with other users. In this way, the performance of the model in personalized recommendation can be evaluated more accurately.
4.5. Hyper-Parametric Sensitivity Analyses
In this section, we report in detail the results of the sensitivity analysis of the four core hyperparameters in the HS-SocialRec model. Specifically, it includes the number of propagation layers (L), the regularization coefficient (), the size of the set of candidate negative samples (S), and the mixing coefficient of positive and negative samples (). L plays an important role in the application of the HS-SocialRec to a new dataset because L determines the depth of the propagation of the information in different graph structures.
In order to comprehensively examine the impact of these hyperparameters on the system performance, we executed a series of experiments, specifically:
We explored the performance variation of the number of propagation layers L over a range of values from 1 to 6, and finally selected L = 3 as the optimal configuration point.
We analyzed the impact of the variation of the regularization factor on the model performance in a specific interval . After careful tuning, we identified an optimal value of as to effectively control the model complexity and avoid the overfitting phenomenon.
Further, we also investigate the variation of the number of negative sample candidate sets S in the sequence of 2 to 8. Ultimately, R is locked at 2, which ensures the generalization ability of the model and improves the computational efficiency at the same time.
When the mixing coefficient is greater than 0.6, the synthetic negative samples have entered the dense area of positive samples. This leads to blurring of the decision boundary and makes the classifier lose its distinguishing power. So we analyze the effect of positive and negative sample mixing coefficients at [0.1–0.6] on the model, with a step size of 0.1. In the end, the model performs best when is at 0.3.
The detailed results of the above sensitivity analyses are displayed in
Table 5,
Table 6,
Table 7 and
Table 8. These tables clearly show the performance fluctuations under different hyperparameter settings, providing empirical support for HS-SocialRec’s optimal configuration. These experiments not only validate our hyperparameter selections but also offer tuning strategies for HS-SocialRec across different applications.
Table 5 shows that for LastFM and Delicious datasets, HS-SocialRec’s performance significantly improves when
L increases from 1 to 3. The model performance peaks when the
L value is set to 4. However, once the
L value exceeds 5, the model performance starts to decrease. Experimental results on the Ciao and Douban datasets show a similar pattern, where the model performance reaches its peak when the
L value equals 3. These findings reveal a key point; if the value of
L is set too large, an over-smoothing effect is triggered, which weakens the model’s recommendation ability. This suggests that choosing an appropriate value of
L is crucial to maintain the recommendation accuracy of the model.
From the trend of the data presented in
Table 6, when the value of
is relatively small (from 0 to
), we observe that increasing the value of
even degrades some of the performances in HS-SocialRec. HS-SocialRec exhibits the best recommended performance when
is set to
. It is worth noting that once the
value exceeds
, the performance of the model shows a significant decline. These experimental results suggest that over-regularization can instead adversely affect the model performance.
Due to the sparse data in the social graph, we adjusted the size of the negative sample candidate set
S within a smaller range of values such as
and recorded the corresponding model performance in detail. As shown in
Table 7, this gives us a detailed understanding of the impact of different sizes of negative sample candidate sets on the performance of the recommendation model.
On the LastFM and Douban datasets, the recommendation models show optimal performance, i.e., both precision and recall, when S is set to 4 and 5, respectively. And when we turn to the Ciao and Delicious datasets, the optimal value of S falls on a more conservative 2. This means that a small but carefully selected number of negative samples in a low-density social data environment is sufficient to guide the model in learning the core features of user preferences. There is no need to bear the additional burden of computational overhead and potential noise interference associated with too many negative samples. As the value of S increases to 7, the performance of the model on the LastFM and Ciao datasets degrades significantly.
In conclusion, choosing the right size of the negative sample candidate set is crucial for optimizing the recommendation model. This needs to be flexibly adjusted according to different dataset characteristics, model structure and specific business scenarios, in order to achieve the best recommendation results.
As shown in
Table 8, the model achieves optimal performance on the LastFM and Delicious datasets when
is 0.3, and the Ciao and Douban datasets have the best performance when
is 0.2 and 0.4. However, when
exceeds 0.4, the performance of all datasets shows a significant decrease, which indicates that sample mixing coefficients at [0.2–0.4] can effectively enhance the model discriminative power, while too high mixing ratios lead to blurring of decision boundaries and loss of discriminative power of the classifiers. This law provides important guidance for the negative sample synthesis strategy. We finally set the mixing coefficient at 0.3.
Author Contributions
Conceptualization, Z.S. and L.W.; methodology, Z.S.; software, L.W.; validation, Z.S. and L.W.; formal analysis, Z.S. and L.W.; investigation, Z.S. and L.W.; resources, Z.S. and L.W.; data curation, Z.S. and L.W.; writing—original draft preparation, Z.S.; writing—review and editing, Z.S. and L.W.; visualization, Z.S.; supervision, L.W.; project administration, Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sankar, A.; Liu, Y.; Yu, J.; Shah, N. Graph neural networks for friend ranking in large-scale social platforms. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 2535–2546. [Google Scholar]
- Wang, L.; Lim, E.P.; Liu, Z.; Zhao, T. Explanation guided contrastive learning for sequential recommendation. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 2017–2027. [Google Scholar]
- Yu, J.; Yin, H.; Xia, X.; Chen, T.; Cui, L.; Nguyen, Q.V.H. Are graph augmentations necessary? simple graph contrastive learning for recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 1294–1303. [Google Scholar]
- Huang, C.; Xia, L.; Wang, X.; He, X.; Yin, D. Self-supervised learning for recommendation. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 5136–5139. [Google Scholar]
- Lu, Y.; Xie, R.; Shi, C.; Fang, Y.; Wang, W.; Zhang, X.; Lin, L. Social influence attentive neural network for friend-enhanced recommendation. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: Applied Data Science Track: European Conference, ECML PKDD 2020, Ghent, Belgium, 14–18 September 2020; Part IV. Springer: Berlin/Heidelberg, Germany, 2021; pp. 3–18. [Google Scholar]
- Zhang, Y.; Zhu, J.; Zhang, Y.; Zhu, Y.; Zhou, J.; Xie, Y. Social-aware graph contrastive learning for recommender systems. Appl. Soft Comput. 2024, 158, 111558. [Google Scholar] [CrossRef]
- Sun, F.; Liu, J.; Wu, J.; Pei, C.; Lin, X.; Ou, W.; Jiang, P. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 1441–1450. [Google Scholar]
- Li, L.; Zhang, Y.; Chen, L. Prompt distillation for efficient llm-based recommendation. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 1348–1357. [Google Scholar]
- He, X.; Deng, K.; Wang, X.; Li, Y.; Zhang, Y.; Wang, M. Lightgcn: Simplifying and powering graph convolution network for recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; pp. 639–648. [Google Scholar]
- Liu, T. XsimGCL’s cross-layer for group recommendation using extremely simple graph contrastive learning. Clust. Comput. 2024, 27, 11537–11552. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, C.; Dong, J.; Yu, Y. Globally Informed Graph Contrastive Learning for Recommendation. In Proceedings of the International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; pp. 274–286. [Google Scholar]
- Yang, Z.; Ding, M.; Zou, X.; Tang, J.; Xu, B.; Zhou, C.; Yang, H. Region or global? A principle for negative sampling in graph-based recommendation. IEEE Trans. Knowl. Data Eng. 2022, 35, 6264–6277. [Google Scholar] [CrossRef]
- Ma, H.; Xie, R.; Meng, L.; Chen, X.; Zhang, X.; Lin, L.; Kang, Z. Plug-in diffusion model for sequential recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 8886–8894. [Google Scholar]
- Yang, Z.; Ding, M.; Zhou, C.; Yang, H.; Zhou, J.; Tang, J. Understanding negative sampling in graph representation learning. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 1666–1676. [Google Scholar]
- Marques, G.A.; Rigo, S.; Alves, I.M.D.R. Graduation mentoring recommender-hybrid recommendation system for customizing the undergraduate student’s formative path. In Proceedings of the 2021 XVI Latin American Conference on Learning Technologies (LACLO), Arequipa, Peru, 19–21 October 2021; pp. 342–349. [Google Scholar]
- Amara, S.; Subramanian, R.R. Collaborating personalized recommender system and content-based recommender system using TextCorpus. In Proceedings of the 2020 6th International Conference on Advanced Computing and Communication Systems (ICACCS), Tianjin, China, 23–26 April 2020; pp. 105–109. [Google Scholar]
- Kannikaklang, N.; Wongthanavasu, S.; Thamviset, W. A hybrid recommender system for improving rating prediction of movie recommendation. In Proceedings of the 2022 19th International Joint Conference on Computer Science and Software Engineering (JCSSE), Bangkok, Thailand, 22–25 June 2022; pp. 1–6. [Google Scholar]
- Chen, C.; Wu, X.; Chen, J.; Pardalos, P.M.; Ding, S. Dynamic grouping of heterogeneous agents for exploration and strike missions. Front. Inf. Technol. Electron. Eng. 2022, 23, 86–100. [Google Scholar] [CrossRef]
- Li, Z.; Xia, L.; Huang, C. Recdiff: Diffusion model for social recommendation. In Proceedings of the 33rd ACM International Conference on Information and Knowledge Management, Boise, ID, USA, 21–25 October 2024; pp. 1346–1355. [Google Scholar]
- Liu, C.; Zhang, J.; Wang, S.; Fan, W.; Li, Q. Score-based generative diffusion models for social recommendations. arXiv 2024, arXiv:2412.15579. [Google Scholar]
- Zang, X.; Xia, H.; Liu, Y. Diffusion social augmentation for social recommendation. J. Supercomput. 2025, 81, 208. [Google Scholar] [CrossRef]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph neural networks for social recommendation. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Yu, J.; Yin, H.; Li, J.; Wang, Q.; Hung, N.Q.V.; Zhang, X. Self-supervised multi-channel hypergraph convolutional network for social recommendation. In Proceedings of the Web Conference 2021, Ljubljana, Slovenia, 19–23 April 2021; pp. 413–424. [Google Scholar]
- Kang, W.C.; McAuley, J. Self-attentive sequential recommendation. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 197–206. [Google Scholar]
- Yun, S.; Jeong, M.; Kim, R.; Kang, J.; Kim, H.J. Graph transformer networks. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Karpov, I.; Kartashev, N. SocialBERT–Transformers for Online Social Network Language Modelling. In Proceedings of the International Conference on Analysis of Images, Social Networks and Texts, Virtual Event, 15–17 July 2021; pp. 56–70. [Google Scholar]
- Li, J.; Wang, H. Graph diffusive self-supervised learning for social recommendation. In Proceedings of the 47th International ACM SIGIR Conference on Research and Development in Information Retrieval, Washington, DC, USA, 14–18 July 2024; pp. 2442–2446. [Google Scholar]
- Cai, T.T.; Frankle, J.; Schwab, D.J.; Morcos, A.S. Are all negatives created equal in contrastive instance discrimination? arXiv 2020, arXiv:2010.06682. [Google Scholar]
- Jiang, R.; Nguyen, T.; Ishwar, P.; Aeron, S. Supervised contrastive learning with hard negative samples. In Proceedings of the 2024 International Joint Conference on Neural Networks (IJCNN), Yokohama, Japan, 30 June–5 July 2024; pp. 1–8. [Google Scholar]
- Xia, L.; Huang, C.; Xu, Y.; Zhao, J.; Yin, D.; Huang, J. Hypergraph contrastive collaborative filtering. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 70–79. [Google Scholar]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph neural networks in recommender systems: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Huang, J.T.; Sharma, A.; Sun, S.; Xia, L.; Zhang, D.; Pronin, P.; Padmanabhan, J.; Ottaviano, G.; Yang, L. Embedding-based retrieval in facebook search. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 2553–2561. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Lai, R.; Chen, R.; Han, Q.; Zhang, C.; Chen, L. Adaptive hardness negative sampling for collaborative filtering. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 8645–8652. [Google Scholar]
- Che, F.; Tao, J. M2ixKG: Mixing for harder negative samples in knowledge graph. Neural Netw. 2024, 177, 106358. [Google Scholar] [CrossRef] [PubMed]
- Rendle, S.; Freudenthaler, C.; Gantner, Z.; Schmidt-Thieme, L. BPR: Bayesian personalized ranking from implicit feedback. arXiv 2012, arXiv:1205.2618. [Google Scholar]
- Zhao, T.; McAuley, J.; King, I. Leveraging social connections to improve personalized ranking for collaborative filtering. In Proceedings of the 23rd ACM International Conference on Information and Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 261–270. [Google Scholar]
- Hu, B.; Zhou, N.; Zhou, Q.; Wang, X.; Liu, W. DiffNet: A learning to compare deep network for product recognition. IEEE Access 2020, 8, 19336–19344. [Google Scholar] [CrossRef]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T.S. Neural graph collaborative filtering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar]
- Lin, Z.; Tian, C.; Hou, Y.; Zhao, W.X. Improving graph collaborative filtering with neighborhood-enriched contrastive learning. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 2320–2329. [Google Scholar]
- Wei, Y.; Wang, X.; Nie, L.; He, X.; Chua, T.S. Graph-refined convolutional network for multimedia recommendation with implicit feedback. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 3541–3549. [Google Scholar]
- Yi, Z.; Wang, X.; Ounis, I.; Macdonald, C. Multi-modal graph contrastive learning for micro-video recommendation. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval, Madrid, Spain, 11–15 July 2022; pp. 1807–1811. [Google Scholar]
- Guo, Z.; Li, J.; Li, G.; Wang, C.; Shi, S.; Ruan, B. LGMRec: Local and global graph learning for multimodal recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 8454–8462. [Google Scholar]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).