1. Introduction
Corporate fraud is defined as the use of one’s occupation for personal enrichment through the deliberate misuse or misapplication of the employing organization’s resources or assets [
1]. According to 2023 Global Fraud Survey, corporate fraud cases from countries all over the world have incurred a total loss of more than 3.1 billion USD, which is estimated to be equivalent to 5% of the company’s revenue [
2]. Due to its huge financial impact, corporate fraud has attracted interest from researchers and regulators since the mid-20th century. The history of corporate fraud detection dates back to the early 1950s when Cressey [
3] proposed the famous fraud triangle framework. This framework remains a classic model to date, and it is often combined with quantitative methods to carry out fraud prediction. With the emergence of artificial intelligence in the past two decades, research in the domain of corporate fraud detection has shifted toward the application of data analytics and machine learning models.
In China, corporate fraud is regulated by the China Securities Regulatory Commission (CSRC). Between 2000 and 2020, the CSRC has revealed more than 5000 violation cases, with the number of violations showing an upward trend in recent years. This is due to the shift in the CSRC regulatory focus from market reform to strengthened supervision following the Chinese stock market crash in 2015 [
4]. The rising fraud rate has drawn the attention of researchers to investigate the occurrence of corporate fraud in China. Despite the increasing number of studies on this topic over the past five years, there are still some important aspects that are not properly addressed in the literature. In particular, we find that none of the extant research considers the population drift problem, which is one of the vital issues in credit scoring [
5]. In addition, although the data contain firms from 19 different industries, fraud analysis based on industry sector is rarely seen in the literature, with a few research works focusing on specific industries which are large [
6,
7]. Furthermore, most of the existing studies utilizing Chinese data focus on financial statement frauds [
8,
9]. Even though there are more than ten different fraud types, only a few studies consider all of them [
10,
11]. We believe that information about industry and fraud type can be used to extract useful information.
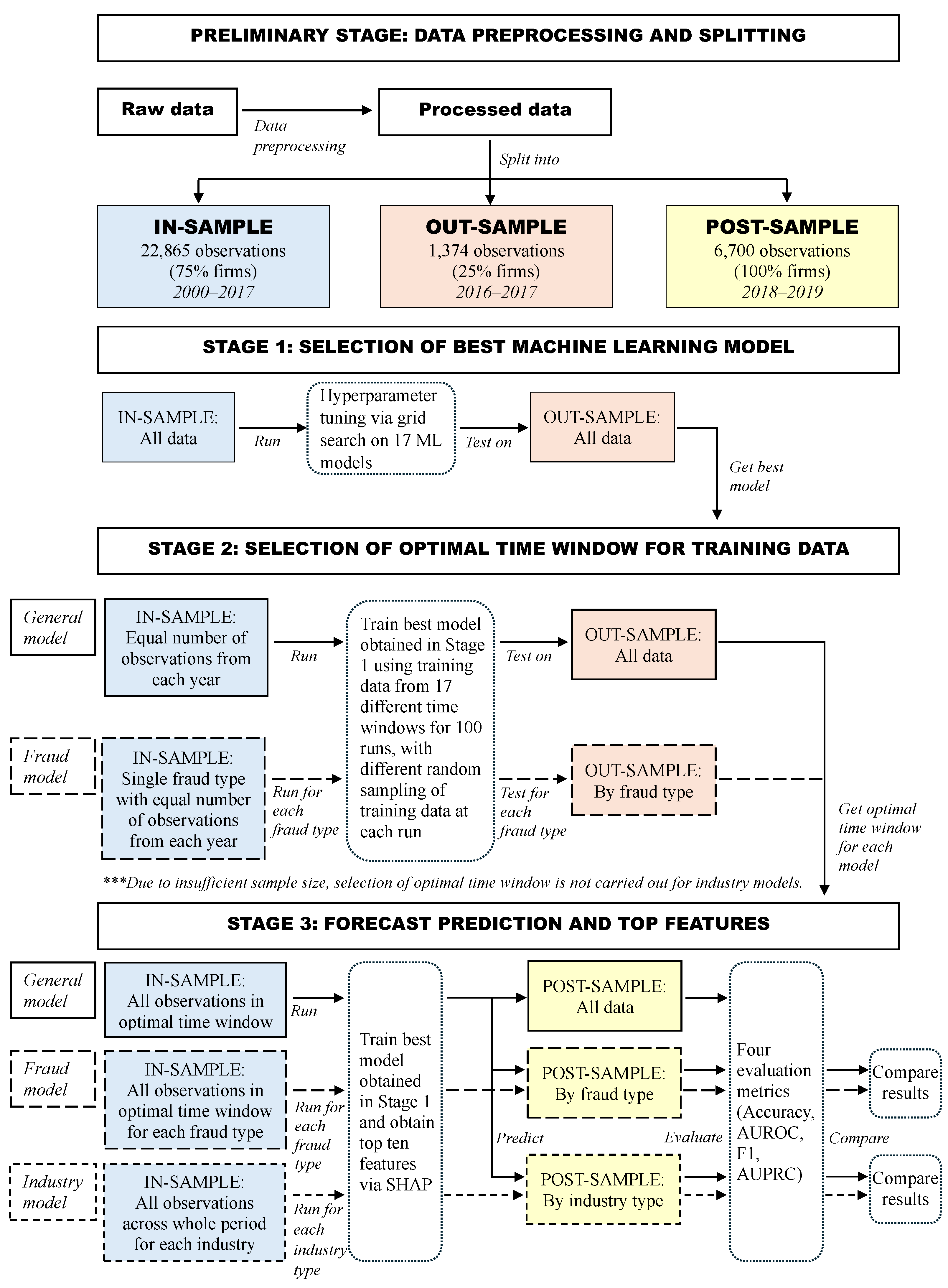
Complementing the above literature, we propose a comprehensive framework for Chinese corporate fraud prediction which incorporates the unaddressed or rarely addressed aspects in the literature. We first collected observations for all fraud types from 2000 to 2020 and extract yearly corporate governance information and financial indices from firm’s annual reports as features. These data were combined as firm-year observations to form the full dataset. To accommodate for segmented models, the full dataset was broken down into data by fraud type and data by industry. The experiments were divided into three stages, each serving a different purpose. In the first stage, we carried out the selection of best machine learning model with the full data. Five machine learning classifiers were selected and combined with three resampling techniques that handle the class imbalance problem to form 15 classifier–resampling combinations. We further employed two ensemble-based resampling approaches to make up a total of 17 candidate models. We found that the random forest classifier without resampling performed best among the 17 models according to the average ranking of four performance measures.
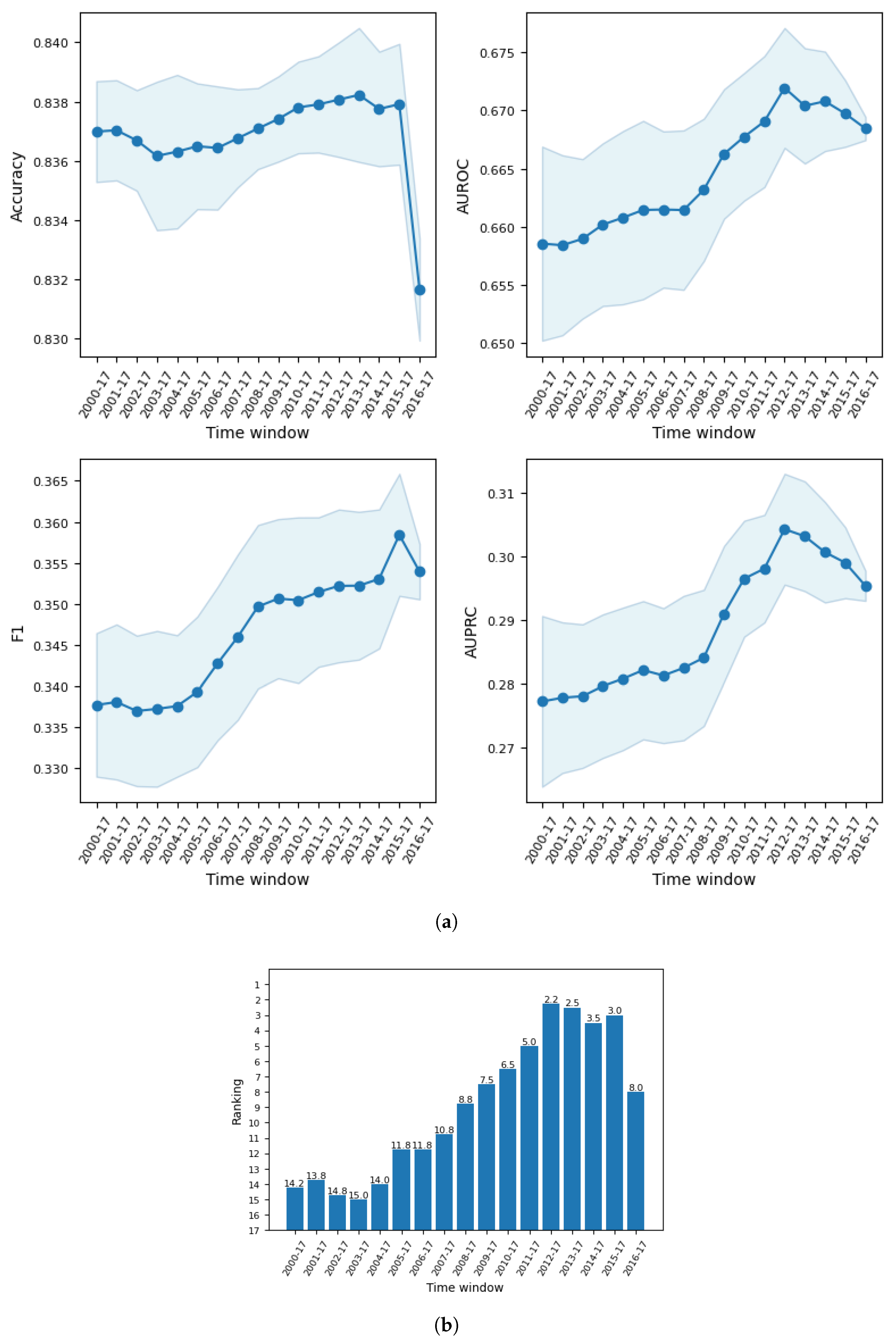
The second stage involved dealing with population drift, where selection of optimal time window for training data was carried out for the general model based on the full data and the fraud segmented models based on the data by fraud type. Our results indicate that the predictive performance increased gradually as older data were discarded from the training sample until at some time period when the number of training examples became too small and performance began to decline. In particular, when predicting fraud occurrences in 2016 to 2017, the general model reported the best performance when training data prior to 2012 were discarded. For the same test window, all the optimal time windows found in the fraud segmented models excluded training data before 2010. This suggests that population drift exists in our data, and it may be caused by several reasons such as changing corporate behavior, socio-economic conditions, and regulatory policy. This manifests the need to balance the tradeoff between the most recent data and sufficient data in order to obtain the best model performance.
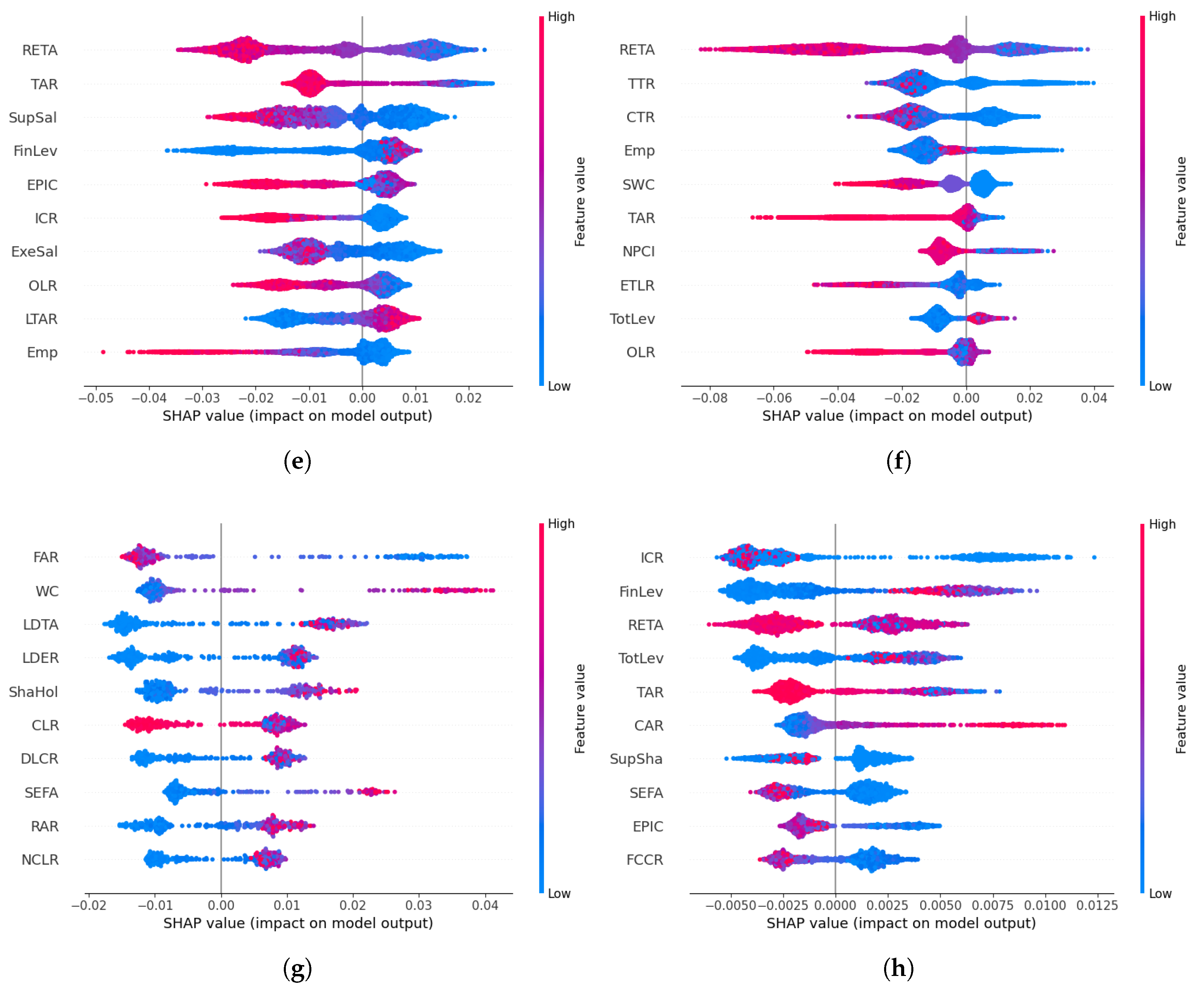
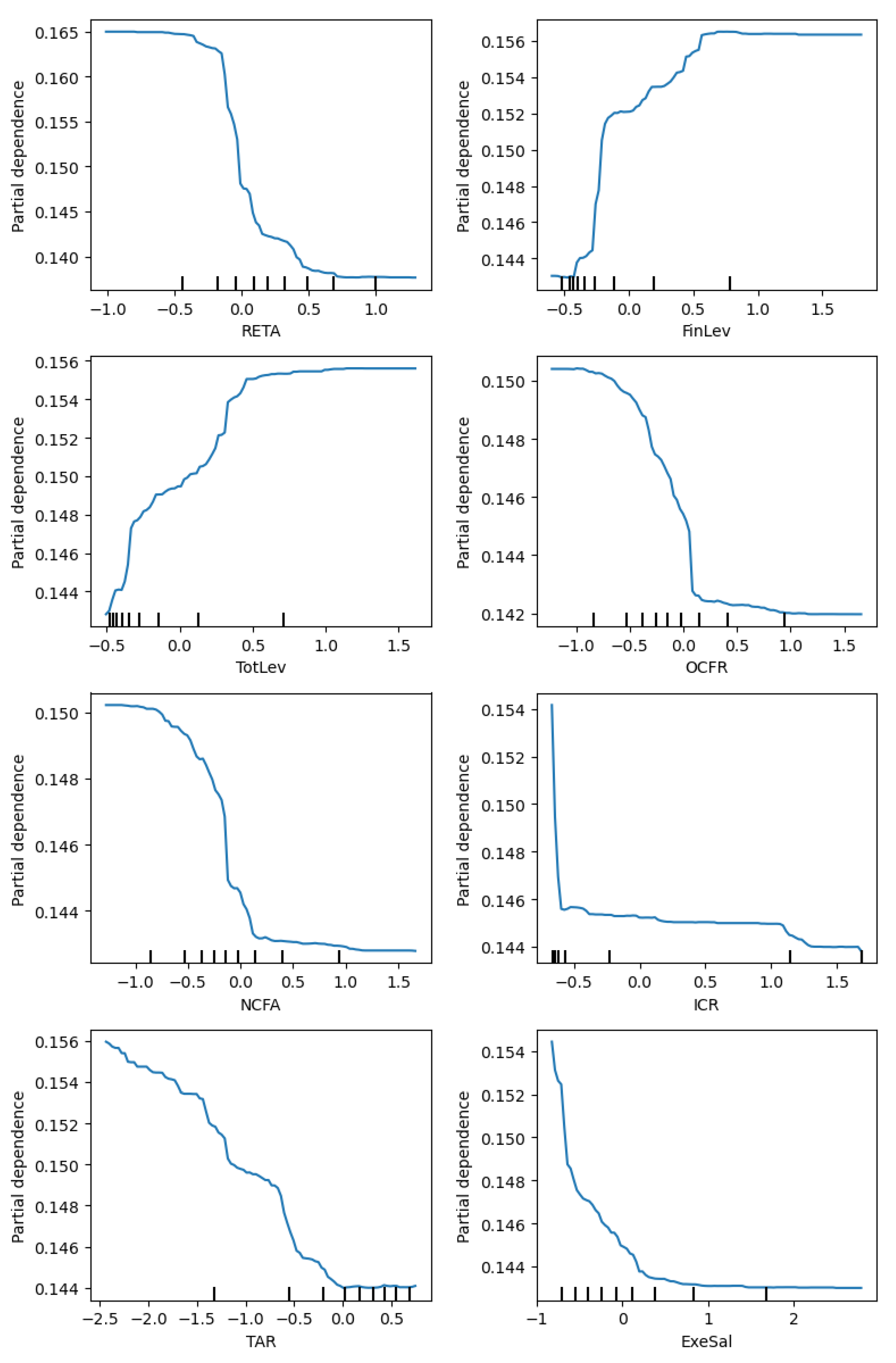
Thirdly, using the best model and optimal time window, we built a general model and segmented models for fraud types and industries. The forecast performance results of the general model, evaluated by four metrics, are comparable to the model performance reported in the previous literature. In terms of feature importance, the risk level and solvency features emerged as top features in the general model. Next, we compared the general model with each segmented model according to predictive performance and top features associated with fraud occurrence. Our findings revealed that five out of nine segmented models for fraud type achieved a better performance than their respective predictions using the general model. Among these fraud types, four of them have low fraud rates (<2%), and two of them show a significant discrepancy in terms of top features. On the other hand, only 2 out of 12 segmented models for industry performed better than their respective predictions in the general model. Our further investigation indicates that this is due to the insufficient training sample for most of the industries. In particular, we found that when we controlled the training size, the segmented models were as good as, or even better than the general model in terms of the AUROC for 11 of the 12 industries. These results suggest that segmented models are more informative than the general model for fraud types with low fraud rates and most industries given sufficient training data and that they should be employed to investigate fraud occurrence for important fraud types and industries.
This paper contributes to the literature on Chinese corporate fraud detection in the following ways. Firstly, to the best of our knowledge, our study is the first paper to address the population drift problem in corporate fraud prediction. This is a common yet important subject in credit scoring, and methods have been proposed to handle this in multiple credit scoring scenarios [
12,
13,
14]. However, none of the previous research considered population drift when building models to predict corporate fraud. We fill this gap by incorporating the selection of an optimal time window for training data before the main model is built. Our results shed new light on the impact of handling population drift in corporate fraud detection.
Secondly, our research provides new insights on the use of segmented models in corporate fraud prediction by introducing new dimensions for segmentation according to fraud type and industry. This is rarely seen in the literature, as previous studies focus on model for specific fraud types and large industries. Fraud predictions for less prevalent fraud types and small industries are understudied. We built segmented models for nine fraud types and 12 industries with sufficiently large sample sizes. The segmented models allow us to (1) compare the predictive performances between general model and segmented model; (2) understand which fraud types/industries are more difficult to predict; and (3) investigate the main risk features associated with each fraud/industry. This offers a new perspective on corporate fraud prediction to researchers, practitioners, and regulators.
Thirdly, our paper complements the growing literature on Chinese corporate fraud detection by providing a comprehensive framework to predict corporate fraud. In particular, we include all observations and fraud types in our model. The features employed in our model can be easily extracted from readily available annual reports and directly used without sophisticated feature engineering approaches. We have also proposed a clear three-stage experimental design that takes into account data splitting, machine learning algorithms, evaluation metrics, and methods to handle the class imbalance and population drift problems which are common in fraud prediction problem. Furthermore, we introduce segmented models for fraud type and industry to carry out comparisons between general and segmented models based on predictive performance and top features. We argue that we have taken into account most if not all aspects of corporate fraud prediction in our framework. Our work may serve as a practical reference for future research.
The remainder of the paper is organized as follows: We start with a review of the existing research on corporate fraud detection in
Section 2. In
Section 3, we discuss the data used in our study and how the data are split to carry out the experiments, as well as the methodology implemented in our experiments, which includes methods to handle the population drift problem, segmented models, and experimental design, which is divided into three stages. The results for each stage are reported in
Section 4, with discussion and analysis to draw meaningful insights. Concluding remarks are provided in
Section 5.
2. Related Studies
There is ample research on implementing machine learning for corporate fraud prediction in the literature. We focus on some of the most frequently cited research findings in the past 15 years. Most of these studies carry out fraud prediction based on data obtained from US companies. Cecchini et al. [
15] proposed a financial kernel for support vector machine which managed to identify 80% of management frauds using basic financial data. Perols [
16] compared the performances of six machine learning models in detecting financial statement frauds under different assumptions of fraud-to-non-fraud ratios. Surprisingly, they found that logistic regression and support vector machine outperformed artificial neural network and ensemble models.
Kim et al. [
17] developed multiclass classifiers to carry out financial misstatement predictions which classified the violations into intentional, unintentional, and no violation instead of the usual binary classification approach. Hájek and Henriques [
18] proposed a fraud detection system which incorporates automatic feature selection of financial and linguistic data. Their findings show that random forest and Bayesian belief network performed best in terms of true positive rate and true negative rate, respectively. Perols et al. [
19] introduced observation undersampling to address class imbalance and variable undersampling by fraud type, which improved the model prediction results by approximately 10% compared to the best-performing benchmark model. Brown et al. [
20] utilized a topic modeling algorithm to predict financial misreporting and found that thematic content of financial statement improved fraud prediction by up to 59%.
Bao et al. [
21] compared fraud prediction performance using different combinations of classifiers and input variables. Their findings indicate that the combination of RUSBoost and raw financial data outperformed the other combinations across four evaluation metrics. Bertomeu et al. [
22] carried out misstatement predictions and found that gradient-boosting regression tree and RUSBoost performed best on likelihood-based and classification-based measure performance, respectively. Khan et al. [
23] proposed a fraud detection framework based on minimizing the loss function and maximizing the recall that was optimized using a meta-heuristic algorithm called Beetle Antennae Search (BAS), which outperformed several benchmark models across different evaluation metrics. Also using the optimization approach, Yi et al. [
24] incorporated the Egret Swarm Optimization Algorithm (ESOA) into their fraud detection framework. The proposed model outperformed several benchmark models, including BAS, over four performance measures.
Since we utilized Chinese data in our research, we also report some recent studies related to corporate fraud prediction in Chinese firms in
Table 1. We present several important aspects of this research in the table for a clear and concise comparison. These include the time period of the data, fraud type of interest, number of observations, fraud rate, and categories of features employed. The feature categories will be further discussed in
Section 3.1. We also report the number of machine learning algorithms and evaluation metrics used, as well as four binary indicators on whether the class imbalance problem, population drift problem, segmented models, or feature importance was implemented in these studies.
Ravisankar et al. [
25] compared the performance of six machine learning models for detecting financial statement fraud with and without feature selection. They found that a probabilistic neural network model outperformed the remaining models in both cases. Song et al. [
26] proposed a hybrid framework which combines machine learning models and a rule-based system for financial statement fraud detection. Using the ensemble of four classifiers, their results indicate that non-financial risk factors and rule-based system reduce the error rates of predictions. Liu et al. [
27] documented that random forest performed best in the detection of financial frauds, and the ratio of debt to equity was the most important variable in the model. Yao et al. [
28] compared the combination six machine learning models with the dimensionality reduction method and found that the combination of support vector machine and stepwise regression dimension reduction performed best in financial statement fraud detection.
Achakzai and Juan [
8] built a voting classifier and stacked classifier for financial statement fraud predictions and found that these meta-classifiers performed better than standalone classifiers in detecting fraudulent observations. Wu and Du [
29] implemented deep learning models on the combination of numerical and textual data to detect financial statement frauds. Their results indicate that LSTM and GRU with textual data showed considerable improvement in model performance compared to traditional models with numerical data. Xu et al. [
10] compared six machine learning models and studied the effects of different features categorized by greed, opportunity, need, exposure (GONE) on corporate fraud prediction. Their findings revealed that random forest performed best and suggest that exposure variables are more important than other variables. Chen and Zhai [
30] utilized data from China to compare the performance of five ensemble learning models on financial statement fraud detection and found that bagging outperformed boosting in several evaluation indicators. Lu et al. [
11] documented that XGBoost performed best among five models in corporate fraud prediction, and their results indicate that financial condition has the greatest impact in fraud detection among different feature groups. Rahman and Zhu [
31] investigated accounting fraud detection in Chinese family firms and found that imbalanced ensemble classifiers performed better than conventional classifiers.
Cai and Xie [
32] proposed an explainable financial statement fraud detection approach based on a two-layer knowledge graph (FSFD-TLKG). They compared the proposed method with 17 different explainable and non-explainable models and found that it outperformed all models except the non-explainable XGBoost model. Duan et al. [
9] used ensemble learning to investigate financial statement frauds with the proposal of an ex ante fraud risk index which improves the integrity of the financial information. Li et al. [
6] utilized textual data from company’s financial statements and media’s news reports to represent internal and external perceptions, respectively. They found that using multiperspective enhanced the effectiveness of financial fraud detection. Sun et al. [
33] documented that the XGBoost model outperformed traditional models in identifying financial frauds among Chinese companies. Tang and Liu [
7] proposed a transformer-based architecture which implements feature extraction and handles class imbalance problem using the multiattention algorithm to carry out financial fraud detection. The proposed method outperformed traditional models across five performance metrics.
Based on the literature review, we observe three aspects which are rarely addressed or are completely unaddressed in the existing studies. Firstly, to the best of our knowledge, none of the research related to corporate fraud in China addresses the population drift problem in their studies. Population drift occurs due to the change in distribution over time, and it is a common problem in credit scoring. Over the years, approaches have been proposed to handle this problem in different credit scoring scenarios such as mortgage arrear prediction [
12], bad rate among accepts (BRAA) prediction [
13,
35], consumer behavioral scoring [
14], and credit card fraud detection [
36]. Since we employed data that span multiple years to carry out corporate fraud detection, we believe that the population drift problem is present and should be addressed in our experiments.
Secondly, we observe that the uses of segmented models are mainly for subsets of different features [
28,
29,
34] or time periods [
8,
31,
33] in existing studies regarding Chinese corporate fraud. Since the data consist of firms from different industries, we hypothesize that a segmented model can be utilized to investigate fraud occurrence in each industry. This is rarely seen in the literature, as existing studies focus on specific industries which are large [
6,
7].
Thirdly, most of the extant research focuses on a single fraud type, with financial statement fraud being the most commonly investigated fraud type. Even though there are more than ten fraud types in the data, only a few studies considered all of them [
10,
11]. We hypothesize that all fraud types should receive equal attention regardless of their prevalence. This can be achieved by building a general model which takes into account all types of violation and extending the idea of a segmented model to each fraud type, which is unseen in the literature so far.