Distantly Supervised Relation Extraction Method Based on Multi-Level Hierarchical Attention

Abstract

Distantly Supervised Relation Extraction (DSRE) aims to automatically identify semantic relationships within large text corpora by aligning with external knowledge bases. Despite the success of current methods in automating data annotation, they introduce two main challenges: label noise and data long-tail distribution. Label noise results in inaccurate annotations, which can undermine the quality of relation extraction. The long-tail problem, on the other hand, leads to an imbalanced model that struggles to extract less frequent, long-tail relations. In this paper, we introduce a novel relation extraction framework based on multi-level hierarchical attention. This approach utilizes Graph Attention Networks (GATs) to model the hierarchical structure of the relations, capturing the semantic dependencies between relation types and generating relation embeddings that reflect the overall hierarchical framework. To improve the classification process, we incorporate a multi-level classification structure guided by hierarchical attention, which enhances the accuracy of both head and tail relation extraction. A local probability constraint is introduced to ensure coherence across the classification levels, fostering knowledge transfer from frequent to less frequent relations. Experimental evaluations on the New York Times (NYT) dataset demonstrate that our method outperforms existing baselines, particularly in the context of long-tail relation extraction, offering a comprehensive solution to the challenges of DSRE.

1. Introduction

Relation extraction (RE) is a fundamental task in natural language processing (NLP) that aims to uncover semantic relationships between pairs of entities within sentences drawn from large text corpora [1,2,3,4]. This process is crucial for various downstream applications, such as question answering [5], knowledge graph construction [6], information retrieval [7], and cybersecurity [8], making it a cornerstone of many practical systems. As a result, RE has attracted significant attention from both researchers [9,10,11] and practitioners [12,13].

Traditional RE methods rely on supervised learning [14,15], which is hindered by the lack of large, manually annotated datasets [16,17,18]. To address the high cost of manual annotation, the concept of distantly supervised relation extraction (DSRE) was introduced [19,20,21]. In DSRE, training data are automatically generated by aligning a knowledge base, such as Freebase, with unstructured text, such as news articles. The goal of DSRE is to develop a relation extractor that can identify semantic relationships within large text corpora using these automatically labeled data [22,23].

Although DSRE has made significant strides in automating data annotation [24,25], it faces two major challenges: label noise [26] and the long-tail distribution of data [27]. Several promising approaches have been proposed to mitigate the negative effects of noisy data [28,29]. For example, Ref. [3] introduced a method that combines a selective gate mechanism with a noise correction framework. The selective gate filters sentence features within a bag of sentences, while the noise correction module adjusts misclassified instances, particularly those from underrepresented categories, reducing the detrimental impact of label noise. Similarly, Ref. [30] tackled noisy data by segmenting them with a Gaussian Mixture Model (GMM) to analyze the loss distribution and applied a guided label generation approach to progressively refine the dataset, improving the overall performance.

While label noise have been extensively studied, the extraction of long-tail relations has received less attention [31]. However, the introduction of a relation hierarchy structure offers a practical solution to address the long-tail problem. Recent advancements in relation extraction have leveraged this hierarchical structure, resulting in improved capabilities for identifying long-tail relations [32,33,34]. For instance, Ref. [27] proposed a contrastive learning approach for long-tail awareness, utilizing hyperaugmentation techniques to distinguish between prevalent and underrepresented segments while creating new positive and negative pairs to improve representations. Similarly, Ref. [35] introduced a joint learning framework that integrates relation extraction with contrastive learning, enabling the model to better differentiate between subtle categories and enhance long-tail relation extraction. Beyond these efforts, the hierarchical attention mechanism has proven effective in leveraging the information embedded within the relation hierarchy [36]. This method employs sentence-level selective attention at each hierarchical level, aligning with the true relation r, and combines the bag representations from each level before feeding them into a softmax classifier. However, this approach falls short of fully capturing the relational details within the hierarchy, relying on simplistic representations of entity bags and the hierarchical structure, which limits the accuracy of the classification process.

Semantic relationships often exist between relation labels [19,37,38,39]. For instance, the sentence “Nanjing is the capital city of Jiangsu Province” expresses the fact <. Nanjing, capital, Jiangsu> and also implies <Nanjing, belongs to, Jiangsu>. By exploring these semantic ties between relation categories and facilitating the knowledge transfer between common head relations and less frequent long-tail relations, the extraction of long-tail relations can be significantly improved. In [32], the concept of a relation hierarchy was introduced, employing a hierarchical tree structure to represent dependencies among relation labels. Figure 1 illustrates the localized aspects of this structure, where relation nodes such as “/ people/person/place_of_birth” and “/people/person/nationality” are children of the parent node “/people/person”. Semantically, a person’s birthplace in a specific country and their nationality in that country represent two closely related events, underscoring the value of hierarchical structures in capturing the relational information between labels.

To address the challenges of label noise and data long-tail distribution, we introduce a novel model called the Multi-level Classification Hierarchical Relation Extraction (MCHRE). Unlike traditional methods that either initialize relation embeddings arbitrarily or rely on external knowledge via knowledge graphs, our approach focuses on encoding the hierarchical structure of relations without using external resources. As the relation hierarchy is a graph-structured dataset, we employ Graph Attention Networks (GATs) [40] as the structural encoder. The self-attention mechanism in GATs enables the derivation of information transfer weight matrices independent of external inputs, facilitating the propagation of semantic information across relation nodes. Additionally, by stacking multiple GAT layers, we enable the exchange of information between nodes at different hierarchical levels. Optionally, multi-head attention can replace self-attention to enhance the encoder’s robustness and uncover deeper latent semantic relationships among relation labels. For classification, traditional hierarchical attention mechanisms rely on bag representations from multiple levels for a single-step prediction. However, these methods often neglect the tight relationships between representations at different levels. To address this, we propose a multi-level classification framework that independently processes the bag representations at each hierarchical level for classification, establishing a tiered classification procedure. While classifications at each level are performed separately, the prediction probabilities of adjacent levels should ideally align. For example, the combined probabilities of child nodes should match the probability of their parent node from the previous level. This alignment ensures the consistency of the multi-level classification framework, which is a condition we term the local probability constraint.

The key contributions of this work are as follows:

• We propose a hierarchical structure encoder using GATs to explore the relational details within the hierarchy, establishing new pathways for knowledge transmission and generating relation embeddings that capture the global hierarchical structure.
• We introduce a multi-level classification framework integrated with hierarchical attention, enabling relation classification across multiple granularities. This framework effectively uses sentence bag features and hierarchical relational insights, promoting data denoising and enhancing long-tail relation extraction.
• We conduct extensive experiments on the NYT dataset, comparing the proposed model to several baseline models. The results demonstrate the model’s effectiveness in data denoising and its success in extracting long-tail relations.

The remainder of this paper is structured as follows: Section 2 reviews related works, Section 3 details the proposed method, Section 4 presents experimental results, and Section 5 discusses the conclusions and future work.

2. Related Works

DSRE is highly regarded for its ability to automatically annotate training datasets. The overarching goal of DSRE is to develop relation extractors that effectively reduce data noise and maintain balance in the extracted relations [41]. In recent years, deep learning-based approaches have become a central focus in this area, leading to the development of several significant methods. This section provides an overview of the current research landscape in DSRE, examining key advancements in label noise correction and the optimization of data long-tail issues.

2.1. Label Noise Correction

Various approaches have been proposed to address the challenge of label noise in DSRE, achieving effective results. For instance, ref. [22] introduced a novel DSRE method that utilizes global sentence context to guide denoising, thereby producing robust bag-level representations. This method enhances sentence representations through knowledge-aware word embeddings, leveraging structured knowledge from external graphs and semantic insights from the text corpus. Ref. [31] proposed a Type Affinity Network (TAN), which explicitly captures dependencies between relational features. TAN extracts high-quality representations using entity-type and local context data while dynamically integrating type dependencies via a type affinity matrix, which improves the handling of long-tail relations. This approach stands out by aggregating implicit relational features into base points, offering a versatile alternative to traditional hierarchical methods.

Similarly, ref. [42] introduced the Contextual Information Interaction and Relation Embeddings (CIRE) method, which employs BERT and Bi-LSTM to strengthen contextual interactions by refining sequence data with error-correcting gates in the Bi-LSTM. This method also enhances the accuracy of relation embeddings by incorporating the vector differences between entity pairs. Ref. [43] proposed a Multi-Encoder with Entity-Aware Embedding Framework (MEEA) for DSRE. The MEEA improves entity relation predictions by thoroughly capturing contextual features, using an entity-aware embedding approach with an attention fusion mechanism. This system blends relative position and dual-entity data, emphasizing the importance of entity pairs while leveraging a multi-encoder setup to extract varied features and grasp global contextual dependencies.

In addition to utilizing contextual information, attention mechanisms have proven effective in mitigating label noise. For example, ref. [44] presented a DSRE method based on knowledge-aware embeddings, where entity type and relation alias data were used to enhance extraction accuracy. The entity-aware embedding technique integrates entity type information, while intrabag attention is refined with relation alias data. Bag representations are aggregated to facilitate relation classification. In [45], an end-to-end network was developed to model relation correlations from two perspectives. Globally, an undirected connected graph based on relation hierarchies was constructed, with Graph Attention Networks (GATs) employed to aggregate node information for correlation-aware Global Hierarchy Embeddings (GHEs). Locally, Local Probability Constraints (LPCs) were introduced to capture the interdependencies between adjacent classification levels, which were integrated into a branch network for sentence-level and bag-level classification.

2.2. Optimization for Data Long-Tail

To address the issue of long-tail data, several researchers have proposed innovative methods with promising results. Ref. [36] tackled long-tail relations by modeling heuristic interactions across relation levels and propagating top-down information in a recursive structure. This process generated relation-enhanced sentence representations, and the introduction of an Entity-Order Perception (EOP) training objective helped preserve entity occurrence details within the sentence encoder. Ref. [35] proposed a joint learning framework that combines relation extraction with contrastive learning, enabling the model to detect subtle category differences and improve long-tail relation extraction. Ref. [27] introduced a contrastive learning method specifically designed for long-tail awareness. This method distinguishes between dominant and underrepresented data segments using hyperaugmentation strategies and constructs new positive and negative pairs in contrastive learning to improve representations across categories.

Beyond contrastive learning [46,47], ref. [36] proposed the Recursive Hierarchy-Interactive Attention (RHIA) network to address long-tail relations. This method models heuristic effects between levels and recursively passed down information to generate relation-augmented sentence representations. Ref. [33] designed a DSRE approach targeting long-tailed, imbalanced data. It leverages knowledge from data-rich head classes to improve performance in data-scarce tail classes and integrates implicit relational knowledge from knowledge graph embeddings with explicit knowledge from graph convolution networks through a coarse-to-fine knowledge-aware attention mechanism. Ref. [48] tackled incorrect labeling and long-tail relations in DSRE by employing a relation-augmented attention network. This network mitigates mislabeling through sentence-to-relation attention and enhances long-tail performance by sharing collaborating relation features across hierarchical relations, which are supported by an auxiliary objective that improves bag-level representations.

In [35], the focus was on learning subtle intercategory differences rather than assuming correlations between head and tail relations via hierarchical trees. This approach significantly improved long-tail relation extraction. Furthermore, ref. [27] enhanced multi-instance learning by using hyperaugmentation strategies to differentiate between major and tail data. By constructing novel contrastive pairs and capturing mutual information, the approach improved the utilization of long-tail data in DSRE.

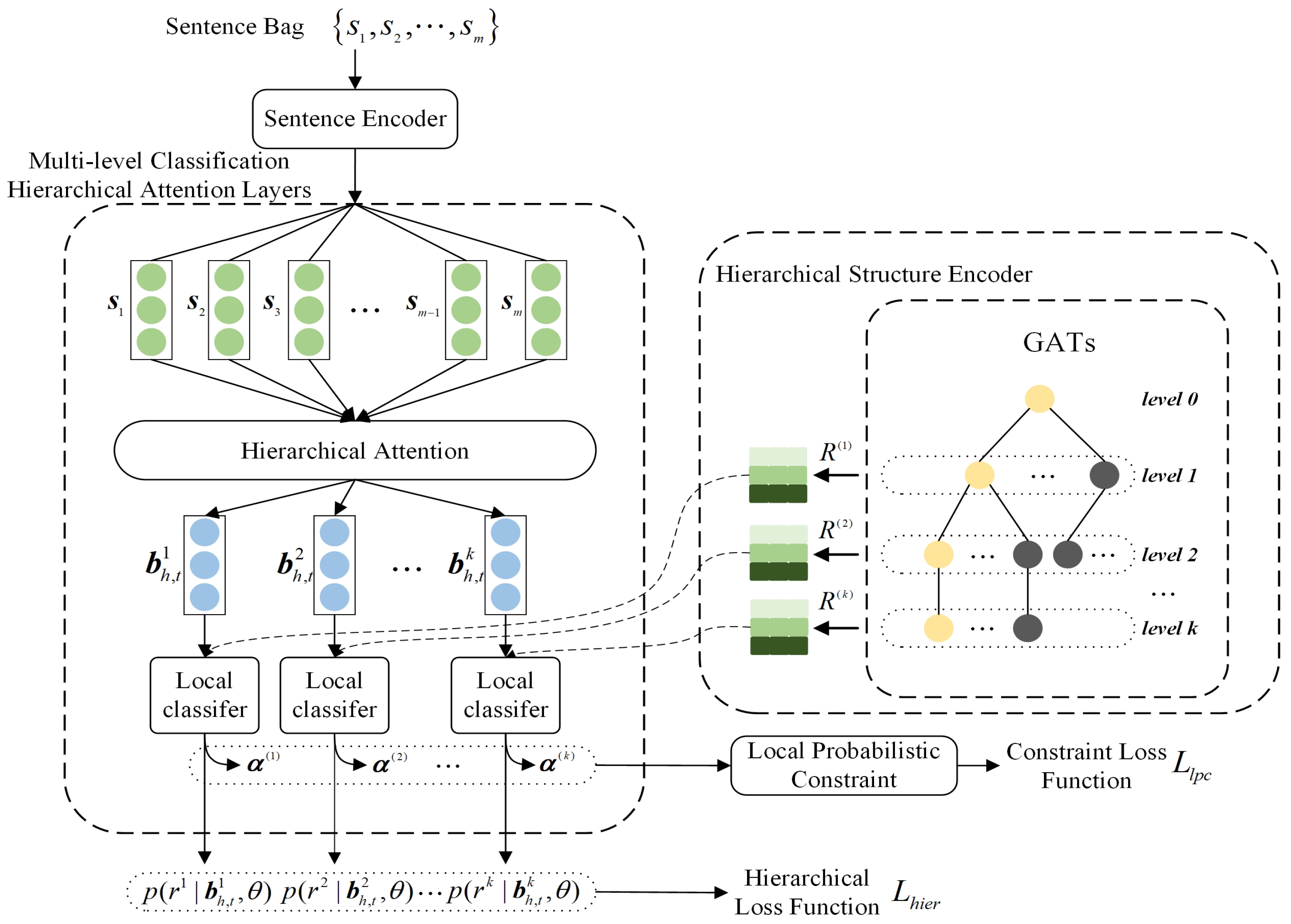
3. Methodology

This section provides a detailed description of the proposed Multi-level Classification Hierarchical Relation Extraction (MCHRE) model, as illustrated in Figure 2. The MCHRE model is composed of three primary components: the hierarchical structure encoder, the sentence encoder, and the multi-level classification hierarchical attention layer. The hierarchical structure encoder takes the relational hierarchy as input and employs Graph Attention Networks (GATs) to represent this structure. It extracts relational insights across labels from a global perspective and generates relation embeddings that reflect the overall hierarchy. The sentence encoder is responsible for extracting features from individual sentences, utilizing networks such as Convolutional Neural Networks (CNNs), Piecewise Convolutional Neural Networks (PCNNs), or Directed Acyclic Graph Attention Networks (DAGATs) for sentence-level feature extraction. The multi-level classification hierarchical attention layer processes the feature vectors of sentence bags, applying a selective attention mechanism to generate bag representations at each hierarchical level. It then performs independent relation classifications for each bag and ensures coherence across the multi-level classification outcomes by enforcing local probability constraints. The following subsections provide a detailed explanation of each component, including the multi-level classification hierarchical attention layer, the hierarchical structure encoder, and the local probability constraint.

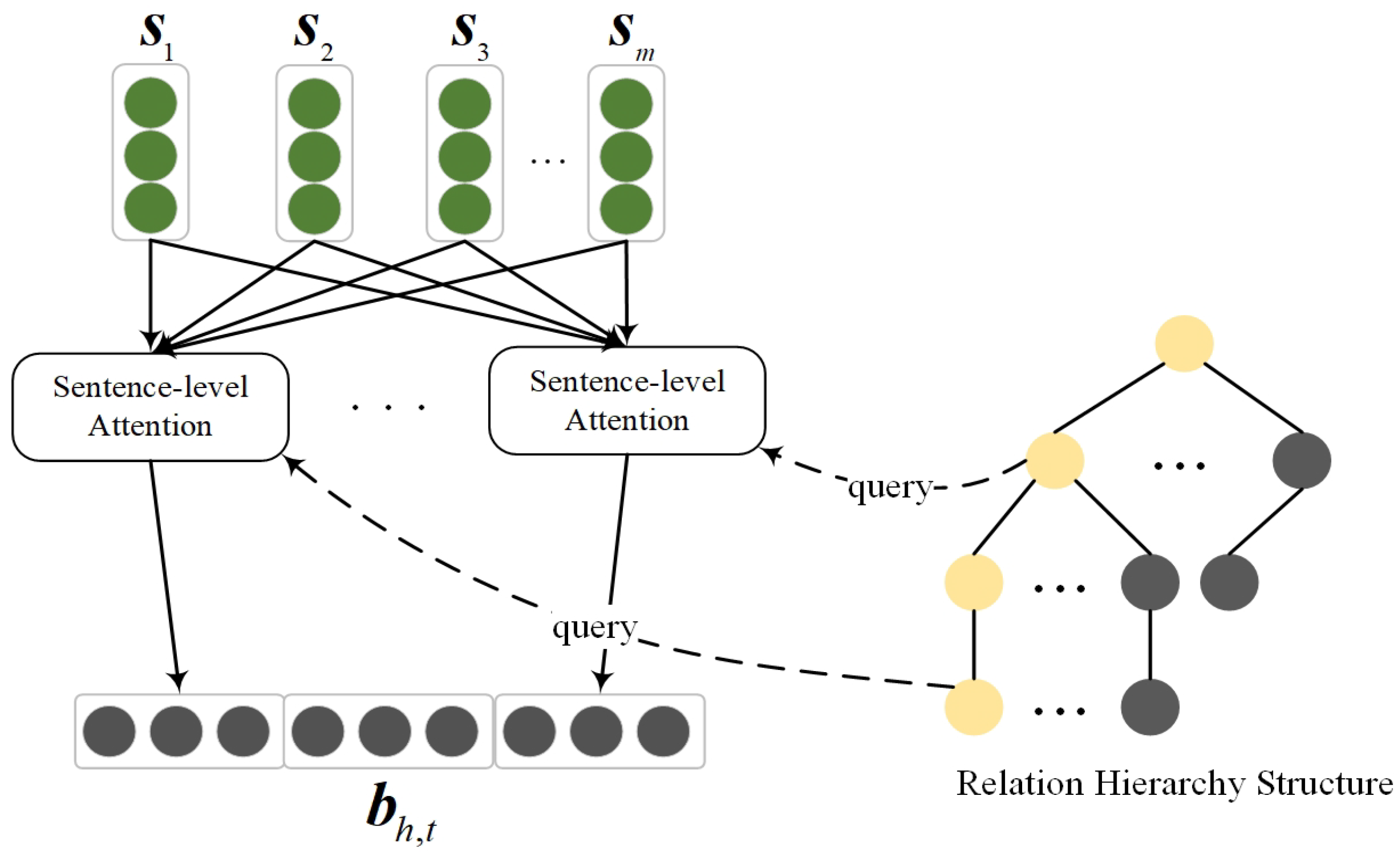
3.1. Hierarchical Structure Encoder

The hierarchical arrangement of relations imparts relational information to each relation category, allowing for the imposition of constraints on the feature embeddings of various relation nodes without relying on external data. The hierarchical structure encoder interprets the hierarchy as an undirected graph and uses GATs to represent it, generating relation embeddings that encapsulate the global structure.

The hierarchical structure encoder is implemented by stacking multiple GAT layers. Each layer receives the embeddings of all relation nodes within the hierarchy as input. Let there be $n_z$ nodes, with the input relation embeddings denoted as $\left\{{\mathit{h}}_1,{\mathit{h}}_2,\dots ,{\mathit{h}}_{n_z}\right\}$, where each embedding ${\mathit{h}}_i$ belongs to the space ${\mathbb{R}}^{d_g}$. The dimensionality of the relation embeddings, denoted as $d_g$, represents the size of the vector space in which each embedding ${\mathit{h}}_i$ resides. The initial GAT layer uses randomly initialized embeddings, where each embedding is drawn from a uniform distribution within the range $[-\sqrt{3/d_g},\sqrt{3/d_g}]$, where $d_g$ is the dimensionality of the embedding vector. Each subsequent layer takes the output of the previous layer as input. Specifically, in the GAT mechanism, the output embeddings from one layer are used as the input embeddings for the next layer, where each layer computes attention weights between nodes and aggregates information from neighboring nodes. This recursive process helps refine the node embeddings at each layer. The core mechanism of GATs is to compute attention weights between nodes. The update weight of node j relative to node i is given by

$${\alpha }_{i,j}={\mathrm{softmax}}_j\left(\mathrm{LeakyRelu}\left({\mathit{W}}_{\mathrm{att}}\left[\mathit{W}{\mathit{h}}_i;\mathit{W}{\mathit{h}}_j\right]+b_{\mathrm{att}}\right)\right),$$

(1)

where $\mathrm{LeakyRelu}(·)$ is a nonlinear activation function, used here to allow for small, nonzero gradients when the input is negative, which helps avoid dead neurons. The matrix $\mathit{W}\in {\mathbb{R}}^{d_g^{\prime }\times d_g}$ is a learnable weight parameter shared across all nodes, transforming node embeddings. The attention weight matrix, ${\mathit{W}}_{\mathrm{att}}\in {\mathbb{R}}^{2d_g^{\prime }\times d_g}$, is used to compute the attention scores between nodes i and j. The softmax operation ${\mathrm{softmax}}_j$ normalizes the attention scores for each node i, ensuring that the sum of the attention weights across all neighbors of node i equals 1. This normalization is crucial for the attention mechanism to focus more on the relevant neighbors.

After computing the attention weight matrix, the updated relation embedding for node i is obtained through a neighbor aggregation process:

$${\mathit{h}}_i^{\prime }=\mathrm{LeakyRelu}\left(\sum _{j\in N_i}{\alpha }_{i,j}{\mathit{W}}_{gat}{\mathit{h}}_j+{\mathit{b}}_{gat}\right)$$

(2)

where $N_i$ represents the set of adjacent nodes to node i, ${\mathit{W}}_{gat}\in {\mathbb{R}}^{d_g\times d_g}$ is a learnable weight matrix, ${\mathit{b}}_{gat}\in {\mathbb{R}}^{d_g}$ is the bias term, and $\mathrm{LeakyRelu}(·)$ is a nonlinear activation function.

The updated embeddings for all relation nodes, $\left\{{\mathit{h}}_1^{\prime },{\mathit{h}}_2^{\prime },\dots ,{\mathit{h}}_{n_z}^{\prime }\right\}$, are obtained in this manner. To stabilize this process and explore more subspaces, a multi-head attention mechanism is employed. The updated process for generating new relation embeddings is as follows:

$${\mathit{h}}_i^{\prime }=\sigma \left(\sum _{h=1}^H\sum _{j\in N_i}\left({\alpha }_{i,j}{\mathit{W}}_{gat}{\mathit{h}}_j+{\mathit{b}}_{gat}\right)\right)$$

(3)

where H represents the number of heads in the multi-head attention mechanism. After obtaining the updated embeddings for all relation nodes, the embeddings from each hierarchical level are stacked to form k level-specific embedding matrices $\left\{{\mathit{R}}^{\left(1\right)},{\mathit{R}}^{\left(2\right)},\dots ,{\mathit{R}}^{\left(k\right)}\right\}$, which are then passed into the multi-level classification hierarchical attention mechanism for further processing.

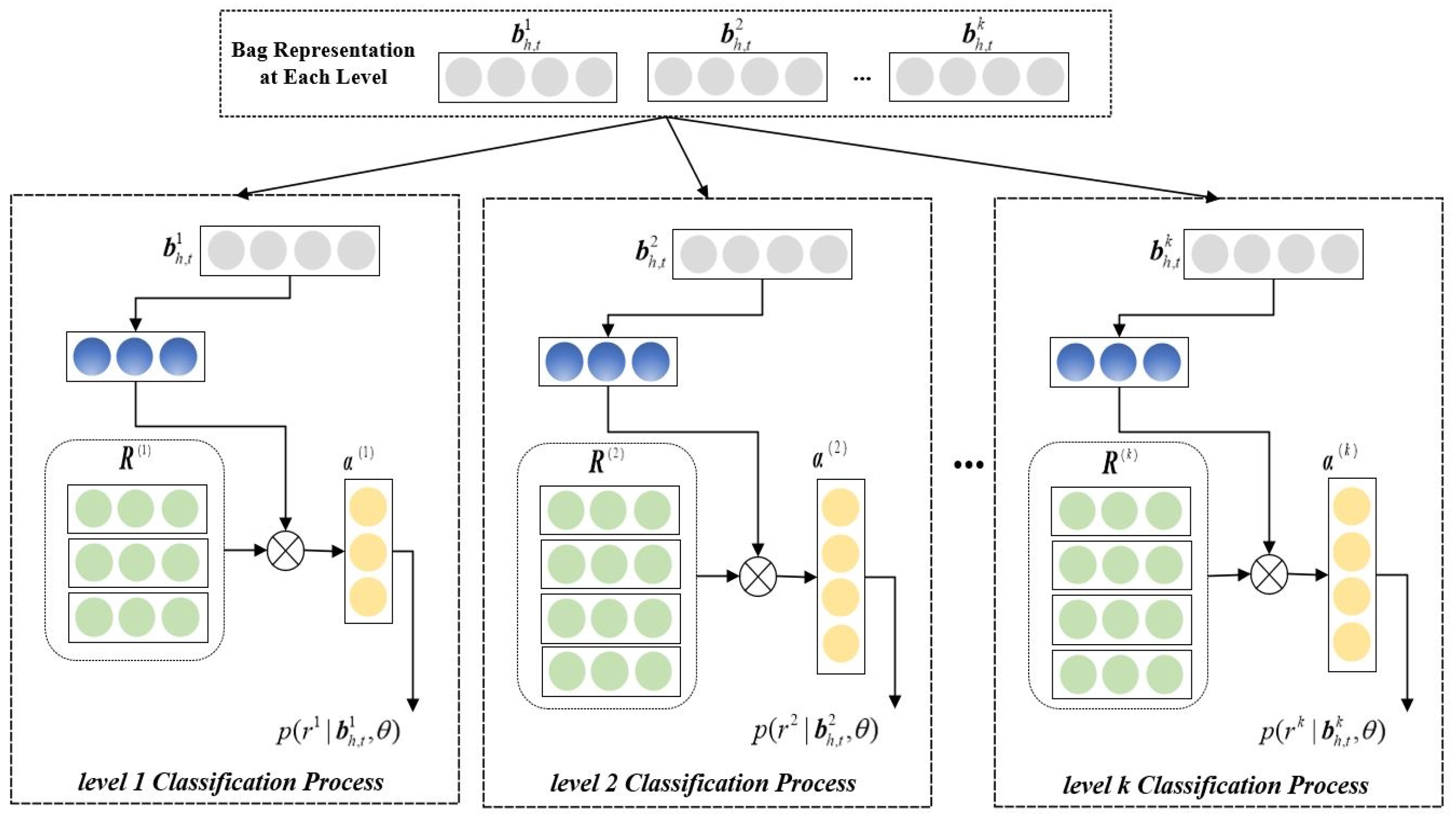
3.2. Multi-Level Classification Hierarchical Attention Layer

The traditional hierarchical attention mechanism utilizes bag representations from each level to classify relation types. However, it neglects the strong interdependence between these bag representations and their corresponding hierarchical relation sets. To more effectively harness both the entity bag features and the information within the hierarchical structure, we propose a multi-level classification framework that integrates seamlessly with the hierarchical attention mechanism, resulting in the multi-level classification hierarchical attention layer within the MCHRE. This layer follows the standard hierarchical attention procedures, deriving the feature vectors (bag representations) from a set of sentences related to a given relation, which are then used for classification tasks at various levels of the hierarchy.

Hierarchical attention is built on sentence-level selective attention, which aggregates weighted features of the sentences in the sentence bag. The bag representation is the weighted sum of these sentence features. The configuration of this attention mechanism is shown in Figure 3. For each level aligned with the true relation r, sentence-level selective attention is applied. Subsequently, the bag representations from each level are combined and fed into a softmax layer, which outputs the probability distribution over relation categories.

Sentence-level selective attention is a core technique used to address label noise, contributing to the robustness of relation extraction methods. The attention mechanism applies a query to establish a normalized weight distribution over the sentence bag, and the weighted sum of the sentence features is used to derive the bag representation, which is ultimately used to predict the relation label for the given entity pair.

Given a sentence bag $\mathit{B}=\left\{{\mathit{s}}_1,{\mathit{s}}_2,\dots ,{\mathit{s}}_n\right\}$, where ${\mathit{s}}_i$ is the feature vector of the i-th sentence, the attention weight for ${\mathit{s}}_i$ is computed as follows:

$${\alpha }_i={\displaystyle \frac{\exp \left(e_i\right)}{{\sum }_{j=1}^n\exp \left(e_j\right)}}$$

(4)

where $e_i$ represents the relevance score of the i-th sentence with respect to the true relation r. This score is computed via a dot product with the attention query vector:

$$e_i={\mathit{q}}_r^T{\mathit{s}}_i$$

(5)

where ${\mathit{q}}_r$ is the attention query vector for relation r.

The resulting attention weight distribution is used to compute the weighted sum of the sentence features, producing the following bag representation:

$${\mathit{b}}_{h,t}=\sum _{i=1}^n{\alpha }_i{\mathit{s}}_i$$

(6)

Equation (6) computes the bag representation by performing a weighted sum of the sentence features, where ${\alpha }_i$ represents the attention weight for the i-th sentence, and ${\mathit{s}}_i$ is the feature vector of the i-th sentence. This process captures the overall relation between the sentences in the bag.

The process of obtaining the bag representation using sentence-level attention can be simplified as follows:

$${\mathit{b}}_{h,t}=\mathrm{ATT}\left({\mathit{q}}_r,\left\{{\mathit{s}}_1,{\mathit{s}}_2,\dots ,{\mathit{s}}_n\right\}\right)$$

(7)

Equation (7) is a simplified version of Equation (6) that explicitly incorporates a query vector ${\mathit{q}}_r$ for the relation label r to calculate the bag representation. In this case, the attention mechanism is applied to a set of sentence features, with the query vector ${\mathit{q}}_r$ guiding the attention based on the relation label r. This highlights how the sentence-level attention is tailored to the specific relation label and how it influences the bag representation.

For a sentence bag with relation label r, which is located at the lowest level of the hierarchy, the relation nodes along the path from the leaf node to the root form a relation chain $\left(r^0,r^1,\dots ,r^k\right)$, where $r=r^k$ and $r^0$ represents a virtual root node. Multiple rounds of selective attention are performed using the relation nodes along this chain to derive bag representations at each hierarchical level. The bag representation at the i-th level is computed as

$${\mathit{b}}_{h,t}^i=\mathrm{ATT}\left({\mathit{q}}_r,\left\{{\mathit{s}}_1,{\mathit{s}}_2,\dots ,{\mathit{s}}_n\right\}\right)$$

(8)

where i refers to the hierarchical level of the relation node from the leaf to the root. Each level produces its own bag representation corresponding to different levels in the relation hierarchy. The set of bag representations across all hierarchical levels, $\left\{{\mathit{b}}_{h,t}^1,{\mathit{b}}_{h,t}^2,\dots ,{\mathit{b}}_{h,t}^k\right\}$, is thus obtained.

The multi-level classification framework processes these bag representations, applying localized classifiers at each level. The framework’s structure is shown in Figure 4.

Each classifier in the multi-level classification framework computes matching scores by leveraging the bag representation and the relation embedding matrix, which are then processed by a softmax function to obtain the probability distribution for relation classification. Specifically, for the j-th level, the relation embedding matrix ${\mathit{R}}^{\left(j\right)}\in {\mathbb{R}}^{N_j\times d_g}$ is used, where $N_j$ is the number of relation nodes at level j, and $d_g$ is the dimension of the relation embeddings. The bag representation ${\mathit{b}}_{h,t}^j$ is first input into a perceptron for dimensional transformation, yielding the following feature vector ${\mathit{s}}_j$ for classification:

$${\mathit{s}}_j=\mathrm{ReLU}\left({\mathit{W}}_l{\mathit{b}}_{h,t}^j+{\mathit{b}}_l\right)$$

(9)

where ${\mathit{W}}_l\in {\mathbb{R}}^{d_g\times d_c}$ is the weight matrix, $d_c$ is the dimensionality of the transformed feature vector, and ${\mathit{b}}_l$ is the bias term.

The relation embedding matrix at the j-th level is multiplied by the classification feature vector ${\mathit{s}}_j$, and a softmax normalization is applied to obtain the following classification probability distribution:

$${\mathit{\alpha }}^{\left(j\right)}=\mathrm{softmax}\left({\mathit{R}}^{\left(j\right)}{\mathit{s}}_j\right)$$

(10)

where j ranges from 1 to k, representing the levels in the hierarchical structure, with k being the total number of levels from leaf to root. Each j corresponds to a different level of the relation hierarchy, and $N_j$ is the number of relation nodes at level j. The “virtual root node” in our context refers to a conceptual starting point for traversing the hierarchical relation structure, not an actual node in the tree. We use this node as the root for the calculation of hierarchical relations. The “relation embedding matrix” ${\mathit{R}}^{\left(j\right)}$ is a matrix containing the relation embeddings at each hierarchical level. This matrix is used to calculate the classification probabilities at each level of the hierarchy.

The probability $p\left(r^j\mid {\mathit{b}}_{h,t}^j,\theta \right)$ for the relation r at the j-th level is retrieved as

$$p\left(r^j\mid {\mathit{b}}_{h,t}^j,\theta \right)={\mathit{\alpha }}_{r^j}^{\left(j\right)}$$

(11)

Here, r represents the same relation across the hierarchical levels, but $r^j$ is used to denote the representation of the relation at the j-th level. In this hierarchical structure, $r^j$ emphasizes the representation of the relation at a particular level of the hierarchy. Thus, r is consistent across levels, while $r^j$ is its corresponding representation at the j-th level.

3.2.1. Local Probability Constraint

The hierarchical structure of relations follows a pyramid-like organization, where classification outcomes at adjacent levels are highly interdependent. To effectively capture and leverage this dependency, we introduce a local probability constraint that ensures the consistency of classification probabilities across these levels. Specifically, this constraint aligns the classification probabilities at each level with those of the preceding level, enforcing coherence throughout the hierarchical structure.

After multi-level classification, each level generates a classification probability distribution, denoted as ${\mathit{\alpha }}^{\left(i\right)}$ for the i-th level. The expected probability distribution ${\mathit{\alpha }}_e^{(i-1)}$ for the previous level is constructed by summing the probability values of child nodes for each relation node. The probability distribution for the next level is used to construct ${\mathit{\alpha }}_e^{(i-1)}$, ensuring the alignment between adjacent levels. The Kullback–Leibler (KL) divergence is used to measure the discrepancy between the expected and actual distributions:

$$L_{lpc}={\displaystyle \frac{1}{\left|B\right|\times (k-1)}}\sum _{i=1}^{\left|B\right|}\sum _{l=1}^{k-1}\mathrm{KL}\left({\mathit{\alpha }}^{\left(l\right)},{\mathit{\alpha }}_e^{\left(l\right)}\right)$$

(12)

where B represents the set of sentence bags in the training batch, and $\mathrm{KL}(·)$ denotes the Kullback–Leibler divergence between two probability distributions.

3.2.2. Model Training

To train the model, we enhance the traditional cross-entropy loss function by incorporating following the hierarchical loss function:

$$L_{\mathrm{hier}}=-{\displaystyle \frac{1}{\left|B\right|}}\sum _{i=1}^{\left|B\right|}\sum _{j=1}^k\log p(r_i^j\mid {\mathit{b}}_{h_i,t_i}^j,\theta )$$

(13)

The final loss function combines this with the local probability constraint term as follows:

$$L=L_{\mathrm{hier}}+{\lambda }_{\mathrm{lpc}}{L}_{lpc}+{\lambda }_{\mathrm{reg}}{∥\theta ∥}^2$$

(14)

where ${\lambda }_{\mathrm{lpc}}\in [0,1]$ is the weighting coefficient for the local probability constraint term, ${\lambda }_{\mathrm{reg}}\in [0,1]$ is the weighting coefficient for the L2 regularization term, and ${∥\theta ∥}^2$ represents the L2 regularization term.

4. Experiments

4.1. Datasets

To evaluate the performance of the proposed model in distant supervision relation extraction (DSRE), we used the commonly employed New York Times (NYT) dataset. This dataset was created by aligning the New York Times corpus with the Freebase knowledge base, which contains structured knowledge about entities and their relationships. By aligning the unstructured news articles in the NYT corpus with the structured Freebase data, this allows us to automatically generate labeled data for training and testing DSRE models.

The NYT dataset consists of a large number of sentences and entity pairs, which are annotated with relation facts derived from Freebase. The data have been split into training and testing subsets, following the official data split, which is detailed in

Table 1. The NYT dataset splitting, showing the number of sentences, entity pairs, and relation facts in the training and testing subsets. #Sentences refers to the total number of sentences in each subset, #Entity Pairs denotes the number of unique entity pairs identified in the sentences, and #Relation Facts indicates the number of labeled relation facts associated with these entity pairs.

NYT	#Sentences	#Entity Pairs	#Relation Facts
Train	522,611	281,270	18,252
Test	172,448	96,678	1950

. The training set includes 522,611 sentences with 281,270 entity pairs and 18,252 relation facts, while the test set includes 172,448 sentences with 96,678 entity pairs and 1950 relation facts. This dataset is widely used in the DSRE literature and serves as a benchmark for evaluating the performance of relation extraction models.

The details of the data split are provided in Table 1, which shows the number of sentences, entity pairs, and relation facts in both the training and testing subsets. The NYT dataset is challenging due to its large scale and noisy data, making it an ideal testbed for evaluating the effectiveness of our proposed model in real-world settings.

4.2. Baselines

This section outlines the baseline models used for comparison in our experiments. These models are categorized into two types: denoising models and long-tail optimization models. It is important to note that all long-tail optimization models also incorporate denoising capabilities. The denoising models used in the experiments are described as follows:

(1)

PCNN_MIL [49]: A relation extraction model utilizing a piecewise convolutional neural network (PCNN) for sentence feature encoding, within a multi-instance learning (MIL) framework. PCNN_MIL selects the highest-probability sample from a bag for classification.

(2)

PCNN_ATT [50]: This model introduces sentence-level selective attention to address dataset noise, enhancing extraction accuracy.

(3)

RESIDE: [51]: This model integrates external information, such as entity type aliases, to enhance the discriminative capability of classification features.

(4)

SeG [52]: A model that uses a lightweight gating mechanism instead of attention to address noisy bags in the dataset.

The long-tail optimization models used for comparison are described as follows:

(1)

DPEN [53]: This model explores the relationship between relation labels and query entity types, proposing a dynamic parameter augmentation network that selects parameter sets based on different entity types.

(2)

PCNN_HATT [32]: This model introduces the hierarchical structure of relations and employs a multi-level attention mechanism to leverage this hierarchy.

(3)

PCNN_KATT [33]: An extension of PCNN_HATT, this model delves deeper into the relational information between relation labels, further enhancing the extraction of long-tail relations.

(4)

CoRA [48]: A model that uses a relation-augmented attention network as a replacement for selective attention mechanisms.

(5)

ToHRE [34]: This model treats the DSRE task as a multi-pass classification problem and introduces a top-down classification strategy to improve relation extraction.

(6)

GCEK [22]: This model uses global contextual sentence information to guide the denoising process, generating effective bag-level representations.

(7)

MLNRNN [1]: This model uses an iterative keyword semantic aggregator (IKSA) to filter out noisy words and highlights key features, leveraging multi-objective multi-instance learning (MOMIL) and cross-level contrastive learning (CCL) to mitigate the impact of incorrect labels.

(8)

MRConRE [24]: This model introduces a meta-relation pattern (MRP) to distinguish clean from noisy instances in each bag, transforming noisy instances into valuable data via relabeling while using contrastive learning for accurate sentence representations.

(9)

TAN [31]: This method captures dependencies among relational features by utilizing entity-type and local context information, incorporating a type affinity matrix for improved relation extraction accuracy.

(10)

MGCL [9]: This model mitigates noise by leveraging multi-granularity features to create contrastive learning samples and employing an asymmetrical contrastive classification strategy to gain deeper, multi-dimensional insights from text.

4.3. Implementation

In all experiments, the proposed MCHRE model used PCNN as the sentence encoder, with hyperparameters following the settings from [50]. Other hyperparameters were tuned using a grid search approach. For instance, the Relation Embedding Size $d_g$ was tested with values of 100, 150, and 200, and the Learning Rate $\alpha$ was varied between 0.01 and 0.1. The Batch Size B was tested in the range of 128 to 256 to find the best configuration.

The word2vec model was used to convert words into vectors, with an embedding dimension of 50. The convolution window size for the PCNN sentence encoder was set to 3, which controls the size of the local context window considered during sentence encoding. The positional feature dimension (representing relative distances between words) was set to 5, allowing the model to capture relative distances between words within the sentence.

The hidden layer size of the PCNN was set to 230, determining the size of the feature representation learned for each sentence. The dimensionality of the relation embeddings output by the hierarchical structure encoder was set to 150, which defines the size of the relation-specific representation learned by the model. The optimal coefficient for the local probability constraint term was set to 0.6, which helps maintain consistency between the predicted probabilities of adjacent hierarchical levels during the classification process.

To prevent overfitting, a dropout strategy with a rate of 0.5 was applied to the hidden layers of the PCNN encoder. This technique randomly disables a portion of the network’s units during training, enhancing generalization. The training batch size was set to 160, which determines the number of training examples processed before the model’s parameters are updated. The total number of iterations was set to 100, representing the number of complete passes through the training dataset. The SGD optimizer was used with a learning rate of 0.1, controlling the step size during the optimization process. Hyperparameters for all baseline models were set according to the configurations provided in their respective original papers (

Table 2. Hyperparameter settings.

Hyperparameters	Value
Window Size l	3
Relation Embedding Size $d_g$	150
Sentence Embedding Size $d_c$	230
Word Embedding Size $d_w$	50
Position Embedding Size $d_p$	5
LPC coefficient $\lambda$	0.6
Batch Size B	160
Epoch Size	100
Learning Rate $\alpha$	0.1
Dropout Probability p	0.5

).

4.4. Evaluation Metrics

The performance of the proposed MCHRE model in DSRE was evaluated using several metrics: Precision–Recall (PR) curve, Top-N Precision (P@N), Area Under Curve (AUC), and macro-averaged Hits@K. These metrics were selected to capture both the general and long-tail relation extraction performance. A brief description of these metrics is provided below:

(1)

PR Curve: This plot shows the tradeoff between precision and recall at various thresholds, with recall on the x axis and precision on the y axis. A model that has its PR curve entirely enclosed by another model’s PR curve outperforms the latter.

(2)

P@N: This metric calculates precision by selecting the top N samples with the highest predicted probabilities from the prediction results.

(3)

AUC: The area under the PR curve. A higher AUC indicates better model performance.

(4)

Hits@K: This metric measures the accuracy of predictions by relaxing the condition for a correct prediction. For each prediction, if the true class appears within the top-K predicted classes, the prediction is considered correct.

4.5. Results Analysis

In this section, we present the results of our experiments to evaluate the proposed MCHRE model. The following subsections detail the different experimental aspects:

• Denoising Evaluation: This subsection focuses on the model’s performance in mitigating the impact of label noise, comparing the MCHRE model with baseline methods and demonstrating its robustness in noisy data environments.
• Long-Tail Relation Evaluation: Here, we assess the MCHRE model’s capability to extract long-tail relations by using the Hits@K metric and comparing the model’s performance on long-tail relations against existing methods.
• Ablations: In this subsection, we perform an ablation study to evaluate the contribution of each component of the MCHRE model. By removing certain components, we investigate how each part of the model impacts overall performance.
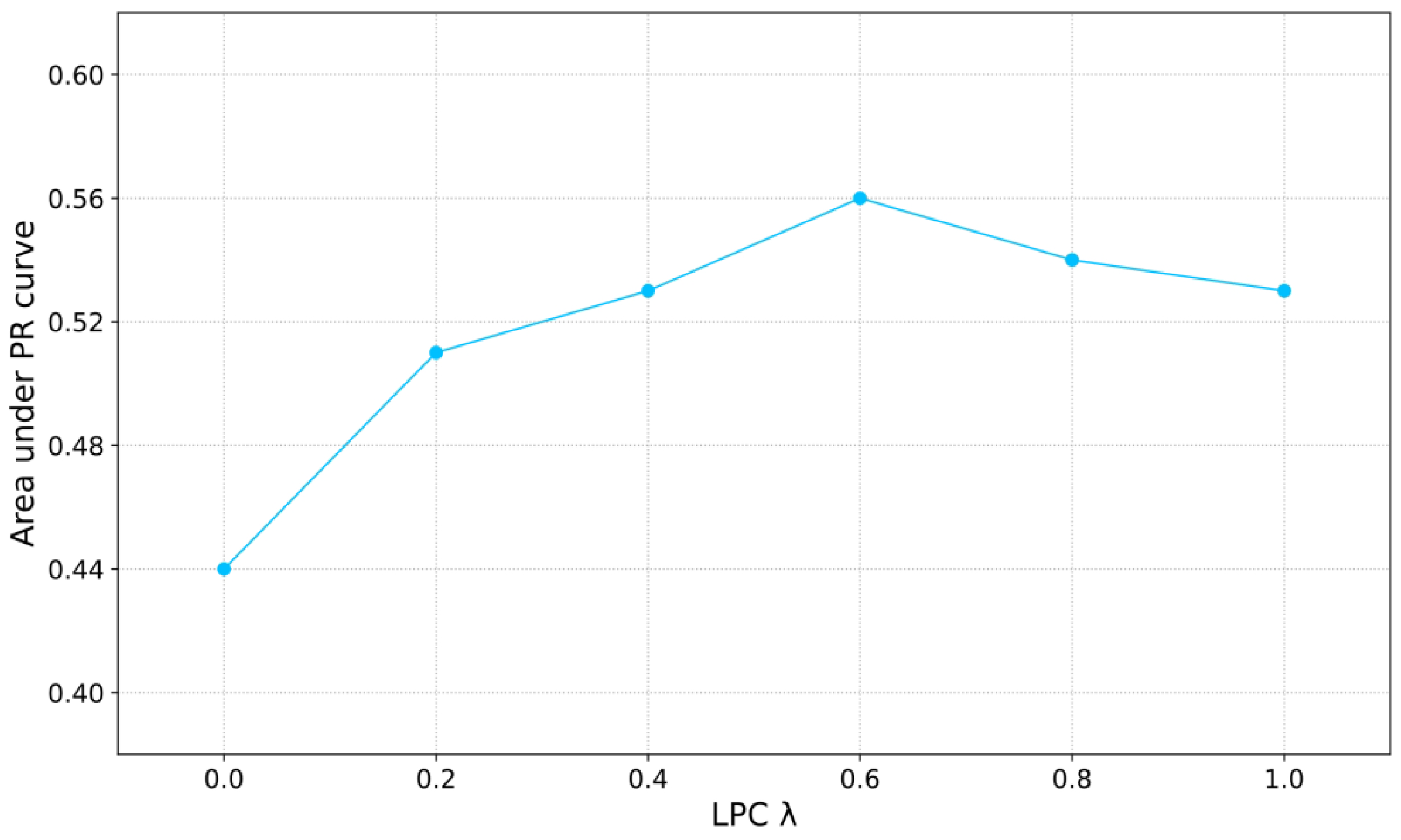
• Selection of The Local Probability Constraint Coefficient: We conduct experiments to explore the effect of varying the local probability constraint coefficient on the model’s performance. This evaluation helps to determine the optimal value for this parameter.

These experiments provide a comprehensive evaluation of the MCHRE model, confirming its effectiveness in various key areas, including noise resistance, long-tail extraction, component contributions, and optimization of the local probability constraint.

4.5.1. Denoising Evaluation

To quantitatively evaluate the relation extraction performance of the models,

Table 3. The results of each model under different evaluation metrics.

Models	Evaluation Metrics
	P@100	P@200	P@300	Mean	AUC
PCNN_MIL [49]	72.3	69.7	64.1	68.7	0.36
PCNN_ATT [50]	76.2	73.1	67.4	72.2	0.39
RESIDE [51]	84.0	78.5	75.6	79.4	0.41
SeG [52]	93.0	90.0	86.0	89.3	0.51
GCEK [22]	85.44	80.38	74.66	80.16	0.41
MLNRNN [1]	94.2	88.4	83.4	88.7	0.49
MRConRE [24]	86.1	80.6	80.1	82.3	0.38
TAN [31]	93.2	89.5	82.1	88.3	0.51
MGCL [54]	89.1	86.5	82.0	86.1	0.53
DPEN [53]	85.0	83.0	82.7	83.6	0.35
PCNN_HATT [32]	88.0	79.5	75.3	80.9	0.42
CoRA [48]	98.0	92.5	88.3	92.9	0.53
ToHRE [34]	91.5	82.9	79.6	84.7	0.44
MCHRE (Ours)	97.6	94.1	91.0	94.2	0.56

presents the evaluation results for all the models, excluding PCNN_KATT. The decision to exclude PCNN_KATT was based on the fact that PCNN_KATT and PCNN_ATT share substantial similarities. Since PCNN_KATT is an extended version of PCNN_ATT, including both would have resulted in redundant comparisons. By focusing on distinct baselines, we aim to provide a clearer analysis of the performance improvements brought by the proposed MCHRE model. The metrics include P@100, P@200, P@300, Mean (the average of P@100, P@200, and P@300), and AUC, with the highest value for each metric highlighted in bold. As seen in the table, the MCHRE model achieved near-optimal results across all metrics. Compared to the best baseline model, CoRA, MCHRE experienced only a 0.4% drop in P@100 but demonstrated improvements of 1.6%, 2.7%, 1.3%, and 0.03 in P@200, P@300, Mean, and AUC, respectively. Among all models, the P@N results for PCNN_MIL were the lowest. The introduction of selective attention in PCNN_ATT led to improvements of 3.9%, 3.4%, 3.3%, 3.5%, and 0.03 in the respective metrics.

The hierarchical structure of relations used in our model is based on the Freebase knowledge base. This structure organizes relations into a multi-level hierarchy, where high-level categories (such as “person” or “location”) are located at the top, and more specific relations (such as “place of birth” or “nationality”) are found at lower levels. This hierarchy guides the model in understanding the dependencies between different types of relations and ensures that the model can leverage these dependencies to improve the extraction of long-tail relations. The ${\alpha }_e$ values represent the expected probability distributions that align the classification probabilities at each hierarchical level with those at the preceding level. These values are derived by aggregating the classification probabilities of child nodes for each relation node and are used to enforce consistency in the hierarchical structure. These expected probabilities are critical in aligning the model’s outputs and ensuring coherence across the multi-level classification framework.

Due to space constraints, a more detailed analysis of the experimental results is provided for a subset of representative methods:

(1)

PCNN_ATT: By incorporating sentence-level selective attention into PCNN_MIL, PCNN_ATT showed significant improvements in relation extraction performance. This highlights the effectiveness of the attention mechanism’s dynamic selection ability in mitigating accuracy issues caused by noisy data. Furthermore, the minimal computational cost of selective attention makes it a valuable component in remote supervision relation extraction models.

(2)

RESIDE: RESIDE optimized the sentence encoder and demonstrated improvements across all metrics compared to PCNN_ATT. Additionally, it incorporated external information, further enhancing the model’s ability to resist noise interference. This indicates that both enhancing the sentence encoder and integrating external data are effective strategies for improving DSRE performance.

(3)

PCNN_HATT: By introducing relational hierarchy and employing a hierarchical attention mechanism to leverage semantic dependencies between relation labels, PCNN_HATT achieved significant improvements over PCNN_ATT. This suggests that hierarchical structure information is effective for filtering out noisy data.

(4)

ToHRE and MCHRE: Both models built upon PCNN_HATT by more effectively utilizing available information. However, MCHRE outperformed ToHRE in terms of P@N and AUC, indicating that MCHRE leverages multiple types of information more efficiently than ToHRE.

(5)

Other Methods: Although models like GCEK, MLNRNN, MRConRE, TAN, and MGCL showed some performance improvements, none surpassed the performance of MCHRE, highlighting the crucial role of hierarchical attention and local probability constraints in DSRE.

In summary, the MCHRE model demonstrated superior performance in resisting noise interference. The effectiveness of the MCHRE model can be attributed to two key factors: (1) Hierarchical Attention: The integration of hierarchical attention and multi-level classification enhances the utilization of both sentence bag features and hierarchical structure information. (2) Local Probability Constraint: The local probability constraint fully accounts for the strong dependencies between adjacent hierarchical classifications, resulting in a more robust model.

4.5.2. Long-Tail Relation Evaluation

In this section, we used the Hits@K (macro) metric to evaluate the performance of each model in extracting long-tail relations. Hits@K relaxes the correctness criterion by considering a prediction correct if the true label appears within the top-K highest-probability predicted labels. We evaluated the models for K values of 10, 15, and 20, which are typical for long-tail relations.

The term “(macro)” refers to the macro-averaging technique, where the model’s performance is evaluated across all relation categories (regardless of their frequency), ensuring that each relation, including long-tail relations, is treated equally. This provides a balanced evaluation of the model’s ability to extract both frequent and rare relations.

Macro-averaging was applied by computing the Hits@K metric for each relation category independently and then averaging these results to obtain a single performance score. This method gives equal weight to the model’s performance on each relation, regardless of its frequency, ensuring a fair assessment of the model’s ability to handle long-tail relations.

Relations with fewer than 100 or 200 samples in the training set were classified as long-tail relations. We then filtered the corresponding test samples to create two subsets: the “<100” and “<200” test sets. The evaluation results for MCHRE and the baseline models on these long-tail relations are shown in

Table 4. Hits@K accuracy of MCHRE and baseline models.

Testing Subset Conditions	<100			<200
Hits@K(macro)	10	15	20	10	15	20
PCNN_ATT [50]	<5.0	7.4	40.7	17.2	24.2	51.5
PCNN_HATT [32]	29.6	51.9	61.1	41.4	60.6	68.2
PCNN_KATT [33]	35.3	62.4	65.1	43.2	61.3	69.2
DPEN [53]	57.6	62.1	66.7	64.1	68.0	71.8
CoRA [48]	66.6	72.0	87.0	72.7	77.3	89.4
ToHRE [34]	62.9	75.9	81.4	69.7	80.3	84.8
MGCL [54]	38.6	61.9	65.5	50.9	67.2	72.2
MCHRE (Ours)	68.3	79.0	88.5	73.9	82.5	90.8

.

From the results, we draw the following conclusions:

(1)

PCNN_ATT: This model performed the weakest on long-tail relation extraction. The Hits@10 accuracy on the <100 test set is below 5%, demonstrating the severity of the long-tail issue in DSRE datasets.

(2)

Hierarchical Optimization: Models such as PCNN_HATT, PCNN_KATT, CoRA, ToHRE, and MCHRE showed substantial improvements in long-tail relation extraction. The effectiveness of leveraging relational hierarchy for mitigating data scarcity is evident, with deeper hierarchical structure utilization further enhancing long-tail extraction.

(3)

MCHRE vs. ToHRE: MCHRE outperformed ToHRE across all evaluation metrics, achieving improvements of 5.4%, 3.1%, 7.1%, 4.2%, 2.2%, and 6%. This demonstrates that MCHRE’s multi-level classification framework is more effective in addressing long-tail data.

(4)

State-of-the-Art Results: MCHRE achieved the highest accuracy across all six evaluation metrics for both test subsets and all K values. The model demonstrated consistent improvements over baseline methods, making it the leading solution for long-tail relation extraction.

In conclusion, the long-tail issue remains a significant challenge in DSRE. Models optimized for hierarchical structures significantly enhance long-tail extraction performance, with the MCHRE model emerging as the state-of-the-art solution due to its effective use of hierarchical structure information and multi-level classification.

4.5.3. Ablations

To assess the contribution of each component of the MCHRE model, we performed an ablation study, focusing on the hierarchical structure encoder and the multi-level classification hierarchical attention layer.

Table 5. Ablation results of MCHRE components. † represents the removal of the hierarchical structure encoder, ‡ represents the removal of the multi-level classification hierarchical attention Layer, and so on.

Models	P@100	P@200	P@300	Mean	AUC
MCHRE	97.6	94.1	91.0	94.2	0.56
†	94.3	87.5	82.1	88.0	0.49
‡	90.3	82.7	77.9	83.6	0.43
† and ‡	88.0	79.5	75.3	80.9	0.42

presents the extraction performance results under different ablation combinations.

The ablation results show that removing the hierarchical structure encoder resulted in a 6.2% decrease in Mean and a 0.07 drop in AUC. Removing the multi-level classification hierarchical attention layer led to a 10.6% decrease in Mean and a 0.13 reduction in AUC. These findings indicate that both components are critical to the model’s performance, with the multi-level classification hierarchical attention layer having a more significant impact.

4.5.4. Selection of the Local Probability Constraint Coefficient

To evaluate the impact of the local probability constraint, we experimented with different coefficients for the local probability constraint term. The results, shown in Figure 5, demonstrate that removing the constraint ($\lambda =0$) led to a significant drop in AUC. As $\lambda$ increased, performance improved, reaching a peak at $\lambda =0.6$. Beyond this point, the performance began to decline slightly, suggesting that while the local probability constraint is beneficial, overly emphasizing it can limit the flexibility of classification levels. Additionally, the expected probability distribution, denoted as ${\alpha }_e$, was computed dynamically during the training process. It is based on the relation labels at the previous hierarchical level, ensuring that the classification probabilities between adjacent levels are consistent.

5. Conclusions

In this paper, we propose the Multi-level Classification Hierarchical Relation Extraction (MCHRE) model, which is a novel approach for distant supervision relation extraction (DSRE) based on multi-level classification hierarchical attention. The MCHRE model leverages Graph Attention Networks (GATs) to model the hierarchical structure of relations, capturing the semantic dependencies between relation labels. This results in the generation of relation embeddings that reflect the global hierarchical framework. The integration of a multi-level classification framework with hierarchical attention allows for improved utilization of both sentence-level features and hierarchical information, enabling multi-granularity relation classification. Furthermore, the introduction of local probability constraints ensures coherence across the multi-level classification process.

We evaluated MCHRE on the New York Times (NYT) dataset, comparing it against several state-of-the-art denoising models and long-tail optimized models. The experimental results demonstrate that (1) MCHRE outperformed all baseline models across various evaluation metrics, achieving superior performance in relation extraction and showing strong resilience to noise interference; (2) MCHRE excelled in long-tail relation extraction, significantly improving the extraction of underrepresented relations and effectively addressing the data long-tail problem in DSRE.

In summary, the MCHRE model successfully addresses the key challenges of label noise and data long-tail distribution in DSRE, providing a robust and effective solution for relation extraction tasks.