Abstract
The rapid development of vehicular networks has facilitated the extensive acquisition of vehicle trajectory data, which serve as a crucial cornerstone for a variety of intelligent transportation system (ITS) applications, such as traffic flow management and urban mobility optimization. Trajectory similarity computation has become an essential tool for analyzing and understanding vehicle movements, making it indispensable for these applications. Nonetheless, most existing methods neglect the temporal dimension in trajectory analysis, limiting their effectiveness. To address this limitation, we integrate the temporal dimension into trajectory similarity evaluations and present a novel contrastive learning framework, termed Spatio-Temporal Trajectory Similarity with Contrastive Learning, aimed at training effective representations for spatio-temporal trajectory similarity. The STT-CL framework introduces the innovative concept of spatio-temporal grids and leverages two advanced grid embedding techniques to capture the coarse-grained features of spatio-temporal trajectory points. Moreover, we design a Spatio-Temporal Trajectory Cross-Fusion Encoder (STT-CFE) that seamlessly integrates coarse-grained and fine-grained features. Experiments on two large-scale real-world datasets demonstrate that STT-CL surpasses existing methods, underscoring its potential in trajectory-driven ITS applications.
1. Introduction
The widespread use of GPS-enabled devices and interconnected vehicular networks has revolutionized the ability to collect and analyze large volumes of vehicle trajectory data. These data form the backbone of various applications in intelligent transportation systems (ITSs), such as improving traffic flow, reducing congestion, and optimizing urban mobility [1,2,3]. By analyzing how vehicles move over time and space, ITS technologies aim to make transportation more efficient and improve the overall travel experience in modern cities [4,5,6,7].
A critical aspect of this analysis is understanding the similarities between vehicle trajectories, which plays a fundamental role in many ITS functions [8,9]. For example, in dynamic route optimization, trajectory similarity computation enables real-time identification of alternative paths by comparing current vehicle movements with historical traffic patterns, ensuring smoother and faster travel during congestion. Similarly, in traffic anomaly detection, analyzing trajectory similarities can help identify irregular behaviors, such as sudden stops or deviations, which may indicate accidents or hazardous conditions. By accurately measuring these similarities, transportation systems can uncover patterns, predict future movements, and respond to disturbances more effectively. Despite its importance, developing reliable and efficient methods for comparing trajectories remains a significant challenge and an active area of research within ITS.
For trajectory similarity computation, various conventional heuristic similarity methods have been proposed, such as DTW [10], EDR [11], Hausdorff [12], and Fréchet [13]. These methods rely on point-wise matching computation, thus resulting in high computational costs. Learning-based similarity methods [14] utilize deep neural networks to represent trajectories as d-dimensional vectors. The similarity between two trajectories is expressed directly as the Euclidean distance between the representation vectors. However, most of these methods only consider trajectories as sequences of spatial points, overlooking the significance of temporal information in real-world trajectories.
Why spatio-temporal similarity? For two trajectories with similar spatial structures, it is reasonable to expect them to be very close when using spatial similarity measures. However, in many real-world scenarios, the time at which these two trajectories occur can significantly influence their degree of similarity. For example, in urban settings, two trajectories with similar starting and ending points, as shown in Figure 1, but occurring at different times, may correspond to going to work and returning home, respectively. Given the varying traffic flow at different time periods of the day, these trajectories should be considered to have more significant dissimilarity than suggested by spatial similarity methods alone.
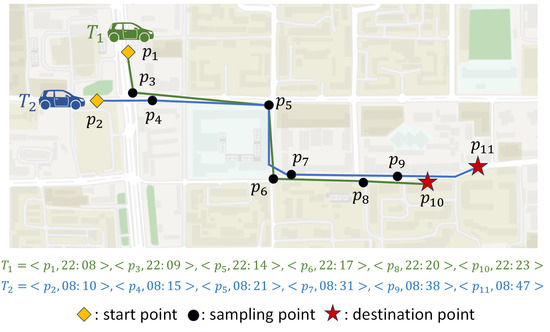
Figure 1.
Illustration of spatio-temporal similarity. The first vehicle traveled the green trajectory at a higher speed at night, while the second vehicle traveled the blue trajectory at a slower speed in the morning. Both have similar spatial similarity but do not have similar spatio-temporal similarity.
To effectively represent the influence of time on different trajectories, we introduce temporal information into trajectory similarity measurement. Moreover, considering the temporal information of the trajectories, we can analyze the movement patterns of objects from more aspects. This contributes to performance improvements in various trajectory-related tasks. Therefore, we use spatio-temporal rather than spatial similarity to measure different trajectories.
Why contrastive learning? Although the acquisition of trajectory data has become much easier these days, how to accurately annotate it remains a challenging problem. To avoid the problem of lacking precise temporal and spatial annotation for trajectories, we employ a self-supervised learning approach. Most self-supervised learning models adopt an encoder–decoder structure. The encoder encodes input samples into representations and the decoder reconstructs these representations back to their original forms. However, recent research [15,16] suggests that reconstruction is unnecessary when computing the similarity between samples. Since the encoder in an encoder–decoder structure aims to learn a representation suitable for reconstructing rather than evaluating similarity, this model is obviously not suitable for our specific task.
Contrastive learning exhibits remarkable generalizability and robustness. It has been widely applied in various fields due to its exceptional performance [17,18]. Contrastive learning is typically used to learn the similarity between data, so we use it to address the issue of trajectory similarity evaluation in self-supervised learning.
We introduce STT-CL, an innovative framework for evaluating Spatio-Temporal Trajectory similarity using Contrastive Learning. This approach considers views of the same trajectory as positive samples, while treating views of different trajectories as negative samples. By utilizing spatio-temporal grids to extract rich features of trajectories at different scales, our model trains a Spatio-Temporal Trajectory Cross-Fusion Encoder to generate representations by learning the similarity between different trajectories.
Our contributions can be summarized as follows.
- We propose STT-CL, a contrastive learning model for spatio-temporal trajectory computation. To the best of our knowledge, it is the first work to introduce the contrastive learning method in the study of spatio-temporal trajectory similarity.
- We innovatively introduce the concept of spatio-temporal grids and present two methods of spatio-temporal grid embedding to capture coarse-grained features.
- We design a spatio-temporal trajectory backbone encoder, namely, Spatio-Temporal Trajectory Cross-Fusion Encoder, which focuses on the correlations between coarse-grained features and fine-grained features of trajectories and fuses them into representation. It exhibits better performance for low-quality trajectories compared with previous encoders.
- We conduct extensive experiments on two real-world datasets. The experimental results illustrate that STT-CL surpasses existing baseline models in terms of performance, particularly in terms of robustness when dealing with low-quality trajectories.
2. Related Work
2.1. Spatial Trajectory Similarity
Spatial trajectory similarity methods can be divided into two types: heuristic methods and learning-based methods. The former typically involve point-wise matching between two trajectories and regard the distance between matched points as a similarity metric. The latter embed trajectories into similarity representation vectors, and the distance between these vectors reflects the similarity between the represented trajectories. Depending on the specific embedding methods, they can be further categorized into supervised learning-based methods and self-supervised learning-based methods.
Heuristic methods are characterized by their reliance on point-wise comparisons between trajectories, where the similarity is determined based on the distances between matched points. For example, DTW (dynamic time warping) [10] matches all points in one trajectory with one or more consecutive points in another trajectory and calculates the Euclidean distance. EDR (edit distance on real sequence) [11] is based on the concept of edit distance, counting the number of edit operations required to make the point sequences identical. The Hausdorff distance [12] measures the maximum distance from a point in one trajectory to the nearest point in another trajectory, treating the trajectory points as sets. The Fréchet distance [13], similar to the Hausdorff distance, considers trajectories as ordered curves while calculating the distance. Due to the necessity of traversing all point pairs between trajectories, heuristic methods have a quadratic computational complexity.
Supervised learning-based methods aim to train a model to approximately learn a heuristic method, which is the ground-truth for trajectory similarity. For example, T3S [19] first introduced structural and spatial features for trajectory similarity, which can adaptively learn various heuristic methods by the proportion of the two features. Aries [20] employs a bidirectional LSTM and aggregates multiple methods to enhance the performance of trajectory similarity in the top-k query task. TSNE [21] proposed a graph embedding method on the k-nearest neighbor graph (k-NNG) to improve the efficiency and interpretability of the model.
Self-supervised learning-based methods also learn trajectory representations but without heuristic method annotations. They compare similar trajectories to capture the implicit corrections between trajectories. For example, t2vec [14] first adopts an RNN-based encoder–decoder model, which reduces the spatial proximity-aware loss between the original trajectories and the reconstructed ones to train the model. AdvTraj2Vec [22] employs a GAN (generative adversarial network) structure, which is also an encoder–decoder structure, and improves the robustness of trajectory similarity computation by harnessing the perturbation with GAN momentum.
2.2. Spatio-Temporal Trajectory Similarity
In recent years, some studies have gradually realized the importance of the time dimension for trajectory similarity and have been used to fuse temporal and spatial features. TS-join [23] introduces the temporal dimension into trajectory similarity, obtaining spatio-temporal similarity methods by separately combining spatial and temporal similarity methods at different scales. STS [24] represents each point in a trajectory as a result observed from a probability distribution to calculate the spatio-temporal overlap. However, these artificially designed heuristic methods still suffer from issues such as high time consumption and ineffectiveness. Some studies have attempted to use deep neural networks for spatio-temporal trajectory similarity computation. ST2Vec [25] proposes a temporal modeling model to capture temporal features and a co-attention fusion module to fuse temporal and spatial features. GTS+ [26] proposes a graph-based framework for spatio-temporal trajectory similarity, which encodes the embeddings of each POI (point of interest) by a GNN. However, both ST2Vec and GTS+ additionally introduce urban road network information for spatio-temporal trajectory similarity.
In other trajectory mining tasks, some methods have also recognized the importance of time. For instance, START [27] acknowledges the importance of spatio-temporal characteristics in trajectories, such as temporal regularities and travel semantics. It extracts both temporal and spatial features from the trajectories and employs a self-supervised approach to embed these representations.
2.3. Contrastive Learning for Trajectory Similarity
Contrastive learning [28] is a prominent self-supervised learning approach that focuses on learning meaningful representations by comparing data instances. The fundamental principle behind contrastive learning is to encourage the model to bring the representations of similar objects (referred to as positive pairs) closer together in the feature space, while simultaneously pushing apart the representations of dissimilar objects (negative pairs). This is achieved without the need for labeled data, as positive and negative pairs are constructed directly from the input dataset. By learning these relationships, contrastive learning facilitates the training of a representation generation model, typically realized through a backbone encoder, which can then be leveraged for a variety of downstream tasks. Notably, this technique has been successfully applied to spatial trajectory similarity analysis, with methods such as CL-TSim [15] and TrajCL [29] integrating contrastive learning principles to improve the representation of trajectory data for better similarity measurements and related applications. CL-TSim is the first method to introduce contrastive learning for spatial trajectory similarity; however, it employs a simple LSTM encoder, which limits its performance in capturing complex trajectory patterns. TrajCL, a more recent approach, improves upon this by utilizing a dual-feature encoder, which significantly enhances the quality of trajectory similarity computation. The dual-feature encoder in TrajCL served as an inspiration for the method presented in this paper, as it effectively captures richer representations of trajectory data. In addition, we use TrajCL as a baseline in our experiments to compare and validate the performance of our proposed model.
3. Preliminaries
In this section, we present fundamental concepts and formally define the problem essential to understanding the subsequent analysis.
Definition 1 (Spatio-Temporal Trajectory).
A spatio-temporal trajectory is a recorded path that depicts the movement of an object in geographical space over time. Formally, it is represented as an ordered sequence:
where denotes the trajectory length. Each sampling point comprises spatial coordinates and the corresponding timestamp. This parametrization establishes a continuous mapping between spatial displacement and temporal progression.
Conventional learning-based methods for spatial trajectory similarity analysis predominantly employ discrete spatial decomposition with equally sized, non-overlapping, and adjacent grids. To capture temporal dynamics while preserving spatial granularity, we propose a dimensional extension of this paradigm into the spatio-temporal domain.
Definition 2 (Spatio-Temporal Grid).
This is created by partitioning the continuous space–time domain into discrete units using fixed spatial intervals and temporal durations. Trajectory points within the same grid unit occupy identical spatial regions and temporal intervals.
Problem 1.
Given a set of spatio-temporal trajectories , learn an encoder function
such that for any two trajectories :
where denotes the similarity between two trajectories.
4. The STT-CL Approach
4.1. Framework Overview
Figure 2 shows the framework overview of STT-CL. It follows the classical contrastive learning framework, similar to MOCO [28] and BYOL [30], both of which adopt a dual-branch structure.
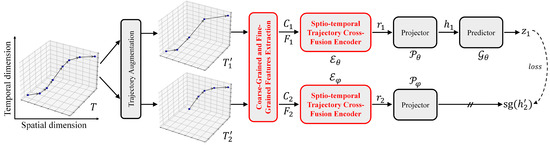
Figure 2.
Framework overview of STT-CL (the red modules are our key contributions).
Given a spatio-temporal trajectory T, first obtain two different views ( and ) of T through the trajectory augmentation module. We employ trajectory down-sampling and trajectory distortion as augmentation methods. Furthermore, we adopt the latest trajectory truncation and simplification [29].
Then, the coarse-grained and fine-grained feature extraction modules produce point-wise features using the generated views . Instead of structural features and spatial features [19], we distinguish point-wise features as coarse-grained features and fine-grained features based on their level of detail (more details are given in Section 4.3). These feature vectors form the coarse-grained feature matrix C and the fine-grained feature matrix F, respectively.
Next, the Spatio-Temporal Trajectory Cross-Fusion Encoder (STT-CFE) takes in C and F, then outputs the representation r for . The STT-CFE we designed is adapted from DualSTB [29], which fuses coarse-grained features and fine-grained features into representations of trajectories (more details are given in Section 4.4).
Finally, we train the STT-CFE through contrastive learning, which maximizes the similarity between and while maintaining dissimilarity between the views of different trajectories (more details are given in Section 4.5).
4.2. Trajectory Augmentation
Trajectory distortion. Trajectory distortion introduces minor spatial perturbations to each point in a trajectory, simulating the inherent noise in GPS data collection. Given a trajectory , the distorted trajectory is generated as
where and are random offsets sampled from a bounded Gaussian distribution.
Trajectory down-sampling. Trajectory down-sampling randomly removes a subset of points from the trajectory, simulating scenarios with missing data or varying sampling rates. For a trajectory T, the down-sampling trajectory is defined as
where is a strictly increasing sequence of indices, and . The masking ratio determines the proportion of points removed.
Trajectory truncation. Trajectory truncation generates partial trajectories by removing a prefix or suffix, simulating scenarios where only a portion of the trajectory is available. Given a trajectory T, the truncated trajectory is
where i is a random starting index, and controls the proportion of points retained.
Trajectory simplification. Trajectory simplification reduces the number of points while preserving the overall shape and critical features of the trajectory. We adopt the Douglas–Peucker [29,31] simplification algorithm, which identifies and retains key points that contribute significantly to the structure of the trajectory. The simplified trajectory is defined as
4.3. Coarse-Grained and Fine-Grained Feature Extraction
In previous studies, point-wise features of a trajectory have been commonly categorized into structural and spatial attributes, focusing primarily on the spatial dimension of trajectory analysis. However, the true value of the trajectory data is not limited to the spatial aspect. The introduction of the temporal dimension offers additional insight into individual mobility patterns. In light of this, our research further refines point-wise features into coarse-grained and fine-grained features, enabling a more detailed and comprehensive analysis of spatio-temporal trajectories.
In order to better understand and characterize the complexities of spatio-temporal trajectories, we design two specific feature extraction modules, called Coarse-Grained Feature Extraction (CFE) and Fine-Grained Feature Extraction (FFE), which are capable of, respectively, extracting coarse-grained and fine-grained features.
4.3.1. Coarse-Grained Feature Extraction
The CFE module aims to capture coarse-grained features, emphasizing the overall movement trends and patterns of a trajectory. The CFE module partitions trajectory points into spatio-temporal grids and trains the grids embeddings to represent the points’ coarse-grained features. These embeddings collectively form the coarse-grained feature matrix C of the trajectory T, where , l denotes the trajectory length, and represents the dimensionality of the embedding of the grid. The key of the CFE module is the methodology of training spatio-temporal grid embeddings. To address the crucial issue, we introduce two improved training methods.
Grid embeddings as nodes. Intuitively, we consider the spatio-temporal grids as nodes within a graph framework, with their temporal and spatial adjacency relations representing the edges that connect these nodes. Using the node2vec algorithm, our aim is to train the embedding representations of these grid nodes. The optimization principle of node2vec is to maximize the probability of observing a node’s neighborhood by strategically sampling walks from the graph, thereby learning representations that encapsulate the structural nuances of the graph.
However, in previous studies [25,29], graphs have been constructed with edges of equal weight based solely on spatio-temporal adjacency between grids. Such an approach fails to accurately capture the actual topological structure of the spatio-temporal grid graph. To better reflect the genuine topological structure of the spatio-temporal grid graph, we propose a novel method for setting edge weights, which incorporates historical trajectory data. The formula for our designed weight calculation is as follows:
where denotes the weight of the edge from grid u to grid v, is a tuning factor, represents the hit rate at which grid v serves as an -step successor of grid u in historical trajectories, and is the set of neighboring grids of v. Modulating the parameter allows for precise control over the impact of historical trajectory data on the discerned strength of connections between spatio-temporal grids. Additionally, the parameter is defined as the temporal step used to determine the number of time intervals over which the hit rate is computed. This parameter plays a crucial role in defining the temporal depth of the historical trajectories engaged during the hit rate computation. A larger can discover more complex relationships between spatio-temporal grids; however, it also incurs a greater computational time cost.
Grid embeddings as words. In the domain of trajectory analysis, some studies [14,15] have conceptualized spatio-temporal grids as words, with the sequence of grids traversed by trajectory points in a single trajectory forming a “sentence”. A corpus is constituted by a vast collection of such trajectory data, providing data support for training grids embeddings with algorithms such as Skip-gram and other word2vec models. However, when employing the Skip-gram model for embedding training, it is often found that the model performs suboptimally with newly emerging or rare words (grids). To address this issue, we adopt a morpheme-based word formation approach in conjunction with the word2vec method in the FastText framework [32].
Initially, spatio-temporal grid words are decomposed into three morphemic parts, representing the divisions of longitude, latitude, and time sequence numbers, such as “X10Y5T6”. Subsequently, we employ the FastText method for word embedding training on the constructed corpus. The optimization goal of FastText is similar to that of the conventional word2vec method, aiming to maximize the logarithmic probability of the context given a center word. However, FastText extends word embeddings to character-level n-grams. The optimization goal of FastText can be expressed as
where T denotes the total number of words (grids) in the training corpus, represents the set of context words surrounding the center word , refers to a word within the context, and encapsulates the parameters of the module. Vector embeddings and correspond to the context and center words, respectively. V is the vocabulary (set of unique grids).
In this manner, the module is able to leverage the internal structural information of spatio-temporal grid words, enhancing its capability to recognize and process new or rare words.
4.3.2. Fine-Grained Feature Extraction
The FFE module manually enhances the features that reflect both the temporal cyclical patterns and physical characteristics of the trajectory points.
For a point , that is, , the enhanced fine-grained features can be represented as a tuple . Here, correspond to the longitude and latitude coordinates, denotes the timestamps, represents the radian value of the segments before and after the point, and finally indicates the average speed of the segments.
Upon enhancement by the FFE module, the spatio-temporal trajectory T is transformed, producing a fine-grained feature matrix F, where , and denotes the length of the fine-grained features.
4.4. Spatio-Temporal Trajectory Cross-Fusion Encoder
Figure 3 illustrates the architecture of our proposed Spatio-Temporal Trajectory Cross-Fusion Encoder (STT-CFE). The encoder consists of three components: the position encoding section, the Bi-Feature Interaction Module (BFIM) section, and the fusion section. These components will be detailed in the following sections.
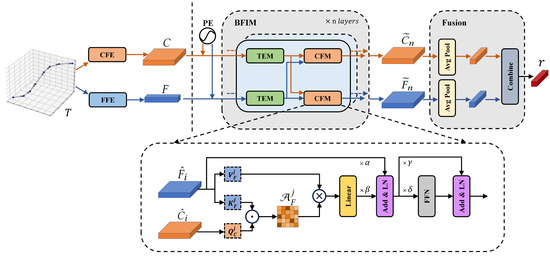
Figure 3.
The architecture of STT-CFE (located to the right of the dividing line).
4.4.1. Position Encoding Section
Just like many modules that employ attention mechanisms for processing sequential data, our encoder also relies on positional encoding to endow features with relative positional information.
We employ the sine and cosine functions [33] for position encoding. The formula for position encoding is as follows:
where represents the encoded positional information for the i-th point in the trajectory, added to the j-th dimensional value of the feature embeddings, and d stands for the overall dimensionality of the feature embeddings. The coarse-grained and fine-grained feature matrices C and F are updated through position encoding as follows:
where represents the position in the i-th row and j-th column of the matrices. and are the updated matrices obtained from C and F, respectively, and serve as input to the next BFIM.
4.4.2. BFIM Section
The BFIM module consists of multiple layers with identical structures, each mainly formed by a Transformer encoder module (TEM) and a cross-attention fusion module (CFM). Each layer of the BFIM receives two feature matrices from the previous layer and outputs the feature matrices after interactive fusion. The operation of the i-th layer is expressed by the following formula:
where represents the output feature matrices of the i-th layer, is a function that denotes the functionality of the BFIM module, interacting with the input feature matrices . The feature matrices , where denotes the final encoding representation length.
Taking the i-th layer as an example, the TEM and CFM are detailed as follows.
Transformer encoder module. The TEM employs the classic encoder structure in Transformer [33] for preliminary encoding of features. We omit a detailed description of its internal components, and describe its processing with the following formula:
where represents the output feature matrices of the TEM, is a function that denotes the functionality of the TEM module.
Cross-attention fusion module. The CFM takes as inputs and utilizes a cross-attention mechanism for interaction between features. During this process, one of the two features acts as the primary feature, while another serves as an auxiliary feature to assist in encoding the primary feature. Given that the CFMs of both branches are mirror images of each other, we specifically describe the structure of the CFM that employs fine-grained features as the primary feature, as shown in the bottom row of Figure 3.
Firstly, through multi-head linear transformations, a value matrix and a key matrix are obtained from the feature matrix , whereas a query matrix is obtained from the feature matrix , where , , and ; j denotes the j-th head; and h is the number of heads (all processes in this subsection occur at the i-th layer; to simplify, we have removed the subscript i from certain matrices, such as and ). The formulas are as follows:
where , , and are the multi-head linear weight matrices.
Then, we calculate the attention matrix between and , which is formulated as follows:
where represents the correlation between the two branch features in the j-th head.
Subsequently, we multiply the value matrix with the attention matrix, then merge the multiple heads and perform a linear transformation, which is formulated as follows:
where || represents the concatenation function, and is the linear weight matrix.
Finally, following the standard Transformer encoder model [33], we employ a feed-forward network (FFN) and two residual connections with layer normalization to obtain the final output feature matrix. Furthermore, we have introduced simple learnable scaling coefficients to residual connections, which have been proven to enhance performance to some extent [34,35]. The process is formulated as follows:
where denotes layer normalization, and refers to two fully connected layers. , , , and are the learnable scaling coefficients.
4.4.3. Fusion Section
The fusion section takes in the coarse-grained and fine-grained feature matrices, and , output by the BFIM (n denotes the number of the BFIM layers, thus and represent the outputs of the BFIM), and fuses them into the final representation.
Firstly, we perform average pooling on the coarse-grained and fine-grained feature matrices and to integrate the features of each point on the trajectory, producing the coarse-grained and fine-grained feature vectors and , respectively.
Then, we design four schemes to combine these two feature vectors. (a) ; (b) ; (c) ; (d) . Through experimentation, we select the best-performing scheme (a), thus the formula is as follows:
where denotes the average pooling function, and r is the output of the section, which also serves as the feature vector that represents the spatio-temporal trajectory T encoded by the STT-CFE.
4.5. STT-CL Contrastive Learning Procedure
STT-CL’s training follows the standard BYOL contrastive learning framework [30], as illustrated on the right of Figure 2, employing two networks: the online network and the target network. The online network, parameterized by , comprises an encoder , a projector , and a predictor . The target network mimics the architecture of the online network, but uses a distinct set of weights , which are updated as an exponential moving average of the online network parameters . More precisely, given a target decay rate , after each training step we perform the following update:
During training, STT-CL creates two augmented trajectories and . Then, the online network processes to produce a representation and a projection . Similarly, the target network processes to generate and a target projection . A prediction of is made, and both and are normalized, where means stop-gradient. The networks are trained by minimizing the mean squared error between the normalized predictions and the target projections . The loss is formulated as follows:
where the angle brackets denote the inner product, and means L2 normalization.
5. Experiments
5.1. Experimental Settings
We conducted experiments on two large-scale real-world datasets.
- Porto comprises 1.7 million GPS trajectory data from taxi fleets in Porto, Portugal, offering rich insights into urban mobility and traffic patterns.
- BJ was collected in Beijing cabs in November 2015 [27,36]. It is made up of one million road network trajectories with timestamps and road network data. We utilize these to perform sampling, resulting in the GPS trajectories.
Following previous research [14,29], we filter the trajectories within the urban area, having between 20 and 200 trajectory points. The preprocessed trajectory statistics are illustrated in Table 1. In addition, each dataset is randomly partitioned into training, validation, and testing sets in a 7:1:2 ratio.

Table 1.
Statistics of preprocessed datasets.
Baselines. We compare our method, STT-CL, with three heuristic similarity measures, DTW [10], EDwP [37] (an improved version of EDR [11]), and Fréchet [13], as well as with two self-supervised learning-based methods: t2vec [14] and TrajCL [29]. To ensure a fair comparison, we incorporate the time dimension as the third input dimension and also integrate the time dimension into the grid embeddings for both t2vec and TrajCL.
Implementation details. Following previous studies, the spatial division distance of the spatio-temporal grid is fixed to 100 m, and the duration of the time divisions is fixed to one hour, in order to capture the cyclical patterns of urban traffic throughout one day. For comparison, STT-CL utilizes the same trajectory augmentation techniques as TrajCL: point masking, and trajectory truncation. For both TrajCL and STT-CL, the number of multi-heads, encoder layers, and the contrastive temperature are 8, 2, and 0.05, respectively. For all learning-based methods, we set the dimensions of the similarity representation r at 256, and employ the Euclidean distance for similarity representation distance computation. For training, we employ Adam as the optimizer, with the initial learning rate, batch size, and maximum epochs set at 0.001, 256, and 20, respectively.
Our method is implemented using Python 3.9 and PyTorch 12.2.2. All experiments are carried out on a platform equipped with a 64-core Intel Xeon Platinum 8358P CPU and an NVIDIA GeForce RTX 3090 GPU.
Metrics. Following previous studies [14,15,29], we evaluate the methods in terms of two aspects, i.e., self-similarity and cross-similarity.
Self-similarity. We randomly select some trajectories from the test set to form the query set Q, where each trajectory T is a series of points, denoted as . We construct two subtrajectories, and , from each trajectory based on the parity of their point indices, with containing all odd-indexed points, , and containing all even-indexed points, . These subtrajectories are assigned to sets and , respectively. Additionally, we select some other trajectories from the test set to form the database D with , which is used for searching.
Following this methodology, we calculate two key metrics for self-similarity, mean rank () and precision (P), formulated as follows:
where denotes the rank of the most similar trajectory to in the search database D. equals 1 if the most similar trajectory to in ranks first in D; otherwise, equals 0. A lower or larger P indicates a better self-similarity performance, as similar trajectories are ranked higher.
Cross-similarity. We utilize the cross-distance deviation () metric to assess the robustness of the similarity measure in maintaining the similarity between two distinct trajectories, irrespective of the data augmentation strategies employed. The is computed as follows:
where and are two distinct trajectories, denotes the similarity distance between two trajectories, is a variant of obtained by trajectory augmentation, and is obtained in a similar manner. A lower value of indicates that the measured similarity is closer to the actual similarity, demonstrating a more robust similarity measure.
5.2. Experimental Comparison
We compare STT-CL with baselines in two aspects: effectiveness and robustness.
5.2.1. Effectiveness
Firstly, we explore the general effectiveness of the models, shown in Table 2. Keeping the size of the query set fixed at 1000 trajectories (|| = 1 k), we compare the performance of the self-similarity metric across various sizes of search database D, where ranges from 20 k to 100 k. Furthermore, to assess the statistical significance of the performance differences between STT-CL and TrajCL, we conduct a significance analysis using t-tests. Specifically, we calculate the p-values to evaluate the significance of the observed performance differences across the various metrics.

Table 2.
MR and precision performance across different database sizes (20 k to 100 k).
Heuristic methods exhibit superior performance in the spatio-temporal trajectory similarity computation task over the general spatial trajectory similarity computation task due to the increased emphasis on temporal dimension similarity, among which the Fréchet distance method exhibits the most outstanding performance. However, compared to all learning-based methods, the effectiveness of heuristic approaches remains inferior. STT-CL and TrajCL, two contrastive learning techniques, exhibit greater effectiveness than t2vec. However, according to the significance analysis, when the size of the search database is relatively small, there is no significant performance difference between the two models, especially in terms of precision.
The comparison between the two datasets clearly shows that the Porto dataset exhibits a lower trajectory similarity compared to the BJ dataset, which better facilitates model performance assessment and makes it a more appropriate choice for an experimental dataset.
5.2.2. Robustness
Furthermore, we evaluate the robustness of the models by comparing self-similarity and cross-similarity metrics in the context of low-quality trajectories, as shown in Table 3 and Table 4. We fix the sizes of query set and search database D at 1 k and 100 k, respectively, applying an equal down-sampling rate to both and D for down-sampling, and perform the calculation of metrics under these conditions, where the down-sampling rate is varied from 0.1 to 0.5 (the higher the down-sampling rate, the lower the trajectory quality). Similarly, we also conduct a significance analysis to compare STT-CL and TrajCL.

Table 3.
MR and precision performance across different down-sampling rates (0.1 to 0.5) in self-similarity evaluation.

Table 4.
CDD performance across different down-sampling rates (0.1 to 0.5) in cross-similarity evaluation.
Contrary to a previous study [15], we do not assess performance on a distorted trajectory dataset, as it has been shown that trajectory distortion has negligible effects on the computation of trajectory similarity [29].
Self-similarity. Among all heuristic methods, EDwP demonstrated the best performance on low-quality trajectory data, while the Fréchet method showed a rapid decline in performance as the trajectory degradation increased (with higher down-sampling rates).
STT-CL exhibits the lowest MR and highest precision metrics among all methods, regardless of down-sampling rates. This underscores the optimal robustness of STT-CL in environments with low-quality trajectories. Furthermore, it is observed that TrajCL experiences a significant disparity in self-similarity metrics compared to STT-CL, especially when the trajectory quality is exceedingly low (with a down-sampling rate exceeding 0.3). This discrepancy is attributed to the inferior performance of the grid embedding method and the TrajCL backbone encoder, a finding corroborated by the subsequent ablation study.
Cross-similarity. Due to computational differences, at a down-sampling rate of 0.1, certain heuristic methods (EDwP and Fréchet) exhibit a lower CDD than learning-based methods. However, as the down-sampling rate increases, the similarity distance between trajectories considerably expands, resulting in a decrease in the cross-similarity performance of heuristic methods compared to learning-based ones.
Comparing STT-CL with TrajCL, it is observed that when the down-sampling rate is below 0.2, TrajCL exhibits a lower CDD, reflecting superior cross-similarity performance. In contrast, when the down-sampling rate exceeds 0.2, the CDD for TrajCL exceeds that of STT-CL. This clearly indicates that a decline in trajectory quality severely and broadly affects TrajCL’s performance, thereby further confirming STT-CL’s robust performance in the context of low-quality trajectories.
5.2.3. Efficiency
The efficiency of trajectory similarity computation is equally crucial, especially for real-world applications where large-scale datasets are involved. In this section, we compare the training and testing efficiency of different models on the Porto dataset, as shown in Figure 4.
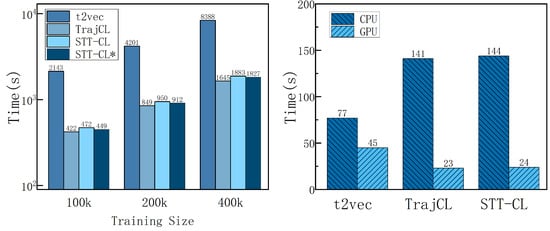
Figure 4.
Training and testing times of different models (STT-CL∗ removes the fusion section in STT-CFE).
Training time. To evaluate the training efficiency of different models on datasets of varying sizes, we conducted experiments using training sets of 100 k, 200 k, and 400 k trajectories. For each training set size, we recorded the one-epoch training times of different models and compared their performance in terms of training efficiency on large-scale datasets. In the experiments, contrastive learning-based methods, STT-CL and TrajCL, were nearly five times faster than t2vec in terms of training time. However, STT-CL took slightly longer to train than TrajCL. Considering that STT-CL involves an additional feature fusion step, we performed further tests by removing the fusion part in STT-CFE and measuring the training time, as shown in Figure 4. It can be seen that the fusion step in STT-CL accounts for 4% of the total time, and the remaining part still takes slightly longer than TrajCL.
Testing time. To evaluate the testing efficiency of different models, we conducted experiments on the Porto dataset using a fixed query set of size 1 k and search database D of size 100 k. We measured the time taken by each model to compute the trajectory similarities between the query and the search dataset. The results showed that t2vec performed better on the CPU, exhibiting faster testing times compared to STT-CL and TrajCL. However, on the GPU, t2vec exhibited slower testing times. This is due to the recursive matrix computations involved in t2vec, which are less optimized for parallel computation on GPU. The testing time for STT-CL and TrajCL did not show significant differences on either CPU or GPU. Despite the overall increased computational cost of the STT-CL model, this difference during testing is not noticeable when handling smaller query sets and datasets.
5.3. Ablation Study
We analyze the impact of the model components by comparing self-similarity metrics (MR and precision) at different down-sampling rates. We present the results solely for the Porto dataset, and the BJ dataset demonstrates a similar trend.
The impact of grid embedding. We assessed our two proposed optimized grid embedding techniques against the method utilized in TrajCL, as depicted in Figure 5. ‘node2vec’ and ‘node2vec+’ in the figure, respectively, denote the original and optimized versions of the node2vec methodology, while ’word2vec+’ signifies the refined FastText approach (used in the comparative experiments).
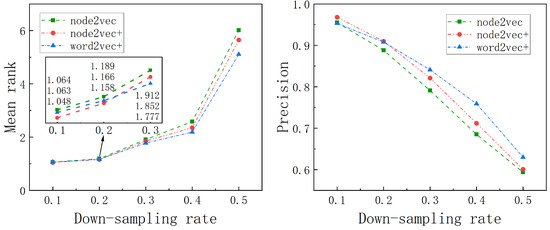
Figure 5.
The impact of grid embedding.
The results reveal that the robustness of the node2vec method substantially increases following optimization. Additionally, the ‘node2vec+’ approach exhibits superior performance to the ‘word2vec+’ method when the down-sampling rate is below 0.2; however, its effectiveness diminishes at higher down-sampling rates. This phenomenon is attributed to high-quality trajectories more accurately representing trajectory similarities through spatial–temporal proximity relations, whereas low-quality trajectories more effectively convey similarity through spatial semantic relationships embedded in historical trajectories.
The impact of the encoder. We conduct a comparison between our proposed STT-CFE model and the encoder implemented in Transformer and TrajCL, as depicted in Figure 6. Within these experiments, the input to the Transformer’s encoder comprises concatenated coarse-grained and fine-grained matrices, while TrajCL’s encoder, DualSTB, is capable of directly integrating coarse-grained and fine-grained matrices as its inputs.
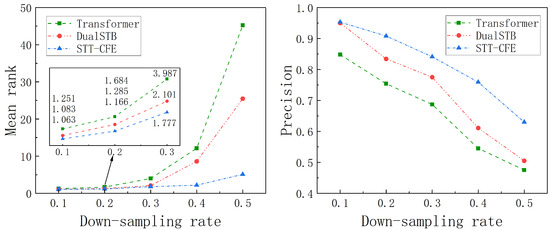
Figure 6.
The impact of the encoder.
The result indicates that STT-CFE performs well at all evaluated down-sampling rates. Furthermore, we observed a notable decline in DualSTB’s robustness when faced with low-quality trajectories (specifically, when the down-sampling rate exceeds 0.3), which aligns with the significant performance degradation previously noted in TrajCL experiments.
The impact of feature combination. In Section 4.4.3, we introduced four schemes for feature combination, and we conducted experimental comparisons among these schemes, as shown in Figure 7.
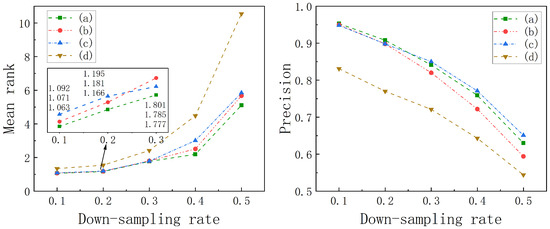
Figure 7.
The impact of feature combination ((a–d) represent the four fusion schemes in Section 4.4.3).
The result indicates that scheme (a) overall exhibits the best performance in the MR experiments. However, scheme (c) outperforms scheme (a) in terms of precision metrics when the down-sampling rate exceeds 0.3, but it shows poorer MR metrics. This is due to strategy (c)’s exclusive reliance on the coarse-grained branch, which leads to difficulty in distinguishing between trajectories with similar structures.
Parameter Study
In this section, we focus on studying the effect of various parameters on the performance of the model, particularly how they influence the handling of low-quality trajectories, i.e., when the down-sampling rate is greater than or equal to 0.3. In the subsequent parameter experiment figures, the symbol represents the down-sampling rate.
The impact of the number of encoder layers. We explore the impact of the number of encoder layers on model performance by varying the number of encoder layers from one to five, as shown in Figure 8. The experimental results show that the overall performance improves as the number of encoder layers increases. However, when the number of layers reaches three, the performance improvement becomes marginal, indicating that additional layers do not contribute significantly beyond this point. Given that increasing the number of layers also leads to a substantial increase in computational overhead, we conclude that using two encoder layers strikes a balance between performance enhancement and computational efficiency.
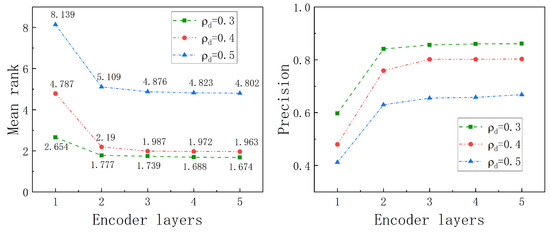
Figure 8.
The impact of the number of encoder layers.
The impact of the number of embedding dimensions. We explore the impact of the number of embedding dimensions by varying it from 64 to 1024, as shown in Figure 9. The experimental results show that overall performance increases with the number of embedding dimensions up to a certain point, but then starts to decline. This trend can be attributed to overfitting when the number of embedding dimensions becomes too large. Notably, the overfitting phenomenon becomes more pronounced as the quality of the trajectories decreases. However, it is important to highlight that the precision metric is less sensitive to overfitting compared to the mean rank. Thus, we default the number of embedding dimensions to 256.
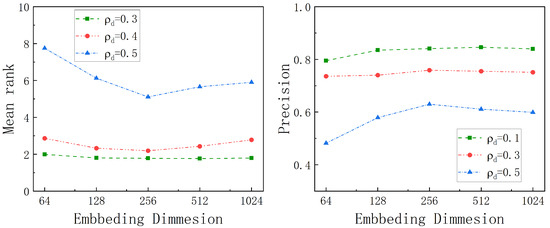
Figure 9.
The impact of the number of embedding dimensions.
6. Conclusions
This study presents STT-CL, an innovative contrastive learning framework for spatio-temporal trajectory similarity computation that systematically captures latent spatio-temporal dependencies. Our primary theoretical contribution lies in the proposed Spatio-Temporal Trajectory Cross-Fusion Encoder (STT-CFE), which establishes a hierarchical feature integration paradigm that adeptly integrates coarse-grained and fine-grained features. The encoder demonstrates exceptional robustness in processing low-quality trajectories with irregular sampling rates and missing data points.
Through rigorous empirical validation on large-scale urban mobility datasets, STT-CL achieves consistent performance gains of 12.7–18.4% over state-of-the-art baselines across a range of critical metrics. These results underline the necessity of joint spatio-temporal embedding spaces for trajectory representation learning and highlight the robustness of contrastive learning in addressing the challenges of trajectory similarity evaluation.
The framework advances ITS by enabling more accurate trajectory analysis for congestion prediction, route optimization, and mobility pattern discovery. Future extensions may explore (a) integration with graph neural networks for network-constrained movement modeling, and (b) domain adaptation techniques for cross-city deployment.
Author Contributions
Conceptualization, Q.T. and Z.-C.X.; methodology, Q.T. and Z.-C.X.; software, Z.-C.X.; validation, Q.T. and N.L.; formal analysis, Q.T. and Z.-C.X.; investigation, Z.-C.X.; data curation, Z.-C.X.; writing—original draft preparation, Z.-C.X.; writing—review and editing, Q.T. and S.H.; supervision, W.N., N.L. and S.H.; project administration, W.N. and N.L.; funding acquisition, W.N. and S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 62202060); the Young Elite Scientists Sponsorship Program by BAST (Grant No. BYESS2023311); the Young Backbone Teacher Support Plan of BISTU (Grant No. YBT202426).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Porto public dataset can be downloaded from https://www.kaggle.com/c/pkdd-15-predict-taxi-service-trajectory-i (accessed on 15 March 2025). BJ dataset can be downloaded from https://github.com/aptx1231/START (accessed on 15 March 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhang, H.; Ge, S.; Luo, G.; Tian, Y.; Ye, P.; Li, Y. Internet of Vehicular Intelligence: Enhancing Connectivity and Autonomy in Smart Transportation Systems. IEEE Trans. Intell. Veh. 2024, 1–5. [Google Scholar] [CrossRef]
- Cheng, X.; Duan, D.; Gao, S.; Yang, L. Integrated sensing and communications (ISAC) for vehicular communication networks (VCN). IEEE Internet Things J. 2022, 9, 23441–23451. [Google Scholar] [CrossRef]
- Amini, A.; Vaghefi, R.M.; de la Garza, J.M.; Buehrer, R.M. Improving GPS-based vehicle positioning for intelligent transportation systems. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 8–11 June 2014; pp. 1023–1029. [Google Scholar]
- Jiang, Q.; Yu, L.; Ziran, D.; Shun, S. Behavior pattern mining based on spatiotemporal trajectory multidimensional information fusion. Chin. J. Aeronaut. 2023, 36, 387–399. [Google Scholar] [CrossRef]
- Glake, D.; Panse, F.; Lenfers, U.; Clemen, T.; Ritter, N. Spatio-temporal Trajectory Learning using Simulation Systems. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 592–602. [Google Scholar]
- Sheng, Z.; Xu, Y.; Xue, S.; Li, D. Graph-based spatial-temporal convolutional network for vehicle trajectory prediction in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17654–17665. [Google Scholar] [CrossRef]
- Li, L.; Erfani, S.; Chan, C.A.; Leckie, C. Multi-scale trajectory clustering to identify corridors in mobile networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 2253–2256. [Google Scholar]
- Hu, D.; Chen, L.; Fang, H.; Fang, Z.; Li, T.; Gao, Y. Spatio-Temporal Trajectory Similarity Measures: A Comprehensive Survey and Quantitative Study. arXiv 2023, arXiv:2303.05012. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, P.; Chen, W.; Zheng, Z.; Guo, M. Embedding-based similarity computation for massive vehicle trajectory data. IEEE Internet Things J. 2021, 9, 4650–4660. [Google Scholar] [CrossRef]
- Yi, B.K.; Jagadish, H.V.; Faloutsos, C. Efficient retrieval of similar time sequences under time warping. In Proceedings of the 14th International Conference on Data Engineering, Orlando, FL, USA, 23–27 February 1998; pp. 201–208. [Google Scholar]
- Chen, L.; Özsu, M.T.; Oria, V. Robust and fast similarity search for moving object trajectories. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Baltimore, MD, USA, 14–16 June 2005; pp. 491–502. [Google Scholar]
- Alt, H. The computational geometry of comparing shapes. In Efficient Algorithms: Essays Dedicated to Kurt Mehlhorn on the Occasion of His 60th Birthday; Springer: Berlin/Heidelberg, Germany, 2009; pp. 235–248. [Google Scholar]
- Alt, H.; Godau, M. Computing the Fréchet distance between two polygonal curves. Int. J. Comput. Geom. Appl. 1995, 5, 75–91. [Google Scholar] [CrossRef]
- Li, X.; Zhao, K.; Cong, G.; Jensen, C.S.; Wei, W. Deep representation learning for trajectory similarity computation. In Proceedings of the 2018 IEEE 34th International Conference on Data Engineering (ICDE), Paris, France, 16–19 April 2018; pp. 617–628. [Google Scholar]
- Deng, L.; Zhao, Y.; Fu, Z.; Sun, H.; Liu, S.; Zheng, K. Efficient Trajectory Similarity Computation with Contrastive Learning. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 365–374. [Google Scholar]
- Liu, X.; Tan, X.; Guo, Y.; Chen, Y.; Zhang, Z. Cstrm: Contrastive self-supervised trajectory representation model for trajectory similarity computation. Comput. Commun. 2022, 185, 159–167. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Gao, T.; Yao, X.; Chen, D. Simcse: Simple contrastive learning of sentence embeddings. arXiv 2021, arXiv:2104.08821. [Google Scholar]
- Yang, P.; Wang, H.; Zhang, Y.; Qin, L.; Zhang, W.; Lin, X. T3s: Effective representation learning for trajectory similarity computation. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; pp. 2183–2188. [Google Scholar]
- Feng, C.; Pan, Z.; Fang, J.; Xu, J.; Zhao, P.; Zhao, L. Aries: Accurate Metric-based Representation Learning for Fast Top-k Trajectory Similarity Query. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 499–508. [Google Scholar]
- Ding, J.; Zhang, B.; Wang, X.; Zhou, C. TSNE: Trajectory similarity network embedding. In Proceedings of the 30th International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 1–4 November 2022; pp. 1–4. [Google Scholar]
- Jing, Q.; Liu, S.; Fan, X.; Li, J.; Yao, D.; Wang, B.; Bi, J. Can Adversarial Training benefit Trajectory Representation? An Investigation on Robustness for Trajectory Similarity Computation. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2022; pp. 905–914. [Google Scholar]
- Shang, S.; Chen, L.; Wei, Z.; Jensen, C.S.; Zheng, K.; Kalnis, P. Trajectory similarity join in spatial networks. Proc. VLDB Endow. 2017, 10, 1178–1198. [Google Scholar] [CrossRef]
- Li, G.; Hung, C.C.; Liu, M.; Pan, L.; Peng, W.C.; Chan, S.H.G. Spatial-temporal similarity for trajectories with location noise and sporadic sampling. In Proceedings of the 2021 IEEE 37th International Conference on Data Engineering (ICDE), Chania, Greece, 19–22 April 2021; pp. 1224–1235. [Google Scholar]
- Fang, Z.; Du, Y.; Zhu, X.; Hu, D.; Chen, L.; Gao, Y.; Jensen, C.S. Spatio-temporal trajectory similarity learning in road networks. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 347–356. [Google Scholar]
- Zhou, S.; Han, P.; Yao, D.; Chen, L.; Zhang, X. Spatial-temporal fusion graph framework for trajectory similarity computation. World Wide Web 2023, 26, 1501–1523. [Google Scholar] [CrossRef]
- Jiang, J.; Pan, D.; Ren, H.; Jiang, X.; Li, C.; Wang, J. Self-supervised Trajectory Representation Learning with Temporal Regularities and Travel Semantics. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 9729–9738. [Google Scholar]
- Chang, Y.; Qi, J.; Liang, Y.; Tanin, E. Contrastive Trajectory Similarity Learning with Dual-Feature Attention. In Proceedings of the 2023 IEEE 39th International Conference on Data Engineering (ICDE), Anaheim, CA, USA, 3–7 April 2023; pp. 2933–2945. [Google Scholar]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.; Buchatskaya, E.; Doersch, C.; Avila Pires, B.; Guo, Z.; Gheshlaghi Azar, M.; et al. Bootstrap your own latent-a new approach to self-supervised learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21271–21284. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Bojanowski, P.; Grave, E.; Joulin, A.; Mikolov, T. Enriching word vectors with subword information. Trans. Assoc. Comput. Linguist. 2017, 5, 135–146. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30 (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Shen, Z.; Liu, Z.; Xing, E. Sliced recursive transformer. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 727–744. [Google Scholar]
- Liu, F.; Gao, M.; Liu, Y.; Lei, K. Self-adaptive scaling for learnable residual structure. In Proceedings of the 23rd Conference on Computational Natural Language Learning (CoNLL), Hong Kong, China, 3–4 November 2019; pp. 862–870. [Google Scholar]
- Wang, J.; Jiang, J.; Jiang, W.; Li, C.; Zhao, W.X. LibCity: An Open Library for Traffic Prediction. In Proceedings of the SIGSPATIAL/GIS, ACM, Beijing, China, 2 November 2021; pp. 145–148. [Google Scholar]
- Ranu, S.; Deepak, P.; Telang, A.D.; Deshpande, P.; Raghavan, S. Indexing and matching trajectories under inconsistent sampling rates. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Republic of Korea, 13–17 April 2015; pp. 999–1010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).