Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices
Abstract
1. Introduction
- Development of an ultralow-power memristor-based unsupervised on-chip and online-learning system for edge security applications.
- Resolution of circuit challenges for implementing online threshold computation to support real-time learning.
- Design and simulation of a Euclidean Distance computation circuit, integrated into the memristor-based neuromorphic system for unsupervised online training.
2. Network Dataset
3. Unsupervised Learning
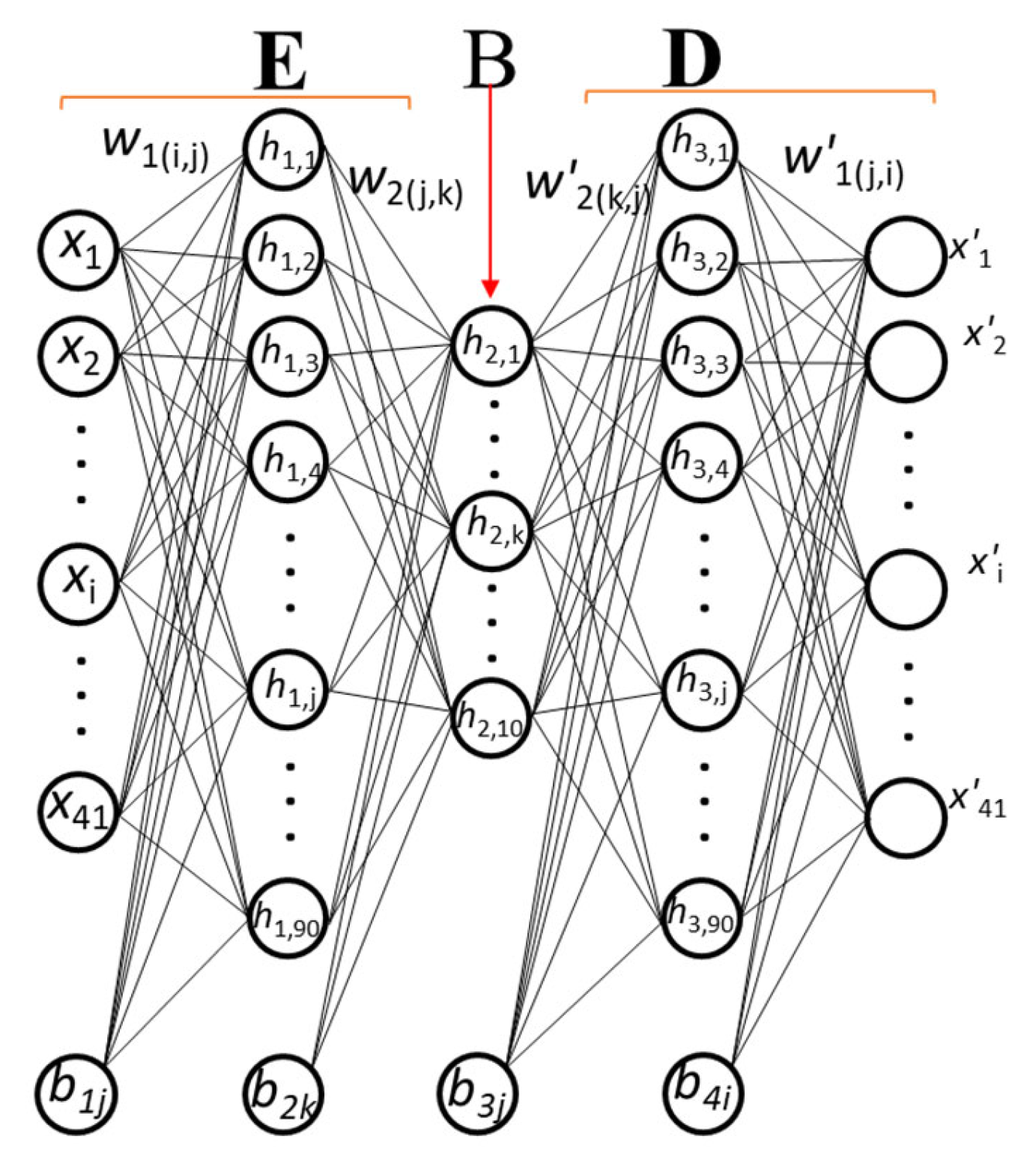
4. Memristor Implementation
4.1. Memristor Device Model
4.2. Memristor Neuron Circuit
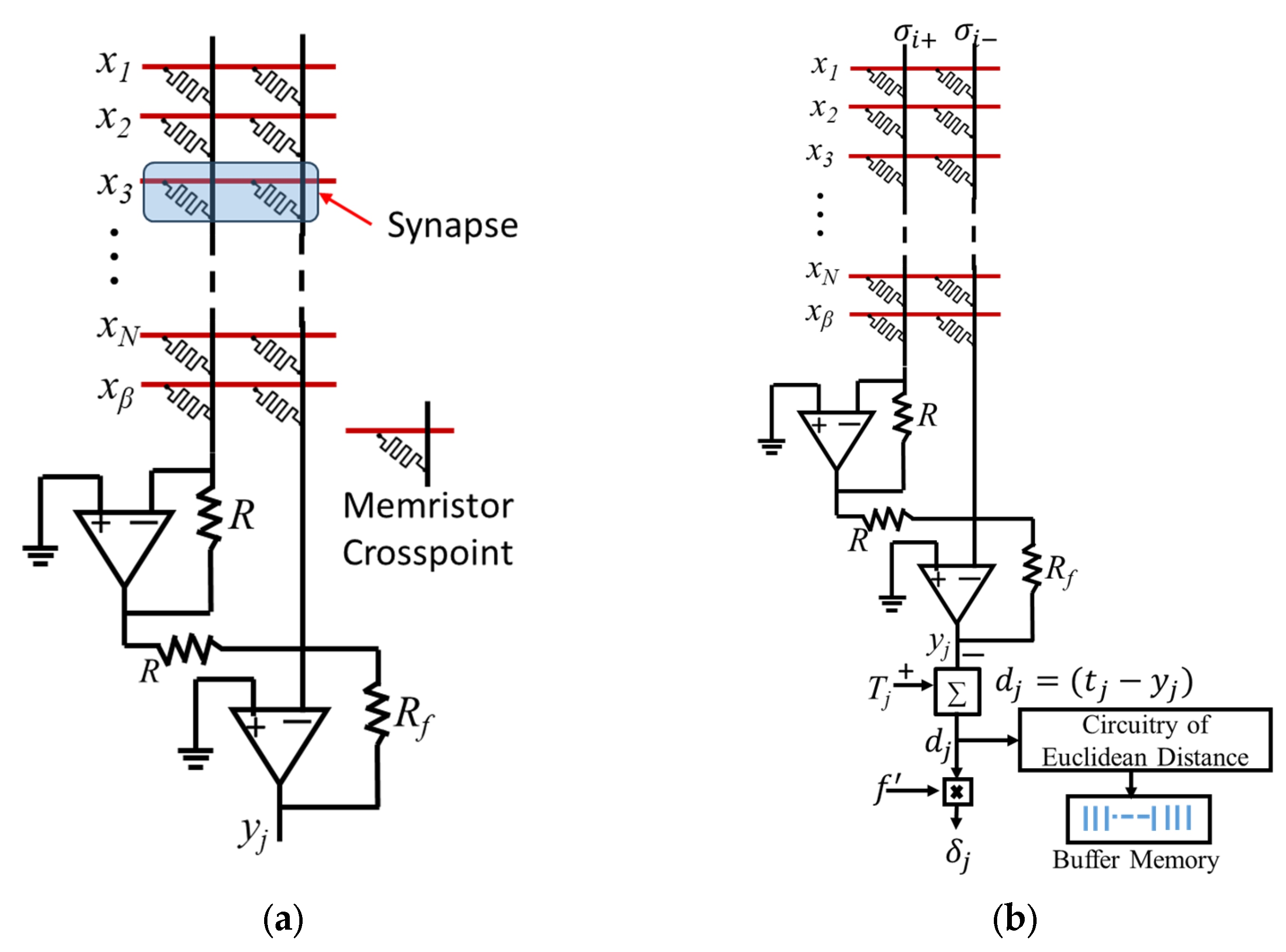
4.3. Crossbar Training Circuit
5. Online Learning and Related Works
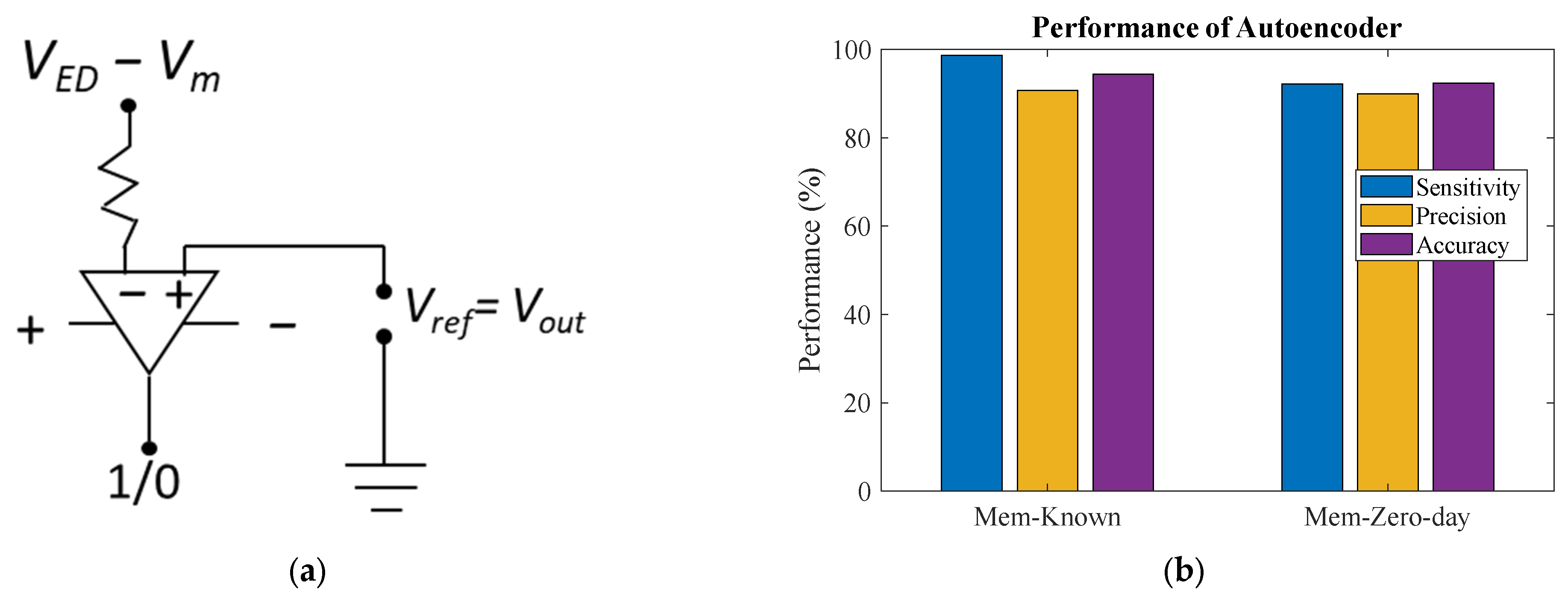
5.1. Online-Learning Memristor Neuron Circuit
5.2. Related Works on Online Learning
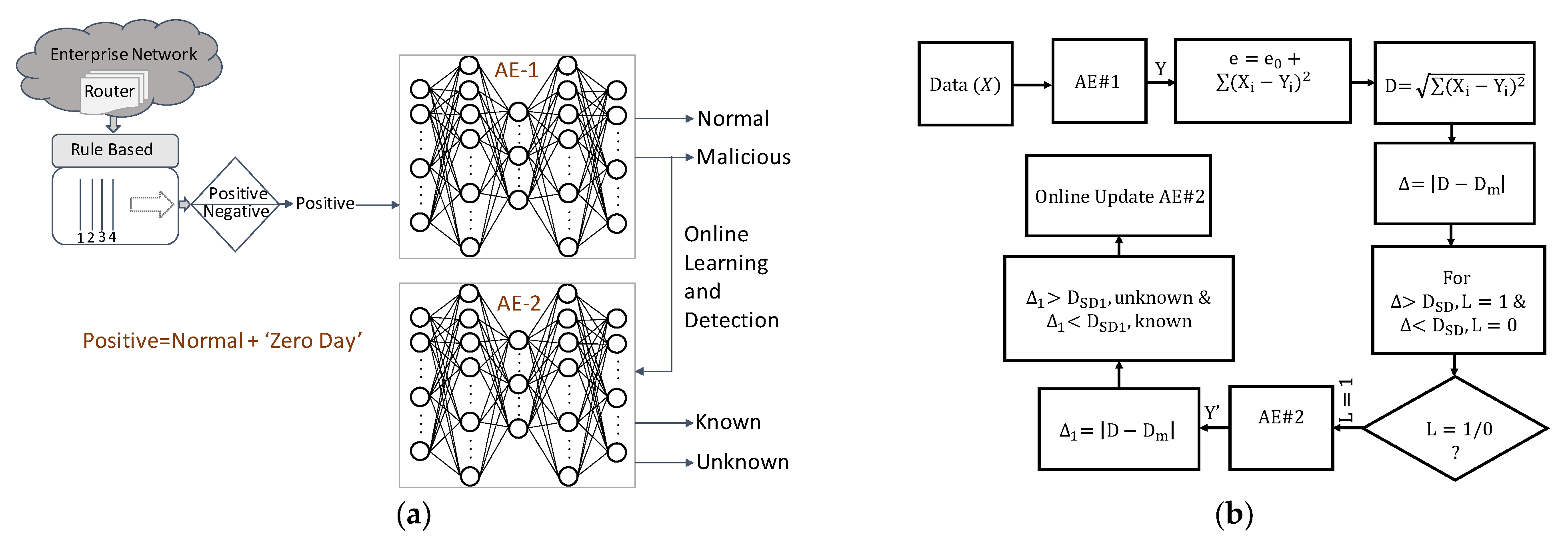
5.3. Online-Learning Systems
6. Memristor-Based Online-Learning Systems
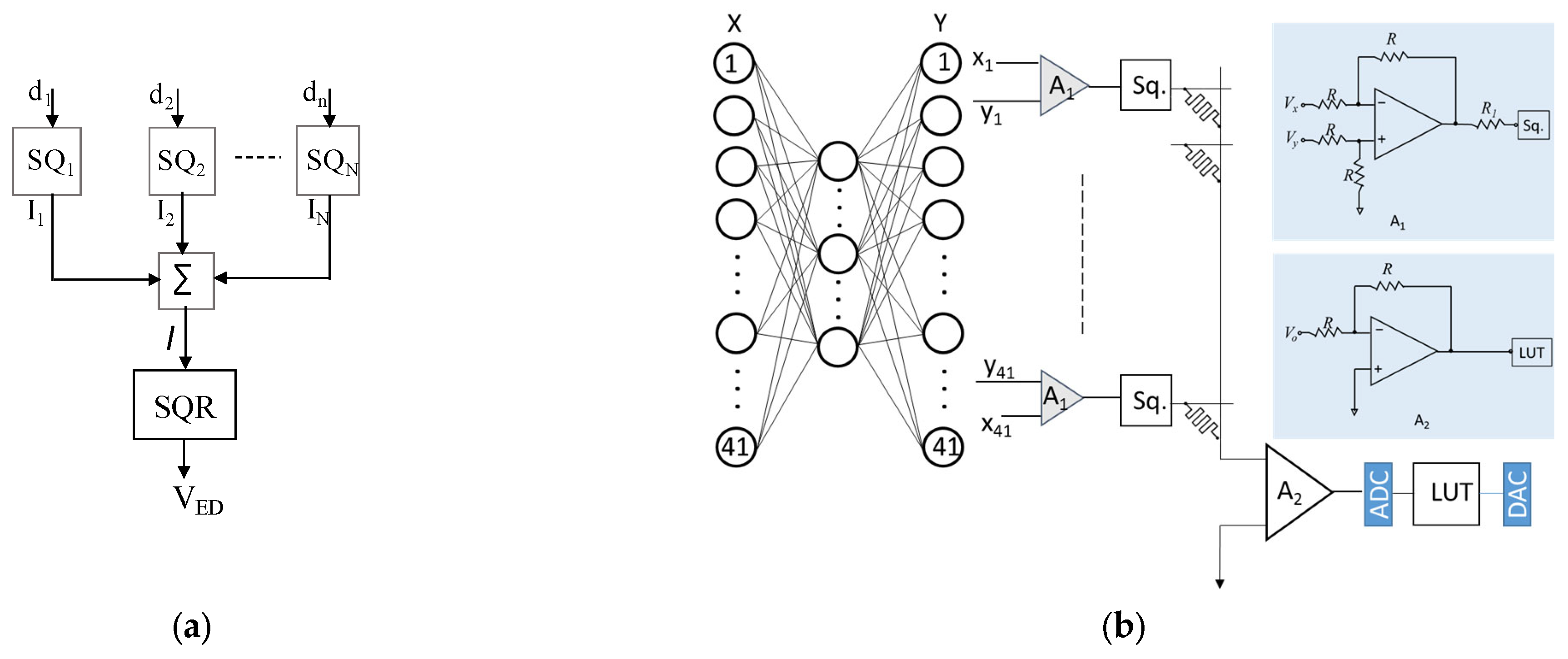
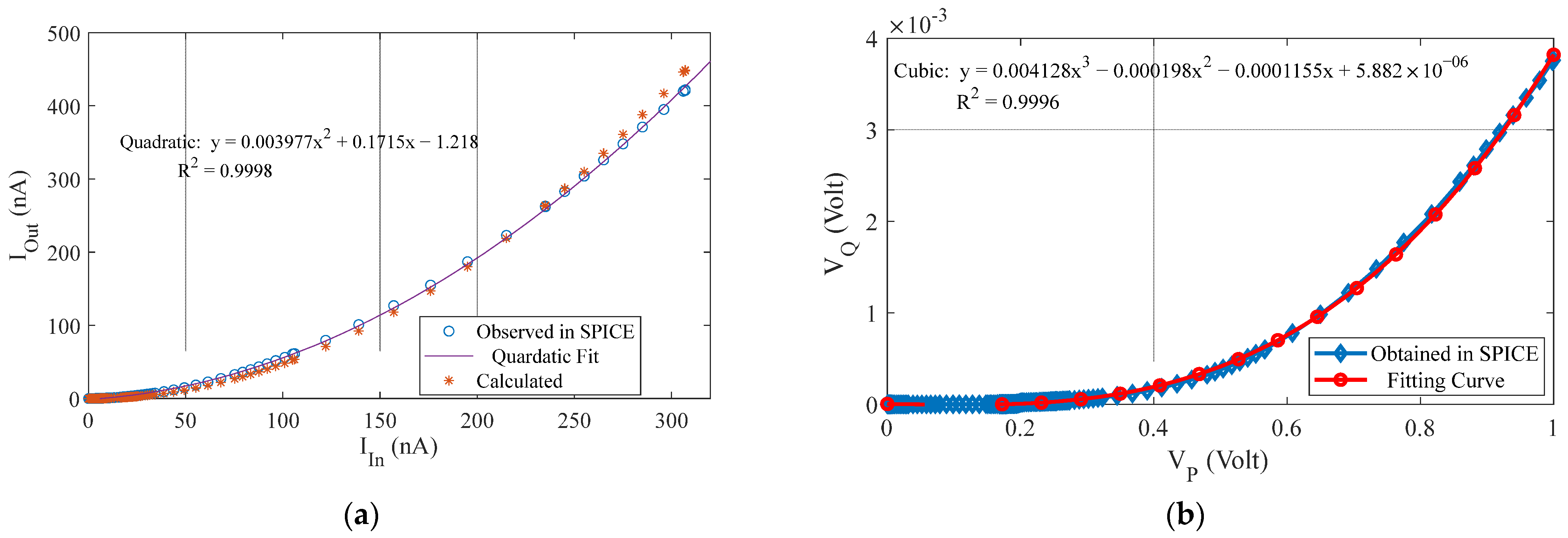
7. Analog Threshold Computing
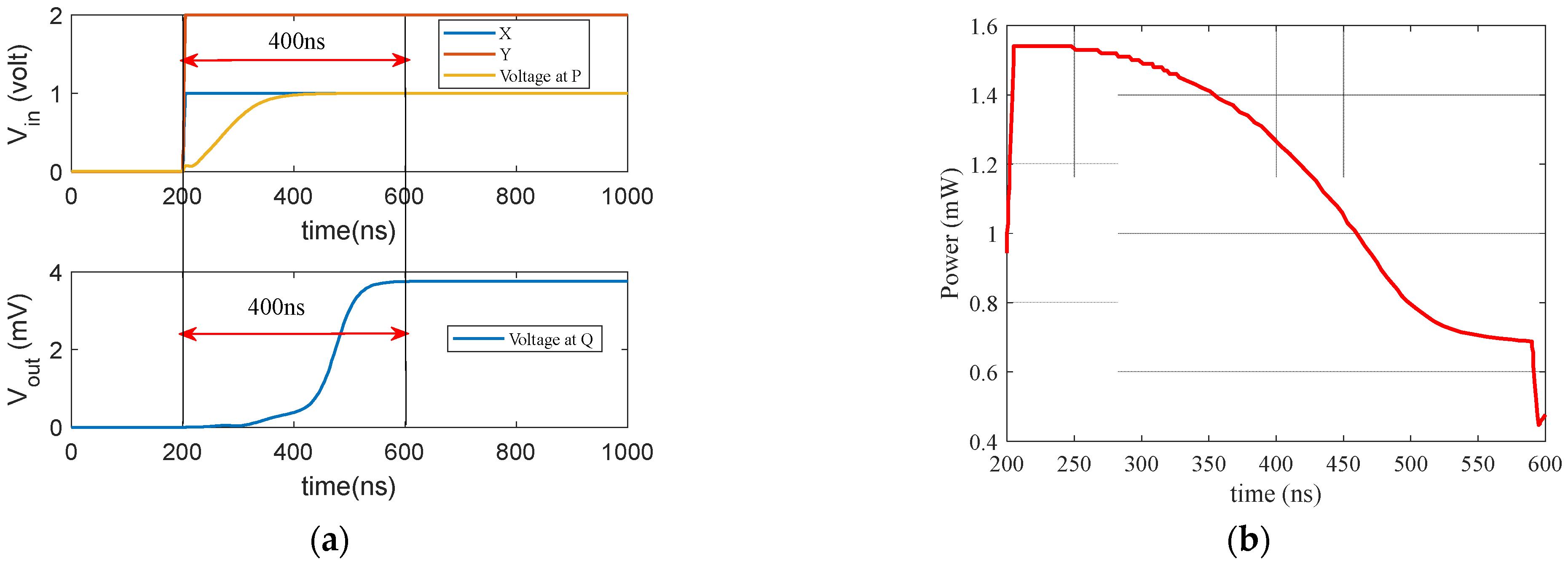
8. Simulation of Online Threshold-Computing Circuit
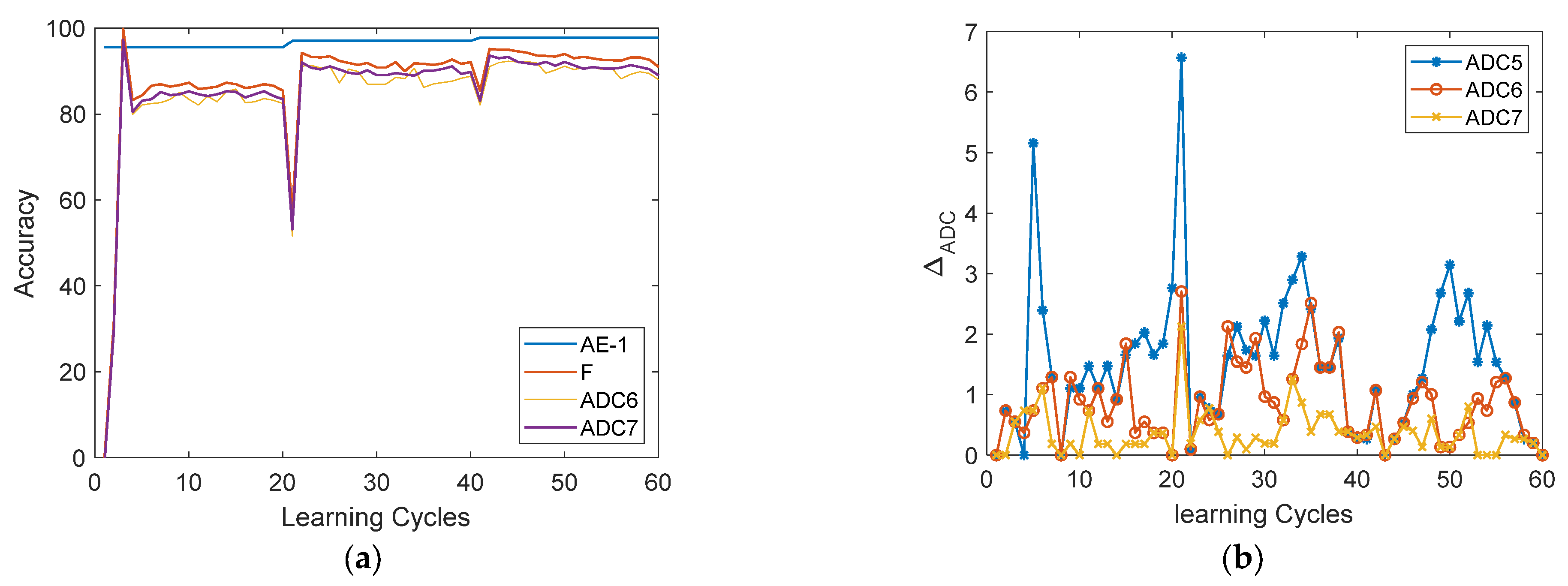
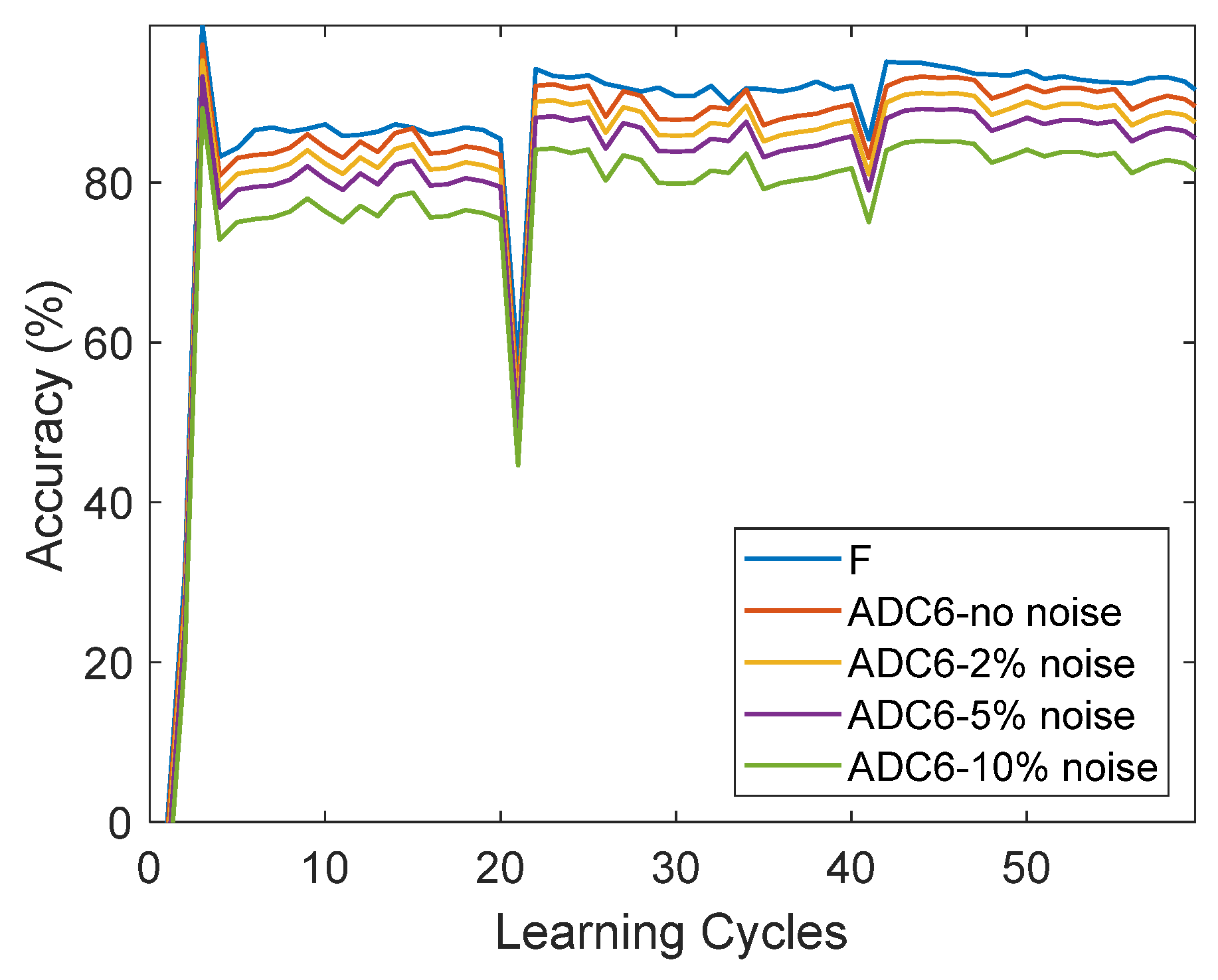
9. Results and Discussion
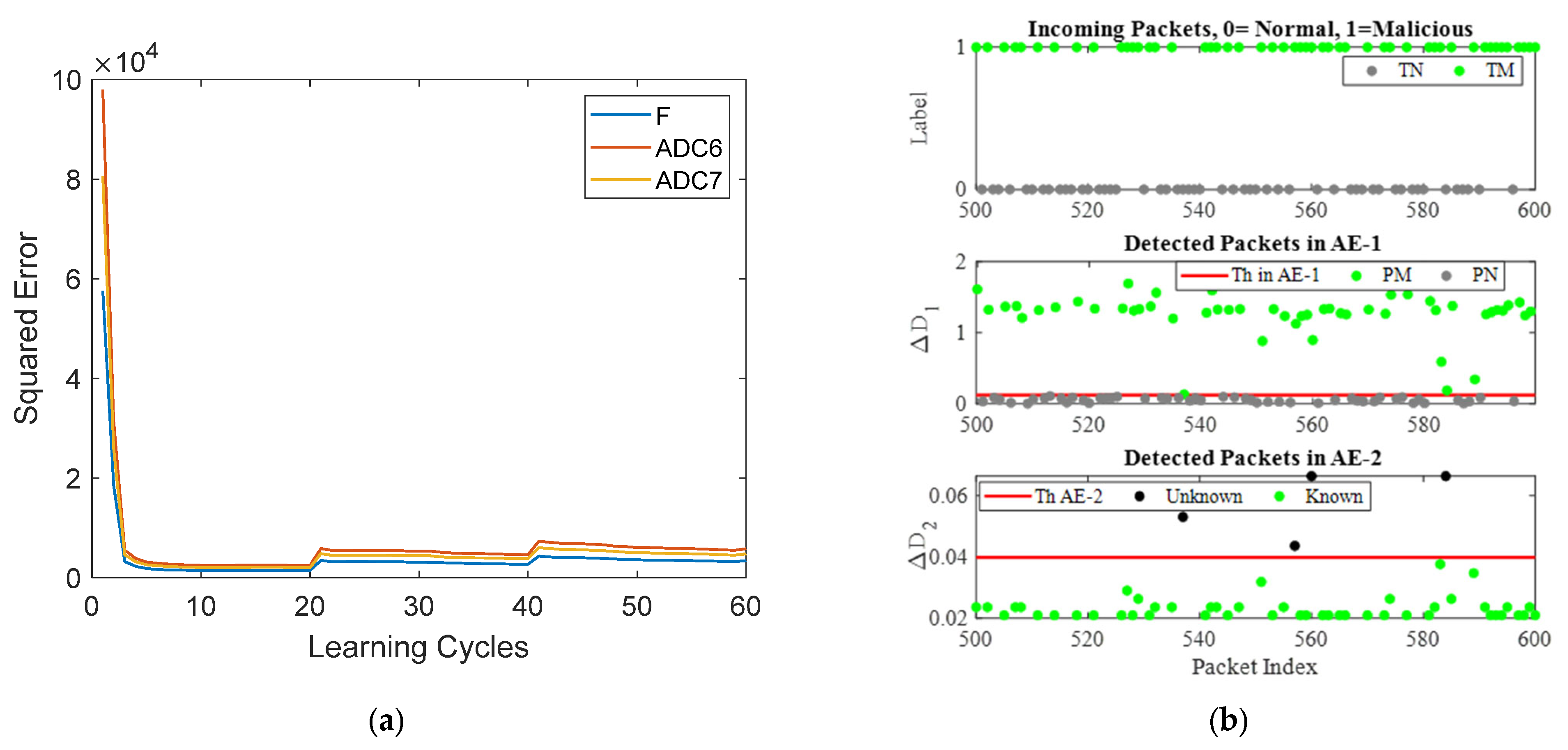
9.1. Crossbar Training Analysis
9.2. Pretrained AE
9.3. Online-Training Analysis
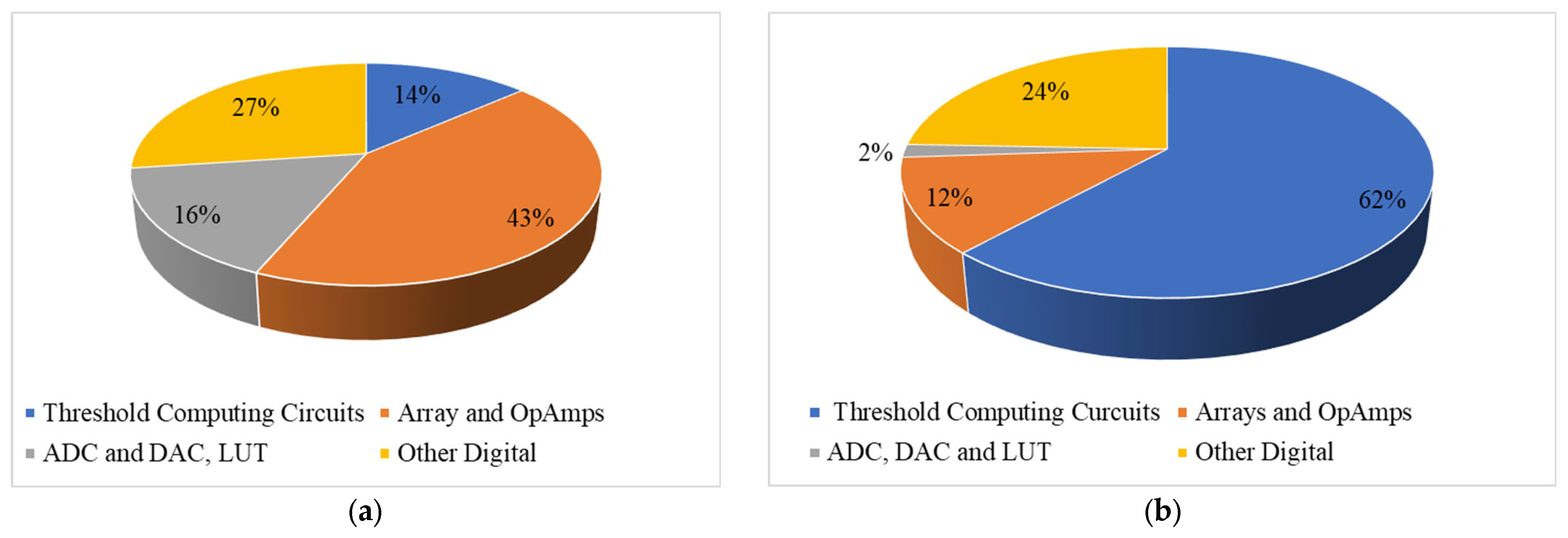
9.4. System Energy, Power, and Performance Analysis
10. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, R.; Gill, S.S. Edge AI: A survey. Internet Things Cyber-Phys. Syst. 2023, 3, 71–92. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, H.; Qian, K.; Zhan, X.; Wang, J. Edge computing and AI-driven intelligent traffic monitoring and optimization. Appl. Comput. Eng. 2024, 67, 225–230. [Google Scholar] [CrossRef]
- Bhavsar, M.; Roy, K.; Kelly, J.; Olusola, O. Anomaly-based intrusion detection system for IoT application. Discov. Internet Things 2023, 3, 5. [Google Scholar] [CrossRef]
- Zarpelão, B.B.; Miani, R.S.; Kawakani, C.T.; de Alvarenga, S.C. A survey of intrusion detection in Internet of Things. J. Netw. Comput. Appl. 2017, 84, 25–37. [Google Scholar] [CrossRef]
- Thudumu, S.; Branch, P.; Jin, J.; Singh, J. A comprehensive survey of anomaly detection techniques for high dimensional big data. J. Big Data 2020, 7, 42. [Google Scholar] [CrossRef]
- Srinivas, T.; Aditya Sai, G.; Mahalaxmi, R. A comprehensive survey of techniques, applications, and challenges in deep learning: A revolution in machine learning. Int. J. Mech. Eng. 2022, 7, 286–296. [Google Scholar]
- Naumov, M.; Kim, J.; Mudigere, D.; Sridharan, S.; Wang, X.; Zhao, W.; Yilmaz, S.; Kim, C.; Yuen, H.; Ozdal, M.; et al. Deep learning training in facebook data centers: Design of scale-up and scale-out systems. arXiv 2020, arXiv:2003.09518. [Google Scholar]
- Lin, J.; Zhu, L.; Chen, W.M.; Wang, W.C.; Gan, C.; Han, S. On-device training under 256 kb memory. Adv. Neural Inf. Process. Syst. 2022, 35, 22941–22954. [Google Scholar]
- Luo, Y.; Peng, X.; Yu, S. MLP + NeuroSimV3. 0: Improving on-chip learning performance with device to algorithm optimizations. In Proceedings of the International Conference on Neuromorphic Systems, Knoxville, TN, USA, 23–25 July 2019; pp. 1–7. [Google Scholar]
- Sebastian, A.; Le Gallo, M.; Khaddam-Aljameh, R.; Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 2020, 15, 529–544. [Google Scholar] [CrossRef]
- Rao, M.; Tang, H.; Wu, J.; Song, W.; Zhang, M.; Yin, W.; Zhuo, Y.; Kiani, F.; Chen, B.; Jiang, X.; et al. Memristor devices denoised to achieve thousands of conductance levels. Nature 2023, 615, 823–829. [Google Scholar] [CrossRef]
- Zidan, M.A.; Strachan, J.P.; Lu, W.D. The future of electronics based on memristive systems. Nat. Electron. 2018, 1, 22–29. [Google Scholar] [CrossRef]
- Lv, Z.; Zhu, S.; Wang, Y.; Ren, Y.; Luo, M.; Wang, H.; Zhang, G.; Zhai, Y.; Zhao, S.; Zhou, Y.; et al. Development of Bio-Voltage Operated Humidity-Sensory Neurons Comprising Self-Assembled Peptide Memristors. Adv. Mater. 2024, 36, 2405145. [Google Scholar] [CrossRef] [PubMed]
- Lv, Z.; Jiang, M.; Liu, H.; Li, Q.; Xie, T.; Yang, J.; Wang, Y.; Zhai, Y.; Ding, G.; Zhu, S.; et al. Temperature-Resilient Polymeric Memristors for Effective Deblurring in Static and Dynamic Imaging. Adv. Funct. Mater. 2025, 2424382. [Google Scholar] [CrossRef]
- NSL-KDD Dataset. Available online: https://www.unb.ca/cic/datasets/nsl.html (accessed on 5 May 2020).
- Takiddin, A.; Ismail, M.; Zafar, U.; Serpedin, E. Deep autoencoder-based anomaly detection of electricity theft cyberattacks in smart grids. IEEE Syst. J. 2022, 16, 4106–4117. [Google Scholar] [CrossRef]
- Sorrenson, P.; Draxler, F.; Rousselot, A.; Hummerich, S.; Zimmerman, L.; Köthe, U. Maximum Likelihood Training of Autoencoders. arXiv 2023, arXiv:2306.01843. [Google Scholar]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E. Memristor SPICE model and crossbar simulation based on devices with nanosecond switching time. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar]
- Yakopcic, C.; Taha, T.M.; Mountain, D.J.; Salter, T.; Marinella, M.J.; McLean, M. Memristor model optimization based on parameter extraction from device characterization data. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2019, 39, 1084–1095. [Google Scholar] [CrossRef]
- Alam, M.S.; Fernando, B.R.; Jaoudi, Y.; Yakopcic, C.; Hasan, R.; Taha, T.M.; Subramanyam, G. Memristor based autoencoder for unsupervised real-time network intrusion and anomaly detection. In Proceedings of the International Conference on Neuromorphic Systems, Knoxville, TN, USA, 23–25 July 2019; pp. 1–8. [Google Scholar]
- Alam, M.S.; Yakopcic, C.; Taha, T.M. Unsupervised Learning of Memristor Crossbar Neuromorphic Processing Systems. U.S. Patent Application 17/384,306, 23 July 2021. [Google Scholar]
- Hasan, R.; Taha, T.M.; Yakopcic, C. On-chip training of memristor based deep neural networks. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 3527–3534. [Google Scholar]
- Krestinskaya, O.; Salama, K.N.; James, A.P. Learning in memristive neural network architectures using analog backpropagation circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 66, 719–732. [Google Scholar] [CrossRef]
- Tsai, S.; Ambrogio, S.; Narayanan, P.; Shelby, B.; Mackin, C.; Burr, G. Analog memory-based techniques for accelerating the training of fully-connected deep neural networks. In Proceedings of the SPIE Advanced Lithography, San Jose, CA, USA, 26–27 February 2019. [Google Scholar]
- Hayes, T.L.; Kanan, C. Lifelong machine learning with deep streaming linear discriminant analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 220–221. [Google Scholar]
- Shao, C.; Feng, Y. Overcoming catastrophic forgetting beyond continual learning: Balanced training for neural machine translation. arXiv 2022, arXiv:2203.03910. [Google Scholar]
- Chaudhri, Z.; Liu, B. Lifelong Machine Learning; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- SRebuffi, A.; Kolesnikov, A.; Sperl, G.; Lampert, C.H. iCaRL: Incremental Classifier and Representation Learning. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5533–5542. [Google Scholar]
- Ashfahani, A.; Pratama, M.; Lughofer, E.; Ong, Y.-S. DEVDAN: Deep evolving denoising autoencoder. Neurocomputing 2020, 390, 297–314. [Google Scholar] [CrossRef]
- Sarwar, S.S.; Ankit, A.; Roy, K. Incremental Learning in Deep Convolutional Neural Networks Using Partial Network Sharing. IEEE Access 2020, 8, 4615–4628. [Google Scholar] [CrossRef]
- Malawade, A.V.; Costa, N.D.; Muthirayan, D.; Khargonekar, P.P.; Al Faruque, M.A. Neuroscience-Inspired Algorithms for the Predictive Maintenance of Manufacturing Systems. IEEE Trans. Ind. Inform. 2021, 17, 7980–7990. [Google Scholar] [CrossRef]
- Monakhov, V.; Thambawita, V.; Halvorsen, P.; Riegler, M.A. GridHTM: Grid-Based Hierarchical Temporal Memory for Anomaly Detection in Videos. Sensors 2023, 23, 2087. [Google Scholar] [CrossRef] [PubMed]
- Faezi, S.; Yasaei, R.; Barua, A.; Al Faruque, M.A. Brain-Inspired Golden Chip Free Hardware Trojan Detection. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2697–2708. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Wang, S.-H.; Zhang, Y.-D. A review on extreme learning machine. Multimed. Tools Appl. 2022, 81, 41611–41660. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xiao, W. Adaptive online sequential extreme learning machine for dynamic modeling. Soft Comput. 2021, 25, 2177–2189. [Google Scholar] [CrossRef]
- Wang, X.; Tu, S.; Zhao, W.; Shi, C. A novel energy-based online sequential extreme learning machine to detect anomalies over real-time data streams. Neural Comput. Appl. 2022, 34, 823–831. [Google Scholar] [CrossRef]
- Albadr, M.A.A.; Tiun, S.; Ayob, M.; Al-Dhief, F.T.; Abdali, T.-A.N.; Abbas, A.F. Extreme Learning Machine for Automatic Language Identification Utilizing Emotion Speech Data. In Proceedings of the 2021 International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Kuala Lumpur, Malaysia, 12–13 June 2021; pp. 1–6. [Google Scholar]
- Alam, M.S.; Yakopcic, C.; Subramanyam, G.; Taha, T.M. Memristor based neuromorphic adaptive resonance theory for one-shot online learning and network intrusion detection. In Proceedings of the International Conference on Neuromorphic Systems, 2020 (ICONS 2020), Oak Ridge, TN, USA, 28–30 July 2020; pp. 1–8, Article No. 25. [Google Scholar]
- Jones, C.B.; Carter, C.; Thomas, Z. Intrusion Detection & Response using an Unsupervised Artificial Neural Network on a Single Board Computer for Building Control Resilience. In Proceedings of the 2018 Resilience Week (RWS), Denver, CO, USA, 20–23 August 2018; pp. 31–37. [Google Scholar]
- Kumar, A.; Sachdeva, N. Cyberbullying checker: Online bully content detection using Hybrid Supervised Learning. In International Conference on Intelligent Computing and Smart Communication: Proceedings of ICSC 2019; Springer: Singapore, 2020; pp. 371–382. [Google Scholar]
- Dong, Z.; Lai, C.S.; Zhang, Z.; Qi, D.; Gao, M.; Duan, S. Neuromorphic extreme learning machines with bimodal memristive synapses. Neurocomputing 2021, 453, 38–49. [Google Scholar] [CrossRef]
- Liang, H.; Cheng, H.; Wei, J.; Zhang, L.; Yang, L.; Zhao, Y.; Guo, H. Memristive neural networks: A neuromorphic paradigm for extreme learning machine. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 15–23. [Google Scholar] [CrossRef]
- Bureneva, O.I.; Prasad, M.S.; Verma, S. FPGA-based Hardware Implementation of the ART-1 classifier. In Proceedings of the 2023 XXVI International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 24–26 May 2023; pp. 171–174. [Google Scholar]
- Govorkova, E.; Puljak, E.; Aarrestad, T.; James, T.; Loncar, V.; Pierini, M.; Pol, A.A.; Ghielmetti, N.; Graczyk, M.; Summers, S.; et al. Autoencoders on field-programmable gate arrays for real-time, unsupervised new physics detection at 40 MHz at the Large Hadron Collider. Nat. Mach. Intell. 2022, 4, 154–161. [Google Scholar] [CrossRef]
- Nag, A.; Paily, R.P. Low power squaring and square root circuits using subthreshold MOS transistors. In Proceedings of the 2009 International Conference on Emerging Trends in Electronic and Photonic Devices & Systems, Varanasi, India, 22–24 December 2009; pp. 96–99. [Google Scholar]
- Jiang, H.; Li, W.; Huang, S.; Cosemans, S.; Catthoor, F.; Yu, S. Analog-to-Digital Converter Design Exploration for Compute-in-Memory Accelerators. IEEE Des. Test 2022, 39, 48–55. [Google Scholar] [CrossRef]
- Yu, S.; Wu, Y.; Wong, H.-S.P. Investigating the switching dynamics and multilevel capability of bipolar metal oxide resistive switching memory. Appl. Phys. Lett. 2011, 98, 103514. [Google Scholar] [CrossRef]
- ASUS. Tinkerboard. Available online: https://tinker-board.asus.com/product/tinker-board.html (accessed on 1 January 2020).
- Suleiman, M.F.; Issac, B. Performance Comparison of Intrusion Detection Machine Learning Classifiers on Benchmark and New Datasets. In Proceedings of the 2018 28th International Conference on Computer Theory and Applications (ICCTA), Alexandria, Egypt, 30 October–1 November 2018; pp. 19–23. [Google Scholar]
- Sidharth, V.; Kavitha, C.R. Network intrusion detection system using stacking and boosting ensemble methods. In Proceedings of the 2021 Third International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 2–4 September 2021; pp. 357–363. [Google Scholar]
- Hamolia, V.; Melnyk, V.; Zhezhnych, P.; Shilinh, A. Intrusion detection in computer networks using latent space representation and machine learning. Int. J. Comput. 2020, 19, 442–448. [Google Scholar] [CrossRef]






| Parameter | Magnitude | Unit |
|---|---|---|
| R | 1000 | Ohm |
| R1 | 1.50 × 106 | Ohm |
| M1 | 1.99/0.65 | W/L |
| M2 | 1.99/0.65 | W/L |
| M3 | 0.2/0.16 | W/L |
| M4 | 0.24/0.18 | W/L |
| M5 | 1.28/0.65 | W/L |
| M6 | 1.85/0.65 | W/L |
| M7 | 1.85/0.65 | W/L |
| Vbias | 0.4 | volt |
| Ibias | 210 | nA |
| RH | 10,000 | Ohm |
| Parameter | Magnitude | Unit |
|---|---|---|
| Cycle time | 2 × 10−9 | s |
| Max training pulse duration | 5 × 10−9 | s |
| Roff | 10 | MΩ |
| Ron | 50 | KΩ |
| Ravg | 5.025 | MΩ |
| Wire resistance | 5 | Ω |
| Vmem | 1.3 | V |
| Pmem | 0.336 | µW |
| Op-amp power | 3 | µW |
| Max read voltage | 1.3 | V |
| Feature size, F | 45 | nm |
| Transistor size | 50 | F2 |
| Memristor area | 10,000 | nm2 |
| Cycle time | 2 | ns |
| Crossbar processing time | 50 | ns |
| Parameters | Tinker Board | Memristor System |
|---|---|---|
| Test sample | 2000 | 2000 |
| Time (sec) | 1.807563 | 2.3 × 10−3 |
| Time/sample | 9.04 × 10−4 | 1.17 × 10−6 |
| Speedup | 1 | 774 |
| Energy (joule) | 4.52 × 10−3 | 2.08 × 10−7 |
| Power (W) | 5 | 0.0205 |
| Performance (OPS) | 20 × 106 | 16.1 × 109 |
| Energy efficiency (OPS/W) | 4.12 × 106 | 7.83 × 1011 |
| Area (mm2) | --- | 4.43 × 10−3 |
| Test sample | 2000 | 2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, M.S.; Yakopcic, C.; Hasan, R.; Taha, T.M. Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices. Information 2025, 16, 222. https://doi.org/10.3390/info16030222
Alam MS, Yakopcic C, Hasan R, Taha TM. Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices. Information. 2025; 16(3):222. https://doi.org/10.3390/info16030222
Chicago/Turabian StyleAlam, Md Shahanur, Chris Yakopcic, Raqibul Hasan, and Tarek M. Taha. 2025. "Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices" Information 16, no. 3: 222. https://doi.org/10.3390/info16030222
APA StyleAlam, M. S., Yakopcic, C., Hasan, R., & Taha, T. M. (2025). Memristor-Based Neuromorphic System for Unsupervised Online Learning and Network Anomaly Detection on Edge Devices. Information, 16(3), 222. https://doi.org/10.3390/info16030222







