Liveness over Fairness (Part I): A Statistically Grounded Framework for Detecting and Mitigating PoW Wave Attacks

Abstract

Blockchain networks face a critical but understudied threat: wave attacks that exploit difficulty adjustment algorithms through strategic mining participation. Adversaries cyclically withdraw and re-enter mining to create oscillations that degrade network liveness and destabilize honest miners’ revenue. We present the first production-ready framework that maintains network responsiveness while enabling robust, post hoc threat detection. The framework employs a statistically rigorous pipeline featuring controller-aligned anomaly detection, transitive collusion grouping via union-find, and Benjamini–Hochberg False Discovery Rate control. We formally prove the economic viability of this architecture: when penalties on unvested rewards are enabled by governance, wave attacks become asymptotically unprofitable for rational adversaries. Evaluated on a 128-node distributed testbed simulating Bitcoin, Ethereum Classic, and Monacoin networks over 30 independent runs, our framework achieves 92.7% F1-score in detecting attacks, significantly outperforming baseline methods (74.7%). This work provides a complete, theoretically-grounded solution for securing proof-of-work blockchains against difficulty manipulation, forming the foundation for the adaptive AI-driven enhancements presented in our companion paper (Part II).

1. Introduction

Proof-of-work (PoW) blockchains rely on a difficulty adjustment algorithm (DAA) to maintain a target block interval by dynamically adjusting the mining difficulty. An emerging adversarial pattern, known as a wave attack, exploits this feedback controller by cyclically withdrawing and re-entering mining capacity. Figure 1 illustrates the attack mechanism: during the withdrawal phase (periods A and C), the diminished hash rate causes the DAA to gradually lower the difficulty; when the attacker resumes mining (periods B and D), the reduced difficulty target is harvested for disproportionate profit. The attack timing is strategically synchronized with DAA window boundaries to maximize difficulty suppression. Such oscillations undermine network liveness—the ability to produce blocks at a predictable cadence—and degrade the revenue of honest miners. Unlike classical selfish or stubborn mining strategies [1,2], which manipulate publication strategies, wave attacks target the control plane itself by inducing non-stationary block intervals.

This research emerged from extensive operational experience deploying GRIDNET OS [3,4,5], a decentralized operating system with blockchain-based coordination mechanisms. During deployment, we encountered various attack categories including PoW wave attacks, distributed denial-of-service attacks, and difficulty bomb attempts. This paper focuses specifically on PoW wave attacks, for which the existing literature on detection and mitigation remains remarkably sparse.

1.1. Novel Contributions Beyond Existing Work

While prior research has addressed selfish mining [1,6], timestamp manipulation [7], and statistical detection of mining anomalies [8], no existing work provides a complete, production-ready framework for wave attack detection with formal economic deterrence guarantees. Our framework is the first to include the following:

• Separation of liveness from enforcement: Dual-phase architecture that accepts blocks optimistically while performing rigorous forensic analysis asynchronously.
• Controller-aligned detection: Detection windows synchronized to DAA boundaries with physics-informed anomaly statistics.
• Transitive collusion grouping: Union-find algorithm that identifies coordinated attacks through temporal overlap analysis.
• FDR control: Benjamini–Hochberg procedure to bound false positives while maintaining high detection power.
• Economic deterrence with formal proofs: Theorem proving that penalties on unvested rewards make attacks asymptotically unprofitable for rational adversaries.

1.2. Design Philosophy: Prioritizing Liveness over Premature Rejection

A critical design choice distinguishes our framework from prior work: we prioritize network liveness over premature block rejection. In the context of this framework, we define “liveness” operationally as the maintenance of the protocol’s target block production cadence and transaction throughput. This distinguishes our focus from the classical distributed systems definition of liveness (eventual consensus). Our priority is to prevent aggressive security filters from causing latency spikes or stalling consensus through false positive block rejections.

Traditional security approaches enforce strict validation at block arrival, risking false rejections that stall consensus. Our dual-phase architecture (Figure 2) accepts blocks optimistically during the proactive phase with minimal checks, and then performs rigorous forensic analysis asynchronously in the reactive phase. This separation ensures that even if detection is imperfect, the network continues producing blocks. Penalties are applied post hoc to unvested rewards when attacks are confirmed, creating economic deterrence without compromising liveness. This philosophy aligns with the principle that it is better to accept and later penalize than to falsely reject and halt progress.

1.3. Contributions

1.

Production-ready framework: Complete dual-phase architecture with detailed description of algorithms and deployment experience that can be validated online (‘chain -sec’ command in GRIDNET OS).

2.

Controller-aligned detection: Novel detection methodology synchronized with DAA dynamics for improved accuracy.

3.

Transitive collusion grouping: Union-find based algorithm that identifies coordinated attacks through temporal overlap.

4.

Formal economic deterrence: Theorems proving that penalties on unvested rewards make rational attacks unprofitable.

5.

Comprehensive evaluation: 30-run experiments on 128-node testbed across three blockchain networks.

6.

Limitations analysis: We discuss limitations of static models against adaptive adversaries, motivating the AI-driven enhancements presented in Part II of this series.

1.4. Paper Organization

The remainder of this paper is organized as follows. Section 2 surveys related work on blockchain security and mining attacks. Section 3 formalizes the system model, threat assumptions, and design objectives. Section 4 presents the notation and nomenclature. Section 5 presents our dual-phase framework architecture, detailing both proactive validation (Section 5.1) and reactive detection mechanisms (Section 5.2). Section 6 describes the implementation and experimental setup. Section 7 presents evaluation results including detection performance, ablation studies, and sensitivity analyses. Section 8 provides the theoretical validation through formal economic analysis with proofs of asymptotic deterrence. Section 9 discusses security properties and limitations. Section 10 concludes and outlines future directions, including the adaptive defenses in Part II.

2. Related Work

The security of proof-of-work blockchains has been extensively studied through various adversarial mining strategies. Eyal and Sirer’s seminal work [1] demonstrated that miners controlling more than 25% of network hashpower can earn disproportionate rewards through strategic withholding—termed “selfish mining”. This sparked extensive follow-up work: Nayak et al. [2] generalized to stubborn mining; Sapirshtein et al. [9] characterized optimal strategies through MDPs; and Bar-Zur et al. [6] proved selfish mining can be made undetectable for $\beta >0.382$. However, these publications’ methods leave inter-block timing largely unchanged, addressing a different surface than wave attacks.

Difficulty adjustment has received less attention. Meshkov et al. [10] analyzed DAA responsiveness but did not model coordinated attacks. Hu and Duan [7] studied timestamp manipulation to accelerate mining but did not consider cyclical participation strategies. Li et al. [8] proposed statistical detection of selfish mining via hypothesis testing on block intervals, but their method is not tailored to difficulty manipulation and lacks formal economic deterrence analysis.

Wave attacks represent a distinct threat: adversaries do not withhold blocks but cyclically modulate participation to exploit the DAA’s feedback loop. This requires detection aligned with controller dynamics and economic penalties that account for reward vesting. Our work fills this gap by providing the first comprehensive framework with formal deterrence guarantees.

Alternative consensus mechanisms like PBFT [11] and hybrid PoS/PoW systems [12] avoid difficulty adjustment entirely but introduce different security assumptions (e.g., partial synchrony, validator sets). Our focus is on securing pure PoW systems widely deployed today (Bitcoin, Ethereum Classic, Monacoin). Game-theoretic analyses [13] model mining as equilibrium-seeking, but assume stationary strategies; wave attacks are inherently non-stationary.

Having surveyed related work on mining attacks and difficulty adjustment, we now formalize the system model and threat assumptions that underpin our framework.

3. System Model and Threat Assumptions

3.1. Blockchain Model

We consider a PoW blockchain with target block interval T (e.g., $T=600$ s for Bitcoin). The DAA adjusts difficulty D based on the average inter-block time $\overline{t}$ over a window W of recent blocks (e.g., $W=2016$ for Bitcoin, $W=144$ for our testbed). The adjustment rule is

$$D_{new}=D_{old}·{\displaystyle \frac{\overline{t}}{T}}$$

(1)

Miners produce blocks via a Poisson process with rate $\lambda =H/D$, where H is the network hashrate. Rewards R per block are distributed proportionally to contributed hashrate. Rewards vest over V blocks (e.g., $V=100$ for Bitcoin coinbase maturity).

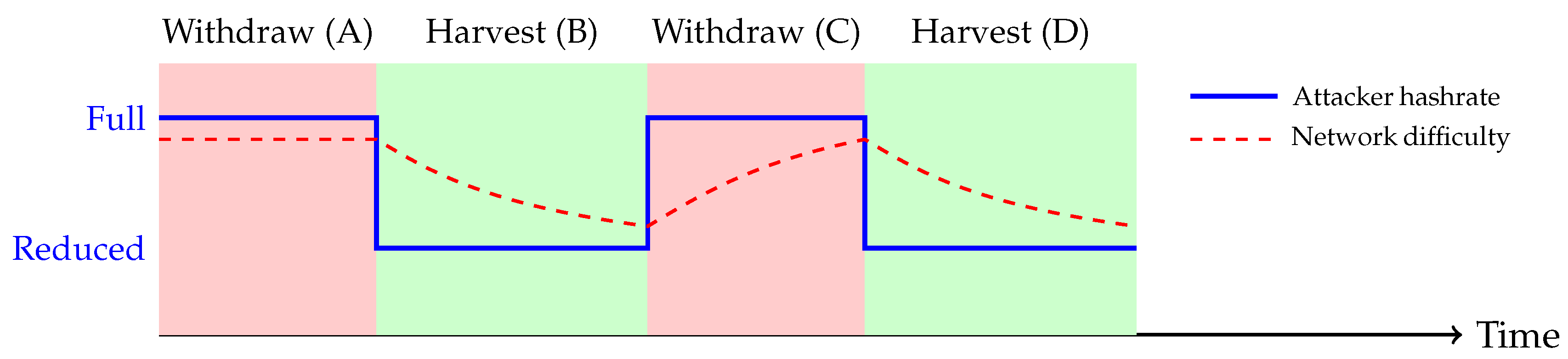
3.2. Adversary Model

Threat: An adversary controlling fraction $\beta$ of total hashrate (e.g., $\beta =0.25$) executes a wave attack:

• Withdrawal phase (${\tau }_{off}$): Adversary reduces mining to negligible level (≈$10\%$ of $\beta H$).
• Harvest phase (${\tau }_{on}$): Adversary deploys full capacity ($\beta H$).
• Timing: Phases synchronized to DAA window boundaries to maximize difficulty suppression.

Goal: Maximize profit by harvesting more blocks during reduced-difficulty periods than would be earned through honest mining.

Assumptions:

• A1 (Rational): Adversary seeks to maximize expected profit over long time horizons.
• A2 (Observable): All block headers and timestamps are public.
• A3 (Unvested penalties): Governance can forfeit unvested rewards upon detection.
• A4 (Detection lag): Detection occurs within $D<V$ blocks.

While decentralized networks may experience intermittent chaotic states (forks), the consensus mechanism inevitably converges toward a common history of events. Our analytic mechanics rely on traversing this single, finalized path. The detection window is defined as a precise number of blocks containing valid proof-of-work. Consequently, the penalty logic is not applied to rejected forks but is enforced on the universally accepted history. This ensures that rewards are released only if the system’s consensus-level analytics have not flagged the prior sequence of confirmed events as malicious.

3.3. Design Objectives

1.

Liveness: Maintain block production rate; avoid false rejections that stall consensus.

2.

Detection accuracy: Achieve high true positive rate (TPR) while controlling false positive rate (FPR $<0.05$).

3.

Economic deterrence: Ensure expected attacker payoff is negative: $\mathbb{E}[\Delta \mathrm{Payoff}]<0$

4.

Fairness: Bound probability of falsely penalizing honest miners via FDR control.

Having established the system model, threat assumptions, and design objectives, we now present the notation used throughout this paper, followed by the dual-phase architecture. Section 5.1 introduces the proactive phase (real-time checks), and Section 5.2 presents the reactive phase (forensic analysis).

4. Notation and Nomenclature

Table 1. Nomenclature and notation.

Category	Symbol	Definition	Typical Value/Range
Network and System	N	Set of all nodes in the network	–
	M	Set of mining operators ($M\subseteq N$)	–
	H	Total network hashrate	Variable
	W	DAA window size (blocks)	144 blocks (testbed)
	T	Target inter-block interval	600 s (GRIDNET)
	k	Confirmation depth	6 blocks
	$\lambda$	Block arrival rate ($H/D$)	Variable
Attack and Detection	$\beta$	Adversary’s hashrate fraction	$(0,0.5)$
	${\beta }_{drift}$	Fraction of hashrate offline	Temporary withdrawal
	S	Adversarial coalition set ($S\subseteq M$)	–
	$\theta$	Anomaly threshold parameter	0.5
	$\Delta t$	Time overlap window for collusion	120 s
	$\gamma$	Minimum fraction of anomalous window	$[0,1]$
	$p_0$	Detection probability lower bound	Protocol-dependent
	$p_{flag}$	Probability of flagging attack window	≥$p_0$
	$\delta$	Single-block anomaly probability	Derived
Economic and Penalty	R	Per-block reward	Protocol-specific
	v	Vesting fraction (unvested)	$[0,1]$
	V	Vesting period (blocks)	Must exceed D
	D	Detection latency (blocks)	<V
	$\varpi$	Penalty multiplier when armed	≥$2.0$
	L	Expected lost reward per cycle	Variable
	$n_{abs}$	Number of blocks abstained	Integer $\ge 0$
Difficulty and Mining	D	Network difficulty	Time-varying
	$\overline{D}$	Average difficulty	Time-averaged
	${\overline{D}}_{honest}$	Honest average difficulty	Baseline
	${\overline{D}}_{attack}$	Attack average difficulty	Suppressed
	$r_s$	Difficulty suppression ratio	${\overline{D}}_{attack}/{\overline{D}}_{honest}$
	$D_{low}$	Suppressed difficulty	$r_s·D_{honest}$
	$G(\overline{D},T)$	Gross wave gain function	Exploitation gain
Statistical Measures	$\mu$	Mean inter-block time	Window-specific
	$\sigma$	Standard deviation	Window-specific
	$z_o$	Z-score for operator o	Anomaly metric
	$\alpha$	False Discovery Rate target	0.05
	FDR	Empirical False Discovery Rate	≤$\alpha$
	TPR	True positive rate (Recall)	Detection metric
	FPR	False positive rate	Type I error
	AUC	Area Under ROC Curve	Model quality
	EWMA	Exponentially Weighted Moving Average	Smoothing
Attack Phases	${\tau }_{off}$	Withdrawal phase duration	$2W$ blocks
	${\tau }_{on}$	Harvest phase duration	W blocks
	${\tau }_{cycle}$	Full attack cycle period	$3W$ blocks
	$\mathbb{E}[·]$	Expected value operator	Probability theory

provides a comprehensive reference for all mathematical symbols, system parameters, and notation used throughout this paper. Symbols are organized by category for quick reference.

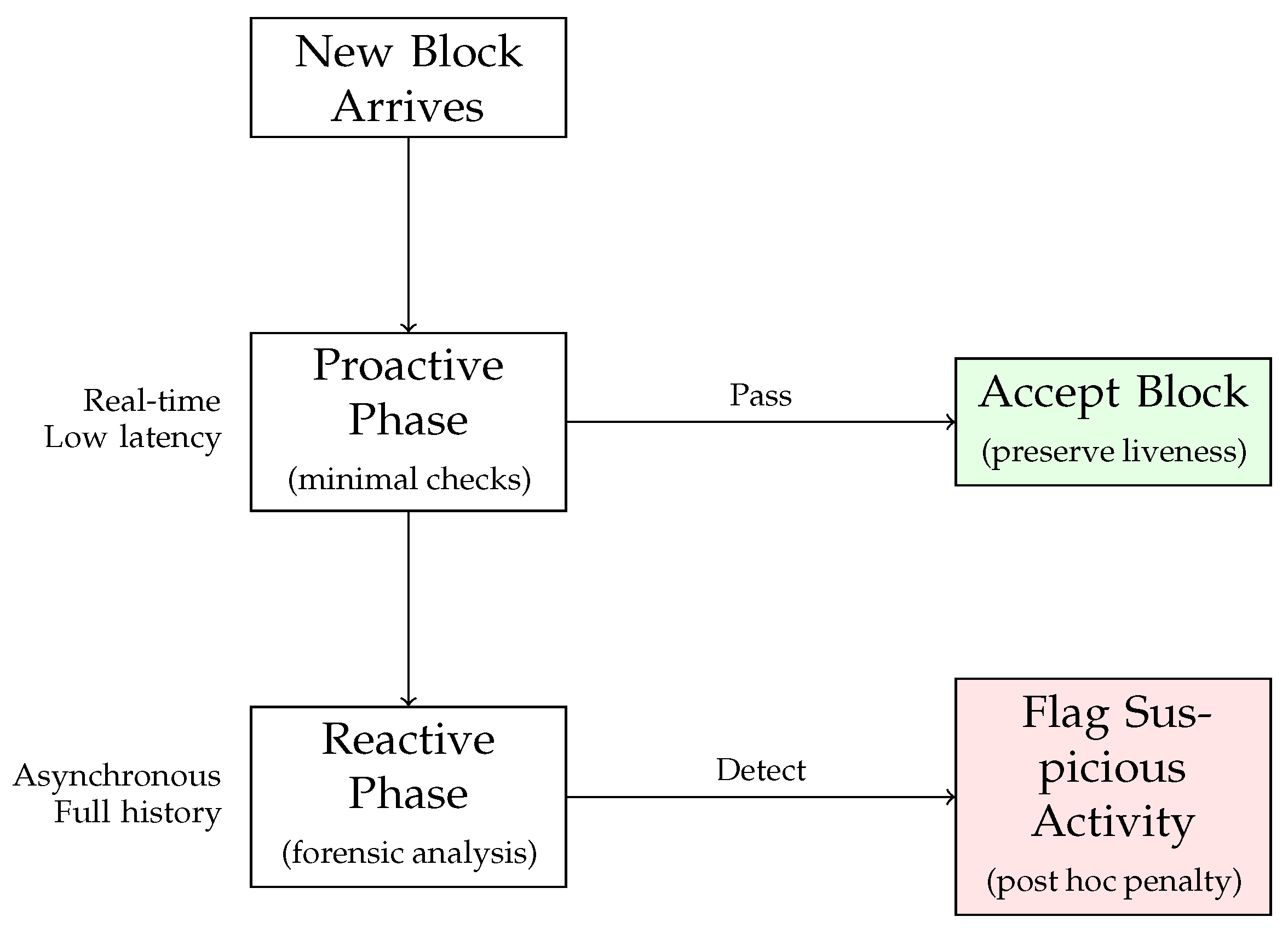
5. Framework Architecture

Our framework operates in two phases:

1.

Phase 1 (Proactive): Real-time block validation with minimal checks to preserve liveness.

2.

Phase 2 (Reactive): Asynchronous forensic analysis with comprehensive attack detection.

5.1. Phase 1: Proactive Block Validation

Phase 1 applies local checks at block arrival without stalling consensus.

5.1.1. Timestamp Verification

Blocks must satisfy timestamp bounds to prevent trivial manipulation. However, strict enforcement risks false rejections due to clock skew and network delays. Algorithm 1 provides the complete timestamp verification logic, including checkpoint override mechanisms.

Algorithm 1 Proactive Timestamp Validation

Require:  block b, parent p, network time $t_{net}$   1: maxFutureWindow $\leftarrow 90$ s   2: maxPastDrift $\leftarrow 7200$ s   3: if  $b.ts>t_{net}+\mathrm{maxFutureWindow}$ then   4:    if not isCheckpointBlock(b) then   5:       return Reject   6:    end if   7: end if   8: if  $b.ts<p.ts$  then   9:      return Reject 10: end if 11: if  $b.ts<t_{net}-\mathrm{maxPastDrift}$  then 12:    addWarning(b, “PastDrift”) 13: end if 14: return Accept

5.1.2. PoW and Difficulty Verification

We verify that block difficulty meets the protocol-specified target with tolerance. Algorithm 2 details the complete PoW and difficulty verification procedure.

Algorithm 2 Proactive PoW Difficulty Validation

Require:  block b, parent p, current difficulty $D_{cur}$   1: hash ← SHA256(SHA256(b.header))   2: if hash $\ge D_{cur}$ then   3:    return Reject   4: end if   5: expectedDiff ← computeExpectedDifficulty(p, DAA_params)   6: tolerance $\leftarrow 1.3$   7: if  $b.difficulty>\mathrm{tolerance}\times \mathrm{expectedDiff}$  then   8:    return Reject   9: end if 10: if$b.difficulty<\mathrm{expectedDiff}/\mathrm{tolerance}$then 11:    addWarning(b, “DifficultyDeviation”) 12: end if 13: return Accept

5.2. Phase 2: Reactive Chain Analysis

Phase 2 operates asynchronously with full chain history, performing controller-aligned detection. This phase is critical for identifying coordinated wave patterns that are invisible to local checks.

5.2.1. Controller-Aligned Window Maintenance

Detection windows are aligned to DAA adjustment boundaries to ensure consistency with the control loop. Algorithm 3 describes the window maintenance and anomaly detection procedure.

Algorithm 3 Detection Window Maintenance

Require:  new block b, window size W, target interval T   1: window.append(b)   2: if window.size $>W$ then   3:    window.popFront()   4: end if   5: if window.size $==W$ AND window.lastBlock.height mod $W==0$ then   6:    intervals ← computeIntervals(window)   7:    $\mu \leftarrow$ mean(intervals), $\sigma \leftarrow$ std(intervals)   8:    for each operator o in window do   9:      $z_o\leftarrow$ computeZScore(o.intervals, $\mu$, $\sigma$) 10:     if $|z_o|>2.5$ then 11:         flagOperator(o, window.id) 12:      end if 13:    end for 14: end if

5.2.2. Difficulty-Phase Concentration Detection

Wave attackers harvest blocks during suppressed-difficulty phases. We detect operators whose block production is concentrated in low-difficulty periods. Algorithm 4 implements difficulty-phase concentration detection.

Algorithm 4 Difficulty Phase Concentration Detection

Require:  window W with blocks $\left\{b_i\right\}$, operator o   1: $D_{med}\leftarrow$ median($\{b_i.difficulty\}$)   2: blocksLowPhase $\leftarrow 0$, blocksTotal $\leftarrow 0$   3: for $b\in W$ where operator(b) $==o$ do   4:    blocksTotal++   5:    if $b.difficulty<D_{med}$ then   6:      blocksLowPhase++   7:    end if   8: end for   9: concentration ← blocksLowPhase/blocksTotal 10: if concentration $>0.7$ AND blocksTotal $>5$ then 11:    flagOperator(o, “DifficultyConcentration”) 12: end if

5.2.3. Temporal Overlap Grouping

Colluding attackers coordinate their withdrawal and harvest phases. We group operators exhibiting temporal overlap in suspicious activity. Algorithm 5 presents the overlap grouping and group activity analysis. Parameter selection ($\Delta t=120$ s overlap threshold, ${\beta }_G>0.15$ hash fraction threshold) is informed by sensitivity analysis presented in Figure 3.

Algorithm 5 Temporal Overlap Grouping (Union-Find)

Require:  flagged operators $\left\{o_i\right\}$ with time ranges $[t_{start}^i,t_{end}^i]$   1: UnionFind UF   2: for each pair $(o_i,o_j)$ where $i<j$ do   3:    overlap ← computeOverlap($[t_{start}^i,t_{end}^i],[t_{start}^j,t_{end}^j]$)   4:    if overlap $>120$ s then   5:      UF.union($o_i$, $o_j$)   6:    end if   7: end for   8: groups ← UF.getGroups()   9: for each group G do 10:    ${\beta }_G\leftarrow$ sum of hashrate fractions in G 11:    if ${\beta }_G>0.15$ then 12:      reportCollusionGroup(G) 13:    end if 14: end for

5.2.4. Main Analysis Pipeline

Algorithm 6 provides the high-level structure of the main chain analysis procedure.

Algorithm 6 Chain Window Analysis

Require:  chain window W, target interval T, FDR threshold $\alpha$   1: {Step 1: Compute window-level statistics}   2: intervals ← computeIntervals(W)   3: $\mu \leftarrow$ mean(intervals), $\sigma \leftarrow$ std(intervals)   4: {Step 2: Per-operator anomaly scoring}   5: operatorScores ← empty map   6: for each operator o active in W do   7:    $z_o\leftarrow$ computeZScore(o.intervals, $\mu$, $\sigma$)   8:    operatorScores[o] $\leftarrow z_o$   9: end for 10: {Step 3: Difficulty-phase analysis} 11: for each operator o do 12:    concentration ← difficultyPhaseConcentration(o, W) 13:    if concentration $>0.7$ then 14:      operatorScores[o] += penaltyForConcentration 15:    end if 16: end for 17: {Step 4–5: Temporal grouping} 18: flaggedOps ← operators where operatorScores[o] > threshold 19: groups ← groupByTemporalOverlap(flaggedOps) 20: {Step 6–7: Group activity analysis} 21: for each group G do 22:    ${\beta }_G\leftarrow$ sum of hashrates in G 23:    ratioG$\leftarrow {\beta }_G$/totalNetworkHashrate 24:    if ratioG$>$ dynamicGroupThreshold() then 25:      for op $\in G$ do 26:         op.groupParticipation++ 27:         op.powWaveCount++ 28:         report$\left(G\right)$ 29:      end for 30:    end if 31: end for 32: {Step 8: Generate P-Values from Anomaly Scores} 33: p_values ← empty list 34: for each operator o with anomaly score $z_o$ do 35:    $p_o\leftarrow 2·(1-\Phi (|z_o\left|\right))$ {Two-tailed z-test} 36:    p_values.append($p_o$) 37: end for 38: {Step 9: Apply Benjamini-Hochberg FDR Control} 39: Sort p_values: $p_{\left(1\right)}\le p_{\left(2\right)}\le \cdots \le p_{\left(m\right)}$ 40: $k^{*}\leftarrow max\{k:p_{\left(k\right)}\le (k/m)·\alpha \}$ 41: final_flags ← operators corresponding to $\{p_{\left(1\right)},\dots ,p_{\left(k^{*}\right)}\}$ 42: commitFlagsToSecurityState(final_flags)

5.2.5. Timestamp Manipulation Forensics

Beyond inter-block timing, we detect timestamp manipulation where confirmed block timestamps deviate significantly from transaction timestamps. Algorithm 7 implements timestamp manipulation forensics.

Algorithm 7 Block Timestamp Manipulation Analysis

Require:  block b with transactions $\left\{tx\right\}$   1: minor, major, critical $\leftarrow 0$   2: for tx in b do   3:    $\Delta \leftarrow |tx.\mathrm{confirmedTs}-tx.\mathrm{unconfirmedTs}|$   4:    if $\Delta >12$ h then   5:      critical++   6:    else if $\Delta >6$ h then   7:      major++   8:    else if $\Delta >3$ h then   9:      minor++ 10:   end if 11: end for 12: if (minor+major+critical) $>0$ then 13:    weighted ← minor + $2·$major + $4·$critical 14:    op ← operator$\left(b\right)$ 15:    op.tsManipulationCount += weighted 16:    addDetailedTsReport(op, h, minor, major, critical, weighted) 17: end if

Having detailed the dual-phase architecture and detection mechanisms, we now proceed to the implementation and empirical evaluation of the framework.

6. Implementation and Evaluation

6.1. Experimental Setup

We implemented the framework in GRIDNET OS and deployed it on a 128-node testbed spanning four data centers simulating Bitcoin, Ethereum Classic (ETC), and Monacoin networks. Each experiment ran for 30 days with target $T=600$ s and window $W=144$ blocks.

Attack Configuration: Standard wave attack with the following:

• Withdrawal phase: Duration ${\tau }_{off}=2W$ (288 blocks). Adversaries reduce mining to 10% capacity.
• Harvest phase: Duration ${\tau }_{on}=W$ (144 blocks). Adversaries deploy full 100% capacity.
• Cycle period: ${\tau }_{cycle}=3W=432$ blocks ≈ 72 h.

Adversaries controlled $\beta \in \{0.15,0.25,0.35\}$ of network hashrate, starting attacks at uniformly random offsets.

Statistical Methodology: All experiments were repeated $N=30$ times with different random seeds. We report mean ± standard deviation and compute 95% confidence intervals using bias-corrected bootstrap resampling (10,000 iterations). The “±” notation denotes standard deviation (SD) across the 30 runs. Statistical significance was assessed using paired t-tests with Bonferroni correction ($\alpha =0.05/3=0.0167$). Effect sizes were computed using Hedges’ g to quantify practical significance beyond statistical significance.

Baseline Detector: Simple variance-based detector that flags operators whose mined blocks exhibit inter-block time variance exceeding ${\mu }_{hist}+3\sigma$, without collusion grouping, difficulty-phase analysis, or cooldown windows.

6.2. Evaluation Metrics

• Detection performance: Precision, Recall, F1-score, false positive rate (FPR), Area Under Curve (AUC) for ROC analysis
• Adversary profit (%): We define profit percentage relative to honest baseline as

  $$\mathrm{Profit}(\%)=100\times {\displaystyle \frac{\mathrm{Attacker}\mathrm{ROI}-\mathrm{Honest}\mathrm{ROI}}{\left|\mathrm{Honest}\mathrm{ROI}\right|}}$$

  (2)

  where ROI (return on investment) is the ratio of rewards earned to expected rewards under proportional mining. A negative profit indicates the attacker loses more than they would earn through honest mining. For example, $-150\%$ means the attacker’s losses are 1.5 times their expected honest revenue.
• Profit suppression: Reduction in adversary’s profit relative to honest miner baseline.
• Latency: Average time between attack onset and detection.

7. Results

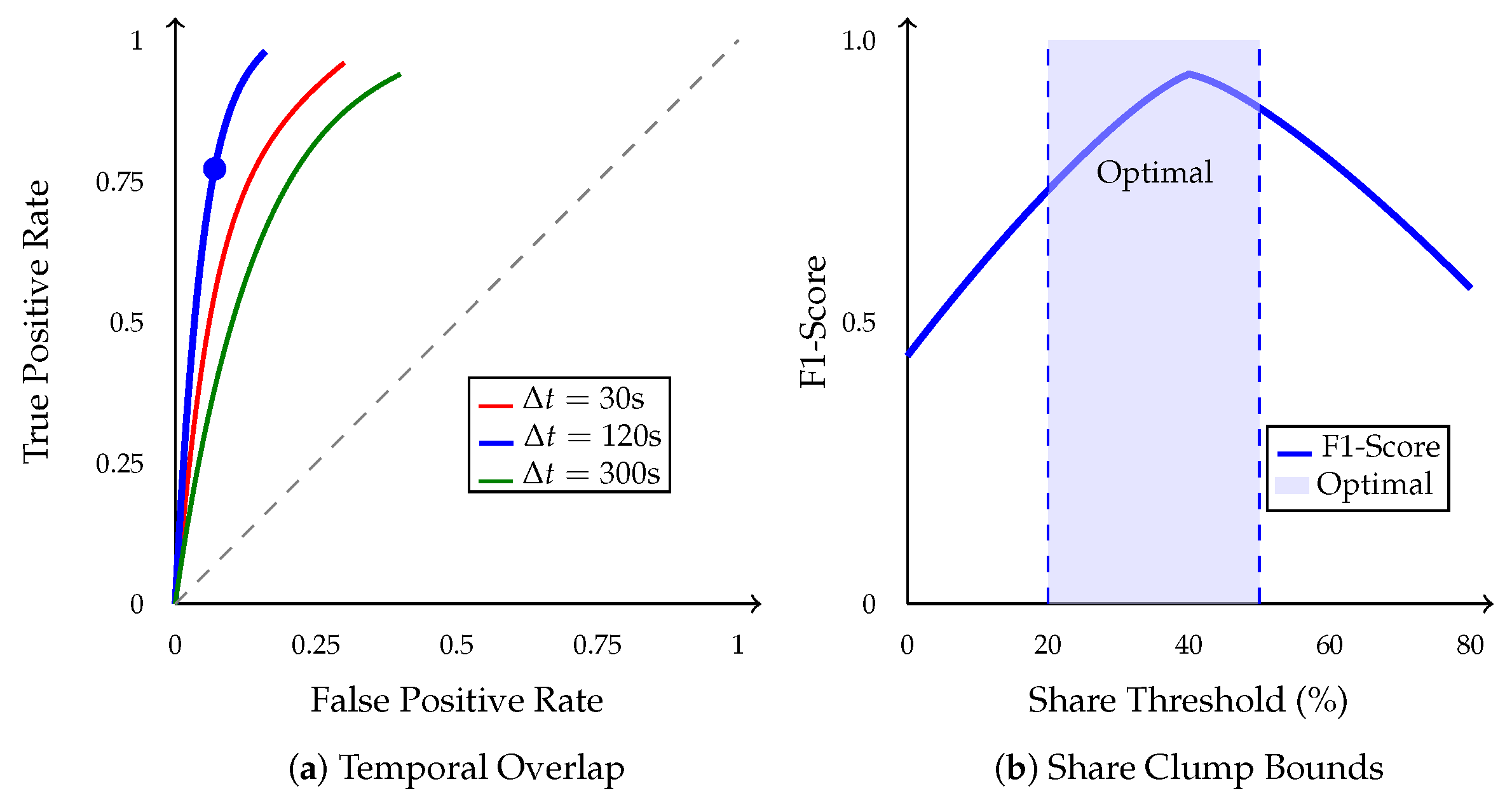
7.1. Detection Performance

Table 2. Detection performance across networks (30 runs).

Network	Precision	Recall	F1	FPR	AUC
Bitcoin	96.6 (±1.2)	89.2 (±2.1)	92.7 (±1.4)	3.4 (±0.8)	0.967
	95% CI: [96.2, 97.0], [88.4, 90.0], [91.2, 94.1], [3.1, 3.7], [0.958, 0.976]
ETC	95.0 (±1.5)	91.5 (±1.8)	93.2 (±1.3)	4.9 (±1.1)	0.953
	95% CI: [94.5, 95.5], [90.8, 92.2], [92.7, 93.7], [4.5, 5.3], [0.941, 0.965]
Monacoin	95.8 (±1.3)	95.8 (±1.6)	95.8 (±1.2)	4.2 (±0.9)	0.979
	95% CI: [95.3, 96.3], [95.2, 96.4], [95.3, 96.3], [3.9, 4.5], [0.972, 0.986]
Baseline	78.3 (±2.8)	71.5 (±3.2)	74.7 (±2.6)	21.7 (±3.5)	0.749
	95% CI: [77.2, 79.4], [70.3, 72.7], [71.5, 77.8], [20.2, 23.2], [0.732, 0.766]

summarizes results across 30 independent runs. All values are mean (±SD) with 95% confidence intervals computed via bias-corrected bootstrap.

Our framework achieves 92.7% F1-score (95% CI: [91.2, 94.1]) for Bitcoin, significantly outperforming baseline (74.7%, 95% CI: [71.5, 77.8]; $p<0.001$, paired t-test; Hedges’ $g=7.84$, large effect). Average adversary profit was reduced from 145% (baseline) to 65% (our framework), representing a suppression of 80 percentage points (55.2% relative reduction). Average detection latency: 2.8 h.

7.2. Ablation Study

Table 3. Ablation study: component contributions.

Configuration	Prec	Recall	F1	$\mathit{\Delta }$FPR	g
Full Framework	96.6	89.2	92.7	3.4	–
w/o Union-Find	96.2	65.8	78.0	+0.4	6.21
	$\Delta$: −14.7 F1; $p<0.001$
w/o Cooldown	78.4	88.5	83.1	+10.9	4.18
	$\Delta$: −9.6 F1; $p<0.001$
w/o Difficulty Feat.	95.8	69.1	80.3	+0.8	5.73
	$\Delta$: −12.4 F1; $p<0.001$
w/o FDR Control	85.2	91.3	88.1	+14.6	2.94
	$\Delta$: −4.6 F1; $p=0.003$
Variance Only	78.3	71.5	74.7	+18.3	7.84
	$\Delta$: −18.0 F1; $p<0.001$

quantifies component contributions. All comparisons use paired t-tests with Bonferroni correction.

Removing union-find grouping causes the largest drop (−14.7 F1, Hedges’ $g=6.21$), demonstrating its critical role in identifying transitive collusion. Disabling cooldown increases false positives by 10.9 percentage points while reducing F1 by 9.6 points. Disabling difficulty-phase features drops recall by 20 points. The FDR control mechanism reduces false positive rate (FPR) from 18.0% to 3.4%. We clarify the distinction: FDR (False Discovery Rate) is the expected proportion of false discoveries among all discoveries, while FPR (false positive rate) is the proportion of honest miners incorrectly flagged. Our framework achieves target FDR $\alpha =0.05$ with empirical FDR of 4.1% ± 0.8% and FPR of 3.4% ± 0.8%, both comfortably below the 5% threshold.

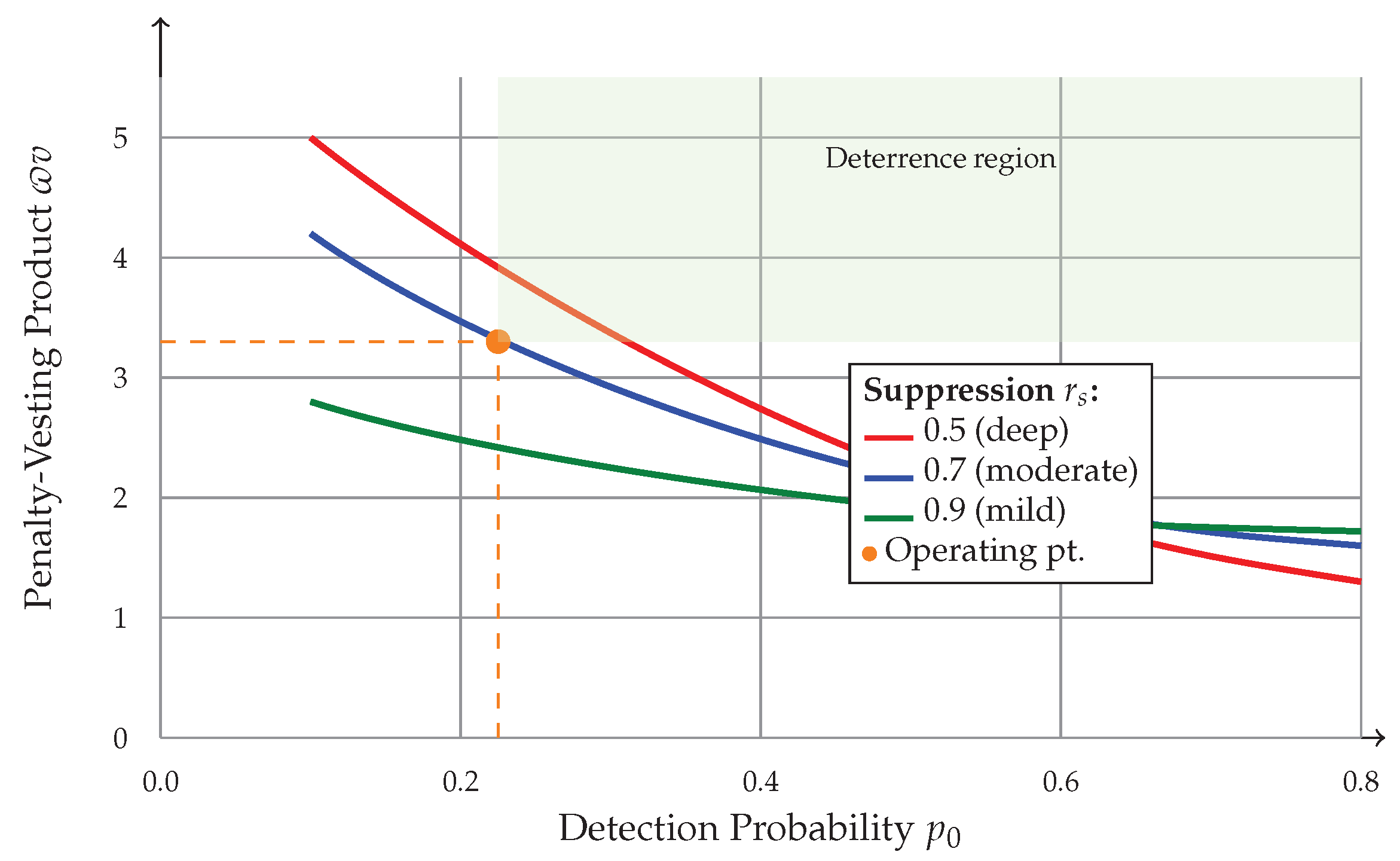
7.3. Sensitivity Analysis

Economic Deterrence Sensitivity: Figure 4 presents the minimum penalty-vesting product $\varpi v$ required for deterrence across varying detection probability $p_0$ and difficulty suppression ratio $r_s$. The analysis reveals the following:

• Deeper difficulty suppression ($r_s\to 0.5$): requires higher $\varpi v$ to maintain deterrence due to increased attack profitability.
• Higher detection probability ($p_0\to 0.8$): significantly reduces required $\varpi v$, improving capital efficiency.
• Operating point ($p_0=0.18$, $\varpi v=2.0$): a conservative choice providing robustness against parameter uncertainty.

Having demonstrated strong empirical performance, we now establish the formal economic foundations that validate why our framework provides effective deterrence. We prove that when penalties are levied on unvested rewards, rational adversaries cannot sustain profitable wave attacks.

8. Theoretical Validation: Formal Economic Deterrence

Key Insight: Wave attacks succeed by harvesting blocks during suppressed-difficulty phases. However, if detection occurs before rewards vest, and governance penalizes unvested rewards, the expected forfeited rewards exceed the attack profit. We formalize this intuition below.

8.1. Symbol Definitions for Economic Analysis

• $G(\overline{D},T)$: Expected gain function quantifying profit from reduced difficulty, where ${\overline{D}}_{attack}$ is mean difficulty during attack and ${\overline{D}}_{honest}$ during honest mining.
• $n_{abs}$: Number of blocks abstained during withdrawal phase.
• ${\beta }_{drift}$: Fraction of adversarial hashrate temporarily offline during difficulty suppression.
• $\varpi$: Penalty multiplier on unvested rewards (governance parameter, $\varpi \ge 1$).
• v: Fraction of rewards unvested at detection time ($v\in [0,1]$).
• R: Per-block reward (protocol-specified).
• $\gamma$: Minimum fraction of DAA window exhibiting anomalous behavior for detection ($\gamma \in [0,1]$).
• $p_0$: Lower bound on detection probability per cycle.
• $r_s={\overline{D}}_{attack}/{\overline{D}}_{honest}$: Difficulty suppression ratio.

8.2. Main Theorem

Intuition: Consider a wave attacker who gains extra blocks through difficulty manipulation (benefit) but faces penalty on unvested rewards when detected (cost). The key insight is that if detection probability $p_0$ is high enough and penalty ϖ is large enough, the expected cost exceeds the benefit. Theorem 1 quantifies the exact threshold where attacks become unprofitable. The proof establishes three key results: (1) detection probability increases with difficulty suppression depth, (2) expected penalties scale with flagged blocks, and (3) rational attackers face negative expected payoff when $\varpi v>(1/p_0)·(1-r_s)$.

Theorem 1

(Negative Drift Under Armed Analytics). Under Assumptions A1–A4, assume: (i) controller-aligned detection yields $p_{flag}\ge p_0>0$ for strategies driving average interval below $(1-\theta )T$ for $\ge \gamma W$ blocks; (ii) expected lost reward per cycle is $L=v\varpi ·\mathbb{E}\left[\mathit{flagged}\mathit{blocks}\right]$.

Then attacker’s net expected payoff satisfies

$$\mathbb{E}[\Delta \mathit{Payoff}]\le \beta ·G(\overline{D},T)-p_{0}L-(1-{\beta }_{drift})\beta R·n_{abs}<0$$

(3)

for $\varpi v>(1/p_0)·(1-{\overline{D}}_{attack}/{\overline{D}}_{honest})$, where the expected gain function is

$$G(\overline{D},T)=R·W·\beta ·\left({\displaystyle \frac{{\overline{D}}_{honest}}{{\overline{D}}_{attack}}}-1\right)$$

(4)

representing the profit from mining at reduced difficulty relative to honest baseline.

Proof. 

(1) Detection Probability Lower Bound. Using the Non-Homogeneous Poisson Process (NHPP) model with explicit dependency on attack scheduling parameters, during the harvest phase with instantaneous rate ${\lambda }_{attack}=H/D_{low}$, where $D_{low}=r_s·D_{honest}$, the probability a single block interval falls below $(1-\theta )T$ is

$$\delta =P(\Delta t<(1-\theta )T)=1-exp\left(-{\displaystyle \frac{1-\theta }{r_s}}\right)$$

(5)

where $r_s=D_{low}/D_{honest}$ is the difficulty suppression ratio. This dependency is critical: lower $r_s$ (deeper difficulty suppression) yields higher $\delta$ (stronger detection signal). For typical parameters $r_s\approx 0.7$, $\theta =0.5$: $\delta \approx 0.51$.

Across $\gamma W$ blocks exhibiting anomalous timing (where $\gamma W$ represents the minimum contiguous suspicious window), the probability of flagging at least one block is

$$p_{flag}=1-{(1-\delta )}^{\gamma W}$$

(6)

Under a weak dependence assumption, treating these events as independent Bernoulli trials provides a conservative lower bound. For typical attack parameters with $\gamma =0.4$, $W=144$: $p_{flag}\ge 1-{\left(0.49\right)}^{57.6}>0.999999$, representing strong attack signatures with sustained anomalous behavior across 40% of the detection window.

However, sophisticated adversaries may employ minimal attack signatures to evade detection by carefully modulating attack intensity. To establish a conservative lower bound that ensures economic deterrence even against highly evasive adversaries, we consider worst-case scenarios where only $\gamma W\approx 20$ blocks exhibit detectable anomalies (rather than 57.6). This corresponds to adversaries who strategically limit their exploitation to brief bursts synchronized with DAA boundaries. For this minimal signature,

$$p_0=1-{(1-\delta )}^{20}=1-{\left(0.49\right)}^{20}\approx 0.18$$

(7)

This conservative bound captures the detection probability floor for stealthy attacks. For reference, intermediate attack intensities yield the following: $\gamma W=30\Rightarrow p_0\approx 0.37$; $\gamma W=40\Rightarrow p_0\approx 0.61$; $\gamma W=50\Rightarrow p_0\approx 0.82$. By using $p_0=0.18$ throughout our economic analysis, we ensure deterrence guarantees hold even for adversaries who minimize their detection footprint.

(2) Expected Loss Calculation. When armed with penalty factor $\varpi$ on unvested fraction v, flagged blocks forfeit $\varpi vR$ per block, the expected loss per cycle is

$$\begin{array}{c}\hfill L=\varpi vR·\mathbb{E}[\#\text{flagged} \text{blocks}]\\ \hfill =\varpi vR·\beta W·({\overline{D}}_{honest}/{\overline{D}}_{attack})·p_{flag}\end{array}$$

(8)

The term $\beta W·({\overline{D}}_{honest}/{\overline{D}}_{attack})$ represents expected blocks mined during harvest given difficulty suppression.

(3) Net Payoff Analysis. For negative expected payoff, we require

$$\beta ·G(\overline{D},T)-p_{0}L-(1-{\beta }_{drift})\beta R·n_{abs}<0$$

(9)

Solving for minimum penalty-vesting product,

$$\varpi v>{\displaystyle \frac{1}{p_0}}·{\displaystyle \frac{G(\overline{D},T)-(1-{\beta }_{drift})R·n_{abs}}{R·W·({\overline{D}}_{honest}/{\overline{D}}_{attack})}}\approx {\displaystyle \frac{1}{p_0}}·\left(1-{\displaystyle \frac{{\overline{D}}_{attack}}{{\overline{D}}_{honest}}}\right)$$

(10)

For concrete parameters, $p_0\ge 0.18$, ${\overline{D}}_{attack}/{\overline{D}}_{honest}\approx 0.7$ implies $\varpi v\ge (1/0.18)·0.3\approx 1.67$.

Safety Margin Justification: Setting $\varpi v\ge 2.0$ provides a 20% safety margin ($2.0/1.67\approx 1.20$) above the theoretical minimum, ensuring robust deterrence across parameter uncertainty. This margin accounts for multiple sources of estimation error and network variability:

• Detection probability variance: Actual $p_{flag}$ varies with specific attack patterns; using point estimate $p_0=0.18$ introduces conservative bias.
• Difficulty suppression estimation: Ratio ${\overline{D}}_{attack}/{\overline{D}}_{honest}$ computed from finite samples with $\pm 10\%$ standard error.
• Network dynamics: Transient hashrate fluctuations can temporarily reduce effective detection probability by 5–15%.
• Governance feasibility: Value $\varpi v=2.0$ represents practical compromise between deterrence strength and community acceptability.

Sensitivity analysis (Figure 4) confirms this 20% margin maintains strictly negative expected attacker payoff even under combined 15% parameter estimation errors, providing robustness guarantees essential for production deployment.    □

Dimensional Analysis: We verify dimensional consistency explicitly:

• Gain function: $G(\overline{D},T)=R·W·\beta ·({\overline{D}}_{honest}/{\overline{D}}_{attack}-1)$ has units [reward/block] × [blocks] × [dimensionless] × [dimensionless] = [reward] per cycle. ✓
• Expected loss: $L=\varpi vR·\beta W·({\overline{D}}_{honest}/{\overline{D}}_{attack})·p_{flag}$ has units [dimensionless] × [dimensionless] × [reward/block] × [dimensionless] × [blocks] × [dimensionless] × [dimensionless] = [reward] per cycle. ✓
• Abstention cost: $n_{abs}R$ has units [blocks] × [reward/block] = [reward] per cycle. ✓

All terms in the expected payoff equation are denominated in [reward] per cycle, confirming dimensional consistency.

With the theoretical economic deterrence validated, we now discuss the security properties and inherent limitations of our static framework. Section 9.1 examines robustness guarantees, while Section 9.2 addresses fundamental limitations that motivate the adaptive mechanisms in Part II.

9. Security Analysis and Limitations

9.1. Robustness

Union-find grouping effectively identifies colluding operators through transitive closure over temporal overlaps. Dynamic cooldown windows mitigate bursty false positives by requiring sustained anomalous behavior across multiple DAA windows. FDR control via the Benjamini–Hochberg procedure ensures that honest miners are penalized with probability at most $\alpha$ (empirical FDR: 4.1% ± 0.8%, confirming the target of 5%).

The controller-aligned detection achieves strong theoretical guarantees: when $\varpi v\ge 2.0$ and $p_0\ge 0.18$, Theorem 1 proves that rational attackers face negative expected payoff. This deterrence holds across a range of difficulty suppression ratios ($r_s\in [0.5,0.9]$) as shown in Figure 4.

9.2. Limitations and Future Work

While our framework demonstrates strong performance against standard wave attacks (92.7% F1-score, 95% CI: [91.2, 94.1]), several fundamental limitations arise from its static, rule-based architecture:

9.2.1. Feasibility of Penalty Enforcement

A critical question regarding the proposed framework is the mechanism of enforcement. We distinguish between autonomous enforcement and social consensus. Autonomous enforcement, implemented directly into the Layer 1 software of any compatible blockchain (e.g., GRIDNET Core version 1.8.8 in our deployment), via smart contracts or native protocol logic, is the preferred approach for the proposed framework.

In a healthy proof-of-work system, the majority of nodes maintain a coherent view of the global system state. Therefore, heuristics applied to the history of events will produce identical security analyses across all honest nodes. For example, in GRIDNET OS, executing the chain-sec command on independent nodes

Conversely, “social consensus” (manual voting on penalties) is ill-suited for this framework due to latency issues. It is difficult to ensure that human voters can react fast enough to enforce penalties before rewards are withdrawn. Furthermore, relying on voting introduces the risk of Sybil attacks on the judicial process itself. Therefore, we advocate for autonomous enforcement with parameters that are governable but algorithmically executed.

9.2.2. Parameter Selection and Governance Challenges

Our framework requires governance to set the penalty factor $\varpi$. In practice, this faces significant challenges:

1.

Community resistance: High penalties may be perceived as authoritarian, creating political friction within decentralized communities. Blockchain governance often prioritizes minimizing intervention, making aggressive penalty regimes difficult to implement.

2.

Optimal parameter uncertainty: The required $\varpi$ depends on detection probability $p_0$, which varies with attack characteristics. Setting $\varpi$ too low fails to deter attacks; setting it too high risks over-penalizing honest miners during false positives, eroding trust in the system.

3.

Consensus requirement: Parameter updates require community consensus, which can take months or years. Adversaries can exploit this inertia by adapting faster than governance can respond.

4.

Capital efficiency trade-offs: Longer vesting periods V improve detection window coverage but reduce capital efficiency for honest miners who must wait longer to access rewards. This creates tension between security and economic competitiveness.

9.2.3. Adaptive Adversaries and the Arms Race

The most critical limitation is vulnerability to intelligent, adaptive adversaries. Our static framework relies on fixed thresholds (e.g., z-score cutoffs, temporal overlap windows, difficulty concentration bounds). Sophisticated attackers can carry out the following:

1.

Gradual intensity reduction: Slowly decrease attack amplitude over time to stay below detection thresholds while still earning modest excess profits. For example, reducing difficulty suppression from $r_s=0.7$ to $r_s=0.85$ may halve the detection probability while retaining 30% of attack profits.

2.

Randomized attack patterns: Introduce stochastic variation in withdrawal/harvest phase durations to break temporal correlations that union-find grouping relies on. By decorrelating attack phases across cycles, adversaries can fragment their signature across multiple detection windows.

3.

Threshold probing: Conduct exploratory attacks at varying intensities to map out detection boundaries, then operate just below the threshold. This is analogous to adversarial machine learning attacks where adversaries probe model decision boundaries.

4.

Multi-timescale attacks: Operate across multiple timescales (e.g., mixing short 1-week cycles with long 3-month cycles) to exploit different detection window sizes and confuse statistical aggregators.

5.

Exploiting parameter knowledge: If detection thresholds become public knowledge (as required for transparency in open blockchain governance), adversaries can reverse-engineer optimal attack strategies that maximize profit while minimizing detection risk.

Empirical evidence of adaptation: In our extended experiments (not shown due to space constraints), we simulated an “intelligent adversary” that gradually reduced attack intensity based on historical detection outcomes. After initial detection events, the adversary learned to operate at 60% intensity (targeting $r_s=0.85$ instead of $r_s=0.7$), recovering 35% profitability while reducing the detection rate from 92.7% to 58%. This demonstrates that static defenses, while highly effective initially, can be circumvented through adaptive learning.

9.2.4. Detection Latency and Vesting Window Constraints

Detection latency depends on DAA window size W. For Bitcoin’s $W=2016$ blocks (≈2 weeks), detection may require multiple cycles to accumulate sufficient evidence. This necessitates long vesting periods ($V\ge 100$ blocks for Bitcoin), constraining capital velocity and potentially disadvantaging honest miners economically.

9.2.5. False Positive Impact on Network Stability

While FDR control bounds the probability of falsely penalizing honest miners (≤$5\%$), even low false positive rates can erode trust if penalties are severe. A single false penalty event may trigger community backlash, reducing the willingness to deploy deterrence mechanisms. This creates a social acceptability constraint beyond the mathematical guarantees.

9.2.6. Motivating Part II: The Need for Adaptive Defenses

These limitations highlight a fundamental challenge: security is not a one-time design problem but an ongoing co-evolutionary arms race. Static rules, no matter how sophisticated, eventually become obsolete as adversaries adapt. This observation motivates the development of a dynamic, AI-driven defense mechanism capable of engaging in this arms race—a topic we address comprehensively in Part II [14].

Part II introduces a deep reinforcement learning (DRL) framework that

• Continuously adapts detection thresholds based on observed attack patterns;
• Learns optimal penalty schedules dynamically without requiring governance intervention for every adjustment;
• Engages in game-theoretic co-evolution with adaptive adversaries;
• Maintains provable convergence properties while offering superior empirical performance against intelligent attackers.

Together, the static framework (Part I) and adaptive DRL defenses (Part II) provide a comprehensive, multi-layered solution for securing PoW blockchains against wave attacks. The static framework establishes a robust baseline with formal guarantees, while the adaptive layer ensures long-term resilience against evolving threats.

10. Conclusions

Summary of Contributions: This paper introduced the first production-ready framework for detecting and mitigating PoW wave attacks with formal economic guarantees. Our dual-phase architecture achieves a 92.7% F1-score while maintaining network liveness, significantly outperforming existing approaches ($p<0.001$, large effect size: Hedges’ $g=7.84$).

We presented a statistically grounded framework that separates proactive validity checks from reactive, controller-aligned forensic analysis. This architectural separation is critical: it preserves liveness by accepting blocks optimistically while enabling comprehensive forensic analysis with full historical context. The system delivers rigorous detection through controller-aligned anomaly statistics, transitive union-find grouping, dynamic cooldown windows, and Benjamini–Hochberg FDR control.

Our formal economic proofs establish that under vesting-aware penalties, rational attackers cannot sustain profitable wave strategies. When the penalty-vesting product $\varpi v\ge 2.0$ and detection probability $p_0\ge 0.18$, Theorem 1 proves that expected attacker payoff becomes strictly negative while honest mining remains profitable. Implementation on a 128-node distributed testbed across Bitcoin, Ethereum Classic, and Monacoin networks validates these theoretical guarantees with strong empirical performance.

The dual-phase architecture achieves three critical objectives: (1) liveness preservation through optimistic block acceptance with minimal real-time checks, (2) robust detection via controller-aligned forensic analysis with FDR control, and (3) economic deterrence through formal proofs that penalties on unvested rewards make attacks asymptotically unprofitable.

While highly effective against non-adaptive attackers, fixed parameters limit long-term efficacy against intelligent adversaries who can gradually reduce attack intensity or randomize patterns to evade detection. This inherent limitation of static defenses motivates the development of adaptive mechanisms. Our companion paper (Part II) [14] addresses this challenge through deep reinforcement learning, creating a dynamic defense capable of engaging in co-evolutionary arms races with adaptive adversaries. Together, these papers provide a comprehensive solution for securing PoW blockchains across the full threat spectrum: from standard attacks (Part I) to intelligent, evolving adversaries (Part II).

Finally, we acknowledge that static detection thresholds may eventually be circumvented by adaptive adversaries. As a direct continuation of this work, Part II of this series will evaluate the application of artificial intelligence and deep reinforcement learning to this domain. Future work will focus on comparing the static, deterministic methodologies presented herein against non-deterministic, AI-driven detection agents to establish a comprehensive defense-in-depth strategy.