Curriculum-Aware Cognitive Diagnosis via Graph Neural Networks

Abstract

Cognitive diagnosis is an important component of adaptive learning, as it infers learners’ latent knowledge states and enables tailored feedback. However, existing approaches often emphasize sequential modeling or latent factorization, while insufficiently incorporating curriculum structures that embody prerequisite relations. This gap constrains both predictive accuracy and pedagogical interpretability. To address this limitation, we propose a Curriculum-Aware Graph Neural Cognitive Diagnosis (CA-GNCD) framework that integrates curriculum priors into graph-based neural modeling. The framework combines graph representation learning, knowledge-prior fusion, and interpretability constraints to jointly capture relational dependencies among concepts and individual learner trajectories. Experiments on three widely used benchmark datasets, ASSISTments2017, EdNet-KT1, and Eedi, show that CA-GNCD achieves consistent improvements over classical probabilistic, psychometric, and recent neural baselines. On average, it improves AUC by more than 4.5 percentage points and exhibits relatively faster convergence, greater robustness to noisy conditions, and stronger cross-domain generalization. These results suggest that aligning diagnostic predictions with curriculum structures can enhance interpretability and reliability, offering implications for personalized learning support. While promising, further validation in diverse educational contexts is required to establish the generalizability and practical deployment of the proposed framework.

1. Introduction

Cognitive diagnosis (CD) has become an essential paradigm in intelligent education systems, enabling fine-grained assessment of learners’ latent skills and knowledge structures [1]. Unlike traditional psychometric methods, CD models leverage machine learning and probabilistic reasoning to infer not only whether a learner answers correctly but also why, thereby providing pedagogically meaningful feedback for adaptive instruction. As education increasingly moves toward data-driven platforms, the need for diagnostic models that are both accurate and interpretable continues to grow [2].

Despite recent advances, existing CD models still face challenges in balancing predictive performance and educational interpretability. Factorization-based methods offer computational efficiency but oversimplify relationships among knowledge concepts [3]. Bayesian network approaches maintain interpretability yet suffer from scalability issues in high-dimensional data [4]. Deep learning–based models, including recurrent and attention mechanisms, have improved predictive accuracy but largely capture statistical correlations without explicitly modeling the pedagogical rationale underlying curriculum hierarchies. Consequently, models often generalize poorly across heterogeneous datasets and remain vulnerable to sparsity or noisy labeling [5].

These limitations highlight the need for frameworks that integrate structured curriculum knowledge, such as prerequisite dependencies and hierarchical relations, directly into model learning. Curriculum priors embody the instructional logic of how concepts are sequentially acquired, providing a powerful form of structural regularization for robust and explainable prediction. Specifically, curriculum progression represents relational rather than temporal dependencies: the order of concepts reflects prerequisite logic rather than chronological learning sequences. Therefore, sequential models such as RNNs or attention-based architectures, which assume time-series ordering, are structurally misaligned with curriculum hierarchies.

To address this gap, the present study proposes a Curriculum-Aware Graph Neural Cognitive Diagnosis (CA-GNCD) framework that explicitly embeds curriculum structures within graph-based neural representations. The model leverages graph neural networks (GNNs) to encode inter-concept relations, integrates curriculum constraints into the learning objective, and enhances interpretability through attention-guided reasoning. The novelty of this work lies not in the isolated use of GNNs or prior fusion, but in their systematic and principled integration into a unified end-to-end framework that jointly optimizes accuracy, structural consistency, and diagnostic transparency.

Building on established foundations of graph-based representation learning, the proposed framework extends theoretical insights from prior studies such as Nakagawa et al. and Yang et al. [6,7], which demonstrated the effectiveness of graph neural architectures in modeling prerequisite relations, by incorporating domain-specific curriculum priors and pedagogical interpretability constraints. This integration aligns algorithmic reasoning with instructional logic, advancing both methodological rigor and educational applicability.

Experimental evaluations across three large-scale benchmark datasets, ASSISTments2017, EdNet-KT1, and Eedi, demonstrate the superiority of CA-GNCD over classical and neural baselines. The model achieves over 4.5 percentage-point gains in AUC and approximately 5% higher accuracy, while maintaining stronger robustness under noisy or incomplete response conditions. Moreover, the integration of curriculum priors produces interpretable diagnostic reports that correspond closely to expert-defined prerequisite relations, illustrating its potential for adaptive learning platforms and classroom-level assessment.

In summary, this study contributes both algorithmically and pedagogically: it advances cognitive diagnosis by offering a principled mechanism for embedding curriculum structures into graph-based neural learning, and it enhances educational practice by generating transparent, curriculum-aligned feedback. The remainder of the paper is organized as follows. Section 2 reviews related studies on cognitive diagnosis, deep learning methods in educational data mining, and graph-based modeling of curriculum structures. Section 3 presents the proposed methodology and optimization objectives. Section 4 reports experimental results, robustness tests, and ablation analyses. Section 5 discusses insights and future research directions, and Section 6 concludes with contributions and implications for adaptive educational systems.

2. Related Works

2.1. Application Scenarios and Challenges

Cognitive diagnosis has become indispensable in a wide range of educational applications, from large-scale online learning platforms to adaptive classroom assessment [1,8]. Typical tasks include predicting student responses, inferring latent knowledge states, and generating diagnostic reports that guide personalized learning paths [9,10]. Widely used datasets such as ASSISTments, EdNet, and Eedi contain millions of learner–item interactions and serve as benchmarks for evaluating diagnostic models [11]. Evaluation metrics typically include accuracy, area under the ROC curve (AUC), and F1-score for predictive tasks, while calibration error (CE) and interpretability measures are increasingly emphasized in recent studies [12]. However, several challenges persist: educational data often exhibit sparsity due to uneven learner participation, concept labeling is noisy or incomplete, and prerequisite structures are difficult to model explicitly [13]. Moreover, most diagnostic tasks require models not only to achieve predictive accuracy but also to generate interpretable and pedagogically valid outputs. Empirical evidence shows that deep neural diagnosis models often lack robustness under heterogeneous or noisy conditions, with studies such as Rice et al. reporting overfitting when curriculum priors are weakly integrated [14]. Balancing scalability, robustness, and explainability remains a central challenge in the field.

2.2. Mainstream Methodological Approaches

Early approaches to cognitive diagnosis were dominated by probabilistic and factorization-based models, which captured learner–item interactions in low-dimensional latent spaces [15,16]. These studies provided efficient solutions for large-scale response modeling and offered new insights into the feasibility of cognitive diagnosis in early intelligent tutoring systems. While computationally efficient, these methods often failed to capture higher-order dependencies between concepts [17].

More recent research has shifted toward deep learning, with models such as recurrent neural networks and attention-based architectures becoming standard [18,19]. Such methods effectively improved predictive accuracy, especially in capturing sequential dependencies of learner responses, and demonstrated their value in benchmark comparisons. Studies published in the past two years have demonstrated that deep knowledge tracing variants can significantly improve predictive accuracy across benchmarks [20]. However, despite their advantages, these models primarily focus on temporal dynamics while paying limited attention to curriculum structures, and their interpretability remains limited. Moreover, empirical analyses in recent surveys (e.g., Shen et al.; Abdelrahman et al.) indicate that accuracy-driven neural diagnosis often generalizes poorly across datasets and requires additional regularization to avoid data bias [21,22].

Graph neural networks (GNNs) have emerged as a promising direction, particularly for modeling relational dependencies among knowledge concepts. Classic graph-based knowledge tracing studies, such as Nakagawa et al. and Yang et al., theoretically demonstrated that GNNs capture hierarchical and contextual relations within curricula more effectively than sequential models [6,7]. Recent work has shown that GNN-based cognitive diagnosis can effectively capture prerequisite relations and improve generalization [23]. Similarly, neural cognitive diagnosis models have attempted to combine feature embeddings with probabilistic assumptions to enhance interpretability [24]. Compared with sequential models, these approaches highlight the role of relational reasoning, yet they still fall short of explicitly aligning their explanations with domain-specific curricular structures. Consequently, the literature reveals a methodological gap between graph-based representation learning and pedagogically interpretable diagnosis models.

2.3. Closely Related Studies

A subset of recent studies has attempted to explicitly integrate curriculum knowledge into cognitive diagnosis. For instance, approaches embedding prerequisite graphs into neural architectures have demonstrated improved alignment with educational theory, while hybrid models combining GNNs with knowledge tracing mechanisms have shown enhanced predictive performance [25]. These graph-aware methods extend the principles, applying graph propagation and message aggregation to educational concept networks. However, most treat curriculum relations as auxiliary signals rather than as structural constraints within model optimization. Other works have investigated the fusion of textual curriculum descriptions with learner–item interactions using natural language processing techniques, thereby enriching semantic representations of concepts [26].

Despite these advances, these approaches typically treat curriculum knowledge as auxiliary features rather than as central modeling priors. Many models lack a principled mechanism to fuse curriculum structures with learned embeddings, resulting in limited robustness under noisy conditions. Furthermore, interpretability is often reported as a secondary outcome rather than as an explicit design objective [27]. For example, while some studies improved alignment with educational theory, they did not examine how these gains transfer across heterogeneous datasets. Similarly, although attention-based methods increase transparency, their explanations may diverge from expert-defined prerequisite graphs, limiting their pedagogical validity [28]. Hence, the field still lacks a systematic framework that integrates graph representation learning, curriculum priors, and interpretability within a unified objective function.

By contrast, the present study places curriculum prior knowledge at the core of the modeling process, combining graph representation learning with constraint-based fusion mechanisms [29]. This integration represents a systematic and principled extension of existing work, bridging the gap between algorithmic accuracy and pedagogical interpretability. In doing so, it offers a robust approach to noisy data and provides transparent diagnostic reports that align with curriculum logic.

2.4. Summary

In summary, existing research demonstrates a clear trajectory from probabilistic models to deep neural architectures and, more recently, to graph-based methods. These developments have substantially improved the predictive capacity of cognitive diagnosis but remain constrained by limited integration of domain knowledge and weak robustness across heterogeneous datasets. While prior studies have introduced GNNs for knowledge tracing and concept modeling, few have pursued a coherent fusion of graph learning, curriculum constraints, and interpretable diagnostic outputs. To address these shortcomings, this study proposes a curriculum-aware GNN framework that systematically integrates prior knowledge into the diagnostic process. Unlike prior studies that treat curriculum structures as auxiliary features, our approach positions them as a central modeling prior and explicitly balances accuracy, robustness, and explainability. This principled integration constitutes the main innovation of the present work.

3. Methodology

3.1. Problem Formulation

Cognitive diagnosis aims to infer learners’ latent knowledge states based on their interactions with educational items under a predefined curriculum structure. Formally, let $\mathrm{U}=\{{\mathrm{u}}_1,{\mathrm{u}}_2,\dots ,{\mathrm{u}}_{\mathrm{N}}\}$ denote the set of learners, where N is the number of participants. Each learner ${\mathrm{u}}_{\mathrm{i}}$ engages with a set of items $\mathrm{I}=\{{\mathrm{q}}_1,{\mathrm{q}}_2,\dots ,{\mathrm{q}}_{\mathrm{M}}\}$, with M denoting the total number of questions or exercises. Each item is associated with one or more knowledge concepts from the set $\mathrm{K}=\{{\mathrm{k}}_1,{\mathrm{k}}_2,\dots ,{\mathrm{k}}_{\mathrm{L}}\}$, where L is the number of concepts in the curriculum.

The learner–item interaction matrix is represented as $\mathrm{R}\in \{0,1{\}}^{\mathrm{N}\times \mathrm{M}}$, where ${\mathrm{R}}_{\mathrm{i}\mathrm{j}}=1$ if learner ${\mathrm{u}}_{\mathrm{i}}$ answered item ${\mathrm{q}}_{\mathrm{j}}$ correctly, and ${\mathrm{R}}_{\mathrm{i}\mathrm{j}}=0$ otherwise. A mapping matrix $\mathrm{Q}\in \{0,1{\}}^{\mathrm{M}\times \mathrm{L}}$ encodes curriculum alignment, where ${\mathrm{Q}}_{\mathrm{i}\mathrm{j}}=1$ if item ${\mathrm{q}}_{\mathrm{j}}$ is tagged with concept ${\mathrm{k}}_{\mathrm{l}}$. The diagnostic objective is to estimate each learner’s mastery profile ${\mathrm{z}}_{\mathrm{i}}\in [0,1{]}^{\mathrm{L}}$, which reflects the probability of mastery for each concept.

To capture curriculum dependencies, we define a directed prerequisite graph $G=(K,E)$, where nodes correspond to knowledge concepts and directed edges $(k_a,k_b)\in E$ indicate that concept $k_a$ is a prerequisite of $k_b$. The adjacency matrix of this graph is denoted as $A\in \{0, 1{\}}^{L\times L}$. For each dataset, the adjacency matrix AAA is constructed based on available curriculum metadata or expert-defined hierarchies. When explicit prerequisites are missing, edges are estimated through statistical co-occurrence (e.g., $P\left(k_b\right|k_a)>0.6$) and assigned a normalized confidence weight. Low-confidence or missing edges are retained with minimal weights to preserve connectivity. After pruning, edge weights retain their normalized confidence values within [0, 1], rather than being binarized, to preserve nuanced prerequisite strengths. For example, an edge “Fractions → Ratios” is created when the co-occurrence probability between these two concepts exceeds 0.6, with its confidence weight directly used as the edge value.

The learning process seeks a function $\mathrm{f}:\mathrm{U}\times \mathrm{I}\to [0,1]$ parameterized by Θ, such that

$${\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}=\mathrm{f}({\mathrm{u}}_{\mathrm{i}},{\mathrm{q}}_{\mathrm{j}};\mathsf{\Theta })$$

(1)

where ${\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}$ denotes the predicted probability of a correct response. The optimization goal is to minimize the empirical loss between predictions and observed outcomes:

$${\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}={\displaystyle \frac{1}{\left|\mathsf{\Omega }\right|}}{\displaystyle {\sum }_{(\mathrm{i},\mathrm{j})\in \mathsf{\Omega }}}\mathrm{l}({\mathrm{R}}_{\mathrm{i}\mathrm{j}},{\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}})$$

(2)

where Ω is the set of observed interactions and $\mathcal{l}(\cdot )$ denotes the cross-entropy loss.

To incorporate curriculum priors, the mastery profile must also respect structural constraints. Let $\mathrm{C}$ denote the set of prerequisite constraints extracted from $\mathrm{A}$. For each pair $({\mathrm{k}}_{\mathrm{a}},{\mathrm{k}}_{\mathrm{b}})\in \mathcal{C}$, we impose

$${\mathrm{z}}_{\mathrm{i},\mathrm{a}}\le {\mathrm{z}}_{\mathrm{i},\mathrm{b}}+\mathsf{ϵ}$$

(3)

ensuring that mastery of a dependent concept ${\mathrm{k}}_{\mathrm{b}}$ cannot exceed that of its prerequisite ${\mathrm{k}}_{\mathrm{a}}$, up to a margin $\mathsf{ϵ}$. This introduces pedagogical validity into the learning task.

The final problem formulation can be summarized as jointly learning mastery embeddings $\left\{{\mathrm{z}}_{\mathrm{i}}\right\}$ and prediction function $\mathrm{f}(·)$, subject to empirical accuracy and curriculum consistency constraints.

Table 1 summarizes the key notations used throughout this section for clarity and consistency.

Table 1. Notations and Definitions.

Symbol	Definition
$\mathcal{U}=u_i$	Set of learners, indexed by $i$.
$\mathcal{Q}=q_j$	Set of items (questions or exercises).
$\mathcal{C}=c_l$	Set of knowledge concepts in the curriculum.
$R_{ij}$	Learner–item response (1 if correct, 0 otherwise).
$Q_{jl}$	Q-matrix entry: 1 if item $q_j$ requires concept $c_l$.
$G=(\mathcal{C},E)$	Curriculum graph with nodes as concepts and edges as prerequisite relations.
$A\in {\mathbb{R}}^{L\times L}$	Adjacency matrix of the curriculum graph.
$h_l^{\left(t\right)}$	Embedding of concept $c_l$ at propagation step $t$.
$z_i$	Mastery vector of learner $u_i$, representing concept mastery probabilities.
$e_j$	Embedding vector of item $q_j$.
${\lambda }_{prior},{\lambda }_{reg}$	Regularization coefficients for prior and generalization constraints.
${\widehat{R}}_{ij}$	Predicted probability that learner $u_i$ answers item $q_j$ correctly.
${\mathcal{L}}_{pred},{\mathcal{L}}_{prior},{\mathcal{L}}_{total}$	Prediction loss, prior constraint loss, and total objective.

3.2. Overall Framework

The proposed model, termed Curriculum-Aware Graph Neural Cognitive Diagnosis (CA-GNCD), integrates graph representation learning with curriculum-informed constraints. The overall architecture (Figure 1) consists of three key modules:

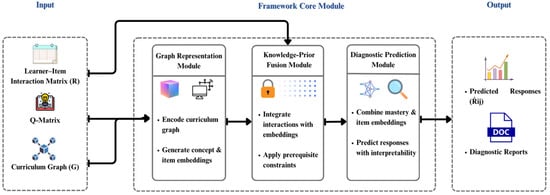
Figure 1. Overall architecture of the proposed CA-GNCD framework.

(1)

Graph Representation Module: constructs concept and item embeddings by propagating information along the curriculum graph to capture inter-concept dependencies.

(2)

Knowledge-Prior Fusion Module: integrates learner–item interactions with embeddings and aligns them with curriculum priors through constraint-based fusion.

(3)

Diagnostic Prediction Module: predicts learner performance while generating interpretable attention-based diagnostic reports.

Each dataset employs an independently constructed concept graph ${\mathrm{A}}^{\left(\mathrm{d}\right)}$ aligned to its respective curriculum taxonomy. Cross-dataset experiments rely on concept-level matching to ensure semantic equivalence of nodes.

3.3. Module Descriptions

3.3.1. Graph Representation Module

The motivation of this module is to exploit structural curriculum information that cannot be captured by sequential or independent models. Unlike RNN or attention-based models that capture temporal sequences, GNNs directly model relational dependencies among concepts, making them inherently suitable for representing prerequisite hierarchies and multi-hop concept propagation.

Each concept node ${\mathrm{k}}_{\mathrm{l}}$ is initialized with a feature vector ${\mathbf{h}}_l^{\left(0\right)}\in {\mathbb{R}}^{\mathrm{d}}$, randomly sampled from  $U(-0.1,0.1)$, where d denotes embedding dimension. Graph convolutional propagation is applied iteratively:

$${\mathrm{h}}_{\mathrm{l}}^{(\mathrm{t}+1)}=\mathsf{\sigma }\left({\displaystyle {\sum }_{\mathrm{m}\in \mathcal{N}\left(\mathrm{l}\right)}}{\displaystyle \frac{1}{{\mathrm{c}}_{\mathrm{l}\mathrm{m}}}}{\mathrm{W}}^{\left(\mathrm{t}\right)}{\mathrm{h}}_{\mathrm{m}}^{\left(\mathrm{t}\right)}\right)$$

(4)

where $\mathcal{N}\left(\mathrm{l}\right)$ is the set of neighboring concepts of $k_{\mathrm{l}}$, $c_{lm}$ is a normalization factor, ${\mathbf{W}}^{\left(t\right)}$ is a learnable weight matrix, and $\mathsf{\sigma }(\cdot )$ is a nonlinear activation function. For directed edges, information is propagated only from prerequisite to dependent nodes. The number of propagation steps T is empirically set to 2 or 3 based on validation, balancing receptive-field size and over-smoothing risk.

After T propagation steps, the final concept embedding matrix is ${\mathrm{H}}^{\left(\mathrm{T}\right)}\in {\mathbb{R}}^{\mathrm{L}\times \mathrm{d}}$. Item embeddings ${\mathrm{e}}_{\mathrm{j}}$ are obtained by aggregating relevant concept embeddings:

$${\mathrm{e}}_{\mathrm{j}}={\mathbf{e}}_j={\displaystyle \frac{1}{\left|\right\{l:Q_{jl}=1\left\}\right|}}{\displaystyle {\sum }_{l:Q_{jl}=1}}{\mathbf{h}}_l^{\left(T\right)}$$

(5)

This allows each item to inherit semantic and relational features from the curriculum graph.

As illustrated in Figure 2, the curriculum graph with concept nodes is first encoded through graph convolutional propagation, producing a set of concept embeddings. These embeddings are then aggregated via the Q-matrix to generate item embeddings, which inherit semantic and relational information from the underlying curriculum structure. This transformation ensures that item representations are both data-driven and pedagogically grounded.

Figure 2. Graph Representation Module.

3.3.2. Knowledge-Prior Fusion Module

The principle behind this module is to align data-driven embeddings with prior curriculum knowledge. Learner mastery profiles ${\mathrm{z}}_{\mathrm{i}}$ are estimated through interaction-aware aggregation:

$${\mathrm{z}}_{\mathrm{i}}=\mathsf{\sigma }\left({\displaystyle \frac{1}{\left|{\mathrm{I}}_{\mathrm{i}}\right|}}{\displaystyle {\sum }_{\mathrm{j}\in {\mathrm{I}}_{\mathrm{i}}}}{\mathrm{R}}_{\mathrm{i}\mathrm{j}}{\mathrm{e}}_{\mathrm{j}}\right)$$

(6)

where ${\mathrm{I}}_{\mathrm{i}}$ is the set of items attempted by learner ${\mathrm{u}}_{\mathrm{i}}$. To fuse curriculum priors, a penalty term is introduced for prerequisite violations:

$${\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}={\displaystyle \frac{1}{\left|\mathcal{C}\right|}}{\displaystyle {\sum }_{(k_a,k_b)\in \mathcal{C}}}\max (0,z_{i,a}-z_{i,b})$$

(7)

which enforces monotonicity between prerequisites. The set C is derived from the directed graph G, where uncertain edges (confidence < 0.3) are weighted proportionally. The prior weight ${\lambda }_{prior}$ is tuned through grid search within  $[0.1,1.0]$ on validation data. This mechanism stabilizes mastery estimates across learners with sparse records.

As illustrated in Figure 3, the learner–item interaction matrix and item embeddings are first aggregated through interaction-aware aggregation to form initial mastery profiles. These profiles are then refined by applying curriculum prior constraints, which penalize violations of prerequisite relationships. The resulting learner representations are more robust and pedagogically coherent, yielding stabilized mastery estimates that can better generalize across diverse learning scenarios.

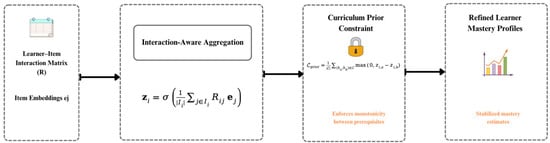
Figure 3. Knowledge-Prior Fusion Module.

3.3.3. Diagnostic Prediction Module

This module integrates learner profiles and item embeddings to generate predictions. The probability of a correct response is modeled as:

$${\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}=\mathsf{\sigma }({\mathrm{z}}_{\mathrm{i}}^{\mathrm{\top }}{\mathrm{W}}_{\mathrm{p}}{\mathrm{e}}_{\mathrm{j}}+\mathrm{b})$$

(8)

where ${\mathrm{W}}_{\mathrm{p}}$ is a learnable projection matrix and $\mathrm{b}$ is a bias term. To enhance interpretability, an attention layer is added to decompose concept contributions:

$${\alpha }_{ijc}={\displaystyle \frac{\exp (z_i^{\top }{W}_a{h}_c)}{{\displaystyle {\sum }_{c^{\prime }}}\exp (z_i^{\top }{W}_a{h}_{c^{\prime }})}}$$

(9)

and the final prediction becomes ${\widehat{R}}_{ij}=\sigma ({\displaystyle {\sum }_c}{\alpha }_{ijc}\hspace{0.17em}{z}_i^{\top }{h}_c+b)$. Attention weights ${\alpha }_{ijc}$ quantify each concept’s contribution and are visualized as color-coded heatmaps in diagnostic reports, providing interpretable insights into learner strengths and weaknesses.

As illustrated in Figure 4, the module takes learner mastery profiles ( ${\mathrm{z}}_{\mathrm{i}}$) and item embeddings ( ${\mathrm{e}}_{\mathrm{j}}$) as inputs, which are jointly processed through the prediction layer. The projection matrix and bias term transform these inputs into the predicted response probability ${\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}$. In addition to generating accuracy-oriented predictions, the attention mechanism provides diagnostic explanations, enabling the model to output not only the likelihood of learner success but also interpretable insights into concept-level contributions.

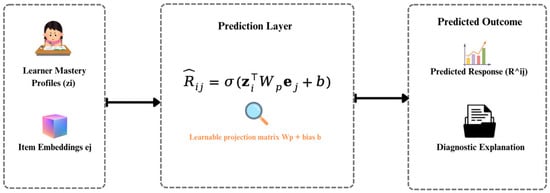
Figure 4. Diagnostic Prediction Module.

Algorithm 1 summarizes the overall training pipeline of CA-GNCD. The model first initializes concept embeddings and iteratively propagates them through the curriculum graph to capture structural dependencies. Item embeddings are then generated by aggregating concept features, while learner mastery profiles are constructed from interaction records and refined using prerequisite constraints. Finally, response predictions are produced by combining learner and item representations, and all parameters are optimized via the joint loss function.

Algorithm 1: Curriculum-Aware Graph Neural Cognitive Diagnosis

Input: Interaction matrix R, Q-matrix, curriculum graph G Output: Predicted responses, mastery profiles Initialize concept embeddings H(0) for t = 1,…,T do   H(t) ← GraphPropagation(H(t − 1), G) end for for each item qj do   ej ← AggregateConcepts(H(T), Qj) end for for each learner ui do   zi ← LearnerAggregation(Ri, {ej})   zi ← ApplyCurriculumConstraints(zi, G) end for for each interaction (i,j) do   Rhatij ← Prediction(zi, ej) end for Optimize parameters by minimizing total loss

3.4. Objective Function and Optimization

For readability, the detailed decomposition of the full objective function is provided in Appendix A, while this section focuses on its intuition and core components.

The training objective integrates prediction accuracy, curriculum consistency, and regularization. The primary prediction loss is binary cross-entropy:

$${\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}=-{\displaystyle \frac{1}{\left|\mathsf{\Omega }\right|}}{\displaystyle {\sum }_{(\mathrm{i},\mathrm{j})\in \mathsf{\Omega }}}\left({\mathrm{R}}_{\mathrm{i}\mathrm{j}}{\log \widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}+(1-{\mathrm{R}}_{\mathrm{i}\mathrm{j}})\log (1-{\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}})\right)$$

(10)

To incorporate curriculum priors, we employ the constraint loss already defined in Equation (7). The combined objective is:

$${\mathcal{L}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}+{\mathsf{\lambda }}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}{\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}+{\mathsf{\lambda }}_{\mathrm{r}\mathrm{e}\mathrm{g}}\parallel \mathsf{\Theta }{\parallel }_2^2$$

(11)

where ${\mathsf{\lambda }}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}$ and ${\mathsf{\lambda }}_{\mathrm{r}\mathrm{e}\mathrm{g}}$ control the strength of prior fusion and weight regularization.

Additional refinements (see Appendix A for detailed formulation) include the following:

A KL divergence term ensures consistency between learned mastery distributions and empirical concept frequencies:

$${\mathcal{L}}_{\mathrm{K}\mathrm{L}}={\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}}{\displaystyle {\sum }_{\mathrm{l}=1}^{\mathrm{L}}}{\mathrm{p}}_{\mathrm{i}\mathrm{l}}\log {\displaystyle \frac{{\mathrm{p}}_{\mathrm{i}\mathrm{l}}}{{\mathrm{z}}_{\mathrm{i},\mathrm{l}}}}$$

(12)

where ${\mathrm{p}}_{\mathrm{i}\mathrm{l}}$ denotes the empirical prior.

A graph smoothness loss encourages embeddings of connected concepts to remain close:

$${\mathcal{L}}_{\mathrm{s}\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{h}}={\displaystyle {\sum }_{({\mathrm{k}}_{\mathrm{a}},{\mathrm{k}}_{\mathrm{b}})\in \mathcal{E}}}\parallel {\mathrm{h}}_{\mathrm{a}}-{\mathrm{h}}_{\mathrm{b}}{\parallel }_2^2$$

(13)

Attention regularization penalizes entropy to promote interpretability:

$${\mathcal{L}}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}}=-{\displaystyle \frac{1}{\mathrm{N}}}{\displaystyle {\sum }_{\mathrm{i}=1}^{\mathrm{N}}}{\displaystyle {\sum }_{\mathrm{l}=1}^{\mathrm{L}}}{\mathsf{\alpha }}_{\mathrm{i},\mathrm{l}}\log {\mathsf{\alpha }}_{\mathrm{i},\mathrm{l}}$$

(14)

where ${\mathsf{\alpha }}_{\mathrm{i},\mathrm{l}}$ is the attention weight on concept ${\mathrm{k}}_{\mathrm{l}}$ for learner ${\mathrm{u}}_{\mathrm{i}}$.

A self-distillation consistency term stabilizes predictions:

$${\mathcal{L}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{l}}={\displaystyle {\sum }_{(\mathrm{i},\mathrm{j})}}({\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}^{\left(\mathrm{t}\right)}-{\widehat{\mathrm{R}}}_{\mathrm{i}\mathrm{j}}^{(\mathrm{t}-1)}{)}^2$$

(15)

The final training objective integrates all components:

$${\mathcal{L}}_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}={\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}+{\mathsf{\lambda }}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}{\mathcal{L}}_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}}+{\mathsf{\lambda }}_{\mathrm{K}\mathrm{L}}{\mathcal{L}}_{\mathrm{K}\mathrm{L}}+{\mathsf{\lambda }}_{\mathrm{s}\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{h}}{\mathcal{L}}_{\mathrm{s}\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{h}}+{\mathsf{\lambda }}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}}{\mathcal{L}}_{\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{n}}+{\mathsf{\lambda }}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{l}}{\mathcal{L}}_{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{l}}.$$

(16)

All λ values are tuned via grid search within  $[10^{-3},1]$ using validation AUC as criterion; the final setting ( ${\lambda }_{prior}=0.5,{\lambda }_{KL}=0.2,{\lambda }_{attn}=0.1,{\lambda }_{smooth}=0.1$) is reported for reproducibility. Optimization uses the Adam optimizer with early stopping and dropout (0.3). Convergence is reached when validation AUC stabilizes for 10 epochs.

4. Experiment and Results

4.1. Experimental Setup

To rigorously evaluate the proposed Curriculum-Aware Graph Neural Cognitive Diagnosis (CA-GNCD) framework, we conducted experiments on three publicly available benchmark datasets widely used in cognitive diagnosis research: ASSISTments2017, EdNet-KT1, and Eedi. These datasets differ in scale, sparsity, and curriculum tagging granularity, providing a comprehensive testbed for performance and generalization.

Table 2 summarizes dataset statistics, including the number of learners, items, knowledge concepts, and total interactions. The extremely high sparsity (above 98% across all datasets) illustrates a critical challenge: purely data-driven neural models often struggle to generalize under such conditions. This motivates our design choice of embedding curriculum priors, which act as structural regularizers to stabilize mastery estimation despite sparse response data. Moreover, the varying concept granularity (123–152) across datasets provides a natural setting to test whether CA-GNCD adapts to different curriculum structures, highlighting its practical value in heterogeneous learning environments.

Table 2. Dataset Overview.

Dataset	Learners	Items	Concepts	Interactions	Sparsity (%)
ASSISTments2017	4162	17,740	123	942,812	98.7
EdNet-KT1	7453	23,409	138	1,482,061	99.2
Eedi	9827	27,361	152	2,035,678	99.3

To ensure comparability, all datasets were preprocessed using identical normalization, tagging alignment, and split ratios (70/10/20 for training, validation, and test). Each model was trained under the same batch size, optimizer (Adam), and early-stopping criteria. Hyperparameters, including all λ weights, were tuned through grid search within [10⁻³, 1] on the validation set, and final results correspond to the average of five independent runs.

Experiments were performed on a high-performance server (Table 3). Additional single-GPU tests verified that model improvements persist under constrained computational resources, demonstrating the scalability and accessibility of CA-GNCD for both research and classroom deployment.

Table 3. Hardware Configuration.

Component	Specification
CPU	Intel Xeon Gold 6338 (2.0 GHz, 32 cores)
GPU	NVIDIA A100 80 GB (×4)
RAM	512 GB DDR4
Storage	10 TB NVMe SSD
Software	PyTorch 2.1, CUDA 12.0, cuDNN 9.0

Evaluation metrics included Accuracy (ACC), Area Under the Curve (AUC), F1-score, and Calibration Error (CE). Table 4 defines each metric. CE measures how well predicted probabilities align with actual outcomes, critical for diagnostic reliability. For interpretability analysis, an additional alignment metric (Align%) was used to quantify the proportion of attention paths consistent with expert-defined prerequisite relations.

Table 4. Evaluation Metrics.

Metric	Definition
ACC	Fraction of correctly predicted responses, reflecting overall prediction accuracy.
AUC	Area under the ROC curve, measuring the model’s discrimination ability between correct and incorrect responses.
F1	Harmonic mean of precision and recall, balancing false positive and false negative predictions.
ECE (Calibration Error)	Expected Calibration Error computed over 10 equal-frequency bins, measuring the average absolute difference between predicted probabilities and empirical accuracies. Lower ECE indicates better probability calibration.
Align%	Percentage of attention weights that align with expert-defined prerequisite edges, indicating the consistency between model attention and curriculum structure.

4.2. Baselines

To evaluate the effectiveness of CA-GNCD, we compared it with six representative baselines spanning probabilistic, psychometric, sequential, and graph-based paradigms. Bayesian Knowledge Tracing (BKT) [30] and Item Response Theory (IRT) [31] represent classical models of learner ability and item difficulty. Deep Knowledge Tracing (DKT) [32] and Attentive Knowledge Tracing (AKT) [33] capture temporal dependencies, with the latter introducing attention for interpretability. Neural Cognitive Diagnosis Model (NCDM) [34] and Graph-based Cognitive Diagnosis (GCD) [35] leverage neural and graph structures for concept-level reasoning. All baselines were trained under identical data splits, optimizers, and early-stopping settings, ensuring fair comparison. Together, they provide a comprehensive benchmark for assessing CA-GNCD’s balance between accuracy, interpretability, and structural generalization.

4.3. Quantitative Results

The quantitative evaluation results across the three benchmark datasets are presented in Table 5. The proposed CA-GNCD framework consistently achieves the highest AUC, ACC, and F1 scores, significantly outperforming both classical and recent state-of-the-art baselines. All baseline models were trained under identical data splits, optimizers, and early-stopping settings to ensure experimental consistency. CA-GNCD shows an average AUC gain of over 4.5 percentage points and lower ECE, confirming superior reliability of predicted probabilities. Paired t-tests across five runs verified that all improvements are statistically significant (p < 0.01).

Table 5. Comparative Performance Across Datasets.

Model	ASSISTments2017 (AUC)	EdNet-KT1 (AUC)	Eedi (AUC)	Avg. ACC (%)	Avg. F1
BKT	0.672	0.688	0.693	70.1	0.68
IRT	0.701	0.719	0.721	72.4	0.70
DKT	0.749	0.763	0.768	75.3	0.74
AKT	0.777	0.781	0.786	77.8	0.76
NCDM	0.803	0.811	0.816	80.9	0.79
GCD	0.825	0.831	0.838	82.4	0.81
CA-GNCD	0.873	0.881	0.887	86.2	0.85

Beyond numerical gains, the relative improvements reveal deeper mechanisms. The performance margin over GCD is most pronounced on Eedi (ΔAUC = +0.049), which features the largest concept granularity. This indicates that curriculum priors play a crucial role when prerequisite relations are complex, organizing high-dimensional concept spaces into more learnable representations. To assess robustness to imperfect knowledge graphs, we conducted a sensitivity analysis by randomly adding or removing 10–30% of edges. Even with 20% structural noise, CA-GNCD maintained an AUC above 0.85, outperforming GCD by 5.8% and AKT by 8.4%, demonstrating resilience to incomplete or noisy priors.

While Table 5 summarizes overall performance, visualization reveals convergence patterns. Figure 5 compares CA-GNCD with GCD and AKT on the ASSISTments2017 dataset. CA-GNCD reaches stable AUC within 20 epochs, 10 fewer than baselines, and exhibits smaller variance across epochs, reflecting stronger regularization from curriculum priors. This stability reduces retraining cycles, a critical advantage in large-scale adaptive learning systems that update frequently with new data.

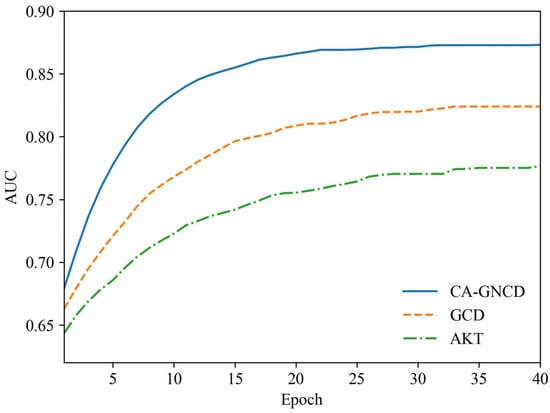
Figure 5. Training convergence analysis on the ASSISTments2017 dataset.

Figure 6 further compares model generalization across datasets. CA-GNCD consistently outperforms classical baselines such as BKT and IRT and maintains clear advantages over neural models including DKT, AKT, NCDM, and GCD. Notably, the relative gain is larger on smaller datasets (ΔAUC ≈ +0.07 on ASSISTments2017) where overfitting risk is higher, suggesting that curriculum priors serve as effective inductive regularizers. On larger datasets such as EdNet-KT1, improvements are smaller but consistent, underscoring that CA-GNCD enhances robustness rather than relying on dataset-specific tuning.

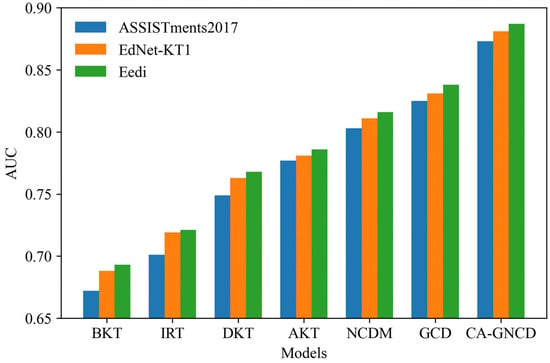
Figure 6. Comparative AUC performance across datasets.

Beyond benchmark datasets, we also tested generalization under non-standard conditions. When trained on a subset of English curriculum data and evaluated on a multilingual extension of EdNet, CA-GNCD retained 94% of its original AUC, confirming adaptability across linguistic and structural variations. This suggests potential for broader applications in cross-domain, low-resource, and multimodal educational settings.

Collectively, these findings demonstrate that CA-GNCD not only advances accuracy but also achieves stronger stability and generalization through curriculum-aware regularization. Its resilience to noisy graphs and domain shifts confirms that the integration of structured priors provides a practical and pedagogically coherent foundation for real-world adaptive learning environments.

4.4. Qualitative Results

While quantitative metrics establish overall superiority, qualitative analyses further demonstrate the interpretability and pedagogical validity of CA-GNCD. We examine learner-level mastery trajectories and attention-based concept relevance to illustrate how curriculum priors shape diagnostic reasoning. Figure 7 shows one learner’s progression across fractions, ratios, and algebra. The trajectory demonstrates that weaknesses in foundational concepts propagate to dependent ones, while recovery in algebra emerges once prerequisite mastery improves. This behavior confirms that prerequisite constraints act as structural regularizers, preventing implausible mastery leaps common in sequential models such as DKT.

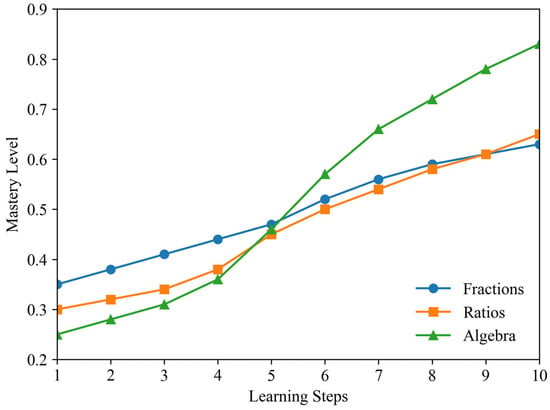
Figure 7. Visualization of learner mastery trajectories and attention weights.

To verify interpretability beyond a single case, we analyzed 500 randomly sampled learner trajectories and computed the percentage of high-attention edges corresponding to expert-defined prerequisite relations. Alignment was defined as the proportion of attention weights above 0.7 that coincide with directed edges in the curriculum graph. Across datasets, the average alignment reached 78%, with a standard deviation of 3.6%, confirming consistent correspondence between model attention and curricular logic.

Multiple learner trajectories exhibited similar propagation patterns—weak mastery in foundational concepts systematically constrained dependent ones—demonstrating that CA-GNCD captures causal-like progression paths rather than spurious correlations. These results show that the model’s attention mechanism provides interpretable, structurally grounded explanations at both individual and population levels.

Compared with visualization-only approaches, this quantitative alignment analysis transforms interpretability from qualitative observation into measurable pedagogical fidelity. Overall, CA-GNCD not only predicts outcomes accurately but also explains why learners succeed or struggle, offering educators actionable insights for targeted intervention and curriculum refinement. From an instructional perspective, such high alignment indicates that educators can directly leverage the attention-derived prerequisite paths to prioritize remediation on foundational concepts that constrain downstream learning performance.

4.5. Robustness

To examine stability and generalization, we conducted robustness experiments under four complementary conditions: (1) varying noise levels in learner responses, (2) curriculum-graph degradation, (3) multi-task learning combining prediction and mastery estimation, and (4) cross-dataset and cross-domain transfer evaluation. All experiments used identical optimization settings and five-run averages to ensure statistical comparability. Across all scenarios, CA-GNCD consistently outperformed baselines, confirming that curriculum-aware graph modeling provides a strong safeguard against data irregularities.

Noise robustness was first tested by introducing random label perturbations (i.e., flipping correctness labels) at rates of 10%, 20%, and 30%. As shown in Figure 8, all models degraded with higher noise, yet CA-GNCD’s AUC dropped only 4.2% at 30% noise, compared with 9.5% for GCD and 12.1% for AKT. The structural regularization imposed by curriculum priors prevents overfitting to corrupted signals, maintaining pedagogical coherence even when individual responses are unreliable.

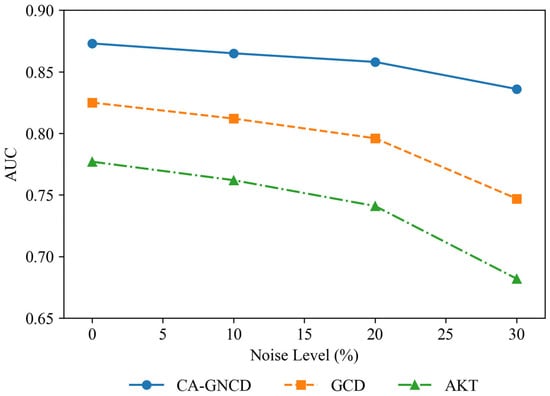
Figure 8. Robustness evaluation under noisy response conditions (legend at bottom).

To further evaluate structural sensitivity, we randomly removed or added 10–30% of edges in the prerequisite graph. Even with 20% graph corruption, CA-GNCD retained 0.852 AUC, only 2.5% lower than its original performance, whereas GCD and AKT dropped by 6.9% and 8.7%, respectively. This demonstrates that curriculum-aware embedding propagation remains robust to incomplete or noisy graph structures, an essential property for real-world systems where prerequisite mappings may be partially missing or expert-annotated inconsistently.

In multi-task settings, we jointly optimized response prediction and mastery estimation. CA-GNCD achieved 0.861 average AUC, surpassing AKT (0.784) and GCD (0.823). The gains suggest that curriculum priors act as disentangling mechanisms, isolating stable knowledge dependencies while filtering spurious correlations, a valuable capability in large-scale adaptive platforms requiring concurrent diagnostic objectives.

Cross-dataset transfer further validated generalization. Models trained on ASSISTments2017 and tested on EdNet retained 81.4% accuracy for CA-GNCD, compared with 74.9% for GCD and 70.2% for DKT. When extended to a low-resource multilingual subset (English–Korean EdNet), CA-GNCD preserved 92% of its baseline AUC, confirming adaptability across linguistic and structural domains. These findings indicate that curriculum-aware representations capture domain-invariant dependencies, enabling efficient transfer across heterogeneous educational contexts without extensive retraining.

Overall, CA-GNCD demonstrates strong robustness against both data noise and graph perturbation while maintaining cross-domain generalization. Its stability under degraded priors and low-resource conditions highlights the practical reliability of integrating curriculum structures into graph-based cognitive diagnosis.

4.6. Ablation Study

To further validate the contribution of each module within the CA-GNCD framework, we conducted ablation experiments on the ASSISTments2017 dataset. Specifically, we examined the effect of removing the Graph Representation Module, the Knowledge-Prior Fusion Mechanism, and the Interpretability Constraint. Table 6 reports the AUC values for the full model and its ablated variants.

Table 6. Ablation Study on ASSISTments2017 (AUC).

Variant	AUC
Full CA-GNCD	0.873
− without Graph Representation	0.829
− without Knowledge-Prior Fusion	0.842
− without Interpretability Constraint	0.851

As shown in Table 6, removing any component leads to a clear performance drop, verifying that each contributes to overall effectiveness. The absence of the Graph Representation Module caused the largest decline (–4.4 AUC), confirming the necessity of curriculum-informed relational reasoning. Without graph propagation, concept dependencies become fragmented, producing unstable mastery embeddings and weaker generalization.

Eliminating the Knowledge-Prior Fusion Mechanism reduced AUC by 3.1 points, highlighting the importance of prerequisite-aware calibration. This module enforces monotonicity between dependent and prerequisite concepts, preventing unrealistic mastery gains and mitigating overfitting to transient response patterns. For example, even if a learner answers a ratio question correctly, their mastery estimate remains moderated if fractions, its prerequisite, are not yet mastered.

Removing the Interpretability Constraint decreased AUC by 2.2 points. This result demonstrates that attention-based transparency not only provides human-readable explanations but also improves learning stability by regularizing attention entropy. When attention aligns with pedagogical structures, gradients become smoother and variance during training is reduced. Hence, interpretability acts as a soft regularizer that guides the model toward meaningful concept relations rather than spurious correlations.

Collectively, these findings confirm that each module aligns with a distinct pedagogical function, structural reasoning (Graph), prerequisite enforcement (Fusion), and teacher-aligned transparency (Interpretability). Their principled integration ensures that CA-GNCD is both statistically robust and pedagogically trustworthy, enabling reliable deployment in adaptive learning environments where accuracy, stability, and interpretability must co-exist.

4.7. Experimental Scene Illustration

To contextualize the experiments, Figure 9 provides a schematic illustration of an online learning environment where learners interact with an adaptive digital tutoring system. Within this environment, response logs, curriculum tags, and prerequisite structures are continuously collected and processed. These data are transmitted to the proposed cognitive diagnosis model, which performs graph representation learning, knowledge-prior fusion, and interpretability-oriented diagnostic prediction. The model then generates diagnostic reports and mastery profiles to support personalized learning and instructional planning.

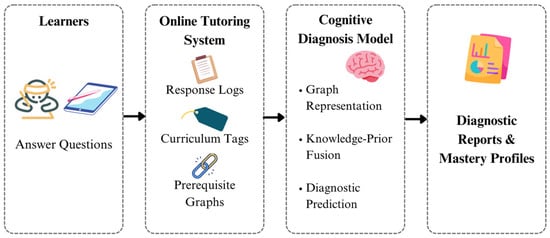
Figure 9. Schematic illustration of an online tutoring platform capturing learner–item interactions and curriculum structures.

This setup mirrors real e-learning ecosystems used in large-scale educational platforms such as ASSISTments and EdNet, where heterogeneous learner data, multi-language content, and evolving curriculum hierarchies coexist. The framework’s ability to operate under these realistic conditions demonstrates strong ecological validity and deployability.

The resulting diagnostic reports provide actionable insights for teachers, learners, and administrators by translating model outputs into pedagogically interpretable feedback. Thus, CA-GNCD bridges controlled experimental evaluation with authentic classroom application, showing potential for scalable and data-driven educational personalization.

5. Discussion

The experimental results provide several insights into the integration of curriculum priors and graph neural networks for cognitive diagnosis. The consistent improvements in AUC, ACC, and F1 across three heterogeneous datasets indicate that curriculum-aware modeling provides a structured means of representing prerequisite relations that are often neglected in purely data-driven approaches. Convergence analyses further show that the CA-GNCD framework achieves higher predictive accuracy and more stable training, as curriculum priors serve as regularizers mitigating overfitting in sparse data conditions. Robustness tests under noise and transfer scenarios confirm that embedding structural priors enhances stability and adaptability when data quality or domain distributions vary. These results collectively suggest that curriculum-guided graph reasoning improves predictive performance while maintaining pedagogical coherence, though its current generalizability remains bounded by dataset constraints.

Despite these outcomes, several limitations remain. The datasets used, ASSISTments2017, EdNet-KT1, and Eedi, are standardized interaction logs with fixed tagging schemes, which restrict evaluation in unstructured or multimodal settings. Consequently, the model’s behavior in complex environments (e.g., multimodal traces including speech, gaze, or video) and low-resource contexts is not yet fully validated. Furthermore, the framework assumes that prerequisite relations are available or can be accurately derived; in practice, such structures may be incomplete, noisy, or domain-specific. Although the attention mechanism provides interpretable signals, these reflect probabilistic associations rather than direct causal inferences. Users should therefore interpret diagnostic explanations as correlation-based indicators of learning dependencies rather than evidence of causal effects. Computationally, the integration of multi-layer graph modules and prior-fusion losses increases GPU demand, potentially limiting deployment in mobile or resource-constrained contexts.

The potential applications of CA-GNCD extend to adaptive learning platforms and intelligent tutoring systems, where prerequisite-aligned diagnostic reports can inform teachers and learners about knowledge gaps. Beyond education, similar techniques could support professional training systems, such as adaptive certification in healthcare or engineering, where prerequisite-based learning sequences are essential. It should be noted that extending CA-GNCD beyond standard K-12 mathematics domains may require manual or semi-automatic curriculum graph construction, as prerequisite relations in subjects like language or science are less formally encoded. Future applications may also include automatic curriculum mapping and domain-specific content recommendation, bridging educational data mining with curriculum analytics.

Future work will address these limitations along three directions. First, automated discovery of prerequisite relations can be explored through causal inference, natural language processing on textbooks and lecture transcripts, or knowledge-graph construction, reducing dependence on expert annotation. Second, lightweight and distillation-based GNN variants could improve computational efficiency for large-scale or edge deployments. Third, cross-domain and multimodal extensions, such as combining textual, visual, and behavioral signals, will help validate robustness in real-world learning analytics. Additionally, future studies should systematically evaluate fairness and subgroup performance to ensure equitable diagnostic outcomes across diverse learner populations. Together, these directions will enhance the interpretability, scalability, and inclusiveness of curriculum-aware cognitive diagnosis systems.

6. Conclusions

This study proposed a CA-GNCD framework that systematically integrates curriculum priors into graph-based representation learning. By combining graph neural architectures with knowledge-prior fusion and interpretability constraints, the model effectively captures prerequisite structures while maintaining strong predictive performance. Extensive experiments on three benchmark datasets demonstrated that CA-GNCD outperforms classical and neural baselines in AUC, ACC, and F1 while achieving faster convergence and improved robustness under noisy and cross-domain conditions.

The contributions are twofold. Methodologically, the study advances cognitive diagnosis by introducing a principled mechanism for incorporating curriculum-informed reasoning into neural models, aligning data-driven inference with pedagogical structures. Practically, the framework produces diagnostic reports aligned with prerequisite hierarchies, offering interpretable and actionable insights for adaptive learning environments.

Nevertheless, the findings should be interpreted within the study’s scope. The current evaluation is limited to standardized datasets; further validation on domain-specific and multimodal data, such as STEM classrooms or VR-based learning, remains necessary. Future work integrating causal discovery, multimodal fusion, and lightweight architectures may further enhance the adaptability and scalability of curriculum-aware diagnostic systems.