Abstract
Autonomous racing serves as a challenging testbed that exposes the limitations of perception-decision-control algorithms in extreme high-speed environments, revealing safety gaps not addressed in existing autonomous driving research. However, traditional control techniques (e.g., FGM and MPC) and reinforcement learning-based approaches (including model-free and Dreamer variants) struggle to simultaneously satisfy sample efficiency, prediction reliability, and real-time control performance, making them difficult to apply in actual high-speed racing environments. To address these challenges, we propose LiDAR Dreamer, a novel world model specialized for LiDAR sensor data. LiDAR Dreamer introduces three core techniques: (1) efficient point cloud preprocessing and encoding via Cartesian Polar Bar Charts, (2) Light Structured State-Space Cells (LS3C) that reduce RSSM parameters by 14.2% while preserving key dynamic information, and (3) a Displacement Covariance Distance divergence function, which enhances both learning stability and expressiveness. Experiments in PyBullet F1TENTH simulation environments demonstrate that LiDAR Dreamer achieves competitive performance across different track complexities. On the Austria track with complex corners, it reaches 90% of DreamerV3’s performance (1.14 vs. 1.27 progress) while using 81.7% fewer parameters. On the simpler Columbia track, while model-free methods achieve higher absolute performance, LiDAR Dreamer shows improved sample efficiency compared to baseline Dreamer models, converging faster to stable performance. The Treitlstrasse environment results demonstrate comparable performance to baseline methods. Furthermore, beyond the 14.2% RSSM parameter reduction, reward loss converged more stably without spikes, improving overall training efficiency and stability.
1. Introduction
Autonomous racing serves as a uniquely strict test bed for autonomous driving research, providing the extreme conditions essential for ensuring long-term safety [1,2]. At racing speeds, vehicles must detect road surface conditions and climate gradients in milliseconds to assess tire grip limits. They must execute high-risk decisions, such as high-speed corner entry, energy strategy, and overtaking, under severe prediction uncertainty. Steering and drive forces must be controlled within milliseconds in acceleration and deceleration environments exceeding 5G. Technologies validated in this autonomous racing environment directly translate to everyday driving scenarios such as non-standard road conditions, uncertain urban intersections, and emergency avoidance maneuvers, enhancing the robustness of perception, decision-making, and control. Thus, autonomous racing research not only pushes the boundaries of vehicle dynamics and autonomous driving algorithms but also acts as a catalyst for accelerating the implementation of safer, more reliable autonomous driving systems on public roads [3,4].
Existing autonomous racing algorithms vary, each with distinct limitations. The Follow the Gap Method [5] selects only the widest available space in the current environment, potentially causing delays when trapped in local minima with multiple obstacles present. Disparity Extender [6] excessively expands distant and fine obstacles, causing conservative steering, while Pure Pursuit [7] frequently weaves and deviates from the path in sharp curvature sections because it references only a single look-ahead point. Vector Pursuit [8] improves tracking performance by reflecting dynamic states, but computational complexity increases sharply during high-speed driving. Model Predictive Control [9] theoretically offers the best performance by optimizing future trajectories, yet securing real-time stability is difficult due to large-scale numerical optimization computational costs and model mismatch issues.
Reinforcement learning (RL) has also been applied to autonomous racing and can be broadly categorized into model-free RL and model-based RL. Model-free RL directly optimizes value functions or policies based on rewards obtained during interactions, without separately learning the environment’s dynamics. Conversely, Model-based RL learns and utilizes the environment’s transition and reward models to predict and plan for the future, thereby optimizing policies. However, both approaches have distinct limitations.
Model-free RL (i) requires massive interaction data, resulting in extremely low sample efficiency on real vehicles or expensive simulators; (ii) relies on random exploration until rewards are received, posing high safety accident risks in the initial stages; and (iii) struggles with reliable credit assignment in tasks requiring long-term dependencies, leading to poor learning stability [10,11]. Particularly in high-speed, high-risk environments like racing, securing sufficient training iterations within physical constraints remains challenging, which limits practical application.
Model-based RL (i) offers the advantage of high data efficiency by predicting and planning future states and rewards. However, (ii) model uncertainty and cumulative error rapidly degrade planning quality, potentially causing fatal decision errors during high-speed driving; and (iii) reflecting complex vehicle dynamics, sensor noise, and road friction variations requires massive parameters and computations, making it difficult to meet real-time control cycles [10,11]. Furthermore, accurately modeling high-dimensional inputs like LiDAR and RGB probabilistically incurs significant computational and memory costs. When deployed on embedded controllers, this creates bottlenecks in thermal, power, and latency aspects.
Therefore, both approaches reveal limitations in sample efficiency, prediction reliability, and real-time requirements demanded by autonomous racing, necessitating a new approach to overcome these challenges.
To address these challenges, World Model-based approaches such as Dreamer become necessary. Traditional Reinforcement Learning exhibits limitations when handling high-dimensional sensory input and long-horizon tasks, requiring massive data collection and computational resources. In contrast, approaches leveraging World Models offer a promising alternative by enabling agents to generalize from past experiences and predict future outcomes through latent imagination. Specifically, Dreamer demonstrates a particular strength by learning actions solely within a compressed latent space extracted from high-dimensional inputs. This architecture efficiently optimizes policies by backpropagating analytical gradients of learned state values along imagined trajectories, directly addressing the shortsightedness that traditional model-based methods suffer from due to finite imagination horizons. Building on this, Dreamer demonstrates superior data efficiency, shorter computation times, and higher final performance than existing approaches on challenging visual control tasks. This shows its potential to solve complex, long-term problems using raw sensor data in domains like autonomous driving, which demand advanced visual understanding and prediction capabilities.
While the Dreamer family of World Models advances Model-based RL, existing Dreamer-based algorithms are not suitable for autonomous racing. First, they rely on high-resolution RGB predictions, significantly increasing memory and latency. Pathdreamer [12] trains two large networks to generate 1024 × 512 panoramas, requiring 400,000 viewpoint trajectories. Second, most variants require powerful GPUs and lengthy training periods. Think2Drive [13] requires three days of training on an A6000 GPU to solve CARLA v2, while MV-MWM [14] uses an A100 GPU and a ViT encoder–decoder with a 1k batch size during the representation learning phase. Third, as DayDreamer [15] also pointed out, reliance solely on camera sensors makes these methods vulnerable to lighting changes, and massive data collection in real environments accelerates hardware wear. Finally, additional techniques like curriculum design or replay strategies are still needed to handle long-tail corner cases, and Think2Drive suffers from policy collapse and scenario imbalance issues. All these constraints result in models that are large, have high power consumption, and slow to respond.
Therefore, algorithm lightweighting is crucial when deploying algorithms in vehicles. We propose a lightweight, LiDAR-specialized autonomous racing dreamer model. The proposed method optimizes LiDAR input, reduces model size, and employs a distance (divergence) metric optimized for LiDAR input. For comparison, we used representative model-free RL algorithms: D4PG, MPO, PPO, and SAC. Evaluation metrics include trajectory progress, model size, and reward loss. We constructed a driving environment similar to the real world using the PyBullet simulator.
The main contributions of our paper are as follows:
- Utilizing a Cartesian Polar Bar Chart enables the use of more input information compared to existing Dreamer-based autonomous driving algorithms. While it maintains a consistent input representation format across different maps, showing better results on tracks with gradual curves than those with sharp corners.
- Proposing and utilizing Light Structured State-Space Cell (LS3C) resulted in smaller model size and better performance when using LiDAR-based images.
- Utilizing Displacement-Covariance Distance reduces the probability of model collapse compared to the KL-divergence used in the baseline dreamer model.
2. Related Works
2.1. Model-Free Reinforcement Learning
Model-Free Reinforcement Learning (Model-Free RL) is a method that directly optimizes value functions or policies based on rewards obtained through interaction, without separately learning the environment’s dynamics. Several key algorithms have emerged in the Model-Free RL domain to solve complex control tasks. Distributed Distributional Deterministic Policy Gradients (D4PG) [16] is an off-policy actor-critic method that integrates distributed critic updates with distributed parallel actors, enabling efficient experience collection and demonstrating state-of-the-art performance across diverse control tasks. However, its prioritization component offers limited benefits for challenging problems and can lead to unstable updates, particularly in manipulation tasks. Maximum a Posteriori Policy Optimization (MPO) [17] is a novel off-policy algorithm that leverages the duality between control and estimation via Expectation Maximization, demonstrating excellent sample efficiency and robustness. However, selecting an appropriate temperature parameter for an unconstrained objective can be challenging. Proximal Policy Optimization (PPO) [18] is an on-policy policy gradient method. It achieves a balance between simplicity, reliable performance, and good sample complexity by introducing a clipped surrogate objective function that enables multiple mini-batch update epochs on the same data. Nevertheless, it may show lower data efficiency than off-policy methods in some situations and can be sensitive to the fixed penalty coefficient. Finally, Soft Actor-Critic (SAC) [19] is an off-policy actor-critic deep RL algorithm based on maximum entropy reinforcement learning. It aims to maximize both reward and policy entropy, demonstrating stable performance with high robustness across various tasks. However, its performance is sensitive to the reward scaling hyperparameter, which acts as the temperature for the optimal policy.
2.2. Model-Based Reinforcement Learning
Model-Based Reinforcement Learning (Model-Based RL) is a method that learns the environment’s transition and reward models to predict and plan for the future, thereby optimizing the policy. Representative approaches for solving complex control problems have also been proposed within the Model-Based RL field. Probabilistic Inference for Learning Control (PILCO) [20] models dynamics using Gaussian Processes (GP) and directly differentiates the long-term expected reward of a policy over the prediction distribution. This approach demonstrated outstanding sample efficiency in robot manipulation and balance control with only minimal actual interactions. However, the ) computational complexity of GPs and the Gaussian assumption can limit computational capacity and expressiveness for high-dimensional observations or discontinuous/non-Gaussian dynamics. Meanwhile, Model-Based Policy Optimization (MBPO) [21] estimates model uncertainty using neural network ensembles, and achieves sample efficiency and stability comparable to off-policy methods in randomly initialized motor and locomotion tasks by repeatedly injecting “short virtual rollouts” into an experience replay buffer to balance model bias and variance. However, it is sensitive to model accuracy, and incorrectly setting hyperparameters like rollout length or ensemble size can drastically degrade policy quality. It also does not fully resolve the simulation-reality gap.
2.3. Dreamer
The Dreamer series has evolved incrementally within the lineage of model-based reinforcement learning (World Model), extending the potential of “latent space planning” pioneered by PlaNet [22] to policy learning. PlaNet compressed pixel observations into latent states using a Recurrent State-Space Model (RSSM) and ran a CEM-based planner on these latent dynamics to generate actions. However, it did not directly learn the policy and value functions, limiting its scalability for large-scale rollouts and real-time control. Dreamer V1 [23] leveraged the same RSSM but mass-generated imagined sequences in the latent space, batch-updating policy π and value . This achieved significantly faster convergence and higher sample efficiency than model-free techniques. Subsequently, DreamerV2 [24] maintained advantages in environments combining pixel inputs and discrete actions, like Atari, by redesigning latent variables as discrete codes and introducing KL Balancing and resampling techniques. It outperformed powerful model-free RL methods like Rainbow DQN with under 200 million steps of data. Finally, DreamerV3 [25] added stabilization strategies minimizing hyperparameter dependency such as input/reward scale normalization, KL separation, and Symlog transformation achieving consistent performance across diverse complex environments with varying observation/reward structures, including 3D robot manipulation, sparse-reward mazes, and Minecraft, using a single configuration. In summary, while PlaNet laid the foundation for “latent planning,” Dreamer V1 extended this to policy/value learning to demonstrate sample efficiency, V2 expanded its applicability through continuous to discrete domain extension, and V3 proved practicality through universality and low tuning. These steps progressively elevated the potential for model-based RL to be widely applied to real-world problems.
2.4. Dreamer-Based Autonomous Driving
Pathdreamer, proposed by Koh et al. [12], is a visual World Model for indoor exploration robots. It can generate high-resolution 360° observations based on RGB and depth for unseen locations within buildings not observed during training. This model employs a hierarchical two-stage approach: first, a structure generator predicts depth and semantic segmentation based on latent noise tensors to capture probabilistic information about the layout of unseen rooms; then, an image generator renders this into photorealistic RGB images. This method enables corner prediction and reasonable imagination of the entire contents of unseen spaces, allowing generation of semantically plausible diverse scene layouts. Pathdreamer has demonstrated performance improvements in downstream tasks like Vision-and-Language Navigation (VLN), and pre-planning using its predictions provides an effect similar to previewing unobserved parts in real environments at roughly half the cost.
Think2Drive, proposed by Li et al. [13], is an RL-based autonomous driving approach designed to solve corner situations in complex urban driving on the challenging CARLA Leaderboard v2 benchmark. This method utilizes a neural network simulator as a latent World Model, enabling the planner to efficiently “think” and learn by performing hundreds of parallel rollouts in a low-dimensional latent space. This significantly improved training efficiency compared to direct interaction with a physical simulator, successfully processing all 39 scenarios in CARLA v2 and achieving expert-level driving performance within three days on a single A6000 GPU. Furthermore, Think2Drive integrates various techniques to address common autonomous driving challenges: (i) preventing policy degradation through planner reinitialization, (ii) handling long-tail scenarios via automated scenario generation and termination-priority replay, and (iii) ensuring vehicle steering stability based on a steering cost function.
While Pathdreamer by Koh et al. [12] and Think2Drive by Li et al. [13] represent significant advancements in navigation and autonomous driving using World Models, they have limitations in meeting the specific demands of autonomous racing, particularly the need for smaller model sizes and faster response times. Pathdreamer focuses on generating a 360° panorama from high-resolution (1024 × 512) visual observations (RGB, depth, semantic segmentation). This pixel-obvious generation approach inherently incurs significant computational demands and large model sizes, potentially slowing inference speed. Therefore, it is unsuitable for applications requiring very compact models or fast real-time responsiveness, and its application domains are primarily limited to indoor navigation. Conversely, Think2Drive demonstrated improved training efficiency through latent World Models, but its complex and large-scale DreamerV3 architecture (approximately 104 million parameters) makes deployment challenging in environments with strict constraints on model size and real-time inference speed. Furthermore, its reliance on privileged information inputs like bounding boxes or HD maps means it requires a separate perception pipeline rather than being a fully end-to-end system processing raw sensor data, increasing the overall system’s complexity and scale.
2.5. Dreamer-Based Autonomous Racing
Brunnbauer et al. [26] applied Dreamer to autonomous racing, demonstrating its superiority over various model-free algorithms in a sim2real setting with high-dimensional LiDAR inputs, particularly in terms of sample efficiency, task completion rates, and generalization to unseen tracks. The research compared two observation models: one reconstructing raw LiDAR scans (LiDAR Observation) and another reconstructing local occupancy grid maps (Occupancy Reconstruction), finding that the latter, while learning faster on a specific track, tended to show reduced generalization performance. As such, this prior work focused on analyzing the impact of Dreamer’s observation model without altering its core internal architecture. In contrast, our paper aims to enhance the fundamental structure of the Dreamer model itself to further maximize its performance and generalization capabilities in autonomous racing.
3. LiDAR-Dreamer
LiDAR-Dreamer is a model based on DreamerV1, specialized for LiDAR sensor data to maximize autonomous racing performance, as shown in Figure 1. Given Dreamer’s characteristic of receiving image input, a Cartesian Polar Bar Chart was used as the input plot to process LiDAR data. Based on the characteristics of this modified input plot, the DreamerV1 architecture was lightweighted and optimized for the changed input by using the Light Structured State-Space Cell proposed in this paper instead of the conventional GRUcell. Furthermore, Displacement Covariance Distance was utilized to stabilize training and maximize performance. Section 3.1 explains the Cartesian Polar Bar Chart, Section 3.2 explains the Light Structured State-Space Cell, and finally, Section 3.3 explains Displacement Covariance Distance.
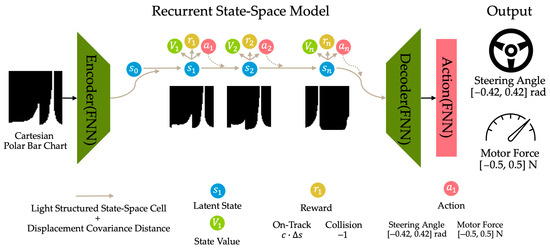
Figure 1.
Structure of LiDAR Dreamer.
3.1. Cartesian Polar Bar Chart
Dreamer receives input as images. Brunnbauer et al. [26] used distance reconstruction and occupancy reconstruction to convert LiDAR input into images, as shown in Figure 2. However, we use the Cartesian Polar Bar Chart method to convert LiDAR input into images by transforming the Polar Bar Chart into a Cartesian coordinate system.

Figure 2.
Dreamer input plot.
LiDAR Observation simply plots points at distances corresponding to the angle of each LiDAR ray from the center of the image. That is, it represents “the location of an obstacle when the actual sensor is pointed in this direction.”
Occupancy Reconstruction is a model that takes a latent state and reconstructs the surrounding map as a 2D occupancy grid. It uses transposed convolution (decoder) to generate a two-dimensional map, similar to a grayscale image, and outputs the “probability of an obstacle” at each pixel as a Bernoulli distribution parameter. During training, small patches of the actual occupancy map are provided as ground truth to ensure the decoder accurately reconstructs the spatial structure.
The two methods above produce results that vary significantly depending on the LiDAR detection angle, making it difficult for the model to make optimal decisions.
The Cartesian Polar Bar Chart is a method for converting a Polar Bar Chart into a Cartesian coordinate system. A Polar Bar Chart displays data magnitude by placing bars radially around a circle. To match the model’s input (square shape), it is converted to a Cartesian coordinate system as shown in Figure 3. The X-axis represents angle (), and the Y-axis represents distance (). This transformation ensures that data changes proportionally from the center of the LiDAR outward as the vehicle moves. Furthermore, input changes remain consistent based on the steering state, making it easier for the model to predict future states.
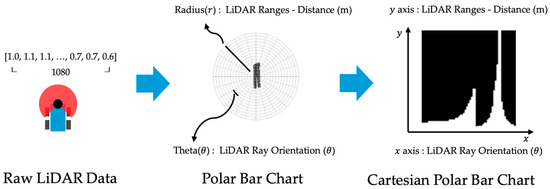
Figure 3.
Process of Raw LiDAR data to Cartesian Polar Bar Chart.
3.2. Light Structured State-Space Cell
In Dreamer, a GRU cell was used as the internal structure of the RSSM. The GRU cell is a recurrent neural network structure that efficiently learns long-term dependencies in sequences by selectively retaining and resetting past memories using Update and Reset Gates. By using the GRU cell, Dreamer’s RSSM can effectively model long-term dependencies through the gate mechanism while reducing parameters and computational load.
We propose a new lightweight cell structure, the Light Structured State-Space Cell (LS3C), which combines the advantages of RNN gate mechanisms and state-space models. LS3C is a recurrent cell designed to stably learn long-term dependencies with fewer parameters, demonstrating efficient and high performance in reinforcement learning environments.
The state update in LS3C is based on a structured state-space model. Specifically, LS3C operates by linearly transforming the previous state to preserve long-term information and then performing a weighted sum of nonlinear transformations applied to the new input. The state of LS3C is defined by the following equation:
Here, is the input at time step , and is the cell state at the previous time step. is the structured state transition matrix of LS3C, a learnable parameter with a fixed structure (e.g., a diagonal stable matrix), which applies a linear transformation to the previous state . in Equation (1) is the update gate, taking values between 0 and 1, computed from the current input and previous state. in Equation (2) is the new candidate state, the result of a nonlinear transformation applied to the current input and previous state, using the tanh activation function (). Finally, in Equation (3), the current state of LS3C is synthesized as a weighted sum of the previous state transformed by the structured matrix and the new candidate state , weighted by the gate .
Compared to the GRUcell, the results are as shown in Table 1 and Table 2. The proposed cell fully removes the reset gate from the standard GRU, eliminating the associated weights , , and operations to lighten the model. Instead, it directly learns the time-series dynamics by applying a structured linear transition matrix A to the past hidden state . As a result, the final update equation changes to (3), reducing the number of parameters and computational load by approximately one-third while retaining the advantage of controlling long-term information via the update gate . The reset gate was removed because, due to the characteristics of racing data where inputs change slowly in 25 ms increments, past information is almost always beneficial. Erasing the past via reset is therefore unhelpful or potentially harmful. In essence, this structure preserves GRU-level long-term dependency handling capabilities while significantly reducing model size and computational cost, making it a lightweight GRU variant.

Table 1.
Mathematical notation for Light Structured State-Space Cell (LS3C).

Table 2.
Comparison between GRU cell and LS3 cell.
In summary, LS3C maintains past state information with a single gate () while efficiently incorporating new information, managing long-term dependencies through structural state propagation via A. This design simplifies the complex gate structure of GRUs while introducing the long-term memory characteristics of state space models.
3.3. Displacement Covariance Distance
Divergence is a function that measures how different two probability distributions and are. The closer it is to 0, the more identical the two distributions are. In Dreamer, the difference between the model’s predicted future and the actual state is measured and learned using KL-Divergence. In this paper, since the shape of the input plot changed, Displacement Covariance Distance was used instead of KL-Divergence to achieve better performance.
Displacement Covariance Distance is a metric based on the concept of distance that primarily measures the difference in the covariance structure between two probability distributions. Intuitively, it serves as an indicator of how different the “spread” or “shape” of the two distributions are; the closer the value is to zero, the more identical the variance-covariance structure of the distributions. It is defined as follows and detailed explanation of the symbols is in Table 3:

Table 3.
Mathematical notation for Displacement Covariance Distance.
Here, the first term is the Wasserstein-1 distance between the means, and the second term represents the difference between the covariance matrices of the two distributions. Notably, when , the above expression simplifies to the definition of the Bures distance between covariance matrices, which is a symmetric metric computed solely from the covariances of the two distributions. Like basic distances, the Displacement Covariance Distance is derived from the optimal transport perspective between distributions. Therefore, it yields finite values even when the support sets of the distributions do not overlap, and it naturally captures differences in both location and shape between distributions. In other words, it is stable, measuring distribution differences without diverging when there is no overlap between distributions, unlike KL divergence. As a distance function, it satisfies symmetry and the triangle inequality, offering analytical advantages.
Cartesian Polar Bar Charts frequently encounter scene transitions where mass ‘moves’ to adjacent bar graphs due to rotation. Due to the nature of bar graphs, KL divergence tends to diverge near values close to zero, specifically where and this situation occurs frequently in Cartesian Polar Bar Charts. In contrast, Displacement Covariance Distance naturally quantifies mass displacement as the optimal transport cost according to the metric and incorporates the covariance term to reflect differences in spread/directionality of distributions. Thus, it simultaneously captures both the displacement and shape changes observed in the Cartesian Polar Bar Chart.
In summary, Displacement Covariance Distance is a metric designed to effectively incorporate the difference between the model’s predicted distribution and the actual distribution into learning. It does this by focusing on the covariance differences in the distributions while maintaining the geometric interpretability and stability of distance.
3.4. Synergy of the Three Components
The three elements of this model are not a simple sum of independent components, but rather an integrated structure designed so that Representation–Dynamics–Objective are interlocking.
First, the Cartesian Polar Bar Chart aligns the geometry of LiDAR observations onto a Cartesian coordinate plane. This ensures that changes in the vehicle’s yaw appear as nearly parallel translations along the angular axis (), while maintaining local smoothness and sparsity along the radial axis () due to distance decay. The statistical outcome of this transformation is summarized by the shift-equivariant approximation:
exhibiting a gradual time-series variation at 40 Hz (≈25 ms).
Second, LS3C possesses a dynamical inductive bias precisely tailored to the above characteristics. Dynamical inductive bias means that the learning model incorporates specific structural constraints or assumptions in advance, enabling it to generalize from data with temporal and dynamic structures. The structured transition matrix approximates the recurrent operator , capturing translation and mild deformation (expansion/contraction) as linear terms. The single update gate suppresses unnecessary forgetting in slow time series, progressively integrating only new evidence (benefit of removing the reset gate). As a result, the prior distribution generated by LS3C tends to form a “translation + weak shape distortion” relationship with the observation-calibrated posterior .
Third, using Displacement Covariance Distance as the loss function to measure the distribution relationship at this point allows the mean displacement component to directly supervise the parallel translation A should predict, while covariance mismatch between distributions normalizes local deformations. Furthermore, even when frequently occurs near the zero region of the Cartesian Polar Bar Chart’s bars, the Displacement Covariance Distance provides a stable gradient that does not diverge as an optimal transport-based distance, making learning robust.
In summary, the three components are designed for synergistic interaction. First, the Cartesian Polar Bar Chart visualizes LiDAR information such that angular variations manifest as horizontal translations on the screen. This ensures high temporal correlation between frames, which appear as incrementally shifting images. Second, LS3C is architected to model these incremental changes. It employs a transition matrix to capture translation and gentle deformations, while a single update gate prevents catastrophic forgetting. This results in a prior that is essentially a slightly displaced and moderately reshaped version of the posterior. Third, the Displacement Covariance Distance metric is tailored to quantify this relationship by decomposing it into two axes: mean displacement (displacement) and covariance dissimilarity (shape). This effectively disentangles the magnitude of the shift from the degree of shape alteration. A key benefit is its robustness; it does not diverge with sparse, near-zero LiDAR readings, which stabilizes the learning process.
Thus, the representation (Cartesian Polar Bar Chart), dynamics model (LS3C), and loss function (Displacement Covariance Distance) are fundamentally aligned. This coherence allows the model to achieve more stable convergence with greater data efficiency compared to the standard Dreamer architecture.
4. Experiment Results
The experiment was conducted in the PyBullet-based F1TENTH simulator environment on three maps (Austria, Columbia, Treitlstrasse) as shown in Table 4. Austria has the longest map length and the sharpest corner. Columbia has the widest map width and the lowest curvature. Treitlstrasse has the narrowest section. The final reward for reinforcement learning is progress. Starting from the origin, the reward is 0, and as progress increases (approaching the black area), a reward of 1 is obtained. If there is no collision, the vehicle’s progress is tracked for a limited time (40 s). Progress is defined as the fraction of track distance completed, where 1.0 represents one complete lap. For instance, a progress value of 1.0 means one full lap is completed, while 1.5 means the vehicle has completed one and a half laps.

Table 4.
Test Maps used in the experiments.
Section 4.1, Section 4.2 and Section 4.3 compare existing methods with the proposed method based on DreamerV1. They show the reward loss, indicating how accurately the World Model predicted the reward one step ahead. If the reward loss consistently decreases, it means the World Model accurately predicts rewards, and the rollout aligns well with reality, leading to steady policy performance improvement. If it stagnates, increases, or fluctuates wildly, reward prediction is likely inaccurate or unstable, distorting the rollout. This often results in lower test returns or policy instability. Progress is also compared to show how much of the map the vehicle traverses in the actual driving environment. Progress is a metric showing either the number of obstacles collided with within a specified time or the extent of map exploration achieved within that time.
Section 4.4 compares Progress between the model applying all proposed methods and Model-free RL, Model-based RL, and base Dreamer V1, 2, and 3. The Model-free RL methods used for comparison are D4PG, MPO, PPO, and SAC. The Model-based RL methods are MBPO and PILCO.
4.1. Input Plot—Cartesian Polar Bar Chart
Three input plots were used in the experiment: LiDAR Observation (lidar), Occupancy Reconstruction (lidaroccupancy), and Cartesian Polar Bar Chart (polarbarchart). The remaining parameters (RNN, Divergence) used the base DreamerV1 configuration.
Figure 4 shows the Reward Loss converged to approximately 0.92 overall. While similar performance was observed on Austria and Treitlstrasse, a noticeable difference emerged on Columbia. This indicates that the map is very simple, making it more efficient to predict average values rather than accurately predicting the future.
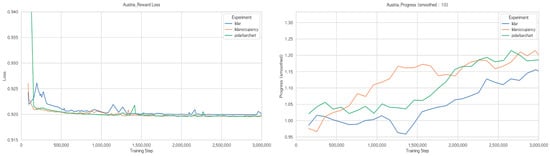
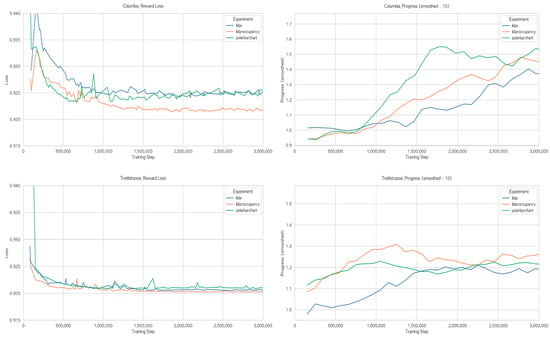
Figure 4.
Comparison of input representations on Austria, Columbia, and Treitlstrasse tracks.
Progress showed that the proposed Cartesian Polar Bar Chart method achieved the best performance at approximately 2,600,000 steps on Austria and 1,800,000 steps on Columbia. However, on Treitlstrasse, it performed slightly worse than Occupancy Reconstruction. This indicates that additional methods are needed for the proposed approach to demonstrate good performance on all maps.
4.2. Recurrent Neural Network—Light Structured State-Space Cell
The experiment compared GRUcell and LS3C. Additionally, experiments were conducted using the same three input plots as before, resulting in a total of six comparison cases. The dashed line represents the existing method, GRU, while the solid line represents the proposed method, LS3C. The number of parameters for RSSM is as follows: RSSM using GRUcell has 568,320 parameters, while RSSM using LS3C has 487,520 parameters. This represents a difference of 80,800 parameters, achieving approximately 14.2% parameter reduction.
Figure 5 shows the Reward Loss converges to approximately 0.92 overall. Columbia’s results show that for lidar and lidaroccupancy, using LS3C instead of the original GRU increases the loss value. However, the proposed polar bar chart shows a decrease in loss when using LS3C. This indicates that LS3C performs well in combination with the polar bar chart for simple map layouts, suggesting that the reduced parameters heuristically improve prediction accuracy. Additionally, results from Treitlstrasse show that using LS3C can cause learning to collapse in certain regions due to the emergence of local minima.
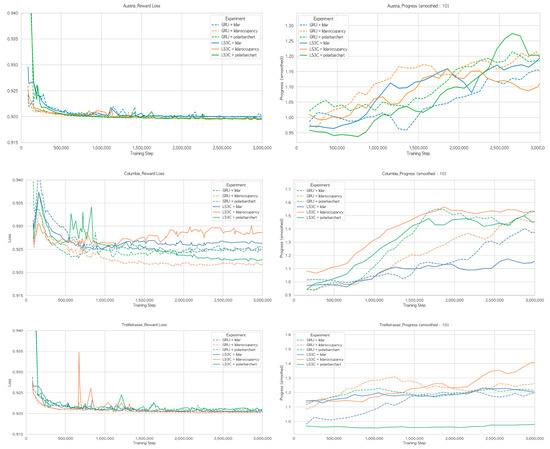
Figure 5.
Comparison of recurrent neural network architectures (GRU vs. LS3C) on Austria, Columbia, and Treitlstrasse tracks.
Progress shows the model using LS3C and Polar Bar Chart performs best in Austria. However, it shows moderate performance in Columbia and particularly poor performance in Treitlstrasse.
4.3. Divergence—Displacement Covariance Distance
The experiment compared three divergence measures: Hellinger Distance, KL Divergence used in DreamerV1, and the proposed Displacement Covariance Distance. The dotted line represents lidar, the dashed line represents lidar occupancy, and the solid line represents the polar bar chart. Blue indicates Hellinger Distance, orange indicates KL Divergence, and green indicates Displacement Covariance Distance.
Figure 6 shows the reward loss converged to approximately 0.92 overall. Examining the results from Columbia, the solid line representing the polar bar chart had the lowest reward loss among the input plots, but it also exhibited the most peaks, leading to frequent collapses during training. However, the green lines using the Displacement Covariance Distance method on Austria and Treitlstrasse had the fewest peaks, indicating they experienced the least learning collapse. This demonstrates their strong performance on complex maps.
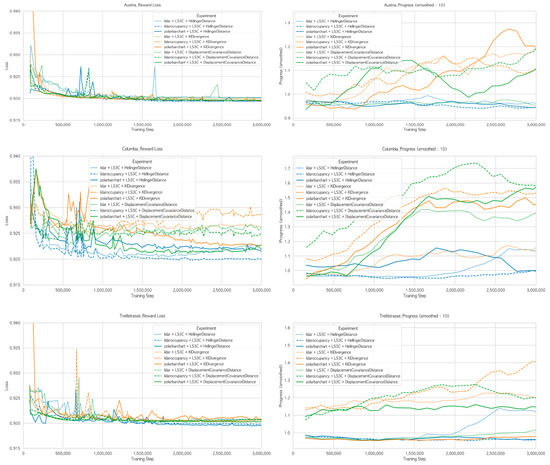
Figure 6.
Comparison of divergence measures (Hellinger Distance, KL Divergence, and Displacement Covariance Distance) on Austria, Columbia, and Treitlstrasse tracks.
Progress shows that the combination of LS3C and Displacement Covariance Distance achieves the fastest learning speed.
4.4. Compare with Other Reinforcement Learning Models
To demonstrate the effectiveness of the proposed model, we compare its progress with other reinforcement learning models. For model-free RL, we used D4PG, MPO, PPO, and SAC as comparison models, while for model-based RL, we used MBPO and PILCO. We also compared it with base Dreamer V1, V2, and V3. Model-free RL and Model-based RL employed hyperparameters optimized via Optuna [27], while the base Dreamer models used the default Dreamer hyperparameters. To distinguish each model’s characteristics, model-free and model-based models are shown as dotted lines, base Dreamer V1, V2, and V3 as dash lines, and the proposed model as solid lines. Vertical lines were added at the training points where maximum progress was achieved, and the corresponding progress values were displayed at the top of the graph.
Figure 7 and Table 5 show the proposed method on Austria achieved the maximum progress at the second fastest rate after DreamerV2+lidaroccupancy. It also achieved the second-highest maximum progress value second highest after DreamerV1+lidaroccupancy. On the Columbia track, while model-free methods (particularly MPO and PPO) achieved superior absolute performance with progress values exceeding 2.0, the proposed method demonstrated competitive performance among the Dreamer-V1, V2, V3, reaching a progress of 1.56 compared to DreamerV2+lidaroccupancy’s 1.71. This represents an approximately 8.8% difference while using significantly fewer parameters. On Treitlstrasse, the proposed method does not achieve the maximum progress value but reaches a progress value greater than 1 at one of the fastest rates.
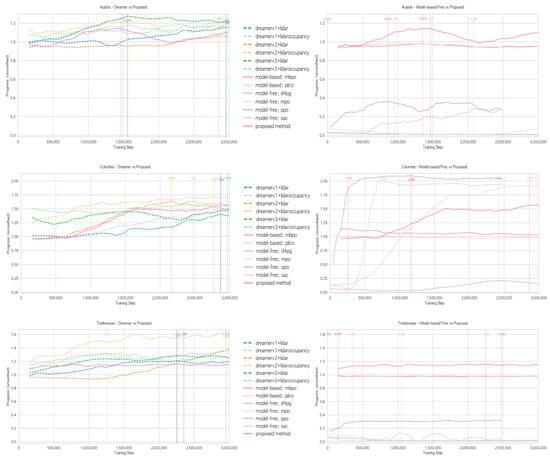
Figure 7.
Performance comparison with other reinforcement learning models on Austria, Columbia, and Treitlstrasse tracks.

Table 5.
Performance comparison with other reinforcement learning models.
To summarize, in complex environments with numerous rounded corners such as Austria, our method recorded the second-best step-to-peak ratio among the Dreamer models. Its progress was just 0.1314 less than the top score of 1.2742 (DreamerV3+lidar). This result is reasonable, considering the RSSM parameter counts of DreamerV2 (5,379,848) and DreamerV3 (2,669,072). Conversely, the method did not stand out on maps with sharp corners like Treitlstrasse in either step at peak or progress. For simple maps such as Columbia, model-free methods generally performed better. While our method’s absolute progress on Columbia does not match the best-performing model-free methods, it shows improved efficiency compared to baseline DreamerV1 models, which is significant given the 14.2% reduction in RSSM parameters.
5. Conclusions
This study proposed LiDAR Dreamer, a lightweight LiDAR-specialized architecture derived from Dreamer V1, to solve the autonomous racing problem demanding simultaneous sample efficiency, prediction reliability, and real-time performance under extreme driving conditions. We first transformed LiDAR distance and direction information into a Cartesian Polar Bar Chart, normalizing the input space into a uniform orthogonal coordinate system. This enabled RSSM to converge quickly and stably even on tracks with high curvature variations. Next, we designed a Light Structured State-Space Cell, reducing parameters by 14.2% compared to the original GRU while maintaining and enhancing long-term dependency representation. Finally, we introduced Displacement Covariance Distance to suppress distribution collapse, simultaneously improving learning stability and final performance.
On complex tracks such as Austria, LiDAR Dreamer achieved competitive performance (1.14 progress) compared to DreamerV3 (1.27 progress) while using 14.2% fewer parameters, demonstrating efficiency in parameter usage. On Treitlstrasse, it showed comparable results to baseline methods. However, on the simpler Columbia track, while model-free methods (MPO, PPO) achieved superior absolute performance exceeding 2.0 progress, our method reached 1.56 progress. This shows improved sample efficiency compared to DreamerV1 but lower final performance than DreamerV2 and V3.
This performance pattern, where World Models excel on complex tracks but show diminished advantages on simple ones, represents a limitation shared across the Dreamer family. The overhead of learning a World Model may not be justified for environments where direct policy optimization suffices. Future research aims to achieve maximized performance even on simple tracks through adaptive rollout lengths and hybrid search strategies. Furthermore, research will continue exploring extension to MCU-class controllers by applying fine-grained quantization and graph pruning.
Author Contributions
Conceptualization, M.K.; Methodology, M.K. and G.-W.K.; Software, M.K. and J.-C.P.; Formal analysis, S.-M.C. and G.-W.K.; Investigation, M.K. and J.-C.P.; Data curation, M.K.; Writing—original draft, M.K. and G.-W.K.; Writing—review and editing, S.-M.C. and G.-W.K.; Supervision, S.-M.C. and G.-W.K.; Project administration, S.-M.C. and G.-W.K.; Funding acquisition, S.-M.C. and G.-W.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the research grant of the Gyeongsang National University in 2024; This research was supported by “Regional Innovation Strategy (RIS)” through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (MOE) (2021RIS-003).
Data Availability Statement
The datasets used and/or analyzed during the current research are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lyu, C.; Lu, D.; Xiong, C.; Hu, R.; Jin, Y.; Wang, J.; Zeng, Z.; Lian, L. Toward a gliding hybrid aerial underwater vehicle: Design, fabrication, and experiments. J. Field Robot. 2022, 39, 543–556. [Google Scholar] [CrossRef]
- Kabzan, J.; Valls, M.I.; Reijgwart, V.J.; Hendrikx, H.F.; Ehmke, C.; Prajapat, M.; Bühler, A.; Gosala, N.; Gupta, M.; Sivanesan, R.; et al. AMZ driverless: The full autonomous racing system. J. Field Robot. 2020, 37, 1267–1294. [Google Scholar] [CrossRef]
- Law, C.K.; Dalal, D.; Shearrow, S. Robust model predictive control for autonomous vehicles/self driving cars. arXiv 2018, arXiv:1805.08551. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Learning how to autonomously race a car: A predictive control approach. IEEE Trans. Control. Syst. Technol. 2019, 28, 2713–2719. [Google Scholar] [CrossRef]
- Sezer, V.; Gokasan, M. A novel obstacle avoidance algorithm: “follow the gap method”. Robot. Auton. Syst. 2012, 60, 1123–1134. [Google Scholar] [CrossRef]
- Otterness, N. Disparity Extender. Available online: https://www.nathanotterness.com/2019/04/the-disparity-extender-algorithm-and.html (accessed on 9 October 2025).
- Scharf, L.L.; Harthill, W.P.; Moose, P.H. A comparison of expected flight times for intercept and pure pursuit missiles. IEEE Trans. Aerosp. Electron. Syst. 1969, AES-5, 672–673. [Google Scholar] [CrossRef]
- Wit, J.; Crane, C.D., III; Armstrong, D. Autonomous ground vehicle path tracking. J. Robot. Syst. 2004, 21, 439–449. [Google Scholar] [CrossRef]
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, UK, 1998; Volume 1, pp. 9–11. [Google Scholar]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Koh, J.Y.; Lee, H.; Yang, Y.; Baldridge, J.; Anderson, P. Pathdreamer: A world model for indoor navigation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 14738–14748. [Google Scholar]
- Li, Q.; Jia, X.; Wang, S.; Yan, J. Think2Drive: Efficient Reinforcement Learning by Thinking with Latent World Model for Autonomous Driving (in CARLA-V2). In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer Nature: Cham, Switzerland, 2024; pp. 142–158. [Google Scholar]
- Seo, Y.; Kim, J.; James, S.; Lee, K.; Shin, J.; Abbeel, P. Multi-view masked world models for visual robotic manipulation. In Proceedings of the International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; PMLR: New York, NY, USA, 2023; pp. 30613–30632. [Google Scholar]
- Wu, P.; Escontrela, A.; Hafner, D.; Abbeel, P.; Goldberg, K. Daydreamer: World models for physical robot learning. In Proceedings of the Conference on Robot Learning, Auckland, New Zealand, 14–18 December 2022; PMLR: New York, NY, USA, 2023; pp. 2226–2240. [Google Scholar]
- Barth-Maron, G.; Hoffman, M.W.; Budden, D.; Dabney, W.; Horgan, D.; Tb, D.; Muldal, A.; Heess, N.; Lillicrap, T. Distributed distributional deterministic policy gradients. arXiv 2018, arXiv:1804.08617. [Google Scholar] [CrossRef]
- Abdolmaleki, A.; Springenberg, J.T.; Tassa, Y.; Munos, R.; Heess, N.; Riedmiller, M. Maximum a posteriori policy optimisation. arXiv 2018, arXiv:1806.06920. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; PMLR: New York, NY, USA, 2018; pp. 1861–1870. [Google Scholar]
- Deisenroth, M.; Rasmussen, C.E. PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 465–472. [Google Scholar]
- Janner, M.; Fu, J.; Zhang, M.; Levine, S. When to trust your model: Model-based policy optimization. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada, 8–14 December 2019; Volume 32. Available online: https://proceedings.neurips.cc/paper_files/paper/2019/file/5faf461eff3099671ad63c6f3f094f7f-Paper.pdf (accessed on 9 October 2025).
- Hafner, D.; Lillicrap, T.; Fischer, I.; Villegas, R.; Ha, D.; Lee, H.; Davidson, J. Learning latent dynamics for planning from pixels. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: New York, NY, USA, 2019; pp. 2555–2565. [Google Scholar]
- Hafner, D.; Lillicrap, T.; Ba, J.; Norouzi, M. Dream to control: Learning behaviors by latent imagination. arXiv 2019, arXiv:1912.01603. [Google Scholar]
- Hafner, D.; Lillicrap, T.; Norouzi, M.; Ba, J. Mastering atari with discrete world models. arXiv 2020, arXiv:2010.02193. [Google Scholar]
- Hafner, D.; Pasukonis, J.; Ba, J.; Lillicrap, T. Mastering diverse domains through world models. arXiv 2023, arXiv:2301.04104. [Google Scholar]
- Brunnbauer, A.; Berducci, L.; Brandstátter, A.; Lechner, M.; Hasani, R.; Rus, D.; Grosu, R. Latent imagination facilitates zero-shot transfer in autonomous racing. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: New York, NY, USA, 2022; pp. 7513–7520. [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).


