Strategic Launch Pad Positioning: Optimizing Drone Path Planning Through Genetic Algorithms †
Abstract
1. Introduction
Motivation & Contribution
- Formulates UAV launch pad positioning as a planar location-routing problem and demonstrates genetic algorithm effectiveness in continuous space optimization for multi-drone operations.
- Provides a comprehensive systematic comparison of a genetic algorithm against both exhaustive search methods and alternative metaheuristics (PSO, SA) for optimizing launch pad location in UAV applications, establishing the GA’s superior computational efficiency despite marginally lower accuracy compared to PSO.
- Introduces and evaluates smart initialization and adaptive termination techniques for genetic algorithms in the LRP context, demonstrating modest but consistent improvements in convergence characteristics while maintaining solution quality.
- Provides a validated methodological framework with empirical benchmarks enabling practitioners to select appropriate optimization approaches based on accuracy requirements versus computational constraints.
- Enhances the framework presented in [2] with multiple algorithmic approaches that aid in the prediction of optimal launch pad positioning.
- Establishes computational benchmarks and parameter optimization guidelines for metaheuristic applications in continuous location-routing problems, contributing to the broader UAV optimization literature.
2. Background and Related Work
2.1. Planar Location-Routing Problems in UAV Applications
2.2. UAV Path Planning Optimization Methodologies
2.3. Environmental Adaptability and Swarm Intelligence
2.4. Green Drone Delivery and Energy-Aware Routing
2.5. Energy-Aware Planning and Launch Pad Optimization
2.6. Metaheuristic Approaches to PLRP
2.7. Research Gap and Contribution Positioning
3. Proposed Method
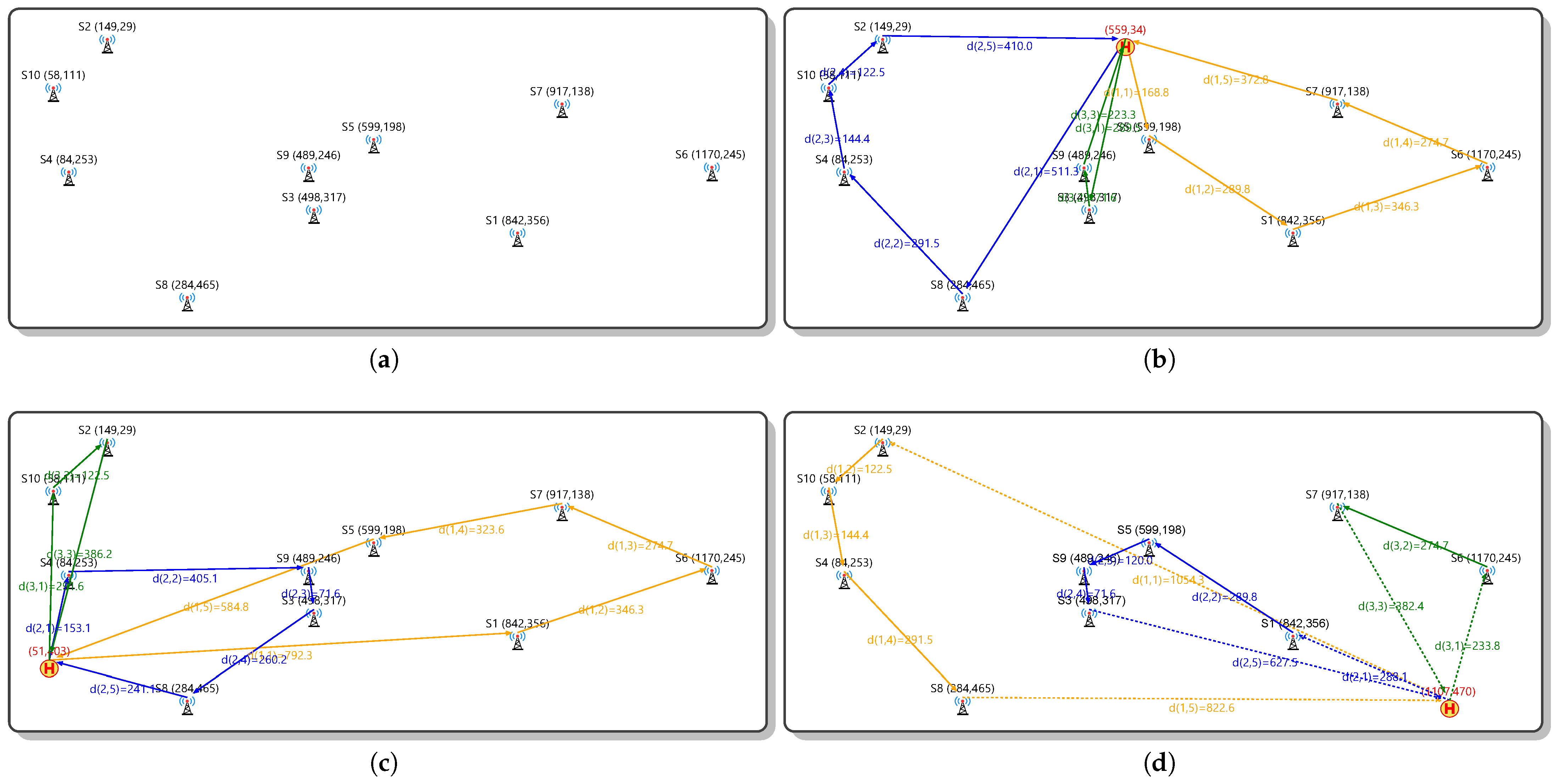
3.1. Establishing the Ground Truth
3.2. The Implementation of GA with mTSP
3.2.1. Rationale for Genetic Algorithm Selection
3.2.2. The Approach
| Algorithm 1 FindOptimalStartingPoint |
|
| Algorithm 2 Genetic algorithm for optimal starting point in MTSP |
|
4. Experimental Evaluation
4.1. The Setup
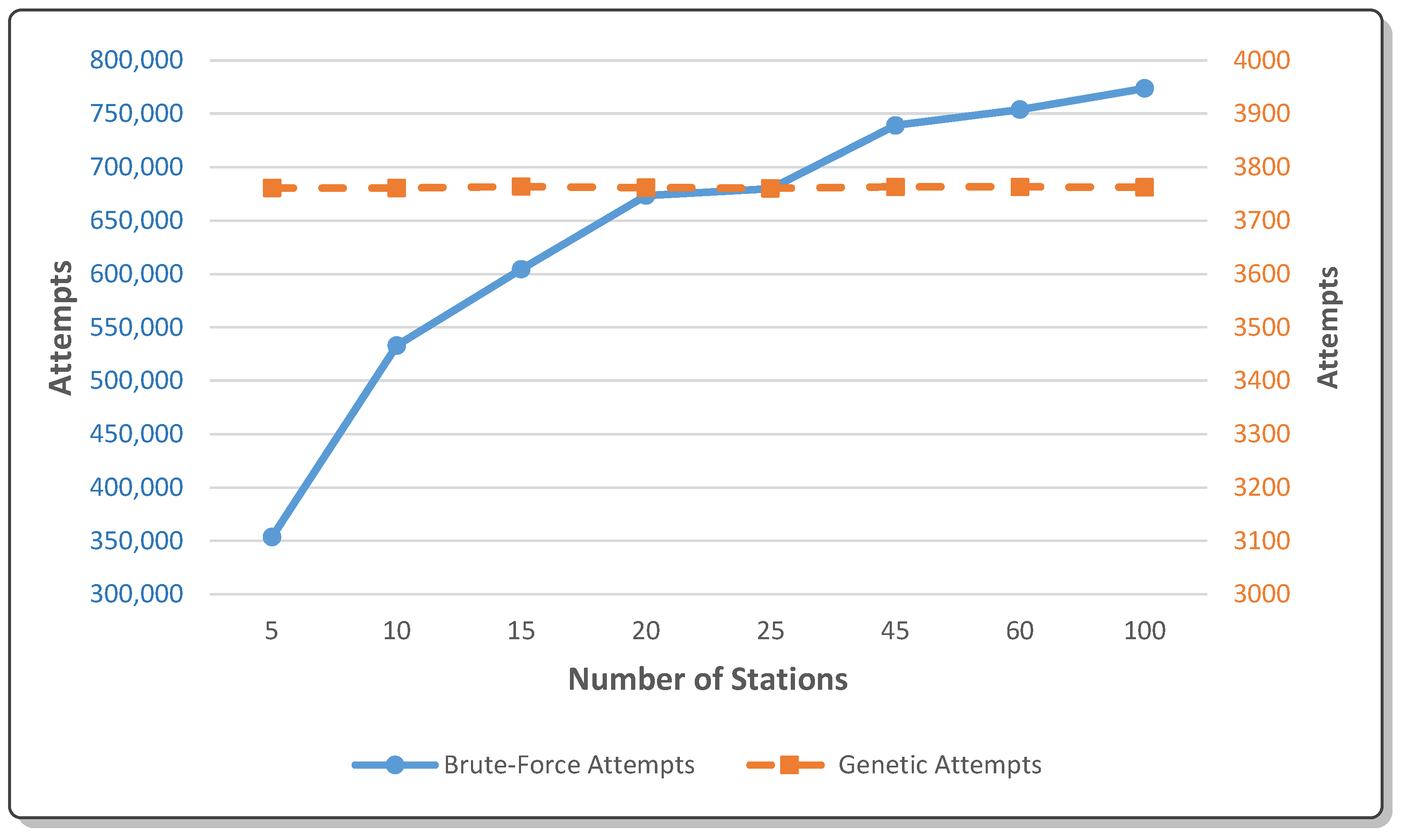
4.2. The Results
- Provides a near-optimal solution with accuracy levels exceeding 97%.
- Drastically reduces computation time, achieving results up to 4 orders of magnitude faster than brute-force.
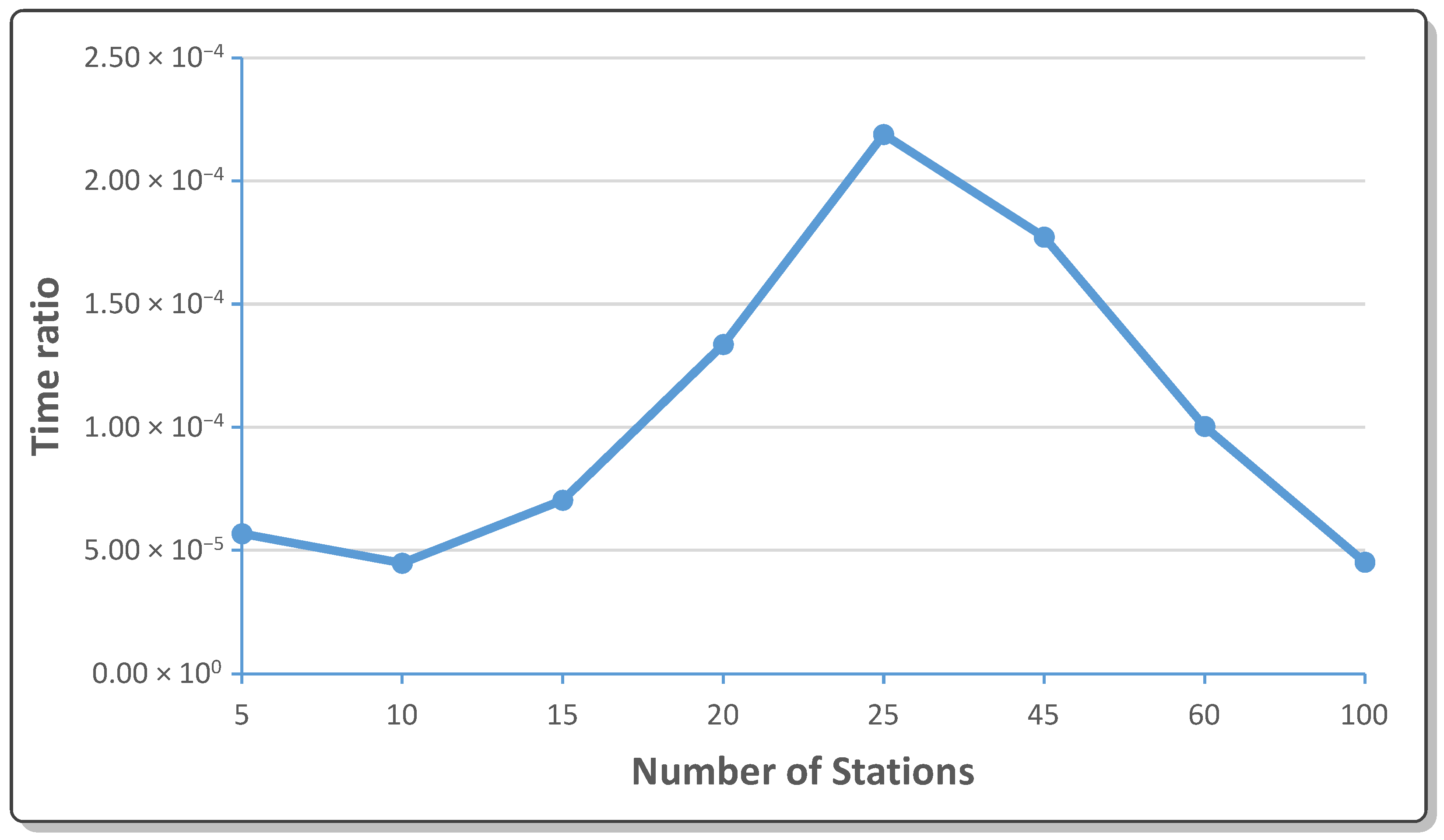
4.3. Solidifying the Results
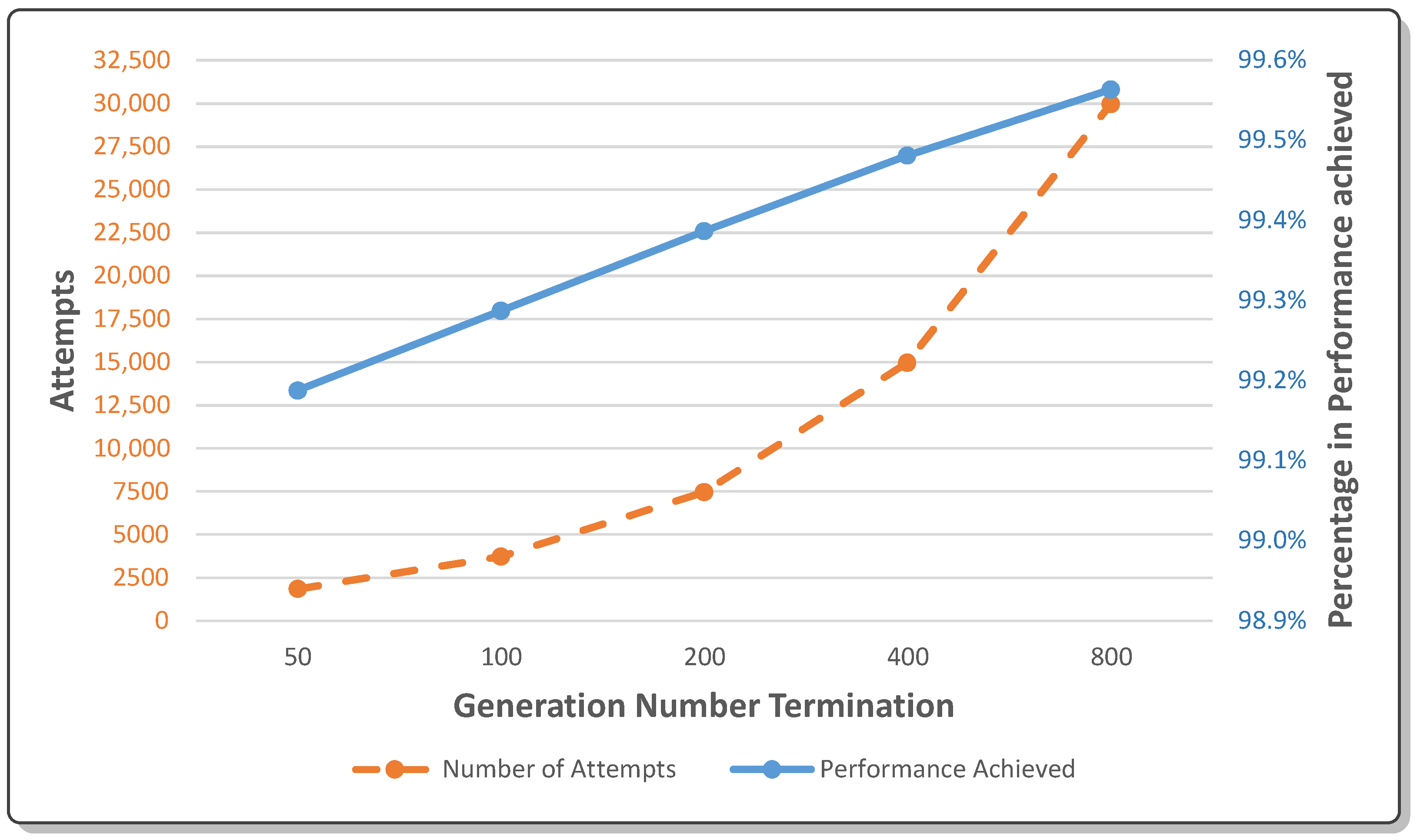
4.4. Taking It Further
4.4.1. Smart Initial Population
4.4.2. Striking the Right Balance
4.4.3. Mitigating Local Minima
4.4.4. Comparative Analysis with Alternative Metaheuristics
Parameter Configuration and Sensitivity Analysis
Comparative Methodology and Iteration Metrics
Experimental Results and Performance Analysis
Computational Efficiency Considerations
Algorithmic Behavior Analysis
Validation of Initial Algorithm Selection
4.5. Limitations
5. Conclusions
5.1. Future Work
5.1.1. Integration of Realistic UAV Energy Dynamics
5.1.2. Dynamic and Adaptive Launch Pad Strategies
5.1.3. Hybrid Optimization Algorithms
5.1.4. Advanced Genetic Algorithm Refinements
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vashisth, A.; Batth, R.S.; Ward, R. Existing Path Planning Techniques in Unmanned Aerial Vehicles (UAVs): A Systematic Review. In Proceedings of the 2021 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), Dubai, United Arab Emirates, 17–18 March 2021; pp. 366–372. [Google Scholar] [CrossRef]
- Gasteratos, G.; Karydis, I. Path Planning Optimisation for Multiple Drones: Repositioning the Starting Point. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Corfu, Greece, 27–30 June 2024; pp. 211–223. [Google Scholar] [CrossRef]
- Quamar, M.M.; Al-Ramadan, B.; Khan, K.; Shafiullah, M.; El Ferik, S. Advancements and Applications of Drone-Integrated Geographic Information System Technology—A Review. Remote Sens. 2023, 15, 5039. [Google Scholar] [CrossRef]
- Saeed, R.A.; Omri, M.; Abdel-Khalek, S.; Ali, E.S.; Alotaibi, M.F. Optimal path planning for drones based on swarm intelligence algorithm. Neural Comput. Appl. 2022, 34, 10133–10155. [Google Scholar] [CrossRef]
- Gasteratos, G.; Karydis, I. Efficient Drone Path Planning through Strategic Launch Pad Positioning. In Proceedings of the 1st International Conference on Drones and Unmanned Systems (DAUS’ 2025), Granada, Spain, 19–21 February 2025; IFSA Publishing: Barcelona, Spain, 2025; pp. 254–259. [Google Scholar] [CrossRef]
- Drezner, Z.; Wesolowsky, G.O. A Trajectory Approach to the Round-Trip Location Problem. Transp. Sci. 1982, 16, 56–66. [Google Scholar] [CrossRef]
- Drezner, Z.; Wesolowsky, G.O. Facility Location on a Sphere. J. Oper. Res. Soc. 1978, 29, 997–1004. [Google Scholar] [CrossRef]
- Drezner, Z.; Wesolowsky, G.O. Obnoxious Facility Location in the Interior of a Planar Network. J. Reg. Sci. 1995, 35, 675–688. [Google Scholar] [CrossRef]
- Salhi, S.; Rand, G.K. The effect of ignoring routes when locating depots. Eur. J. Oper. Res. 1989, 39, 150–156. [Google Scholar] [CrossRef]
- Nagy, G.; Salhi, S. Location-routing: Issues, models and methods. Eur. J. Oper. Res. 2007, 177, 649–672. [Google Scholar] [CrossRef]
- Fan, X. A path-planning method for uav swarm under multiple environmental threats. Drones 2024, 8, 171. [Google Scholar] [CrossRef]
- Xiong, T.; Li, H.; Ding, K.; Liu, H.; Li, Q. A Hybrid Improved Symbiotic Organisms Search and Sine–Cosine Particle Swarm Optimization Method for Drone 3D Path Planning. Drones 2023, 7, 633. [Google Scholar] [CrossRef]
- Boccadoro, P.; Striccoli, D.; Grieco, L.A. An extensive survey on the Internet of Drones. Ad Hoc Networks 2021, 122, 102600. [Google Scholar] [CrossRef]
- Shirabayashi, J.V.; Ruiz, L.B. Toward uav path planning problem optimization considering the internet of drones. IEEE Access 2023, 11, 136825–136854. [Google Scholar] [CrossRef]
- Jones, M.; Djahel, S.; Welsh, K. Path-planning for unmanned aerial vehicles with environment complexity considerations: A survey. ACM Comput. Surv. 2023, 55, 234. [Google Scholar] [CrossRef]
- Wu, Y.; Low, K.; Pang, B.; Tan, Q. Swarm-based 4d path planning for drone operations in urban environments. IEEE Trans. Veh. Technol. 2021, 70, 7464–7479. [Google Scholar] [CrossRef]
- Lu, F.; Tian, S.; Feng, W.; Bi, H. Green drone multi-package delivery routing problem and its efficient algorithms. Int. J. Gen. Syst. 2025, 1–32. [Google Scholar] [CrossRef]
- Diller, J.; Han, Q. Energy-aware drone path finding with a fixed-trajectory ground vehicle. J. Auton. Transp. Syst. 2023, 2, 17. [Google Scholar] [CrossRef]
- Dang, S.; Liu, Y.; Luo, Z.; Liu, Z.; Shi, J. A Survey of the Routing Problem for Cooperated Trucks and Drones. Drones 2024, 8, 550. [Google Scholar] [CrossRef]
- Brimberg, J.; Hansen, P.; Mladenovic, N.; Salhi, S. A Survey of Solution Methods for the Continuous Location-Allocation Problem. Int. J. Oper. Res. 2008, 5, 1–12. [Google Scholar]
- Mara, S.T.W.; Kuo, R.; Asih, A.M.S. Location-routing problem: A classification of recent research. Int. Trans. Oper. Res. 2021, 28, 2941–2983. [Google Scholar] [CrossRef]
- Bektaş, T. The multiple traveling salesman problem: An overview of formulations and solution procedures. Omega-Int. J. Manag. Sci. 2006, 34, 209–219. [Google Scholar] [CrossRef]
- Cheikhrouhou, O.; Khoufi, I. A comprehensive survey on the Multiple Traveling Salesman Problem: Applications, approaches and taxonomy. Comput. Sci. Rev. 2021, 40, 100369. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Storn, R.; Price, K.V. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kang, M.; Lee, C. An Exact Algorithm for Heterogeneous Drone-Truck Routing Problem. Transp. Sci. 2021, 55, 1088–1112. [Google Scholar] [CrossRef]
- Liang, Y.J.; Luo, Z.X. A Survey of Truck–Drone Routing Problem: Literature Review and Research Prospects. J. Oper. Res. Soc. China 2022, 10, 343–377. [Google Scholar] [CrossRef]
- Fang, S.; Luo, Z. Multi-Traveling Salesman Algorithm for UAV Swarms Based on Improved Genetic Algorithm. In Proceedings of the 2024 IEEE 6th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 26–28 July 2024; pp. 1027–1032. [Google Scholar] [CrossRef]
- C# Genetic Algorithm Library. Available online: https://github.com/giacomelli/GeneticSharp (accessed on 5 December 2024).
- Whitley, D. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Back, T. Selective pressure in evolutionary algorithms: A characterization of selection mechanisms. In Proceedings of the First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994; Volume 1, pp. 57–62. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Stützle, T.; Dorigo, M. Ant Colony Optimization: A Component-Wise Overview. In Handbook of Heuristics; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–37. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications. In Mathematics and Its Applications; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Bernard, R.; Robert, J.G.; Mei-Ling, T.L. The Wilcoxon signed rank test for paired comparisons of clustered data. Biometrics 2006, 62, 185–192. [Google Scholar] [CrossRef]
- Deakin, R.; Bird, S.; Grenfell, R. The Centroid? Where would you like it to be be? Cartography 2002, 31, 153–167. [Google Scholar] [CrossRef]
- Minsker, S.; Strawn, N. The Geometric Median and Applications to Robust Mean Estimation. arXiv 2023, arXiv:2307.03111. [Google Scholar] [CrossRef]
- Kwon, H.; Oh, S.; Baek, J.W. Algorithmic Efficiency in Convex Hull Computation: Insights from 2D and 3D Implementations. Symmetry 2024, 16, 1590. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Deng, D. DBSCAN clustering algorithm based on density. In Proceedings of the 2020 7th international forum on electrical engineering and automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 949–953. [Google Scholar]
- Gu, R.; Zhao, Y.; Ren, X. Integrating wind field analysis in UAV path planning: Enhancing safety and energy efficiency for urban logistics. Chin. J. Aeronaut. 2025, 103605. [Google Scholar] [CrossRef]
- Thibbotuwawa, A.; Nielsen, P.; Zbigniew, B.; Bocewicz, G. Factors Affecting Energy Consumption of Unmanned Aerial Vehicles: An Analysis of How Energy Consumption Changes in Relation to UAV Routing. In Proceedings of the Information Systems Architecture and Technology: 39th International Conference on Information Systems Architecture and Technology—ISAT 2018, Nysa, Poland, 16–18 September 2018; Świątek, J., Borzemski, L., Wilimowska, Z., Eds.; Springer: Cham, Switzerland, 2019; pp. 228–238. [Google Scholar]
- Nagy, I.; Laufer, E. Energy-Optimized 3D Path Planning for Unmanned Aerial Vehicles. Appl. Sci. 2024, 14, 6988. [Google Scholar] [CrossRef]
- Lv, S.; Wang, X.; Lu, W.; Zhang, J.; Ni, H. The Influence of Temperature on the Capacity of Lithium Ion Batteries with Different Anodes. Energies 2022, 15, 60. [Google Scholar] [CrossRef]
- Ercan, H.; Ayaz, F.A.; Ulucan, H. Effect of Temperature, Pressure and Humidity on Battery Consumption in Unmanned Aerial Vehicles. J. Aviat. 2025, 9, 5–12. [Google Scholar] [CrossRef]
- Seth, A.; James, A.; Kuantama, E.; Mukhopadhyay, S.; Han, R. Aerodynamics and Sensing Analysis for Efficient Drone-Based Parcel Delivery. In Proceedings of the 2023 16th International Conference on Sensing Technology (ICST), Hyderabad, India, 17–20 December 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Qi, Y.; Jiang, H.; Huang, G.; Yang, L.; Wang, F.; Xu, Y. Multi-UAV path planning considering multiple energy consumptions via an improved bee foraging learning particle swarm optimization algorithm. Sci. Rep. 2025, 15, 14755. [Google Scholar] [CrossRef] [PubMed]
- Su, S.; Shan, X.; Yu, P.; Wang, H. Energy Consumption Performance of a VTOL UAV In and Out of Ground Effect by Flight Test. Drones 2024, 8, 625. [Google Scholar] [CrossRef]
- Pasala, S.; Kumar, B.N.; Satapathy, S.C. A Study of Roulette Wheel and Elite Selection on GA to Solve Job Shop Scheduling. In Proceedings of the International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA); Satapathy, S.C., Udgata, S.K., Biswal, B.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 477–485. [Google Scholar] [CrossRef]
- Pencheva, T.; Atanassov, K.; Shannon, A. Modelling of a stochastic universal sampling selection operator in genetic algorithms using generalized nets. In Proceedings of the Tenth International Workshop on Generalized Nets, Sofia, Bulgaria, 5 December 2009; pp. 1–7. [Google Scholar]
- Bell, O. Applications of Gaussian Mutation for Self Adaptation in Evolutionary Genetic Algorithms. arXiv 2022, arXiv:2201.00285. [Google Scholar] [CrossRef]




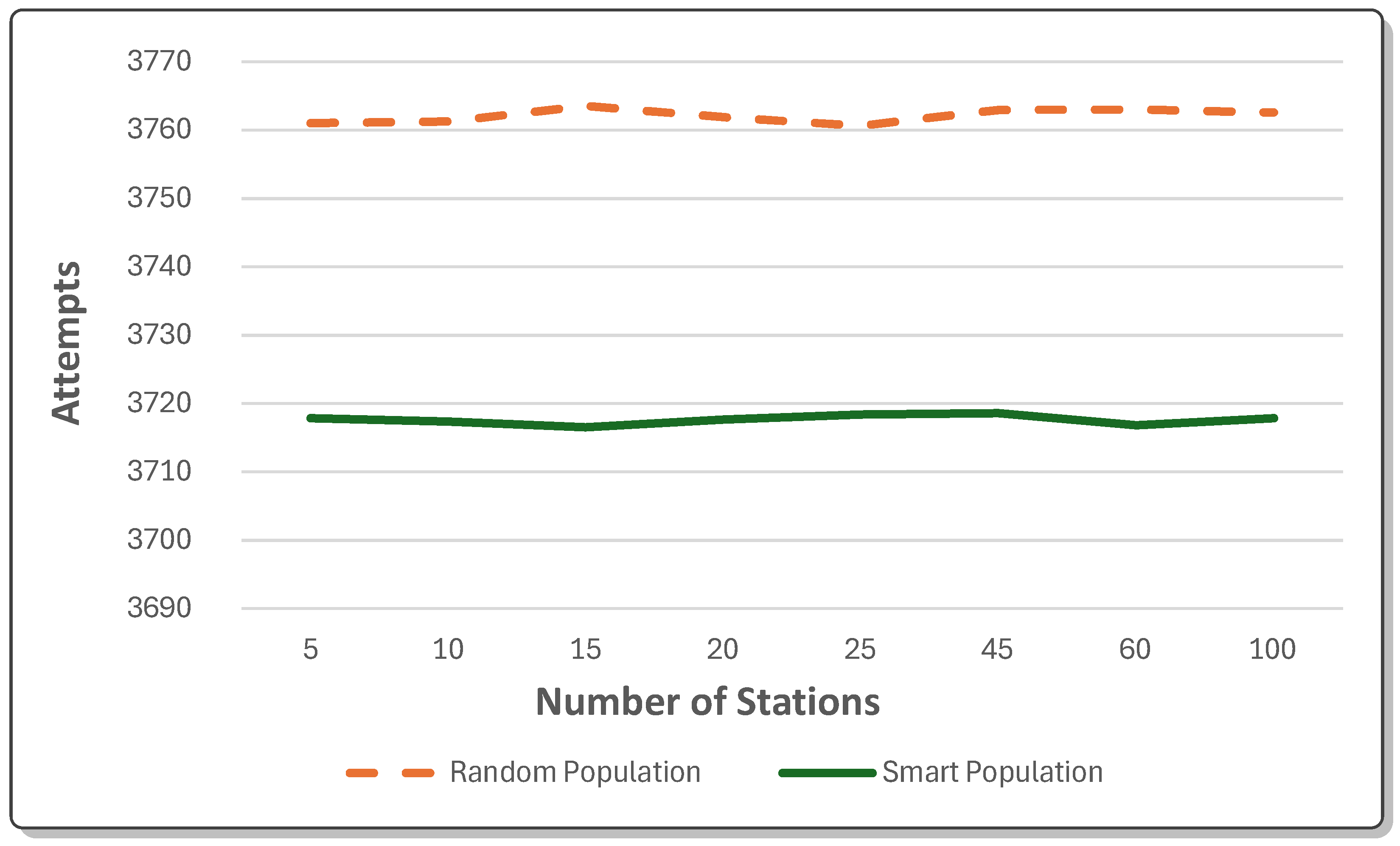

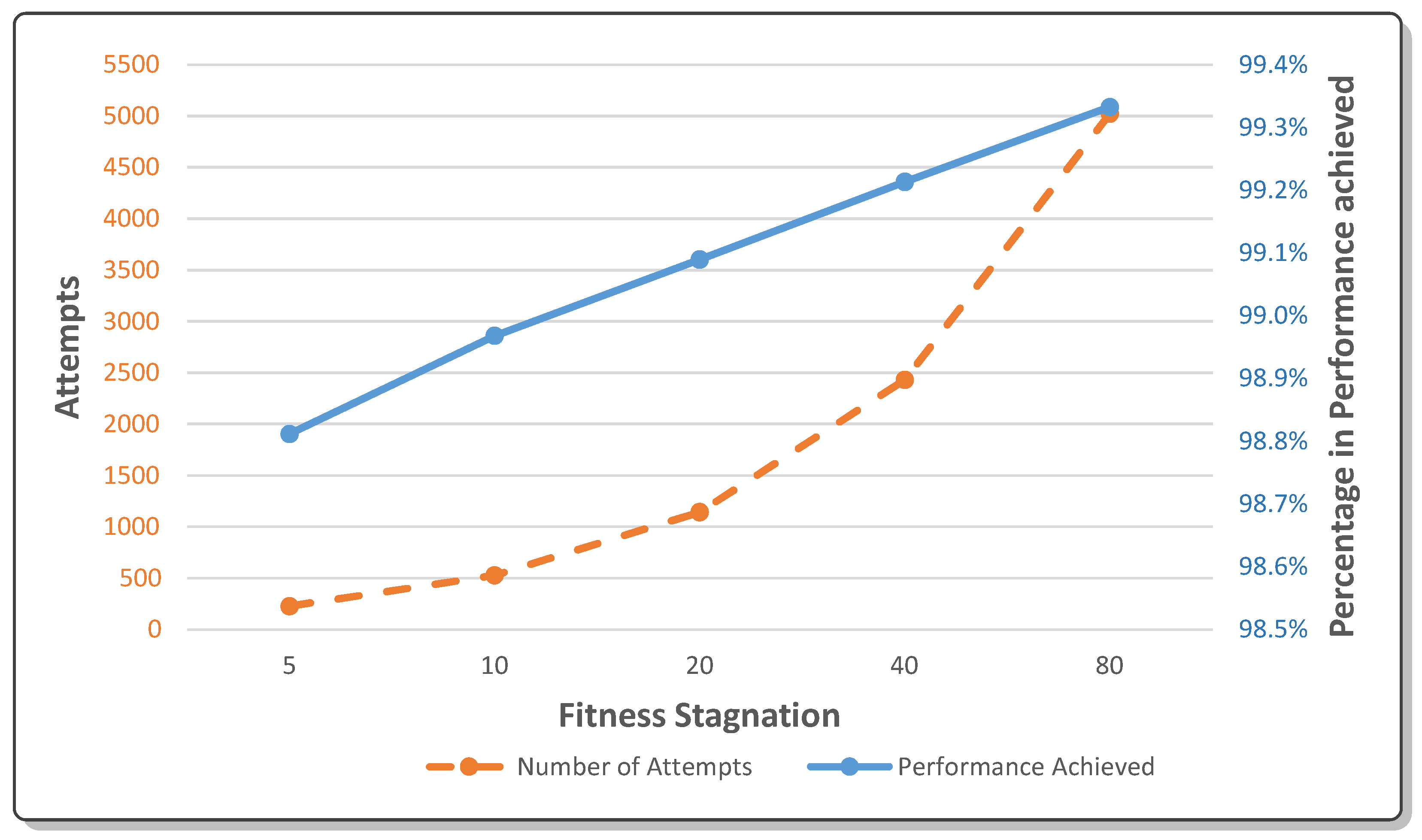



| Parameter | Value/Description |
|---|---|
| Fitness Function | mTSP total distance |
| Selection Process | Elite selection |
| Crossover Operator | Uniform crossover |
| Probability 0.75 per chromosome pair (default) | |
| Mix probability 0.5 per gene (default) | |
| Mutation Operator | Uniform mutation |
| Probability 0.1 (default) | |
| Initial Population | 50 (minimum) to 100 (maximum, adaptive) |
| Generations | 100 |
| Metric | Brute-Force | Genetic Algorithm | Advantage (GA) |
|---|---|---|---|
| Accuracy (Distance) | Exact solution | 97% to 100% | Near-optimal |
| Computation Time | Prohibitively High | Significantly lower | 4 orders of magnitude faster |
| Parameter | Values | Description |
|---|---|---|
| Social Coefficient | 1, 1.5, 2, 2.5 | This parameter controls how much the particle is influenced by the best solution found by its neighbors in the swarm. Higher values make particles more likely to move toward the swarm’s best known position. |
| Cognitive Coefficient | 1, 1.5, 2, 2.5 | Determines how much the particle is influenced by its own best known position. Values between 1 and 2.5 are commonly used in PSO implementations. |
| Inertia Weight | 0.4, 0.6, 0.7, 0.8, 0.9 | Controls the momentum of the particle, with higher values allowing more exploration and lower values favoring exploitation. The range covers typical values used in the literature. |
| Total Iterations | 300, 500, 1000, 1500, 2000 | The maximum number of iterations the algorithm will run. More iterations allow for better convergence but increase computation time. |
| Swarm Size | 10, 30, 50, 75, 100 | Number of particles in the swarm. Larger swarms can explore more space but require more computational resources. These values represent common swarm sizes used in practice. |
| Parameter | Value |
|---|---|
| Social Coefficient | 1 |
| Cognitive Coefficient | 2.5 |
| Inertia Weight | 0.9 |
| Total Iterations | 1000 |
| Swarm Size | 30 |
| Parameter | Values | Description |
|---|---|---|
| Cooling Rate | 0.9, 0.93, 0.95, 0.97, 0.99 | Controls the rate at which the temperature decreases. A value of 0.99 means the temperature reduces by 1% each iteration, allowing gradual convergence. |
| Total Iterations | 100, 300, 1000, 2000, 5000 | The maximum number of iterations for the algorithm. Higher values improve solution quality but increase computation time. |
| Temperature | 100, 500, 1000, 2000, 5000 | Initial temperature for the annealing process. Higher temperatures allow more exploration, while lower temperatures focus on exploitation. |
| Parameter | Value |
|---|---|
| Cooling Rate | 0.99 |
| Total Iterations | 1000 |
| Temperature | 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gasteratos, G.; Karydis, I. Strategic Launch Pad Positioning: Optimizing Drone Path Planning Through Genetic Algorithms. Information 2025, 16, 897. https://doi.org/10.3390/info16100897
Gasteratos G, Karydis I. Strategic Launch Pad Positioning: Optimizing Drone Path Planning Through Genetic Algorithms. Information. 2025; 16(10):897. https://doi.org/10.3390/info16100897
Chicago/Turabian StyleGasteratos, Gregory, and Ioannis Karydis. 2025. "Strategic Launch Pad Positioning: Optimizing Drone Path Planning Through Genetic Algorithms" Information 16, no. 10: 897. https://doi.org/10.3390/info16100897
APA StyleGasteratos, G., & Karydis, I. (2025). Strategic Launch Pad Positioning: Optimizing Drone Path Planning Through Genetic Algorithms. Information, 16(10), 897. https://doi.org/10.3390/info16100897







