Autonomous Navigation Approach for Complex Scenarios Based on Layered Terrain Analysis and Nonlinear Model
Abstract
1. Introduction
2. Materials and Methods
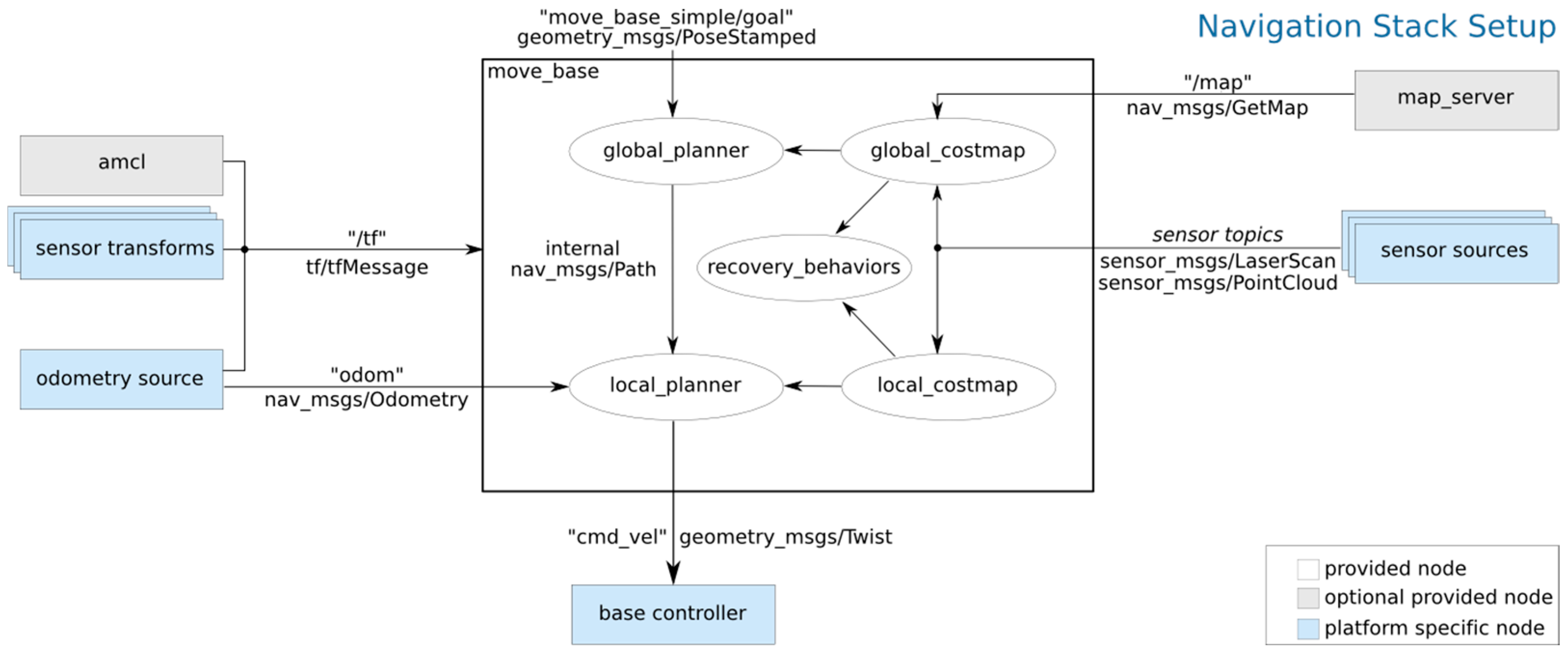
2.1. Basic Framework for Autonomous Navigation
2.2. Global Path Planning Based on Hierarchical Terrain Cost Maps
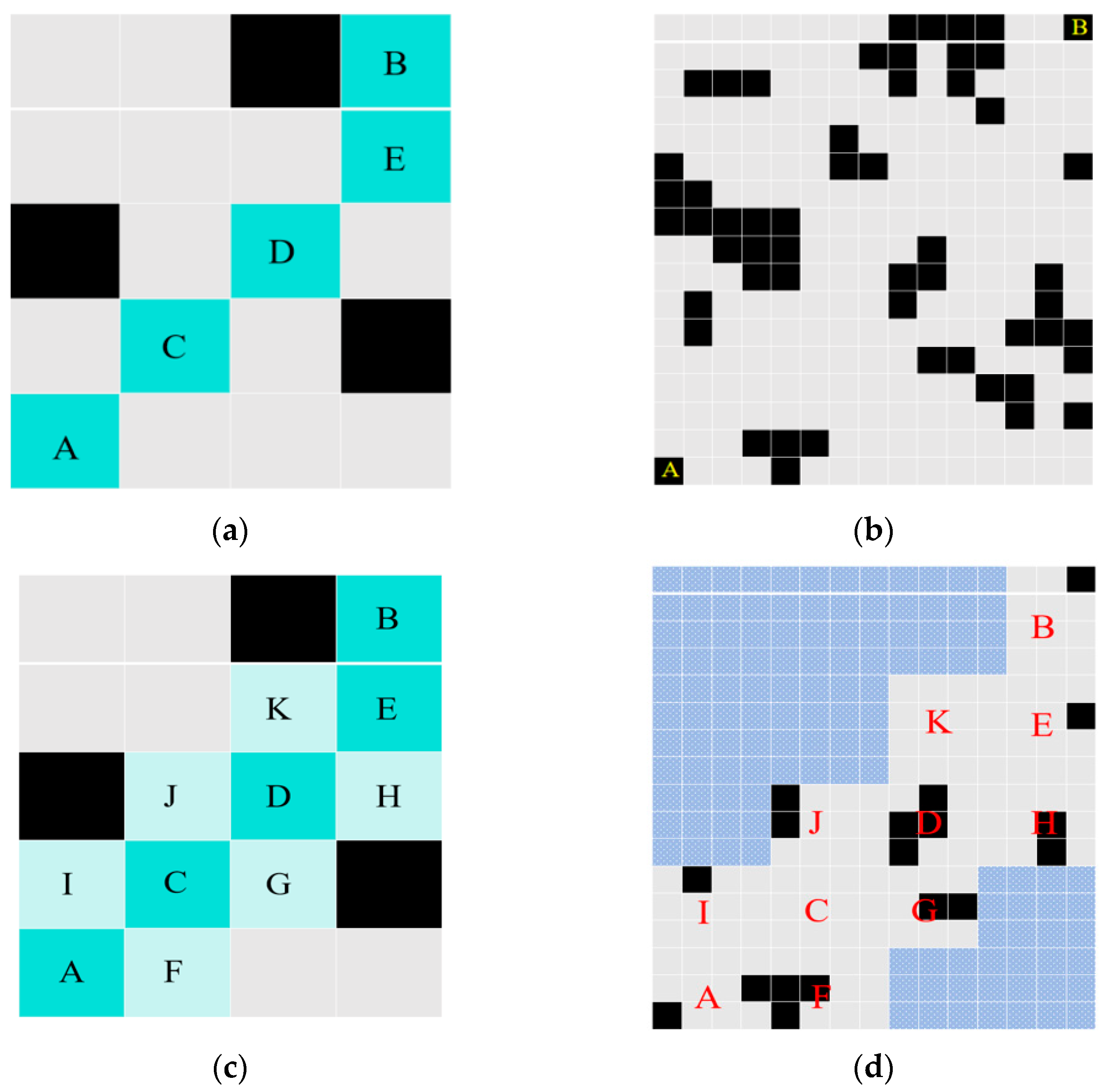
2.2.1. Raster Map Based A* Path Planning Method
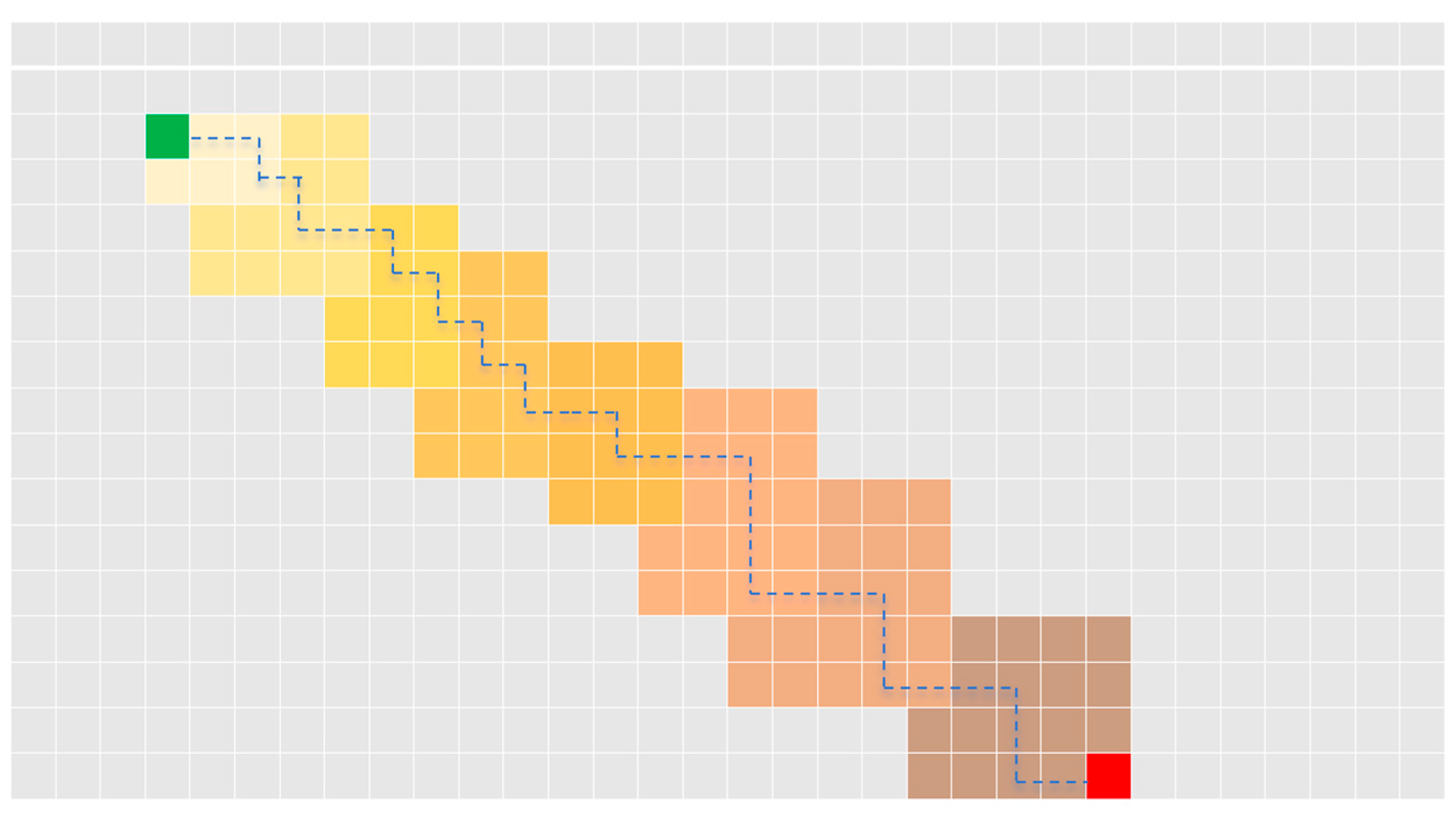
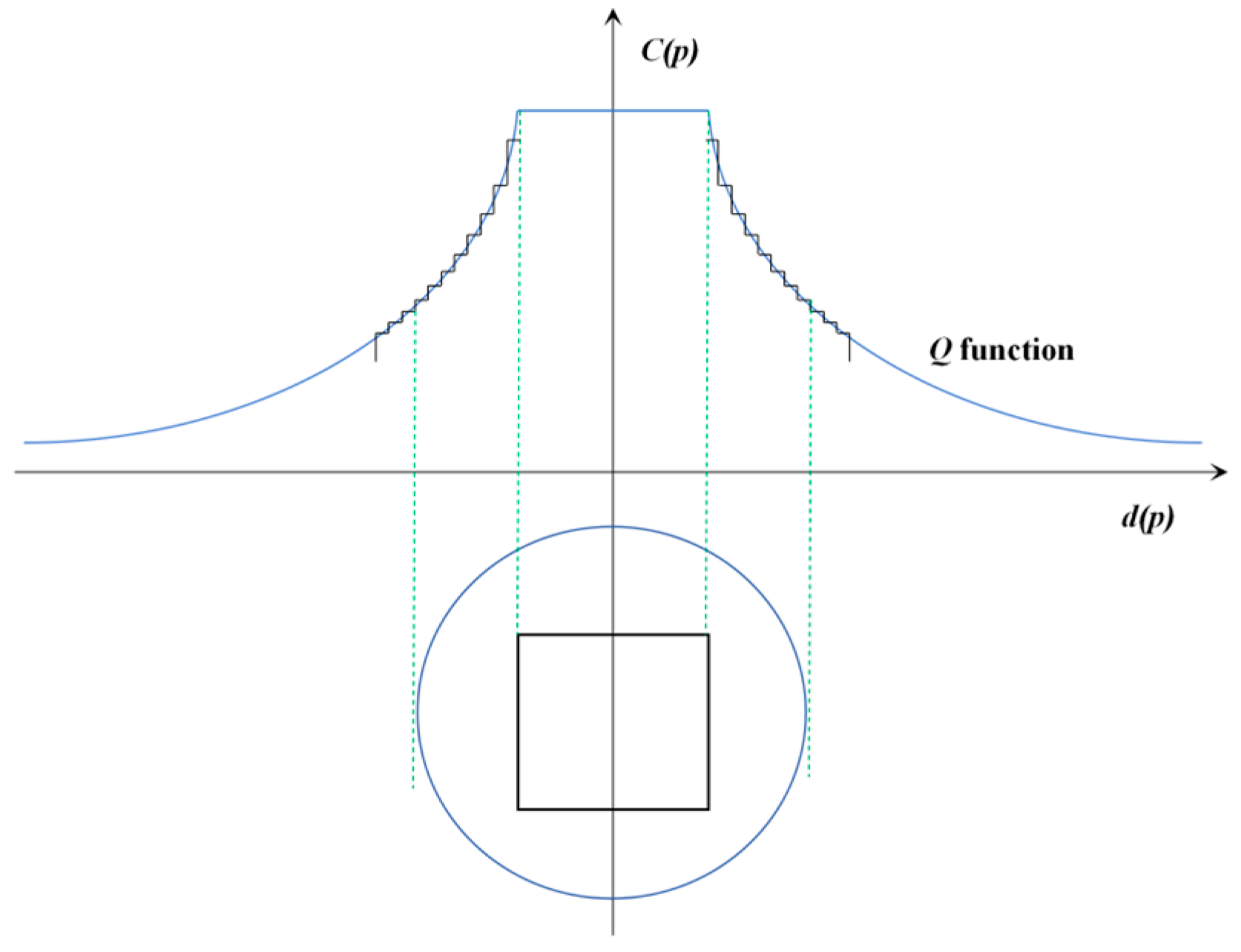
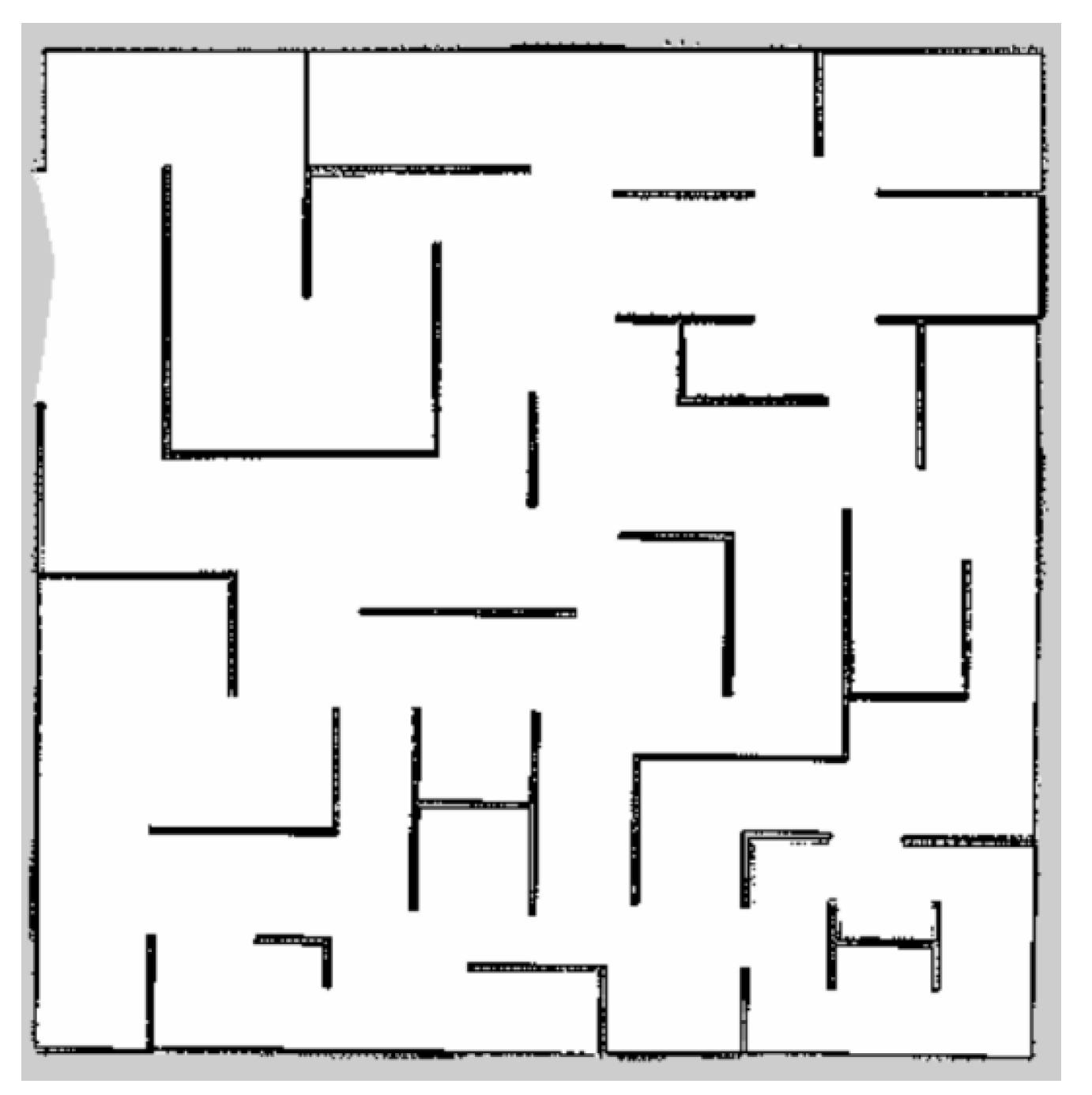
2.2.2. Cost Map
2.2.3. Layered Terrain Method
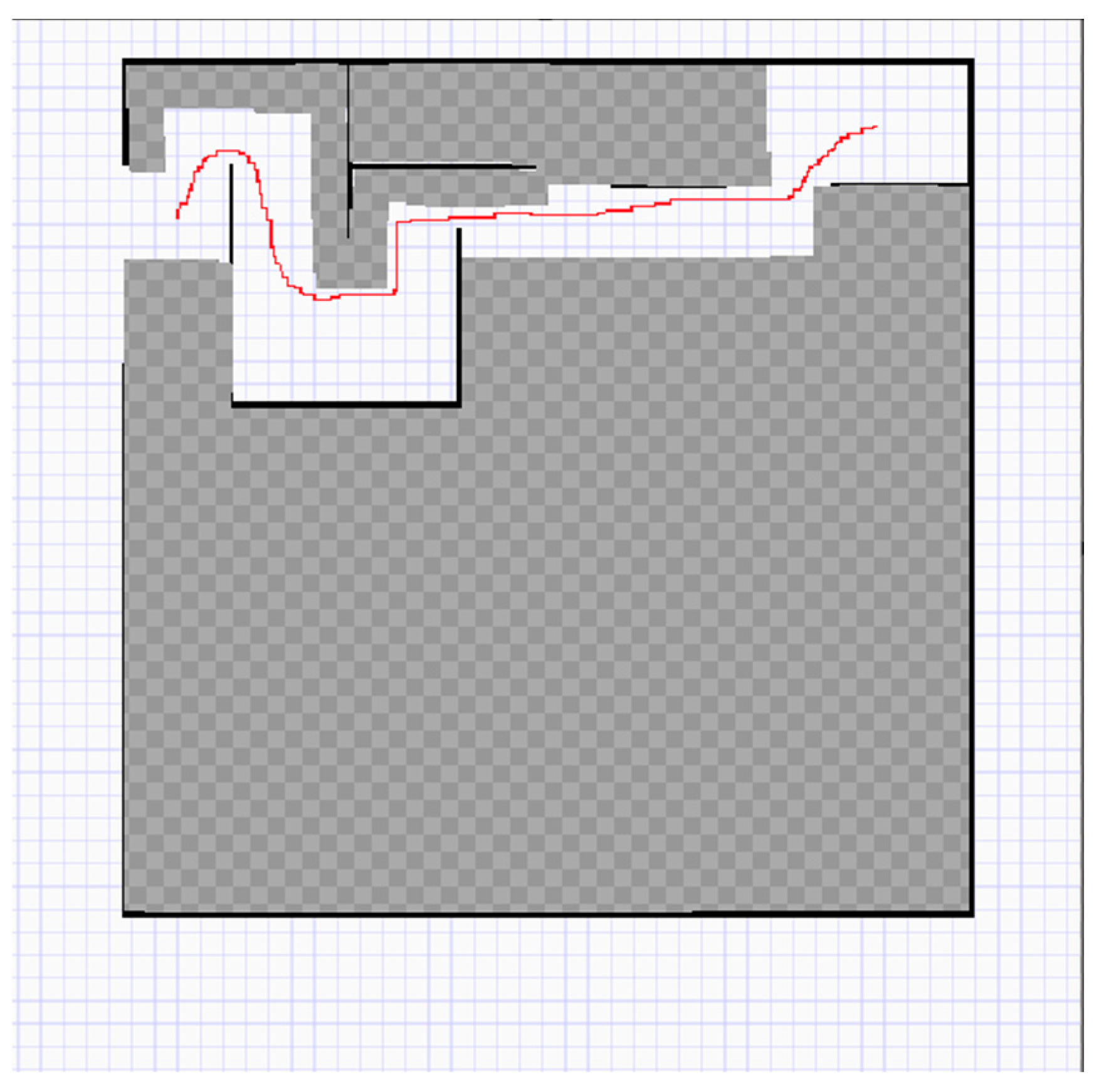
2.3. Local Path Planning
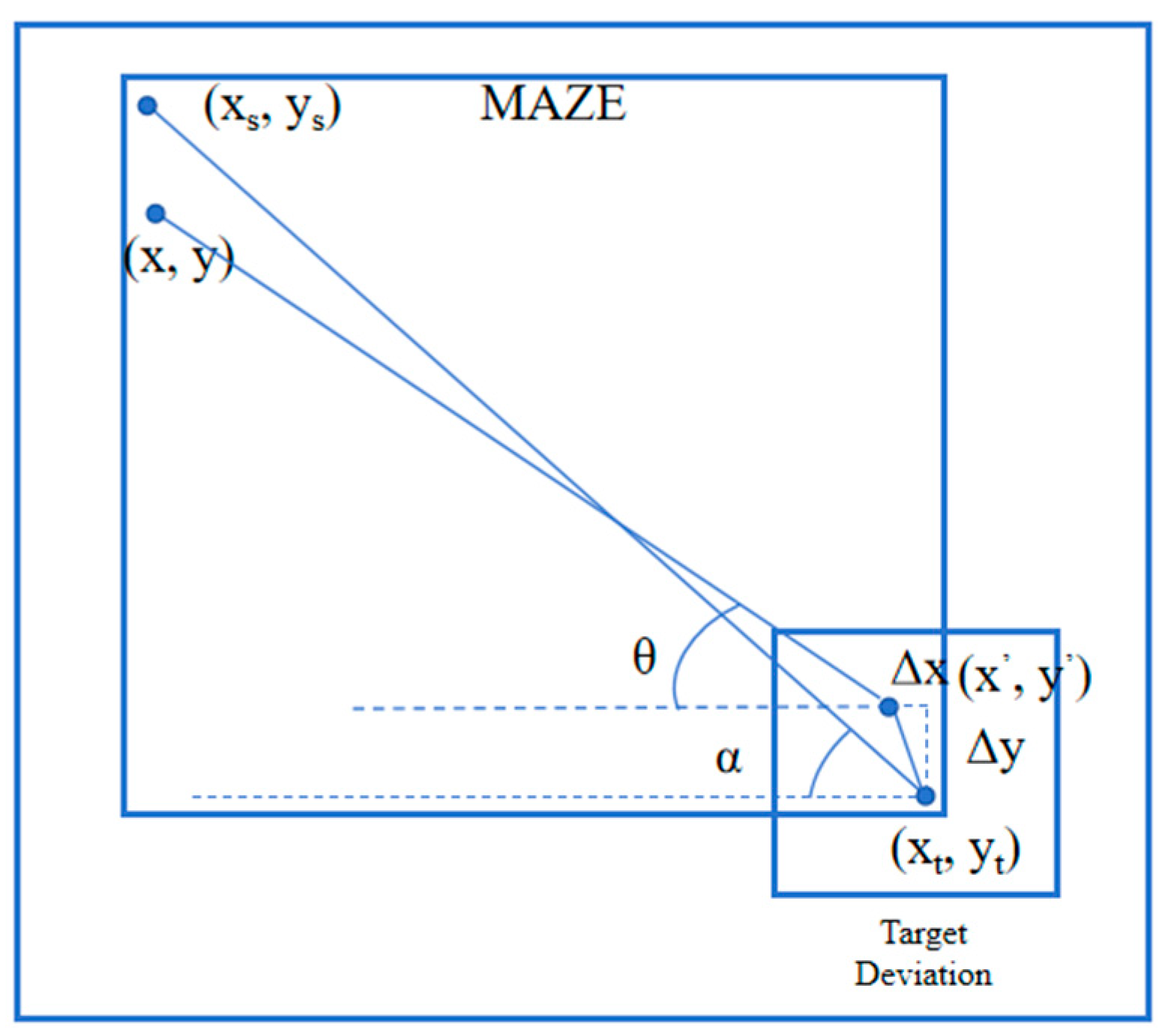
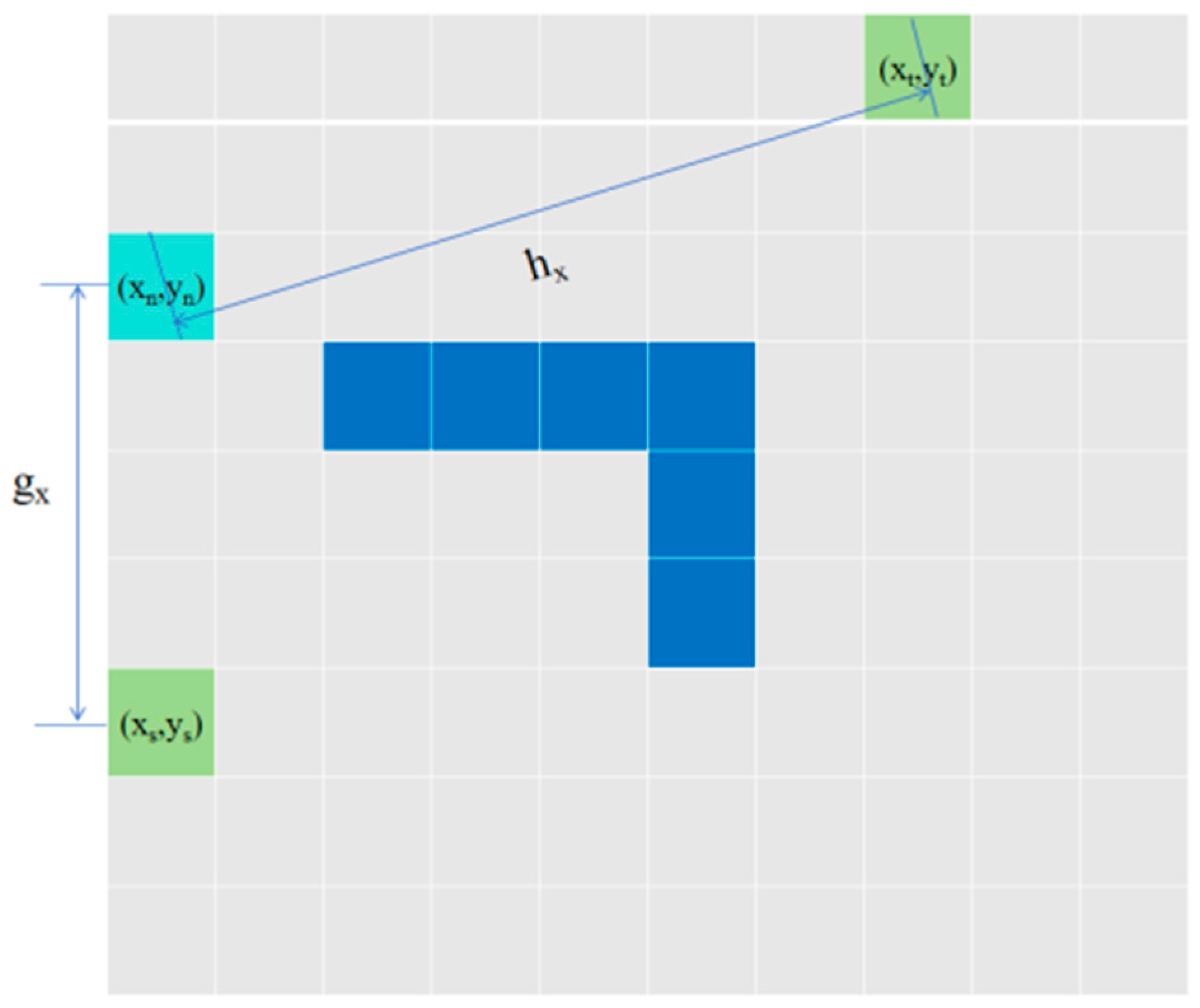
2.3.1. Linear Interpolation
2.3.2. Nonlinear Control Model
3. Results
3.1. Experimental Details
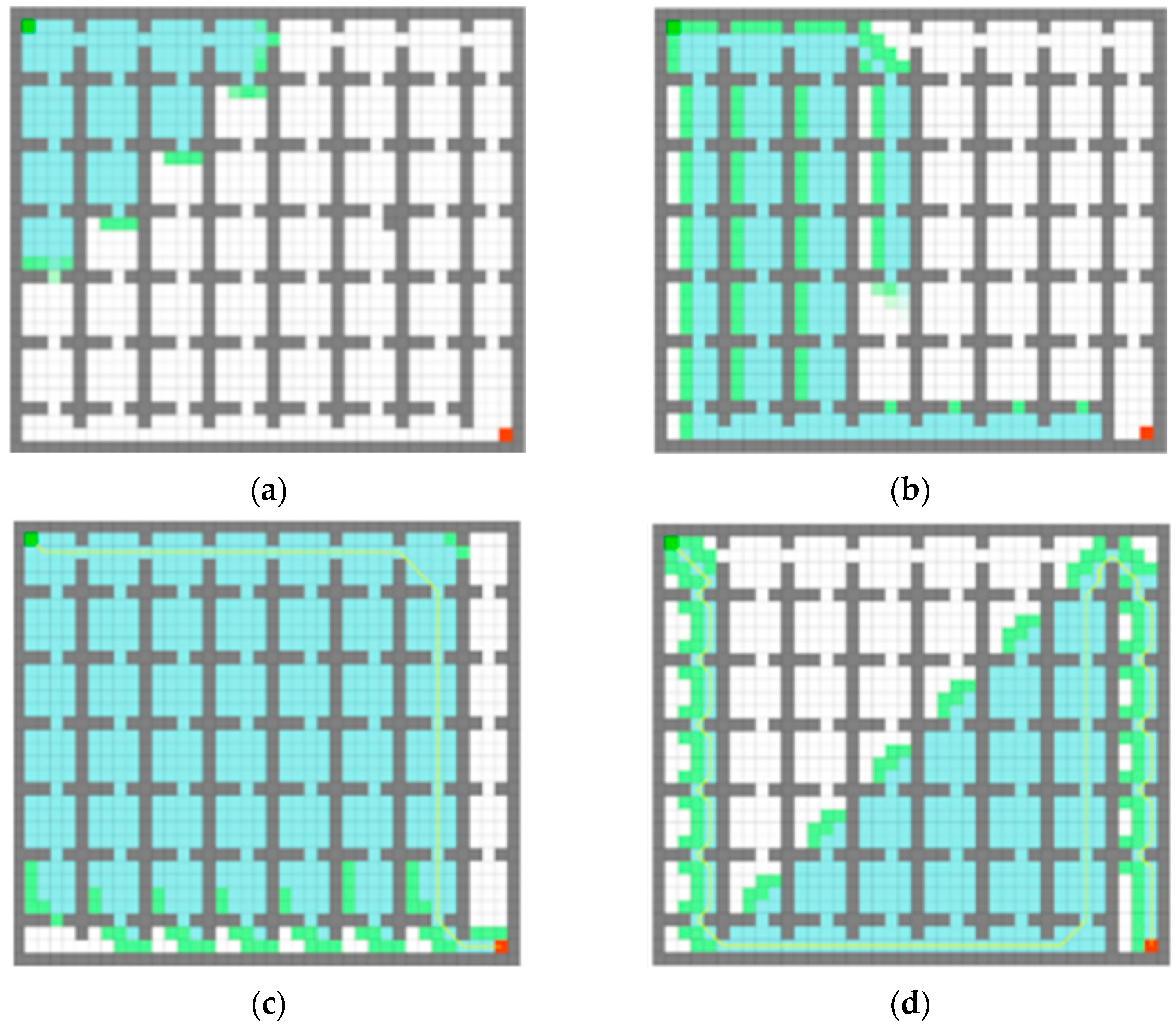
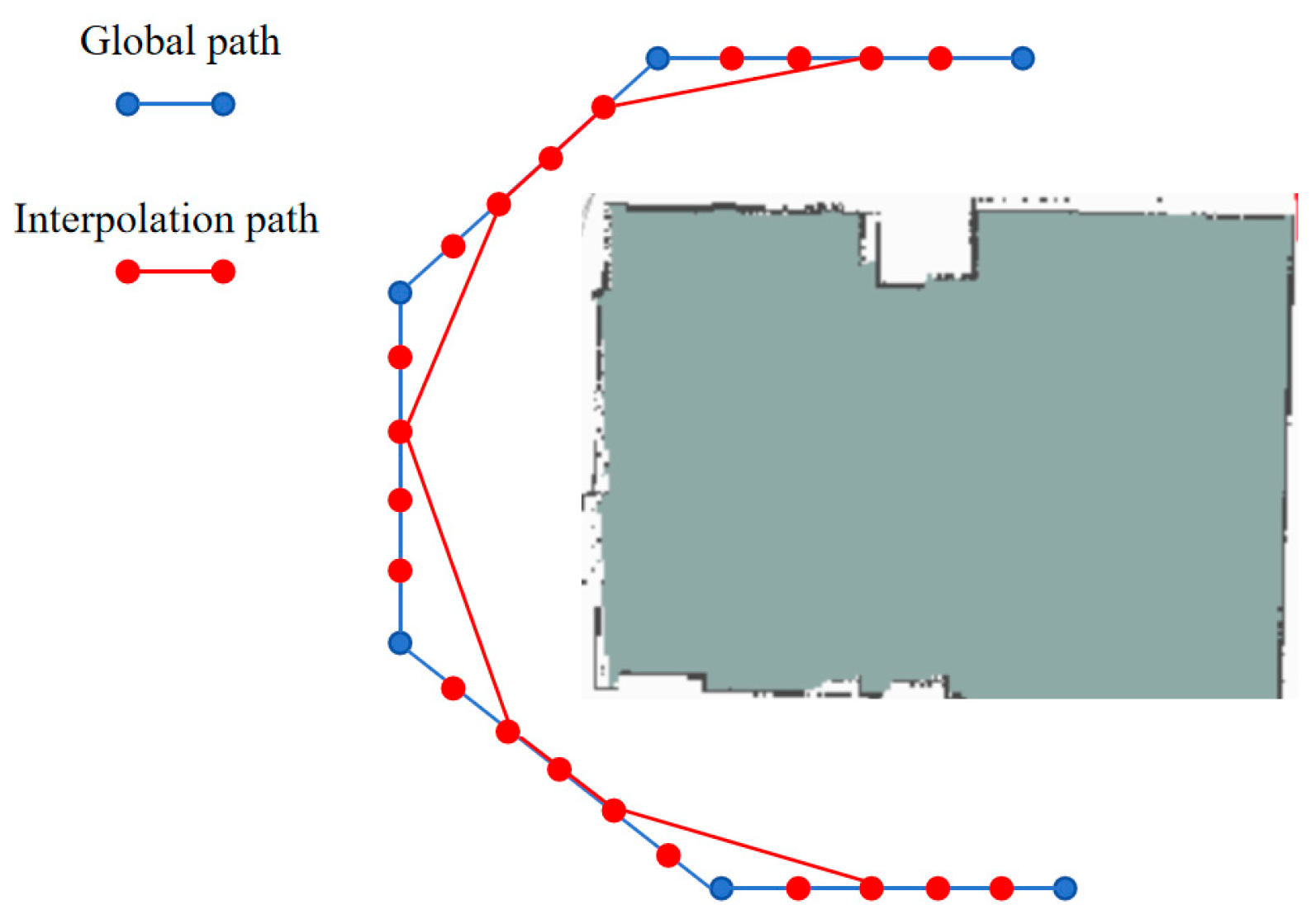
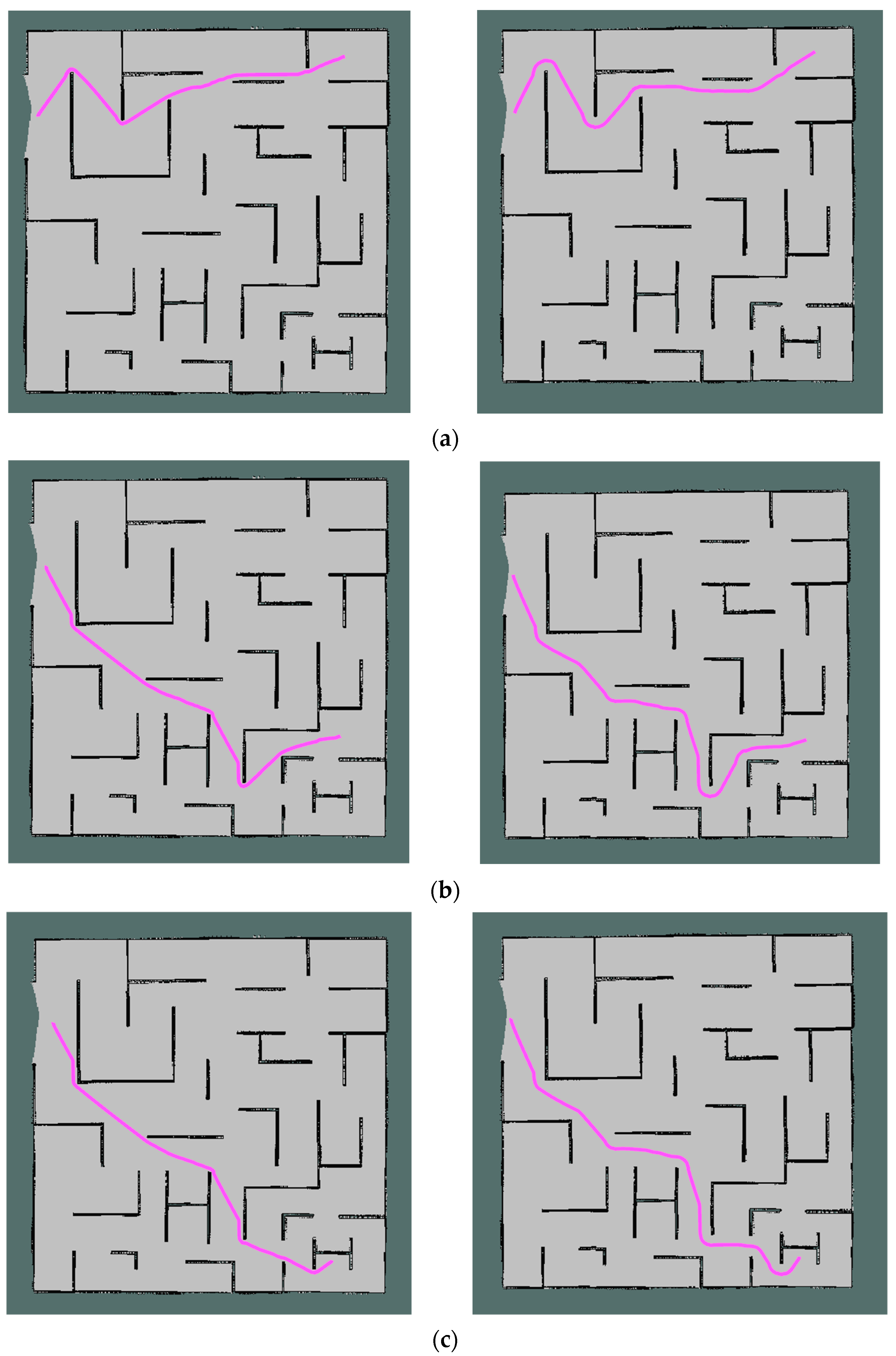
3.2. Qualitative Experiment on the Simulation Platform
3.3. Simulation Platform Ablation Experiment
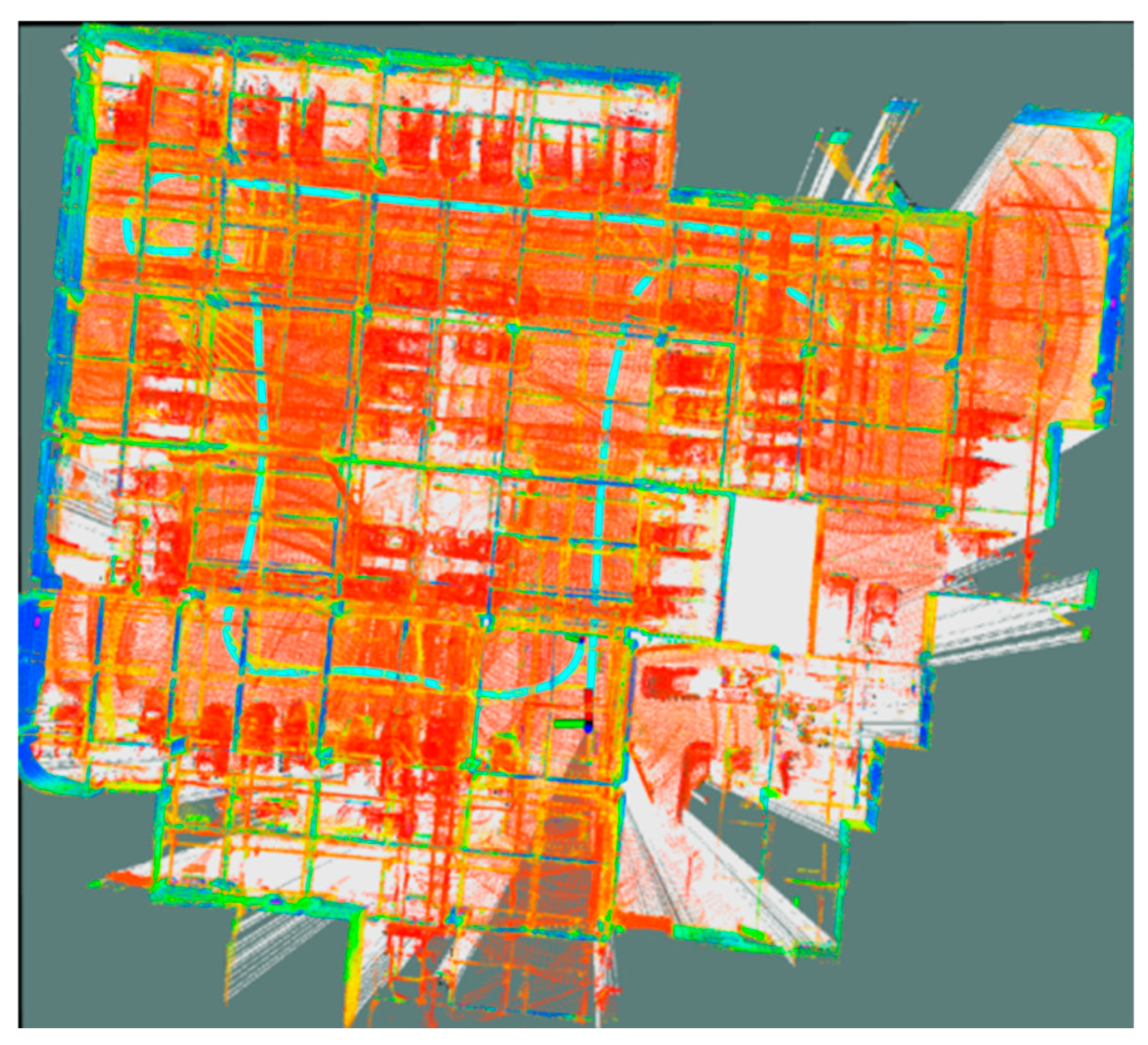
3.4. Experiments in Real Scenes
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, C.; Mees, O.; Zeng, A.; Burgard, W. Visual language maps for robot navigation. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; IEEE: New York, NY, USA, 2023; pp. 10608–10615. [Google Scholar]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 7464–7475. [Google Scholar]
- Liu, S.; Zeng, Z.; Ren, T.; Li, F.; Zhang, H.; Yang, J.; Jiang, Q.; Li, C.; Yang, J.; Su, H.; et al. Grounding dino: Marrying dino with grounded pre-training for open-set object detection. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer Nature: Cham, Switzerland, 2024; pp. 38–55. [Google Scholar]
- Tzafestas, S.G. Mobile robot control and navigation: A global overview. J. Intell. Robot. Syst. 2018, 91, 35–58. [Google Scholar] [CrossRef]
- Ginting, M.F.; Kim, S.K.; Fan, D.D.; Palieri, M.; Kochenderfer, M.J. Seek: Semantic reasoning for object goal navigation in real world inspection tasks. arXiv 2024, arXiv:2405.09822. [Google Scholar] [CrossRef]
- Gadd, M.; Newman, P. A framework for infrastructure-free warehouse navigation. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: New York, NY, USA, 2015; pp. 3271–3278. [Google Scholar]
- Ackerman, E. A Robot for the Worst Job in the Warehouse: Boston Dynamics’ Stretch can move 800 heavy boxes per hour. IEEE Spectr. 2022, 59, 50–51. [Google Scholar] [CrossRef]
- Shiomi, M.; Kanda, T.; Ishiguro, H.; Hagita, N. Interactive humanoid robots for a science museum. In Proceedings of the 1st ACM SIGCHI/SIGART Conference on Human-Robot Interaction, Salt Lake City, UT, USA, 2–3 March 2006; pp. 305–312. [Google Scholar]
- Huang, C.M.; Iio, T.; Satake, S.; Kanda, T. Modeling and Controlling Friendliness for An Interactive Museum Robot. In Proceedings of the Robotics: Science and Systems, Berkeley, CA, USA, 12–16 July 2014; pp. 12–16. [Google Scholar]
- Hossain, M. Autonomous delivery robots: A literature review. IEEE Eng. Manag. Rev. 2023, 51, 77–89. [Google Scholar] [CrossRef]
- Vaussard, F.; Fink, J.; Bauwens, V.; Rétornaz, P.; Hamel, D.; Dillenbourg, P.; Mondada, F. Lessons learned from robotic vacuum cleaners entering the home ecosystem. Robot. Auton. Syst. 2014, 62, 376–391. [Google Scholar] [CrossRef]
- Xiao, X.; Liu, B.; Warnell, G.; Stone, P. Motion planning and control for mobile robot navigation using machine learning: A survey. Auton. Robot. 2022, 46, 569–597. [Google Scholar] [CrossRef]
- Elfes, A. Using occupancy grids for mobile robot perception and navigation. Computer 2002, 22, 46–57. [Google Scholar] [CrossRef]
- Filliat, D.; Meyer, J.A. Map-based navigation in mobile robots: I. a review of localization strategies. Cogn. Syst. Res. 2003, 4, 243–282. [Google Scholar] [CrossRef]
- Behzadian, B.; Agarwal, P.; Burgard, W.; Tipaldi, G.D. Monte Carlo localization in hand-drawn maps. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; IEEE: New York, NY, USA, 2015; pp. 4291–4296. [Google Scholar]
- Boniardi, F.; Behzadian, B.; Burgard, W.; Tipaldi, G.D. Robot navigation in hand-drawn sketched maps. In Proceedings of the 2015 European conference on mobile robots (ECMR), Lincoln, UK, 2–4 September 2015; IEEE: New York, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Xu, C.; Amato, C.; Wong, L.L.S. Robot navigation in unseen environments using coarse maps. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: New York, NY, USA, 2024; pp. 2932–2938. [Google Scholar]
- Wijmans, E.; Kadian, A.; Morcos, A.; Lee, S.; Essa, I.; Parikh, D.; Savva, M.; Batra, D. Dd-ppo: Learning near-perfect pointgoal navigators from 2.5 billion frames. arXiv 2019, arXiv:1911.00357. [Google Scholar]
- Ye, J.; Batra, D.; Das, A.; Wijmans, E. Auxiliary tasks and exploration enable objectgoal navigation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 16117–16126. [Google Scholar]
- Maksymets, O.; Cartillier, V.; Gokaslan, A.; Wijmans, E.; Galuba, W.; Lee, S.; Batra, D. Thda: Treasure hunt data augmentation for semantic navigation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 15374–15383. [Google Scholar]
- Ramrakhya, R.; Undersander, E.; Batra, D.; Das, A. Habitat-web: Learning embodied object-search strategies from human demonstrations at scale. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5173–5183. [Google Scholar]
- Batra, D.; Gokaslan, A.; Kembhavi, A.; Maksymets, O.; Mottaghi, R.; Savva, M.; Toshev, A.; Wijmans, E. Objectnav revisited: On evaluation of embodied agents navigating to objects. arXiv 2020, arXiv:2006.13171. [Google Scholar] [CrossRef]
- Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A.; Fei-Fei, L.; Farhadi, A. Target-driven visual navigation in indoor scenes using deep reinforcement learning. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: New York, NY, USA, 2017; pp. 3357–3364. [Google Scholar]
- Hussein, A.; Gaber, M.M.; Elyan, E.; Jayne, C. Imitation learning: A survey of learning methods. ACM Comput. Surv. (CSUR) 2017, 50, 1–35. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An introduction; MIT Press: Cambridge, UK, 1998. [Google Scholar]
- Gervet, T.; Chintala, S.; Batra, D.; Malik, J.; Chaplot, D.S. Navigating to objects in the real world. Sci. Robot. 2023, 8, eadf6991. [Google Scholar] [CrossRef]
- Chaplot, D.S.; Gandhi, D.; Gupta, S.; Gupta, A.; Salakhutdinov, R. Learning to explore using active neural slam. arXiv 2020, arXiv:2004.05155. [Google Scholar] [CrossRef]
- Chaplot, D.S.; Jiang, H.; Gupta, S.; Gupta, A. Semantic curiosity for active visual learning. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 309–326. [Google Scholar]
- Ramakrishnan, S.K.; Chaplot, D.S.; Al-Halah, Z.; Malik, J.; Grauman, K. Poni: Potential functions for objectgoal navigation with interaction-free learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18890–18900. [Google Scholar]
- Chen, J.; Li, G.; Kumar, S.; Ghanem, B.; Yu, F. How to not train your dragon: Training-free embodied object goal navigation with semantic frontiers. arXiv 2023, arXiv:2305.16925. [Google Scholar] [CrossRef]
- Zhou, K.; Zheng, K.; Pryor, C.; Shen, Y.; Jin, H.; Getoor, L.; Wang, X.E. Esc: Exploration with soft commonsense constraints for zero-shot object navigation. In Proceedings of the International Conference on Machine Learning (PMLR), Honolulu, HI, USA, 23–29 July 2023; pp. 42829–42842. [Google Scholar]
- Yokoyama, N.; Ha, S.; Batra, D.; Wang, J.; Bucher, B. Vlfm: Vision-language frontier maps for zero-shot semantic navigation. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: New York, NY, USA, 2024; pp. 42–48. [Google Scholar]
- Soltani, A.; Tawfik, H.; Goulermas, J.; Fernando, T. Path planning in construction sites: Performance evaluation of the Dijkstra, A∗, and GA search algorithms. Adv. Eng. Inform. 2002, 16, 291–303. [Google Scholar]
- Liu, X.; Gong, D. A comparative study of A-star algorithms for search and rescue in perfect maze. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; IEEE: New York, NY, USA, 2011; pp. 24–27. [Google Scholar]
- Masehian, E.; Amin-Naseri, M.R. A voronoi diagram-visibility graph-potential field compound algorithm for robot path planning. J. Robot. Syst. 2004, 21, 275–300. [Google Scholar] [CrossRef]
- Sariff, N.B.; Buniyamin, N. Comparative study of genetic algorithm and ant colony optimization algorithm performances for robot path planning in global static environments of different complexities. In Proceedings of the 2009 IEEE International Symposium on Computational Intelligence in Robotics and Automation-(CIRA), Daejeon, Republic of Korea, 15–18 December 2009; IEEE: New York, NY, USA, 2009; pp. 132–137. [Google Scholar]
- Park, K.H.; Kim, Y.J.; Kim, J.H. Modular Q-learning based multi-agent cooperation for robot soccer. Robot. Auton. Syst. 2001, 35, 109–122. [Google Scholar] [CrossRef]
- Engedy, I.; Horváth, G. Artificial neural network based local motion planning of a wheeled mobile robot. In Proceedings of the 2010 11th International Symposium on Computational Intelligence and Informatics (CINTI), Budapest, Hungary, 18–20 November 2010; IEEE: New York, NY, USA, 2010; pp. 213–218. [Google Scholar]
- Zhu, A.; Yang, S.X. Neurofuzzy-based approach to mobile robot navigation in unknown environments. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 610–621. [Google Scholar]
- Ghorbani, A.; Shiry, S.; Nodehi, A. Using genetic algorithm for a mobile robot path planning. In Proceedings of the 2009 International Conference on Future Computer and Communication, Kuala Lumpar, Malaysia, 3–5 April 2009; IEEE: New York, NY, USA, 2009; pp. 164–166. [Google Scholar]
- Garcia, M.P.; Montiel, O.; Castillo, O.; Sepúlveda, R.; Melin, P. Path planning for autonomous mobile robot navigation with ant colony optimization and fuzzy cost function evaluation. Appl. Soft Comput. 2009, 9, 1102–1110. [Google Scholar] [CrossRef]
- Wang, X.; Yang, S.X. A neuro-fuzzy approach to obstacle avoidance of a nonholonomic mobile robot. In Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2003), Online, 20–24 July 2003; IEEE: New York, NY, USA, 2003; Volume 1, pp. 29–34. [Google Scholar]
- Schøler, F. 3d Path Planning for autonomous Aerial Vehicles in Constrained Spaces. Ph.D. Thesis, Section of Automation & Control, Department of Electronic Systems, Aalborg University, Aalborg, Denmark, 2012. [Google Scholar]
- Alshammrei, S.; Boubaker, S.; Kolsi, L. Improved Dijkstra algorithm for mobile robot path planning and obstacle avoidance. Comput. Mater. Contin. 2022, 72, 5939–5954. [Google Scholar] [CrossRef]
- Han, C.; Li, B. Mobile robot path planning based on improved A* algorithm. In Proceedings of the 2023 IEEE 11th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 8–10 December 2023; IEEE: New York, NY, USA, 2023; Volume 11, pp. 672–676. [Google Scholar]
- Kiani, F.; Seyyedabbasi, A.; Aliyev, R.; Gulle, M.U.; Basyildiz, H.; Shah, M.A. Adapted-RRT: Novel hybrid method to solve three-dimensional path planning problem using sampling and metaheuristic-based algorithms. Neural Comput. Appl. 2021, 33, 15569–15599. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T. Global path planning for mobile robot based on Artificial Bee Colony and Dijkstra’s algorithms. In Proceedings of the 2021 IEEE 19th International Power Electronics and Motion Control Conference (PEMC), Gliwice, Poland, 25–29 April 2021; IEEE: New York, NY, USA, 2021; pp. 724–730. [Google Scholar]
- Goto, T.; Kosaka, T.; Noborio, H. On the Heuristics of A* or A Algorithm in ITS and Robot Path-Planning. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003) (Cat. No.03CH37453), Las Vegas, NV, USA, 27–31 October 2003. [Google Scholar]
- Foead, D.; Ghifari, A.; Kusuma, M.B.; Hanafiah, N.; Gunawan, E. A systematic literature review of A* pathfinding. Procedia Comput. Sci. 2021, 179, 507–514. [Google Scholar] [CrossRef]
- LaValle, S.M.; Kuffner, J.J., Jr. Randomized kinodynamic planning. Int. J. Robot. Res. 2001, 20, 378–400. [Google Scholar] [CrossRef]
- Gammell, J.D.; Srinivasa, S.S.; Barfoot, T.D. Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; IEEE: New York, NY, USA, 2014; pp. 2997–3004. [Google Scholar]
- Montaner, M.B.; Ramirez-Serrano, A. Fuzzy knowledge-based controller design for autonomous robot navigation. Expert Syst. Appl. 1998, 14, 179–186. [Google Scholar] [CrossRef]
- Yang, X.S. Cuckoo search and firefly algorithm: Overview and analysis. In Cuckoo Search and Firefly Algorithm: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–26. [Google Scholar]









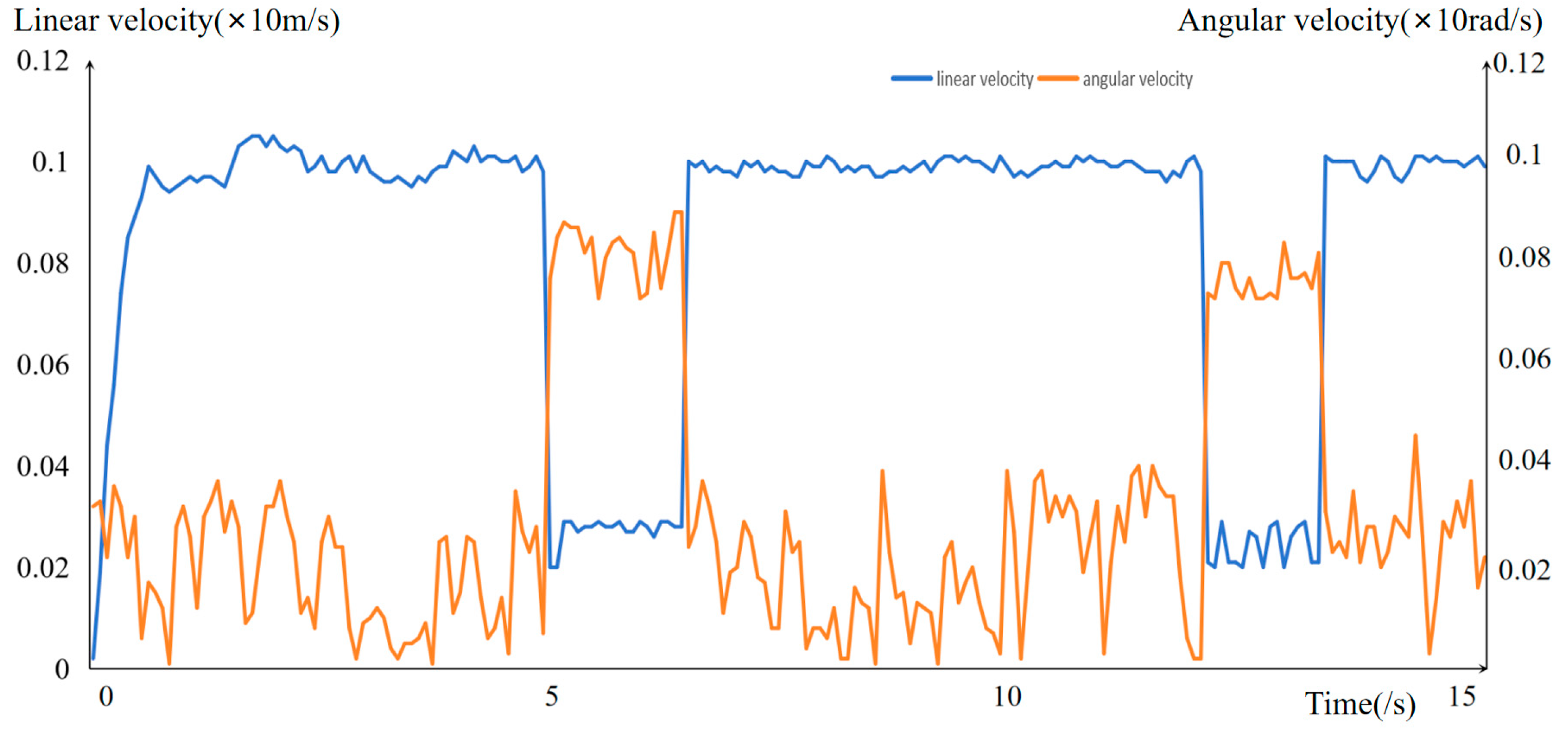

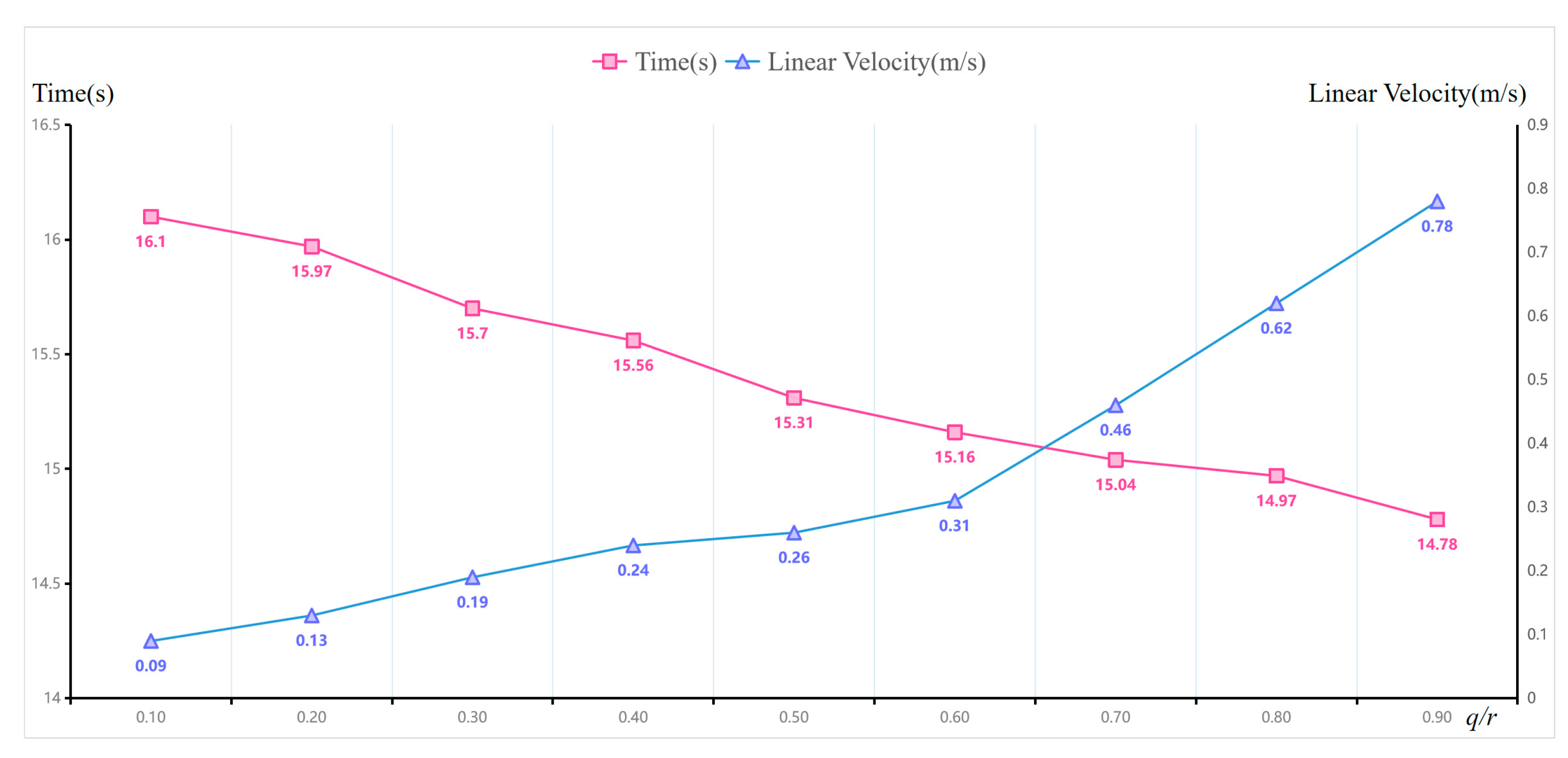
| Method Metrics | Original A* Method | Layered Terrain Method |
|---|---|---|
| Total path length (number of rasters) | 523 | 546 |
| Proximity to obstacles (number of line segments) | 5 | 0 |
| Method operation time (seconds) | 5.121 | 4.091 |
| Method Metrics (s) | Layered Terrain Method | Layered Terrain + Local Path Planning Method |
|---|---|---|
| Corner region runtime | 2.517 | 2.941 |
| Straight ahead region runtime | 1.574 | 0.476 |
| Method computation time | 4.091 | 3.417 |
| Method Index (s) | Layered Terrain Method | Layered Terrain Method + Local Path Planning Calculation |
|---|---|---|
| Corner area running time | 6.41 | 4.73 |
| Straight ahead region running time | 6.12 | 7.01 |
| Pedestrian avoidance running time | 7.00 | 3.42 |
| Method computation time | 19.53 | 15.16 |
| Methods (s) | Straight Ahead Area | Corner Area | Circumvention of Pedestrians | Total Running Time |
|---|---|---|---|---|
| RRT* | 7.94 | 4.24 | 3.11 | 15.29 |
| PF-RRT* | 7.52 | 4.61 | 3.38 | 15.51 |
| A* | 8.27 | 3.96 | 3.13 | 15.36 |
| FL | 8.31 | 4.27 | 3.15 | 15.73 |
| PSO | 8.28 | 4.59 | 2.71 | 15.58 |
| CSA | 8.18 | 4.18 | 3.07 | 15.43 |
| ABC | 8.22 | 4.28 | 3.31 | 18.81 |
| ACO | 8.74 | 4.31 | 3.18 | 16.23 |
| Ours | 7.01 | 4.73 | 3.42 | 15.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Hua, L.; Shen, S.; Wang, Y.; Pu, Q.; Ma, X. Autonomous Navigation Approach for Complex Scenarios Based on Layered Terrain Analysis and Nonlinear Model. Information 2025, 16, 896. https://doi.org/10.3390/info16100896
Chen W, Hua L, Shen S, Wang Y, Pu Q, Ma X. Autonomous Navigation Approach for Complex Scenarios Based on Layered Terrain Analysis and Nonlinear Model. Information. 2025; 16(10):896. https://doi.org/10.3390/info16100896
Chicago/Turabian StyleChen, Wenhe, Leer Hua, Shuonan Shen, Yue Wang, Qi Pu, and Xundiao Ma. 2025. "Autonomous Navigation Approach for Complex Scenarios Based on Layered Terrain Analysis and Nonlinear Model" Information 16, no. 10: 896. https://doi.org/10.3390/info16100896
APA StyleChen, W., Hua, L., Shen, S., Wang, Y., Pu, Q., & Ma, X. (2025). Autonomous Navigation Approach for Complex Scenarios Based on Layered Terrain Analysis and Nonlinear Model. Information, 16(10), 896. https://doi.org/10.3390/info16100896







