MoCap-Impute: A Comprehensive Benchmark and Comparative Analysis of Imputation Methods for IMU-Based Motion Capture Data
Abstract
1. Introduction
2. Background and Related Work
2.1. IMUs
2.2. Data Imputation
2.3. Single Imputation Methods
2.4. Multiple Imputation Methods
2.5. Gap Analysis
- Lack of comprehensive performance evaluation for IMU-based MoCap imputation: To date, no research has systematically examined and compared the performance of well-established data imputation strategies, including ML and DL statistical methods, specifically for MoCap data acquired from IMU sensors. This absence limits the ability of researchers and practitioners to select the most appropriate imputation technique for specific MoCap missing data scenarios, hindering accurate data reconstruction and subsequent analysis.
- Absence of a standardized MoCap benchmark dataset for imputation: A fundamental requirement for reproducible research and comparative analysis is the availability of a standardized dataset. Currently, there is no publicly available MoCap dataset explicitly designed and proposed for benchmarking the performance of various data imputation methods. This hinders the consistent evaluation and advancement of imputation techniques tailored to the unique complexities of MoCap data.
3. Methodology
3.1. Overview
3.2. Dataset and Preprocessing
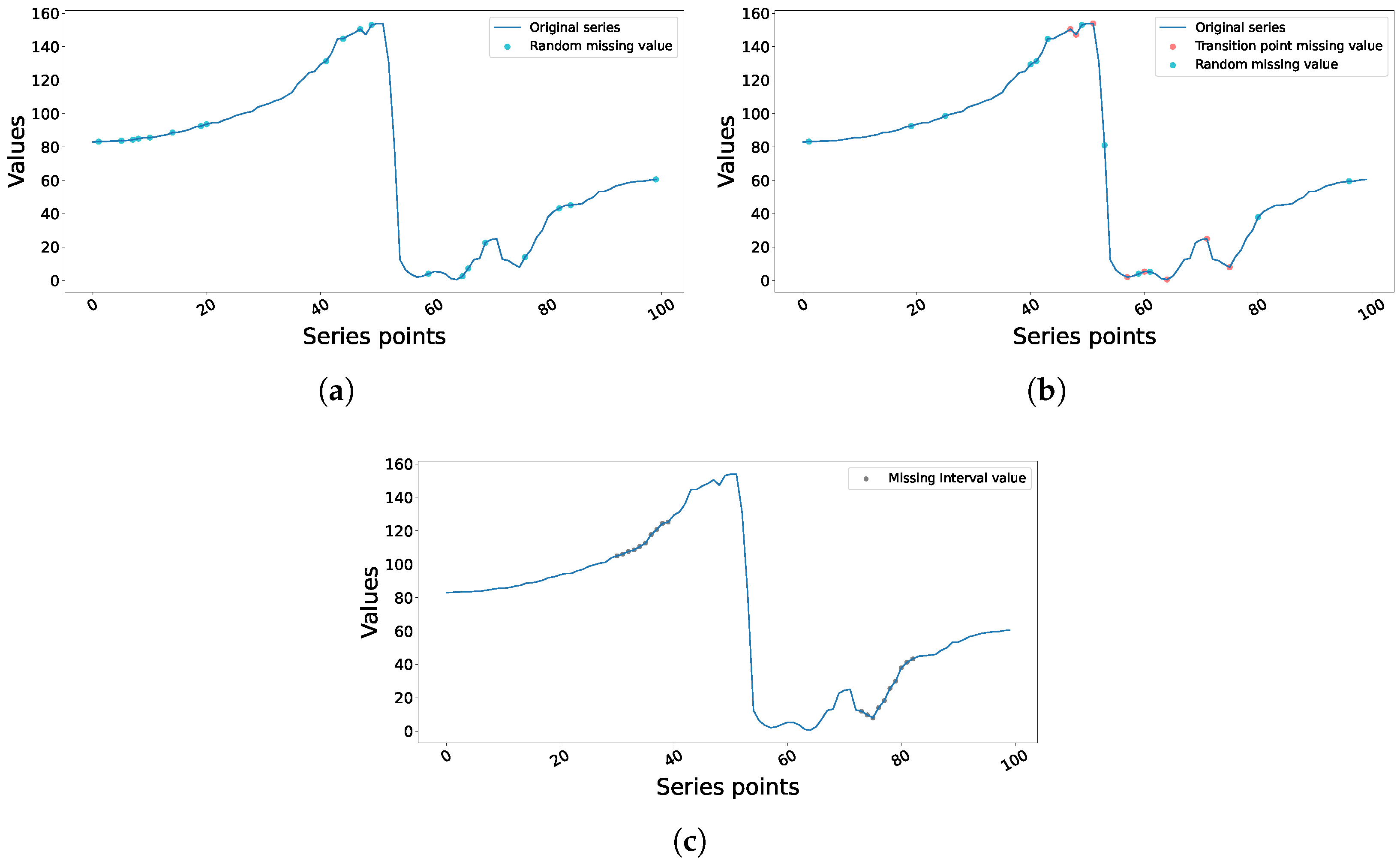
3.3. Simulation of Missing Data
- Missing Completely At Random (MCAR): From , k unique time indices were sampled uniformly without replacement for each series , and the corresponding entries in were assigned a value of 1. This mechanism assumes that missingness was completely independent of observed and unobserved values. A sample of this approach is depicted in Figure 2a.
- Value-Dependent Missingness at Transition Points: This mechanism emulates a form of value-dependent missingness, where the probability of data loss is intentionally correlated with the local dynamics of the signal itself. Specifically, we target transition points (local minima and maxima), as these points of high kinetic change can be more susceptible to measurement error or signal clipping in real-world MoCap applications. First, for each time series , we identify the complete set of transition point indices . Then, we randomly sample indices from these transition points. If the total number of missing points to be introduced, k, is greater than the number of available transition points, we sample the remaining indices from the non-transition points. All sampled indices were set to missing (). Figure 2b shows a sample of this approach.
- Block Missingness (Structured): We introduced blocks of contiguous missing values. For the purposes of sampling blocks, the total length of the time series T was conceptually divided into segments of . For each segment, we placed a block of a predetermined size (where was identified to approximate the total count of k across all blocks) starting from a random index within the limits of the segment. Again, all sample indices in these blocks were converted to missing in . In the case of overlaps in blocks or deviations in total segment length which deemed the total count < k (or >k), we made adjustments. Figure 2c depicts a sample of this dataset.
| Algorithm 1 GenerateMissingMask () |
|
3.4. Imputation Framework Contexts
- Univariate Context: Here, data are processed independently for each individual time series . Univariate algorithms will only learn from information in the individual series being completed; a limitation of univariate context is that we ignore any potential relationships across players or angles. Input data is treated as a vector with length T.
- Multivariate Context (Across Players): For a given angle a, we conceptualize imputation as the data matrix (or the transpose). As a result, algorithms that in the multivariate context can model correlations or similarities across different players and time series across angles will take advantage of information from the cohort.
- Multivariate Context (Across Angles): For a given player p, we represent imputation as the data matrix . Algorithms that operate in the multivariate context can take advantage of inter-feature correlations, essentially learning about how various angles (kinematic variables) are related to the same subject over time.
3.5. Imputation Algorithms
- Statistical Baselines: Simple, computationally economical methods including Mean, Median, and Random Sample Imputation applied within the relevant context (univariate series or multivariate scope across players/angles for calculating the statistic or sampling pool).
- Classical Machine Learning Methods: Algorithms primarily sourced from the fancyimpute library.
- –
- KNN estimates missing values using a weighted average of the values from the K most similar samples (neighbors), based on observed features.
- –
- Matrix Factorization (SoftImpute, IterativeSVD): These methods approximate the data matrix with a low-rank factorization, effectively filling missing entries based on learned latent factors. SoftImpute uses nuclear norm regularization, while IterativeSVD employs truncated SVD iteratively.
- –
- IterativeImputer models each feature with missing values as a function of the other features using a regression model (e.g., Bayesian Ridge). It iteratively predicts and updates missing values until convergence.
- –
- Optimal Transport Imputation (OT) [62]: This method utilizes Optimal Transport theory, specifically minimizing the Sinkhorn divergence between empirical distributions formed by batches of data. We utilize the BatchSinkhornImputation approach, where the missing values themselves are treated as learnable parameters . In the following text, we will call this method BSI. These parameters are optimized by minimizing the expected Sinkhorn divergence between pairs of randomly drawn mini-batches from the currently filled dataset :The expectation is approximated using samples per gradient step.
- Deep Learning Methods:
- –
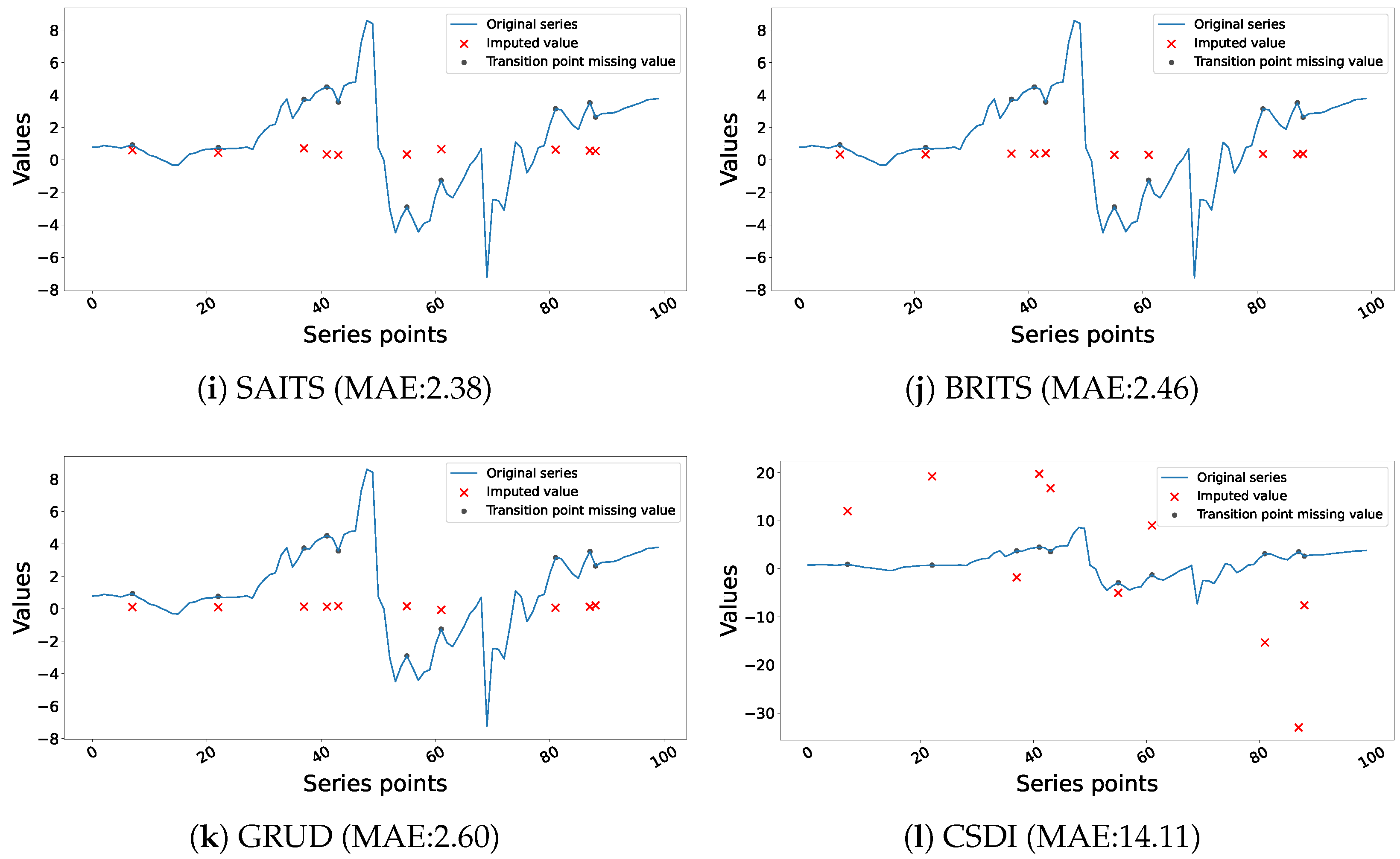
- SAITS [63]: Self-Attention-based Imputation for Time Series (SAITS) is a deep learning model that can impute missing data from complex time series data. SAITS addresses an important challenge of many previous imputation models, which is the lack of a self-attention-based mechanism to capture long-range dependencies detectable within the time series data [63]. Capturing these long-term relationships is particularly important when attempting to impute values in irregularly sampled time series and/or partially observed time series.
- –
- BRITS [64]: BRITS is a novel technique that uses bidirectional recurrent neural networks (RNNs) to impute missing values in multivariate time series data. Unlike earlier techniques, BRITS makes no particular data assumptions and learns missing values directly within a recurrent dynamical system. It enables efficient backpropagation updates by treating missing values as variables in the RNN graph. The model increases overall accuracy by carrying out imputation and classification/regression at the same time. This method tackles issues such as nonlinear dynamics in time series and correlated missing values.
- –
- GRU-D [65] is proposed specifically for multivariate time series with missing values, with an emphasis on “informative missingness.” It employs a Gated Recurrent Unit (GRU) architecture and integrates time interval and masking as two representations of missing patterns. GRU-D successfully captures long-term temporal dependencies and employs missingness for better prediction by incorporating these patterns into the inputs and hidden states of the GRU through trainable decay mechanisms. This method improves classification performance on synthetic and real-world clinical datasets.
- –
- CSDI [24]: The CSDI (Conditional Score-based Diffusion Model) is a deep generative approach for probabilistic time series imputation. To deal with missing values, it makes use of score-based diffusion models, which use iterative denoising to learn data distributions. CSDI produces diverse and realistic imputations by conditioning the diffusion process on observed portions of the time series. It is appropriate for probabilistic forecasting since it offers imputations and uncertainty estimates.
- –
- GAIN [66]: GAIN utilizes a minimax game between a Generator (G) and a Discriminator (D). The Generator (G) attempts to impute the missing values in the data tensor given a mask M and a noise tensor Z, producing the final imputed tensor . The discriminator D attempts to differentiate observed components from imputed ones based on and a hint vector (partially revealing ). The objectives arewhere ⊙ denotes element-wise multiplication and is a hyperparameter balancing the adversarial loss and a direct reconstruction (MSE) loss on observed components.
3.6. Evaluation Metrics
3.7. Experimental Setup and Implementation
| Algorithm 2 Experimental Configuration |
|
| Algorithm 3 ApplyImputation() |
|
4. Results and Discussion
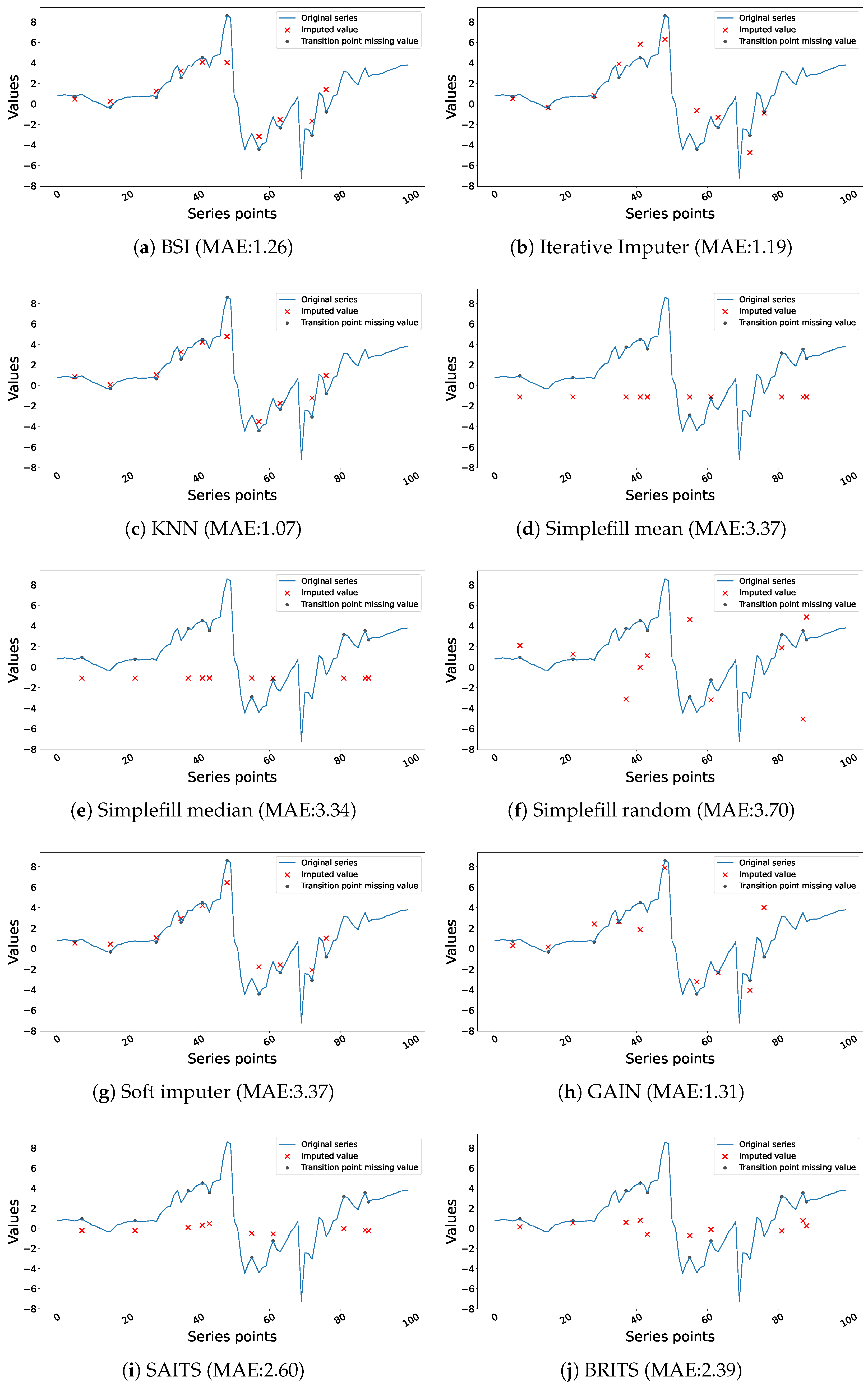
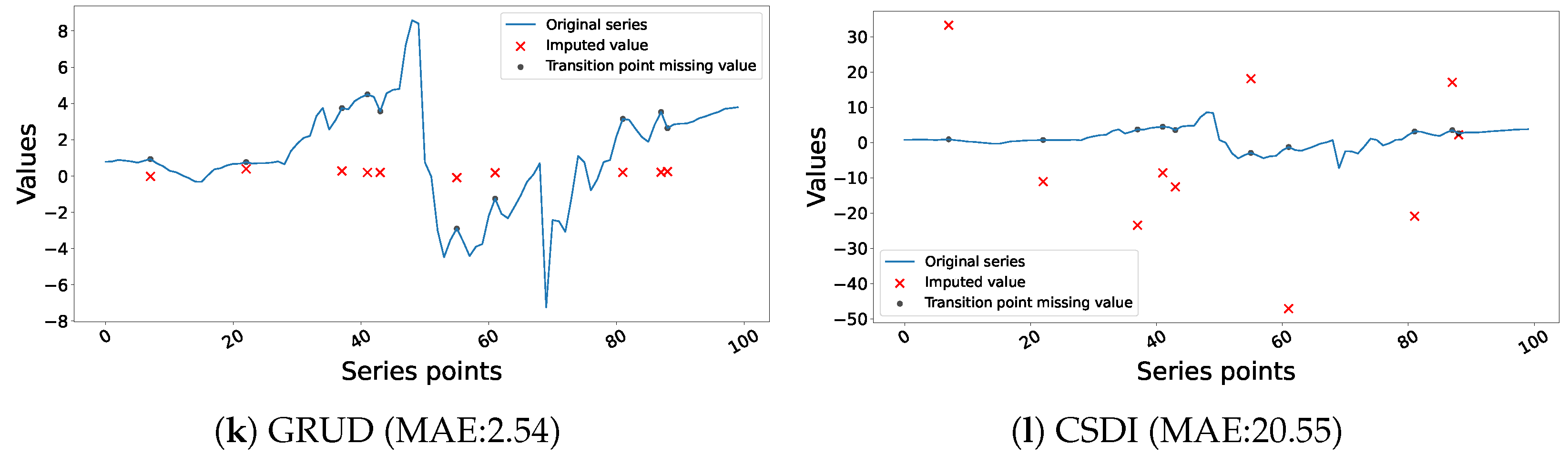
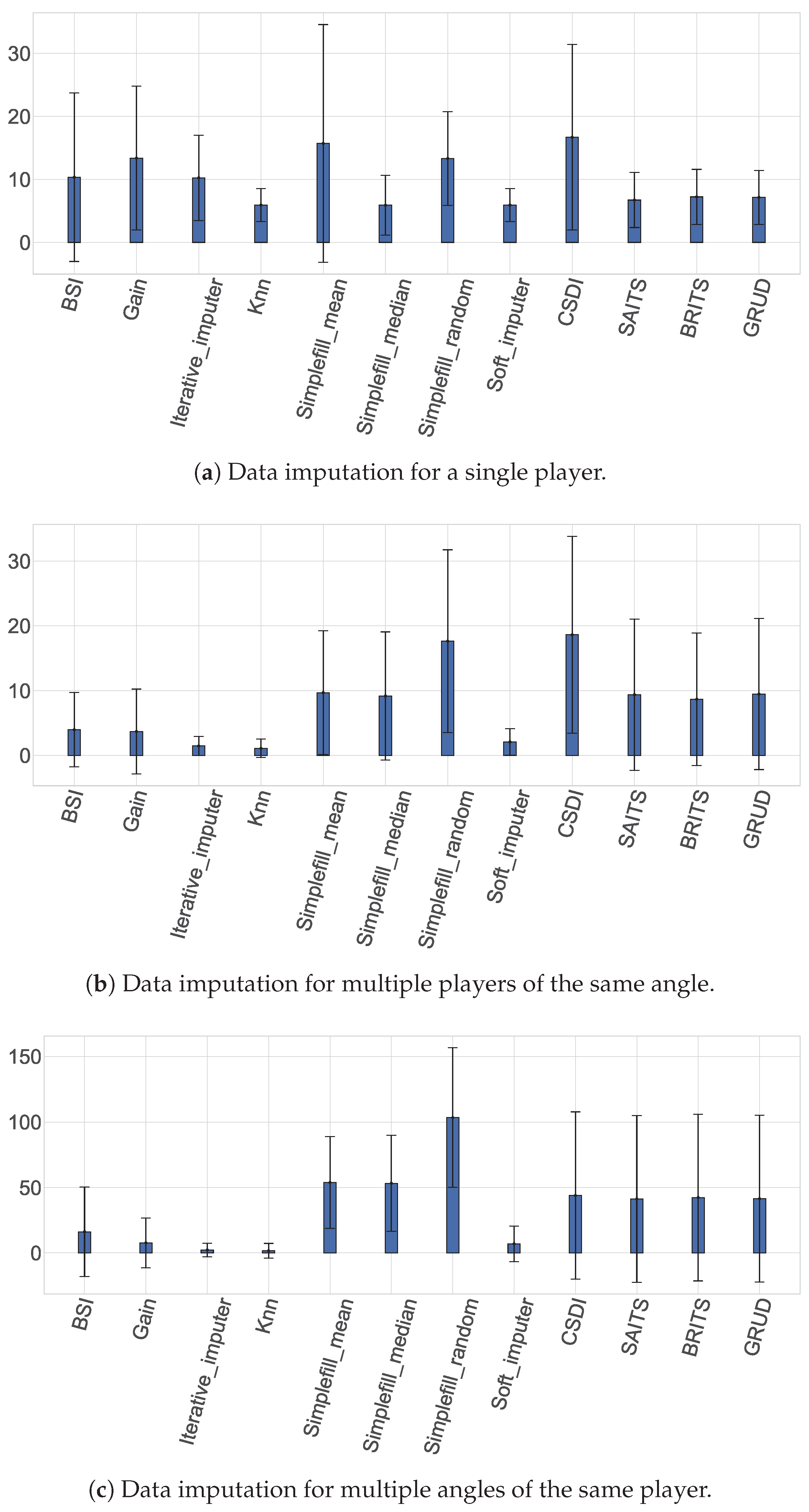
4.1. Performance and Interpretation of Univariate Imputation
4.2. Results and Comparative Interpretation of Multivariate Contexts
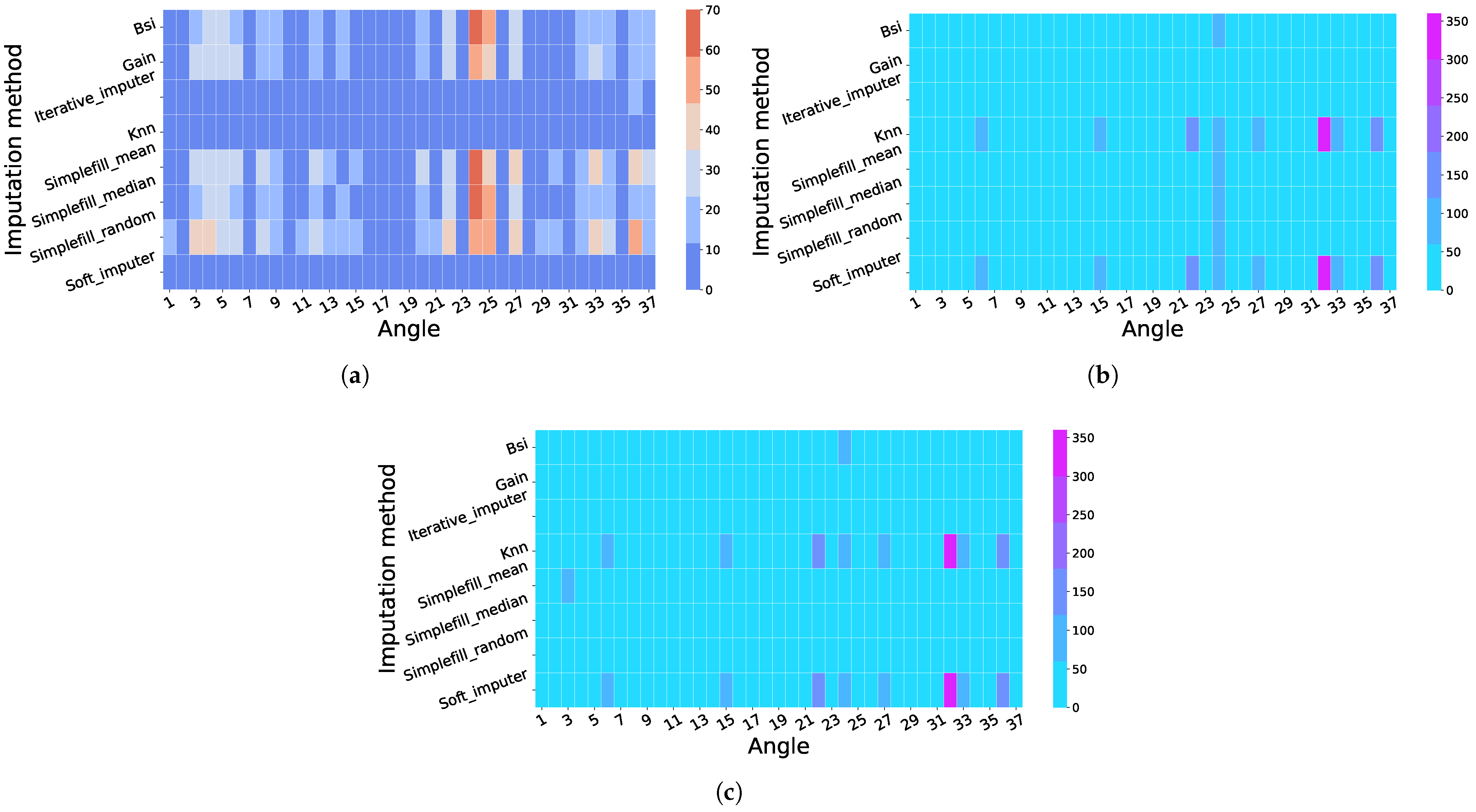
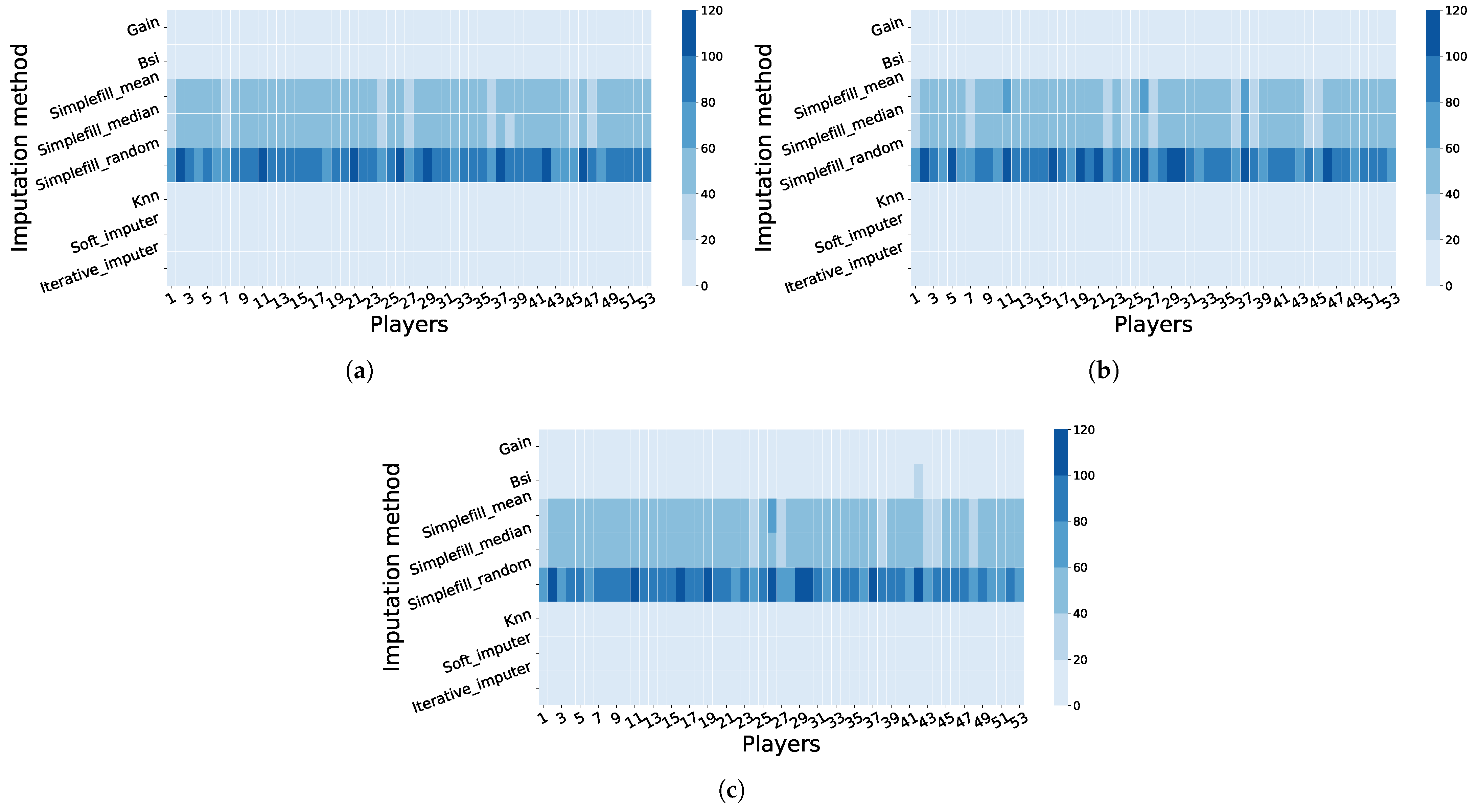
4.2.1. Across-Player Imputation: Results and Cohort-Based Interpretation
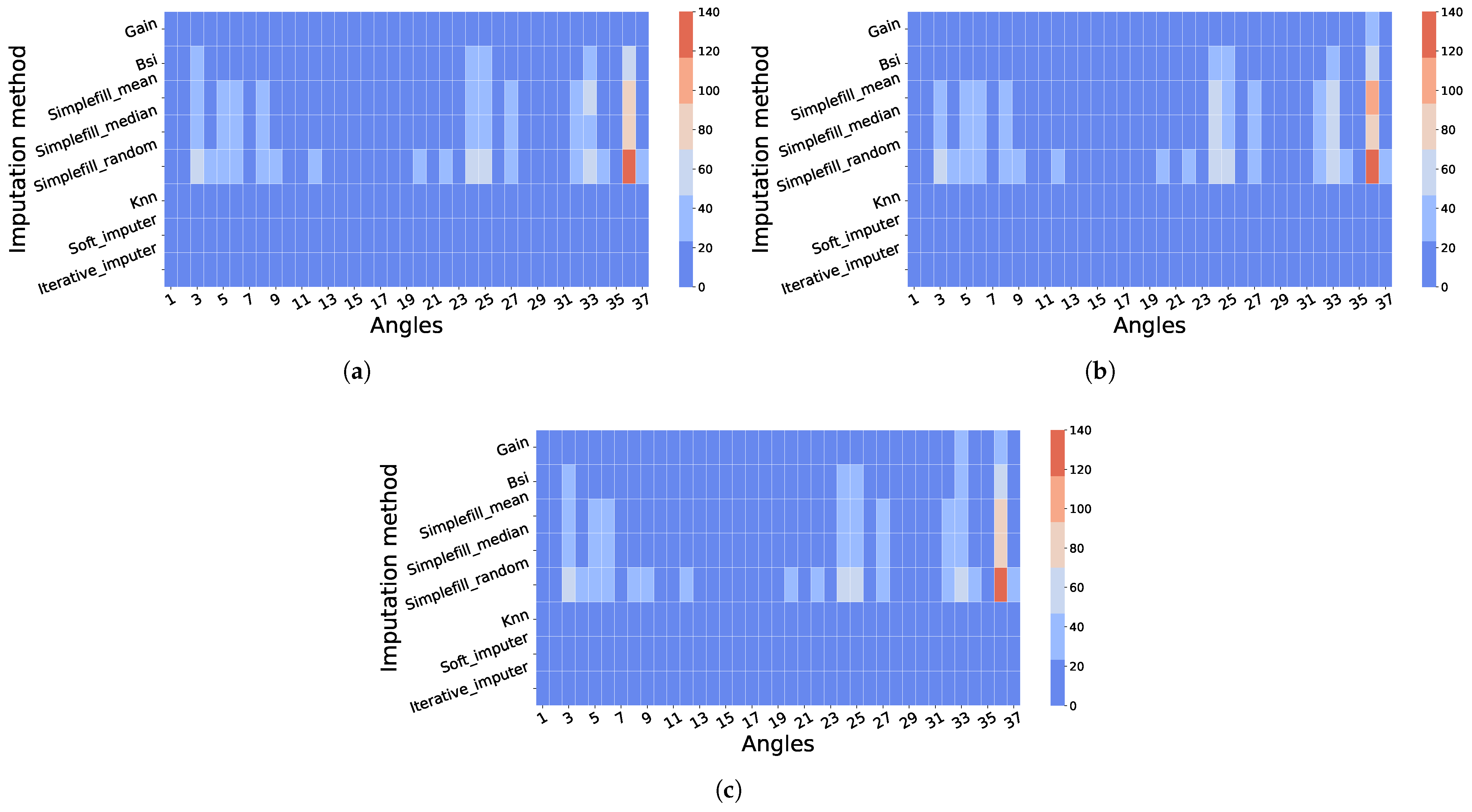
4.2.2. Across-Angle Imputation: Results and Biomechanical Interpretation
4.3. Biomechanical Interpretation of Multivariate Gains
4.4. Discussion
4.5. Study Limitations and Implications for Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van der Kruk, E.; Reijne, M.M. Accuracy of human motion capture systems for sport applications; state-of-the-art review. Eur. J. Sport Sci. 2018, 18, 806–819. [Google Scholar] [CrossRef]
- Fathalla, A.; Salah, A.; Bekhit, M.; Eldesouky, E.; Talha, A.; Zenhom, A.; Ali, A. Real-Time and Automatic System for Performance Evaluation of Karate Skills Using Motion Capture Sensors and Continuous Wavelet Transform. Int. J. Intell. Syst. 2023, 2023, 1561942. [Google Scholar] [CrossRef]
- Jalata, I.K.; Truong, T.D.; Allen, J.L.; Seo, H.S.; Luu, K. Movement analysis for neurological and musculoskeletal disorders using graph convolutional neural network. Future Internet 2021, 13, 194. [Google Scholar] [CrossRef]
- Arlotti, J.S.; Carroll, W.O.; Afifi, Y.; Talegaonkar, P.; Albuquerque, L.; Ball, J.E.; Chander, H.; Petway, A. Benefits of IMU-based Wearables in Sports Medicine: Narrative Review. Int. J. Kinesiol. Sport. Sci. 2022, 10, 36–43. [Google Scholar] [CrossRef]
- Adel, B.; Badran, A.; Elshami, N.E.; Salah, A.; Fathalla, A.; Bekhit, M. A Survey on Deep Learning Architectures in Human Activities Recognition Application in Sports Science, Healthcare Security. In Proceedings of the the International Conference on Innovations in Computing Research, Athens, Greece, 5–7 July 2022; pp. 121–134. [Google Scholar]
- Ismail, A.R.; Zainal Abidin, N.; Maen, M.K. Systematic Review on Missing Data Imputation Techniques with Machine Learning Algorithms for Healthcare. J. Robot. Control (JRC) 2022, 3, 143–152. [Google Scholar] [CrossRef]
- Kaseris, M.; Kostavelis, I.; Malassiotis, S. A Comprehensive Survey on Deep Learning Methods in Human Activity Recognition. Mach. Learn. Knowl. Extr. 2024, 6, 842–876. [Google Scholar] [CrossRef]
- Guignard, B.; Ayad, O.; Baillet, H.; Mell, F.; Simbaña Escobar, D.; Boulanger, J.; Seifert, L. Validity, reliability and accuracy of inertial measurement units (IMUs) to measure angles: Application in swimming. Sport. Biomech. 2021, 23, 1471–1503. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y.; Li, Q.; Liu, T.; Yi, J. Two shank-mounted IMUs-based gait analysis and classification for neurological disease patients. IEEE Robot. Autom. Lett. 2020, 5, 1970–1976. [Google Scholar] [CrossRef]
- Karuzaki, E.; Partarakis, N.; Patsiouras, N.; Zidianakis, E.; Katzourakis, A.; Pattakos, A.; Kaplanidi, D.; Baka, E.; Cadi, N.; Magnenat-Thalmann, N.; et al. Realistic virtual humans for cultural heritage applications. Heritage 2021, 4, 4148–4171. [Google Scholar] [CrossRef]
- Yahya, M.; Shah, J.A.; Kadir, K.A.; Yusof, Z.M.; Khan, S.; Warsi, A. Motion capture sensing techniques used in human upper limb motion: A review. Sens. Rev. 2019, 39, 504–511. [Google Scholar] [CrossRef]
- Clemente, F.M.; Akyildiz, Z.; Pino-Ortega, J.; Rico-González, M. Validity and reliability of the inertial measurement unit for barbell velocity assessments: A systematic review. Sensors 2021, 21, 2511. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on various inertial measurement unit (IMU) sensor applications. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Behrmann, N.; Hillebrecht, M.; Pöppl, N.; Pöppl, S.; Seiler, S. Is the EnodePro® a Valid Tool to Determine the Bar Velocity in the Bench Press and Barbell Back Squat? A Comparative Analysis. Sensors 2025, 25, 549. [Google Scholar] [CrossRef] [PubMed]
- Dragutinovic, S.; Djuric, S.; Petruzzi, S. Validation of the VmaxPro Sensor for Assessing Velocity and Load-Velocity Variables During Back Squat and Bench Press Exercises. Sports 2024, 12, 101. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, Z. A real-time articulated human motion tracking using tri-axis inertial/magnetic sensors package. IEEE Trans. Neural Syst. Rehabil. Eng. 2004, 12, 295–302. [Google Scholar]
- Cai, Q.; Song, N.; Yang, G.; Liu, Y. Accelerometer calibration with nonlinear scale factor based on multi-position observation. Meas. Sci. Technol. 2013, 24, 105002. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, C.; Chao, F.; Lin, C.M.; Yang, L.; Shang, C.; Shen, Q. Low-cost inertial measurement unit calibration with nonlinear scale factors. IEEE Trans. Ind. Inform. 2021, 18, 1028–1038. [Google Scholar] [CrossRef]
- Sohrabi, H.; Ebadollahi, S. Accuracy enhancement of MEMS accelerometer by determining its nonlinear coefficients using centrifuge test. Measurement 2017, 112, 29–37. [Google Scholar] [CrossRef]
- Olivares, A.; Olivares, G.; Gorriz, J.; Ramirez, J. High-efficiency low-cost accelerometer-aided gyroscope calibration. In Proceedings of the 2009 International Conference on Test and Measurement, Hong Kong, China, 5–6 December 2009; Volume 1, pp. 354–360. [Google Scholar]
- Kozlov, A.; Sazonov, I.; Vavilova, N. IMU calibration on a low grade turntable: Embedded estimation of the instrument displacement from the axis of rotation. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–4. [Google Scholar]
- Aktakka, E.E.; Woo, J.K.; Najafi, K. On-chip characterization of scale-factor of a MEMS gyroscope via a micro calibration platform. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; pp. 1–4. [Google Scholar]
- Renner, J.; Rumpf, M.C.; Wagner, M.; Zoch, M.; Pöppl, S. Concurrent Validity of Novel Smartphone-Based Apps Monitoring Barbell Velocity in Powerlifting Exercises. Sensors 2024, 24, 882. [Google Scholar] [CrossRef]
- Tashiro, Y.; Song, J.; Song, Y.; Ermon, S. Csdi: Conditional score-based diffusion models for probabilistic time series imputation. Adv. Neural Inf. Process. Syst. 2021, 34, 24804–24816. [Google Scholar]
- Adhikari, D.; Jiang, W.; Zhan, J.; He, Z.; Rawat, D.B.; Aickelin, U.; Khorshidi, H.A. A comprehensive survey on imputation of missing data in internet of things. ACM Comput. Surv. 2022, 55, 1–38. [Google Scholar] [CrossRef]
- Hasan, M.K.; Alam, M.A.; Roy, S.; Dutta, A.; Jawad, M.T.; Das, S. Missing value imputation affects the performance of machine learning: A review and analysis of the literature (2010–2021). Inform. Med. Unlocked 2021, 27, 100799. [Google Scholar] [CrossRef]
- Luo, Y. Evaluating the state of the art in missing data imputation for clinical data. Briefings Bioinform. 2022, 23, bbab489. [Google Scholar] [CrossRef]
- Singh, G.; Jaiswal, A.K. Efficient Imputation Methods to Handle Missing Data in Sample Surveys. J. Stat. Theory Pract. 2022, 16, 40. [Google Scholar] [CrossRef]
- Donders, A.R.T.; Van Der Heijden, G.J.; Stijnen, T.; Moons, K.G. A gentle introduction to imputation of missing values. J. Clin. Epidemiol. 2006, 59, 1087–1091. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.C.; Tsai, C.F. Missing value imputation: A review and analysis of the literature (2006–2017). Artif. Intell. Rev. 2020, 53, 1487–1509. [Google Scholar] [CrossRef]
- Little, T.D.; Jorgensen, T.D.; Lang, K.M.; Moore, E.W.G. On the joys of missing data. J. Pediatr. Psychol. 2014, 39, 151–162. [Google Scholar] [CrossRef] [PubMed]
- Leurent, B.; Gomes, M.; Faria, R.; Morris, S.; Grieve, R.; Carpenter, J.R. Sensitivity analysis for not-at-random missing data in trial-based cost-effectiveness analysis: A tutorial. Pharmacoeconomics 2018, 36, 889–901. [Google Scholar] [CrossRef]
- de Goeij, M.C.; van Diepen, M.; Jager, K.J.; Tripepi, G.; Zoccali, C.; Dekker, F.W. Multiple imputation: Dealing with missing data. Nephrol. Dial. Transplant. 2013, 28, 2415–2420. [Google Scholar] [CrossRef]
- Bakar, A.A.; Ahmad, I.B.; Yusof, Y.S.; Zakaria, I.H.; Yacob, H. A hybrid CNN-LSTM model with attention mechanism for missing data imputation. Artif. Intell. Med. 2023, 145, 102587. [Google Scholar] [CrossRef]
- Rubin, D.B. Multiple Imputation for Nonresponse in Surveys; John Wiley & Sons: Hoboken, NJ, USA, 2004; Volume 81. [Google Scholar]
- Kang, J.; Yuan, Y.; Emery, C. Assessing remedies for missing weekly individual exposure in sport injury studies. Inj. Prev. 2014, 20, 177–182. [Google Scholar] [CrossRef]
- Wood, A.M.; White, I.R.; Hillsdon, M.; Carpenter, J. Comparison of imputation and modelling methods in the analysis of a physical activity trial with missing outcomes. Int. J. Epidemiol. 2005, 34, 89–99. [Google Scholar] [CrossRef]
- Jekauc, D.; Völkle, M.; Lämmle, L.; Woll, A. Missing values in sport scientific studies: A practical guide to multiple imputation with SPSS. Sportwissenschaft 2012, 42, 126–136. [Google Scholar] [CrossRef]
- Wang, C.; Stokes, T.; Steele, R.; Wedderkopp, N.; Shrier, I. Implementing multiple imputation for missing data in longitudinal studies when models are not feasible: A tutorial on the random hot deck approach. arXiv 2020, arXiv:2004.06630. [Google Scholar] [CrossRef]
- Solaro, N.; Barbiero, A.; Manzi, G.; Ferrari, P. A simulation comparison of imputation methods for quantitative data in the presence of multiple data patterns. J. Stat. Comput. Simul. 2018, 88, 3588–3619. [Google Scholar] [CrossRef]
- Takahashi, M. Multiple ratio imputation by the EMB algorithm: Theory and simulation. J. Mod. Appl. Stat. Methods 2017, 16, 34. [Google Scholar] [CrossRef]
- Jang, J.H.; Choi, J.; Roh, H.W.; Son, S.J.; Hong, C.H.; Kim, E.Y.; Kim, T.Y.; Yoon, D. Deep learning approach for imputation of missing values in actigraphy data: Algorithm development study. JMIR MHealth UHealth 2020, 8, e16113. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.S.; Thongam, K.; Choudhary, P.; Bhagat, P. An integrated machine learning approach for congestive heart failure prediction. Diagnostics 2024, 14, 736. [Google Scholar] [CrossRef]
- Benson, L.C.; Stilling, C.; Owoeye, O.B.; Emery, C.A. Evaluating methods for imputing missing data from longitudinal monitoring of athlete workload. J. Sport. Sci. Med. 2021, 20, 188. [Google Scholar] [CrossRef]
- Hammerling, D.; Cefalu, M.; Cisewski, J.; Dominici, F.; Parmigiani, G.; Paulson, C.; Smith, R.L. Completing the results of the 2013 Boston marathon. PLoS ONE 2014, 9, e93800. [Google Scholar] [CrossRef]
- Kato, T.; Kasugai, R.; Sakai, K. Relationship Between the Total Quality Recovery Scale and Race Performance in Competitive College Swimmers over Two Seasons. Sports 2025, 13, 139. [Google Scholar] [CrossRef]
- Barker, J.; McCarthy, P.; Jones, M.; Moran, A. Single-Case Research Methods in Sport and Exercise Psychology; Routledge: London, UK, 2011. [Google Scholar]
- Ramli, M.N.; Yahaya, A.S.; Ramli, N.; Yusof, N.F.F.M.; Abdullah, M. Roles of imputation methods for filling the missing values: A review. Adv. Environ. Biol. 2013, 7, 3861–3870. [Google Scholar]
- Ette, E.I.; Chu, H.M.; Ahmad, A. Data Imputation; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 245–262. [Google Scholar] [CrossRef]
- Kishore, C.L.; Rao, C.R. A Comparative Study on Missing Value Imputation Techniques in Machine Learning. In Proceedings of the SHS Web of Conferences, Paris, France, 20–22 May 2025; Volume 218, p. 02014. [Google Scholar] [CrossRef]
- Alwateer, M.; Atlam, E.S.; Abd El-Raouf, M.M.; Ghoneim, O.A.; Gad, I. Missing data imputation: A comprehensive review. J. Comput. Commun. 2024, 12, 53–75. [Google Scholar] [CrossRef]
- Ser, G.; Keskin, S.; Yilmaz, M. The performance of multiple imputations for different number of imputations. Sains Malays. 2016, 45, 1755–1761. [Google Scholar]
- Sterne, J.A.; White, I.R.; Carlin, J.B.; Spratt, M.; Royston, P.; Kenward, M.G.; Wood, A.M.; Carpenter, J.R. Multiple imputation for missing data in epidemiological and clinical research: Potential and pitfalls. Bmj 2009, 338, b2393. [Google Scholar] [CrossRef] [PubMed]
- Mistler, S.A.; Enders, C.K. A comparison of joint model and fully conditional specification imputation for multilevel missing data. J. Educ. Behav. Stat. 2017, 42, 432–466. [Google Scholar] [CrossRef]
- Zhang, L.C. Nonparametric Markov chain bootstrap for multiple imputation. Comput. Stat. Data Anal. 2004, 45, 343–353. [Google Scholar] [CrossRef]
- White, I.R.; Daniel, R.; Royston, P. Avoiding bias due to perfect prediction in multiple imputation of incomplete categorical variables. Comput. Stat. Data Anal. 2010, 54, 2267–2275. [Google Scholar] [CrossRef]
- Ae Lee, J.; Gill, J. Missing value imputation for physical activity data measured by accelerometer. Stat. Methods Med Res. 2018, 27, 490–506. [Google Scholar] [CrossRef]
- Nguyen, Q.; Matthews, G.J. Filling the gaps: A multiple imputation approach to estimating aging curves in baseball. J. Sport. Anal. 2024, 10, 77–85. [Google Scholar] [CrossRef]
- Epp-Stobbe, A.; Tsai, M.-C.; Klimstra, M. Comparison of Imputation Methods for Missing Rate of Perceived Exertion Data in Rugby. Mach. Learn. Knowl. Extr. 2022, 4, 827–838. [Google Scholar] [CrossRef]
- Woods, A.D.; Gerasimova, D.; Van Dusen, B.; Nissen, J.; Bainter, S.; Uzdavines, A.; Davis-Kean, P.E.; Halvorson, M.; King, K.M.; Logan, J.A.; et al. Best practices for addressing missing data through multiple imputation. Infant Child Dev. 2024, 33, e2407. [Google Scholar] [CrossRef]
- Li, P.; Stuart, E.A.; Allison, D.B. Multiple imputation: A flexible tool for handling missing data. JAMA 2015, 314, 1966–1967. [Google Scholar] [CrossRef]
- Muzellec, B.; Josse, J.; Boyer, C.; Cuturi, M. Missing data imputation using optimal transport. In Proceedings of the International Conference on Machine Learning, Vienna, Austria, 12–18 July 2020; pp. 7130–7140. [Google Scholar]
- Du, W.; Côté, D.; Liu, Y. Saits: Self-attention-based imputation for time series. Expert Syst. Appl. 2023, 219, 119619. [Google Scholar] [CrossRef]
- Cao, W.; Wang, D.; Li, J.; Zhou, H.; Li, L.; Li, Y. Brits: Bidirectional recurrent imputation for time series. Adv. Neural Inf. Process. Syst. 2018, 31, 6776–6786. [Google Scholar]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent neural networks for multivariate time series with missing values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef]
- Yoon, J.; Jordon, J.; Schaar, M. Gain: Missing data imputation using generative adversarial nets. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 5689–5698. [Google Scholar]

| Imputation Method | Type | Percentage of Missing Data | |||||
|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | ||
| BSI | ML | 10.88 ± 5.99 | 11.12 ± 5.6 | 9.52 ± 5.12 | 9.69 ± 5.74 | 11.45 ± 5.74 | 10.0 ± 6.57 |
| Iterative Imputer | ML | 11.93 ± 8.21 | 10.67 ± 6.06 | 9.5 ± 7.21 | 10.22 ± 6.82 | 10.8 ± 6.9 | 9.71 ± 7.19 |
| KNN | ML | 8.73 ± 6.98 | 14.2 ± 10.09 | 9.56 ± 7.05 | 10.99 ± 8.8 | 12.0 ± 9.89 | 12.19 ± 8.92 |
| Simplefill mean | Statistical | 11.93 ± 8.21 | 10.67 ± 6.06 | 9.5 ± 7.21 | 10.22 ± 6.82 | 10.8 ± 6.9 | 9.71 ± 7.19 |
| Simplefill median | Statistical | 13.78 ± 9.8 | 10.05 ± 8.62 | 10.18 ± 9.33 | 10.75 ± 8.65 | 10.99 ± 8.57 | 9.97 ± 9.0 |
| Simplefill random | Statistical | 20.79 ± 11.95 | 13.89 ± 8.18 | 18.74 ± 12.77 | 15.46 ± 12.66 | 17.24 ± 10.06 | 17.27 ± 12.73 |
| Soft imputer | ML | 8.73 ± 6.98 | 14.2 ± 10.09 | 9.56 ± 7.05 | 10.99 ± 8.8 | 12.0 ± 9.89 | 12.19 ± 8.92 |
| GAIN | DL | 11.99 ± 8.25 | 10.69 ± 6.0 | 13.51 ± 9.55 | 10.21 ± 6.73 | 10.8 ± 6.85 | 9.71 ± 7.2 |
| CSDI | DL | 26.1 ± 18.77 | 16.54 ± 11.12 | 12.09 ± 9.73 | 32.08 ± 21.72 | 14.88 ± 13.34 | 13.31 ± 10.24 |
| SAITS | DL | 7.42 ± 4.15 | 7.12 ± 3.52 | 6.64 ± 2.79 | 7.55 ± 2.69 | 6.68 ± 2.79 | 7.23 ± 2.99 |
| BRITS | DL | 7.56 ± 4.08 | 7.4 ± 3.74 | 6.74 ± 3.02 | 7.7 ± 2.76 | 7.37 ± 2.97 | 7.52 ± 2.95 |
| GRUD | DL | 7.48 ± 4.03 | 7.16 ± 3.79 | 6.03 ± 2.66 | 7.07 ± 2.64 | 6.95 ± 2.8 | 7.26 ± 2.91 |
| Imputation Method | Type | Percentage of Missing Data | |||||
|---|---|---|---|---|---|---|---|
| 5% | 10% | 15% | 20% | 25% | 30% | ||
| BSI | ML | 6.47 ± 5.16 | 6.65 ± 5.47 | 7.21 ± 4.95 | 7.68 ± 4.99 | 8.48 ± 5.15 | 8.12 ± 5.21 |
| Iterative Imputer | ML | 0.86 ± 0.88 | 3.29 ± 4.13 | 2.74 ± 2.5 | 2.49 ± 2.42 | 5.82 ± 5.52 | 4.4 ± 4.33 |
| KNN | ML | 0.77 ± 0.87 | 2.19 ± 3.37 | 2.26 ± 3.46 | 2.48 ± 3.5 | 4.29 ± 7.06 | 6.96 ± 8.57 |
| Simplefill mean | Statistical | 10.96 ± 5.99 | 11.1 ± 4.97 | 9.08 ± 4.77 | 10.06 ± 4.72 | 10.8 ± 5.15 | 10.07 ± 4.76 |
| Simplefill median | Statistical | 10.3 ± 2.94 | 11.81 ± 5.13 | 8.92 ± 3.14 | 10.06 ± 3.97 | 10.89 ± 4.8 | 10.53 ± 4.21 |
| Simplefill random | Statistical | 9.12 ± 6.31 | 12.95 ± 8.19 | 18.75 ± 12.39 | 16.89 ± 12.8 | 15.27 ± 12.28 | 14.71 ± 13.44 |
| Soft imputer | ML | 3.06 ± 1.75 | 5.7 ± 7.89 | 2.99 ± 3.23 | 3.91 ± 5.24 | 5.87 ± 7.82 | 4.81 ± 6.63 |
| GAIN | DL | 2.21 ± 1.36 | 6.99 ± 7.67 | 2.89 ± 2.18 | 14.72 ± 6.89 | 6.2 ± 6.87 | 4.38 ± 5.45 |
| CSDI | DL | 19.29 ± 14.21 | 13.89 ± 10.8 | 23.2 ± 14.84 | 16.89 ± 11.97 | 19.38 ± 13.45 | 13.7 ± 10.11 |
| SAITS | DL | 2.8 ± 3.07 | 3.03 ± 3.72 | 3.0 ± 3.43 | 2.89 ± 3.36 | 2.96 ± 3.35 | 2.93 ± 3.27 |
| BRITS | DL | 2.67 ± 3.0 | 3.07 ± 3.75 | 3.01 ± 3.42 | 2.79 ± 3.41 | 2.91 ± 3.36 | 2.91 ± 3.28 |
| GRUD | DL | 2.86 ± 3.07 | 3.15 ± 3.72 | 3.07 ± 3.41 | 3.04 ± 3.41 | 3.01 ± 3.32 | 2.99 ± 3.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekhit, M.; Salah, A.; Alrawahi, A.S.; Attia, T.; Ali, A.; Eldesouky, E.; Fathalla, A. MoCap-Impute: A Comprehensive Benchmark and Comparative Analysis of Imputation Methods for IMU-Based Motion Capture Data. Information 2025, 16, 851. https://doi.org/10.3390/info16100851
Bekhit M, Salah A, Alrawahi AS, Attia T, Ali A, Eldesouky E, Fathalla A. MoCap-Impute: A Comprehensive Benchmark and Comparative Analysis of Imputation Methods for IMU-Based Motion Capture Data. Information. 2025; 16(10):851. https://doi.org/10.3390/info16100851
Chicago/Turabian StyleBekhit, Mahmoud, Ahmad Salah, Ahmed Salim Alrawahi, Tarek Attia, Ahmed Ali, Esraa Eldesouky, and Ahmed Fathalla. 2025. "MoCap-Impute: A Comprehensive Benchmark and Comparative Analysis of Imputation Methods for IMU-Based Motion Capture Data" Information 16, no. 10: 851. https://doi.org/10.3390/info16100851
APA StyleBekhit, M., Salah, A., Alrawahi, A. S., Attia, T., Ali, A., Eldesouky, E., & Fathalla, A. (2025). MoCap-Impute: A Comprehensive Benchmark and Comparative Analysis of Imputation Methods for IMU-Based Motion Capture Data. Information, 16(10), 851. https://doi.org/10.3390/info16100851







