Adaptive Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks
Abstract
1. Introduction
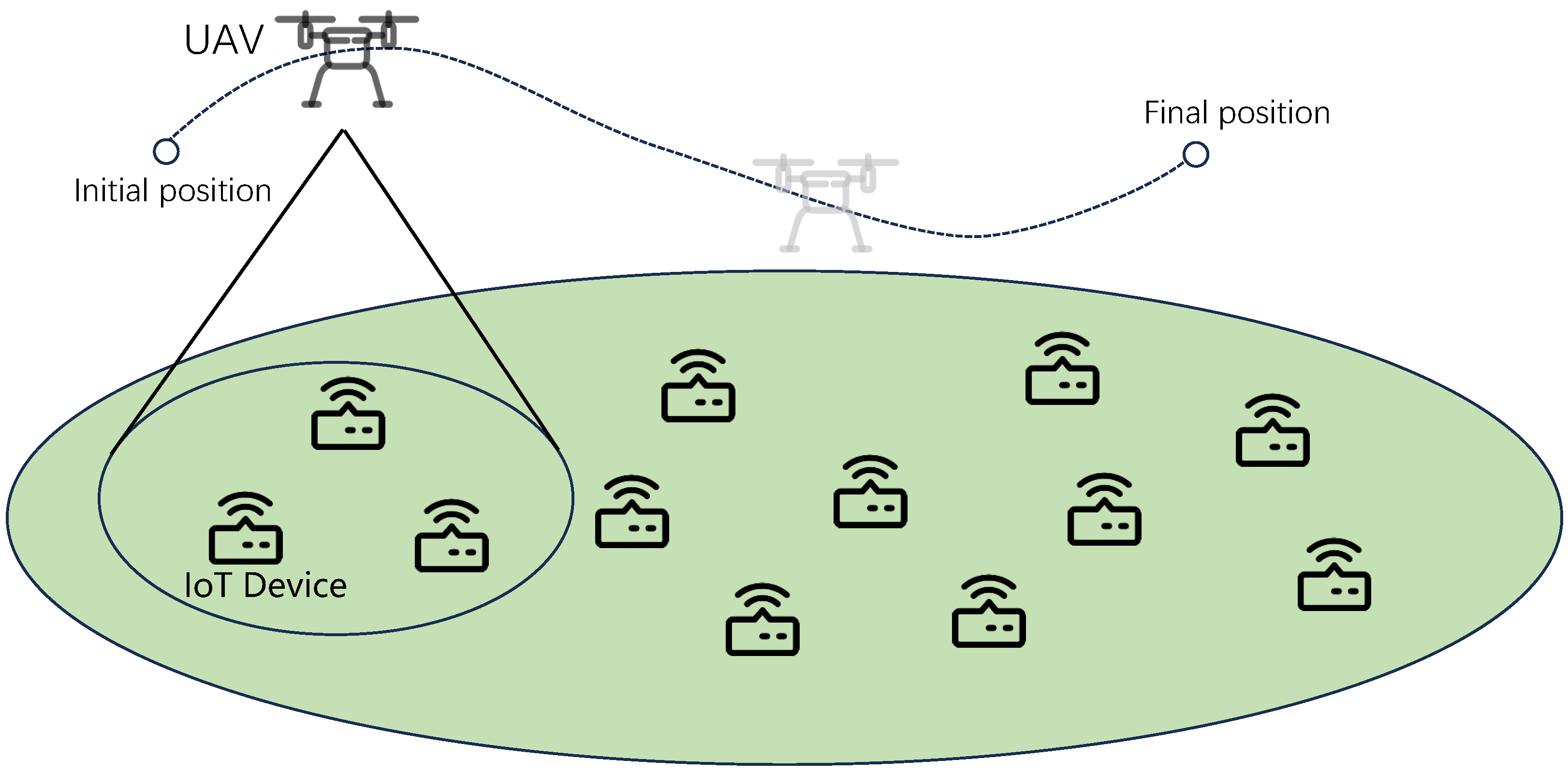
- We consider a UAV-assisted wireless powered IoT network in which IoT devices generate real-time data and require sustainable energy supply. A rotary-wing UAV equipped with a full-duplex hybrid access point (HAP) follows a fly–hover–communicate protocol to collect data from target devices and wirelessly charge surrounding nodes within its coverage.
- We formulate a dynamic multi-objective optimization problem that maximizes the system sum rate and harvested energy while minimizing UAV propulsion energy consumption. To solve it, we extend the classic DDPG by introducing a multi-dimensional reward and a state-conditioned weight generator (WeightNet). Unlike fixed or manually tuned scalarization, WeightNet adaptively outputs preferences at each step. Trained with the actor–critic, it performs online scalarization of the vector reward, enabling adaptive preference learning in time-varying UAV-assisted IoT networks.
- Simulation results confirm that our proposed DW-MODDPG approach achieves better flexibility and coordination across multiple objectives. By adjusting weight outputs in real time, the UAV policy exhibits strong generalization and responsiveness to different task priorities.
2. Related Work
2.1. UAV-Enabled Wireless Powered IoT Systems
2.2. Optimization Objectives and Trade-Offs
2.3. Reinforcement Learning for UAV Control
3. System Description and Problem Formulation
3.1. System Model
3.2. Problem Formulation
4. Preliminaries
5. Method
- -
- encourages high data rate during hovering:
- -
- rewards efficient energy transfer to multiple devices:
- -
- penalizes propulsion energy consumption:
- -
- is an auxiliary reward:
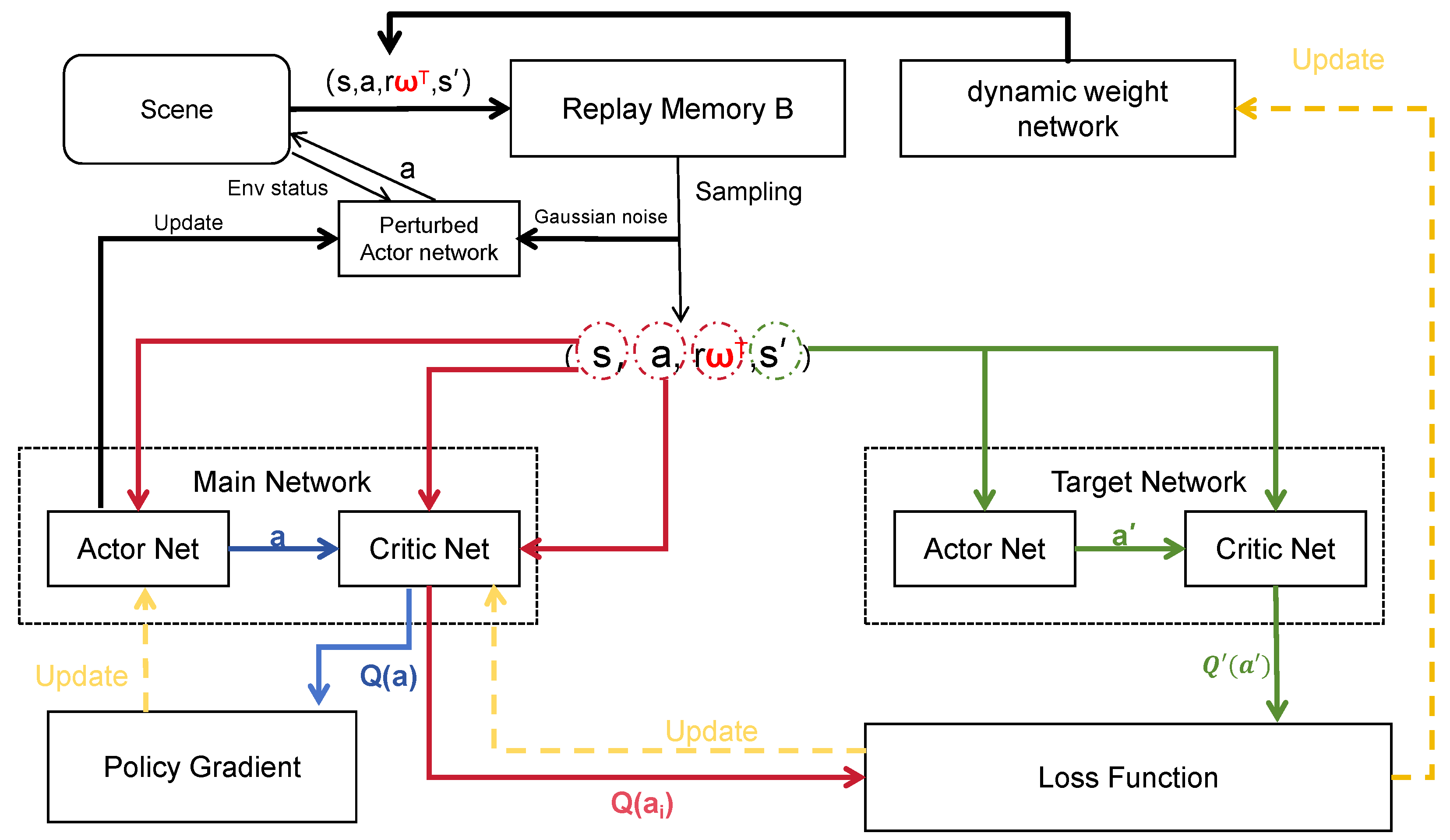
5.1. DW-MODDPG Algorithm
5.1.1. Network Architecture and Initialization
- The actor network maps the current state s to an action a, representing the control policy.
- The critic network estimates the expected cumulative reward given state–action pairs, providing feedback for policy improvement.
5.1.2. Vector-Valued Rewards and Adaptive Weighting
5.1.3. Training Procedure
5.1.4. Algorithmic Steps
| Algorithm 1 MODDPG with dynamic WeightNet. |
|
6. Simulation Results and Discussion
6.1. Simulation Settings
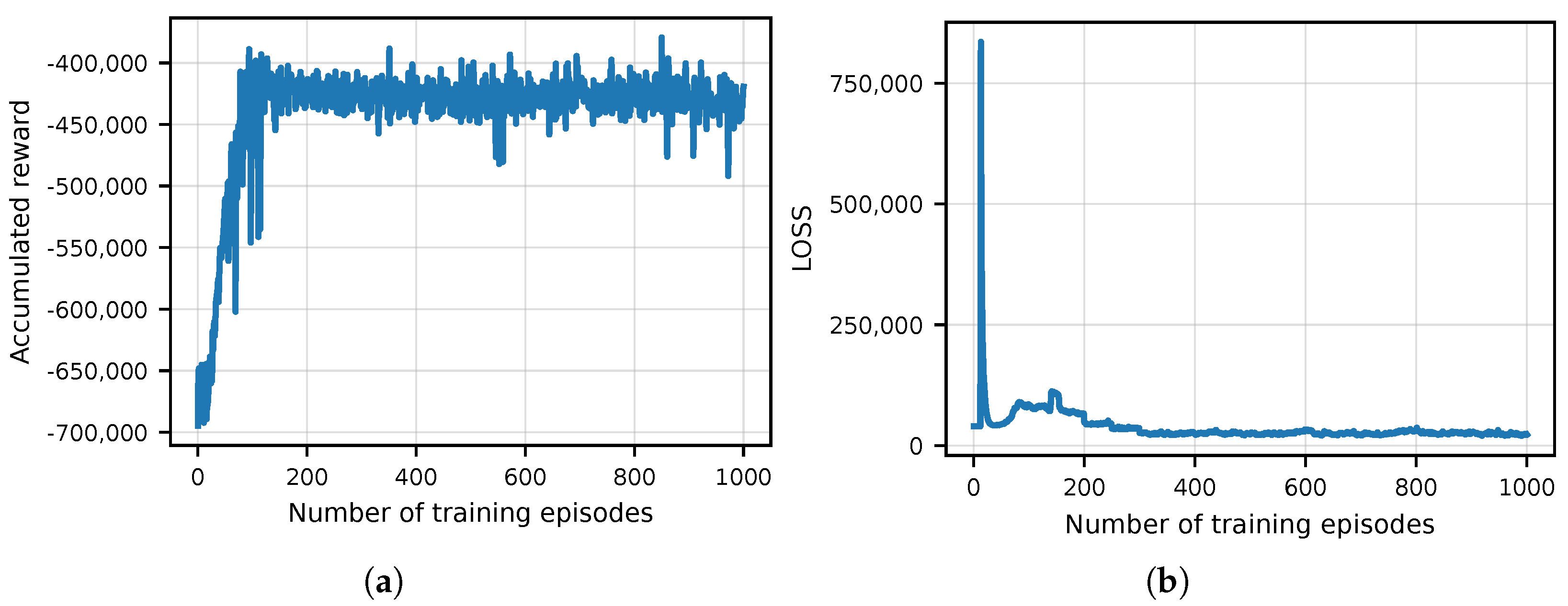
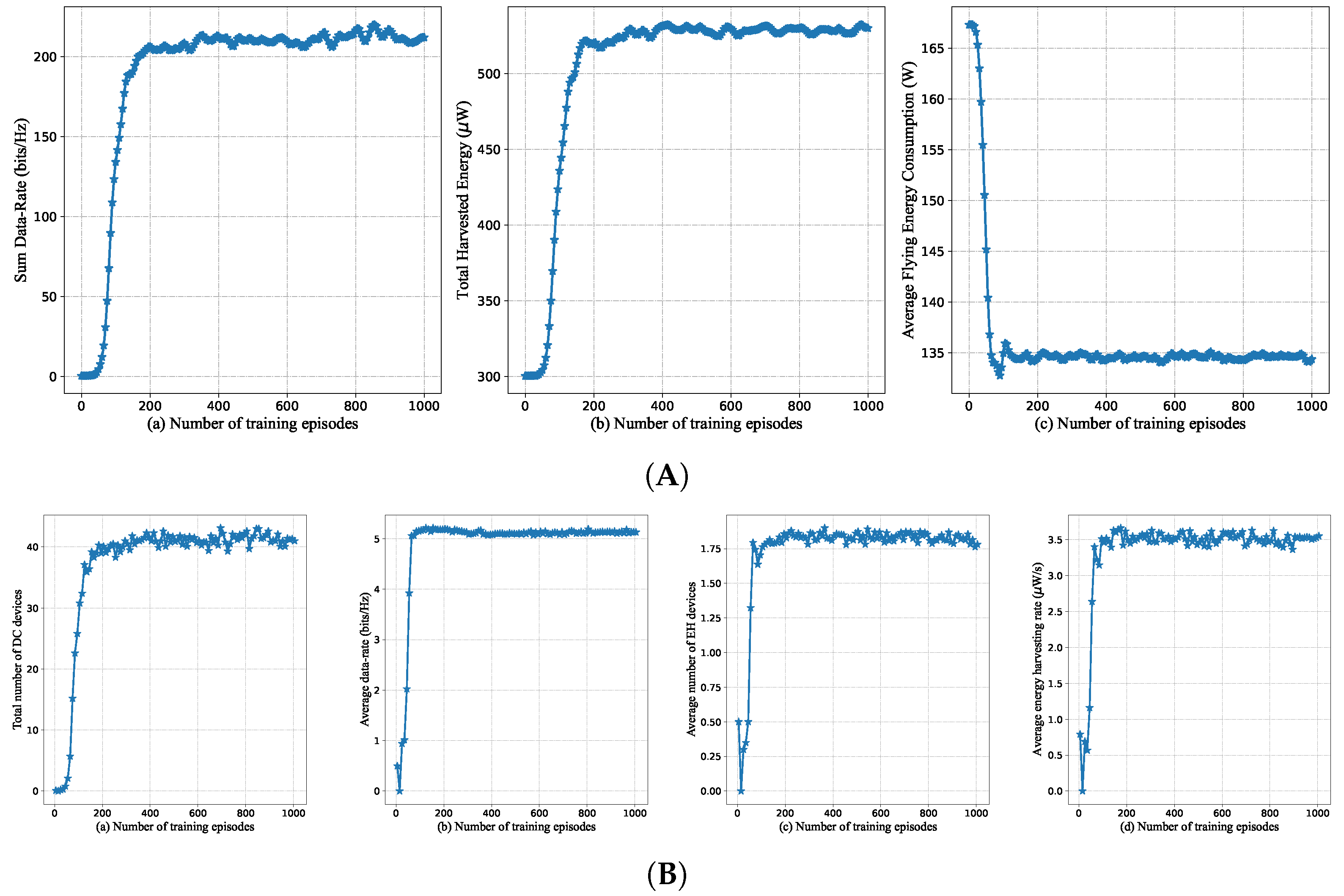
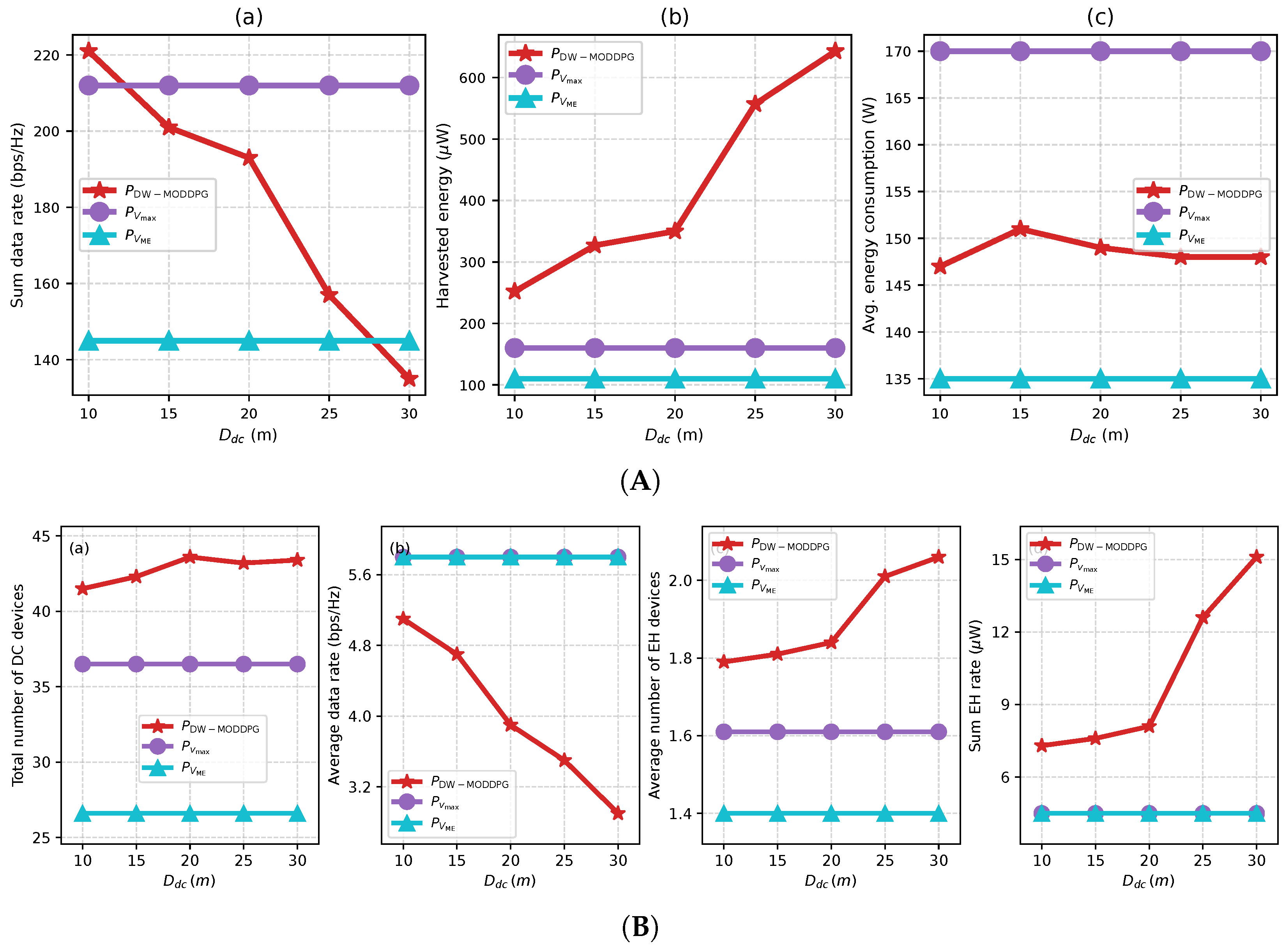
6.2. Performance Comparison with Benchmark Policies
- : The UAV flies at the maximum speed and hovers directly above each target device to collect data.
- : The UAV travels at the maximum endurance speed and also hovers above target devices for data collection.
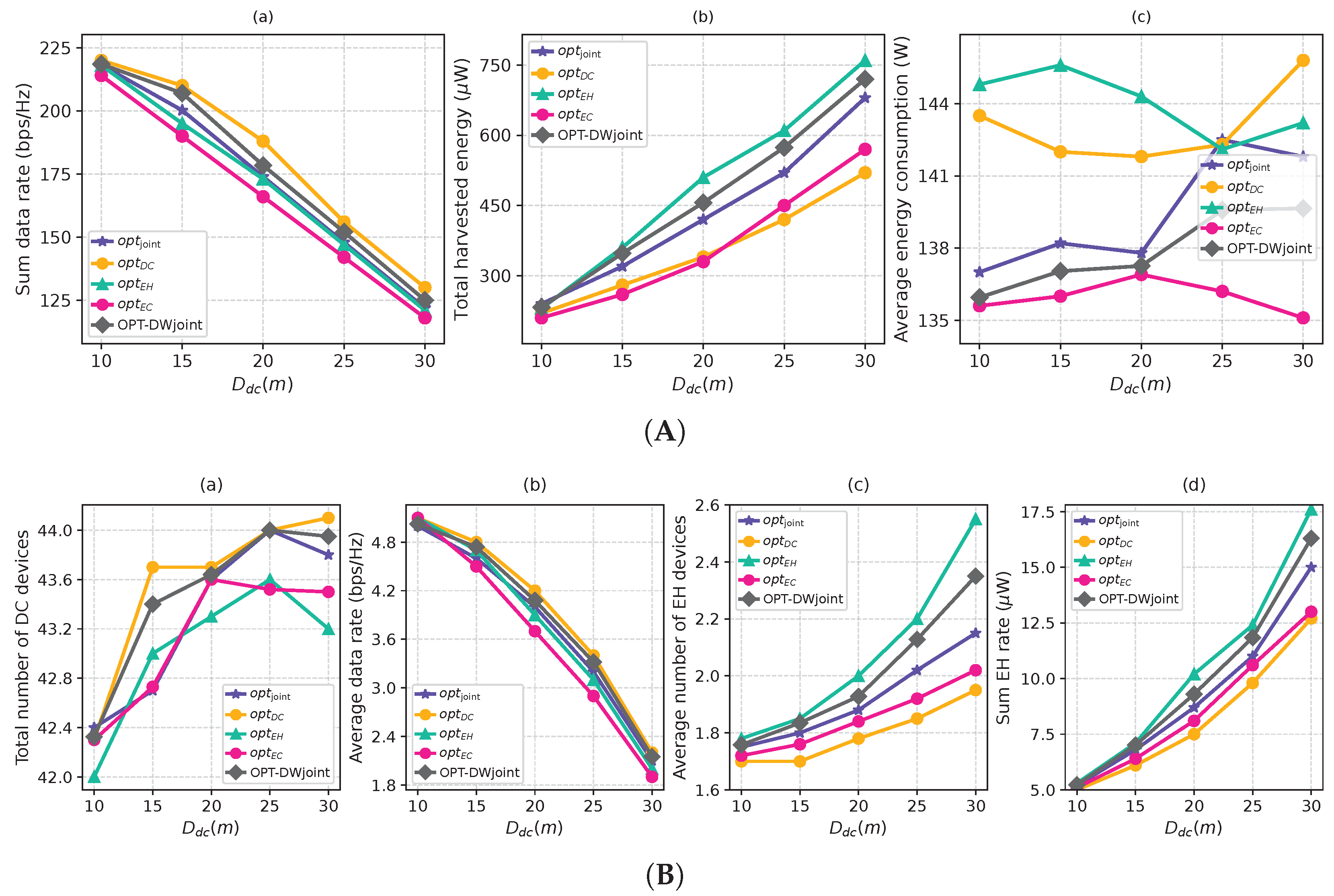
6.3. Effect of Weight Preferences on Control Policies
- optDC: Prioritizes data collection with and .
- optEH: Focuses on maximizing harvested energy, setting and others to 0.0.
- optEC: Aims to minimize UAV energy consumption with .
- optJoint: Considers all objectives equally with .
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. The Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of Things for smart cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of Things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutor. 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Kalør, A.E.; Popovski, P. Timely monitoring of dynamic sources with observations from multiple wireless sensors. arXiv 2020, arXiv:2012.12179. [Google Scholar] [CrossRef]
- Tsai, C.-W.; Lai, C.-F.; Chiang, M.-C.; Yang, L.T. Data mining for Internet of Things: A survey. IEEE Commun. Surv. Tutor. 2014, 16, 77–97. [Google Scholar] [CrossRef]
- Kaul, S.; Yates, R.; Gruteser, M. Real-time status: How often should one update? In Proceedings of the 31st Annual IEEE International Conference on Computer Communications (IEEE INFOCOM 2012), Orlando, FL, USA, 25–30 March 2012; pp. 2731–2735. [Google Scholar]
- Clerckx, B.; Zhang, R.; Schober, R.; Ng, D.W.K.; Kim, D.I.; Poor, H.V. Fundamentals of wireless information and power transfer: From RF energy harvester models to signal and system designs. IEEE J. Sel. Areas Commun. 2019, 37, 4–33. [Google Scholar] [CrossRef]
- Bi, S.; Zeng, Y.; Zhang, R. Wireless powered communication networks: An overview. IEEE Wirel. Commun. 2016, 23, 10–18. [Google Scholar] [CrossRef]
- Zhang, R.; Ho, C.K. MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Trans. Wirel. Commun. 2013, 12, 1989–2001. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate–energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Nam, Y.H.; Debbah, M. A tutorial on UAVs for wireless networks: Applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 2019, 21, 2334–2360. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Energy-efficient data collection in UAV-enabled wireless sensor networks. IEEE Wirel. Commun. Lett. 2018, 7, 328–331. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Ye, H.-T.; Kang, X.; Joung, J.; Liang, Y.-C. Optimization for full-duplex rotary-wing UAV-enabled wireless-powered IoT networks. IEEE Trans. Wirel. Commun. 2020, 19, 5057–5072. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Xie, L.; Xu, J.; Zeng, Y. Common throughput maximization for UAV-enabled interference channel with wireless powered communications. IEEE Trans. Commun. 2020, 68, 3197–3212. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, J.; Huang, J.; Zhang, X.; So, D.K.C.; Wong, K.-K. Multi-objective optimization for UAV-assisted wireless powered IoT networks based on extended DDPG algorithm. IEEE Trans. Commun. 2021, 69, 6361–6373. [Google Scholar] [CrossRef]
- Wan, S.; Lu, J.; Fan, P.; Letaief, K.B. Toward big data processing in IoT: Path planning and resource management of UAV base stations in mobile-edge computing systems. IEEE Internet Things J. 2020, 7, 3555–3572. [Google Scholar] [CrossRef]
- Zhou, F.; Hu, R.Q.; Qian, Y. Wireless power transfer and data collection in wireless sensor networks. IEEE Internet Things J. 2020, 7, 14915–14927. [Google Scholar]
- Jin, K.; Zhou, W. Wireless Laser Power Transmission: A Review of Recent Progress. IEEE Trans. Power Electron. 2019, 34, 3842–3859. [Google Scholar] [CrossRef]
- Brown, W.C. The History of Wireless Power Transmission. Sol. Energy 1996, 56, 3–21. [Google Scholar] [CrossRef]
- Pahlavan, S.; Shooshtari, M.; Jafarabadi Ashtiani, S. Star-Shaped Coils in the Transmitter Array for Receiver Rotation Tolerance in Free-Moving Wireless Power Transfer Applications. Energies 2022, 15, 8643. [Google Scholar] [CrossRef]
- Lu, X.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Wireless Charging Technologies: Fundamentals, Standards, and Network Applications. IEEE Commun. Surv. Tutorials 2015, 18, 1413–1452. [Google Scholar] [CrossRef]
- Long, Y.; Zhao, S.; Gong, S.; Gu, B.; Niyato, D.; Shen, X.S. AoI-aware sensing scheduling and trajectory optimization for multi-UAV-assisted wireless backscatter networks. IEEE Trans. Veh. Technol. 2024, 73, 15440–15455. [Google Scholar] [CrossRef]
- Fathollahi, L.; Mohassel Feghhi, M.; Atashbar, M. Energy optimization for full-duplex wireless-powered IoT networks using rotary-wing UAV with multiple antennas. Comput. Commun. 2024, 215, 62–73. [Google Scholar] [CrossRef]
- Li, Y.; Ding, H.; Yang, Z.; Li, B.; Liang, Z. Integrated trajectory optimization for UAV-enabled wireless powered MEC system with joint energy consumption and AoI minimization. Comput. Netw. 2024, 254, 110842. [Google Scholar] [CrossRef]
- Liu, X.; Chai, Z.-Y.; Li, Y.-L.; Cheng, Y.-Y.; Zeng, Y. Multi-objective deep reinforcement learning for computation offloading in UAV-assisted multi-access edge computing. Inf. Sci. 2023, 642, 119154. [Google Scholar] [CrossRef]
- Pham, Q.-V.; Le, L.B.; Huynh, V.-N.; Fang, F.; Hwang, W.-J. UAV communications in 5G and beyond: Recent advances and future trends. IEEE Internet Things J. 2021, 8, 11664–11684. [Google Scholar]
- Liu, Y.; Zhang, S.; Cheng, N.; Shi, W.; Wang, J. Reinforcement learning-enhanced trajectory planning in UAV-enabled mobile edge computing. IEEE Trans. Veh. Technol. 2022, 71, 8770–8783. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Yang, Y.; Zhang, M.; Zhang, D.; Li, K. Deep reinforcement learning for task offloading in UAV-enabled edge computing networks. IEEE Internet Things J. 2020, 7, 11173–11185. [Google Scholar]
- Sun, Y.; Sun, H.; Ding, M.; Poor, H.V. Age-optimal trajectory planning for UAV-assisted data collection. IEEE Trans. Commun. 2021, 69, 6570–6585. [Google Scholar]
- Qu, Y.; Song, Y.; Zhang, H.; Cao, X.; Niyato, D. Multi-agent RL-based control for UAV swarm deployment in IoT coverage scenarios. Sensors 2021, 21, 460. [Google Scholar]
- Li, M.; Lin, Y.; Fu, X.; Zhao, J. Deep reinforcement learning-based trajectory optimization for UAV-aided data collection. IEEE Trans. Mob. Comput. 2021, 20, 2226–2239. [Google Scholar]
- Zeng, Y.; Zhang, R. Energy-efficient UAV communication with trajectory optimization. IEEE Trans. Wirel. Commun. 2017, 16, 3747–3760. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Kaelbling, L.P.; Littman, M.L.; Moore, A.W. Reinforcement learning: A survey. J. Artif. Intell. Res. 1996, 4, 237–285. [Google Scholar] [CrossRef]
- Watkins, C.J.C.H.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Konda, V.R.; Tsitsiklis, J.N. Actor–critic algorithms. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2000; pp. 1008–1014. [Google Scholar]
- Hu, H.; Xiong, K.; Qu, G.; Ni, Q.; Fan, P.; Ben Letaief, K. AoI-minimal trajectory planning and data collection in UAV-assisted wireless powered IoT networks. IEEE Internet Things J. 2021, 8, 1211–1223. [Google Scholar] [CrossRef]
- Wang, L.; Chen, M.; Sun, Y.; Zhang, R. UAV-aided wireless powered communication networks: Trajectory optimization and resource allocation for maximizing minimum throughput. IEEE Access 2019, 7, 134978–134991. [Google Scholar]
| Parameter | Value |
|---|---|
| Bandwidth (B) | 1 MHz |
| Noise power () | −90 dBm |
| Reference channel power gain () | −30 dB |
| Attenuation coefficient of NLoS link () | 0.2 |
| Path loss exponent () | 2.3 |
| Parameters of LoS probability (a, b) | 10, 0.6 |
| Blade profile power () | 79.86 |
| Induced power () | 88.63 |
| Tip speed of rotor blade () | 120 m/s |
| Mean rotor induced velocity in hover () | 4.03 |
| Fuselage drag ratio () | 0.6 |
| Air density () | 1.225 kg/m3 |
| Rotor solidity (s) | 0.05 |
| Rotor disc area (A) | 0.503 m2 |
| Maximum output DC power () | 9.079 W |
| Parameters of EH model (c, d) | 47,083, 2.9 W |
| Parameters | Values |
|---|---|
| Actor–Critic Network | |
| Network structure for actor | [400, 300] |
| Network structure for critic | [400, 300] |
| Number of training episodes | 1600 |
| Learning rate for actor | |
| Learning rate for critic | |
| Reward discount factor | 0.9 |
| Replay memory size | 8000 |
| Batch size | 64 |
| Initial exploration variance | 2.0 |
| Final exploration variance | 0.1 |
| Soft target update parameter | 0.001 |
| Weight Scheduler Network | |
| Hidden layer sizes | [64, 64] |
| Activation function | ReLU |
| Output dimension (weights) | 3 |
| Output activation | Softmax |
| Name | Parameters |
|---|---|
| optjoint | |
| optDC | |
| optEH | |
| optEC |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; He, J.; Zhao, M. Adaptive Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks. Information 2025, 16, 849. https://doi.org/10.3390/info16100849
Zhu X, He J, Zhao M. Adaptive Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks. Information. 2025; 16(10):849. https://doi.org/10.3390/info16100849
Chicago/Turabian StyleZhu, Xu, Junyu He, and Ming Zhao. 2025. "Adaptive Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks" Information 16, no. 10: 849. https://doi.org/10.3390/info16100849
APA StyleZhu, X., He, J., & Zhao, M. (2025). Adaptive Multi-Objective Optimization for UAV-Assisted Wireless Powered IoT Networks. Information, 16(10), 849. https://doi.org/10.3390/info16100849






