Efficient Algorithms for Range Mode Queries in the Big Data Era
Abstract
1. Introduction
1.1. Preliminaries
1.1.1. Notation
1.1.2. Related Work
1.1.3. Rank Space Reduction
| Algorithm 1 Randomized rank-space-reduction algorithm |
|
- uniq represents a selection from a set to {1,2, …,|D(k)|}.
- is the reduction of produced by applying uniq bijections to each element.
1.2. Applications of Range Mode Query in Various Fields
1.2.1. Big Data Analysis
1.2.2. Audit and Compliance
1.2.3. Economic Data Analysis
1.2.4. Healthcare
1.2.5. Retail and Marketing
1.2.6. Technology and AI
2. Background and Related Work
2.1. Role of Big Data Analytics in Internal Audit
2.2. Range Mode Queries in Identifying Anomalies for Internal Audit
2.3. Utilizing Range Mode Queries for Risk Assessment
2.4. Big Data and Range Mode Queries
2.5. RMQ Applications in the Big Data Era
2.6. Various Big Data Use Cases of RMQ
- Finding the Minimum Value in a Range
- Definition: Given an array A of n elements, preprocess A so that, for any given range , the minimum value can be found efficiently.
- Example: In stock price analysis, one might want to quickly determine the minimum stock price over a certain period.
- Mathematical Expression:
- Finding the Most Frequent Item in a Range
- Definition: Given an array A of n elements, preprocess A to efficiently find the most frequent item within any subarray .
- Example: In analyzing user behavior on a website, one might need to determine which page was visited most frequently within a certain timeframe.
- Mathematical Expression:
- Finding the Sum of Elements in a Range
- Definition: Preprocess the array A to quickly compute the sum of elements within any given subarray .
- Example: Summing up sales figures over a specified period.
- Mathematical Expression:
2.7. Detailed Use Case: Finding the Most Frequent Item in a Range
- Methodology
- Preprocessing:
- Construct a segment tree where each node stores the most frequent item and its count for the corresponding segment of the array.
- Time Complexity: for building the segment tree.
- Querying:
- For a given range , traverse the segment tree to combine results from relevant segments to determine the most frequent item in that range.
- Time Complexity: per query.
- Mathematical Explanation
- Define each node as , where “value” is the most frequent item in the segment represented by the node and “frequency” is its count.
- Merge function: When merging two nodes and ,
2.7.1. Data Preprocessing
- Firstly, this will take advantage of the RMQ algorithm to efficiently find out minimum values within specific ranges of data points. For example, when dealing with time series or geographical information datasets like temporal or spatial data, respectively, RMQ algorithms can find minimums and maximums very fast for predefined intervals [38]. This feature is useful when solving problems like trend analysis or anomaly detection where knowing differences within some ranges becomes necessary before making decisions about them [39].
- These also help in the cleaning of data and control of its quality during preprocessing. In certain ranges, these flags can be set by these algorithms to help check whether there are any issues with data quality [40]. For example, such robots may indicate faults or errors in measurements by the sensors as they assay readings from them.
- Additionally, RMQs participate in feature extraction and selection procedures [41]. Dimensionality reduction and focusing on the most significant attributes of data are common operations for many analytical tasks. As such, RMQs help find out the least values within some given feature ranges [42]. For example, this might include finding the darkest or brightest regions in an image that could be very important features for subsequent classification or segmentation stages in image processing.
- Normalization and scaling are supported in RMQ algorithms during preprocessing. These algorithms swiftly discover the minimum and maximum values across given ranges, which helps to normalize or scale data attributes [43]. This forms a basis for comparative purposes while maintaining the same range among the features and it is vital in normalizing the data before proceeding to any further analysis such as clustering or classification.
- In other words, RMQ algorithms enable the efficient identification of the minimum value within a specific data range thus making them essential tools for preprocessing big data analytics [44]. By ensuring that there is no compromise on either the quality or relevance of information manipulated by a given application, this step has contributed towards reducing the computational complexity associated with subsequent analysis tasks [45].
2.7.2. Time Series Analysis
2.7.3. Data Compression and Summarization
2.7.4. Parallel and Distributed Computing
3. Naive Algorithm
3.1. Variant One
| Algorithm 2 Naive Algorithm |
|
3.1.1. Memory Complexity Analysis
3.1.2. Time Complexity Analysis
3.2. Variant Two
Memory Complexity Analysis
4. Offline Algorithm
4.1. MultiMode Structure
- INSERT(x)—insert x into the multiset M;
- REMOVE(x)—remove x from the multiset M;
- QUERY()—return the dominant and its frequency.
| Algorithm 3 Insert Operation |
|
| Algorithm 4 Remove Operation |
|
| Algorithm 5 Query Operation |
|
4.1.1. Insert Operation
4.1.2. Remove Operation
4.1.3. Query Operation
4.1.4. Interval Transformation
| Algorithm 6 Interval transformation |
|
4.1.5. Alternative Implementation of MultiMode
4.1.6. Offline Queries
| Algorithm 7 Offline Query Algorithm |
|
4.1.7. Time Complexity Analysis
4.1.8. Memory Complexity Analysis
4.1.9. Implementation
5. KMS(s) Data Structure
- COUNT(x,i,j)—returns in time.
- QUERY(i,j)—returns the dominant and its frequency in the interval in time .
5.1. KMS(s) Structure Construction
5.2. Count Operation
| Algorithm 8 Operation Count |
|
5.3. Query Operation
| Algorithm 9 Query Operation |
|
5.4. Time Complexity Analysis
5.5. Operation Count
5.6. Operation Query
5.7. Memory Complexity Analysis
5.8. Selection of Parameter s
6. CDLMW(s) Data Structure
- COUNT(—Calculates in time . We assume that .
- QUERY()—Calculates the dominant and its frequency in time.
6.1. CDLMW(s) Structure Construction
6.2. Count Operation
| Algorithm 10 Count Operation |
|
6.3. Query Operation
| Algorithm 11 Query Operation |
|
- It lies within the range .
- It occurs at least times in the interval .
6.4. Computational Complexity Analysis
6.4.1. Construction
6.4.2. Count Operation
6.4.3. Query Operation
6.4.4. Memory Complexity Analysis
6.4.5. Count and Query Operations
7. CDLMW BP(s) Data Structure
- BCOUNT(—Calculates the dominant with the frequency of the intervalin time when .
- COUNT(—Calculates in time .We assume that .
- QUERY()—Calculates the dominant and its frequency over time .
7.1. Construction
7.2. RANK and SELECT Operations
7.3. BCount Operation
| Algorithm 12 Bcount Operation |
|
7.4. Count and Query Operations
7.5. Time Complexity Analysis
7.5.1. Construction
7.5.2. Bcount Operation
7.5.3. Count Operation
7.6. Query Operation
7.7. Memory Complexity Analysis
7.7.1. Construction
7.7.2. Bcount Operation
7.7.3. Count and Query Operations
7.8. Selection of Parameters
7.9. Implementation
7.9.1. RANK
7.9.2. SELECT
- The abbreviated sequence of sequence B has a 1 in the i-th position when any bit of the block is not feeding. Otherwise, = 0.
- The interrupting sequence of B has a 1 in the i-th position when -all 1 of B is the first one in the block containing it. Otherwise, = 0.
8. CDLMW SF Data Structure
8.1. Construction
8.2. Memory Complexity Analysis
8.3. Time Complexity Analysis
8.4. Implementation
9. CDLMW BP+SF Data Structure
9.1. Construction
Query Operation
| Algorithm 13 Query Operation |
|
9.2. Time Complexity Analysis
9.2.1. Construction
9.2.2. Query Operation
9.3. Memory Complexity Analysis
9.3.1. Construction
9.3.2. Query Operation
10. Proposed Methods
- When i mod t = 0, we keep the original target range.
- Otherwise, it is separated into two parts which are the prefix and the suffix .
| Algorithm 14 Precomputation of Array1 and Array2 |
|
Query Algorithm
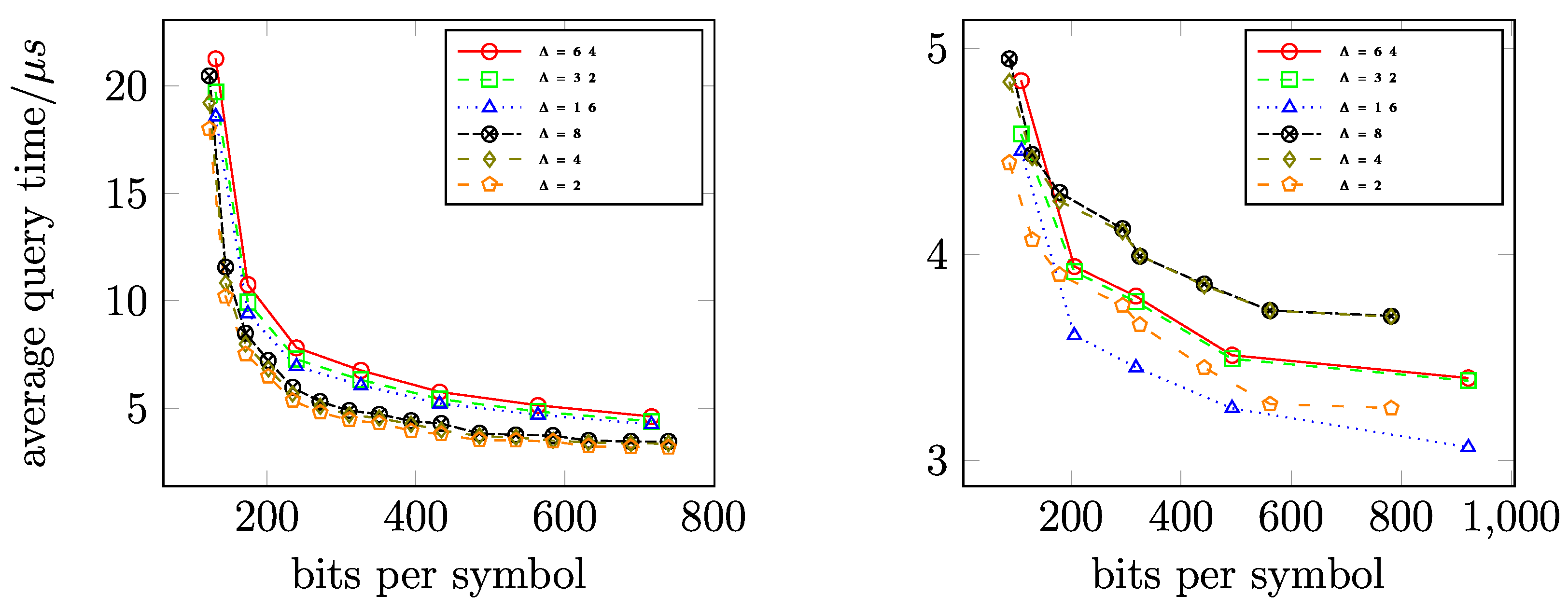
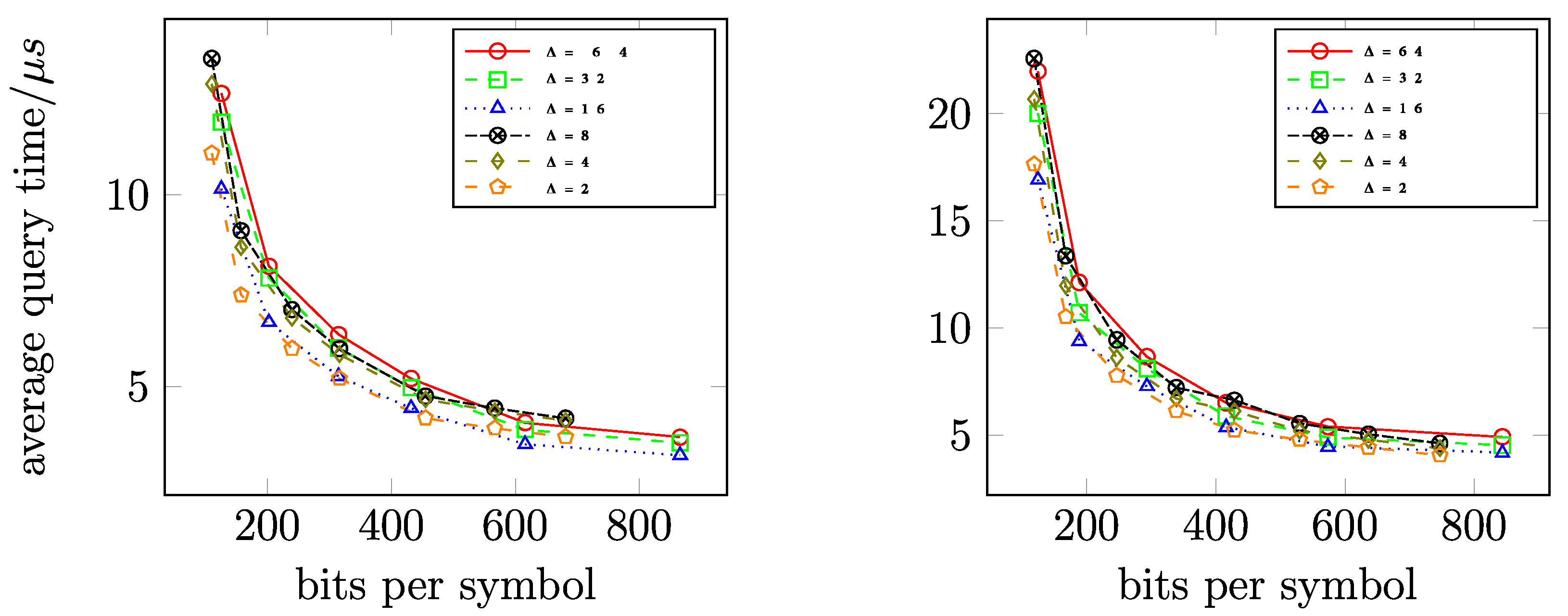
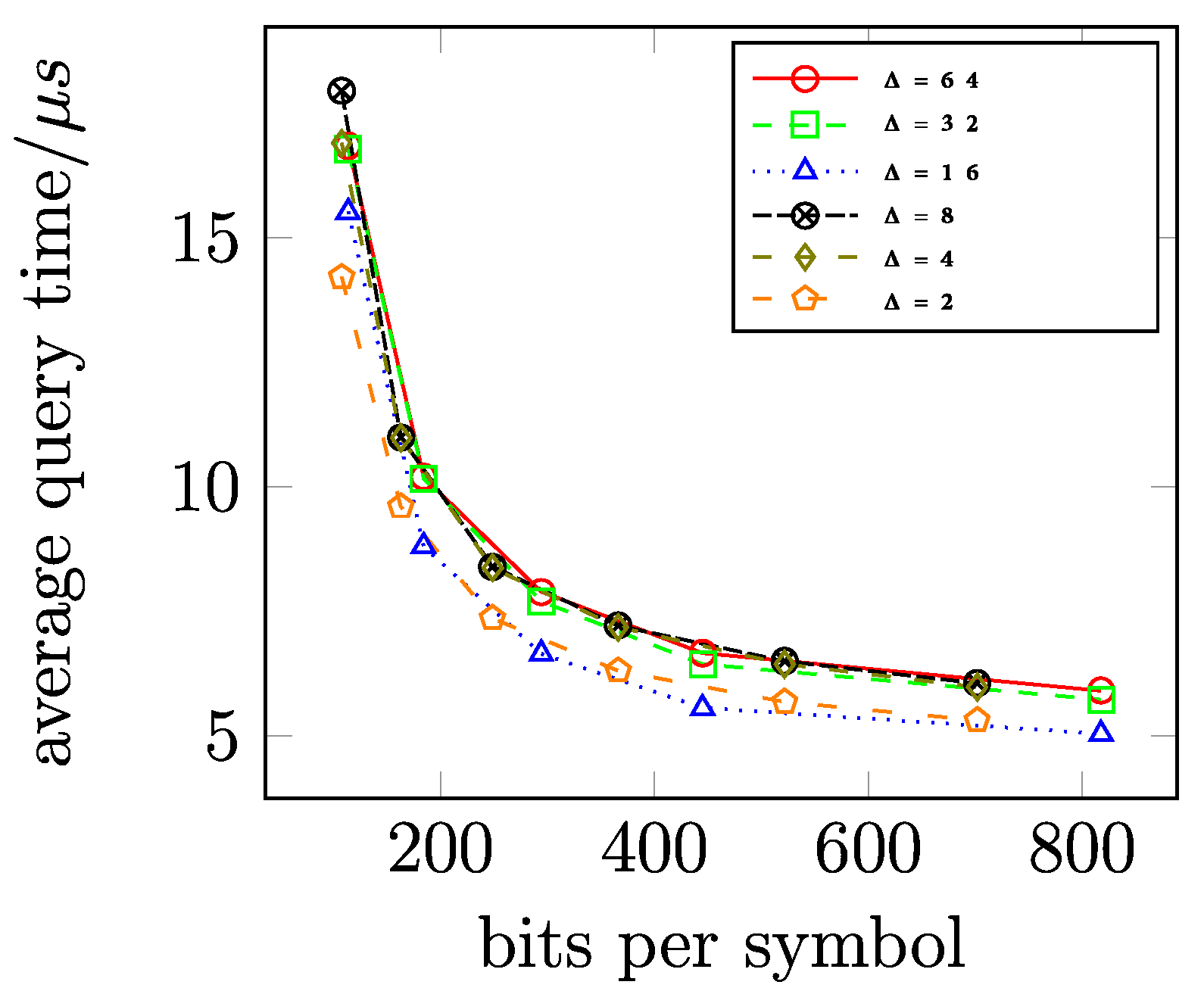
11. Experimental Results
11.1. Test Data and Queries
11.2. Naive Algorithm
11.2.1. Initialization Time
11.2.2. Query Time
11.3. Offline Algorithm
11.3.1. Initialization Time
11.3.2. Query Time
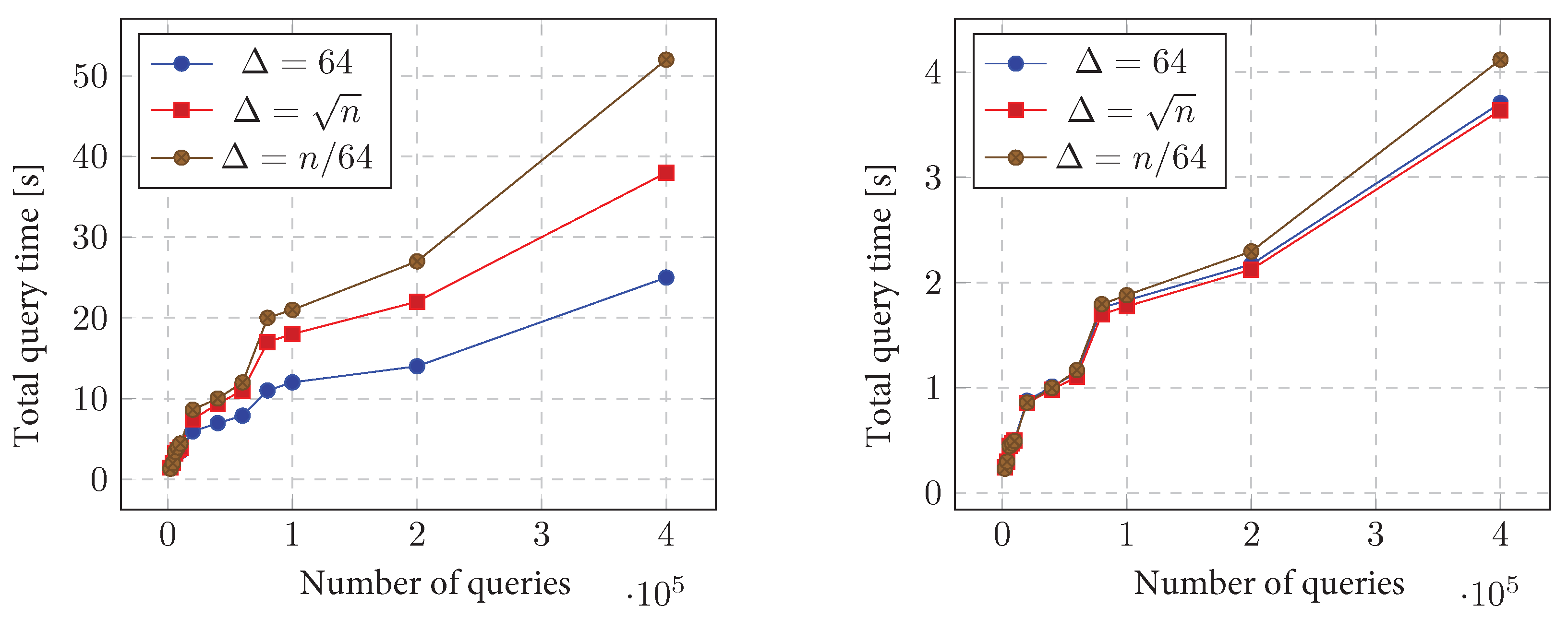
11.3.3. Query Time vs. Number of Queries
11.4. CDLMW and CDLMW BP Data Structures
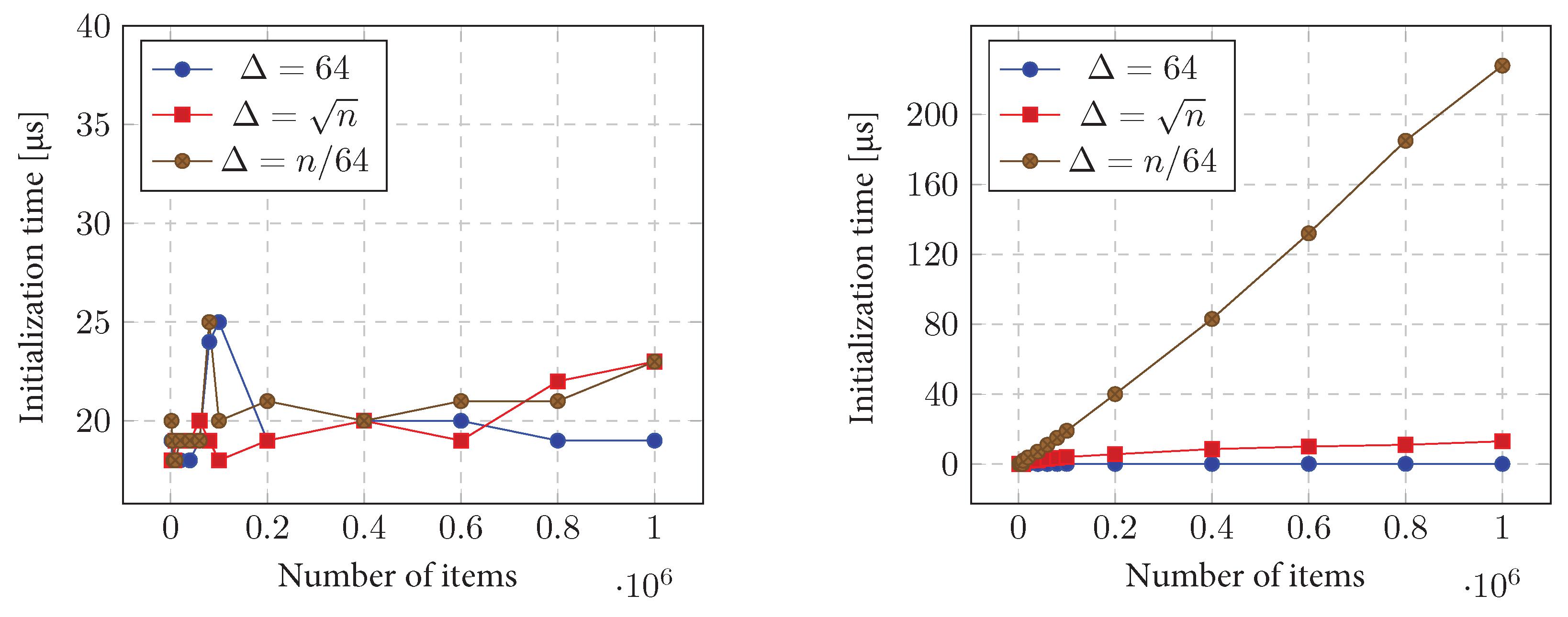
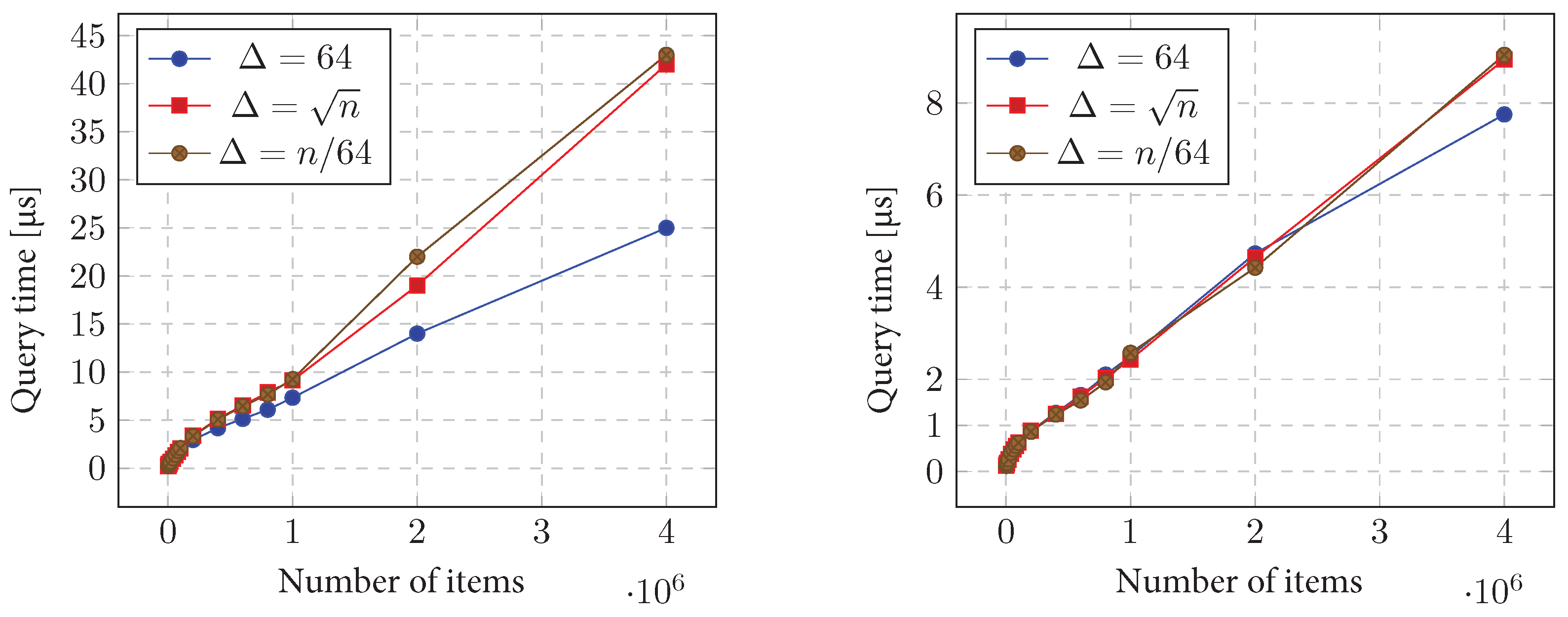
11.4.1. Initialization Time
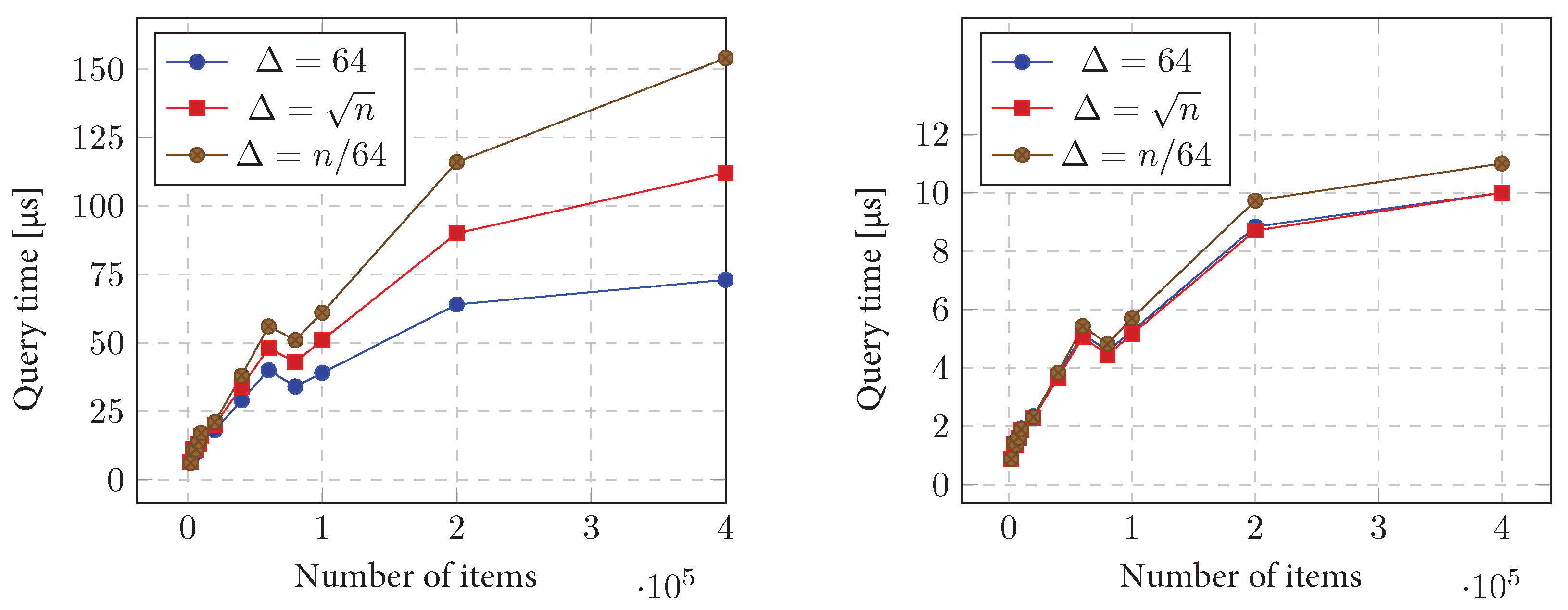
11.4.2. Query Time
11.5. CDLMW SF Data Structure
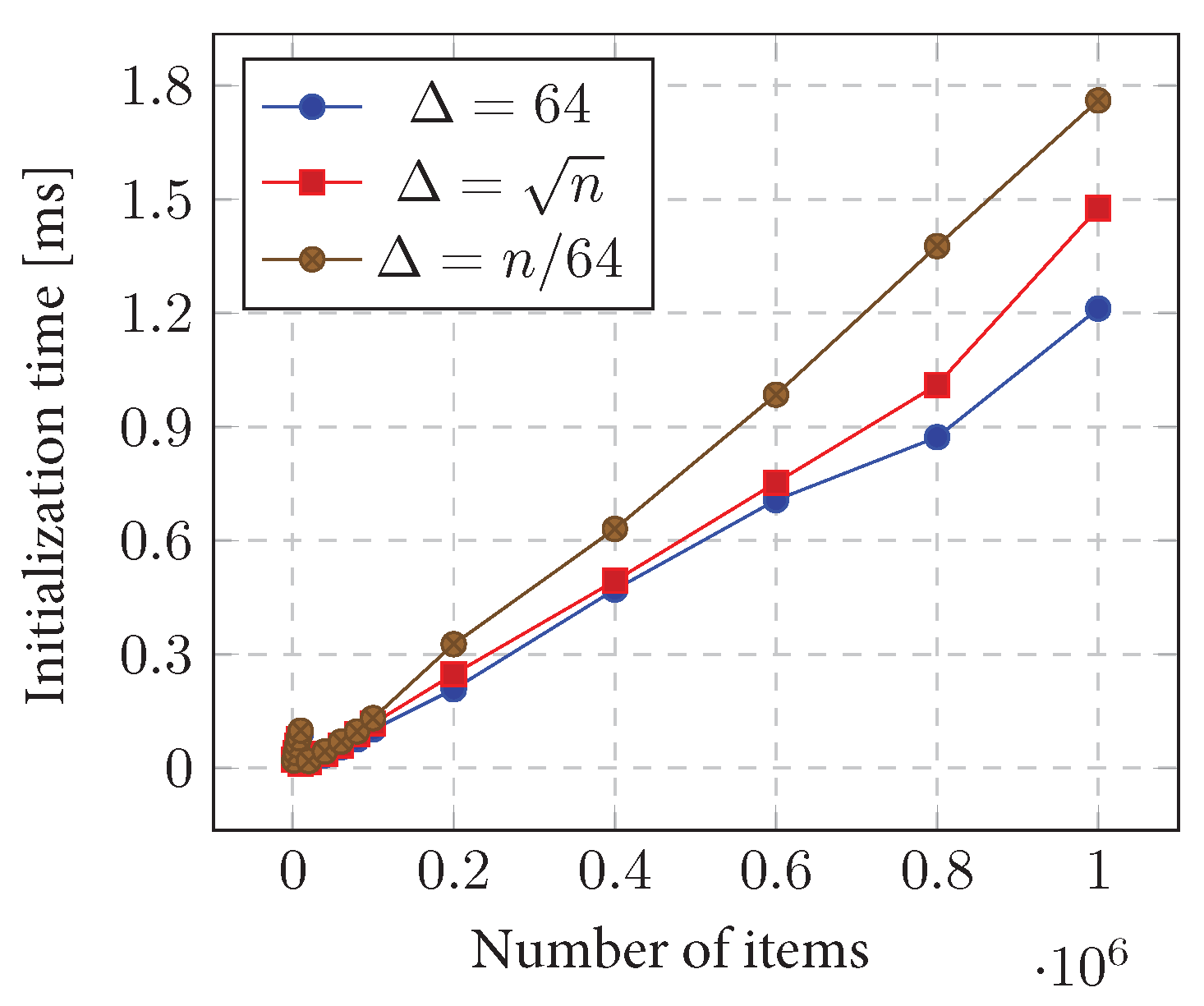
11.5.1. Initialization Time
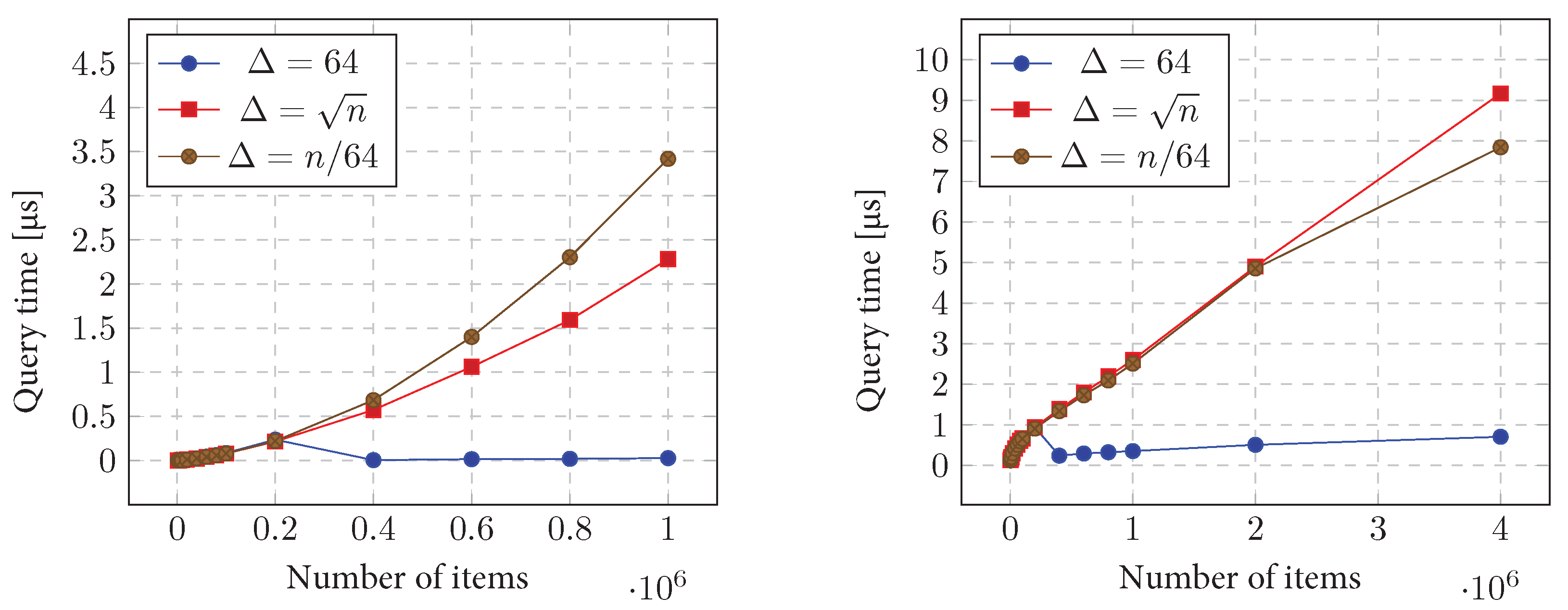
11.5.2. Query Time
11.6. CDLMW BP+SF Data Structure
Initialization and Query Time
11.7. Assessment of Size
12. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krizanc, D.; Morin, P.; Smid, M. Range mode and range median queries on lists and trees. Nord. J. Comput. 2005, 12, 1–17. [Google Scholar]
- Chan, T.M.; Durocher, S.; Larsen, K.G.; Morrison, J.; Wilkinson, B.T. Linear-space data structures for range mode query in arrays. Theory Comput. Syst. 2014, 55, 719–741. [Google Scholar] [CrossRef][Green Version]
- Durocher, S.; Morrison, J. Linear-space data structures for range mode query in arrays. arXiv 2011, arXiv:1101.4068. [Google Scholar]
- El-Zein, H.; He, M.; Munro, J.I.; Sandlund, B. Improved time and space bounds for dynamic range mode. arXiv 2018, arXiv:1807.03827. [Google Scholar]
- Petersen, H.; Grabowski, S. Range mode and range median queries in constant time and sub-quadratic space. Inf. Process. Lett. 2009, 109, 225–228. [Google Scholar] [CrossRef]
- Theodorakopoulos, L.; Antonopoulou, H.; Mamalougou, V.; Giotopoulos, K. The drivers of volume volatility: A big data analysis based on economic uncertainty measures for the Greek banking system. Banks Bank Syst. 2022, 17, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Rakipi, R.; De Santis, F.; D’Onza, G. Correlates of the internal audit function’s use of data analytics in the big data era: Global evidence. J. Int. Account. Audit. Tax. 2021, 42, 100357. [Google Scholar] [CrossRef]
- Álvarez-Foronda, R.; De-Pablos-Heredero, C.; Rodríguez-Sánchez, J.L. Implementation model of data analytics as a tool for improving internal audit processes. Front. Psychol. 2023, 14, 1140972. [Google Scholar] [CrossRef]
- Tang, F.; Norman, C.S.; Vendrzyk, V.P. Exploring perceptions of data analytics in the internal audit function. Behav. Inf. Technol. 2017, 36, 1125–1136. [Google Scholar] [CrossRef]
- Shabani, N.; Munir, A.; Mohanty, S.P. A Study of Big Data Analytics in Internal Auditing. In Intelligent Systems and Applications, Proceedings of the 2021 Intelligent Systems Conference (IntelliSys), Virtual, 2–3 September 2021; Springer: Cham, Switzerland, 2022; Volume 2, pp. 362–374. [Google Scholar]
- De Santis, F.; D’Onza, G. Big data and data analytics in auditing: In search of legitimacy. Meditari Account. Res. 2021, 29, 1088–1112. [Google Scholar] [CrossRef]
- Alrashidi, M.; Almutairi, A.; Zraqat, O. The impact of big data analytics on audit procedures: Evidence from the Middle East. J. Asian Financ. Econ. Bus. 2022, 9, 93–102. [Google Scholar]
- Sihem, B.; Ahmed, B.; Alzoubi, H.M.; Almansour, B.Y. Effect of Big Data Analytics on Internal Audit Case: Credit Suisse. In Proceedings of the 2023 International Conference on Business Analytics for Technology and Security (ICBATS), Dubai, United Arab Emirates, 7–8 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–11. [Google Scholar]
- Popara, J.; Savkovic, M.; Lalic, D.C.; Lalic, B. Application of Digital Tools, Data Analytics and Machine Learning in Internal Audit. In Proceedings of the IFIP International Conference on Advances in Production Management Systems, Trondheim, Norway, 17–21 September; Springer: Cham, Switzerland, 2023; pp. 357–371. [Google Scholar]
- Tanuska, P.; Spendla, L.; Kebisek, M.; Duris, R.; Stremy, M. Smart anomaly detection and prediction for assembly process maintenance in compliance with industry 4.0. Sensors 2021, 21, 2376. [Google Scholar] [CrossRef]
- Sayedahmed, N.; Anwar, S.; Shukla, V.K. Big Data Analytics and Internal Auditing: A Review. In Proceedings of the 2022 3rd International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 15–17 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Si, Y. Construction and application of enterprise internal audit data analysis model based on decision tree algorithm. Discret. Dyn. Nat. Soc. 2022, 2022, 4892046. [Google Scholar] [CrossRef]
- Bu, S.J.; Cho, S.B. A convolutional neural-based learning classifier system for detecting database intrusion via insider attack. Inf. Sci. 2020, 512, 123–136. [Google Scholar] [CrossRef]
- Yusupdjanovich, Y.S.; Rajaboevich, G.S. Improvement the schemes and models of detecting network traffic anomalies on computer systems. In Proceedings of the 2020 IEEE 14th International Conference on Application of Information and Communication Technologies (AICT), Tashkent, Uzbekistan, 7–9 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Hegde, J.; Rokseth, B. Applications of machine learning methods for engineering risk assessment—A review. Saf. Sci. 2020, 122, 104492. [Google Scholar] [CrossRef]
- Putra, I.; Sulistiyo, U.; Diah, E.; Rahayu, S.; Hidayat, S. The influence of internal audit, risk management, whistleblowing system and big data analytics on the financial crime behavior prevention. Cogent Econ. Financ. 2022, 10, 2148363. [Google Scholar] [CrossRef]
- Liu, H.C.; Chen, X.Q.; You, J.X.; Li, Z. A new integrated approach for risk evaluation and classification with dynamic expert weights. IEEE Trans. Reliab. 2020, 70, 163–174. [Google Scholar] [CrossRef]
- Turetken, O.; Jethefer, S.; Ozkan, B. Internal audit effectiveness: Operationalization and influencing factors. Manag. Audit. J. 2020, 35, 238–271. [Google Scholar] [CrossRef]
- Alazzabi, W.Y.E.; Mustafa, H.; Karage, A.I. Risk management, top management support, internal audit activities and fraud mitigation. J. Financ. Crime 2023, 30, 569–582. [Google Scholar] [CrossRef]
- Hou, W.-H.; Wang, X.-K.; Zhang, H.-Y.; Wang, J.-Q.; Li, L. A novel dynamic ensemble selection classifier for an imbalanced data set: An application for credit risk assessment. Knowl.-Based Syst. 2020, 208, 106462. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C.; Zhang, J.; Zhong, R. Big data analytics for intelligent manufacturing systems: A review. J. Manuf. Syst. 2022, 62, 738–752. [Google Scholar] [CrossRef]
- Zheng, Y.; Lu, R.; Guan, Y.; Shao, J.; Zhu, H. Efficient and privacy-preserving similarity range query over encrypted time series data. IEEE Trans. Dependable Secur. Comput. 2021, 19, 2501–2516. [Google Scholar] [CrossRef]
- Müller, I.; Fourny, G.; Irimescu, S.; Berker Cikis, C.; Alonso, G. Rumble: Data independence for large messy data sets. Proc. VLDB Endow. 2020, 14, 498–506. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Huang, J.Z.; Salloum, S.; Emara, T.Z.; Sadatdiynov, K. A survey of data partitioning and sampling methods to support big data analysis. Big Data Min. Anal. 2020, 3, 85–101. [Google Scholar] [CrossRef]
- Karras, A.; Karras, C.; Samoladas, D.; Giotopoulos, K.C.; Sioutas, S. Query optimization in NoSQL databases using an enhanced localized R-tree index. In Proceedings of the International Conference on Information Integration and Web, Virtual, 28–30 November 2022; Springer: Cham, Switzerland, 2022; pp. 391–398. [Google Scholar]
- Karras, A.; Karras, C.; Pervanas, A.; Sioutas, S.; Zaroliagis, C. SQL query optimization in distributed nosql databases for cloud-based applications. In Proceedings of the International Symposium on Algorithmic Aspects of Cloud Computing, Potsdam, Germany, 5–6 September 2022; Springer: Cham, Switzerland, 2022; pp. 21–41. [Google Scholar]
- Karras, C.; Karras, A.; Theodorakopoulos, L.; Giannoukou, I.; Sioutas, S. Expanding queries with maximum likelihood estimators and language models. In Proceedings of the International Conference on Innovations in Computing Research, Athens, Greece, 29–31 August 2022; Springer: Cham, Switzerland, 2022; pp. 201–213. [Google Scholar]
- Karras, A.; Karras, C.; Schizas, N.; Avlonitis, M.; Sioutas, S. Automl with bayesian optimizations for big data management. Information 2023, 14, 223. [Google Scholar] [CrossRef]
- Theodorakopoulos, L.; Theodoropoulou, A.; Stamatiou, Y. A State-of-the-Art Review in Big Data Management Engineering: Real-Life Case Studies, Challenges, and Future Research Directions. Eng 2024, 5, 1266–1297. [Google Scholar] [CrossRef]
- Samoladas, D.; Karras, C.; Karras, A.; Theodorakopoulos, L.; Sioutas, S. Tree Data Structures and Efficient Indexing Techniques for Big Data Management: A Comprehensive Study. In Proceedings of the 26th Pan-Hellenic Conference on Informatics, Athens, Greece, 25–27 November 2022; pp. 123–132. [Google Scholar]
- Luengo, J.; García-Gil, D.; Ramírez-Gallego, S.; García, S.; Herrera, F. Big Data Preprocessing; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Rahman, A. Statistics-based data preprocessing methods and machine learning algorithms for big data analysis. Int. J. Artif. Intell. 2019, 17, 44–65. [Google Scholar]
- Asadi, R.; Regan, A. Clustering of time series data with prior geographical information. arXiv 2021, arXiv:2107.01310. [Google Scholar]
- Raja, R.; Sharma, P.C.; Mahmood, M.R.; Saini, D.K. Analysis of anomaly detection in surveillance video: Recent trends and future vision. Multimed. Tools Appl. 2023, 82, 12635–12651. [Google Scholar] [CrossRef]
- Liu, J.; Li, J.; Li, W.; Wu, J. Rethinking big data: A review on the data quality and usage issues. ISPRS J. Photogramm. Remote Sens. 2016, 115, 134–142. [Google Scholar] [CrossRef]
- Mendes, A.; Togelius, J.; Coelho, L.d.S. Multi-stage transfer learning with an application to selection process. arXiv 2020, arXiv:2006.01276. [Google Scholar]
- Akingboye, A.S. RQD modeling using statistical-assisted SRT with compensated ERT methods: Correlations between borehole-based and SRT-based RMQ models. Phys. Chem. Earth Parts A/B/C 2023, 131, 103421. [Google Scholar] [CrossRef]
- Pena, J.C.; Nápoles, G.; Salgueiro, Y. Normalization method for quantitative and qualitative attributes in multiple attribute decision-making problems. Expert Syst. Appl. 2022, 198, 116821. [Google Scholar] [CrossRef]
- García, S.; Ramírez-Gallego, S.; Luengo, J.; Benítez, J.M.; Herrera, F. Big data preprocessing: Methods and prospects. Big Data Anal. 2016, 1, 9. [Google Scholar] [CrossRef]
- Hatala, M.; Nazeri, S.; Kia, F.S. Progression of students’ SRL processes in subsequent programming problem-solving tasks and its association with tasks outcomes. Internet High. Educ. 2023, 56, 100881. [Google Scholar] [CrossRef]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 2020. [Google Scholar]
- McWalter, T.A.; Rudd, R.; Kienitz, J.; Platen, E. Recursive marginal quantization of higher-order schemes. Quant. Financ. 2018, 18, 693–706. [Google Scholar] [CrossRef]
- Rudd, R.; McWalter, T.A.; Kienitz, J.; Platen, E. Robust product Markovian quantization. arXiv 2020, arXiv:2006.15823. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ahmed, M. Data summarization: A survey. Knowl. Inf. Syst. 2019, 58, 249–273. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, M.; Gao, L.; Jin, Y.; Du, L.; Zhao, H.; Zhang, H.; Haffari, G. Summpip: Unsupervised multi-document summarization with sentence graph compression. In Proceedings of the 43rd International ACM Sigir Conference on Research and Development in Information Retrieval, Xi’an, China, 25–30 July 2020; pp. 1949–1952. [Google Scholar]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- Jo, S.; Mozes, S.; Weimann, O. Compressed range minimum queries. In Proceedings of the International Symposium on String Processing and Information Retrieval, Lima, Peru, 9–11 October 2018; Springer: Cham, Switzerland, 2018; pp. 206–217. [Google Scholar]
- Wang, J.; Ma, Q. Numerical techniques on improving computational efficiency of spectral boundary integral method. Int. J. Numer. Methods Eng. 2015, 102, 1638–1669. [Google Scholar] [CrossRef]
- Oussous, A.; Benjelloun, F.Z.; Lahcen, A.A.; Belfkih, S. Big Data technologies: A survey. J. King Saud Univ.-Comput. Inf. Sci. 2018, 30, 431–448. [Google Scholar] [CrossRef]
- Zhao, Z.; Min, G.; Gao, W.; Wu, Y.; Duan, H.; Ni, Q. Deploying edge computing nodes for large-scale IoT: A diversity aware approach. IEEE Internet Things J. 2018, 5, 3606–3614. [Google Scholar] [CrossRef]
- Wang, S.; Sheng, H.; Yang, D.; Zhang, Y.; Wu, Y.; Wang, S. Extendable multiple nodes recurrent tracking framework with RTU++. IEEE Trans. Image Process. 2022, 31, 5257–5271. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.-l.; Cheng, H.; Zuo, T.-s.; Jiao, G.-s.; Han, Z.-h.; Qin, H. NeuDATool: An open source neutron data analysis tools, supporting GPU hardware acceleration, and across-computer cluster nodes parallel. Chin. J. Chem. Phys. 2020, 33, 727–732. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, J. Data transmission and management based on node communication in opportunistic social networks. Symmetry 2020, 12, 1288. [Google Scholar] [CrossRef]
- Nietert, S.; Goldfeld, Z.; Sadhu, R.; Kato, K. Statistical, robustness, and computational guarantees for sliced wasserstein distances. Adv. Neural Inf. Process. Syst. 2022, 35, 28179–28193. [Google Scholar]
- Günther, W.A.; Mehrizi, M.H.R.; Huysman, M.; Feldberg, F. Debating big data: A literature review on realizing value from big data. J. Strateg. Inf. Syst. 2017, 26, 191–209. [Google Scholar] [CrossRef]
- Jacobson, G. Space-efficient static trees and graphs. In Proceedings of the 30th Annual Symposium on Foundations of Computer Science, Raleigh, NC, USA, 30 October–1 November 1989; IEEE Computer Society: Washington, DC, USA, 1989; pp. 549–554. [Google Scholar]
- Clark, D.R.; Munro, J.I. Efficient suffix trees on secondary storage. In Proceedings of the Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, Atlanta, Georgia, 28–30 January 1996; pp. 383–391. [Google Scholar]
- Raman, R.; Raman, V.; Satti, S.R. Succinct indexable dictionaries with applications to encoding k-ary trees, prefix sums and multisets. ACM Trans. Algorithms (TALG) 2007, 3, 43-es. [Google Scholar] [CrossRef]
- Na, J.C.; Kim, J.E.; Park, K.; Kim, D.K. Fast computation of rank and select functions for succinct representation. IEICE Trans. Inf. Syst. 2009, 92, 2025–2033. [Google Scholar] [CrossRef]
- Vigna, S. Broadword implementation of rank/select queries. In Proceedings of the International Workshop on Experimental and Efficient Algorithms, Provincetown, MA, USA, 30 May–1 June 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 154–168. [Google Scholar]
- Baatwah, S.R.; Aljaaidi, K.S. Dataset for audit dimensions in an emerging market: Developing a panel database of audit effectiveness and efficiency. Data Brief 2021, 36, 107061. [Google Scholar] [CrossRef]

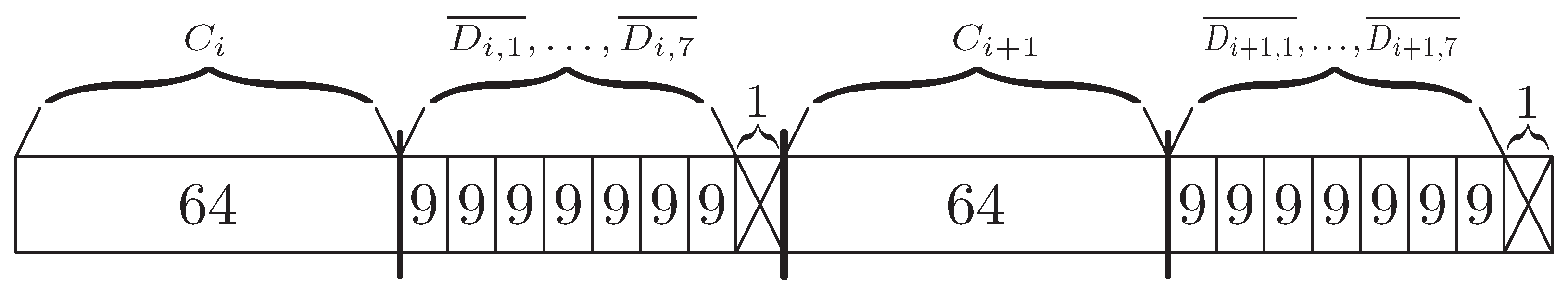
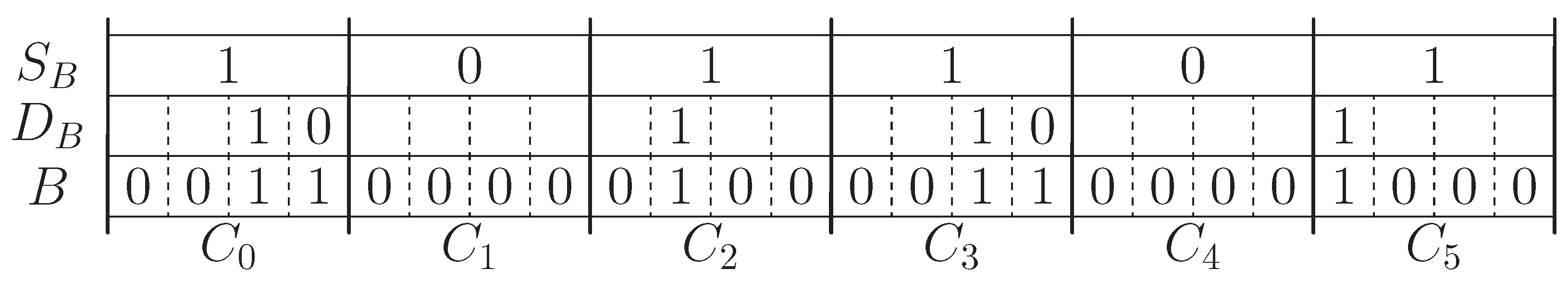




| Reference | Query Time | Update Time | Space | Type |
|---|---|---|---|---|
| [4] | Dynamic | |||
| [2] | Dynamic | |||
| [2] | Dynamic | |||
| [2] | − | − | ||
| [3] | − | |||
| [3] | − | − | ||
| [3] | − | − | ||
| [3] | − | − | ||
| [5] | − | − | ||
| [5] | − | |||
| [5] | − | − | ||
| [5] | − | − | ||
| [1] | − |
| Operating system | Windows 11 |
| Kernel version | 22H2 |
| Processor | Intel i9-10850k CPU @ |
| Cache L1/L2/L3 | // |
| Cache patency | 5 |
| Processor extensions used | AVX512VL, MBI2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karras, C.; Theodorakopoulos, L.; Karras, A.; Krimpas, G.A. Efficient Algorithms for Range Mode Queries in the Big Data Era. Information 2024, 15, 450. https://doi.org/10.3390/info15080450
Karras C, Theodorakopoulos L, Karras A, Krimpas GA. Efficient Algorithms for Range Mode Queries in the Big Data Era. Information. 2024; 15(8):450. https://doi.org/10.3390/info15080450
Chicago/Turabian StyleKarras, Christos, Leonidas Theodorakopoulos, Aristeidis Karras, and George A. Krimpas. 2024. "Efficient Algorithms for Range Mode Queries in the Big Data Era" Information 15, no. 8: 450. https://doi.org/10.3390/info15080450
APA StyleKarras, C., Theodorakopoulos, L., Karras, A., & Krimpas, G. A. (2024). Efficient Algorithms for Range Mode Queries in the Big Data Era. Information, 15(8), 450. https://doi.org/10.3390/info15080450








