Optimizing Energy Efficiency in Opportunistic Networks: A Heuristic Approach to Adaptive Cluster-Based Routing Protocol

Abstract

Opportunistic Networks (OppNets) are characterized by intermittently connected nodes with fluctuating performance. Their dynamic topology, caused by node movement, activation, and deactivation, often relies on controlled flooding for routing, leading to significant resource consumption and network congestion. To address this challenge, we propose the Adaptive Clustering-based Routing Protocol (ACRP). This ACRP protocol uses the common member-based adaptive dynamic clustering approach to produce optimal clusters, and the OppNet is converted into a TCP/IP network. This protocol adaptively creates dynamic clusters in order to facilitate the routing by converting the network from a disjointed to a connected network. This strategy creates a persistent connection between nodes, resulting in more effective routing and enhanced network performance. It should be noted that ACRP is scalable and applicable to a variety of applications and scenarios, including smart cities, disaster management, military networks, and distant places with inadequate infrastructure. Simulation findings demonstrate that the ACRP protocol outperforms alternative clustering approaches such as kRop, QoS-OLSR, LBC, and CBVRP. The analysis of the ACRP approach reveals that it can boost packet delivery by 28% and improve average end-to-end, throughput, hop count, and reachability metrics by 42%, 45%, 44%, and 80%, respectively.

1. Introduction

The concept of smart cities revolves around merging information communication technologies (ICTs) with the Internet of Things (IoT) to achieve efficient urban resource management [1]. Integrating intelligent vehicles into these frameworks has the potential to improve safety, traffic flow, and environmental sustainability within cities [2]. Wireless technologies have enabled communication systems based on vehicles, leading to the development of Vehicular Ad Hoc Networks (VANETs). VANETs, a subset of Mobile Ad Hoc Networks (MANETs), are characterized by highly dynamic network connectivity and frequent topology changes due to vehicle movement [3,4]. VANETs play a crucial role in enhancing safety and traffic conditions through Intelligent Transport Systems (ITSs), marking a significant advancement in transportation management [5]. However, the dynamic nature of VANETs often results in a dispersed network structure, leading to intermittent connectivity and forming an opportunistic network [6]. Consequently, VANETs face challenges such as high node mobility, frequent disconnections, and significant end-to-end delays.

Delay-Tolerant Networking (DTN) is a network paradigm specifically designed to facilitate communication in environments where continuous end-to-end connectivity is unreliable or unavailable [7]. Unlike traditional networks that rely on stable connections, DTNs operate in scenarios with intermittent connectivity, common in rural areas, disaster zones, or space missions. Data transmission in DTNs is opportunistic, utilizing store-and-forward techniques where nodes store messages and forward them to other nodes when direct communication is not possible. DTNs offer a solution to the challenges mentioned earlier for VANETs by being specifically designed to manage prolonged and unpredictable delays in delivering messages. Within DTNs, messages are relayed through intermediary nodes in a step-by-step fashion, leveraging intermittent connections to eventually reach their intended destination [7]. Opportunistic Networks (OppNets), a subset of DTNs, emphasize the sporadic nature of communication, where nodes exploit encounters with other nodes to exchange data. OppNet protocols commonly employ store-carry-forward techniques, where nodes store messages in their buffers and relay them to other nodes when suitable opportunities arise [8] (see Figure 1). However, the limitations of supporting TCP/IP routing protocols in DTNs due to frequent disconnections and network fragmentation pose significant challenges. DTN routing protocols, although robust in highly partitioned environments, typically result in higher delays, lower delivery ratios, and increased overhead, as they rely on store-and-forward mechanisms and opportunistic forwarding [9]. To overcome these challenges and leverage the well-established efficiencies of TCP/IP protocols, the conversion of the DTN into a more connected network structure can be achieved by implementing a cluster-based routing protocol within the DTN. The core idea is to dynamically group nodes into clusters based on their connectivity and proximity. Cluster heads (CHs) are then responsible for relaying traffic within their clusters, and clusters can communicate with each other during periods of temporary network stability. This enables reliable end-to-end communication required for TCP/IP protocols [10]. This approach represents a significant enhancement in DTNs to address the practical challenges of operating in highly dynamic and disrupted environments. Nevertheless, there remain several hurdles to overcome, including the selection of cluster heads, dynamic network conditions, limited network awareness, and scalability [11].

Overcoming the aforementioned challenges necessitates the development of sophisticated, adaptive clustering routing protocols that can dynamically adjust to network conditions and minimize the end-to-end path between source and destination nodes [12]. This paper proposes a novel cluster-centric routing protocol that establishes network connectivity through dynamic clustering. This method adapts cluster configuration based on shared nodes between clusters. Additionally, a heuristic function extends the radio range of the cluster head, effectively transforming a fragmented network into an ad hoc network. As a result, our proposed protocol offers significant performance improvements for OppNets, making it a compelling solution for managing transportation routes and determining optimal paths between source and destination nodes. This paper presents the following key contributions:

• Adaptive Clustering with Extended Radio Range: We propose an adaptive clustering method that leverages a new heuristic function to increase the cluster head’s radio range, thus enhancing network efficiency. This approach allows the OppNet to function similarly to a TCP/IP network, making it suitable for dynamic network topologies.
• Infrastructure-Independent Clustering for Efficient Routing: We introduce a novel common member constraint-based routing algorithm for clustering. This algorithm facilitates the creation of optimal clusters, enabling faster data transmission and shorter paths between source and destination nodes. Notably, this technique eliminates reliance on network infrastructure like roadside units (RSUs), which can introduce delays and routing inefficiencies.
• Demonstrated Performance Improvement: We present a method that achieves significant improvements across various performance metrics, including delivery ratio (approximately 28% increase), end-to-end delay (approximately 42% decrease), throughput (approximately 45% increase), hop count (approximately 44% decrease), and reachability (approximately 80% increase).

2. Related Work

Sharma et al. [13] introduce k-Means clustering-based routing protocol for opportunistic networks (kROp), a routing protocol for DTNs that leverages k-means clustering. It utilizes network features like contact duration, frequency, buffer occupancy, and delivery predictability for next-hop selection, and whereas kROp demonstrates improvements over other protocols in terms of dropped packets, overhead, and average hop count, its effectiveness might be limited in scenarios with low node mobility due to its assumptions about cluster creation and maintenance. Location-Based Clustering Approach for Next-Hop Selection in Opportunistic Networks (LBC), presented in [14] by Dutta et al., identifies cluster points based on human interaction patterns, achieving lower latency compared to existing protocols. However, LBC may incur higher energy consumption due to frequent location updates and cluster computations. Chaurasia et al. [15] introduce Metaheuristic-Based Optimized Opportunistic Routing Protocol (MOORP), a routing protocol designed for Wireless Sensor Networks (WSNs) that utilizes a metaheuristic approach combined with opportunistic routing strategies. MOORP focuses on optimizing data transmission efficiency and reducing energy consumption by selecting optimal forwarder nodes and routes, and whereas it shows potential for DTNs, its complexity and scalability limitations require careful consideration during implementation in resource-constrained DTN environments. The study by Saravankumar et al. [16] presents a novel routing protocol for wireless mobile networks that employs a cluster-based approach with innovative techniques to improve coverage delay performance. It utilizes a sophisticated algorithm considering factors like residual energy, node mobility, and distance to optimize cluster head selection. Additionally, a fuzzy logic system adjusts node transmission power based on network conditions. However, the protocol lacks clear explanations on how the DTN technique integrates with the clustering algorithm, and it also lacks validation through real-world experiments or testbeds, limiting its applicability to DTNs. Kadadha et al. [17] propose a cluster-based, QoS-optimized OLSR protocol for urban VANETs. The protocol incorporates cluster formation, cluster head election, and QoS-aware routing, prioritizing metrics like bandwidth, delay, and packet loss for path selection. However, it lacks an analytical model or theoretical proof for the protocol’s effectiveness, hindering its wider adoption in DTNs. Cheng et al. [18] introduce a novel model for clustering and routing VANETs in urban environments. This model comprises two key components: a connectivity prediction method (CP) and a dynamic clustering model (DC). CP forecasts connectivity based on vehicle features, whereas DC forms clusters and selects core nodes as cluster heads, adapting to network changes. This method also includes a routing approach based on DC. However, this approach may introduce overhead and complexity due to prediction and clustering processes, potentially impacting its suitability for resource-constrained DTNs. A clustering-based routing method for vehicular networks called CRLLR is introduced in [19] by Fakhar et al. Utilizing Ant Colony Optimization (ACO), CRLLR aims to determine optimal routes between communicating vehicles, emphasizing four quality of service (QoS) metrics: reliability, end-to-end latency, throughput, and energy consumption. Although showing potential in delivering dependable and low-latency routing, further research is needed to evaluate its performance in real-world DTN scenarios and compare it with other advanced routing schemes. It is important to assess how CRLLR’s reliance on ACO translates to the more intermittent connectivity patterns of DTNs compared to VANETs. Pal et al. [20] introduced the AMRBC, a MAC protocol for VANETs, focusing on stable clustering and communication range to improve network stability. AMRBC offers an adaptive, range-based MAC protocol tailored for VANETs, prioritizing safety messages to reduce safety message delay. However, its applicability to DTNs is limited as it primarily focuses on VANET-specific challenges and lacks comparison with other state-of-the-art MAC protocols designed for DTNs. The work by Mohammad Nasr et al. [21] introduces CBVRP, a cluster-based VANET routing protocol tailored for non-populated areas like deserts. CBVRP achieves high communication efficiency and reliable information delivery by implementing a cluster structure and cluster head election suitable for desert environments. However, its effectiveness may be limited to specific network conditions with sparse node distribution. Its performance in more dynamic or dense DTN environments might require further investigation. Feyzi et al. [22] introduced fuzzy logic into the Ad Hoc On-Demand Distance Vector Routing AODV routing protocol for VANETs to enhance route selection. This integration enables more flexible decision-making by considering factors like vehicle speed, distance, and traffic conditions. Fuzzy logic facilitates stable route selection, enhancing network efficiency. However, implementing the fuzzy system may demand additional computational resources, potentially increasing overhead; whereas this approach focuses on VANETs, it highlights the potential benefits of incorporating fuzzy logic for dynamic routing decisions in DTNs. However, the trade-off between routing efficiency and overhead requires careful consideration in resource-constrained DTN environments.

This section reviewed various cluster-based routing protocols proposed for DTNs or related network types, and these studies offer valuable insights and techniques. However, limitations exist, including scalability concerns, increased overhead due to complex clustering algorithms, and challenges in achieving high delivery ratios and low end-to-end delays inherent to DTNs. Our proposed Adaptive Clustering-based Routing Protocol (ACRP) addresses these shortcomings by focusing on dynamic cluster formation, efficient cluster head selection, and a lightweight routing mechanism to improve network performance in OppNets.

3. Proposed Method

Clustering within an OppNet entails organizing vehicles according to factors like proximity and geographic positioning. This arrangement fosters adaptable groups with basic data exchange and effective communication among vehicle nodes, prompting the development of various clustering algorithms. An important aspect in clustering is the selection of CHs, which can be accomplished via either a centralized approach utilizing network infrastructure such as RSU, or a decentralized method where CHs are chosen based on decisions made by vehicles within each cluster. In this study, we propose an Adaptive Clustering-based Routing Protocol (ACRP) that utilizes dynamic clustering, resulting in improved packet delivery and a dynamic clustering approach that groups nodes based on distance and location. The protocol is divided into four phases:

• Phase 1: calculating the Euclidean distance between vehicles.
• Phase 2: selecting a node as a CH.
• Phase 3: network addressing architecture.
• Phase 4: dynamic clustering adaptively.

In the first phase of the proposed ACRP, we consider an area where each vehicle ($V_i$) is randomly positioned. We assume that GPS data are globally available for all nodes that contribute to the calculation of distances between nodes. This is based on the individual capability of each node (e.g., vehicle) to independently access GPS signals from satellites directly, rather than relying on the transmission of GPS data between nodes. Accordingly, we calculate the Euclidean distance between two vehicles as follows $d_{(V_i,V_j)}=\sqrt{{(X_{V_i}-X_{V_j})}^2+{(Y_{V_i}-Y_{V_j})}^2}$ where the selected vehicles are assumed to be ($V_i$) and ($V_j$) and the corresponding coordinates are ($X_{V_i},Y_{V_i}$) and $(X_{V_j},Y_{V_j}$). This distance makes the closest node to be placed in the cluster and also two nodes communicate with each other in a lesser time interval.

In the second phase, we utilize two crucial criteria for choosing the cluster head: Encounter Rate ($\varphi$) and Remaining Energy ($\Psi$).

The cluster head (${\chi }_i$) is chosen based on the encounter value of other neighbors within a specific range. In order to monitor the frequency of encounters for a note, the ACRP keeps track of two local variables: an encounter history (${\varphi }_i$) and a current window counter ($CW$). The ${\varphi }_i$ reflects the node’s historical encounter rate, calculated as a weighted moving average. On the other hand, the $CW$ provides information about the number of encounters within the current time interval. Periodically, the ${\varphi }_i$ is updated to incorporate the most recent $CW$, ensuring that the latest rate of encounter information is taken into account. The calculations for updating the ${\varphi }_i$ are conducted in the following manner:

$${{\varphi }_i}_{\left(New\right)}=\gamma \ast CW+(1-\gamma )\ast {{\varphi }_i}_{\left(Current\right)}$$

(1)

The exponentially weighted moving average gives greater importance to the most recent complete current window ($CW$), with the emphasis being proportional to the factor $\gamma$. Updating the $CW$ is a simple process: for each encounter, the $CW$ is incremented. After the current window update is finished, the history of encounters is updated, and the $CW$ is set back to zero. According to Equation (1), it represents a simple filter for updating the encounter rate such that the recent encounter rate receives a higher weight compared to the previous encounter rate. Through our experiments, we discovered that using a $\gamma$ value of $0.85$ and an update interval of approximately 30 s yielded good results. Based on this interval time, if the interval duration is long, the encounter rate becomes uneven, whereas with shorter intervals, nodes fail to encounter neighboring nodes (best in our test of 30 s). With this knowledge, the node with the highest ${\varphi }_i$ can be selected as a candidate cluster head. The objective of this optimization problem is to maximize the sum of the weights of the links between the ${\chi }_i$ and its neighbors. This means each vehicle has a list of neighboring nodes and the node with the highest ${\varphi }_i$ to its neighbors is selected as the ${\chi }_i$. We consider ${\varphi }_i$ to be the encounter history of node i, representing the number of encounters node i has had with its neighbors, which can be expressed as follows:

$${{\varphi }_i}_{max}=max(V_i,V_j),\sum (\varphi (V_i,V_j)forall{V}_j\in neighbors{V}_i)$$

(2)

A higher ${\varphi }_i$ indicates greater efficiency in terms of easily sending and receiving more packets. Therefore, the node with the highest ${{\varphi }_i}_{max}$ is a good candidate for ${\chi }_i$ as it helps maintain long-term stability in the cluster and enables communication with nearest neighbors. The encounter rate as used in our study refers specifically to the number of times vehicles come within their communication range of each other, rather than the duration for which they remain in mutual proximity.

${\Psi }_i$ is employed for gauging the remaining energy of a node, which can be computed using Equation (3), where ${\Psi }_i^{Current}\left(t\right)$ denotes the remaining energy of node i at time slot t, and ${\Psi }_i^{Initial}\left(o\right)$ represents the initial energy of node i. By utilizing this equation, we are able to identify the node with the highest remaining energy, which has the potential to serve as a cluster head.

$${\Psi }_i=\frac{{\Psi }_i^{Current}\left(t\right)}{{\Psi }_i^{Initial}\left(o\right)}$$

(3)

To choose cluster heads, we propose a heuristic function. Initially, we need to compare two factors: the highest encounter rate (${\varphi }_i$) and the most remaining energy (${\Psi }_i$). To make this comparison fair, we can apply min–max normalization. This process standardizes the data, making sure all features are scaled equally. This prevents any one feature from dominating others due to differences in their sizes. This process involves rescaling the data to a fixed range, usually between 0 and 1. In general, we determine the minimum (${{\sigma }_i}_{\left(min\right)}$) and maximum (${{\sigma }_i}_{\left(max\right)}$) values of the feature we want to normalize. Then, we calculate the range of the feature by subtracting the minimum value from the maximum value: ${{\sigma }_i}_{\left(max\right)}-{{\sigma }_i}_{\left(min\right)}$. Therefore, for each data point (${\sigma }_i$) in the feature, we apply the min–max normalization formula. The min–max(${{\sigma }_i}_{\left(normalized\right)}$) scale is as follows:

$${{\sigma }_i}_{\left(normalized\right)}=\frac{{\sigma }_i-{{\sigma }_i}_{\left(min\right)}}{{{\sigma }_i}_{\left(max\right)}-{{\sigma }_i}_{\left(min\right)}}$$

(4)

By following Equation (4), we guarantee uniform scaling across all nodes, ensuring that each node’s data are standardized to the same scale relative to the entire dataset. Normalization not only ensures that both factors are scaled within the range of $[0,1]$, but also ensures equal contribution from both factors in the analysis, facilitating a balanced consideration of encounter rate and remaining energy when selecting cluster heads. Consequently, the normalized expressions for encounter rate (${\varphi }_i$) and remaining energy (${\Psi }_i$) for node i, utilizing the min–max scaling technique, can be articulated as follows:

$${{\varphi }_i}_{\left(normalized\right)}=\frac{{\varphi }_i-{{\varphi }_i}_{\left(min\right)}}{{{\varphi }_i}_{\left(max\right)}-{{\varphi }_i}_{\left(min\right)}}$$

(5)

and

$${{\Psi }_i}_{\left(normalized\right)}=\frac{{\psi }_i-{{\psi }_i}_{\left(min\right)}}{{{\psi }_i}_{\left(max\right)}-{{\varphi }_i}_{\left(min\right)}}$$

(6)

Therefore, utilizing Equations (5) and (6), we introduce a heuristic function for the selection of cluster heads. The heuristic function ${\xi }_i$ is as follows:

$${\xi }_i={{\varphi }_i}_{\left(normalized\right)}+{{\Psi }_i}_{\left(normalized\right)}$$

(7)

The ${\chi }_i$ is a vehicle selected as the group leader and maintains a routing table for every vehicle in its cluster. Based on the ${\chi }_i$, clusters are formed ($C_i$), with each cluster containing some nodes ($M_i$) that are supported by its respective cluster head ${\chi }_i$. However, due to estimation errors in contact probabilities and unpredictable sequencing of meetings among mobile nodes, it is possible for numerous small or large clusters to form, some of which may have significant overlap with other clusters. To address this problem, we propose a novel strategy where each cluster ($C_i$) maintains an Overlapping Degree ($OD$) with other clusters, indicating the count of shared members among them. Assume $C_i$ represents the i-th cluster, ${\aleph }_q$ represents the q-th common member, and ${\beta }_{{\chi }_i}$ represents the transmission range of the i-th $\chi$, whereas every cluster head maintains a consistent maximum transmission distance (${\beta }_{{\chi }_i}\le R$). In cases where there is no overlap ($OD=0$), the cluster head can adjust its transmission range (${\beta }_{{\chi }_i}$) to establish communication with other clusters. Additionally, we introduce a limit of common members between clusters. After experimenting with different values, we found that a maximum of five common members between clusters provides ideal clustering. Put differently, we establish a boundary wherein clusters can share a maximum of five common members and a minimum of two. Having a cluster size larger than five common members results in less ideal conditions with significant overlap among clusters. Moreover, the cluster head should not be a common member (${\chi }_i\ne {\aleph }_q$) among the clusters. This ensures that the clusters remain ideal and do not overlap completely, thereby increasing their clustering effectiveness. Furthermore, clusters interact with each other through common members and also have members that are unique to each cluster. In other words, each cluster has common members and non-common members between other clusters. Additionally, if members within each cluster are unable to communicate with their cluster head, they have the capability to independently increase their transmission range. Whenever a node has difficulty communicating with its cluster head, it can extend its transmission range. Our experiment shows that even a slight increase in transmission range allows a node to communicate with the cluster head, given their Euclidean distance proximity. In addition, clusters must have minimal connectivity with other clusters to facilitate communication through shared members. Ultimately, the cluster must satisfy one of the constraints listed below.

$$(2\le OD\le 5)OR(M_i\ge 5)$$

(8)

According to Equation (8), if the specific cluster $C_i$ has less than two members in common, the ${\chi }_i$ should increase the transmit range to be able to connect with other clusters. In this way, the communication between the clusters is permanent and it becomes possible to send the packet in the whole network through common members. Furthermore, if the cluster is unable to satisfy the specified constraint ($2\le OD\le 5$), it must consist of a minimum of $M_i=5$ members. This ensures that the cluster head can extend its transmission range in cases where the cluster comprises fewer than five members ($M_i<5$). For clarity, we highlight that these numbers are obtained based on our simulation studies and the value depends on the network specifications. This implies that the values could be different within a different network with different specifications to achieve better results. We assume that if ${\chi }_i$ has fewer than two common members ($OD<2$), or if the cluster head has fewer than five members ($Mi<5$), the cluster head will increase its transmission range by the amount of $\Delta$, where $\Delta$ represents the minimum distance between a cluster head and its members. We expand the transmission range of the cluster head by integrating the value of $\Delta$ until it fulfills one of the conditions specified in Equation (8). Put simply, if the cluster head fails to meet the specified constraints, it should augment its transmission range (${\beta }_{{\chi }_i}$) by adding $\Delta$ to it (${\beta }_{{\chi }_i}={\beta }_{{\chi }_i}+\Delta$).

In the third stage, after clustering, a new routing method is introduced for improved results between the source (S) and destination (D). This routing method focuses on inter-cluster communication, allowing each cluster to have limited connections with other clusters. This enables optimal selection of subsequent transfer and forwarding nodes towards the destination. Limiting the common members serves two purposes. Firstly, it ensures optimal clustering and unique members for each cluster. Secondly, the common members are responsible for routing as they can carry packets between clusters. 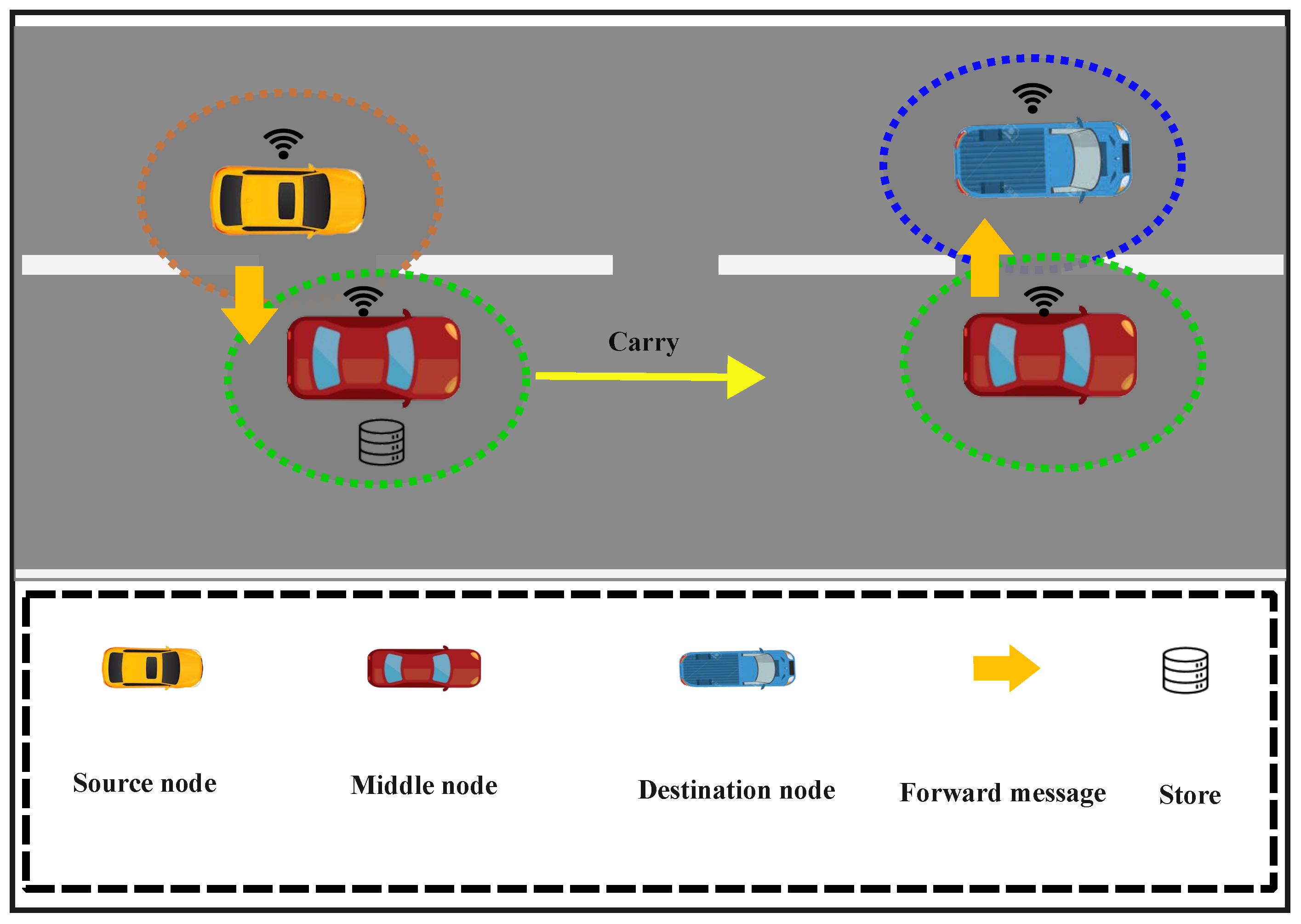Figure 2 illustrates a cluster configuration with common members, which means that each cluster communicates with other clusters ($2\le OD\le 5$) through common members. For example, envision a situation where the source node $V_1$ inside cluster $C_1$ sends a packet intended for $V_{10}$ to its cluster head ${\chi }_1$. Afterward, ${\chi }_1$ relays the packet to a common member, ${\aleph }_1$, which serves as the intermediary node shared between clusters $C_1$ and $C_2$. As ${\aleph }_1$ is a shared member between the two clusters, it is able to communicate with the cluster head of the other cluster ${\chi }_2$ and transfer packets to ${\chi }_2$. If ${\chi }_2$ finds the destination node in its list, it dispatches the packet to $V_{10}$. Otherwise, the packet is routed to the shared node ${\aleph }_2$ in other clusters until it reaches the intended destination. This packet routing process can be depicted as follows:

$$V_1\to {\chi }_1\to {\aleph }_1\left\{\begin{array}{c}{V}_{10}if{V}_{10}\in {\chi }_2\\ {\chi }_2\to {\aleph }_2\to {\chi }_3\to V_{10},\dots \end{array}\right.$$

(9)

This method follows a reliable routing to the destination of the packet. In the final stage, after a time interval, clustering is conducted again and phases one, two, and three are repeated. Due to the high mobility of nodes in these networks, any node can leave the cluster and new nodes can join the cluster.

According to the four phases mentioned above, we present the proposed Algorithm 1. As shown in the algorithm, when a node $V_2$ wants to send a message to a vehicle at a great distance ($V_{12}$), vehicles receive information from GPS. The distance between each vehicle is then calculated using the Euclidean distance (from lines 1 to 5). ${\chi }_i$ with the highest encounter rate and maximum remaining energy is selected for a group of vehicles (lines 6, 7, and 8). As long as conditions ($M_i<5$ OR $OD<2$) AND $({\beta }_{{\chi }_i}\le RAND{\chi }_i\ne {\aleph }_q)$ are not fulfilled, the cluster head maintains the capability to enhance its transmission range by the value of $\Delta$ (lines 9 and 10). The routing phase starts, and the source node $V_2$ into cluster sends a message to its cluster head ${\chi }_1$ (line 12). The ${\chi }_1$ looks into the list of members, and as explained above, each cluster head has its own table (list) of members. If the destination node is not on the ${\chi }_i$’s list of members, the packet is sent to the ${\aleph }_q$ (it can be seen in lines 13 to 17). The next step is for the ${\aleph }_q$ to send the packets to the neighboring cluster head ${\chi }_2$ that it is a member of, and so on until the packet reaches its destination $V_{12}$, these steps will be repeated (line 20). Furthermore, the updating interval is independent of the contact duration, emphasizing that the number of encounters is the determining factor in our algorithm.

Algorithm 1 ACRP

Input: GPS data

1: for  $V_i\in V$  do

2:     for $V_j\in V$ do

3:           Calculate the distance between $V_i$ and $V_j$ Euclidean distance $d_{(V_i,V_j)}=\sqrt{{(X_{V_i}-X_{V_j})}^2+{(Y_{V_i}-Y_{V_j})}^2}$

4:     end for

5: end for

6: Calculate ${\xi }_i$

7: $\xi$ sorted from maximum to minimum value

8: The cluster heads (${\chi }_1,{\chi }_2,{\chi }_3,\dots ,{\chi }_i$) are selected from the maximum $\xi$ value, respectively.

9: while ($M_i<5$ OR $OD<2$) AND $({\beta }_{{\chi }_i}\le R$ AND ${\chi }_i\ne {\aleph }_q)$ do

10:    ${\beta }_{{\chi }_i}={\beta }_{{\chi }_i}+\Delta$

11: end while

12: $V_i\to$ Send packet to ${\chi }_i$

13: ${\chi }_i\leftarrow$ Receive the packet

14: ${\chi }_i$ check its list

15: if the destination address is at ${\chi }_i$ list then

16:    ${\chi }_i\to$ send the packet to the destination

17:    $V_i\leftarrow$ Receive the packet through ${\chi }_i$

18: else

19:    ${\chi }_i\to$ Send packet to ${\aleph }_q$ in $C_i$

20:    Repeat lines 12 to 19

21: end if

22: interval time=0

23: Repeat line 1

4. Simulation Studies

4.1. Parameters of Simulation

We compare our work against well-known clustering-based routing protocols such as [13,14,17,19,20,21,22]. The evaluation is based on hop count, delivery ratio average, throughput, and end-to-end delay. To evaluate the ACRP in relation to mobility patterns and vehicle movement, we have simulated a DTN with specific configurations given in

Table 1. Experimental parameters.

No.	Parameters	Value
1	Simulation tool	The ONE and MATLAB
2	Routing protocols	Cluster-based routing
3	Number of nodes	50, 100, 150, 200, and 250
4	Network size	4000 × 3500 m2
5	Mobility model	Shortest Path Map
6	Channel type	Wireless channel
7	Message size	250–750 KB
8	Buffer size	5, 10, 15, and 20 Mb
9	Total simulation time	1 h
10	Source and distention selection	Random
11	Message TTL	300 MS
12	Interval time	30 S
13	Maximum transmit range of vehicles	100 M
14	Maximum transmit range of trams	300 M
15	Vehicle speeds	$2.7$–13.9 m/s
16	Tram speeds	7–10 m/s

. Using the ACRP, we strategically convert this simulated DTN into a network employing TCP/IP protocols through the adaptive clustering of nodes. This transformation is a pivotal component of our protocol’s capability to enhance network connectivity and performance. We utilized the Opportunistic Network Environment (ONE) simulator. ONE is an open-source simulation tool for the development and testing of routing protocols, based on Java [23]. It can be extended for analyzing protocols and network mobility models for delay-tolerant networking. With ONE, it is easy to integrate contact records, route modules, applications, and reports [24]. For the ACRP, we used the default ONE simulation map from Helsinki, Finland. The geographical space for this experiment is 4000 × 3500 m² in size, with 50, 100, 150, 200, and 250 nodes distributed at random. In this setting, 64% of the nodes represent vehicles moving from their current location to a randomly selected point via the shortest route. These vehicles travel in one direction at speeds of $2.7$ to 13.9 m/s. The remaining nodes follow predefined routes like tram lines and travel at a speed between 7 and 10 m/s. All nodes have a transmission range of 20 m, except trams, which can transmit up to 200 m. Each message generated in the network has a time-to-live value of 300 s. The generated messages range in size from 250 to 750 KB. The nodes’ buffer sizes are 5, 10, 15, and 20, respectively, and the starting point is 5 MB. The coordinates of the cluster head nodes in each clustering can be acquired during a specific round of data collection, following the cluster head election procedure described in Equation (7). Table 1 shows the summary of the parameters.

4.2. Delivery Ratio

In brief, delivery rate is the main network metric used to evaluate network performance. It is defined as the ratio of the number of packets successfully delivered to the destination to the number of packets sent by the source node. The equation for the Number of Delivered Bundles ($NDB$) against the Number of Generated Bundles ($NGB$) is as follows [25]:

$$DeliveryRatio=\frac{NDB}{NGB}$$

(10)

4.3. End-to-End Delay

It is defined as the time it takes for a packet to travel from source to destination on a network [26]. As shown by

$$\mathit{End-to-End}delay=\frac{ET-ST}{NC}$$

(11)

where $ET$ is the end time and $ST$ is the start time. $NC$ represents how many hops there are between the source and destination.

4.4. Hop Count

A hop count refers to the total number of intermediate devices, such as nodes, that a data packet must traverse between its source and destination. Each node along the data path represents a hop, transferring data from one source to another [27].

4.5. Throughput

This metric shows the amount of data transmitted from a source to a destination per time unit over a communication link. It is measured in bits per second [28].

$$AverageThroughput=\frac{PDR}{ST-SPT}$$

(12)

$PDR$ stands for packet delivery ratio, and $ST-SPT$ stands for start time and stop time.

4.6. Reachability

It is calculated as the proportion of successful route discovery attempts out of the total number of route discovery operations [29].

5. Experiment and Result

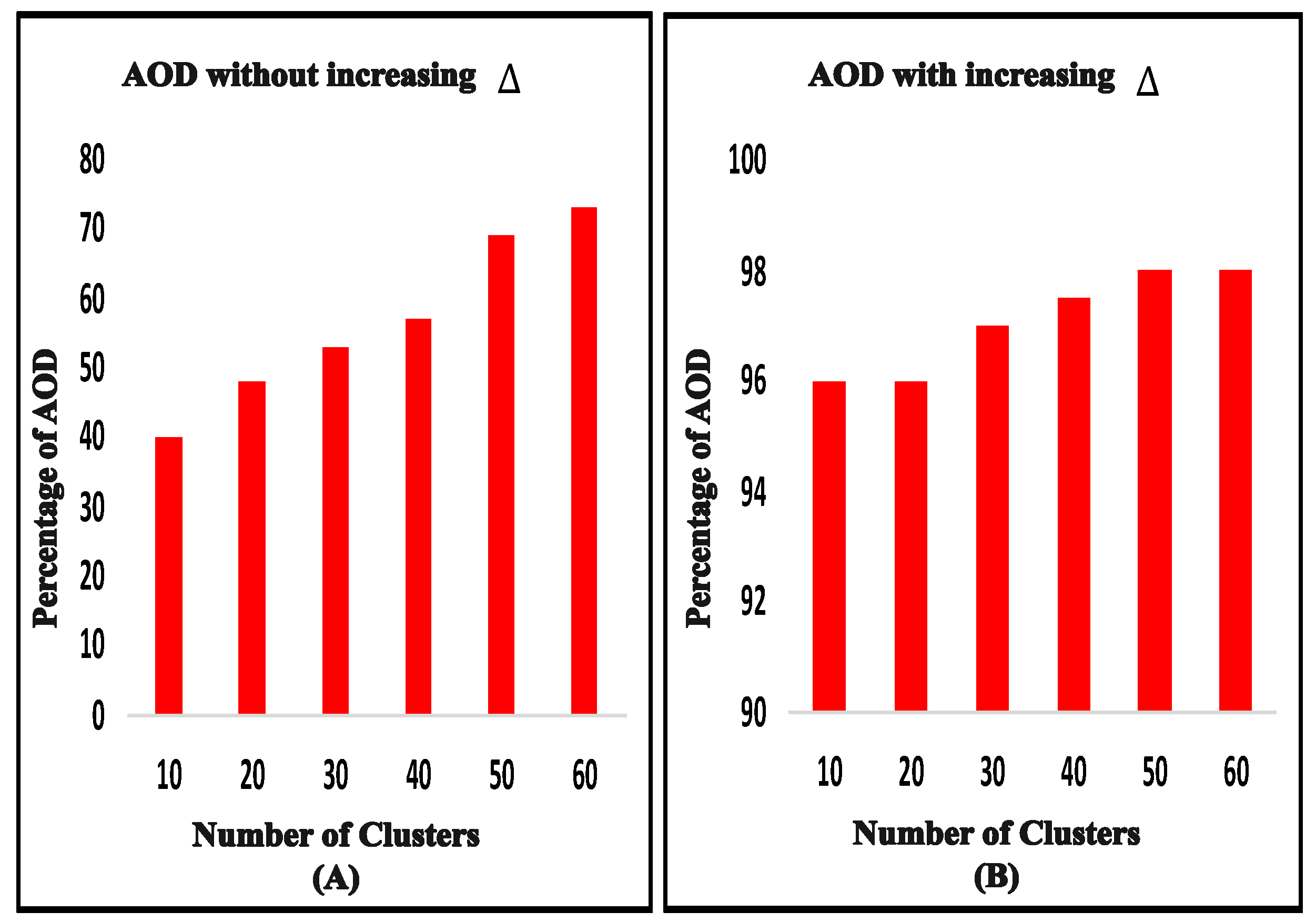
Average Overlapping Degree ($AOD$) is defined as the average overlap degree between any two overlapping clusters in the network. Let us consider that A and B are the cluster head nodes in two clusters. We assume that $OD$ is the maximum overlapping degree between the two clusters, where $OD\ne 0$. Two symmetrical circles with radius R = maximum ${\beta }_C$ = maximum ${\beta }_{{\chi }_i}$, where ${\beta }_C$ is the range of communication between sensors, which are present in cluster A or B. Notice that $OD$ is specifically defined for clusters that overlap ($OD\ne 0$). We calculate the $AOD$ as the mean value of this random variable $OD$. $d_{(A,B)}$ is the Euclidean distance between the two nodes A and B. In other words, $d_{(A,B)}$ is a continuous random variable that can contain values ranging from 0 to $2R$. In the case of $d_{(A,B)}$ = 0, there should be complete overlaps between two clusters; on the other hand, when $d_{(A,B)}$ is greater than or equal to $2R$, there should be no overlap. In the simulation study, we investigated the degree of overlap with increasing $\Delta$ value and without increasing $\Delta$ value. Our method might not achieve complete overlap (100%). Moreover, there could be instances where a direct path between the source and destination is unavailable at certain times, but with $\Delta$, achieving satisfactory $AOD$ is feasible.

In Figure 3A,B, it is shown that as the number of clusters increases, the average overlap between clusters increases. However, Figure 3B demonstrates a significant improvement in the overlapping degree between clusters when comparing clustering with and without increasing $\Delta$. Therefore, this method enhances routing and reduces delay. During several practical experiments, utilizing 60 clusters, we observed a 34% improvement with increasing $\Delta$ compared to without increasing $\Delta$, and we also found an almost 98% overlap between clusters.

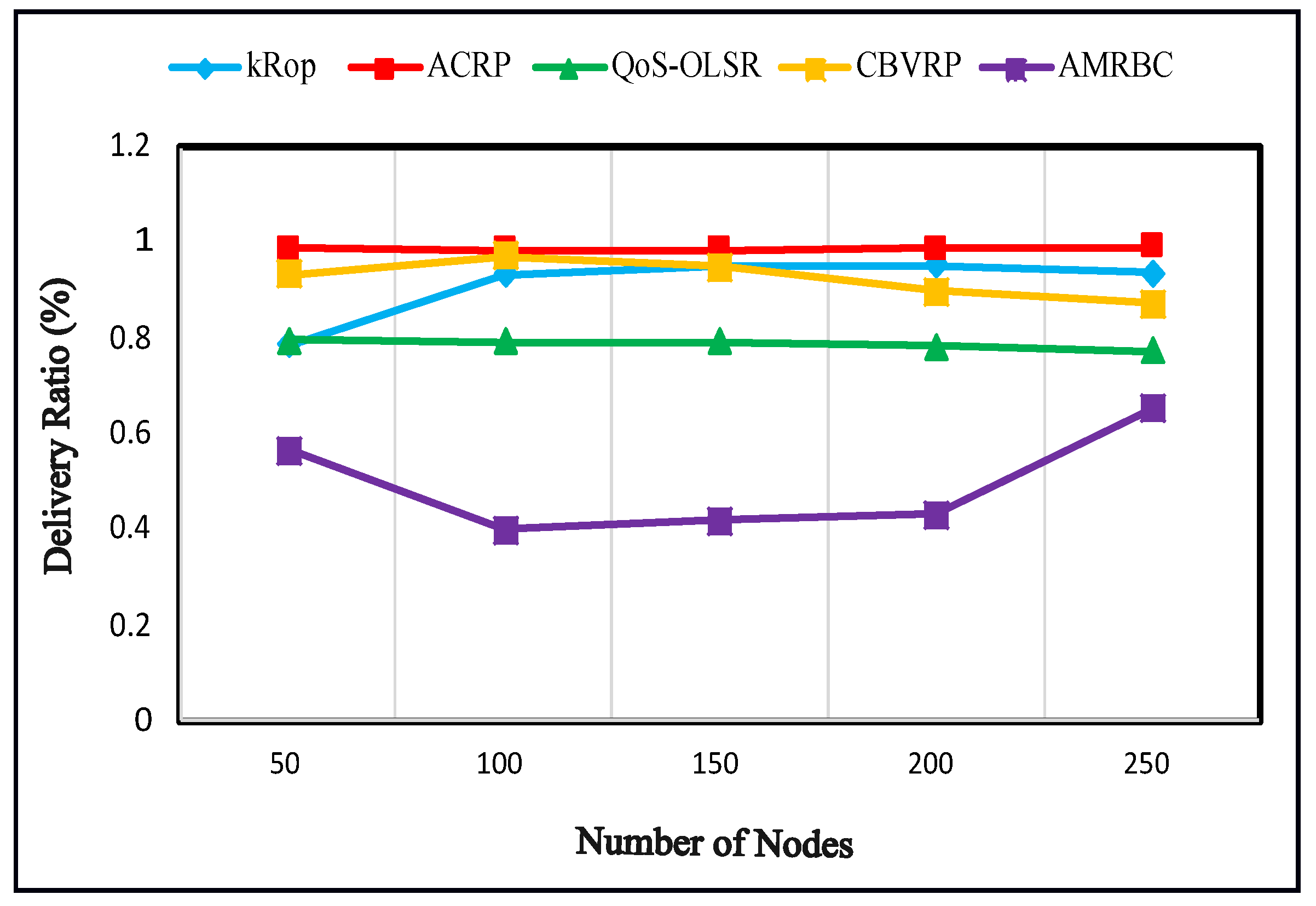
Figure 4 shows the efficient performance ACRP method in the DR compared to other clustering methods such as QoS-OLSR [17], CBVRP [21], kRop [13], and AMRBC [20]. ACRP routing protocols illustrate a very high and approximately stable DR during the simulation. This is because ACRP considers the encounter rate, giving more weight to nodes in high-density areas to be considered as cluster heads. This strategy increases the likelihood of a high delivery ratio, contributing to the consistent performance observed across different node densities. Figure 4 illustrates that the ACRP, when deployed with 250 nodes, achieved a DR improvement exceeding 28% in comparison to QoS-OLSR. Furthermore, the AMRBC exhibited suboptimal performance, lagging behind other protocols. In contrast, ACRP outperformed AMRBC by a substantial margin, achieving an impressive 51% enhancement. Additionally, when considering the highest number of nodes (250), ACRP exhibited superiority over both kRop and CBVRP, with enhancements exceeding 5% and 13%, respectively. Our approach selects the cluster head based on the highest encounter rate and the highest remaining energy. This prioritizes both network connectivity and energy efficiency, ensuring that the cluster head effectively manages message forwarding while conserving energy resources. In contrast, the KRop method, which relies on the k-Means algorithm, may suffer from suboptimal cluster formations due to sensitivity to initial cluster centroid selection. Similarly, in the CBVRP approach, clusters formed may not consistently optimize communication efficiency or network coverage. However, with ACRP, by enforcing constraints on cluster overlap and member count, we aim to create optimal clusters that maximize both communication efficiency and coverage.

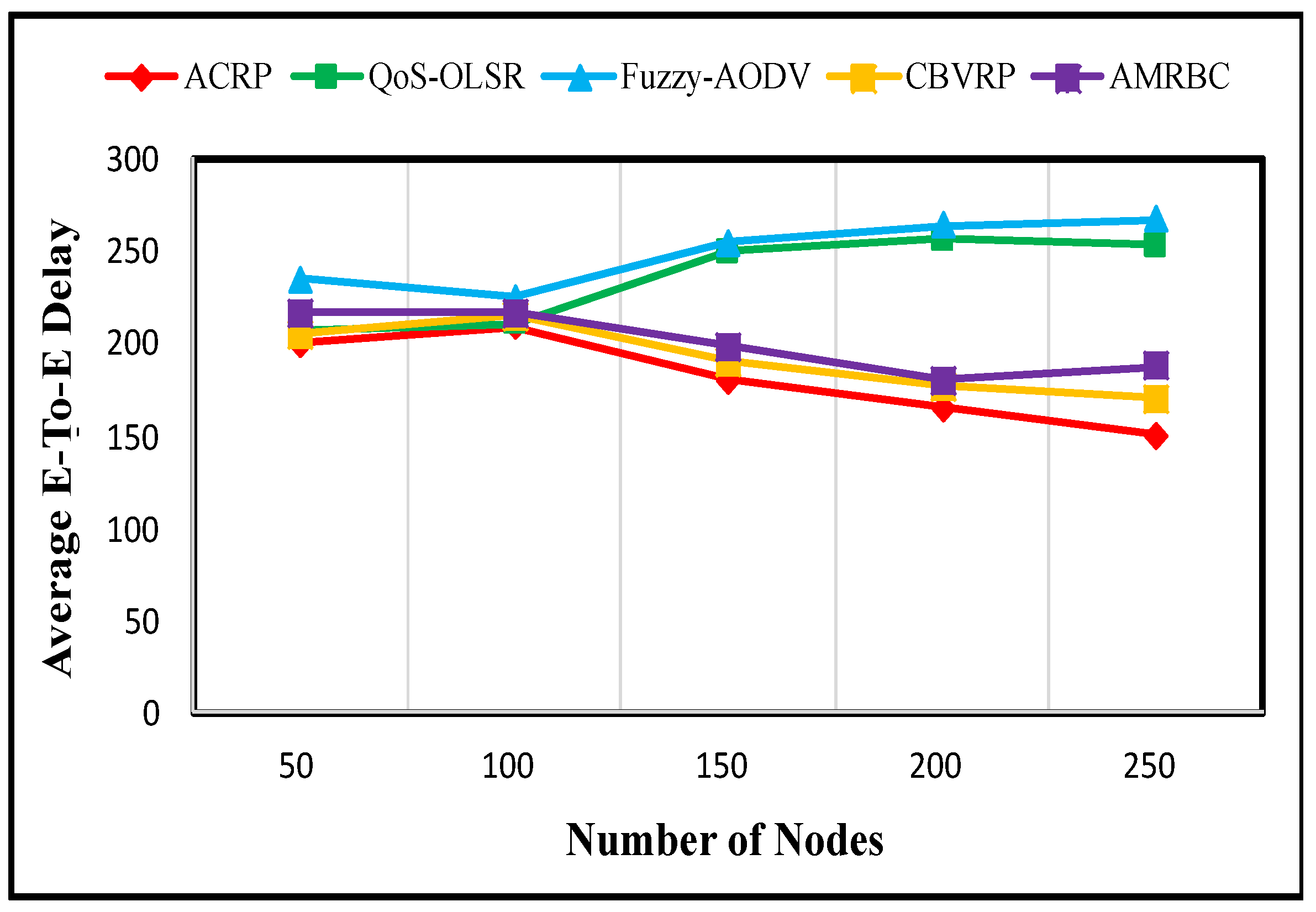
The end-to-end average delay refers to the time taken for a packet to traverse a network from its source to its destination. In the context of networking, this metric captures the average duration between a packet leaving its origin and reaching its final endpoint. Figure 5 demonstrates that the ACRP protocol exhibits a reduced end-to-end delay compared to other protocols. Specifically, compared to fuzzy-AODV [22] and QoS-OLSR [17], CBVRP [21], and AMRBC [20], ACRP was able to reduce end-to-end delay more effectively. Additionally, under conditions of both lowest density and highest density, ACRP experiences significant reductions: over 17%, 3%, 3%, and 7% for the former, and an impressive 42%, 38%, 13%, and 20% for the latter. This improvement can be attributed to the presence of common nodes, which facilitate shorter packet travel distances and consequently lead to reduced delays from source to destination.

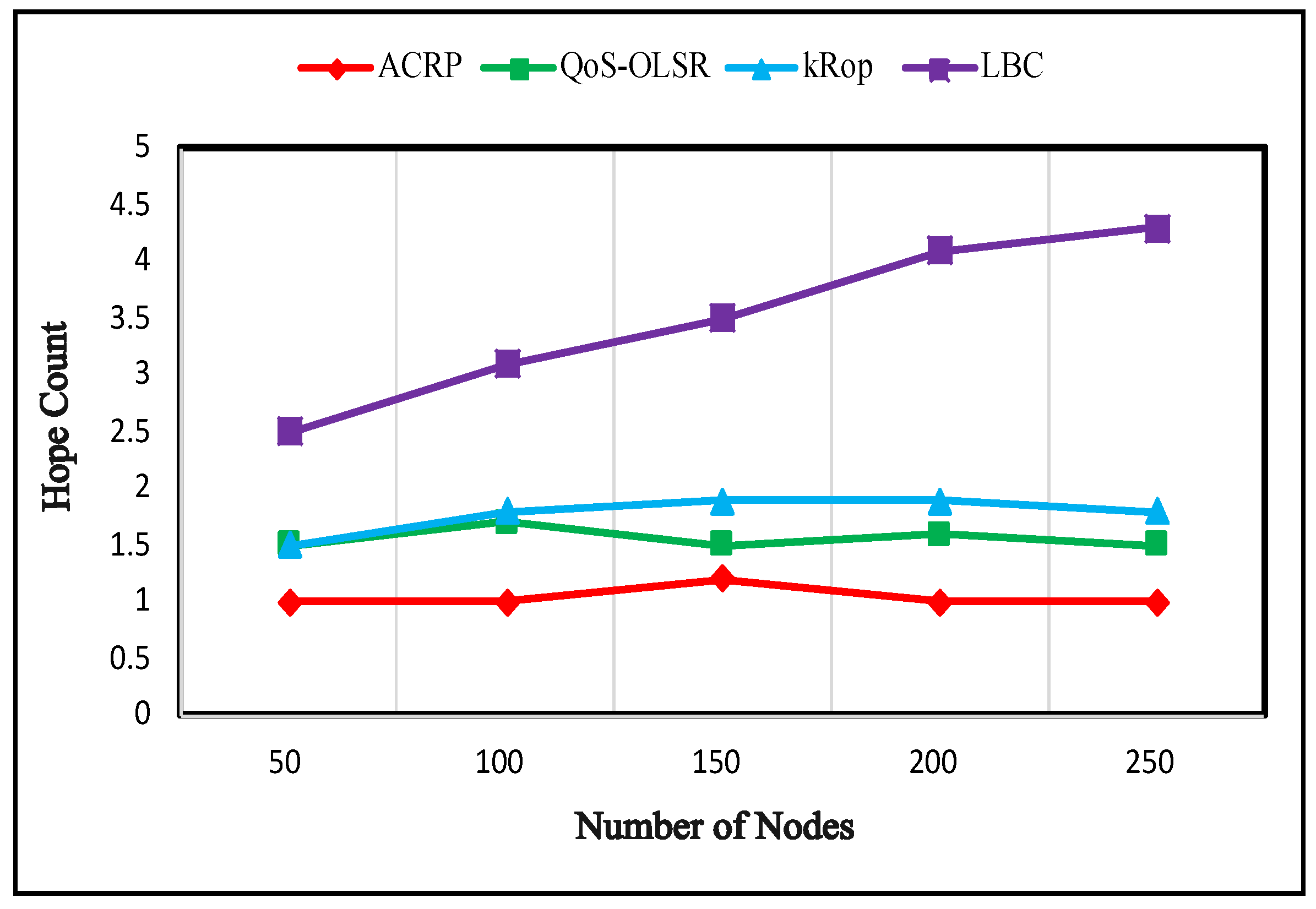
Figure 6 shows the total number of intermediate nodes that a data packet must traverse between the source and destination. Along the data path, each node forms a hop, transferring data from one source to another. When compared to QoS-OLSR [17], kRop [13], and LBC [14] methods, the ACRP method reduced hop count by over 33%, 44%, and 76% at the highest node densities (250), respectively. Due to the fact that this protocol only uses the common member and cluster head to transmit packets, communication between the source and destination does not require sending packets to every member.

A decreased hop count indicates shorter transmission distances between nodes, leading to lower energy consumption in relaying messages within the network. Therefore, the reduced energy expenditure per hop contributes to an overall decrease in energy usage across the network. Additionally, extended network longevity is achieved through decreased energy consumption, thereby preserving energy resources.

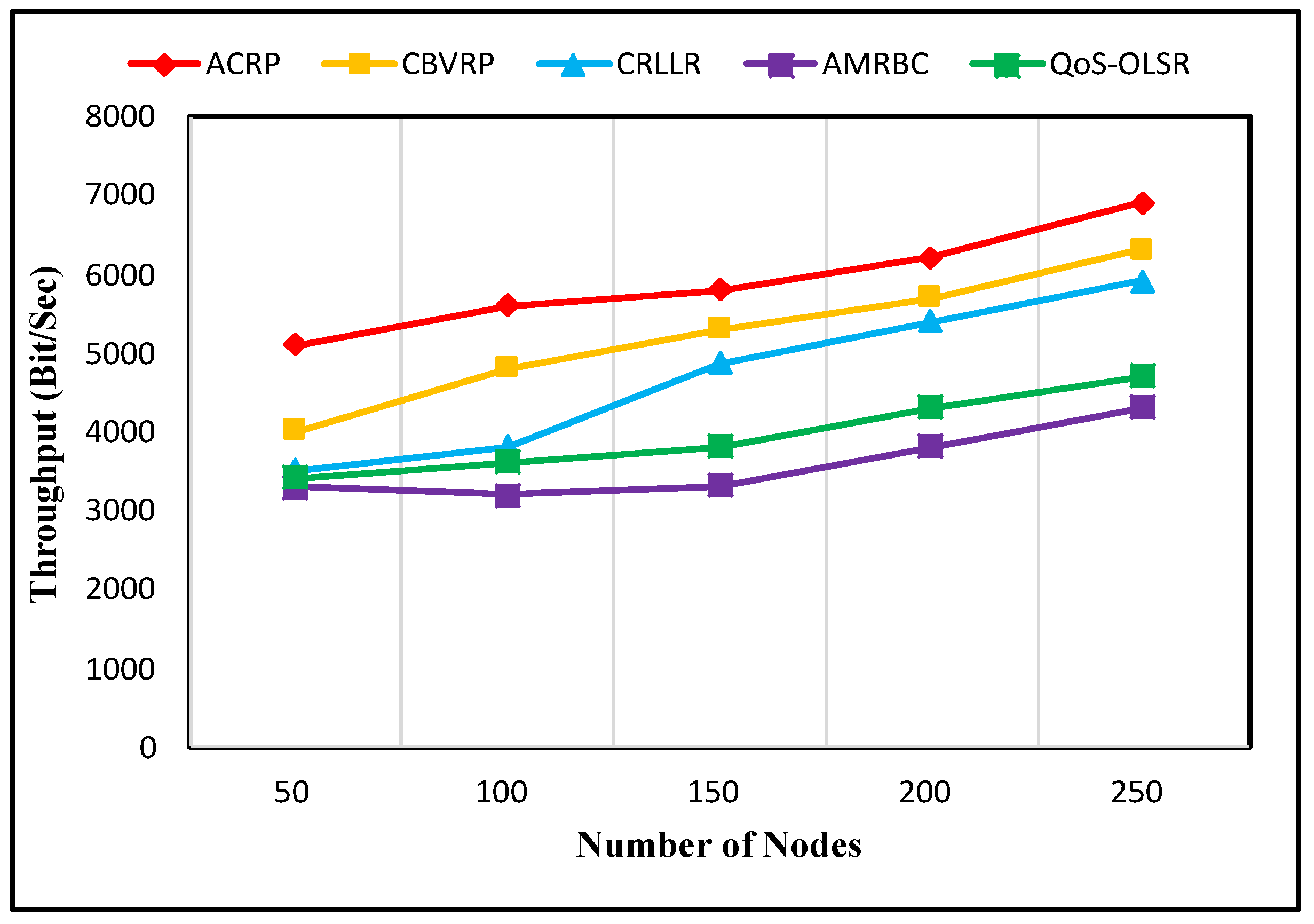
Figure 7 shows the number of packets that transmit from source to destination (throughput) based on Bit/Sec, and the performance of the ACRP method reached the highest amount when compared to other protocols. It is evident that the ACRP method exhibits superior performance when compared to the CBVRP [21], QoS-OLSR [17], AMRBC [20], and CRLLR [19] approaches. Among the examined methods, ACRP demonstrates superior performance with a 27%, 50%, 54%, and 54% advantage over CBVRP, QoS-OLSR, AMRBC, and CRLLR, respectively, in the scenario with the lowest node numbers (50). Additionally, in the highest density scenario (250), ACRP outperforms other methods by 9%, 46%, 60%, and 16%, respectively. Two factors contribute to this: firstly, as indicated by Equation (7), the proper selection of the cluster head establishes a robust link between the member node and its respective cluster head. Secondly, transmitting data via shared members across clusters has led to an augmentation of this parameter.

Speeding up the node causes a change in reachability. As the success of route discovery is influenced by the change in network topology, reachability is correlated with node speed. With increasing the speed of vehicles, reachability is decreased. This means network topology changes accelerate as node speed increases, which reduces reachability. The ACRP method remains stable during simulation over 80% with different densities. Due to connection and routing by cluster head, each cluster can be viewed as a node that moves throughout the network. The network topology is less affected by node mobility. As a result, this reduces the number of routing table updates since the network topology changes only when a cluster is changed. As shown in Figure 8, we can see that ACRP achieved more than 80% access from the lowest speed to the highest speed. For example, it reached 87% with the highest speed.

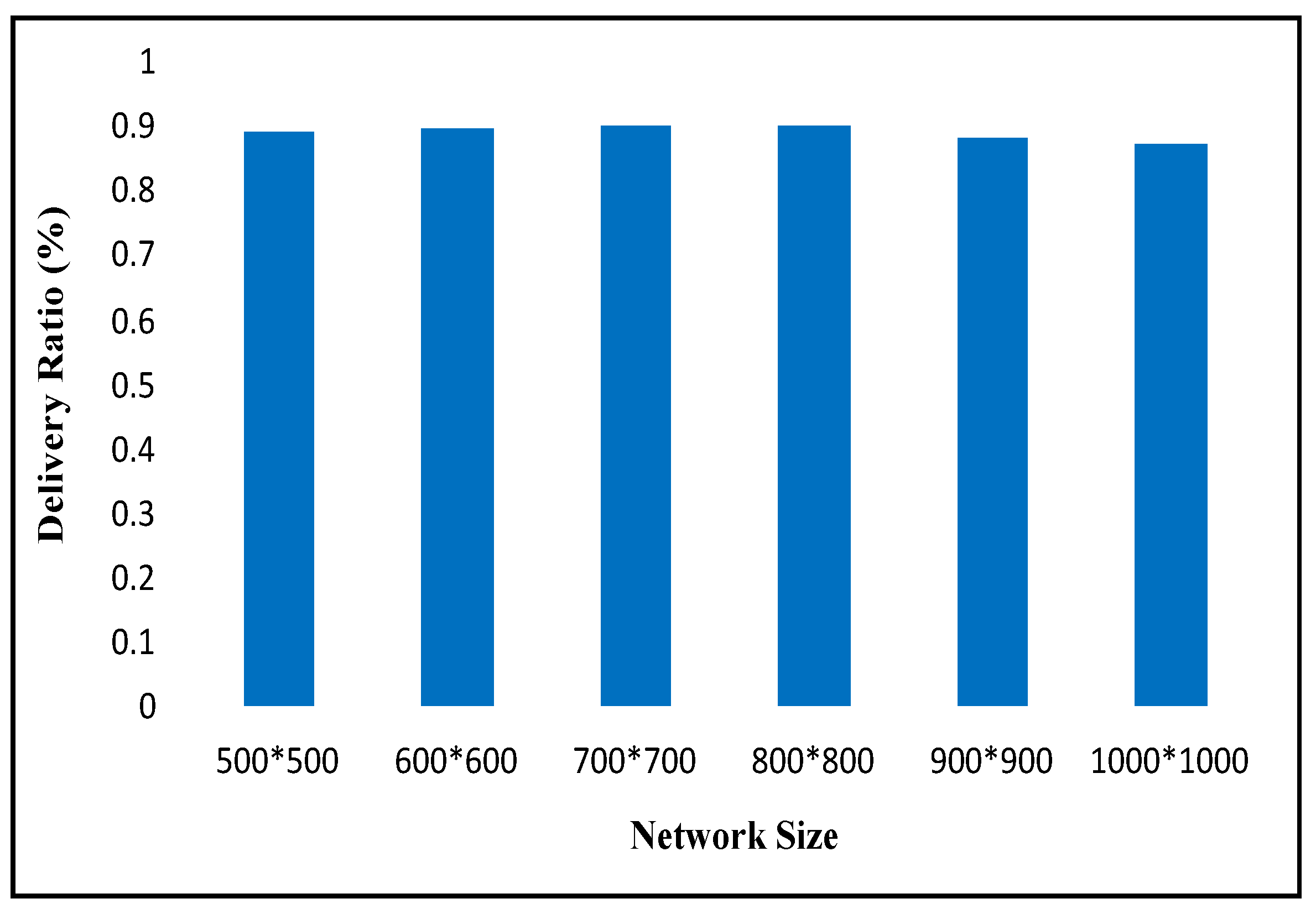
The efficacy of the ACRP was evaluated across a range of network sizes (500, 600, 700, 800, 900, and 1000) in terms of packet delivery ratio. Figure 9 demonstrates that the ACRP consistently exhibits the highest packet delivery ratios across varying network sizes. For example, in the lowest and highest network sizes, the ACRP achieves a remarkable delivery ratio exceeding 89%.

6. Conclusions and Future Work

OppNets present unique challenges due to their intermittent connectivity and dynamic network topologies. Traditional routing protocols struggle in these environments, often leading to high resource consumption and inefficient performance. This paper proposes a novel Adaptive Clustering-based Routing Protocol (ACRP) specifically designed for OppNets. ACRP leverages a member-based adaptive dynamic clustering approach to create a structured network that facilitates efficient routing. Our simulation results demonstrate that ACRP outperforms existing clustering protocols in terms of packet delivery ratio (increased by 28%), end-to-end delay (reduced by 42%), throughput (increased by 45%), hop count (reduced by 44%), and network reachability (increased by 80%). These improvements highlight the effectiveness of ACRP in enhancing communication performance within OppNets.

In our future work, we aim to reduce energy consumption and improve important network parameters using machine learning algorithms.