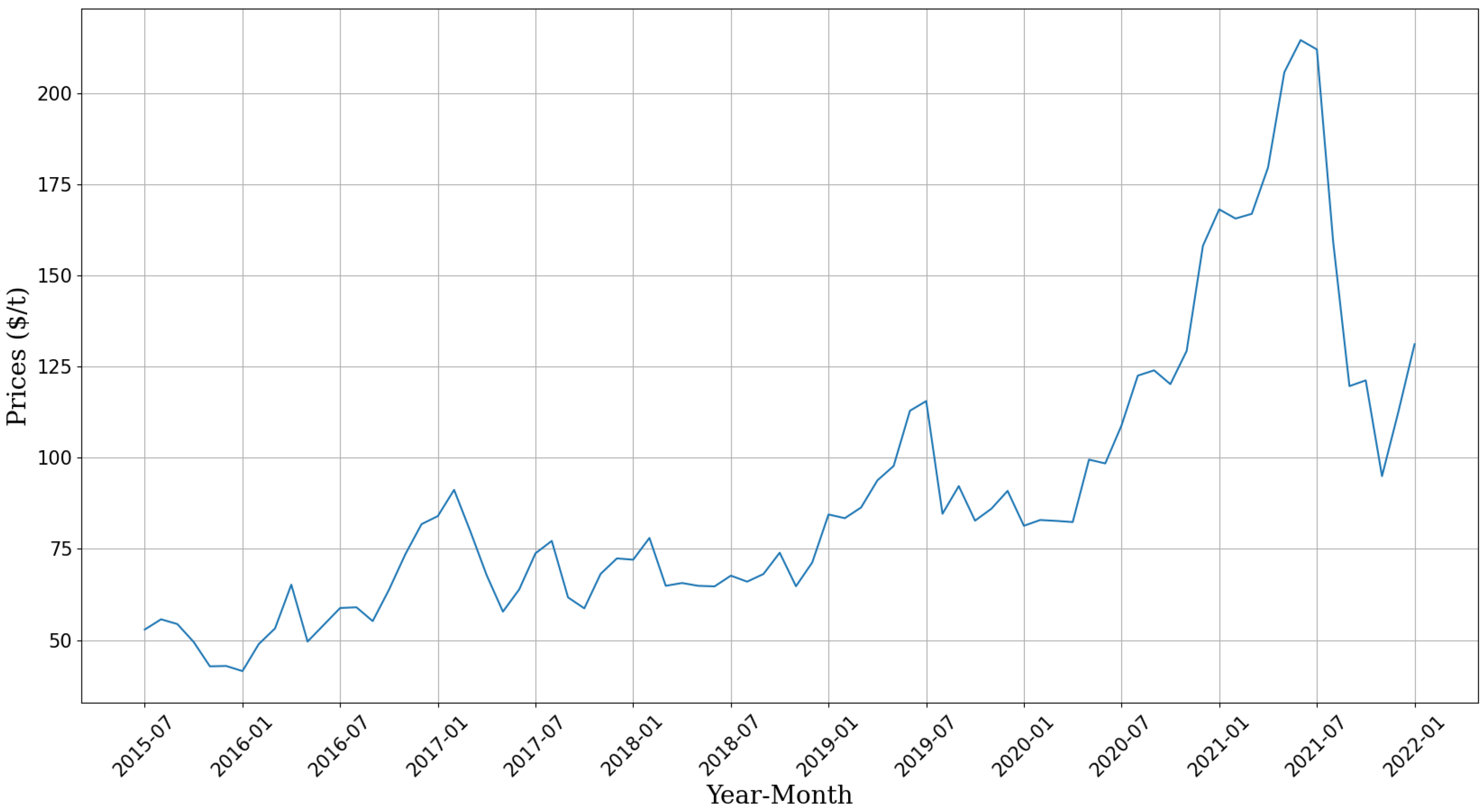
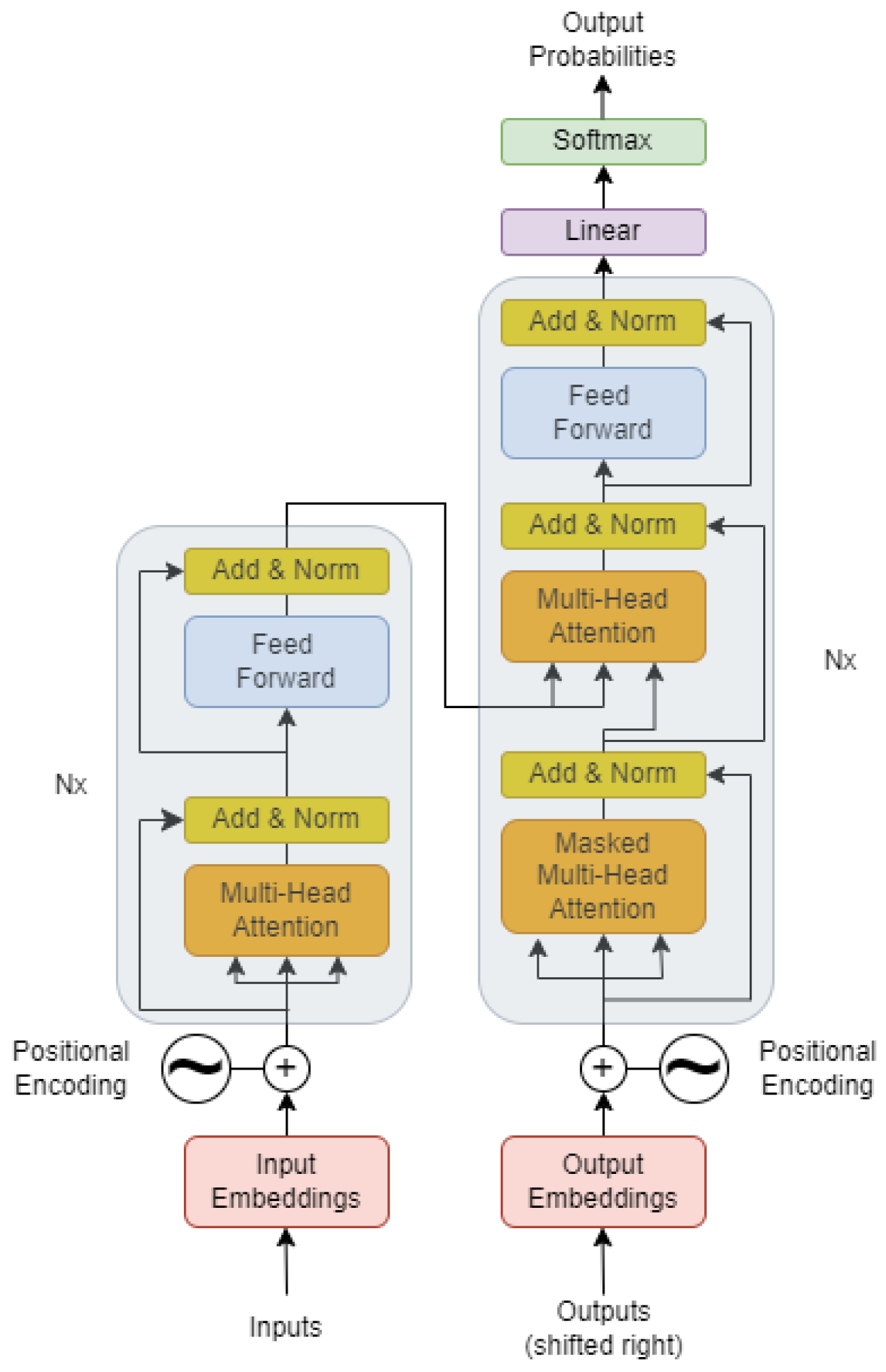
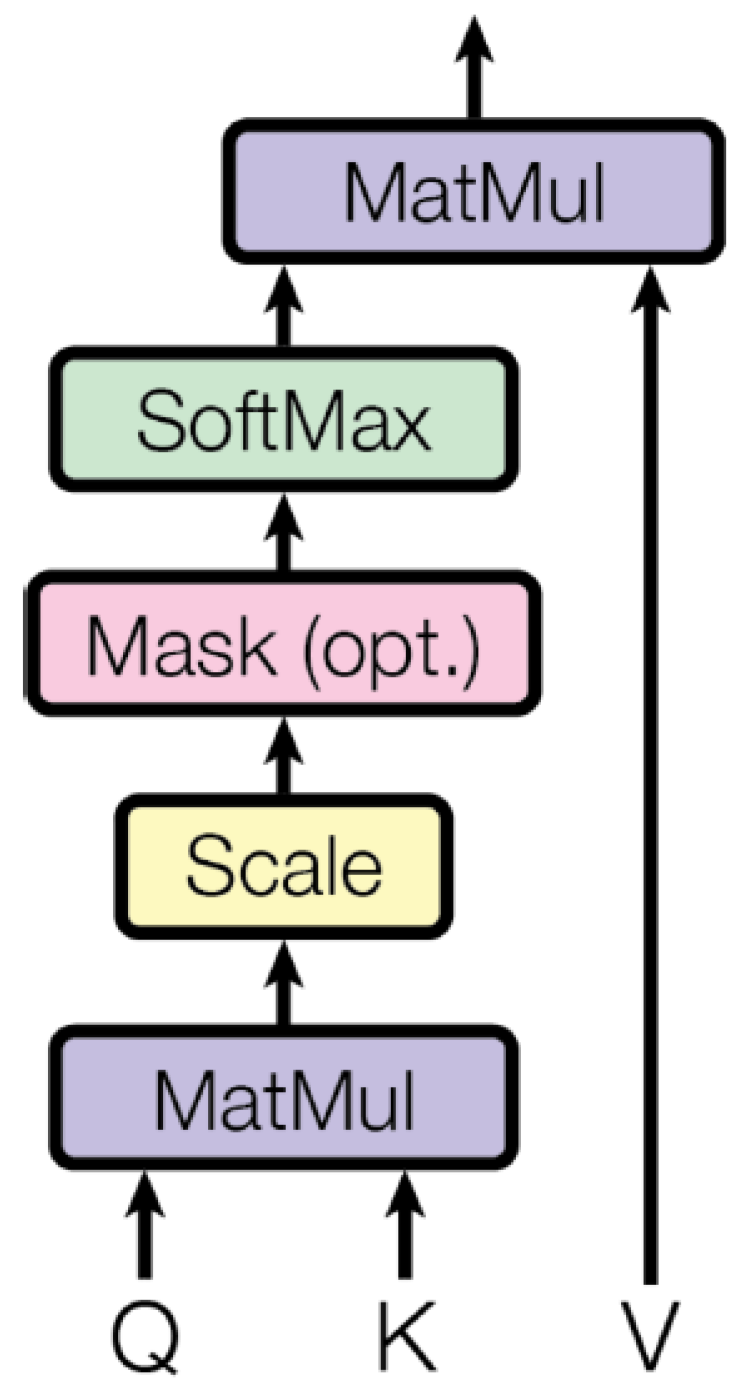
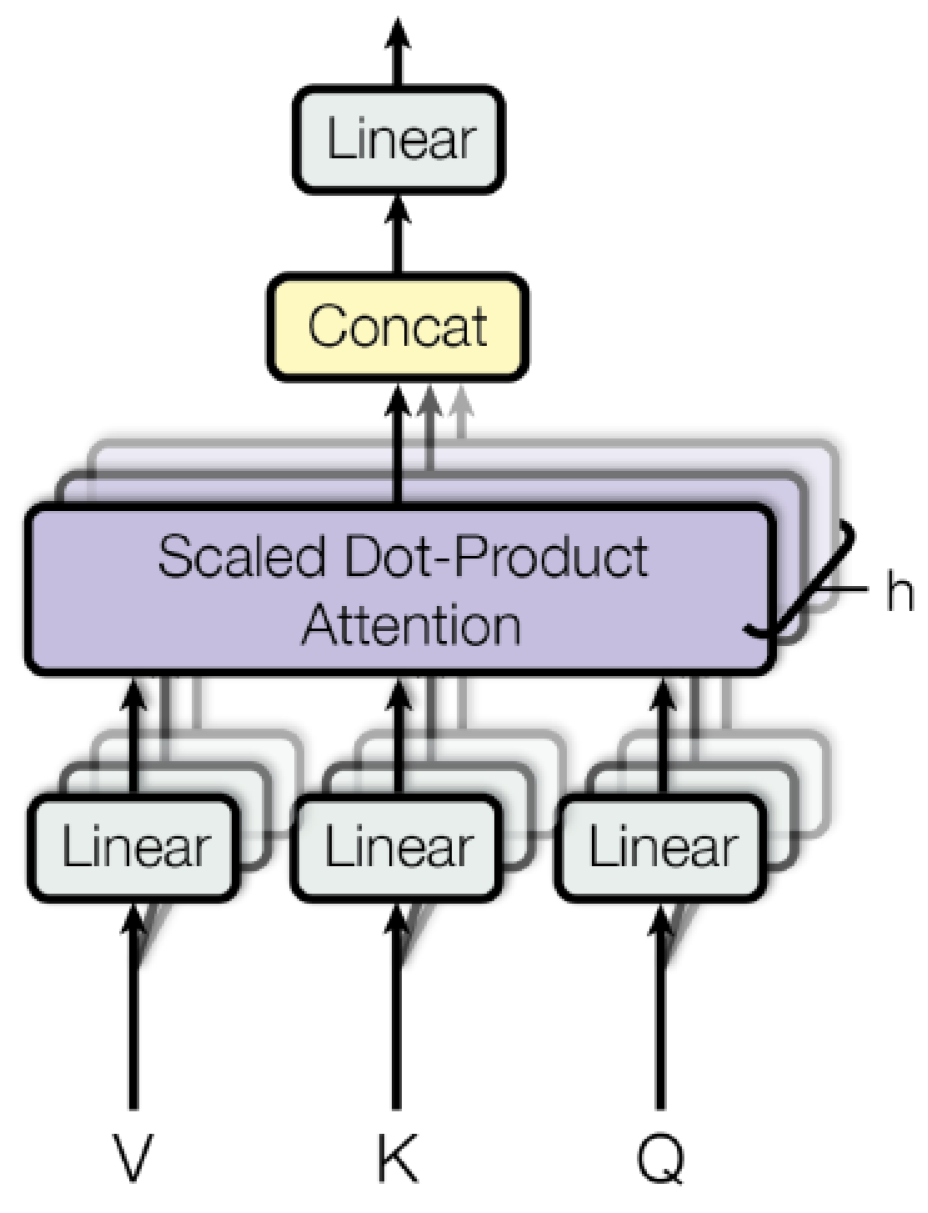
1. Introduction
Iron stands as one of the most extensively utilized metals globally [
1]. The international pricing of iron ore is shaped by demand and supply, as well as influenced by a plethora of quantitative factors, including steel prices, production volumes, oil prices, gold prices, interest rates, inflation rates, iron production, and aluminum prices [
2]. Given iron ore’s critical role in steel manufacturing, accurate price forecasting is essential for effective risk management in associated ventures and projects [
3]. For mining companies like VALE, iron ore price projections are instrumental in assessing the operational viability of specific mines and in managing production surplus.
Unlike other commodities, iron ore pricing follows a unique path, thereby commonly relying on two primary sources. The benchmark index, set daily by key reference companies, represents one source. However, its transparency may be compromised due to behind-the-scenes contractual negotiations, thus affecting market price and quantity predictability. Conversely, the futures market offers nearly round-the-clock trading with transparent transactions, including detailed information on contract volumes, potential buyers and sellers, and their willing transaction prices while the market remains open [
4].
The advent of digitalization in corporate governance has unlocked access to vast quantities of both quantitative and subjective market data. With the enhanced processing capabilities of today’s computers, artificial intelligence (AI) methods have become increasingly feasible and effective for prediction tasks [
5,
6].
Taking advantage of this data wealth, research into future iron ore prices has revealed that hybrid forecasting methodologies offer promising results. Proposals by Li et al. and Ewees et al. have successfully merged optimization techniques with artificial neural networks [
2,
7]. Similarly, Tuo and Zhang have introduced a hybrid model that combines signal decomposition technology with an artificial neural network [
3].
Nonetheless, these methods, which mainly target technical analysis data, struggle to anticipate market shifts in the iron ore sector driven by fundamentally oriented issues. The significant impacts of events like the COVID-19 pandemic, analyzed by Jowitt [
8], and carbon emission reduction policies, explored by Ma and Wang [
9], underscore the profound effect of fundamental variables on pricing.
In their innovative work, Li et al. merged Rank-Dependent Expected Utility (RDEU) with game theory to examine the behaviors of mining and steelmaking companies in commercial conflicts. Their findings reveal the extensive influence of subjective factors—such as industry growth expectations, as well as the production capacity and surplus availability of mining firms—on strategic corporate decision making and market positioning. By analyzing market actors’ data and their production chain expectations, it is possible to delineate behavioral responses, isolate specific flow patterns, and devise tools and signals for enhanced negotiation, investment, and risk management strategies [
10].
In recent years, AI methods employing Natural Language Processing (NLP), like sentiment analysis and opinion mining, have shown notable predictive success in the stock market through fundamental analyses, thus highlighted by studies from Alves [
11] and Igarashi et al. [
12].
Given the unique characteristics of the iron ore market and the cutting-edge predictive tools for similar assets discussed earlier, developing a dedicated decision support system for iron ore assets is crucial. Such a system, being capable of accurately forecasting iron ore prices using time series analysis, assessing asset-related risks via textual information, and recommending optimal resource management strategies, would provide immense value to companies and managers within this sector.
The successful application of sentiment analysis on news articles and the aggregation of indexes using hesitant fuzzy sets demonstrate the potential for creating an index to quantify subjective market variables specific to the iron ore sector. Moreover, this index could serve as an input variable in a fuzzy time series predictive model, thus potentially enhancing the accuracy of iron ore price forecasts beyond current literature methods.
This study aims to explore the use of alternative variables—derived from industry-related news—as inputs in multivariate fuzzy predictive models to forecast the future trends of the average price time series for 62% refined iron ore. To achieve this, an index will be developed through the hesitant fuzzy aggregation of sentiments extracted from iron ore-related news via sentiment analysis. Furthermore, the quantity of news will be evaluated as an exogenous variable in a predictive model employing fuzzy time series, thus aiming to bolster the model’s robustness compared to existing iron ore price forecasting methods in the literature.
The structure of this document is as follows: An overview and discussion of work relevant to this field are provided in
Section 2. The methodology behind the development of the model we propose is detailed in
Section 3. The findings from our investigation are explored and interpreted in
Section 4. Conclusions drawn from this study, alongside suggestions for future research avenues, are offered in
Section 5.
5. Conclusions and Future Works
Given the objectives set forth in the introduction, this study aimed to evaluate the application of alternative variables as exogenous inputs within a predictive model based on fuzzy time series with the goal of enhancing robustness compared to existing methods in the literature for forecasting iron ore prices. To this end, an index was constructed through the hesitant fuzzy aggregation of sentiments extracted from news articles related to iron ore, and the volume of news was considered as a variable.
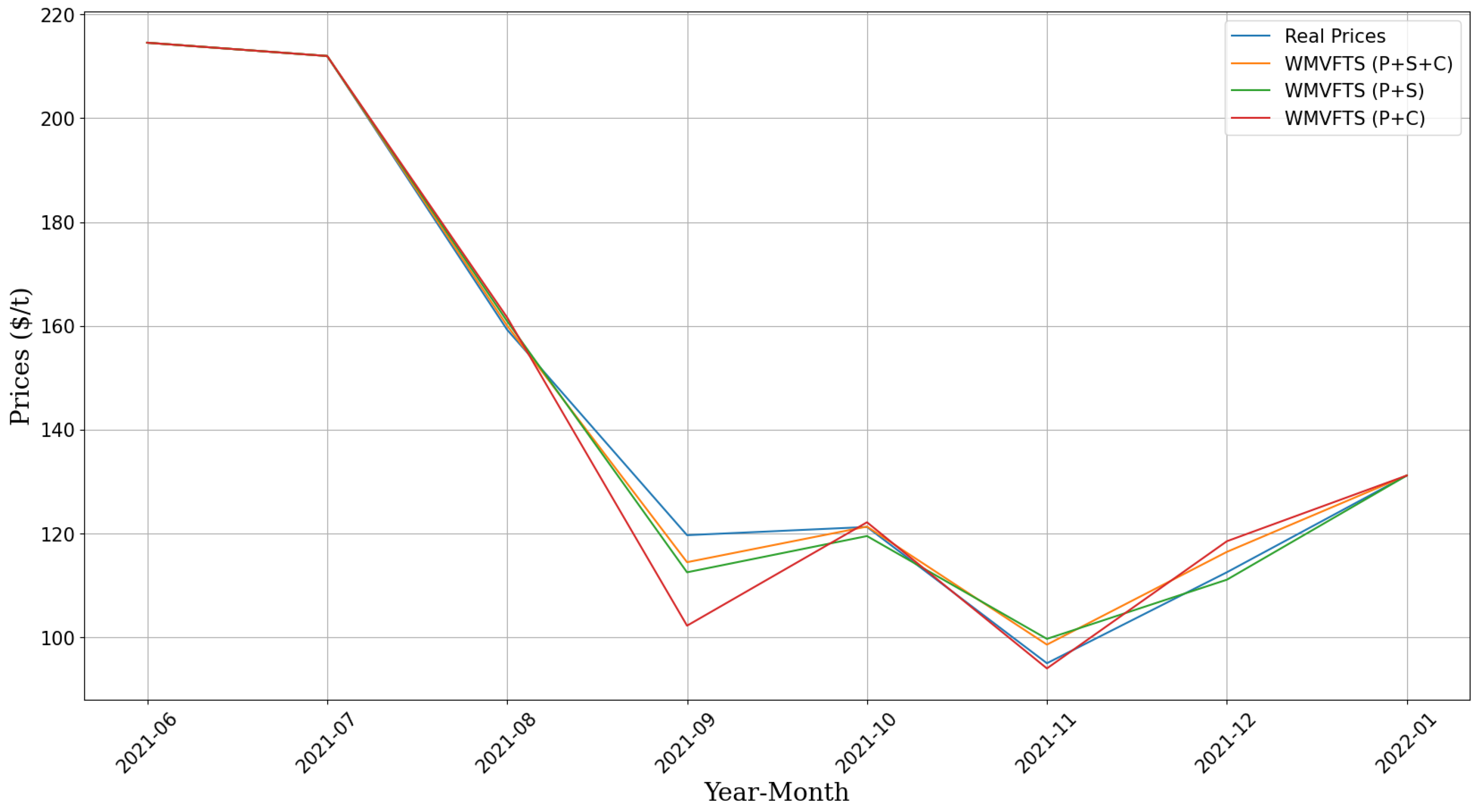
The findings of this research demonstrate the feasibility and positive impact of using an index constructed from aggregated sentiments derived from iron ore-related news for price forecasting, as well as incorporating news volume.
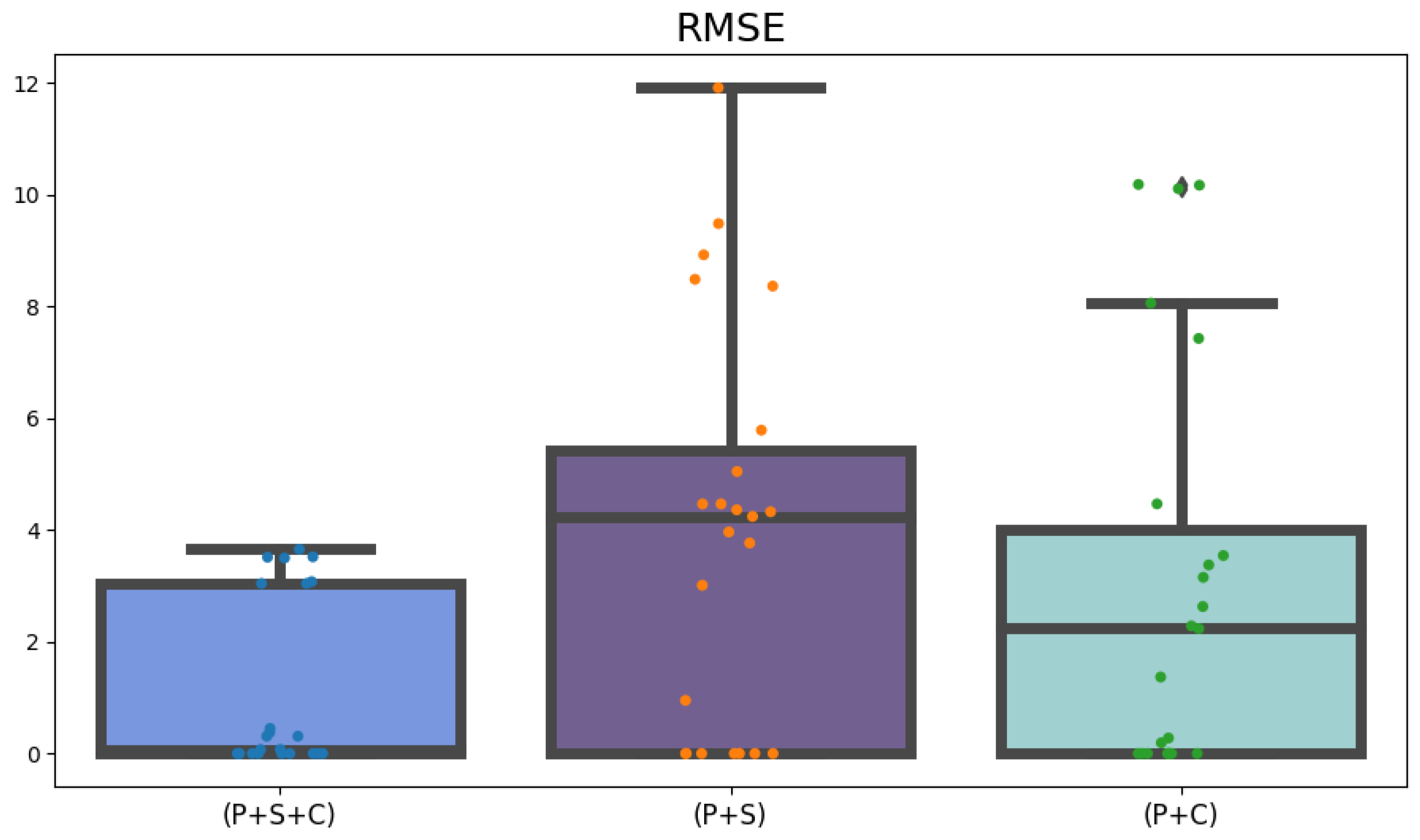
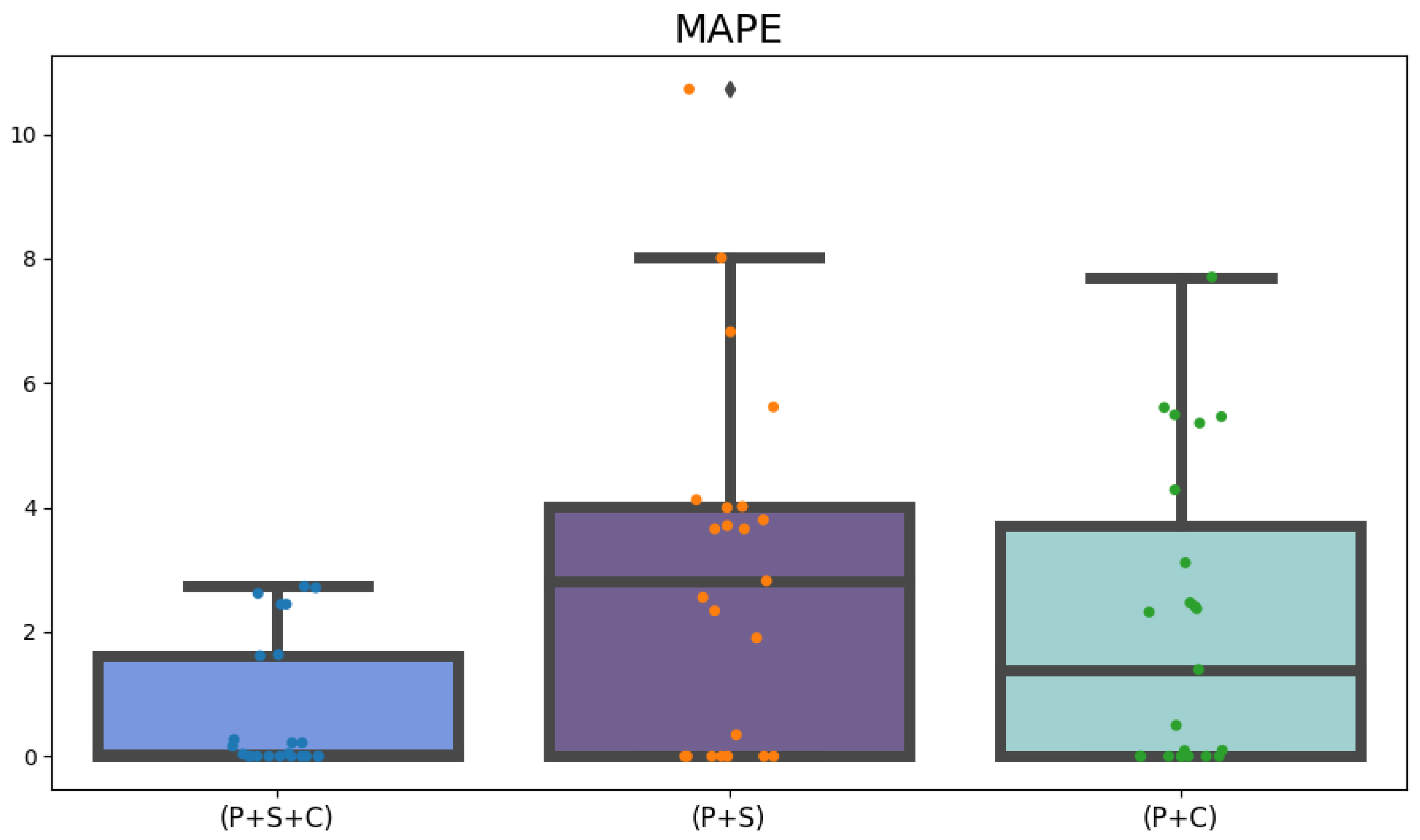
The proposed approach, utilizing the WMVFTS for data analysis, showed improved outcomes when the input dataset included all correlated variables. This predictive method also proved to be superior to the multivariate approaches referenced, as evidenced by descriptive statistical analyses of the RMSE and MAPE. From a planning perspective and aiding analysts in decision making regarding future iron ore prices, the analysis of the MDA metric, with an accuracy above 80% in all tests, suggests that the model presented in this study is promising and reliable for forecasting, especially short- to medium-term trends and fluctuations of the variable of interest.
Throughout the research, some challenges were encountered, and the results had limitations. Identifying an unbiased news source compatible with the BERT parameters for delivering coherent sentiment analysis proved challenging. News articles that influence the rise in iron ore prices may be perceived positively by mining companies but negatively by steel manufacturers. The same news can have different connotations depending on the market sector to which the publishing media are aligned.
Employing a sentiment analysis model trained on a dataset with labeled sentiments from textual sources specialized in the iron ore market and aimed at the relevant segment, mining, or steel manufacturing is likely to enhance the outcomes of this study. However, building such a dataset would require significant effort, as it would necessitate the manual labeling by experts of a large number of news articles impacting the iron ore market in some manner.
Suggestions for future works that build upon this study to refine the employed methodology include several key areas of focus. First, incorporating additional variables that may correlate with the iron ore price series into the predictive model could significantly improve its accuracy. Furthermore, exploring other textual information sources about iron ore and correlated variables, such as reports and specialized articles, could enhance sentiment extraction processes. There is also potential in enhancing the model with modules for automatic decision making that utilize deep learning techniques, with a subsequent comparison of their decisions against those made by human experts. Lastly, applying the methodology proposed in this study to forecast other types of variables could broaden the scope and utility of the research findings.
Author Contributions
Conceptualization, F.M.d.C.S.; methodology, F.M.d.C.S.; validation, F.M.d.C.S., G.P.R.F. and G.P.; resources, F.M.d.C.S.; writing—original draft preparation, F.M.d.C.S., G.P.R.F., F.G.G., R.I.M. and G.P.; writing—review and editing, F.M.d.C.S., G.P.R.F., F.G.G., R.I.M. and G.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mendes, J.A. O ferro na história: Das artes mecânicas às Belas-Artes. Gestáo Desenvolv. 2000, 9, 301–318. [Google Scholar] [CrossRef]
- Li, D.; Moghaddam, M.R.; Monjezi, M.; Jahed Armaghani, D.; Mehrdanesh, A. Development of a Group Method of Data Handling Technique to Forecast Iron Ore Price. Appl. Sci. 2020, 10, 2364. [Google Scholar] [CrossRef]
- Tuo, J.; Zhang, F. Modelling the iron ore price index: A new perspective from a hybrid data reconstructed EEMD-GORU model. J. Manag. Sci. Eng. 2020, 5, 212–225. [Google Scholar] [CrossRef]
- Market Index. FAQs. Market Index. 2022. Available online: https://www.marketindex.com.au/ (accessed on 25 April 2024).
- Arias, M.; Arratia, A.; Xuriguera, R. Forecasting with twitter data. ACM Trans. Intell. Syst. Technol. (TIST) 2014, 5, 1–24. [Google Scholar] [CrossRef]
- Nobre, R.A.; Nascimento, K.C.d.; Vargas, P.A.; Valejo, A.D.B.; Pessin, G.; Villas, L.A.; Filho, G.P.R. AURORA: An autonomous agent-oriented hybrid trading service. Neural Comput. Appl. 2022, 34, 1–16. [Google Scholar] [CrossRef]
- Ewees, A.A.; Elaziz, M.A.; Alameer, Z.; Ye, H.; Jianhua, Z. Improving multilayer perceptron neural network using chaotic grasshopper optimization algorithm to forecast iron ore price volatility. Resour. Policy 2020, 65, 101555. [Google Scholar] [CrossRef]
- Jowitt, S.M. COVID-19 and the global mining industry. SEG Discov. 2020, 122, 33–41. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, J. Time-varying spillovers and dependencies between iron ore, scrap steel, carbon emission, seaborne transportation, and China’s steel stock prices. Res. Policy 2021, 74, 102254. [Google Scholar] [CrossRef]
- Keenan, M.J.S. Advanced Positioning, Flow, and Sentiment Analysis in Commodity Markets: Bridging Fundamental and Technical Analysis; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Alves, D.S. Uso de Técnicas de Computação Social para Tomada de Decisão de Compra e Venda de Ações no Mercado Brasileiro de Bolsa de Valores. Ph.D. Thesis, Departamento de Engenharia Elétrica, Faculdade de Tecnologia, Universidade de Brasília, Brasília, DF, Brazil, 2015; 133p. [Google Scholar]
- Igarashi, W.; Valdevieso, G.S.; Igarashi, D.C.C. Análise de sentimentos e indicadores técnicos: Uma análise da correlação dos preços de ativos com a polaridade de notícias do mercado de ações. Braz. J. Bus. 2020, 3, 470–486. [Google Scholar] [CrossRef]
- Sousa, M.G.; Sakiyama, K.; de Souza Rodrigues, L.; Moraes, P.H.; Fernandes, E.R.; Matsubara, E.T. BERT for stock market sentiment analysis. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 1597–1601. [Google Scholar]
- Dolabela Dias, B.C.; Sadaei, H.J.; De Lima e Silva, P.C.; Guimarães, F.G. Aggregation of Sentiment Analysis Index with Hesitant Fuzzy Sets for Financial Time Series Forecasting. In Proceedings of the 2021 IEEE World AI IoT Congress (AIIoT), Virtual, 10–13 May 2021; pp. 433–439. [Google Scholar] [CrossRef]
- Li, W.; Huang, S.; Qi, Y.; Haizhong, A. Rdeu Hawk-Dove Game Analysis of the China-Australia Iron Ore Trade Conflict. Resour. Policy 2022, 77, 102643. [Google Scholar] [CrossRef]
- Tonidandel, H., Jr.; Guimarães, F.G. Aplicação de Modelos Nebulosos Univariados e Multivariados na Previsão de Preços de Minério De Ferro: Um Estudo Comparativo. In Proceedings of the Congresso Brasileiro de Automática-CBA: 2022, Fortaleza, Brazil, 16–19 October 2022. [Google Scholar]
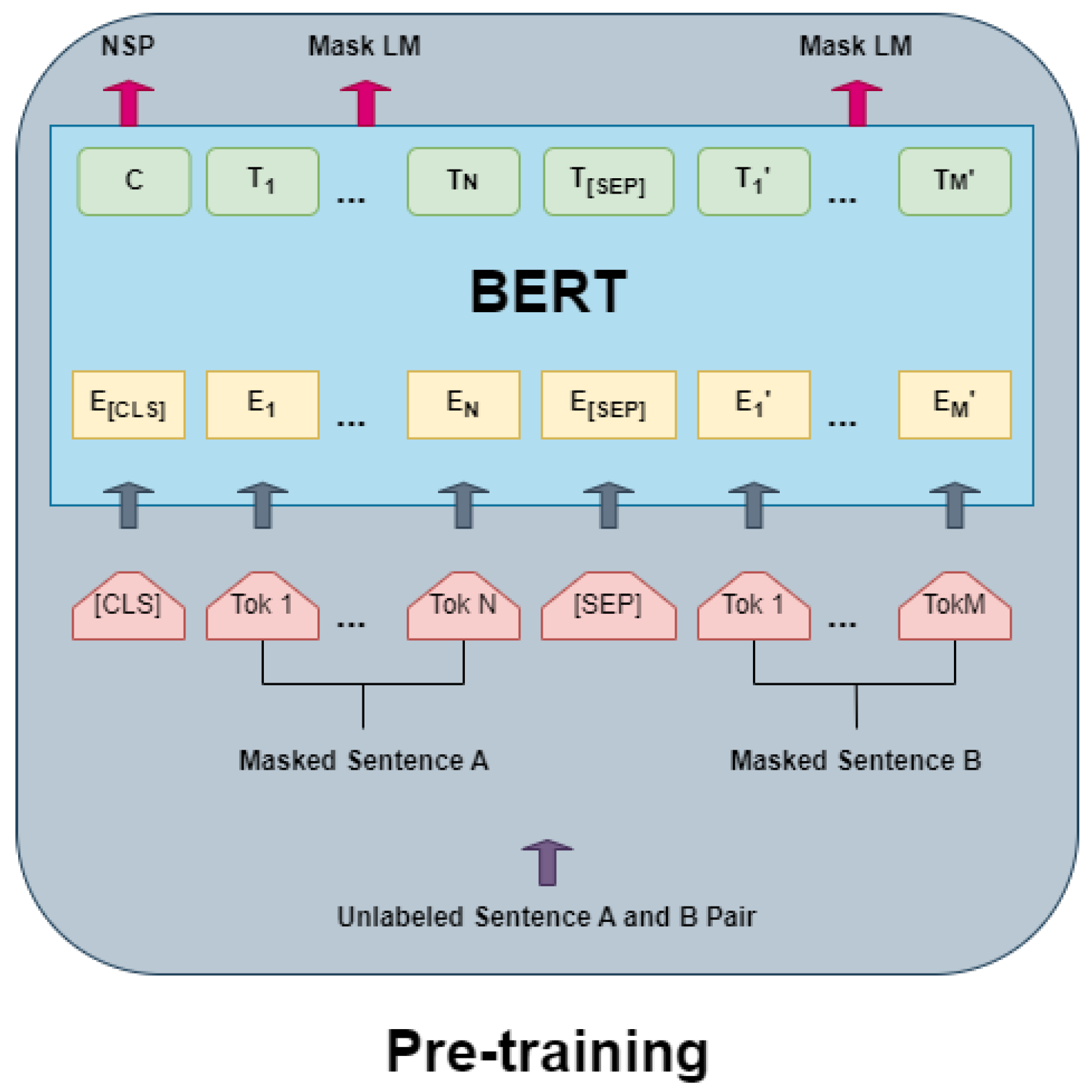
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2018, arXiv:1810.04805. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Song, Q.; Chissom, B.S. Fuzzy time series and its models. Fuzzy Sets Syst. 1993, 54, 269–277. [Google Scholar] [CrossRef]
- Cheng, C.H.; Chen, C.H. Fuzzy time series model based on weighted association rule for financial market forecasting. Expert Syst. 2018, 35, e12271. [Google Scholar] [CrossRef]
- de Lima, P.C. Scalable Models for Probabilistic Forecasting with Fuzzy Time Series. 2019. Available online: https://repositorio.ufmg.br/bitstream/1843/30040/1/Final_Thesis.pdf (accessed on 17 March 2024).
- Silva, P.C.; e Lucas, P.d.O.; Sadaei, H.J.; Guimaraes, F.G. Distributed evolutionary hyperparameter optimization for fuzzy time series. IEEE Trans. Netw. Serv. Manag. 2020, 17, 1309–1321. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).