A Critical Analysis of Deep Semi-Supervised Learning Approaches for Enhanced Medical Image Classification
Abstract
1. Introduction
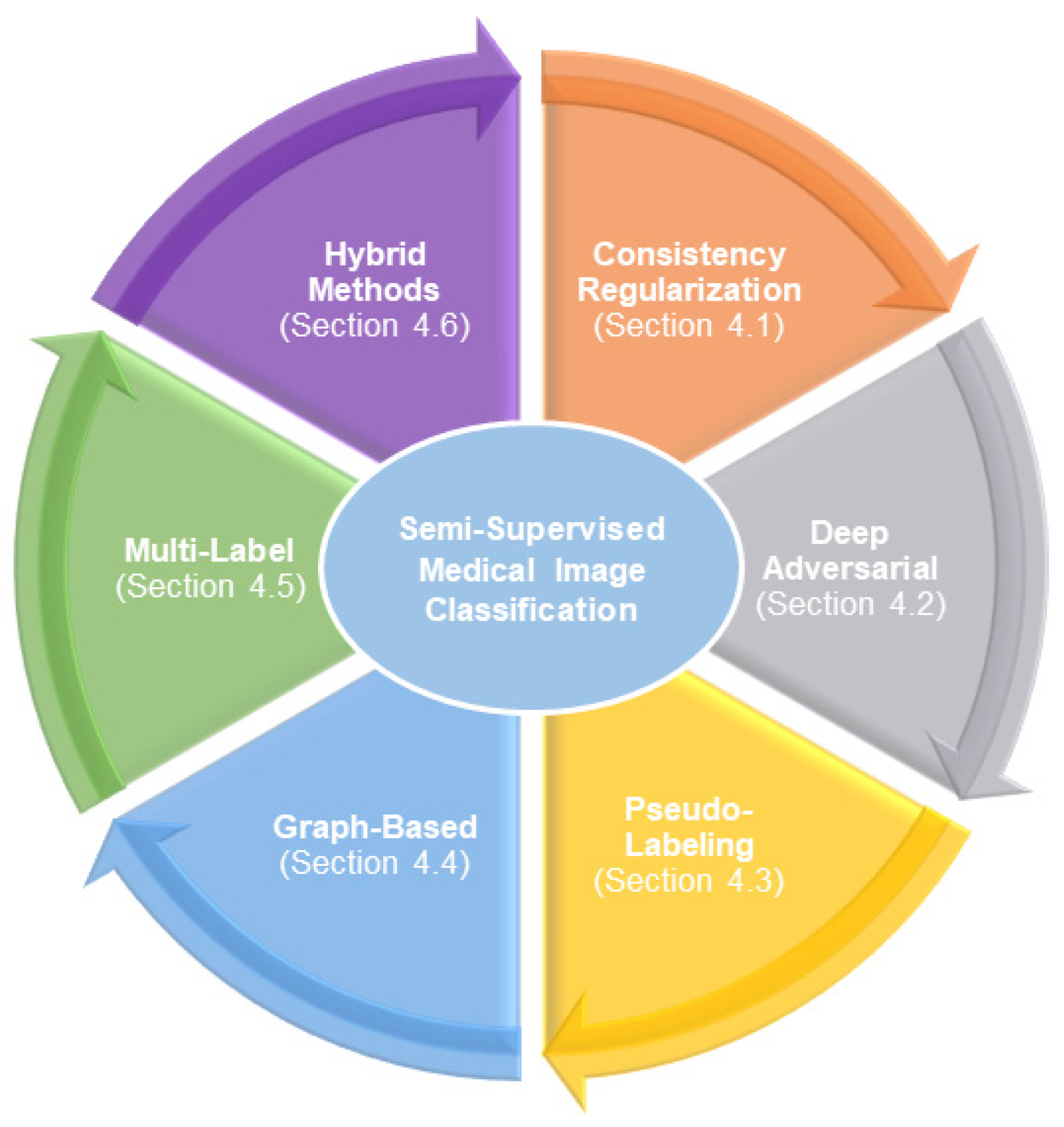
- We propose a comprehensive categorization for primary DSSL methods applied to medical image classification, categorizing these methods into six main groups. Each category is examined for variations, accompanied by standardized descriptions and unified schematic representations.
- We extensively explain each approach, frequently including important equations, elucidate the developmental context underlying the methods, and provide essential performance comparisons.
- A compilation of resources for DSSL is assembled, comprising open-source codes for several reviewed methods, well-known benchmark datasets, and performance evaluations across various label rates on these benchmark datasets.
- We pinpoint three undetermined issues and explore potential research directions for future studies, drawing insights from recent notable research in this area.
2. Background
2.1. Classification Overview
2.1.1. Consistency Regularization Methods
2.1.2. Deep Adversarial Methods
2.1.3. Pseudo-Labeling Methods
2.1.4. Graph-Based Methods
2.1.5. Multi-Label Methods
2.1.6. Hybrid Methods
2.2. Estimations
3. Methodology
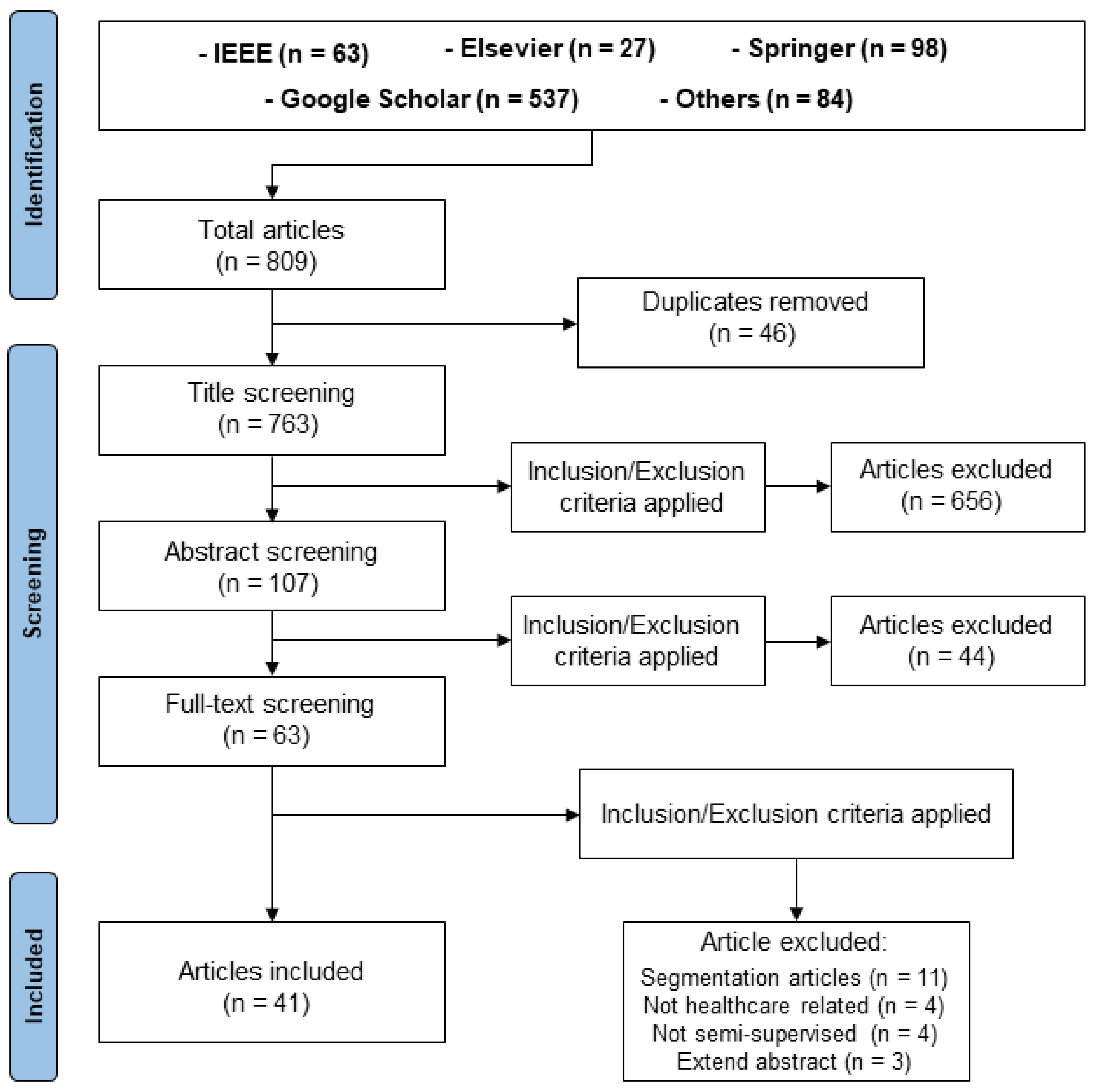
- Review: The primary inquiry driving the literature review was focused on conducting a comparative analysis of various DSSL techniques for medical image classification, with an emphasis on loss function and model design;
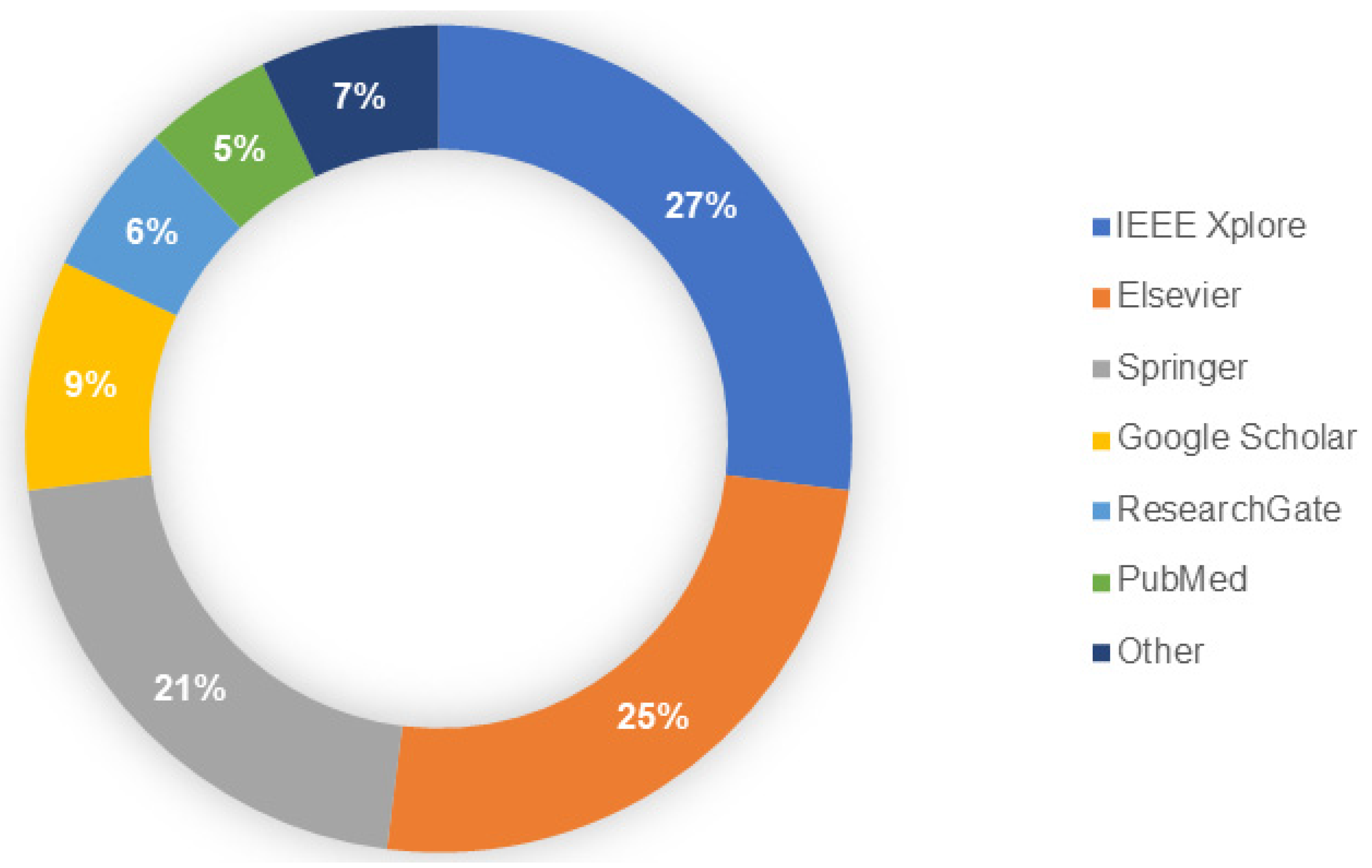
- Search: This search encompassed journal articles, conference articles, published reports, and official websites (Figure 2).
- The primary focus of the study should be on SSL.
- Inclusion of a thorough description of the model architecture and a clear presentation of the classification algorithm’s results.
- For instance, we consider originality, significance of findings, and high number of citation factors.
- There is no peer review or trustworthy records indexing for the research.
- The research has not introduced relevant augmentation or alteration to the established deep learning algorithm.
- The research provides an ambiguous explanation of the experimentation and classification results. The literature review process is delineated in the PRISMA representation depicted in Figure 3.
4. Methods
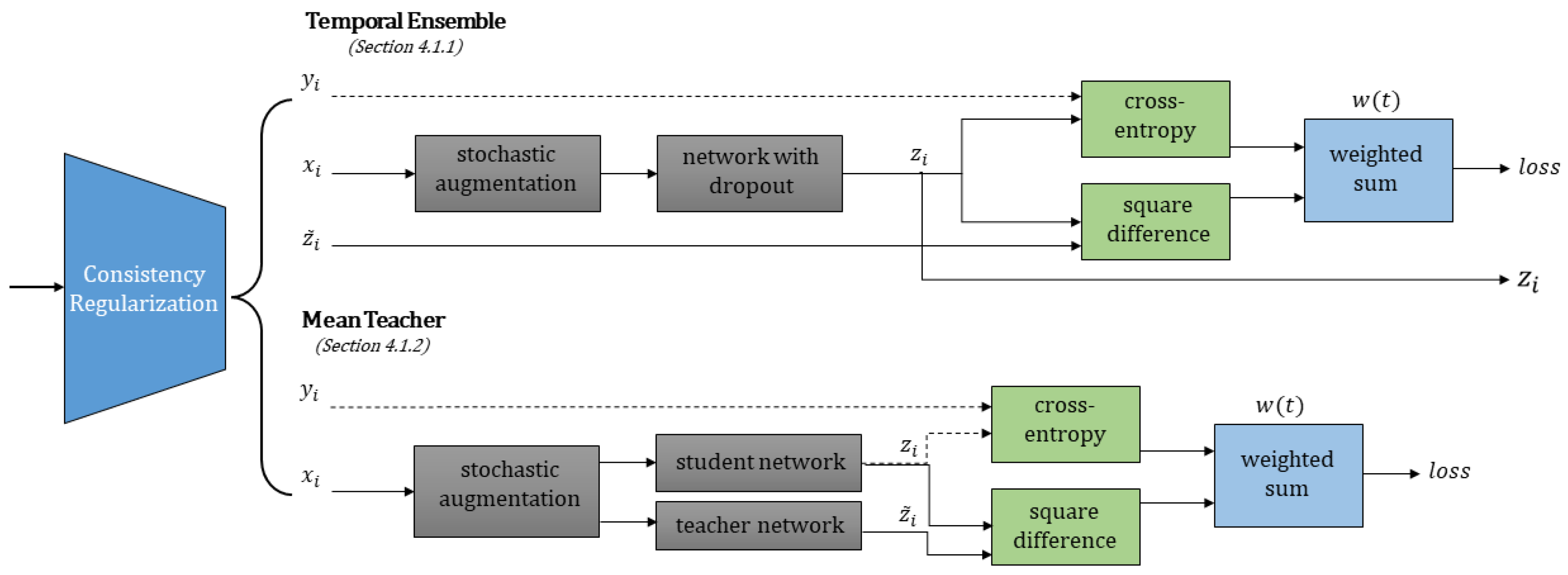
4.1. Consistency Regularization
4.1.1. Temporal Ensemble
4.1.2. Mean Teacher
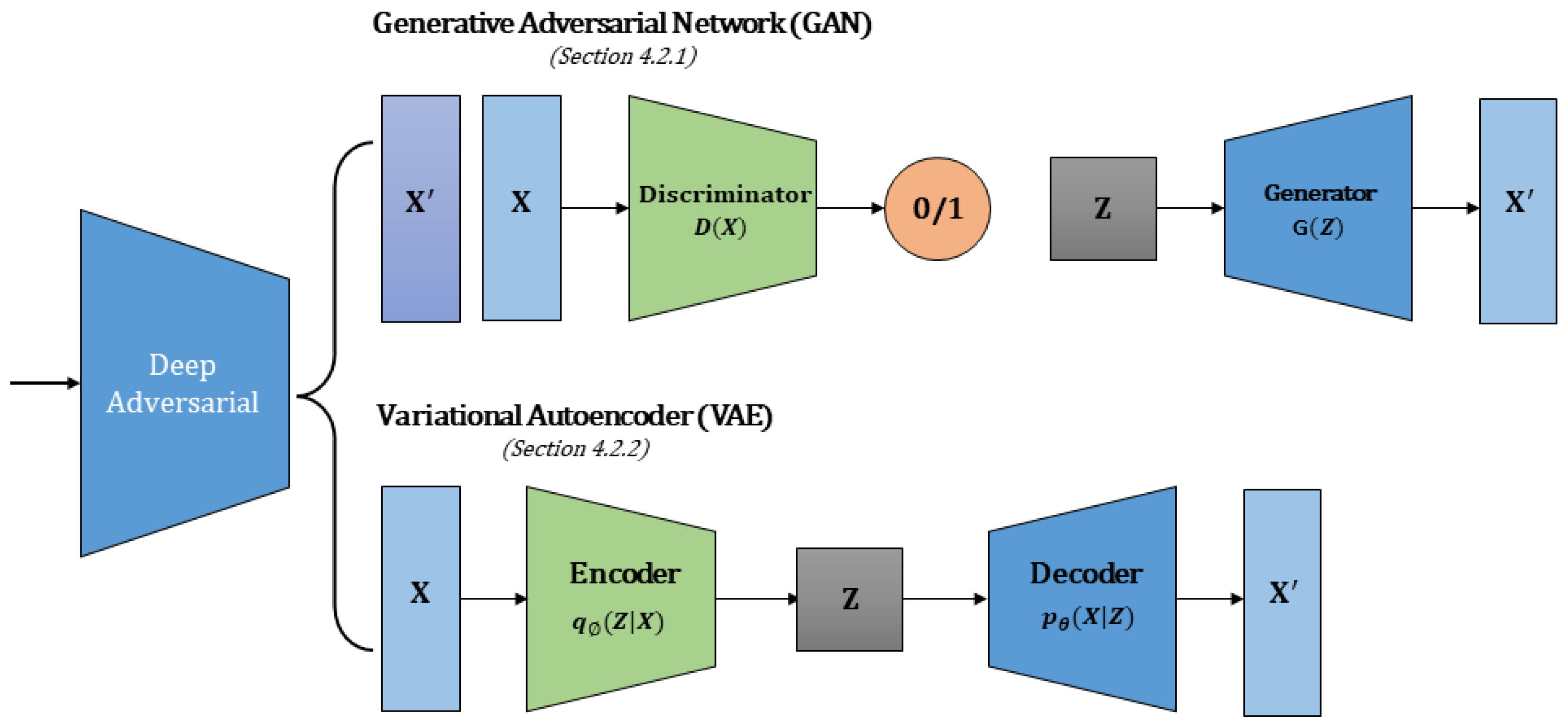
4.2. Deep Adversarial Methods
4.2.1. Generative Adversarial Network (GAN)
4.2.2. Variational Autoencoder (VAE)
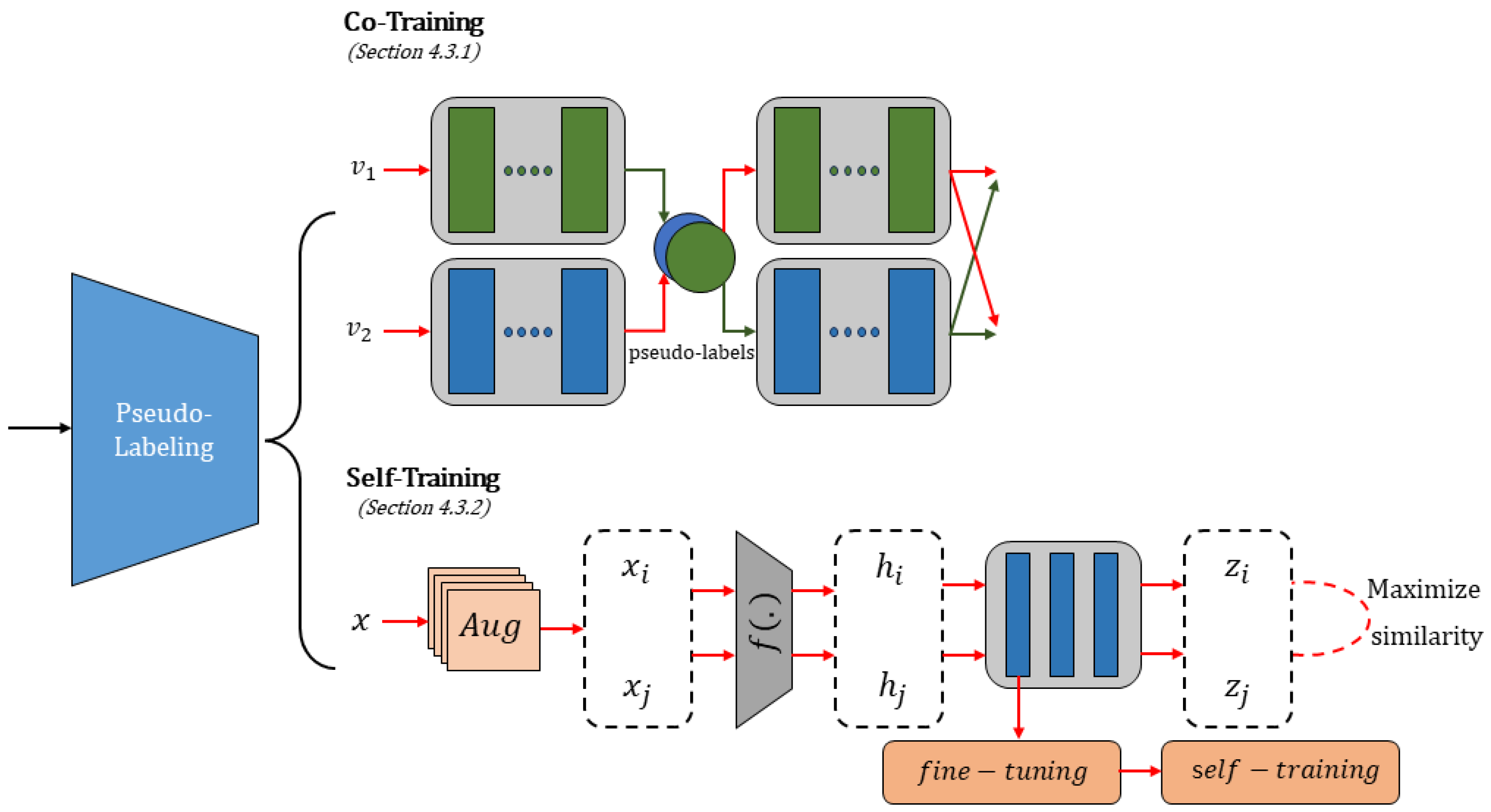
4.3. Pseudo-Labeling Methods
4.3.1. Co-Training
4.3.2. Self-Training
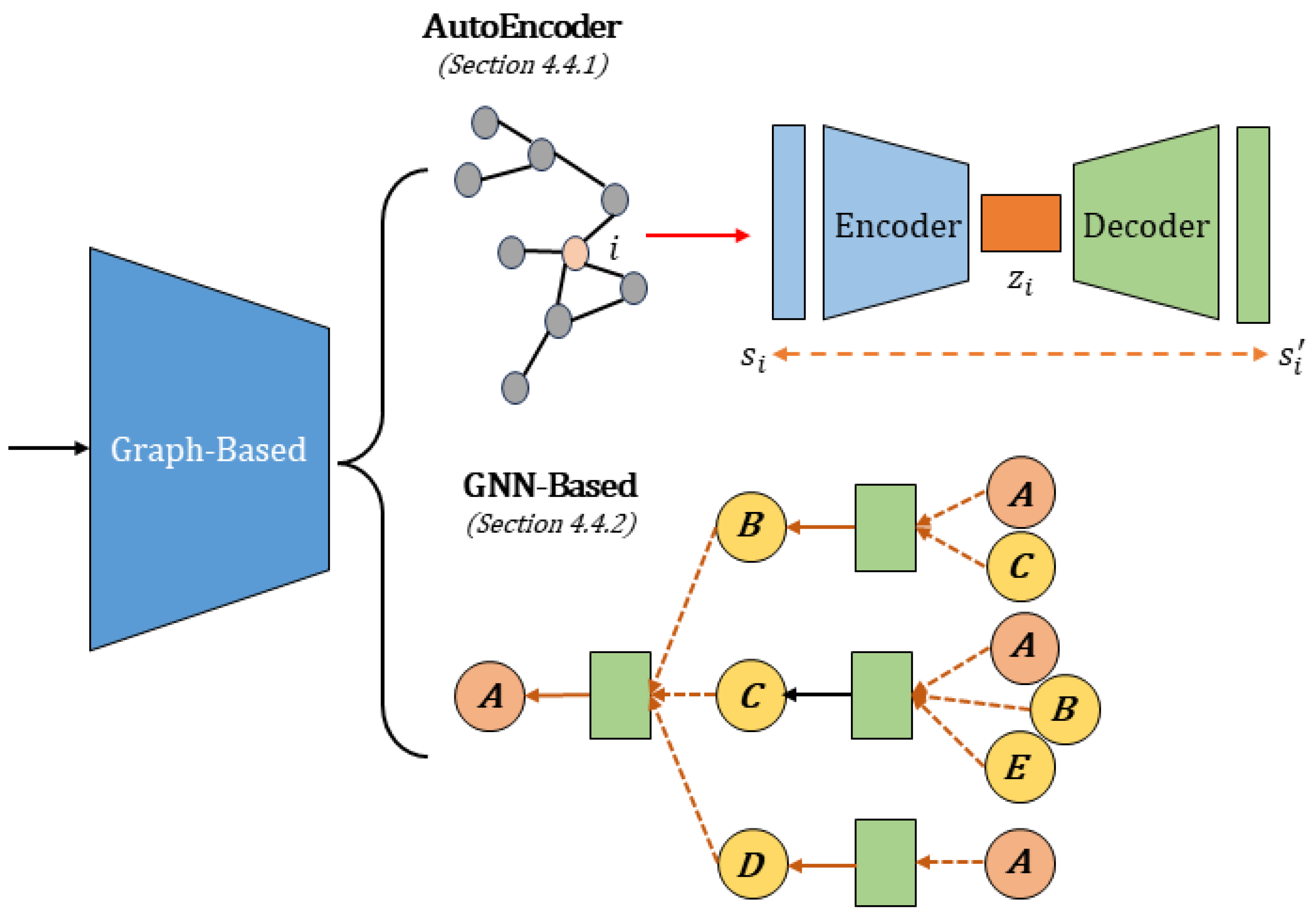
4.4. Graph-Based Methods
4.4.1. AutoEncoder
4.4.2. GNN-Based
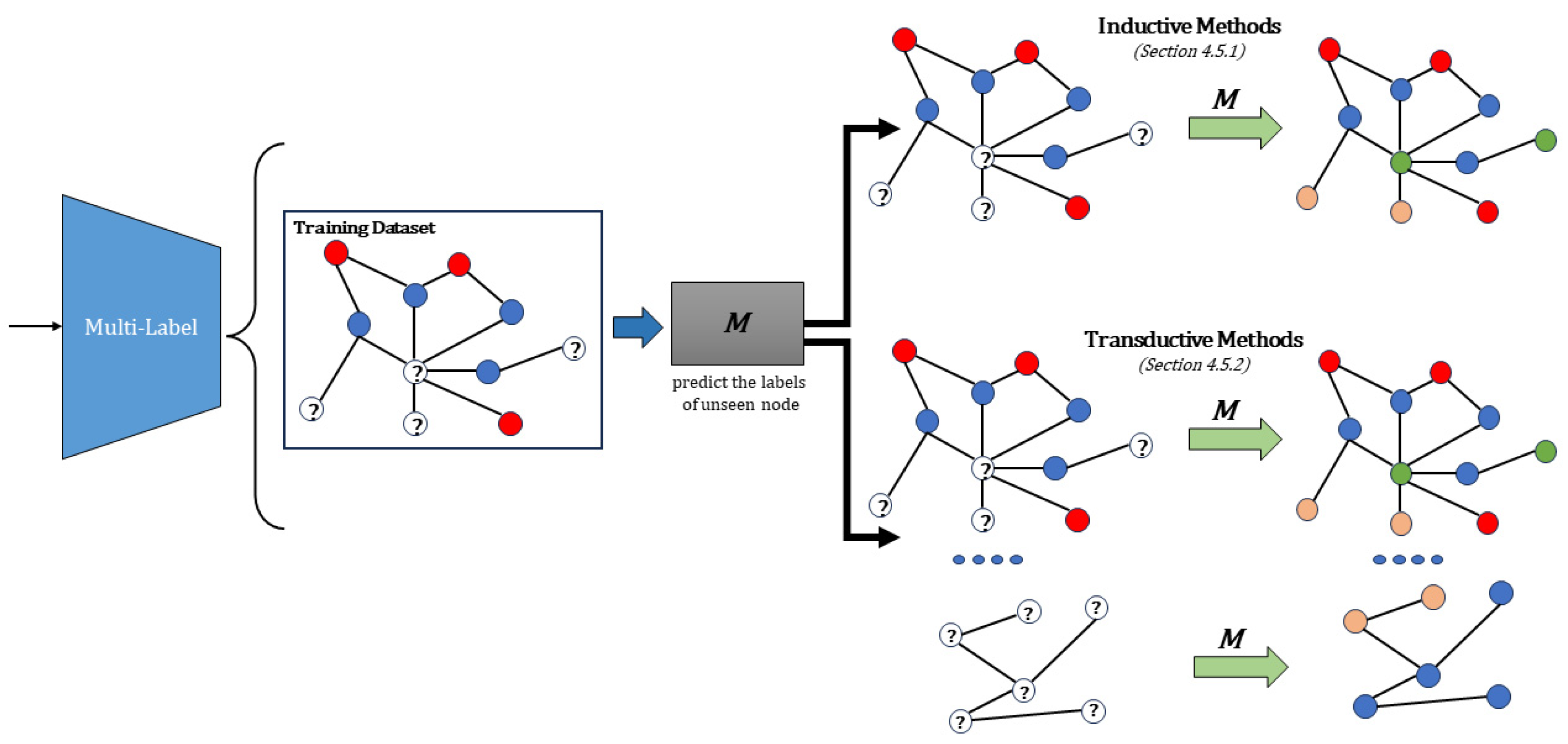
4.5. Multi-Label Methods
4.5.1. Inductive Methods
4.5.2. Transductive Methods
4.6. Hybrid Methods
4.7. Advantages and Disadvantages of DSSL Approaches
5. Comparative Analysis and Discussion
5.1. Datasets
5.2. Experimental Analysis
5.2.1. Experiments on CheXpert and ChestX-ray14 Datasets
5.2.2. Experiments on ISIC2018 Dataset
6. Discussion on Challenges and Future Directions
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DSSL | Deep Semi-Supervised Learning |
| AI | Artificial Intelligence |
| SIFT | Scale-Invariant Feature Transform |
| CNN | Convolutional Neural Network |
| SSL | Semi-Supervised Learning |
| SL | Supervised Learning |
| EM | Expectation Maximization |
| GAN | Generative Adversarial Networks |
| VAE | Variational Auto-Encoders |
| JS | Jensen-Shannon |
| MSE | Mean Squared Error |
| KL | Kullback-Leibler |
| UKSSL | Underlying Knowledge-based Semi-Supervised Learning |
| MedCLR | Contrastive Learning of Medical Visual Representations |
| LTrans | Light Transformer |
| MSA | Multi-Head Self-Attention |
| MLP | Multi-Layer Perceptron |
| EMA | Exponential Moving Average |
| SRC | Sample Relation Consistency |
| S2MTS2 | Mean Teacher for Self-supervised and Semi-supervised Learning |
| NoT | NoTeacher |
| SSAC | Semi-supervised Adversarial Classification |
| GAP | Global Average Pooling |
| PET | Positron Emission Tomography |
| MRI | Magnetic Resonance Imaging |
| SPECT | Single Photon Emission Computed Tomography |
| CS | Clinically Significant |
| ELBO | Evidence Lower Bound |
| DTFD-MIL | Double-Tier Feature Distillation Multiple Instance Learning |
| MIMS | Multi-Instance Multi-Scale |
| WSI | Whole Slide Image |
| CDSI | Cross-Distribution Sample Informativeness |
| GMM | Gaussian Mixture Model |
| KNN | K-Nearest Neighbor |
| ASP | Anchor Set Purification |
| CE | Cross-Entropy |
| GSSL | Graph-Based Semi-Supervised Learning |
| Semi-Supervised HGCN | Semi-Supervised Hypergraph Convolutional Network |
| CRC | Classifying Colorectal Cancer |
| HGNN | Hypergraph Neural Network |
| DNNs | Deep Neural Networks |
| BCE | Binary Cross-Entropy |
| SSMLL | Semi-Supervised Multi-Label Learning |
| MSML | Multi-Symptom Multi-Label |
| SSAL | Semi-Supervised Active Learning |
| AL | Active Learning |
| LC | Least Confidence |
| MLE | Multi-label Entropy |
| MLM | Multi-Label Margin |
| DFUs | Diabetic Foot Ulcers |
| SVD | Singular Value Decomposition |
| MLRF | Multi-Label Relative Feature |
| GCN | Graph Convolutional Network |
| AU | Aleatoric Uncertainty |
| LP | Label Propagation |
| PLGAN | Pseudo-Labeling Generative Adversarial Networks |
| CL | Contrastive Learning |
| OCT | Optical Coherence Tomography |
References
- Sidey-Gibbons, J.A.; Sidey-Gibbons, C.J. Machine learning in medicine: A practical introduction. BMC Med. Res. Methodol. 2019, 19, 64. [Google Scholar] [CrossRef]
- Ker, J.; Wang, L.; Rao, J.; Lim, T. Deep learning applications in medical image analysis. IEEE Access 2017, 6, 9375–9389. [Google Scholar] [CrossRef]
- AlAmir, M.; AlGhamdi, M. The Role of generative adversarial network in medical image analysis: An in-depth survey. ACM Comput. Surv. 2022, 55, 96. [Google Scholar] [CrossRef]
- Kazeminia, S.; Baur, C.; Kuijper, A.; van Ginneken, B.; Navab, N.; Albarqouni, S.; Mukhopadhyay, A. GANs for medical image analysis. Artif. Intell. Med. 2020, 109, 101938. [Google Scholar] [CrossRef] [PubMed]
- Solatidehkordi, Z.; Zualkernan, I. Survey on recent trends in medical image classification using semi-supervised learning. Appl. Sci. 2022, 12, 12094. [Google Scholar] [CrossRef]
- Wang, W.; Liang, D.; Chen, Q.; Iwamoto, Y.; Han, X.-H.; Zhang, Q.; Hu, H.; Lin, L.; Chen, Y.-W. Medical image classification using deep learning. In Deep Learning in Healthcare: Paradigms and Applications; Springer: Cham, Switzerland, 2020; pp. 33–51. [Google Scholar]
- Swati, Z.N.K.; Zhao, Q.; Kabir, M.; Ali, F.; Ali, Z.; Ahmed, S.; Lu, J. Brain tumor classification for MR images using transfer learning and fine-tuning. Comput. Med. Imaging Graph. 2019, 75, 34–46. [Google Scholar] [CrossRef] [PubMed]
- O’Mahony, N.; Campbell, S.; Carvalho, A.; Harapanahalli, S.; Hernandez, G.V.; Krpalkova, L.; Riordan, D.; Walsh, J. Deep learning vs. traditional computer vision. In Proceedings of the Advances in Computer Vision: Proceedings of the 2019 Computer Vision Conference (CVC), Volume 1, Las Vegas, NV, USA, 2–3 May 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Wang, Z.; Tang, C.; Sima, X.; Zhang, L. Research on application of deep learning algorithm in image classification. In Proceedings of the 2021 IEEE Asia-Pacific Conference on Image Processing, Electronics and Computers (IPEC), Dalian, China, 14–16 April 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Liu, P.; Choo, K.-K.R.; Wang, L.; Huang, F. SVM or deep learning? A comparative study on remote sensing image classification. Soft Comput. 2017, 21, 7053–7065. [Google Scholar] [CrossRef]
- Wang, P.; Fan, E.; Wang, P. Comparative analysis of image classification algorithms based on traditional machine learning and deep learning. Pattern Recognit. Lett. 2021, 141, 61–67. [Google Scholar] [CrossRef]
- Devi, M.R.S.; Kumar, V.V.; Sivakumar, P. A review of image classification and object detection on machine learning and deep learning techniques. In Proceedings of the 2021 5th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 2–4 December 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Ciompi, F.; de Hoop, B.; van Riel, S.J.; Chung, K.; Scholten, E.T.; Oudkerk, M.; de Jong, P.A.; Prokop, M.; van Ginneken, B. Automatic classification of pulmonary peri-fissural nodules in computed tomography using an ensemble of 2D views and a convolutional neural network out-of-the-box. Med. Image Anal. 2015, 26, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.-C.; Roth, H.R.; Gao, M.; Lu, L.; Xu, Z.; Nogues, I.; Yao, J.; Mollura, D.; Summers, R.M. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Trans. Med. Imaging 2016, 35, 1285–1298. [Google Scholar] [CrossRef]
- Erickson, B.J.; Korfiatis, P.; Akkus, Z.; Kline, T.L. Machine learning for medical imaging. Radiographics 2017, 37, 505–515. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.-Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Sindhwani, V.; Niyogi, P.; Belkin, M. A co-regularization approach to semi-supervised learning with multiple views. In Proceedings of the ICML Workshop on Learning with Multiple Views, Bonn, Germany, 11 August 2005. [Google Scholar]
- Tao, H.; Hou, C.; Nie, F.; Zhu, J.; Yi, D. Scalable multi-view semi-supervised classification via adaptive regression. IEEE Trans. Image Process. 2017, 26, 4283–4296. [Google Scholar] [CrossRef] [PubMed]
- Nie, F.; Xiang, S.; Liu, Y.; Zhang, C. A general graph-based semi-supervised learning with novel class discovery. Neural Comput. Appl. 2010, 19, 549–555. [Google Scholar] [CrossRef]
- Zhao, Y.; Ball, R.; Mosesian, J.; de Palma, J.-F.; Lehman, B. Graph-based semi-supervised learning for fault detection and classification in solar photovoltaic arrays. IEEE Trans. Power Electron. 2014, 30, 2848–2858. [Google Scholar] [CrossRef]
- Druck, G.; McCallum, A. High-performance semi-supervised learning using discriminatively constrained generative models. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Druck, G.; Pal, C.; McCallum, A.; Zhu, X. Semi-supervised classification with hybrid generative/discriminative methods. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007. [Google Scholar]
- Chapelle, O.; Scholkopf, B.; Zien, A. Semi-supervised learning (chapelle, o. et al., eds.; 2006) [book reviews]. IEEE Trans. Neural Netw. 2009, 20, 542. [Google Scholar] [CrossRef]
- Han, K.; Sheng, V.S.; Song, Y.; Liu, Y.; Qiu, C.; Ma, S.; Liu, Z. Deep semi-supervised learning for medical image segmentation: A review. Expert Syst. Appl. 2024, 245, 123052. [Google Scholar] [CrossRef]
- Cheplygina, V.; de Bruijne, M.; Pluim, J.P. Not-so-supervised: A survey of semi-supervised, multi-instance, and transfer learning in medical image analysis. Med. Image Anal. 2019, 54, 280–296. [Google Scholar] [CrossRef]
- Yang, J.; Du, B.; Wang, D.; Zhang, L. ITER: Image-to-pixel Representation for Weakly Supervised HSI Classification. IEEE Trans. Image Process. 2023, 33, 257–272. [Google Scholar] [CrossRef]
- Mehyadin, A.E.; Abdulazeez, A.M. Classification based on semi-supervised learning: A review. Iraqi J. Comput. Inform. 2021, 47, 1–11. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhang, K.; Fung, K.-M.; Thai, T.C.; Moore, K.; Mannel, R.S.; Liu, H.; Zheng, B.; Qiu, Y. Recent advances and clinical applications of deep learning in medical image analysis. Med. Image Anal. 2022, 79, 102444. [Google Scholar] [CrossRef] [PubMed]
- Huynh, T.; Nibali, A.; He, Z. Semi-supervised learning for medical image classification using imbalanced training data. Comput. Methods Programs Biomed. 2022, 216, 106628. [Google Scholar] [CrossRef] [PubMed]
- Cevikalp, H.; Benligiray, B.; Gerek, Ö.N.; Saribas, H. Semi-Supervised Robust Deep Neural Networks for Multi-Label Classification. In Proceedings of the CVPR Workshops, Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Cevikalp, H.; Benligiray, B.; Gerek, O.N. Semi-supervised robust deep neural networks for multi-label image classification. Pattern Recognit. 2020, 100, 107164. [Google Scholar] [CrossRef]
- Mustafa, A.; Mantiuk, R.K. Transformation consistency regularization–a semi-supervised paradigm for image-to-image translation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XVIII 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Tsai, K.-H.; Lin, H.-T. Learning from label proportions with consistency regularization. In Proceedings of the Asian Conference on Machine Learning, Bangkok, Thailand, 18–20 November 2020. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Langr, J.; Bok, V. GANs in Action: Deep Learning with Generative Adversarial Networks; Simon and Schuster: New York, NY, USA, 2019. [Google Scholar]
- Larsen, A.B.L.; Sønderby, S.K.; Larochelle, H.; Winther, O. Autoencoding beyond pixels using a learned similarity metric. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016. [Google Scholar]
- Sabuhi, M.; Zhou, M.; Bezemer, C.-P.; Musilek, P. Applications of generative adversarial networks in anomaly detection: A systematic literature review. IEEE Access 2021, 9, 161003–161029. [Google Scholar] [CrossRef]
- Mostapha, M.; Prieto, J.; Murphy, V.; Girault, J.; Foster, M.; Rumple, A.; Blocher, J.; Lin, W.; Elison, J.; Gilmore, J. Semi-supervised VAE-GAN for out-of-sample detection applied to MRI quality control. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part III 22. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Lee, D.-H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. Workshop Chall. Represent. Learn. ICML 2013, 3, 896. [Google Scholar]
- Donyavi, Z.; Asadi, S. Diverse training dataset generation based on a multi-objective optimization for semi-supervised classification. Pattern Recognit. 2020, 108, 107543. [Google Scholar] [CrossRef]
- Reed, S.; Lee, H.; Anguelov, D.; Szegedy, C.; Erhan, D.; Rabinovich, A. Training deep neural networks on noisy labels with bootstrapping. arXiv 2014, arXiv:1412.6596. [Google Scholar]
- Zou, Y.; Yu, Z.; Liu, X.; Kumar, B.; Wang, J. Confidence regularized self-training. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Liu, F.; Tian, Y.; Chen, Y.; Liu, Y.; Belagiannis, V.; Carneiro, G. ACPL: Anti-curriculum pseudo-labelling for semi-supervised medical image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Wang, R.; Qi, L.; Shi, Y.; Gao, Y. Better pseudo-label: Joint domain-aware label and dual-classifier for semi-supervised domain generalization. Pattern Recognit. 2023, 133, 108987. [Google Scholar] [CrossRef]
- Sheikhpour, R.; Sarram, M.A.; Gharaghani, S.; Chahooki, M.A.Z. A survey on semi-supervised feature selection methods. Pattern Recognit. 2017, 64, 141–158. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F. Graph-based semi-supervised learning. Artif. Life Robot. 2009, 14, 445–448. [Google Scholar] [CrossRef]
- Song, Z.; Yang, X.; Xu, Z.; King, I. Graph-based semi-supervised learning: A comprehensive review. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8174–8194. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Song, R. Semi-supervised learning for multi-label classification. Reconstruction 2017, 1, 1–6. [Google Scholar]
- Wang, Q.; Jia, N.; Breckon, T.P. A baseline for multi-label image classification using an ensemble of deep convolutional neural networks. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar]
- Bachman, P.; Alsharif, O.; Precup, D. Learning with pseudo-ensembles. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Laine, S.; Aila, T. Temporal ensembling for semi-supervised learning. arXiv 2016, arXiv:1610.02242. [Google Scholar]
- Zhang, W.; Zhu, L.; Hallinan, J.; Zhang, S.; Makmur, A.; Cai, Q.; Ooi, B.C. Boostmis: Boosting medical image semi-supervised learning with adaptive pseudo labeling and informative active annotation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Balaram, S.; Nguyen, C.M.; Kassim, A.; Krishnaswamy, P. Consistency-Based Semi-supervised Evidential Active Learning for Diagnostic Radiograph Classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18–22 September 2022; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Shi, W.; Gong, Y.; Ding, C.; Tao, Z.M.; Zheng, N. Transductive semi-supervised deep learning using min-max features. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Wang, D.; Zhang, Y.; Zhang, K.; Wang, L. Focalmix: Semi-supervised learning for 3d medical image detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Pang, T.; Wong, J.H.D.; Ng, W.L.; Chan, C.S. Semi-supervised GAN-based radiomics model for data augmentation in breast ultrasound mass classification. Comput. Methods Programs Biomed. 2021, 203, 106018. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lv, Q.; Lee, C.H.; Shen, L. GSDA: Generative adversarial network-based semi-supervised data augmentation for ultrasound image classification. Heliyon 2023, 9, e19585. [Google Scholar] [CrossRef] [PubMed]
- Sellars, P.; Aviles-Rivero, A.I.; Schönlieb, C.-B. Laplacenet: A hybrid energy-neural model for deep semi-supervised classification. arXiv 2021, arXiv:2106.04527. [Google Scholar]
- Li, Z.; Togo, R.; Ogawa, T.; Haseyama, M. Chronic gastritis classification using gastric X-ray images with a semi-supervised learning method based on tri-training. Med. Biol. Eng. Comput. 2020, 58, 1239–1250. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Hong, B.; Li, Y.; Zhang, X.; Wu, J.; Wang, C.; Zhang, X.; Gong, T.; Zheng, Y.; Meng, D. A semi-supervised multi-task learning framework for cancer classification with weak annotation in whole-slide images. Med. Image Anal. 2023, 83, 102652. [Google Scholar] [CrossRef] [PubMed]
- Calderon-Ramirez, S.; Giri, R.; Yang, S.; Moemeni, A.; Umana, M.; Elizondo, D.; Torrents-Barrena, J.; Molina-Cabello, M.A. Dealing with scarce labelled data: Semi-supervised deep learning with mix match for COVID-19 detection using chest X-ray images. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Zhou, Y.; He, X.; Huang, L.; Liu, L.; Zhu, F.; Cui, S.; Shao, L. Collaborative learning of semi-supervised segmentation and classification for medical images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Mall, P.K.; Singh, P.K. Credence-Net: A semi-supervised deep learning approach for medical images. Int. J. Nanotechnol. 2023, 20, 897–914. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Huang, X.; Yang, S.; Hu, Z.; Duan, Q.; Metaxas, D.N.; Li, H.; Zhang, S. Hybrid supervision learning for pathology whole slide image classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Oliver, A.; Odena, A.; Raffel, C.A.; Cubuk, E.D.; Goodfellow, I. Realistic evaluation of deep semi-supervised learning algorithms. In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Xie, Q.; Dai, Z.; Hovy, E.; Luong, T.; Le, Q. Unsupervised data augmentation for consistency training. Adv. Neural Inf. Process. Syst. 2020, 33, 6256–6268. [Google Scholar]
- Park, S.; Park, J.; Shin, S.-J.; Moon, I.-C. Adversarial dropout for supervised and semi-supervised learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Ke, Z.; Wang, D.; Yan, Q.; Ren, J.; Lau, R.W. Dual student: Breaking the limits of the teacher in semi-supervised learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. arXiv 2017, arXiv:1703.01780. [Google Scholar]
- Tranfield, D.; Denyer, D.; Smart, P. Towards a methodology for developing evidence-informed management knowledge by means of systematic review. Br. J. Manag. 2003, 14, 207–222. [Google Scholar] [CrossRef]
- Grant, M.J.; Booth, A. A typology of reviews: An analysis of 14 review types and associated methodologies. Health Inf. Libr. J. 2009, 26, 91–108. [Google Scholar] [CrossRef] [PubMed]
- Bilotta, G.S.; Milner, A.M.; Boyd, I. On the use of systematic reviews to inform environmental policies. Environ. Sci. Policy 2014, 42, 67–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, R.; Liao, Q.; Li, D.; Zhang, J. Uncertainty-guided mutual consistency learning for semi-supervised medical image segmentation. Artif. Intell. Med. 2023, 138, 102476. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Kim, S.; Kim, I.; Cheon, Y.; Cho, M.; Han, W.-S. Contrastive regularization for semi-supervised learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Zhang, Y.; Deng, L.; Zhu, H.; Wang, W.; Ren, Z.; Zhou, Q.; Lu, S.; Sun, S.; Zhu, Z.; Gorriz, J.M. Deep learning in food category recognition. Inf. Fusion 2023, 98, 101859. [Google Scholar] [CrossRef]
- Zhu, X. Semi-Supervised Learning with Graphs; Carnegie Mellon University: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Sajjadi, M.; Javanmardi, M.; Tasdizen, T. Regularization with stochastic transformations and perturbations for deep semi-supervised learning. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Montreal, QC, Canada, 22–25 May 2016. [Google Scholar]
- Irvin, J.; Rajpurkar, P.; Ko, M.; Yu, Y.; Ciurea-Ilcus, S.; Chute, C.; Marklund, H.; Haghgoo, B.; Ball, R.; Shpanskaya, K. Chexpert: A large chest radiograph dataset with uncertainty labels and expert comparison. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Gyawali, P.K.; Li, Z.; Ghimire, S.; Wang, L. Semi-supervised learning by disentangling and self-ensembling over stochastic latent space. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part VI 22. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Chartsias, A.; Joyce, T.; Papanastasiou, G.; Semple, S.; Williams, M.; Newby, D.E.; Dharmakumar, R.; Tsaftaris, S.A. Disentangled representation learning in cardiac image analysis. Med. Image Anal. 2019, 58, 101535. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Xie, W.; Wong, K.K.; Liao, Z. Classification of myocardial fibrosis in DE-MRI based on semi-supervised semantic segmentation and dual attention mechanism. Comput. Methods Programs Biomed. 2022, 225, 107041. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Ren, Z.; Kong, X.; Zhang, Y.; Wang, S. UKSSL: Underlying knowledge based semi-supervised learning for medical image classification. IEEE Open J. Eng. Med. Biol. 2023; 1–8. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020. [Google Scholar]
- Becker, S.; Hinton, G.E. Self-organizing neural network that discovers surfaces in random-dot stereograms. Nature 1992, 355, 161–163. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Montreal, QC, Canada, 22–25 May 2016. [Google Scholar]
- Wu, Z.; Xiong, Y.; Yu, S.X.; Lin, D. Unsupervised feature learning via non-parametric instance discrimination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Weng, Y.; Zhang, Y.; Wang, W.; Dening, T. Semi-supervised information fusion for medical image analysis: Recent progress and future perspectives. Inf. Fusion 2024, 106, 102263. [Google Scholar] [CrossRef]
- Liu, Q.; Yu, L.; Luo, L.; Dou, Q.; Heng, P.A. Semi-supervised medical image classification with relation-driven self-ensembling model. IEEE Trans. Med. Imaging 2020, 39, 3429–3440. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Cao, J.; Li, B.; Yuan, C.; Hu, W.; Li, Y.; Duan, Y. Knowledge distillation via instance relationship graph. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar]
- Battaglia, P.W.; Hamrick, J.B.; Bapst, V.; Sanchez-Gonzalez, A.; Zambaldi, V.; Malinowski, M.; Tacchetti, A.; Raposo, D.; Santoro, A.; Faulkner, R. Relational inductive biases, deep learning, and graph networks. arXiv 2018, arXiv:1806.01261. [Google Scholar]
- Liu, F.; Tian, Y.; Cordeiro, F.R.; Belagiannis, V.; Reid, I.; Carneiro, G. Self-supervised mean teacher for semi-supervised chest X-ray classification. In Proceedings of the International Workshop on Machine Learning in Medical Imaging, Strasbourg, France, 27 September 2021; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Cai, Q.; Wang, Y.; Pan, Y.; Yao, T.; Mei, T. Joint contrastive learning with infinite possibilities. Adv. Neural Inf. Process. Syst. 2020, 33, 12638–12648. [Google Scholar]
- Unnikrishnan, B.; Nguyen, C.; Balaram, S.; Li, C.; Foo, C.S.; Krishnaswamy, P. Semi-supervised classification of radiology images with NoTeacher: A teacher that is not mean. Med. Image Anal. 2021, 73, 102148. [Google Scholar] [CrossRef] [PubMed]
- Harshvardhan, G.; Gourisaria, M.K.; Pandey, M.; Rautaray, S.S. A comprehensive survey and analysis of generative models in machine learning. Comput. Sci. Rev. 2020, 38, 100285. [Google Scholar]
- Zhang, X.; Yao, L.; Yuan, F. Adversarial variational embedding for robust semi-supervised learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Diaz-Pinto, A.; Colomer, A.; Naranjo, V.; Morales, S.; Xu, Y.; Frangi, A.F. Retinal image synthesis and semi-supervised learning for glaucoma assessment. IEEE Trans. Med. Imaging 2019, 38, 2211–2218. [Google Scholar] [CrossRef] [PubMed]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Durgadevi, M. Generative adversarial network (gan): A general review on different variants of gan and applications. In Proceedings of the 2021 6th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 8–10 July 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Li, D.; Liu, S.; Lyu, Z.; Xiang, W.; He, W.; Liu, F.; Zhang, Z. Use mean field theory to train a 200-layer vanilla GAN. In Proceedings of the 2021 IEEE 33rd International Conference on Tools with Artificial Intelligence (ICTAI), Washington, DC, USA, 1–3 November 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Alrashedy, H.H.N.; Almansour, A.F.; Ibrahim, D.M.; Hammoudeh, M.A.A. BrainGAN: Brain MRI image generation and classification framework using GAN architectures and CNN models. Sensors 2022, 22, 4297. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Zhang, J.; Xia, Y. Semi-supervised adversarial model for benign–malignant lung nodule classification on chest CT. Med. Image Anal. 2019, 57, 237–248. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Yang, X.; Lin, Y.; Wang, Z.; Li, X.; Cheng, K.-T. Bi-modality medical image synthesis using semi-supervised sequential generative adversarial networks. IEEE J. Biomed. Health Inform. 2019, 24, 855–865. [Google Scholar] [CrossRef] [PubMed]
- Moseley, M.; Donnan, G. Multimodality imaging: Introduction. Stroke 2004, 35 (Suppl. S11), 2632–2634. [Google Scholar] [CrossRef]
- Deshpande, I.; Zhang, Z.; Schwing, A.G. Generative modeling using the sliced wasserstein distance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Wu, J.; Huang, Z.; Acharya, D.; Li, W.; Thoma, J.; Paudel, D.P.; Gool, L.V. Sliced wasserstein generative models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Yang, Q.; Yan, P.; Zhang, Y.; Yu, H.; Shi, Y.; Mou, X.; Kalra, M.K.; Zhang, Y.; Sun, L.; Wang, G. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Trans. Med. Imaging 2018, 37, 1348–1357. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Zheng, G. Handling Imbalanced Data: Uncertainty-Guided Virtual Adversarial Training with Batch Nuclear-Norm Optimization for Semi-Supervised Medical Image Classification. IEEE J. Biomed. Health Inform. 2022, 26, 2983–2994. [Google Scholar] [CrossRef]
- Cui, S.; Wang, S.; Zhuo, J.; Li, L.; Huang, Q.; Tian, Q. Towards discriminability and diversity: Batch nuclear-norm maximization under label insufficient situations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Lazo, J.F.; Rosa, B.; Catellani, M.; Fontana, M.; Mistretta, F.A.; Musi, G.; de Cobelli, O.; de Mathelin, M.; De Momi, E. Semi-supervised Bladder Tissue Classification in Multi-Domain Endoscopic Images. IEEE Trans. Biomed. Eng. 2023, 70, 2822–2833. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Rezende, D.J.; Mohamed, S.; Wierstra, D. Stochastic backpropagation and approximate inference in deep generative models. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Imran, A.-A.-Z.; Terzopoulos, D. Multi-adversarial variational autoencoder nets for simultaneous image generation and classification. Deep Learn. Appl. 2021, 2, 249–271. [Google Scholar]
- Durugkar, I.; Gemp, I.; Mahadevan, S. Generative multi-adversarial networks. arXiv 2016, arXiv:1611.01673. [Google Scholar]
- Mordido, G.; Yang, H.; Meinel, C. Dropout-gan: Learning from a dynamic ensemble of discriminators. arXiv 2018, arXiv:1807.11346. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Ji, C.; Wang, Y.; Gao, Z.; Li, L.; Ni, J.; Zheng, C. A semi-supervised learning method for MiRNA-disease association prediction based on variational autoencoder. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 19, 2049–2059. [Google Scholar] [CrossRef] [PubMed]
- Bartel, D.P. MicroRNAs: Genomics, biogenesis, mechanism, and function. Cell 2004, 116, 281–297. [Google Scholar] [CrossRef] [PubMed]
- Ambros, V. The functions of animal microRNAs. Nature 2004, 431, 350–355. [Google Scholar] [CrossRef] [PubMed]
- Bhaskaran, M.; Mohan, M. MicroRNAs: History, biogenesis, and their evolving role in animal development and disease. Vet. Pathol. 2014, 51, 759–774. [Google Scholar] [CrossRef] [PubMed]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-vae: Learning basic visual concepts with a constrained variational framework. In Proceedings of the International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Hsu, T.-C.; Lin, C. Learning from small medical data—Robust semi-supervised cancer prognosis classifier with Bayesian variational autoencoder. Bioinform. Adv. 2023, 3, vbac100. [Google Scholar] [CrossRef] [PubMed]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998. [Google Scholar]
- Qiao, S.; Shen, W.; Zhang, Z.; Wang, B.; Yuille, A. Deep co-training for semi-supervised image recognition. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Yang, Z.; Wu, W.; Zhang, J.; Zhao, Y.; Gu, L. Deep co-training active learning for mammographic images classification. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar]
- Ren, Z.; Wang, S.; Zhang, Y. Weakly supervised machine learning. CAAI Trans. Intell. Technol. 2023, 8, 549–580. [Google Scholar] [CrossRef]
- Zhou, Z.-H. A brief introduction to weakly supervised learning. Natl. Sci. Rev. 2018, 5, 44–53. [Google Scholar] [CrossRef]
- Zhu, X.J. Semi-Supervised Learning Literature Survey; University of Wisconsin-Madison: Madison, WI, USA, 2005. [Google Scholar]
- Zhang, H.; Meng, Y.; Zhao, Y.; Qiao, Y.; Yang, X.; Coupland, S.E.; Zheng, Y. Dtfd-mil: Double-tier feature distillation multiple instance learning for histopathology whole slide image classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Yan, C.; Yao, J.; Li, R.; Xu, Z.; Huang, J. Weakly supervised deep learning for thoracic disease classification and localization on chest X-rays. In Proceedings of the 2018 ACM International Conference on Bioinformatics, Computational Biology, and Health Informatics, Washington, DC, USA, 29 August–1 September 2018. [Google Scholar]
- Li, S.; Liu, Y.; Sui, X.; Chen, C.; Tjio, G.; Ting, D.S.W.; Goh, R.S.M. Multi-instance multi-scale CNN for medical image classification. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part IV 22. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, R.; Chen, B.; Meng, D.; Wang, L. Weakly supervised lesion detection from fundus images. IEEE Trans. Med. Imaging 2018, 38, 1501–1512. [Google Scholar] [CrossRef] [PubMed]
- Radosavovic, I.; Dollár, P.; Girshick, R.; Gkioxari, G.; He, K. Data distillation: Towards omni-supervised learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Grandvalet, Y.; Bengio, Y. Semi-supervised learning by entropy minimization. In Proceedings of the Advances in Neural Information Processing Systems 17 (NIPS 2004), Vancouver, BC, Canada, 13–18 December 2004. [Google Scholar]
- Shakya, K.S.; Jaiswal, M.; Porteous, J.; K, P.; Kumar, V.; Alavi, A.; Laddi, A. SellaMorph-Net: A Novel Machine Learning Approach for Precise Segmentation of Sella Turcica Complex Structures in Full Lateral Cephalometric Images. Appl. Sci. 2023, 13, 9114. [Google Scholar] [CrossRef]
- Abu, A.; Abdukarimov, Y.; Tu, N.A.; Lee, M.-H. Meta Pseudo Labels for Chest X-ray Image Classification. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022. [Google Scholar]
- Pham, H.; Dai, Z.; Xie, Q.; Le, Q.V. Meta pseudo labels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Shakya, K.S.; Jaiswal, M.; Priti, K.; Alavi, A.; Kumar, V.; Li, M.; Laddi, A. A novel SM-Net model to assess the morphological types of Sella Turcica using Lateral Cephalogram. Res. Sq. 2022, preprint. [Google Scholar]
- Sharma, C.M.; Goyal, L.; Chariar, V.M.; Sharma, N. Lung disease classification in CXR images using hybrid inception-ResNet-v2 model and edge computing. J. Healthc. Eng. 2022, 2022, 9036457. [Google Scholar] [CrossRef] [PubMed]
- Chapelle, O.; Zien, A. Semi-supervised classification by low density separation. In Proceedings of the International Workshop on Artificial Intelligence and Statistics, Bridgetown, Barbados, 6–8 January 2005. [Google Scholar]
- Zhu, X.; Ghahramani, Z. Learning from Labeled and Unlabeled Data with Label Propagation; Carnegie Mellon University: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Aviles-Rivero, A.I.; Papadakis, N.; Li, R.; Sellars, P.; Fan, Q.; Tan, R.T.; Schönlieb, C.-B. GraphXNET-Chest X-ray Classification Under Extreme Minimal Supervision. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part VI 22. Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, X.; Peng, Y.; Lu, L.; Lu, Z.; Bagheri, M.; Summers, R.M. Chestx-ray8: Hospital-scale chest X-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Gu, L.; Zhang, X.; You, S.; Zhao, S.; Liu, Z.; Harada, T. Semi-supervised learning in medical images through graph-embedded random forest. Front. Neuroinformatics 2020, 14, 601829. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Song, M.; Tao, D.; Liu, Z.; Zhang, L.; Chen, C.; Bu, J. Random forest construction with robust semisupervised node splitting. IEEE Trans. Image Process. 2014, 24, 471–483. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.-C.; You, Z.-H.; Huang, D.-S.; Kwoh, C.K. Graph representation learning in bioinformatics: Trends, methods and applications. Brief. Bioinform. 2022, 23, bbab340. [Google Scholar] [CrossRef] [PubMed]
- Kang, Z.; Peng, C.; Cheng, Q.; Liu, X.; Peng, X.; Xu, Z.; Tian, L. Structured graph learning for clustering and semi-supervised classification. Pattern Recognit. 2021, 110, 107627. [Google Scholar] [CrossRef]
- Ge, C.; Gu, I.Y.-H.; Jakola, A.S.; Yang, J. Deep semi-supervised learning for brain tumor classification. BMC Med. Imaging 2020, 20, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bakht, A.B.; Javed, S.; AlMarzouqi, H.; Khandoker, A.; Werghi, N. Colorectal cancer tissue classification using semi-supervised hypergraph convolutional network. In Proceedings of the 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI), Nice, France, 13–16 April 2021. [Google Scholar]
- Ponzio, F.; Macii, E.; Ficarra, E.; Di Cataldo, S. Colorectal cancer classification using deep convolutional networks. In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies, Funchal, Portugal, 19–21 January 2018. [Google Scholar]
- Shakya, K.S.; Priti, K.; Jaiswal, M.; Laddi, A. Segmentation of Sella Turcica in X-ray Image based on U-Net Architecture. Procedia Comput. Sci. 2023, 218, 828–835. [Google Scholar] [CrossRef]
- Liu, W.; Wang, H.; Shen, X.; Tsang, I.W. The emerging trends of multi-label learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7955–7974. [Google Scholar] [CrossRef] [PubMed]
- Coulibaly, S.; Kamsu-Foguem, B.; Kamissoko, D.; Traore, D. Deep Convolution Neural Network sharing for the multi-label images classification. Mach. Learn. Appl. 2022, 10, 100422. [Google Scholar] [CrossRef]
- Song, H.; Kim, M.; Park, D.; Shin, Y.; Lee, J.-G. Learning from noisy labels with deep neural networks: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8135–8153. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Xu, J.; Shi, R.; Yang, K.; Zhang, D.; Gao, M.; Ma, H.; Qian, W. A multi-label deep learning model with interpretable grad-CAM for diabetic retinopathy classification. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020. [Google Scholar]
- Selvaraju, R.R.; Das, A.; Vedantam, R.; Cogswell, M.; Parikh, D.; Batra, D. Grad-CAM: Why did you say that? arXiv 2016, arXiv:1611.07450. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chattopadhay, A.; Sarkar, A.; Howlader, P.; Balasubramanian, V.N. Grad-cam++: Generalized gradient-based visual explanations for deep convolutional networks. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018. [Google Scholar]
- Liu, L.; Lei, W.; Wan, X.; Liu, L.; Luo, Y.; Feng, C. Semi-supervised active learning for COVID-19 lung ultrasound multi-symptom classification. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2020. [Google Scholar]
- Gao, M.; Zhang, Z.; Yu, G.; Arık, S.Ö.; Davis, L.S.; Pfister, T. Consistency-based semi-supervised active learning: Towards minimizing labeling cost. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part X 16. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Tomanek, K.; Hahn, U. Semi-supervised active learning for sequence labeling. In Proceedings of the Joint Conference of the 47th Annual Meeting of the ACL and the 4th International Joint Conference on Natural Language Processing of the AFNLP, Suntec, Singapore, 2–7 August 2009. [Google Scholar]
- Guo, J.; Shi, H.; Kang, Y.; Kuang, K.; Tang, S.; Jiang, Z.; Sun, C.; Wu, F.; Zhuang, Y. Semi-supervised active learning for semi-supervised models: Exploit adversarial examples with graph-based virtual labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Shakya, K.S.; Laddi, A.; Jaiswal, M. Automated methods for sella turcica segmentation on cephalometric radiographic data using deep learning (CNN) techniques. Oral Radiol. 2023, 39, 248–265. [Google Scholar] [CrossRef] [PubMed]
- Alavi, A.; Akhoundi, H. Deep Subspace Analysing for Semi-supervised Multi-label Classification of Diabetic Foot Ulcer. In Diabetic Foot Ulcers Grand Challenge; Springer: Berlin/Heidelberg, Germany, 2021; pp. 109–120. [Google Scholar]
- Yap, M.H.; Cassidy, B.; Pappachan, J.M.; O’Shea, C.; Gillespie, D.; Reeves, N.D. Analysis towards classification of infection and ischaemia of diabetic foot ulcers. In Proceedings of the 2021 IEEE EMBS International Conference on Biomedical and Health Informatics (BHI), Athens, Greece, 27–30 July 2021. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Van Engelen, J.E.; Hoos, H.H. A survey on semi-supervised learning. Mach. Learn. 2020, 109, 373–440. [Google Scholar] [CrossRef]
- Zhang, M.-L.; Zhou, Z.-H. Multilabel neural networks with applications to functional genomics and text categorization. IEEE Trans. Knowl. Data Eng. 2006, 18, 1338–1351. [Google Scholar] [CrossRef]
- McCallum, A.K. Multi-label text classification with a mixture model trained by EM. In Proceedings of the AAAI’99 Workshop on Text Learning, Orlando, FL, USA, 18–19 July 1999. [Google Scholar]
- Sun, L.; Ji, S.; Ye, J. Hypergraph spectral learning for multi-label classification. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008. [Google Scholar]
- Kong, X.; Ng, M.K.; Zhou, Z.-H. Transductive multilabel learning via label set propagation. IEEE Trans. Knowl. Data Eng. 2011, 25, 704–719. [Google Scholar] [CrossRef]
- Schapire, R.E.; Singer, Y. BoosTexter: A boosting-based system for text categorization. Mach. Learn. 2000, 39, 135–168. [Google Scholar] [CrossRef]
- Lin, J.; Cai, Q.; Lin, M. Multi-label classification of fundus images with graph convolutional network and self-supervised learning. IEEE Signal Process. Lett. 2021, 28, 454–458. [Google Scholar] [CrossRef]
- Liu, Y.; Jin, M.; Pan, S.; Zhou, C.; Zheng, Y.; Xia, F.; Philip, S.Y. Graph self-supervised learning: A survey. IEEE Trans. Knowl. Data Eng. 2022, 35, 5879–5900. [Google Scholar] [CrossRef]
- Wu, L.; Lin, H.; Tan, C.; Gao, Z.; Li, S.Z. Self-supervised learning on graphs: Contrastive, generative, or predictive. IEEE Trans. Knowl. Data Eng. 2021, 35, 4216–4235. [Google Scholar] [CrossRef]
- Ghesu, F.C.; Georgescu, B.; Mansoor, A.; Yoo, Y.; Gibson, E.; Vishwanath, R.; Balachandran, A.; Balter, J.M.; Cao, Y.; Singh, R. Quantifying and leveraging predictive uncertainty for medical image assessment. Med. Image Anal. 2021, 68, 101855. [Google Scholar] [CrossRef] [PubMed]
- Sensoy, M.; Kaplan, L.; Kandemir, M. Evidential deep learning to quantify classification uncertainty. In Proceedings of the Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montréal, Canada, 3–8 December 2018. [Google Scholar]
- Jsang, A. Subjective Logic: A Formalism for Reasoning under Uncertainty; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Zhao, X.; Chen, F.; Hu, S.; Cho, J.-H. Uncertainty aware semi-supervised learning on graph data. Adv. Neural Inf. Process. Syst. 2020, 33, 12827–12836. [Google Scholar]
- Fujino, A.; Ueda, N.; Saito, K. A hybrid generative/discriminative approach to semi-supervised classifier design. In Proceedings of the National Conference on Artificial Intelligence, Pittsburgh, PA, USA, 9–13 July 2005. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond empirical risk minimization. arXiv 2017, arXiv:1710.09412. [Google Scholar]
- Su, H.; Shi, X.; Cai, J.; Yang, L. Local and global consistency regularized mean teacher for semi-supervised nuclei classification. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China, 13–17 October 2019. [Google Scholar]
- Zhou, D.; Bousquet, O.; Lal, T.; Weston, J.; Schölkopf, B. Learning with local and global consistency. In Proceedings of the Advances in Neural Information Processing Systems 16 (NIPS 2003), Vancouver, BC, Canada, 8–13 December 2003. [Google Scholar]
- Bromley, J.; Guyon, I.; LeCun, Y.; Säckinger, E.; Shah, R. Signature verification using a “siamese” time delay neural network. In Proceedings of the Advances in Neural Information Processing Systems 6 (NIPS 1993), Denver, CO, USA, 29 November–2 December 1993. [Google Scholar]
- Guo, L.; Wang, C.; Zhang, D.; Xu, K.; Huang, Z.; Luo, L.; Peng, Y. Semi-supervised medical image classification based on CamMix. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Virtual, 18–22 July 2021. [Google Scholar]
- Berthelot, D.; Carlini, N.; Goodfellow, I.; Papernot, N.; Oliver, A.; Raffel, C.A. Mixmatch: A holistic approach to semi-supervised learning. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Mao, J.; Yin, X.; Zhang, G.; Chen, B.; Chang, Y.; Chen, W.; Yu, J.; Wang, Y. Pseudo-labeling generative adversarial networks for medical image classification. Comput. Biol. Med. 2022, 147, 105729. [Google Scholar] [CrossRef] [PubMed]
- Arazo, E.; Ortego, D.; Albert, P.; O’Connor, N.E.; McGuinness, K. Pseudo-labeling and confirmation bias in deep semi-supervised learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Khosla, P.; Teterwak, P.; Wang, C.; Sarna, A.; Tian, Y.; Isola, P.; Maschinot, A.; Liu, C.; Krishnan, D. Supervised contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 18661–18673. [Google Scholar]
- Chen, T.; Kornblith, S.; Swersky, K.; Norouzi, M.; Hinton, G.E. Big self-supervised models are strong semi-supervised learners. Adv. Neural Inf. Process. Syst. 2020, 33, 22243–22255. [Google Scholar]
- Luisier, F.; Blu, T.; Unser, M. Image denoising in mixed Poisson–Gaussian noise. IEEE Trans. Image Process. 2010, 20, 696–708. [Google Scholar] [CrossRef] [PubMed]
- Yeh, C.-H.; Hong, C.-Y.; Hsu, Y.-C.; Liu, T.-L.; Chen, Y.; LeCun, Y. Decoupled contrastive learning. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Liu, X.; Cao, J.; Fu, T.; Pan, Z.; Hu, W.; Zhang, K.; Liu, J. Semi-supervised automatic segmentation of layer and fluid region in retinal optical coherence tomography images using adversarial learning. IEEE Access 2018, 7, 3046–3061. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Xiang, H.; Lin, H.; Lin, X.; Heng, P.-A. Deep virtual adversarial self-training with consistency regularization for semi-supervised medical image classification. Med. Image Anal. 2021, 70, 102010. [Google Scholar] [CrossRef] [PubMed]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; March, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 1–35. [Google Scholar]
- Zhang, H.; Zhang, Z.; Odena, A.; Lee, H. Consistency regularization for generative adversarial networks. arXiv 2019, arXiv:1910.12027. [Google Scholar]
- Qu, A.; Wu, Q.; Wang, J.; Yu, L.; Li, J.; Liu, J. TNCB: Tri-net with Cross-Balanced Pseudo Supervision for Class Imbalanced Medical Image Classification. IEEE J. Biomed. Health Inform. 2024, 28, 2187–2198. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Shen, Y.; Wang, H.; Fei, J.; Li, W.; Wu, L.; Zhao, R.; Fu, Z.; Liu, Q. Learning from future: A novel self-training framework for semantic segmentation. Adv. Neural Inf. Process. Syst. 2022, 35, 4749–4761. [Google Scholar]
- Otálora, S.; Marini, N.; Müller, H.; Atzori, M. Semi-weakly supervised learning for prostate cancer image classification with teacher-student deep convolutional networks. In Proceedings of the Interpretable and Annotation-Efficient Learning for Medical Image Computing: Third International Workshop, iMIMIC 2020, Second International Workshop, MIL3ID 2020, and 5th International Workshop, LABELS 2020, Held in Conjunction with MICCAI 2020, Lima, Peru, 4–8 October 2020; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Marini, N.; Otálora, S.; Müller, H.; Atzori, M. Semi-supervised learning with a teacher-student paradigm for histopathology classification: A resource to face data heterogeneity and lack of local annotations. In Proceedings of the Pattern Recognition. ICPR International Workshops and Challenges, Virtual Event, 10–15 January 2021; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Kingma, D.P.; Mohamed, S.; Jimenez Rezende, D.; Welling, M. Semi-supervised learning with deep generative models. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Filipovych, R.; Davatzikos, C.; Initiative, A.s.D.N. Semi-supervised pattern classification of medical images: Application to mild cognitive impairment (MCI). NeuroImage 2011, 55, 1109–1119. [Google Scholar] [CrossRef] [PubMed]
- Mabu, S.; Miyake, M.; Kuremoto, T.; Kido, S. Semi-supervised CycleGAN for domain transformation of chest CT images and its application to opacity classification of diffuse lung diseases. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 1925–1935. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Walia, E.; Babyn, P. Unsupervised and semi-supervised learning with categorical generative adversarial networks assisted by wasserstein distance for dermoscopy image classification. arXiv 2018, arXiv:1804.03700. [Google Scholar]
- Guo, X.; Yuan, Y. Semi-supervised WCE image classification with adaptive aggregated attention. Med. Image Anal. 2020, 64, 101733. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.Y.; Chen, R.J.; Wang, J.; Dillon, D.; Mahmood, F. Semi-supervised histology classification using deep multiple instance learning and contrastive predictive coding. arXiv 2019, arXiv:1910.10825. [Google Scholar]
- Marini, N.; Otálora, S.; Müller, H.; Atzori, M. Semi-supervised training of deep convolutional neural networks with heterogeneous data and few local annotations: An experiment on prostate histopathology image classification. Med. Image Anal. 2021, 73, 102165. [Google Scholar] [CrossRef] [PubMed]
- Madani, A.; Moradi, M.; Karargyris, A.; Syeda-Mahmood, T. Semi-supervised learning with generative adversarial networks for chest X-ray classification with ability of data domain adaptation. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018. [Google Scholar]
- Gong, C.; Tao, D.; Maybank, S.J.; Liu, W.; Kang, G.; Yang, J. Multi-modal curriculum learning for semi-supervised image classification. IEEE Trans. Image Process. 2016, 25, 3249–3260. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Kim, D.; Sclaroff, S.; Darrell, T.; Saenko, K. Semi-supervised domain adaptation via minimax entropy. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Baid, U.; Ghodasara, S.; Mohan, S.; Bilello, M.; Calabrese, E.; Colak, E.; Farahani, K.; Kalpathy-Cramer, J.; Kitamura, F.C.; Pati, S. The rsna-asnr-miccai brats 2021 benchmark on brain tumor segmentation and radiogenomic classification. arXiv 2021, arXiv:2107.02314. [Google Scholar]
- Baltruschat, I.M.; Nickisch, H.; Grass, M.; Knopp, T.; Saalbach, A. Comparison of deep learning approaches for multi-label chest X-ray classification. Sci. Rep. 2019, 9, 6381. [Google Scholar] [CrossRef] [PubMed]
- Armato III, S.G.; McLennan, G.; Bidaut, L.; McNitt-Gray, M.F.; Meyer, C.R.; Reeves, A.P.; Zhao, B.; Aberle, D.R.; Henschke, C.I.; Hoffman, E.A. The lung image database consortium (LIDC) and image database resource initiative (IDRI): A completed reference database of lung nodules on CT scans. Med. Phys. 2011, 38, 915–931. [Google Scholar] [CrossRef]
- Tiwari, L.; Raja, R.; Awasthi, V.; Miri, R.; Sinha, G.; Alkinani, M.H.; Polat, K. Detection of lung nodule and cancer using novel Mask-3 FCM and TWEDLNN algorithms. Measurement 2021, 172, 108882. [Google Scholar] [CrossRef]
- Ragab, D.A.; Sharkas, M.; Marshall, S.; Ren, J. Breast cancer detection using deep convolutional neural networks and support vector machines. PeerJ 2019, 7, e6201. [Google Scholar] [CrossRef]
- Scholzen, T.; Gerdes, J. The Ki-67 protein: From the known and the unknown. J. Cell. Physiol. 2000, 182, 311–322. [Google Scholar] [CrossRef]
- Gutman, D.; Codella, N.C.; Celebi, E.; Helba, B.; Marchetti, M.; Mishra, N.; Halpern, A. Skin lesion analysis toward melanoma detection: A challenge at the international symposium on biomedical imaging (ISBI) 2016, hosted by the international skin imaging collaboration (ISIC). arXiv 2016, arXiv:1605.01397. [Google Scholar]
- Diaz-Pinto, A.; Morales, S.; Naranjo, V.; Köhler, T.; Mossi, J.M.; Navea, A. CNNs for automatic glaucoma assessment using fundus images: An extensive validation. Biomed. Eng. Online 2019, 18, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Decencière, E.; Zhang, X.; Cazuguel, G.; Lay, B.; Cochener, B.; Trone, C.; Gain, P.; Ordonez, R.; Massin, P.; Erginay, A. Feedback on a publicly distributed image database: The Messidor database. Image Anal. Stereol. 2014, 33, 231–234. [Google Scholar] [CrossRef]
- Kather, J.N.; Weis, C.-A.; Bianconi, F.; Melchers, S.M.; Schad, L.R.; Gaiser, T.; Marx, A.; Zöllner, F.G. Multi-class texture analysis in colorectal cancer histology. Sci. Rep. 2016, 6, 27988. [Google Scholar] [CrossRef] [PubMed]
- Paton, R.W. Screening in developmental dysplasia of the hip (DDH). Surgeon 2017, 15, 290–296. [Google Scholar] [CrossRef] [PubMed]
- Richterstetter, M.; Wullich, B.; Amann, K.; Haeberle, L.; Engehausen, D.G.; Goebell, P.J.; Krause, F.S. The value of extended transurethral resection of bladder tumour (TURBT) in the treatment of bladder cancer. BJU Int. 2012, 110, E76–E79. [Google Scholar] [CrossRef] [PubMed]
- Bien, N.; Rajpurkar, P.; Ball, R.L.; Irvin, J.; Park, A.; Jones, E.; Bereket, M.; Patel, B.N.; Yeom, K.W.; Shpanskaya, K. Deep-learning-assisted diagnosis for knee magnetic resonance imaging: Development and retrospective validation of MRNet. PLoS Med. 2018, 15, e1002699. [Google Scholar] [CrossRef] [PubMed]
- Kavakiotis, I.; Alexiou, A.; Tastsoglou, S.; Vlachos, I.S.; Hatzigeorgiou, A.G. DIANA-miTED: A microRNA tissue expression database. Nucleic Acids Res. 2022, 50, D1055–D1061. [Google Scholar] [CrossRef] [PubMed]
- Verma, R.; Kumar, N.; Patil, A.; Kurian, N.C.; Rane, S.; Graham, S.; Vu, Q.D.; Zwager, M.; Raza, S.E.A.; Rajpoot, N. MoNuSAC2020: A multi-organ nuclei segmentation and classification challenge. IEEE Trans. Med. Imaging 2021, 40, 3413–3423. [Google Scholar] [CrossRef] [PubMed]
- Miyato, T.; Maeda, S.-i.; Koyama, M.; Ishii, S. Virtual adversarial training: A regularization method for supervised and semi-supervised learning. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1979–1993. [Google Scholar] [CrossRef] [PubMed]
- Majkowska, A.; Mittal, S.; Steiner, D.F.; Reicher, J.J.; McKinney, S.M.; Duggan, G.E.; Eswaran, K.; Cameron Chen, P.-H.; Liu, Y.; Kalidindi, S.R. Chest radiograph interpretation with deep learning models: Assessment with radiologist-adjudicated reference standards and population-adjusted evaluation. Radiology 2020, 294, 421–431. [Google Scholar] [CrossRef] [PubMed]
- Sohn, K.; Zhang, Z.; Li, C.-L.; Zhang, H.; Lee, C.-Y.; Pfister, T. A simple semi-supervised learning framework for object detection. arXiv 2020, arXiv:2005.04757. [Google Scholar]
- Nartey, O.T.; Yang, G.; Wu, J.; Asare, S.K. Semi-supervised learning for fine-grained classification with self-training. IEEE Access 2019, 8, 2109–2121. [Google Scholar] [CrossRef]
- Wu, D.; Shang, M.; Luo, X.; Xu, J.; Yan, H.; Deng, W.; Wang, G. Self-training semi-supervised classification based on density peaks of data. Neurocomputing 2018, 275, 180–191. [Google Scholar] [CrossRef]
- Rizve, M.N.; Duarte, K.; Rawat, Y.S.; Shah, M. In defense of pseudo-labeling: An uncertainty-aware pseudo-label selection framework for semi-supervised learning. arXiv 2021, arXiv:2101.06329. [Google Scholar]
- Codella, N.; Rotemberg, V.; Tschandl, P.; Celebi, M.E.; Dusza, S.; Gutman, D.; Helba, B.; Kalloo, A.; Liopyris, K.; Marchetti, M. Skin lesion analysis toward melanoma detection 2018: A challenge hosted by the international skin imaging collaboration (isic). arXiv 2019, arXiv:1902.03368. [Google Scholar]
- Al-Masni, M.A.; Kim, D.-H.; Kim, T.-S. Multiple skin lesions diagnostics via integrated deep convolutional networks for segmentation and classification. Comput. Methods Programs Biomed. 2020, 190, 105351. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Yeh, R.; Schwing, A. Not all unlabeled data are equal: Learning to weight data in semi-supervised learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21786–21797. [Google Scholar]
- Athiwaratkun, B.; Finzi, M.; Izmailov, P.; Wilson, A.G. There are many consistent explanations of unlabeled data: Why you should average. arXiv 2018, arXiv:1806.05594. [Google Scholar]
- Zoph, B.; Ghiasi, G.; Lin, T.-Y.; Cui, Y.; Liu, H.; Cubuk, E.D.; Le, Q. Rethinking pre-training and self-training. Adv. Neural Inf. Process. Syst. 2020, 33, 3833–3845. [Google Scholar]
- Ghosh, A.; Thiery, A.H. On data-augmentation and consistency-based semi-supervised learning. arXiv 2021, arXiv:2101.06967. [Google Scholar]
- Xie, X.; Niu, J.; Liu, X.; Chen, Z.; Tang, S.; Yu, S. A survey on incorporating domain knowledge into deep learning for medical image analysis. Med. Image Anal. 2021, 69, 101985. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Fang, Q.; Huang, Y.; Xu, K. Semi-supervised method for image texture classification of pituitary tumors via CycleGAN and optimized feature extraction. BMC Med. Inform. Decis. Mak. 2020, 20, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Enguehard, J.; O’Halloran, P.; Gholipour, A. Semi-supervised learning with deep embedded clustering for image classification and segmentation. IEEE Access 2019, 7, 11093–11104. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Luo, L.; Dou, Q.; Heng, P.-A. Triplet attention and dual-pool contrastive learning for clinic-driven multi-label medical image classification. Med. Image Anal. 2023, 86, 102772. [Google Scholar] [CrossRef]
- Yang, Y.; Zhan, D.-C.; Wu, Y.-F.; Liu, Z.-B.; Xiong, H.; Jiang, Y. Semi-supervised multi-modal clustering and classification with incomplete modalities. IEEE Trans. Knowl. Data Eng. 2019, 33, 682–695. [Google Scholar] [CrossRef]
- Mao, B.; Jia, C.; Huang, Y.; He, K.; Wu, J.; Gong, T.; Li, C. Uncertainty-guided Mutual Consistency Training for Semi-supervised Biomedical Relation Extraction. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022. [Google Scholar]
- Singh, K.K.; Yu, H.; Sarmasi, A.; Pradeep, G.; Lee, Y.J. Hide-and-seek: A data augmentation technique for weakly-supervised localization and beyond. arXiv 2018, arXiv:1811.02545. [Google Scholar]
- DeVries, T.; Taylor, G.W. Improved regularization of convolutional neural networks with cutout. arXiv 2017, arXiv:1708.04552. [Google Scholar]
- Chen, P.; Liu, S.; Zhao, H.; Jia, J. Gridmask data augmentation. arXiv 2020, arXiv:2001.04086. [Google Scholar]
- Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; Yang, Y. Random erasing data augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. Autoaugment: Learning augmentation strategies from data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Cubuk, E.D.; Zoph, B.; Shlens, J.; Le, Q.V. Randaugment: Practical automated data augmentation with a reduced search space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020. [Google Scholar]
- Lu, Z.; Wang, L. Noise-robust semi-supervised learning via fast sparse coding. Pattern Recognit. 2015, 48, 605–612. [Google Scholar] [CrossRef]
- Kim, J.; Hur, Y.; Park, S.; Yang, E.; Hwang, S.J.; Shin, J. Distribution aligning refinery of pseudo-label for imbalanced semi-supervised learning. Adv. Neural Inf. Process. Syst. 2020, 33, 14567–14579. [Google Scholar]
- Deng, J.; Yu, J.-G. A simple graph-based semi-supervised learning approach for imbalanced classification. Pattern Recognit. 2021, 118, 108026. [Google Scholar] [CrossRef]
- Singh, A.; Nowak, R.; Zhu, J. Unlabeled data: Now it helps, now it doesn’t. In Proceedings of the Advances in Neural Information Processing Systems 21 (NIPS 2008), Vancouver, BC, Canada, 8–11 December 2008. [Google Scholar]
- Yang, T.; Priebe, C.E. The effect of model misspecification on semi-supervised classification. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2093–2103. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Karakoulas, G. Learning from labeled and unlabeled data: An empirical study across techniques and domains. J. Artif. Intell. Res. 2005, 23, 331–366. [Google Scholar] [CrossRef]
| Related Articles | Classification | Application | Estimation | |
|---|---|---|---|---|
| Integrated Database | Integrated Database Setting | |||
| Cheplygina, Bruijne et al., 2019 [25] | Regularization and graph-based, Self-training and co-training | Analysis | - | - |
| Aska et al., 2021 [27] | Self-Training, co-training and expectation maximization (EM), transudative SVMs, and graph-based methods | Classification | - | - |
| Chen, Wang et al., 2022 [28] | Pseudo-labeling, consistency regularization | Analysis | - | - |
| Zahra and Imran, 2022 [5] | Consistency-Based, adversarial, graph-based and hybrid method | Classification | ✓ | × |
| Our | Consistency regularization, deep adversarial (GANs and VAEs), pseudo-labeling, graph-based, multi-label, and hybrid methods | Classification | ✓ | ✓ |
| Methods | Description | Key Points |
|---|---|---|
| Consistency Regularization Methods | Formulating constraints on consistency | Assumptions are evident and rational; relying on the utilization of data augmentation and perturbation techniques. |
| Deep Adversarial Methods | Involving generative models like GAN, VAE, and their derivatives | Induce new training instances; challenging to attain optimal outcomes for both the generative and downstream task. |
| Pseudo-Labeling Methods | Pseudo-labeling unlabeled examples using labeled examples | Generating pseudo-labels; these labels produced artificially may contain inaccuracies. |
| Graph-Based Methods | Constructing graphs from training datasets and employing graph-based approaches to address subsequent tasks | Acquiring additional knowledge through graphs; dependent on effectively representing the relationships among training samples. |
| Multi-Label Methods | Labels or sets of labels are used to extract useful information from both labeled and unlabeled instances | Controls complexity and make smooth predictions; optimize combine methods. |
| Hybrid Methods | Combining different learning approaches, such as incorporating consistency regularization and employing pseudo-labeling techniques | Enhanced efficiency and resilience; increased size of the model. |
| Methods | Advantages | Disadvantages |
|---|---|---|
| Consistency Regularization |
|
|
| Deep Adversarial |
|
|
| Pseudo-Labeling |
|
|
| Graph-Based |
|
|
| Multi-Label |
|
|
| Hybrid |
|
|
| Dataset | 2D/3D | Consistency Regularization | Deep Adversarial | Pseudo-Labeling | Graph-Based | Multi-Label | Hybrid |
|---|---|---|---|---|---|---|---|
| MICCAI [217] | 2D, 3D | ✓ | |||||
| LIDC-IDRI [219] | 2D, 3D | ✓ | ✓ | ✓ | ✓ | ||
| TianChi [220] | 2D, 3D | ✓ | ✓✓ | ||||
| Ki-67 [222] | 2D, 3D | ✓ | |||||
| Tumor (TURBT) [228] | 2D, 3D | ✓ | |||||
| CheXpert [78] | 2D | ✓✓ | ✓ | ✓ | ✓✓ | ||
| ChestX-ray14 [218] | 2D | ✓✓✓ | ✓ | ✓✓ | |||
| CBIS-DDSM [221] | 2D | ✓ | ✓ | ✓ | |||
| ISIC2018 [223] | 2D | ✓✓ | ✓ | ✓ | ✓ | ✓✓ | |
| ACRIMA [224] | 2D | ✓ | ✓ | ||||
| Messidor [225] | 2D | ✓ | ✓ | ✓✓ | |||
| Colorectal Cancer [226] | 2D | ✓ | ✓ | ||||
| DDH [227] | 2D | ✓ | |||||
| DFUC_2021 [169] | 2D | ✓ | |||||
| MoNuSeg [231] | 2D | ✓ | |||||
| Knee (MRNet) [229] | 3D | ✓ | |||||
| miRNAs [230] | 3D | ✓ |
| Methods | Reference | Metrics form Published Articles | Proposed Study Metrics | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10% Proportion | 20% Proportion | |||||||||
| Acc (%) | AUC (%) | F1 (%) | Acc (%) | AUC (%) | F1 (%) | Acc (%) | AUC (%) | F1 (%) | ||
| Consistency Regularization | ||||||||||
| Baseline | ResNet50 [218] | - | 66.40 | - | 67.51 | 69.84 | 66.70 | 74.49 | 81.06 | 80.49 |
| Temporal Ensemble | Unsupervised VAE [79] | - | 65.81 | - | - | - | - | - | - | - |
| Mean Teacher | SRC-MT [92] | 91.04 | 92.27 | 58.61 | 93.13 | 92.89 | 85.01 | 96.56 | 94.12 | 87.84 |
| [95] | - | 82.50 | - | - | - | - | - | - | - | |
| NoTeacher [97] | - | 78.87 | - | - | - | - | - | - | - | |
| Deep Adversarial | ||||||||||
| GAN | BiModality SS-GAN [107] | - | - | - | 82.67 | 79.03 | 80.32 | 88.45 | 86.01 | 83.79 |
| Uncertainty-Guided [112] | 79.49 | 69.75 | 80.69 | - | - | - | - | - | - | |
| 𝐶𝑦𝑐𝑙𝑒GAN [114] | - | - | - | - | - | - | - | - | - | |
| VAE | MAVEN [117] | 52.57 | - | - | 63.85 | 60.89 | 61.22 | 65.77 | 63.07 | 63.62 |
| SVAEMDA [121] | - | - | - | - | - | - | - | - | - | |
| SCAN [126] | - | - | - | 67.39 | 61.05 | 63.81 | 73.56 | 74.08 | 70.67 | |
| Pseudo-Labeling | ||||||||||
| Self-Training | ACPL [43] | - | 94.36 | 62.23 | 87.16 | 90.3 | 64.54 | 94.01 | 94.69 | 69.53 |
| Meta Pseudo-Label [140] | 85.92 | - | - | - | - | - | - | - | - | |
| Graph-Based | ||||||||||
| AutoEncoder | GraphXNET V1.0 [146] | - | 62.12 | - | 68.30 | 64.51 | 67.08 | 72.84 | 69.09 | 71.02 |
| GraphXNET V2.0 [146] | - | 76.14 | - | 77.56 | 78.16 | 75.16 | 82.43 | 89.38 | 86.70 | |
| GNN-Based | Label Propagation [152] | - | - | - | - | - | - | - | - | - |
| SS-HGCN [153] | - | - | - | 82.37 | 85.61 | 80.73 | 88.09 | 91.79 | 90.37 | |
| Multi-Label | ||||||||||
| Inductive | MSML [163] | 95.72 | - | - | 90.43 | 91.19 | 88.01 | 96.07 | 94.03 | 93.23 |
| Transductive | MCG-Net [177] | - | - | - | 87.27 | 85.04 | 81.49 | 89.48 | 88.76 | 84.22 |
| MCGS-Net [177] | - | - | - | 91.54 | 92.06 | 89.88 | 93.01 | 94.97 | 93.06 | |
| Hybrid | ||||||||||
| CamMix [189] | - | 95.34 | - | 93.08 | 92.03 | 88.54 | 96.02 | 97.37 | 94.89 | |
| PLGAN [191] | 97.50 | - | - | - | - | - | - | - | - | |
| Deep Virtual Adversarial CR [199] | - | - | - | 93.02 | 92.79 | 89.09 | 95.21 | 98.02 | 93.27 | |
| TNCB [202] | 96.24 | 99.23 | - | 91.06 | 92.37 | 89.26 | 97.08 | 99.69 | 94.22 | |
| Methods | Reference | Metrics form Published Articles | Proposed Study Metrics | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10% Proportion | 20% Proportion | |||||||||
| Acc (%) | AUC (%) | F1 (%) | Acc (%) | AUC (%) | F1 (%) | Acc (%) | AUC (%) | F1 (%) | ||
| Consistency Regularization | ||||||||||
| Baseline | ResNet50 [239] | 89.28 | - | 81.28 | 83.43 | 85.88 | 76.04 | 90.03 | 91.83 | 81.71 |
| Temporal Ensemble | Unsupervised VAE [79] | - | - | - | - | - | - | - | - | - |
| Mean Teacher | SRC-MT [92] | 92.54 | 93.58 | 60.68 | 89.20 | 87.91 | 57.03 | 89.04 | 91.37 | 60.49 |
| [95] | - | 94.71 | 62.67 | - | - | - | - | - | - | |
| Deep Adversarial | ||||||||||
| GAN | BiModality SS-GAN [107] | - | - | - | 89.17 | 91.10 | 79.83 | 91.24 | 92.63 | 78.09 |
| Uncertainty-Guided [112] | 94.27 | 96.04 | 69.97 | - | - | - | - | - | - | |
| VAE | MAVEN [117] | 82.12 | - | - | 80.52 | 81.37 | 71.02 | 83.45 | 86.07 | 76.03 |
| SCAN [126] | - | - | - | 80.83 | 82.33 | 71.87 | 83.59 | 87.29 | 76.71 | |
| Pseudo-Labeling | ||||||||||
| Co-Training | COAL [129] | - | - | - | - | - | - | - | - | - |
| Self-Training | ACPL [43] | - | 74.44 | - | 69.49 | 71.05 | 62.03 | 73.11 | 75.07 | 63.98 |
| Graph-Based | ||||||||||
| AutoEncoder | GraphXNET V1.0 [146] | - | - | - | 73.44 | 71.63 | 65.93 | 81.27 | 73.26 | 74.92 |
| GraphXNET V2.0 [146] | - | - | - | 77.29 | 73.57 | 68.39 | 81.29 | 77.29 | 78.73 | |
| SS-HGCN [153] | - | - | - | 88.05 | 83.99 | 77.84 | 88.70 | 84.31 | 79.47 | |
| Multi-Label | ||||||||||
| Inductive | MSML [163] | - | - | - | 87.74 | 84.54 | 78.46 | 89.28 | 87.16 | 81.28 |
| Transductive | MCG-Net [177] | - | - | - | 72.30 | 69.17 | 66.05 | 79.95 | 74.44 | 68.94 |
| MCGS-Net [177] | 81.36 | - | 72.07 | 78.25 | 73.64 | 68.02 | 83.79 | 79.60 | 74.40 | |
| Hybrid | ||||||||||
| CamMix [189] | - | 94.04 | - | 82.60 | 78.00 | 65.80 | 85.41 | 81.60 | 76.30 | |
| Deep Virtual Adversarial CR [199] | - | - | - | 86.60 | 84.70 | 79.19 | 92.62 | 87.50 | 81.01 | |
| TNCB [202] | 95.94 | 96.14 | - | 88.89 | 90.78 | 79.27 | 92.20 | 92.32 | 92.98 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shakya, K.S.; Alavi, A.; Porteous, J.; K, P.; Laddi, A.; Jaiswal, M. A Critical Analysis of Deep Semi-Supervised Learning Approaches for Enhanced Medical Image Classification. Information 2024, 15, 246. https://doi.org/10.3390/info15050246
Shakya KS, Alavi A, Porteous J, K P, Laddi A, Jaiswal M. A Critical Analysis of Deep Semi-Supervised Learning Approaches for Enhanced Medical Image Classification. Information. 2024; 15(5):246. https://doi.org/10.3390/info15050246
Chicago/Turabian StyleShakya, Kaushlesh Singh, Azadeh Alavi, Julie Porteous, Priti K, Amit Laddi, and Manojkumar Jaiswal. 2024. "A Critical Analysis of Deep Semi-Supervised Learning Approaches for Enhanced Medical Image Classification" Information 15, no. 5: 246. https://doi.org/10.3390/info15050246
APA StyleShakya, K. S., Alavi, A., Porteous, J., K, P., Laddi, A., & Jaiswal, M. (2024). A Critical Analysis of Deep Semi-Supervised Learning Approaches for Enhanced Medical Image Classification. Information, 15(5), 246. https://doi.org/10.3390/info15050246








