Intuitionistic Fuzzy Sets for Spatial and Temporal Data Intervals
Abstract
1. Introduction
2. Methods and Materials
2.1. Relevant Background
2.1.1. Temporal Information Research
2.1.2. Spatial Information Research
2.2. Fuzzy Set Theory
2.2.1. Fuzzy Sets
2.2.2. Intuitionistic Fuzzy Sets
2.2.3. Interval Representation
3. Results
3.1. Simple and Complex Intervals
3.2. Interval Relationships
- Non-intersecting: NI(S1, S2)
- Simple interval: Sh1 < Sl2
- Complex interval: OSh1 < OSl2
- 2.
- Abutting: AB (S1, S2)
- Simple interval: Sh1 = Sl2
- Simple to complex: Sh1 = OSl2
- Complex interval: OSh1 = OSl2
- 3.
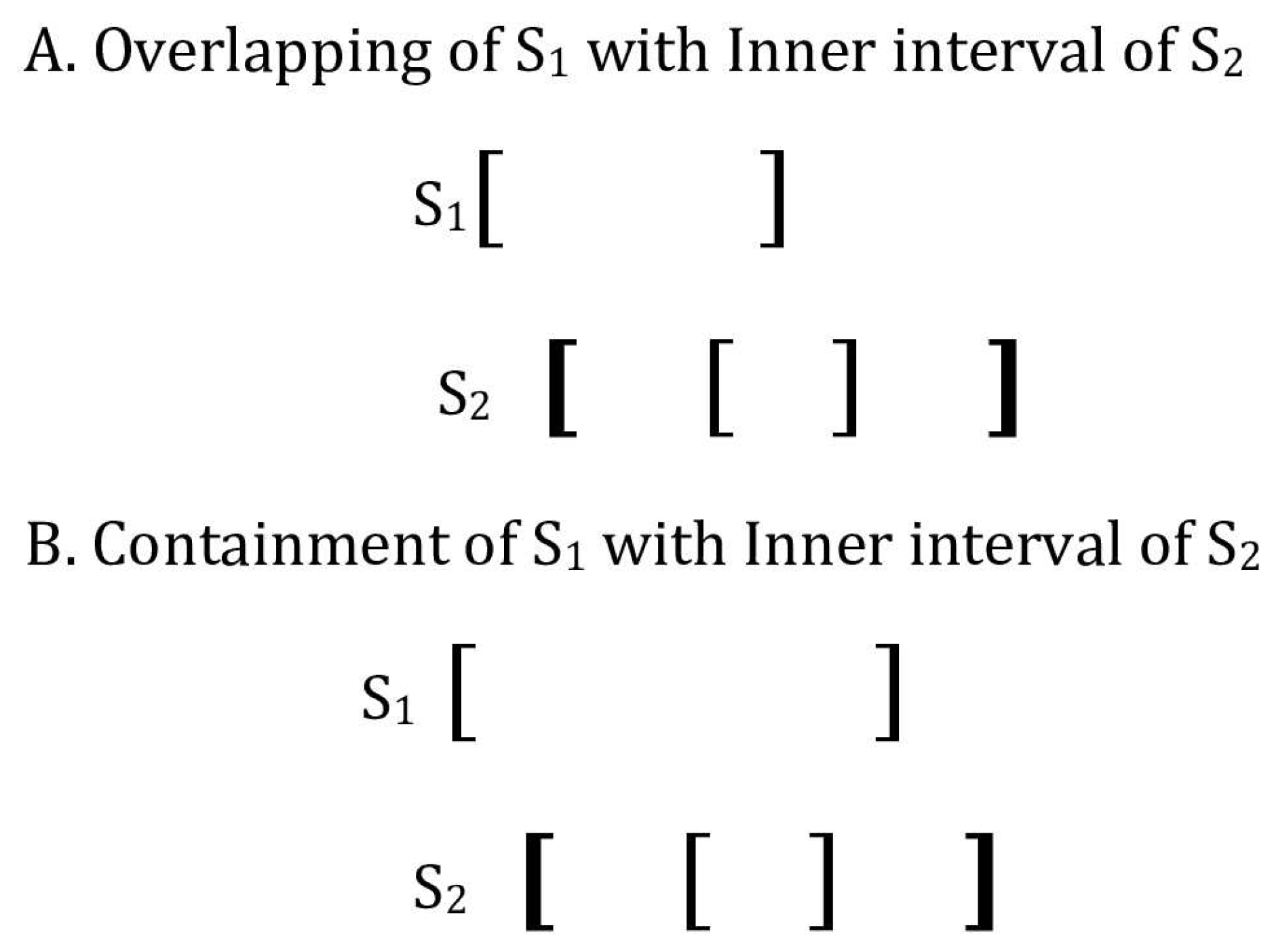
- Overlapping: OV(S1, S2)
- Sh1 > Sl2; Example on the left side of Figure 2.
- For example, S1 = [1305, 1345], S2 = [1340, 1420]
- Case 1. Outer overlap only: Sh1 > OSl2 and Sh1 ≤ ISl2
- For example, S1 =[50, 100]; S2 = [90 [160, 180] 200]
- Case 2. Figure 2A. Inner overlap but not contained: Sh1 > ISl2
- and Sh1 ≤ ISh2
- Outer interval overlap: OSh1 > OSl2
- Outer–inner interval overlap: OSh1 > ISl2
- 4.
- Contained: CO(S1, S2)
- S2 contained in S1: Sl2 > Sl1 and Sh2 < Sh1. Therefore, note that if the intervals satisfy the containing condition this means an overlap condition is also implied. The right side of Figure 3 illustrates this.
- For example, S1 = [1340, 1420], S2 = [1345, 1400]
- Inner interval of S2 contained in S1 (Figure 2B):
- S11 < ISl2 and Sh1 > ISh2
3.3. Interval Aggregation
3.3.1. Simple Intervals
3.3.2. Complex Intervals
3.3.3. Aggregation of Memberships
3.3.4. Selection Criteria for Full Aggregations
3.3.5. Bathymetry Aggregation Application Example
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
References
- Fingar, T. Reducing Uncertainty: Intelligence Analysis and National Security; Stanford University Press: Stanford, CA, USA, 2011. [Google Scholar]
- Nickell, J.; Fischer, J. Crime Science: Methods of Forensic Detection; University Press of Kentucky: Lexington, KY, USA, 1999. [Google Scholar]
- Canter, D.; Youngs, D. Principles of Geographical Offender Profiling; Ashgate Publishing: Farnham, UK, 2008. [Google Scholar]
- Li, C. Handbook of Research on Computational Forensics, Digital Crime, and Investigation: Methods and Solutions; IGI Global: Hershey, PA, USA, 2011. [Google Scholar]
- Anderson, M.; Anderson, D.; Wescott, D. Estimation of adult age-at-death using the Sugeno fuzzy integral. J. Phys. Anthropol. 2010, 142, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.; Charrow, R. Upper and lower bounds for probability of guilt based on circumstantial evidence. J. Am. Stat. Assoc. 1975, 70, 555–560. [Google Scholar]
- Trinanes, J.; Olascoaga, M.; Goni, G.; Maximenko, N.; Griffin, D.; Hafner, J. Analysis of flight MH370 potential debris trajectories using ocean observations and numerical model results. J. Oper. Oceanogr. 2016, 9, 126–138. [Google Scholar] [CrossRef]
- Ryabov, V.; Puurouen, S.; Terziyan, V. Representation and reasoning with uncertain temporal relations. In Proceedings of the Twelfth International Florida Artificial Intelligence Research Society Conference, Orlando, FL, USA, 1–5 May 1999. [Google Scholar]
- Freska, C. Temporal reasoning based on semi-intervals. Artif. Intell. 1992, 54, 199–227. [Google Scholar]
- Kanhuba, N. Temporal Information Retrieval; Now Publishers: Boston, MA, USA, 2015. [Google Scholar]
- Tang, Y.; Peng, Z.; Liu, D.; Zhang, W. From time data to temporal information. In Temporal Information Processing Technology and Its Applications; Tang, Y., Tang, N., Ye, X., Eds.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Dubois, D.; Prade, H. Processing fuzzy temporal knowledge. IEEE Trans Syst. Man Cybern. 1989, 19, 729–744. [Google Scholar] [CrossRef]
- Dubois, D.; HadjAli, A.; Prade, H. Fuzziness and uncertainty in temporal reasoning. J. Univers. Comput. Sci. 2003, 9, 1168–1194. [Google Scholar]
- Conradie, W.; Monica, D.; Muñoz-Velasco, E.; Sciavicco, G.; Stan, I. Fuzzy Halpern and Shoham’s interval temporal logics. Fuzzy Sets Syst. 2023, 456, 107–124. [Google Scholar] [CrossRef]
- Foulloy, L.; Clivillé, V.; Berrah, L. Fuzzy temporal approach to the overall equipment effectiveness measurement. Comput. Ind. Eng. 2019, 127, 103–111. [Google Scholar] [CrossRef]
- Knyazeva, M.; Bozhenyuk, A.; Kaymak, U. Fuzzy Temporal Graphs and Sequence Modelling in Scheduling Problem. In Information Processing and Management of Uncertainty in Knowledge-Based Systems, Proceedings of the IPMU 2020, Lisbon, Portugal, 15–19 June 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Liu, L.; Huang, L.; Dai, D.; Zhang, X.; Tian, Y.; Ma, L.; Liu, Y.; Yuji, Y. Integrating Multi-Source Heterogeneous Fuzzy Spatiotemporal Data. In Proceedings of the 2023 3rd International Conference on Mobile Networks and Wireless Communications, Tumkur, India, 4–5 December 2023. [Google Scholar]
- Wang, Y.; Bai, L. Fuzzy Spatiotemporal Data Modeling Based on UML. IEEE Access 2019, 7, 45405–45416. [Google Scholar] [CrossRef]
- Khan, M.; Banerjee, M.; Panda, S. Logics for Temporal Information Systems in Rough Set Theory. ACM Trans. Comput. Logic. 2023, 2, 1–29. [Google Scholar] [CrossRef]
- Selvakumar, K.; Karuppiah, M.; SaiRamesh, L.; Islam, H.; Hassan, M.; Fortino, G.; Choo, K. Intelligent temporal classification and fuzzy rough set-based feature selection algorithm for intrusion detection system in WSNs. Inf. Sci. 2019, 497, 77–90. [Google Scholar] [CrossRef]
- Goodchild, M. Twenty years of progress: GIScience in 2010. J. Spat. Inf. Sci. 2010, 1, 3–20. [Google Scholar] [CrossRef]
- Couclelis, H. The Certainty of Uncertainty: GIS and the Limits of Geographic Knowledge. Trans. GIS 2003, 7, 165–175. [Google Scholar] [CrossRef]
- Chang, K. Introduction to Geographic Information Systems, 9th ed.; McGraw-Hill: Boston, MA, USA, 2016. [Google Scholar]
- Zhang, J.; Goodchild, M. Uncertainty in Geographical Information; Taylor and Francis: London, UK, 2002. [Google Scholar]
- Stoms, D. Reasoning with uncertainty in intelligent geographic information systems. GIS 1987, 87, 693–699. [Google Scholar]
- Mobarakeh, M.; Jazi, M.; Rahmani, A. Direction based method for representing and querying fuzzy regions. Multimed. Tools Appl. 2024, 1, 1–28. [Google Scholar] [CrossRef]
- Carniel, A.; Borges de Venancio, P.; Schneider, M. fsr: An R package for fuzzy spatial data handling. Trans. GIS 2023, 27, 900–911. [Google Scholar] [CrossRef]
- Xu, J.; Pan, X. A Fuzzy Spatial Region Extraction Model for Object’s Vague Location Description from Observer Perspective. ISPRS Int. J. Geo-Inf. 2020, 9, 703–711. [Google Scholar] [CrossRef]
- Bloch, I.; Ralescu, A. Fuzzy Spatial Objects. In Fuzzy Sets Methods in Image Processing and Understanding; Bloch, I., Ralescu, A., Eds.; Springer: Cham, Switzerland, 2023; pp. 53–78. [Google Scholar]
- Carniel, A.; Galdino, F.; Schneider, M. Evaluating Region Inference Methods by Using Fuzzy Spatial Inference Models. In Proceedings of the 2022 IEEE International Conference on Fuzzy Systems, Padua, Italy, 18–23 July 2022. [Google Scholar]
- Boudet, L.; Poli, J.; Bergé, L.; Rodriguez, M. Situational assessment of wildfires: A fuzzy spatial approach. In Proceedings of the 2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI), Baltimore, MD, USA, 9–11 November 2022. [Google Scholar]
- Beaubouef, T.; Petry, F.; Breckenridge, J. Rough Set Based Uncertainty Management for Spatial Databases and Geographical Information Systems. In Soft Computing in Industrial Applications; Suzuki, Y., Ed.; Springer: London, UK, 2000; Chapter 6a; pp. 471–479. [Google Scholar]
- Cross, V.; Firat, A. Fuzzy objects for geographical information systems. Fuzzy Sets Syst. 2000, 113, 19–36. [Google Scholar] [CrossRef]
- Kruse, R.; Borgelt, C.; Braune, C.; Mostaghim, S.; Steinbrecher, M. Computational Intelligence: A Methodological Introduction, 2nd ed.; Springer: London, UK, 2016. [Google Scholar]
- Elmore, P.; Petry, F.; Yager, R. Geospatial Modeling using Dempster-Shafer Theory. IEEE Trans Cybern. 2017, 47, 1551–1561. [Google Scholar] [CrossRef]
- Elmore, P.; Petry, F.; Yager, R. Dempster-Shafer Approach to Temporal Uncertainty. IEEE Trans. Emerg. Top. Comput. Intell. 2017, 1, 316–325. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Klir, G. Uncertainty and Information; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Atanassov, K. Intuitionstic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R. Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst. 2013, 22, 958–965. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R. Fermatean fuzzy sets. J. Ambient Intell. Humaniz. Comput. 2020, 11, 663–674. [Google Scholar] [CrossRef]
- Moore, R. Interval Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Moore, R.; Kearfott, B.; Cloud, M. Introduction to Interval Analysis; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Burrilo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Syst. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Petry, F.; Yager, R. Interval-valued fuzzy sets aggregation and evaluation approaches. Appl. Soft Comput. 2022, 124, 122–134. [Google Scholar] [CrossRef]
- Calvo, T.; Kolesárová, A.; Komorníková, M.; Mesiar, R. Aggregation operators: Properties, classes and construction methods. In Aggregation Operators—New Trends and Applications; Calvo, T., Mayor, G., Mesiar, R., Eds.; Physica-Verlag: Heidelberg, Germany, 2002; pp. 3–104. [Google Scholar]
- Xu, Z.; Da, Q. An overview of operators for aggregating information. Int. J. Intell. Syst. 2003, 18, 953–969. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic Fuzzy Aggregation Operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Elmore, P.; Calder, B.; Petry, F.; Masetti, G.; Yager, R. Aggregation Methods Using Bathymetry Sources of Differing Subjective Reliabilities for Navigation Mapping. Mar. Geod. 2023, 46, 99–128. [Google Scholar] [CrossRef]
- Calder, B. On risk-based expression of hydrographic uncertainty. Mar. Geod. 2015, 38, 99–127. [Google Scholar] [CrossRef]
- Bakdi, A.; Glad, I.; Vanem, E.; Engelhardtsen, O. AIS-based multiple vessel collision and grounding risk identification based on adaptive safety domain. J. Mar. Sci. Eng. 2019, 8, 5. [Google Scholar] [CrossRef]
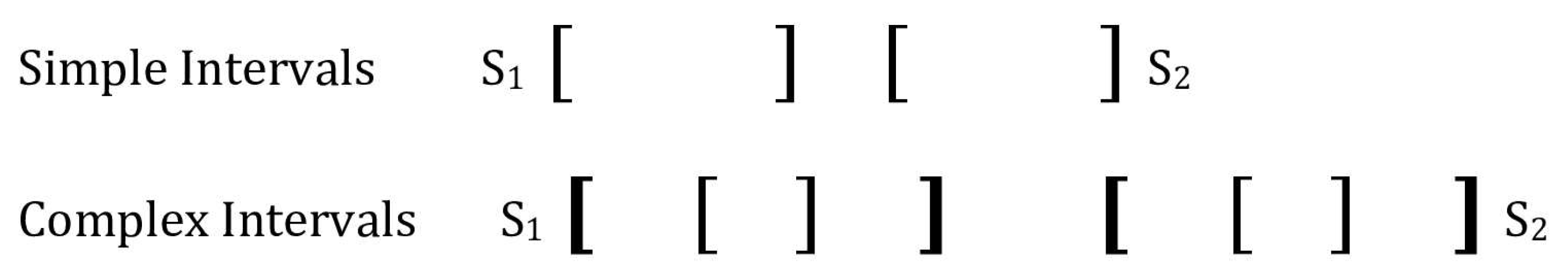

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petry, F. Intuitionistic Fuzzy Sets for Spatial and Temporal Data Intervals. Information 2024, 15, 240. https://doi.org/10.3390/info15040240
Petry F. Intuitionistic Fuzzy Sets for Spatial and Temporal Data Intervals. Information. 2024; 15(4):240. https://doi.org/10.3390/info15040240
Chicago/Turabian StylePetry, Frederick. 2024. "Intuitionistic Fuzzy Sets for Spatial and Temporal Data Intervals" Information 15, no. 4: 240. https://doi.org/10.3390/info15040240
APA StylePetry, F. (2024). Intuitionistic Fuzzy Sets for Spatial and Temporal Data Intervals. Information, 15(4), 240. https://doi.org/10.3390/info15040240






