Ensemble Modeling with a Bayesian Maximal Information Coefficient-Based Model of Bayesian Predictions on Uncertainty Data

Abstract

Uncertainty presents unfamiliar circumstances or incomplete information that may be difficult to handle with a single model of a traditional machine learning algorithm. They are possibly limited by inadequate data, an ambiguous model, and learning performance to make a prediction. Therefore, ensemble modeling is proposed as a powerful model for enhancing predictive capabilities and robustness. This study aims to apply Bayesian prediction to ensemble modeling because it can encode conditional dependencies between variables and present the reasoning model using the BMIC model. The BMIC has clarified knowledge in the model which is ready for learning. Then, it was selected as the base model to be integrated with well-known algorithms such as logistic regression, K-nearest neighbors, decision trees, random forests, support vector machines (SVMs), neural networks, naive Bayes, and XGBoost classifiers. Also, the Bayesian neural network (BNN) and the probabilistic Bayesian neural network (PBN) were considered to compare their performance as a single model. The findings of this study indicate that the ensemble model of the BMIC with some traditional algorithms, which are SVM, random forest, neural networks, and XGBoost classifiers, returns 96.3% model accuracy in prediction. It provides a more reliable model and a versatile approach to support decision-making.

1. Introduction

Uncertainty prediction holds significant importance across various fields and applications, particularly in high-stakes decision-making scenarios. The presence of data uncertainty poses a challenge when dealing with observed datasets. Since machine learning (ML) algorithms have introduced a widely favored approach for the analysis and prediction of data, they can be problematic in scenarios dealing with uncertainty. Deep learning (DL) is required for manipulation. Moreover, the challenge of data availability that needs to be handled with big data will not return more accurate results through the use of purely traditional models [1].

Data analysis employs various techniques in order to capture the classifications or predictions that can help to support decision-making [2,3]. It concerns the accuracy of outputs that are returned from insufficient data. The detection of relationships among features can be input to the learning algorithm for training with its data. One of the popular network model representations is the Bayesian network (BN) which is a probabilistic graphical model (PGM) that represents probabilistic relationships between variables using a directed acyclic graph (DAG). It is based on Bayes’ theorem and encodes conditional dependencies between variables, allowing for efficient inference and reasoning under uncertainty. In [4], the authors applied the BN with the maximal information coefficient (MIC) to construct a good model as the Bayesian maximal information coefficient (BMIC) which demonstrates the clear relationship among features with the BIC score. However, it was found that a single model representation might present less accurate results in prediction.

Moreover, another approach is the application of DL, which can be used in the neural network domain. It can rely on Bayes’ theorem, which is the Bayesian neural network model (BNN). It treats model parameters as probability distributions rather than fixed values. The weights and biases of the neural network are treated as random variables with associated probability distributions. The BNN allows for a more nuanced understanding of uncertainty in predictions. It also extends to the application of another algorithm, the probabilistic Bayesian neural network (PBN) which shares similarities with the BNN. The PBN can provide a posterior distribution that reflects the uncertainty in the model’s parameters and delivers precise decision-making.

However, the combination of multiple models can improve prediction accuracy compared to using a single model. This is also a possible approach to provide a more robust estimate of uncertainty through ensemble learning. Models can be combined through the particular learning algorithm between each pairwise combination. Therefore, ensemble models can be particularly useful when the amount of data is limited, as they can help to reduce overfitting and improve the generalization performance of the model. Also, they deserve more accurate estimates of portfolio risk by accounting for uncertainty in the underlying data and modeling assumptions.

This study emphasizes determining the high accuracy of ensemble model prediction. It is applied in the agricultural domain which focuses on price prediction, especially Thai rice prices. According to Thai rice prices, it relates to uncertainty data, and many factors (features) can be affected. The model of the BMIC [4] presents a clear relationship model, which impacts predictive accuracy. Since it has been found that the statistics of the Bayesian approach can present the probability distribution of the model, in this study, we thus selected the model of the BMIC [4] which integrates various forms of knowledge of Bayes’ theorem and the MIC to be the base model for incorporation with other traditional algorithms. Aggregation between different learning algorithms can extract new knowledge and reduce the occurrence of overfitting. Consequently, this paper will employ both single and ensemble models to determine better predictive accuracy in uncertainty data. The findings will show a suitable approach for Thai rice price prediction that works well with the base model of the BMIC.

2. Related Works

2.1. Uncertainty in Machine Learning Prediction

Data uncertainty refers to insufficient knowledge or imprecision about the values and characteristics of data. It refers to the ambiguity level that is presented in observations, measurements, or predictions. There are common sources that can increase uncertainty in data, as follows:

• Measurement errors occur during the measurement process in equipment, sensors, or human observation.
• Human subjectivity relates to the judgment or interpretation of any situation, such as survey responses or subjective assessments.
• Expert judgement refers to opinions or estimations which typically serve as inputs for models or influence decision-making outcomes.
• Sampling variability can be found in a large sample dataset.
• Environment variability may be affected by external factors or environmental conditions during data collection.
• Incomplete or missing data presents the unavailability of data or values, which provides insufficient information to process.
• Modeling assumptions can happen during the development of statistical or machine learning models which can lead to errors in predictions.
• Model complexity may occur due to many parameters in modeling and this tends to affect the overfit model.
• Stochastic processes occur with random phenomena that are uncontrollable.
• Evolving systems emphasize changes over time, such as time-series data.

In addition to the above, this study focuses on machine learning prediction, especially in the context of Bayesian modeling. Therefore, the two characteristics of uncertainty, which are modeled in a probabilistic way, are epistemic and aleatoric uncertainty [5]. Epistemic uncertainty is caused by the limitation of knowledge or data, which means that it is not possible to capture the statistical dependencies defined by auxiliary variables. It can imply model uncertainty. In machine learning prediction, the more accurate the prediction, the more reliable the information presented in real-world data. There are possible scenarios in various domains that can be found, such as incomplete knowledge or data about economic factors, market dynamics, and geopolitical events in financial forecasting. On the other hand, aleatoric uncertainty presents the randomness or variability in the data themselves which arises from noise in the data and cannot be eliminated by the model, such as the volatility of stock prices due to various factors [6].

Thus, uncertainty data commonly arise due to measurement errors, variability, or ambiguity in real-world observations. Examples of uncertainty data are sentiment analysis or language translation by natural language processing models, machine learning in medical diagnostics with the variability of blood sampling, calibration errors, or fluctuations in blood sugar levels [7], and Bitcoin price prediction [8]. On the other hand, non-uncertainty data refer to data that have a known ground truth or are obtained under controlled conditions where uncertainty is minimized. Examples are datasets containing labeled data or data collected in a controlled laboratory setting with minimal or accounted-for measurement errors.

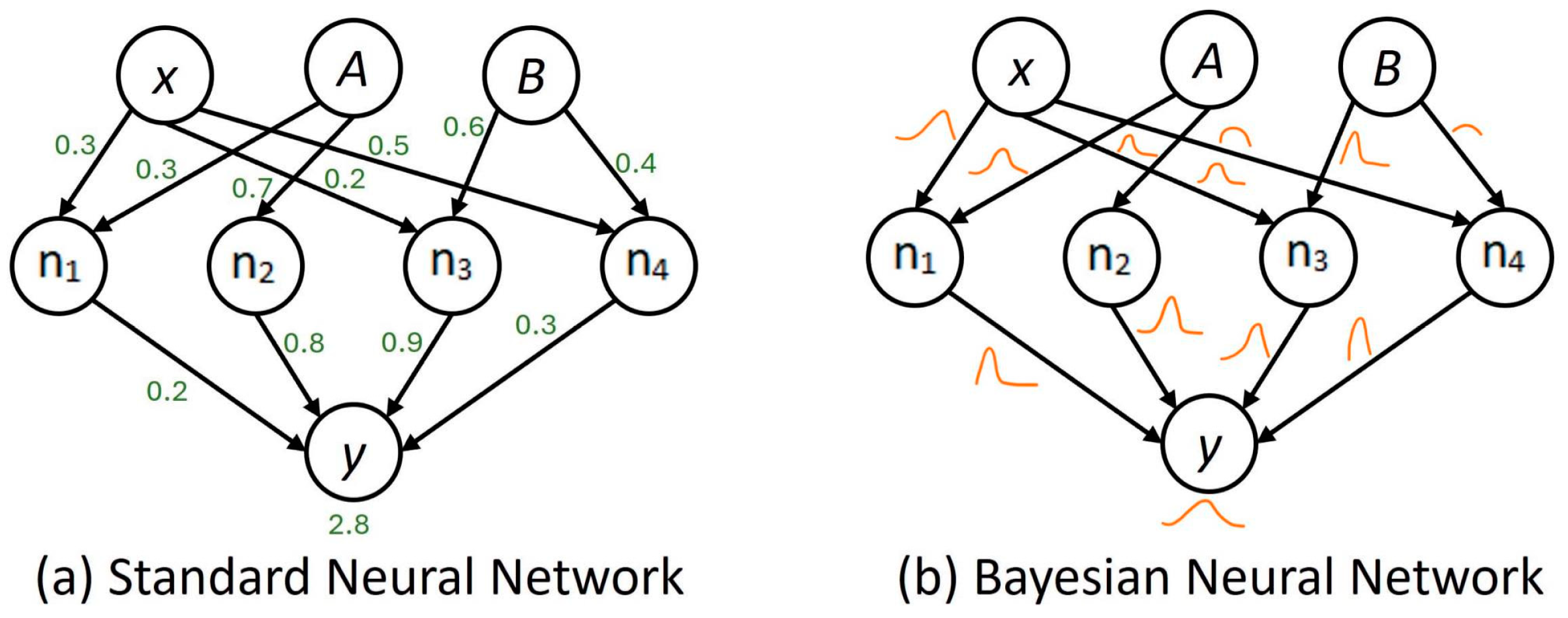
2.2. Bayesian Neural Network (BNN)

A Bayesian neural network (BNN) [9] is a stochastic artificial neural network that integrates Bayesian principles into its structure. BNNs differ from traditional neural networks by representing weights and biases as probability distributions rather than point estimates, as shown in Figure 1. Applications that require precise comprehension and quantification of uncertainty can benefit from the incorporation of uncertainty into model predictions. BBNs are widely used in the application of model predictions, such as in medical diagnoses [10] and financial forecasting [11], and also apply to time-series data forecasting [12]. A BNN is a specific type of artificial neural network (ANN) that incorporates stochastic elements into its network. It is achieved by providing the network with either stochastic activation or stochastic weights to implement multiple models along with their associated probability distributions. Therefore, BNNs can be regarded as a specific instance of ensemble learning.

From a theoretical perspective, a BNN uses Bayesian inference to train the stochastic artificial neural network model to address the uncertainty output through posterior distribution. Both epistemic and aleatoric uncertainty come from different sources of uncertainty. Epistemic uncertainty requires more data to capture the probability distribution of the model: $p\left(\theta \right|D)$ where $\theta$ is a particular parameter. This type can help the small sample in which the Bayesian theorem combines expert knowledge with empirical data. The prior distribution of the parameters, $P\left(\theta \right)$, is allowed to be updated into the posterior distribution. On the other hand, aleatoric uncertainty is naturally found in data, and it can capture the probability of the parameter $P\left(y\right|\theta )$.

The probabilistic parameterization in a BNN estimates the weights and biases of the parameter, $\theta$, as a posterior probability distribution, $p\left(\theta |D_x,D_y\right)$, which refers to a simple application of Bayes theorem [13].

$$p\left(\theta |D_x,D_y\right)=\frac{p\left(D_y|D_x,\theta \right)p\left(\theta \right)}{{\int }_{\mathsf{\Theta }}p\left(D_y|D_x,{\theta }^{\prime }\right)p\left({\theta }^{\prime }\right)d{\theta }^{\prime }}$$

(1)

The data $D$ comprises the input set of $x$, $D_x$ and the corresponding data of output of $y$, $D_y$, which will be used for network modeling based on $D_x$. It can alternatively determine in a pair of $x,y$ by $D={\{y_i,x_i\}}_{i=1}^N$, where $N$ is the sample size. Then, it can imply the input $x$ and output $y$ of the $i$th sample as $D_x={\left\{x_i\right\}}_{i=1}^N$ and $D_y={\left\{y_i\right\}}_{i=1}^N$. From the equation, the probability of $D_y$ is conditional on the input sample of $D_x$, which is parsed specific parameter values of the input into predictions. Meanwhile, the output adheres to a determined likelihood function.

Theorem 1.

The inference procedure of the Bayesian neural network from Equation (1) when the sample data of $x$ and $y$ are considered as $D$.

• for $i=0$ to $N$ do
• Draw ${\theta }_i~p\left(\theta \right|D)$;
• $y_i={\Phi }_{{\theta }_i\left(x\right)}$;
• end for
• return $Y=\left\{y_i|iϵ\left[0,N\right)\right\}$, $\Theta =\left\{{\theta }_i\right|iϵ\left[0,N\right)\}$; where $Y$ is a sample set of $p\left(y\right|x,D)$ and $\Theta$ is a collection sample of $p\left(\theta \right|D)$.

With the return values of $Y$ and $\Theta$ in Theorem 1, the uncertainty of the BNN can be computed and summarized by those returned samples. Also, the estimator can be acquired for output $y$ with $\widehat{y}$. The average model prediction for classification will provide the relative probability of each class, which can be regarded as an indicator of uncertainty.

$$\widehat{p}=\frac{1}{\Theta }{\sum }_{{\theta }_i\in \Theta }{\Phi }_{{\theta }_i}\left(x\right)$$

(2)

Then, the final prediction will return as

$$\widehat{y}=\mathit{arg}\underset{i}{\max } p_i\in \widehat{p}$$

(3)

According to this definition, BNNs are discriminative models which focus on constructing the target variable $y$ on the given observation variable $x$ [9].

In addition, there is a type of artificial intelligence, the probabilistic Bayesian neural network (PBN) [14], which extends beyond representing uncertainty in parameters to also explicitly modeling uncertainty in predictions. This means that instead of providing a single deterministic output, the PBN yields a distribution of possible outputs, reflecting the inherent uncertainty in predictions. PBNs provide a promising avenue for probabilistic modeling in deep learning, and they have the potential to improve the accuracy and interpretability of neural network predictions in various fields. Both epistemic and aleatoric uncertainty can be captured. The conversion of a BN to a PBN is proposed to provide uncertainty estimates for the predictions, which can be particularly useful in applications where risk assessment is important. The model will learn from mean and variance parameters to obtain the output as a normal distribution. As in [15], we used the BNN-based probabilistic prediction model to analyze the results of the prediction model and uncertainty. It returned high accuracy in prediction and brought the uncertainty of prediction.

Therefore, all BNNs are probabilistic in nature due to the treatment of parameters as probability distributions. A PBN may specifically highlight the inclusion of explicit modeling of uncertainty in the predictions, making it a more refined and encompassing approach to uncertainty representation in neural networks.

2.3. Ensemble Model

An ensemble model in machine learning refers to a technique where multiple individual models are combined to form a stronger, more robust predictive model. This approach leverages the diversity of different models to enhance overall performance and generalization. Instead of relying on a single model, an ensemble model aggregates predictions from its constituent models, often resulting in improved accuracy and stability. There are two strategies in ensemble learning, which are homogeneous ensemble and heterogeneous ensemble.

• Homogeneous ensemble involves using multiple models of the same type or family to create an ensemble. In this approach, identical base learners, often sharing the same algorithm, are trained on different subsets of the data or with variations in training parameters. The individual models work collectively to provide a more robust and accurate prediction. Bagging, where multiple decision trees are trained independently, is an example of a homogeneous ensemble approach.
• Heterogeneous ensemble employs diverse types of base learners within the ensemble. This approach combines models that may belong to different algorithm families, utilizing their unique strengths and characteristics. Heterogeneous ensembles aim to enhance predictive performance by leveraging the complementary nature of different algorithms. Stacking, where models with distinct architectures or learning algorithms are combined, exemplifies a heterogeneous ensemble strategy.

Regarding ensemble learning, the ensemble model can be formed through the main methods of bagging (bootstrap aggregating), boosting, stacking, blending, and voting, which are widely used and allow one to capture a broader range of patterns and nuances present in the data.

• Bagging (bootstrap aggregating) involves training several instances of the same base learning algorithm on diverse subsets of the dataset. These subsets are often created through bootstrap sampling, and the predictions from individual models are then aggregated, commonly through averaging or voting. The goal of bagging is to mitigate overfitting and improve overall model robustness.
• Boosting focuses on sequential training models, with each subsequent model assigning higher weights to instances misclassified by previous models. This adaptive approach aims to correct errors and improve the model’s performance, particularly in challenging instances. AdaBoost and gradient boosting are popular boosting algorithms used to create strong predictive models.
• Stacking (stacked generalization) involves training diverse base models, often of different types or families, and combining their predictions through a meta-model. Instead of directly aggregating predictions, a meta-model is trained to learn how to combine the outputs of the individual models best. Stacking is a more sophisticated ensemble method that aims to capture complex relationships within the data.
• Blending is an ensemble technique whereby different models are trained independently on the dataset and their predictions are combined through a weighted average or a simple linear model. Unlike stacking, blending typically involves using a holdout validation set to create the ensemble model.
• Voting is also known as majority voting and is a straightforward ensemble method where multiple models make predictions, and the final prediction is determined based on a majority vote. In the case of classification, the class that receives the most votes is chosen as the overall prediction. This approach is commonly used in both binary and multiclass classification scenarios.

In summary, the key distinction lies in the nature of the base learners who can employ the techniques in both types of homogeneous and heterogeneous ensembles. Homogeneous ensembles use identical or similar base learners, while heterogeneous ensembles leverage diverse types of base learners. There is a study by [16] which introduced cost-sensitive learning in multi-class data prediction with probability. They proposed the heterogeneous ensemble model. Their experiment combined it with various classifiers and worked with homogeneous models which demonstrated high accuracy when using a probability-driven weighted voting approach. Also, in the environmental area, researchers applied ensemble learning with conditional probability to predict landslide susceptibility [17]. They focused on statistical theory with machine learning to improve the accuracy of boost regression tree (BRT) model prediction. In [18,19], the authors presented ensemble learning with classification models in the context of financial data classification, particularly in corporate bankruptcy prediction. The resulting scoring model was applied to prove that ensemble classification systems outperform existing models. Moreover, in [20], the authors studied feature ensemble to predict anxiety disorders for the improvement of health care.

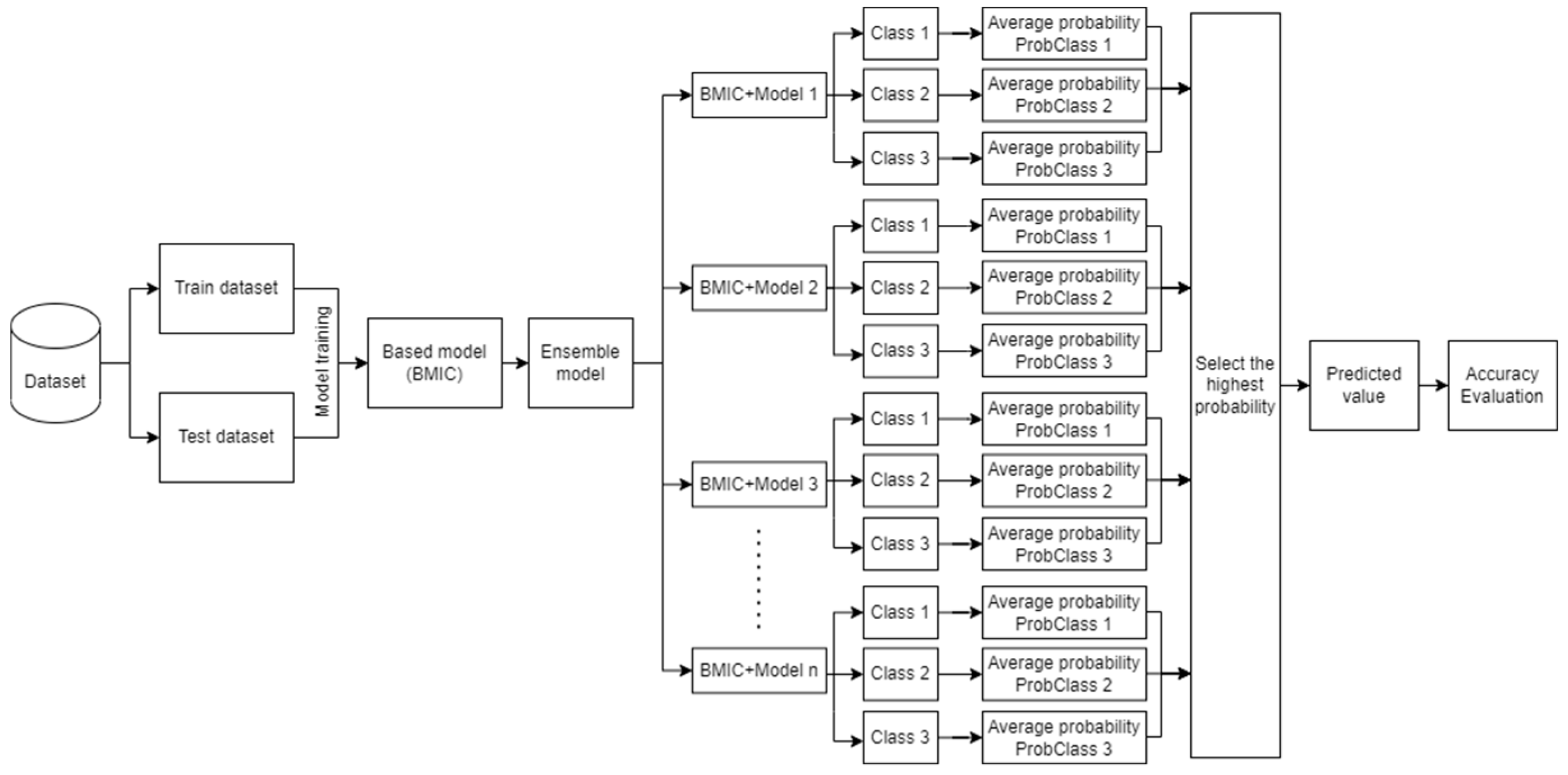
3. Methods

3.1. Methodology

The purpose of this study was to explore the methodology of ensemble prediction models based on the Bayesian approach that helps to measure uncertainty data through probability theory. Our main aim was to apply the BMIC which is a Bayesian classification model that relies on a BN for estimating the probability of each class and considers class predictions. Every class is linked to a probability distribution across the feature space. Upon encountering a new instance, its characteristics are utilized to determine the probability of it belonging to each class based on the class-conditional probability distributions. The probabilities are combined with the prior probabilities of each class to calculate the posterior probability of each class based on the observed features. The label, for instance, is predicted by selecting the class with the highest posterior probability.

The approach of ensemble prediction models involves combining the probability distribution of multiple individual models using Bayesian inference. It has been found that a single model typically relies on a single set of assumptions and parameters, which may lead to less accurate predictions. Therefore, ensemble learning provides a more comprehensive and robust prediction by considering the uncertainty and variability of the integration among individual models.

According to the Bayesian theorem we focused on in this study, it provides a versatile and powerful foundation for prediction in machine learning. One key benefit lies in its ability to seamlessly integrate prior knowledge or beliefs about model parameters, enabling a principled combination of existing information with observed data. This approach is particularly advantageous in situations with limited data. Bayesian inference facilitates the quantification of uncertainty by providing probability distributions over parameters, leading to more nuanced and insightful predictions. The methodological framework of this study is presented in Figure 2 to describe the flow of the ensemble model, which is the integration of a traditional model with the BMIC model [4].

The ensemble learning in this experiment was set to test the model accuracy of ensemble model prediction, as shown in Figure 2. Ensemble models often involve combining predictions from multiple models. The BMIC was selected as the base model that returns the best cause-and-effect relationship model. It is a novel model based on the integration of the probability inference of a Bayesian network (BN) in the form of a probabilistic graphical model (PGM) and MIC correlation. The method formed the efficiency model to find the causal relationship between data uncertainty which includes relevant factors and Thai rice prices. Bayesian inference plays a crucial role in ensemble models, especially when considering the uncertainty associated with model parameters and predictions. It treats model parameters as probability distributions rather than fixed values. The Bayesian approach enables the incorporation of prior beliefs about parameter values, and as new data are observed, the posterior distribution over parameters is updated, capturing the uncertainty in their estimates. Therefore, the ensemble model with the BMIC can be more accurate in prediction, as with the assumption of this study.

Ensemble models and Bayesian networks are two distinct concepts in machine learning and combining them may be uncommon. However, combining Bayesian networks within an ensemble framework could imply creating an ensemble of Bayesian networks or using Bayesian methods to improve specific aspects of ensemble models. We found the predictive model which embeds Bayesian principles in comparison. The Bayesian neural network (BNN) model was selected to be compared since it can capture uncertainty within model parameters, treating them as probability distributions instead of fixed values. However, BNNs diverge from ensemble models; they can be incorporated into ensemble strategies to boost overall performance. Therefore, in this experiment, we set two approaches to focus on.

The first approach is the ensemble learning of the BMIC with the other models illustrated in Figure 2, which is our study purpose. Ensemble learning incorporates Bayesian methods, such as Bayesian model averaging, to assign probabilistic weights to $n$ different models in the ensemble. The different models emphasize the traditional classification models, which are logistic regression, K-nearest neighbors, decision tree classifiers, random forest classifiers, support vector machines, neural networks, naive Bayes classifiers, and XGBoost classifiers. The BMIC and selected classification models utilize three distinct labels to categorize input data into corresponding classes. These labels serve as the target variables during the training phase, in which the model learns patterns and relationships between input features and the assigned labels. Subsequently, during prediction, the model utilizes these learned patterns to classify new instances into one of the three predefined categories. We merged the probability distributions generated by model $n$ and the BMIC for each label and then averaged the results to make predictions. It can be valuable in ensemble models for understanding the robustness of predictions to extract the probabilistic dependencies of the ensemble models of the BMIC.

Algorithm 1 describes the approach of ensemble learning between two models of BMIC and traditional classification model algorithms. This method emphasizes the predicted probability value on different labels. The avg_PredProb stores the average value of the predicted probability of each label. Then, the label which holds the maximum value of predicted probability is returned.

Algorithm 1 Ensemble learning of the BMIC and traditional classification model algorithms

Input: dataset $D$ from csv file   Read data from $D$   Split $D$ into features(X)80% and target variable(y)20% Procedure BMIC prediction   Define the structure of the Bayesian Network:     Define the nodes and their dependencies   Initialize the BMIC on the structure of the Bayesian Network   Fit the BMIC on the training data   Predict probabilities of three distinct labels for testing data   Store predicted probability results in PredProb_BMIC    Procedure traditional classification models prediction   Define a list of classification models to loop through:   models = [LogisticRegression(), K-nearestNeighbors(), DecisionTree(), RandomForest(), SVM(), NeuralNetwork(), NaiveBayes(), XGBoost()]   Define a list to store model performance metrics:     model_acc = []   Loop each model in the list of classification models:     For each model in models:       Initialize the model       Fit the model on the training data       Predict probabilities of three distinct labels for testing data       Store predicted probability results in PredProb_model Procedure ensemble model of BMIC and each traditional classification model   Calculate the average probabilities of BMIC and each traditional classification model     avg_PredProb = (PredProb_BMIC + PredProb_model)/2   Select the maximum value of predicted probability among three distinct labels     If label1.value is greater than label2.value and label1.value is greater than label3.value:       PredMaxLable = label1.value     Else if num2 is greater than num1 and num2 is greater than num3:       PredMaxLable = label2.value     Else:       PredMaxLable = label3.value   Calculate the accuracy score true labels of y test and PredMaxLable   Store in testing_acc   Print PredMaxLable   Print testing_acc

Secondly, there are Bayesian neural networks (BNNs) in the ensemble which utilize neural networks (NNs) as base models in an ensemble with the Bayesian inference. This study focuses on the model predictions of a BNN and another type of probabilistic Bayesian neural network (PBN). The PBN in the ensemble provides probabilistic predictions, capturing the uncertainty in its parameters. We combined the predictions of multiple BNNs to obtain a more reliable and uncertainty-aware ensemble prediction. It is necessary to manually extract the probabilistic dependencies from the BN and use them to inform the probabilistic model for the weights and biases in a PBN. PBNs treat these parameters as probability distributions, allowing for a more flexible representation of uncertainty. In [8,12,21], the authors applied a BNN to reveal its predictive ability and compared it with traditional predictive models. Also, in [22], the authors compared the predictive accuracy of traditional and ensemble models.

3.2. Data Preparation

The environment concentrated on Thai rice price prediction, which was used to emphasize multi-label classification. According to BMIC model selection, it is a novel predictive model that integrates the Bayesian theorem and MIC correlation to describe the causal relationship between variables. The ensemble learning executes on the same dataset, which is the Thai rice price data with nine different features, which relied on the study of [4]. Then, nine different features of the BMIC model were described in the form of a Bayesian network which shows the relationship among features in

Table 1. The causal relationships between the features of the BMIC-based model.

Cause Features	Effect Feature
Export Vietnamese white rice price	Export Pakistani white rice price
Export Pakistani white rice price	Export Thai white rice price
Export Thai white rice price	Gold price in Thailand
Export Thai jasmine rice price	Jasmine rice price in Thailand
Export Thai jasmine rice price	Paddy price in Thailand
Export Thai jasmine rice price	Exchange rate of US Dollar with Thai Baht
Paddy price in Thailand	Jasmine rice price in Thailand
Jasmine rice price in Thailand	Exchange rate of US Dollar with Thai Baht
Exchange rate of US Dollar with Thai Baht	Gasoline price in Thailand

, which were used to train the model in this study. The dataset was collected from the sources of the Office of Agricultural Economics [23], the Thai Rice Exporter Association [24], Thai Customs [25], and the Thai Meteorological Department [26], which cover 11 years (2008–2018). The dataset was determined as the uncertainty data that were collected over time as the time-series data.

The data were separated into three labels, and then, the results were tested on voting for the highest predicted posterior probability among the three labels. They take the average predicted probability from ensembled models in the case of classification. The data is split into training and testing datasets with 80% as the training dataset and 20% as the testing dataset.

4. Results and Discussion

The predicted probability has been measured via single model and ensembled models. We experimented to present the predictive accuracy of the ensemble model between the BMIC model and traditional classification models. There are eight models, which are logistic regression (LR), K-nearest neighbors (KNN), decision tree classifiers, random forest classifiers, support vector machines (SVMs), neural networks, naive Bayes classifiers, and the XGBoost classifier, which were focused upon to be ensembled.

To follow the selected study of Thai rice prices, we included the BNN and PBN to reveal the model’s accuracy on uncertain data. This is particularly relevant in ensemble methods like Bayesian neural networks (BNNs), where the weights and biases of individual models are represented by probability distributions. Focusing on BNNs and PBNs, these activation functions are utilized to model uncertainty in predictions by propagating probability distributions instead of deterministic values through the network. The activation function was declared as the “Softmax function”, which is commonly used when the task involves classification with more than two classes. When given an input $z$, the softmax function computes the output $y$.

$$y_i=\frac{e^{z_i}}{{\sum }_{j=1}^K{e}^{z_j}}$$

(4)

where $K$ is the number of labels

$z_i$ is the $i$-th element of an input $z$

$y_i$ is the $i$-th element of an output $y$

The Softmax function ensures that the output values lie between 0 and 1 and sum up to 1, making them interpretable as probabilities. It is often used in the output layer of classification models to predict the probability distribution over different classes. It implies that the highest predicted probabilities among the three labels can be returned. The model distribution of the output with classification implemented the OneHotCategorical for multiple classes. In a BNN, the OneHotCategorical distribution is often employed in the output layer to model the probability distribution over multiple classes in classification tasks. Instead of producing a single deterministic output, the output layer of a Bayesian neural network with OneHotCategorical distribution outputs a probability distribution over classes. During training, the network learns the parameters (probabilities) of the OneHotCategorical distribution from the data, incorporating uncertainty into predictions. During inference, the network provides predictions in the form of probability distributions, enabling uncertainty estimation in classification tasks.

To reveal the performance of predictions, both single and ensemble models are considered. The single model of a BNN and a PBN was selected to test the model’s accuracy compared with the ensemble models. The BNN and PBN treat model parameters as probability distributions, applying Bayesian principles to capture uncertainty in model parameters. This method contrasts with ensemble techniques, which involve training multiple models independently and then combining their predictions using methods like averaging or voting. Ensemble models enhance overall performance by aggregating predictions from multiple individual models. The model’s accuracy was measured using the accuracy score provided by the scikit-learn library. This function calculates accuracy by matching the predicted label for a sample to y_true labels.

Therefore, the accuracy of prediction on training models is shown in

Table 2. Evaluating the predictive accuracy on the training model of single and ensemble models.

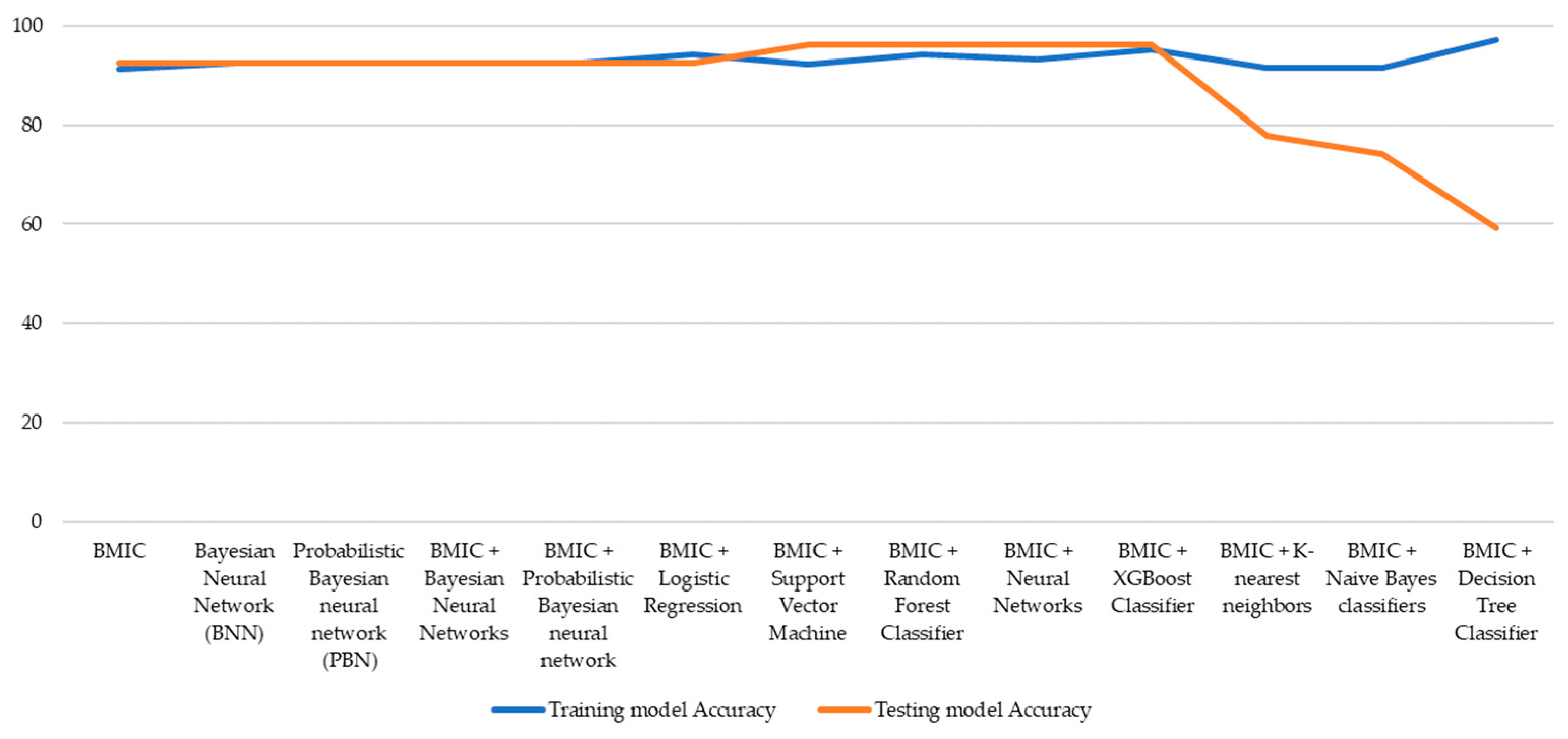
Models	Training Model Accuracy
BMIC	91.42
Bayesian Neural Network (BNN)	92.59
Probabilistic Bayesian neural network (PBN)	92.59
BMIC + Bayesian Neural Networks	92.59
BMIC + Probabilistic Bayesian neural network	92.59
BMIC + Logistic Regression	94.29
BMIC + Support Vector Machine	92.38
BMIC + Random Forest Classifier	94.29
BMIC + Neural Networks	93.33
BMIC + XGBoost Classifier	95.24
BMIC + K-Nearest Neighbors	91.43
BMIC + Naive Bayes Classifiers	91.43
BMIC + Decision Tree Classifier	97.14

.

The performance of prediction on the training model of single and ensemble models reached more than 90% in every model. There are 11 models including single and ensemble models which return predictive accuracies of around 91–94%. In particular, the two ensembled models with accuracy higher than 95% are the combination of the BMIC with the XGBoost classifier and decision tree classifier, which reached 95.24 and 97.14, respectively. The decision tree classifier reduces variance by capturing data patterns, while XGBoost iteratively corrects errors to reduce bias. Therefore, the models learned enough with the dataset and returned high results.

Moreover, the comparison results for the testing model are shown in

Table 3. Evaluating the predictive accuracy on the testing model of single and ensemble models.

Model	Testing Model Accuracy
BMIC	92.58
Bayesian Neural Network (BNN)	92.58
Probabilistic Bayesian neural network (PBN)	92.58
BMIC + Bayesian Neural Networks	92.59
BMIC + Probabilistic Bayesian neural network	92.59
BMIC + Logistic Regression	92.59
BMIC + Support Vector Machine	96.3
BMIC + Random Forest Classifier	96.3
BMIC + Neural Networks	96.3
BMIC + XGBoost Classifier	96.3
BMIC + K-Nearest Neighbors	77.77
BMIC + Naive Bayes classifiers	74.1
BMIC + Decision Tree Classifier	59.26

.

The analysis shows that individual models of the BMIC, BNN, and PBN, as well as the ensemble models of the BMIC with a BNN and the BMIC with a PBN, all achieve an accuracy of approximately 92%. The equal outcome implies that the support from the same domain of the Bayesian theorem does not significantly enhance predictive performance. They lack the diversity of base classifiers. If the base classifiers in the ensemble are similar or biased in the same way, the ensemble may not provide much improvement over individual classifiers. Moreover, the BMIC combined with LR gives approximately 92%. This implies that LR can boost predictive modeling’s ability, which estimates the probability of a given sample belonging to a particular class. This is particularly useful when the relationship between the features and the target variable is linear, offering interpretable results that indicate the influence of each feature.

While ensemble models demonstrate good accuracy compared to the ensemble model with other individual traditional models, each of the combinations of the BMIC with SVM, the BMIC with the random forest classifier, the BMIC with neural networks, and the BMIC with the XGBoost classifier returned 96.3% model accuracy. SVMs, random forest classifier, neural networks, and XGBoost classifier are diverse in terms of their learning algorithms, feature representations, or hyperparameters. SVMs excel at classifying data in high dimensions by finding the best-dividing line (hyperplane) to separate different categories. They achieve good performance while efficiently using memory by focusing on critical data points (support vectors) for decision-making. Also, the random forest classifier combines predictions from numerous decision trees to enhance accuracy and combat overfitting. Neural networks are masters of pattern recognition. They analyze data by passing them through layers of interconnected nodes, each performing basic calculations. This enables them to capture intricate patterns and relationships within the data, making them versatile for various tasks. Lastly, XGBoost classifiers take an innovative approach to prediction by combining the predictions of multiple weak learners. They effectively handle missing data and boast resilience against overfitting through built-in regularization. Traditional models may be sensitive to outliers or noise in the data, leading to suboptimal performance in certain cases. Ensemble methods, by combining predictions from multiple models, can be more robust to outliers and noise, as outliers are less likely to significantly impact the aggregated predictions, resulting in higher accuracy overall. Therefore, the ensemble models of the four particular traditional algorithms can capture a wider range of patterns and dependencies present in the data and work properly with the BMIC model.

On the other hand, a few traditional models obtained around 74% and 77%, namely the BMIC with KNN and the BMIC with naive Bayes classifiers, respectively, which are less accurate. Since naive Bayes classifiers operate under the assumption that features are conditionally independent given the class label, it can be unrealistic that features might have some level of interdependence in many real-world scenarios. This makes the naive Bayes model miss crucial relationships between features, potentially leading to worse performance. Moreover, KNN analyzes a new point by examining its closest neighbors in the dataset, using their known classes to predict the unknown one. It does not estimate parameters or model the underlying distribution of the data explicitly. It relies solely on the proximity of data points in the feature space to make predictions. This makes it difficult to directly apply Bayesian inference, which typically involves modeling probability distributions over parameters. Consequently, improper algorithms cannot operate ensemble learning among the same base model of the BMIC.

However, the BMIC with the decision tree classifier returned the worst model accuracy of around 59%. The decision tree classifier predicts the class of a sample by traversing a tree-like structure based on feature splits. It is capable of handling both numerical and categorical data and is resistant to outliers. However, decision trees can easily overfit the training data, especially if the tree is deep or has high variance in the data. Regularization techniques like pruning are often used to mitigate this issue. Then, this is the reason why it gives inaccurate predictions when working with the BMIC.

The predictive accuracy results of both the training and testing models are demonstrated in Figure 3. There are five models, including the BMIC, the BMIC with support vector machine, the BMIC with the random forest classifier, the BMIC with neural networks, and the BMIC with the XGBoost classifier, that provide improved prediction results on the testing model. Optimal tuning of the hyperparameters in the training data will ultimately lead to improved predictions in the testing data. Except for the single BMIC model, it was noticed that the BMIC can be integrated with individual traditional models. The ensemble approach can enhance the accuracy of predictions by capitalizing on the advantages of each individual model while minimizing their weaknesses. However, it was noticed to a significant degree that the ensembled models between the BMIC with the decision tree classifier returned the highest result in the training model but the lowest result in the testing model. This might have occurred due to the insufficient test dataset since Bayesian methods use prior knowledge and regularization to reduce overfitting. Regarding the remaining models, there was no improvement in the training and testing models, with them returning similar predictive accuracy results.

As a result, the experimental results demonstrate the predictive accuracy among the single and ensemble models which capture the different characteristics of the models. Each individual traditional method may have its own ability in terms of handling different aspects of data and modeling. While the ensemble method can leverage the complementary strengths of diverse BMICs as a base model to compensate for the weaknesses of individual models, this study reveals that the pairwise combination models of SVMs, the random forest classifier, neural networks, and the XGBoost classifier with the BMIC exhibit the highest accuracy, as evidenced by their respective characteristics. They handle the high-dimensional space of the input data which can capture the non-linear relationship between features and class labels. Also, they train their models with the ensemble method which aggregates predictions from multiple layers. Moreover, these learners are robust to noise and outliers.

The findings of this study show that ensemble models return the best accuracy in prediction. They can support human decision-making when applied to various domains, especially financial ones. Since this study focused on Thai rice prices, it can be used as a tool to reveal the predicted prices which can help relevant stakeholders in this field estimate future trends and prevent the occurrence of unexpected situations.

5. Conclusions

The ability of ensemble models comprising a Bayesian-based model with the MIC (BMIC) can provide high accuracy in prediction when combined with other models within various domains. By combining Bayesian approaches with traditional machine learning, practitioners can build models that are more robust, adaptive, and capable of providing meaningful uncertainty estimates. The hybrid framework enhances the flexibility and reliability of machine learning models, especially in situations where uncertainty and limited data pose challenges. This study focuses on uncertainty data and compares the results with the single models of a BNN, a PBN, and ensemble traditional models with the BMIC. We found that some of the single models, such as SVMs, the random forest classifier, neural networks, and the XGBoost classifier, can work effectively with the BMIC to deal with uncertainty in data.

It was noticed that the BNN and PBN have several advantages over traditional machine learning. Firstly, they can provide more robust predictions by accounting for the uncertainty in the data. This can be particularly useful in situations where the data are noisy or incomplete. Secondly, they can avoid overfitting by incorporating prior knowledge into the model. Finally, they produce a probability distribution over possible outcomes rather than a single-point estimate. However, the BNN and PBN return lower prediction accuracy compared to ensemble models because of the same domain of the Bayesian theorem with the BMIC model.

Therefore, the ensemble model integrates various individual models or learning algorithms (learners) to enhance performance which is known as “learners” and work together to achieve a more accurate prediction than any single one could on its own. These learners can be diverse, employing different model types or even variations of the same model with distinct parameter settings which contribute to the prediction. They integrate the predictions of multiple models and facilitate more effective decision-making support in addressing uncertainty data or ambiguous scenarios.