Domain-Specific Dictionary between Human and Machine Languages

Abstract

In the realm of artificial intelligence, knowledge graphs have become an effective area of research. Relationships between entities are depicted through a structural framework in knowledge graphs. In this paper, we propose to build a domain-specific medicine dictionary (DSMD) based on the principles of knowledge graphs. Our dictionary is composed of structured triples, where each entity is defined as a concept, and these concepts are interconnected through relationships. This comprehensive dictionary boasts more than 348,000 triples, encompassing over 20,000 medicine brands and 1500 generic medicines. It presents an innovative method of storing and accessing medical data. Our dictionary facilitates various functionalities, including medicine brand information extraction, brand-specific queries, and queries involving two words or question answering. We anticipate that our dictionary will serve a broad spectrum of users, catering to both human users, such as a diverse range of healthcare professionals, and AI applications.

1. Introduction

Knowledge representation refers to the process of crafting a structured framework that represents information related to a particular domain of interest. The purpose of knowledge representation is to facilitate reasoning and decision-making concerning the domain of interest [1]. In order to represent scientific knowledge through a structured framework, knowledge graphs are widely used. A knowledge graph can be described as a systematic representation of facts through entities, relationships, and a semantic framework. Knowledge graphs can also be defined as semantic networks. Semantic networks are structured representations of knowledge or concepts, where nodes represent entities or concepts, and edges represent relationships between entities [2]. The primary objective of both semantic networks and knowledge graphs is to capture the semantics or meaning of the relationships between entities. Knowledge graphs facilitate the spontaneous exploration and analysis of complex datasets. They enhance decision-making processes and accelerate knowledge discovery.

A significant number of knowledge graphs have been developed so far, such as Freebase, WordNet, ConceptNet, DBpedia, YAGO, and NELL [1]. These systems have been extensively used for question-answering systems, search engines, and recommendation systems. Since the introduction of semantic networks by Quillian [3] in 1963, research in this area has been continuously conducted, with various algorithms, mechanisms, and applications being presented. Semantic webs and ontology [4] are considered to represent the second wave of this research, in which the merging of local and universal ontologies was proposed. Compared with semantic networks, the second wave represents knowledge in a hierarchal structure, and hence, inheritance becomes possible. The most fundamental and influential work was RDF and OWL by the World Wide Web Consortium (W3C). W3C also developed standards and guidelines for web information representation and extraction. Knowledge graphs and knowledge graph learning, which represent the third wave of this research, were introduced in recent years. Information is represented as tuples which form knowledge graphs. Significant progress has been made in recent years in terms of applying machine learning algorithms to knowledge graphs. In their recent survey article [1], Ji et al. provided a comprehensive summary of the research in this area. In the academic and industrial research communities, the expressions knowledge graph and knowledge base are used indiscriminately [1]. There is a negligible difference between these two expressions. When considering the graph structure, a knowledge graph can be seen as a graph [1]. However, when formal semantics are applied, it can be regarded as a knowledge base used for interpreting and inferring facts [1]. 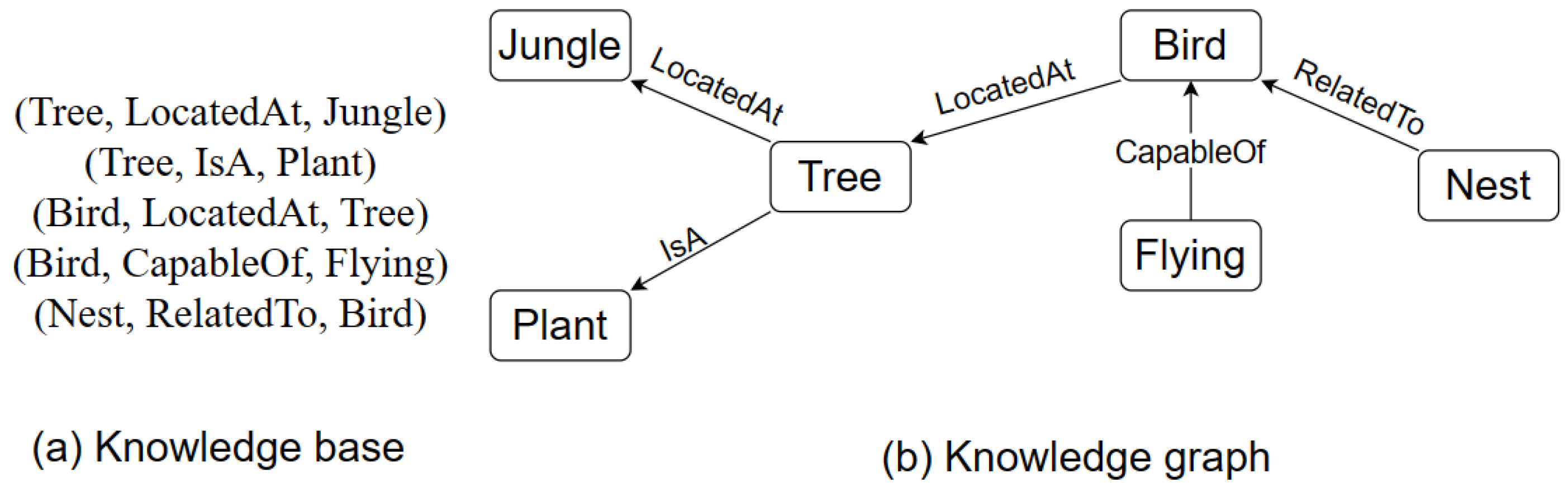In Figure 1a, we can see an example of a knowledge base and Figure 1b an example of a knowledge graph. In the knowledge base (Figure 1a) example, knowledge is represented in the form of factual triples. Triples comprise the subject, predicate, and object. For example, Bird, locatedAt, and Tree. In triples, a relationship between subject and object is established through the predicate.

On the other hand, the knowledge graph (Figure 1b) contains a set of entities (nodes) linked by directed and labeled edges. Each edge represents a relation. The two entities linked by a relation represent a relationship. The entity pointed to by the relation is the head of the relationship, whereas the other entity is called the tail. An entity can be a head as well as a tail in a knowledge graph. For instance, the entity “tree” is the head in the relationship “tree isA plant”, whereas it is a tail in the relation “bird locatedAt tree”.

Structured information can be useful outside of knowledge graphs as well. OMRKBC [5] is a machine-readable knowledge base designed to enable efficient data access and utilization. The authors of OMRKBC [5] structured it using the fundamental concept of knowledge graph triples, making it accessible via a variety of systems. OMRKBC [5] allows users to extract valuable information efficiently through diverse applications and interfaces. Moreover, the authors have introduced an additional framework known as NLIKR [6], which allows an application to extract definitions of a concept from their dictionary and understand its meaning. This framework provides a definition corresponding to each concept [6]. The application possesses the capability of accurately estimating the distance and similarity between concepts, thereby enhancing its understanding of their meaning.

In this paper, we propose a domain-specific dictionary between human and machine languages. The inspiration for this dictionary stemmed from an extensive survey of knowledge graphs. There is a unique opportunity to enhance the way medicine information is organized, accessed, and understood. The ultimate goal of this dictionary is to improve the quality of healthcare services. This knowledge graph-driven medicine dictionary will serve as a cornerstone in the realm of medical information systems. Its foundation lies in a well-structured ontology that utilizes knowledge graph triples to represent essential information about medications, their classifications, strengths, side effects, and various attributes. These triples, such as “A-Cold, has dosage form, Syrup”, “A-Cold, type of, allopathic”, etc., form the backbone of our ontology, enabling us to organize and present information in a format that is both machine-readable and human-understandable. This paper will explore the rationale, methodology, and potential benefits of constructing such a medicine dictionary.

The primary aim of this paper is to introduce a novel framework for constructing a comprehensive medicine dictionary using structured triples. While existing resources, such as The Danish Fetal Medicine database [7], YaTCM [8], and MEDI database [9], and knowledge graphs, such as SMR [10] and SnoMed kg [11], have contributed to the field, they typically present data in relational table formats or contain triples that are not exclusively focused on medicine-related information. Furthermore, these knowledge graphs primarily serve as repositories of medical knowledge within the medical sector.

What sets our proposed dictionary apart is its unique capability to represent medicine attributes through entities and relations, thereby enabling advanced reasoning abilities. Users of this dictionary will be empowered to effortlessly extract crucial medicine-related details, including generic names, types, strengths, manufacturers, pharmacological descriptions, side effects, and, significantly, a wide range of alternative medicine brands for each primary medicine brand.

The rest of the paper will be organized as follows. Section 2 will briefly discuss the previous research on knowledge graphs and the findings from the literature survey on knowledge representation learning, acquisition, and applications. In the next section, we will delve into the methodology employed to construct a medicine dictionary. Here, we will briefly lay out our approach, detailing how we harness structured triples to construct our comprehensive medicine dictionary. The methodology section will unveil the techniques and tools utilized in this project. After that, we will explore the practical application of our medicine dictionary. Real-world applications, such as the information extraction mechanism and question-answering techniques, will be discussed. Furthermore, we will showcase our experimental results and compare our work with existing mechanisms. Lastly, this paper will conclude with future research directions and the broader implications of our work.

2. Related Works

The domain of artificial intelligence has an extensive and well-established history of knowledge representation and reasoning, often facilitated by knowledge graphs. These graphs are primarily used to predict missing links within a vast network of information. Knowledge reasoning ability is crucial for representing knowledge in a structured format. Reasoning can be described as the process of analyzing, consolidating, and deriving new information on various aspects based on known facts and inference rules (relationships). It involves accumulating facts, identifying relationships between entities, and developing advanced understandings. Reasoning relies on prior knowledge and experience. Mining, organizing, and effectively managing knowledge from large-scale data are conducted through reasoning capabilities [12].

The concept of semantic net, proposed by Richens in 1956, can be identified as the origins of diagram-based knowledge interpretation [1]. The roots of symbolic logic knowledge trace back to the General Problem Solver in 1959 [1]. As knowledge representation progressed, various methods emerged, including framework-driven language, reasoning-driven systems, and blended manifestation systems. MYCIN [1], the renowned knowledge reasoning system in medical diagnosis, utilized a rule-based approach. The semantic web’s essential standards, such as Web Ontology Language (OWL) and resource description framework (RDF), were inspired by knowledge representation and reasoning systems [1]. Semantic databases offer flexibility in depicting complex data relationships and enable sophisticated querying through semantic technologies such as OWL, RDF, and SparQl. Nonetheless, their management complexity and potential performance overhead demand proficiency in semantic standards. Despite scalability, the steep learning curve and limited tooling support can hinder widespread use. RDF serves as a framework for organizing web-based knowledge through structured triples, facilitating the development of interconnected datasets represented in a graph format [5]. Additionally, it facilitates the querying of these datasets via SparQl. OWL, as a language designed for crafting web ontologies, enables the specification of classes, properties, and logical axioms within specific domains [5]. OWL builds on RDF and handles complex knowledge models with detailed meanings, enabling automated reasoning and inference based on asserted knowledge. Apart from these, various systems and resources, including WordNet, DBpedia, ConceptNet, YAGO, and Freebase, have been developed to capture and represent knowledge effectively and efficiently.

WordNet [13] can be described as a lexical database of English words defined through synonyms. In the database, words are bundled as synsets. One synset can be defined as one unique concept. Concepts are linked through lexical relations, thus allowing machines to apply knowledge to reason over the meaning of words. However, the authors of NLIKR [6] argue that synsets are not enough to describe a word. Their argument was based on the fact that a word representing existence may reveal its characteristics in various ways, and WordNet is not capable of expressing them [6]. ConceptNet [14] was constructed using words and phrases connected by relations to model general human knowledge. ConceptNet has the ability to supply a comprehensive collection of general knowledge required by computer applications for the analysis of text based on natural language. However, ConceptNet has a significant drawback in that its relationships are inflexible and limited. Users cannot define custom relationships for their choice of words or phrases. DBPedia [15] is a collection of structured information on various domains that has been extracted from Wikipedia. However, the knowledge is limited to named entities or concepts.

In recent years, knowledge representation learning has become essential for various applications, such as knowledge graph completion and reasoning. Researchers have explored multiple geometric spaces, including Euclidean, complex, and hyperbolic spaces. A Euclidean space can be described as a three-dimensional geometric space in which the points are denoted by their Cartesian co-ordinates [1]. It utilizes the principles of Euclidean geometry for calculating distances. A complex space refers to a mathematical concept where numbers are denoted by complex numbers [16]. This framework expands the one-dimensional real number line into a two-dimensional plane, where each point is depicted by a distinct complex number comprising both real and imaginary parts [16]. A hyperbolic space refers to a mathematical space that has a negative curvature. It is employed to model complex hierarchical structures to capture the inherent geometry of the dataset [17]. Notable models, such as RotatE [16], leverage complex spaces, while ATTH [17] focuses on hyperbolic spaces to encode hierarchical relationships. TransModE [18] takes an innovative approach by utilizing modulus spaces, and DiriE [19] introduces Bayesian inference to tackle uncertainty in knowledge graphs.

RotatE [16] introduced a novel approach by leveraging complex spaces to encode entities and relations. This model is based on Euler’s identity and treats unitary complex numbers as rotational transformations within the complex plane. RotatE aims to capture relationship structures, including symmetry/anti-symmetry, inversion, and composition. Symmetry refers to a relationship between entities where if entity A is related to entity B, entity B is likewise related to entity A, for example, (Barack Obama, MarriedTo, Michelle Obama), (Michelle Obama, MarriedTo, Barack Obama). If a relationship between entities exists in one direction, it cannot exist in the opposite direction unless the entities are the same; this is known as anti-symmetry. For example, (Parent, IsParentOf, Child). The opposite relationship (Child, IsParentOf, Parent) is not true. Inversion can be defined as a relationship where the direction of a relationship is reversed. For example, (Doctor, Treats, Patient), (Patient, TreatedBy, Doctor). Composition refers to combining multiple relationships to derive new relationships or discover new knowledge. For example, (Alex, StudiesAt, University Of Melbourne), (University Of Melbourne, LocatedIn, Melbourne). By composing the two relationships “StudiesAt” and “LocatedIn”, we can infer another relationship (Alex, LivesIn, Melbourne). Another approach delves into hyperbolic spaces, as seen in the ATTH [17] model. This model focuses on encoding hierarchical and logical relations within a knowledge graph. The curvature of the hyperbolic space is a crucial parameter that dictates whether relationships should be represented within a curved, tree-like structure or a flatter Euclidean space. Similarly, MuRP [20] employs hyperbolic geometry to embed hierarchical relationship structures. This model is suitable for encoding hierarchical data with relatively few dimensions, offering scalability benefits. TransModE [18] takes a unique approach by utilizing modulus spaces, which involves replacing numbers with their remainders after division by a given modulus value. This model is capable of encoding a wide range of relationship structures, including symmetry, anti-symmetry, inversion, and composition. DiriE [19] adopts a Bayesian inference approach to address the uncertainty associated with knowledge graphs. Entities are represented as Dirichlet distributions and relations as multinomial distributions, allowing the model to quantify and model the uncertainty of large and incomplete knowledge frameworks.

Knowledge graphs require continuous expansion, as they often contain incomplete data. Knowledge graph completion (KGC) aims to add new triples from unstructured text, employing tasks such as relation path analysis. Relation extraction and entity discovery play vital roles in discovering new knowledge from unstructured text. Path analysis entails examining sequences of relations between entities to infer missing or potential relations. Relation extraction and entity discovery are essential for discovering new knowledge from unstructured text, involving tasks such as determining relationships between entities and aligning entities with their types. Distant supervision, also known as weak supervision or self-supervision, is primarily used to infer missing relations [1]. This approach generates training data by heuristically matching sentences that mention the same entities under the assumption that they may express the same relation [1]. It is used under the guidance of a relational database. RECON [21] is a relation extraction model (introduced in 2021) that effectively represents knowledge derived from knowledge graphs using a graph neural network (GNN). This model leverages textual and multiple instance-based mechanisms to learn the background characteristics of concepts, analyze triple context, and aggregate context. Knowledge graph embedding (KGE) has become a popular approach for KGC, with models such as TransMS [22] addressing the limitations of earlier translation-based models. TransMS projects entities and relations into different embedding spaces, allowing for more flexible and accurate modeling of complex relations. Type-aware attention path reasoning (TAPR) [23], proposed in 2020, tackles path reasoning in knowledge graphs. It offers greater flexibility in path prediction by considering the structural facts, recorded facts, and characteristic information of knowledge graphs (KG). TAPR leverages character-level information to enrich entity and relation representations and employs path-level attention mechanisms to weight paths and calculate relations between entities.

The integration of structured knowledge, especially knowledge graphs, has significant implications for AI systems. Knowledge-aware applications have emerged in various domains, including language representation learning and recommendation systems. Models such as K-BERT [24] and ALBERT [25] offer solutions to integrate knowledge graphs and enhance AI capabilities. For domain-specific knowledge in language representation (LR), K-BERT [24] was introduced in 2020 as a notable advancement. It addresses the challenges of integrating heterogeneous embedding spaces and handling noise in knowledge graphs. K-BERT extends existing BERT models, allowing them to incorporate domain-specific knowledge from a knowledge graph. ALBERT [25], introduced in 2022, focuses on fact retrieval from knowledge graphs. This model leverages schema graph expansion (SGE) to extract relevant knowledge from a knowledge graph and integrate it into a pre-trained language model. ALBERT consists of five modules, including a text encoder, classifier, knowledge extractor, graph encoder, and schema graph expander.

As we conclude our exploration of knowledge representation learning, knowledge acquisition, and integration, it becomes evident that while previous endeavors have made significant strides, a distinct opportunity lies on the horizon—a chance to pioneer a revolutionary approach tailored specifically to the field of medicine: the creation of a dynamic and comprehensive medicine dictionary. Unlike prior initiatives, which have generally covered a broad spectrum of medical data, this endeavor focuses solely on consolidating medicine information into a structured knowledge graph format. Inspired by the architecture of knowledge graphs and various other databases, this opportunity presents unparalleled potential to transform the way we understand and utilize medicine knowledge. The uniqueness of this approach lies in its focused representation of medical information as entities and relations, facilitating enhanced information retrieval and question-answering capabilities. Incorporating this approach into medicine holds the potential for substantial benefits, significantly enhancing healthcare practices and outcomes.

3. The Domain-Specific Medicine Dictionary (DSMD) and Its Construction

One perspective of defining a domain-specific dictionary is to characterize it as a knowledge base organized in a knowledge graph architecture comprising entities and relations. Each entity is interconnected with other entities through relationships. A domain-specific dictionary is centered around a particular field of expertise, such as medicine, economics, finance, electronics, cellular biology, etc. The primary objective is to populate this knowledge base with triples to facilitate information extraction and question-answering. Let’s take an example of a knowledge base or knowledge graph in medicine domain:

$$\begin{array}{cc}\hfill & (\text{A-Cold}, \mathrm{generic\_name\_is}, \mathrm{Bromhexine}\mathrm{Hydrochloride})\hfill \\ \hfill & (\text{A-Cold}, \mathrm{type\_of}, \mathrm{Allopathic})\hfill \\ \hfill & (\text{A-Cold}, \mathrm{has\_dosage\_form}, \mathrm{Syrup})\hfill \\ \hfill & (\text{A-Cold}, \mathrm{has\_strength\_of}, 4\mathrm{mg}/5\mathrm{mL})\hfill \\ \hfill & (\text{A-Cold}, \mathrm{manufactured\_by}, \mathrm{ACME}\mathrm{Laboratories}\mathrm{Ltd}.)\hfill \\ \hfill & (\mathrm{Bromhexine}\mathrm{Hydrochloride}, \mathrm{pharmacology\_description}, \mathrm{definition})\hfill \\ \hfill & (\mathrm{Bromhexine}\mathrm{Hydrochloride}, \mathrm{side\_effects}, \mathrm{side}\mathrm{effects}\mathrm{description})\hfill \end{array}$$

This domain-specific dictionary serves as a structured and interconnected repository of knowledge tailored to a specific field, which is important for enhancing information retrieval and analysis within that domain.

In this section, we present a structured approach to construct a human-machine dictionary in the medicine domain smoothly and effectively. The open source ‘Assorted Medicine Dataset of Bangladesh’ [26] was used to build a prototype dictionary. Before moving on to the prototype design, we will explore the properties of the dictionary.

3.1. Concepts and Relations

Our knowledge graph will consist of entities and relations. Each entity will be considered a concept, and the concepts will be connected through relations. Examples of entities include A-Cold, A-Cof, Syrup, Allopathic, etc. Entities can be names of medicine brands, generic names, types of medicine, such as herbal or allopathic, dosage forms of medicine, such as tablet or syrup, the strength of medicine, etc. On the other hand, relations will express the connection between concepts. For example, if A-Cold and Syrup are both concepts in the dictionary, what is the appropriate connection or link between them? The link between them can be defined as a relation. Here, the appropriate link between A-Cold and Syrup would be ‘dosage form’. Once the links are identified, we can add a form of triple, such as “(A-Cold, has dosage form, Syrup)”.

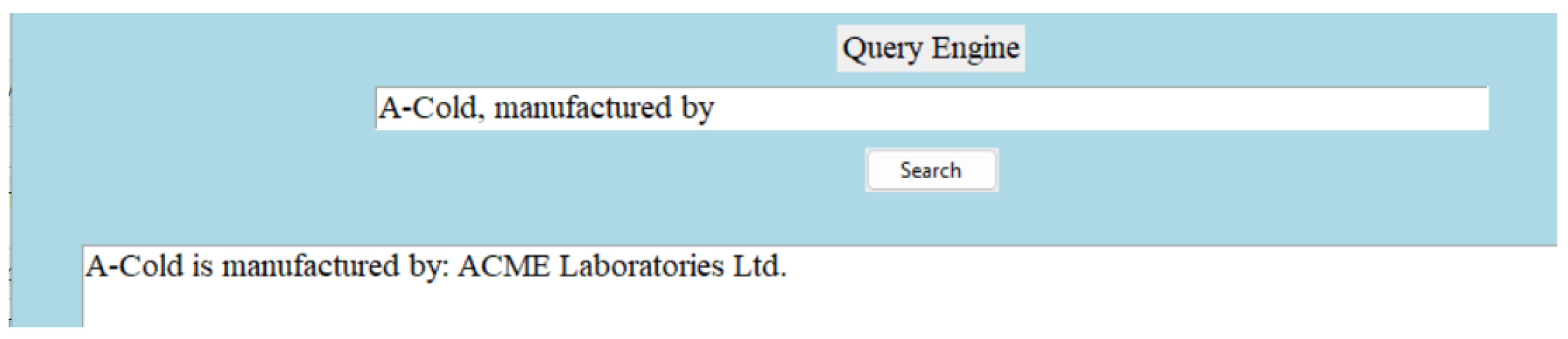
Relations are useful when they establish meaningful connections between entities. Consistency is the most important attribute of a relation. For example, in the triple “(‘A-Cold’, ’manufactured by’, ‘ACME Laboratories Ltd.’)”, the relation ‘manufactured by’ indicates that the medicine ‘A-Cold’ is manufactured by ACME Laboratories Ltd. In order to ensure consistency, whenever the relation ’manufactured by’ is used in the entire knowledge base, it should always point towards the manufacturer. Other valuable attributes of relations are relevance and the clarity of semantics. In the triple “(‘A-Cold’, ‘type of’, ’allopathic’)”, the relation ‘type of’ is relevant, as it specifies the classification of the medicine ‘A-Cold’ within the context of medical domain. In the triple “(‘Bromhexine Hydrochloride’, ‘pharmacology description’, ‘definition’)”, the relation ‘pharmacology description’ has clear semantics, implying that it provides a description or definition of the pharmacology of ’Bromhexine Hydrochloride’. Our dictionary provides a broad definition of the pharmacology for each generic medicine. The word ‘definition’ is used here in the triple to keep it short. All these attributes of relations ensure that machines can interpret the relationship between entities accurately. For instance, the relation ‘generic name is’ indicates that ‘Bromhexine Hydrochloride’ serves as the generic name for ‘A-Cold,’ enabling the machine to understand the relationship between the medicine and its generic identifier. Similarly, the relation ’manufactured by’ indicates that ‘ACME Laboratories Ltd.’ is the manufacturer of ‘A-Cold,’ providing crucial information about the entity responsible for producing the medication. By interpreting these relations appropriately, machines can navigate the knowledge base, extract relevant information, and generate comprehensive insights.

While concepts are collected easily from data, discovering relations is the tricky part. Khanam et al. [5] established certain rules for discovering relations. One such rule is that a verb, common noun, or an adjective followed by a preposition can be considered as a relation. For example, type of, strength of, manufactured by, etc. We followed this rule to establish a few relations for our dictionary. Some new rules have been discovered as well. The following are two example rules that we have discovered:

• Rule number one: a verb phrase can be considered as a relation.
• Rule number two: a noun or noun phrase can be considered a relation.

An example of a verb phrase is ‘has dosage form’. Examples of noun phrases are ‘generic name’, ‘side effects’, and ’pharmacology description’.

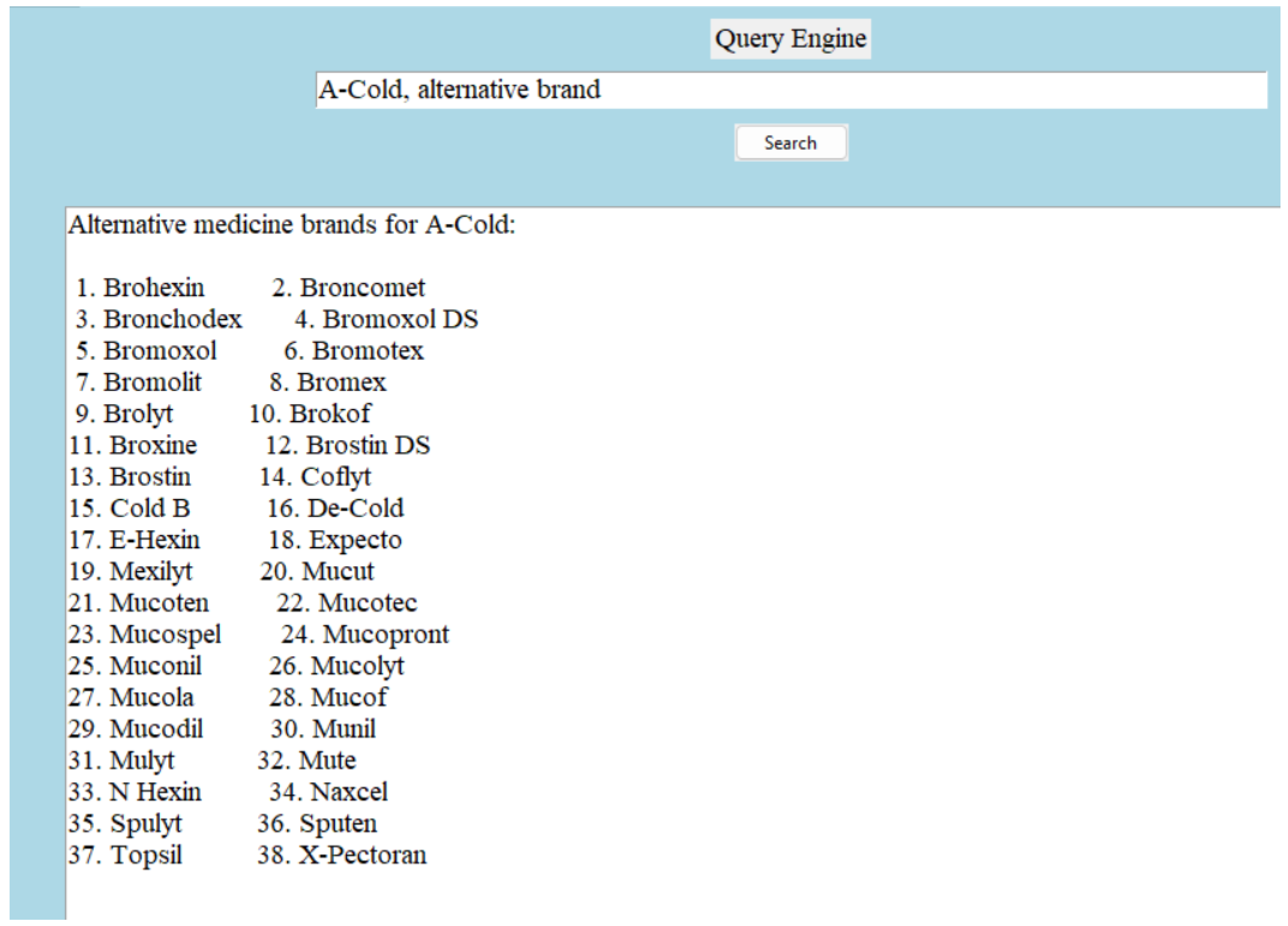
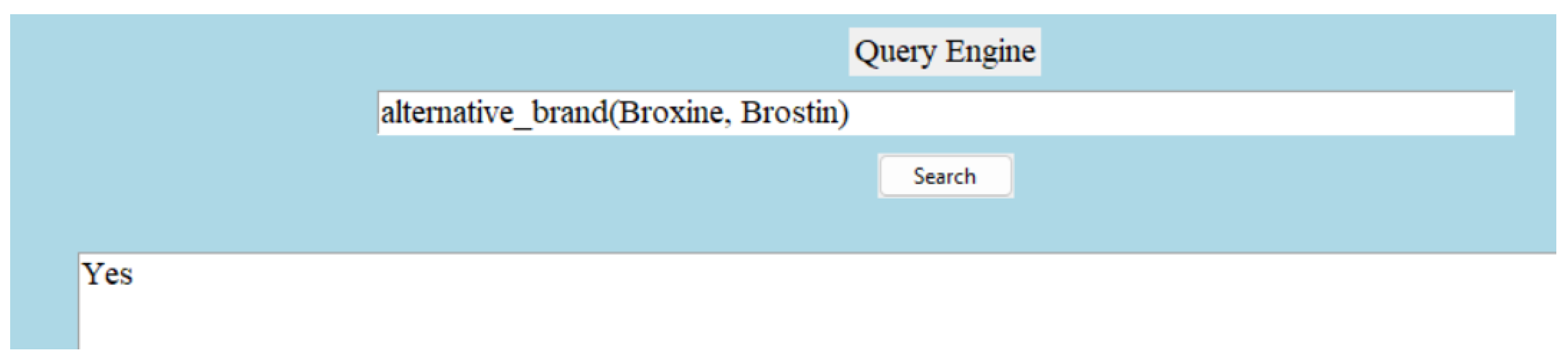
Since we are constructing a medicine dictionary with a limited number of attributes, we decided to keep a limited number of relations in the knowledge graph. The relation types are symmetric, complex, and asymmetric. A symmetric relation is the one in which the positions of the head and tail can be swapped. Let us take an example of a symmetric relation—(A-Cold, alternative brand, Brohexin). The reverse triple—(Brohexin, alternative brand, A-Cold) is true as well. Not all relationships are symmetric, but an inverse relationship can be created easily. For example, (‘A-Cold’, ’has dosage form’, ’Syrup’) can be written as (‘Syrup’, ‘is a form of dosage for’, ‘A-Cold’). A complex relation is defined as a more intricate or multi-layered connection between entities. Complex relation—(A-Cold, pharmacology description, description); this is true because of—(Bromhexine Hydrochloride, pharmacology description, description). More explanations can be found on this in the hierarchical structure and inheritance section. An example of an asymmetric relation is “(A-Cold, type of, allopathic)”. An example of the architecture of the structured triples can be found in Figure 2.

3.2. The Hierarchical Structure and Inheritance

Following the knowledge graph architecture, a hierarchical structure is maintained in the dictionary. Hierarchy in a knowledge graph refers to the phenomenon that an entity can be a type of another entity; hence, attribute inheritance becomes possible. For instance, “Cat” as an entity is a type of “Mammal”, which is another entity in a knowledge graph. As such, Cat can be defined as a descendant of Mammal and inherits attributes such as being “warm-blooded” and “produce milk to feed their young” from a Mammal. In our knowledge graph, the hierarchy is as follows: each generic medicine has multiple medicine brands manufactured by multiple manufacturers. Each medicine brand has four different attributes, including type, dosage form, strength, and manufacturer. Generic names, brand names, and attributes form a hierarchy, which is true for the entire database. Limiting the number of relations or attributes aims to simplify database structures, uphold data quality, enhance semantic clarity, ensure consistency and prioritize relevant information.

Moreover, each medicine brand inherits the attributes of generic medicine. Each generic medicine has two definitions as its attributes, including the pharmacology description and side effects. Let us take an example of a complex relation—(Bromhexine Hydrochloride, pharmacology description, description). Since each medicine brand inherits attributes from generic medicine, when the dictionary connects all the triples together, it will find that the medicine brand will have a definition. We did not explicitly mention in the database that A-Cold has a description. However, through complex relations, each brand should find a definition and description of side effects description. So that we end up with—(A-Cold, pharmacology description, description).

3.3. Prototype Dictionary

In this section, we will provide an overview of the process involved in building a prototype dictionary, encompassing data collection, processing, mapping, structured triple formation, and functional programming design and implementation. The architecture of the prototype dictionary is detailed in Figure 3, and the process is explained in the following subsections.

The ‘Assorted Medicine Dataset of Bangladesh’ [26], an open source medicine data repository that is available on Kaggle, serves as the foundation for our prototype dictionary. This repository contains real-world medicine data and is extensively described in Section 3.4 of this paper. With information on over 21,715 medicine brands, this dataset provides a comprehensive resource for our project.

Creating the prototype dictionary involves discovering entities and relations from the dataset and forming triples. This process is elaborated upon in the data processing section (Section 3.5), where we outline the steps involved in transforming raw data into structured triples.

Furthermore, the Section 4 delves into the application developed using Python for information retrieval and question-answering experiments. This section provides insights into the practical implementation of our prototype dictionary and its functionality.

3.4. Brief Description of the Dataset

In order to build our dictionary, we used an open sourced medicine dataset called Assorted Medicine Dataset of Bangladesh [26]. This dataset consists of medicine brands with their generics, drug classes, indications, dosage forms, manufacturer’s information, descriptions, side effects, etc. The dataset contains more than 20,000 different medicine brands. All information is stored in six different csv files. For our research purposes, we only used two csv files, medicine.csv and generic.csv. Figure 4 presents a preview of the medicine.csv dataset.

‘Medicine.csv’ contains information on many different brands of medicine with their attributes. Attributes include brand ID, brand name, type, slug, dosage form, generic, strength, manufacturer, package container, and package size. Some of the information is not useful, while others are very important. We decided to keep the useful information and remove unnecessary information, such as brand ID, slug, package container, and package size. Package size can be useful, but there was a lot of missing information in that specific column. Hence, the decision is to remove the package size. ‘Generic.csv’ consists of many columns, such as generic ID, generic name, slug, monographic link, drug class, indication, therapeutic class description, pharmacology description, dosage description, side effects description, and many more. For our research purposes, we decided to use the generic name, pharmacology description, and side effects description column. We simply removed the other information. There are more than 1,400 different generic medicine names, with their associated information in the dataset.

3.5. Data Processing

Data processing involves selecting concepts, discovering the relations between them, mapping data, and forming structured triples. The collected instances from generic.csv and medicine.csv were used to select concepts for the dictionary. For example, A-Cold, allopathic, Syrup, Bromhexine Hydrochloride, 4 mg/5 mL, ACME Laboratories Ltd. In the above instance, A-Cold is a medicine brand, allopathic is the type of the brand, Syrup is the dosage form of the brand, Bromhexine Hydrochloride is the generic name of the brand, 4 mg/5 mL is the strength of the brand, and ACME Laboratories Ltd. is the manufacturer of the brand. Each attribute is treated as a concept for the dictionary. We also have a pharmacology definition of each generic name and the side effects of each generic name. They have also been included in the dictionary. After selecting our concepts, we started the task of discovering relations. Relations represent the link between two concepts. Hence, it is considered the most important and challenging task in our dictionary construction.

After discovering concepts and relations, we focus on mapping entities and relations to form structured triples. The generic.csv file contains pharmacology descriptions and side effects descriptions for each generic medicine. We encountered an issue where the pharmacology descriptions and side effects descriptions in the ‘generic.csv’ file contained HTML tags throughout the text. Since our goal was to extract definitions and side effects for each medicine from this file and ensure they are usable as triples, we needed to remove these HTML tags. In order to accomplish this, we utilized Python libraries such as pandas and BeautifulSoup. First, we loaded the csv file using pandas csv reader and identified the columns containing pharmacology descriptions and side effects descriptions. Next, we applied a function written in Python, leveraging BeautifulSoup, to extract the text from the HTML content in these columns. The algorithm for extracting text from HTML content can be found in Figure 5. Once the HTML tags were removed, we saved the cleaned data as a new csv file. With the ‘medicine.csv’ and ‘generic.csv’ files now cleaned and ready for use, we proceeded to transform the rows of information into triples. Using a Python function and pandas data frames, we mapped the discovered entities and linked them with the appropriate relations. The algorithm to transform rows of data into triples can be found in the public repository of my program, which is available at (https://github.com/Saif0013/DSMD (accessed on 15 February 2024)). In order to ensure data integrity, we checked for and removed any duplicate rows in the database before saving the triples as a csv file.

3.6. Dealing with Uncertainties

During data processing, we encountered a range of uncertainties, including missing data, duplicate entries, and data in incorrect formats, among others. Uncertainty within the dictionary can be detrimental, as it undermines data accuracy and integrity, leading to inaccurate information. In our commitment to enhancing the quality and reliability of our dictionary, we made the deliberate decision to systematically address and eliminate these uncertainties. The original medicine dataset contains information for 21,715 medicine brands. However, some entries in the dataset have missing information. While it is common for real-world knowledge graphs to be incomplete, ensuring accuracy and completeness is crucial, especially in the context of medicine. In order to maintain data integrity, we have opted to remove all medicine brands with missing or incomplete information from our database. After removing missing information, our dataset now contains information for 20,311 medicine brands. This meticulous effort ensures that our dictionary offers users accurate and trustworthy information, enhancing its utility for both healthcare professionals and AI applications.

4. Experiments

A program was designed to implement a prototype dictionary. The application was built using Python, leveraging rich libraries such as Pandas for data management and Tkinter for GUI development. It employs a functional programming approach to process user queries efficiently. Queries are submitted through the GUI interface, where users input questions or specific queries about medicine brands and their attributes. These queries are then transformed and formatted as needed before being submitted to the database. Unlike SparQL, which is commonly used for querying RDF databases, this application interacts directly with a Pandas DataFrame to retrieve information rather than using a specialized query language. The program has been open source and made available on GitHub for public access. The program can be found at https://github.com/Saif0013/DSMD (accessed on 15 February 2024) The architecture of our application is presented in Figure 6.

There are more than 20,000 medicine brands, and their associated information is available in the dictionary. We selected 50 different medicine brands as part of our experiment. The dictionary contains no missing information, and all the brands have similar information, including the generic name, type, dosage form, strength, manufacturer, pharmacology description, and side effects. Therefore, we think 50 brands for the experiment provide a representative sample of the entire dataset. The experiment was conducted on different types of questions, such as brand information extraction, specific information extraction about a brand, and question-answering with a yes or no. Please navigate to the Section 5 to find out how a question can be asked and how information can be extracted. The overall accuracy of the experiment is 100%. Overall accuracy was calculated based on the following formula:

$$\mathrm{Overall}\mathrm{Accuracy}=\frac{\mathrm{Number}\mathrm{of}\mathrm{Correct}\mathrm{Answers}}{\mathrm{Total}\mathrm{Number}\mathrm{of}\mathrm{Answers}}$$

(1)

Our DSMD is truly unique, setting it apart from any other database. Our database boasts an impressive repository of over 348,000 triples, encompassing information on more than 20,000 medicine brands and 1,500 plus details on generic medicines. In contrast to the databases that served as our inspiration, which span a wide range of domains, our dictionary distinguishes itself by its focused approach. When compared to well-known databases, such as DBpedia, ConceptNet, WordNet, and NLIKR, our dictionary notably contains a leaner volume of data. This not only streamlines information retrieval but also results in faster access when compared to these larger databases. Despite the differences in the nature of these databases, we’ve made deliberate efforts to emphasize the unique characteristics of our DSMD, which are outlined in

Table 1. Comparison with other databases.

	DBpedia	WordNet	ConceptNet	NLIKR	DSMD
Meaningful and well-structured properties	N	N	N	Y	Y
Supporting multiple types of relations	N	N	Y	Y	Y
Concepts are linked in various ways	N	N	Y	Y	Y
Allows Inheritance	N	Y	N	Y	Y
Allows Queries between two words	Y	N	N	Y	Y
Faster query execution time	Y	Y	Y	N	Y

. Our database shares many characteristics with NLIKR. However, when it comes to executing searches or queries, our dictionary outperforms NLIKR significantly. The author of NLIKR notes that while DBPedia, WordNet, and ConceptNet operate at an O(n) complexity level for searches, NLIKR’s complexity is $O(n^2)$, where ’n’ represents the number of concepts [6]. During our experiments, we noted that our fastest query execution time was 0.034 s, while the slowest query execution time was 0.057 s.

5. Applications

DSMD has diverse applications across multiple sectors, benefiting healthcare professionals, medical researchers, pharmacies, healthcare educators, healthcare writers, journalists, regulatory authorities, and pharmaceutical experts. It offers a wealth of information about medicines and drugs, including generic names, dosage forms, medicine types, strengths, side effects, pharmacological descriptions, manufacturers, and alternative brands. Notably, our dictionary excels in providing multiple alternative brands for the same medicine, a highly valuable feature for pharmacists, doctors, medicine students, and researchers. Additionally, DSMD enables users to compare two medicines by calculating their distance and similarity. BERT models, such as K-BERT [24] and ALBERT [25], can seamlessly integrate knowledge graph databases as an external source of information. Given the adherence of our dictionary to the knowledge graph structure, it serves as a valuable source of information for AI language models. In the following subsections, we will illustrate example use cases, including retrieving information about medicine brands, comparing different medicines, and conducting word-based queries.

5.1. Medicine Comparison

As a dictionary, DSMD allows the distance and similarity of two medicines to be estimated based on their percentage of common ancestor (PCA), percentage of common association (PCAS), and percentage of binding association (PBAS).

Given two entities, $e_1$ and $e_2$, the distance between the two is calculated as [6]

$$D(e_1,e_2)=W_{CA}log\frac{1}{PCA(e_1,e_2)}+W_{CAS}log\frac{1}{PCAS(e_1,e_2)}+W_{AB}PBAS(e_1,e_2)$$

(2)

where $W_{CA}$, $W_{CAS}$, and $W_{BAS}$ are three weights. The similarity of $e_1$ and $e_2$ can be estimated as [6]

$$S(e_1,e_2)=f_{CA}PCA(e_1,e_2)+f_{CAS}PCAS(e_1,e_2)$$

(3)

where $f_{CA}$ and $f_{CAS}$ are two coefficients satisfying $f_{CA}\ge 0$ and $f_{CAS}\ge 0$ and $f_{CA}$ + $f_{CAS}$ = 1.

The capability of estimating the distance and similarity is extremely important. It enables us to systematically compare the effects and side effects of two drugs or even explore their interaction.

5.2. Brand Information Extraction

Figure 7 illustrates how the dictionary presents information for each medicine brand through relationships.

In Figure 7, A-Cold is the medicine brand. The extracted information, for example, ‘Bromhexine Hydrochloride’ is represented by the relation ‘generic name is’ and ‘allopathic’ is represented by the relation ‘type of’.

5.3. Alternative Medicine Information Extraction

Figure 8 depicts how the dictionary provides alternative medicine brands for a given medicine brand.

The dictionary contains information on 38 different alternative medicine brands for ‘A-Cold’.

5.4. Question-Answering

Our dictionary is also capable of answering specific questions about a medicine brand. Figure 9 is an example of answering a specific question related to a particular medicine brand.

Figure 9 demonstrates how the dictionary can provide answers to a specific question.

Along with the above information extraction capabilities, the dictionary also offers the ability to answer questions with a yes or no. For example:

Figure 10 demonstrates the ability to answer a question with ‘Yes’ if the provided information is true.

Here is another example:

Figure 11 demonstrates the ability of answering a question with ‘No’ if the provided information is false.

5.5. A Brief Overview of Information Extraction and Question-Answering

The domain-specific medicine dictionary can be used by both human users and machines, such as language models, including BERT models, ChatGpt, etc. By accessing the dictionary, a machine or a user can extract the following information:

• Medicine Information

1.

Medicine brand information by searching a medicine brand name such as ‘A-Cof’.

• Specific Information about a Particular Medicine Brand

• Generic name: ‘A-Cof’, ‘generic name is’
• Medicine type: ‘A-Cof’, ‘type of’
• Dosage form: ‘A-Cof’, ‘has dosage form’
• Strength: ‘A-Cof’, ‘has strength of’
• Manufacturer: ‘A-Cof’, ‘manufactured by’
• Pharmacology description: ‘A-Cof’, ‘pharmacology description’
• Side effects: ‘A-Cof’, ‘side effects’
• Alternative brand: ‘A-Cof’, ‘alternative brand’

• Yes or No Answers

• generic_name_is(A-Cold, Bromhexine Hydrochloride)
• type_of(A-Cold, allopathic)
• has_dosage_form(A-Cold, Syrup)
• has_strength_of(A-Cold, 4 mg/5 mL)
• manufactured_by(A-Cold, ACME Laboratories Ltd.)

6. Conclusions

We have introduced a comprehensive framework for creating a domain-specific medicine dictionary designed to serve both human users and AI applications. In our dictionary, we represent each entity as a concept and establish connections between concepts through meaningful relations. This dictionary excels in its ability to extract essential information related to medicine brands, offer specific insights into individual medicine brands, and respond to inquiries effectively.

A standout feature of our dictionary is its capacity to provide multiple alternative brand options for a single medicine brand, enhancing its practicality and versatility. We anticipate that our dictionary will find valuable application across a diverse spectrum of healthcare fields, including general practice, medical research, pharmacies, healthcare education, and regulatory authorities. Furthermore, the dictionary serves as a rich source of information for various AI applications.

A further research direction has been identified: the incorporation of more comprehensive details for each medicine brand, such as additional attributes related to manufacturers and generic medicines. These additions may encompass data on drug class, drug indications, and the specific diseases for which the drugs are prescribed. Apart from these, we would like to automate the relation extraction process so that triples are automatically extracted from plain text and added to the knowledge base. A number of machine learning-based tools for natural language processing, such as BERT and spaCy, can be used. Research in the area is less mature. The accuracy of general-purpose information extraction normally has low accuracy. As such, we aim to pursue our goal in a domain-specific area, which is likely to achieve accuracy at a satisfactory level. Additionally, some limitations of our dictionary have also been identified, including a limited number of relations due to the nature of the available data and a constrained number of concepts due to limited data availability. Our original focus was on identifying alternative medicine options for a given brand and providing the essential attributes related to medicine brands, such as medicine type, strength, dosage form, and manufacturer. With this framework, a domain-specific dictionary can be constructed in the same or any other domain of choice.