An Efficient Ensemble Approach for Brain Tumors Classification Using Magnetic Resonance Imaging
Abstract
1. Introduction
- Our proposed ensemble model provides prominent results. We observed a significant improvement in evaluation parameters, especially improved classification accuracy using our approach.
- This study provides the implementation of ten SOTA DCNN models, i.e., EfficientNetB0, ResNet50, DenseNet169, DenseNet121, SqueezeNet, ResNet34, ResNet18, VGG16, VGG19, and LeNet, and a detailed performance comparison of them. We also observe better results when we compare our proposed ensemble technique’s with SOTA DCNN models.
- We compare results using two LRs of 0.001 and 0.0001 and two BS of 64 and 128. We highlight the best LR and BS for the respective model.
2. Related Work
3. Materials and Methods
3.1. Dataset Description
3.2. Dataset Preprocessing
3.3. Proposed Ensemble of DL DCNN Models
3.3.1. Model Architecture
3.3.2. Global Average Pooling (GAP)
3.3.3. Concatenation and Dense Layer
3.3.4. Output Layer
3.3.5. Ensemble Voting Mechanism
3.3.6. Model Optimization and Evaluation
3.4. SOTA DL Models
3.5. Hyperparameters
3.6. Training Parameters
3.7. Experimental Setup
3.8. Evaluation Protocols
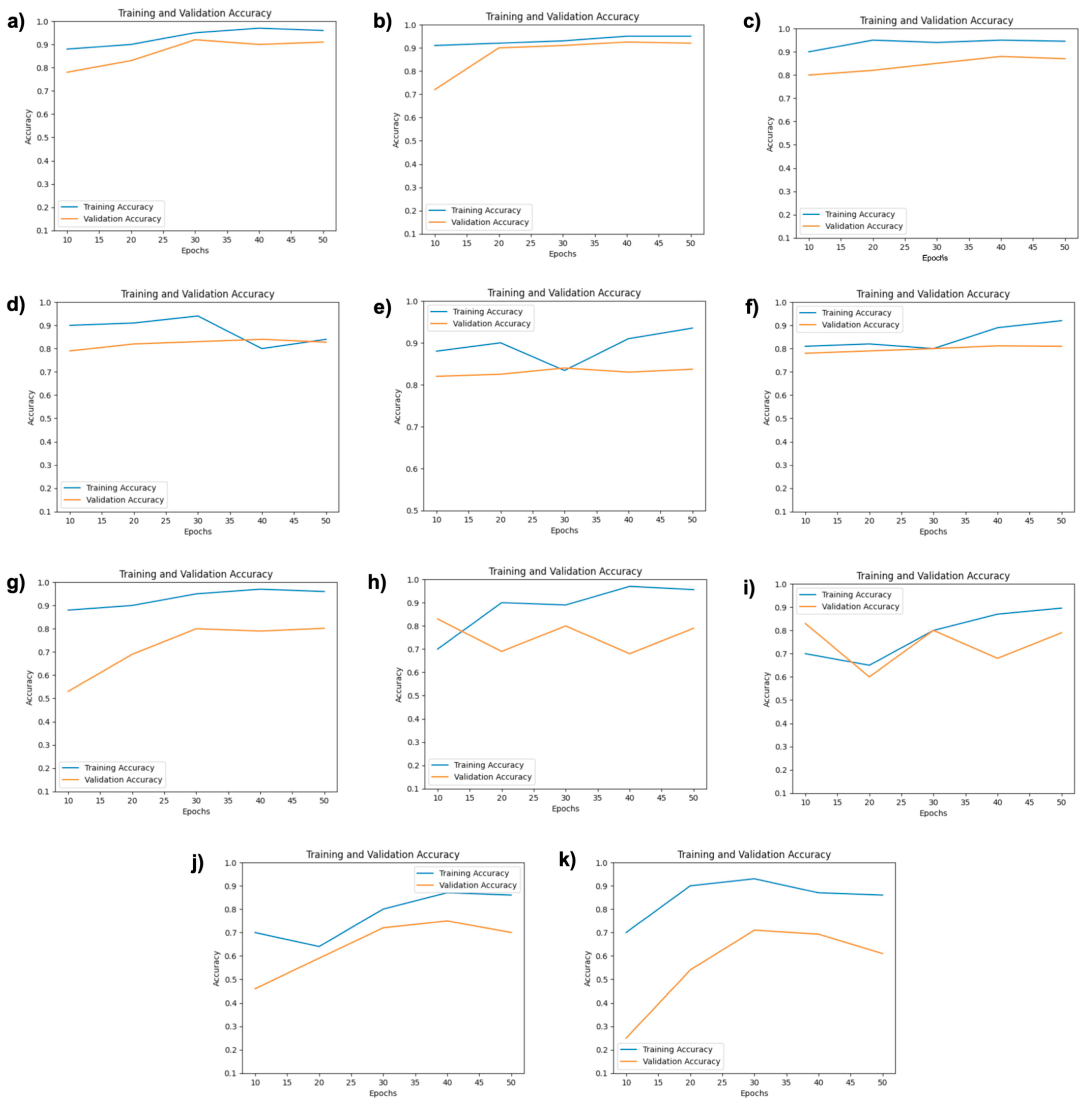
4. Results and Analysis
Comparison of Proposed Ensemble Model vs. Latest Techniques
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mukadam, S.B.; Patil, H.Y. Machine learning and computer vision based methods for cancer classification: A systematic review. Arch. Comput. Methods Eng. 2024, 31, 3015–3050. [Google Scholar] [CrossRef]
- International Agency for Research on Cancer. Cancer Today. 2023. Available online: https://gco.iarc.fr/today/data/factsheets/cancers/20-Brain.cancer (accessed on 16 April 2024).
- Raza, A.; Khan, M.U.; Saeed, Z.; Samer, S.; Mobeen, A.; Samer, A. Classification of eye diseases and detection of cataract using digital fundus imaging (DFI) and inception-V4 deep learning model. In Proceedings of the 2021 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 13–14 December 2021; IEEE: New York, NY, USA, 2021; pp. 137–142. [Google Scholar]
- Saeed, Z.; Khan, M.U.; Raza, A.; Khan, H.; Javed, J.; Arshad, A. Classification of pulmonary viruses X-ray and detection of COVID-19 based on invariant of inception-V 3 deep learning model. In Proceedings of the 2021 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 26–27 October 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Naqvi, S.Z.H.; Khan, M.U.; Raza, A.; Saeed, Z.; Abbasi, Z.; Ali, S.Z.E.Z. Deep Learning Based Intelligent Classification of COVID-19 & Pneumonia Using Cough Auscultations. In Proceedings of the 2021 6th International Multi-Topic ICT Conference (IMTIC), Jamshoro & Karachi, Pakistan, 10–12 November 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Byun, Y.H.; Ha, J.; Kang, H.; Park, C.K.; Jung, K.W.; Yoo, H. Changes in the Epidemiologic Pattern of Primary CNS Tumors in Response to the Aging Population: An Updated Nationwide Cancer Registry Data in the Republic of Korea. JCO Glob. Oncol. 2024, 10, e2300352. [Google Scholar] [CrossRef] [PubMed]
- Srinivas, C.; KS, N.P.; Zakariah, M.; Alothaibi, Y.A.; Shaukat, K.; Partibane, B.; Awal, H. Deep transfer learning approaches in performance analysis of brain tumor classification using MRI images. J. Healthc. Eng. 2022, 2022, 3264367. [Google Scholar] [CrossRef] [PubMed]
- Khairandish, M.O.; Sharma, M.; Jain, V.; Chatterjee, J.M.; Jhanjhi, N.Z. A hybrid CNN-SVM threshold segmentation approach for tumor detection and classification of MRI brain images. Irbm 2022, 43, 290–299. [Google Scholar] [CrossRef]
- Khan, A.H.; Abbas, S.; Khan, M.A.; Farooq, U.; Khan, W.A.; Siddiqui, S.Y.; Ahmad, A. Intelligent model for brain tumor identification using deep learning. Appl. Comput. Intell. Soft Comput. 2022, 2022, 8104054. [Google Scholar] [CrossRef]
- Assam, M.; Kanwal, H.; Farooq, U.; Shah, S.K.; Mehmood, A.; Choi, G.S. An efficient classification of MRI brain images. IEEE Access 2021, 9, 33313–33322. [Google Scholar] [CrossRef]
- Noreen, N.; Palaniappan, S.; Qayyum, A.; Ahmad, I.; Imran, M.; Shoaib, M. A deep learning model based on concatenation approach for the diagnosis of brain tumor. IEEE Access 2020, 8, 55135–55144. [Google Scholar] [CrossRef]
- Ghassemi, N.; Shoeibi, A.; Rouhani, M. Deep neural network with generative adversarial networks pre-training for brain tumor classification based on MR images. Biomed. Signal Process. Control 2020, 57, 101678. [Google Scholar] [CrossRef]
- Musallam, A.S.; Sherif, A.S.; Hussein, M.K. A new convolutional neural network architecture for automatic detection of brain tumors in magnetic resonance imaging images. IEEE Access 2022, 10, 2775–2782. [Google Scholar] [CrossRef]
- Ismael SA, A.; Mohammed, A.; Hefny, H. An enhanced deep learning approach for brain cancer MRI images classification using residual networks. Artif. Intell. Med. 2020, 102, 101779. [Google Scholar] [CrossRef] [PubMed]
- Sekhar, A.; Biswas, S.; Hazra, R.; Sunaniya, A.K.; Mukherjee, A.; Yang, L. Brain tumor classification using fine-tuned GoogLeNet features and machine learning algorithms: IoMT enabled CAD system. IEEE J. Biomed. Health Inform. 2021, 26, 983–991. [Google Scholar] [CrossRef] [PubMed]
- Irmak, E. Multi-classification of brain tumor MRI images using deep convolutional neural network with fully optimized framework. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 1015–1036. [Google Scholar] [CrossRef]
- Kaggle Dataset. Available online: https://www.kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset (accessed on 13 August 2023).
- Mahesh, T.R.; Vinoth Kumar, V.; Vivek, V.; Karthick Raghunath, K.M.; Sindhu Madhuri, G. Early predictive model for breast cancer classification using blended ensemble learning. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 188–197. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, X.; Wang, Q.; Lv, J.; Chen, L.; Du, Y.; Du, L. An Area-Efficient CNN Accelerator Supporting Global Average Pooling with Arbitrary Shapes. In Proceedings of the 2024 IEEE 6th International Conference on AI Circuits and Systems (AICAS), Abu Dhabi, The United Arab Emirates, 22–25 April 2024; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Hussain, D.; Al-Masni, M.A.; Aslam, M.; Sadeghi-Niaraki, A.; Hussain, J.; Gu, Y.H.; Naqvi, R.A. Revolutionizing tumor detection and classification in multimodality imaging based on deep learning approaches: Methods, applications and limitations. J. X-ray Sci. Technol. 2024, 32, 857–911. [Google Scholar] [CrossRef] [PubMed]
- Pareek, M.; Jha, C.K.; Mukherjee, S. Brain tumor classification from MRI images and calculation of tumor area. In Soft Computing: Theories and Applications: Proceedings of SoCTA 2018; Springer: Singapore, 2020; pp. 73–83. [Google Scholar]
- Decuyper, M.; Bonte, S.; Deblaere, K.; Van Holen, R. Automated MRI based pipeline for glioma segmentation and prediction of grade, IDH mutation and 1p19q co-deletion. arXiv 2020, arXiv:2005.11965. [Google Scholar] [CrossRef] [PubMed]
- Gupta, M.; Sasidhar, K. Non-invasive brain tumor detection using magnetic resonance imaging based fractal texture features and shape measures. In Proceedings of the 2020 3rd International Conference on Emerging, Kolkata, India, 23–25 February 2020. [Google Scholar]
- Saxena, P.; Maheshwari, A.; Maheshwari, S. Predictive modeling of brain tumor: A deep learning approach. In Innovations in Computational Intelligence and Computer Vision: Proceedings of ICICV 2020; Springer: Singapore, 2020; pp. 275–285. [Google Scholar]
- Cheng, J.; Huang, W.; Cao, S.; Yang, R.; Yang, W.; Yun, Z.; Wang, Z.; Feng, Q. Enhanced performance of brain tumor classification via tumor region augmentation and partition. PLoS ONE 2015, 10, e0140381. [Google Scholar] [CrossRef] [PubMed]
- Saeed, Z.; Bouhali, O.; Ji, J.X.; Hammoud, R.; Al-Hammadi, N.; Aouadi, S.; Torfeh, T. Cancerous and Non-Cancerous MRI Classification Using Dual DCNN Approach. Bioengineering 2024, 11, 410. [Google Scholar] [CrossRef] [PubMed]

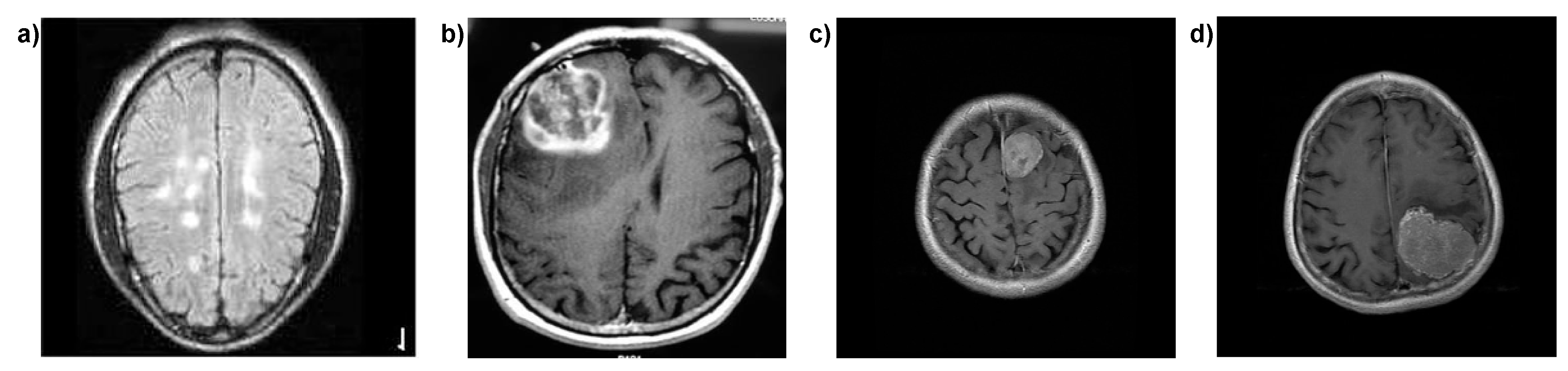
| Reference | Dataset | Technique Used | Total Scans | Classes | Advantages | Limitations |
|---|---|---|---|---|---|---|
| [8], Khairandish et al. | BRATS’15 | Hybrid CNN for feature extraction and SVM for classification | 64 LGG 220 HGG MRIs | Normal and tumor | Combines strengths of CNN for feature extraction and SVM for classification; good accuracy on BRATS’15 dataset | Limited to normal and tumor classification only |
| [9], Khan et al. | Public | Hierarchical DL model | 3264 | Normal, Meningioma, Pituitary and Glioma, | Hierarchical approach allows for better multi-class tumor classification | Limited description of the exact performance; needs further evaluation on large datasets |
| [10], Assam et al. | Self-collected acquired from Harvard Medical College (T2 weighted scans) | Median filter, DWT, color moments for feature extraction, FF-ANN, RF, RSS classifiersPre-trained DCNN (InceptionV3, DenseNet201), multi-level feature extraction and concatenation |
25 Normal 45 Tumors scans | Normal and tumor | Combination of feature extraction techniques improves classification performance | Small dataset (self-collected, 70 samples); limited generalization capability |
| [11], Noreen et al. | 3064 T1-CE MRI scans | Pre-trained DCNN (InceptionV3, DenseNet201), multi-level feature extraction and concatenation | 3064 | Glioma, Meningioma, and Pituitary | Pre-trained models reduce the need for large datasets, multi-level feature extraction enhances classification | Lacks of novality and better performance, exploration of lightweight models |
| [12], Ghassemi et al. |
(1) 3064 T1-CE MRI scans (2) Whole brain MRI scans consisting of 373 longitudinal scans via 150 subjects | DCNN as a discriminator in GAN, data augmentation via image transformations | (1) 3064 (2) 156 | Pituitary, Meningioma and, Glioma. | GAN enhances robustness by distinguishing genuine/fake MRI scans; data augmentation improves model performance | GAN training can be unstable; limited evaluation on more diverse datasets |
| [13], Musallam et al. |
(1) Sartaj brain MRI dataset (2) Navoneel brain tumor MRI dataset that has two kinds of MRI | DCNN with pre-processing (noise reduction, histogram equalization) | (1) 3394 (2) 3394 | Glioma, Meningioma, and Pituitary | Pre-processing improves MRI scan quality; robust validation on different tumor types | Focused on specific MRI types (T1 and T2); lacks broader generalization on unseen datasets |
| [14], Ismael et al. | Public | Modified ResNet50 with data augmentation | 3064 | Meningioma, Glioma, and Pituitary | ResNet50 provides good accuracy; data augmentation helps improve model generalization | Their approach may not perform well on smaller datasets |
| [15], Sekhar et al. | FigShare CE-MRI dataset | Modified GoogleNet with SVM and K-NN classifiers | 3064 | Glioma, Meningioma, and Pituitary | Combination of GoogleNet and traditional classifiers yields high classification accuracy | Needs comparison with more advanced deep learning models; computationally expensive |
| [16], Irmak et al. |
(1) RIDER (2) REMBRANDT (3) TCGA-LGG | Multi-class classification with CNN and grid search for hyperparameters |
(1) 70,220 RIDER (2) 110,020 REMBRANDT (3) 241,183 TCGA-LGG |
Model I: Tumor and non-tumor; Model II: Glioma, pituitary, meningioma, metastatic, and normal; Model III: Different grades of glioma tumors | Use of grid search optimizes hyperparameters; CNN models for multi-level tumor classification | Computational complexity increases with multiple CNN models |
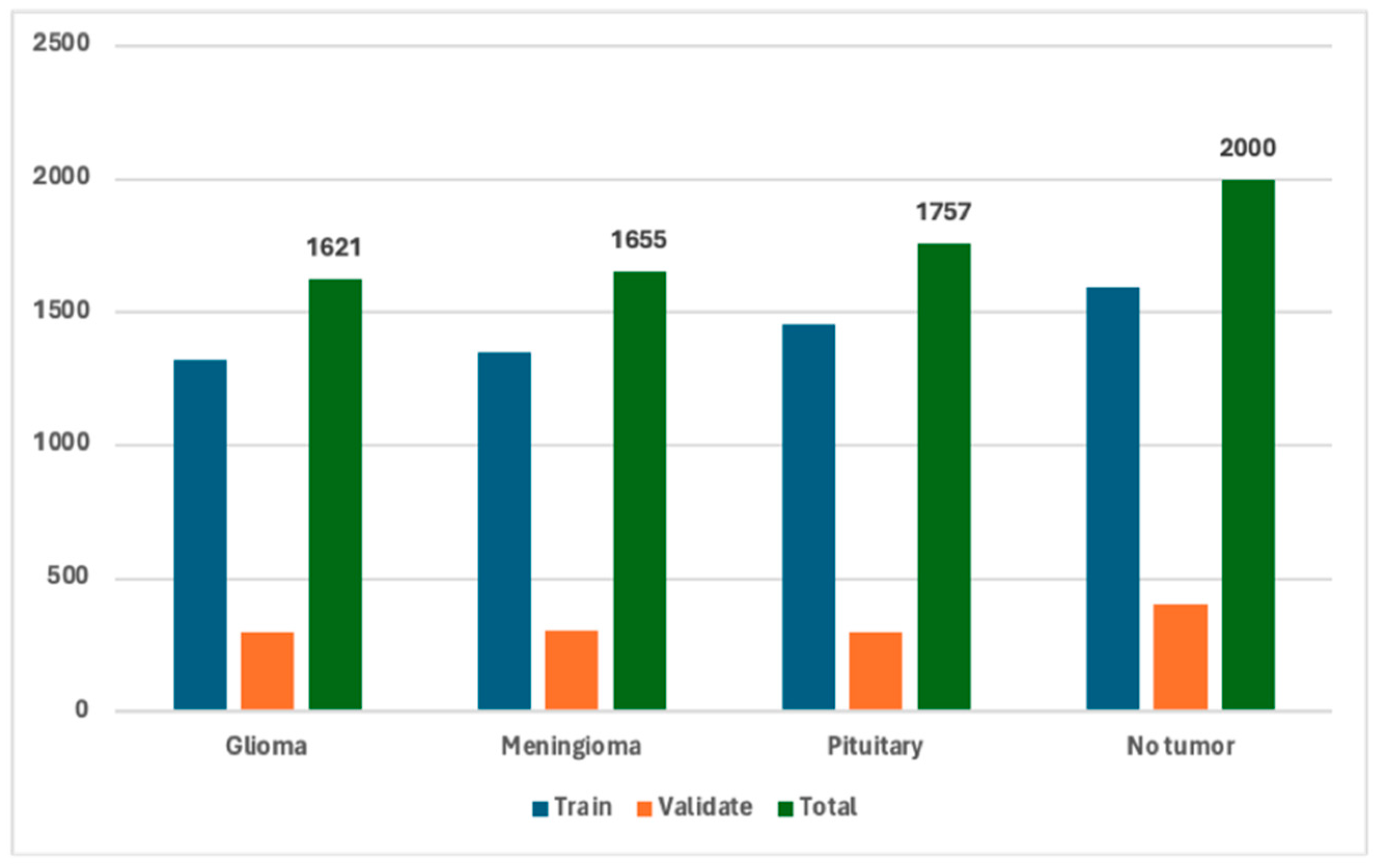
| Class | Train | Validate | Total | Class Label |
|---|---|---|---|---|
| Glioma | 1321 | 300 | 1621 | “0” |
| Meningioma | 1349 | 306 | 1655 | “1” |
| Pituitary | 1457 | 300 | 1757 | “2” |
| No tumor | 1595 | 405 | 2000 | “3” |
| Total | 5722 | 1311 | 7033 |
| Sr. No | Parameters | Value |
|---|---|---|
| 1. | No.s of epochs | 50 |
| 2. | Learning Rates | 0.001 and 0.0001 |
| 3. | Batch Sizes | 64 and 128 Against Each Learning Rate |
| 4. | Shuffle | Every Epoch |
| 5. | Optimizer and Loss Function | Adam Optimizer (AO) and Stochastic Gradient Decent (SGD) with Categorical Cross-Entrophy |
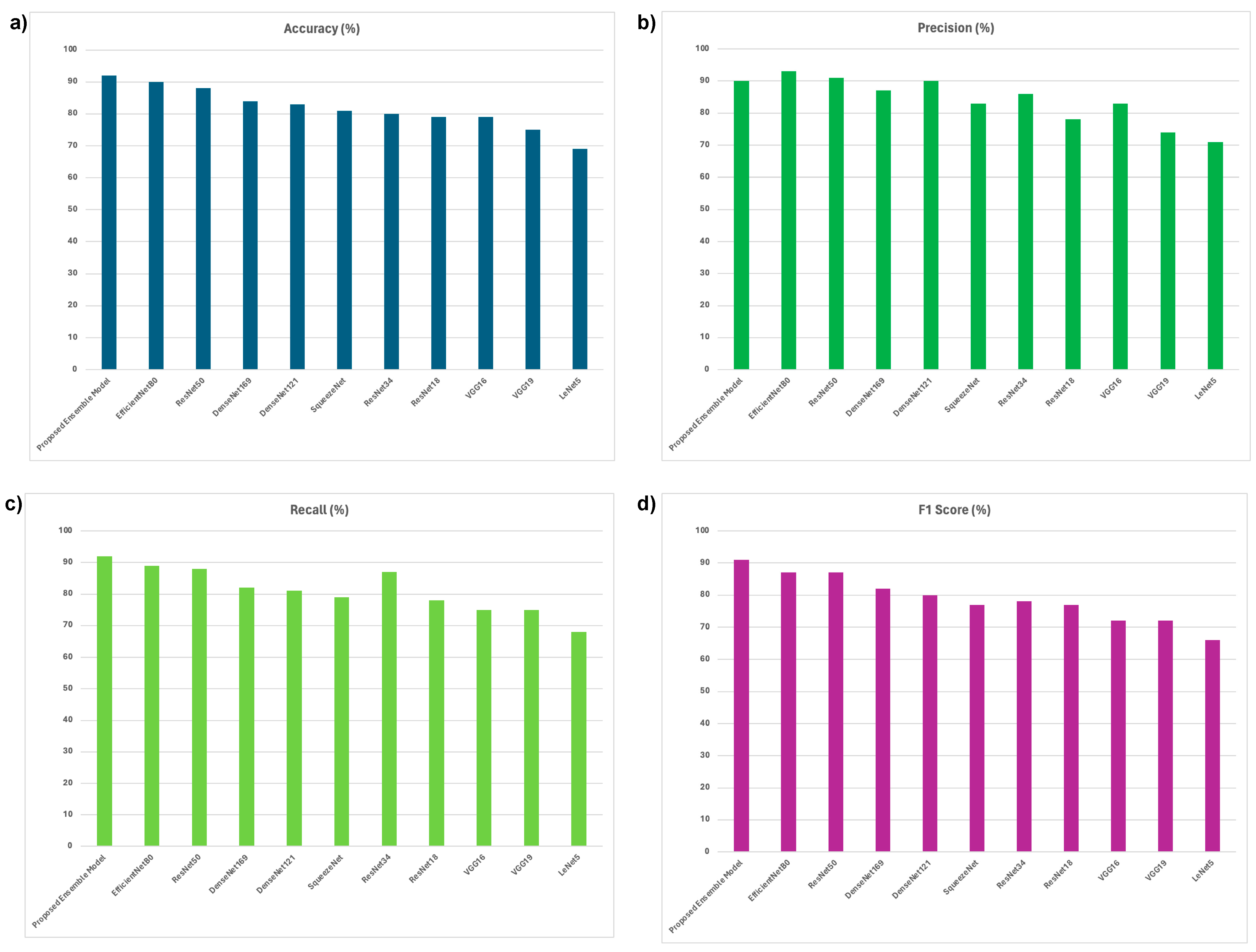
| Model | Batch size (BS) | Learning Rate (LR) | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|---|---|
| Proposed Ensemble Model | 64 | 0.001 | 89 | 88 | 85 | 87 |
| 0.0001 | 92 | 90 | 92 | 91 | ||
| 128 | 0.001 | 83 | 83 | 80 | 81 | |
| 0.0001 | 89 | 88 | 84 | 86 | ||
| EfficientNetB0 | 64 | 0.001 | 88 | 97 | 88 | 85 |
| 0.0001 | 90 | 93 | 89 | 87 | ||
| 128 | 0.001 | 83 | 95 | 82 | 79 | |
| 0.0001 | 89 | 93 | 88 | 86 | ||
| ResNet50 | 64 | 0.001 | 80 | 86 | 87 | 78 |
| 0.0001 | 88 | 91 | 88 | 87 | ||
| 128 | 0.001 | 79 | 88 | 79 | 74 | |
| 0.0001 | 84 | 86 | 83 | 83 | ||
| DenseNet169 | 64 | 0.001 | 84 | 87 | 82 | 82 |
| 0.0001 | 65 | 72 | 65 | 64 | ||
| 128 | 0.001 | 83 | 85 | 82 | 81 | |
| 0.0001 | 70 | 74 | 70 | 69 | ||
| DenseNet121 | 64 | 0.001 | 83 | 90 | 81 | 80 |
| 0.0001 | 45 | 53 | 46 | 42 | ||
| 128 | 0.001 | 79 | 86 | 78 | 77 | |
| 0.0001 | 65 | 66 | 66 | 64 | ||
| SqueezeNet | 64 | 0.001 | 81 | 83 | 79 | 77 |
| 0.0001 | 63 | 64 | 64 | 63 | ||
| 128 | 0.001 | 79 | 77 | 73 | 72 | |
| 0.0001 | 54 | 58 | 56 | 54 | ||
| ResNet34 | 64 | 0.001 | 79 | 88 | 79 | 74 |
| 0.0001 | 80 | 86 | 87 | 78 | ||
| 128 | 0.001 | 74 | 80 | 72 | 74 | |
| 0.0001 | 79 | 88 | 78 | 77 | ||
| ResNet18 | 64 | 0.001 | 79 | 78 | 78 | 77 |
| 0.0001 | 78 | 77 | 78 | 78 | ||
| 128 | 0.001 | 67 | 81 | 65 | 62 | |
| 0.0001 | 72 | 70 | 69 | 73 | ||
| VGG16 | 64 | 0.001 | 75 | 84 | 74 | 70 |
| 0.0001 | 71 | 75 | 70 | 69 | ||
| 128 | 0.001 | 79 | 83 | 75 | 72 | |
| 0.0001 | 66 | 68 | 65 | 63 | ||
| VGG19 | 64 | 0.001 | 70 | 75 | 70 | 71 |
| 0.0001 | 71 | 70 | 70 | 69 | ||
| 128 | 0.001 | 75 | 74 | 75 | 72 | |
| 0.0001 | 69 | 68 | 66 | 66 | ||
| LeNet5 | 64 | 0.001 | 69 | 71 | 68 | 66 |
| 0.0001 | 63 | 68 | 62 | 65 | ||
| 128 | 0.001 | 67 | 77 | 66 | 64 | |
| 0.0001 | 64 | 71 | 64 | 62 |
| Model | Batch size (BS) | Learning Rate (LR) | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|---|---|
| Proposed Ensemble Model | 64 | 0.0001 | 92 | 90 | 92 | 91 |
| EfficientNetB0 | 64 | 0.0001 | 90 | 93 | 89 | 87 |
| ResNet50 | 64 | 0.0001 | 88 | 91 | 88 | 87 |
| DenseNet169 | 64 | 0.001 | 84 | 87 | 82 | 82 |
| DenseNet121 | 64 | 0.001 | 83 | 90 | 81 | 80 |
| SqueezeNet | 64 | 0.001 | 81 | 83 | 79 | 77 |
| ResNet34 | 64 | 0.001 | 80 | 86 | 87 | 78 |
| ResNet18 | 64 | 0.001 | 79 | 78 | 78 | 77 |
| VGG16 | 128 | 0.001 | 79 | 83 | 75 | 72 |
| VGG19 | 128 | 0.001 | 75 | 74 | 75 | 72 |
| LeNet5 | 64 | 0.001 | 69 | 71 | 68 | 66 |
| Reference | Method | Model | Dataset Medical Modality | Performance |
|---|---|---|---|---|
| [21], Pareek, M. et al. | Machine Learning | SVM with linear kernal | MRI images | Acc: 78.12 |
| [22], Decuyper, M. et al. | Deep Learning for feature learning and SVM for classification | DL-SVM | MRI images | Acc: 83.30, P: 86.7, R: 79.2 |
| [23], Gupta, M. et al. | Machine Learning | Segmentation-based fractal texture analysis (SFTA) | MRI images | Acc: 87%, P: 88%, R: 86% |
| [24], Saxena, P. et al. | Deep Learning based DCNN model | (1) VGG16 (2) InceptionV3 | MRIs Images | (1) Acc: 90%, P: 90.9% (2) Acc: 55%, P: 68.9% |
| [25], Cheng, J. et al. | Machine Learning | Spatial Pyramid Matching (SPM) | MRI images | Acc: 91.2%, P:89.7%, R:90.8%, F1: 90% |
| Proposed Ensemble Technique | Deep Learning | DCNN | MRI images | Acc: 92, P: 90, R: 92, F1: 91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeed, Z.; Torfeh, T.; Aouadi, S.; Ji, X.; Bouhali, O. An Efficient Ensemble Approach for Brain Tumors Classification Using Magnetic Resonance Imaging. Information 2024, 15, 641. https://doi.org/10.3390/info15100641
Saeed Z, Torfeh T, Aouadi S, Ji X, Bouhali O. An Efficient Ensemble Approach for Brain Tumors Classification Using Magnetic Resonance Imaging. Information. 2024; 15(10):641. https://doi.org/10.3390/info15100641
Chicago/Turabian StyleSaeed, Zubair, Tarraf Torfeh, Souha Aouadi, (Jim) Xiuquan Ji, and Othmane Bouhali. 2024. "An Efficient Ensemble Approach for Brain Tumors Classification Using Magnetic Resonance Imaging" Information 15, no. 10: 641. https://doi.org/10.3390/info15100641
APA StyleSaeed, Z., Torfeh, T., Aouadi, S., Ji, X., & Bouhali, O. (2024). An Efficient Ensemble Approach for Brain Tumors Classification Using Magnetic Resonance Imaging. Information, 15(10), 641. https://doi.org/10.3390/info15100641









