A Traceable Universal Designated Verifier Transitive Signature Scheme

Abstract

A transitive signature scheme enables anyone to obtain the signature on edge $(i,k)$ by combining the signatures on edges $(i,j)$ and $(j,k)$, but it suffers from signature theft and signature abuse. The existing work has solved these problems using a universal designated verifier transitive signature (UDVTS). However, the UDVTS scheme only enables the designated verifier to authenticate signatures, which provides a simple way for the signer to deny having signed some messages. The fact that the UDVTS is not publicly verifiable prevents the verifier from seeking help arbitrating the source of signatures. Based on this problem, this paper proposes a traceable universal designated verifier transitive signature (TUDVTS) and its security model. We introduce a tracer into the system who will trace the signature back to its true source after the verifier has submitted an application for arbitration. To show the feasibility of our primitive, we construct a concrete scheme from a bilinear group pair $(\mathbb{G},{\mathbb{G}}_{\mathbb{T}})$ of prime order and prove that the scheme satisfies unforgeability, privacy, and traceability.

1. Introduction

In today’s information age, network information security is a hot topic all over the world. As a cryptographic technique to provide authentication services for electronic data, digital signatures allow a signer who has generated a public/private key pair to sign a message, and any other entity who knows the public key can verify the integrity and the source of data.

However, using traditional digital signatures to authenticate graph-based big data with chain relationships can result in significant communication costs. Given an administrative domain that involves four nodes, as depicted in Figure 1, A and B both belong to the same administrative domain if the edge $(A,B)$ is authentic. If both the edge $(A,B)$ and the edge $(B,C)$ are authentic, then A and C are in the same administrative domain. We need to provide two signatures (${\sigma }_{AB}$ and ${\sigma }_{BC}$) when disclosing the relationship between A and C to others using traditional digital signatures. Such an authentication method is very costly with big data. In 2002, Micali and Rivest [1] proposed the concept of a transitive signature, where anyone can compute a valid signature of the edge $(A,C)$, from the signatures of two edges $(A,B)$ and $(B,C)$.

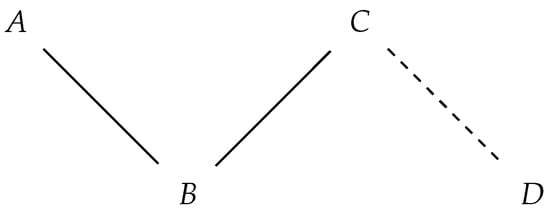
Figure 1. An administrative domain. (Solid lines represent actual edges in the administrative domain, while dotted lines represent non-existent edges).

This method greatly reduces communication costs, but it creates the problem that transitive signatures may be abused, i.e., the signer cannot control who verifies the data, as the signature is publicly verifiable, allowing any entity to verify its validity.

To remove the public verifiability of transitive signatures, Hou et al. [2] introduced a universal designated verifier transitive signature (UDVTS), where only the designated verifier authenticates signatures. The verifier is designated by the combiner who combines transitive signatures. However, disputes may arise regarding the source of a signature. There are two cases: (1) the signer denies the signature generated by himself, e.g., we assume the edge $(A,B)$ is signed by a signer in Figure 1. B can convince the verifier (not in the same administrative domain as B) that A and C are in the same administrative domain. The signer denies that he had signed the edge $(A,B)$ when the private information was leaked. (2) The signer did not sign an edge $(C,D)$, but the verifier framed the signer by using a simulated signature to make it appear as if the signer had signed the edge. This is because the non-transferability of the designated verifier signature requires the verifier to generate a signature that is indistinguishable from a designated verifier signature. It is also clear that, in the dispute, no arbitration service whatsoever is provided.

The above issues arise from the lack of public verifiability in the UDVTS. Arbitration service is, therefore, a closely watched issue in designated verifier signatures.

1.1. Our Contributions

While transitive signature disputes are easily resolved, the public verifiability also facilitates verifiers leaking signatures to a third party. Furthermore, UDVTS implementation sacrifices the public verifiability of transitive signatures to control the verifier (only the designated verifier can authenticate signatures). To achieve both the goal of controlling the verifier and arbitrability, this paper introduces the concept of a traceable universal designated verifier transitive signature (TUDVTS). Meanwhile, in order to avoid creating a huge arbitration institution, this article mandates a single individual with tracking and arbitration abilities, known as the tracer. The tracer can determine whether the disputed signature originated from the signer.

The specific contributions of this paper are as follows:

(1)

Our goal is to substitute the public verifiability of transitive signatures with single entity verifiability, where the entity is trusted. Therefore, we adopt the UDVTS proposed by [2]. Considering that the common issue of designated verifier signatures is that arbitration service cannot be provided when there is a signature dispute, we have introduced a tracer into the system that can find the true source of the signature.

(2)

We propose the concept of TUDVTS. We introduce to the UDVTS a tracer who is responsible for arbitrating any disputed data, and the chain relationships in the graphic remain hidden from other entities except the tracer. Therefore, this scheme protects the rights and interests of the signer and the verifier.

(3)

We describe definitions of TUDVTS and its security model. The security requirements of TUDVTS include unforgeability, privacy, and traceability. The unforgeability of TUDVTS means that any adversary cannot forge a transitive signature or a designated verifier signature even if it is allowed to obtain signatures on many other messages and public keys of its choice. The TUDVTS scheme encompasses two distinct forms of privacy: the non-transferability of TUDVTS and the privacy of transitive signatures. The former means that there is no way for anyone to distinguish between the two designated verifier signatures produced by the combiner or the verifier. The latter means that there is no way for anyone to distinguish between the two transitive signatures produced by the signer or the combiner. The traceability implies that the tracer can determine whether the signer signed the message.

(4)

We construct a TUDVTS scheme. By incorporating traceability, our scheme not only achieves the goal of controlling the verifier but also provides an arbitration service when signature disputes arise. We have conducted proofs to establish that our scheme satisfies the unforgeability, privacy, and traceability.

1.2. Related Works

We recall transitive signatures and universally designated verifier signatures in this section.

• Transitive Signatures (TS). The earliest transitive signature schemes, DLTS and RSATS-1, were proposed by Micali and Rivest [1], where their security relies on the discrete logarithm problem and the RSA assumption, respectively. Note that the former can resist adaptive chosen-message attacks, while the latter can only resist non-adaptive chosen-message attacks. In the same year, Bellare and Neven [3] proposed the “node certification paradigm” and constructed two schemes based on RSA assumption and factoring, respectively. In addition, they proposed other new schemes based on the one-more discrete logarithm problem and one-more gap Diffie-Hellman problem [4]. By employing braid groups, Wang et al. [5] designed a transitive signature scheme that was not susceptible to quantum attacks at the time. Previous schemes required special hash functions, which made them less efficient. Lin et al. [6] introduced a scheme that utilizes general hash functions to achieve improved efficiency by reducing computational time.

Hou et al. [2] proposed the UDVTS scheme to solve the problem of transitive signatures being stolen or abused; only the designated verifier has the ability to authenticate the signature. To serve more scenarios, Zhu et al. [7] proposed a transitive signature scheme with multiple verifiers designated and named it UDMVTS. Lin et al. [8] proposed a more efficient UDVTS scheme based on RSA assumption. Geontae et al. [9] designed the first lattice-based transitive signature scheme, which has the advantage of being resistant to quantum attacks. Then, Geontae et al. [10] designed the first identity-based transitive signature scheme.

All the above schemes are only applicable to undirected graphs. Currently, there are no proposed transitive signature schemes for general directed graphs. In fact, Hohenberger [11] shared that it is difficult to construct a general transitive signature scheme for directed graphs because it requires a special Abel TGII group, and there is no construction of such a group yet. Kuwakado and Tanaka [12] first proposed a TS scheme for directed trees but did not provide a concrete proof. Yi et al. [13] pointed out that Kuwakado’s scheme was not secure and then constructed a directed transitive signature scheme provably secure under the standard model. Neven et al. [14] designed a simpler transitive signature scheme to reduce the signature size. Camacho and Hcvia [15] constructed a scheme using a hash function with a common-prefix proof. Xu et al. [16] constructed a scheme using the RSA accumulator that preserves the composed signature size and protects its path information.

• Universal Designated Verifier Signatures (UDVS). Steinfeld et al. [17] introduced the concept of UDVS: only the verifier designated by the signature holder is allowed to authenticate signatures. Steinfeld et al. [17] proposed the first UDVS scheme by utilizing a BLS [18] short signature in the same year. They then combined the standard RSA and Schnor schemes to propose two identity-based UDVS schemes [19]. Ng et al. [20] proposed another scheme with multiple verifiers designated, allowing multiple verifiers to authenticate the signature. Zhang et al. [21] use the model proposed by Steinfeld et al. [17] to design two new identity-based UDVS schemes. The security of the above schemes all rely on the random oracle model. Zhang et al. [22] designed the first UDVS scheme that is provably secure in the standard model. Shahandashti et al. [23] provided a generic construction of UDVS from standard digital signatures. Since then, a multitude of UDVS schemes with distinct features have been put forward, such as multi-signer and multiple designated verifiers UDVS [24], UDVS without delegatability [25], universal designated verifier ring signatures [26], and universal designated multi-verifiers content extraction signatures [27]. To resist quantum attacks, Li et al. [28] constructed the first lattice-based UDVS scheme. Moreover, Tang et al. [29] pointed out that the strong privacy in traditional universal designated verifier signature schemes leads to the problem of unfairness to the verifier and, thus, designed a traceable universal designated verifier signature proof scheme.

2. Preliminaries

This section first gives a description of related symbols and introduces some basic concepts and related knowledge.

2.1. Notations

The notation $a\stackrel{R}{\leftarrow }A$ means that an element a is randomly sampled from the set A. A $\mathcal{PPT}$ (probabilistic polynomial-time) algorithm means that the algorithm is both probabilistic and runs in polynomial time. We define $\mathcal{O}(·)$ as a random oracle that responds to every unique query with a random response chosen uniformly from its output domain. If a query is repeated, it responds the same way every time that query is submitted. The notation $Pr\left[X\right]$ denotes the probability of event X happening. We equate the notion of “negligible probability” with probabilities smaller than any inverse polynomial in n.

2.2. Graphs

This paper considers an undirected graph $G=(V,E)$, where V is a points set and $E\subseteq V\times V$ is an edges set. $\tilde{G}=(V,\tilde{E})$ represents the transitive closure of G. It means that $(i,j)\in \tilde{E}$ if and only if G contains a path from i to j. $G^{*}=(V^{*},E^{*})$ represents the transitive reduction in G. It is the graph with the minimum number of edges that possesses the equivalent transitive closure as G.

2.3. Admissible Bilinear Pairing

Let $\mathbb{G}$, ${\mathbb{G}}_{\mathbb{T}}$ be two groups of prime order p and let g be a generator of $\mathbb{G}$. An admissible bilinear mapping $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_{\mathbb{T}}$ has the following properties:

(1)

Bilinearity: $e(g^a,g^b)=e{(g,g)}^{ab}$, for all $a,b\stackrel{R}{\leftarrow }{\mathbb{Z}}_p$.

(2)

Non-degeneracy: $e(g,g)\ne 1$.

(3)

Computability: $e(g_1,g_2)$ is efficiently computable for all $g_1,g_2\stackrel{R}{\leftarrow }\mathbb{G}$.

2.4. Complexity Assumptions

Definition 1

(One-more Bilinear Diffie–Hellman (BDH) problem [30]). Let $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_{\mathbb{T}}$ be a bilinear mapping, where $\mathbb{G}$ and ${\mathbb{G}}_{\mathbb{T}}$ are groups of prime order p, and g is a generator of $\mathbb{G}$. Let $A=g^a,B=g^b$, where $a,b\stackrel{R}{\leftarrow }{\mathbb{Z}}_p$. Given $(e,\mathbb{G},{\mathbb{G}}_{\mathbb{T}},p,g,A,B)$ and the following two oracles:

(1)

The $H_1$ oracle ${\mathcal{O}}^{{\mathcal{H}}_1}$: inputs a point $i\in N$, returns a random point $h_i\in \mathbb{G}$.

(2)

The CDH oracle ${\mathcal{O}}^{\mathcal{CDH}}$: inputs a point $h_i\in \mathbb{G}$, returns a point ${\left(h_i\right)}^a\in \mathbb{G}$.

An adversary is said to have solved the one-more BDH problem if it successfully computes n values of $e{(g,h_i)}^{ab}$ when the number of ${\mathcal{O}}^{\mathcal{CDH}}$ has queried strictly less than n.

3. Traceable Universal Designated Verifier Transitive Signature Scheme

The following describes the definitions and security model of the TUDVTS scheme. Hou et al. [2] proposed a universal designated verifier transitive signature (UDVTS). As a special case of UDVTS, the idea of the TUDVTS scheme is to allow the combiner to convert a composed signature into a translated signature before designating a verifier. Translation is performed by using the tracer’s public key. After the verification, the tracer can seek the true source of a designated verifier signature by using his own secret key. A TUDVTS scheme consists of ten efficient algorithms as follows:

• $pp\leftarrow \mathbf{Setup}\left(1^k\right)$. The initialization algorithm that takes as input the security parameter k, outputs the public parameters $pp$.
• $(p{k}_i,s{k}_i)\leftarrow \mathbf{KGen}\left(pp\right)$. The key generation algorithm that takes as input the public parameters $pp$, outputs all users’ public/secret key pairs $(p{k}_i,s{k}_i)$.
• ${\sigma }_{ij}\leftarrow \mathbf{TSign}(i,j,s{k}_s)$. The transitive signing algorithm that takes as input the signer’s secret key $s{k}_s$ and nodes $i,j\in \mathbb{N}$ and outputs an original signature of edge $(i,j)$ relative to $s{k}_s$.
• $\left\{0,1\right\}\leftarrow \mathbf{TVry}(i,j,p{k}_s,{\sigma }_{ij})$. The verification algorithm that takes as input the signer’s public key $p{k}_s$, nodes $i,j\in \mathbb{N}$, and a candidate signature ${\sigma }_{ij}$, which outputs 1 if accepting the signature or 0 for rejecting it.
• $\left\{\perp ,{\sigma }_{ik}\right\}\leftarrow \mathbf{Comp}(i,j,k,p{k}_s,{\sigma }_{ij},{\sigma }_{jk})$. The composition algorithm that takes as input the signer’s public key $p{k}_s$,nodes $i,j,k\in \mathbb{N}$, and two signatures ${\sigma }_{ij},{\sigma }_{jk}$, which outputs the composed signature ${\sigma }_{ik}$ or the symbol ⊥to indicate failure.
• $\left\{{\widehat{\sigma }}_{ij},t\right\}\leftarrow \mathbf{Trans}(p{k}_t,{\sigma }_{ij})$. The translation algorithm that takes as input the tracer’s public key $p{k}_t$ and a transitive signature ${\sigma }_{ij}$ of edge $(i,j)$ and outputs a translated signature ${\widehat{\sigma }}_{ij}$. In addition, the combiner selects and saves a secret value t.
• ${\sigma }_{DV}\leftarrow \mathbf{DS}(i,j,p{k}_v,{\widehat{\sigma }}_{ij},t)$. The signature holder’s designation algorithm that takes as input the verifier’s public key $p{k}_v$, nodes $i,j\in \mathbb{N}$, a secret value t, and a translated signature ${\widehat{\sigma }}_{ij}$, which outputs a designated verifier signature ${\sigma }_{DV}$.
• ${\widehat{\sigma }}_{DV}\leftarrow \mathbf{Sim}(i,j,p{k}_s,p{k}_t,s{k}_v,{\widehat{\sigma }}_{ij})$. The transcript simulation algorithm that takes as input the signer’s public key $p{k}_s$, the tracer’s public key $p{k}_t$, the verifier’s secret key $s{k}_v$, nodes $i,j\in \mathbb{N}$, and the translated signature ${\widehat{\sigma }}_{ij}$, which outputs a simulated signature ${\widehat{\sigma }}_{DV}$.
• $\left\{0,1\right\}\leftarrow \mathbf{DV}(i,j,p{k}_s,s{k}_v,{\sigma }_{DV})$. The designated verifying algorithm that takes as input the signer’s public key $p{k}_s$, the verifier’s secret key $s{k}_v$, nodes $i,j\in \mathbb{N}$, and a designated verifier signature ${\sigma }_{DV}$, which outputs 1 if accepting the signature or 0 for rejecting it.
• ${\sigma }_{ij}\leftarrow \mathbf{Trace}(s{k}_t,{\widehat{\sigma }}_{ij})$. The tracing algorithm that takes as input the tracer’s secret key $s{k}_t$ and the translated signature ${\widehat{\sigma }}_{ij}$, which outputs the transitive signature ${\sigma }_{ij}$.

• Correctness: we require five obvious correctness properties in TUDVTS. The first four points are the correctness requirements of UDVTS. Algorithm TVry checks the correctness of TSign and Comp. Algorithm DV checks the correctness of DS and Sim. Algorithm Trans checks the correctness of Trace.

• Correctness of TSign: If ${\sigma }_{ij}\leftarrow \mathbf{TSign}(i,j,s{k}_s)$, then

  $$Pr[1\leftarrow \mathbf{TVry}(i,j,p{k}_s,{\sigma }_{ij})]=1.$$
• Correctness of Comp: If ${\sigma }_{ik}\leftarrow \mathbf{Comp}(i,j,k,p{k}_s,{\sigma }_{ij},{\sigma }_{jk})$, then

  $$Pr[1\leftarrow \mathbf{TVry}(i,k,p{k}_s,{\sigma }_{ik})]=1,$$

  where ${\sigma }_{ij},{\sigma }_{jk}$ are legitimate signatures (the signature is either obtained by the signer or by running Comp on legitimate signatures).
• Correctness of DS: If ${\sigma }_{DV}\leftarrow \mathbf{DS}(i,j,p{k}_v,{\widehat{\sigma }}_{ij})$, then

  $$Pr[1\leftarrow \mathbf{DV}(i,j,p{k}_s,s{k}_v,{\sigma }_{DV})]=1.$$
• Correctness of Sim: If ${\sigma }_{DV}\leftarrow \mathbf{Sim}(i,j,p{k}_s,p{k}_t,s{k}_v,{\widehat{\sigma }}_{ij})$, then

  $$Pr[1\leftarrow \mathbf{DV}(i,j,p{k}_s,s{k}_v,{\sigma }_{DV})]=1.$$
• Correctness of Trace: If ${\widehat{\sigma }}_{ij}\leftarrow \mathbf{Trans}(p{k}_t,{\sigma }_{ij})$, then ${\sigma }_{ij}\leftarrow \mathbf{Trace}(s{k}_t,{\widehat{\sigma }}_{ij})$.

Security Models

A secure TUDVTS scheme satisfies unforgeability, privacy, and traceability. The following are definitions of these security properties.

• Unforgeability: the unforgeability of TUDVTS is similar to the unforgeability of UDVTS. TUDVTS encompasses two distinct forms of unforgeability. The first property refers to the fact that any adversary cannot output a forgery even if it is allowed to obtain transitive signatures on many other messages of its choice, i.e., the transitive signature unforgeability (TS-unforgeability). The second property refers to the impossibility for any adversary to forge a valid designated verifier signature even if they possess a valid translated signature from before, i.e., the designated verifier signature unforgeability (DV-unforgeability). Note that it is possible that the translated signature in DV-unforgeability is forged. As described in reference [29], we only consider this case where the translated signature is sent by the designator.

TS-unforgeability requires that any adversary cannot output a transitive signature on a disconnected edge. A disconnected edge is one that does not belong to the transitive closure of the graph composed of all pairs signed by the signer.

We let ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TS}}^{cma}$ denote an execution of the experiment for a given TUDVTS and adversary $\mathcal{A}$. The experiment is defined as follows:

• Setup: the public parameters $pp$ and the signer’s public/secret key-pair $(p{k}_s,s{k}_s)$ are generated by running Setup and KGen, respectively. Then, it is sent to $\mathcal{A}$.
• TSign Query: $\mathcal{A}$ picks an edge $(i,j)$. Then, the transitive signature ${\sigma }_{ij}$ is generated by running TSign and sent to $\mathcal{A}$.

In the end, $\mathcal{A}$ outputs an edge $(i^{\prime },j^{\prime })$ and its signature ${\sigma }_{i^{\prime }{j}^{\prime }}$. The experiment outputs 1 if $1\leftarrow \mathbf{TVry}(i^{\prime },j^{\prime },p{k}_s,{\sigma }_{i^{\prime }{j}^{\prime }})$ and $(i^{\prime },j^{\prime })\notin \tilde{G}$, where $\tilde{G}$ is the transitive closure of the graph G composed of all pairs $(i,j)$ submitted to TSign Query.

The advantage of $\mathcal{A}$ in the ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TS}}^{cma}$ is defined as

$${\mathrm{Adv}}_{\mathcal{A},\mathrm{TS}}^{cma}\left(k\right)=Pr[{\mathrm{Forge}}_{\mathcal{A},\mathrm{TS}}^{cma}=1].$$

Definition 2

(TS-Unforgeability). The transitive signature is unforgeable under adaptive chosen-message attacks if ${\mathrm{Adv}}_{\mathcal{A},\mathrm{TS}}^{cma}\left(k\right)$ is negligible for any $\mathcal{PPT}$ adversary $\mathcal{A}$.

DV-unforgeability requires that any adversary cannot output a designated verifier signature on an edge using the designated verifier’s public key, where the edge and the public key have not been used as input to query the designated verifier signature.

We let ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}$ denote an execution of the experiment for a given TUDVTS and adversary $\mathcal{A}$. The experiment is defined as follows:

• Setup: the public parameters $pp$ and all users’ public/secret key-pairs $(p{k}_i,s{k}_i)$ are generated by running Setup and KGen, respectively. Then, it is sent to $\mathcal{A}$.
• Trans Query: $\mathcal{A}$ picks an edge $(i,j)$. The transitive signature ${\sigma }_{ij}$ is first generated by running TSign. Then, the translated signature ${\widehat{\sigma }}_{ij}$ is generated by running Trans and sent to $\mathcal{A}$. The secret value t is kept private.
• DS Query: $\mathcal{A}$ picks an edge ($i,j$), a verifier’s public key $p{k}_{v_i}$ and the corresponding translated signature ${\widehat{\sigma }}_{ij}$. He initially acquires the signature ${\widehat{\sigma }}_{ij}$ using the aforementioned procedure in the absence of the translated signature. Then, ${\sigma }_{DV}$ is generated by running DS and sent to $\mathcal{A}$.
• DV Query: $\mathcal{A}$ requests the verification result of ($(i,j),{\sigma }_{DV}$) using the chosen public key $p{k}_{v_i}$. The verification result is generated by running DV and sent to $\mathcal{A}$.
• SKey Query: $\mathcal{A}$ picks a verifier’s public key $p{k}_{v_i}$. Then, the corresponding private key $s{k}_{v_i}$ is sent to $\mathcal{A}$.

In the end, it returns a forgery ${\sigma }_{DV}^{\prime }$ on edge $(i^{\prime },j^{\prime })$ with $p{k}_{v_k}$ chosen by himself. The experiment outputs 1 if:

-

$1\leftarrow$DV($i^{\prime },j^{\prime },p{k}_s,s{k}_{v_k},{\sigma }_{DV}^{\prime }$).

-

$((i^{\prime },j^{\prime }),p{k}_{v_k})$ has never been submitted to DS Query.

-

$p{k}_{v_k}$ has never been submitted to SKey Query.

The advantage of $\mathcal{A}$ in the ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}$ is defined as

$${\mathrm{Adv}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)=Pr[{\mathrm{Forge}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}=1].$$

Definition 3

(DV-Unforgeability). A TUDVTS scheme is unforgeable under adaptive chosen-message and chosen-public-key attacks if ${\mathrm{Adv}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)$ is negligible for any $\mathcal{PPT}$ adversary $\mathcal{A}$, where $\mathcal{A}$ invokes at most $q_1$ Trans Query, $q_2$ DS Query, $q_3$ DV Query and $q_4$ SKey Query in time t.

The main difference between the above definition and [2] is that here, $\mathcal{A}$ queries the translated signature instead of the transitive signature.

Privacy: the privacy has been systematically discussed by Hou et al. in [2]. There are two types of privacy in the TUDVTS scheme: non-transferability of TUDVTS and privacy of transitive signature. As stated in [17], the designated verifier has the capability to produce a signature that cannot be distinguished from the signature generated by the signature holder. That is, the verifier is unable to provide convincing evidence to others that the signer has indeed signed the message. As stated in [1], The second condition states that a transitive signature and a composed signature on the same edge cannot be distinguished. This implies that the Comp algorithm can operate properly even if its input was generated using Comp itself.

The non-transferability of TUDVTS requires that any distinguisher cannot distinguish a designated verifier signature and the corresponding simulated signature.

We let ${\mathrm{Priv}}_{\mathcal{D},\mathrm{TUDVTS}}^{cma,cpka}$ denote an execution of the experiment for a given TUDVTS and distinguisher $\mathcal{D}$. The experiment is defined as follows:

• Setup: the public parameters $pp$ and all users’s public/secret key-pairs $(p{k}_i,s{k}_i)$ are generated by running Setup and KGen, respectively. Then, it is sent to $\mathcal{D}$.
• Stage 1: the distinguisher $\mathcal{D}$ adaptively makes Trans Query, DS Query, DV Query, Sim Query, SKey Query: it responds to $\mathcal{D}$ in the same way as in game ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}$.

  -

  Sim Query: assuming that $\mathcal{D}$ requests a simulated signature on edge ($i,j$) using the chosen public key $p{k}_{v_i}$, he initially acquires the signature ${\widehat{\sigma }}_{ij}$ using the aforementioned procedure in the absence of the translated signature. Then, the simulated signature ${\widehat{\sigma }}_{DV}$ is generated by running Sim and sent to $\mathcal{D}$.

• Challenge stage: $\mathcal{D}$ returns $(i^{\prime },j^{\prime })$ and $p{k}_{v_k}$ that satisfy the following conditions:

  -

  $(i^{\prime },j^{\prime })\notin G$.

  -

  $((i^{\prime },j^{\prime }),p{k}_{v_k})$ has never been submitted to DS Query and Sim Query.

  -

  $p{k}_{v_k}$ has never been submitted to SKey Query.

  In reply, the experiment randomly samples $b\in \left\{0,1\right\}$. If $b=1$, then the signature ${\sigma }_{DV}$ is generated by running DS and returned to $\mathcal{D}$. Otherwise, the signature ${\widehat{\sigma }}_{DV}$ is generated by running Sim and returned to $\mathcal{D}$.
• Stage 2. Upon the receipt of the signature, $\mathcal{D}$ can still proceed with the query in stage 1. However, he cannot choose $((i^{\prime },j^{\prime }),p{k}_{v_k})$ for DS Query or Sim Query.
• Guess stage. $\mathcal{D}$ outputs his guess $b^{\prime }\in \left\{0,1\right\}$.

If $b^{\prime }=b$, then $\mathcal{D}$ wins the game. The advantage of $\mathcal{D}$ in the ${\mathrm{Priv}}_{\mathcal{D},\mathrm{TUDVTS}}^{cma,cpka}$ is defined as

$${\mathrm{Adv}}_{\mathcal{D},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)=\left|Pr[b^{\prime }=b]-1/2\right|.$$

Definition 4

(Non-Transferability of TUDVTS). If ${\mathrm{Adv}}_{\mathcal{D},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)$ is negligible for any $\mathcal{PPT}$ distinguisher $\mathcal{D}$, then the TUDVTS scheme is non-transferable under adaptive chosen-message and chosen-public-key attacks.

Privacy of transitive signatures requires that any distinguisher cannot distinguish between transitive signatures and composed signatures on the same edges.

Definition 5

(Privacy of Transitive Signature). If the input of Comp is legitimate signatures, then the distributions that the composed signature and the signature generated by the signer follow are statistically indistinguishable.

• Traceability: as stated in [29], in order to determine whether the signer signed the message, we introduce a tracer in UDVTS. The tracer can restore the translated signature ${\widehat{\sigma }}_{ij}$ to its corresponding transitive signature ${\sigma }_{ij}$. According to TV-unforgeability, only the signer and the combiner have the ability to obtain valid transitive signatures. Thus, the tracer can track the identity of the translated signature generator by checking whether the transitive signature is valid.

Definition 6

(Traceability). If the translated signature is calculated by the combiner, then the transitive signature can be recovered by the tracer.

4. Our TUDVTS Scheme

In this section, we present a concrete construction of the TUDVTS scheme and its security results.

4.1. Construction

Our scheme TUDVTS = (Setup, KGen, TSign, TVry, Comp, Trans, DS, DV, Sim, Trace) is constructed as follows: Given a group generator GGen that takes as input $1^k$ and outputs a triple $(\mathbb{G},{\mathbb{G}}_{\mathbb{T}},p)$, where p is a lagre prime and $\mathbb{G},{\mathbb{G}}_{\mathbb{T}}$ are two p-order multiplicative cyclic groups. Denote $H_1:\mathbb{N}\to \mathbb{G}$ and $H_2:{\{0,1\}}^{*}\to {\mathbb{Z}}_p$ as two hash functions.

• Setup($1^k$): this algorithm first obtains $(\mathbb{G},{\mathbb{G}}_{\mathbb{T}},p)$ by running GGen. Then, it generates a bilinear map $e:\mathbb{G}\times \mathbb{G}\to {\mathbb{G}}_{\mathbb{T}}$ and a generator g of $\mathbb{G}$ and outputs the public parameters $pp=(p,g,e,\mathbb{G},{\mathbb{G}}_{\mathbb{T}},H_1,H_2$).
• KGen($pp$): this algorithm takes as input the public parameters $pp$. It computes $A=g^a,B=g^b,D=g^d$, where $a,b,d\stackrel{R}{\leftarrow }{Z}_p^{*}$. It outputs three pairs of public/secret keys $\left\{(A=g^a,a),(B=g^b,b),(D=g^d,d)\right\}$, which denote the signer, the verifier, and the tracer, respectively.
• TSign($i,j,s{k}_s$): this algorithm takes as input the signer’s secret key a and nodes $i,j\in \mathbb{N}$. It computes ${\sigma }_{ij}={\left(h_i{h}_j^{-1}\right)}^a$ if $i<j$, where $h_i=H_1\left(i\right),h_j=H_1\left(j\right)$. If $i>j$, swap i and j.
• TVry($i,j,p{k}_s,{\sigma }_{ij}$): this algorithm takes as input the signer’s public key A, nodes $i,j\in \mathbb{N}$, and a signature ${\sigma }_{ij}$. If $e({\sigma }_{ij},g)=e(h_i{h}_j^{-1},A)$, then it outputs 1 (accept). Otherwise, it outputs 0 (reject).
• Comp($i,j,k,p{k}_s,{\sigma }_{ij},{\sigma }_{jk}$): this algorithm takes as input the signer’s public key A, nodes $i,j,k\in \mathbb{N}$, and two signatures ${\sigma }_{ij}$ of $(i,j)$ and ${\sigma }_{jk}$ of $(j,k)$. If ${\sigma }_{ij}$ and ${\sigma }_{jk}$ are both valid signatures, then it outputs the composed signature ${\sigma }_{ik}\leftarrow {\sigma }_{ij}·{\sigma }_{jk}$ of $(i,k)$. Otherwise, it outputs ⊥.
• Trans(${\sigma }_{ij},p{k}_t$): this algorithm takes as input the tracer’s public key D and the signature ${\sigma }_{ij}$ of $(i,j)$. The combiner computes $T_1=g^t,T_2={\sigma }_{ij}{D}^t$, where $t\stackrel{R}{\leftarrow }{Z}_p^{*}$. He outputs the translated signature ${\widehat{\sigma }}_{ij}=(T_1,T_2)$.
• DS($i,j,p{k}_v,{\widehat{\sigma }}_{ij},t$): this algorithm takes as input the verifier’s public key B and the translated signature ${\widehat{\sigma }}_{ij}$. The combiner randomly chooses $r\in {\mathbb{Z}}_p$, and calculates $R=e{(g,B)}^r,h=H_2(i,j,h_i,h_j,R),R_1=e(D^{th},B),T=T_2^h{g}^r\left(\mathrm{mod}p\right)$ and $c=e(T,B).$ Then, he outputs the designated verifier signature ${\sigma }_{DV}=(R_1,h,c)$.
• Sim($i,j,p{k}_s,p{k}_t,s{k}_v,{\widehat{\sigma }}_{ij}$): this algorithm takes as input the signer’s public key A, the tracer’s public key D and notes $i,j\in \mathbb{N}$. The verifier randomly picks $r^{\prime }\in {\mathbb{Z}}_q$, and calculates $R^{\prime }=e{(g,B)}^{r^{\prime }},h^{\prime }=H_2(i,j,h_i,h_j,R^{\prime }),R_1^{\prime }=e(D^{h^{\prime }},T_1^b),T^{\prime }=T_2^{h^{\prime }}{g}^{r^{\prime }}\left(\mathrm{mod}p\right)$ and $c^{\prime }=e(T^{\prime },B).$ Then, he outputs a simulated signature ${\widehat{\sigma }}_{DV}=(R_1^{\prime },h^{\prime },c^{\prime })$.
• DV($i,j,p{k}_s,s{k}_v,{\sigma }_{DV}$): this algorithm takes as input the signer’s public key A, the tracer’s public key D, notes $i,j\in \mathbb{N}$ and the signature ${\sigma }_{DV}$. The designated verifier calculates $P_1=e(h_i{h}_j^{-1},A^{bh})R_1,P=c{P}_1^{-1}$ and checks whether $h=H_2(i,j,h_i,h_j,P)$. If this holds, then the algorithm outputs 1 (accept). Otherwise, it outputs 0 (reject).
• Trace($s{k}_t,{\widehat{\sigma }}_{ij}$): this algorithm takes as input the translated signature ${\widehat{\sigma }}_{ij}$. The tracer computes ${\sigma }_{ij}=T_2/T_1^d$ and checks whether $e({\sigma }_{ij},g)=e(h_i{h}_j^{-1},A)$. If this holds then ${\sigma }_{ij}$ is legitimate.

4.2. Correctness

Here, we show five correctness properties in our TUDVTS.

• Correctness of TSign: if ${\sigma }_{ij}={\left(h_i{h}_j^{-1}\right)}^a\leftarrow \mathbf{TSign}(i,j,s{k}_s)$, where $h_i=H_1\left(i\right),h_j=H_1\left(j\right)$, then

  $$e({\sigma }_{ij},g)=e({\left(h_i{h}_j^{-1}\right)}^a,g)=e(h_i{h}_j^{-1},g^a)=e(h_i{h}_j^{-1},A).$$
• Correctness of Comp: If ${\sigma }_{ik}={\sigma }_{ij}·{\sigma }_{jk}={\left(h_i{h}_j^{-1}\right)}^a·{\left(h_j{h}_k^{-1}\right)}^a={\left(h_i{h}_k^{-1}\right)}^a$, where $h_k=H_1\left(k\right)$, then

  $$e({\sigma }_{ik},g)=e({\left(h_i{h}_k^{-1}\right)}^a,g)=e(h_i{h}_k^{-1},g^a)=e(h_i{h}_k^{-1},A).$$
• Correctness of DS: if $R_1=e(D^{th},B)$ and

  $$\begin{array}{cc}\hfill P& =e(T_2^h{g}^r,B){\left[e(h_i{h}_j^{-1},A^{bh})R_1\right]}^{-1}\hfill \\ \hfill & =e({\sigma }_{ij}^h,B)e(D^{th},B)e(g^r,B){\left[e(h_i{h}_j^{-1},A^{bh})R_1\right]}^{-1}\hfill \\ \hfill & =e(h_i{h}_j^{-1},A^{bh})e(D^{th},B)e(g^r,B){\left[e(h_i{h}_j^{-1},A^{bh})R_1\right]}^{-1}\hfill \\ \hfill & =e(g^r,B),\hfill \end{array}$$

  then $h=H_2(i,j,h_i,h_j,P)$.
• Correctness of Sim: If $R_1^{\prime }=e(D^{h^{\prime }},T_1^b)$ and

  $$\begin{array}{cc}\hfill P& =e(T_2^{h^{\prime }}{g}^{r^{\prime }},B){\left[e(h_i{h}_j^{-1},A^{b{h}^{\prime }})R_1^{\prime }\right]}^{-1}\hfill \\ \hfill & =e({\sigma }_{ij}^{h^{\prime }},B)e(D^{t{h}^{\prime }},B)e(g^{r^{\prime }},B){\left[e(h_i{h}_j^{-1},A^{b{h}^{\prime }})R_1^{\prime }\right]}^{-1}\hfill \\ \hfill & =e(h_i{h}_j^{-1},A^{b{h}^{\prime }})e(D^{h^{\prime }},T_1^b)e(g^{r^{\prime }},B){\left[e(h_i{h}_j^{-1},A^{b{h}^{\prime }})R_1^{\prime }\right]}^{-1}\hfill \\ \hfill & =e(g^{r^{\prime }},B),\hfill \end{array}$$

  then $h^{\prime }=H_2(i,j,h_i,h_j,P)$.
• Correctness of Trace: if $T_1=g^t,T_2={\sigma }_{ij}{D}^t$, then

  $${\sigma }_{ij}=T_2/T_1^d={\sigma }_{ij}{D}^t/g^{td}={\sigma }_{ij}{D}^t/D^t={\sigma }_{ij}.$$

4.3. Security Analysis

Here, we show the following theorems and provide rigorous formal proofs.

Theorem 1

(DV-Unforgeability). Assuming the one-more BDH assumption holds in ($\mathbb{G},{\mathbb{G}}_{\mathbb{T}}$) using the public parameters $pp$, we can conclude that the TUDVTS scheme satisfies DV-unforgeability under adaptive chosen-message and chosen-public-key attacks, with parameters ($t,q_1,q_2,q_3,q_4$).

Proof. 

Suppose there are n verifiers in the system. If there exist a $\mathcal{PPT}$ adversary $\mathcal{A}$ for breaking DV-unforgeability of TUDVTS with ${\mathrm{Adv}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)$, we construct a challenger $\mathcal{C}$ for solving one-more BDH problem with ${\mathrm{Adv}}_{\mathcal{C}}^{one-moreBDH}\left(k\right)$, such that

$$\frac{1}{n}{(1-\frac{1}{n})}^{q_5}{\mathrm{Adv}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)\le {\mathrm{Adv}}_{\mathcal{C}}^{one-moreBDH}\left(k\right),\forall k\in \mathbb{N}.$$

Given an instance $pp=(e,\mathbb{G},{\mathbb{G}}_{\mathbb{T}},p,g,A,B)$ of one-more BDH problem, a public parameter D, ${\mathcal{O}}^{{\mathcal{H}}_1}(·)$ and ${\mathcal{O}}^{\mathcal{CDH}}(·)$, where $A=g^a,B=g^b,D=g^d$. $\mathcal{C}$’s aim is to output n values of $e{(H_1\left(i\right),g)}^{ab}$, under the requirement that has been made ${\mathcal{O}}^{\mathcal{CDH}}(·)$ less than n queries. Denote the set that comprises all queried vertices as V. Denote the function that stores all queried edge signatures as $\Delta :V\times V\to \mathbb{G}$. $\mathcal{C}$ performs the simulation work according to this instance as follows with adversary $\mathcal{A}$:

• Setup:

  1.

  $\mathcal{C}$ sets A as the signer’s public key and sets D as the tracer’s public key.

  2.

  $\mathcal{C}$ computes $y_i=g^{x_i}$ as the public key of the verifier $i(i\ne l)$, where $x_i\stackrel{R}{\leftarrow }{Z}_p^{*}$ is his private key. For $i=l$, $\mathcal{C}$ sets B as his public key. Then, $\mathcal{C}$ maintains a list L and adds all the pairs ($y_i,x_i$) to L, where $x_l=\perp$.

  3.

  $\mathcal{C}$ sends ($pp,A,B,D,y_1,\cdots ,y_n$) to $\mathcal{A}$.

• ${\mathrm{H}}_1$Query:

  1.

  $\mathcal{C}$ maintains a list $L_1$ to record the hash values output by calling ${\mathcal{O}}^{{\mathcal{H}}_1}(·)$.

  2.

  When $\mathcal{A}$ queries $H_1\left(i\right)$, $\mathcal{C}$ completes the following:

  -

  If $i\notin V$, then $V\leftarrow V\bigcup \left\{i\right\}$; $h_i\stackrel{R}{\leftarrow }\mathbb{G}$; $H_1\left(i\right)\leftarrow h_i$; $L_1\leftarrow L_1\cup h_i$; $\Delta (i,i)\leftarrow 1$.

  -

  $\mathcal{C}$ returns $H_1\left(i\right)$ to $\mathcal{A}$.

• ${\mathrm{H}}_2$Query:

  1.

  $\mathcal{C}$ maintains a list $L_2$ to record the hash values output by $H_2$ oracle. $\mathcal{A}$ randomly picks a verifier’s public key $y_i$ and a number $r_i\in {\mathbb{Z}}_p$ and computes $R=e{(g,y_i)}^{r_i}$.

  2.

  When $\mathcal{A}$ queries $H_2(i,j,h_i,h_j,R)$, $\mathcal{C}$ completes the following:

  -

  Firstly, obtains $h_i$ and $h_j$ as above if the two hash values do not exist.

  -

  Returns $h\stackrel{R}{\leftarrow }{\mathbb{Z}}_p$ to $\mathcal{A}$. Then, $\mathcal{C}$ adds all the message/value pairs $(R,h)$ to $L_2$.

• Trans Query: assuming that $\mathcal{A}$ requests a translated signature on an edge ($i,j$) that he has chosen. In reply, $\mathcal{C}$ firstly obtains the signature ${\sigma }_{ij}$ if $\Delta (i,j)$ is empty. $\mathcal{C}$ performs the following (assume $i<j$):

  1.

  If $i\notin V$ or $j\notin V$, $\mathcal{C}$ invokes ${\mathcal{O}}^{{\mathcal{H}}_1}(·)$ to obtain $H_1\left(i\right)$ or $H_1\left(j\right)$.

  2.

  If $\Delta (i,j)$ is empty, then

  $\Delta (i,j)\leftarrow {\mathcal{O}}^{\mathcal{CDH}}\left(H_1\left(i\right)H_1{\left(j\right)}^{-1}\right)$; $\Delta (j,i)\leftarrow \Delta {(i,j)}^{-1}$.

  3.

  For all $k\in V\setminus \left\{i,j\right\}$,

  If $\Delta (k,i)$ is empty, then $\Delta (k,j)\leftarrow \Delta (k,i)·\Delta (i,j)$; $\Delta (j,k)\leftarrow \Delta {(k,j)}^{-1}$.

  If $\Delta (k,j)$ is empty, then $\Delta (k,i)\leftarrow \Delta (k,j)·\Delta (j,i)$; $\Delta (i,k)\leftarrow \Delta {(k,i)}^{-1}$.

  4.

  ${\sigma }_{ij}\leftarrow \Delta (i,j)$.

  5.

  $\mathcal{C}$ randomly picks $t\in {\mathbb{Z}}_p$, computes $T_1=g^t$ and $T_2={\sigma }_{ij}{D}^t$. $\mathcal{C}$ maintains a list $L_T$ and stores all the random numbers t to $L_T$.

  6.

  Returns ($T_1,T_2$) to $\mathcal{A}$, and stores the corresponding t in $L_T$.

• DS Query: assuming that $\mathcal{A}$ requests a designated verifier signature on edge ($i,j$) using the chosen public key $y_i$, $\mathcal{C}$ firstly obtains the translated signature $(T_1,T_2)$ as above if the signature does not exist. Then, $\mathcal{C}$ randomly selects $r\in {\mathbb{Z}}_p$ and calculates $R=e{(g,B)}^r,R_1=e(D^{th},B),T=T_2^h{g}^r\left(\mathrm{mod}p\right)$ and $c=e(T,B)$, returns ${\sigma }_{DV}=(R_1,h,c)$ to adversary $\mathcal{A}$.
• DV Query: assuming that $\mathcal{A}$ requests a verification result of ($(i,j),{\sigma }_{DV}$) using the chosen public key $y_i$, $\mathcal{C}$ calculates $P_1=e(h_i{h}_j^{-1},A^{bh})R_1,P=c{P}_1^{-1}$, returns 1 if $h=H_2(i,j,h_i,h_j,P)$, otherwise returns 0.
• SKey Query: assuming that $\mathcal{A}$ requests the corresponding private key using the chosen public key $y_i$, $\mathcal{C}$ outputs the corresponding private key $x_i$ if $i\ne l$. Otherwise, the operation aborts. The probability of $\mathcal{C}$ not aborting is ${(1-\frac{1}{n})}^{q_5}$.
• Forgery: eventually, $\mathcal{A}$ takes as input $r^{*}\stackrel{R}{\leftarrow }{\mathbb{Z}}_P$ and $R^{*}=e{(g,y_k)}^{r^{*}}$, obtains $h^{*}$ by asking for the ${\mathrm{H}}_2$ oracle, when the edge $(i^{*},j^{*})$ and the verifier’s public key $y_k$ chosen by himself. Then, he obtains a translated signature ${\widehat{\sigma }}_{ij}^{*}=(T_1^{*},T_2^{*})$ by Trans Query and computes $c^{*}=e({T_2^{\prime }}^{h^{*}}{g}^{r^{*}},y_k)$. In the end, $\mathcal{A}$ returns a forgery signature ${\sigma }_{DV}^{*}=(R_1^{*},h^{*},c^{*})$. If $y_k\ne B$, then the operation aborts. The probability of $\mathcal{C}$ not aborting is $\frac{1}{n}$. We assume $i^{*},j^{*}\in V$, otherwise $\mathcal{C}$ can query the ${\mathcal{O}}^{{\mathcal{H}}_1}$ by himself. Let the graph $G=(V,E)$ be composed of all pairs $(i,j)$ submitted to Trans Query and let $\tilde{G}=(V,\tilde{E})$ be the transitive closure of G. ${\sigma }_{DV}^{*}$ is valid if it satisfies the following:

  -

  $1\leftarrow$DV($i,j,p{k}_s,s{k}_{v_k},{\sigma }_{DV}^{*}$).

  -

  $((i^{*},j^{*}),B)$ has never been submitted to DS Query.

  -

  $y_k$ has never been submitted to SKey Query.

$\mathcal{C}$ can compute the BDH values of all vertices in V by using ${\sigma }_{DV}^{*}$. V is decomposed into m disjoint subsets $V_t\subset V,\forall t=1,2,\cdots ,m$, which is intended to separate $i^{*}$ and $j^{*}$. Let $i^{*}\in V_1$ but $j^{*}\notin V_1$. For all $t\ne 1$, $\mathcal{C}$ picks a reference node $s_t\in V_t$. The BDH values for all nodes in $V_t$ can be calculated by performing the following steps:

1.

${\sigma }_{s_t}={\left(h_{s_t}\right)}^a={\left(H_1\left(s_t\right)\right)}^a\leftarrow {\mathcal{O}}^{\mathcal{CDH}}\left(H_1\left(S_t\right)\right)$.

2.

$c_{s_t}\leftarrow e({\sigma }_{s_t},B)$.

For all $z\in V_t\setminus \left\{s_t\right\}$,

3.

$c_{z{s}_t}\leftarrow e({\sigma }_{z{s}_t},B)$.

4.

$c_z\leftarrow c_{z{s}_t}·c_{s_t}$.

Otherwise, the BDH values for all nodes in $V_1$ can be calculated by performing the following steps:

1.

$c_{i^{*}{j}^{*}}\leftarrow {[c^{*}·{R^{*}}^{-1}]}^{h^{-1}}·{R_1^{*}}^{-1}$.

2.

$c_{i^{*}}\leftarrow c_{i^{*}{j}^{*}}·c_{j^{*}}$.

For all $k\in V_1\setminus \left\{i^{*}\right\}$,

3.

$c_{k{i}^{*}}\leftarrow e({\sigma }_{k{i}^{*}},B)$.

4.

$c_k\leftarrow c_{k{i}^{*}}·c_{i^{*}}$.

Now $\mathcal{C}$ outputs the BDH values $c_i=e({\sigma }_i,B)=e{(g,H_1\left(i\right))}^{ab}$ for all $i\in V$. For each $V_t(t\ne 1)$, $\mathcal{C}$ queried ${\mathcal{O}}^{\mathcal{CDH}}(·)$$\left|V_t\right|-1$ times to compute the signature ${\sigma }_{z{s}_t}$ (the number of edges in a minimal spanning tree of $V_t$), and queried ${\mathcal{O}}^{\mathcal{CDH}}(·)$ once to compute ${\sigma }_{s_t}$, the number of ${\mathcal{O}}^{\mathcal{CDH}}(·)$ for each $V_t(t\ne 1)$ is summed to $\left|V_t\right|$. For $V_1$, $\mathcal{C}$ did not need the additional query to compute the ${\sigma }_{i^{*}}$. Therefore, $\mathcal{C}$ outputs $\left|V\right|$ BDH values using ${\sum }_{t\ne 1}\left|V_t\right|+\left|V_1\right|-1=\left|V\right|-1$ CDH oracle and, hence, solves the one-more BDH problem.

Below, we consider the probability of $\mathcal{C}$ not aborting. If $\mathcal{C}$ does not abort, the following conditions must be satisfied:

-

$y_l=B$ has never been submitted to SKey Query.

-

In the output forgery, $\mathcal{A}$ chooses the public key B.

Obviously, the probability that both conditions are satisfied is greater than $\frac{1}{n}{(1-\frac{1}{n})}^{q_5}$; hence,

$$\frac{1}{n}{(1-\frac{1}{n})}^{q_5}{\mathrm{Adv}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}\left(k\right)\le {\mathrm{Adv}}_{\mathcal{C}}^{one-moreBDH}\left(k\right).$$

This completes the proof. □

Theorem 2

(TS-Unforgeability). Assuming the one-more BDH assumption holds in the bilinear group pair ($\mathbb{G},{\mathbb{G}}_{\mathbb{T}}$) using the public parameters $pp$, we can conclude that the transitive signature is unforgeable under an adaptive chosen-message attack.

Proof. 

Given an instance $pp=(e,\mathbb{G},{\mathbb{G}}_{\mathbb{T}},p,g,A,B)$ of one-more BDH problem, $H_1$ oracle ${\mathcal{O}}^{{\mathcal{H}}_1}(·)$ and the CDH oracle ${\mathcal{O}}^{\mathcal{CDH}}(·)$. $\mathcal{C}$’s aim is to output n values of $e{(H_1\left(i\right),g)}^{ab}$, but the CDH oracle has been made strictly less than n queries. Let V denote the set that comprises all queried vertices. $\mathcal{C}$ performs the simulation work according to this instance as follows with adversary $\mathcal{A}$:

• Setup: $\mathcal{C}$ sets A as the signer’s public key and returns $(A,pp)$ to $\mathcal{A}$.
• TSign Query: assuming that $\mathcal{A}$ requests a signature on an edge ($i,j$) that he has chosen. In reply, $\mathcal{C}$ performs the following (Assume $i<j$):

  1.

  If $i\notin V$ or $j\notin V$, $\mathcal{C}$ invokes ${\mathcal{O}}^{{\mathcal{H}}_1}(·)$ to obtain $H_1\left(i\right)$ or $H_1\left(j\right)$.

  2.

  If $\Delta (i,j)$ is empty, then

  $\Delta (i,j)\leftarrow {\mathcal{O}}^{\mathcal{CDH}}\left(H_1\left(i\right)H_1{\left(j\right)}^{-1}\right)$; $\Delta (j,i)\leftarrow \Delta {(i,j)}^{-1}$.

  3.

  For all $k\in V\setminus \left\{i,j\right\}$,

  If $\Delta (k,i)$ is empty, then $\Delta (k,j)\leftarrow \Delta (k,i)·\Delta (i,j)$; $\Delta (j,k)\leftarrow \Delta {(k,j)}^{-1}$.

  If $\Delta (k,j)$ is empty, then $\Delta (k,i)\leftarrow \Delta (k,j)·\Delta (j,i)$; $\Delta (i,k)\leftarrow \Delta {(k,i)}^{-1}$.

  4.

  ${\sigma }_{ij}\leftarrow \Delta (i,j)$.

  5.

  Returns ${\sigma }_{ij}$ to $\mathcal{A}$.

• Then, $\mathcal{A}$ adaptively invokes the $H_1$ oracle. $\mathcal{C}$ responds to $\mathcal{A}$ in the same way as in the proof above.

In the end, $\mathcal{A}$ outputs an edge $(i^{\prime },j^{\prime })$ and the signature ${\sigma }_{i^{\prime }{j}^{\prime }}$. If $1\leftarrow \mathbf{TVry}(i^{\prime },j^{\prime },A,{\sigma }_{i^{\prime }{j}^{\prime }})$ and $(i^{\prime },j^{\prime })\notin \tilde{G}$, then ${\sigma }_{i^{\prime }{j}^{\prime }}$ is said to be a valid forgery.

The one-more BDH problem is solved based on this forgery, as in the proof of the Theorem 1 method. ${\sigma }_{i^{\prime }{j}^{\prime }}$ is used to find the BDH value of vertex $i^{\prime }$. Thus, solving for the BDH values of all vertices in V, $\mathcal{C}$ queries at most $\left|V\right|-1$${\mathcal{O}}^{\mathcal{CDH}}(·)$. This completes the proof. □

Theorem 3

(Non-Transferability of TUDVTS). Our scheme satisfies the non-transferability of TUDVTS against the adaptive chosen-message and chosen-public-key $\mathcal{PPT}$ distinguisher $\mathcal{D}$.

Proof. 

Suppose $\mathcal{C}$ is a challenger. $\mathcal{C}$’s goal is to distinguish between a designated verifier signature and its corresponding simulated signature.

• Setup:

  1.

  $\mathcal{C}$ sets $A=g^a,D=g^d$ as the public key of the signer and the tracer, respectively, where $a,d\stackrel{R}{\leftarrow }{Z}_p^{*}$.

  2.

  $\mathcal{C}$ sets $y_i=g^{x_i}$ as the ith ($i\ne l$) verifier’s public/private key-pair, where $x_i\stackrel{R}{\leftarrow }{Z}_p^{*}$. Then, $\mathcal{C}$ maintains a list L and adds all the public/private key-pairs $(y_i,x_i)$ to L.

  3.

  $\mathcal{C}$ sends ($pp,A,y_1,\cdots ,y_n$) to $\mathcal{D}$.

• Stage 1: the distinguisher $\mathcal{D}$ adaptively invokes ${\mathrm{H}}_1$ Query, ${\mathrm{H}}_2$ Query, Trans Query, DS Query, DV Query, Sim Query, SKey Query. It responds to $\mathcal{D}$ in the same way as in game ${\mathrm{Forge}}_{\mathcal{A},\mathrm{TUDVTS}}^{cma,cpka}$.

  -

  SKey Query: if $\mathcal{D}$ requests the private key associated with a chosen public key $y_i$, $\mathcal{C}$ verifies the list L and provides the matching private key $x_i$ in response.

  -

  Sim Query: assuming that $\mathcal{D}$ requests a simulated signature on edge ($i,j$) using the chosen public key $y_i$, $\mathcal{C}$ firstly obtains the translated signature $(T_1,T_2)$ as above if the signature does not exist. Then, $\mathcal{C}$ randomly selects $r\in {\mathbb{Z}}_p$ and calculates $R^{\prime }=e{(g,y_i)}^{r^{\prime }},R_1^{\prime }=e(D^{h^{\prime }},T_1^b),T^{\prime }=T_2^{h^{\prime }}{g}^{r^{\prime }}\left(\mathrm{mod}p\right)$ and $c^{\prime }=e(T^{\prime },y_i).$, returns ${\widehat{\sigma }}_{DV}=(R_1^{\prime },h^{\prime },c^{\prime })$ to distinguisher $\mathcal{D}$.

• Challenge stage: $\mathcal{D}$ returns $(i^{\prime },j^{\prime })$ and $y_k$ that satisfy the following conditions:

  -

  $(i^{\prime },j^{\prime })\notin G$.

  -

  $((i^{\prime },j^{\prime }),y_k)$ has never been submitted to DS Query and Sim Query.

  -

  $y_k$ has never been submitted to SKey Query.

  In reply, $\mathcal{C}$ randomly samples $b\in \left\{0,1\right\}$. If $b=1$, then the signature ${\sigma }_{DV}=(R_1,h,c)$ is generated by running DS and returned to $\mathcal{D}$. Otherwise, the signature ${\widehat{\sigma }}_{DV}=(R_1^{\prime },h^{\prime },c^{\prime })$ is generated by running Sim and returned to $\mathcal{D}$.
• Stage 2: upon the receipt of the signature, $\mathcal{D}$ can still proceed with the query in Stage 1. However, he cannot query the translated signature on edge $(i^{\prime },j^{\prime })$, and cannot choose $((i^{\prime },j^{\prime }),y_k)$ for DS Query or Sim Query.
• Guess stage: $\mathcal{D}$ outputs his guess $b^{\prime }\in \left\{0,1\right\}$.

Suppose ${\sigma }_{DV}^{*}=(R_1^{*},h^{*},c^{*})$ is a valid designated verifier signature, since

$$Pr\left[{\sigma }_{DV}^{*}={\sigma }_{DV}\right]=Pr\left[\begin{array}{cc}& R^{*}=e{(g,B)}^{r^{*}}=e{(g,B)}^r=R\hfill \\ & h^{*}=h,\hfill \\ & R_1^{*}=e(D^{t^{*}{h}^{*}},B)=e(D^{th},B)=R_1\hfill \\ & c^{*}=c\hfill \end{array}\right]=Pr\left[\begin{array}{cc}& r^{*}=r\hfill \\ & t^{*}=t\hfill \end{array}\right]=\frac{1}{p^2},$$

where $r,r^{*},t,t^{*}\in {\mathbb{Z}}_p$. Similarly,

$$Pr\left[{\sigma }_{DV}^{*}={\widehat{\sigma }}_{DV}\right]=Pr\left[\begin{array}{cc}& R^{*}=e{(g,B)}^{r^{*}}=e{(g,B)}^{r^{\prime }}=R^{\prime }\hfill \\ & h^{*}=h^{\prime }\hfill \\ & R_1^{*}=e(D^{t^{*}{h}^{*}},B)=e(D^{t^{\prime }{h}^{\prime }},B)=R_1^{\prime }\hfill \\ & c^{*}=c^{\prime }\hfill \end{array}\right]=Pr\left[\begin{array}{cc}& r^{*}=r^{\prime }\hfill \\ & t^{*}=t^{\prime }\hfill \end{array}\right]=\frac{1}{p^2},$$

where $r^{\prime },r^{*},t^{\prime },t^{*}\in {\mathbb{Z}}_p$.

Therefore, the designated verifier signature and the simulated signature on the same edge and public key are statistically indistinguishable. This completes the proof. □

Theorem 4

(Privacy of Transitive Signature). If the input of Comp is legitimate signatures, then the distributions of the composed signature and the signature generated by the signer are statistically indistinguishable.

Proof. 

Let ${\sigma }_{ij}$ and ${\sigma }_{jk}$ be the legitimate signatures of edge $(i,j)$ and edge $(j,k)$ with respect to the public key A. Then, ${\sigma }_{ij}={\left(h_i{h}_j^{-1}\right)}^a$ and ${\sigma }_{jk}={\left(h_j{h}_k^{-1}\right)}^a$, where $h_i=H_1\left(i\right),h_j=H_1\left(j\right),h_k=H_1\left(k\right)$. Taking $(A,i,j,k,{\sigma }_{ij},{\sigma }_{jk})$ as input Comp, it outputs the composed signature

$${\sigma }_{ik}={\sigma }_{ij}·{\sigma }_{jk}={\left(h_i{h}_j^{-1}\right)}^a·{\left(h_j{h}_k^{-1}\right)}^a={\left(h_i{h}_k^{-1}\right)}^a.$$

Hence, the signature generated by the signer and the composed signature on the same edge are statistically indistinguishable. This completes the proof. □

Theorem 5

(Traceability). The TUDVTS scheme is traceable, which can check whether the signer signed the message.

Proof. 

Suppose the verifier sends a translated signature ${\widehat{\sigma }}_{ij}=(T_1,T_2)$ to the tracer. The tracer can calculate:

$${\sigma }_{ij}=T_2/T_1^d.$$

Then, the tracer checks whether $e({\sigma }_{ij},g)=e(h_i{h}_j^{-1},A)$ holds. If this holds then ${\sigma }_{ij}$ is legitimate, i.e., the signer signed the edge. This completes the proof. □

5. Efficiency Analysis

Since no other TUDVTS schemes have been proposed, we mainly discuss the size of the signature generated by the scheme and the time cost of its sub-algorithms and compare its efficiency with UDVTS. Let $\left|{\mathbb{Z}}_p\right|,\left|\mathbb{G}\right|,\left|{\mathbb{G}}_T\right|$ denote the bit length of the element in ${\mathbb{Z}}_p,\mathbb{G}$ and ${\mathbb{G}}_T$, respectively. Let $t_1,t_2,t_3,t_4,t_5$ be the time cost of performing one exponentiation, pairing, hash, inverse, and multiply operation, respectively. We have the following Table 1 and Table 2.

Table 1. Signature size.

Algorithm	TSign	TVry	Comp	Trans	DS	DV	Sim
UDVTS	$\left|\mathbb{G}\right|$	—	$\left|\mathbb{G}\right|$	—	$\left|{\mathbb{G}}_T\right|$	—	$\left|{\mathbb{G}}_T\right|$
TUDVTS	$\left|\mathbb{G}\right|$	—	$\left|\mathbb{G}\right|$	$2\left|\mathbb{G}\right|$	$\left|{\mathbb{Z}}_p\right|+2\left|{\mathbb{G}}_T\right|$	—	$\left|{\mathbb{Z}}_p\right|+2\left|{\mathbb{G}}_T\right|$

Table 2. Time cost.

Algorithm	TSign	TVry	Comp	Trans	DS	DV	Sim
UDVTS	$t_1+2t_3+t_4+t_5$	$2t_2+2t_3+t_4$	$t_5$	—	$t_2$	$t_1+t_2+2t_3+t_4+t_5$	$t_1+t_2+2t_3+t_4+t_5$
TUDVTS	$t_1+2t_3+t_4+t_5$	$2t_2+2t_3+t_4$	$t_5$	$2t_1+t_5$	$4t_1+3t_2+t_3+2t_5$	$t_1+t_2+t_3+2t_4+4t_5$	$5t_1+3t_2+t_3+t_5$

6. Conclusions

This paper introduces the concept of traceable universal designated verifier transitive signatures (TUDVTS) and formally depicts the framework of TUDVTS and its security model. In the new framework, the tracer can find the true source of the disputed signature. We next construct a concrete scheme in the random oracle model, whose unforgeability relies on the one-more BDH assumption. The public key, the transitive signature, the translated signature, and the designated verifier signature in our construction are $3\left|\mathbb{G}\right|$ bits, $\left|\mathbb{G}\right|$ bits, $2\left|\mathbb{G}\right|$ bits, and $2\left|{\mathbb{G}}_T\right|+\left|{\mathbb{Z}}_p\right|$ bits, respectively.