Abstract
This paper presents a multi-material dual “contouring” method used to convert a digital 3D voxel-based atlas of basal ganglia to a deformable discrete multi-surface model that supports surgical navigation for an intraoperative MRI-compatible surgical robot, featuring fast intraoperative deformation computation. It is vital that the final surface model maintain shared boundaries where appropriate so that even as the deep-brain model deforms to reflect intraoperative changes encoded in ioMRI, the subthalamic nucleus stays in contact with the substantia nigra, for example, while still providing a significantly sparser representation than the original volumetric atlas consisting of hundreds of millions of voxels. The dual contouring (DC) algorithm is a grid-based process used to generate surface meshes from volumetric data. The DC method enables the insertion of vertices anywhere inside the grid cube, as opposed to the marching cubes (MC) algorithm, which can insert vertices only on the grid edges. This multi-material DC method is then applied to initialize, by duality, a deformable multi-surface simplex model, which can be used for multi-surface atlas-based segmentation. We demonstrate our proposed method on synthetic and deep-brain atlas data, and a comparison of our method’s results with those of traditional DC demonstrates its effectiveness.
1. Introduction
1.1. Background
There are several computer-assisted therapy applications, including image-guided surgery and surgical simulation, which are founded on a descriptive patient-specific model of the anatomy that is typically derived from magnetic resonance imaging (MRI) or computed tomography (CT) datasets of the patient. Image-guided surgery and surgical robotics can both utilize the image-based anatomical representation through a registration process between this representation and the space in the operating room that coincides with the corresponding anatomy. The latter is defined in a coordinate system associated with either an optically tracked probe or a surgical robot. The registration process can exploit fiducials present on the patient or robot. Both surgical technologies strive for a high degree of accuracy between the image space and the patient space. This is typically achieved through a rigid transformation with an error on the order of 1 mm or less, particularly in surgical applications where the anatomical targets are compact. This level of accuracy is particularly desirable in deep-brain stimulation (DBS), which is a procedure that uses a needle to position an electrode lead (connected by wires to stimulation hardware outside the cranium) to a point on a neuroanatomical target. This target varies according to the neuro disorder under consideration. For example, Parkinson’s Disease treatment involves the delivery of electrode leads to a point on the subthalamic nucleus (STN), as depicted in Figure 1, whereas obsessive-compulsive disorder treatment involves the targeting of the nucleus accumbens. The STN is found on both the left and right sides of the subcortical portion of the brain. Its morphology is near-ellipsoidal, as shown in Figure 1, and its size is estimated to be, on average, 5.9 mm anteroposteriorly, 3.7 mm mediolaterally, and 5 mm dorsoventrally [1]. More importantly, the STN is composed of the limbic, motor, and associative zones, as depicted in Figure 1b. It is vital that the stimulation be accurately positioned in the motor portion. Inaccurate targeting can have dire implications. For example, an error of 2 mm, which can easily occur through intraoperative brain shift during DBS, can displace the target from the motor to the limbic or associative zone with dire consequences. Not surprisingly, there is also an increasing clinical interest in updating the anatomical model over time to account for intraoperative soft-tissue shift, particularly in neurosurgery and certainly in deep-brain stimulation, given the scale of the STN motor zone.
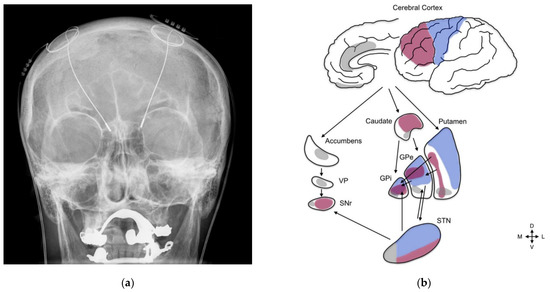
Figure 1.
Clinical context for this project: deep-brain stimulation. (a) DBS probes shown in an X-ray of the skull (white areas around the maxilla and mandible represent metal dentures; reproduced from Wikipedia). (b) Three-zone STN model, emphasizing the functional organization of the STN, basal ganglia structures, and cortical regions. The motor circuit (blue) includes the motor cortical areas, the dorsolateral postcommissural putamen, the lateral two-thirds of the globus pallidus (GPe and GPi), and a small portion of the substantia nigra (SNr). The motor regions of the STN comprise the dorsal-lateral aspects of the rostrocaudal third of the nucleus. The associative circuits (purple) consist of the associative cortical regions, the bulk of the caudate nucleus, the putamen rostral to the anterior commissure, the dorsal portion of the medial third of the globus pallidus (GPe and GPi), and finally, most of the substantia nigra. The associative regions of the STN coincide with its ventral–lateral–rostral portions. The limbic circuits (gray) are comprised of the limbic cortical areas, the nucleus accumbens, the rostral striatum, the subcommissural ventral pallidum (VP), limbic regions in the ventral area of the medial third of the globus pallidus (GPe and GPi), and the medial tip of the substantia nigra. The limbic STN lies in the mediorostral portions of the nucleus. Reproduced from [2].
Traditionally, commercial image-guided surgery systems used highly onerous manual labeling of tissues in order to achieve anatomical representations of the patient; however, given the progress in computer algorithms in terms of labeling or segmentation and the myriad approaches to programming MRI pulse sequences, there is considerable impetus to automate this process, possibly by leveraging multimodal MRI. Broadly speaking, there are three basic approaches to mapping intensities in 3D medical images to tissues: voxel-based, atlas-based, and boundary-based [3], and hybrid methods are also feasible. Voxel approaches map intensities or local measurements to a tissue label, often in the context of feature-based classification, and increasingly exploit a deep learning formalism in order to learn the most discriminating features conducive to robust classification [4]. In the second approach, a digital atlas represents a spatial map of anatomical structures that is usually derived from expert labeling; tissues are segmented by warping this 3D atlas to the subject image. Boundary models, also known as codimension-1 models, consist of deformable 2D contour models and 3D surface models that are defined in the image domain and change their shape under the influence of forces. In addition, codimension-2 models are used to segment curvilinear tissues in 3D [5]. Codimension-2 models are more relevant to segmentation. In this approach, the tissue boundary is shrink-wrapped with a contour or surface that is attracted to it, using external forces that are founded on image attractors such as image gradients. These forces are balanced by internal forces that regularize the resulting boundary based on continuity or stabilize it using shape statistics. These deformable models are either implicit, such as in Level Sets, or explicit, such as the snakes and simplex models. The interior of the 2D contour or 3D surface is assumed to coincide with the anatomical structure of interest. In general, complex anatomies must be identified piecemeal, one surface at a time, with little consideration of the agreement between boundaries in contact with each other.
The latter piecemeal approach to deformable surfaces makes it unlikely that multiple surfaces are identified in a manner that results in boundaries in perfect agreement (i.e., pairs of polygonalized boundaries flush with each other). If, in turn, this resulting segmentation were to serve as input for further segmentations within an image sequence, e.g., for intraoperative soft-tissue tracking, given a starting segmentation based on preoperative images, the lack of agreement may, in fact, worsen. As a result, neighboring surfaces can either overlap spatially or nudge each other apart. Although existing multi-surface techniques have used static collision detection to force neighboring surfaces to push each other away [6], this formalism does not enforce agreement between neighboring faces. As a result, there can be space between neighboring surfaces. Likewise, volumetric warping, such as FreeSurfer, which extracts anatomical boundaries based on volumetric nonrigid registration between image volumes, cannot guarantee that the initial configuration based on preoperative images maintains neighboring surfaces while updating the anatomy to account for intraoperative soft-tissue shift. Furthermore, biomechanical applications, in particular musculoskeletal modeling, may require large-scale representations of the anatomy such as a scoliotic spine. These anatomies may entail spaces between tissue boundaries, which may not be visible at coarse visualization scales and may undermine the accuracy of biomechanical (finite element) studies. To address this limitation in single-surface deformable surface models and make these surface models compatible with the use of elaborate digital atlases that are highly descriptive from a functional or anatomical perspective, this paper proposes a boundary-based segmentation technique that combines multi-material mesh generation and deformable surface models. As such, it builds on technical considerations that bridge two communities otherwise isolated from each other: surface meshing, which is founded on rigorous computational geometry, and deformable surface model-based segmentation.
1.2. Brief Overview of Mesh Generation
Mesh generation is an important component in visualization and is used in scientific disciplines such as engineering, simulation, medicine, and architecture. The marching cubes (MC) algorithm [7] introduced the concept of producing surface meshes by analyzing the intersections of a volume and a uniform grid. Other methods, such as dual contouring [8] and marching tetrahedra [9], expand on this concept in order to produce surface or volumetric meshes and non-grid-based methods such as dynamic particle systems [10,11] use physics-based forces to position vertices in an implicit volume. Although surface mesh generation has come a long way since the introduction of MC, defects in meshes, such as non-manifold geometry, cracks/gaps, and intersecting polygons, are still common and require post-processing mesh corrections before the surface mesh can be further used. Recently, there has been a trend toward multi-material surfaces and volumetric meshing, which can compound the above-mentioned meshing errors.
Multi-material surface meshing is the next evolution in surface mesh generation. For multi-labeled data, Bloomenthal and Ferguson [12] decomposed a cube into six tetrahedral cells. For each tetrahedron that intersected the surface, the edges, faces, and interior of each tetrahedron were examined for vertices and polygons were produced. Hege et al. [13] presented a variation of the MC algorithm that produced meshes for non-binary volumes. This involved subdividing a cube into a number of sub-cells whose probable material indices were established using trilinear interpolation. In [14], Bonnell et al. used volume fraction information on a dual grid constructed from regular hexahedral grids, which were then split into six tetrahedral cells to generate non-manifold multi-material boundary surfaces. Wu and Sullivan [15] extended the classical marching cubes algorithm to produce 2D and 3D multi-material meshes, where every faceted surface separated two materials. Reitinger et al. [16] presented a modified MC-based method that produced consistent non-manifold meshes from multi-labeled datasets. A cube whose corners had more than one material label was subdivided into eight smaller cubes and the faces of the cube whose corners had more than one material label were subdivided into four sub-cells. A constrained Laplacian filter was used on the output mesh to reduce staircase-like artifacts. Bertram et al. [17] used a method similar to [13] but relied on a dual grid. In [18], Bischoff and Kobbelt simplified topological ambiguities by subdividing voxels that contained critical edges or vertices before extracting the material interface. In [19], Boissonnat and Oudot presented a Delaunay-based surface mesh generator that produced provably good meshes and Oudot et al. extended this to volumetric meshing in [20]. Pons et al. [21] further extended these Delaunay-based methods to produce surface and volumetric meshes from multi-labeled medical datasets. Zhang and Qian [22] used a modified dual contouring algorithm, where ambiguous grid cubes were decomposed into tetrahedral cells to generate tetrahedrons and polyhedrons for multi-material datasets. Dillard et al. [23] presented an interpolation method using a simple physical model to find likely region boundaries between image slices and then applied marching tetrahedra [9] to produce a surface mesh. Smoothing and simplification methods have also been presented to reduce the number of triangles. Meyer presented a variation of dynamic particle systems [24] to produce multi-material surface and tetrahedral meshes.
The standard dual contouring algorithm is unable to produce two-manifold and watertight surface meshes due to the presence of ambiguous cubes. Our previous work in [25] presented a modified dual contouring algorithm that was capable of overcoming the limitations of standard DC. Ambiguous cubes were subdivided into a number of tetrahedral cells with regular sizes and shapes. The centroids of these tetrahedral cells were used as minimizers and novel polygon generation rules were used to produce single-material surface meshes that were two-manifold and watertight.
Atlas-based segmentation is a paradigm where anatomical atlases are used as a guide for the segmentation of new images, which effectively transforms a segmentation problem into a non-rigid registration problem. This category of segmentation can be divided into two parts: single-atlas-based and multiple-atlas-based. In single-atlas-based segmentation, an atlas is constructed from one or more labeled images and then registered to the target image. The accuracy of the segmentation depends on the registration process. Examples of single-atlas-based segmentation can be found in [26,27,28,29]. In multi-atlas-based segmentation, many independently built atlases are registered to the target image and the resulting segmentation labels are combined. The advantage of multiple-atlas-based segmentation over the single-atlas-based approach is that more information is available due to the use of many independent atlases and the drawback is the number of registration steps required to produce the final segmentation. Examples of multiple-atlas-based segmentation can be found in [29,30,31,32].
Deformable models were first presented in 1986 by Sederberg and Parry in [33]. Terzopoulos [34] coined the term deformable models and applied physical properties to objects. The basic idea behind the use of deformable models for segmentation is that the model will evolve using internal and external forces. The internal force will ensure a smooth surface and the external force will move the surface of the model toward the object boundary. Meier provided a thorough survey of the various deformable models in [35]. Snakes [36] was the first deformable model to be used for segmentation and has been used to demonstrate that deformable models produce superior segmentation results, even for datasets with large variations, noise, and discontinuities. Cootes et al. [37] introduced the notion of using statistical shape information to aid in the segmentation process.
Delingette formulated a specific deformable model, the simplex mesh [38,39,40], for 3D shape reconstruction and segmentation. A k-simplex mesh is defined as a k-manifold discrete mesh, where each vertex is linked to exactly k + 1 neighboring vertices. Delingette specified the simplex angle and metric parameters, which can be used to represent the position of any vertex with respect to its neighbors. The simplex angle can be considered the height of a vertex above the plane made by its three neighbors and the metric parameters are expressed as a function of the three neighboring vertices. Simplex meshes are dual to triangular meshes and have predefined resolution control through topology operators. Simplex forces include internal forces based on mesh geometry and external forces based on input image gradients. Various enhancements, such as shape constraints [41], smoothing parameters, shape memory, internal and external constraints [6,42], and statistical shape information [43,44,45,46,47,48], have allowed simplex meshes to be used for the accurate segmentation of anatomical structures. Gilles used the simplex mesh for segmenting and registering muscles and bone from MR data [6,42]. Tejos extended the 2D Diffusion Snakes process [49,50,51] and combined it with simplex meshes and statistical shape information for segmenting the patellar and femoral cartilage. Schmidt et al [43] as well as Haq et al. [52,53,54] incorporated statistical shape information into the two-simplex framework, whereas Sultana et al. [55] incorporated statistical shape information into a 1-simplex framework to segment intra-cranial nerves.
2. Materials and Methods
2.1. Overview of Method and Summary of Contributions
The method presented below is a multi-material (MM) dual contouring (DC) technique suitable for producing a triangulated surface boundary from a labeled volume or voxel-based digital atlas, where any shared boundary between two tissue labels is represented as a single triangulated mesh. In turn, this triangulated surface can serve as input to a tetrahedral meshing stage, where shared boundaries are each represented as a single mesh and are used to anchor tetrahedral elements on both sides. Alternatively, the aggregate triangulated surface model can be warped to a target image to produce a surface-based segmentation of that image. The advantage of this approach is that a functional representation of the anatomy is feasible in the target image, beyond the simple decomposition based strictly on conspicuous tissues.
As described in detail in Section 2.2, MM DC consists of decomposing the image domain into cubic grids, determining the nature of the intersections of the volumetric label map with each grid, and then finally stitching together a triangulated surface mesh that is optimally consistent with these grid intersection points. The preceding statement could apply to any contouring technique but what is specific to dual contouring is the particular nature of the intersection point within the grid cell, which can be anywhere within the cell and, as emphasized by Ju [8], enables the surface to capture discontinuous surfaces.
Moreover, the aspect that relates to multi-material meshing and the major contribution of this paper is the consideration of multiple tissue labels on either side of the boundary, which results in triangulated surface models with shared boundaries. In contrast, it is feasible to mesh the surface boundaries of any digital atlas (or labeled volume) through the iterative application of single-surface contouring; however, that approach would be plagued by double boundaries at the interface of each pair of labels, with no guarantee of agreement between the vertices, edges, and faces and the likelihood of subtle pockets of space in between. These spaces could then undermine a tetrahedral mesh needed for a biomechanical study or lead to drift between deformable surface models in a segmentation application. Multi-material dual contouring addresses the weaknesses of single-surface contouring. The main steps of the process are depicted in Figure 2.
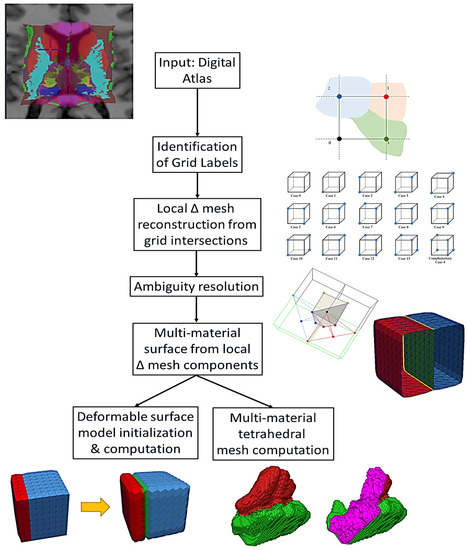
Figure 2.
Algorithmic workflow of MM DC-based surface meshing and its extension to deformable surface models and tetrahedral meshing.
The work presented here is an extension of the algorithm presented by the authors in [25]. The new contribution, beyond the originally published algorithm, is the generation of geometrically correct multi-material surface meshes that contain non-manifold elements at the junctions where materials meet. The sub-meshes of each material are 2-manifold and watertight on their own. The proposed method is capable of producing multi-material interfaces or shared boundaries that are consistent between sub-meshes. It is also demonstrated that these multi-material surface meshes can be used to easily initialize multi-material tetrahedral meshes. The final contribution consists of utilizing these multi-material surface meshes to initialize multi-material 2-simplex deformable surface meshes for segmentation purposes.
2.2. Contouring
2.2.1. An Overview of the Single-Surface Dual Contouring Algorithm
Dual contouring [8] is a method used for extracting the surface of an implicit volume. The method is dual in the sense that the vertices generated by DC are topologically dual to the faces generated by the marching cubes [7] (MC) algorithm. A labeled input volume is first subdivided using a uniform grid of an appropriate size and an octree is then used to represent and parse through the grid cubes. Once the volume is divided using the uniform grid, the values of the corners of each cube are noted and stored. In standard, single-material DC, the corners are labeled as inside or outside the volume. This results in a single-material mesh. In multi-material DC, each corner of the cube is assigned an integer value, where each integer represents a particular material of the labeled volume. The leaves of the tree represent the grid cubes at their finest level of division.
For each cube that intersects the volume, dual vertices or minimizers are computed using Quadratic Error Functions (QEFs). The general formulation of a QEF is given in Equation (1):
where represents a vertex on the contour or surface mesh (Figure 3a), are the intersection points of the isosurface with the grid, and are the normals defined at those intersections. Typically, one minimizer is computed for each grid cube that intersects the volume of interest. This minimizer can theoretically be anywhere inside the grid cube, rather than being restricted to the edges of the cube as in MC. This feature allows DC to produce meshes with sharp features.
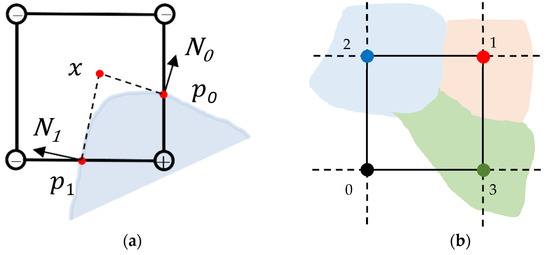
Figure 3.
Multi-material dual contouring geometry. (a) Contouring geometry and quadratic error function. The blue region represents the tissue volume. The position is an MM DC vertex, which is optimized according to the isosurface intersection points and the normals (drawn in 2D). (b) A 2D example of a uniform grid superimposed on a multi-material domain. The four corners of the square occupy three different material domains, as well as the background.
The function can be expressed as the inner product where A is a matrix whose rows map to the normals and b is a vector whose entries are . The function can then be expanded into the following:
In Equation (2), is a symmetric 3 × 3 matrix, is a column vector of length three, and is a scalar. This representation of a QEF can be solved using the QR decomposition method of Golub and Van Loan [56] or by computing the pseudoinverse of the matrix using Singular Value Decomposition (SVD) [57,58]. The implementation time depends on the dimensions of the image and the grid size, but in general, SVD is linear in the larger dimension (the number of rows of ) and quadratic in the smaller dimension (3).
Once the octree is generated and simplified and all the minimizers for the leaf cells are computed, the recursive functions EdgeProc(), CellProc(), and FaceProc(), as defined in [8], are used to locate the common minimal edge shared by four neighboring octree cells. The minimal edge is defined as the smallest edge shared by 4 neighboring octree cells. The concept of a minimal edge is necessary due to the fact that some octrees used in DC are adaptive octrees, meaning that the leaves of the octree are not all at the same level. In such a case, it may be that the four neighboring octree cells are not always the same size.
2.2.2. Multi-Material vs. Two-Manifold Contouring
A mesh is defined as being 2-manifold if every edge of the mesh is shared by exactly two faces and if the neighborhood of each vertex is the topological equivalent of a disk. A closed 2-manifold mesh S satisfies the Euler–Poincaré condition . The closed surface mesh is also watertight if it does not contain any holes or cracks.
Since a multi-material surface will inherently contain non-manifold elements along the material interfaces due to its multi-material nature, it is important to present a formal description of a mesh being multi-material, watertight, and 2-manifold. A triangular mesh can be described as a set where V is a set of n vertices For each , E is a set of k edges where each tuple is an edge made up of two vertices and F is a set of t triangular faces where each tuple describe a triangle made up of three vertices.
In regular, single-material, grid-based surface meshing algorithms such as marching cubes [7] or dual contouring [8], the input data are a binary volume or implicit function that describes a point as being either greater than or less than a given isovalue. A uniform grid is superimposed on the input data and the corners of the grid cubes are designated as inside or outside the volume.
Multi-label or multi-material input data have material indices describing the different material subdomains of the input data. The material indices are typically implemented in the form of integer values, with 0 indicating the background and the positive integers describing the different materials/labels. The corners of the grid cubes are assigned these integer material indices, indicating that the cube’s corner resides inside that material region of the input data. Figure 3b shows an example of a 2D uniform grid superimposed on a multi-material domain. There are three materials in this example, red with material index 1, blue with material index 2, and green with material index 3, along with the background whose material index is 0. The four corners of the square are within each of these regions and are assigned their respective material indices.
A multi-material mesh would have additional material information associated with its vertices and/or faces. In our implementation of a multi-material and 2-manifold dual contouring algorithm, we assigned pairwise integer values to the faces only, with the mechanism of the assignment explained in the next section. The triangular faces of a multi-material mesh SM of M materials can be described by the set , where p and q are the assigned pairwise material indices for a triangular face and and . For example, denotes the first triangle of the mesh with material indices 0 and 1. This means that the first triangle forms a plane between the background and Material 1. As another example, the face describes the triangle, with index 80 forming a plane between Materials 2 and 3. Figure 4 depicts a more complete example. Figure 4a shows a simple mesh comprising two materials with material indices 1 and 2 in red and blue, respectively. This is the actual, whole, and complete mesh. Figure 4b shows a cutout of the mesh. The green-colored part of the mesh is the interface or shared boundary that lies between the two materials. In this example, all the faces of Material 1 (red) are of the form , all the faces of Material 2 (blue) are of the form and all the faces of the shared boundary (green) are of the form . Figure 4c,d show what the sub-meshes of each material and the shared boundary would look like if they were viewed separately.
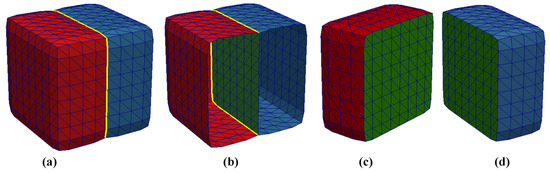
Figure 4.
A synthetic example of a multi-material mesh of two materials with a shared boundary. (a) The whole and complete multi-material mesh, (b) a cutout of the mesh showing the green shared boundary, (c) the sub-mesh for Material 1, (d) the sub-mesh for Material 2.
One aspect of a multi-material mesh with shared boundaries is that non-manifold elements will occur at the junction where two or more materials meet. In Figure 4a,b, the junction where Materials 1 and 2 meet is outlined in yellow and these edges are non-manifold, i.e., they are shared by more than two faces. Although the multi-material mesh (Figure 4a) as a whole is not purely 2-manifold due to the presence of these non-manifold elements, the sub-meshes (Figure 4c,d) of individual materials, along with the shared boundary, are completely 2-manifold and watertight.
Figure 5 shows another synthetic example of a multi-material mesh containing non-manifold elements, with sub-meshes for Materials 1, 2, and 3 shown in red, blue, and purple, respectively. In Figure 5a,b, there is an additional non-manifold vertex, which is shared between the sub-meshes of Material 1 and Material 2, along with the non-manifold edges (demarcated in yellow). Figure 5b shows a cutout of the mesh and the shared boundary between the sub-meshes for Material 1 and Material 3 is shown in green. Figure 5c–e show the separated sub-meshes for each of the materials. Again, although the whole and complete multi-material mesh is not purely 2-manifold, the three sub-meshes are 2-manifold and watertight.
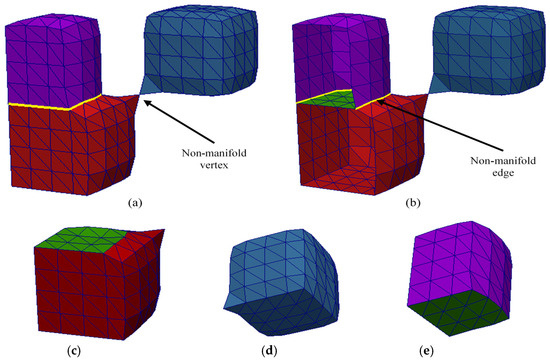
Figure 5.
A synthetic example of a multi-material mesh with three materials with non-manifold edges and vertex. (a) The whole and complete multi-material mesh, (b) a cutout of the mesh to show the shared boundary between the red and purple meshes, (c) sub-mesh for Material 1, (d) sub-mesh for Material 2, (e) sub-mesh for Material 3. All three sub-meshes are 2-manifold and watertight.
2.2.3. Ambiguous vs. Unambiguous Grid Cubes
The surface meshing process begins by superimposing a uniform grid over the multi-labeled volume in question. As stated earlier, the corners of the grid cubes are assigned material indices to indicate which material domain they occupy. An octree is used to represent the uniform grid. The corner configuration of the grid cubes can be one of two types: (1) all the corners have the same material index, or (2) at least one corner has a material index that is different from the rest. The cubes whose corners all have the same material index are completely inside a particular material and are, therefore, discarded from the octree. Quadratic Error Functions (QEF), as shown in Equation (2), are used to generate a single minimizer for each grid cube.
In the single-material case, each grid cube can have 28 or 256 possible configurations; however, these can be reduced to 14 fundamental cases when rotation and symmetry are taken into account, as shown in Figure 6. Out of these 14 configurations, Cases 0, 1, 2, 5, 8, 9, and 11 are simple cases for which there is only a single surface that intersects the grid cube (no surface for Case 0) [59].
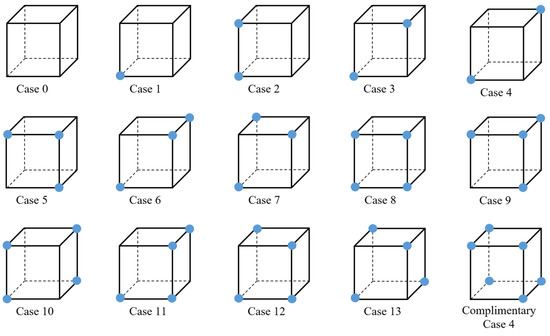
Figure 6.
The 14 fundamental cube configurations for a grid cube with binary labels.
In standard DC, the presence of ambiguous cubes, along with its single minimizer, is the reason that non-manifold elements occur in the resulting surface mesh. Once the octree is generated, it is, therefore, necessary to identify ambiguous and unambiguous grid cubes. A grid cube is called ambiguous because there is more than one possible surface intersecting the cube. Ambiguous cubes have either a face ambiguity or an interior ambiguity. Face ambiguity occurs when the material indices of two diagonal corners of a face are the same while the other two corners have different material indices. Interior ambiguity occurs when the material indices of two diagonally opposite corners of the cube have the same value. Figure 7a and Figure 7b show an example of face and interior ambiguities, respectively. It may be possible, although costly, to identify each ambiguous case in a single-material case. However, in a multi-material case where a cube can have a total of 88 permutations (since there are 8 corners and each corner can have 8 possible labels for a given cube), it is simply not feasible to identify ambiguity for each grid cube. Indicator variables can be used, as demonstrated in [22], to reduce a multi-labeled cube into a series of binary labeled cubes for each material and then determine ambiguity for each material.
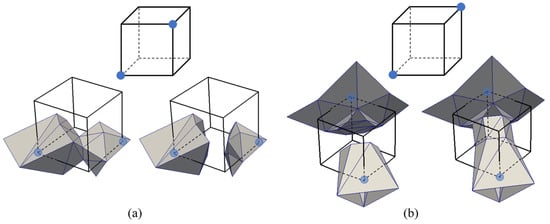
Figure 7.
Examples of ambiguous cubes. (a) Face ambiguity and the two possible surfaces. (b) Interior ambiguity and the two possible surfaces.
To determine ambiguity, we note that each ambiguous cube (Cases 3, 6, 7, 10, 12, and 13), with the exception of Case 4, shows at least one instance of face ambiguity. One face of the cube consisting of four points can have a total of 24 and 44 permutations for single- and multi-material situations, respectively. After taking symmetry and rotation into account, the number of permutations for a single face exhibiting face ambiguity can be reduced to 1 and 2 for single- and multi-material situations, respectively, as shown in Figure 8 (top row).
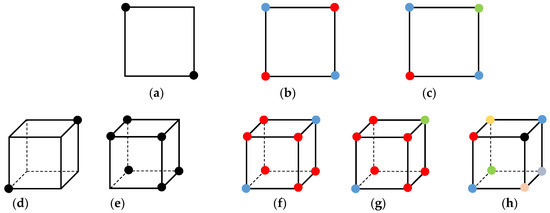
Figure 8.
Identifying ambiguity for multi-material domains. (Top row) Face ambiguity: (a) one possible configuration for single-material contouring, (b,c) two possible configurations for multi-material contouring. (Bottom row) Interior ambiguity: (d,e) two possible configurations for single-material contouring, (f–h) three possible configurations for multi-material contouring.
The situation is slightly more complex for the Case 4 ambiguity. In the single-material case, standard DC produces a non-manifold vertex when (1) only two diagonally opposite corners of the cube are inside the volume and the remaining corners are outside the volume, as shown in Figure 8d, or (2) when only two diagonally opposite corners are outside the volume and the remaining corners are inside the volume, as shown in Figure 8e. This concept holds in the multi-material case involving two materials, three materials, or more than three materials in the most extreme circumstance, as shown in Figure 8f–h. In the proposed multi-material and 2-manifold dual contouring method, a cube is identified as either ambiguous or unambiguous by determining face or interior ambiguity. The exact nature of the ambiguity (i.e., Case 3, Case 4, Case 10, or Case 12) is not necessary. This allows the proposed method to be extremely generalized in its approach.
2.2.4. Tetrahedral Decomposition of Ambiguous Cubes
Once grid cubes have been classified into ambiguous and unambiguous cubes, the next stage is to compute the minimizers for each cube. In standard DC, one minimizer is computed for each cube. This single minimizer in ambiguous cubes is insufficient to adequately represent the different topologies that are possible in ambiguous cubes. Hence, when used in conjunction with the minimizers of neighboring cubes to generate surfaces, non-manifold edges and vertices appear in the resulting surface mesh.
Volume smoothing is one method that can be used to reduce the chances of generating non-manifold edges and vertices. However, such approaches do not address the underlying issue of what to do when ambiguous cubes are inevitably encountered. Since the presence of a single minimizer in ambiguous cubes is the main reason for the creation of non-manifold elements, the obvious solution is to introduce multiple minimizers into ambiguous cubes. In [59], based on the intersections between the isosurface and the cube, multiple minimizers were introduced into the cube and new polygons were created by reconnecting the vertices of the mesh to the newly inserted minimizers.
Sohn [60] shows that a cube can be decomposed into a number of tetrahedrons while preserving the topology. Our proposed method decomposes an ambiguous cube into a maximum of twelve tetrahedral cells in the same manner as [22]. The center of the cube acts as a common point for all tetrahedrons. The basic rules for creating the diagonal are as follows:
- If the two diagonally opposite corners are contiguous with each other through the interior of the volume, create a face diagonal between the two corners.
- If the two diagonally opposite corners are inside the volume but not contiguous with each other through the interior, create a face diagonal using the other two corners.
- For all other cases, any appropriate face diagonal can be used.
This rule also allows two adjacently placed ambiguous cubes that share a face to have consistent face diagonals. The consistency of the diagonal of shared faces between two ambiguous cubes is particularly important during polygon generation. Figure 9 Right shows an example of two ambiguous cubes with a shared face (purple). The red and blue dashed lines represent two tetrahedrons for the red and blue cubes, respectively, and the shared face serves as the base for all four tetrahedrons. Notice that the face diagonal (purple dashed line) is the same for both cubes.
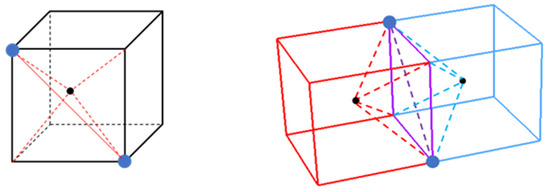
Figure 9.
An illustration of the decomposition of ambiguous cubes. (Left) A partially decomposed ambiguous cube with two tetrahedra. The front face is the base of two tetrahedra (red lines) and the center of the cube is a common point for all tetrahedra. (Right) Two adjacently placed ambiguous cubes sharing a face (purple square). The face diagonal (purple dashed line) across the shared face of the cubes is consistent between both cubes.
An interior edge is an edge of a tetrahedron that is made up of a corner of the parent cube and the center of the cube. A sign-change edge is an edge of a tetrahedron or a grid cube whose end points have different material indices. A valid tetrahedron is one in which at least one edge is a sign-change edge. Although an ambiguous cube is decomposed into a total of twelve tetrahedrons, our proposed strategy makes use of only valid tetrahedra for polygon generation. For each valid tetrahedron, the centroid is computed and used as its minimizer.
As mentioned above, in the case of single-material surfacing, a cube can have 31 unique configurations when face and interior ambiguity are taken into consideration. The number of configurations drastically increases when dealing with multi-material surfacing. Each cube configuration is representative of a different surface and/or topology. Establishing polygon generation rules for each configuration is difficult at best for single-material surfacing and near impossible when dealing with multi-material surfacing. In order to be effective and feasible, polygon generation rules need to be generalized enough to handle unambiguous cubes, as well as any ambiguous case, for both single- and multi-material surfacing. The next section describes the set of polygon generation rules that are applied to unambiguous cubes and any ambiguous cubes that have been subdivided into a number of tetrahedral cells.
2.2.5. Polygon Generation
In standard DC, polygon generation is based on analyzing minimal edges. For each minimal edge, a polygon is created using the minimizers of all cubes that contain the minimal edge. For DC using non-adaptive octrees, a minimal edge will be contained by 4 cubes, and the cubes’ four minimizers are used to create a quad or two triangles. The proposed method for generating multi-material surfaces also relies on analyzing the minimal edges contained by four cubes. Additionally, since ambiguous cubes will contain a number of interior edges due to their decomposition into a set of tetrahedral cells, it is also necessary to analyze these interior edges and face diagonals. The proposed method for generating multi-material and 2-manifold surface meshes is only applicable to non-adaptive octrees. Minimal edges will always be shared by four cubes. If all four cubes are unambiguous, we create two triangles using the minimizers of the four cubes. On the other hand, if any of the four cubes exhibit ambiguity, the following rules are applied: (1) the minimal edge rule, (2) the face diagonal rule, and (3) the interior edge rule.
Minimal Edge Rule: Create an n-sided polygon, also known as an n-gon, using the minimizers of all the unambiguous cubes and tetrahedral cells that contain the minimal edge.
This rule follows the same concept as standard DC, that is, if the minimal edge is a sign-change edge, there must be a surface intersecting the minimal edge. The n-sided polygon is generated by linking together the minimizers of unambiguous grid cubes and tetrahedral cells that share the minimal edge and then triangulating the n-gon. Each ambiguous grid cube will have exactly two valid tetrahedral cells sharing the minimal edge. It should be noted that the resulting n-gon does not necessarily have to be convex. It is also worth mentioning that extra care should be taken when using triangulation algorithms such as regular or conventional Delaunay tessellation, which have a tendency to generate convex polygons. In our implementation, we utilized CGAL’s [61] 2D triangulation library. The vertices were first projected onto the appropriate XY, YZ, or XZ plane. Then, an n-sided polygon (which may or may not be convex) was created and used with Constrained Delaunay Triangulation (CDT) to produce a triangulated surface. CDT uses the n-sided polygon as a template to determine if triangles are contained inside or outside the n-gon.
Figure 10 illustrates the minimal edge rule. In this figure, the small black square represents one end of the minimal edge that is shared by the four grid cubes. There are two ambiguous grid cubes (green) and two unambiguous grid cubes (grey). The blue and red squares represent the vertices of the tetrahedral cells. The blue and red lines represent the four tetrahedral cells of the two ambiguous grid cubes. All four tetrahedral cells share the minimal edge. In Figure 10, a 6-sided polygon is created by first linking together the minimizers of the two unambiguous grid cubes, as well as the minimizers of the four tetrahedral cells sharing the minimal edge, and then triangulating the polygon.
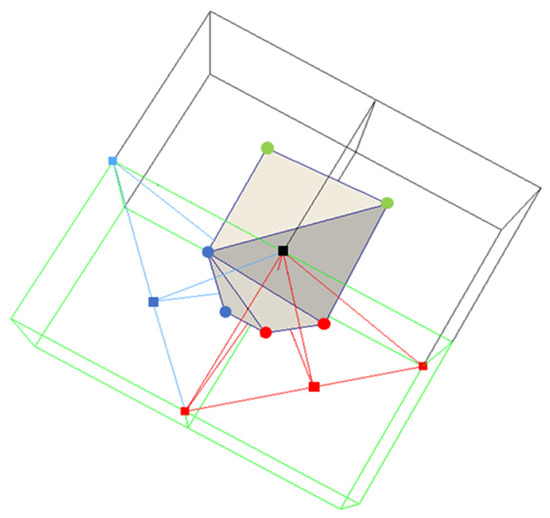
Figure 10.
An illustration of the minimal edge rule. Triangulation using six minimizers, which is an example of a forced convex triangulation. The green cubes represent ambiguous cubes and the gray cubes are unambiguous cubes. The green dots represent the single minimizers of the unambiguous cubes and the red/blue dots represent the minimizers of the tetrahedral cells of the ambiguous cubes. The red/blue squares represent the center/corners of the ambiguous cubes.
Face Diagonal Rule: For any ambiguous cube sharing a face with another cube, if the face diagonal of the shared face is a sign-change edge, create a polygon using all the minimizers surrounding the face diagonal.
Ambiguous grid cubes can share a face with another ambiguous or unambiguous grid cube. In the case of two ambiguous cubes sharing a face, if the face diagonal is a sign-change edge, there are four valid tetrahedral cells that share the face diagonal. The four minimizers are used to generate a quadrangle, which equates to two triangles. In the case of an ambiguous cube sharing a face with an unambiguous cube, there are two valid tetrahedral cells whose bases comprise the shared face. The minimizers of these two tetrahedral cells, as well as the minimizer of the ambiguous cube, are used to generate a triangle.
Figure 11 illustrates the application of this rule. In Figure 11a, the two green cubes are the ambiguous cubes and the red and blue lines represent the four tetrahedral cells sharing the face diagonal. The face diagonal is a sign-change edge. The black cubes are unambiguous. The purple square represents the shared face between the two ambiguous cubes. The red and blue round points represent the four minimizers used to generate the two yellow triangles. In Figure 11b, the green cube is the sole ambiguous cube and the red lines represent the two tetrahedral cells making up the shared face with a neighboring unambiguous cube (purple square). The two round red points are the minimizers of the two tetrahedral cells and the round blue point is the minimizer of the unambiguous cube in question. The three minimizers are used to generate a triangle (yellow).
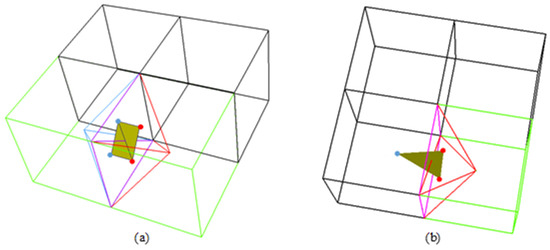
Figure 11.
An illustration of the face diagonal rule. The purple square is the shared face between two cubes. Ambiguous cubes are green and unambiguous cubes are black. (a) The case of two ambiguous cubes sharing a face. (b) The case of an ambiguous cube and an unambiguous cube sharing a face.
Interior Edge Rule: For a sign-change interior edge of a tetrahedral cell, which has one end point that is also shared with the minimal edge, create a polygon using the minimizers of all the tetrahedral cells of the parent cube that share the sign-change interior edge.
An interior edge can be shared by multiple tetrahedral cells. If the interior edge is a sign-change edge, it follows that there is a surface intersecting the interior edge and this surface can be constructed using the minimizers of the surrounding tetrahedral cells. Figure 12 depicts the interior edge rule. In this figure, there is one ambiguous grid cube (green) and three unambiguous grid cubes (black). The center of the ambiguous cube (yellow square) is a shared vertex for all the tetrahedral cells. The small red squares are the vertices of the tetrahedral cells. The round white and black points make up the minimal edge. The interior edge with a sign-change edge in this figure is made of the round white point and the center of the ambiguous cube. The red lines represent four tetrahedral cells that share the sign-change interior edge. The round blue points are the minimizers of the tetrahedral cells. A polygon is created using these four minimizers.
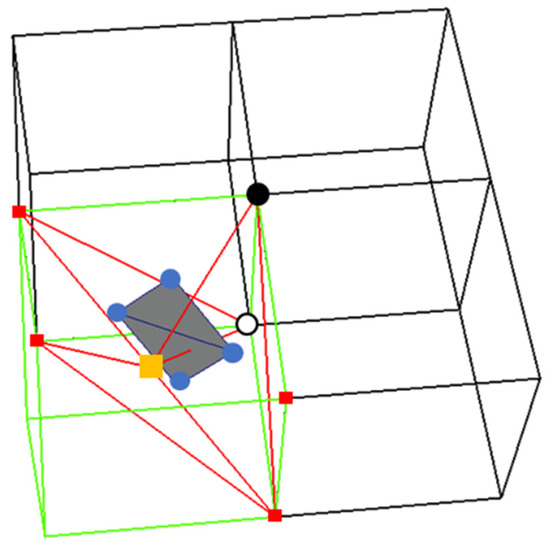
Figure 12.
An illustration of the interior edge rule. The round white and black points represent the minimal edge. The red squares depict the vertices of the four tetrahedral cells incident on the minimal edge: the vertices of the minimal edge are also vertices of two tetrahedral cells. The round green point and the orange square make up the sign-change interior edge. The red lines represent the four tetrahedral cells that share the sign-change edge. The round blue points are the minimizers of the tetrahedral cells that are used to create a polygon.
2.2.6. Verifying Two-Manifoldness and Quality of Multi-Material Meshes
Multi-material meshes are inherently non-manifold due to their multi-material nature. Specifically, the junctions where two or more materials meet will contain non-manifold edges and/or vertices. The proposed algorithm is capable of generating multi-material surface meshes where each material’s sub-mesh is a watertight and 2-manifold mesh. In order to verify this, the whole multi-material mesh is split into each material’s sub-meshes, as shown in Figure 4 and Figure 5. For each sub-mesh, the open source software MeshLab [62] is used rather than relying on visual inspection to detect the presence of non-manifold edges and vertices and boundary edges. MeshLab is an open source mesh processing tool that makes extensive use of the VCG (Visualization and Computer Graphics) library (http://vcg.isti.cnr.it/vcglib; accessed on 2 March 2023). Our experiments show that even though an entire multi-material mesh can have non-manifold elements, an individual material’s sub-mesh is always watertight and 2-manifold. A commonly used metric to describe the quality of triangles in surface meshes is the radius ratio described in [63], as shown in Equation (3).
In Equation (3), describes the radius of the circle inscribed in the triangle and is the radius of the circumscribing circle. A value close to 1 indicates a very good quality triangle (close to an equilateral triangle) and a value near zero indicates a poor-quality triangle (a triangle that is collapsing to an edge). Section 3 demonstrates the application of these techniques to a digital atlas of basal ganglia [64].
2.3. Multi-Material Tetrahedral Mesh Generation
One type of mesh that is commonly used in engineering and biomedical research is tetrahedral mesh. Tetrahedral mesh generation can be classified [65] into the following four categories: (1) octree-based, (2) Delaunay, (3) advancing front, and (4) optimization-based. Among these categories, Delaunay-based techniques are the most frequently used. In many applications, an initial surface mesh, known as a piecewise linear complex (PLC) that coincides with the boundary of the problem domain, is used as an initial starting point for the tetrahedralization process. In such cases, the user has to ensure (either manually or by using mesh-editing software) that the input surface mesh does not contain geometric errors such as holes, slivers, intersecting triangles, or non-manifold elements. Software such as TetGen [66] and the open source library CGAL (Computational Geometry Algorithms Library) [67] are able to generate tetrahedral meshes from an input PLC using Delaunay-based methods.
As mentioned previously, the geometric errors are further compounded when using multi-material surface meshes as the input PLC. Apart from requirements such as 2-manifold, watertight, and intersection-free polygons, there is a further need to ensure that the shared boundary or material interface between two materials remains consistent. The proposed DC algorithm can produce multi-material 2-manifold surface meshes, where the shared boundary or material interface is consistent and each sub-mesh is watertight and 2-manifold. These multi-material meshes can be readily used as the input PLC in the generation of multi-material tetrahedral meshes.
2.4. Deformable Multi-Surface Models
In this section, we present an application for the proposed multi-material and 2-manifold surface mesh. Specifically, we use the multi-material triangular surface mesh to initialize a multi-material 2-simplex mesh. A 2-simplex mesh is a 2-manifold discrete mesh where every vertex is connected to three neighboring vertices. A 2-simplex mesh undergoes deformations based on geometry-based internal forces and image-based external forces. The dynamics of each vertex can be modeled using the Newtonian law of motion shown in Equation (4).
where is the mass and is the position of a vertex of the mesh. represents the sum of all internal forces, represents the aggregate of all the external forces acting on and represents a damping coefficient.
The internal force can be a linear sum of any number of geometry-based forces. Gilles [6] defined several internal forces for a 2-simplex mesh based on Laplacian smoothing, shape memory, and global volume preservation, as follows, respectively:
Equation (5) summarizes the internal force resulting from the difference between an idealized position based on internal shape-driven considerations and the current vertex position (subscript i is dropped for readability). Equation (6) represents the barycentric weighted Laplacian smoothing-based internal force, where , , and represent the surfaces associated with the neighboring vertices , and . The operator represents the averaging around the neighborhood of vertex P. Therefore, represents the average elevation around the neighborhood of P. A reference shape model can be used to represent the prior shape information in the deformation. In Equation (7), , and represent predefined metric parameters. Volume preservation can be used to exploit the fact that biological tissue is incompressible. In Equation (8), represents the target volume, represents the current volume, and represents the surface area of the closed mesh.
In the context of the segmentation of anatomical structures, the main criterion by which an organ or anatomical structure is identified without human assistance is through the use of image gradients that delineate the boundaries of the target structure. For the 2-simplex discrete deformable mesh, external forces are derived from maximal image gradients. The idea is to derive a force function based on the gradient values around the neighborhood of a vertex’s position. The neighborhood of a vertex’s position can be defined as a fixed space along the bidirectional surface normal of the vertex.
To compute an external force, this maps to a force that nudges the vertex of interest toward a desired position that is defined from image information such as a strong gradient.
In this case, we define a vertex , with normal n (defined at that vertex) and a predefined step size s, and the sample points for the image gradient can be defined as:
where j is an integer representing the optimal shifts in the surface normal direction. An interpolation method such as trilinear interpolation can be used to interpolate the values between the voxels of the gradient image intensities. The maximal gradient magnitude at can be obtained using:
where represents the image gradient of the input image T.
In order to achieve model-to-image registration, the goal is to align a source image S to the target T using model deformations. The model is initially aligned to S and its initial vertex positions are given by P0. It is iteratively deformed until each vertex matches the target, where a maximum similarity metric is achieved in the vertex neighborhood :
As mentioned above, the vertex neighborhood is constructed using sampling points with Equation (10) along the direction of the surface normal n. The weights and determine the relative contributions of the internal and external forces.
Initializing Multi-Material Two-Simplex Meshes
A 2-simplex mesh is the topological dual of a triangular mesh [39]. This geometric duality can be exploited to generate 2-simplex meshes from triangular surface meshes, with the assumption that a triangular mesh is watertight and 2-manifold. Figure 13 shows an illustration of the duality.
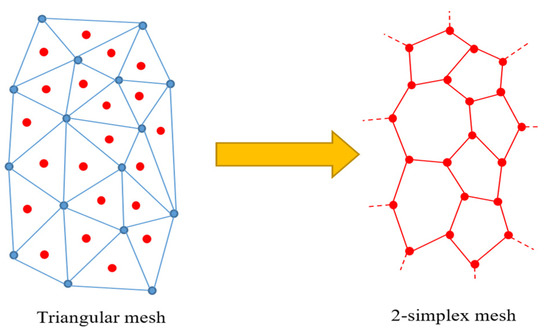
Figure 13.
Converting a triangular mesh into a simplex mesh using duality.
A closed 2-simplex mesh is a watertight 2-manifold mesh with no gaps and/or boundary edges. On the other hand, a multi-material 2-simplex (MM2S) mesh will contain non-manifold edges and/or vertices. This situation is analogous to the multi-material triangular surface meshes discussed in the previous section. The multi-material and 2-manifold dual contouring methods described in the previous section were used to generate multi-material triangular surface meshes, which can be used to initialize MM2S meshes in the following manner:
- Step 1: Compute the centroids of each triangle of the triangular mesh.
- Step 2: For each material index, perform the following:
- ○
- Step 2.1: For each ith vertex of the triangular mesh,
- ▪
- Step 2.1.1: Locate all the triangles with the current material index that contain the ith vertex;
- ▪
- Step 2.1.2: Use the centroids of these triangles to create one simplex cell.
Once the initial MM2S mesh is generated from the triangular mesh, it can be split into its constituent sub-meshes. Each sub-mesh is a pure 2-simplex mesh where every vertex is connected to exactly three neighboring vertices. Since simplex vertices and cells are being created for each material index, care must be taken to avoid duplicate and overlapping cells along the shared boundaries. Figure 14 illustrates the conversion process for a multi-material triangular mesh. Figure 14a shows a synthetic box comprising two materials shown in red and blue, respectively. Figure 14b shows the converted 2-simplex mesh and Figure 14c shows the separated sub-meshes. The green surfaces of the two sub-meshes represent the shared boundary.
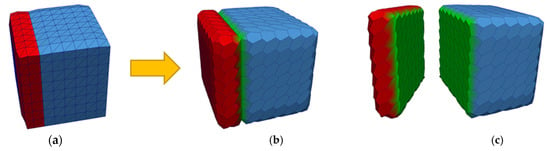
Figure 14.
Converting a multi-material triangular mesh into a multi-material 2-simplex mesh. (a) A multi-material triangular mesh of two materials shown in red and blue with a shared boundary, (b) converted multi-material 2-simplex mesh, (c) split multi-material 2-simplex mesh, where the green surfaces represent the shared boundary.
For every iteration of the deformation, the internal and external forces are computed. The internal forces are based on mesh geometry and the external forces are based on an input image or volume. The input image or volume is not used directly in the deformation process. Instead, an edge-preserving anisotropic diffusion smoothing filter (implemented in VTK’s vtkImageAnisotropicDiffusion3D filter) is applied and then the gradient of the volume is computed. This gradient image is used to determine the external forces for each vertex. Both the internal and external forces are computed independently of each sub-mesh.
Since the forces are computed independently of the sub-meshes, the corresponding vertices making up the shared boundary may not necessarily remain consistent after deformation. Therefore, after each deformation iteration, it is necessary to ensure that all corresponding vertices of the sub-meshes making up the shared boundary are aligned and consistent. This is done by averaging the positions of each corresponding shared boundary vertex and then updating the shared boundary vertices in the MM2S mesh, as well as the sub-meshes, with these newly computed vertex positions. Figure 15 shows a flowchart of the deformation process.
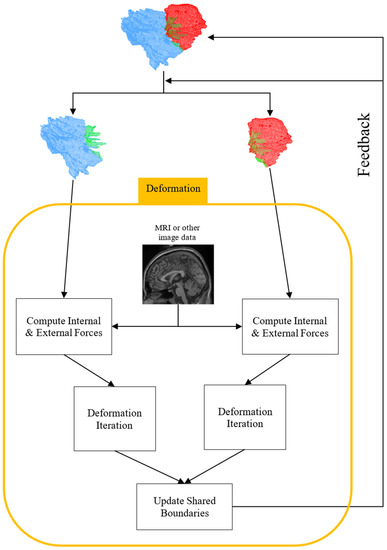
Figure 15.
A flowchart of the multi-material 2-simplex deformation process.
3. Results
3.1. Multi-Material Surface Meshing
Figure 4 and Figure 5 show two examples of multi-material and two-manifold surface meshes generated using the proposed method. The proposed method has also been applied to a digital atlas [64] of the basal ganglia and thalamus to produce multi-material surface meshes of anatomical structures. The atlas is in MINC 2.0 format (Medical Imaging NetCDF) and contains a total of 92 labeled structures. The atlas consists of 334 × 334 × 334 voxels with a step size of 0.3 mm.
A multi-material mesh of five anatomical structures in close proximity was generated using the proposed method. Figure 16 shows a multi-material mesh of the striatum (purple), interior capsule (yellow), globus pallidus (green), globus pallidus external (red), and globus pallidus internal (blue). The upper figure shows both (left and right) parts of the mesh and the lower figure shows a close-up of the right side of the mesh. Typically, the striatum and internal capsule almost completely surround the globus pallidus so the striatum and internal capsule are rendered transparent in this figure. The white lines denote the non-manifold edges along the material interfaces. For the sake of simplicity, the shared boundaries between materials have not been differentiated in Figure 16, even though they do exist. The shared boundaries are shown in Figure 17.
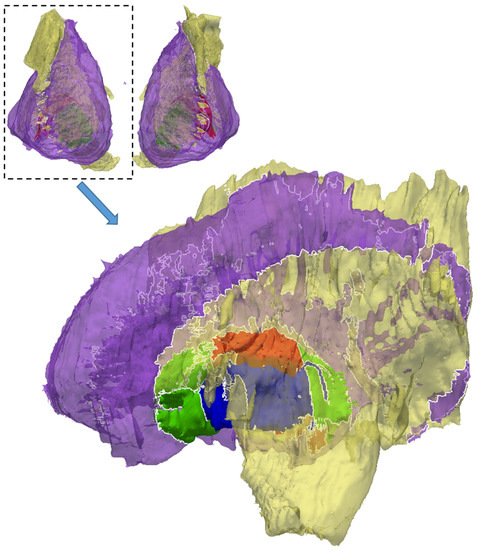
Figure 16.
A multi-material representation of the striatum (purple), internal capsule (yellow), globus pallidus (green), globus pallidus external (red), and globus pallidus internal (blue). The striatum and internal capsule are rendered transparent. The black lines represent the non-manifold edges where two materials meet. Each structure is represented by a single color. The shared boundaries are not depicted here.
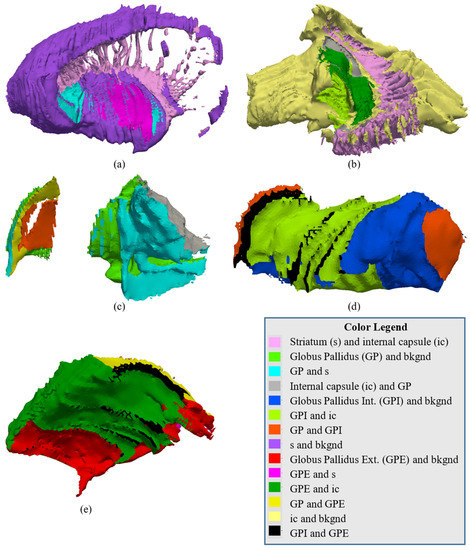
Figure 17.
An illustration of the complexity of the shared boundaries between the (a) striatum, (b) internal capsule, (c) globus pallidus, (d) globus pallidus internal, and (e) globus pallidus external. The different colors represent the parts of the mesh that are shared between the structures.
Figure 18 shows a cross-section of the multi-material mesh in Figure 16 and Figure 17. Table 1 shows the quality of the triangles of the meshes. The overall quality of the triangles of the meshes is roughly 0.81 on average and the worst value is 0.11. The poor-quality triangles of the mesh are a result of the implementation of the minimal edge rule. In the current implementation of the surface meshing method, constrained Delaunay triangulations are used, which may not always result in high-quality triangulations.
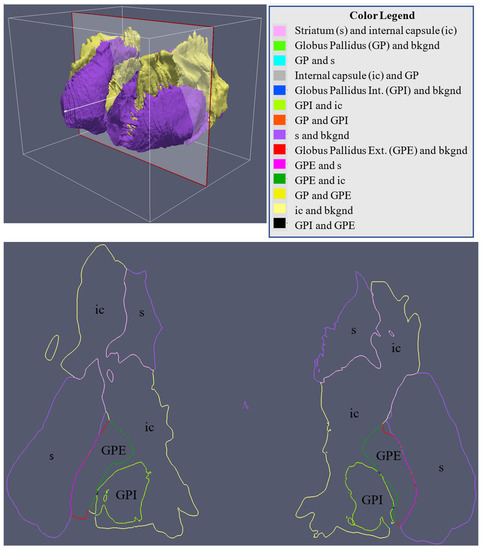
Figure 18.
A coronal slice of the multi-material mesh of the striatum (s), internal capsule (ic), globus pallidus (GP), globus pallidus internal (GPI), and globus pallidus external (GPE). The different colors represent the different shared boundaries between the two structures.

Table 1.
Mesh quality report for the striatum, internal capsule, and globus pallidus group.
A multi-material surface mesh of the thalamus consisting of 34 separate labels is shown in Figure 19. In this figure, the different colors represent the different parts of the thalamus and the white lines represent the non-manifold edge of the material interfaces. Figure 20 shows a cross-section of the mesh of the thalamus with the major regions labeled. Table 2 shows the quality of the triangles for all the components of the thalamus. The average radius ratio for this mesh is approximately 0.81 and the average worst value is 0.12.
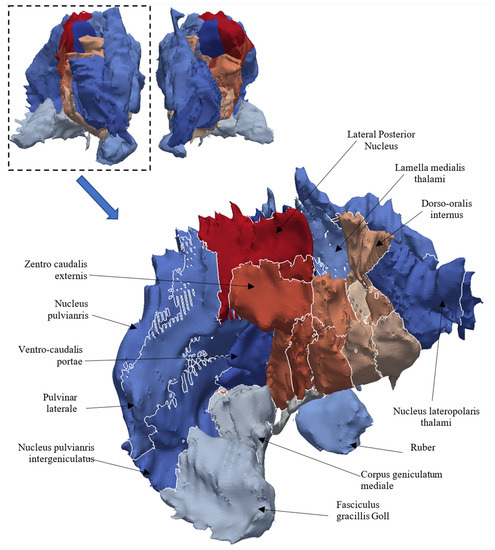
Figure 19.
A multi-material representation of the thalamus.
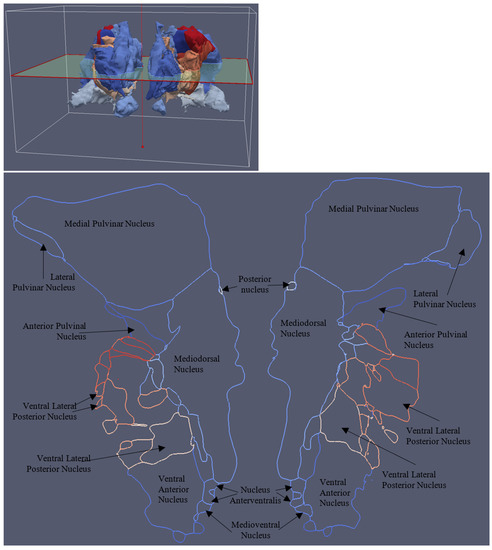
Figure 20.
A cross-section slice of the multi-material mesh of the thalamus. The different colors represent the different constituent components of the thalamus.

Table 2.
Mesh quality for the components of the thalamus.
3.2. Multi-Material Tetrahedral Mesh Generation
Figure 21 shows an example of a multi-material tetrahedral mesh. Figure 21a shows a multi-material surface mesh of the subthalamic nucleus and substantia nigra that was generated using the proposed surface meshing algorithm and was used in TetGen [66] to generate a multi-material tetrahedral mesh. Figure 21b shows a cutout of the generated multi-material tetrahedral mesh, with the internal tetrahedra shown in purple. Figure 21c and Figure 21d show cutouts of the tetrahedral meshes in Figure 16 and Figure 19, respectively. In the three cases, the multi-material surface mesh generated using the proposed surface meshing algorithm was used as the input PLC for TetGen.
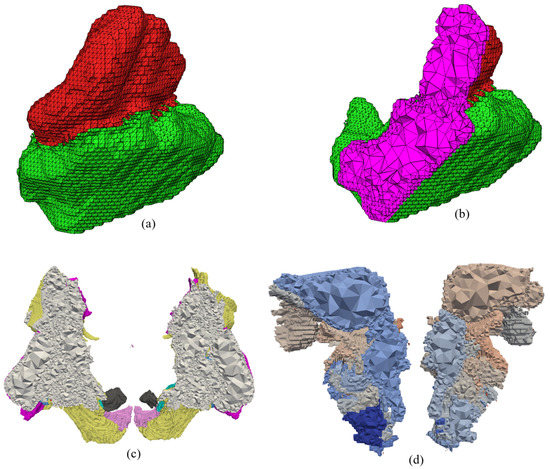
Figure 21.
An example of a multi-material tetrahedral mesh. (Top row) (a) The multi-material 2-manifold surface mesh of the subthalamic nucleus (red) and substantia nigra (green), (b) cutout of tetrahedral mesh of the subthalamic nucleus and substantia nigra, (c) cutout of the basal ganglia mesh in Figure 16, (d) cutout of the tetrahedral mesh in Figure 19.
3.3. Deformable Multi-Surface Models
The multi-material two-simplex deformable system was used on realistic data to achieve meaningful segmentation of anatomical structures. The subthalamic nucleus (STN) and the substantia nigra (SN) are two deep-brain structures that are difficult to detect and segment from MRI. T2-weighted MR data were used. O’Gorman [68] studied the visibility of the STN and GP internal segments using eight different MR protocols and concluded that the different iron levels present in the basal ganglia structures can affect the contrast-to-noise ratio.
The MR data used in this section are freely available from Neuroimaging Informatics Tools and Resources Clearinghouse (https://www.nitrc.org/projects/deepbrain7t; accessed on 2 March 2023) and were produced as part of the research in [69]. In [69], T1- and T2-weighted MR images of 12 healthy control subjects were acquired using a 7T MR scanner and an unbiased average template with T1w and T2w contrast was generated using groupwise registration. Both images had dimensions of 267 × 367 × 260 voxels and 0.6 mm isotropic spacing. A labeled volume was also provided (and referred to as the Wang atlas) that contained segmentations of the left and right globus pallidus, mammillary body, red nucleus, substantia nigra, and subthalamic nucleus. This labeled volume, which was recently made public, serves as a ground truth for validating our multi-surface atlas-to-image registration approach.
An initial watertight and two-manifold multi-material triangular mesh of the left SN-STN was constructed from Chakravarty’s atlas [64] using the multi-material surface meshing algorithm described in Section 2. This atlas has a step size of 0.3 mm and a triangular mesh generated at this resolution is simply too large (approximately 410 k triangles and 20 k vertices) to be practical. Therefore, the atlas was downsampled to an appropriate size and a much coarser multi-material triangular mesh was generated (2.5 k triangles and 1.2 k vertices). Figure 22a shows a mesh representation of the SN and STN from the Wang atlas and Figure 22b and Figure 22c show the surface mesh and wireframe mesh, respectively, of the SN and STN constructed using Chakravarty’s atlas.
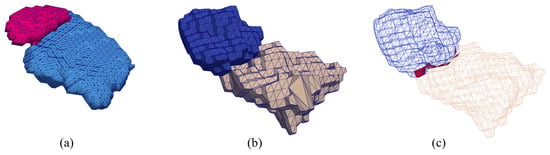
Figure 22.
Meshes of the SN and STN. (a) A mesh representation of the SN (blue) and STN (pink) from the Wang atlas, (b) the multi-material triangular surface mesh of the SN (yellow) and STN (blue), (c) the wireframe representation of the mesh, where the red part represents the shared boundary.
For the deformation process, the T2-weighted MR image was used because the SN and STN are more visible than in T1-weighted MR images. The image was anisotropically filtered and then the gradient image was computed. The external forces for the deformation were computed using the gradient image. Laplacian-based internal forces were used to achieve a smooth mesh. Figure 23 shows the deformation of the SN and STN mesh for several iterations. Figure 24 shows the final deformed mesh of the SN and STN at 160 iterations.
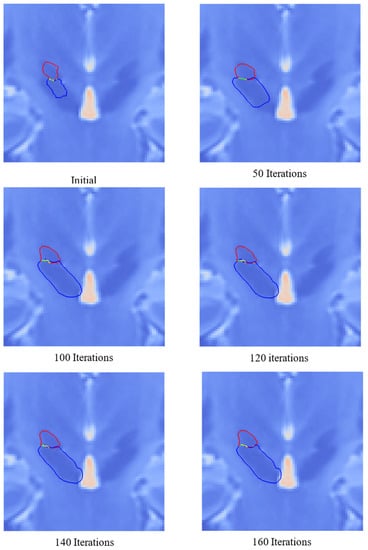
Figure 23.
State of the deformation of the SN and STN. The red outline represents the outline of the STN and the blue outline represents the outline of the SN. The green outline represents the shared boundary.
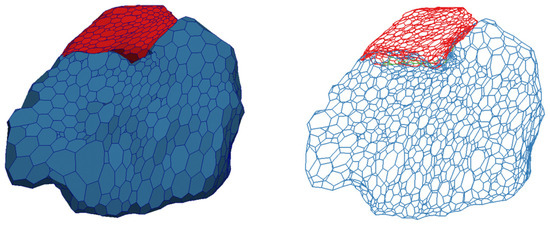
Figure 24.
Final surface mesh (left) and wireframe (right) of the SN (blue) and STN (red).
In another segmentation experiment, the multi-material surface meshing algorithm was used to generate triangular surface meshes of the striatum and combined globus pallidum (globus pallidus, globus pallidus external, and globus pallidus internal segments from the Chakravarty atlas [64]), as shown in Figure 25 (top row). This multi-material triangular mesh was then used to initialize a multi-material two-simplex mesh, as shown in Figure 25 (bottom row).
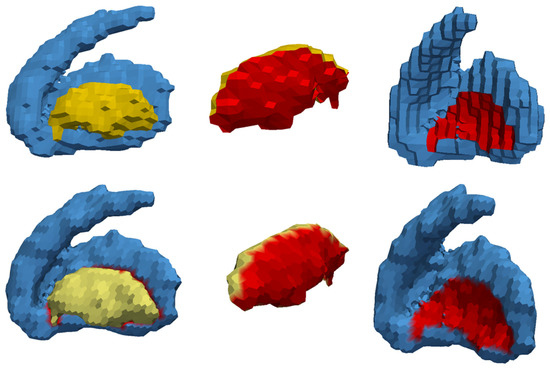
Figure 25.
Simplex mesh generation for the striatum and combined globus pallidum. (Top) The multi-material triangular mesh of the striatum and combined globus pallidus. (Bottom) The multi-material 2-simplex mesh initialized from the triangular mesh. The red part of the mesh depicts the shared boundary between the combined globus pallidus and striatum.
For the deformation, the MR image from [69] was anisotropically smoothed and then the gradient image was computed. The external forces for the deformation were computed using the gradient image. In this experiment, the gradient images for both the T1- and T2-weighted images were computed. The T1-weighted image was used to compute the external forces for the striatum and the T2-weighted image was used to compute the external forces for the combined globus pallidum. Laplacian-based internal forces were used to achieve a smooth mesh.
Figure 26 shows the state of the deformation using both T1- and T2-weighted MRI over several iterations. In this figure, the blue outline represents the outline of the striatum, the yellow outline represents the outline of the GP, and the red outline shows the shared boundary between the GP and striatum. As shown in Figure 26, the deformation achieved a steady state after about 250 iterations. Figure 27 shows the final meshes of the striatum and GP after 250 deformation iterations.
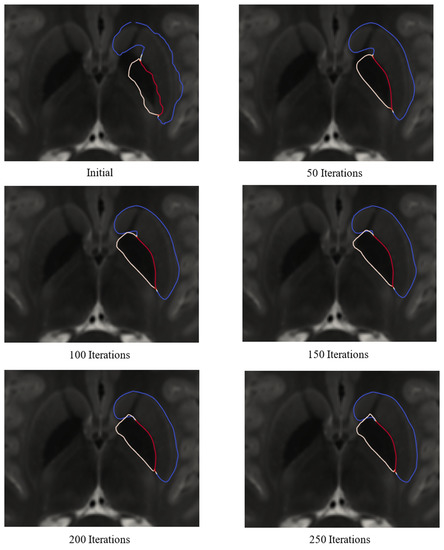
Figure 26.
Cross-sections of the striatum and globus pallidus during deformation using both T1- and T2-weighted MRI. The blue outline represents the striatum, the yellow outline represents the GP, and the red outline represents the shared boundary. The mesh cross-sections are shown on the T2-weighted image.
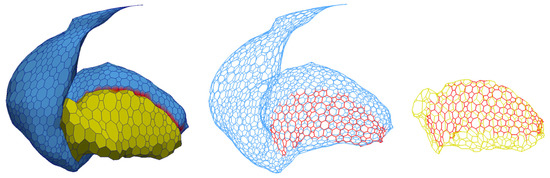
Figure 27.
The final surface mesh (left) of the striatum and combined globus pallidum after deformation using both T1- and T2-weighted MRI. (Middle and right) A wireframe rendering of the striatum and combined globus pallidum.
For validation, surface mesh representations of the SN, STN, and combined GP were created from the labeled volume that is part of the data from [69] and this was used as the ground truth. The open source VTK library implementation of the marching cubes algorithm was used to generate the surface meshes. Unfortunately, a segmentation of the striatum was not available in the data from [69] so a quantitative analysis of the striatum was not possible.
The surface-to-surface distance between the deformed mesh and the ground-truth mesh of the SN and STN was computed using uniform sampling. The metrics calculated were the Hausdorff distance (HD), mean absolute distance (MAD), mean square distance (MSD), and Dice’s coefficient (DC), as reported in Table 3. The Hausdorff distance is the largest error between the deformed mesh and its corresponding ground-truth mesh. Dice’s coefficient measures the amount of similarity/overlap between the deformed mesh and the ground-truth mesh. The mean square distance reports the average squared difference between the sampled points on the deformed mesh and the ground-truth mesh, and the mean absolute distance reports the mean of the absolute difference between the sampled points of the deformed mesh and the ground-truth mesh.

Table 3.
Segmentation results for deformation using the multi-material 2-simplex mesh framework.
Figure 28 shows the final deformed meshes of the SN, STN, and combined GP. The color scheme is as follows: for the deformed meshes, red indicates over-segmentation, blue represents under-segmentation, and green indicates segmentation accurate to within 15% of each extremum (roughly 0.3 mm) with respect to the ground truth. For the deformation of the SN and STN, the maximum over-segmentation is shown in Figure 28. The highest over-segmentation errors for the STN and SN were approximately 1.55 mm and 1.97 mm, respectively. The highest under-segmentation errors for the STN and SN were −0.898 mm and −1.63 mm, respectively. For the combined GP, the maximum over-segmentation was approximately 2.43 mm and the maximum under-segmentation was −2.19.
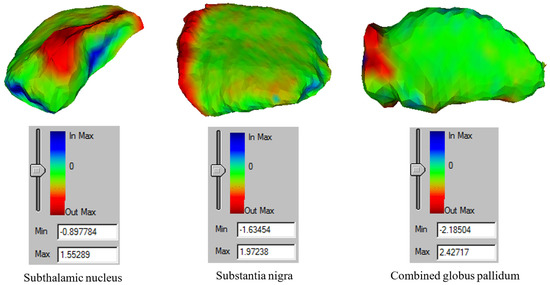
Figure 28.
A visualization of the mesh errors. (Left) deformed mesh of the subthalamic nucleus, (middle) deformed mesh of the substantia nigra, and (right) deformed mesh of the combined globus pallidum.
Table 3 shows the HD, MSD, MAD, and DC values for the deformed STN, SN, and combined GP. The MSD and MAD values of the SN and STN are larger because along the main body of both structures, the segmentation was fairly accurate (as indicated in green in Figure 28), with over and/or under-segmentation occurring at the lateral ends of both structures, coinciding with lower gradient values. The DC values show that there was approximately 77% and 80% similarity, respectively, for the STN and SN with their corresponding ground-truth meshes. The DC value for the combined GP was considerably higher at approximately 93%. This is because the contrast of the GP was more discernable with respect to the surrounding tissue in the T2-weighted image. The HDs for the STN, SN, and GP were 2.11 mm, 2.55 mm, and 2.43 mm, respectively.
4. Discussion
We present a modified dual-contouring (DC) method that can produce surface meshes that are (1) watertight and two-manifold, and (2) multi-material, where each sub-mesh is completely watertight and two-manifold and the material interfaces are consistent. Ambiguous cubes are divided into regular tetrahedral cells and polygons are generated around the sign-change edges of the tetrahedrons or parent cubes. The polygon generation rules are simple, generalizable, and can be applied to any combination of cubes and/or tetrahedrons.
The marching cubes (MC) [7] algorithm is considered the gold standard for meshing. However, as explained in [8], the MC algorithm is not able to reproduce sharp features due to the fact that vertices are produced along the edges of the grid. The DC algorithm in [8] is able to reproduce sharp features by using Hermite data and project the minimizer inside the grid cube but it cannot prevent non-manifold elements in the mesh. The proposed method is capable of reproducing sharp features and preventing the generation of non-manifold elements.
A method for dealing with topology ambiguity in dual contouring was presented by Zhang and Qian in [59]. This approach relied on first generating a base mesh using the standard DC method and then analyzing ambiguous cubes. Depending on a cube’s ambiguity and intersections between the cube and the isosurface, multiple minimizers are introduced into the cube. The final step consists of remeshing using the new minimizers. Although this method can produce topologically correct surface meshes, it relies on complex remeshing rules for each ambiguous cube. These rules may be further compounded by the presence of adjacent ambiguous cubes with their own additional minimizers. Our proposed method is capable of producing topologically correct surface meshes while relying on a consistent rule for inserting additional minimizers into ambiguous cubes and having a single set of polygon generation rules that are applicable to any combination of ambiguous cubes and tetrahedrons. Furthermore, the proposed method does not need to produce an initial base mesh.
The method proposed by Meyer et al. [24] uses a variation of dynamic particle systems and a novel, differentiable representation of material junctions in order to sample corners, edges, and surfaces of material intersections. Delaunay-based meshing algorithms are used to produce high-quality watertight meshes. Although the surface mesh quality (radius ratio) in [24] is reported to be greater than 0.9 on average and a minimum of 0.3, the total execution time is reported to be several hours. In contrast, the multi-material and two-manifold DC method presented here produces surface meshes with an average radius ratio of about 0.8 and a minimum of slightly over 0.1 but the total execution time does not exceed 1 h (approximately 26.5 min for Figure 16 and approximately 11.3 min for Figure 19).
The proposed method exhibits some of the same limitations as the single-material two-manifold DC method [25], namely that the mesh has a staircase-like effect. The cause of the staircase-like effects is the centroids of tetrahedral cells being used as minimizers. Specifically, these minimizers are static and are not able to move around within their respective tetrahedral cells in the same way that minimizers of unambiguous cubes can. This further exacerbates the staircase-like effects exhibited in the surface meshes. A mechanism for adjusting the positions of these minimizers based on the corner values of the tetrahedral cells may result in smoother meshes. This limitation can be somewhat mitigated through the careful use of a post-processing smoothing filter. The current implementation of the proposed DC algorithm only works on non-adaptive octrees. By incorporating an adaptive octree, the standard DC algorithm is more flexible in terms of creating and producing triangles of differing sizes (larger triangles for flat surfaces). However, the current implementation of the proposed multi-material and two-manifold DC algorithm assumes that all grid cubes are the same size (lowest level of the octree) and that each minimal edge shares four cubes. Incorporating an adaptive octree may prove difficult in the sense that new cube decomposition methods and polygon generation methods need to be formulated.
Given the emergence of deep neural networks in image segmentation, medical and otherwise, the question arises of how multi-material meshing and DNNs could co-exist or potentiate each other. The senior author of this paper has recently published a hybrid method that leverages single-surface extraction-mediated ligamentoskeletal meshing of the spine, where the conspicuous vertebrae are used to anchor the transformation of deformable multi-surface anatomy that subsumes inconspicuous ligaments, which is based on a digital atlas of the spine that includes these tissues [70]. For future biomechanical studies, this anatomical modeling method would benefit from a means of converting a multi-surface model constructed piecewise to a multi-surface model with shared boundaries, as this paper advocates. It is also worth mentioning that increasingly, DNNs are successful in incorporating local tissue structure into the learning process, as this paper advocates for meshing [71,72].
5. Conclusions
In conclusion, a modified dual contouring method is introduced that is able to produce error-free surface meshes. These meshes are multi-material and two-manifold in the sense that the sub-meshes of the individual materials are watertight and two-manifold, even though the entire mesh can contain non-manifold elements along the material interfaces. The sub-meshes have consistent shared boundaries. Each triangle of the mesh is identified using pairwise material indices. The proposed method is effective in generating geometrically correct and accurate representations of anatomical structures.
A multi-material two-simplex (MM2S) deformable mesh framework is also presented, along with the results using synthetic and realistic data. One limitation of this method is that the initialized MM2S mesh may not, in fact, be very representative of the target structure, especially when using a single atlas to initialize the deformable mesh of a specific subject. Since the initial MM2S mesh plays a significant role in the accuracy of the deformation, it makes sense to incorporate more structural information when generating the initial MM2S mesh. One potential approach is to utilize statistical shape information similar to [52,53,54] and [5,55,73] in generating the initial MM2S mesh so that the resulting mesh would be a generalization of the specific shape.
The MM2S deformation process uses internal forces, which are based on mesh geometry, and external forces, which are based on image gradients. The accuracy of the deformation relies heavily on the external force, and, therefore, it can be said that the deformation process is dependent on image gradients. In the case of clear and crisp gradients, the deformation will likely result in a good approximation of the target structure. On the other hand, if the gradients are not very clear or if there are competing gradients within the search space, the deformation is likely to result in poor segmentation. The use of specialized imaging protocols such as quantitative susceptibility mapping (QSM) [74,75,76] would likely improve the segmentation results. For example, the subthalamic nucleus (STN) is difficult to detect in standard T1- and T2-weighted MRI. Specialized MR acquisition protocols, such as QSM or the multi-contrast, multi-echo protocol of [77], can be used to produce superior segmentation results.
Multi-resolution registration in terms of discrete deformable meshes implies the ability of the deformable mesh to take on several levels of resolutions: coarser levels for algorithmic robustness and finer levels in order to capture the small and fine features of the target. Finer-resolution meshes have a larger number of cells and vertices and thus incur increased processing times. Moreover, if the deformation starts with a very high-resolution mesh, not only will the overall processing time increase but the mesh may also be susceptible to being trapped in false minima. The solution is to start the deformation with a coarse mesh and then after a suitable number of deformation iterations, switch to a higher-resolution mesh that is based on the previous deformed coarse mesh. The coarse mesh will deform at a much faster pace since it has fewer cells and vertices.
Although it is true that convolutional neural networks (CNNs) have had a significant impact on segmentation in the past decade, CNNs generally only segment tissues that are conspicuous in the target image while atlas-based segmentation can provide functional tissue maps anchored by a subset of visible tissues and is inclusive of functionally separate but inconspicuous tissues. This method makes it possible to produce a multi-surface tissue map with shared boundaries, which goes beyond a strictly bottom-up approach such as CNNs.
Finally, this paper represents a more extensively described and validated update of a previous conference paper [78]. We saw fit to flesh out the discussion on multi-material surface acquisition and simplex deformable models in more detail while also alluding to tetrahedral extensions in specific terms and proposing more descriptive validation studies.
Author Contributions
Conceptualization, T.R., S.S. and M.A.A.; methodology, T.R. and M.A.A.; software, T.R. and M.A.A.; validation, T.R., S.S. and M.A.A.; formal analysis, T.R. and M.A.A.; investigation, T.R. and M.A.A.; resources, M.C. and M.A.A.; data curation, T.R., M.C. and M.A.A.; writing—original draft preparation, T.R. and M.A.A.; writing—review and editing, T.R. and M.A.A.; visualization, T.R.; supervision, M.A.A.; project administration, M.A.A.; funding acquisition, M.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Jeffress Memorial Trust.
Data Availability Statement
A copy of the multi-surface atlas is available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richter, E.O.; Hoque, T.; Halliday, W.; Lozano, A.M.; Saint-Cyr, J.A. Determining the position and size of the subthalamic nucleus based on magnetic resonance imaging results in patients with advanced Parkinson disease. J. Neurosurg. 2004, 100, 541–546. [Google Scholar] [CrossRef] [PubMed]
- Hamani, C.; Florence, G.; Heinsen, H.; Plantinga, B.R.; Temel, Y.; Uludag, K.; Alho, E.; Teixeira, M.J.; Amaro, E.; Fonoff, E.T. Subthalamic nucleus deep brain stimulation: Basic concepts and novel perspectives. Eneuro 2017, 4, ENEURO.0140-17.2017. [Google Scholar] [CrossRef] [PubMed]
- Pham, D.L.; Xu, C.; Prince, J.L. Current methods in medical image segmentation. Annu. Rev. Biomed. Eng. 2000, 2, 315–337. [Google Scholar] [CrossRef] [PubMed]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompim, F.; Ghafoorian, M.; van der Laak, J.A.W.M.; van Ginneken, B.; Sánchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef]
- Sultana, S.; Blatt, J.E.; Gilles, B.; Rashid, T.; Audette, M.A. MRI-based Medial Axis Extraction and Boundary Segmentation of Cranial Nerves through Discrete Deformable 3D Contour and Surface Models. IEEE Trans. Med. Imaging 2017, 36, 1711–1721. [Google Scholar] [CrossRef]
- Gilles, B.; Magnenat-Thalmann, N. Musculoskeletal MRI segmentation using multi-resolution simplex meshes with medial representations. Med. Image Anal. 2010, 14, 291–302. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Ju, T.; Losasso, F.; Schaefer, S.; Warren, J. Dual contouring of hermite data. ACM Trans. Graph. (TOG) 2002, 339–346. Available online: https://pdfs.semanticscholar.org/6fb3/c8bd1d6f3d11f86e1863e9dd861ac128e964.pdf (accessed on 23 March 2023). [CrossRef]
- Treece, G.M.; Prager, R.W.; Gee, A.H. Regularised marching tetrahedra: Improved iso-surface extraction. Comput. Graph. 1999, 23, 583–598. [Google Scholar] [CrossRef]
- Szeliski, R.; Tonnesen, D.; Terzopoulos, D. Modeling surfaces of arbitrary topology with dynamic particles. In Computer Vision and Pattern Recognition, Proceedings of the CVPR’93, 1993 IEEE Computer Society Conference, New York, NY, USA, 15–18 June 1993; IEEE: New York, NY, USA, 1993. [Google Scholar]
- de Figueiredo, L.H.; Gomes, J.; Terzopoulos, D.; Velho, L. Physically-based methods for polygonization of implicit surfaces. In Proceedings of the Graphics Interface, Vancouver, BC, Canada, 11–15 May 1992. [Google Scholar]
- Bloomenthal, J.; Ferguson, K. Polygonization of non-manifold implicit surfaces. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995. [Google Scholar]
- Hege, H.-C.; Stalling, D.; Seebass, M.; Zöckler, M. A Generalized Marching Cubes Algorithm Based on Non-Binary; Citeseer: Princeton, NJ, USA, 1997. [Google Scholar]
- Bonnell, K.S.; Duchaineau, M.A.; Schikore, D.R.; Hamann, B.; Joy, K.I. Material interface reconstruction. IEEE Trans. Vis. Comput. Graph. 2003, 9, 500–511. [Google Scholar] [CrossRef]
- Wu, Z.; Sullivan, J.M. Multiple material marching cubes algorithm. Int. J. Numer. Methods Eng. 2003, 58, 189–207. [Google Scholar] [CrossRef]
- Reitinger, B.; Bornik, A.; Beichel, R. Constructing smooth non-manifold meshes of multi-labeled volumetric datasets. In Proceedings of the 13th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision 2005 in Co-Operation with EUROGRAPHICS, Plzen, Czech Republic, 31 January–4 February 2005. [Google Scholar]
- Bertram, M.; Reis, G.; van Lengen, R.H.; Köhn, S.; Hagen, H. Non-manifold Mesh Extraction from Time-varying Segmented Volumes used for Modeling a Human Heart. In Proceedings of the EuroVis 2005, Leeds, UK, 1–3 June 2005; pp. 199–206. [Google Scholar]
- Bischoff, S.; Kobbelt, L. Extracting consistent and manifold interfaces from multi-valued volume data sets. In Bildverarbeitung Für Die Medizin; Springer: Berlin, Germany, 2006; pp. 281–285. [Google Scholar]
- Boissonnat, J.-D.; Oudot, S. Provably good sampling and meshing of surfaces. Graph. Model. 2005, 67, 405–451. [Google Scholar] [CrossRef]
- Oudot, S.; Rineau, L.; Yvinec, M. Meshing volumes bounded by smooth surfaces. In Proceedings of the 14th International Meshing Roundtable, San Diego, CA, USA, 11–14 September 2005; Springer: Berlin, Germany, 2005. [Google Scholar]
- Pons, J.-P.; Ségonne, E.; Boissonnat, J.D.; Rineau, L.; Yvinec, M.; Keriven, R. High-quality consistent meshing of multi-label datasets. In Proceedings of the Biennial International Conference on Information Processing in Medical Imaging, Kerkrade, The Netherlands, 2–6 July 2007; Springer: Berlin, Germany, 2007. [Google Scholar]
- Zhang, Y.; Qian, J. Resolving topology ambiguity for multiple-material domains. Comput. Methods Appl. Mech. Eng. 2012, 247, 166–178. [Google Scholar] [CrossRef]
- Dillard, S.; Bingert, J.; Thoma, D.; Hamann, B. Construction of simplified boundary surfaces from serial-sectioned metal micrographs. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1528–1535. [Google Scholar] [CrossRef]
- Meyer, M.; Whitaker, R.; Kirby, R.M.; Ledergerber, C.; Pfister, H. Particle-based sampling and meshing of surfaces in multimaterial volumes. Vis. Comput. Graph. IEEE Trans. 2008, 14, 1539–1546. [Google Scholar] [CrossRef] [PubMed]
- Rashid, T.; Sultana, S.; Audette, M.A. 2-manifold surface meshing using dual contouring with tetrahedral decomposition. Adv. Eng. Softw. 2016, 102, 83–96. [Google Scholar] [CrossRef]
- Li, B.; Christensen, G.E.; Hoffman, E.A.; McLennan, G.; Reinhardt, J.M. Establishing a normative atlas of the human lung: Intersubject warping and registration of volumetric CT images. Acad. Radiol. 2003, 10, 255–265. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Bland, P.H.; Meyer, C.R. Construction of an abdominal probabilistic atlas and its application in segmentation. Med. Imaging IEEE Trans. 2003, 22, 483–492. [Google Scholar] [CrossRef]
- Sluimer, I.; Prokop, M.; van Ginneken, B. Toward automated segmentation of the pathological lung in CT. Med. Imaging IEEE Trans. 2005, 24, 1025–1038. [Google Scholar] [CrossRef]
- Stancanello, J.; Romanelli, P.; Modugno, N.; Cerveri, P.; Ferrigno, G.; Uggeri, F.; Cantore, G. Atlas-based identification of targets for functional radiosurgery. Med. Phys. 2006, 33, 1603–1611. [Google Scholar] [CrossRef]
- Isgum, I.; Staring, M.; Rutten, A.; Prokop, M.; Viergever, M.A.; van Ginneken, B. Multi-atlas-based segmentation with local decision fusion—Application to cardiac and aortic segmentation in CT scans. Med. Imaging IEEE Trans. 2009, 28, 1000–1010. [Google Scholar] [CrossRef] [PubMed]
- Rohlfing, T.; Russakoff, D.B.; Maurer, C.R., Jr. Performance-based classifier combination in atlas-based image segmentation using expectation-maximization parameter estimation. Med. Imaging IEEE Trans. 2004, 23, 983–994. [Google Scholar] [CrossRef] [PubMed]
- Artaechevarria, X.; Munoz-Barrutia, A.; Ortiz-de-Solorzano, C. Combination strategies in multi-atlas image segmentation: Application to brain MR data. Med. Imaging IEEE Trans. 2009, 28, 1266–1277. [Google Scholar] [CrossRef] [PubMed]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. ACM Siggraph Comput. Graph. 1986, 151–160. [Google Scholar] [CrossRef]
- Terzopoulos, D.; Platt, J.; Barr, A.; Fleischer, K. Elastically deformable models. ACM Siggraph Comput. Graph. 1987, 205–214. [Google Scholar] [CrossRef]
- Meier, U.; López, O.; Monserrat, C.; Juan, M.C.; Alcañiz, M. Real-time deformable models for surgery simulation: A survey. Comput. Methods Programs Biomed. 2005, 77, 183–197. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active shape models-their training and application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Delingette, H. General object reconstruction based on simplex meshes. Int. J. Comput. Vis. 1999, 32, 111–146. [Google Scholar] [CrossRef]
- Delingette, H. Simplex meshes: A general representation for 3D shape reconstruction. In Computer Vision and Pattern Recognition, Proceedings of the CVPR’94, 1994 IEEE Computer Society Conference, Seattle, WS, USA, 16–18 May 1994; IEEE: New York, NY, USA, 1994. [Google Scholar]
- Delingette, H. Modélisation, Déformation et Reconnaissance D’objets Tridimensionnels à L’aide de Maillages Simplexes; Ecole Centrale Paris: Paris, France, 1994. [Google Scholar]
- Montagnat, J.; Delingette, H. Volumetric medical images segmentation using shape constrained deformable models. In CVRMed-MRCAS’97; Springer: Berlin, Germany, 1997. [Google Scholar]
- Gilles, B.; Moccozet, L.; Magnenat-Thalmann, N. Anatomical modelling of the musculoskeletal system from MRI. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2006; Springer: Berlin, Germany, 2006; pp. 289–296. [Google Scholar]
- Schmid, J.; Magnenat-Thalmann, N. MRI bone segmentation using deformable models and shape priors. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2008; Springer: Berlin, Germany, 2008; pp. 119–126. [Google Scholar]
- Schmid, J.; Iglesias Guitián, J.A.; Gobbetti, E.; Magnenat-Thalmann, N. A GPU framework for parallel segmentation of volumetric images using discrete deformable models. Vis. Comput. 2011, 27, 85–95. [Google Scholar] [CrossRef]
- Schmid, J.; Sandholm, A.; Chung, F.; Thalmann, D.; Delingette, H.; Magnenat-Thalmann, N. Musculoskeletal simulation model generation from MRI data sets and motion capture data. In Recent Advances in the 3D Physiological Human; Springer: Berlin, Germany, 2009; pp. 3–19. [Google Scholar]
- Montagnat, J.; Delingette, H. Space and time shape constrained deformable surfaces for 4D medical image segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2000; Springer: Berlin, Germany, 2000. [Google Scholar]
- Montagnat, J.; Delingette, H. 4D deformable models with temporal constraints: Application to 4D cardiac image segmentation. Med. Image Anal. 2005, 9, 87–100. [Google Scholar] [CrossRef] [PubMed]
- Montagnat, J.; Sermesant, M.; Delingette, H.; Malandain, G.; Ayache, N. Anisotropic filtering for model-based segmentation of 4D cylindrical echocardiographic images. Pattern Recognit. Lett. 2003, 24, 815–828. [Google Scholar] [CrossRef]
- Cremers, D.; Schnorr, C.; Weickert, J. Diffusion-snakes: Combining statistical shape knowledge and image information in a variational framework. In Variational and Level Set Methods in Computer Vision, Proceedings of the IEEE Workshop on Variational and Level Set Methods in Computer Vision, Vancouver, BC, Canada, 13 July 2001; IEEE: New York, NY, USA, 2001. [Google Scholar]
- Cremers, D.; Schnörr, C.; Weickert, J.; Schellewald, C. Diffusion–snakes using statistical shape knowledge. In Algebraic Frames for the Perception-Action Cycle; Springer: Berlin, Germany, 2000; pp. 164–174. [Google Scholar]
- Cremers, D.; Tischhäuser, F.; Weickert, J.; Schnörr, C. Diffusion snakes: Introducing statistical shape knowledge into the Mumford-Shah functional. Int. J. Comput. Vis. 2002, 50, 295–313. [Google Scholar] [CrossRef]
- Haq, R.; Aras, R.; Besachio, D.A.; Borgie, R.C.; Audette, M.A. 3D lumbar spine intervertebral disc segmentation and compression simulation from MRI using shape-aware models. Int. J. Comput. Assist. Radiol. Surg. 2015, 10, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Haq, R.; Besachio, D.A.; Borgie, R.C.; Audette, M.A. Using shape-aware models for lumbar spine intervertebral disc segmentation. In Pattern Recognition (ICPR), Proceedings of the 22nd International Conference on Pattern Recognition, Stockholm, Sweden, 24–28 August 2014; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Haq, R.; Cates, J.E.; Besachio, D.A.; Borgie, R.C.; Audette, M.A. Statistical Shape Model Construction of Lumbar Vertebrae and Intervertebral Discs in Segmentation for Discectomy Surgery Simulation. In International Workshop on Computational Methods and Clinical Applications for Spine Imaging; Springer: Berlin, Germany, 2015. [Google Scholar]
- Sultana, S.; Blatt, J.E.; Lee, Y.; Ewend, M.; Cetas, J.; Costa, A.; Audette, M.A. Patient-specific cranial nerve identification using a discrete deformable contour model for skull base neurosurgery planning and simulation. In Workshop on Clinical Image-Based Procedures; Springer: Berlin, Germany, 2015. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations. In Johns Hopkins Series in the Mathematical Sciences; Johns Hopkins University Press: Baltimore, MD, USA, 1989. [Google Scholar]
- Kobbelt, L.P.; Botsch, M.; Schwanecke, U.; Seidel, H.P. Feature sensitive surface extraction from volume data. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; ACM: New York, NY, USA, 2001. [Google Scholar]
- Lindstrom, P. Out-of-core simplification of large polygonal models. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 23–28 July 2000; ACM Press: New York, NY, USA; Addison-Wesley Publishing Co.: Boston, MA, USA, 2000. [Google Scholar]
- Zhang, Y.; Qian, J. Dual Contouring for domains with topology ambiguity. Comput. Methods Appl. Mech. Eng. 2012, 217–220, 34–45. [Google Scholar] [CrossRef]
- Sohn, B.-S. Topology preserving tetrahedral decomposition of trilinear cell. In Computational Science–ICCS 2007; Springer: Berlin, Germany, 2007; pp. 350–357. [Google Scholar]
- CGAL Editorial Board. The CGAL Project, CGAL User and Reference Manual, 4.13 ed.; CGAL Editorial Board: Glasgow, UK, 2018. [Google Scholar]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. Meshlab: An open-source mesh processing tool. In Proceedings of the Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008. [Google Scholar]
- Shewchuk, J. What is a Good Linear Finite Element? Interpolation, Conditioning, Anisotropy, and Quality Measures (Preprint); University of California at Berkeley: Berkeley, CA, USA, 2002. [Google Scholar]
- Chakravarty, M.M.; Bertrand, G.; Hodge, C.P.; Sadikot, A.F.; Collins, D.L. The creation of a brain atlas for image guided neurosurgery using serial histological data. Neuroimage 2006, 30, 359–376. [Google Scholar] [CrossRef]
- Owen, S.J. A survey of unstructured mesh generation technology. IMR 1998, 239, 267. [Google Scholar]
- Si, H. TetGen, a Delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Softw. (TOMS) 2015, 41, 11. [Google Scholar] [CrossRef]
- CGAL Editorial Board. The CGAL Project, CGAL User and Reference Manual, 4.9 ed.; CGAL Editorial Board: Glasgow, UK, 2016. [Google Scholar]
- O’Gorman, R.L.; Shmueli, K.; Ashkan, K.; Samuel, M.; Lythgoe, D.J.; Shahidiani, A.; Wastling, S.J.; Footman, M.; Selway, R.P.; Jarosz, J. Optimal MRI methods for direct stereotactic targeting of the subthalamic nucleus and globus pallidus. Eur. Radiol. 2011, 21, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.T.; Poirier, S.; Guo, T.; Parrent, A.G.; Peters, T.M.; Khan, A.R. Generation and evaluation of an ultra-high-field atlas with applications in DBS planning. In SPIE Medical Imaging; International Society for Optics and Photonics: Bellingham, WS, USA, 2016. [Google Scholar]
- Tapp, A.; Payer, C.; Schmid, J.; Polanco, M.; Kumi, I.; Bawab, S.; Ringleb, S.; St. Remy, C.; Bennett, J.; Kakar, R.S.; et al. Generation of Patient-Specific, Ligamentoskeletal, Finite Element Meshes for Scoliosis Correction Planning. CLIP/DCL/LL-COVID19/PPML@MICCAI 2021; Springer International Publishing: New York, NY, USA, 2021; pp. 13–23. [Google Scholar]
- Zhang, D.; Yao, L.; Chen, K.; Wang, S.; Chang, X.; Liu, Y. Making Sense of Spatio-Temporal Preserving Representations for EEG-Based Human Intention Recognition. IEEE Trans. Cybern. 2020, 50, 3033–3044. [Google Scholar] [CrossRef]
- Luo, M.; Chang, X.; Nie, L.; Yang, Y.; Hauptmann, A.G.; Zheng, Q.Q. An Adaptive Semisupervised Feature Analysis for Video Semantic Recognition. IEEE Trans. Cybern. 2018, 48, 648–660. [Google Scholar] [CrossRef] [PubMed]
- Sultana, S.; Agrawal, P.; Elhabian, S.Y.; Whitaker, R.T.; Rashid, T.; Blatt, J.E.; Cetas, J.S.; Audette, M.A. Towards a Statistical Shape-Aware Deformable Contour Model for Cranial Nerve Identification. In Workshop on Clinical Image-Based Procedures; Springer: Berlin, Germany, 2016. [Google Scholar]
- de Rochefort, L.; Liu, T.; Kressler, B.; Liu, J.; Spincemaille, P.; Lebon, V.; Wu, J.; Wang, Y. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: Validation and application to brain imaging. Magn. Reson. Med. 2010, 63, 194–206. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Eskreis-Winkler, S.; Schweitzer, A.D.; Chen, W.; Kaplitt, M.G.; Tsiouris, A.J.; Wang, Y. I Improved subthalamic nucleus depiction with quantitative susceptibility mapping. Radiology 2013, 269, 216–223. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, T. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magn. Reson. Med. 2015, 73, 82–101. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Beriault, S.; Pike, G.B.; Collins, D.L. Multicontrast multiecho FLASH MRI for targeting the subthalamic nucleus. Magn. Reson. Imaging 2012, 30, 627–640. [Google Scholar] [CrossRef] [PubMed]
- Rashid, T.; Sultana, S.; Fischer, G.S.; Pilitsis, J.; Audette, M.A. Deformable Multi-Material 2-Simplex Surface Mesh for Intraoperative MRI-Ready Surgery Planning and Simulation, with Deep-Brain Stimulation Applications; Cardoso, M.J., Arbel, T., Tavares, J.M.R.S., Aylward, S., Li, S., Boctor, E., Fichtinger, G., Cleary, K., Freeman, K.B., Kohli, L., et al., Eds.; MICCAI BIVPCS/POCUS-2017. LNCS; Springer: Berlin, Germany, 2017; Volume 10549, pp. 94–102. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).