Abstract
Blockchain, with its characteristics of non-tamperability and decentralization, has had a profound impact on various fields of society and has set off a boom in the research and application of blockchain technology. However, blockchain technology faces the problem of data availability attacks during its application, which greatly limits the scope and domain of blockchain applications. One of the most advantageous researches to address this problem is the scalable data availability solution that integrates coding theory design into the Merkle tree promise. Based on this scheme, this paper combines a zero-knowledge accumulator with higher efficiency and security with local repair coding, and proposes a data availability scheme with strong dataset privacy protection. The scheme first encodes the data block information on the blockchain to ensure tamper-proof data, and then uses a zero-knowledge accumulator to store the encoded data block information. Its main purpose is to use zero-knowledge property to protect the accumulation set information stored in the accumulator from being leaked and to ensure that no other information about the accumulation set is revealed during the data transmission. It fundamentally reduces the possibility of attackers generating fraudulent information by imitating block data and further resists data availability attacks.
1. Introduction
Public blockchains, such as Bitcoin [1] and Ether [2], have proven themselves to be secure in practice. One of them, Bitcoin, has gone through more than a decade of secure and real-time operations, but at the cost of deteriorating performance [3]. To address this problem, various consensus layers and off-chain extension methods have been introduced: For example, ACeD, which is a scalable data availability solution that adds coding theory to the Merkle tree commitment to ensure efficiency and tamper resistance [4]; a new fraud prevention and data availability system that reduces the trade-off between on-chain capacity and security by enabling light clients to receive and verify proofs of fraud for invalid blocks from full nodes; and rollup information scattering with provable retrievability, a scheme that uses linear erasure codes and homomorphic vector commitments to design a storage and communication efficient protocol. These schemes address the scalable data availability problem of blockchain from different perspectives through different implementations. This paper aims to improve the blockchain data availability scheme based on the above scheme, and proposes a blockchain data availability scheme with strong dataset privacy protection (DPP-DA).
This paper proposes an intermediate “data availability verification” mechanism between the side blockchain (i.e., smaller blockchains) and the trusted blockchain (i.e., larger blockchains). The side blockchain transmits data to the verification layer, which then transmits verifiable membership witnesses to the trusted blockchain and ensures that the data is available in the side blockchain. N verification nodes work together to verify whether the proposed blocks are searchable (that is, data is available) before submitting it to the trusted blockchain. The key problem is how to share data securely and efficiently among nodes to verify the availability of data.
The solution of this paper is to use local repair codes [5,6,7] so that different nodes receive different encoding blocks. To ensure the integrity and correctness of the encoded blocks, we use zero-knowledge accumulators [8,9] to provide membership proofs for any block, but malicious block producers can hide malicious data, so the probability of reconstructing a block is very small and negligible. Nodes can detect such attacks by broadcasting what they receive and decoding data forwarded by others to confirm that the data is correct.
In order to find a scalable solution to the problem of data availability verification, the method based on local repair code must prevent error encoding attacks while minimizing the cost of storage and communication. The local repair code has low communication complexity and high data repair ability. When the storage node is a hostile node, the storage and download overhead is also low.
While solving the problem of data availability of blockchain, the threat of data privacy in a blockchain system will become a more important research issue. If there is no data privacy protection, the data will be easily leaked, and attackers will be more likely to attack the blockchain by imitating the leaked data, fraudulently cheating the blockchain in the process of data transmission, thus increasing the probability of data availability attacks. Therefore, it is also important to ensure the data privacy protection performance of the blockchain.
The existing various privacy protection mechanisms [10,11,12] and implementation technologies protect blockchain privacy from different aspects. Therefore, in a blockchain system that actually considers privacy protection, multiple technologies are usually integrated to achieve a more comprehensive privacy protection effect [13,14]. For the privacy of user information, the current protection mechanisms still have a lot of room for development, but the existing implementation technologies can not completely solve the threat to privacy protection. There are deficiencies in security, performance, scalability, and so on. Overall, with the continuous development of applications and demands, blockchain technology will gradually tend to improve in terms of privacy protection. Among them, zero-knowledge proof technology [15,16] is effective in solving the data privacy protection of blockchain.
In this paper, based on the zero-knowledge proof technique, we introduce and design a zero-knowledge accumulator based on bilinear mapping [17] to propose a powerful privacy-preserving enhancement scheme for datasets, which also provides hidden guarantees: accumulation values and witnesses do not leak dynamic sets that evolve through element insertion/deletion. At the same time, in addition to the results that can be queried, they do not disclose any information about the set, protecting not only the initially accumulated set, but also all accumulative updates. It also allows membership and non-membership proofs, it can compute membership witnesses, and it supports efficient updating of accumulative values due to insertions and deletions in sets. Membership and non-membership queries for a set can be responded to without revealing any other information about the set. This scheme not only enhances the security assurance of datasets, but also maintains the same efficient performance.
2. Related Work
Blockchain scaling: For a given node network, achieving the highest throughput and lowest latency blockchain that can be operated by consensus has always been a major focus area [18]. The off-chain payment network indirectly increases the transaction throughput of the system by processing large amounts of transaction data offline while using the blockchain to handle exceptions in the off-chain payment process [19]. The consensus mechanism of Bitcoin PoW [20,21] ensures the consistency of the state of the blockchain in the open network (weak consistency), but it does not consider the efficiency of the blockchain. So, Eyal et al. [22] proposed the Bitcon-NG scheme, which aims to increase the number of transaction confirmations in each round of consensus, so as to improve the transaction throughput of the system. The transaction throughput of the system can also be improved by designing a reliable sharding mechanism in an open blockchain network, based on the sharding technique [23,24] borrowed from the traditional distributed database domain. In this paper, starting from another form of blockchain extension, we design and implement an intermediate verification layer that can carry out scalable security interaction between the side blockchain and trusted blockchain.
Data availability: When blockchain nodes cannot access all data, they are vulnerable to data availability attacks [25]. One solution is to use the light node to provide warnings to the full node to notify the malicious block proponents of misbehavior and encode the blockchain data to improve the efficiency of fraud prevention. It was first used in 2D Reed-Solomon codes [26,27] and was then generalized by cryptographic hash accumulators encoding Merkle trees to generate block promises. In this paper, we propose a local repair encoding for validation operations: this encoding, combined with a zero-knowledge accumulator, allows efficient and secure validation of data between verification nodes.
Improving the scalability of the blockchain leads to a vulnerablilty to data availability attacks. That is, the amount of data increases with the improvement of the scalability of the blockchain, so it is very important for nodes to determine whether malicious transactions are hidden in the block when a new block is generated. Therefore, the aim of the scalable data availability scheme is to improve the scalability of the blockchain and at the same time solve the data availability attacks caused by malicious nodes.
Data privacy protection: With the wide application of blockchain technology, blockchain is facing more and more security threats and challenges [28,29]. Blockchain does not rely on central nodes, and transaction records, such as addresses and transaction amounts of participating users, are often made public on the blockchain, making it easy for nodes to verify, store transaction contents, and reach consensus. However, this open and transparent nature of the blockchain will likely lead to user privacy leaks [30,31]. The varying security performance and ability of each blockchain node to combat information leakage increases the risk of data privacy leakage [32]. The flaws of various programs in the blockchain will also expose the blockchain system to huge security risks. In this paper, we design a powerful data privacy protection scheme using zero-knowledge accumulators, which allow the membership and non-membership of sets to be answered without revealing any other information about the set at query time and allow membership and non-membership proofs, can compute membership witness, and support the efficient updating of accumulation values due to insertions and deletions in sets. Accumulators with zero-knowledge can be thought of as “honest submitter” relaxations of zero-knowledge sets.
3. System and Security Models
The system consists of four parts: trusted blockchain (proof of storage block), client (node providing data in side blockchain), zero knowledge accumulator, and intermediate verification layer to ensure data availability. The system structure is shown in Figure 1.
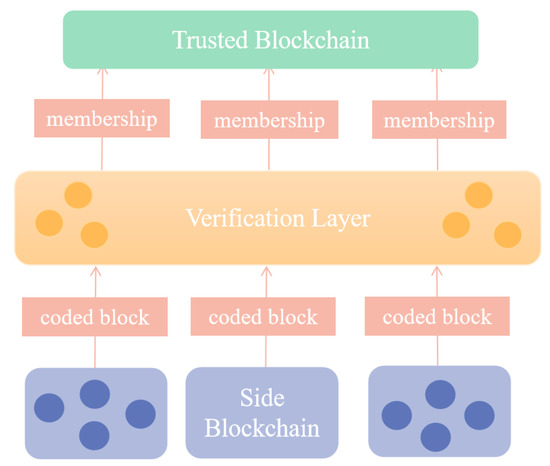
Figure 1.
System structure.
3.1. Network Models and Assumptions
This part contains two types of nodes: verification nodes and client nodes. The specific flow of the intermediate verification layer is shown in Figure 2.
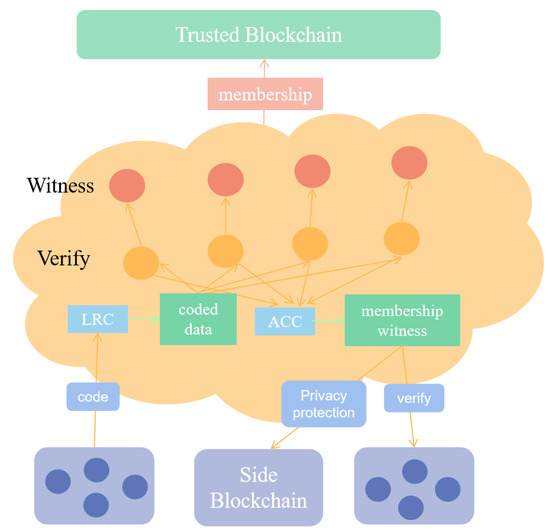
Figure 2.
Intermediate verification layer.
Verification nodes are the main participants in the verification layer. They receive block submitted requests from the client of the side blockchain, including the block header and a set of data blocks. After ensuring that the data is complete and correct, they determine whether the block is available by verification and submit the result to the trusted blockchain.
Zero knowledge accumulator stores the block information on the blockchain to provide privacy for the client, and then the client receives the block and requests the verification layer to submit the block. They update the information periodically based on the membership witness from the trusted blockchain and inquire the verification node about the block witnessed by the non-membership witness as needed.
A key assumption of the verification model is that trusted blockchains have a persistent data sequence and service activeness. In addition, we assume that honest nodes are in the majority in the verification layer. The verification node is connected to all clients. The network is synchronized and the communication is certified and reliable.
3.2. Data Privacy Protection Model
Block data of the blockchain is stored using a zero-knowledge accumulator, where the accumulation values and proofs are not disclosed for dynamic sets inserted and deleted through elements. During data transfer in trusted blockchains and side blockchains, privacy protection is provided for any dynamic changes in data generated by the set in the accumulator, i.e., set membership and non-membership queries can be answered without revealing any other information about the set.
Data storage: Each block is connected to a zero-knowledge accumulator, which compressively stores the encoded block data and forms a large accumulation set in the accumulator.
Dynamic operations: Dynamically and efficiently query, add, delete and other operations to cumulative sets. Accumulated values do not leak for dynamic sets that change through element insertion/deletion.
Set membership and non-membership proofs: Membership and non-membership proofs are generated for sets of data stored in accumulators, and set membership and non-membership proofs can query these proofs without disclosing any other information about these datasets.
3.3. Verification Model
Reducing the storage burden and ensuring data availability through the intermediate verification layer is of vital importance. The verification layer network consists of several zero-knowledge accumulators and blocks to form N verification nodes, which can transmit data with the client and provide data availability services. There are opponents that can damage several authentication nodes. Any node that is not damaged is called an honest node.
In the verification layer, data blocks are the basic data units. The following steps are required to submit and retrieve block b for data availability verification.
- Generation blocks: When a client wants to commit block b to a trusted blockchain, it runs the accumulation set of accumulators connected to the block to generate membership witnesses for block b and a set of D blocks generates membership witnesses .
- Dispersion blocks: The client runs the decentralized protocol disperse , N), and specifies that different data blocks are sent to N different verification nodes.
- Verification termination: Verification nodes query membership witnesses to finalize and accept their witnesses to write certain blocks in the trusted blockchain.
- Retrieve data: The client retrieves a set of blocks of any witnesses that has been verified by the verification layer by initiating a request (retrieve, Wit).
- Decoded data: Any client can run primitive decoding to decode the blocks in the retrieved block . The decoder also returns the proof of the membership associated with the witness for decoding block b.
We describe the security of the verification model, that is, the data availability scheme, and define the data availability verification, as follows.
In the data availability verification of the trusted block chain, the client submits the block and the trusted block chain receives the witness with the following properties:
- Termination: When an honest client requests block b decentralized, block b will eventually be approved and the witness will be transferred to the trusted blockchain.
- Availability: Dispersion is acceptable if a client wants to retrieve and the verification layer is able to provide it with block b or empty block Ø and prove that the client is related to .
- Correctness: If two honest clients running (Retrieve, Wit) at the same time receive and , then . If the client initiating the dispersion is honest, it needs to satisfy the original dispersion block .
4. Technical Description
In this section, bilinear mappings, zero knowledge accumulators, and local repair codes are described and constructed, respectively. These techniques are described in more detail in Refs. [5,8,33], respectively. Readers can refer to these studies for further information.
4.1. Bilinear Mapping
The basic bilinear accumulator is a paired bilinear mapping based on the n-strong Diffie–Hellman assumption [33]. Pairing: e: , where and are cyclic groups of prime order p. We require pairing e to satisfy the following attributes.
Bilinearity: , where .
Non-degeneracy: There is at least element that satisfies .
Calculability: For any , there is a polynomial time algorithm related to a given security parameter , which can efficiently calculate .
We call a bilinear paired tuple as the output of a probabilistic polynomial time algorithm running on input . When choosing cyclic groups and , we usually consider the security of accumulators, that is , we choose asymmetric cyclic groups.
Suppose is the generator of , then is the generator of .
The accumulated value for the dataset is .
For any subset of the set D, its membership witness is the accumulative value of removing from the set .
Verify that the membership witness is correct or not, we can judge whether is true or not.
4.2. Zero-Knowledge Accumulator
The zero-knowledge accumulator is a dynamic universal accumulator based on bilinear mapping. It has all the properties of dynamic universal accumulator and achieves perfect zero-knowledge property. It supports membership witness and non-membership witness, and it supports insertion and deletion of sets for efficient updating of accumulative values. The following is a definition of dynamic universal accumulator and zero-knowledgeability.
There are five probabilistic polynomial-time algorithms in the dynamic universal accumulator (GenKey, Setup, Witness, Verify, Update). It represents the set D with accumulative values, which contains elements from the domain D. It supports queries of the form “?”. Where and the update of the current collection (e.g., using the “insert d” or “delete d” operations). The algorithm for the dynamic universal accumulator runs between the owner, the server, and the client, as described below. A tuple of algorithms constitutes the accumulator.
Five PPT algorithms comprise the dynamic universal accumulator, DUA = (GenKey, Setup, Witness, Verify, Update) defined as follows:
The key generation algorithm takes security parameters as input, and then outputs the public verification key and the secret key saved by the owner, which are responded by the client during the verification query.
The owner runs this setup algorithm. It takes as input the source set D and generates an accumulative value that is published to both the server and client, along with the evaluation key and the auxiliary information that is only sent to the server for proof construction.
The server runs the witness algorithm. It inputs the evaluation keyword , the accumulative value , the set D, and the query element d. It outputs an indication of whether the boolean value b is in the set and the witness w of the answer.
The client runs the verification algorithm. It inputs accumulative value , public key , queried element d, boolean value b, witness w, and outputs accept/reject.
This update algorithm inputs the current set with its accumulative values and auxiliary information and inserts element d into D, if or removes element d from D, if . The algorithm outputs ⊥ if and , (similarly, if and ), indicating that the update is invalid. Otherwise, it outputs , where is the new accumulative value corresponding to the set or is the modified evaluation keyword, and is the auxiliary information of the set (both are sent to the server only).
As a result of changing accumulative values, we need the WitUpdate function in order to update the existing witnesses efficiently.
The WitUpdate algorithm will run after the update is called. It takes as input the old and new accumulative values and auxiliary information based on the binary value , the evaluation keyword that updates the output, and the elements inserted or removed from the set d. It also uses different elements y and their existing witnesses w (which can be membership or non-membership witnesses). A new witness about y of the new set is output. This output must match what can be calculated by running Witness .
Zero-knowledgeness: Let X be a binary function. For a query, , when and only when or update update, when or . Let RealAdv Ideadv, and be the game between the challenger, the adversary Adv, and the simulator , defined as follows:
RealAdv :
Setup: The challenger runs and sends the to Adv. The latter selects the set with and sends it to the challenger, which in turn runs setup to obtain . Then, it sends to Adv and sets , , .
Query: For , where outputs , where op ∈ query, update } and
If op = query: Challenger runs witness and returns output to Adv.
If op = update: Challenger runs , , ). Update the set if the output is not ⊥, and accordingly get and forward to Adv. Otherwise, output ⊥.
Response: The opponent outputs a bit x.
IdealAdv
Setup: The simulator , with input1 , outputs a and forwards it to Adv. The adversary chooses a set with poly responds with and maintains the state . Finally, let .
Query: For , Adv outputs , where ∈{query, update} and
If op = query: The simulator runs , query, and returns the output to Adv.
If op = update: The simulator runs , states, (update, )). If the output of D (update, is 1, such that in and in and according to a valid update, X is always the placeholder variable for the latest set version, but the simulator never observes the variable. The simulator responds to adv with .
4.3. Local Repair Code
Let be a finite field consisting of q elements. Denote the set by . In layman’s terms, a given codeword is a grouping code with local restorability r if each coordinate of a given codeword can be recovered by accessing a maximum of r other coordinates of the codeword, it is a block code with local repairable r.
Let be a q-element grouping code of length n. For each and , define . For a subset , we denote by the projection of onto I. A code E is said to be a locally restorative code with local restorability r if for each , there exists a subset satisfying such that for any , the codes and are disjoint.
5. Performance Guarantee
5.1. Data Privacy Protection Security Analysis
To ensure the security of blockchain data privacy protection, the security of the zero-knowledge accumulator needs to be analyzed. The two main aspects include completeness and reliability.
One of the properties of the cryptographic accumulator is completeness, that is, the witness of the output of any call sequence through the scheme algorithm, because the state of the set at the time of witness generation is correctly verified with an almost negligible probability.
Completeness. Let the elements in D assimilate the set which is constructed after calling the update algorithm (starting from the set ) and for as well. The dynamic universal accumulator is complete if for all sets , where and are polynomials in and for all , for , there is a negligible function , then the dynamic universal accumulator is said to be complete such that:
where the probability of the algorithm exceeds its randomness.
The second property is reliability. It reflects the fact that the adversarial server cannot provide proof of acceptance if the request is incorrect.
Reliability: that is to say, Adv has the right to access all algorithms in the scheme and is required to generate a statement and the witness of the statement in the competition, but Adv cannot win.
For all PPT adversaries Adv and all 1-polynomials in running on input , the randomness of the coins that take over the algorithm and Adv has a negligible probability of winning the following game:
Setup: Challenger runs and sends to Adv, who responds with set . The challenger runs ←set and sends the output to the adversary.
Updates: The challenger starts the list L and inserts the tuple . After this, for , the opponent releases update and receives the updated output from the challenger. After each call to update, if the output is not ⊥, the challenger appends the returned to L. or else, it appends
Challenge: A triple is output by the adversary along with an index j. Let be . The adversary will win the game if the following occurs:
The discussion on the conditions for winning the game should take place on this point. In particular, Adv output set and the accumulative value and may be used to calculate the latter to cater to the randomization of the accumulator.
5.2. Security Analysis of Data Availability Scheme
In order to demonstrate that the data availability scheme is secure if the trusted blockchain is durable and secure, we prove the following properties.
Verification termination: In data availability verification, dispersion is accepted only if a membership witness is submitted to the trusted blockchain. If honest client requests are scattered, but there is no membership witness in the trusted blockchain, then either no membership witness is submitted, or no new transactions are accepted. By querying the membership witness , even if all the damaged nodes cannot provide any information, the data can still be considered available by membership proof and the membership witness will be presented, so the trusted blockchain is not active, which contradicts our assumption.
Availability: If decentralization is accepted, there is a membership witness in the trusted blockchain, and the verification node has proved the block. Because the trusted blockchain is persistent, the membership witness can be obtained as long as the client retrieves the block, and at least nodes will respond through the stored zero-knowledge accumulator connected to the block. On receiving a group block from a partial node of the side blockchain, for applying a local repair code with local repairability r and a feasible dispersion algorithm of the data availability verification layer, if dispersion is accepted, the verification is able to provide block b or empty block Ø and prove its relation to whenever an honest client requests retrieval.
6. Performance Analysis
6.1. Storage and Communication
We deployed our solution implementation on Linux cloud hardware with a 6-core CPU, 32 GB RAM, 128 GB SSD, and 40 Gpbs network interface (for data verification layer and side blockchain nodes). The central goals of the system are dataset privacy protection and data availability. Based on Table 1, we define four key performance metrics for the system, let N be the number of nodes, M be the number of blocks, and b be the size of each block. The coded repair rate of the local repair code measures the fault tolerance of the model. Consider the simplest scaling solution, which is to spread the data across the network without duplication. The “storage overhead” refers to the ratio of the total storage cost to the actual storage information. Considering that the blocks in each node are connected to a zero-knowledge accumulator to compress the stored data, the storage overhead is O(N), which indicates that the storage cost increases linearly with the network size. The system implements O(1) storage in case of client honesty and O(Logb) storage in case of client corruption. When applying 1D-RS codes [34], the worst-case scenario is that the adversary sends a block verification node with incorrect encoding and needs to download O(B) data for fraud prevention. The data availability verification system in this paper achieves a near-optimal overhead, requiring only O(Logb) proofs to be downloaded. For a given block, the communication efficiency of the data availability verification system in this paper is O(B).

Table 1.
System performance indicators.
6.2. Bandwidth Consumption during Local Repair Code Encoding
We can calculate the amount of bandwidth consumed by the nodes during the encoding process. The bandwidth consumption of the node is determined by evaluating the bandwidth consumption of the d encoding fragments stored by each node. The bandwidth consumption of the node during encoding varies for k = 10, 20, 30, 40, 50, 60, and d = 4, 5, 6, where k denotes the total number of encoded fragments. Figure 3 shows the change in bandwidth consumption when the encoding fragments are stored during encoding. When d is fixed, the larger k is fixed, and the less bandwidth is consumed for storing the encoded fragment during encoding, and when k is fixed, the larger d is, and the greater bandwidth is consumed for storing the encoded fragment during encoding. Therefore, the size of bandwidth occupied by nodes for data transmission is related to the amount of encoded data allocated to nodes for storage. When the block size is relatively large, the bandwidth occupation and the amount of stored data can be measured to choose a better solution, but with the current block size of the mainstream blockchain, the bandwidth occupied by data transmission between nodes within a group is small.
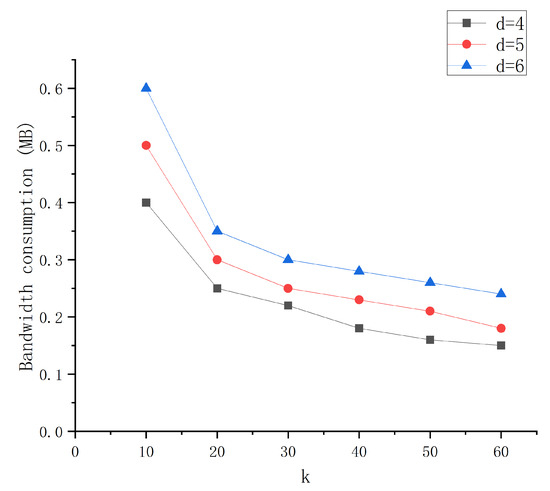
Figure 3.
Bandwidth consumption during encoding.
In the experiments, the repair rate of erroneous nodes was calculated and the total encoded data volume of the nodes was evaluated at the number of erroneous nodes p = 1, 2, 3, respectively. n = 20, 40, 60, 80, 100, 120 is the repair rate of the erroneous nodes. Figure 4 shows the variation of the repair rate of the error nodes. We can know that when p is fixed, the larger n is, and the slower the repair rate of the error nodes in each slice, and when n is fixed, the smaller p is, and the faster the repair rate of the error nodes.
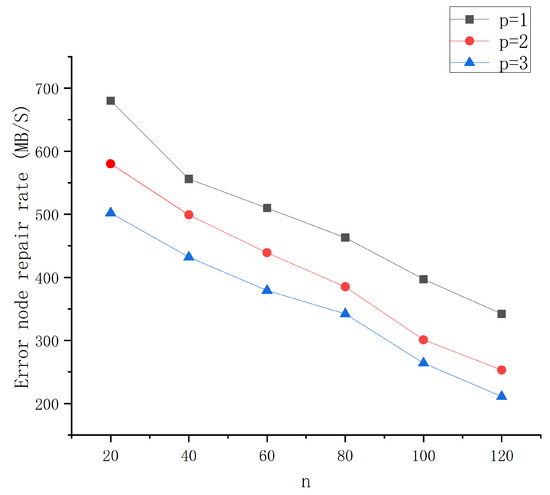
Figure 4.
Error node repair rate.
6.3. Comparison of Schemes
We compare the data availability scheme with strong dataset privacy protection (DPP-DA) in this paper with the ACeD data availability scheme, the 1D-RS scheme [35,36], using regenerable codes, and the AVID [37] scheme. The differences between the three in terms of latency, throughput, and fault tolerance are analyzed, respectively. The results are shown in Table 2. In terms of latency, the local repair codes used in this paper are more efficient compared to Merkle tree coding and regenerable codes. It is more effective in reducing the blockchain time delay. In terms of throughput, DPP-DA has a higher improvement compared with the other two schemes, because compressed storage by accumulator can improve the throughput of blockchain. In terms of fault tolerance, the fault tolerance of blockchain is influenced by the coding repair rate, where the coding repair ability of local repair codes is higher than other codes, so the data availability scheme based on local repair codes is more fault tolerant.

Table 2.
Performance comparison.
7. Conclusions
By investigating previous data availability scheme, this paper puts forward a new blockchain-based data availability scheme. The original coded Merkle tree is replaced by a zero-knowledge accumulator with local repair coding with higher efficiency and security, and then the zero-knowledge performance of the zero-knowledge accumulator is used to achieve strong data privacy protection performance considering the privacy security of the data. Finally, a blockchain data availability scheme with strong privacy protection for datasets is proposed. The scheme first ensures tamper-proof data by encoding the data block information on the blockchain, and then stores the encoded data block information on the blockchain using a zero-knowledge accumulator to protect the accumulation set information stored in the accumulator from being compromised. It fundamentally reduces the possibility of attackers generating fraudulent information by imitating the information of data blocks on the blockchain.
Author Contributions
X.L. and Y.R. were responsible for conceptual analysis, methodological analysis, and writing the original draft. X.W. and L.L. were responsible for thesis revision and review. S.J. was responsible for review, supervision, and project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2021YFB27-00500), and it was also supported by the National Natural Science Foundation of China (Grant No. 62072249, 62076125). This work was also supported by the National Key R&D Program of Guangdong Province (Grant No. 2020B0101090002), and the Natural Science Foundation of Jiangsu Province (Grant No. BK20200418, BE2020106).
Data Availability Statement
The datasets generated and analyzed during the current study are not publicly available due to restricted data sources but are available from the corresponding author on reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Decentralized Bus. Rev. 2008, 21260, 21260. [Google Scholar]
- Chen, H.; Pendleton, M.; Njilla, L.; Xu, S.H. A survey on Ethereum systems security: Vulnerabilities, attacks, and defenses. ACM Comput. Surv. 2021, 53, 1–43. [Google Scholar] [CrossRef]
- Ren, Y.J.; Zhu, F.; Wang, J.; Sharma, P.; Ghosh, U. Novel vote scheme for decision-making feedback based on blockchain in internet of vehicles. IEEE Trans. Intell. Transp. 2021, 21, 1639–1648. [Google Scholar] [CrossRef]
- Sheng, P.Y.; Xue, B.W.; Kannan, S.; Viswanath, P. ACeD: Scalable data availability oracle. In Proceedings of the International Conference on Financial Cryptography and Data Security, Virtual Event, 1–5 March 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 299–318. [Google Scholar]
- Papailiopoulos, D.S.; Dimakis, A.G. Locally repairable codes. IEEE Trans. Inf. Theory 2014, 60, 5843–5855. [Google Scholar] [CrossRef]
- Huang, P.; Yaakobi, E.; Uchikawa, H.; Siegel, P.H. Binary linear locally repairable codes. IEEE Trans. Inf. Theory 2016, 62, 6268–6283. [Google Scholar] [CrossRef]
- Luo, Y.; Xing, C.; Yuan, C. Optimal locally repairable codes of distance 3 and 4 via cyclic codes. IEEE Trans. Inf. Theory 2019, 65, 1048–1053. [Google Scholar] [CrossRef]
- Esha, G.; Olga, O.; Dimitrios, P.; Roberto, T.; Nikos, T. Zero-knowledge accumulators and set operations. Cryptol. Eprint Arch. 2016, 10032, 1–46. [Google Scholar]
- Campanelli, M.; Mathias, H. Curve trees: Practical and transparent zero-knowledge accumulators. Cryptol. Eprint Arch. 2022, 756, 1–18. [Google Scholar]
- Li, T.; Qian, Q.; Ren, Y.J.; Ren, Y.Z.; Xia, J.Y. Privacy-preserving recommendation based on kernel method in cloud computing. Comput. Mater. Contin. 2021, 66, 779–791. [Google Scholar] [CrossRef]
- Feng, Q.; He, D.B.; Zeadally, S.; KhurramKhan, M.; Kumar, N. A survey on privacy protection in blockchain system. J. Netw. Comput. Appl. 2019, 126, 45–58. [Google Scholar] [CrossRef]
- Mohammed, B.; Abdulghani, A.A.; Mohd, A.B.I.; Ali, S.S.; Muhammad, K.K. Comprehensive Survey on Big Data Privacy Protection. IEEE Access 2022, 8, 20067–20079. [Google Scholar]
- Liang, W.; Yang, Y.; Yang, C.; Hu, Y.H.; Xie, S.Y.; Li, K.C.; Cao, J.N. PDPChain: A consortium blockchain-based privacy protection scheme for personal data. IEEE Trans. Reliab. 2022, 1–13. [Google Scholar] [CrossRef]
- Ren, Y.J.; Huang, D.; Wang, W.H.; Yu, X.F. BSMD: A blockchain-based secure storage mechanism for big spatio-temporal data. Future Gener. Comput. Syst. 2023, 138, 328–338. [Google Scholar] [CrossRef]
- Benarroch, D.; Campanelli, M.; Fiore, D.; Kobi, G.; Dimitris, K. Zero-knowledge proofs for set membership: Efficient, succinct, modular. In Proceedings of the International Conference on Financial Cryptography and Data Security, Virtual Event, 1–5 March 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 393–414. [Google Scholar]
- Sun, X.Q.; Yu, F.R.; Zhang, P.; Sun, Z.W.; Xie, W.X.; Peng, X. A survey on zero-knowledge proof in blockchain. IEEE Netw. 2021, 35, 198–205. [Google Scholar] [CrossRef]
- Ren, Y.J.; Qi, J.; Liu, Y.P.; Wang, J.; Kim, G. Integrity verification mechanism of sensor data based on bilinear map accumulator. ACM Trans. Internet Technol. 2021, 21, 1–20. [Google Scholar] [CrossRef]
- Zhou, Q.H.; Huang, H.W.; Zheng, Z.B.; Bian, J. Solutions to scalability of blockchain: A survey. IEEE Access 2020, 8, 16440–16455. [Google Scholar] [CrossRef]
- Novo, O. Scalable access management in IoT using blockchain: A performance evaluation. IEEE Internet Things J. 2019, 6, 4694–4701. [Google Scholar] [CrossRef]
- Panda, S.S.; Mohanta, B.K.; Satapathy, U.; Jena, D.; Gountia, D.; Patra, T.K. Study of blockchain based decentralized consensus algorithms. In Proceedings of the TENCON 2019—2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 908–913. [Google Scholar]
- Ren, Y.J.; Zhu, F.J.; Kumar, S.P.; Wang, T.; Wang, J. Data query mechanism based on hash computing power of blockchain in internet of things. Sensors 2020, 20, 207. [Google Scholar] [CrossRef]
- Eyal, I.; Gencer, A.E.; Renesse, R.V. Bitcoin-NG: A scalable blockchain protocol. In Proceedings of the 13th USENIX Symposium on Networked Systems Design and Implementation (NSDI’16), Santa Clara, CA, USA, 16–18 March 2016; pp. 45–59. [Google Scholar]
- Yun, J.; Goh, Y.; Chung, J.M. DQN-based optimization framework for secure sharded blockchain systems. IEEE Internet Things J. 2021, 8, 708–722. [Google Scholar] [CrossRef]
- Mizrahi, A.; Rottenstreich, O. Blockchain state sharding with space-aware representations. IEEE Trans. Netw. Serv. Manag. 2021, 18, 1571–1583. [Google Scholar] [CrossRef]
- Yu, M.C.; Saeid, S.; Li, S.Z.; Salman, A.; Sreeram, K.; Pramod, V. Coded merkle tree: Solving data availability attacks in blockchains. In Proceedings of the International Conference on Financial Cryptography and Data Security, Kota Kinabalu, Malaysia, 10–14 February 2020; Springer: Cham, Switzerland, 2020; Volume 12059, pp. 114–134. [Google Scholar]
- Martńnez-Peñas, U.; Kschischang, F.R. Reliable and secure multishot network coding using linearized reed-solomon codes. IEEE Trans. Inf. Theory 2019, 65, 4785–4803. [Google Scholar] [CrossRef]
- Papamanthou, C.; Roberto, T.; Nikos, T. Authenticated hash tables based on cryptographic accumulators. Algorithmica 2016, 74, 664–712. [Google Scholar] [CrossRef]
- Ren, Y.J.; Leng, Y.; Cheng, Y.P.; Wang, J. Secure data storage based on blockchain and coding in edge computing. Math. Biosci. Eng. 2019, 16, 1874–1892. [Google Scholar] [CrossRef] [PubMed]
- Tavani, H.T.; Moor, J.H. Privacy protection, control of information, and privacy-enhancing technologies. ACM Sigcas Comput. Soc. 2001, 31, 6–11. [Google Scholar] [CrossRef]
- Gong, J.; Mei, Y.R.; Xiang, F.; Hong, H.S.; Sun, Y.B.; Sun, Z.X. A data privacy protection scheme for Internet of things based on blockchain. Trans. Emerg. Telecommun. Technol. 2021, 32, e4010. [Google Scholar] [CrossRef]
- Ren, Y.J.; Leng, Y.; Qi, J.; Pradip, K.S.; Wang, J. Multiple cloud storage mechanism based on blockchain in smart homes. Future Gener. Comput. Syst. 2021, 115, 304–313. [Google Scholar] [CrossRef]
- Boneh, D.; Bunz, B.; Fisch, B. Batching techniques for accumulators with applications to IOPs and stateless blockchains. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 2019; Springer: Cham, Switzerland, 2019; pp. 561–586. [Google Scholar]
- Thakur, S. Batching non-membership proofs with bilinear accumulators. IACR Cryptol. ePrint Arch. 2019, 1–22. Available online: https://eprint.iacr.org/2019/1147 (accessed on 8 November 2022).
- Halbawi, W.; Liu, Z.; Hassibi, B. Balanced Reed-Solomon codes. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 935–939. [Google Scholar]
- Sarkar, M.N.I.; Meegahapola, L.G.; Datta, M. Reactive power management in renewable rich power grids: A review of grid-codes, renewable generators, support devices, control strategies and optimization algorithms. IEEE Access 2018, 6, 41458–41489. [Google Scholar] [CrossRef]
- Chen, H.C.H.; Lee, P.P.C. Enabling data integrity protection in regenerating-coding-based cloud storage: Theory and implementation. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 407–416. [Google Scholar] [CrossRef]
- Cachin, C.; Tessaro, S. Asynchronous verifiable information dispersal. IEEE Symp. Reliab. Distrib. Syst. 2014, 25, 191–201. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).