Abstract
The problem of finding the global minimum of multidimensional functions is often applied to a wide range of problems. An innovative method of finding the global minimum of multidimensional functions is presented here. This method first generates an approximation of the objective function using only a few real samples from it. These samples construct the approach using a machine learning model. Next, the required sampling is performed by the approximation function. Furthermore, the approach is improved on each sample by using found local minima as samples for the training set of the machine learning model. In addition, as a termination criterion, the proposed technique uses a widely used criterion from the relevant literature which in fact evaluates it after each execution of the local minimization. The proposed technique was applied to a number of well-known problems from the relevant literature, and the comparative results with respect to modern global minimization techniques are shown to be extremely promising.
1. Introduction
An innovative method for finding the global minimum of multidimensional functions is presented here. The functions considered are continuous and differentiable and defined as . The problem of locating the global optimum is usually formulated as:
with S:
A variety of problems in the physical world can be represented as global minimum problems, such as problems from physics [1,2,3], chemistry [4,5,6], economics [7,8], medicine [9,10], etc. During the past years, many methods, especially the stochastic one, have been proposed to tackle the problem of Equation (1), such as Controlled Random Search methods [11,12,13], Simulated Annealing methods [14,15,16], Differential Evolution methods [17,18], Particle Swarm Optimization (PSO) methods [19,20,21], Ant Colony Optimization [22,23], Genetic algorithms [24,25,26], etc. A systematic review of global optimization methods can also be found in the work of Floudas et al. [27]. In addition, during the last few years, a variety of work has been proposed on combinations and modifications to some global optimization methods to more efficiently find the global minimum, such as methods that combine PSO with other methods [28,29,30], methods aimed to discover all the local minima of functions [31,32,33], new stopping rules to efficiently terminate the global optimization techniques [34,35,36], etc. In addition, due to the massive use of parallel processing techniques, several methods have been proposed that take full advantage of parallel processing, such as parallel techniques [37,38,39], methods that utilize the GPU architectures [40,41], etc.
In addition, during the past years, many metaheuristic algorithms have appeared to tackle global optimization problems such as the Quantum-based avian navigation optimizer algorithm [42], a Tunicate Swarm Algorithm (TSA) inspired by simulating the lives of Tunicates at sea and how food is obtained [43], Starling murmuration optimizer [44,45], the Diversity-maintained multi-trial vector differential evolution algorithm (DMDE) used in large-scale global optimization [46], an improved moth-flame optimization algorithm with an adaptation mechanism to solve numerical and mechanical engineering problems [47], the dwarf-mongoose optimization algorithm [48], etc.
In this paper, a new multistart method is proposed that uses a machine learning model, which is trained in parallel with the evolution of the optimization process. Although multistart methods are considered the basis for more modern optimization techniques, they have been successfully used in several problems such as the Traveling Salesman Problem (TSP) [49,50,51], the maximum clique problem [52,53], the vehicle routing problem [54,55], scheduling problems [56,57], etc. In the new technique, a Radial Basis Function (RBF) network [58] is used to construct an approximation of the objective function. This construction is carried out in parallel with the execution of the optimization. A limited number of samples from the objective function and the local minima discovered during the optimization are used to construct the approximation function. During the execution of the method, the samples needed to start local minimizers are taken from the approximation function that is constructed by the neural network. The RBF network was used as an approximation tool as it has been successfully used in a wide range of problems in the field of artificial intelligence [59,60,61,62] and its training procedure is very fast, if compared to artificial neural networks, for example. In addition, for a more efficient termination of the method, a termination method proposed by Tsoulos is used [63], but this termination method is applied after each execution of the local minimization procedure. The mentioned method was applied to some test functions provided by the relevant literature and the results are extremely promising as compared with other global optimization techniques.
The proposed method does not sample the actual function but an approximation of it, which is generated incrementally. The creation of the approximation is done by using an RBF neural network, known for its reliability and its ability to efficiently approximate functions. The initial approximation is created from a limited number of points, and then, it will be improved through the local minimizers that will be found during the execution of the method. With the above procedure, the required number of function calls is drastically reduced, since the actual function is not used to produce samples, but an approximation of them. Only samples with low function values are taken from the approximation function, which means that finding the global minimum is likely to be performed faster than other techniques and more efficiently. Furthermore, the generation of the approximation function does not use any prior knowledge about the objective problem.
2. Method Description
The proposed technique generates an estimation of the objective function during the optimization using an RBF network. This estimation is initially generated from some samples from the objective function and gradually local minima that will have been discovered during the optimization are added to it. In this way, the estimation of the objective function will be continuously improved to approximate the true function as much as possible. At every iteration, several samples are then taken from the estimated function and sorted in ascending order. Those with the lowest value will be starting points of the local minimization method. The local optimization method used here is a BFGS variant of Powell [64]. This process has the effect of drastically reducing the total number of function calls that are made and, at the same time, the points used as initiators of the local minimization technique approach the global minimum of the objective function. In addition, the proposed method checks the termination rule after the application of every local search method. That way, if the absolute minimum has already been discovered with some certainty, no more function calls will be wasted finding it.
In the following subsections, the training procedure of RBF networks as well as the proposed method are fully described.
2.1. RBF Preliminaries
An RBF network can be defined as:
where
- The vector is called the input pattern to the equation.
- The vectors are called the center vectors.
- The vector stands for the the output weight of the RBF network.
In most cases, the function is a Gaussian function:
The training error for the RBF network on a set of points is estimated as
In most approaches, Equation (4) is minimized with respect to the parameters of the RBF network using a two-phase procedure:
- In the first phase, the K-Means algorithm [65] is used to approximate the k centers and the corresponding variances.
- In the second phase, the weight vector is calculated by solving a linear system of equations as follows:
- (a)
- Set.
- (b)
- Set.
- (c)
- Set.
- (d)
- The system to be solved is identified as:With the solution:
2.2. The Main Algorithm
The main steps of the proposed algorithm are as follows:
- 1.
- Initialization step.
- (a)
- Setk the number of weights in the RBF network.
- (b)
- Set the initial samples that will be taken from the function .
- (c)
- Set the number of samples that will be used in every iteration as starting points for the local optimization procedure.
- (d)
- Set the number of samples that will be drawn from the RBF network at every iteration with .
- (e)
- Set the maximum number of allowed iterations.
- (f)
- Set Iter = 0, the iteration number.
- (g)
- Set as the global minimum. Initially,
- 2.
- Creation Step.
- (a)
- Set, the training set for the RBF network.
- (b)
- For do
- i.
- Take a new sample .
- ii.
- Calculate.
- iii.
- .
- (c)
- End For
- (d)
- Train the RBF network on the training set T.
- 3.
- Sampling Step.
- (a)
- Set.
- (b)
- Fordo
- i.
- Take a random sample from the RBF network.
- ii.
- Set.
- (c)
- End For
- (d)
- Sort according to the y values in ascending order.
- 4.
- Optimization Step.
- (a)
- For do
- i.
- Take the next sample from .
- ii.
- , where LS(x) is a predefined local search method.
- iii.
- ; this step updates the training set of the RBF network.
- iv.
- Train the RBF network on the set T.
- v.
- If, then .
- vi.
- Check the termination rule as suggested in [63]. If it holds, then report as the located global minimum and terminate.
- (b)
- End For
- 5.
- Set iter = iter + 1.
- 6.
- Goto to Sampling step.
The steps of the algorithm are illustrated graphically in Figure 1.
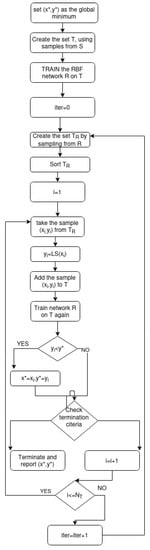
Figure 1.
The steps of the proposed algorithm.
3. Experiments
To estimate the efficiency of the new technique, a number of functions from the relevant literature were used [66,67]. These functions are provided in Appendix A. The proposed technique was tested on these test functions and the results produced were compared with those given by a simple genetic algorithm or a PSO method or differential evolution (DE) method. The used genetic algorithm is based on the algorithm from the work of Kaelo and Ali [68]. In order to have fairness in the comparison of the results, for all global optimization techniques, the same local minimization method as that of the proposed method has been used. In addition, the number of chromosomes in the genetic algorithm and the number of particles in the PSO method are identical to the parameter of the proposed procedure. In addition, for the DE method, the number of agents was set to . The values for the parameters used in the conducted experiments are shown in Table 1. For every function and for every global optimizer, 30 independent runs were executed using a different seed for the random generator each time. The proposed method is implemented as the method with the name NeuralMinimizer in the OPTIMUS global optimization environment, which is freely available from https://github.com/itsoulos/OPTIMUS (accessed on 19 January 2023). All the experiments were conducted on an AMD Ryzen 5950X with 128 GB of RAM and the Debian Linux operating system.

Table 1.
Experimental settings.
The experimental results from the application of the proposed method and the other methods are shown in Table 2. The number in the cells represent average function calls. The number in parentheses indicates the fraction of runs where the global optimum was successfully discovered. Absence of this fraction indicated that the global minimum is discovered for every execution (100% success). At the end of the table, an additional row named AVERAGE has been added to show the total number of function calls and the average success rate in locating the global minimum. In the experimental results, the superiority of the proposed technique over the other two methods in terms of the number of function calls is clear. The proposed technique requires an average of 90% fewer function calls than the other methods. In addition, the proposed technique appears to be more efficient than the other two as it finds, on average, more often the global minimum of most test functions in the experiments. In addition, the statistical comparison between the global optimization methods is shown in Figure 2.

Table 2.
Comparison between the proposed method and the Genetic and PSO methods.
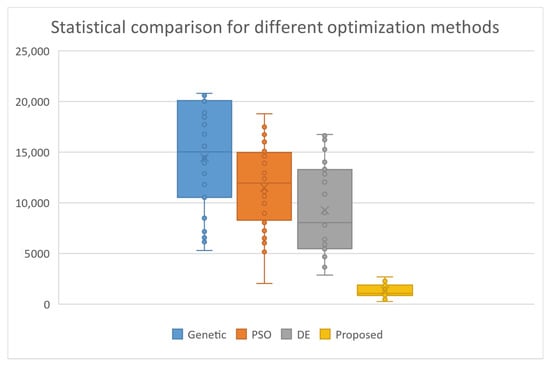
Figure 2.
Statistical comparison between the global optimization methods.
In addition, Table 3 presents the experimental results for the proposed method and for various values of the parameter . As can be seen, the increase in this parameter does not cause a large increase in the total number of function calls, while, at the same time, it improves to some extent the ability of the proposed technique to find the global minimum.

Table 3.
Experimental results for the proposed method and for different values of the critical parameter (50, 100, 200). Numbers in the cells represent averages of 30 runs.
The efficiency of the method is also shown in Table 4, where the proposed method is compared against the genetic algorithm and particle swarm optimization for a range of number of atoms of the Potential problem. As can be seen in the table, the proposed method requires a significantly smaller number of function calls compared with the other techniques and its reliability in finding the global minimum remains high even when the number of atoms in the potential increases significantly.

Table 4.
Optimizing the Potential problem for different number of atoms.
4. Conclusions
An innovative technique for finding the global minimum of multidimensional functions was presented in this work. This new technique is based on the multistart procedure, but also generates an estimation of the objective function through a machine learning model. The machine learning model constructs an estimation of the objective function using a small number of samples from the true function but also with the contribution of local minima discovered during the execution of the method. In this way, the estimation of the objective function is continuously improved and the sampling to perform local minimization is done from the estimated function rather than the actual one. This procedure combined with checking the termination criterion after each execution of the local minimization method led the proposed method to have excellent results both in terms of the speed of finding the global minimum and its efficiency. In addition, the method shows significant stability in its performance even in the presence of large changes of its parameters as presented in the experimental results section.
In the future, the use of the RBF network to construct an approximation of the objective function can be applied to more modern optimization techniques such as genetic algorithms. It would also be interesting to create a parallel implementation of the proposed method, in order to significantly speed up its execution and to be able to be used efficiently in optimization problems of higher dimensions.
Author Contributions
I.G.T., A.T., E.K. and D.T. conceived of the idea and methodology. I.G.T. and A.T. conducted the experiments, employing several test functions and provided the comparative experiments. E.K. and D.T. performed the statistical analysis and all other authors prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
- Bent Cigar function. The function iswith the global minimum . For the conducted experiments, the value was used.
- Bf1 function. The function Bohachevsky 1 is given by the equationwith .
- Bf2 function. The function Bohachevsky 2 is given by the equationwith .
- Branin function. The function is defined by with . The value of global minimum is 0.397887 with .
- CM function. The Cosine Mixture function is given by the equationwith . For the conducted experiments, the value was used.
- Camel function. The function is given byThe global minimum has the value of .
- Discus function. The function is defined aswith global minimum For the conducted experiments, the value was used.
- Easom function. The function is given by the equationwith and global minimum .
- Exponential function.The function is given byThe values were used here and the corresponding function names are EXP4, EXP16, EXP64.
- Griewank10 function, defined as:with .
- Hansen function. , . The global minimum of the function is −176.541793.
- Hartman 3 function. The function is given bywith and andThe value of the global minimum is −3.862782.
- Hartman 6 function.with and andThe value of the global minimum is −3.322368.
- High Conditioned Elliptic function, defined aswith for the conducted experiments.
- Potential function used to represent the lowest energy for the molecular conformation of N atoms via the Lennard–Jones potential [69]. The function is defined as:In the current experiments, two different cases were studied: .
- Rastrigin function. The function is given by
- Shekel 7 function.with and .
- Shekel 5 function.with and .
- Shekel 10 function.with and .
- Sinusoidal function. The function is given byThe global minimum is located at with . For the conducted experiments, the cases of , and were studied.
- Test2N function. This function is given by the equationThe function has local minima in the specified range and, in our experiments, we used .
- Test30N function. This function is given bywith . The function has local minima in the specified range and we used in the conducted experiments.
References
- Honda, M. Application of genetic algorithms to modelings of fusion plasma physics. Comput. Phys. Commun. 2018, 231, 94–106. [Google Scholar] [CrossRef]
- Luo, X.L.; Feng, J.; Zhang, H.H. A genetic algorithm for astroparticle physics studies. Comput. Phys. Commun. 2020, 250, 106818. [Google Scholar] [CrossRef]
- Aljohani, T.M.; Ebrahim, A.F.; Mohammed, O. Single and Multiobjective Optimal Reactive Power Dispatch Based on Hybrid Artificial Physics–Particle Swarm Optimization. Energies 2019, 12, 2333. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Shalloway, D.; Xue, G. Optimization methods for computing global minima of nonconvex potential energy functions. J. Glob. Optim. 1994, 4, 117–133. [Google Scholar] [CrossRef]
- Liwo, A.; Lee, J.; Ripoll, D.R.; Pillardy, J.; Scheraga, A.H. Protein structure prediction by global optimization of a potential energy function. Biophysics 1999, 96, 5482–5485. [Google Scholar] [CrossRef]
- An, J.; He, G.; Qin, F.; Li, R.; Huang, Z. A new framework of global sensitivity analysis for the chemical kinetic model using PSO-BPNN. Comput. Chem. Eng. 2018, 112, 154–164. [Google Scholar] [CrossRef]
- Gaing, Z.-L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans. Power Syst. 2003, 18, 1187–1195. [Google Scholar] [CrossRef]
- Basu, M. A simulated annealing-based goal-attainment method for economic emission load dispatch of fixed head hydrothermal power systems. Int. J. Electr. Power Energy Syst. 2005, 27, 147–153. [Google Scholar] [CrossRef]
- Cherruault, Y. Global optimization in biology and medicine. Math. Comput. Model. 1994, 20, 119–132. [Google Scholar] [CrossRef]
- Lee, E.K. Large-Scale Optimization-Based Classification Models in Medicine and Biology. Ann. Biomed. Eng. 2007, 35, 1095–1109. [Google Scholar] [CrossRef]
- Price, W.L. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
- Křivý, I.; Tvrdík, J. The controlled random search algorithm in optimizing regression models. Comput. Stat. Data Anal. 1995, 20, 229–234. [Google Scholar] [CrossRef]
- Ali, M.M.; Törn, A.; Viitanen, S. A Numerical Comparison of Some Modified Controlled Random Search Algorithms. J. Glob. 1997, 11, 377–385. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, J.; Lampinen, J. A Fuzzy Adaptive Differential Evolution Algorithm. Soft Comput. 2005, 9, 448–462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.K.; Blackwell, T. Particle swarm optimization algorithm: An Overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Trelea, I.C. The particle swarm optimization algorithm: Convergence analysis and parameter selection. Inf. Process. Lett. 2003, 85, 317–325. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Company: Reading, MA, USA, 1989. [Google Scholar]
- Michaelewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer-Verlag: Berlin, Germany, 1996. [Google Scholar]
- Grady, S.A.; Hussaini, M.Y.; Abdullah, M.M. Placement of wind turbines using genetic algorithms. Renew. Energy 2005, 30, 259–270. [Google Scholar] [CrossRef]
- Floudas, C.A.; Gounaris, C.E. A review of recent advances in global optimization. J. Glob. Optim. 2009, 45, 3–38. [Google Scholar] [CrossRef]
- Da, Y.; Xiurun, G. An improved PSO-based ANN with simulated annealing technique. Neurocomputing 2005, 63, 527–533. [Google Scholar] [CrossRef]
- Liu, H.; Cai, Z.; Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Pan, X.; Xue, L.; Lu, Y.; Sun, N. Hybrid particle swarm optimization with simulated annealing. Multimed. Tools Appl. 2019, 78, 29921–29936. [Google Scholar] [CrossRef]
- Ali, M.M.; Storey, C. Topographical multilevel single linkage. J. Glob. Optim. 1994, 5, 349–358. [Google Scholar] [CrossRef]
- Salhi, S.; Queen, N.M. A hybrid algorithm for identifying global and local minima when optimizing functions with many minima. Eur. J. Oper. Res. 2004, 155, 51–67. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Lagaris, I.E. MinFinder: Locating all the local minima of a function. Comput. Phys. Commun. 2006, 174, 166–179. [Google Scholar] [CrossRef]
- Betro, B.; Schoen, F. Optimal and sub-optimal stopping rules for the multistart algorithm in global optimization. Math. Program. 1992, 57, 445–458. [Google Scholar] [CrossRef]
- Hart, W.E. Sequential stopping rules for random optimization methods with applications to multistart local search. Siam J. Optim. 1998, 9, 270–290. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Tsoulos, I.G. Stopping Rules for Box-Constrained Stochastic Global Optimization. Appl. Math. Comput. 2008, 197, 622–632. [Google Scholar] [CrossRef]
- Schutte, J.F.; Reinbolt, J.A.; Fregly, B.J.; Haftka, R.T.; George, A.D. Parallel global optimization with the particle swarm algorithm. Int. J. Numer. Methods Eng. 2004, 61, 2296–2315. [Google Scholar] [CrossRef]
- Larson, J.; Wild, S.M. Asynchronously parallel optimization solver for finding multiple minima. Math. Comput. 2018, 10, 303–332. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Tzallas, A.; Tsalikakis, D. PDoublePop: An implementation of parallel genetic algorithm for function optimization. Comput. Phys. Commun. 2016, 209, 183–189. [Google Scholar] [CrossRef]
- Kamil, R.; Reiji, S. An Efficient GPU Implementation of a Multi-Start TSP Solver for Large Problem Instances. In Proceedings of the 14th Annual Conference Companion on Genetic and Evolutionary Computation, Philadelphia, PA, USA, 7–11 July 2012; pp. 1441–1442. [Google Scholar]
- Van Luong, T.; Melab, N.; Talbi, E.G. GPU-Based Multi-start Local Search Algorithms. In Learning and Intelligent Optimization; Coello, C.A.C., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6683. [Google Scholar]
- Hoda, Z.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar]
- Gharehchopogh, F.S. An Improved Tunicate Swarm Algorithm with Best-random Mutation Strategy for Global Optimization Problems. J. Bionic Eng. 2022, 19, 1177–1202. [Google Scholar] [CrossRef]
- Hoda, Z.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar]
- Nadimi-Shahraki, M.H.; Asghari Varzaneh, Z.; Zamani, H.; Mirjalili, S. Binary Starling Murmuration Optimizer Algorithm to Select Effective Features from Medical Data. Appl. Sci. 2023, 13, 564. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Hoda, Z. DMDE: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization. Expert Syst. Appl. 2022, 198, 116895. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Abualigah, L. An improved moth-flame optimization algorithm with adaptation mechanism to solve numerical and mechanical engineering problems. Entropy 2021, 23, 1637. [Google Scholar] [CrossRef] [PubMed]
- Agushaka, J.O.; Ezugwu, A.E.; Abualigah, L. Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 2022, 391, 114570. [Google Scholar] [CrossRef]
- Li, W. A Parallel Multi-start Search Algorithm for Dynamic Traveling Salesman Problem. In Experimental Algorithms; Pardalos, P.M., Rebennack, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6630. [Google Scholar]
- Martí, R.; Resende, M.G.C.; Ribeiro, C.C. Multi-start methods for combinatorial optimization. Eur. J. Oper. Res. 2013, 226, 1–8. [Google Scholar] [CrossRef]
- Pandiri, V.; Singh, A. Two multi-start heuristics for the k-traveling salesman problem. Opsearch 2020, 57, 1164–1204. [Google Scholar] [CrossRef]
- Wu, Q.; Hao, J.K. An adaptive multistart tabu search approach to solve the maximum clique problem. J. Comb. Optim. 2013, 26, 86–108. [Google Scholar] [CrossRef]
- Djeddi, Y.; Haddadene, H.A.; Belacel, N. An extension of adaptive multi-start tabu search for the maximum quasi-clique problem. Comput. Ind. Eng. 2019, 132, 280–292. [Google Scholar] [CrossRef]
- Bräysy, O.; Hasle, G.; Dullaert, W. A multi-start local search algorithm for the vehicle routing problem with time windows. Eur. J. Oper. Res. 2004, 159, 586–605. [Google Scholar] [CrossRef]
- Michallet, J.; Prins, C.; Amodeo, L.; Yalaoui, F.; Vitry, G. Multi-start iterated local search for the periodic vehicle routing problem with time windows and time spread constraints on services. Comput. Oper. Res. 2014, 41, 196–207. [Google Scholar] [CrossRef]
- Peng, K.; Pan, Q.K.; Gao, L.; Li, X.; Das, S.; Zhang, B. A multi-start variable neighbourhood descent algorithm for hybrid flowshop rescheduling. Swarm Evol. Comput. 2019, 45, 92–112. [Google Scholar] [CrossRef]
- Mao, J.Y.; Pan, Q.K.; Miao, Z.H.; Gao, L. An effective multi-start iterated greedy algorithm to minimize makespan for the distributed permutation flowshop scheduling problem with preventive maintenance. Expert Syst. Appl. 2021, 169, 114495. [Google Scholar] [CrossRef]
- Park, J.; Sandberg, I.W. Approximation and Radial-Basis-Function Networks. Neural Comput. 1993, 5, 305–316. [Google Scholar] [CrossRef]
- Yoo, S.H.; Oh, S.K.; Pedrycz, W. Optimized face recognition algorithm using radial basis function neural networks and its practical applications. Neural Netw. 2015, 69, 111–125. [Google Scholar] [CrossRef]
- Huang, G.B.; Saratchandran, P.; Sundararajan, N. A generalized growing and pruning RBF (GGAP-RBF) neural network for function approximation. IEEE Trans. Neural Netw. 2005, 16, 57–67. [Google Scholar] [CrossRef]
- Majdisova, Z.; Skala, V. Radial basis function approximations: Comparison and applications. Appl. Math. Model. 2017, 51, 728–743. [Google Scholar] [CrossRef]
- Kuo, B.C.; Ho, H.H.; Li, C.H.; Hung, C.C.; Taur, J.S. A Kernel-Based Feature Selection Method for SVM With RBF Kernel for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 317–326. [Google Scholar] [CrossRef]
- Tsoulos, I.G. Modifications of real code genetic algorithm for global optimization. Appl. Math. Comput. 2008, 203, 598–607. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Davis Davis, CA, USA, 27 December 1965–7 January 1966; Volume 1, pp. 281–297. [Google Scholar]
- Ali, M.M.; Khompatraporn, C.; Zabinsky, Z.B. A Numerical Evaluation of Several Stochastic Algorithms on Selected Continuous Global Optimization Test Problems. J. Glob. Optim. 2005, 31, 635–672. [Google Scholar] [CrossRef]
- Floudas, C.A.; Pardalos, P.M.; Adjiman, C.; Esposito, W.R.; Gümüs, Z.H.; Harding, S.; Klepeis, J.; Meyer, C.; Schweiger, C. Handbook of Test Problems in Local and Global Optimization; Kluwer Academic Publishers: Dordrecht, Germany, 1999. [Google Scholar]
- Kaelo, P.; Ali, M.M. Integrated crossover rules in real coded genetic algorithms. Eur. J. Oper. Res. 2007, 176, 60–76. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).