LA-ESN: A Novel Method for Time Series Classification
Abstract
1. Introduction
- (1)
- We propose a simple end-to-end model LA-ESN for handling time series classification tasks;
- (2)
- We modify the output layer of ESN to handle time series better and use CNN and LSTM as output layers to finish feature extraction;
- (3)
- The attention mechanism is deployed behind both CNN and LSTM, which effectively improves the effectiveness and computing efficiency of LA-ESN;
- (4)
- Experiments on various time series datasets show that LA-ESN is efficacious.
2. Associated Work
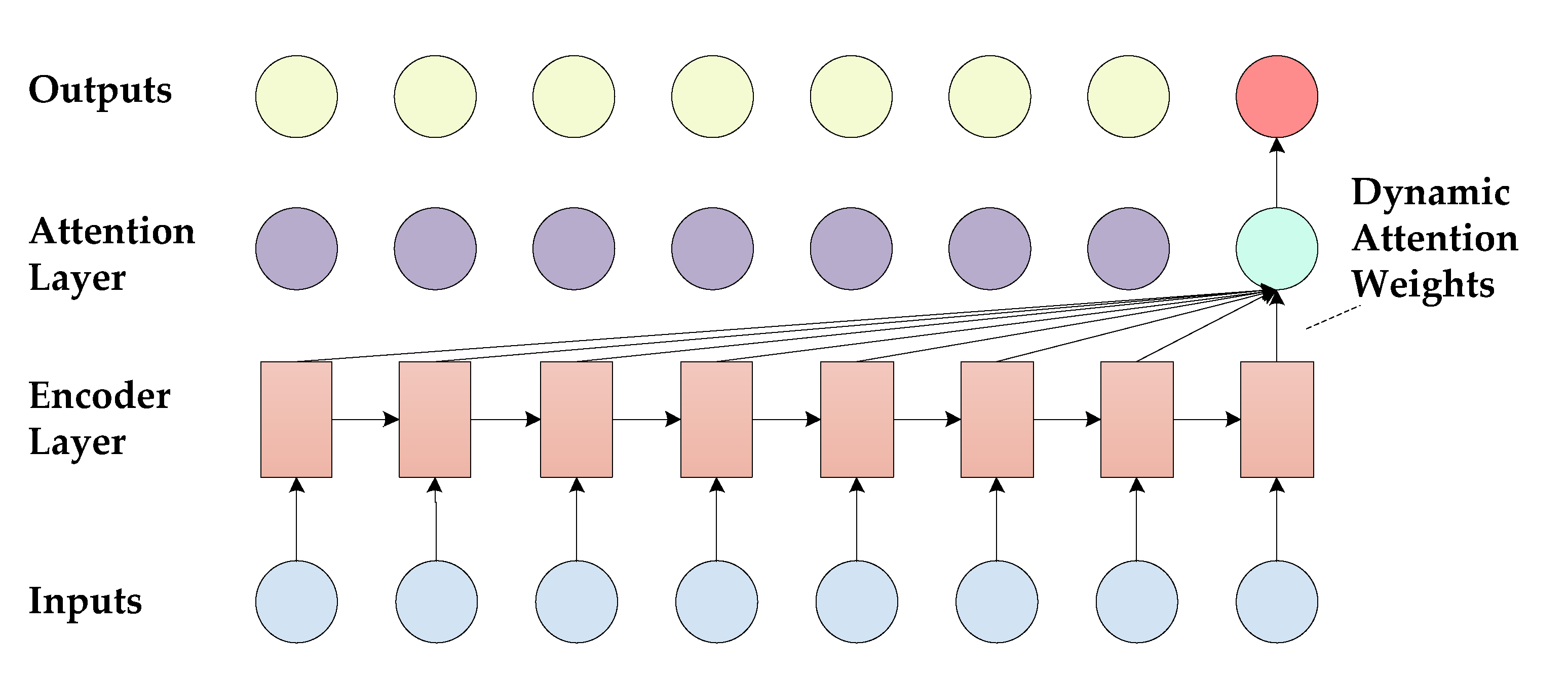
2.1. CNN with Attention
2.2. ESN -Based Classifier
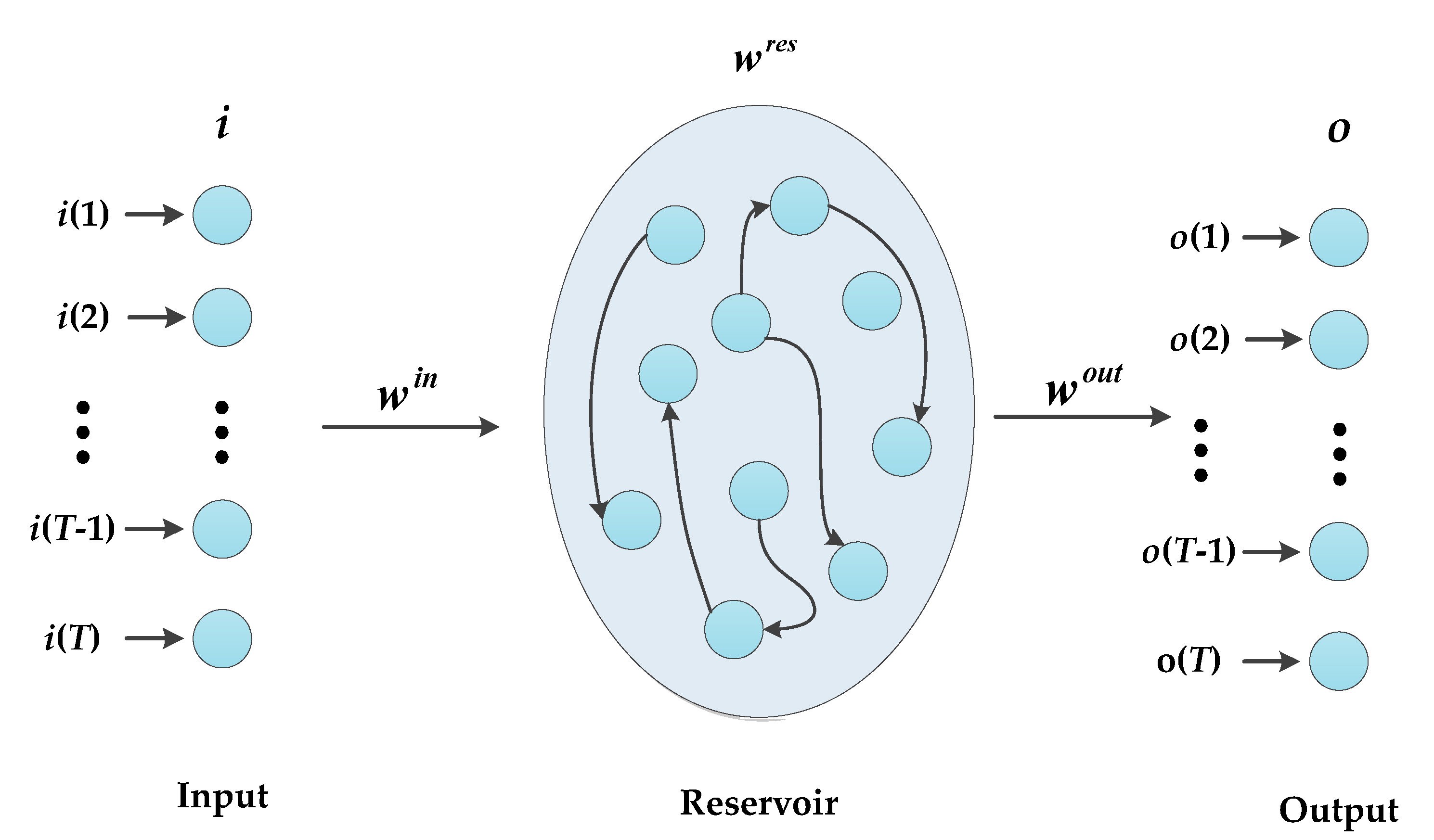
3. The Proposed LA-ESN Framework
3.1. Preliminary
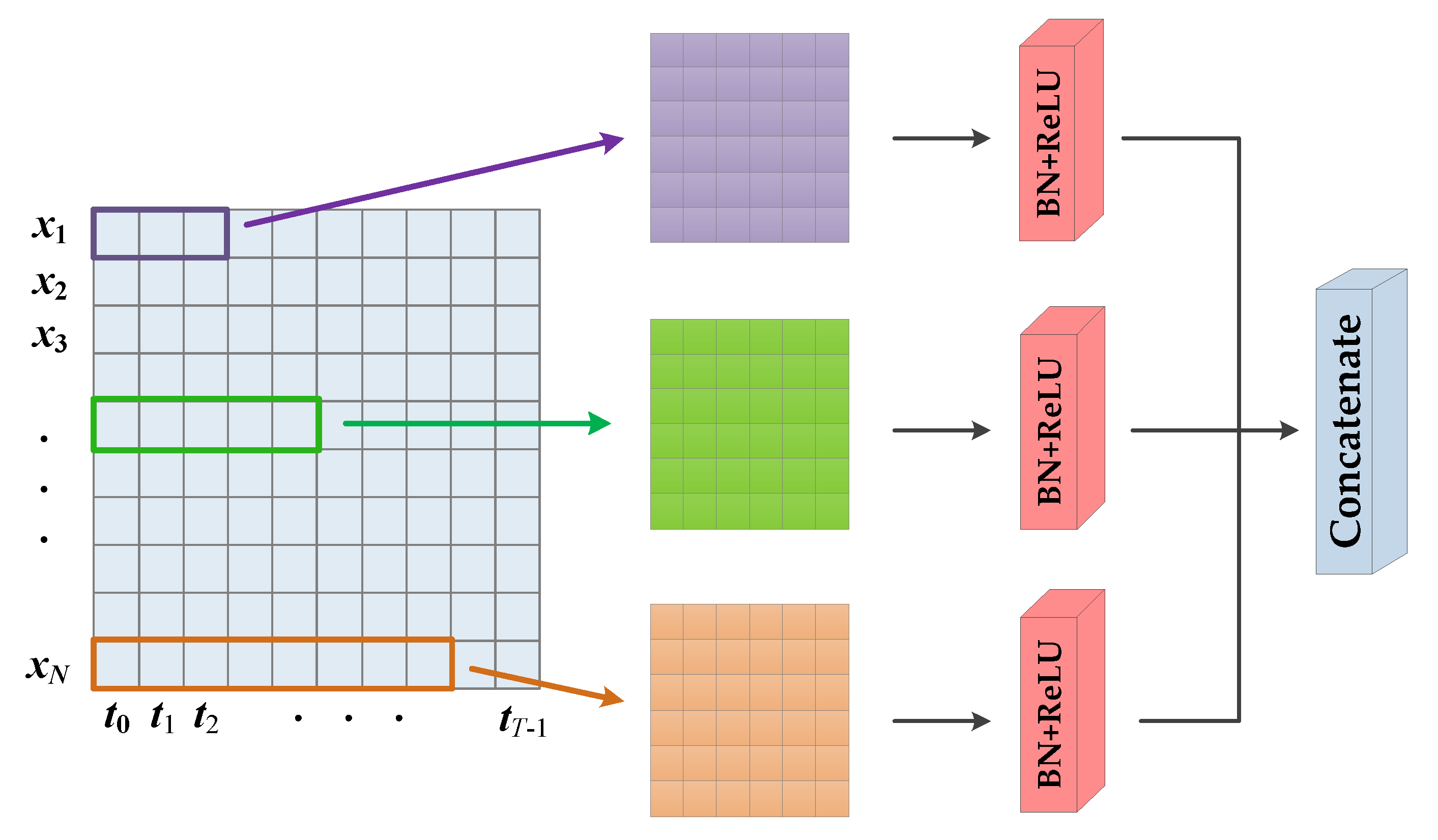
3.2. Encoding Stage
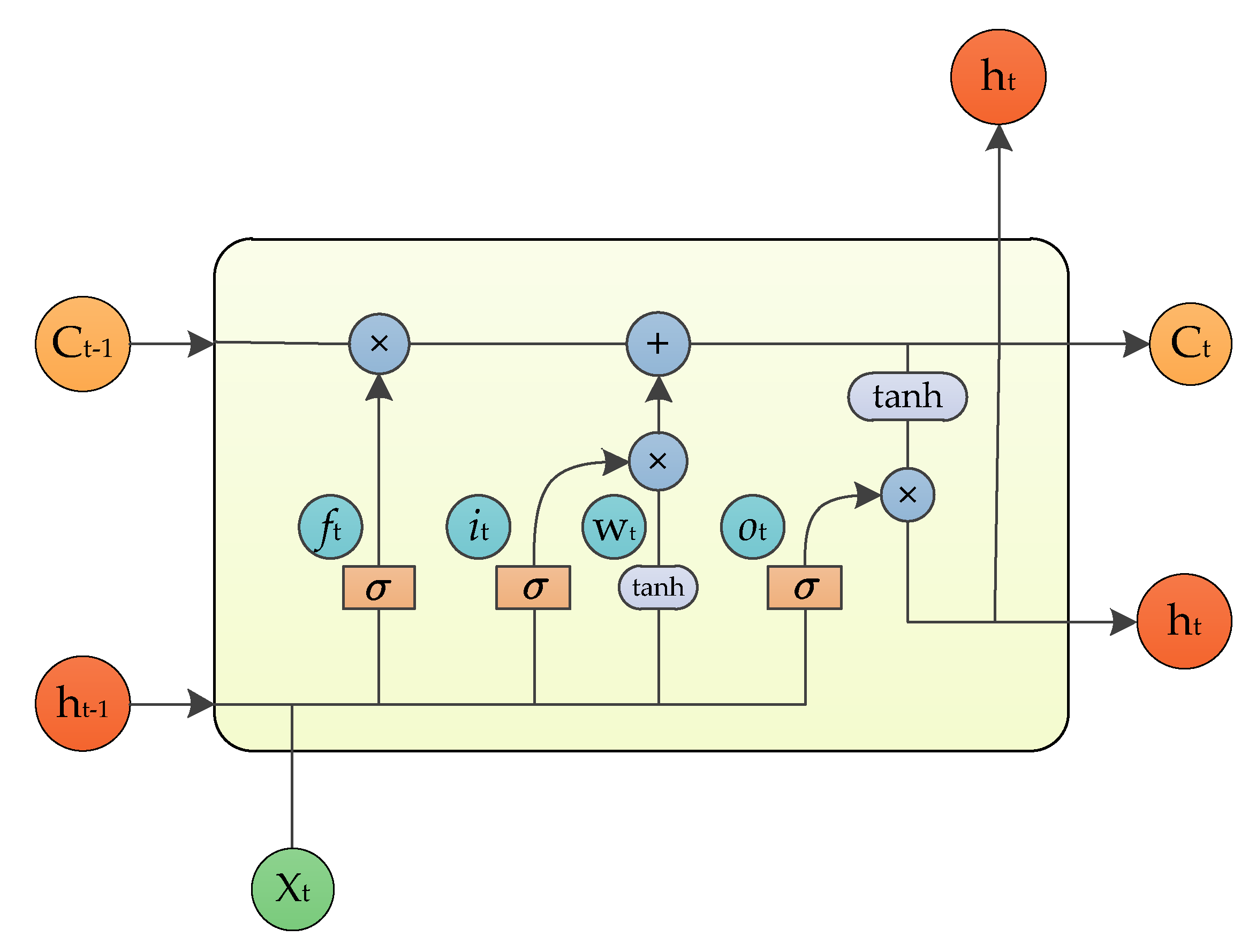
3.3. Decoding Stage
4. Experiments and Results
4.1. Database Description
4.2. Evaluation Metric
4.3. Results and Discussion
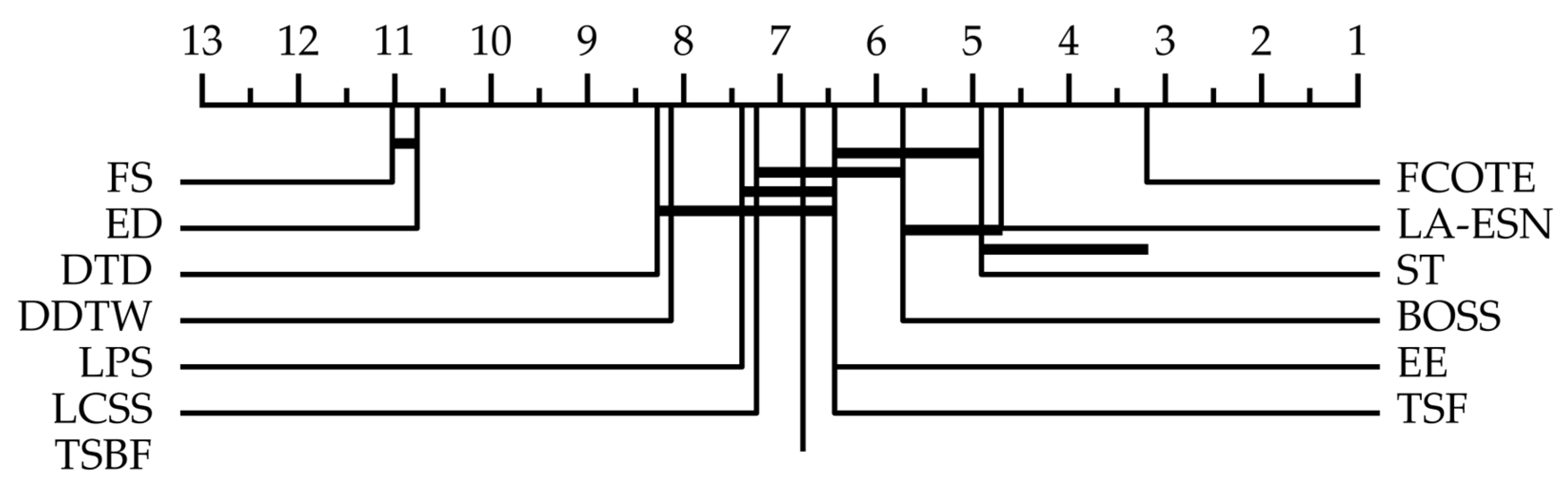
4.3.1. Compared with Traditional Methods
- (1)
- ED (1-Nearest Neighbour with Euclidean Distance). In this method, the Euclidean distance is employed to measure the similarity of two given time series, and then the nearest neighbor is used for classification.
- (2)
- DDTW (Dynamic Derivative Time Warping). This method weights the DTW distance between the two-time series and the DTW distance between the corresponding first-order difference series.
- (3)
- DTD (Derivative Transform Distance). The DTW distance between sequences of sine, cosine, and Hilbert transforms is further considered based on the DDTW.
- (4)
- LCSS (Longest Common Subsequence). In this method, a shapelet transform-based classifier is designed using a heuristic gradient descent-based shapelet search process instead of enumeration.
- (5)
- BOSS (Bag of SFA Symbols). This method uses windows to form ‘words’ on the level and then explores a truncated discrete Fourier transform on each window to obtain features.
- (6)
- EE (Elastic Ensemble). The EE method takes a voting scheme to combine eleven 1-NN classifiers with elastic distance metrics.
- (7)
- FCOTE (Flat Collective of Transform-based Ensembles). The method integrates 35 classifiers by using the cross-validation accuracy of training sets.
- (8)
- TSF (Time Series Forest). The time series is first divided into intervals in this method to calculate the mean, standard deviation and slope as interval features. Then, the intervals are randomly selected to train the tree forest.
- (9)
- TSBF (Time Series Bag Feature). This method selects multiple random length subsequences from random locations and then divides these subsequences into shorter intervals to capture local information.
- (10)
- ST (Shape Transform). This method uses the shapelet transform to obtain a new representation of the original time series. Then, a classifier is constructed on the new representation using a weighted integration of eight different classifiers.
- (11)
- LPS (Learning Pattern Similarity). The method is based on intervals, but the main difference is that the subsequence is used as an attribute rather than the extracted interval features.
- (12)
- FS (Fast Shape Tree). The method speeds up the search process by converting the original time series into a discrete low-dimensional representation by applying a symbolic aggregation approximation to the actual time series. Random projections are then used to find potential shapelet candidates.
4.3.2. Compared with Deep Learning Methods
- (1)
- MLP (Multilayer Perceptrons). The final result is obtained by using a softmax layer and three fully connected layers of 500 cells. Dropout and ReLU are used to activate the model.
- (2)
- FCN (Fully Convolutional Networks). The FCN model stacks three one-dimensional convolutional blocks with 128, 256 and 128 and kernel sizes of 3, 5 and 8. Then the features are fed into the global average pooling layer and the softmax layer to obtain the final result. The FCN model uses the ReLU activation function and batch normalization.
- (3)
- ResNet (Residual Network). The residual network is stacked with three residual blocks. Each residual block consists of 64, 128 and 256 convolutions of sizes 8, 5 and 3, respectively, followed by a ReLU activation function and batch normalization. ResNet extends the neural network to a profound structure by adding shortcut connections in each residual block. ResNet has a higher proclivity for overfitting the training data.
- (4)
- Inception Time (AlexNet). Instead of the usual fully connected layer, it consists of two distinct residual blocks, each made of three Inception sub-blocks. The input of each residual block is transferred to the information of the next block via a fast linear connection, thus alleviating the problem of gradient disappearance by allowing a direct flow of gradients.
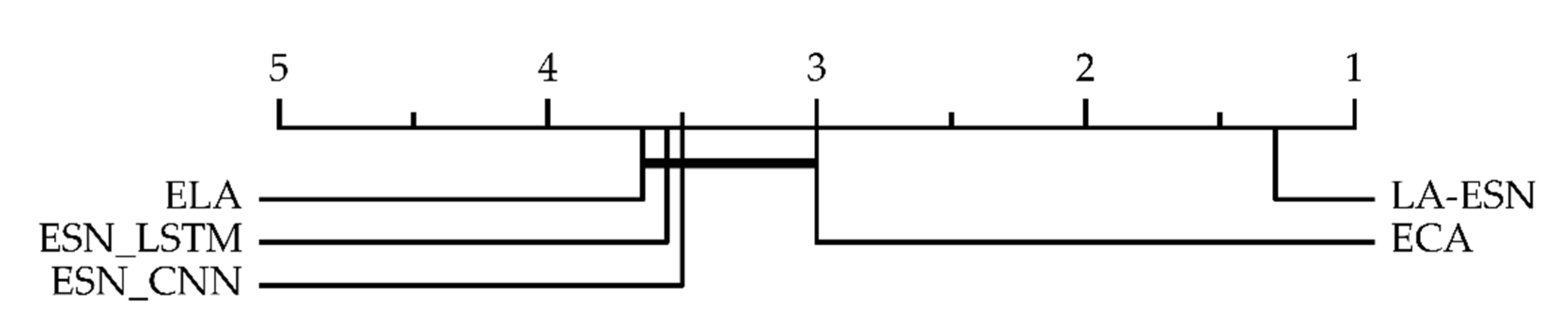
4.3.3. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Oxford, UK, 2020. [Google Scholar]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Xiao, X.; Li, R.; Zheng, H.-T.; Ye, R.; Kumar Sangaiah, A.; Xia, S. Novel dynamic multiple classification system for network traffic. Inf. Sci. 2018, 479, 526–541. [Google Scholar] [CrossRef]
- Michida, R.; Katayama, D.; Seiji, I.; Wu, Y.; Koide, T.; Tanaka, S.; Okamoto, Y.; Mieno, H.; Tamaki, T.; Yoshida, S. A Lesion Classification Method Using Deep Learning Based on JNET Classification for Computer-Aided Diagnosis System in Colorectal Magnified NBI Endoscopy. In Proceedings of the 36th International Technical Conference on Circuits/Systems, Computers and Communications (ITC-CSCC), Jeju, Republic of Korea, 27–30 June 2021; pp. 1–4. [Google Scholar]
- Mori, U.; Mendiburu, A.; Miranda, I.; Lozano, J. Early classification of time series using multi-objective optimization techniques. Inf. Sci. 2019, 492, 204–218. [Google Scholar] [CrossRef]
- Wan, Y.; Si, Y.-W. A formal approach to chart patterns classification in financial time series. Inf. Sci. 2017, 411, 151–175. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Q.J.; Wang, D.; Xin, J.; Yang, Y.; Yu, K. Echo state network with a global reversible autoencoder for time series classification. Inf. Sci. 2021, 570, 744–768. [Google Scholar] [CrossRef]
- Marteau, P.-F.; Gibet, S. On Recursive Edit Distance Kernels with Application to Time Series Classification. IEEE Trans. Neural Networks Learn. Syst. 2014, 26, 1121–1133. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Y. Time Series K-Nearest Neighbors Classifier Based on Fast Dynamic Time Warping. In Proceedings of the 2021 IEEE International Conference on Artificial Intelligence and Computer Applications (ICAICA), Dalian, China, 28–30 June 2021; pp. 751–754. [Google Scholar]
- Gustavo, E.; Batista, A.; Keogh, E.J.; Tataw, O.M.; De Souza, V.M.A. CID: An efficient complexity-invariant distance for time series. Data Min. Knowl. Discov. 2013, 28, 634–669. [Google Scholar] [CrossRef]
- Purnawirawan, A.; Wibawa, A.D.; Wulandari, D.P. Classification of P-wave Morphology Using New Local Distance Transform and Random Forests. In Proceedings of the 6th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 September 2020; pp. 1–6. [Google Scholar]
- Qiao, Z.; Mizukoshi, Y.; Moteki, T.; Iwata, H. Operation State Identification Method for Unmanned Construction: Extended Search and Registration System of Novel Operation State Based on LSTM and DDTW. In Proceedings of the IEEE/SICE International Symposium on System Integration (SII), Virtual Conference, 9–12 January 2022; pp. 13–18. [Google Scholar]
- Rahman, B.; Warnars, H.L.H.S.; Sabarguna, B.S.; Budiharto, W. Heart Disease Classification Model Using K-Nearest Neighbor Algorithm. In Proceedings of the 6th International Conference on Informatics and Computing (ICIC), Virtual Conference, 3–4 November 2021; pp. 1–4. [Google Scholar]
- Górecki, T. Using derivatives in a longest common subsequence dissimilarity measure for time series classification. Pattern Recognit. Lett. 2014, 45, 99–105. [Google Scholar] [CrossRef]
- Baydogan, M.G.; Runger, G.; Tuv, E. A Bag-of-Features Framework to Classify Time Series. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2796–2802. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E.; Vladimir, M. A time series forest for classification and feature extraction. Inf. Sci. 2013, 239, 142–153. [Google Scholar] [CrossRef]
- Ji, C.; Zhao, C.; Liu, S.; Yang, C.; Pan, L.; Wu, L.; Meng, X. A fast shapelet selection algorithm for time series classification. Comput. Networks 2019, 148, 231–240. [Google Scholar] [CrossRef]
- Arul, M.; Kareem, A. Applications of shapelet transform to time series classification of earthquake, wind and wave data. Eng. Struct. 2021, 228, 111564. [Google Scholar] [CrossRef]
- Baydogan, M.G.; Runger, G. Time series representation and similarity based on local autopatterns. Data Min. Knowl. Discov. 2016, 30, 476–509. [Google Scholar] [CrossRef]
- Kate, R.J. Using dynamic time warping distances as features for improved time series classification. Data Min. Knowl. Discov. 2016, 30, 283–312. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Networks 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Ma, Q.; Chen, E.; Lin, Z.; Yan, J.; Yu, Z.; Ng, W.W.Y. Convolutional Multitimescale Echo State Network. IEEE Trans. Cybern. 2019, 51, 1613–1625. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Insights into LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Koh, B.H.D.; Lim, C.L.P.; Rahimi, H.; Woo, W.L.; Gao, B. Deep Temporal Convolution Network for Time Series Classification. Sensors 2021, 21, 603. [Google Scholar] [CrossRef]
- Ku, B.; Kim, G.; Ahn, J.-K.; Lee, J.; Ko, H. Attention-Based Convolutional Neural Network for Earthquake Event Classification. IEEE Geosci. Remote. Sens. Lett. 2020, 18, 2057–2061. [Google Scholar] [CrossRef]
- Tripathi, A.M.; Baruah, R.D. Multivariate Time Series Classification with An Attention-Based Multivariate Convolutional Neural Network. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Sun, J.; Takeuchi, S.; Yamasaki, I. Prototypical Inception Network with Cross Branch Attention for Time Series Classification. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–7. [Google Scholar]
- Li, D.; Lian, C.; Yao, W. Research on time series classification based on convolutional neural network with attention mechanism. In Proceedings of the 11th International Conference on Intelligent Control and Information Processing (ICICIP), Yunnan, China, 3–7 December 2021; pp. 88–93. [Google Scholar]
- Huang, Z.; Yang, C.; Chen, X.; Zhou, X.; Chen, G.; Huang, T.; Gui, W. Functional deep echo state network improved by a bi-level optimization approach for multivariate time series classification. Appl. Soft Comput. 2021, 106. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Wang, D.; Luo, Y.; Tong, C.; Lv, Z. Discriminative and regularized echo state network for time series classification. Pattern Recognit. 2022, 130, 1–14. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Exploiting multi-channels deep convolutional neural networks for multivariate time series classification. Front. Comput. Sci. 2016, 10, 96–112. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.-A.; Petitjean, F. InceptionTime: Finding AlexNet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time series classification using multi-channels deep convolutional neural networks. In Proceedings of the International Conference on Web-Age Information Management, Macau, China, 16–18 June 2014; Springer: Cham, Switzerland, 2014; pp. 298–310. [Google Scholar]
- Dau, H.A.; Bagnall, A.; Kamgar, K.; Yeh, C.-C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Keogh, E. The UCR time series archive. IEEE/CAA J. Autom. Sin. 2019, 6, 1293–1305. [Google Scholar] [CrossRef]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Schäfer, P. The BOSS is concerned with time series classification in the presence of noise. Data Min. Knowl. Discov. 2015, 29, 1505–1530. [Google Scholar] [CrossRef]
- Lines, J.; Bagnall, A. Time series classification with ensembles of elastic distance measures. Data Min. Knowl. Discov. 2015, 29, 565–592. [Google Scholar] [CrossRef]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-Series Classification with COTE: The Collective of Transformation-Based Ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Benavoli, A.; Corani, G.; Mangili, F. Should we really use post-hoc tests based on mean-ranks? J. Mach. Learn. Res. 2016, 17, 152–161. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Demšar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar] [CrossRef]


| Dataset | Train | Test | Class | Length |
|---|---|---|---|---|
| ACSF1 | 100 | 100 | 10 | 1460 |
| Adiac | 390 | 391 | 37 | 176 |
| AllGestureX | 300 | 700 | 10 | 0 |
| AllGestureY | 300 | 700 | 10 | 0 |
| AllGestureZ | 300 | 700 | 10 | 0 |
| ArrowHead | 36 | 175 | 3 | 251 |
| Beef | 30 | 30 | 5 | 470 |
| BeetleFly | 20 | 20 | 2 | 512 |
| BirdChicken | 20 | 20 | 2 | 512 |
| BME | 30 | 150 | 3 | 128 |
| Car | 60 | 60 | 4 | 577 |
| CBF | 30 | 900 | 3 | 128 |
| Chinatown | 20 | 345 | 2 | 24 |
| ChlorineCon | 467 | 3840 | 3 | 166 |
| CinCECGTorso | 40 | 1380 | 4 | 1639 |
| Coffee | 28 | 28 | 2 | 286 |
| Computers | 250 | 250 | 2 | 720 |
| CricketX | 390 | 390 | 12 | 300 |
| CricketY | 390 | 390 | 12 | 300 |
| CricketZ | 390 | 390 | 12 | 300 |
| Crop | 7200 | 16,800 | 24 | 46 |
| DiatomSizeR | 16 | 306 | 4 | 345 |
| DistPhxAgeGp | 400 | 139 | 3 | 80 |
| DistlPhxOutCorr | 600 | 276 | 2 | 80 |
| DistPhxTW | 400 | 139 | 6 | 80 |
| DodgerLoopDay | 78 | 80 | 7 | 288 |
| DodgerLoopGame | 20 | 138 | 2 | 288 |
| DodgerLoopWnd | 20 | 138 | 2 | 288 |
| Earthquakes | 322 | 139 | 2 | 512 |
| ECG200 | 100 | 100 | 2 | 96 |
| ECG5000 | 500 | 4500 | 5 | 140 |
| ECGFiveDays | 23 | 861 | 2 | 136 |
| ElectricDevices | 8926 | 7711 | 7 | 96 |
| EOGHorSignal | 362 | 362 | 12 | 1250 |
| EOGVerticalSignal | 362 | 362 | 12 | 1250 |
| EthanolLevel | 504 | 500 | 4 | 1751 |
| FaceAll | 560 | 1690 | 14 | 131 |
| FaceFour | 24 | 88 | 4 | 350 |
| FacesUCR | 200 | 2050 | 14 | 131 |
| FiftyWords | 450 | 455 | 50 | 270 |
| Fish | 175 | 175 | 7 | 463 |
| FordA | 3601 | 1320 | 2 | 500 |
| FordB | 3636 | 810 | 2 | 500 |
| FreezerRegularT | 150 | 2850 | 2 | 301 |
| FreezerSmallTrain | 28 | 2850 | 2 | 301 |
| Fungi | 18 | 186 | 18 | 201 |
| GestureMidAirD1 | 208 | 130 | 26 | 360 |
| GestureMidAirD2 | 208 | 130 | 26 | 360 |
| GestureMidAirD3 | 208 | 130 | 26 | 360 |
| GesturePebbleZ1 | 132 | 172 | 6 | 0 |
| GesturePebbleZ2 | 146 | 158 | 6 | 0 |
| GunPoint | 50 | 150 | 2 | 150 |
| GunPointAgeSpan | 135 | 316 | 2 | 150 |
| GunPointMaleFe | 135 | 316 | 2 | 150 |
| GunPointOldYg | 135 | 316 | 2 | 150 |
| Ham | 109 | 105 | 2 | 431 |
| HandOutlines | 1000 | 370 | 2 | 2709 |
| Haptics | 155 | 308 | 5 | 1092 |
| Herring | 64 | 64 | 2 | 512 |
| HouseTwenty | 34 | 101 | 2 | 3000 |
| InlineSkate | 100 | 550 | 7 | 1882 |
| InsectEPGRegTra | 62 | 249 | 3 | 601 |
| InsectEPGSmallTra | 17 | 249 | 3 | 601 |
| InsectWingSnd | 30,000 | 20,000 | 10 | 30 |
| ItalyPowerDemand | 67 | 1029 | 2 | 24 |
| LargeKitchenApp | 375 | 375 | 3 | 720 |
| Lightning2 | 60 | 61 | 2 | 637 |
| Lightning7 | 70 | 73 | 7 | 319 |
| Mallat | 55 | 2345 | 8 | 1024 |
| Meat | 60 | 60 | 3 | 448 |
| MedicalImages | 381 | 760 | 10 | 99 |
| MelbournePed | 1194 | 2439 | 10 | 24 |
| MidPhxOutAgeGp | 400 | 154 | 3 | 80 |
| MidPhxOutCorr | 600 | 291 | 2 | 80 |
| MidPhxTW | 399 | 154 | 6 | 80 |
| MixedRegularTrain | 500 | 2425 | 5 | 1024 |
| MixedSmallTrain | 100 | 2425 | 5 | 1024 |
| MoteStrain | 20 | 1252 | 2 | 84 |
| NonFetalECGTh1 | 1800 | 1965 | 42 | 750 |
| NonFetalECGTh2 | 1800 | 1965 | 42 | 750 |
| OliveOil | 30 | 30 | 4 | 570 |
| OSULeaf | 200 | 242 | 6 | 427 |
| PhaOutCorr | 1800 | 858 | 2 | 80 |
| Phoneme | 214 | 1896 | 39 | 1024 |
| PickupGestureWZ | 50 | 50 | 10 | 0 |
| PigAirwayPressure | 104 | 208 | 52 | 2000 |
| PigArtPressure | 104 | 208 | 52 | 2000 |
| PigCVP | 104 | 208 | 52 | 2000 |
| PLAID | 537 | 537 | 11 | 0 |
| Plane | 105 | 105 | 7 | 144 |
| PowerCons | 180 | 180 | 2 | 144 |
| ProxPhxOutAgeGp | 400 | 205 | 3 | 80 |
| ProxPhaxOutCorr | 600 | 291 | 2 | 80 |
| ProxPhxTW | 400 | 205 | 6 | 80 |
| RefDevices | 375 | 375 | 3 | 720 |
| Rock | 20 | 50 | 4 | 2844 |
| ScreenType | 375 | 375 | 3 | 720 |
| SemgHandGenCh2 | 300 | 600 | 2 | 1500 |
| SemgHandMovCh2 | 450 | 450 | 6 | 1500 |
| SemgHandSubCh2 | 450 | 450 | 5 | 1500 |
| ShakeGestureWZ | 50 | 50 | 10 | 0 |
| ShapeletSim | 20 | 180 | 2 | 500 |
| ShapesAll | 600 | 600 | 60 | 512 |
| SmallKitchenApp | 375 | 375 | 3 | 720 |
| SmoothSubspace | 150 | 150 | 3 | 15 |
| SonyAIBORobSur1 | 20 | 601 | 2 | 70 |
| SonyAIBORobSur2 | 27 | 953 | 2 | 65 |
| StarLightCurves | 1000 | 8236 | 3 | 1024 |
| Strawberry | 613 | 370 | 2 | 235 |
| SwedishLeaf | 500 | 625 | 15 | 128 |
| Symbols | 25 | 995 | 6 | 398 |
| SyntheticControl | 300 | 300 | 6 | 60 |
| ToeSegmentation1 | 40 | 228 | 2 | 277 |
| ToeSegmentation2 | 36 | 130 | 2 | 343 |
| Trace | 100 | 100 | 4 | 275 |
| TwoLeadECG | 23 | 1139 | 2 | 82 |
| TwoPatterns | 1000 | 4000 | 4 | 128 |
| UMD | 36 | 144 | 3 | 150 |
| UWaveAll | 896 | 3582 | 8 | 945 |
| UwaveX | 896 | 3582 | 8 | 315 |
| UwaveY | 896 | 3582 | 8 | 315 |
| UwaveZ | 896 | 3582 | 8 | 315 |
| Wafer | 1000 | 6164 | 2 | 152 |
| Wine | 57 | 54 | 2 | 234 |
| WordSynonyms | 267 | 638 | 25 | 270 |
| Worms | 181 | 77 | 5 | 900 |
| WormsTwoClass | 181 | 77 | 2 | 900 |
| Yoga | 300 | 3000 | 2 | 426 |
| Dataset | ED | DDTW | DTD | LCSS | BOSS | EE | FCOTE | TSF | TSBF | ST | LPS | FS | LA-ESN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Adiac | 0.611 | 0.701 | 0.701 | 0.522 | 0.765 | 0.665 | 0.790 | 0.731 | 0.770 | 0.783 | 0.770 | 0.593 | 0.984 (0.002) |
| Beef | 0.667 | 0.667 | 0.667 | 0.867 | 0.800 | 0.633 | 0.867 | 0.767 | 0.567 | 0.900 | 0.600 | 0.567 | 0.935 (0.009) |
| BeetleFly | 0.750 | 0.650 | 0.650 | 0.800 | 0.900 | 0.750 | 0.800 | 0.750 | 0.800 | 0.900 | 0.800 | 0.700 | 0.783 (0.080) |
| BirdChicken | 0.550 | 0.850 | 0.800 | 0.800 | 0.950 | 0.800 | 0.900 | 0.800 | 0.900 | 0.800 | 1.000 | 0.750 | 0.775 (0.048) |
| Car | 0.733 | 0.800 | 0.783 | 0.767 | 0.833 | 0.833 | 0.900 | 0.767 | 0.783 | 0.917 | 0.850 | 0.750 | 0.931 (0.002) |
| CBF | 0.852 | 0.997 | 0.980 | 0.991 | 0.998 | 0.998 | 0.996 | 0.994 | 0.988 | 0.974 | 0.999 | 0.940 | 0.901 (0.030) |
| ChlorineCon | 0.650 | 0.708 | 0.713 | 0.592 | 0.661 | 0.656 | 0.727 | 0.720 | 0.692 | 0.700 | 0.608 | 0.546 | 0.911 (0.009) |
| CinCECGTorso | 0.897 | 0.725 | 0.852 | 0.869 | 0.900 | 0.942 | 0.995 | 0.983 | 0.712 | 0.954 | 0.736 | 0.859 | 0.909 (0.004) |
| Computers | 0.576 | 0.716 | 0.716 | 0.584 | 0.756 | 0.708 | 0.740 | 0.720 | 0.756 | 0.736 | 0.680 | 0.500 | 0.551 (0.012) |
| CricketX | 0.577 | 0.754 | 0.754 | 0.741 | 0.736 | 0.813 | 0.808 | 0.664 | 0.705 | 0.772 | 0.697 | 0.485 | 0.930 (0.004) |
| CricketY | 0.567 | 0.777 | 0.774 | 0.718 | 0.754 | 0.805 | 0.826 | 0.672 | 0.736 | 0.779 | 0.767 | 0.531 | 0.933 (0.002) |
| CricketZ | 0.587 | 0.774 | 0.774 | 0.741 | 0.746 | 0.782 | 0.815 | 0.672 | 0.715 | 0.787 | 0.754 | 0.464 | 0.935 (0.003) |
| DiatomSizeR | 0.935 | 0.967 | 0.915 | 0.980 | 0.931 | 0.944 | 0.928 | 0.931 | 0.899 | 0.925 | 0.905 | 0.866 | 0.978 (0.005) |
| DistPhxAgeGp | 0.626 | 0.705 | 0.662 | 0.719 | 0.748 | 0.691 | 0.748 | 0.748 | 0.712 | 0.770 | 0.669 | 0.655 | 0.803 (0.007) |
| DistPhxCorr | 0.717 | 0.732 | 0.725 | 0.779 | 0.728 | 0.728 | 0.761 | 0.772 | 0.783 | 0.775 | 0.721 | 0.750 | 0.748 (0.009) |
| DistPhxTW | 0.633 | 0.612 | 0.576 | 0.626 | 0.676 | 0.647 | 0.698 | 0.669 | 0.676 | 0.662 | 0.568 | 0.626 | 0.893 (0.005) |
| Earthquakes | 0.712 | 0.705 | 0.705 | 0.741 | 0.748 | 0.741 | 0.748 | 0.748 | 0.748 | 0.741 | 0.640 | 0.705 | 0.734 (0.014) |
| ECG200 | 0.880 | 0.830 | 0.840 | 0.880 | 0.870 | 0.880 | 0.880 | 0.870 | 0.840 | 0.830 | 0.860 | 0.810 | 0.904 (0.010) |
| ECG5000 | 0.925 | 0.924 | 0.924 | 0.932 | 0.941 | 0.939 | 0.946 | 0.939 | 0.940 | 0.944 | 0.917 | 0.923 | 0.973 (0.000) |
| ECGFiveDays | 0.797 | 0.769 | 0.822 | 1.000 | 0.983 | 0.820 | 0.999 | 0.956 | 0.877 | 0.984 | 0.879 | 0.998 | 0.883 (0.040) |
| ElectricDevices | 0.552 | 0.592 | 0.594 | 0.587 | 0.799 | 0.663 | 0.713 | 0.693 | 0.703 | 0.747 | 0.681 | 0.579 | 0.895 (0.003) |
| FaceAll | 0.714 | 0.902 | 0.899 | 0.749 | 0.782 | 0.849 | 0.918 | 0.751 | 0.744 | 0.779 | 0.767 | 0.626 | 0.974 (0.002) |
| FaceFour | 0.784 | 0.829 | 0.818 | 0.966 | 0.996 | 0.909 | 0.898 | 0.932 | 1.000 | 0.852 | 0.943 | 0.909 | 0.910 (0.011) |
| FacesUCR | 0.769 | 0.904 | 0.908 | 0.939 | 0.957 | 0.945 | 0.942 | 0.883 | 0.867 | 0.906 | 0.926 | 0.706 | 0.977 (0.003) |
| FiftyWords | 0.631 | 0.754 | 0.754 | 0.730 | 0.705 | 0.820 | 0.798 | 0.741 | 0.758 | 0.705 | 0.818 | 0.481 | 0.988 (0.001) |
| Fish | 0.783 | 0.943 | 0.926 | 0.960 | 0.989 | 0.966 | 0.983 | 0.794 | 0.834 | 0.989 | 0.943 | 0.783 | 0.965 (0.002) |
| FordA | 0.665 | 0.723 | 0.765 | 0.957 | 0.930 | 0.738 | 0.957 | 0.815 | 0.850 | 0.971 | 0.873 | 0.787 | 0.789 (0.011) |
| FordB | 0.606 | 0.667 | 0.653 | 0.917 | 0.711 | 0.662 | 0.804 | 0.688 | 0.599 | 0.807 | 0.711 | 0.728 | 0.697 (0.014) |
| GunPoint | 0.913 | 0.980 | 0.987 | 1.000 | 0.994 | 0.993 | 1.000 | 0.973 | 0.987 | 1.000 | 0.993 | 0.947 | 0.947 (0.007) |
| Ham | 0.600 | 0.476 | 0.552 | 0.667 | 0.667 | 0.571 | 0.648 | 0.743 | 0.762 | 0.686 | 0.562 | 0.648 | 0.689 (0.009) |
| HandOutlines | 0.862 | 0.868 | 0.865 | 0.481 | 0.903 | 0.889 | 0.919 | 0.919 | 0.854 | 0.932 | 0.881 | 0.811 | 0.903 (0.005) |
| Haptics | 0.370 | 0.399 | 0.399 | 0.468 | 0.461 | 0.393 | 0.523 | 0.445 | 0.490 | 0.523 | 0.432 | 0.393 | 0.783 (0.007) |
| Herring | 0.516 | 0.547 | 0.547 | 0.625 | 0.547 | 0.578 | 0.625 | 0.609 | 0.641 | 0.672 | 0.578 | 0.531 | 0.609 (0.018) |
| InlineSkate | 0.342 | 0.562 | 0.509 | 0.438 | 0.516 | 0.460 | 0.495 | 0.376 | 0.385 | 0.373 | 0.500 | 0.189 | 0.816 (0.004) |
| InsWngSnd | 0.562 | 0.355 | 0.473 | 0.606 | 0.523 | 0.595 | 0.653 | 0.633 | 0.625 | 0.627 | 0.551 | 0.489 | 0.931 (0.001) |
| ItalyPrDmd | 0.955 | 0.950 | 0.951 | 0.960 | 0.909 | 0.962 | 0.961 | 0.960 | 0.883 | 0.948 | 0.923 | 0.917 | 0.958 (0.008) |
| LrgKitApp | 0.493 | 0.795 | 0.795 | 0.701 | 0.765 | 0.811 | 0.845 | 0.571 | 0.528 | 0.859 | 0.717 | 0.560 | 0.637 (0.015) |
| Lightning2 | 0.754 | 0.869 | 0.869 | 0.820 | 0.810 | 0.885 | 0.869 | 0.803 | 0.738 | 0.738 | 0.819 | 0.705 | 0.702 (0.026) |
| Lightning7 | 0.575 | 0.671 | 0.657 | 0.795 | 0.666 | 0.767 | 0.808 | 0.753 | 0.726 | 0.726 | 0.739 | 0.644 | 0.901 (0.009) |
| Mallat | 0.914 | 0.949 | 0.927 | 0.950 | 0.949 | 0.939 | 0.954 | 0.919 | 0.960 | 0.964 | 0.908 | 0.976 | 0.976 (0.005) |
| Meat | 0.933 | 0.933 | 0.933 | 0.733 | 0.900 | 0.933 | 0.917 | 0.933 | 0.933 | 0.850 | 0.883 | 0.833 | 0.917 (0.054) |
| MedicalImages | 0.684 | 0.737 | 0.745 | 0.664 | 0.718 | 0.742 | 0.758 | 0.755 | 0.705 | 0.670 | 0.746 | 0.624 | 0.945 (0.002) |
| MidPhxAgeGp | 0.519 | 0.539 | 0.500 | 0.571 | 0.545 | 0.558 | 0.636 | 0.578 | 0.578 | 0.643 | 0.487 | 0.545 | 0.660 (0.021) |
| MidPhxCorr | 0.766 | 0.732 | 0.742 | 0.780 | 0.780 | 0.784 | 0.804 | 0.828 | 0.814 | 0.794 | 0.773 | 0.729 | 0.779 (0.009) |
| MidPhxTW | 0.513 | 0.487 | 0.500 | 0.506 | 0.545 | 0.513 | 0.571 | 0.565 | 0.597 | 0.519 | 0.526 | 0.532 | 0.855 (0.006) |
| MoteStrain | 0.879 | 0.833 | 0.768 | 0.883 | 0.846 | 0.883 | 0.937 | 0.869 | 0.903 | 0.897 | 0.922 | 0.777 | 0.848 (0.022) |
| NonInv_Thor1 | 0.829 | 0.806 | 0.841 | 0.259 | 0.838 | 0.846 | 0.931 | 0.876 | 0.842 | 0.950 | 0.812 | 0.710 | 0.997 (0.000) |
| NonInv_Thor2 | 0.880 | 0.893 | 0.890 | 0.770 | 0.900 | 0.913 | 0.946 | 0.910 | 0.862 | 0.951 | 0.841 | 0.754 | 0.997 (0.000) |
| OliveOil | 0.867 | 0.833 | 0.867 | 0.167 | 0.867 | 0.867 | 0.900 | 0.867 | 0.833 | 0.900 | 0.867 | 0.733 | 0.750 (0.000) |
| OSULeaf | 0.521 | 0.880 | 0.884 | 0.777 | 0.955 | 0.806 | 0.967 | 0.583 | 0.760 | 0.967 | 0.740 | 0.678 | 0.853 (0.005) |
| PhaOutCorr | 0.761 | 0.739 | 0.761 | 0.765 | 0.772 | 0.773 | 0.770 | 0.803 | 0.830 | 0.763 | 0.756 | 0.744 | 0.784 (0.019) |
| Phoneme | 0.109 | 0.269 | 0.268 | 0.218 | 0.265 | 0.305 | 0.349 | 0.212 | 0.276 | 0.321 | 0.237 | 0.174 | 0.963 (0.000) |
| ProxPhxAgeGp | 0.785 | 0.800 | 0.795 | 0.834 | 0.834 | 0.805 | 0.854 | 0.849 | 0.849 | 0.844 | 0.795 | 0.780 | 0.893 (0.006) |
| ProxPhxCorr | 0.808 | 0.794 | 0.794 | 0.849 | 0.849 | 0.808 | 0.869 | 0.828 | 0.873 | 0.883 | 0.842 | 0.804 | 0.865 (0.026) |
| ProxPhxTW | 0.707 | 0.769 | 0.771 | 0.776 | 0.800 | 0.766 | 0.780 | 0.815 | 0.810 | 0.805 | 0.732 | 0.702 | 0.926 (0.007) |
| RefDev | 0.395 | 0.445 | 0.445 | 0.515 | 0.499 | 0.437 | 0.547 | 0.589 | 0.472 | 0.581 | 0.459 | 0.333 | 0.596 (0.009) |
| ScreenType | 0.360 | 0.429 | 0.437 | 0.429 | 0.464 | 0.445 | 0.547 | 0.456 | 0.509 | 0.520 | 0.416 | 0.413 | 0.593 (0.013) |
| ShapesAll | 0.752 | 0.850 | 0.838 | 0.768 | 0.908 | 0.867 | 0.892 | 0.792 | 0.185 | 0.842 | 0.873 | 0.580 | 0.993 (0.000) |
| SmlKitApp | 0.344 | 0.640 | 0.648 | 0.664 | 0.725 | 0.696 | 0.776 | 0.811 | 0.672 | 0.792 | 0.712 | 0.333 | 0.619 (0.023) |
| SonyAIBORobot | 0.696 | 0.742 | 0.710 | 0.810 | 0.895 | 0.704 | 0.845 | 0.787 | 0.795 | 0.844 | 0.774 | 0.686 | 0.730 (0.054) |
| SonyAIBORobot2 | 0.859 | 0.892 | 0.892 | 0.875 | 0.888 | 0.878 | 0.952 | 0.810 | 0.778 | 0.934 | 0.872 | 0.790 | 0.836 (0.014) |
| StarlightCurves | 0.849 | 0.962 | 0.962 | 0.947 | 0.978 | 0.926 | 0.980 | 0.969 | 0.977 | 0.979 | 0.963 | 0.918 | 0.960 (0.002) |
| Strawberry | 0.946 | 0.954 | 0.957 | 0.911 | 0.976 | 0.946 | 0.951 | 0.965 | 0.954 | 0.962 | 0.962 | 0.903 | 0.947 (0.016) |
| SwedishLeaf | 0.789 | 0.901 | 0.896 | 0.907 | 0.922 | 0.915 | 0.955 | 0.914 | 0.915 | 0.928 | 0.920 | 0.768 | 0.984 (0.001) |
| Symbols | 0.899 | 0.953 | 0.963 | 0.932 | 0.961 | 0.959 | 0.963 | 0.915 | 0.946 | 0.882 | 0.963 | 0.934 | 0.950 (0.009) |
| SynthCntr | 0.880 | 0.993 | 0.997 | 0.997 | 0.967 | 0.990 | 1.000 | 0.987 | 0.994 | 0.983 | 0.980 | 0.910 | 0.990 (0.003) |
| Trace | 0.760 | 1.000 | 0.990 | 1.000 | 1.000 | 0.990 | 1.000 | 0.990 | 0.980 | 1.000 | 0.980 | 1.000 | 0.908 (0.010) |
| TwoLeadECG | 0.747 | 0.978 | 0.985 | 0.996 | 0.985 | 0.971 | 0.993 | 0.759 | 0.866 | 0.997 | 0.948 | 0.924 | 0.795 (0.050) |
| TwoPatterns | 0.907 | 1.000 | 0.999 | 0.993 | 0.991 | 1.000 | 1.000 | 0.991 | 0.976 | 0.955 | 0.982 | 0.908 | 0.980 (0.006) |
| UWaveX | 0.739 | 0.779 | 0.775 | 0.791 | 0.753 | 0.805 | 0.822 | 0.804 | 0.831 | 0.803 | 0.829 | 0.695 | 0.941 (0.001) |
| UWaveY | 0.662 | 0.716 | 0.698 | 0.703 | 0.661 | 0.726 | 0.759 | 0.727 | 0.736 | 0.730 | 0.761 | 0.596 | 0.922 (0.001) |
| UWaveZ | 0.649 | 0.696 | 0.679 | 0.747 | 0.695 | 0.724 | 0.750 | 0.743 | 0.772 | 0.748 | 0.768 | 0.638 | 0.925 (0.001) |
| Wafer | 0.995 | 0.980 | 0.993 | 0.996 | 0.995 | 0.997 | 1.000 | 0.996 | 0.995 | 1.000 | 0.997 | 0.997 | 0.995 (0.000) |
| Wine | 0.611 | 0.574 | 0.611 | 0.500 | 0.912 | 0.574 | 0.648 | 0.630 | 0.611 | 0.796 | 0.629 | 0.759 | 0.497 (0.007) |
| WordSynonyms | 0.618 | 0.730 | 0.730 | 0.607 | 0.659 | 0.779 | 0.757 | 0.647 | 0.688 | 0.570 | 0.755 | 0.431 | 0.970 (0.000) |
| Yoga | 0.830 | 0.856 | 0.856 | 0.834 | 0.918 | 0.879 | 0.877 | 0.859 | 0.819 | 0.818 | 0.869 | 0.695 | 0.844 (0.004) |
| Average | 0.703 | 0.766 | 0.767 | 0.756 | 0.805 | 0.785 | 0.831 | 0.780 | 0.769 | 0.814 | 0.777 | 0.694 | 0.861 |
| Total | 1 | 3 | 2 | 5 | 9 | 4 | 13 | 4 | 7 | 13 | 3 | 1 | 36 |
| MR | 10.605 | 7.855 | 7.947 | 7.026 | 5.474 | 6.158 | 2.961 | 6.224 | 6.566 | 4.750 | 7.263 | 10.921 | 4.684 |
| ME | 0.079 | 0.065 | 0.065 | 0.062 | 0.050 | 0.060 | 0.046 | 0.058 | 0.059 | 0.048 | 0.060 | 0.077 | 0.052 |
| Dataset | MLP | FCN | ResNet | Inception Time | LA-ESN | |
|---|---|---|---|---|---|---|
| AC(SD) | Time(s) | |||||
| ACSF1 | 0.558 | 0.898 | 0.916 | 0.896 | 0.907 (0.004) | 169.4 |
| Adiac | 0.391 | 0.841 | 0.833 | 0.830 | 0.984 (0.002) | 348.8 |
| AllGestureX | 0.477 | 0.713 | 0.741 | 0.772 | 0.904 (0.001) | 257.7 |
| AllGestureY | 0.571 | 0.784 | 0.794 | 0.813 | 0.912 (0.002) | 257.0 |
| AllGestureZ | 0.439 | 0.692 | 0.726 | 0.792 | 0.891 (0.001) | 257.7 |
| ArrowHead | 0.784 | 0.843 | 0.838 | 0.847 | 0.850 (0.016) | 39.0 |
| Beef | 0.713 | 0.680 | 0.753 | 0.687 | 0.935 (0.009) | 40.1 |
| BeetleFly | 0.880 | 0.910 | 0.850 | 0.800 | 0.790 (0.086) | 85.1 |
| BirdChicken | 0.740 | 0.940 | 0.880 | 0.950 | 0.790 (0.037) | 30.8 |
| BME | 0.905 | 0.836 | 0.999 | 0.993 | 0.928 (0.004) | 29.6 |
| Car | 0.783 | 0.913 | 0.917 | 0.890 | 0.931 (0.002) | 107.4 |
| CBF | 0.869 | 0.994 | 0.996 | 0.998 | 0.900 (0.033) | 129.0 |
| Chinatown | 0.872 | 0.980 | 0.978 | 0.983 | 0.706 (0.091) | 39.3 |
| ChlorineCon | 0.800 | 0.817 | 0.853 | 0.873 | 0.911 (0.009) | 892.9 |
| CinCECGTorso | 0.838 | 0.829 | 0.838 | 0.842 | 0.909 (0.004) | 1033.2 |
| Coffee | 0.993 | 1.000 | 1.000 | 1.000 | 1.000 (0.000) | 94.7 |
| Computers | 0.558 | 0.819 | 0.806 | 0.786 | 0.548 (0.010) | 299.5 |
| CricketX | 0.591 | 0.794 | 0.799 | 0.841 | 0.930 (0.004) | 308.2 |
| CricketY | 0.598 | 0.793 | 0.810 | 0.839 | 0.933 (0.002) | 323.2 |
| CricketZ | 0.629 | 0.810 | 0.809 | 0.849 | 0.935 (0.003) | 302.1 |
| Crop | 0.618 | 0.738 | 0.743 | 0.751 | 0.911 (0.136) | 1657.0 |
| DiatomSizeR | 0.909 | 0.346 | 0.301 | 0.935 | 0.978 (0.005) | 108.2 |
| DistPhxAgeGp | 0.647 | 0.718 | 0.718 | 0.734 | 0.803 (0.007) | 123.5 |
| DistlPhxOutCorr | 0.727 | 0.760 | 0.770 | 0.768 | 0.748 (0.009) | 197.1 |
| DistPhxTW | 0.610 | 0.695 | 0.663 | 0.665 | 0.893 (0.005) | 123.7 |
| DodgerLoopDay | 0.160 | 0.143 | 0.150 | 0.150 | 0.875 (0.013) | 49.8 |
| DodgerLoopGame | 0.865 | 0.768 | 0.710 | 0.854 | 0.810 (0.048) | 34.5 |
| DodgerLoopWnd | 0.978 | 0.904 | 0.952 | 0.970 | 0.971 (0.022) | 34.1 |
| Earthquakes | 0.727 | 0.725 | 0.712 | 0.742 | 0.738 (0.012) | 287.4 |
| ECG200 | 0.914 | 0.888 | 0.874 | 0.918 | 0.904 (0.010) | 93.7 |
| ECG5000 | 0.930 | 0.940 | 0.935 | 0.939 | 0.973 (0.000) | 712.0 |
| ECGFiveDays | 0.973 | 0.985 | 0.966 | 1.000 | 0.892 (0.038) | 203.2 |
| ElectricDevices | 0.593 | 0.706 | 0.728 | 0.709 | 0.896 (0.003) | 4303.5 |
| EOGHorSignal | 0.432 | 0.565 | 0.599 | 0.588 | 0.899 (0.005) | 511.0 |
| EOGVerticalSignal | 0.418 | 0.446 | 0.445 | 0.464 | 0.899 (0.003) | 508.3 |
| EthanolLevel | 0.386 | 0.484 | 0.758 | 0.804 | 0.765 (0.030) | 933.2 |
| FaceAll | 0.794 | 0.938 | 0.867 | 0.801 | 0.974 (0.002) | 624.2 |
| FaceFour | 0.836 | 0.930 | 0.955 | 0.957 | 0.910 (0.011) | 47.9 |
| FacesUCR | 0.831 | 0.943 | 0.954 | 0.964 | 0.977 (0.003) | 320.9 |
| FiftyWords | 0.708 | 0.646 | 0.740 | 0.807 | 0.988 (0.001) | 311.3 |
| Fish | 0.848 | 0.961 | 0.981 | 0.976 | 0.965 (0.002) | 165.3 |
| FordA | 0.816 | 0.914 | 0.937 | 0.957 | 0.786 (0.010) | 3204.3 |
| FordB | 0.707 | 0.772 | 0.813 | 0.849 | 0.700 (0.014) | 2970.7 |
| FreezerRegularT | 0.906 | 0.997 | 0.998 | 0.996 | 0.959 (0.013) | 352.7 |
| FreezerSmallTrain | 0.686 | 0.683 | 0.832 | 0.866 | 0.676 (0.007) | 324.5 |
| Fungi | 0.863 | 0.018 | 0.177 | 1.000 | 0.986 (0.006) | 35.4 |
| GestureMidAirD1 | 0.575 | 0.695 | 0.698 | 0.732 | 0.969 (0.002) | 111.8 |
| GestureMidAirD2 | 0.545 | 0.631 | 0.668 | 0.708 | 0.963 (0.002) | 110.5 |
| GestureMidAirD3 | 0.382 | 0.326 | 0.340 | 0.366 | 0.955 (0.002) | 111.3 |
| GesturePebbleZ1 | 0.792 | 0.880 | 0.901 | 0.922 | 0.942 (0.003) | 100.8 |
| GesturePebbleZ2 | 0.701 | 0.781 | 0.777 | 0.875 | 0.922 (0.018) | 104.3 |
| GunPoint | 0.928 | 1.000 | 0.991 | 1.000 | 0.947 (0.007) | 52.7 |
| GunPointAgeSpan | 0.934 | 0.996 | 0.997 | 0.987 | 0.882 (0.009) | 71.4 |
| GunPointMaleFe | 0.980 | 0.997 | 0.992 | 0.996 | 0.985 (0.004) | 70.1 |
| GunPointOldYg | 0.941 | 0.989 | 0.989 | 0.962 | 0.992 (0.007) | 70.6 |
| Ham | 0.699 | 0.707 | 0.758 | 0.705 | 0.688 (0.009) | 119.4 |
| HandOutlines | 0.914 | 0.799 | 0.914 | 0.946 | 0.903 (0.005) | 3273.4 |
| Haptics | 0.425 | 0.490 | 0.510 | 0.549 | 0.783 (0.007) | 368.5 |
| Herring | 0.491 | 0.644 | 0.600 | 0.666 | 0.613 (0.018) | 89.4 |
| HouseTwenty | 0.734 | 0.982 | 0.983 | 0.975 | 0.803 (0.009) | 154.8 |
| InlineSkate | 0.335 | 0.332 | 0.377 | 0.485 | 0.816 (0.004) | 631.9 |
| InsectEPGRegTra | 0.646 | 0.999 | 0.998 | 0.998 | 0.788 (0.015) | 94.3 |
| InsectEPGSmallTra | 0.627 | 0.218 | 0.372 | 0.941 | 0.756 (0.005) | 73.0 |
| InsectWingSnd | 0.604 | 0.392 | 0.499 | 0.630 | 0.931 (0.001) | 497.3 |
| ItalyPowerDemand | 0.953 | 0.963 | 0.962 | 0.964 | 0.958 (0.008) | 166.9 |
| LargeKitchenApp | 0.470 | 0.903 | 0.901 | 0.900 | 0.641 (0.014) | 497.1 |
| Lightning2 | 0.682 | 0.734 | 0.780 | 0.787 | 0.702 (0.028) | 112.5 |
| Lightning7 | 0.616 | 0.825 | 0.827 | 0.803 | 0.901 (0.009) | 86.6 |
| Mallat | 0.923 | 0.967 | 0.974 | 0.941 | 0.976 (0.005) | 1212.1 |
| Meat | 0.893 | 0.803 | 0.990 | 0.933 | 0.916 (0.059) | 93.0 |
| MedicalImages | 0.719 | 0.778 | 0.770 | 0.787 | 0.945 (0.002) | 253.2 |
| MelbournePed | 0.863 | 0.912 | 0.909 | 0.908 | 0.973 (0.004) | 322.6 |
| MidPhxOutAgeGp | 0.522 | 0.535 | 0.545 | 0.523 | 0.660 (0.021) | 143.6 |
| MidPhxOutCorr | 0.755 | 0.795 | 0.826 | 0.816 | 0.781 (0.008) | 208.5 |
| MidPhxTW | 0.536 | 0.501 | 0.495 | 0.508 | 0.855 (0.006) | 173.7 |
| MixedRegularTrain | 0.907 | 0.955 | 0.973 | 0.966 | 0.963 (0.002) | 1101.6 |
| MixedSmallTrain | 0.841 | 0.893 | 0.917 | 0.912 | 0.934 (0.004) | 774.1 |
| MoteStrain | 0.855 | 0.936 | 0.924 | 0.886 | 0.848 (0.022) | 201.1 |
| NonFetalECGTh1 | 0.915 | 0.958 | 0.941 | 0.956 | 0.997 (0.000) | 2374.7 |
| NonFetalECGTh2 | 0.918 | 0.953 | 0.944 | 0.958 | 0.997 (0.000) | 2320.2 |
| OliveOil | 0.653 | 0.720 | 0.847 | 0.820 | 0.750 (0.000) | 63.8 |
| OSULeaf | 0.560 | 0.979 | 0.980 | 0.925 | 0.853 (0.005) | 201.5 |
| PhaOutCorr | 0.756 | 0.818 | 0.845 | 0.838 | 0.777 (0.013) | 512.4 |
| Phoneme | 0.094 | 0.328 | 0.333 | 0.328 | 0.963 (0.000) | 1109.9 |
| PickupGestureWZ | 0.604 | 0.744 | 0.704 | 0.744 | 0.936 (0.006) | 31.8 |
| PigAirwayPressure | 0.065 | 0.172 | 0.406 | 0.532 | 0.969 (0.001) | 302.6 |
| PigArtPressure | 0.105 | 0.987 | 0.991 | 0.993 | 0.971 (0.001) | 303.6 |
| PigCVP | 0.076 | 0.831 | 0.918 | 0.953 | 0.974 (0.000) | 302.1 |
| PLAID | 0.625 | 0.904 | 0.940 | 0.937 | 0.932 (0.001) | 791.3 |
| Plane | 0.977 | 1.000 | 1.000 | 1.000 | 0.993 (0.001) | 79.7 |
| PowerCons | 0.977 | 0.863 | 0.879 | 0.948 | 0.979 (0.010) | 70.1 |
| ProxPhxOutAgeGp | 0.849 | 0.825 | 0.847 | 0.845 | 0.893 (0.006) | 127.1 |
| ProxPhaxOutCorr | 0.730 | 0.907 | 0.920 | 0.918 | 0.865 (0.026) | 183.3 |
| ProxPhxTW | 0.767 | 0.761 | 0.773 | 0.781 | 0.926 (0.007) | 133.6 |
| RefDevices | 0.377 | 0.497 | 0.530 | 0.523 | 0.596 (0.009) | 439.7 |
| Rock | 0.852 | 0.632 | 0.552 | 0.752 | 0.917 (0.029) | 105.3 |
| ScreenType | 0.402 | 0.622 | 0.615 | 0.580 | 0.591 (0.014) | 470.7 |
| SemgHandGenCh2 | 0.822 | 0.816 | 0.824 | 0.802 | 0.825 (0.033) | 599.5 |
| SemgHandMovCh2 | 0.435 | 0.476 | 0.439 | 0.420 | 0.815 (0.015) | 710.8 |
| SemgHandSubCh2 | 0.817 | 0.742 | 0.739 | 0.787 | 0.922 (0.007) | 707.8 |
| ShakeGestureWZ | 0.548 | 0.884 | 0.880 | 0.900 | 0.920 (0.008) | 33.2 |
| ShapeletSim | 0.513 | 0.706 | 0.782 | 0.917 | 0.510 (0.032) | 54.4 |
| ShapesAll | 0.776 | 0.894 | 0.926 | 0.918 | 0.993 (0.000) | 561.3 |
| SmallKitchenApp | 0.380 | 0.777 | 0.781 | 0.756 | 0.615 (0.024) | 452.6 |
| SmoothSubspace | 0.980 | 0.975 | 0.980 | 0.981 | 0.880 (0.021) | 30.4 |
| SonyAIBORobSur1 | 0.692 | 0.958 | 0.961 | 0.864 | 0.734 (0.059) | 116.2 |
| SonyAIBORobSur2 | 0.831 | 0.980 | 0.975 | 0.946 | 0.838 (0.014) | 153.8 |
| StarLightCurves | 0.950 | 0.965 | 0.972 | 0.978 | 0.960 (0.002) | 4779.5 |
| Strawberry | 0.959 | 0.975 | 0.980 | 0.983 | 0.947 (0.016) | 350.3 |
| SwedishLeaf | 0.845 | 0.967 | 0.963 | 0.964 | 0.984(0.001) | 247.5 |
| Symbols | 0.836 | 0.955 | 0.893 | 0.980 | 0.948 (0.009) | 345.0 |
| SyntheticControl | 0.973 | 0.989 | 0.997 | 0.996 | 0.990 (0.003) | 100.6 |
| ToeSegmentation1 | 0.589 | 0.961 | 0.957 | 0.961 | 0.639 (0.025) | 52.9 |
| ToeSegmentation2 | 0.745 | 0.889 | 0.894 | 0.943 | 0.794 (0.026) | 44.2 |
| Trace | 0.806 | 1.000 | 1.000 | 1.000 | 0.910 (0.009) | 78.2 |
| TwoLeadECG | 0.753 | 0.999 | 1.000 | 0.997 | 0.806 (0.048) | 190.0 |
| TwoPatterns | 0.948 | 0.870 | 1.000 | 1.000 | 0.980 (0.006) | 813.6 |
| UMD | 0.949 | 0.988 | 0.990 | 0.982 | 0.925 (0.021) | 33.0 |
| UWaveAll | 0.954 | 0.818 | 0.861 | 0.944 | 0.988 (0.001) | 1740.2 |
| UWaveX | 0.768 | 0.754 | 0.781 | 0.814 | 0.941 (0.001) | 1324.3 |
| UWaveY | 0.699 | 0.642 | 0.666 | 0.755 | 0.922 (0.001) | 1346.0 |
| UWaveZ | 0.697 | 0.727 | 0.749 | 0.750 | 0.925 (0.001) | 1251.3 |
| Wafer | 0.996 | 0.997 | 0.998 | 0.999 | 0.995 (0.000) | 1309.3 |
| Wine | 0.541 | 0.611 | 0.722 | 0.659 | 0.496 (0.007) | 64.2 |
| WordSynonyms | 0.599 | 0.561 | 0.617 | 0.732 | 0.970 (0.000) | 296.5 |
| Worms | 0.457 | 0.782 | 0.761 | 0.769 | 0.794 (0.012) | 176.6 |
| WormsTwoClass | 0.608 | 0.743 | 0.748 | 0.782 | 0.626 (0.056) | 177.2 |
| Yoga | 0.856 | 0.837 | 0.867 | 0.891 | 0.845 (0.004) | 900.2 |
| Average | 0.705 | 0.786 | 0.807 | 0.836 | 0.871 | |
| Total | 2 | 13 | 25 | 32 | 64 | |
| MR | 4.313 | 3.234 | 2.648 | 2.250 | 2.430 | |
| ME | 0.066 | 0.048 | 0.043 | 0.037 | 0.047 | |
| Dataset | ESN_CNN | ECA | ESN_LSTM | ELA | LA-ESN |
|---|---|---|---|---|---|
| Adiac | 0.952 | 0.978 | 0.983 | 0.974 | 0.984 |
| Beef | 0.826 | 0.906 | 0.899 | 0.846 | 0.947 |
| CricketX | 0.930 | 0.925 | 0.928 | 0.925 | 0.930 |
| CricketY | 0.932 | 0.927 | 0.929 | 0.917 | 0.933 |
| ECG5000 | 0.973 | 0.973 | 0.967 | 0.970 | 0.973 |
| HandOutlines | 0.854 | 0.856 | 0.878 | 0.899 | 0.908 |
| Haptics | 0.736 | 0.784 | 0.753 | 0.779 | 0.783 |
| NonInv_Thor2 | 0.995 | 0.990 | 0.995 | 0.992 | 0.997 |
| ProxPhxAgeGp | 0.852 | 0.869 | 0.874 | 0.871 | 0.893 |
| ProxPhxTW | 0.913 | 0.926 | 0.934 | 0.935 | 0.926 |
| ShapesAll | 0.992 | 0.992 | 0.990 | 0.987 | 0.993 |
| SwedishLeaf | 0.982 | 0.983 | 0.978 | 0.978 | 0.984 |
| UWaveX | 0.942 | 0.941 | 0.933 | 0.934 | 0.941 |
| UWaveY | 0.910 | 0.915 | 0.899 | 0.912 | 0.922 |
| UWaveZ | 0.924 | 0.927 | 0.907 | 0.915 | 0.925 |
| Wafer | 0.986 | 0.960 | 0.990 | 0.990 | 0.995 |
| WordSynonyms | 0.967 | 0.967 | 0.966 | 0.964 | 0.970 |
| Average | 0.922 | 0.931 | 0.930 | 0.929 | 0.941 |
| Total | 3 | 3 | 0 | 1 | 13 |
| MR | 3.235 | 2.765 | 3.412 | 3.588 | 1.294 |
| ME | 0.016 | 0.015 | 0.014 | 0.014 | 0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, H.; Liu, M.; Hu, J.; Li, P.; Peng, Y.; Yi, Y. LA-ESN: A Novel Method for Time Series Classification. Information 2023, 14, 67. https://doi.org/10.3390/info14020067
Sheng H, Liu M, Hu J, Li P, Peng Y, Yi Y. LA-ESN: A Novel Method for Time Series Classification. Information. 2023; 14(2):67. https://doi.org/10.3390/info14020067
Chicago/Turabian StyleSheng, Hui, Min Liu, Jiyong Hu, Ping Li, Yali Peng, and Yugen Yi. 2023. "LA-ESN: A Novel Method for Time Series Classification" Information 14, no. 2: 67. https://doi.org/10.3390/info14020067
APA StyleSheng, H., Liu, M., Hu, J., Li, P., Peng, Y., & Yi, Y. (2023). LA-ESN: A Novel Method for Time Series Classification. Information, 14(2), 67. https://doi.org/10.3390/info14020067







