Abstract
Most of the existing estimation methods of spreading code sequence are not suitable for the QPSK-DSSS. We propose a spreading code sequence estimation method based on fast independent component analysis (Fast-ICA). It mainly includes signal preprocessing, calculations of separation matrix, and spreading code sequence. Firstly, the received signal is segmented according to the period of the spreading code sequence, and the covariance matrix can be calculated. Then, the signal subspace and corresponding eigenvalues are obtained by eigenvalue decomposition of the covariance matrix. Subsequently, the received signal matrix needs to be whitened. Finally, the Fast-ICA algorithm is used to find the separation matrix to estimate the in-phase and orthogonal spreading code sequence. The experiment result shows that the estimation of the spreading code sequence can be carried out based on Fast-ICA under a low SNR of −12 dB. Compared with the constant modulus algorithm (CMA) and the decomposition method for the real part of the self-covariance matrix (EVD-R), this method has a better performance.
1. Introduction
The direct sequence spread spectrum (DSSS) signal has the advantages of low power spectral density, low probability of interception, strong anti-interference ability, and good security performance []. Therefore, it is widely used in military and civil communication systems such as code division multiple access (CDMA) communication systems, tactical communication systems, tracking, and data relay satellite systems, etc. []. For non-cooperative receivers, even if the signal is intercepted, when the spreading code sequence cannot be accurately estimated, the original signal cannot be demodulated from the intercepted signal []. Therefore, how to accurately estimate the spreading code sequence of the spread spectrum signal under non-cooperative conditions has been a hot issue in the field of DSSS signal reconnaissance and processing.
The research on blind estimation of the spreading code sequence of DSSS signals mainly focuses on the baseband DSSS signal and the binary phase shift keying (BPSK) modulated DSSS signal. It mainly includes the covariance matrix eigendecomposition method, the correlation coefficient judgment method, the principal component analysis method, and the neural network method, etc. Choi, H. et al. proposed a spreading code sequence estimation method based on turbo processing []. This method can be implemented for both synchronous and asynchronous cases. Sun, X.Y. et al. proposed a spreading code sequence blind estimation algorithm based on fractional low order (FLO) joint M estimation []. This method further reduces the noise component of the received signal by constructing the fractional low order matrix of the received signal and using the weighted M estimation function. Mehboodi, S. et al. proposed a method of estimating the spreading code sequence by judging the correlation coefficient after segmenting the received signal according to the period []. By selecting some symbols in each cycle for the correlation operation, the correlation length is reduced and the calculation amount of the algorithm is reduced. Xiong, G. et al. designed an optimal estimator using the Hebb criterion []. They used the neural network method to estimate the spread spectrum sequence and improved the real-time performance of the algorithm. Some methods for estimating the spreading code sequences of long code DSSS signals have also been proposed [,]. The algorithms above were all researched on DSSS signals with BPSK modulation. They were not suitable for DSSS signals modulated by QPSK.
Because the I/Q (in-phase/quadrature) of the QPSK-DSSS signal used different spreading sequences, the principal component eigenvectors of the signal correlation matrix were stretched by two spreading code sequences. Therefore, these traditional algorithms could not be directly used. Zhang, H.G. et al. pointed out that the two-dimensional signal subspace after the eigendecomposition of the covariance matrix of the QPSK-DSSS signal has a fuzzy emirates matrix, hence it cannot be directly used to estimate the spreading code sequence []. They modeled the question as the solution to emirate the matrix fuzzy problem of the signal subspace, and then optimized the solution according to the constant model characteristic of spreading sequences. However, the performance of this algorithm was seriously degraded in the case of a low signal to noise ratio (SNR). Qiu, Z. Y. et al. studied the problem of QPSK-DSSS signal spreading sequence estimation with residual frequency offset based on Zhang, H.G. et al. []. However, this method has poor performance in the case of low SNR. Chen, X.L. et al. proposed a spreading code sequence estimation method based on signal correlation matrix spectral norms and correlation matrix eigendecomposition combined with an all-digital phase-locked loop []. However, this method is computationally intensive.
Independent component analysis (ICA) is a commonly used signal blind source separation algorithm. It has both fixed point and floating point types. It has applications in feature extraction [], blind separations of speech signals [], images, and underwater acoustic signals [], etc. Fast-ICA algorithm is a fast optimization iterative neural network algorithm proposed by Hyvarinen, A. []. It treats the received signal as a linear combination of multiple independent signals and separates the different types of signals from the mixed signal by using a separation matrix. This method has the characteristics of simple calculation and fast convergence []. In the spread spectrum communication system, it is mainly used to estimate the spread spectrum code sequence of the CDMA system [,,]. In Ref. [], Albataineh, Z. et al. proposed a new blind detection algorithm based on hyper-differential evolution (H-DE) combined with ICA, which improved the accuracy of information code extraction in CDMA signals. In Ref. [], Tian, R.X. et al. proposed an efficient iterative dimension-increasing method based on Fast-ICA algorithms to obtain the spreading code sequence of the DS-CDMA signal. The method blindly estimated the entire or part of the periodic spreading sequence from a small spreading period to a larger spreading period, and then used the two-norm of the vector to separate the spreading code sequences of different spreading periods, and finally obtained the spreading code sequences of all users. These methods can bring some reference to the estimation of the spreading code sequence of the QPSK-DSSS signal.
The motivations and contributions of this paper are as follows:
- This paper mainly focuses on the spreading code sequence estimation problem of QPSK- DSSS signals modulated by two different spreading code sequences with the same period. A blind estimation method of QPSK-DSSS signal spreading code sequences based on Fast-ICA algorithms is proposed.
- The proposed estimation method of spreading code sequences mainly includes signal whitening, separation matrix calculation, and spreading code extraction.
- The computational complexity of the algorithm is analyzed in Section 3.4 and is compared with other algorithms.
- In Section 4, we make experiments to study the influence of different spreading code lengths, information code lengths, frequency offsets, and different SNR on the spreading code estimation method. Finally, it is compared with the existing spreading code estimation method of QPSK-DSSS signal.
The rest of this paper is structured as follows. In Section 2, we elaborate the model of the QPSK-DSSS signal, and analyze the feasibility of Fast-ICA algorithms. In Section 3, we present a spreading code sequence estimation algorithm of the QPSK-DSSS signal based on Fast-ICA, which mainly includes signal whitening, separation matrix calculation, spreading code extraction, and algorithm complexity analysis. Section 4 is the simulation experiment and result analysis where we analyze the estimation performance of the proposed algorithm under different SNR, spreading code lengths, information code lengths, and residual frequency offsets, and compare them with CMA and EVD-R algorithms. Section 5 is the conclusion of this paper and the future work directions.
2. QPSK-DSSS Signal Model
The QPSK-DSSS signal model is shown in Figure 1. The information sequence, S(t), is mapped into in-phase branch, a(t), and quadrature branch, , after serial-to-parallel conversion. Then, two different spreading code sequences with the same period is used to spread the I/Q (in-phase/quadrature) two channels, respectively. When the spread spectrum signal passes through the forming filter, the two channel signals will be carrier modulated with mutually orthogonal carriers. Finally, the two signals can be combined to be the QPSK-DSSS signal.

Figure 1.
QPSK-DSSS signal model diagram.
The QPSK-DSSS signal is equivalent to the synchronized two-user BPSK-DSSS signal. The model can be expressed as:
where A represents the amplitude of the signal, and represents white Gaussian noise. We assume that the spreading code period, carrier frequency, and code rate have been obtained. Therefore, the discrete form of the baseband signal with noise obtained by down-converting and sampling the signal represented by Equation (1) can be expressed as:
where k = 0, 1, 2, …, N − 1, N represents the total number of symbols after spreading. If we segment the received signal, , without overlapping by the spreading code period L, we can obtain the received signal matrix R as the following:
where M is the number of information codes, and L is the length of the spreading code sequence, so N = LM. Substituting Equation (2) into Equation (3), we can get:
Making , , , then
It can be found that the recovery of the spreading code from the received signal is a typical blind source separation problem. Therefore, the spreading code can be extracted by the Fast-ICA algorithm.
3. Spreading Code Estimation Based on Fast-ICA Algorithm
The Fast-ICA algorithm is based on kurtosis, maximum likelihood estimation, maximum negative entropy, and other forms []. In this paper, the Fast-ICA algorithm based on maximum kurtosis is used to estimate the spreading code sequence. According to the central limit theorem, the solution is to find an optimal separation matrix, , by maximizing the non-Gaussian property of . In this paper, the objective function to measure the non-Gaussianity is the kurtosis function. When the kurtosis function reaches the maximum value, the optimal separation matrix, , can be obtained. Then, the two spreading code sequences can be restored from the receiving signal after whitening. The algorithm frame diagram is shown in Figure 2.

Figure 2.
Frame diagram of spreading code estimation algorithm.
3.1. Signal Whitening
Since the signals of each cycle of the received signal, R, are correlated, before using the Fast-ICA algorithm to estimate the spreading code sequence, the received signal needs to be whitened []. The new vector after whitening,, must satisfy . Whitening can remove the correlation between the received signal data, and it can simplify the blind separation algorithm, and then to improve the separation performance of the signal blind separation algorithm []. This process can be achieved by doing eigendecomposition, which is shown in the following:
- (1)
- The first step is calculating the covariance matrix of the received signal, r(t), . The larger means, the richer the information of the spreading sequence contained in the received signal. Therefore, theoretically, under the same condition of the SNR, the longer the information code length, , means the better the estimation effect of the spreading sequence;
- (2)
- Then, the eigendecomposition should be performed on , as shown in Equation (6).where represents the signal subspace, represents the noise subspace, and are the matrices formed by the eigenvalues corresponding to the vectors constituting the signal subspace and the noise subspace, respectively.
- (3)
- Finally, the received signal should be whitened using and .
3.2. Calculate the Separation Matrix
In the process of estimating the spreading code, the absolute value of kurtosis is used as the objective function to measure non-Gaussianity, which is
where is the separation matrix. Therefore, maximizing non-Gaussianity is equivalent to finding the maximum of where the constraint is of . Kurtosis is an index to define the non-Gaussianity of a random variable, which is defined as , where the random variable y is assumed to have zero mean.
Therefore, by calculating the absolute gradient of the kurtosis of , we obtain,
The data after whitening satisfies the Equation , so Equation (9) can be simplified as:
Therefore, , means equivalent, we can get
Equations (11) and (12) are repeated until the convergence condition is achieved. Then, can be used to isolate an independent component. In order to avoid getting the same sequence in every time, it is necessary to perform Schmidt orthogonalization on obtained both this time and before. Assuming that the j-th components has been obtained, it is necessary to orthogonalize before extracting the (j + 1)-th component,
3.3. Calculate the Spreading Code Sequence
After calculating the separation matrix , the operation of Equation (15) is performed through the separation matrix, , to separate the spreading code sequence from the whitened received signal.
The spreading code sequence estimation steps based on the Fast-ICA are shown in Table 1.

Table 1.
The steps of the spreading code estimation method based on Fast-ICA.
3.4. Algorithm Complexity Analysis
In this paper, the proposed estimation method of spreading code sequences mainly includes signal whitening, separation matrix calculation, and spread spectrum code extraction. The computational complexity of signal whitening is . The computational complexity of Equation (11) is . Assuming convergence after k iterations, the computational complexity of calculating the separation matrix is . It is estimated that the computational complexity of spread spectrum code is . Therefore, the total computational complexity of the proposed spread spectrum code estimation method is .
The computational complexity of the CMA is , K represents the number of iterations, and its size depends on the size of the iteration interval and the iteration step. The computational complexity of the EVD-R is . In this paper, k = 2, K = 300, so the complexity of Fsat-ICA is , the complexity of the CMA is . If L is a constant, for example, L = 127, the complexity curves of the three algorithms versus M are shown in Figure 3.

Figure 3.
Complexity variation curve versus M.
It can be seen that when M is less than L, the complexity of the Fast-ICA is less than the other two algorithms. In this condition, the Fast-ICA has a lower complexity. When M is bigger than L, the complexity of the Fast-ICA will no longer be an advantage.
4. Simulation Experiment and Result Analysis
This paper uses the average bit error rate (BER) to evaluate the estimation performance of the spreading sequence [,]:
where errorNum represents the number of different spreading codes from the original spreading codes in the estimation result of spreading codes, and represents the number of experiments. The smaller the average BER, the better the estimation performance. If , it means that the estimated value is equal to the true value.
In order to verify the performance of our algorithm, the influence of SNR, the spreading code length, the information code length, and the residual carrier are researched by simulation experiments. The performance is compared with other algorithms.
4.1. Relationship between BER and Spreading Code Length
In order to study the effect of spreading code length on the estimation performance, m-sequences with lengths of 127, 255, 511, 1023, and 2047 bits are used, respectively. In the simulation, the information code length is 200 bits, the spreading code rate is 1 MHz, the information code rate is MHz, and the sampling rate is 1 MHz; there is no residual carrier. One hundred Monte Carlo experiments are performed with different spreading code sequence lengths, and the results are shown in Figure 4.
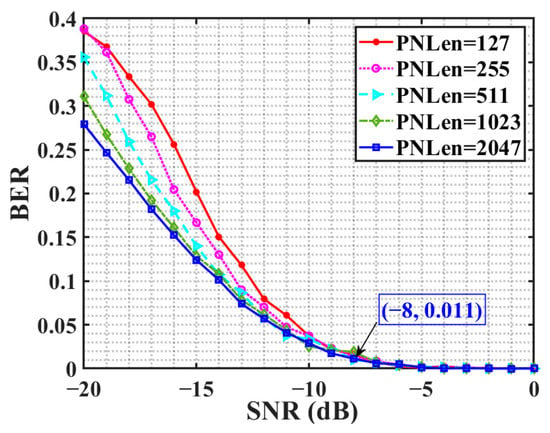
Figure 4.
Variation curve of BER with SNR under different spreading code lengths.
It can be seen that no matter how long the spread spectrum code sequence is, the BER of the estimated result decreases continuously with the increase in the SNR. When the SNR is higher than −8 dB, the spreading code sequence estimation method proposed in this paper is no longer affected by the length of the spreading code. When the SNR is lower than −8 dB, the longer the spreading code is, the lower the average BER is. It shows that in the case of low SNR, the longer the spreading code length is and the better the estimation performance.
4.2. Relationship between BER and Message Code Length
In order to study the influence of the information code length on the estimation performance, the information code length bit is selected. The SNR is −10 dB, the length of the spreading code is 255 bits, and other experimental parameters are the same as those in Section 4.1. One hundred Monte Carlo experiments were performed with different information code lengths, and the results are shown in Figure 5.

Figure 5.
Variation curve of BER with information code length.
From the experimental results in Figure 5, it can be seen that the longer the information code is, the lower the bit error rate. When the length of the information code reaches 750 bits, the method proposed in this paper estimates a nearly completely correct spreading code sequence when the SNR is −10 dB. The larger the length of the information code, the richer the information of the spreading code sequence contained in the received signal. We can get a more accurate estimation result of the spreading code sequence under the same SNR. In practical application, it is easier to estimate the spreading code when the longer signal is intercepted.
4.3. Relationship between BER and Residual Carrier
In order to study the effect of the residual carrier on the estimation performance, the residual frequency offsets in the simulation experiments were selected to be 10, 100, 500, 1000, and 2000 Hz, respectively. The length of the spreading code was 127 bits, the length of the information code was 100 bits, the SNR was [−20 dB, 0 dB], and other experimental parameters were the same as in Section 4.1. One hundred Monte Carlo experiments were performed with different residual frequency offsets, and the results are shown in Figure 6.

Figure 6.
Variation curve of BER with SNR under different residual frequency offset conditions.
From the simulation results in Figure 6, it can be seen that the effect of different residual frequency offsets on the estimation results is smaller with the lower SNR. When the SNR is −20 dB, the maximum difference of the average BER between the different residual frequency offsets is 4%. When the residual frequency offset is less than 100 Hz, the residual frequency offset has little effect on the spreading code estimation, and the estimation result is not affected by the residual carrier when the SNR is greater than 5 dB. When the residual frequency offset is greater than 100 Hz, the larger the residual frequency offset is, and the worse the estimation performance. The algorithm proposed in this paper is not suitable for the situation with a large residual frequency offset.
4.4. Comparison Experiment with Different Methods
In order to study the estimation performance of the method proposed in this paper, it is compared with the QPSK-DSSS signal spreading sequence estimation method based on CMA [] and EVD-R []. In the simulation experiment, the spread spectrum code period is 127 bits, the information code length is 100 bits, the other experimental parameters are the same as in Section 4.1. One hundred Monte Carlo experiments were performed, and the results are shown in Figure 7.
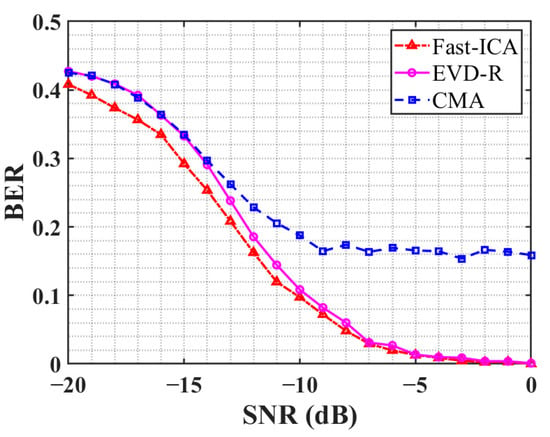
Figure 7.
Variation curve of BER with SNR for different methods.
It can be seen from the Figure 7 that with the increase in the SNR, the average BER of the three algorithms all decreased. However, when the SNR is lower than −14 dB, the average BER of the Fast-ICA is almost 5% lower than the EVD-R and CMA. When the SNR is above −14 dB, the average BER of the EVD-R and Fast-ICA gradually tend to be the same. However, the average BER of CMA has reached a constant of about 15% value when the SNR reaches −9 dB. When the SNR is above −5 dB, the average BER of the Fast-ICA is less than 2%, which is same to the EVD-R. Overall, the spreading code estimation method of Fast-ICA is superior to the EVD-R and CMA.
5. Conclusions
Most research on the estimation of spreading sequences has been aimed at BPSK-DSSS signals. In this paper, by studying the generation principle of QPSK-DSSS signal, it can be equivalent to two channels of the BPSK-DSSS signal, which is similar to a two-user DS-CDMA signal. We proposed a spreading code estimation method of QPSK-DSSS signal based on Fast-ICA algorithm.
Theoretical analysis and simulation results show that the Fast-ICA can effectively estimate the two-channel spreading code sequence of QPSK-DSSS signal under the condition of low SNR. Through a comparative experiment, it shows that the performance of the Fast-ICA is better than CMA and EVD-R. Meanwhile, when the number of information codes, M, is less than the period of spreading codes, L, the computational complexity of the Fast-ICA is less than the other two algorithms. However, the estimation performance of the proposed algorithm is poor in the case of large residual frequency offset, which needs to be improved. Next, we plan to further study how to reduce the influence of frequency shifts on the algorithm estimation results and consider the deep learning method in the spreading code sequence estimation.
Author Contributions
The contributions of all authors in terms of the literature search, theoretical research, experimental simulation, results analysis, and writing are equivalent. All authors have read and agreed to the published version of the manuscript.
Funding
The work leading to this publication has been partially funded by the Natural Science Foundation of Zhejiang Province, China, LQ20F050010, and the Fundamental Research Funds of Zhejiang Sci-Tech University, 2021Q030.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, J. Research on Blind Reconstruction Method of Spreading Code Sequence for Direct Spread Signal; Harbin Engineering University: Harbin, China, 2017. [Google Scholar]
- Choi, H.; Moon, H. Blind Estimation of Spreading Sequence and Data Bits in Direct-Sequence Spread Spectrum Communication Systems. IEEE Access 2020, 8, 148066–148074. [Google Scholar] [CrossRef]
- Sun, X.Y.; Fan, Z.; Ji, Y.F.; Yan, S.Q.; Wang, S.H.; Zhen, W.M. Blind Estimation of PN Sequence Based on FLO Joint M Estimation for Short-Code DSSS Signals. In Proceedings of the 2018 7th International Conference on Digital Home (ICDH), Guilin, China, 30 November–1 December 2018. [Google Scholar]
- Mehboodi, S.; Jamshidi, A.; Farhang, M. Two Algorithms for Spread Spectrum Sequence Estimation for DSSS Signals in Noncooperative Communication Systems. In Proceedings of the 2016 24th Iranian Conference on Electrical Engineering(ICEE), Shiraz, Iran, 10–12 May 2016. [Google Scholar]
- Xiong, G.; Zhao, E.F. Spread Spectrum Code Sequence Recognition Method based on Hebb Optimization Criterion. Commun. Technol. 2019, 52, 2098–2101. [Google Scholar]
- Qiang, X.Z.; Zhang, T.Q. Estimation of Spreading Code in non-periodic Long-Code DSSS Signal. In Proceedings of the 2021 Sixth International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 25–27 March 2021. [Google Scholar]
- Liu, Q.H.; Li, T.Y.; Xu, M.K. Joint Blind Estimation of PN Codes and Channels for Long-Code DSSS Signals in Multiple Paths at Low SNR. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology (ICCT), Nanning, China, 28–31 October 2020. [Google Scholar]
- Zhang, H.G.; Wei, P. Spreading squence estimation based on constant modulus property for QPSK-DSSS signals. Acta Aeroautica Astronaut. Sin. 2013, 34, 1389–1396. [Google Scholar]
- Qiu, Z.Y.; Peng, H.; Li, T.Y. A Blind Despreading and Demodulation Method for QPSK-DSSS Signal with Unknown Carrier Offset Based on Matrix Subspace Analysis. IEEE Access 2019, 7, 125700–125710. [Google Scholar] [CrossRef]
- Chen, X.L.; Zhang, T.Q.; Meng, Y.; Wang, X.Y. Blind Estimation of Pseudo-Code Sequences for QPSK-DSSS Signals with Residual Frequency Offset. J. Beijing Univ. Posts Telecommun. 2022, 45, 90–95. [Google Scholar]
- Wang, Y.; Fu, Y.H.; He, Z.M. Fetal Electrocardiogram Extraction Based on Fast ICA and Wavelet Denoising. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018. [Google Scholar]
- Zhang, X.; Liu, X.M. Frogmen Formation Voice Communication Technology Based on Fast ICA. In Proceedings of the 2021 OES China Ocean Acoustics (COA), Harbin, China, 14–17 July 2021. [Google Scholar]
- Tu, S.J.; Chen, H. Blind Source Separation of Underwater Acoustic Signal by Use of Negentropy-Based Fast ICA Algorithm. In Proceedings of the 2015 IEEE International Conference on Computational Intelligence & Communication Technology, Ghazizbad, India, 13–14 February 2015. [Google Scholar]
- Hyvarinen, A. A family of fixed-point algorithms for independent component analysis. In Proceedings of the 1997 IEEE International Conference on Acoustics, Speech, and Signal Processing, Munich, Germany, 21–24 April 1997. [Google Scholar]
- Naeem, A.; Arslan, H. Joint Radar and Communication based Blind Signal Separation using a New Non-Linear Function for Fast-ICA. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021. [Google Scholar]
- Albataineh, Z.; Salem, F. New Blind Multiuser Detection in DS-CDMA Using H-DE and ICA Algorithms. In Proceedings of the 2013 4th International Conference on Intelligent Systems, Modelling and Simulation, Bangkok, Thailand, 29–31 January 2013. [Google Scholar]
- Tian, R.X.; Hui, X.; Tao, H.Z.; Wang, F.H.; Lu, F.B. Fast-ICA Based Blind Estimation of the Spreading Sequences for Down-link Multi-Rate DS/CDMA Signals. In Proceedings of the 2012 Fifth International Conference on Intelligent Computation Technology and Automation, Zhangjiajie, China, 12–14 January 2012. [Google Scholar]
- Adkhan, S.B.; Mohammed, S.J.; Shubbar, M.M. Fast ICA and JADE Algorithms for DS-CDMA. In Proceedings of the 2017 Second Al-Sadiq International Conference on Multidisciplinary in IT and Communication Science and Applications (AICMITCSA), Baghdad, Iraq, 30–31 December 2017. [Google Scholar]
- Mora, H.R.C.; Garzón, N.V.O.; Almeida, C.D. Mean Bit Error Rate Evaluation of MC-CDMA Cellular Systems Employing Multiuser-Maximum-Likelihood Detector. IEEE Trans. Veh. Technol. 2017, 66, 9838–9851. [Google Scholar] [CrossRef]
- Karan, Y.; Kahveci, S. Extraction of Theoretical Bit and Symbol Error Rates of Dual Carrier Modulation with QPSK. In Proceedings of the 2019 27th Signal Processing and Communications Applications Conference (SIU), Sivas, Turkey, 24–26 April 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).