Model for Interference Evaluation in 5G Millimeter-Wave Ultra-Dense Network with Location-Aware Beamforming
Abstract
1. Introduction
2. Background for Location-Aware Beamforming in 5G Ultra-Dense Networks
3. Link Level Simulation Model for Interference Evaluation in 5G UDN with LAB
3.1. SIR Dependence on the Terrestrial Separation of Two gNB-UE Links in 5G UDN with LAB
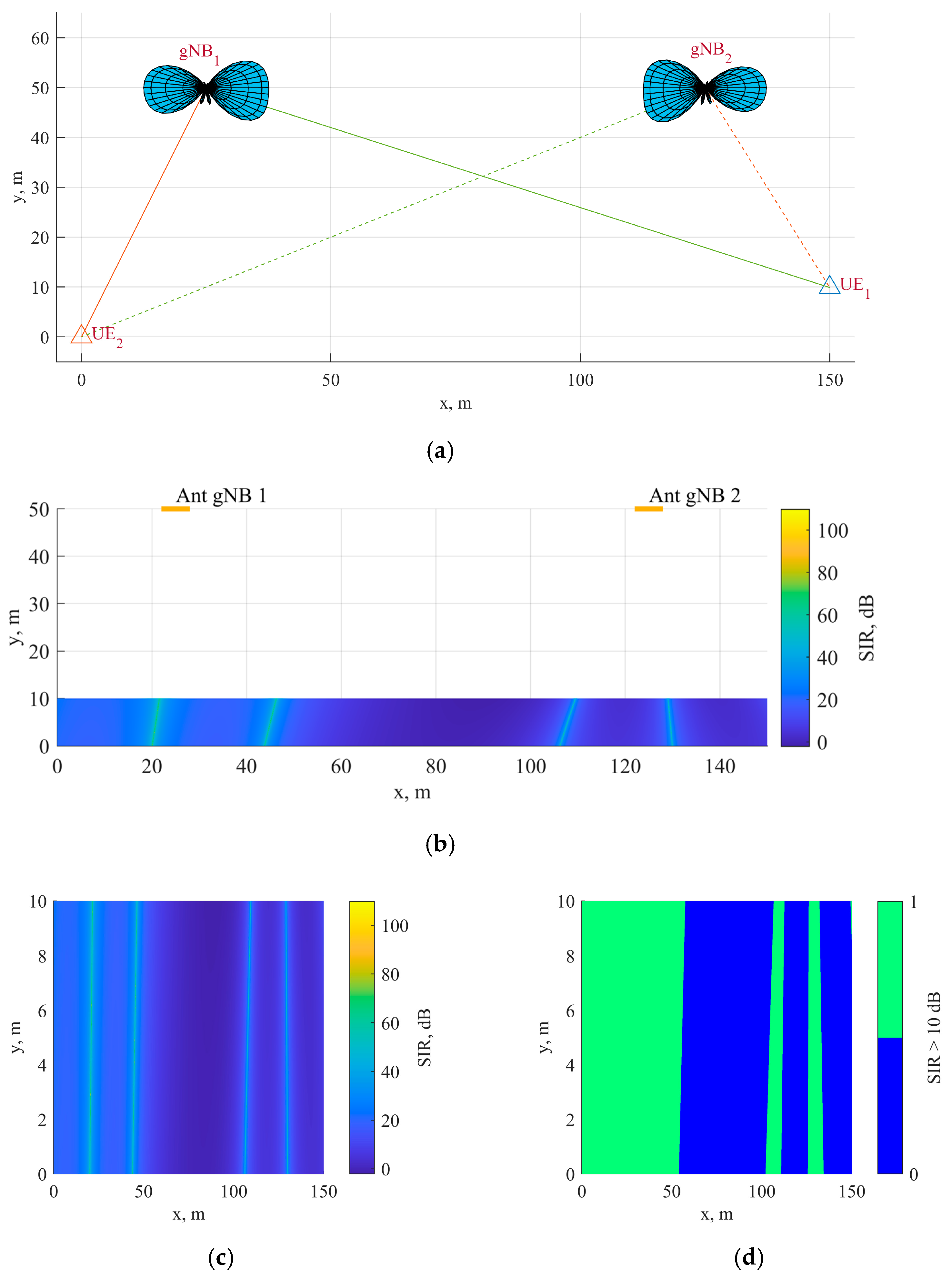
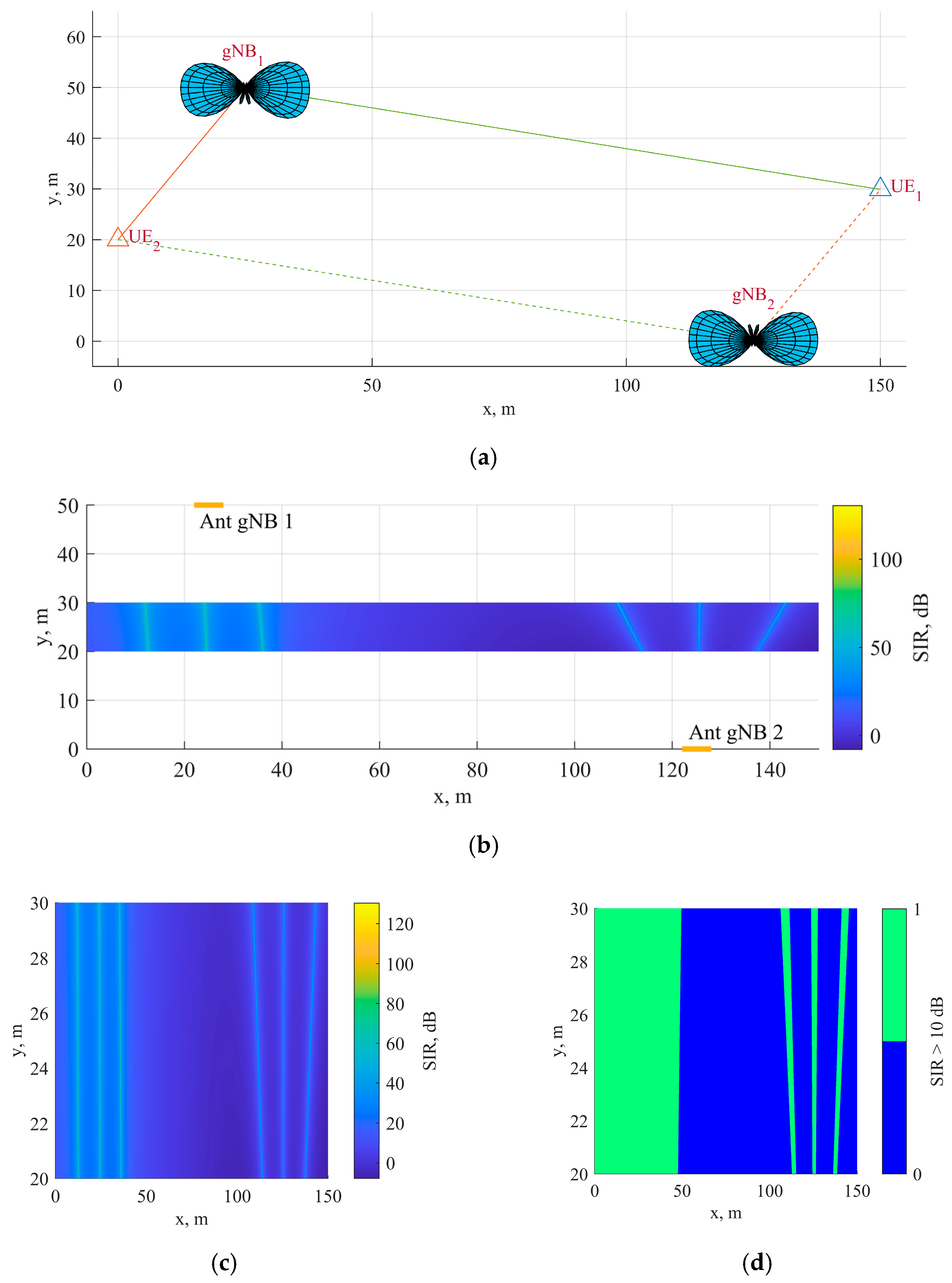
3.1.1. Simulation Model for SIR Dependence on the Terrestrial Separation
3.1.2. Mathematical Model for SIR Dependence on the Terrestrial Separation
3.1.3. Evaluation of SIR Dependence on the Terrestrial Separation
3.2. SIR Dependence on the Angular Separation of Two gNB-UE Links in 5G UDN with LAB
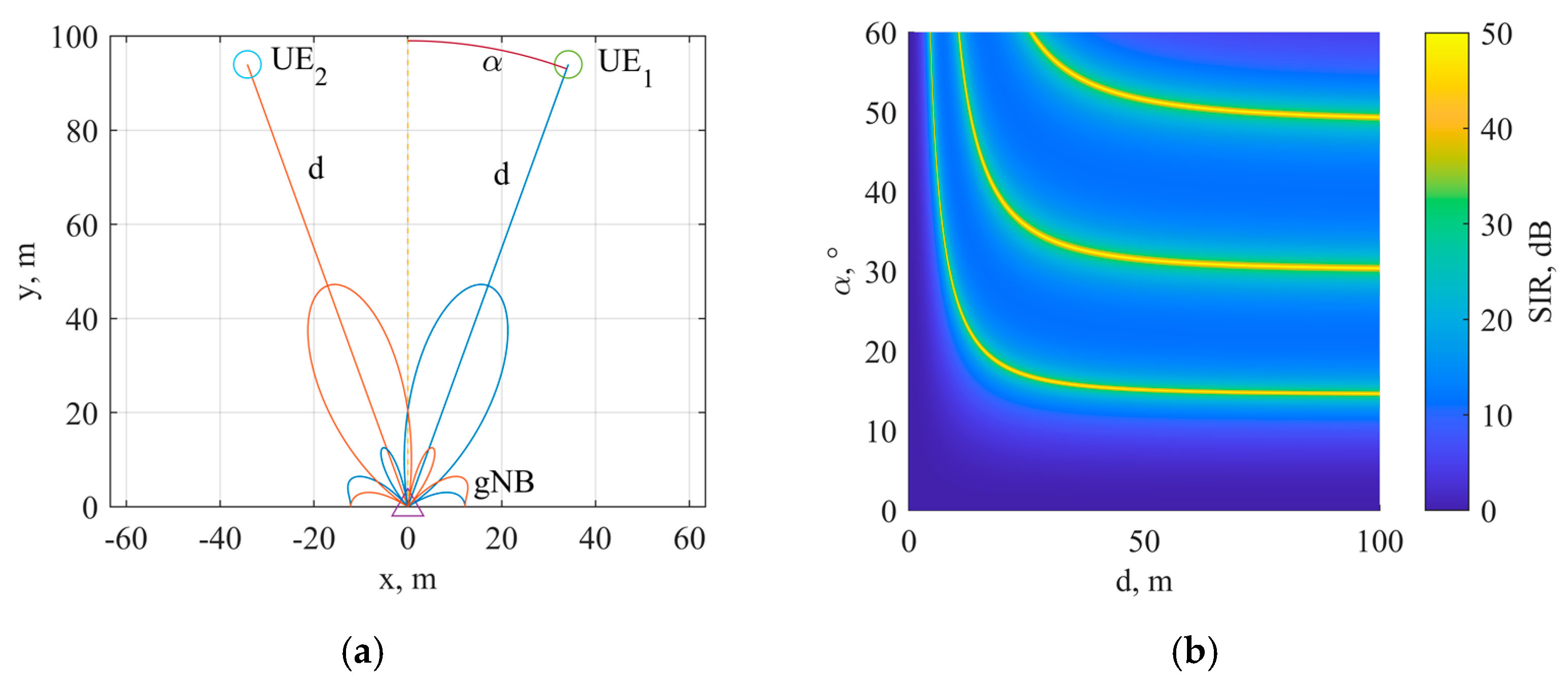
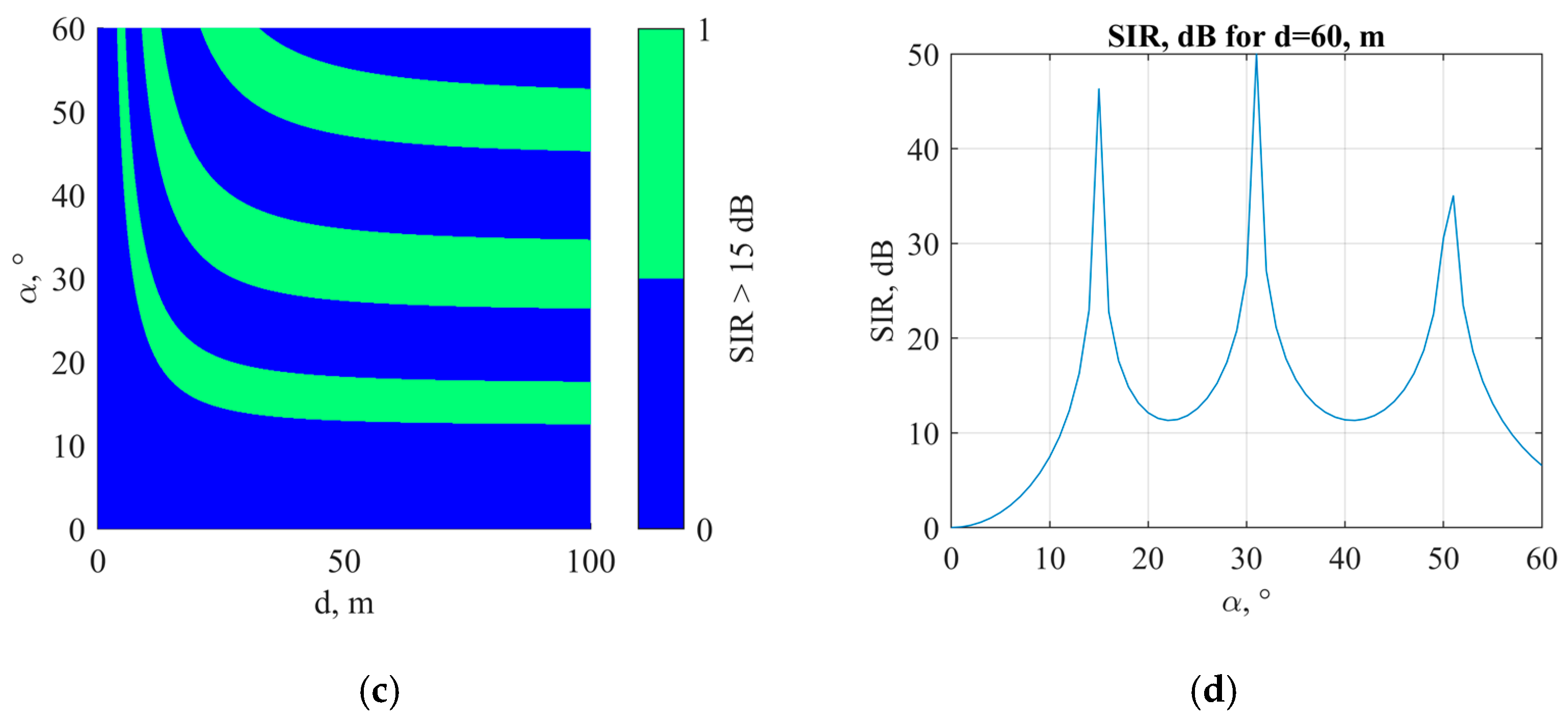
3.2.1. Simulation Model for SIR Dependence on the Angular Separation
3.2.2. Mathematical Model for SIR Dependence on the Angular Separation
3.2.3. Evaluation of SIR Dependence on the Angular Separation
3.3. Transition from the Link to System Level Simulation Model of 5G UDN with LAB
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Davydov, V.; Fokin, G.; Moroz, A.; Lazarev, V. Instantaneous Interference Evaluation Model for Smart Antennas in 5G Ultra-Dense Networks. In Proceedings of the International Conference on Next Generation Wired/Wireless Networking NEW2AN ruSMART 2021, St. Petersburg, Russia, 26–27 August 2021; Volume 13158, pp. 365–376. [Google Scholar] [CrossRef]
- Davydov, V.; Fokin, G.; Lazarev, V.; Makeev, S. Space Division Multiple Access Performance Evaluation in Ultra-Dense 5G Networks. In Proceedings of the International Conference on Next Generation Networks and Systems, NEW2AN ruSMART 2020, St. Petersburg, Russia, 26–28 August 2020; Volume 12525, pp. 86–98. [Google Scholar] [CrossRef]
- Balanis, C. Antenna Theory Analysis and Design, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Gross, F. Smart Antennas with MATLAB, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Mailloux, R.J. Phased Array Antenna Handbook, 3rd ed.; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Stepanets, I.; Fokin, G.; Müller, A. Beamforming Techniques Performance Evaluation for 5G Massive MIMO Systems. In Proceedings of the 5th Collaborative European Research Conference (CERC), Darmstadt, Germany, 29–30 March 2019; pp. 57–68. [Google Scholar]
- Stepanets, I.; Fokin, G. Beamforming Signal Processing Performance Analysis for Massive MIMO Systems. In Proceedings of the International Conference on Next Generation Wired/Wireless Networking NEW2AN ruSMART 2019, St. Petersburg, Russia, 26–28 August 2019; Volume 11660, pp. 329–341. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; MacCartney, G.R.; Molisch, A.F.; Mellios, E.; Zhang, J. Overview of Millimeter Wave Communications for Fifth-Generation (5G) Wireless Networks—With a Focus on Propagation Models. IEEE Trans. Antennas Propag. 2017, 65, 6213–6230. [Google Scholar] [CrossRef]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R.W. Channel Estimation and Hybrid Precoding for Millimeter Wave Cellular Systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Kutty, S.; Sen, D. Beamforming for Millimeter Wave Communications: An Inclusive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 949–973. [Google Scholar] [CrossRef]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Wymeersch, H.; Hoydis, J.; Marzetta, T.L. Massive MIMO is a reality—What is next? Five promising research directions for antenna arrays. Digit. Signal Process. 2019, 94, 3–20. [Google Scholar] [CrossRef]
- Xue, Q.; Li, B.; Zuo, X.; Yan, Z.; Yang, M. Cell capacity for 5G cellular network with inter-beam interference. In Proceedings of the 2016 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Hong Kong, China, 5–8 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Lazarev, V.; Fokin, G. Beamforming and Spatial Multiplexing Performance Evaluation in 5G Ultra-Dense Networks. In Proceedings of the International Youth Conference on Electronics, Telecommunications and Information Technologies, St. Petersburg, Russia, 10–11 July 2020; Volume 255, pp. 709–717. [Google Scholar] [CrossRef]
- Fokin, G. Interference Suppression Using Location Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2020 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2020; pp. 13–17. [Google Scholar] [CrossRef]
- Lazarev, V.; Fokin, G.; Stepanets, I. Positioning for Location-Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2019 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 17–18 October 2019; pp. 136–139. [Google Scholar] [CrossRef]
- Fokin, G.; Bachevsky, S.; Sevidov, V. System Level Performance Evaluation of Location Aware Beamforming in 5G Ultra-Dense Networks. In Proceedings of the 2020 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech), St. Petersburg, Russia, 15–16 October 2020; pp. 94–97. [Google Scholar] [CrossRef]
- Lazarev, V.O.; Fokin, G.A. Positioning Performance Requirements Evaluation for Grid Model in Ultra-Dense Network Scenario. In Proceedings of the 2020 Systems of Signals Generating and Processing in the Field of on-Board Communications, Moscow, Russia, 19–20 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Fokin, G.; Lazarev, V. Location Accuracy of Radio Emission Sources for Beamforming in Ultra-Dense Radio Networks. In Proceedings of the 2019 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 1–2 October 2019; pp. 9–12. [Google Scholar] [CrossRef]
- Laoudias, C.; Moreira, A.; Kim, S.; Lee, S.; Wirola, L.; Fischione, C. A Survey of Enabling Technologies for Network Localization, Tracking, and Navigation. IEEE Commun. Surv. Tutor. 2018, 20, 3607–3644. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, X.; He, S.; Shi, Z. Prospective Positioning Architecture and Technologies in 5G Networks. IEEE Netw. 2017, 31, 115–121. [Google Scholar] [CrossRef]
- Fokin, G.; Lazarev, V. 3D Location Accuracy Estimation of Radio Emission Sources for Beamforming in Ultra-Dense Radio Networks. In Proceedings of the 2019 11th International Congress on Ultra-Modern Telecommunications and Control Systems and Workshops (ICUMT), Dublin, Ireland, 28–30 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Fokin, G. Vehicles Tracking in 5G-V2X UDN Using Range and Bearing Measurements. In Proceedings of the 2021 IEEE Vehicular Networking Conference (VNC), Ulm, Germany, 10–12 November 2021; pp. 103–106. [Google Scholar] [CrossRef]
- Fokin, G. Vehicle Positioning Requirements for Location-Aware Beamforming in 5G UDN. In Proceedings of the 2022 Intelligent Technologies and Electronic Devices in Vehicle and Road Transport Complex (TIRVED), Moscow, Russia, 10–11 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Fokin, G. Bearing Measurement with Beam Sweeping for Positioning in 5G Networks. In Proceedings of the 2021 IEEE Microwave Theory and Techniques in Wireless Communications (MTTW), Riga, Latvia, 7–8 October 2021; pp. 64–67. [Google Scholar] [CrossRef]
- Fokin, G. Bearing Measurement with Beam Refinement for Positioning in 5G Networks. In Proceedings of the 5th International Conference on Future Networks & Distributed Systems (ICFNDS 2021), Dubai, United Arab Emirates, 15–16 December 2021; pp. 537–545. [Google Scholar] [CrossRef]
- Fokin, G.A.; Grishin, I.V. Direction of Arrival Positioning Requirements for Location-Aware Beamforming in 5G mmWave UDN. In Proceedings of the 2022 Wave Electronics and its Application in Information and Telecommunication Systems (WECONF), St. Petersburg, Russia, 30 May–3 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Rastorgueva-Foi, E.; Koivisto, M.; Valkama, M.; Costa, M.; Leppänen, K. Localization and Tracking in mmWave Radio Networks using Beam-Based DoD Measurements. In Proceedings of the 2018 8th International Conference on Localization and GNSS (ICL-GNSS), Guimaraes, Portugal, 26–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rastorgueva-Foi, E.; Costa, M.; Koivisto, M.; Talvitie, J.; Leppäneny, K.; Valkama, M. Beam-based Device Positioning in mmWave 5G Systems under Orientation Uncertainties. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 3–7. [Google Scholar] [CrossRef]
- Rastorgueva-Foi, E.; Costa, M.; Koivisto, M.; Leppänen, K.; Valkama, M. Dynamic Beam Selection for Beam-RSRP Based Direction Finding in mmW 5G Networks. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Rastorgueva-Foi, E.; Costa, M.; Koivisto, M.; Leppänen, K.; Valkama, M. User Positioning in mmW 5G Networks Using Beam-RSRP Measurements and Kalman Filtering. In Proceedings of the 2018 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Bechta, K.; Kelner, J.M.; Ziółkowski, C.; Nowosielski, L. Inter-Beam Co-Channel Downlink and Uplink Interference for 5G New Radio in mm-Wave Bands. Sensors 2021, 21, 793. [Google Scholar] [CrossRef]
- Bechta, K.; Ziółkowski, C.; Kelner, J.M.; Nowosielski, L. Modeling of Downlink Interference in Massive MIMO 5G Macro-Cell. Sensors 2021, 21, 597. [Google Scholar] [CrossRef]
- Bechta, K.; Ziółkowski, C.; Kelner, J.M.; Nowosielski, L. Downlink Interference in Multi-Beam 5G Macro-Cell. In Proceedings of the 2020 23rd International Microwave and Radar Conference (MIKON), Warsaw, Poland, 5–8 October 2020; pp. 140–143. [Google Scholar] [CrossRef]
- Bechta, K.; Du, J.; Rybakowski, M. Rework the Radio Link Budget for 5G and Beyond. IEEE Access 2020, 8, 211585–211594. [Google Scholar] [CrossRef]
- Ziółkowski, C.; Kelner, J.M. Antenna pattern in three-dimensional modelling of the arrival angle in simulation studies of wireless channels. IET Microw. Antennas Propag. 2017, 11, 898–906. [Google Scholar] [CrossRef]
- Kelner, J.M.; Ziółkowski, C. Interference in multi-beam antenna system of 5G network. Int. J. Electron. Telecommun. 2020, 66, 17–23. [Google Scholar] [CrossRef]
- Ziółkowski, C.; Kelner, J.M. Statistical evaluation of the azimuth and elevation angles seen at the output of the receiving antenna. IEEE Trans. Antennas Propag. 2018, 66, 2165–2169. [Google Scholar] [CrossRef]
- Va, V.; Heath, R.W. Basic Relationship between Channel Coherence Time and Beamwidth in Vehicular Channels. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Va, V.; Choi, J.; Heath, R.W. The Impact of Beamwidth on Temporal Channel Variation in Vehicular Channels and Its Implications. IEEE Trans. Veh. Technol. 2017, 66, 5014–5029. [Google Scholar] [CrossRef]
- Va, V.; Shimizu, T.; Bansal, G.; Heath, R.W. Beam design for beam switching based millimeter wave vehicle-to-infrastructure communications. In Proceedings of the 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Talvitie, J.; Levanen, T.; Koivisto, M.; Ihalainen, T.; Pajukoski, K.; Valkama, M. Beamformed Radio Link Capacity Under Positioning Uncertainty. IEEE Trans. Veh. Technol. 2020, 69, 16235–16240. [Google Scholar] [CrossRef]
- Bae, J.; Lim, S.H.; Yoo, J.H.; Choi, J.W. New beam tracking technique for millimeter wave-band communications. arXiv 2017, arXiv:1702.00276. Available online: https://arxiv.org/pdf/1702.00276.pdf (accessed on 8 November 2022).
- Tao, Y.; Liu, Y.; Liu, D. Location-Based Beam Tracking and Doppler-Aware Vehicle Scheduling for V2I Communications. In Proceedings of the 2019 IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019; pp. 803–808. [Google Scholar] [CrossRef]
- Mavromatis, I.; Tassi, A.; Piechocki, R.J.; Nix, A. Beam alignment for millimeter wave links with motion prediction of Autonomous Vehicles. In Proceedings of the Antennas, Propagation & RF Technology for Transport and Autonomous Platforms 2017, Birmingham, UK, 2 February 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Maschietti, F.; Gesbert, D.; de Kerret, P.; Wymeersch, H. Robust Location-Aided Beam Alignment in Millimeter Wave Massive MIMO. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Alexandropoulos, G.C. Position aided beam alignment for millimeter wave backhaul systems with large phased arrays. In Proceedings of the 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), Curacao, The Netherlands, 10–13 December 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Orikumhi, I.; Kang, J.; Park, C.; Yang, J.; Kim, S. Location-Aware Coordinated Beam Alignment in mmWave Communication. In Proceedings of the 2018 56th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–5 October 2018; pp. 386–390. [Google Scholar] [CrossRef]
- Garcia, N.; Wymeersch, H.; Ström, E.G.; Slock, D. Location-aided mm-wave channel estimation for vehicular communication. In Proceedings of the 2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 3–6 July 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Va, V.; Choi, J.; Shimizu, T.; Bansal, G.; Heath, R.W. Inverse Multipath Fingerprinting for Millimeter Wave V2I Beam Alignment. IEEE Trans. Veh. Technol. 2018, 67, 4042–4058. [Google Scholar] [CrossRef]
- Sim, G.H.; Klos, S.; Asadi, A.; Klein, A.; Hollick, M. An Online Context-Aware Machine Learning Algorithm for 5G mmWave Vehicular Communications. IEEE/ACM Trans. Netw. 2018, 26, 2487–2500. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, A.; Lau, V. Successive Localization and Beamforming in 5G mmWave MIMO Communication Systems. IEEE Trans. Signal Process. 2018, 67, 1620–1635. [Google Scholar] [CrossRef]
- Fazliu, Z.L.; Malandrino, F.; Chiasserini, C.F.; Nordio, A. MmWave Beam Management in Urban Vehicular Networks. IEEE Syst. J. 2021, 15, 2798–2809. [Google Scholar] [CrossRef]
- Maiberger, R.; Ezri, D.; Erlihson, M. Location based beamforming. In Proceedings of the 2010 IEEE 26-th Convention of Electrical and Electronics Engineers, Eilat, Israel, 17–20 November 2010; pp. 184–187. [Google Scholar] [CrossRef]
- Fokin, G. Location Aware Beamforming in Mm-Wave Band Ultra-Dense Radio Access Networks. Information about Project, Supported by RSCF. Available online: https://rscf.ru/en/project/22-29-00528/ (accessed on 8 November 2022).
- Andrews, J.G.; Zhang, X.; Durgin, G.D.; Gupta, A.K. Are we approaching the fundamental limits of wireless network densification? IEEE Commun. Mag. 2016, 54, 184–190. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Turco, S.; Bianchi, G.; Blefari-Melazzi, N. “Cellular Network Densification Increases Radio-Frequency Pollution”: True or False? IEEE Trans. Wirel. Commun. 2022, 21, 2608–2622. [Google Scholar] [CrossRef]
- Thors, B.; Furuskär, A.; Colombi, D.; Törnevik, C. Time-Averaged Realistic Maximum Power Levels for the Assessment of Radio Frequency Exposure for 5G Radio Base Stations Using Massive MIMO. IEEE Access 2017, 5, 19711–19719. [Google Scholar] [CrossRef]
- Chiaraviglio, L.; Rossetti, S.; Saida, S.; Bartoletti, S.; Blefari-Melazzi, N. “Pencil Beamforming Increases Human Exposure to ElectroMagnetic Fields”: True or False? IEEE Access 2021, 9, 25158–25171. [Google Scholar] [CrossRef]
- Ali, A.; Karabulut, U.; Awada, A.; Viering, I.; Tirkkonen, O.; Barreto, A.N.; Fettweis, G.P. System Model for Average Downlink SINR in 5G Multi-Beam Networks. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Heng, Y.; Andrews, J.G.; Mo, J.; Va, V.; Ali, A.; Ng, B.L.; Zhang, J.C. Six Key Challenges for Beam Management in 5.5G and 6G Systems. IEEE Commun. Mag. 2021, 59, 74–79. [Google Scholar] [CrossRef]
- Duarte, M.F.; Sarvotham, S.; Baron, D.; Wakin, M.B.; Baraniuk, R.G. Distributed Compressed Sensing of Jointly Sparse Signals. In Proceedings of the Conference Record of the Thirty-Ninth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 30 October–2 November 2005; pp. 1537–1541. [Google Scholar] [CrossRef]
- Bang, J.; Chung, H.; Hong, J.; Seo, H.; Choi, J.; Kim, S. Millimeter-Wave Communications: Recent Developments and Challenges of Hardware and Beam Management Algorithms. IEEE Commun. Mag. 2021, 59, 86–92. [Google Scholar] [CrossRef]
- Va, V.; Zhang, X.; Heath, R.W. Beam Switching for Millimeter Wave Communication to Support High Speed Trains. In Proceedings of the 2015 IEEE 82nd Vehicular Technology Conference (VTC2015-Fall), Boston, MA, USA, 6–9 September 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Doff, A.W.; Chandra, K.; Prasad, R.V. Sensor assisted movement identification and prediction for beamformed 60 GHz links. In Proceedings of the 2015 12th Annual IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2015; pp. 648–653. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Gutierrez, F.; Ben-Dor, E.; Murdock, J.N.; Qiao, Y.; Tamir, J.I. Broadband Millimeter-Wave Propagation Measurements and Models Using Adaptive-Beam Antennas for Outdoor Urban Cellular Communications. IEEE Trans. Antennas Propag. 2013, 61, 1850–1859. [Google Scholar] [CrossRef]
- Nam, Y.-H.; Ng, B.L.; Sayana, K.; Li, Y.; Zhang, J.; Kim, Y.; Lee, J. Full-dimension MIMO (FD-MIMO) for next generation cellular technology. IEEE Commun. Mag. 2013, 51, 172–179. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An Overview of Massive MIMO: Benefits and Challenges. IEEE J. Sel. Top. Signal Process. 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Razavizadeh, S.M.; Ahn, M.; Lee, I. Three-Dimensional Beamforming: A new enabling technology for 5G wireless networks. IEEE Signal Process. Mag. 2014, 31, 94–101. [Google Scholar] [CrossRef]
- Roh, W.; Seol, J.-Y.; Park, J.; Lee, B.; Lee, J.; Kim, Y.; Cho, J.; Cheun, K.; Aryanfar, F. Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results. IEEE Commun. Mag. 2014, 52, 106–113. [Google Scholar] [CrossRef]
- Larsson, E.G.; Edfors, O.; Tufvesson, F.; Marzetta, T.L. Massive MIMO for next generation wireless systems. IEEE Commun. Mag. 2014, 52, 186–195. [Google Scholar] [CrossRef]
- Sun, S.; Rappaport, T.S.; Heath, R.W.; Nix, A.; Rangan, S. Mimo for millimeter-wave wireless communications: Beamforming, spatial multiplexing, or both? IEEE Commun. Mag. 2014, 52, 110–121. [Google Scholar] [CrossRef]
- Han, S.; Chih-lin, I.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Ullah, A.; Abbas, Z.H.; Abbas, G.; Muhammad, F.; Kang, J.-M. Hybrid millimeter wave heterogeneous networks with spatially correlated user equipment. Digit. Commun. Netw. 2022; in press. [Google Scholar] [CrossRef]
- MathWorks. Phased Array System Toolbox. Available online: https://www.mathworks.com/products/phased-array.html (accessed on 8 November 2022).
- LAB Link Level Simulator. Available online: https://github.com/grihafokin/LAB_link_level (accessed on 8 November 2022).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fokin, G.; Volgushev, D. Model for Interference Evaluation in 5G Millimeter-Wave Ultra-Dense Network with Location-Aware Beamforming. Information 2023, 14, 40. https://doi.org/10.3390/info14010040
Fokin G, Volgushev D. Model for Interference Evaluation in 5G Millimeter-Wave Ultra-Dense Network with Location-Aware Beamforming. Information. 2023; 14(1):40. https://doi.org/10.3390/info14010040
Chicago/Turabian StyleFokin, Grigoriy, and Dmitriy Volgushev. 2023. "Model for Interference Evaluation in 5G Millimeter-Wave Ultra-Dense Network with Location-Aware Beamforming" Information 14, no. 1: 40. https://doi.org/10.3390/info14010040
APA StyleFokin, G., & Volgushev, D. (2023). Model for Interference Evaluation in 5G Millimeter-Wave Ultra-Dense Network with Location-Aware Beamforming. Information, 14(1), 40. https://doi.org/10.3390/info14010040







