EACH-COA: An Energy-Aware Cluster Head Selection for the Internet of Things Using the Coati Optimization Algorithm
Abstract
:1. Introduction
- A substantial analysis was conducted on the proposed EACH-COA technique to obtain the best CH in a network. The effectiveness of the EACH-COA strategy was tested using various metrics: throughput, latency, and network longevity.
- EACH-COA performs CH selection and cluster formation. Using the coati optimization method, the best CH is selected, and clusters are grouped together using the nodes that are closest to each other.
- Existing optimization techniques are compared with the proposed EACH-COA methodology to demonstrate that EACH-COA outperforms them in network longevity.
- The fitness function is computed using residential energy (RER) and distance parameters in the CH selection process.
- The proposed EACH-COA technique was simulated using MATLAB 2019a. The overall network lifetime and throughput were improved by 8–15% and 5–10%, respectively.
2. Background
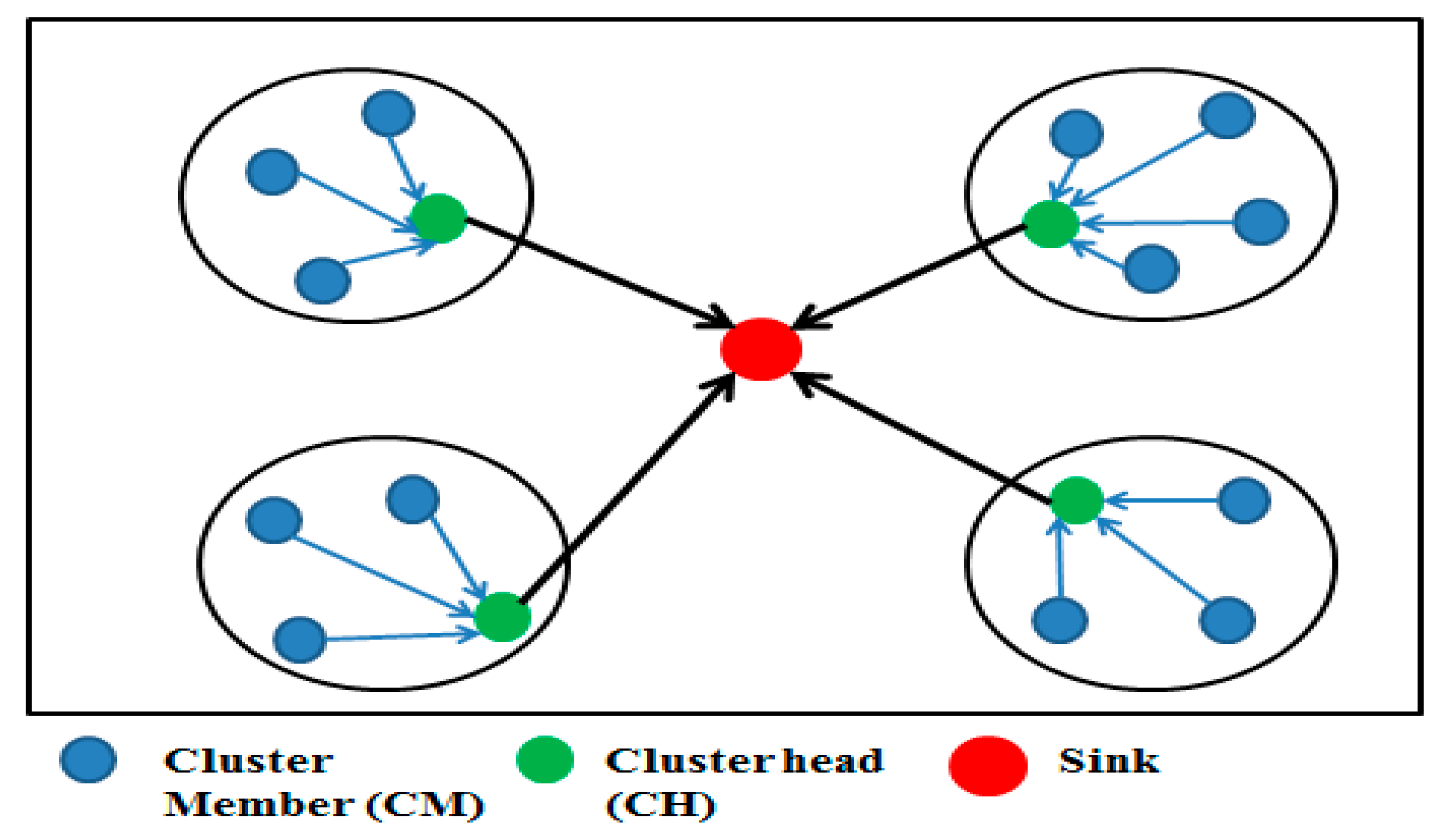
3. System Model
3.1. Network Model
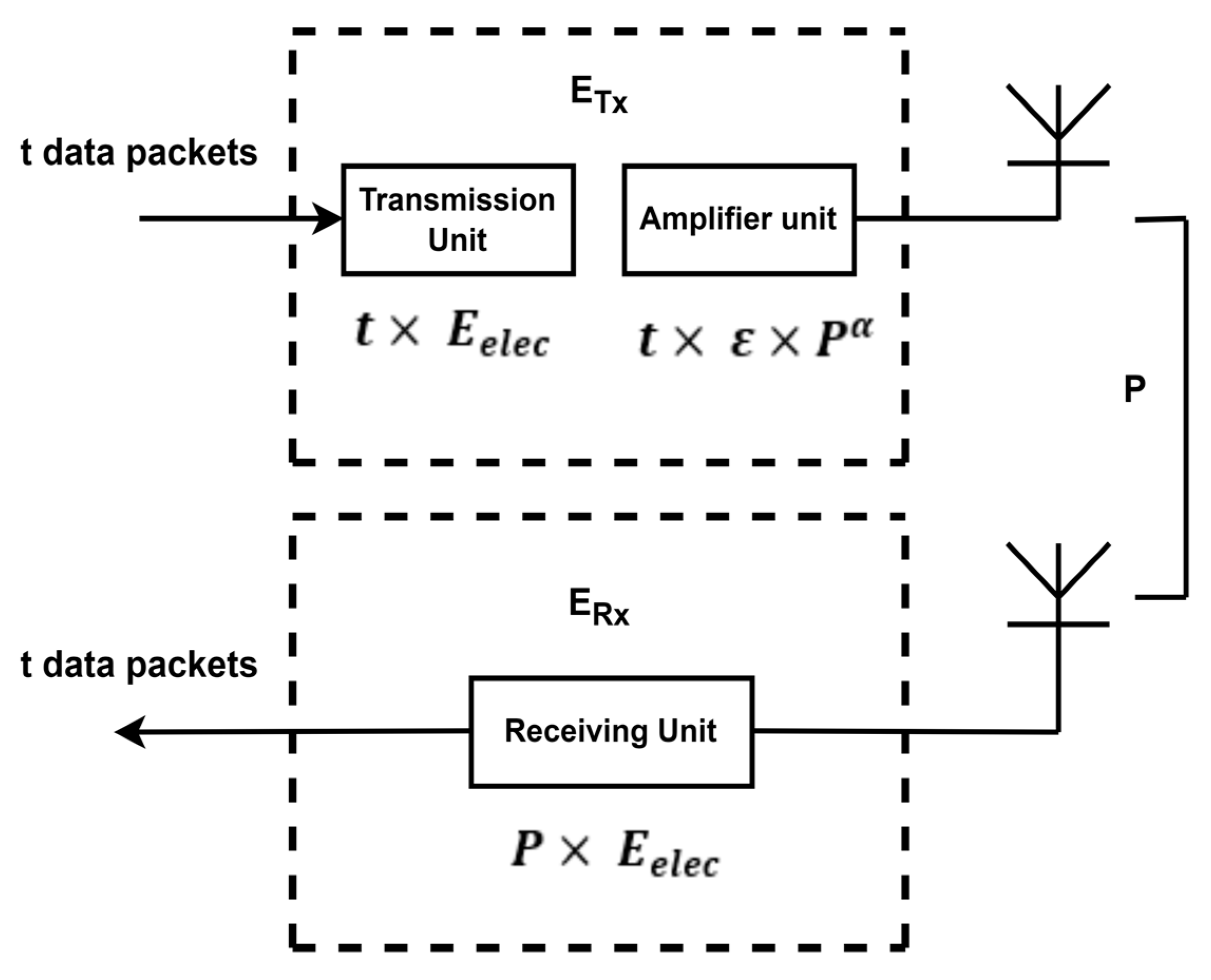
3.2. Energy Model
4. Proposed COA Protocol
4.1. Coati Optimization Algorithm-Based Cluster Head Selection
4.1.1. Exploration Phase
4.1.2. Exploitation Phase
4.1.3. Fitness Function
| Algorithm 1: COA-based CH Selection Algorithm |
| Input: Number of nodes ‘n’ Output: Best position of coati acts as CH 1: initialize the position of nodes using Equation (4) 2: For z = 1 to Z do 3: prey position is updated based on best member position //exploration phase 4: For z = 1 to [Z/2] 5: the new position of coati is calculated using Equation (7) 6: update position of i-th coati using Equation (10) 7: END for 8: For z = 1 + [Z/2]: Z 9: prey random position is computed using Equation (8) 10: coati new position is computed using Equation (9) 11: updated position of i-th coati using Equation (10) 12: END for //exploitation phase 13: For z = 1 to Z 14: Update the position of the ith coati using Equations (11) to (13) 15: END for 16: compute the fitness value using Equation (16) 17: If coati reaches best position, then 18: Best coati acts as CH 19: else 20: Go to step 1 21: END for 22: return optimal CH |
- Residual Energy (RER)
- Computation of Distance
5. Results and Discussion
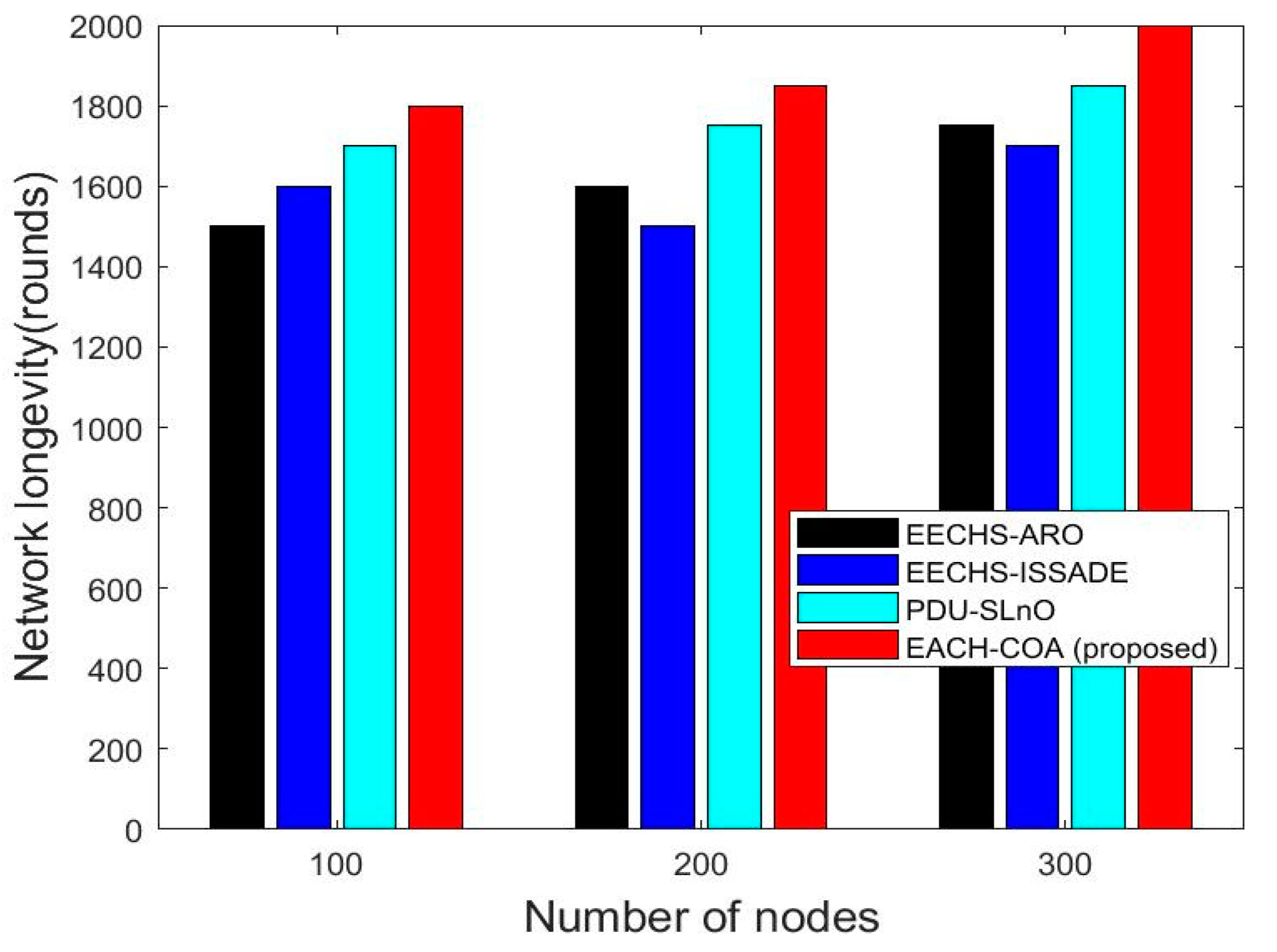
5.1. Network Longevity
5.2. Throughput
5.3. Average Energy Consumption
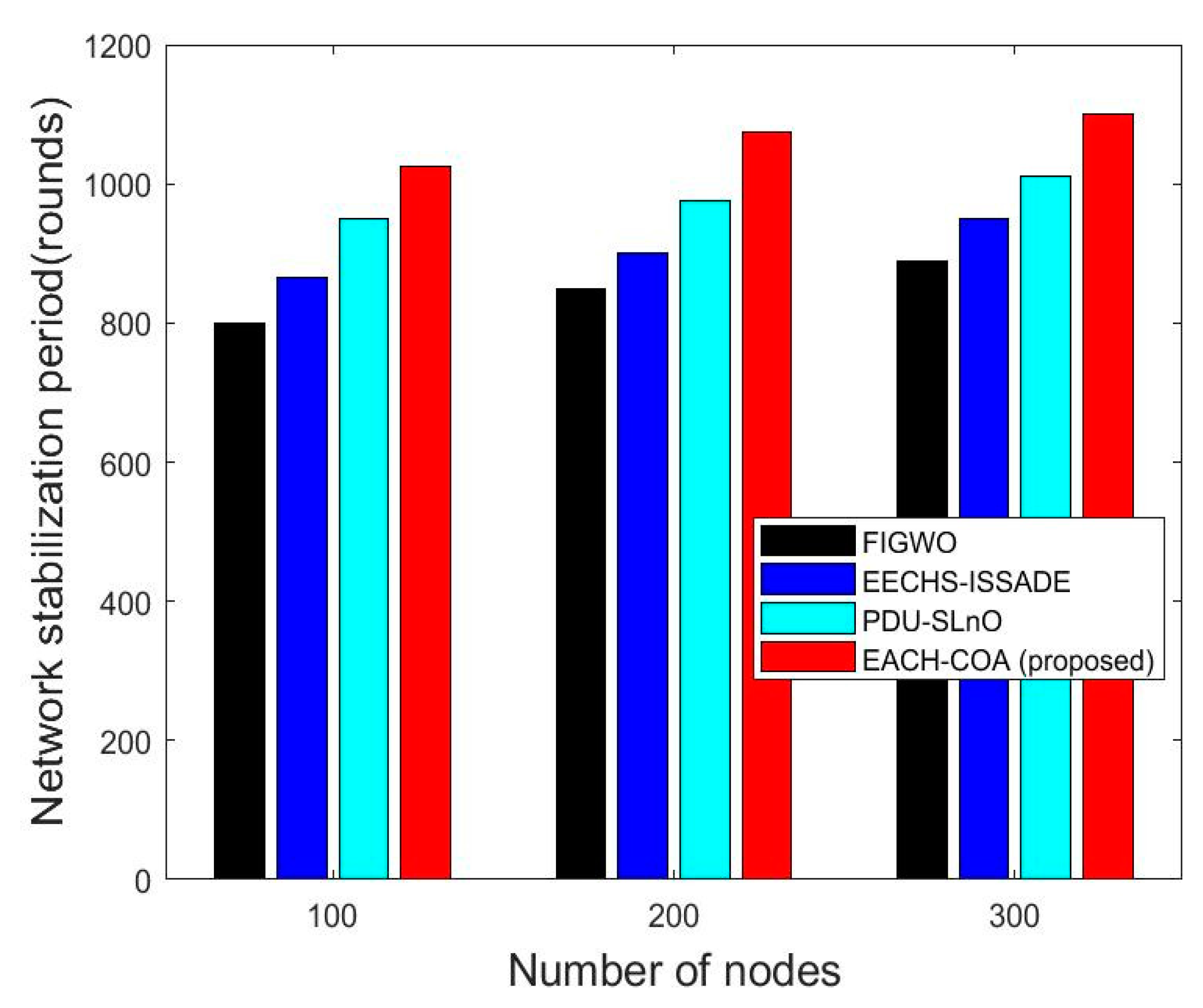
5.4. Network Stabilization Period
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sennan, S.; Ramasubbareddy, S.; Balasubramaniyam, S.; Nayyar, A.; Kerrache, C.A.; Bilal, M. MADCR: Mobility aware dynamic clustering-based routing protocol in Internet of Vehicles. China Commun. 2021, 18, 69–85. [Google Scholar] [CrossRef]
- Nauman, A.; Qadri, Y.A.; Amjad, M.; Zikria, Y.B.; Afzal, M.K.; Kim, S.W. Multimedia Internet of Things: A comprehensive survey. IEEE Access 2020, 8, 8202–8250. [Google Scholar] [CrossRef]
- Sennan, S.; Ramasubbareddy, S.; Balasubramaniyam, S.; Nayyar, A.; Abouhawwash, M.; Hikal, N.A. T2FL-PSO: Type-2 Fuzzy Logic-based Particle Swarm Optimization Algorithm used to Maximize the Lifetime of Internet of Things. IEEE Access 2021, 9, 63966–63979. [Google Scholar] [CrossRef]
- Kassab, W.A.; Darabkh, K.A. A–Z survey of Internet of Things: Architectures, protocols, applications, recent advances, future directions and recommendations. J. Netw. Comput. Appl. 2020, 163, 102663. [Google Scholar] [CrossRef]
- Thuluva AS, S.; Somanathan, M.S.; Somula, R.; Sennan, S.; Burgos, D. Secure and efficient transmission of data based on Caesar Cipher Algorithm for Sybil attack in IoT. EURASIP J. Adv. Signal Process. 2021, 2021, 1–23. [Google Scholar] [CrossRef]
- Roy, S.; Mazumdar, N.; Pamula, R. An optimal mobile sink sojourn location discovery approach for the energy-constrained and delay-sensitive wireless sensor network. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 10837–10864. [Google Scholar] [CrossRef]
- Palanisamy, S.; Sankar, S.; Somula, R.; Deverajan, G.G. Communication Trust and Energy-Aware Routing Protocol for WSN Using DS Theory. Int. J. Grid High Perform. Comput. (IJGHPC) 2021, 13, 24–36. [Google Scholar] [CrossRef]
- Kandris, D.; Nakas, C.; Vomvas, D.; Koulouras, G. Applications of wireless sensor networks: An up-to-date survey. Appl. Syst. Innov. 2020, 3, 14. [Google Scholar] [CrossRef]
- Shahraki, A.; Taherkordi, A.; Haugen, Ø.; Eliassen, F. Clustering objectives in wireless sensor networks: A survey and research direction analysis. Comput. Netw. 2020, 180, 107376. [Google Scholar] [CrossRef]
- Goyat, R.; Kumar, G.; Alazab, M.; Saha, R.; Thomas, R.; Rai, M.K. A secure localization scheme based on trust assessment for WSNs using blockchain technology. Future Gener. Comput. Syst. 2021, 125, 221–231. [Google Scholar] [CrossRef]
- Nabavi, S.R.; Eraghi, N.O.; Torkestani, J.A. WSN routing protocol using a multiobjective greedy approach. Wirel. Commun. Mob. Comput. 2021, 2021, 6664669. [Google Scholar] [CrossRef]
- Sah, D.K.; Amgoth, T. Renewable energy harvesting schemes in wireless sensor networks: A survey. Inf. Fusion 2020, 63, 223–247. [Google Scholar] [CrossRef]
- Priyadarshi, R.; Gupta, B.; Anurag, A. Deployment techniques in wireless sensor networks: A survey, classification, challenges, and future research issues. J. Supercomput. 2020, 76, 7333–7373. [Google Scholar] [CrossRef]
- Ravi, G.; Kashwan, K.R. A new routing protocol for energy efficient mobile applications for ad hoc networks. Comput. Electr. Eng. 2015, 48, 77–85. [Google Scholar] [CrossRef]
- El Khediri, S.; Fakhet, W.; Moulahi, T.; Khan, R.; Thaljaoui, A.; Kachouri, A. Improved node localization using K-means clustering for Wireless Sensor Networks. Comput. Sci. Rev. 2020, 37, 100284. [Google Scholar] [CrossRef]
- Reddy, M.; Babu, M.R. Implementing self adaptiveness in whale optimization for cluster head section in Internet of Things. Clust. Comput. 2019, 22, 1361–1372. [Google Scholar] [CrossRef]
- Amutha, J.; Sharma, S.; Sharma, S.K. Strategies based on various aspects of clustering in wireless sensor networks using classical, optimization and machine learning techniques: Review, taxonomy, research findings, challenges and future directions. Comput. Sci. Rev. 2021, 40, 100376. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Sennan, S.; Balasubramaniyam, S.; Luhach, A.K.; Ramasubbareddy, S.; Chilamkurti, N.; Nam, Y. Energy and delay aware data aggregation in routing protocol for Internet of Things. Sensors 2019, 19, 5486. [Google Scholar] [CrossRef]
- Sankar, S.; Ramasubbareddy, S.; Luhach, A.K.; alnumay, W.S.; Chatterjee, P. NCCLA: New caledonian crow learning algorithm based cluster head selection for Internet of Things in smart cities. J. Ambient Intell. Humaniz. Comput. 2022, 13, 4651–4661. [Google Scholar] [CrossRef]
- Behera, T.M.; Mohapatra, S.K.; Samal, U.C.; Khan, M.S.; Daneshmand, M.; Gandomi, A.H. Residual energy-based cluster-head selection in WSNs for IoT application. IEEE Internet Things J. 2019, 6, 5132–5139. [Google Scholar] [CrossRef]
- Khan, M.A.R.; Shavkatovich, S.N.; Nagpal, B.; Kumar, A.; Haq, M.A.; Tharini, V.J.; Karupusamy, S.; Alazzam, M.B. Optimizing hybrid metaheuristic algorithm with cluster head to improve performance metrics on the IoT. Theor. Comput. Sci. 2022, 927, 87–97. [Google Scholar] [CrossRef]
- Savaglio, C.; Fortino, G. A simulation-driven methodology for IoT data mining based on edge computing. ACM Trans. Internet Technol. (TOIT) 2021, 21, 1–22. [Google Scholar] [CrossRef]
- Ramalingam, R.; Saleena, B.; Basheer, S.; Balasubramanian, P.; Rashid, M.; Jayaraman, G. EECHS-ARO: Energy-efficient cluster head selection mechanism for livestock industry using artificial rabbits optimization and wireless sensor networks. Electron. Res. Arch. 2023, 31, 3123–3144. [Google Scholar] [CrossRef]
- Chaurasia, S.; Kumar, K.; Kumar, N. MOCRAW: A Meta-heuristic Optimized Cluster head selection based Routing Algorithm for WSNs. Ad Hoc Netw. 2023, 141, 103079. [Google Scholar] [CrossRef]
- Sankar, S.; Ramasubbareddy, S.; Dhanaraj, R.K.; Balusamy, B.; Gupta, P.; Ibrahim, W.; Verma, R. Cluster Head Selection for the Internet of Things Using a Sandpiper Optimization Algorithm (SOA). J. Sens. 2023, 2023, 3507600. [Google Scholar] [CrossRef]
- Kumar, A.; Webber, J.L.; Haq, M.A.; Gola, K.K.; Singh, P.; Karupusamy, S.; Alazzam, M.B. Optimal cluster head selection for energy efficient wireless sensor network using hybrid competitive swarm optimization and harmony search algorithm. Sustain. Energy Technol. Assess. 2022, 52, 102243. [Google Scholar] [CrossRef]
- Yadav, R.K.; Mahapatra, R.P. Hybrid metaheuristic algorithm for optimal cluster head selection in wireless sensor network. Pervasive Mob. Comput. 2022, 79, 101504. [Google Scholar] [CrossRef]
- Kathiroli, P.; Selvadurai, K. Energy efficient cluster head selection using improved Sparrow Search Algorithm in Wireless Sensor Networks. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 8564–8575. [Google Scholar] [CrossRef]
- Sengathir, J.; Rajesh, A.; Dhiman, G.; Vimal, S.; Yogaraja, C.A.; Viriyasitavat, W. A novel cluster head selection using Hybrid Artificial Bee Colony and Firefly Algorithm for network lifetime and stability in WSNs. Connect. Sci. 2022, 34, 387–408. [Google Scholar] [CrossRef]
- Abu Salem, A.O.; Shudifat, N. Enhanced LEACH protocol for increasing a lifetime of WSNs. Pers. Ubiquitous Comput. 2019, 23, 901–907. [Google Scholar] [CrossRef]
- Dehghani, M.; Montazeri, Z.; Trojovská, E.; Trojovský, P. Coati Optimization Algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems. Knowl.-Based Syst. 2023, 259, 110011. [Google Scholar] [CrossRef]
- Sankar, S.; Srinivasan, P.; Luhach, A.K.; Somula, R.; Chilamkurti, N. Energy-aware grid-based data aggregation scheme in routing protocol for agricultural internet of things. Sustain. Comput. Inform. Syst. 2020, 28, 100422. [Google Scholar] [CrossRef]
- Sahoo, B.M.; Amgoth, T.; Pandey, H.M. Particle swarm optimization based energy efficient clustering and sink mobility in heterogeneous wireless sensor network. Ad Hoc Netw. 2020, 106, 102237. [Google Scholar] [CrossRef]
- Sathyamoorthy, M.; Kuppusamy, S.; Dhanaraj, R.K.; Ravi, V. Improved K-means based q learning algorithm for optimal clustering and node balancing in WSN. Wirel. Pers. Commun. 2022, 122, 2745–2766. [Google Scholar] [CrossRef]



| S.No | Authors | Proposed CH Selection Optimization Techniques | Advantages | Limitations |
|---|---|---|---|---|
| 1 | Ramalingam et al. [24] | ARO | Network lifetime and packet delivery ratio are improved by 15% and 5% | It takes more time to form clusters in the network |
| 2 | Chaurasia et al. [25] | DA | Minimized energy consumption by 0.0014 J | It consumes more energy during CH selection |
| 3 | Sankar et al. [26] | SOA | Improved throughput and network lifetime by 6–10% and 3–18% | Sensor nodes deplete energy early during CH selection process |
| 4 | Kumar et al. [27] | HSA-CSO | Prolongs network lifetime and minimizes energy consumption | Convergence takes time for CH selection process in network |
| 5 | Yadav et al. [28] | PDU-SLnO | Increased network lifetime and consumes less energy | Sensor nodes deplete energy early during CH selection process |
| 6 | Kathiroli and Selvadurai [29] | SSA | Extended lifetime of sensor nodes | Takes more time to converge |
| 7 | Sengathir et al. [30] | EABC-FA | Prolonged network lifespan by 23.21% and energy stability by 19.84% and reduced network delay 22.88% | It takes more time to select CH selection |
| Parameter | Value |
|---|---|
| Network area | 500 × 500 |
| Sink location | (250, 250) |
| Number of sensor nodes | 100, 200, 300 |
| CH percentage | 5–10% |
| Control packet size | 200 bits |
| Data packet size | 4000 bits |
| Free space energy | 10 PJ/bit/ |
| Multipath energy | 0.0013 PJ/bit/ |
| Number of Nodes | Network Longevity | |||
|---|---|---|---|---|
| EECHS-ARO | EECHS-ISSADE | PDU-SLnO | EACH-COA | |
| 100 | 1500 | 100 | 1500 | 100 |
| 200 | 1600 | 200 | 1600 | 200 |
| 300 | 1750 | 300 | 1750 | 300 |
| Number of Nodes | Network Longevity | |||
|---|---|---|---|---|
| EECHS-ARO | EECHS-ISSADE | PDU-SLnO | EACH-COA | |
| 100 | 130,000 | 140,000 | 170,000 | 180,000 |
| 200 | 220,000 | 200,000 | 240,000 | 260,000 |
| 300 | 310,000 | 300,000 | 360,000 | 400,000 |
| Number of Rounds | Average Energy Consumption (Joule) | |||
|---|---|---|---|---|
| EECHS-ARO | EECHS-ISSADE | PDU-SLnO | EACH-COA | |
| 0 | 0 | 0 | 0 | 0 |
| 500 | 0.17 | 500 | 0.17 | 500 |
| 1000 | 0.18 | 1000 | 0.18 | 1000 |
| 1500 | 0.19 | 1500 | 0.19 | 1500 |
| 2000 | 0.39 | 2000 | 0.39 | 2000 |
| 2500 | 0.44 | 2500 | 0.44 | 2500 |
| 3000 | 0.55 | 3000 | 0.55 | 3000 |
| Number of Nodes | Network Longevity | |||
|---|---|---|---|---|
| EECHS-ARO | EECHS-ISSADE | PDU-SLnO | EACH-COA | |
| 100 | 800 | 100 | 800 | 100 |
| 200 | 850 | 200 | 850 | 200 |
| 300 | 900 | 300 | 900 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somula, R.; Cho, Y.; Mohanta, B.K. EACH-COA: An Energy-Aware Cluster Head Selection for the Internet of Things Using the Coati Optimization Algorithm. Information 2023, 14, 601. https://doi.org/10.3390/info14110601
Somula R, Cho Y, Mohanta BK. EACH-COA: An Energy-Aware Cluster Head Selection for the Internet of Things Using the Coati Optimization Algorithm. Information. 2023; 14(11):601. https://doi.org/10.3390/info14110601
Chicago/Turabian StyleSomula, Ramasubbareddy, Yongyun Cho, and Bhabendu Kumar Mohanta. 2023. "EACH-COA: An Energy-Aware Cluster Head Selection for the Internet of Things Using the Coati Optimization Algorithm" Information 14, no. 11: 601. https://doi.org/10.3390/info14110601
APA StyleSomula, R., Cho, Y., & Mohanta, B. K. (2023). EACH-COA: An Energy-Aware Cluster Head Selection for the Internet of Things Using the Coati Optimization Algorithm. Information, 14(11), 601. https://doi.org/10.3390/info14110601







