Abstract
Deep convolutional neural networks (DCNNs) have manifested significant performance gains for single-image super-resolution (SISR) in the past few years. Most of the existing methods are generally implemented in a fully supervised way using large-scale training samples and only learn the SR models restricted to specific data. Thus, the adaptation of these models to real low-resolution (LR) images captured under uncontrolled imaging conditions usually leads to poor SR results. This study proposes a zero-shot blind SR framework via leveraging the power of deep learning, but without the requirement of the prior training using predefined imaged samples. It is well known that there are two unknown data: the underlying target high-resolution (HR) images and the degradation operations in the imaging procedure hidden in the observed LR images. Taking these in mind, we specifically employed two deep networks for respectively modeling the priors of both the target HR image and its corresponding degradation kernel and designed a degradation block to realize the observation procedure of the LR image. Via formulating the loss function as the approximation error of the observed LR image, we established a completely blind end-to-end zero-shot learning framework for simultaneously predicting the target HR image and the degradation kernel without any external data. In particular, we adopted a multi-scale encoder–decoder subnet to serve as the image prior learning network, a simple fully connected subnet to serve as the kernel prior learning network, and a specific depthwise convolutional block to implement the degradation procedure. We conducted extensive experiments on several benchmark datasets and manifested the great superiority and high generalization of our method over both SOTA supervised and unsupervised SR methods.
1. Introduction
Single-image super-resolution (SISR) aims to estimate a high-resolution (HR) image from its low-resolution (LR) counterpart and has been a fundamental and important low-level vision task for decades. In SISR, the observed LR image is usually assumed to be a low-pass-filtered and downsampled version of the underlying HR image, and multiple solutions for an LR observation may exist, causing the ill-posed nature of the SR problem. To handle this challenging SR problem, numerous methods have been proposed, which mainly are divided into two research lines: the conventional optimization-based pipeline and the learning-based paradigm, and therein, the learning-based methods due to their good performance have been extensively explored.
Recently, deep-convolutional-neural-network (CNN)-based learning methods [1,2,3,4,5,6] have demonstrated great performance superiority over the non-deep SR methods and have become the dominant paradigm for the SR task in recent years. These great successes of the deep learning method for the SR task are mainly beneficial from the well-elaborated deep and complex network architectures and the long training process with large-scale LR/HR pairs. In addition, most existing deep learning methods are usually realized in a fully supervised way, and then, the learned SR model may only be applicable to the LR observations captured in controlled imaging conditions such as with the assumed degradation model: “bicubic” downsampling. The adaptation of these constructed models to real-world LR images often causes unpleasant/artificial structures and leads to great performance degradation because of the domain gap. Moreover, to boost SR performance, the recent state-of-the-art (SOTA) CNN-based methods have struggled to elaborate deeper and more complicated network architectures and, then, result in a large number of parameters and memory overheads in real applications.
To handle the limitation of deeply relying on the prior training with external data, internal learning [7] via extracting training samples from the observed LR image and its downsampled version has been exploited to produce a specific SR model for the under-studied image. To enhance the generalization of the specific SR model, Soh et al. [8] further incorporated meta-transfer learning with the internal learning, which can achieve a good initial state for different degradation procedures and quickly obtain convergence in the online learning for a specific LR image. However, these methods face difficulty in large upscaled SR tasks because of the limited numbers of the available training samples. Further, several works [9,10] have leveraged the strong capability of the CNN architectures for modeling low-level image statistics (priors) and proposed to predict the target HR image using the observed LR image without any prepared supervision signal (label) in an unsupervised manner, which is implemented by assuming the known degradation procedure such as the “bicubic” downsampling operation, restricting its wide applicability in real scenarios.
This study proposes a novel zero-shot blind SR framework (ZSB-SR) via leveraging the generative network’s powerful ability of capturing low-level image statistics with the LR observation instead of the prior training using the predefined imaged samples. The goal of this study was to learn the underlying HR image using the LR observation only without any external dataset, whilst the degradation procedure (blurring kernel and downsampling) for capturing the LR data is unknown, which is called the blind SR problem. To solve the challenge of the blind SR task, we specifically employed two deep networks for respectively modeling the priors of both the target HR image and its corresponding degradation kernel and designed a degradation block to realize the observation procedure of the LR image. Via formulating the loss function as the approximation error of the observed LR image, we established a completely blind end-to-end zero-shot learning framework for simultaneously predicting the target HR image and the degradation kernel without any external data. In particular, we adopted a multi-scale encoder–decoder subnet to serve as the image prior learning network, a simple fully connected subnet to serve as the kernel prior learning network, and a specific depthwise convolutional block to implement the degradation procedure. We conducted extensive experiments on several benchmark datasets and manifested the great superiority and high generalization of our method over both SOTA supervised and unsupervised SR methods.
In summary, our contributions are three-fold:
(1) A novel zero-shot blind SR method, i.e., ZSB-SR, is proposed, where external training samples and prior knowledge about the imaging conditions are not required.
(2) We respectively leveraged an encoder–decoder-based generative network for modeling the prior of the latent HR image, a fully connected network (FCN) for learning the blurring kernel, and a specific depthwise convolutional layer for realizing the degradation model. Moreover, we integrated the SoftMax nonlinearity with the output of the FCN to impose the non-negative and equality constraints on the blurring kernel.
(3) We exploited a joint optimization algorithm to solve the zero-shot blind SR model for simultaneously generating the latent HR image, learning the blurring kernel, and implementing the degradation operation, and thus, we constructed an end-to-end highly generalized SR learning framework applicable to arbitrary imaging conditions.
2. Related Work
In this section, we briefly survey the relevant works including fully supervised-CNN-based image super-resolution, the unsupervised-deep-learning-based method, and zero-shot learning.
Supervised-CNN-based image super-resolution: Recently, extensive research based on convolutional neural networks (CNNs) has been conducted to address the task of SISR and demonstrated remarkable progress in terms of the recovery performance. Dong et al. [1] initially proposed a shallow (three-layer) fully convolutional network for implicitly learning a mapping between LR and HR images and, then, extended it to use LR representative feature pre-learning and post-upsampling for constructing the efficient SR model. Current efforts [2,4,5] mainly focus on the design of deeper and more complicated network architectures for boosting performance. Kim et al. [2] proposed a VDSR model to increase the depth of the SR network to 20 and further leverage the idea of the residual connection from ResNet [11] for easing the training difficulty of the DRCN [3]. Later, Shi et al. proposed an efficient subpixel convolutional layer via upscaling the learned LR features to the HR output at the end of the SR network in the ESPCN [4], while Lim et al. exploited a very deep and wide network, EDSR [5], by stacking residual blocks without the batch normalization (BN) layers. Moreover, to improve the perceptual quality of the SISR results, several researchers [12,13,14] integrated adversarial loss [15] and perceptual loss [16] with the commonly used fidelity loss for SR network training. However, all of these methods are implemented in a fully supervised way and are trained on HR and synthetic LR pairs under a specific degradation operation, which usually cannot be well generalized to real LR images. Thus, Cai et al. [17] attempted to capture LR–HR image pairs under a realistic setting via tuning the focal length of DSLR cameras to collect images with different resolutions. Nevertheless, different devices usually have various imaging settings, and models trained even with the actually captured data under a specific device may not generalize well to LR images captured by other devices. Furthermore, several recent works attempted to incorporate the degradation parameters such as the the blurring kernel into the supervised network learning [18,19,20]. However, these methods rely on estimating blurring kernels existing in the prepared training datasets only and, thus, have an insufficient capability to handle the arbitrary blurring kernel.
Unsupervised-deep-learning-based methods: To address the insufficient generalization issue of the fully supervised methods in real scenarios, unsupervised learning methods have been exploited in recent years [21]. Some work on the GAN [15] have proven that different styles of images can be mutually translated, dubbed as image-to-image translation, without using the paired training samples [22,23]. Image super-resolution can be treated as a special image translation task to translate LR domain images to HR domain images. Yuan et al. [24] proposed Cycle-in-CycleGAN (CinGan) for the unsupervised image SR problem, which includes two translation cycles: one for the real LR and synthetic LR images and the other for the real LR and HR images. However, in CinGan, the used degradation model of the cycle from the HR images to real LR images is deterministic, thus making it restricted to generating diverse and real-world LR images. Motivated by the CycleGAN model, Zhao et al. [25] exploited the unsupervised degradation learning method for image SR via leveraging the cycle of the reconstruction and degradation models and using an additional perceptual loss in the LR domain instead of the HR domain. Later, Lugmayr et al. [26] investigated two stages of the SR framework to firstly generate realistic image pairs with an unsupervised image translation model and then predicted the HR image with an image restoration model, where the translation and restoration models were trained separately, while Fritsche et al. [27] further extended this method by dealing with the low- and high-frequency components separately. Moreover, Bulat et al. [28] proposed to automatically learn the degradation from HR images to real LR images and implemented an end-to-end learning framework via the high-to-low and low-to-high networks for modeling the relation of the HR and the estimated degraded LR images. Chen et al. [29] further expanded another cycle learning network between the real and synthetic LR images to improve the SR performance. Although some performance gains have been achieved with unsupervised learning, these methods usually require previously learning the degradation and restoration models using external image samples. In this study, we aimed to learn the specific prior of an under-studied target via simultaneously modeling the underlying structure of the latent HR image with a generative network and the realistic kernel with a fully connected network without resorting to any external image samples, which is expected to further improve the practicality and generalization of the SR networks, termed as “zero-shot” learning.
Zero-shot learning: Zero-shot learning (ZSL) is popularly investigated in the domains of recognition/classification for the problem setup where the learned model recognizes the objects from classes not previously seen in the training stage. Shocher et al. [7] firstly introduced ZSL for single-image SR, dubbed ZSSR. ZSSR exploits deep internal learning using the synthetic training pairs via treating the LR observation as HR supervision and the downsampled images from the observed LR image as the LR one and constructed a specific CNN model for the under-studied scene. Although ZSSR can potentially address different blurring kernels via varying the downsampling operations in preparing the internal training samples, it requires retraining the reconstruction models for different degradation models. Soh et al. [8] further integrated meta-learning into ZSSR methods and effectively leveraged the advantages of both internal and external learning for boosting SR performance. Since this kind of SR pipeline treats the observed LR image as HR supervision (“HR father”) and generates the “LR son” via downsampling the observation for internal learning, it usually cannot synthesize enough samples for model training, especially for large upscaled images, and thus, it is generally applied for small upscaled factors such as 2–4. Moreover, Ulyanov et al. [9] exploited a different paradigm, which utilizes the powerful modeling ability of deep convolutional neural networks for capturing the inherent structure of nature images and adapted for several image restoration tasks including the image SR problem. Without the generation of any synthesized training samples, DIP directly estimates the latent HR image with a generative network from the observed LR image only and achieved impressive performance even with a large upscaled factor. Thus, DIP can also be considered as a zero-shot (self-supervised) learning paradigm. However, DIP assumes that the LR observation is a “bicubic” downsampling version of the latent HR image and implements the fixed degradation operation with mathematical computation, which restricts the applicability to the data captured under diverse imaging conditions. This study is closely related to DIP [9], but we propose to model not only the latent HR image with a generative network, but also the degradation kernel with a fully connected subnet and further implement the downsampling operation with a specifically designed depthwise convolutional layer to construct an end-to-end blind zero-shot SR learning framework.
3. Proposed Method
In this section, we first introduce the problem formulation of the blind SR task and, then, present our proposed blind zero-shot learning framework including the generative network for modeling the latent HR image, the fully connected subnet for modeling the degradation kernel, and the designed depthwise convolutional block for implementing the degradation operation, as well as the joint optimization algorithm.
3.1. Problem Formulation
Given an observed LR image , the goal of the single-image SR problem aims at reconstructing an HR image with and . In general, the degradation model of the observed can be mathematically formulated as
where ⊗ represents the 2D convolution operation, and denote the blurring kernel and downsampling operation with factor s, respectively, while is the additive white Gaussian noise. Most existing methods including traditional optimization methods and recent appealing deep-learning-based paradigms assume the degradation operations (the blurring kernel and the downsampling operation) are known. Although outstanding performance of the deep-learning-based methods has been achieved, the learned models using the prepared LR–HR pairs with the fixed blurring kernel and downsampling operation can only super-resolve the LR image under the controlled imaging conditions. Then, the estimated results for the observed LR images in real scenarios would be greatly degraded. Thus, this study exploited a novel zero-shot blind SR learning method and is dedicated to reconstructing the underlying HR image from the observed LR image only with the unknown blurring kernel and downsampling operation.
3.2. The Proposed Zero-Shot Blind Learning Network
DIP [9] advocated that the deep CNN architecture itself has a sufficient capability of capturing a large amount of low-level image statistics (priors) [9] and, then, can generate a high-quality natural image from a noisy input to be applied to several low-level vision tasks including image SR. Inspired by this insight, we present a novel zero-shot blind SR learning paradigm for simultaneously modeling the priors of both the underlying HR image and blurring kernel using deep generative networks (with the unknown blurring kernel and downsampling). In particular, we employed a multi-scale encoder–decoder-based generative network for modeling the priors of the underlying HR image, a simple fully connected network for capturing the priors of the blurring kernel, and a specifically designed depthwise convolutional block for realizing the degradation procedure. Then, we established an unsupervised blind SR framework with end-to-end learning for simultaneously predicting the target HR image and the blurring kernel using the observed LR image only. The conceptual flowchart of the proposed zero-shot blind SR learning network is shown in Figure 1. Following the degradation model of the LR observation in Equation (1), we express the loss function of our proposed zero-shot blind learning network as
where and are the to-be-learned network parameters of the image generative network and the kernel learning subnet , respectively, while and denote the input data to and . Moreover, represents the magnitude of the row and column pixel in the target HR image, and is the learned weight of the element in the predicted blurring kernel. Via minimizing the loss function in Equation (2), we aimed to probe the parameter space of the image and kernel learning generative networks and to discover the optimal parameter solution, and therefore, the achieved optimal is used to proficiently generate the underlying target: , whilst is employed to provide an approximation of the blurring kernel: . In the following section, we embody the network architectures of and for the image and kernel learning, the input data to the generative networks, the detailed realization of the degradation block, and the joint optimization algorithm for both and .
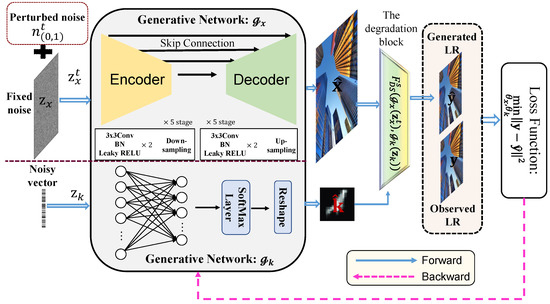
Figure 1.
The schematic concept of the proposed zero-shot blind SR learning framework (ZSB-SR).
The architectures of the generative networks and : Since natural images have diverse contents with various salient structures and abundant textures, the network to generate high-quality HR natural images has to possess a sufficient modeling capability for providing acceptable results. As demonstrated in several data generation methods for different tasks [9,30,31], the multi-scale encoder–decoder architecture has a powerful modeling capability to achieve high-quality images. Therefore, in this study, we employed a symmetric encoder–decoder network with a simple feature transferring block like skip connections between the encoder and decoder for feature reusing, to serve as the image prior learning subnet . The employed encoder–decoder network can capture multi-scale feature representations for modeling various contexts in in the target image. In the generative network , we composed both the encoder and decoder paths with 5 convolutional blocks for learning multi-scale contexts and transferred the outputs of the 5 encoder blocks with a naive pointwise convolution layer to the corresponding decoder blocks for reusing the learned detailed features. Specifically, each block contains 3 convolutional ReLU layers, and a max-pooling layer is employed between the adjacent blocks of the encoder to reduce the feature map to half size, while a bilinear upsampling layer is used between the adjacent blocks of the decoder to extend the feature map to double the size. Finally, given the learned features by the last block of the decoder, a reconstruction block is used to estimate the target HR image.
Contrary to the image prior learning subnet with the encoder–decoder architecture for capturing the low-level statistics of natural images, we adopted a simpler network to model the prior of the blurring kernel since has a much lower dimensionality and simplex spatial structure. Specifically, we employed a fully connected network (FCN) to serve as and used a one-dimensional noise vector as the input data. The overall structure of is shown in the gray background window of Figure 2, which is composed of a hidden layer, an output layer with nodes, and a SoftMax layer to constrain the non-negativity and equality of the learned element in . Finally, the 1D output with the entries is reshaped into the 2D matrix as the predicted blurring kernel.
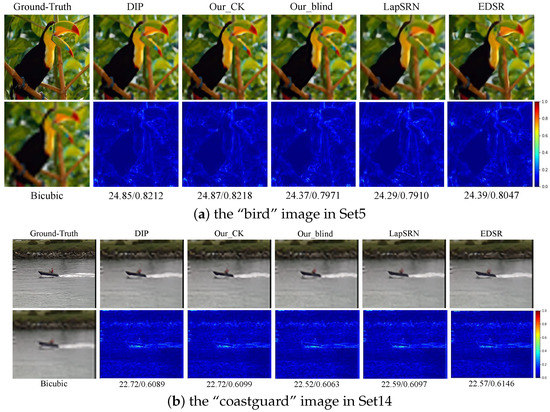
Figure 2.
Comparison of the visualization results of the recovered HR images of different SOTA methods. The first row denotes the resulting HR images, while the second row gives the difference images between the recovered and the ground-truth images.
The input data to the generative networks: As proven in different generative adversarial learning methods such as DCGAN [32] and its variants [33,34,35,36], high-quality natural images can be generated from a random noisy input. Most existing GAN-based methods attempt to generate diverse images with predefined specific concepts by leveraging the powerful modeling capability of CNNs, which transfer the low-dimensional noisy input sampled from a previously defined distribution to the expected images obeying the same distribution with the large-scale training samples. In contrast, the deep image prior [9] advocated that the generative network can be potentially used to learn the prior of a specific image from random noise and is successfully applied to several image restoration tasks. In this study, we similarly leveraged randomly generated noise (* represents or ) as the input of the generative network or . However, utilizing a fixed noise input may cause the optimization solution to drop into a local minimization point due to the ill-posed nature of Equation (2). Thus, to mitigate the above-mentioned limitation, we firstly sampled a random noisy vector as the base input to the generative network while adding a small random perturbation (randomly sampled noise with a uniform distribution in the value range (0, 1)) to the base input at each step of network training. The input to the generative network in the training step can be expressed as:
where denotes the interference degree of the fixed noise and is the randomly sampled noise at the training step. In contrast to , the blurring kernel is not the main estimation target and has a much lower dimensionality and smooth spatial structure. The noise perturbation to the input for the kernel learning subnet would destabilize the training procedure of . Thus, for the kernel prior learning subnet , we maintained the fixed noisy input generated from a uniform distribution in all training steps. Finally, given the trained generative network, we predicted the target HR image from the initial fixed noise as .
The implementation of the degradation block: After generating the HR image with and the learned blurring kernel with , we attempted to obtain an approximated version of the observed LR image for the formulation of the loss function. Specifically, we elaborated a degradation block to realize the procedure. As shown in Equation (1), the degradation procedure consists of the convolution operation with a blurring kernel and a downsampling operation, where the downsampling can be approximated by a blurring procedure with a fixed kernel and a nearest neighbor downsampling operation such as the combination of a Lanczos kernel and the nearest downsampling for the bicubic downsampling. We assumed that the kernel learning subnet can achieve the integrated kernels containing the real blurring kernel and the approximated kernel for the downsampling operation. Then, we realized the degradation procedure using a specific depthwise convolution layer (SDW) with the predicted target HR image as its input, with the learned blurring kernel as its parameters. Moreover, it is well known that each color channel should have the same degradation operation, i.e., the same blurring kernel and downsampling operations, in a real scenario, and thus, we imposed the same kernel weights on the DW layer for all color bands with zero bias and set the stride parameter as the downsampling factor for realizing the nearest neighbor downsampling. The designed DW layer is expressed as
where denotes an approximated version of the degraded LR image from the generated HR image: , and the kernel weights in the SDW layer were set as the learned output of . Therefore, our proposed SR framework has high flexibility to be adapted to various real scenarios including unknown blurring kernels and downsampling operations. Via implementing the degradation procedure (including blurring and downsampling transformation) in Equation (2) with the designed SDW block, the loss function for training the blind SR network can be reformulated as
Via minimizing the loss in Equation (5), we can jointly optimize the parameters of the image and kernel prior learning subnets and . Since there is no requirement to previously prepare the labeled training samples, the learning procedure of the proposed blind SR framework can be considered as a kind of “zero-shot” unsupervised learning with only the observed LR image.
Joint optimization algorithm: The constructed model in Equation (5) for our ZSB-SR is an unconstrained optimization problem and is highly non-convex. Most commonly used solutions such as for the traditional MAP-based framework usually adopt an alternating minimization strategy, which may get stuck at saddle points [37]. Benefiting from the powerful modeling capacity of and , which can avoid implausible HR images and trivial delta kernel solutions, we exploited a joint optimization method instead of using alternating optimization for our ZSB-SR. To update the parameters of the generative networks and , we derived the gradients with respect to and using the automatic differentiation techniques [38]. The proposed joint optimization algorithm is summarized in Algorithm 1, where the parameters and for the two generative networks are jointly updated using the ADAM algorithm [39]. In our experiments, we stopped the optimization procedure after T iterations, and the latent HR image and the degradation kernel can simultaneously be generated as and .
| Algorithm 1 Joint optimization for ZSB-SR. |
|
4. Experimental Results
To verify the effectiveness of our proposed ZSB-SR framework, we firstly conducted an ablation study to analyze the effect of the generative network for approximating different degradation operations. Then, the ZSB-SR was evaluated on several benchmark datasets to be compared with the state-of-the-art methods including the fully supervised non-blind methods and the unsupervised SR methods.
The proposed ZSB-SR was implemented using Pytorch. We set the learning rates for and as 0.01 and , respectively, and adopted the ADAM optimization strategy. The experiments followed the same settings, i.e., 4000 (2000) for a downsampling factor of 8 (4), and the noises , , and were sampled from the uniform distribution with a fixed random seed of 0, while the perturbed parameter was set as 0.05.
4.1. Ablation Study
We conducted an ablation study on the Set5 [40], Set14 [41], and B100 [41] datasets and simulated the LR inputs with different degradation operations including bicubic downsampling only (without the blurring kernel) and the combined Gaussian blurring kernels with different standard deviation values ( from 1.0 to 3) and the bicubic downsampling operation. To validate the learning capability of the generative network , we varied the kernel weights of the degradation operation via setting it as the correct kernel (such as the Lanczos kernel for bicubic downsampling), the wrong kernel, the automatically learning inside , and the learned kernel with . Table 1a provides a quantitative comparison on three datasets from the bicubic downsampled LR images with factors of 4 and 8. From Table 1a, it can be seen that the learned kernels with the generative network provide comparable results using the correct kernel (here, Lanczos kernel for bicubic downsampling).

Table 1.
Quantitative comparison with the varied kernels used in . (a) On the bicubic downsampled LR images; (b) on the LR images with Gaussian blurring kernels and the bicubic downsampling operation. The first numerical result represents the PSNR value, and the second denotes the SSIM value.
Next, we conducted experiments using the simulated LR images with both blurring kernels and the bicubic downsampling operation, where Gaussian kernels with different standard deviation values from 1.0 to 3.0 were adopted without loss of generality. In the experiments, we adopted different experimental settings including the semi-blind conditions, where the bicubic downsampling operation was assumed to be known, but with less knowledge about the blurring kernel such as only the known kernel type (Gaussian) or no knowledge about the kernel and the complete blind condition. In the semi-blind experimental setting, we investigated three values: 0 (without blurring kernel), 1, and the true value of in the known Gaussian type to give the estimated HR image , while we only learned the blurring kernel using for the setup without any knowledge about the blurring kernel. In the blind experimental setting, we automatically learned the integrated kernel of the blurring and downsampling operations with and . Table 1b gives the quantitative comparison on the Set5 and Set14 datasets with a factor of eight and different experimental settings, which manifested comparable performance or better performance using our ZSB-SR under the completely blind condition compared to the varied implementations under some controlled conditions such as the known downsampling operation.
4.2. Comparison with the State-of-the-Art Methods
Since most existing methods generally super-resolve the bicubic downsampled LR images, we firstly verified the performance of the reconstructed HR images on the simulated LR images of the benchmark datasets: Set5 [40], Set14 [41], and B100 [41] with bicubic downsampling to conduct a fair comparison. The compared state-of-the-art methods consisted of an unsupervised/non-blind pipeline including the unsupervised-optimization-based method with TV_Prior, DIP [9], and our method with the correct kernel (Our_CK) and the supervised deep networks (LapSRN [6] and EDSR [5]), where our method falls under the unsupervised and blind paradigm. Table 2a provides a quantitative comparison, which manifests that our ZSB-SR can achieve the best performance under the same experimental setting and comparable performance under completely an unsupervised and blind setting to the fully supervised deep learning methods. The compared visualization results of the recovered HR images with different SOTA methods are shown in Figure 2, where our ZSB-SR (unsupervised and blind) gives comparable performance to both SOTA unsupervised and supervised non-blind methods.

Table 2.
Quantitative comparison of our proposed ZSB-SR with the sate-of-the-art methods.
Moreover, we also evaluated our ZSB-SR on 100 validation images of the NTIRE2018 super-resolution challenge, where the LR images were created with more realistic degradation by the challenge. We adopted the ZSB-SR method for NTIRE17 Track 2, where the LR images were captured with diverse degradations. Since there is no training dataset for this task, the popular methods generally fall into two paradigms: (1) synthesizing training pairs according to the estimated degradation types and, then, constructing the super-resolved model with the deep learning method; (2) the unsupervised image translation method with the GAN. Therefore, we compared our ZSB-SR method with the mentioned SOTA methods for this task, and Table 2b manifests the compared results, which also demonstrates the superior performance of our ZSB-SR.
5. Conclusions
In this study, we investigated a novel zero-shot blind SR model, i.e., ZSB-SR, for reconstructing the underlying HR image from the observed LR image only under an unknown degradation procedure. Instead of learning the prior from the previously prepared data or exploiting hand-crafted priors according to the accumulated experience, we leveraged the powerful modeling capability of generative networks to automatically learn the priors in the latent HR image from the observed LR image. Specifically, we adopted two generative networks: an encoder–decoder-based network architecture to model the latent HR image and a fully connected network (FCN) to learn the degradation knowledge such as the blurring kernel and a specially designed degradation block to implement the imaging procedure, and thus, we constructed an end-to-end learning ZSB-SR framework for jointly predicting the latent HR image and the degradation knowledge. Extensive experiments on several benchmark datasets demonstrated the great superiority and high generalization of our proposed ZSB-SR method over both SOTA supervised and unsupervised SR methods.
Author Contributions
Conceptualization, methodology, and writing, K.Y. and X.-H.H.; software, K.Y.; validation and visualization, K.Y.; supervision, project administration, and funding acquisition, X.-H.H.; investigation and data curation, K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Grant-in Aid for Scientific Research from the Japanese Ministry for Education, Science, Culture and Sports (MEXT) under Grant No. 20K11867, and JSPS KAKENHI Grant Number JP12345678.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available in a publicly accessible repository.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1132–1140. [Google Scholar]
- Lai, W.S.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep laplacian pyramid networks for fast and accurate superresolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; Volume 2. [Google Scholar]
- Shocher, A.; Cohen, N.; Irani, M. “Zero-shot” super-resolution using deep internal learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3118–3126. [Google Scholar]
- Soh, J.W.; Cho, S.; Cho, N.I. Meta-Transfer Learning for Zero-Shot Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3516–3525. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. Deep Image Prior. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Yamawaki, K.; Han, X.H. Deep Blind Un-Supervised Learning Network for Single Image Super Resolution. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 1789–1793. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; Shi, W. Photo-realistic single image superresolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Sajjadi, M.S.M.; Scholkopf, B.; Hirsch, M. Enhancenet: Single image super-resolution through automated texture synthesis. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Chao Dong, Y.Q.; Loy, C.C. ESRGAN: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 63, 2672–2680. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward real-world single image super-resolution: A new benchmark and A new model. arXiv 2019, arXiv:1904.00523. [Google Scholar]
- Gu, J.; Lu, H.; Zuo, W.; Dong, C. Blind super-resolution with iterative kernel correction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1604–1613. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Learning a single convolutional super-resolution network for multiple degradations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. Deep plug-and-play super-resolution for arbitrary blurring kernels. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R.; Fritsche, M.; Gu, S.; Purohit, K.; Kandula, P.; Suin, M.; Rajagoapalan, A.N.; Joon, N.H.; et al. Aim 2019 challenge on real-world image super-resolution: Methods and results. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. arXiv 2017, arXiv:1703.10593. [Google Scholar]
- Yi, Z.; Zhang, H.; Tan, P.; Gong, M. Unsupervised dual learning for image-to-image translation. arXiv 2017, arXiv:1704.02510. [Google Scholar]
- Yuan, Y.; Liu, S.; Zhang, J.; Zhang, Y.; Dong, C.; Lin, L. Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Zhao, T.; Ren, W.; Zhang, C.; Ren, D.; Hu, Q. Unsupervised degradation learning for single image super-resolution. arXiv 2018, arXiv:1812.04240. [Google Scholar]
- Lugmayr, A.; Danelljan, M.; Timofte, R. Unsupervised learning for real-world super-resolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Fritsche, M.; Gu, S.; Timofte, R. Frequency separation for real-world super-resolution. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Korea, 27–28 October 2019. [Google Scholar]
- Bulat, A.; Yang, J.; Tzimiropoulos, G. To learn image super-resolution, use a gan to learn how to do image degradation first. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Chen, S.; Han, Z.; Dai, E.; Jia, X.; Liu, Z.; Liu, X.; Zou, X.; Xu, C.; Liu, J.; Tian, Q. Unsupervised Image Super-Resolution with an Indirect Supervised Path. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Isola, T.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Wang, T.C.; Liu, M.Y.; Zhu, J.Y.; Tao, A.; Kautz, J.; Catanzaro, B. High-Resolution Image Synthesis and Semantic Manipulation with Conditional GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Zhang, H.; Goodfellow, I.; Metaxas, D.; Odena, A. Self-Attention Generative Adversarial Networks. arXiv 2019, arXiv:1805.08318. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive Growing of GANs for Improved Quality, Stability, and Variation. arXiv 2018, arXiv:1710.10196. [Google Scholar]
- Donahue, J.; Krähenbühl, P.; Darrell, T. Adversarial Feature Learning. arXiv 2017, arXiv:1605.09782. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. arXiv 2019, arXiv:1812.04948. [Google Scholar]
- Tseng, P. Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl. 2001, 109, 475–494. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lererr, A. Automatic differentiation in pytorch. In Proceedings of the NIPS Workshop:The Future of Gradient-based Machine Learning Software and Techniques, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi-Morel, M. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the 23rd British Machine Vision Conference (BMVC), Surrey, UK, 3–7 September 2012; pp. 1–10. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Lecture Notes in Computer Science, Proceedings of the International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 711–730. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).