Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis
Abstract
1. Introduction
1.1. State-of-the-Art Methods
1.2. Related Works
2. Problem Definition
3. Objectives and Contributions
- Provide an accurate and fast estimation of IF and instantaneous slope using deep learning, as deep learning for frequency classification is promising. The proposed method can be used for RADAR and medical SONAR applications, where RADAR functions include range (localization), angle, and velocity, while medical SONAR functions include diagnosis, classification, and tracking. The use of the proposed approach can lead to improved RADAR localization and improved medical SONAR diagnosis.
- Create a dataset of noisy LFM signals with varying LCR and frequency.
- Two types of noise are combined by a linear equation, as explained in Section 5.1.
- Convolutional deep learning, rather than recursive networks, estimate parameters. Researchers commonly use convolutional networks to classify signal types.
- A comparison between the classical and convolutional deep learning methods.
- They obtain high accuracy in the presence of impulsive noise without the use of de-noise methods.
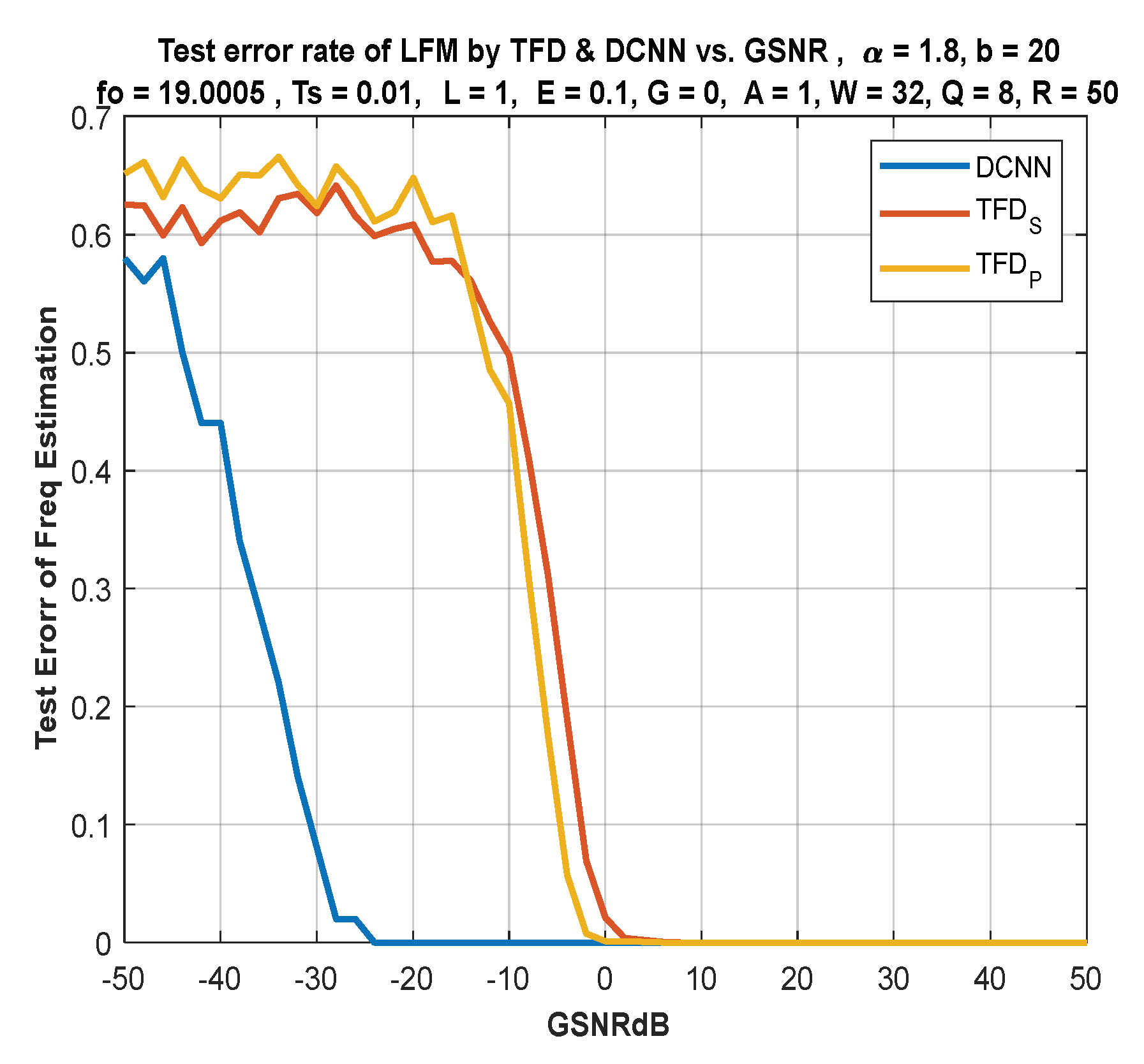
- The performance of the DL approach is compared with the version of the still-active classical techniques based on Fourier analysis. It is shown that the classical time–frequency-based methods are ineffective under the damaging alpha-stable noise, especially under low signal-to-noise ratios, where a difference of 20 dB in performance has been noticed compared to the DL approach. This result is vital for underwater RADAR systems, where impulsive noise is dominant.
- The DL approach is SNR-dependent, so an investigation of the system performance under various SNRs is presented. Based on our previous work [12], a change in SNR will have little effect on the performance of the DL-based approach.
- The reduced complexity introduced by DL-based FE and avoiding complex valued arithmetic will make FE easier and cheaper for IoT communications, sensors, sensor networks, and SDR. This work presents discussions on such possibilities.
4. FM Signals and Noise
4.1. Instantaneous Frequency and FM
4.2. Additive White Gaussian Noise
- Calculating the power contained in the input signal , were
- Converting the supplied ( in ) to a linear scale and finding the noise power in terms of SNR and signal power , were
- Using the following equations to determine the AWG noise:where For a real signal , for a complex signal .
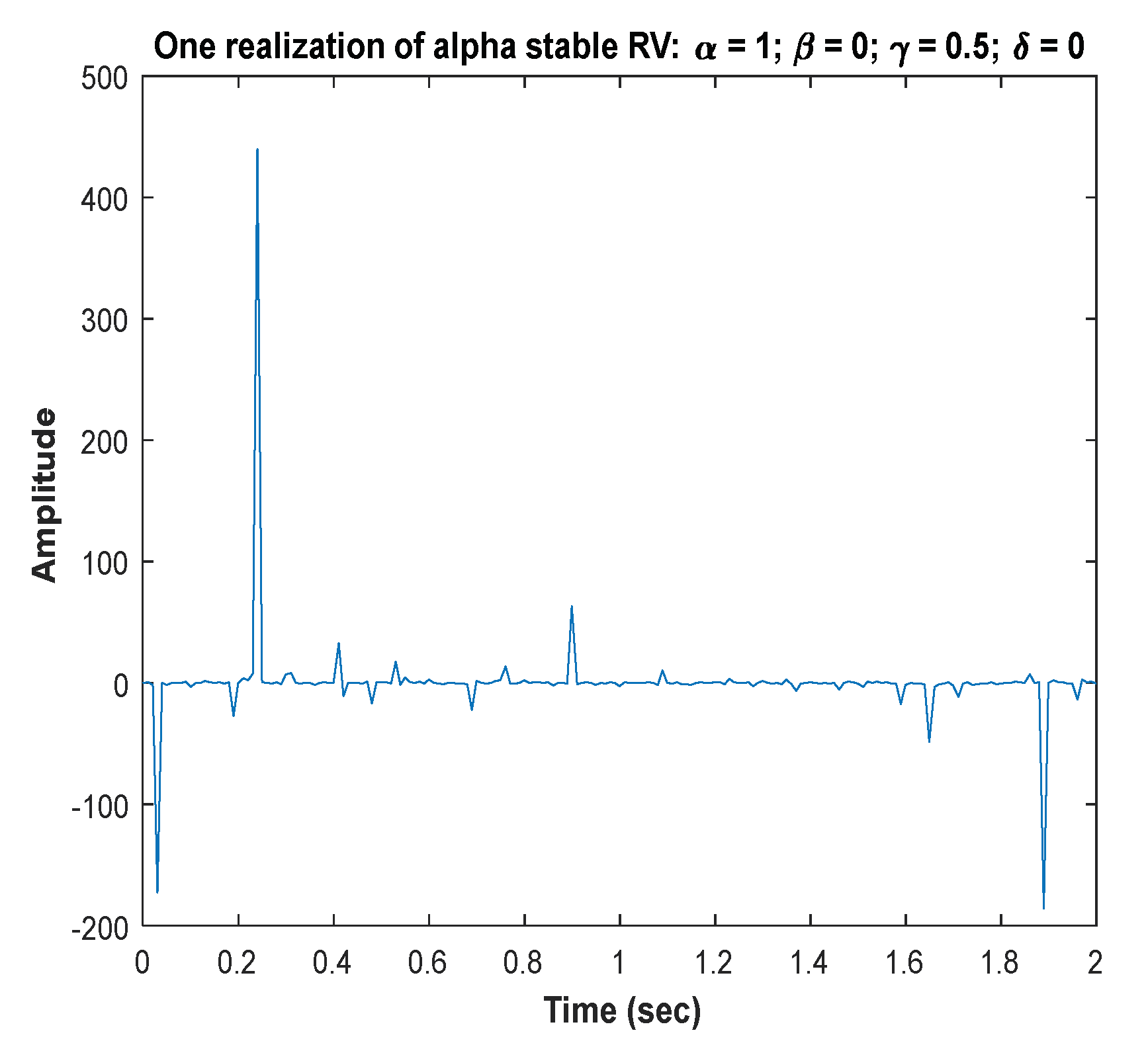
4.3. Symmetric α-Stable Noise
5. The Proposed Method
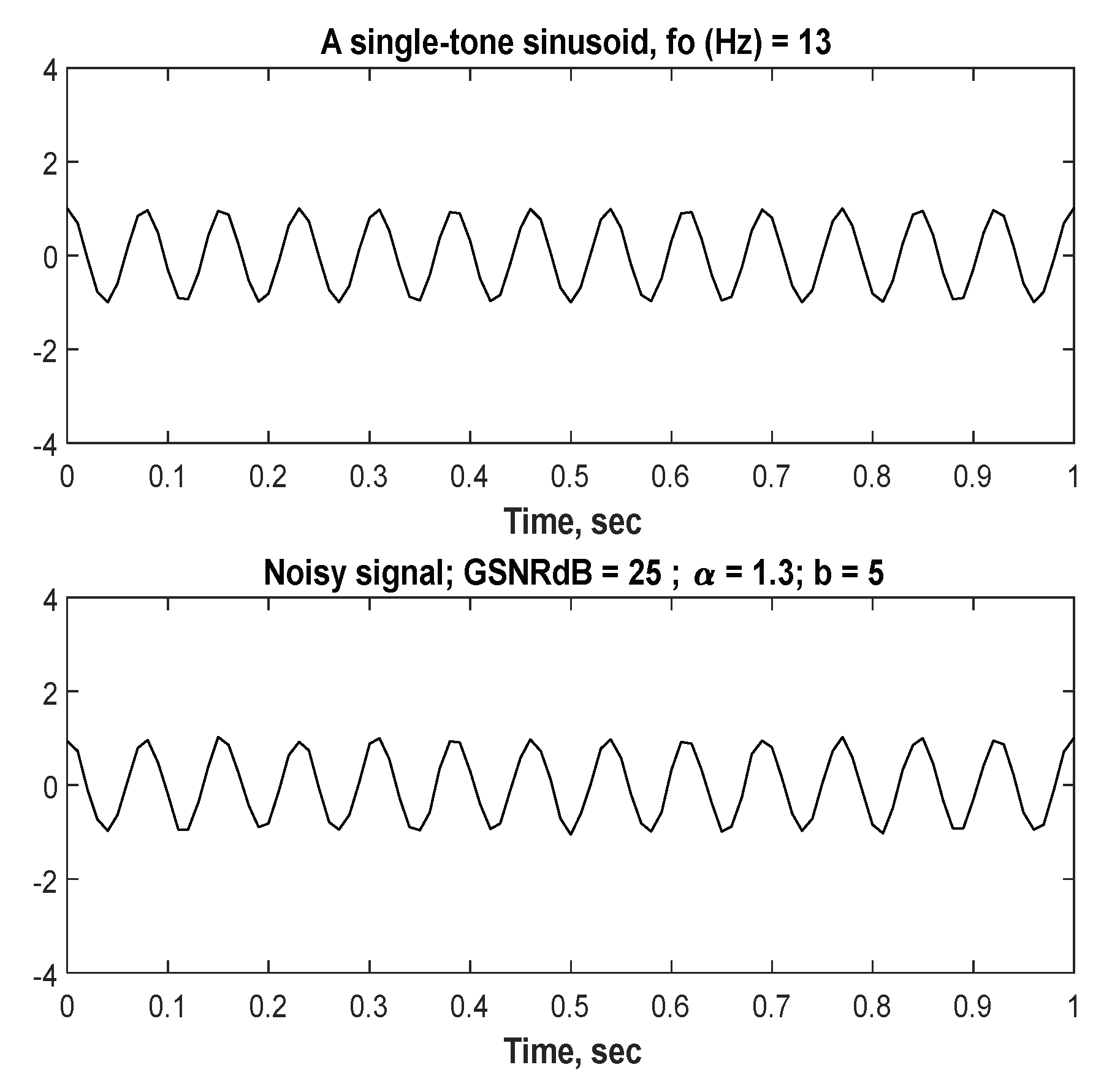
5.1. Hybrid Noise and Noisy Signal Generation
- The frequency () range:
- Initial frequency is
- Final frequency is
- The number of frequencies is
- The differential frequency step is
- The range of frequency is
- The LFM slope () range:
- Initial slope is
- Final slope is
- The number of slopes is
- The differential frequency step is
- The range of slope is
- The time vector () range:
- Initial time is
- Final time is
- Sampling period is
- The range of time in seconds is
- GSNR range is chosen as .
- To generate as shown in Equations (27b), (33) and (35) with four parameters chosen as follows: , while the choice of is (scale parameter) relies on the ratio as shown in Equation (19).
- AWGN ( is generated as shown in Equation (10).
- Total noise ( is a hybrid: AWGN with as shown in Equation (16).
5.2. Converting 1D Signal into 2D Signal and Dataset Creation
| Algorithm 1: Converting 1D Signals into 2D Signals |
| Input:). Output:. Begin: 1.For // 2. initial counter where . 3. tack the values from and place in column by column and row by row as follows: 4. 5. For // 6. For // 7. 8. 9. End for 10. End for 11. 12. End for 13. Return in folders. // name folder is label. End algorithm |
The Dataset Generates
| Algorithm 2: The Dataset is Divided into Training, Validation, and Testing Sets |
| Input:, where each label is presented as frequency and slope. Output: Noisy LFM Signals divided into a . Begin: 1. Select a random index as the following: , where 2. Sorted dataset according to as follows: 3. Select the length of training, validation, and testing percent: 4. Divided dataset into a training set (, and labels ( as follows: 5. Divided dataset into validation set (, and labels ( as follows: 6. Divided dataset into the testing set (, and labels ( as follows: 7. End of algorithm |
5.3. Estimation of IF and LCR by DNN
- True frequency () is the target frequency of a signal
- Estimate frequency () is the predicted frequency of the DNN network
- The relative absolute error of the frequency
- True slope ( is the target slope of a signal
- Estimate slope () is the predicted slope of the DNN network
- The relative absolute error of the slope is
- Estimate IF is
5.4. Estimation of IF and LCR by CNN
- Batch normalization is applied on input signals; it speeds up training by halving the epochs (or faster).
- Feature map is found by computing the sum of product for input node with weights (filters), then summation with bias is performed, where bias is used in the forward stage.
- An activation function is applied to the sum of the product, where the activation function is ReLU.
- Max pooling is applied; it is used to decrease the size of the feature maps.
- The convolution layer is applied three times with the number of filters (60, 90, and 128), and each of them is followed by a ReLU layer and max pooling layer.
- A fully connected network is applied: it is a feedforward neural network where all of the inputs from the previous layer are linked to each node in the next layer.
- Dropout is applied: it is a method of stochastic regularization. It aids in the prevention of overfitting, and the accuracy and loss will gradually improve.
- The classification stage includes three layers that are fully connected, followed by softmax, then a classification operation. The fully connected layer has ten output nodes: a feedforward neural network. The softmax is utilized as the activation function in the output layer for multi-class classification tasks. The loss function is finding the error for a single sample in data training that relies on actual and predicted labels. The loss function is cross entropy loss used to measure how well a classification model in deep learning performs. The loss (or error) is calculated as a number between zero and one, where the zero value referred the perfect model. The cost function is the summation of the loss function for all data training. The objective function is referred to as a cost function (cross-entropy).
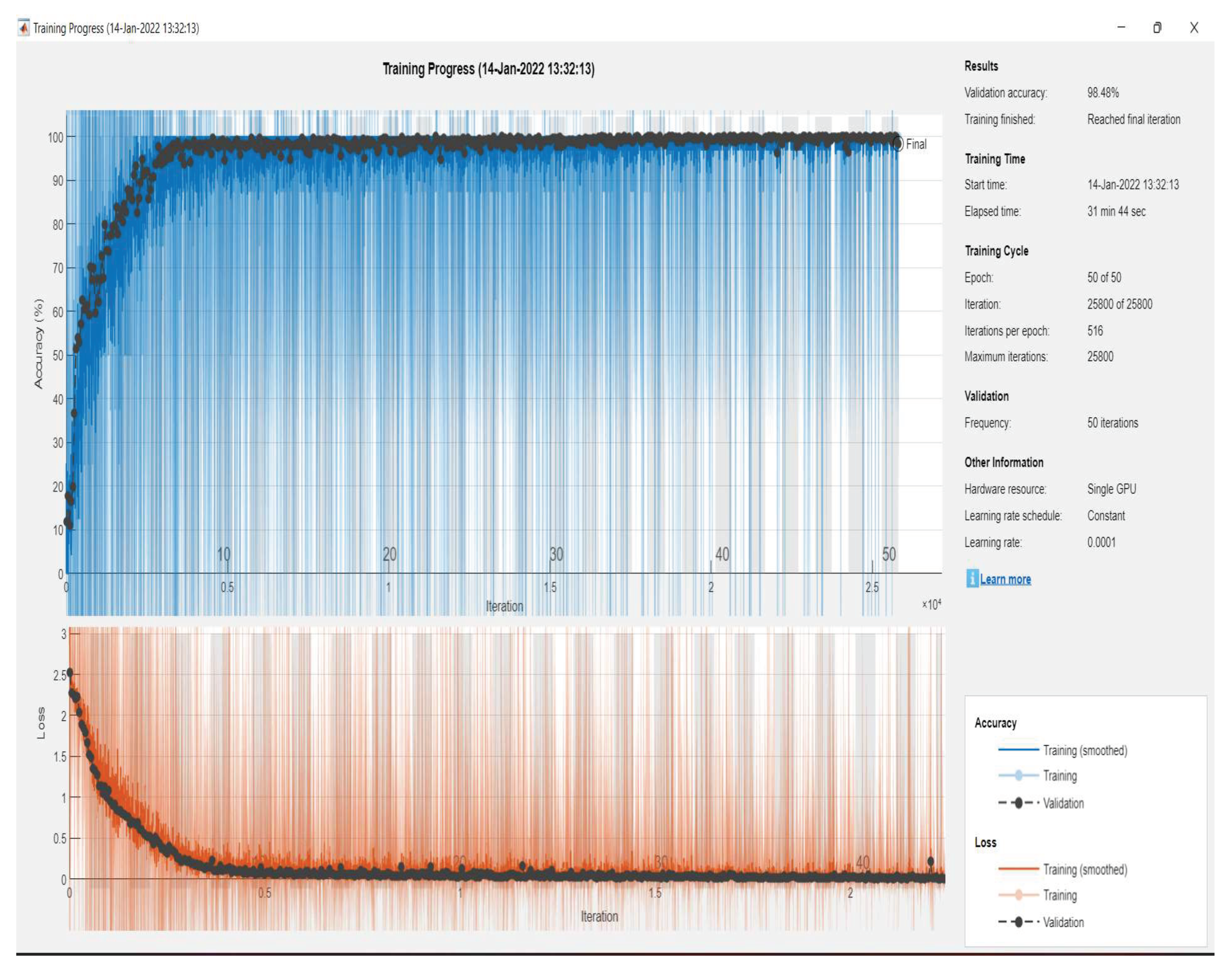
- The parameters of the CNN model are a learning rate of 0.0001, max epochs are 5, and mini-batch size is 8. At the same time, Adam uses an initial learning rate is 0.001, Epsilon is 0.00000001, squared gradient decay factor is 0.999, and Gradient decay factor is 0.9. Hyperparameters in convolution are: the number of filters (30, 60, 90, and 128), the filter size is , and padding and stride are equal to one. In batch normalization, the parameters are , , and , max pooling uses the size , and the stride is . In the dropout layer, the probability of dropout is 50%, and in the fully connected layer, the number of classes is 10.
- In this stage, an optimization algorithm is needed to update the parameters, and each layer’s error should be calculated. The optimization algorithm controls how the parameters of the neural network are adjusted. In this work, Adam is used as the optimization algorithm
- The weights and biases update is given by:
- where are new weights and biases, are old weights and biases, and as explained in reference [22], Adam is updating the weights and biases relying on the derivative of the loss function (entropy). The derivative of the loss function is applied in the backward stage for CNN, while the loss function is applied in the forward stage for CNN. It measures the performance of the network. The training set is evaluated for each epoch using the validation set. The validation loss is similar to the training loss and is calculated as the sum of the errors for each sample in the validation set. Forward and backward stages are performed until reaching the last epoch (end of training).
- The final step is to evaluate the CNN model by applying a testing set to the trained CNN model to predict the label (class) for the test data. The CNN model is evaluated using relevant metrics such as accuracy.
- After the class number (label) prediction, it is possible to estimate the frequency and slope to which it belongs. Then it is possible to calculate the amount of error and the accuracy of the predicted parameters versus the true parameters as follows:
- True frequency () is the target frequency of a signal
- Estimate frequency () is the predicted frequency of the CNN network
- The relative absolute error of the frequency
- True slope ( is the target slope of a signal
- Estimate slope () is the predicted slope of the CNN network
- The relative absolute error of the slope is
- Estimate IF is
| Algorithm 3: CNN Model Procedure |
| Input:, where each label is represented by the . Output: Frequency and slope estimation. Begin: Step 1: A training stage 1. The input layer is the training set with length , and validation set . 2. Divided training set into min-batches, where mini-batch size equals 8. Iteration is one-time processing for forward and backward for a batch of samples. Iterations per epoch = number of training samples mini-batch size. Iterations = iterations per epoch number of epochs. 3. Find the batches, where . 4. Find batch list, where 5. For epoch =1 No of epoch 6. For iteration =1 batches 7. Select data by 8. For 9. The convolutional layer applies convolutional operation between input signals and filters, where the number of filters equals 30. 10. A batch normalization layer is applied as a result of step 2. 11. ReLU is used as an activation function. 12. Max pooling layer is applied to reduce the features map. 13. The convolution layer is applied with several filters 60 to find feature maps, and then ReLU and max pooling layer are used. 14. The convolution layer is applied with several filters 90 to find feature maps, and then ReLU and max pooling layer are used. 15. The convolution layer is applied with the number of filters 128 to find feature maps and then used, ReLU and max pooling layer. 16. A fully connected layer and dropout layer are applied to avoid overfitting. 17. A fully connected layer is used with an equal output number of classes. 18. Softmax is applied to find the output of the network that presents the predicate label ( where each label is predicate frequency and slope. 19. In the classification layer, calculate the performance of the network by entropy as follows: where is the number of classes, is predicate labels, is actual labels in one-hot encoding, , is the number of samples training. 20. In the backward stage, calculate the error by the derivative of the loss function and compute the change of the weights ( as follows: 21. End of k loop 22. Cross entropy is computing the cost function of the network. The sum of loss for each batch in the training set calculates the cost function of the training loss function: Then compute the accuracy of the training data set: 23. The weights ( are updated as follows: 24. Evaluate the network during training by using validation data for each iteration, where applied same network layers on validation data and new weights are used to predict the label of validation data, and the cost of loss for validation is similar to the cost of loss for training as follows. Moreover, find loss as follows: 25. End of iteration 26. End of epoch 27. CNN model trained () is returned. Step 3: Testing stage 1. The testing set It used the CNN model trained, which has the same layers but uses optimal weights. 2. The CNN trained is applied on the testing set to predict the label, where each label is predicate frequency and slope. ● Estimate frequency () is predicted frequency and estimated slope () is the predicted slope from the predicated label () of CNN network as follows: ● Compute the error of frequency and slope as follows: ● The relative absolute error of the frequency ● The relative absolute error of the slope is ● Estimate IF is 3. Evaluation of the CNN model trained using metrics is accuracy, precision, recall, F-Measure, and ROC. End of algorithm |
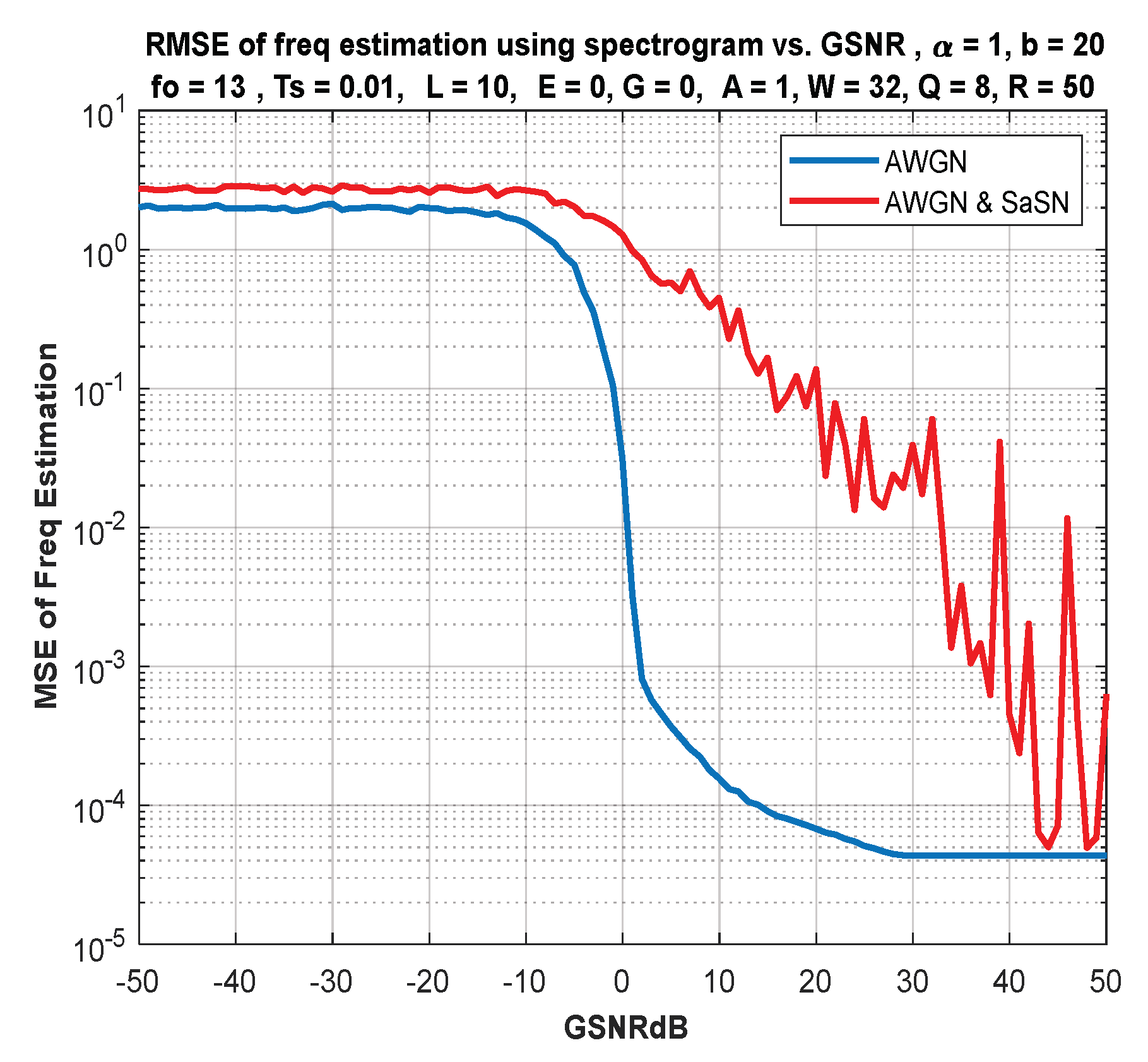
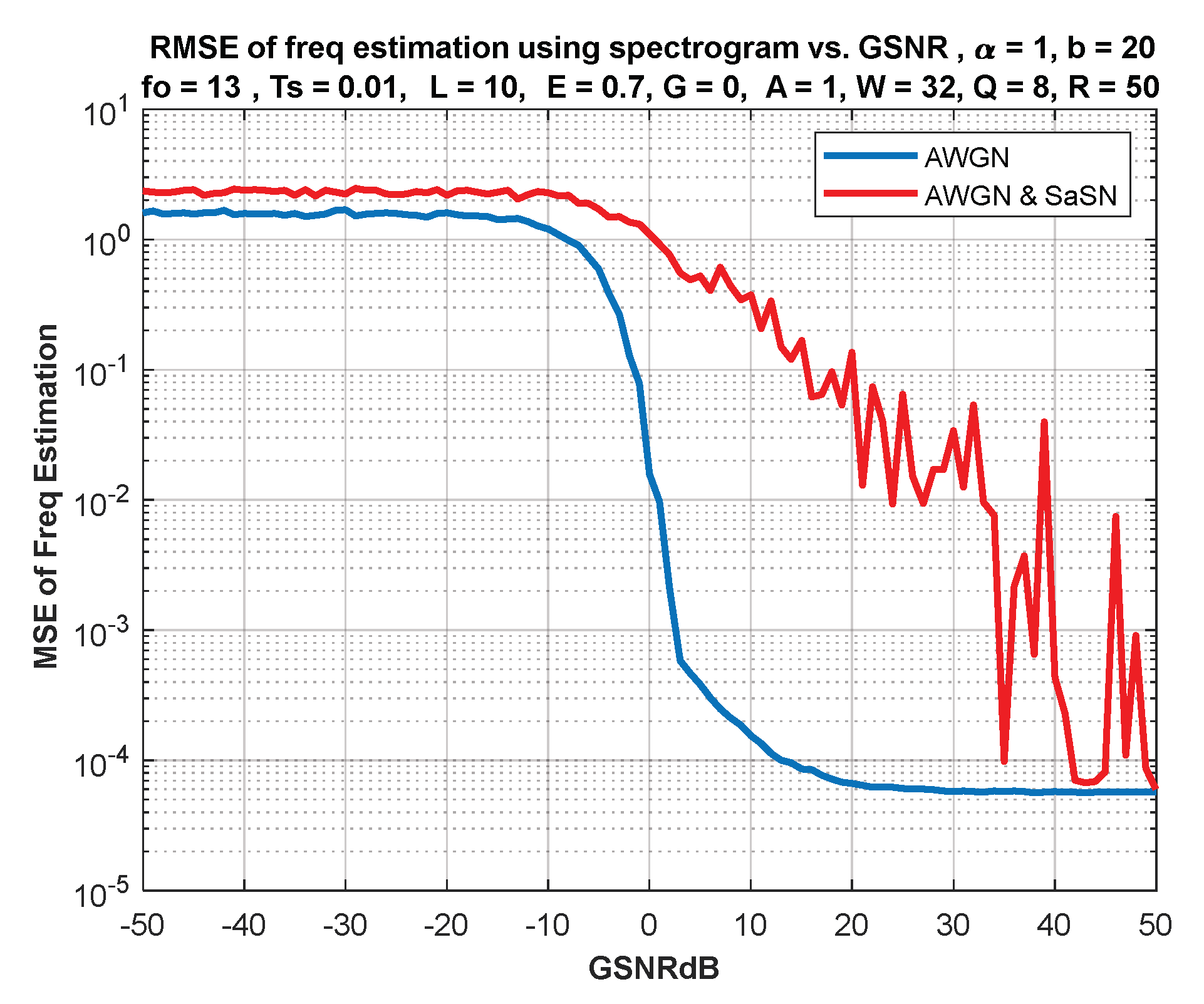
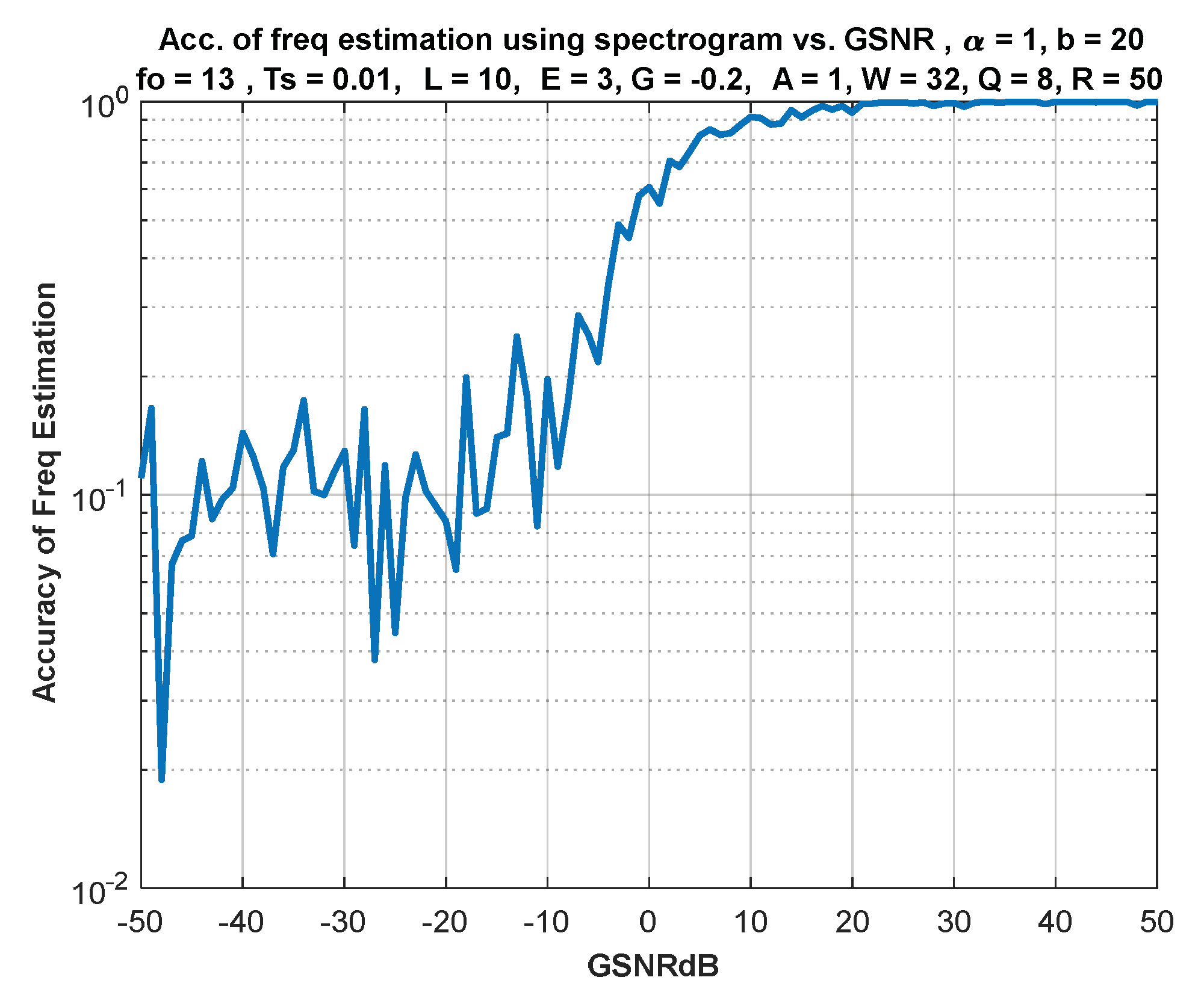
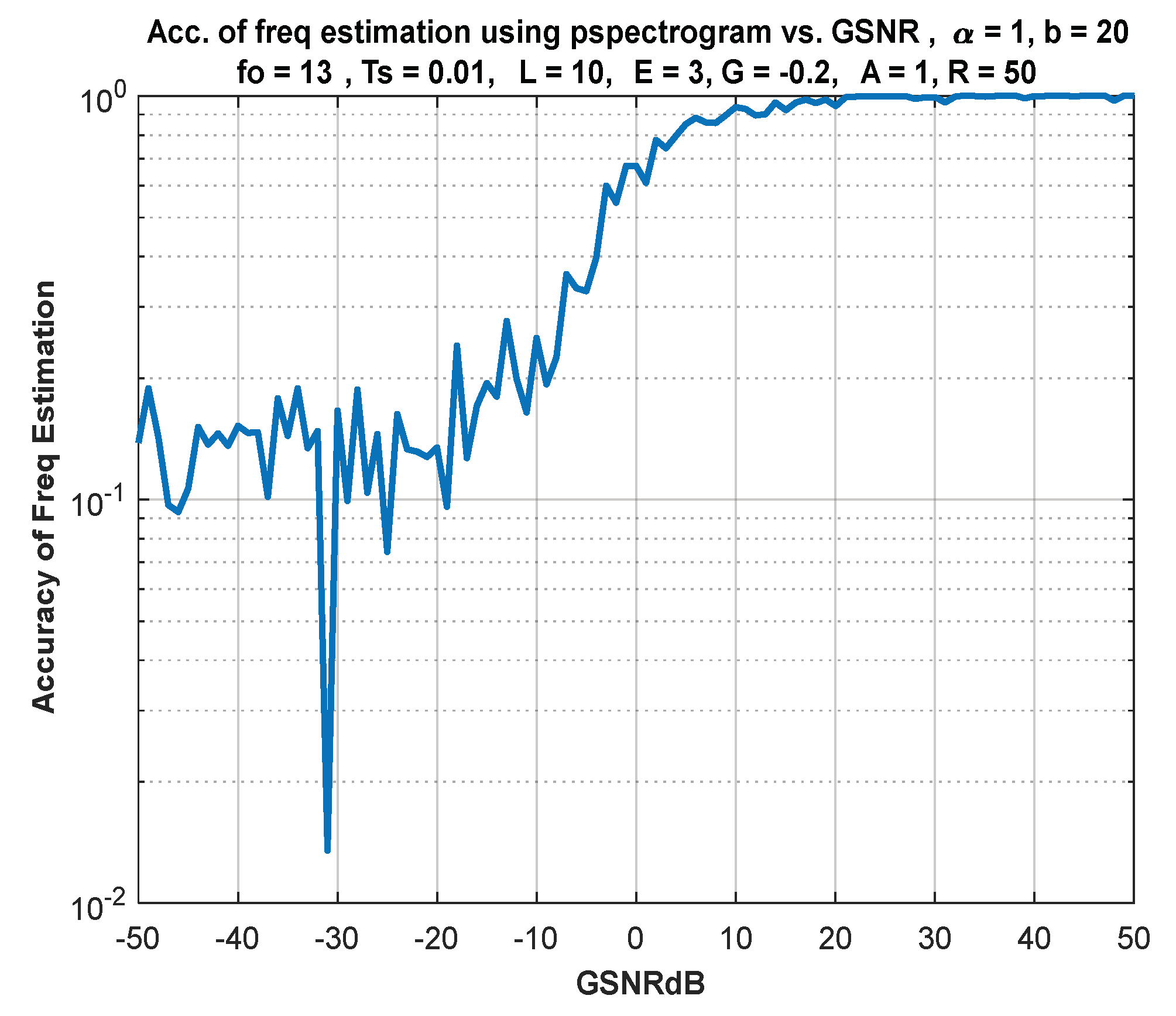
6. IF Estimation Based on TFD
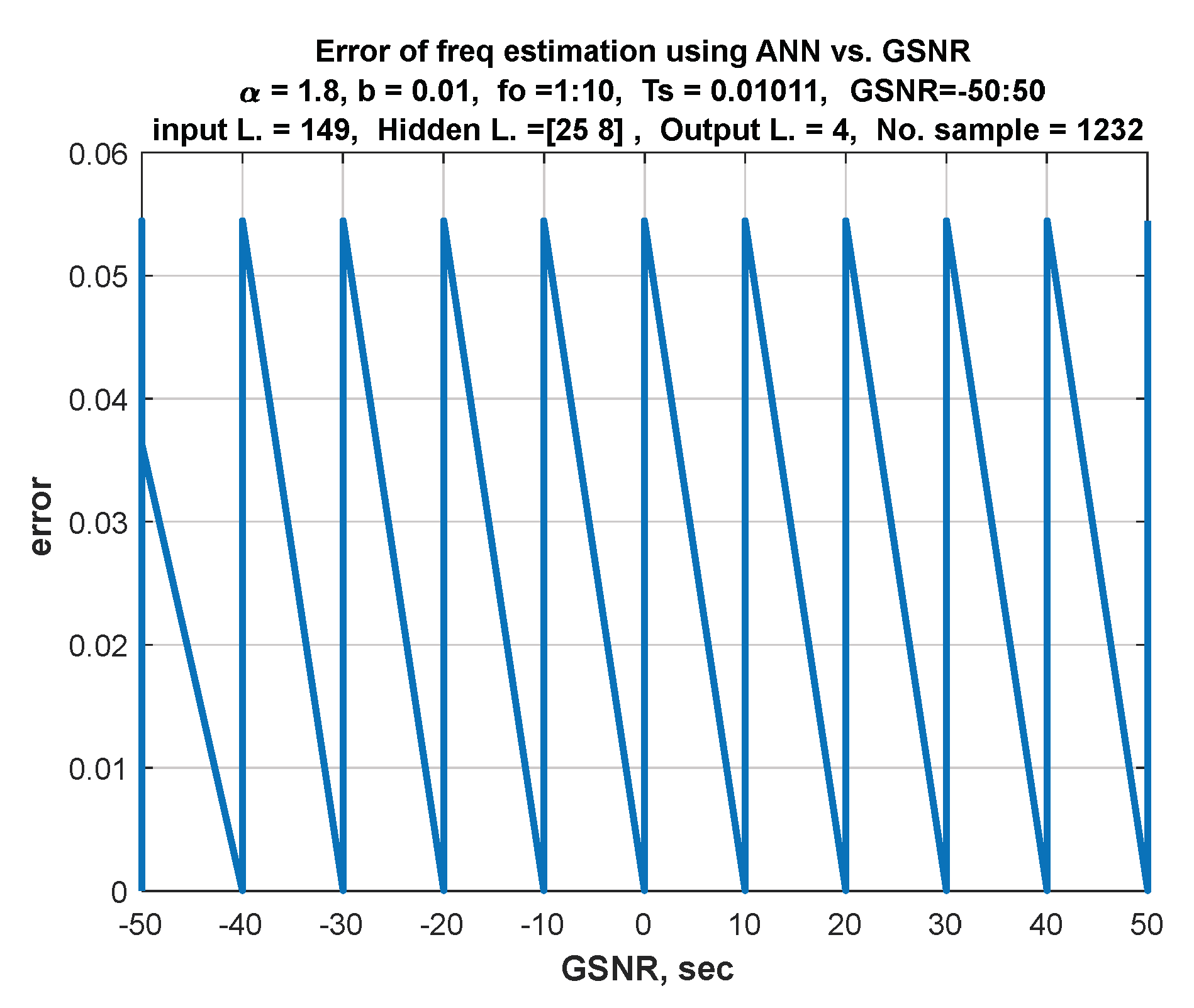
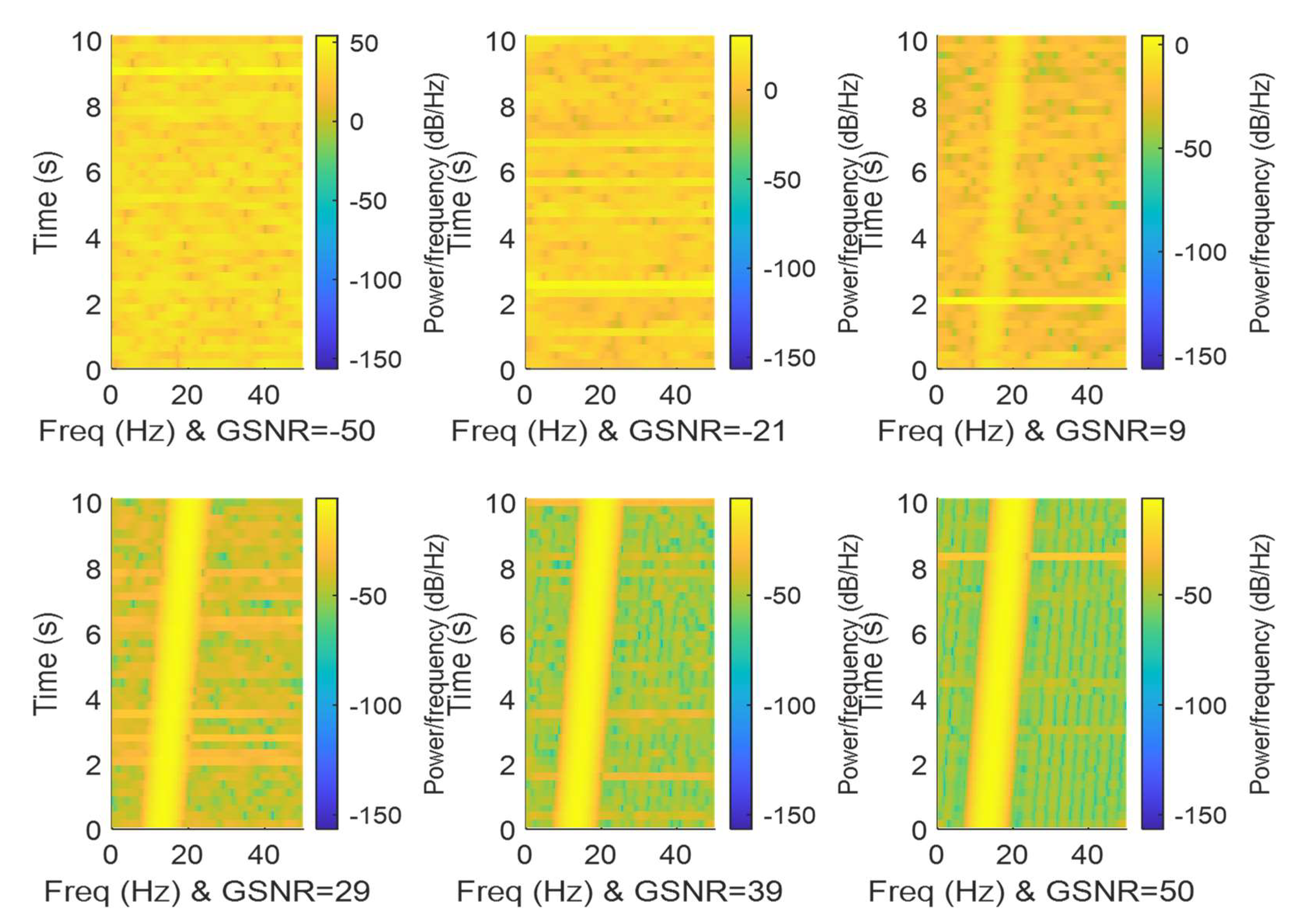
7. Discussion of Results
8. Further Remarks
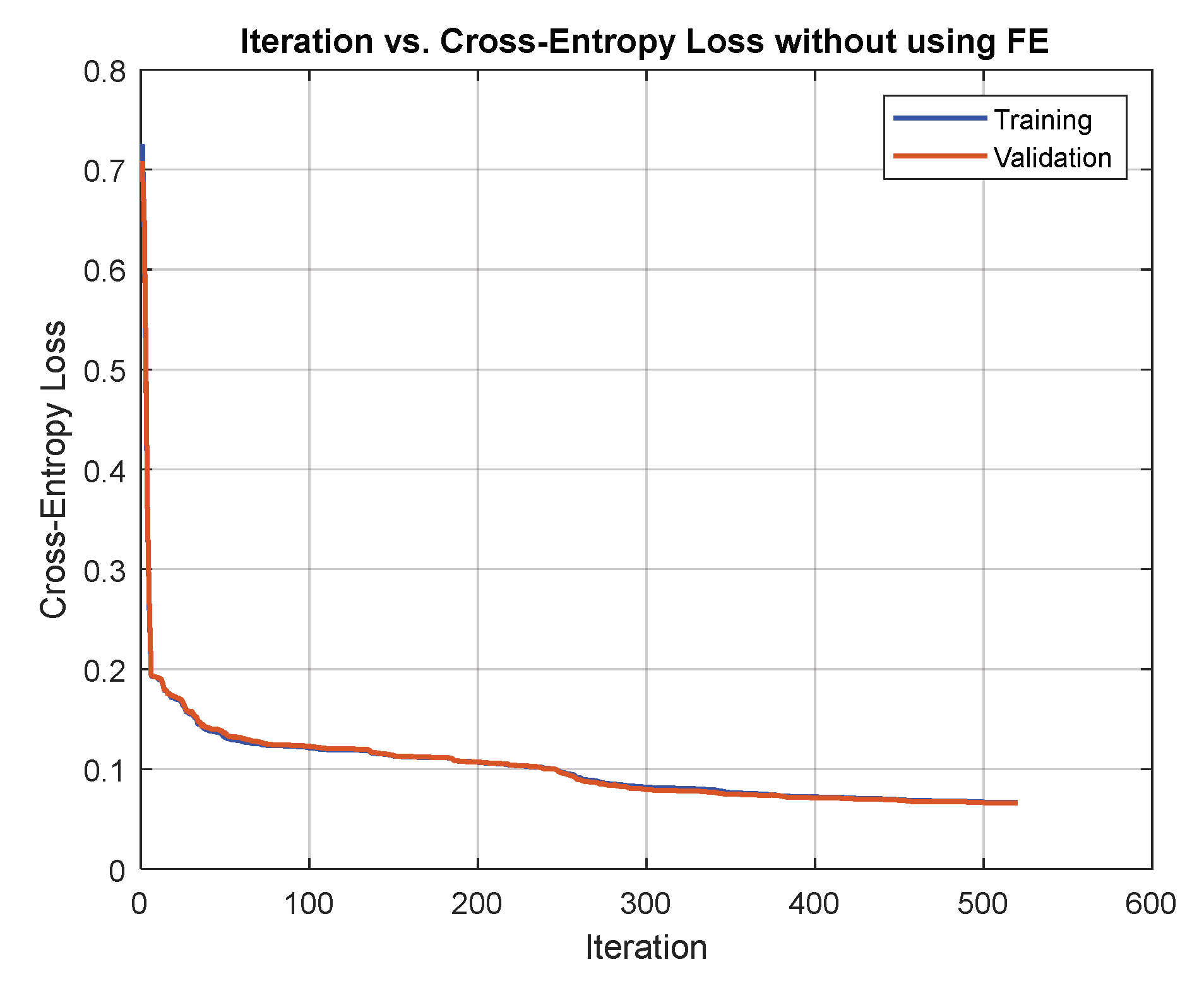
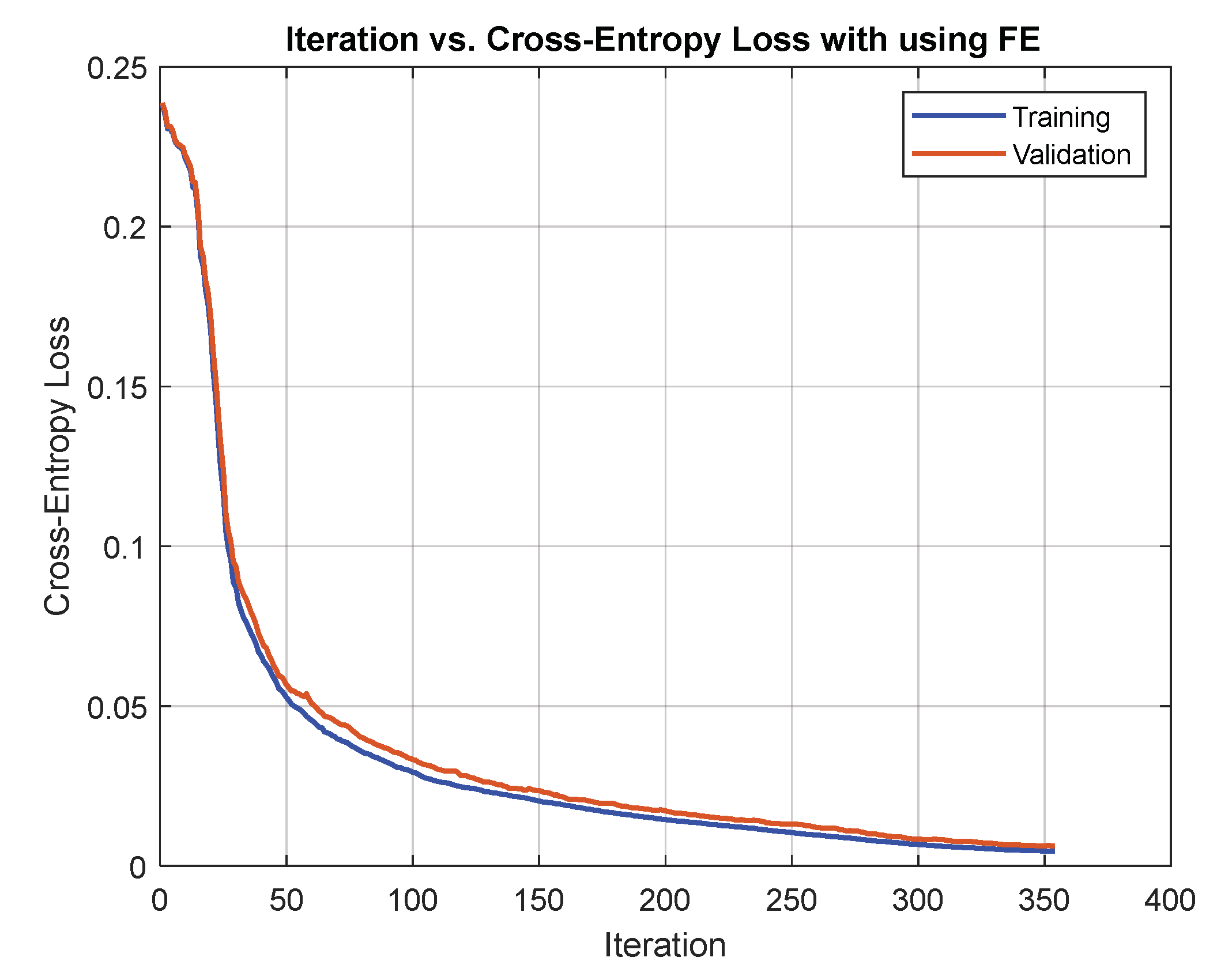
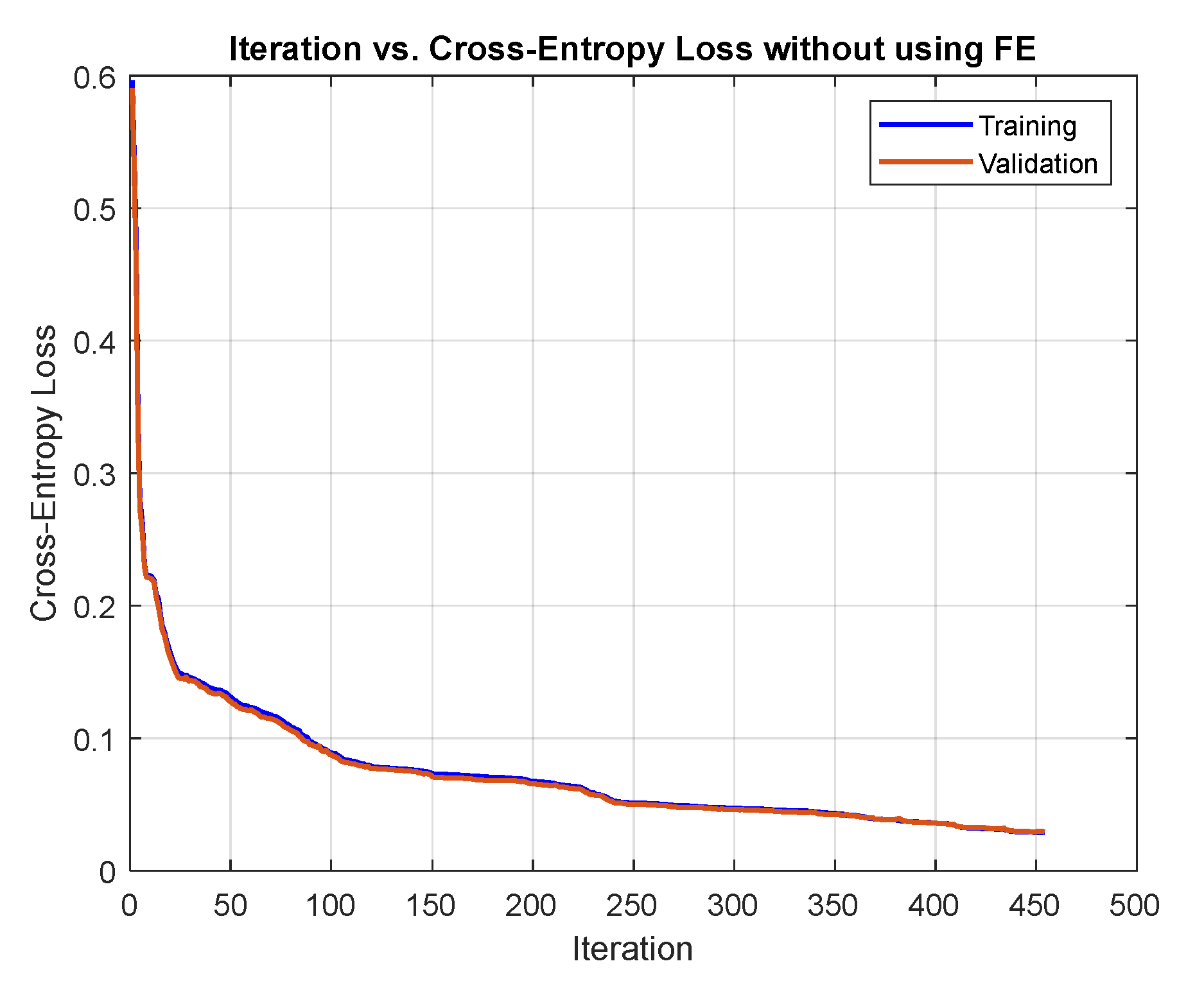
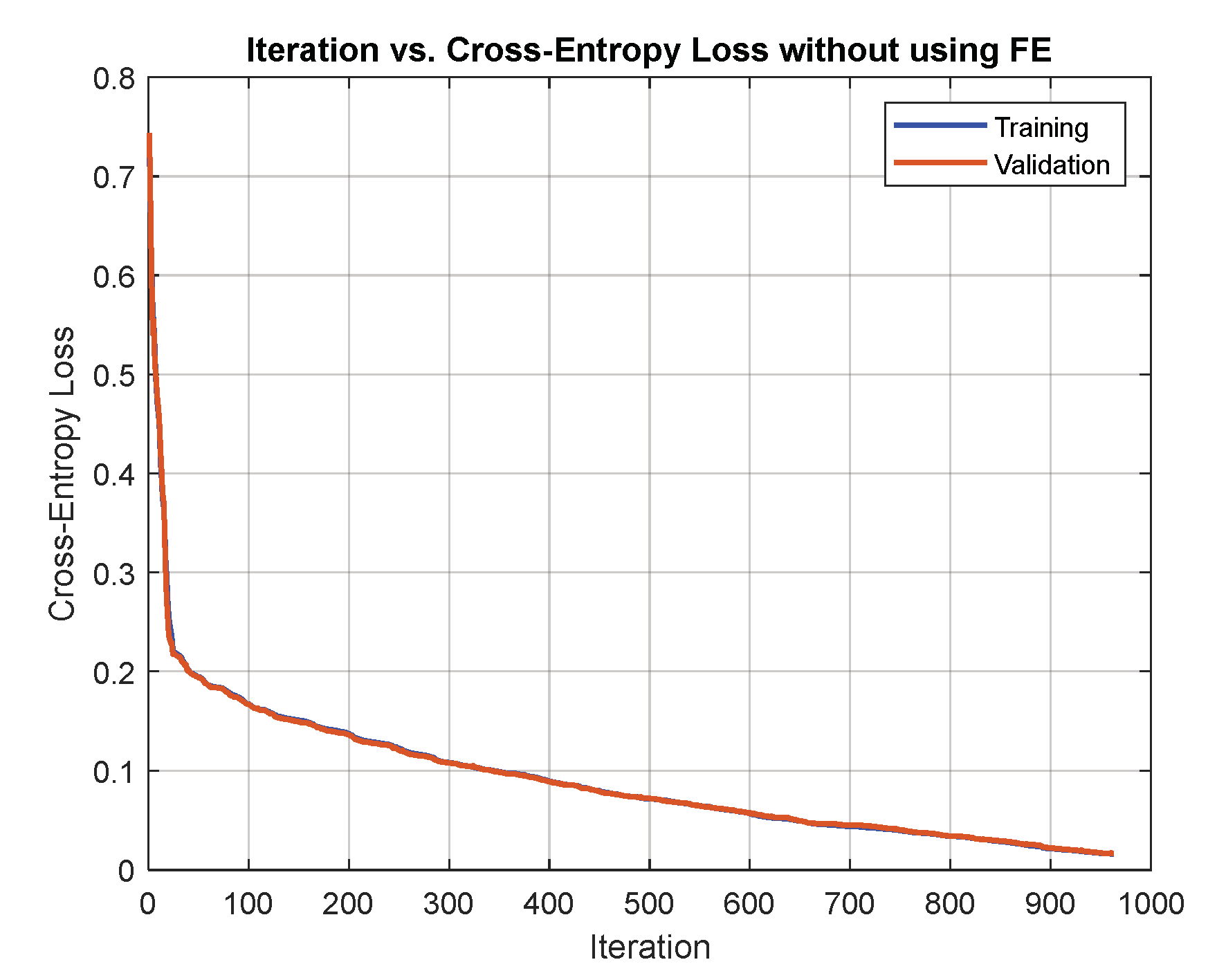
8.1. Comparing Network Training with and without Extracted Features
8.2. Different Lengths for the Input Signal and Feature Vector
8.3. Effect of Network Training by the Number of Layers and Number of Nodes
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- For β = 0: symmetric α-stable noise can be generated as follows. A uniformly distributed random variable V and an independent exponential random variable W are generated as follows:
- 2.
- For , a uniformly distributed random variable and an independent exponential random variable are generated as follows to get :When scale and shift are applied, we have:
- 3.
- For , random variables and are generated as above, then:When scale and shift are applied as an equation, we have:
Appendix B
| Indexes | Layers Name | Input Size | OutputSize | Hyperparameters | Total of Parameters |
|---|---|---|---|---|---|
| 1. | Image Input | 80 × 80 × 1 | 80 × 80 × 1 | Normalization zero-center | 0 |
| 2. | Convolution | 80 × 80 × 1 | 80 × 80 × 30 | 300 | |
| 3. | Batch Normalization | 80 × 80 × 30 | 80 × 80 × 30 | =0, =0, =1 | 0 |
| 4. | ReLU | 80 × 80 × 30 | 80 × 80 × 30 | - | 0 |
| 5. | Max Pooling | 80 × 80 × 30 | 40 × 40 × 30 | 0 | |
| 6. | Convolution | 40 × 40 × 30 | 40 × 40 × 60 | , C=30 | 16,260 |
| 7. | ReLU | 40 × 40 × 60 | 40 × 40 × 60 | - | 0 |
| 8. | Max Pooling | 40 × 40 × 60 | 20 × 20 × 60 | 0 | |
| 9. | Convolution | 20 × 20 × 60 | 20 × 20 × 90 | 48,690 | |
| 10. | ReLU | 20 × 20 × 90 | 20 × 20 × 90 | - | 0 |
| 11. | Max Pooling | 20 × 20 × 90 | 10 × 10 × 90 | 0 | |
| 12. | Convolution | 10 × 10 × 90 | 10 × 10 × 128 | 103,808 | |
| 13. | ReLU | 10 × 10 × 128 | 10 × 10 × 128 | - | 0 |
| 14. | Max Pooling | 10 × 10 × 128 | 5 × 5 × 128 | 0 | |
| 15. | Fully Connected | 5 × 5 × 128 = 3200 | 100 | Nodes = 100 | 320,100 |
| 16. | Dropout | - | - | Probability = 0.5 | 0 |
| 17. | Fully Connected | 100 | 10 | No. class = 10 | 1010 |
| 18. | Softmax | 10 | 10 | - | 0 |
| 19. | Classification | 10 | 1 | Loss Function = cross-entropy | 0 |
| Number of weights for convolution layers = (270 + 16200 + 48600 + 103680) = 168750 Number of biases for convolution layers = (30 + 60 + 90 + 128) = 308 Total parameters for convolution layers = 169058 | |||||
| Total parameters for all network = 169058 + 320100+1010 = 490168 | |||||
Appendix C
| Algorithm A1: Frequency Estimation by TFD |
| Input:. Output: Instantaneous frequency estimate . Begin: Step 1: , . Step 2: , the duplicate input signal in R rows, may repeat run R times to get a good result. Step 3: ● The SS noise ( and Gaussian noise ( are generated as above explained. ● The input signals are corrupted by hybrid noise, where total noise ( is a mixture of both Gaussian noise and SS noise: ● IF error temporary matrix, where (initially). Step 4: ■ Take hth realization, where . ■ Eliminate the negative portion of the signal spectrum by called Alg. (5) with an input parameter () and an output parameter . ■ IF estimate with spectrogram and pspectrum by called Alg. (6) with input parameter and output parameter ■ Estimate the IF from the peak (max) of the as follows: ■ Calculate the relative squared error for each GSNR: theoretical instantaneous frequency. ■ End of loop End of loop End of algorithm |
| Algorithm A2: Hilbert Transform |
| . Begin: have three values as follows: . ) where End of algorithm |
| Algorithm A3: Spectrogram of Short-Time Fourier Transform |
| Input: Analytic signal and . Output: Spectrogram time and frequency vectors Begin: Step 1: Define the parameters of STFT are window length hop size window overlap , sampling frequency (), and the number of FFT points Step 2: Create Hamming window of length and . Step 3: STFT matrix with size where is the number of signal frames. Step 4: Divides the input signal into overlapping segments and multiply each segment by the window (. Then fast Fourier transform is applied to each segment ( For End of loop Step 5: Find the spectrogram , were Step 6: Calculation of the time vector in second and frequency vector in , were End of algorithm |
References
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal—I: Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal—II: Algorithms and applications. Proc. IEEE 1992, 80, 540–568. [Google Scholar] [CrossRef]
- Liu, J.; Fan, L.; Jin, J.; Wang, X.; Xing, J.; He, W. An Accurate and Efficient Frequency Estimation Algorithm by Using FFT and DTFT. In Proceedings of the 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020. [Google Scholar]
- Akram, J.; Khan, N.A.; Ali, S.; Akram, A. Multi-component instantaneous frequency estimation using signal decomposition and time-frequency filtering. Signal Image Video Process. 2020, 14, 1663–1670. [Google Scholar] [CrossRef]
- Xu, S.; Shimodaira, H. Direct F0 Estimation with Neural-Network-Based Regression. In Proceedings of the INTER-SPEECH, Graz, Austria, 15–19 September 2019; pp. 1995–1999. [Google Scholar]
- Silva, B.; Habermann, D.; Medella, A.; Fraidenraich, G. Artificial Neural Networks to Solve Doppler Ambiguities in Pulsed Radars. In Proceedings of the International Conference on Radar (RADAR), Brisbane, Australia, 27–31 August 2018; pp. 1–5. [Google Scholar]
- Chen, X.; Jiang, Q.; Su, N.; Chen, B.; Guan, J. LFM Signal Detection and Estimation Based on Deep Convolutional Neural Network. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, 18–21 November 2019; pp. 753–758. [Google Scholar]
- Xuelian, L.; Wang, C. A novel parameter estimation of chirp signal in α-stable noise. IEICE Electronics Express 2017, 14, 20161053. [Google Scholar]
- Aboutanios, E.; Mulgrew, B. Iterative frequency estimation by interpolation on Fourier coefficients. IEEE Trans. Signal Process. 2005, 53, 1237–1241. [Google Scholar] [CrossRef]
- Ahmet, S. Fast and efficient sinusoidal frequency estimation by using the DFT coefficients. IEEE Trans. Commun. 2018, 67, 2333–2342. [Google Scholar]
- Li, L.; Qiu, T. A Robust Parameter Estimation of LFM Signal Based on Sigmoid Transform Under the Alpha Stable Distribution Noise. Circuits Syst. Signal Process. 2019, 38, 3170–3186. [Google Scholar] [CrossRef]
- Almayyali, H.; Hussain, Z. Deep Learning versus Spectral Techniques for Frequency Estimation of Single Tones: Reduced Complexity for Software-Defined Radio and IoT Sensor Communications. Sensors 2021, 21, 2729. [Google Scholar] [CrossRef]
- Boashash, B. (Ed.) Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, 2nd ed.; Elsevier: Oxford, UK, 2016. [Google Scholar]
- Milczarek, H.; Leśnik, C.; Djurović, I.; Kawalec, A. Estimating the Instantaneous Frequency of Linear and Nonlinear Frequency Modulated Radar Signals—A Comparative Study. Sensors 2021, 21, 2840. [Google Scholar] [CrossRef]
- Boashash, B.; O’Shea, P.; Arnold, M.J. Algorithms for Instantaneous Frequency Estimation: A Comparative Study; SPIE: Bellingham, WA, USA, 1990. [Google Scholar]
- Zhang, J.; Li, Y.; Yin, J. Modulation classification method for frequency modulation signals based on the time–frequency distribution and CNN. IET Radar Sonar Navig. 2018, 12, 244–249. [Google Scholar] [CrossRef]
- Liu, M.; Han, Y.; Chen, Y.; Song, H.; Yang, Z.; Gong, F. Modulation Parameter Estimation of LFM Interference for Direct Sequence Spread Spectrum Communication System in Alpha-Stable Noise. IEEE Syst. J. 2020, 15, 881–892. [Google Scholar] [CrossRef]
- Kristoffer, H. Symmetric Alpha-Stable Adapted Demodulation and Parameter Estimation. Master’s Dissertation, Lulea University of Technology, Lulea, Sweden, 2018. [Google Scholar]
- Braspenning, P.J.; Thuijsman, F.; Weijters, A.J.M.M. Artificial neural networks: An introduction to ANN theory and practice. In Lecture Notes in Computer Science; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995; Volume 931. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Møller, M.F. A scaled conjugate gradient algorithm for fast supervised learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef] [PubMed]
- Moons, B.; Bankman, D.; Verhelst, M. Embedded Deep Learning: Algorithms, Architectures and Circuits for Always-on Neural Network Processing; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Phil, K. Matlab Deep Learning with Machine Learning, Neural Networks and Artificial Intelligence; Apress: New York, NY, USA, 2017. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. arXiv 2011, arXiv:2010.16061. [Google Scholar]
- Hussain, Z.M.; Sadik, A.Z.; O’Shea, P. Digital Signal Processing: An Introduction with MATLAB and Applications; Springer: Berlin, Germany, 2011. [Google Scholar]
- Razzaq, H.S.; Hussain, Z.M. Instantaneous Frequency Estimation for Frequency-Modulated Signals under Gaussian and Symmetric α-Stable Noise. In Proceedings of the 31st International Telecommunication Networks and Applications Conference (ITNAC), Sydney, Australia, 24–26 November 2021. [Google Scholar]
- Gao, J.; Deng, B.; Qin, Y.; Wang, H.; Li, X. Enhanced radar imaging using a complex-valued convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2018, 16, 35–39. [Google Scholar] [CrossRef]
- Djurović, I. Viterbi algorithm for chirp-rate and instantaneous frequency estimation. Signal Process. 2011, 91, 1308–1314. [Google Scholar] [CrossRef]
- Yin, Z.; Chen, W. A New LFM-Signal Detector Based on Fractional Fourier Transform. EURASIP J. Adv. Signal Process. 2010, 2010, 1–7. [Google Scholar] [CrossRef]
- Hussain, Z.M.; Boashash, B. Design of time-frequency distributions for amplitude and IF estimation of multicomponent signals. In Proceedings of the Sixth International Symposium on Signal Processing and its Applications (ISSPA2001), Kuala Lumpur, Malaysia, 13–16 August 2001. [Google Scholar]
- Nelson, D.J. Instantaneous Higher Order Phase Derivatives. Digit. Signal Process. 2002, 12, 416–428. [Google Scholar] [CrossRef]
- Yin, Q.; Shen, L.; Lu, M.; Wang, X.; Liu, Z. Selection of optimal window length using STFT for quantitative SNR analysis of LFM signal. J. Syst. Eng. Electron. 2013, 24, 26–35. [Google Scholar] [CrossRef]
- Hussain, Z.M. Energy-Efficient Systems for Smart Sensor Communications. In Proceedings of the IEEE 30th International Telecommunication Networks and Applications Conference (ITNAC), Melbourne, Australia, 25–27 November 2020. [Google Scholar]
- Alwan, N.; Hussain, Z. Frequency Estimation from Compressed Measurements of a Sinusoid in Moving-Average Colored Noise. Electronics 2021, 10, 1852. [Google Scholar] [CrossRef]



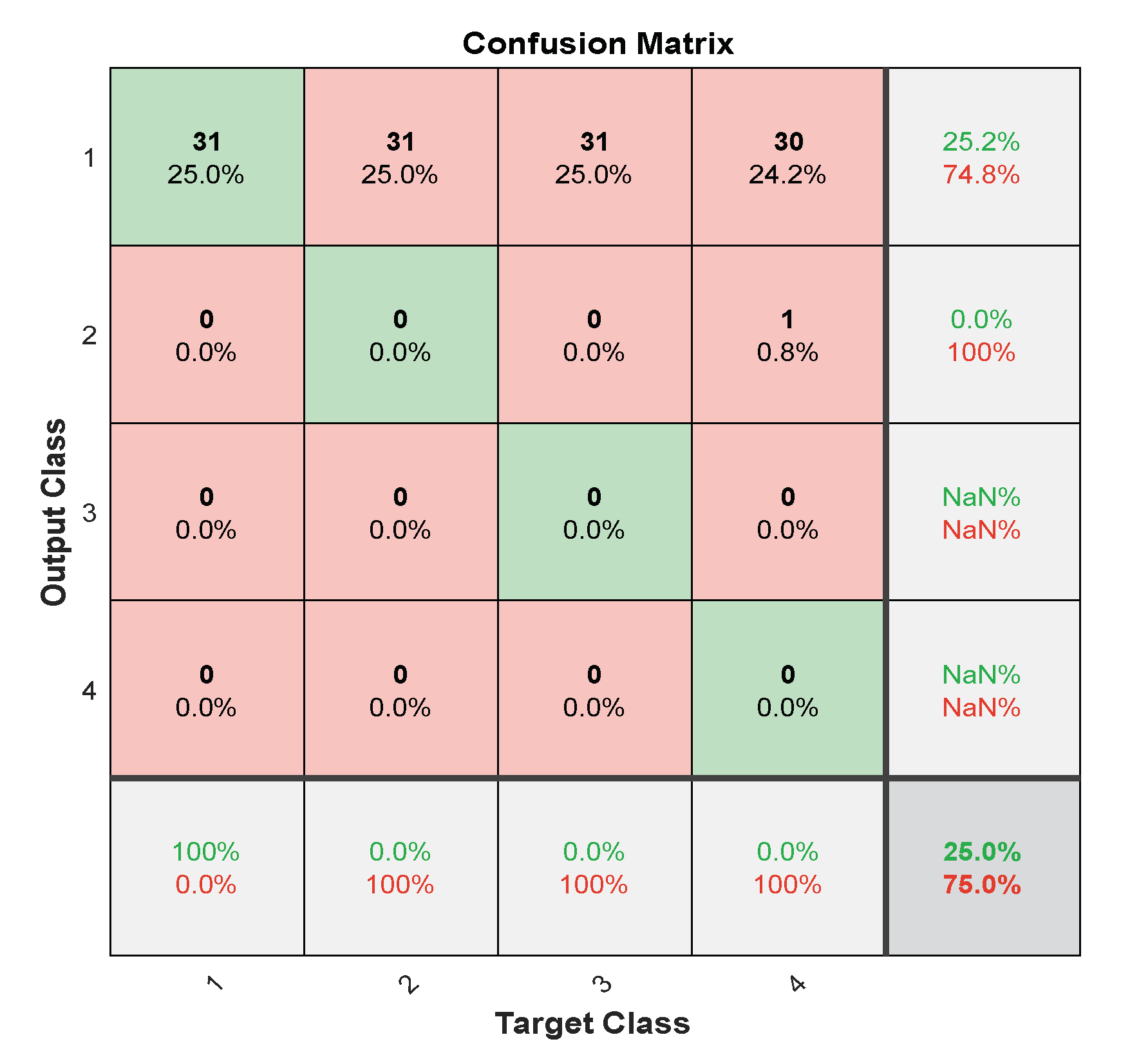


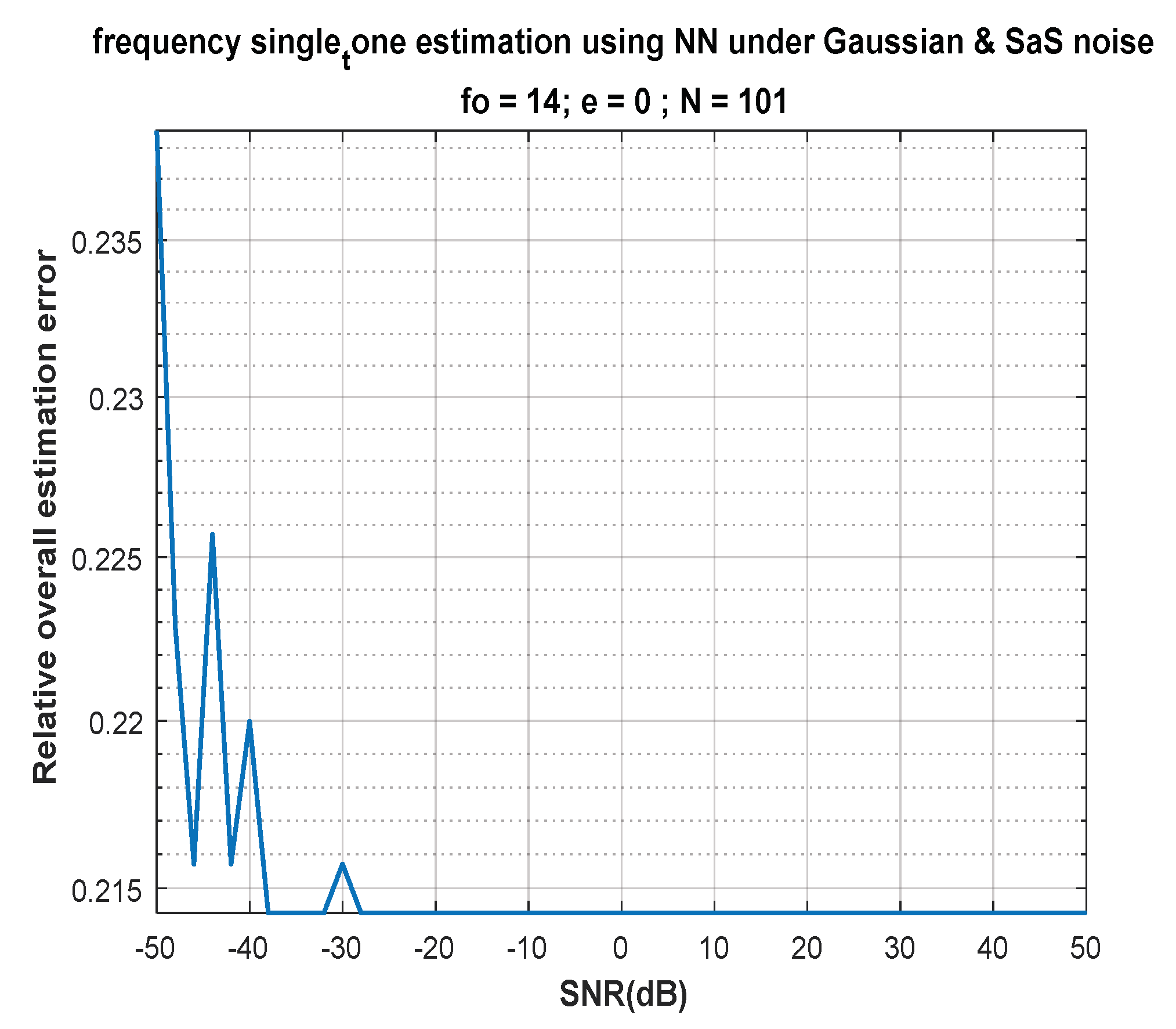

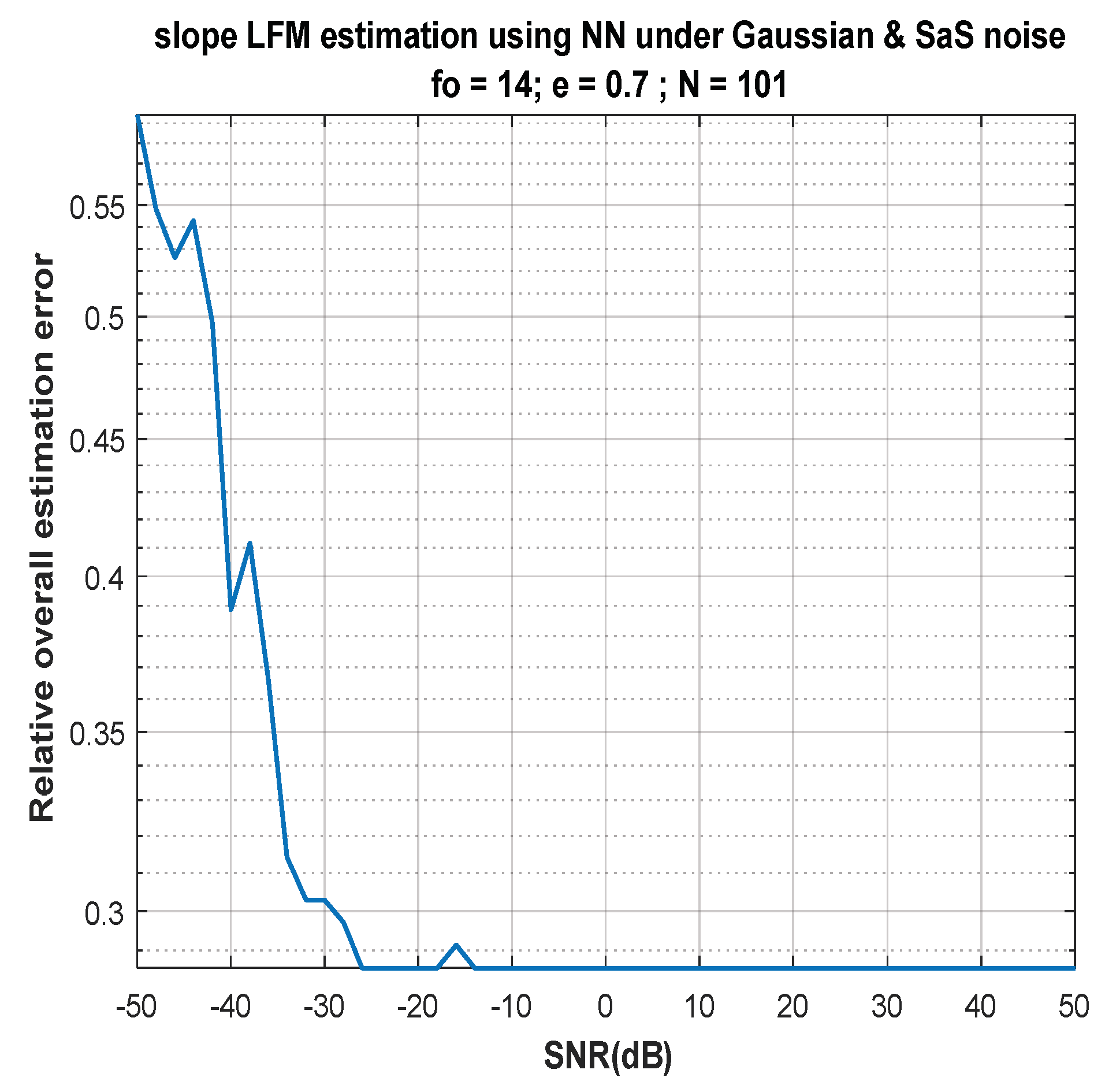

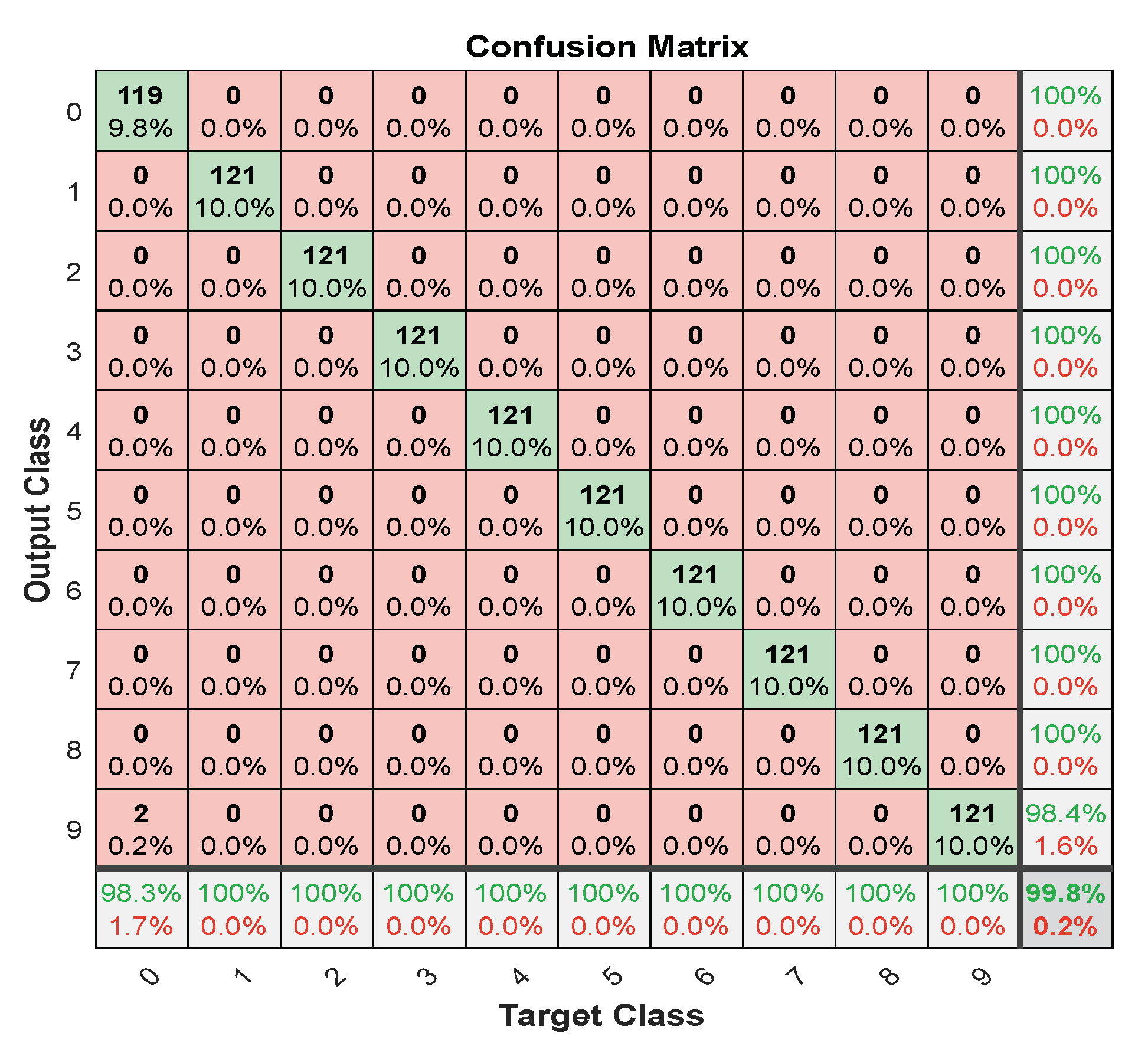
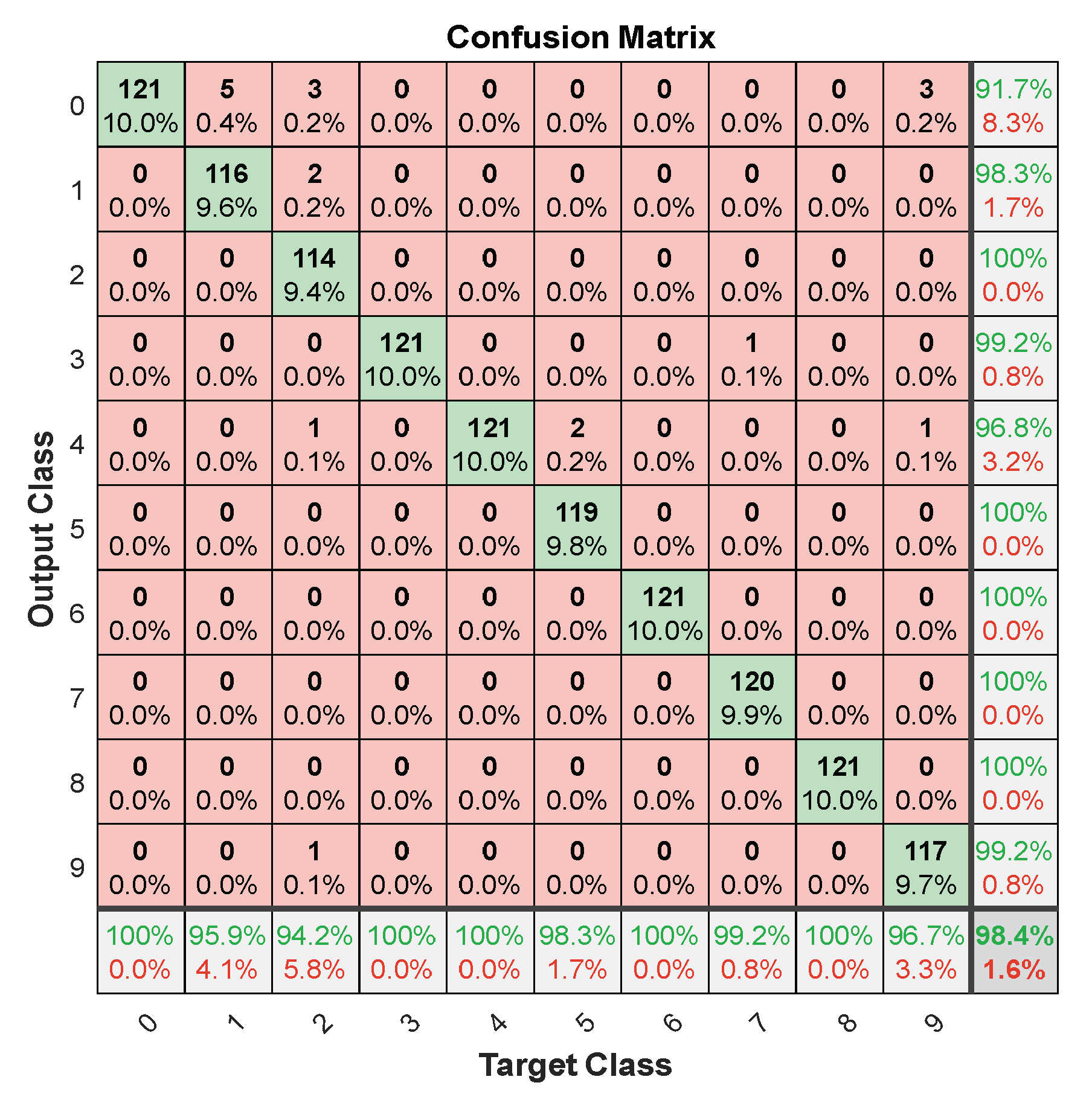


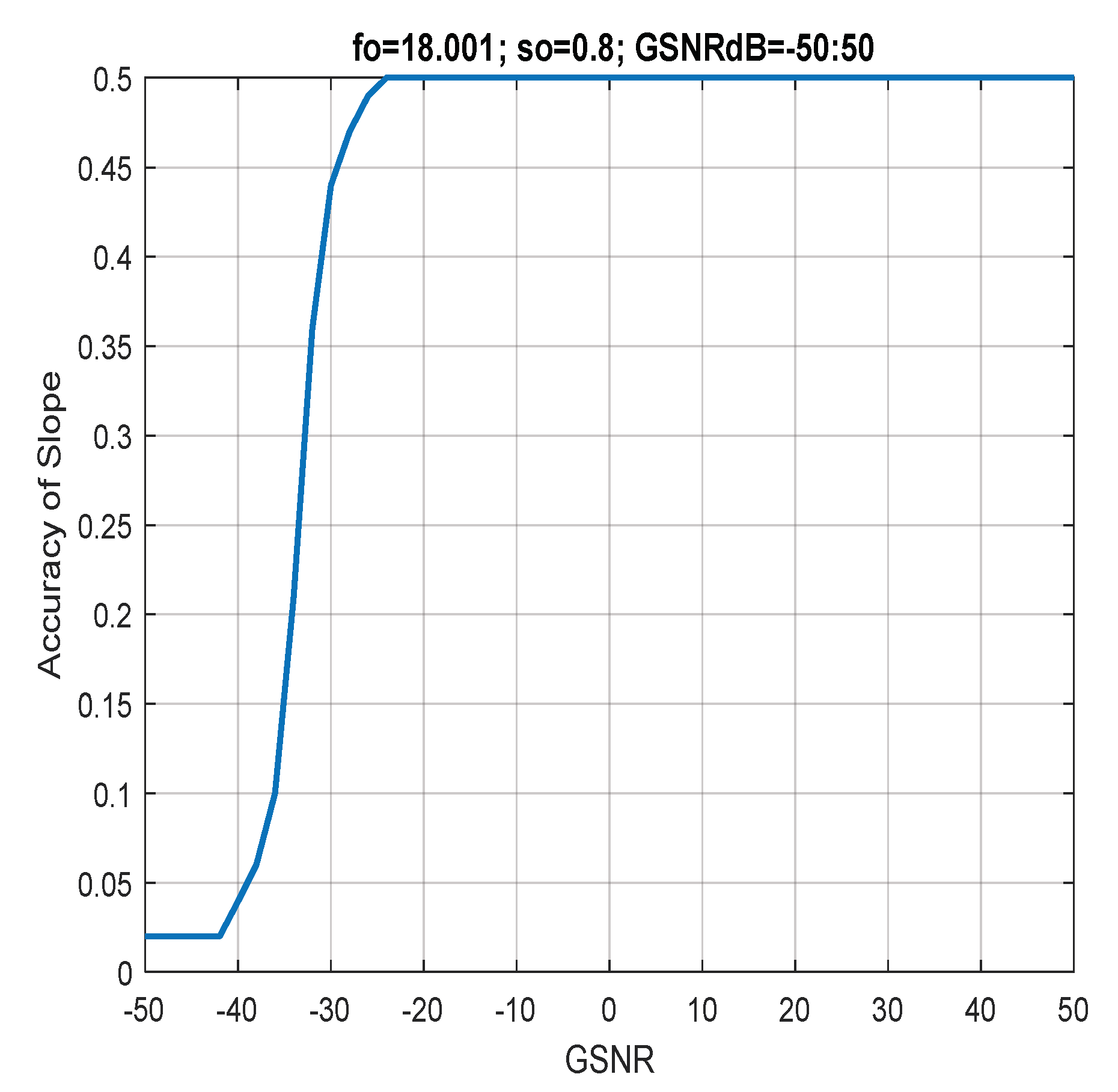
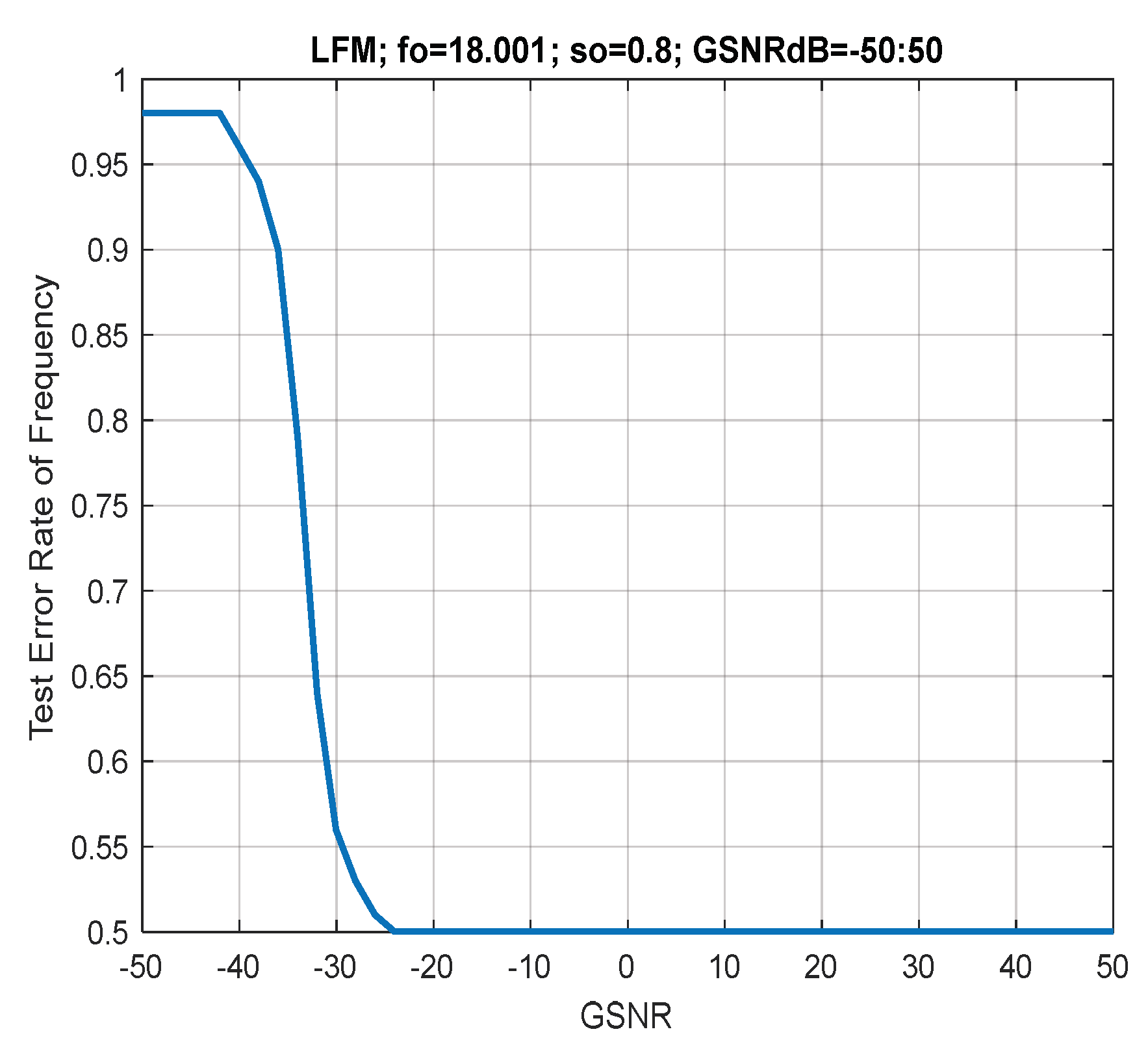



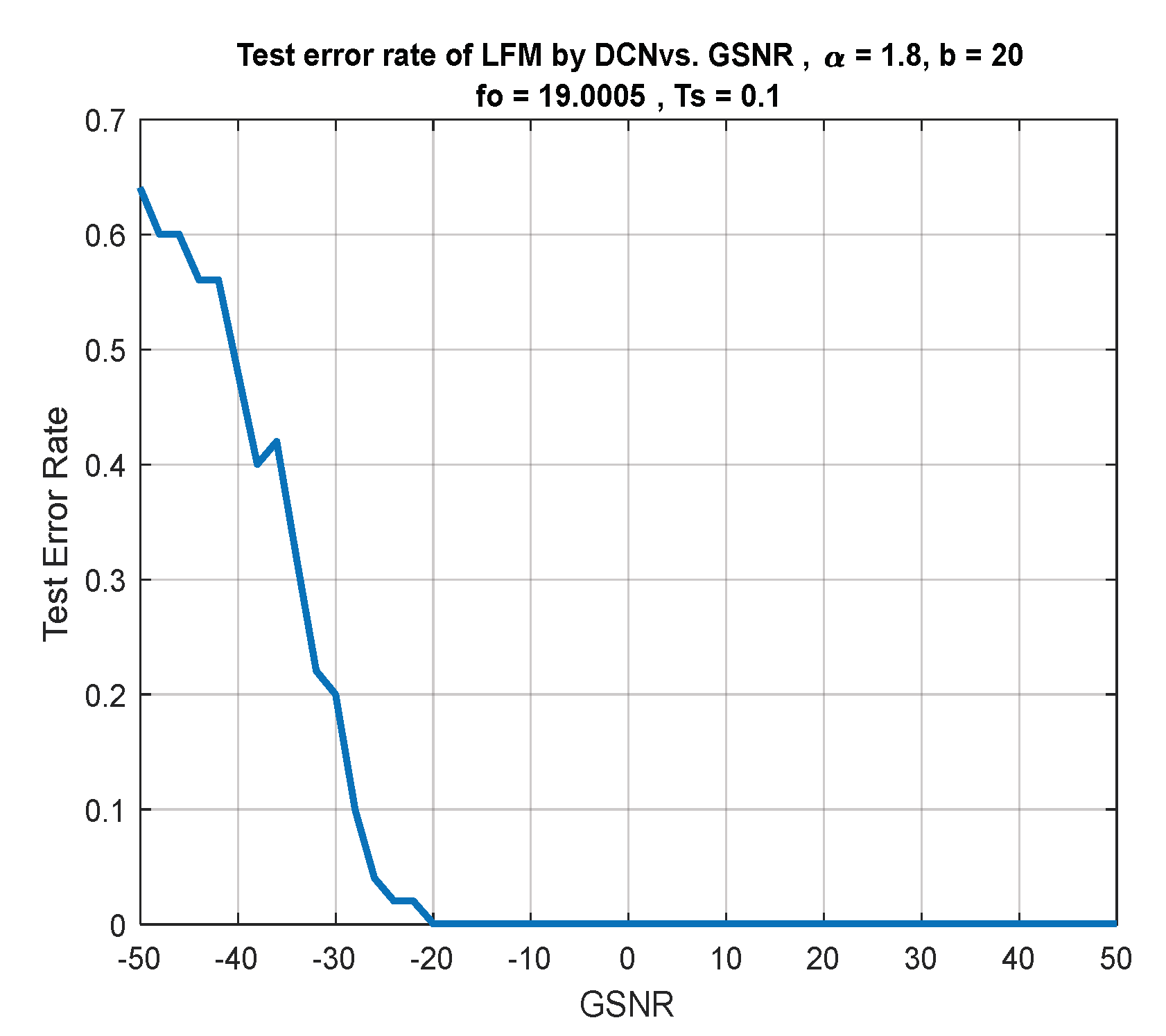
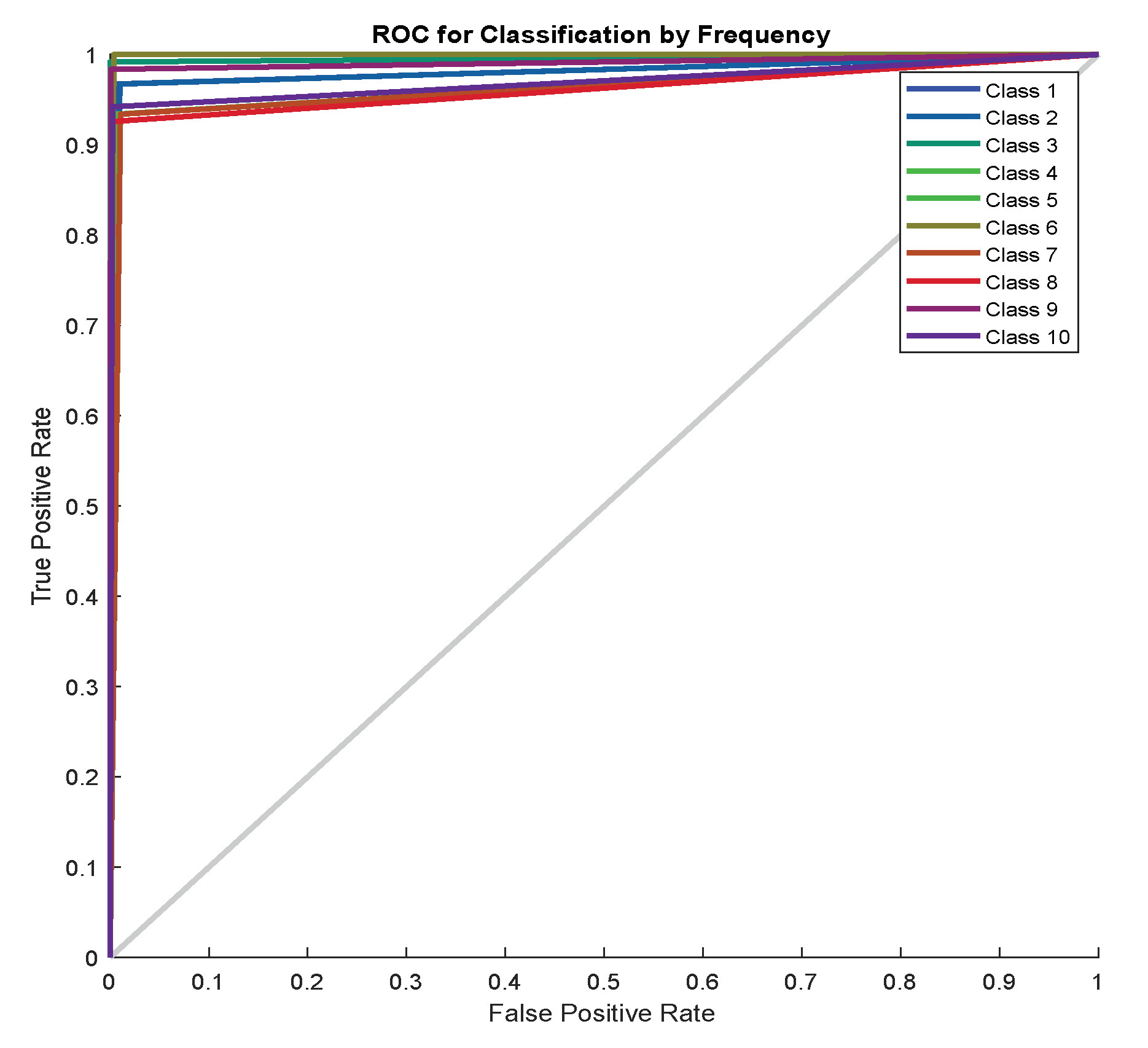

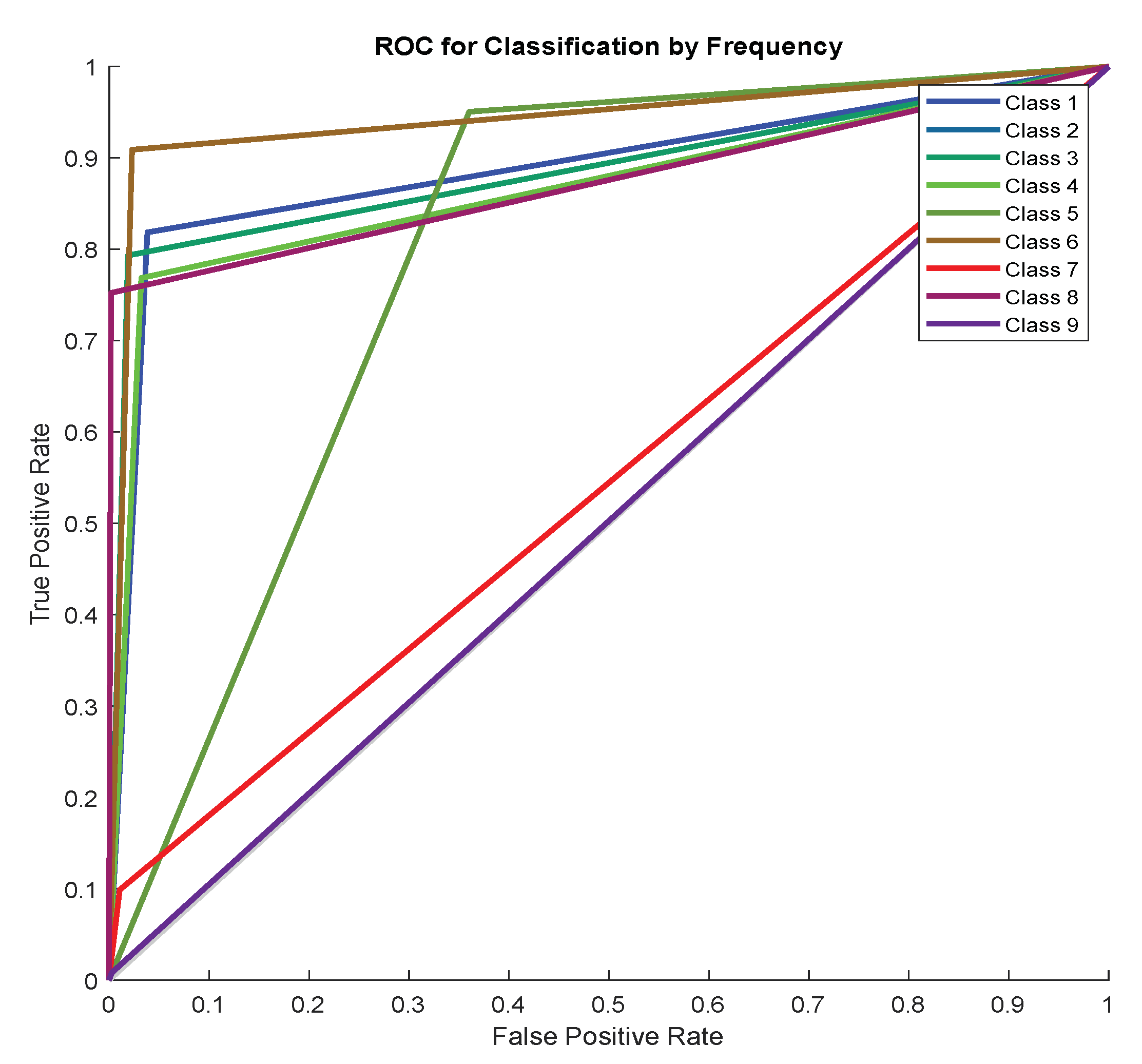
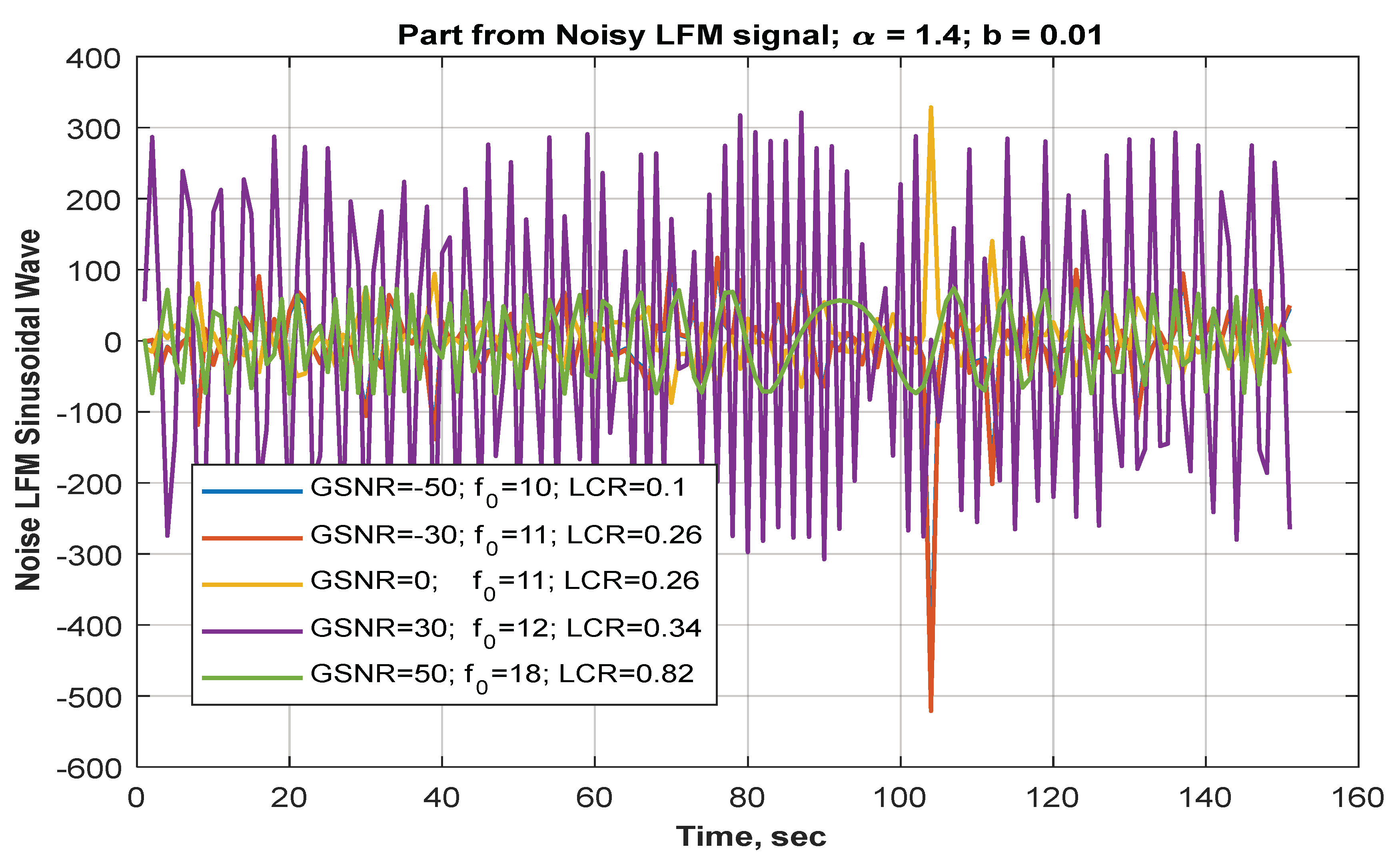

| Measures | LFM | |
|---|---|---|
| Frequency | Slope | |
| Accuracy | 99.8118 | 98.4431 |
| Precision | 99.8303 | 99.0445 |
| Recall | 99.8118 | 98.4432 |
| F1_Score | 99.8210 | 98.5477 |
| FNR | 0.0039 | 0.0216 |
| FPR | 0.0037 | 0.0195 |
| Measures | Values |
|---|---|
| Accuracy | 56.6575 |
| Precision | 57.5019 |
| Recall | 56.6575 |
| F1_Score | 57.0766 |
| Epoch | 10 |
| Parameters | Accuracy | Recall | Precision | F1-Score | |
|---|---|---|---|---|---|
| Learning rate | 10−3 | 90.4959 | 90.4959 | 91.5224 | 91.0062 |
| 10−4 | 96.2810 | 96.2810 | 96.3523 | 96.3166 | |
| 10−5 | 70.4959 | 70.4959 | 77.6223 | 73.8876 | |
| Epoch | 5 | 96.2810 | 96.2810 | 96.3523 | 96.3166 |
| 10 | 97.6033 | 97.6033 | 97.7144 | 97.6588 | |
| 30 | 99.8347 | 99.8347 | 99.8374 | 99.8361 | |
| Min-patch | 8 | 96.2810 | 96.2810 | 96.3523 | 96.3166 |
| 32 | 97.6033 | 97.6033 | 97.7144 | 97.6588 | |
| 64 | 99.8347 | 99.8347 | 99.8374 | 99.8361 | |
| Training Method | SGDA | 74.2149 | 74.2149 | 82.8702 | 78.3041 |
| RMSPROP | 93.7190 | 93.7190 | 94.2774 | 93.9974 | |
| Adam | 96.2810 | 96.2810 | 96.3523 | 96.3166 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razzaq, H.S.; Hussain, Z.M. Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis. Information 2023, 14, 18. https://doi.org/10.3390/info14010018
Razzaq HS, Hussain ZM. Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis. Information. 2023; 14(1):18. https://doi.org/10.3390/info14010018
Chicago/Turabian StyleRazzaq, Huda Saleem, and Zahir M. Hussain. 2023. "Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis" Information 14, no. 1: 18. https://doi.org/10.3390/info14010018
APA StyleRazzaq, H. S., & Hussain, Z. M. (2023). Instantaneous Frequency Estimation of FM Signals under Gaussian and Symmetric α-Stable Noise: Deep Learning versus Time–Frequency Analysis. Information, 14(1), 18. https://doi.org/10.3390/info14010018







