Abstract
The distributor management system has long been a challenge for many organizations and companies. Overall, successful distribution involves several moving entities and methods, requiring a resilient distribution management strategy powered by data analysis. For nonprofit organizations, the distribution system requires efficient distribution and management. This includes minimizing time, distance, and cost. As a consequence, service quality and financial efficiency can be achieved. This paper proposes a methodology to tackle the vehicle routing problems (VRP) faced by nonprofit organizations. The methodology consists of four subsequent approaches—greedy, intraroute, interroute, and tabu search—to improve the functionality and performance of nonprofit organizations. The methodology was validated by applying it to a real nonprofit organization. Furthermore, the proposed system was compared to another state-of-the-art system; the achieved results were satisfactory and suggest that this methodology is capable of handling the VRP accordingly, improving the functionality and performance of nonprofit organizations.
1. Introduction
The issue of global food waste is a major part of the impact of agriculture on climate change. Reducing food waste is essential due to the number of people affected by hunger, which has been on the rise since 2014 according to the United Nations. In addition, the wastage of food is considered one of the most important contributors to landfills. The whole food chain is engaged in the wastage of food, starting from the fields of farmers, then food industries, then retailers and caterers, and at the end, reaching the consumers. Major factors leading to food waste include consumable leftovers, lack of awareness, and unplanned shopping for groceries [1]. Gulf countries are considered at the top of the list for food waste due to many social and traditional gatherings. Further, Saudi Arabia ranks first in food waste; it has been observed that around 427 kg of food is wasted per capita per annum. Moreover, there are limited agriculture and water resources in Saudi Arabia to support agricultural crops to feed the continually growing population. To meet the needs of the population, Saudi Arabia relies heavily on importing food. Although there are numerous restaurants and caterers, the largest amounts of food waste are produced by households [2]. In order to reduce food waste, a number of nonprofit organizations have intervened. Currently, a number of charity organizations have offered their services to distribute surplus food to people in need. These organizations voluntarily take action to address food waste [3]. One of these organizations is Ekram.
Ekram is an organization that collects surplus food and distributes it to people who need food. It plays a crucial role in reducing people’s hunger through redistribution. It also offers a complete process from collection to delivery. A primary objective of Ekram is to create awareness of the impact of food waste. This process includes provisioning of food and delivering it to people, promoting a healthy diet and hygienic practices.
Although Ekram is working to achieve its inspiring mission, it faces issues of optimizing its process. One major issue is the distribution management system, which includes the routes of delivery vehicles and confirmation of requests by clients. A common issue that regularly faces such organizations is that clients are unavailable at delivery times or that they may cancel the request after a vehicle is headed toward their location. This significantly impacts the process and causes time and economic waste of resources. The process needs to be managed in an efficient manner that avoids resource waste. Another problem that such organizations face relates to the amount of donated food, where the number of people who need food and the amount of surplus food do not match. Accordingly, many people who need food will not be able to obtain it; in addition, on some occasions, there can be surplus food that cannot be collected and distributed. This leads to operational issues that require optimization techniques to enhance the process of such organizations. Systems that are able to efficiently handle the vehicle routing problem (VRP) are necessary to avoid such issues and enhance the operation of the organization. This paper proposes a system that potentially addresses the major concerns of surplus food delivery at Ekram. The delivery of food is considered a complex problem. It also includes various kinds of challenging aspects, such as cost-effective routing, uncertainty in donors and clients, and limited transport resources. The main contributions of this work can be summarized as follows:
- To investigate efficient routing modules suitable for the VRP.
- To improve the system’s performance by using effective fleet management.
- To minimize the route cost and time.
The remainder of the paper is organized as follows. Section 2 highlights the vehicle routing problem (VRP) and current available systems. Section 3 presents an implementation of the proposed system. The application of the proposed system on a real-world case is presented in Section 4. Finally, the conclusions are drawn in Section 5.
2. Vehicle Routing Problem (VRP)
The VRP is also known as route optimization, which includes a fleet of vehicles with various capacities along with the depot that services different customers, considering a set of routes to obtain the minimum cost to serve the various requests. In the VRP, there are different itineraries that start and terminate with the depot, and every request is served by a single vehicle. The main objective of a VRP system is to increase the efficiency of transport for the fleet vehicle by determining the shortest routes and tracking each vehicle [4]. Furthermore, the VRP system attempts to improve the efficiency of the transportation for the distribution centers. Further, the VRP problem is considered a combinatorial optimization problem, with the optimal set of routes for a fleet of vehicles to traverse in order to deliver to a given set of customers. For that, mathematical programming formulation and optimization algorithms are required to solve the VRP in an efficient manner. In a general VRP setting, it is assumed that vehicles arrive and depart from the depot at prespecified times. Furthermore, the vehicles can serve multiple customers in one trip. As mentioned previously, the main objective of a VRP system is to find the minimum set of routes that can serve as many demands in a short time-frame achieving customer satisfaction. These requirements of VRP increase the complexity of the problem, as various other constraints may be considered. For example, in heterogeneous VRP settings, the delivery task is assigned to more than one type of vehicle with time windows (VRPTW) [5] and must serve customers in the particular time period. In many works, the VRP is considered with time-window constraints, where penalty costs reflect the violations of time windows. These works examine the optimal routes by which the total routing cost is minimized [6]. In the VRP for a surplus food system, the meals to be delivered must arrive on time, as they are highly perishable. Further, nonprofit organizations offer services for specialized gourmet meals, and they operate in high traffic cities with hundreds of customers on a daily basis. In many organizations, a fleet of refrigerated vehicles are used for the effective distribution of the food. In Ekram and similar organizations, the meals are ordered one day before, and it is expected that customers will receive perishable food within a certain time frame [6]. This requires a VRP system that finds the most efficient route to accomplish these needs.
Currently, numerous nonprofit organizations use VRP systems to reduce the time and cost of products. However, for delivering foods, time windows are essential to assure that perishable foods are delivered in good condition and on time. This can be tackled by using multiobjective frameworks, where the cost of the distribution can be minimized. Simultaneously, this results in foods being delivered in good condition. Further, other objectives are achieved as a result, including a reduction in operational costs [7]. Minimizing the operational costs requires finding the shortest route to a set of locations while considering two constraints: the prespecified time-window constraints and capacity constraints, as several vehicles may collect food from different locations. The VRP objective is to minimize the distance traveled and assist in completing the deliveries in the shortest time.
The implementation of the VRP requires different integrated optimization procedures that are used to facilitate the vehicle to manage the collection and distribution of surplus food. This procedure is used to manage all the resources that are able to operate in a complex network, and it could also manage the VRP for the sustainability of the organization. The operation of an organization depends on the coordination network and uses the proper procedures to create balance among the distribution and collection of food [8].
Other research has shown that food banks in Australia are also engaged in these services, and the basic objective of those organizations is to collect surplus food and redistribute it among needy people. The main donors of food are restaurants and large food store outlets that have extra food at the end of the day, with the utilization of the VRP for costing models [9].
Concerning the requirements of the distribution systems and logistics, many works have developed technology-based solutions for routing models. These models are based on integrating linear programming models that facilitate periodic and unpaired food distribution vehicles. This resolves the challenges associated with the vehicle routing system, including delays and system failures. It was concluded from previous works, that there is a need for efficient solutions for the VRP to bring sustainability to the food supply business without compromising the quality of operations as well as the environmental standards set out by the governmental sectors. Models for routing problems that are capable of reducing waste generated by food businesses, especially focusing on waste elimination in the food supply chain operations by ensuring food safety measures, have been an area of research interest. The linear programming models are effective for the logistics of food rescue. The food vehicles and delivery vehicles of the food supply organizations could work on this linear programming model to control safety issues at rescue points.
3. Implementation of the Proposed System on Ekram
3.1. Overview of the Ekram Problem
The donated food can be categorized based on the quantity and frequency. A comprehensive system is required to collaborate to collect the food from the donors and distribute to people who need it. The composition of this procedure is based on different parameters, such as to avoid the waste of food, reduce the delivery time, and create methods to reach the people who want to use this food. Ekram strives to accomplish this. The system to support this should include the following:
- Mobile application: The application is intended to communicate with users (receiving orders) and vehicle drivers (sending to orders) with simple interfaces.
- Website: The website through which the organization manages, schedules orders and vehicles, and designs the route plan for each vehicle.
The following describes how Ekram operates:
- The user determines the type of order (donor/receiver).
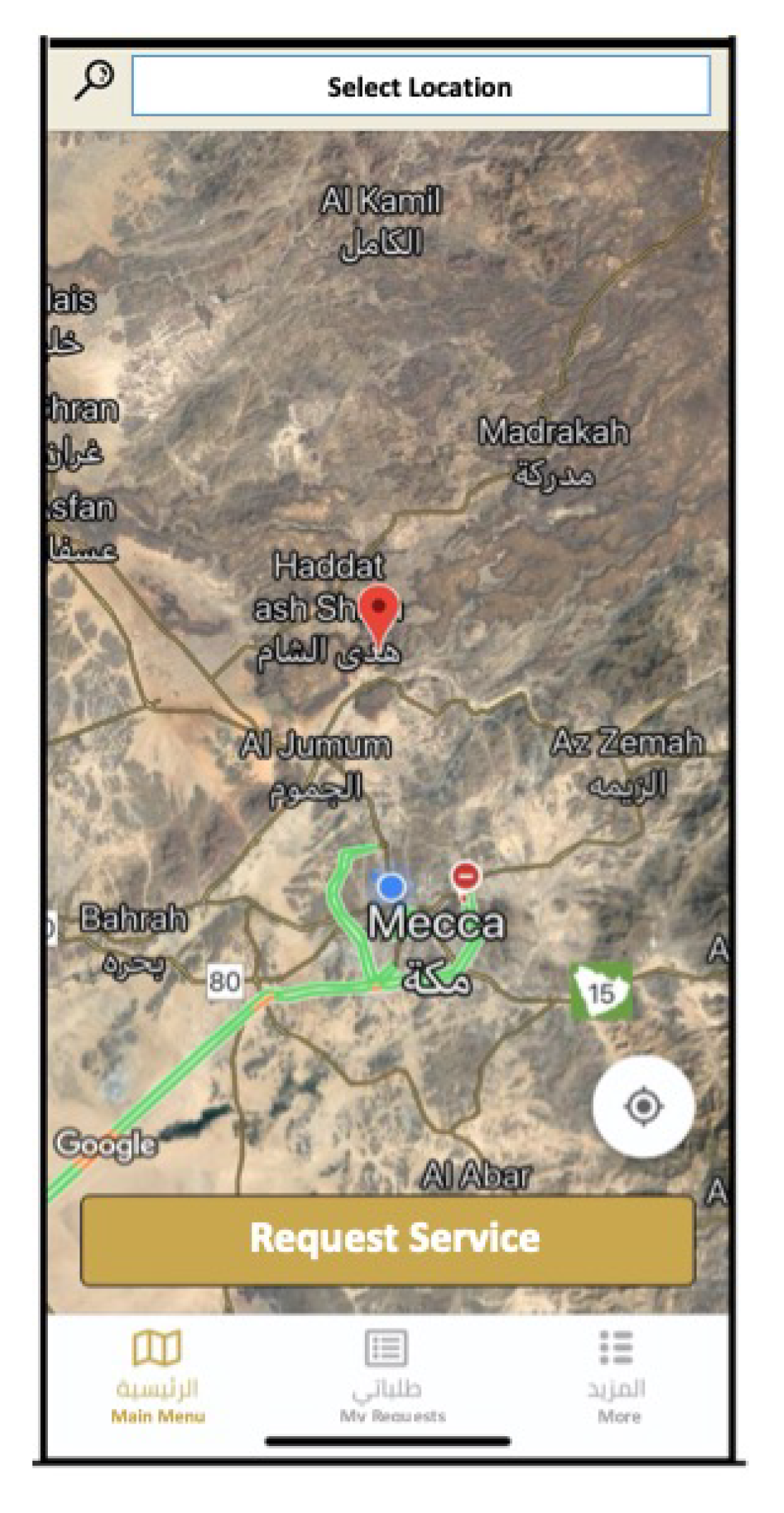
- The user determines their location via the Google map interface (Figure 1).
 Figure 1. User locating interface.
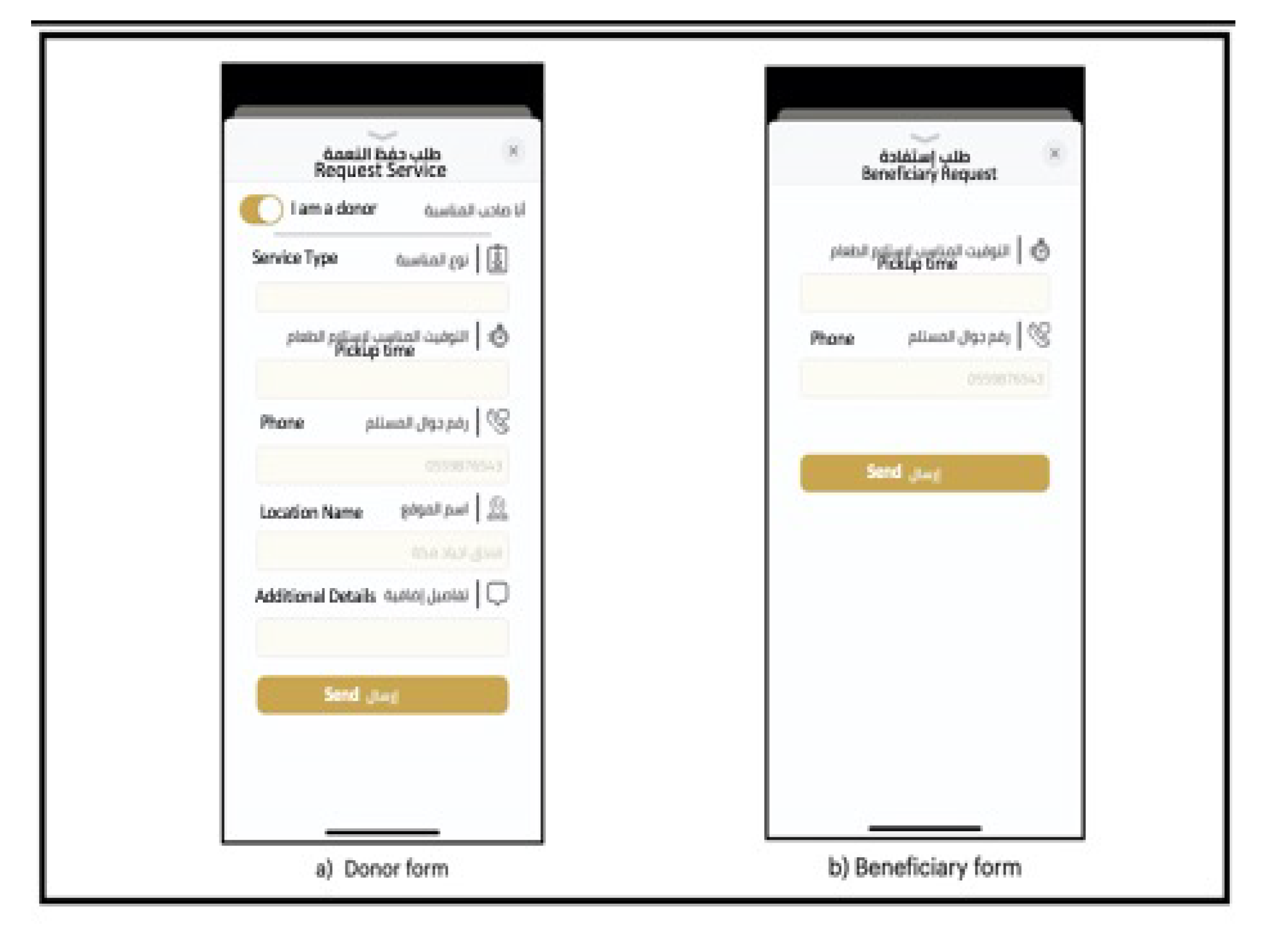
Figure 1. User locating interface. - Then a form is completed by filling in the required information (Figure 2).
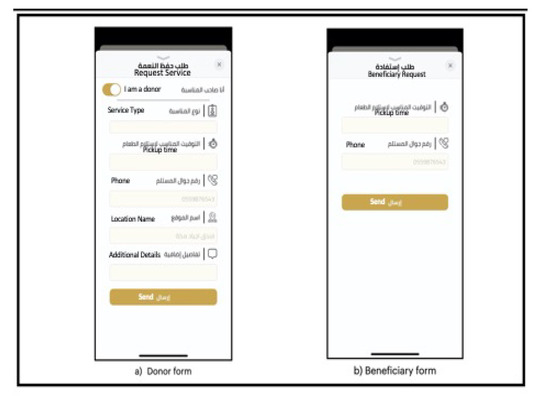 Figure 2. Donor and beneficiary form to complete request with confirmation.
Figure 2. Donor and beneficiary form to complete request with confirmation. - After submitting the request, the employee responsible for managing the requests through the website forwards the request to the vehicle operator through the application, and the driver makes the decision of whether to accept the request based on several factors, such as their current location and capacity of the vehicle.
- After accepting the request, the vehicle is sent to the user and ends with the return of the vehicle to the warehouse.
Ekram’s process starts with collecting the food from the donors and ends with distributing it to the people who request it. Ekram depends upon the number of vehicles to increase the efficacy of the delivery of food products as well as for collecting the food products from the donors. The main concern for Ekram is how to distribute vehicles and manage requests in an efficient manner without the driver having to decide. In some situations, the drivers may make poor decisions that reflect negatively on the organization in terms of wasted time, money, and effort and reduce the quality of the work. Furthermore, food distribution can severely be affected by the problem of late collection of the donated food. Finally, Ekram and similar organizations spend their largest amount of money on distribution.
Developing a model for the VRP should consider making informed decisions to reduce the delivery cost in an effective manner. For that, a set of four search algorithms were considered to optimize the system, namely, greedy, intraroute neighborhood, interroute neighborhood, and tabu search algorithms.
3.2. Steps to Apply the VRP System on Ekram
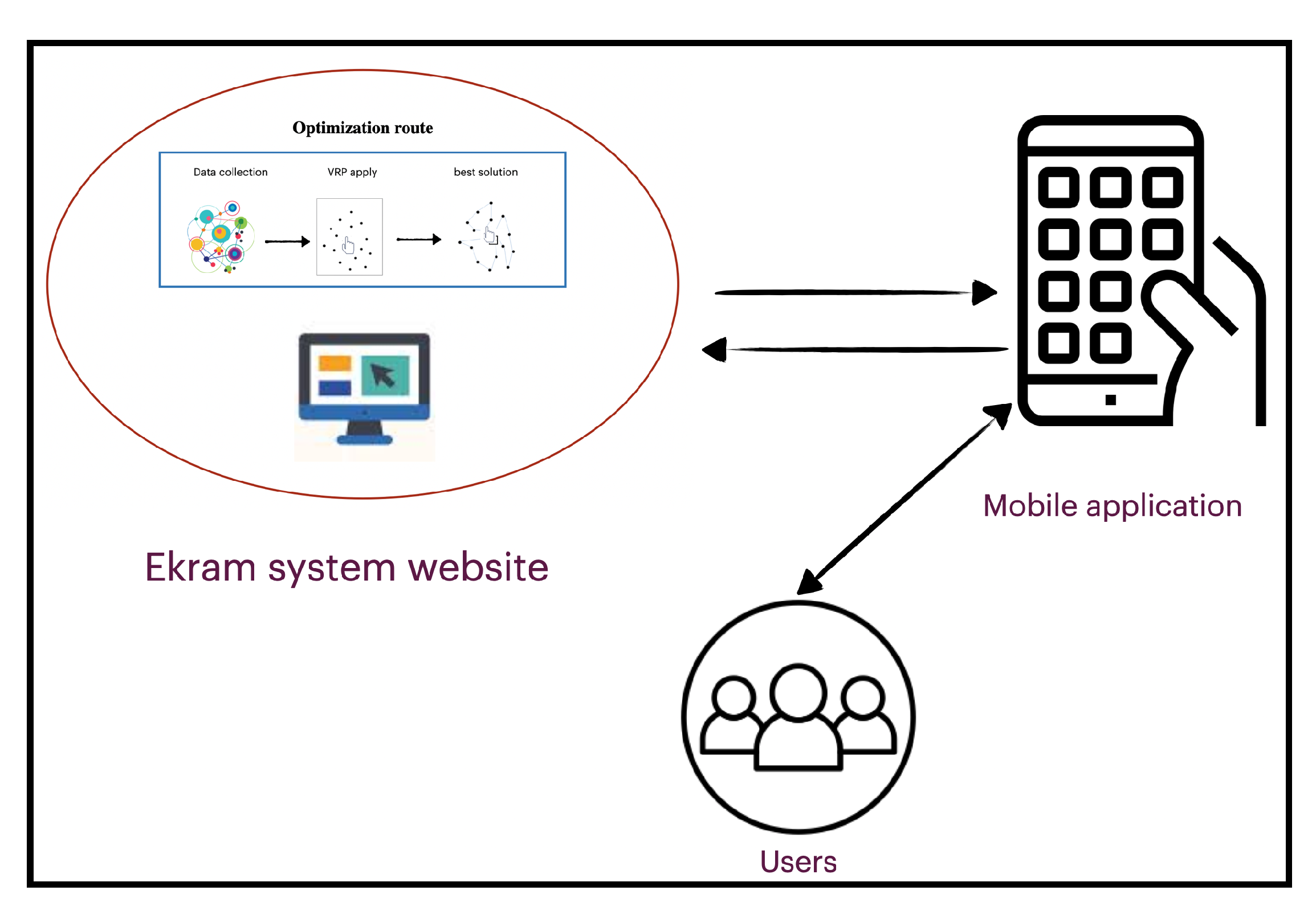
This subsection discusses the VRP system process for business operations in Ekram. Figure 3 illustrates the main steps that cover the process at Ekram:
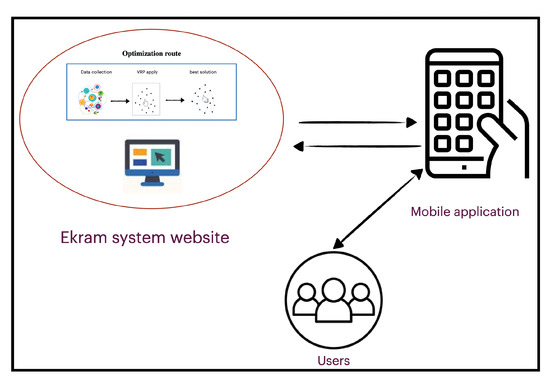
Figure 3.
Ekram system with VRP.
- The user determines the type of order (donor/receiver).
- The user determines their location via the Google map interface.
- Then the user fills out the required details to complete the application.
- The application is then submitted as a request from the user to the system. Once the application is submitted, the optimization process of Figure 3 is applied:
- (a)
- The system collects the required data including the location of the user, amount of food donated, the number of available vehicles, location and capacity of each vehicle, and delivery time requested.
- (b)
- The system then executes the proposed algorithms on the given data; the algorithms find the best solution “best route” and then terminate.
- (c)
- Once the the best solution is obtained, the system sends notifications simultaneously through the mobile application. One notification is sent to the driver that contains the route to be followed and the order details. Another notification is sent to the user that contains the type of delivery vehicle and expected time of arrival.
All of the aforementioned activities begin with the request of the donors and end with the delivery of food. Following this process, the optimized route showed a noticeable improvement in performance and reduction in cost.
3.3. Application of the VRP Algorithm
The purpose of the VRP was to manage the Ekram process to find the shortest route and reduce the effort and time for vehicles to collect and deliver surplus food in an optimized and effective manner.
This case can be defined as a graph , where is the set of the nodes along with the depot of at the various locations, with each pair of locations denoted through (i,j). The set of the various arcs , represent the donor set, which is also connected to the nonprofit organization’s set of vehicles . , , and are the binary variables, and is the continuous variable. L is the vehicle capacity. i, j, and k represent the node the vehicle visits, along with , known as the demand node.
The first binary decision variable , which is equal to 1, if and only if it has the optimal solution with the vehicle solution k, also visits the customer j, after customer i; is equal to 1, where the vertex of i is served through vehicle k. The problem is defined as
subject to the following terms.
We determine the vehicle capacity:
The objective function aims to minimize the total traveled distance. Constraint (2) ensures that each customer is served by at least one vehicle. The arc within which the vehicle will leave or enter the node i is shown in constraints (3) and (4). The leave and entry node enforces the following condition: if node i is visited by vehicle k, then vehicle k will use one arc entering the node and then another arc that leaves node i. Additionally, if node i is not visited by vehicle k, then no arc entering or leaving node i should be used by vehicle k. The flow conservation at the nodes for each vehicle is present in constraint (5), and constraint (6) ensures that no vehicle can be overloaded, and the amount of the product in each vehicle must always be less or equal to the vehicle capacity L. Finally, constraint (7) shows when the vehicle is at the depot.
As mentioned previously, four algorithms were utilized to optimize the VRP of Ekram. These algorithms were heuristic and metaheuristic algorithms. The algorithms were implemented on a MacBook Pro (Intel Core i5 1.4GHz CPU and 8GB RAM), and the programming language was Java.
3.3.1. Greedy Search Algorithm
The greedy search method was used in this research to solve the VRP. The greedy search algorithm is an effective method that considers all data in solving problems. The algorithm then selects the nodes to add into the solution at every step. Further, it generates the solution step by step and always selects the next node, offering the most rapid and obvious path. By giving the data set and applying the greedy search algorithm, a rule for searching and providing the optimal path will select the largest number at every level in the tree during the search. After selecting the largest numbers at each level, the algorithm presents the result which represents the sum of all of the selections in searching. Greedy search can be applied to solve the VRP, considering it has both greedy choice and an optimal substructure property. In our case, the problem has both properties, so the greedy algorithm can be applied. In this problem, the optimal substructure was identified by the presented solution.
3.3.2. Intraroute Heuristic Neighborhood Search
The intraroute heuristic neighborhood algorithm is a searching method that works on the basis of heuristics and is useful in complex searching systems. The searching algorithm basically works to reduce the number of vehicles in the VRP, which is the main purpose of using an intraroute heuristics search in this problem. Furthermore, the algorithm basically works by considering neighbors and works on reducing the total traveled distance in a given route. Three different kinds of challenges are involved in the VRP that require attention for its further progression, which include priority orders, unmatched pickups and deliveries, and interroute restrictions.
The number of interroute and intraroute structures is engaged in the deterministic order for the local and the shaking search operators. Four intraroute structures, including swap, 3-opt, 2-opt, and insertion are used by both variable neighborhood descent (VND) and variable neighborhood search (VNS), where both use four neighborhood structures, namely, cross, exchange (m,n), replace (1,1) as well as shift (0,1). When the algorithm reaches the shaking step, it will choose two subtours randomly; only in the case of the next operator of VNS is it an interroute operator. Then, the operator will be applied randomly to the subtours. The total delivery (starting) and the total pickup (returning) load are checked in the calculations of the fitness value [10].
3.3.3. Interroute Heuristic Neighborhood Search
Changes also appear in the intraroute neighborhood search according to progress in the VRP. These changes include 2OPT neighborhood, SWAP, and RELOCATE according to the neighborhood with a sufficient guarantee that a local search contains the TSP optimal routes, providing the promising solution. This involves short routes with up to 15 to 20 visits. To develop optimal tours, simple neighborhood search methods of TSP are used to handle small-level problems [11]. Interroute operators are used to reduce the complete distance, where the different cases could also reduce the number of vehicles.
3.3.4. Tabu Search Algorithm
The tabu search algorithm is a metaheuristic method to obtain the optimized solution for a VRP. It is inspired by the principles of human memory. The tabu search functions by applying mathematical principles for search methods. The main advantage of this method includes preventing repetition in the searching phases, as repetitions may increase the cost of the search. For this, the tabu search is an effective solution that potentially satisfies specific situations. The fundamental point of a tabu search is to fill in the missing pieces of a straightforward slope-climbing heuristic. In hill climbing, new arrangement competitors are contrasted, and closeness among arrangements and results are chosen.
4. Simulation Results
In this section, we describe how the proposed system was verified and compared with other existing manual dispatching systems. Further, a comparison with a state-of-the-art capacitated VRP based on Time Windows CVRPTW [3] is presented.
4.1. Proposed System Results
In Ekram, there are donors that must be visited on specific times and dates. For example, there are donors that are to be visited on Monday and Friday. From the distribution center of the organization, 15 vehicles are dispatched on each weekday. Every weekday, each vehicle is responsible for visiting 15 to 20 donors in order to collect the donated food. One donor is visited by only one vehicle consuming an average of 10–20 min in order to load the products.
To illustrate this, we examine a Thursday. A total of 60 donors were to be visited for food collection. The donors were located in the city of Makkah, Saudi Arabia. There were about 15 vehicles available for collecting food from 9:00 a.m. to 11:00 p.m.
This problem involved evaluating a set of various vehicle routes, which must include the following:
- The start and end must be at the depot.
- Exactly one vehicle is required to visit each single customer.
- The quantity L is associated with the total demand of any route.
- The total routing cost must be minimized.
The major aim of this study was to reduce the total travel time and the number of vehicles to minimize transportation costs. In this study, the performance was evaluated using the following metrics:
Travel time: the time for the vehicle to reach its destination, which can be calculated using this formula:
Travel distance: the route distance from the vehicle location to the destination, which can be calculated by
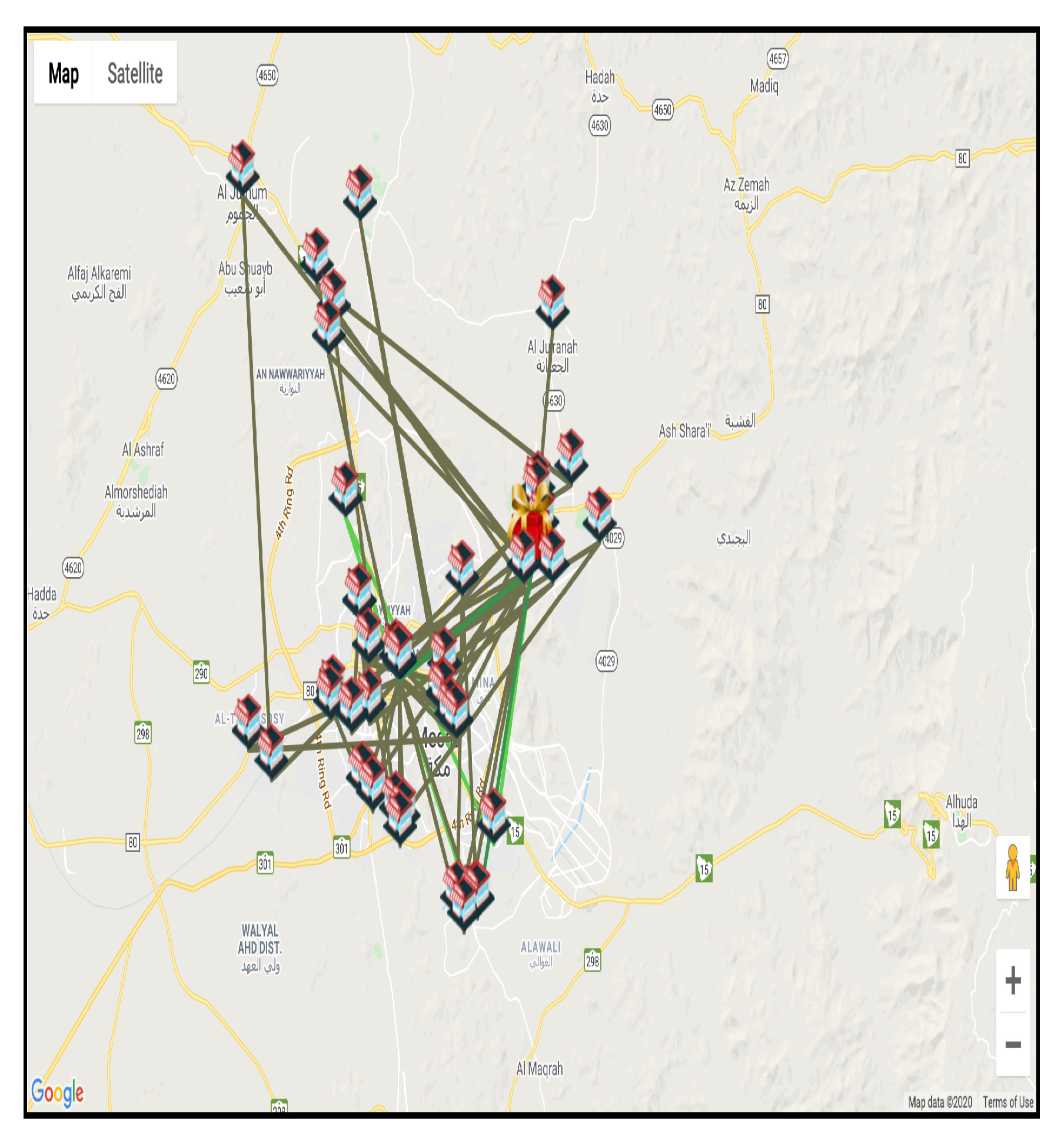
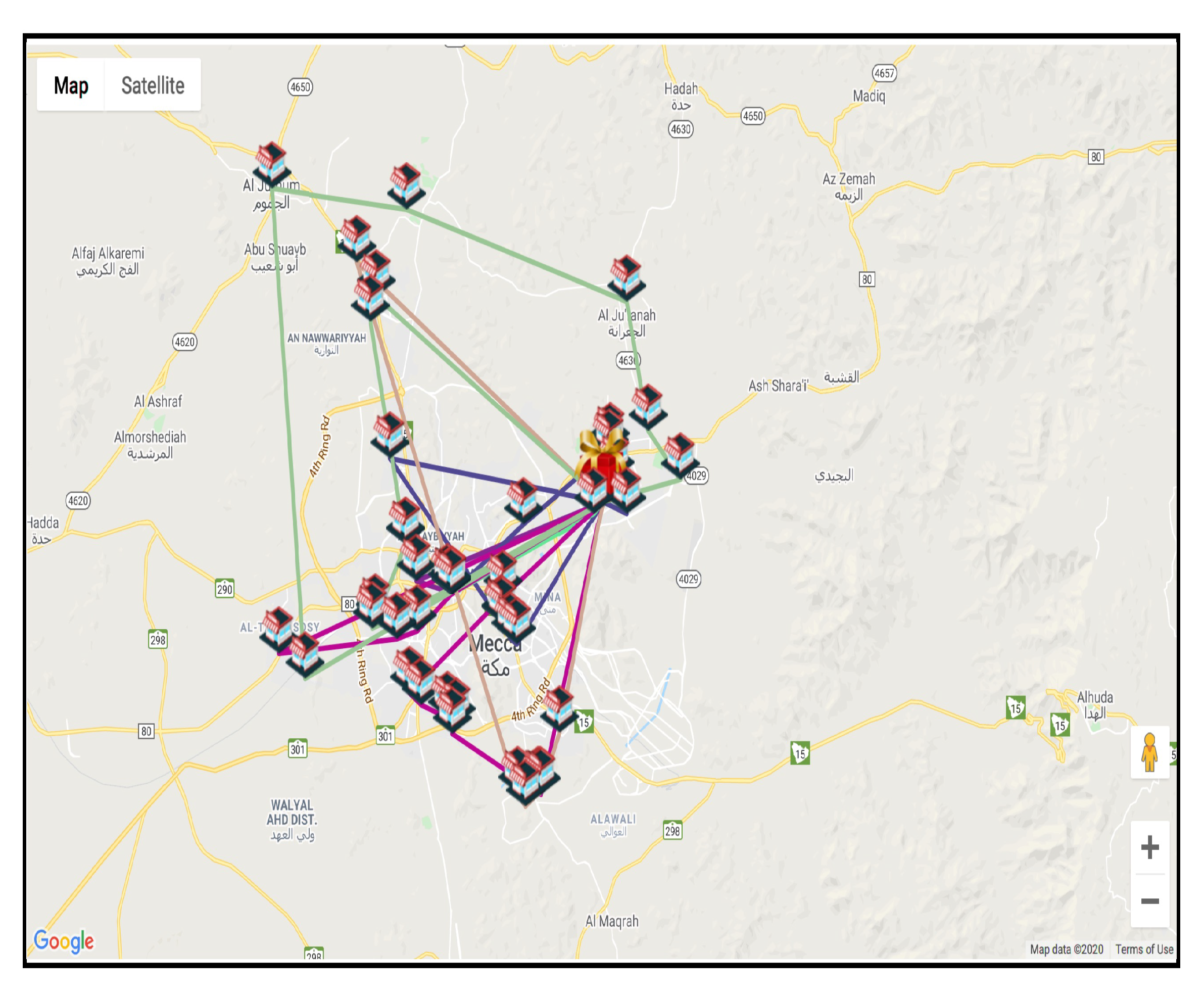
The objective was to minimize the total travel time and number of vehicles while ensuring all food was collected from the donors. In this case, there were 54 donors. Figure 4 shows the output of the system and the proposed route plan for drivers to serve these donors with “random selection” on Google maps before solving the problem.
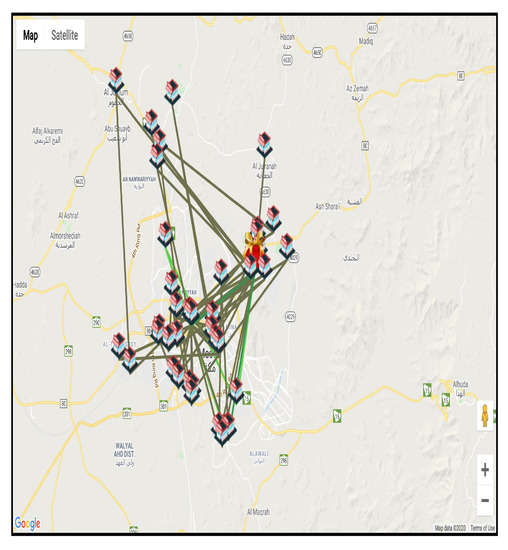
Figure 4.
Route plan proposed by the Ekram system before applying VRP.
Figure 5 shows the output after applying the VRP algorithms and optimizing the system on Google maps.
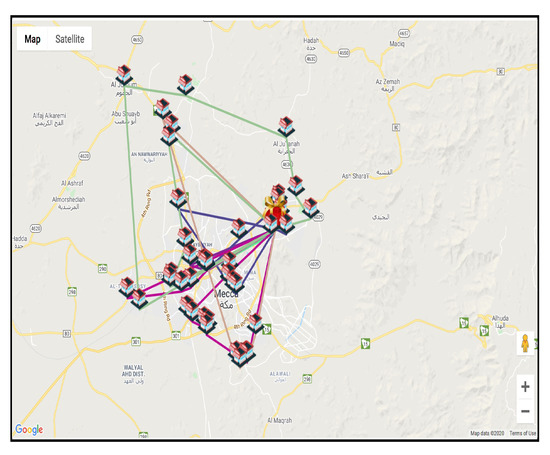
Figure 5.
Route plan proposed by the Ekram system after applying VRP.
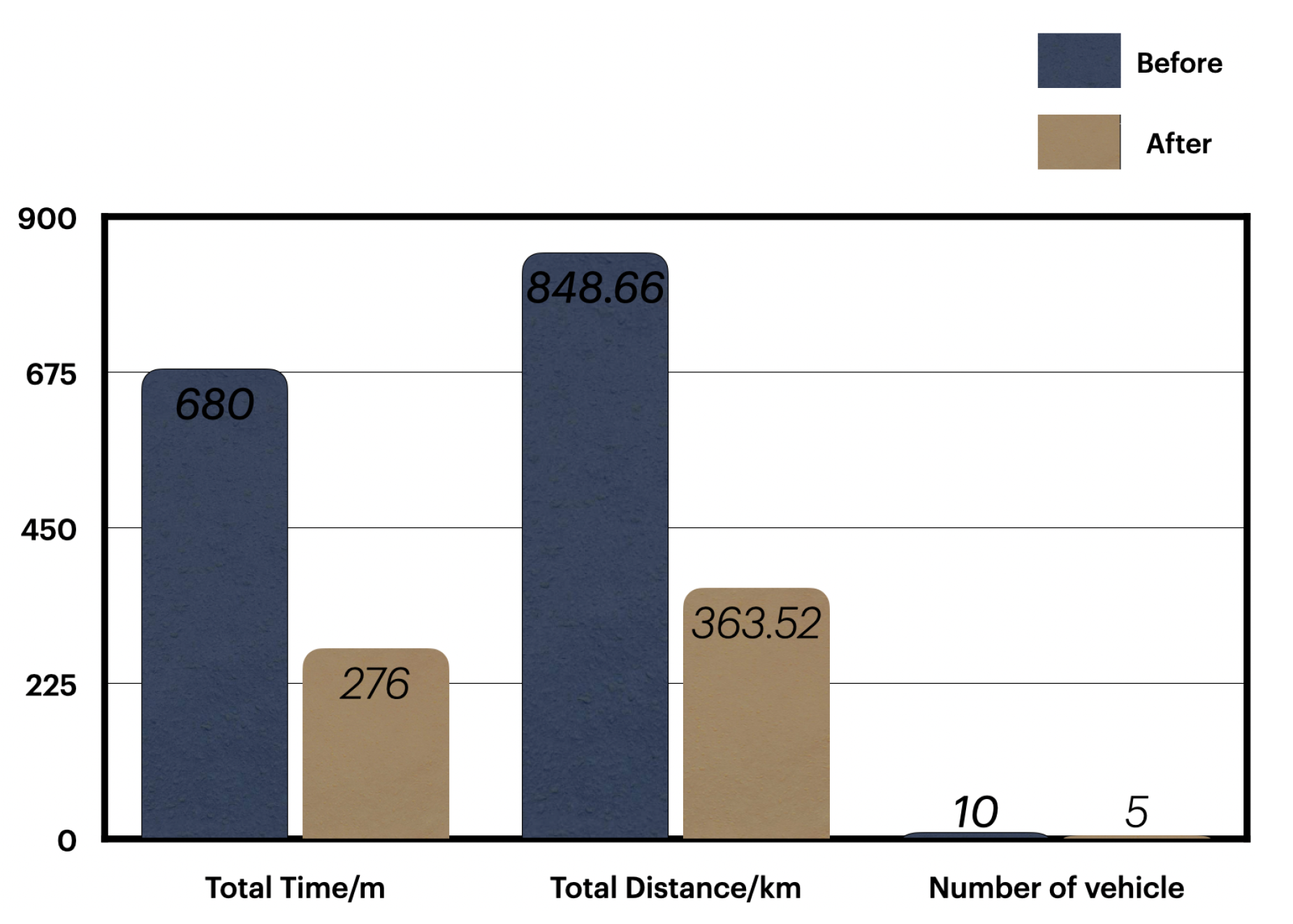
Figure 6 shows the initial results (without applying VRP) and the optimized results (after applying VRP); the first column represents the total time in minutes, the second column represents the total traversed distance in kilometers (km), and the last column presents the total number of vehicles used.
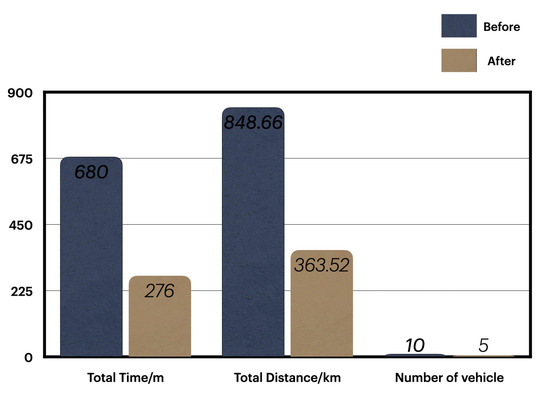
Figure 6.
A graph showing the difference between the results before and after applying the proposed solution.
When comparing the results between the current Ekram system and the proposed solution, the proposed solution reduced the total time by 59% and the total travel distances by 57%. Further, the total number of vehicles was reduced by 50%. Accordingly, the proposed algorithms presented an effective solution that optimized the operation of Ekram.
4.2. Comparison with the CVRPTW System
This section compares the proposed VRP system with the state-of-the-art method [3]. The authors of [3] solved the capacitated vehicle routing problem with time windows (CVRPTW). It used the Clarke and Wright algorithm to generate the initial solution, after which local search operators improved the solution. For the time-windows problem, the multiple ant colony system (MACS) was utilized. The methods were evaluated by three benchmarks, Christofides’ benchmark and Taillard’s benchmark to test the algorithms in the CVRP and Solomon’s instances to test the algorithms in the VRPTW. For Christofides’ problem, local search operators generated solutions within 1.9% of the best-known results, and for Taillard’s problem, the local search generated solutions that were on average 1.61% above the best-known results, and MACS produced the best-known result in the number of vehicles.
The case study of Thursday was used to evaluate the performance of [6]. Table 1 presents the problem’s features and compares the proposed method with [3]. The table has four columns: the first column is the number of routes or vehicles, the second column is the time, the third column is the food demand for each vehicle, and the fourth column is the number of donors visited on each route. From Table 2, the proposed solution outperformed [3] by 1.7%.

Table 1.
Considered features.

Table 2.
Comparison of the proposed solution and [3].
5. Conclusions
Nonprofit organizations provide services in accordance with principles of charity. Such organizations are in need of solutions to function in an effective manner. In this study, Ekram, a nonprofit organization, was used as a case study to improve the operations of collecting and delivering food to people. For Ekram, the vehicle routing problem (VRP) was one major problem. Furthermore, when several customers are being served by delivering/collecting food, it is important to find a range of optimizing routes, which not only satisfies the requirements of the customers but also assists Ekram in saving costs and time. In this study, four methods to find the optimized route for food collection and delivery were utilized, namely, greedy, intraroute, interroute, and tabu search algorithms. Furthermore, a mobile application to ease the process was developed. From the obtained results, the proposed algorithms significantly improved the operation process of Ekram. Furthermore, the results of the proposed method showed that it outperformed the state-of-the-art method. Thus, utilizing the proposed system for VRPs enhances the service quality and financial efficiency for such organizations.
Author Contributions
Conceptualization, A.A. (Ahmad Alhindi) and A.A. (Abrar Alsaidi); methodology, A.A. (Ahmad Alhindi), A.A. (Abrar Alsaidi) and A.M.; software, A.A. (Ahmad Alhindi) and A.A. (Abrar Alsaidi); validation, A.A. (Ahmad Alhindi) and A.M.; formal analysis, A.A. (Ahmad Alhindi) and A.A. (Abrar Alsaidi); resources, A.A. (Ahmad Alhindi); data curation, A.A. (Ahmad Alhindi); writing—original draft preparation, A.A. (Abrar Alsaidi) and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Behnassi, M.; Pollmann, O.; Gupta, H. Climate Change, Food Security and Natural Resource Management: Regional Case Studies from Three Continents; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Baig, M.B.; Al-Zahrani, K.H.; Schneider, F.; Straquadine, G.S.; Mourad, M. Food waste posing a serious threat to sustainability in the Kingdom of Saudi Arabia–A systematic review. Saudi J. Biol. Sci. 2019, 26, 1743–1752. [Google Scholar] [CrossRef] [PubMed]
- Li, X. Capacitated Vehicle Routing Problem with Time Windows: A Case Study on Pickup of Dietary Products in Nonprofit Organization; Arizona State University: Tempe, AZ, USA, 2015. [Google Scholar]
- Prescott-Gagnon, E.; Desaulniers, G.; Rousseau, L.M. A branch-and-price-based large neighborhood search algorithm for the vehicle routing problem with time windows. Netw. Int. J. 2009, 54, 190–204. [Google Scholar] [CrossRef]
- Kallehauge, B.; Larsen, J.; Madsen, O.B.; Solomon, M.M. Vehicle Routing Problem with Time Windows. In Column Generation; Desaulniers, G., Desrosiers, J., Solomon, M.M., Eds.; Springer: Boston, MA, USA, 2005; pp. 67–98. [Google Scholar] [CrossRef]
- Hsu, C.I.; Hung, S.F.; Li, H.C. Vehicle routing problem with time-windows for perishable food delivery. J. Food Eng. 2007, 80, 465–475. [Google Scholar] [CrossRef]
- Amorim, P.; Almada-Lobo, B. The impact of food perishability issues in the vehicle routing problem. Comput. Ind. Eng. 2014, 67, 223–233. [Google Scholar] [CrossRef]
- Kopfer, H.W.; Kopfer, H.; Wang, X. Limit and Degree of Autonomy in Groupage Systems: Challenges, Chances and Barriers for Horizontal Cooperation in Operational Transportation Planning. In Autonomous Cooperation and Control in Logistics; Springer: Berlin/Heidelberg, Germany, 2011; pp. 61–75. [Google Scholar]
- Motoyama, Y.; Knowlton, K. Examining the connections within the startup ecosystem: A case study of St. Louis. Entrep. Res. J. 2017, 7. [Google Scholar] [CrossRef]
- Lei, H.; Laporte, G.; Guo, B. A generalized variable neighborhood search heuristic for the capacitated vehicle routing problem with stochastic service times. Top 2012, 20, 99–118. [Google Scholar] [CrossRef]
- Belhaiza, S.; M’Hallah, R.; Brahim, G.B. A new hybrid genetic variable neighborhood search heuristic for the vehicle routing problem with multiple time windows. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1319–1326. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).