Improving Performance and Quantifying Uncertainty of Body-Rocking Detection Using Bayesian Neural Networks
Abstract
:1. Introduction
- With enough model capacity, our Bayesian framework provided better performance and was less sensitive to overfitting;
- Higher capacity alone did not consistently result on higher performance for a given model when compared to the Bayesian framework;
- Although transfer learning did not impact significantly the performance, it prevented the calibrated probability degradation as model complexity increased;
- The calibrated probability obtained from our Bayesian framework is an interpretable quantity that accurately represents the likelihood of correctness of the prediction of the specific dataset;
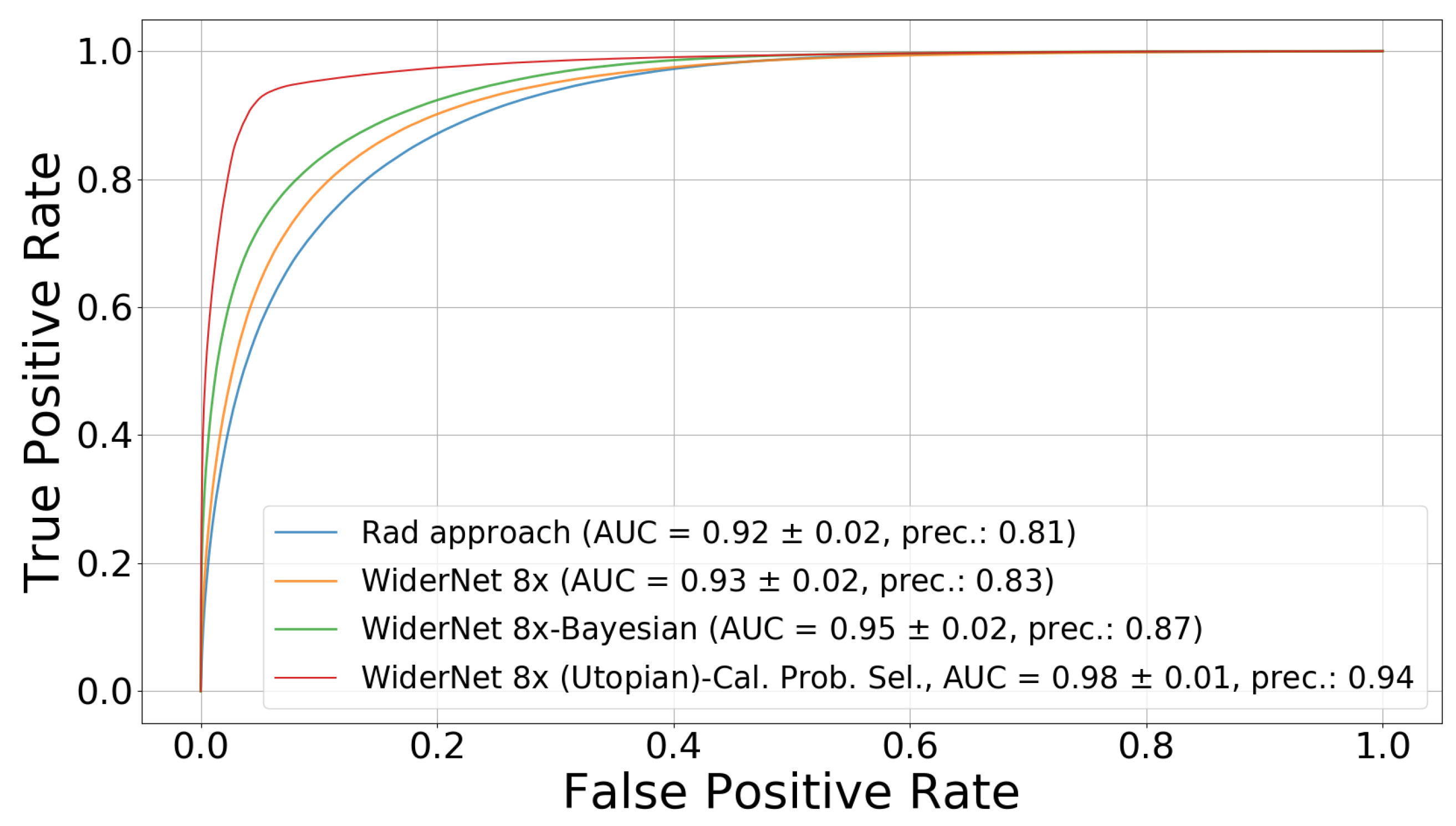
- Using the calibrated probability as a criterion for selecting reliable detection, we observe a clear improvement on precision with relatively low trade-off in other metrics (e.g., F1-score).
2. Related Work
3. Materials and Methods
3.1. Datasets
3.2. Bayesian Neural Networks
3.3. Probability Calibration
3.4. The Models
3.5. Dataset Pre-Processing and Evaluation Strategy
3.5.1. Transfer Learning for Model Improvement
3.5.2. Uncertainty Quantification as a Criterion for Choosing Reliable Predictions
3.5.3. Metrics
4. Results
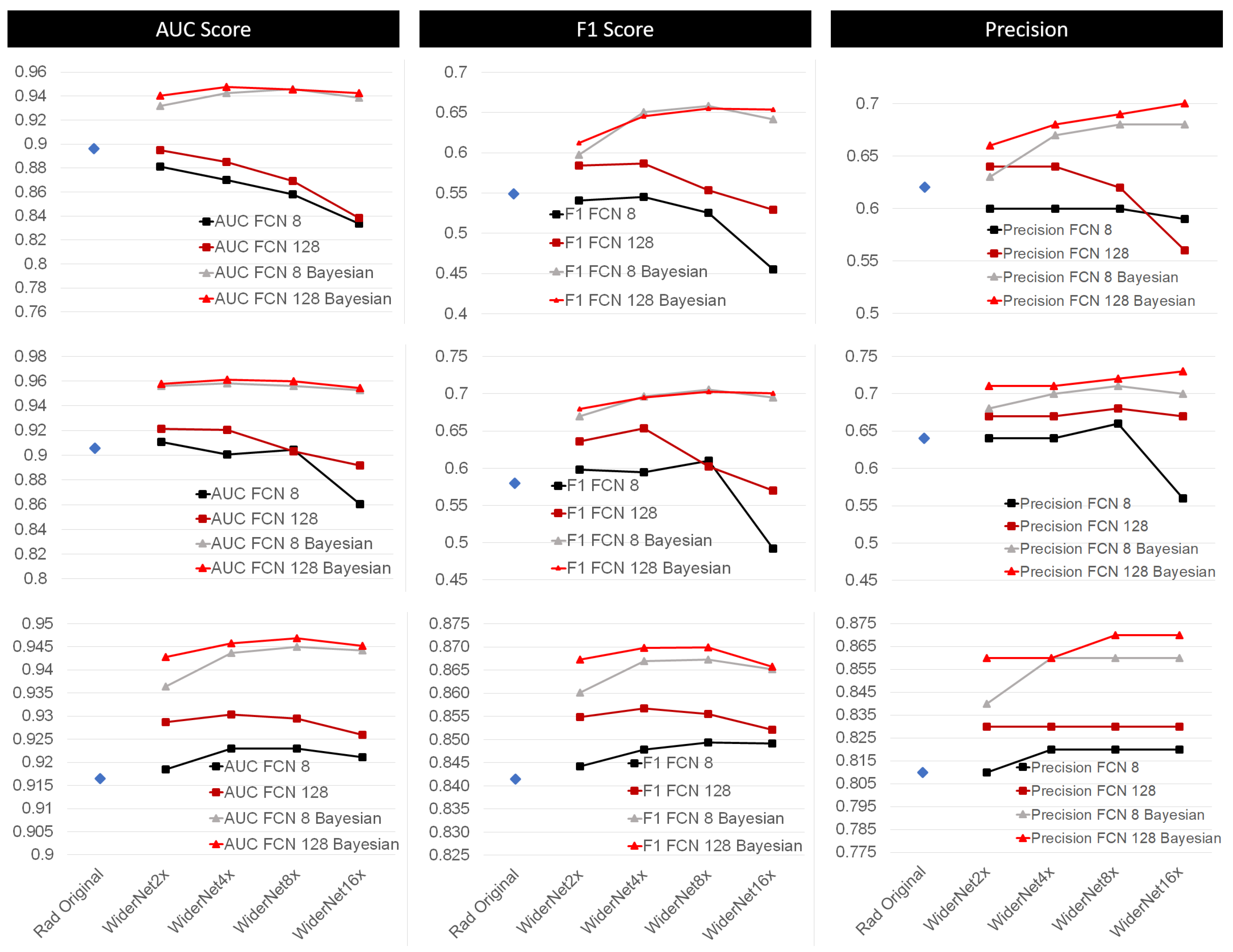
4.1. Bayesian Approach Compared to Current Methods
4.2. Effect of Transfer Learning (TF)
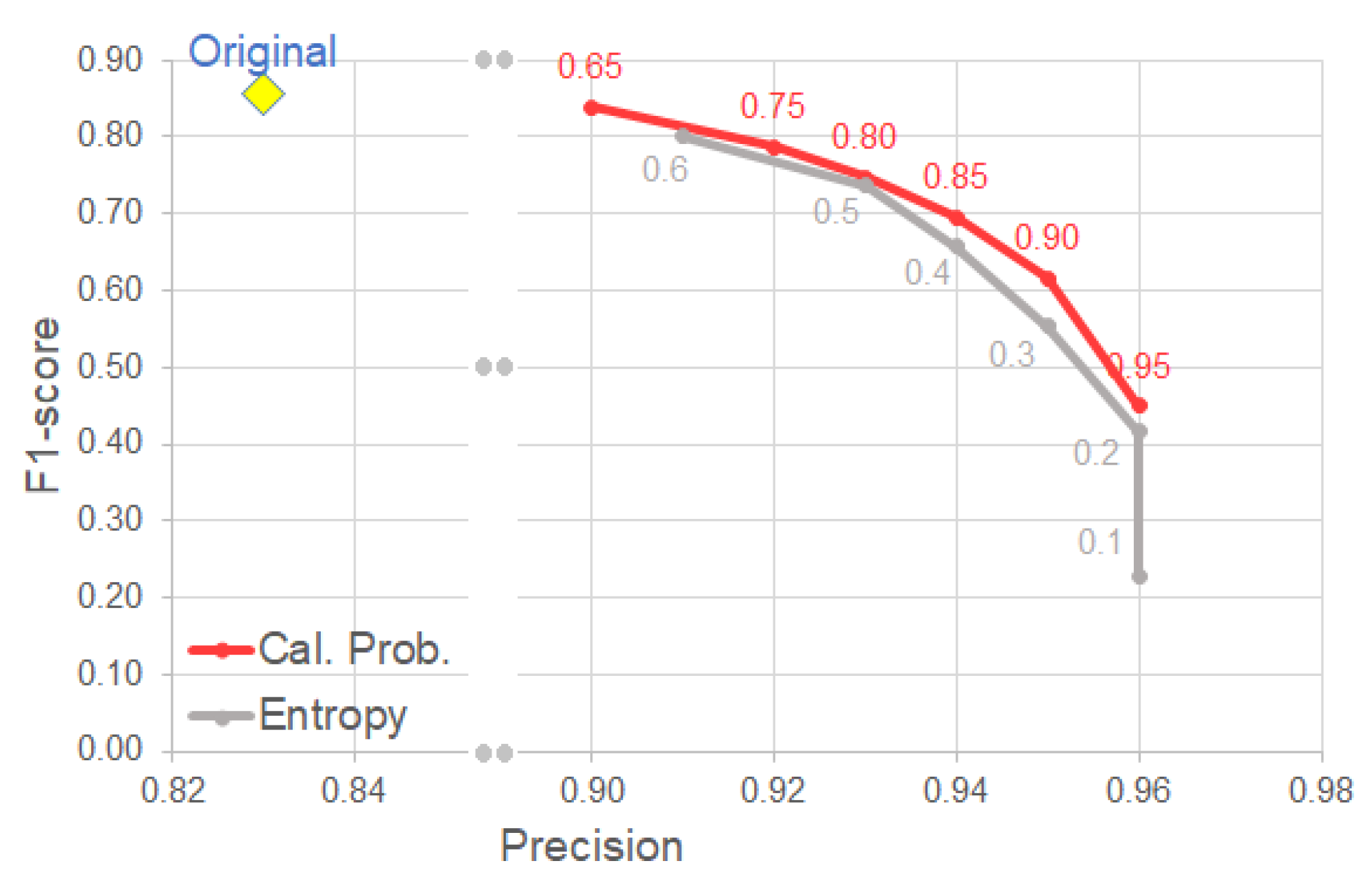
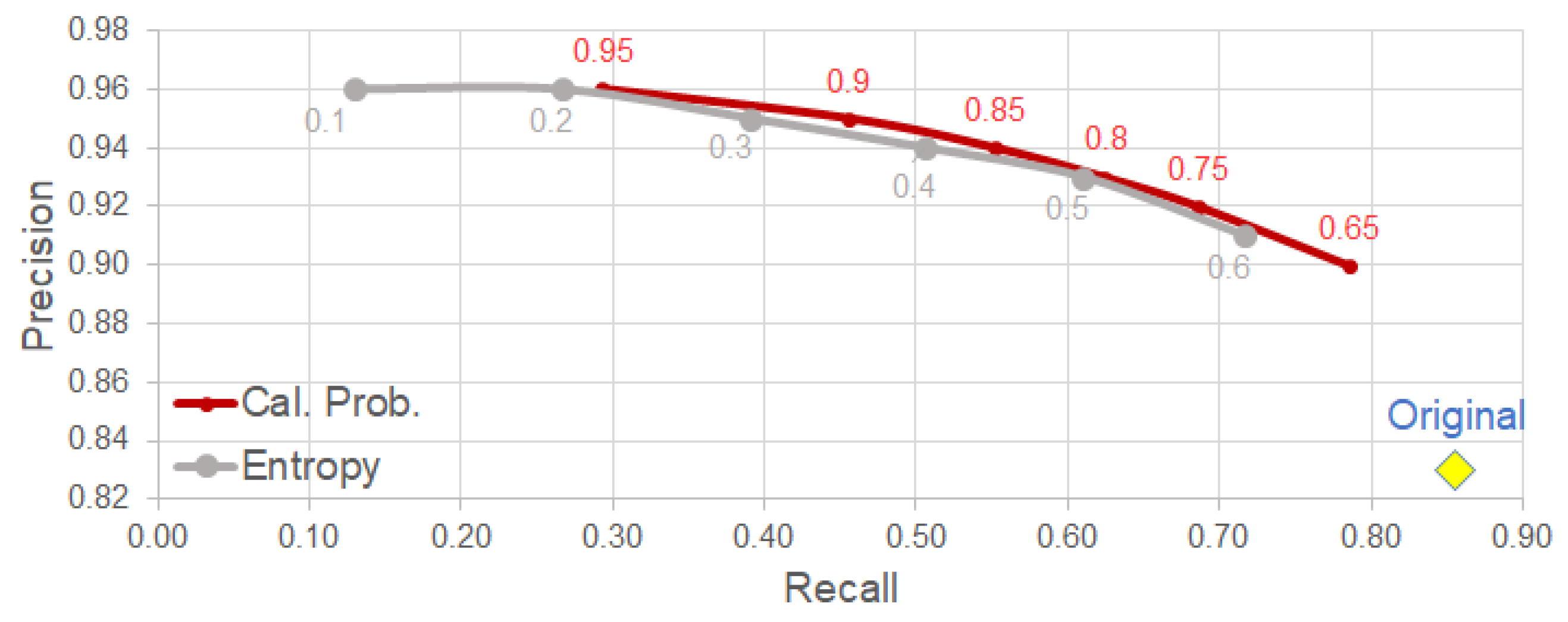
4.3. Uncertainty-Based Detection Selection
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Czapliński, A.; Steck, A.J.; Fuhr, P. Tic syndrome. Neurol. Neurochir. Pol. 2002, 36, 493–504. [Google Scholar] [PubMed]
- Singer, H.S. Stereotypic movement disorders. Handb. Clin. Neurol. 2011, 100, 631–639. [Google Scholar] [PubMed]
- Mahone, E.M.; Bridges, D.D.; Prahme, C.; Singer, H.S. Repetitive arm and hand movements (complex motor stereotypies) in children. J. Pediatr. 2004, 145, 391–395. [Google Scholar] [CrossRef] [PubMed]
- Troester, H.; Brambring, M.; Beelmann, A. The age dependence of stereotyped behaviours in blind infants and preschoolers. Child Care Health Dev. 1991, 17, 137–157. [Google Scholar] [CrossRef]
- McHugh, E.; Pyfer, J.L. The Development of Rocking among Children who are Blind. J. Vis. Impair. Blind. 1999, 93, 82–95. [Google Scholar] [CrossRef]
- Rafaeli-Mor, N.; Foster, L.G.; Berkson, G. Self-reported body-rocking and other habits in college students. Am. J. Ment. Retard. 1999, 104, 1–10. [Google Scholar] [CrossRef]
- Miller, J.M.; Singer, H.S.; Bridges, D.D.; Waranch, H.R. Behavioral therapy for treatment of stereotypic movements in nonautistic children. J. Child Neurol. 2006, 21, 119–125. [Google Scholar] [CrossRef]
- Subki, A.; Alsallum, M.; Alnefaie, M.N.; Alkahtani, A.; Almagamsi, S.; Alshehri, Z.; Kinsara, R.; Jan, M. Pediatric Motor Stereotypies: An Updated Review. J. Pediatr. Neurol. 2017, 15, 151–156. [Google Scholar] [CrossRef]
- Da Silva, R.L.; Stone, E.; Lobaton, E. A Feasibility Study of a Wearable Real-Time Notification System for Self-Awareness of Body-Rocking Behavior. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 3357–3359. [Google Scholar]
- Wang, X.; Gao, Y.; Lin, J.; Rangwala, H.; Mittu, R. A Machine Learning Approach to False Alarm Detection for Critical Arrhythmia Alarms. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 202–207. [Google Scholar]
- Eerikäinen, L.M.; Vanschoren, J.; Rooijakkers, M.J.; Vullings, R.; Aarts, R.M. Reduction of false arrhythmia alarms using signal selection and machine learning. Physiol. Meas. 2016, 37, 1204–1216. [Google Scholar] [CrossRef]
- Hinton, G.E.; Neal, R.M. Bayesian Learning for Neural Networks; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- MacKay, D.J.C. A Practical Bayesian Framework for Backpropagation Networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian approximation: Representing model uncertainty in deep learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Zhong, B.; Silva, R.L.D.; Li, M.; Huang, H.; Lobaton, E. Environmental Context Prediction for Lower Limb Prostheses with Uncertainty Quantification. IEEE Trans. Autom. Sci. Eng. 2020, 18, 458–470. [Google Scholar] [CrossRef]
- Zhong, B.; Huang, H.; Lobaton, E. Reliable Vision-Based Grasping Target Recognition for Upper Limb Prostheses. IEEE Trans. Cybern. 2020, 52, 1750–1762. [Google Scholar] [CrossRef]
- Thakur, S.; van Hoof, H.; Higuera, J.C.G.; Precup, D.; Meger, D. Uncertainty Aware Learning from Demonstrations in Multiple Contexts using Bayesian Neural Networks. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 768–774. [Google Scholar] [CrossRef] [Green Version]
- Akbari, A.; Jafari, R. Personalizing Activity Recognition Models Through Quantifying Different Types of Uncertainty Using Wearable Sensors. IEEE Trans. Biomed. Eng. 2020, 67, 2530–2541. [Google Scholar] [CrossRef]
- Gilchrist, K.H.; Hegarty-Craver, M.; Christian, R.P.K.B.; Grego, S.; Kies, A.C.; Wheeler, A.C. Automated Detection of Repetitive Motor Behaviors as an Outcome Measurement in Intellectual and Developmental Disabilities. J. Autism Dev. Disord. 2018, 48, 1458–1466. [Google Scholar] [CrossRef]
- Grossekathöfer, U.; Manyakov, N.V.; Mihajlovic, V.; Pandina, G.; Skalkin, A.; Ness, S.; Bangerter, A.; Goodwin, M.S. Automated Detection of Stereotypical Motor Movements in Autism Spectrum Disorder Using Recurrence Quantification Analysis. Front. Neuroinform. 2017, 11, 9. [Google Scholar] [CrossRef] [Green Version]
- Min, C.H.; Tewfik, A.H.; Kim, Y.; Menard, R. Optimal sensor location for body sensor network to detect self-stimulatory behaviors of children with autism spectrum disorder. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 3489–3492. [Google Scholar]
- Goodwin, M.S.; Haghighi, M.; Tang, Q.; Akçakaya, M.; Erdogmus, D.; Intille, S.S. Moving towards a real-time system for automatically recognizing stereotypical motor movements in individuals on the autism spectrum using wireless accelerometry. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014. [Google Scholar]
- Goodwin, M.S.; Intille, S.S.; Albinali, F.; Velicer, W.F. Automated detection of stereotypical motor movements. J. Autism Dev. Disord. 2011, 41, 770–782. [Google Scholar] [CrossRef]
- Min, C.H.; Tewfik, A.H. Automatic characterization and detection of behavioral patterns using linear predictive coding of accelerometer sensor data. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 220–223. [Google Scholar]
- Albinali, F.; Goodwin, M.S.; Intille, S.S. Recognizing stereotypical motor movements in the laboratory and classroom: A case study with children on the autism spectrum. In Proceedings of the 11th International Conference on Ubiquitous Computing, Orlando, FL, USA, 30 September–3 October 2009. [Google Scholar]
- Rad, N.M.; Kia, S.M.; Zarbo, C.; van Laarhoven, T.; Jurman, G.; Venuti, P.; Marchiori, E.; Furlanello, C. Deep learning for automatic stereotypical motor movement detection using wearable sensors in autism spectrum disorders. Signal Process. 2018, 144, 180–191. [Google Scholar]
- Sadouk, L.; Gadi, T.; Essoufi, E.H. A Novel Deep Learning Approach for Recognizing Stereotypical Motor Movements within and across Subjects on the Autism Spectrum Disorder. Comp. Int. Neurosc. 2018, 2018, 7186762. [Google Scholar] [CrossRef] [Green Version]
- Rad, N.M.; Furlanello, C. Applying Deep Learning to Stereotypical Motor Movement Detection in Autism Spectrum Disorders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 1235–1242. [Google Scholar]
- Rad, N.M.; Kia, S.M.; Zarbo, C.; Jurman, G.; Venuti, P.; Furlanello, C. Stereotypical Motor Movement Detection in Dynamic Feature Space. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 487–494. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Wu, H.H.; Lemaire, E.D.; Baddour, N.C. Combining low sampling frequency smartphone sensors and video for a Wearable Mobility Monitoring System. F1000Research 2015, 3, 170. [Google Scholar] [CrossRef]
- Akbari, A.; Jafari, R. A Deep Learning Assisted Method for Measuring Uncertainty in Activity Recognition with Wearable Sensors. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical Health Informatics (BHI), Chicago, IL, USA, 19–22 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Steinbrener, J.; Posch, K.; Pilz, J. Measuring the Uncertainty of Predictions in Deep Neural Networks with Variational Inference. Sensors 2020, 20, 6011. [Google Scholar] [CrossRef]
- Barandas, M.; Folgado, D.; Santos, R.; Simão, R.; Gamboa, H. Uncertainty-Based Rejection in Machine Learning: Implications for Model Development and Interpretability. Electronics 2022, 11, 396. [Google Scholar] [CrossRef]
- Cicalese, P.A.; Mobiny, A.; Shahmoradi, Z.; Yi, X.; Mohan, C.; Van Nguyen, H. Kidney Level Lupus Nephritis Classification Using Uncertainty Guided Bayesian Convolutional Neural Networks. IEEE J. Biomed. Health Inform. 2021, 25, 315–324. [Google Scholar] [CrossRef]
- Wang, X.; Tang, F.; Chen, H.; Luo, L.; Tang, Z.; Ran, A.R.; Cheung, C.Y.; Heng, P.A. UD-MIL: Uncertainty-Driven Deep Multiple Instance Learning for OCT Image Classification. IEEE J. Biomed. Health Inform. 2020, 24, 3431–3442. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Zeng, Z.; Xu, K.; Chen, C.; Guan, C. DSAL: Deeply Supervised Active Learning From Strong and Weak Labelers for Biomedical Image Segmentation. IEEE J. Biomed. Health Inform. 2021, 25, 3744–3751. [Google Scholar] [CrossRef] [PubMed]
- Wickstrøm, K.; Mikalsen, K.Ø.; Kampffmeyer, M.; Revhaug, A.; Jenssen, R. Uncertainty-Aware Deep Ensembles for Reliable and Explainable Predictions of Clinical Time Series. IEEE J. Biomed. Health Inform. 2021, 25, 2435–2444. [Google Scholar] [CrossRef] [PubMed]
- Silvestro, D.; Andermann, T. Prior choice affects ability of Bayesian neural networks to identify unknowns. arXiv 2020, arXiv:2005.04987. [Google Scholar]
- Tejero-Cantero, Á.; Boelts, J.; Deistler, M.; Lueckmann, J.M.; Durkan, C.; Gonccalves, P.J.; Greenberg, D.S.; Neuroengineering, J.H.M.C.; Electrical, D.; Engineering, C.; et al. SBI—A toolkit for simulation-based inference. J. Open Source Softw. 2020, 5, 2505. [Google Scholar] [CrossRef]
- Teng, X.; Pei, S.; Lin, Y.R. StoCast: Stochastic Disease Forecasting with Progression Uncertainty. IEEE J. Biomed. Health Inform. 2021, 25, 850–861. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Williams, C.K.I. Computing with Infinite Networks. In Proceedings of the NIPS, Denver, CO, USA, 2–5 December 1996. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; p. 463. [Google Scholar]
- Zhong, B. Reliable Deep Learning for Intelligent Wearable Systems; North Carolina State University: Raleigh, NC, USA, 2020. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Appendix. arXiv 2015, arXiv:1506.02157. [Google Scholar]
- Smith, L.; Gal, Y. Understanding measures of uncertainty for adversarial example detection. arXiv 2018, arXiv:1803.08533. [Google Scholar]
- Kendall, A.; Gal, Y. What uncertainties do we need in bayesian deep learning for computer vision? In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5574–5584. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Houlsby, N.; Huszár, F.; Ghahramani, Z.; Lengyel, M. Bayesian active learning for classification and preference learning. arXiv 2011, arXiv:1112.5745. [Google Scholar]
- Zhong, B.; da Silva, R.L.; Tran, M.; Huang, H.; Lobaton, E. Efficient Environmental Context Prediction for Lower Limb Prostheses. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3980–3994. [Google Scholar] [CrossRef]
- Kendall, A.; Badrinarayanan, V.; Cipolla, R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding. arXiv 2017, arXiv:1511.02680. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Bayesian convolutional neural networks with Bernoulli approximate variational inference. arXiv 2015, arXiv:1506.02158. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2017, arXiv:1611.03530. [Google Scholar] [CrossRef]
- Wenzel, F.; Roth, K.; Veeling, B.S.; Swiatkowski, J.; Tran, L.; Mandt, S.; Snoek, J.; Salimans, T.; Jenatton, R.; Nowozin, S. How Good is the Bayes Posterior in Deep Neural Networks Really? In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020. [Google Scholar]
- Vladimirova, M.; Verbeek, J.; Mesejo, P.; Arbel, J. Understanding Priors in Bayesian Neural Networks at the Unit Level. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
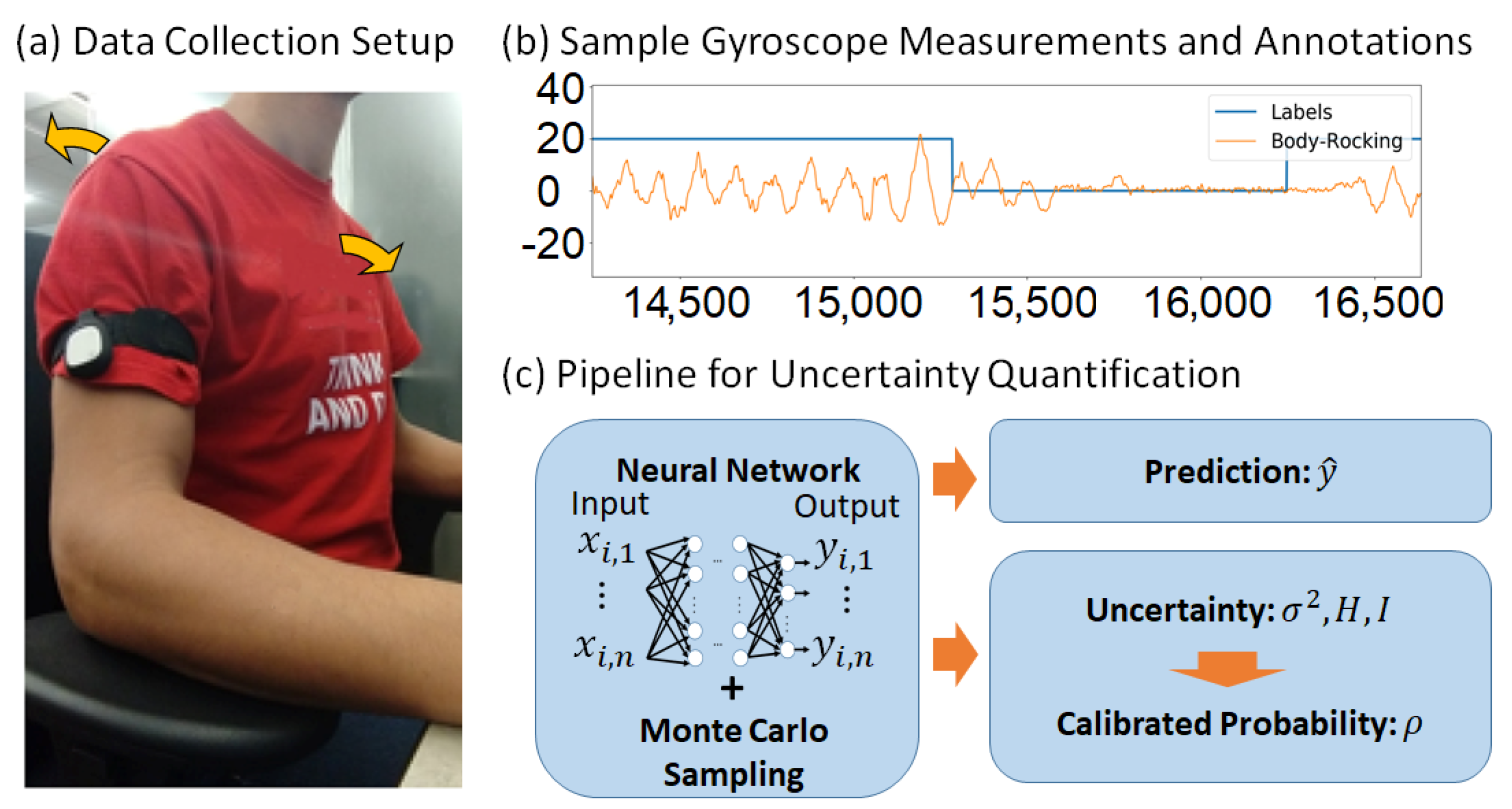





| Name | Subject | Session | Total Length | Occurrences | Behavior Duration | Sensors |
|---|---|---|---|---|---|---|
| ESDB | 1 | 14 | 11.74 h | 526 | 7 h (59.7%) | Acc, Gyro |
| EDAQA | 6 | 25 | 10.63 h | 792 | 2 h (20.3%) | Acc |
| Equation | Title | |
|---|---|---|
| (1) | Representation of a DNN with L layers | |
| (2) | Standard loss function for a DL model | |
| (3) | Model predictive probability | |
| (4) | Loss function of Gaussian Process | |
| (5) | Monte Carlo approximation of (4) | |
| (6) | Regression loss obtained from (5) | |
| (14) | Classification loss obtained from (5) | |
| (10) | Model predictive variance | |
| (11) | Model predictive entropy | |
| + | (12) | Mutual information |
| Study 1 | Study 2 | ESDB | ||
|---|---|---|---|---|
| Rad Original | AUC: | 0.896 | 0.906 | 0.916 |
| F1: | 0.549 | 0.580 | 0.841 | |
| Precision | 0.620 | 0.680 | 0.810 | |
| Rad Bayes | AUC: | 0.891 | 0.920 | 0.925 |
| F1: | 0.502 | 0.530 | 0.852 | |
| Precision | 0.690 | 0.720 | 0.820 | |
| WiderNet 2× | AUC: | 0.895 | 0.921 | 0.929 |
| F1: | 0.584 | 0.636 | 0.855 | |
| Precision | 0.640 | 0.670 | 0.830 | |
| WiderNet 2× | AUC: | 0.941 | 0.958 | 0.943 |
| Bayes | F1: | 0.612 | 0.679 | 0.867 |
| Precision | 0.660 | 0.710 | 0.860 | |
| WiderNet 4× | AUC: | 0.885 | 0.920 | 0.930 |
| F1: | 0.587 | 0.653 | 0.857 | |
| Precision | 0.640 | 0.670 | 0.830 | |
| WiderNet 4× | AUC: | 0.948 | 0.961 | 0.946 |
| Bayes | F1: | 0.645 | 0.695 | 0.870 |
| Precision | 0.680 | 0.710 | 0.860 | |
| WiderNet 8× | AUC: | 0.869 | 0.903 | 0.929 |
| F1: | 0.554 | 0.602 | 0.856 | |
| Precision | 0.620 | 0.680 | 0.830 | |
| WiderNet 8× | AUC: | 0.945 | 0.960 | 0.947 |
| Bayes | F1: | 0.655 | 0.703 | 0.870 |
| Precision | 0.690 | 0.720 | 0.870 | |
| WiderNet 16× | AUC: | 0.838 | 0.892 | 0.926 |
| F1: | 0.529 | 0.570 | 0.852 | |
| Precision | 0.560 | 0.670 | 0.830 | |
| WiderNet 16× | AUC: | 0.943 | 0.954 | 0.945 |
| Bayes | F1: | 0.654 | 0.700 | 0.866 |
| Precision | 0.700 | 0.730 | 0.870 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, R.L.; Zhong, B.; Chen, Y.; Lobaton, E. Improving Performance and Quantifying Uncertainty of Body-Rocking Detection Using Bayesian Neural Networks. Information 2022, 13, 338. https://doi.org/10.3390/info13070338
da Silva RL, Zhong B, Chen Y, Lobaton E. Improving Performance and Quantifying Uncertainty of Body-Rocking Detection Using Bayesian Neural Networks. Information. 2022; 13(7):338. https://doi.org/10.3390/info13070338
Chicago/Turabian Styleda Silva, Rafael Luiz, Boxuan Zhong, Yuhan Chen, and Edgar Lobaton. 2022. "Improving Performance and Quantifying Uncertainty of Body-Rocking Detection Using Bayesian Neural Networks" Information 13, no. 7: 338. https://doi.org/10.3390/info13070338
APA Styleda Silva, R. L., Zhong, B., Chen, Y., & Lobaton, E. (2022). Improving Performance and Quantifying Uncertainty of Body-Rocking Detection Using Bayesian Neural Networks. Information, 13(7), 338. https://doi.org/10.3390/info13070338







