Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Peak Distribution Function
2.2. Classical Savitizky–Golay Filtering
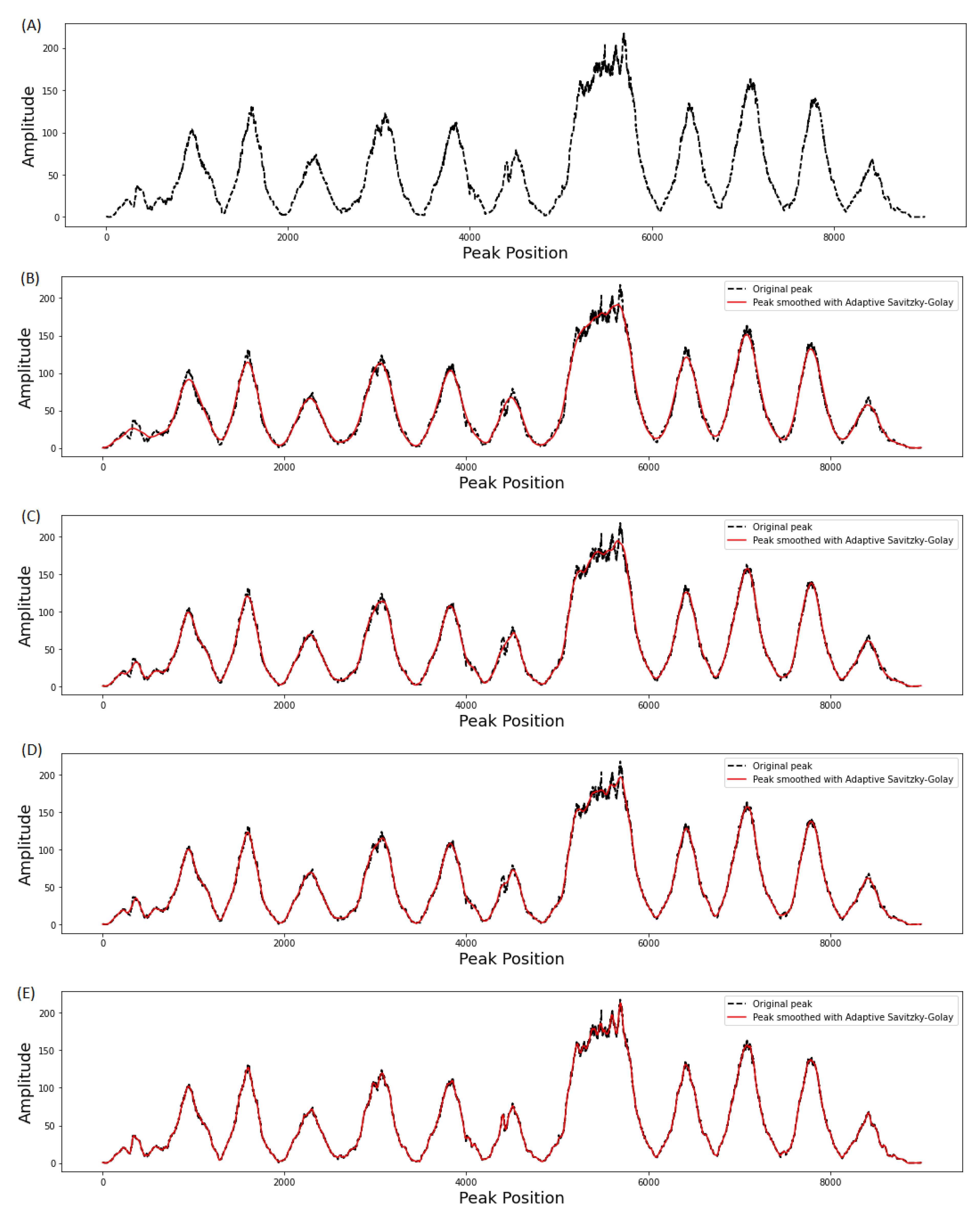
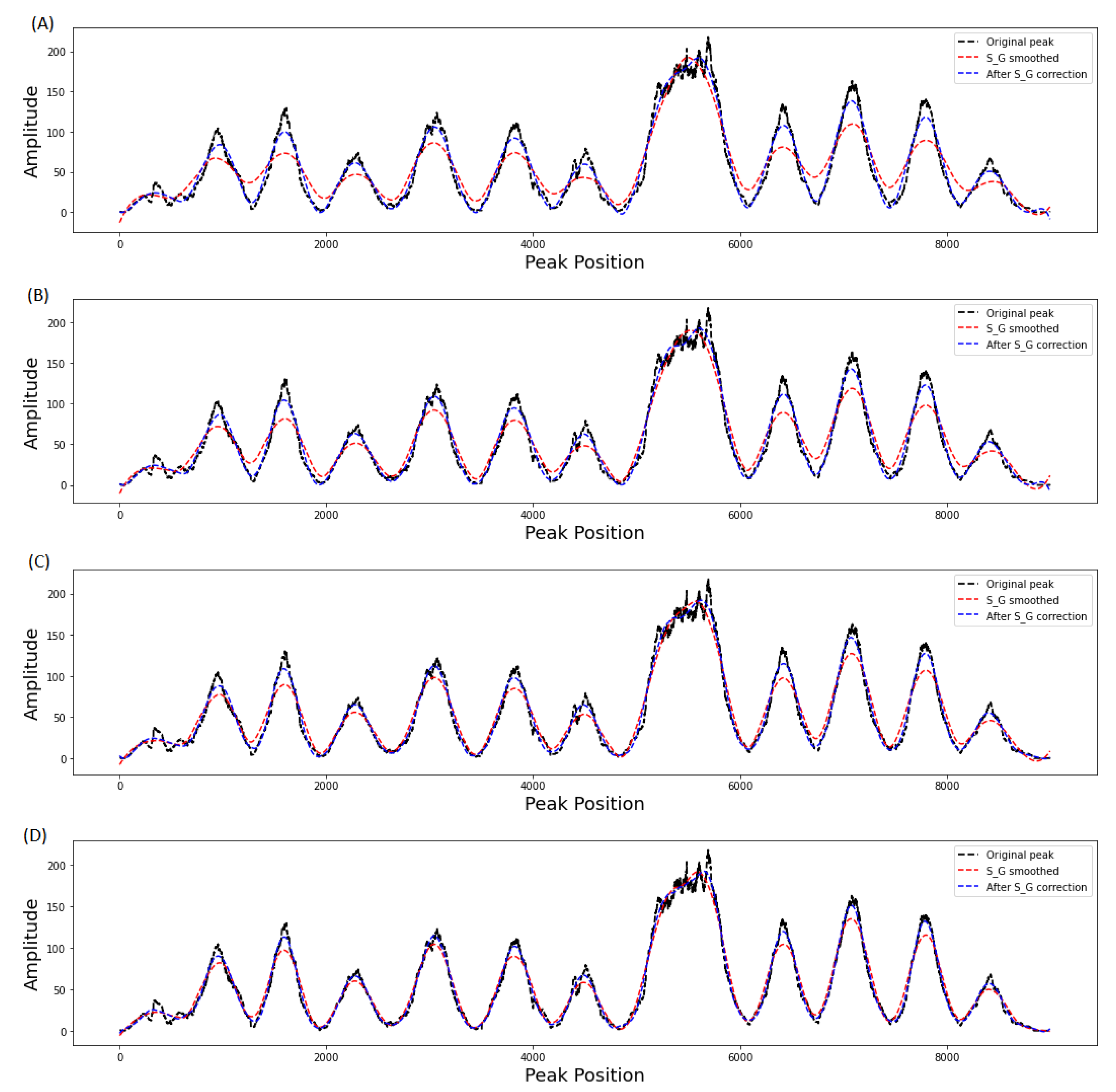
2.3. Adaptive Savitizky–Golay Filtering
2.4. Feature Extraction
3. Results
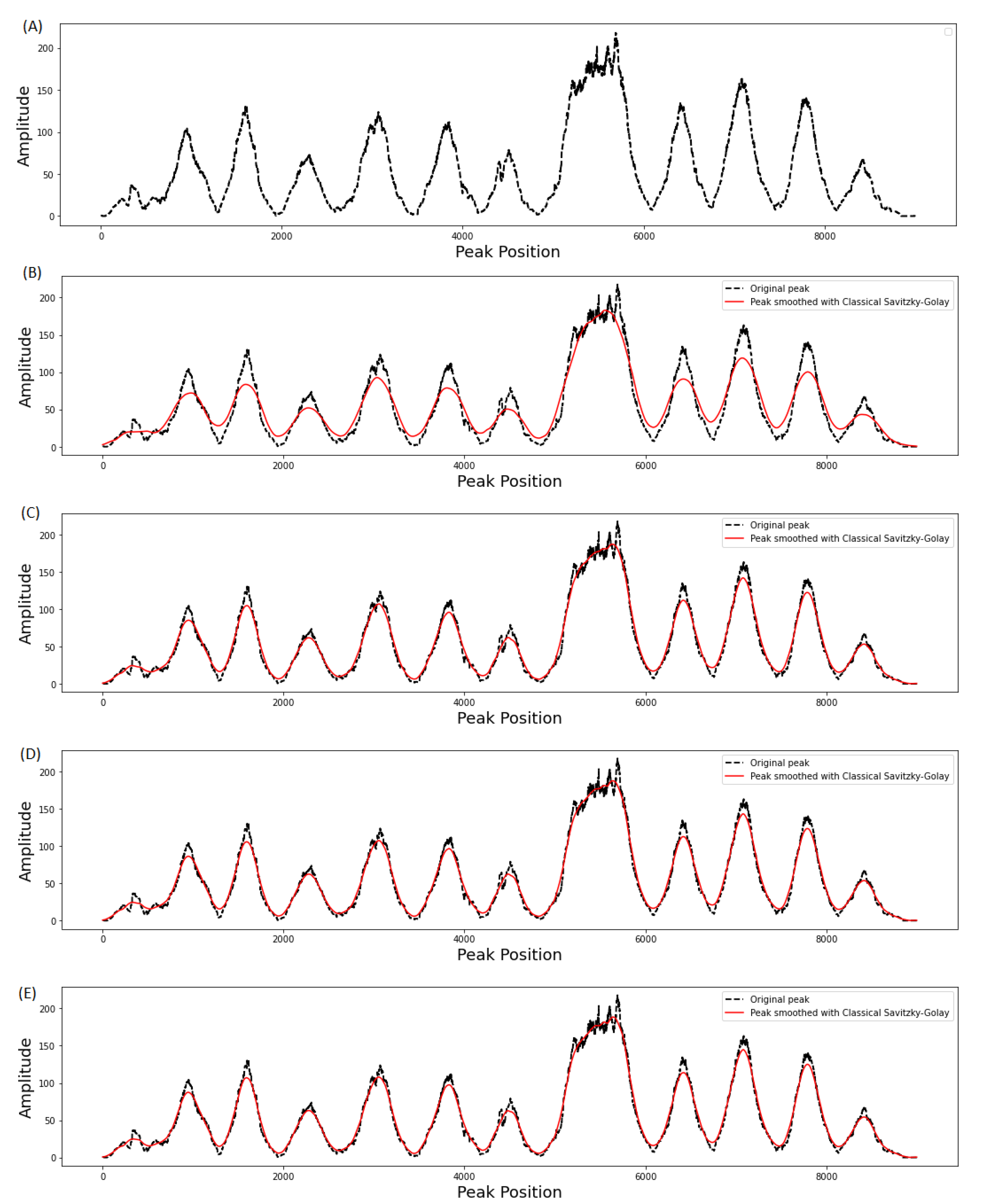
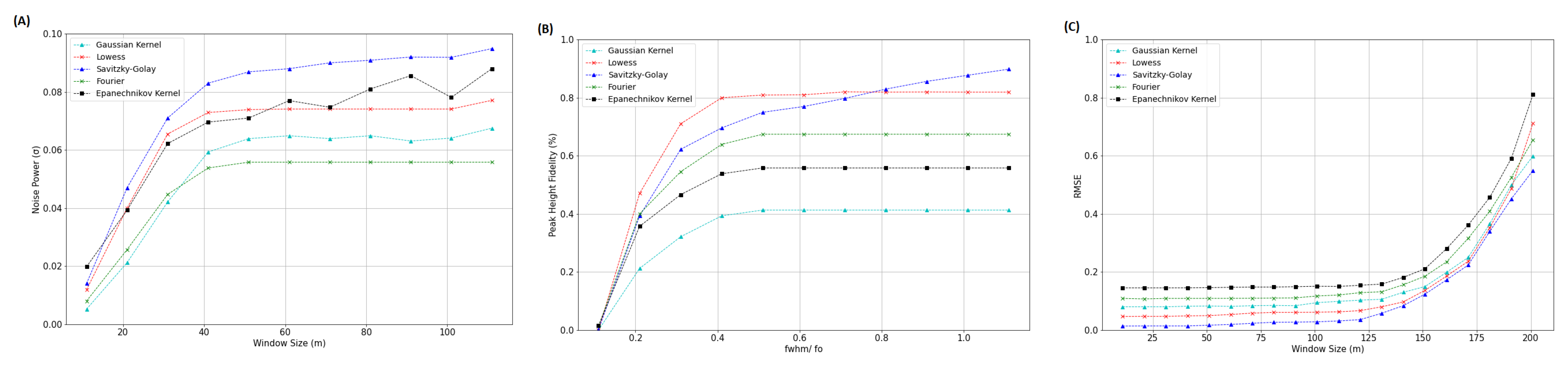
3.1. Effect of Window Length on Smoothing Performance
3.2. Evaluation of Filter Order on Smoothing Performance
3.3. Comparison of Adaptive Savitzky–Golay Filtering with Peer Methods
3.4. Application in CNVs Peak Analysis
3.4.1. Data Preparation
3.4.2. Simulation Studies
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
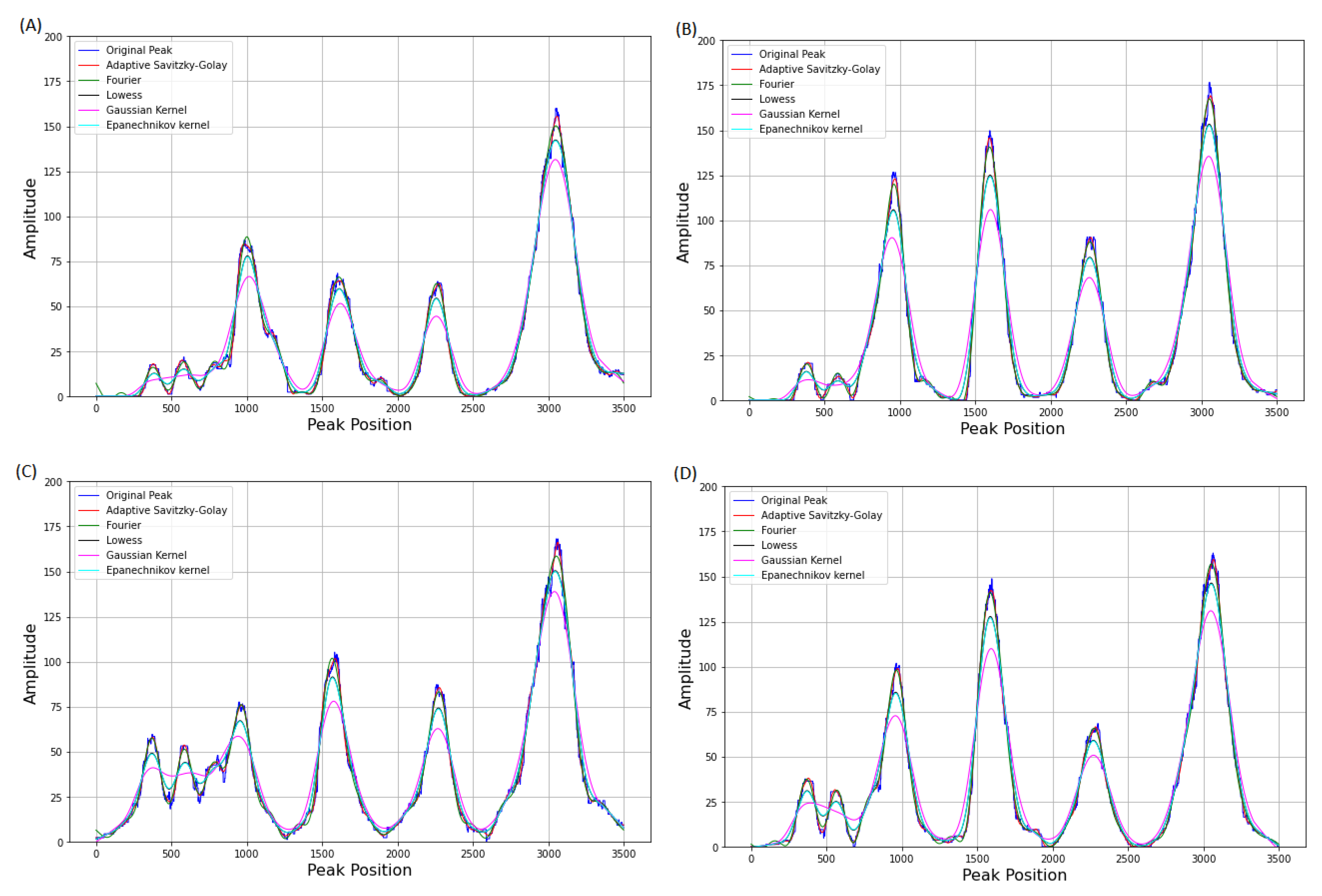
Appendix B
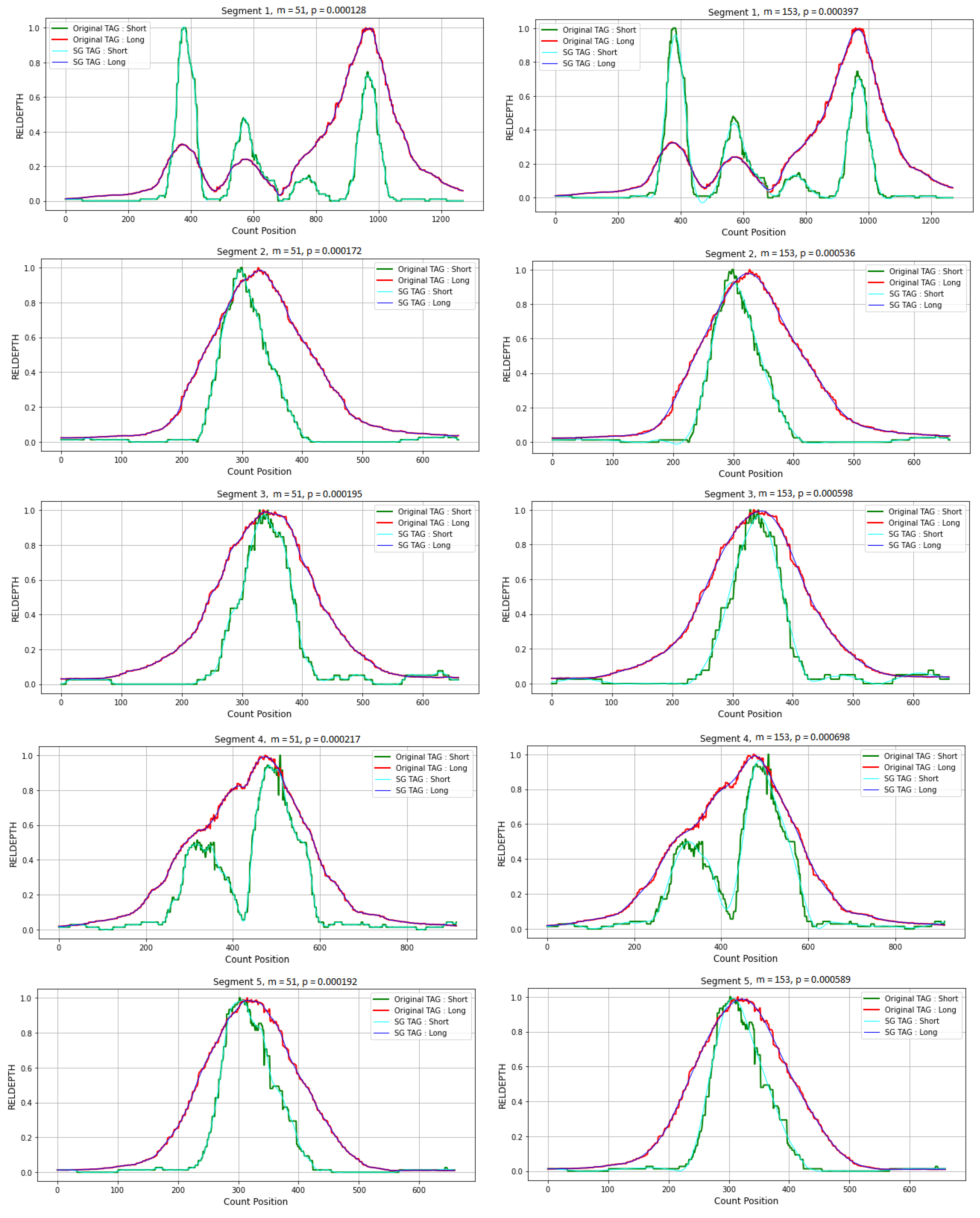
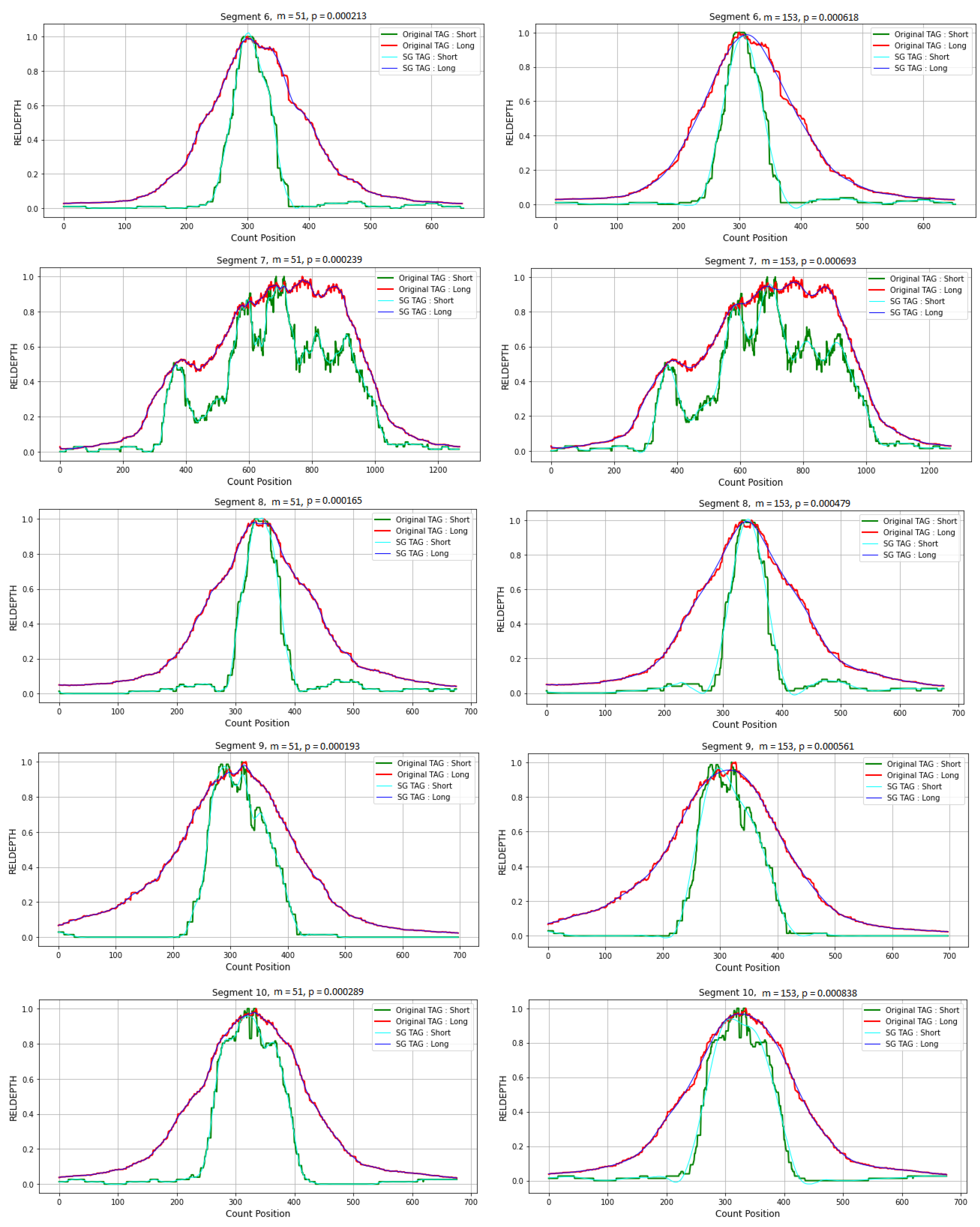
References
- Zhang, L.; Bai, W.; Yuan, N.; Du, Z. Comprehensively benchmarking applications for detecting copy number variation. PLoS Comput. Biol. 2019, 15, e1007069. [Google Scholar] [CrossRef]
- Sarihan, E.I.; Pérez-Palma, E.; Niestroj, L.M.; Loesch, D.; Inca-Martinez, M.; Horimoto, A.R.; Cornejo-Olivas, M.; Torres, L.; Mazzetti, P.; Cosentino, C.; et al. Genome-Wide Analysis of Copy Number Variation in Latin American Parkinson’s Disease Patients. Mov. Disord. 2021, 36, 434–441. [Google Scholar] [CrossRef] [PubMed]
- Grillova, L.; Cokelaer, T.; Mariet, J.F.; da Fonseca, J.P.; Picardeau, M. Core genome sequencing and genotyping of Leptospira interrogans in clinical samples by target capture sequencing. bioRxiv 2022. [Google Scholar] [CrossRef]
- Naslavsky, M.S.; Scliar, M.O.; Yamamoto, G.L.; Wang, J.Y.T.; Zverinova, S.; Karp, T.; Nunes, K.; Ceroni, J.R.M.; de Carvalho, D.L.; da Silva Simões, C.E.; et al. Whole-genome sequencing of 1171 elderly admixed individuals from Brazil. Nat. Commun. 2022, 13, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Qiao, H.; Gao, Y.; Liu, Q.; Wei, Y.; Li, J.; Wang, Z.; Qi, H. Oligo replication advantage driven by GC content and Gibbs free energy. Biotechnol. Lett. 2022, 44, 1189–1199. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.; Zhang, J.G.; Deng, H.W.; Wang, Y.P. Comparative studies of copy number variation detection methods for next-generation sequencing technologies. PLoS ONE 2013, 8, e59128. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Lee, B.; Kim, D.G.; Cho, Y.A.; Kim, J.S.; Suh, Y.L. Detection of TERT promoter mutations using targeted next-generation sequencing: Overcoming GC bias through trial and error. Cancer Res. Treat. Off. J. Korean Cancer Assoc. 2022, 54, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Povysil, G.; Tzika, A.; Vogt, J.; Haunschmid, V.; Messiaen, L.; Zschocke, J.; Klambauer, G.; Hochreiter, S.; Wimmer, K. panelcn. MOPS: Copy-number detection in targeted NGS panel data for clinical diagnostics. Hum. Mutat. 2017, 38, 889–897. [Google Scholar] [CrossRef]
- Wang, Y.; Li, X.Y.; Xu, W.J.; Wang, K.; Wu, B.; Xu, M.; Chen, Y.; Miao, L.J.; Wang, Z.W.; Li, Z.; et al. Comparative genome anatomy reveals evolutionary insights into a unique amphitriploid fish. Nat. Ecol. Evol. 2022, 6, 1354–1366. [Google Scholar] [CrossRef]
- Chen, L.; Qing, Y.; Li, R.; Li, C.; Li, H.; Feng, X.; Li, S.C. Somatic variant analysis suite: Copy number variation clonal visualization online platform for large-scale single-cell genomics. Briefings Bioinform. 2022, 23, bbab452. [Google Scholar] [CrossRef]
- Stalder, L.; Oggenfuss, U.; Mohd-Assaad, N.; Croll, D. The population genetics of adaptation through copy number variation in a fungal plant pathogen. Mol. Ecol. 2022, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Kuśmirek, W.; Nowak, R. CNVind: An open source cloud-based pipeline for rare CNVs detection in whole exome sequencing data based on the depth of coverage. BMC Bioinform. 2022, 23, 85. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Yu, J.; Chen, Y.; Zhong, W.; Ma, P. Smoothing splines approximation using Hilbert curve basis selection. J. Comput. Graph. Stat. 2022, 31, 802–812. [Google Scholar] [CrossRef] [PubMed]
- Virta, J.; Lietzen, N.; Nyberg, H. Robust signal dimension estimation via SURE. arXiv 2022, arXiv:2203.16233. [Google Scholar]
- Cięszczyk, S.; Skorupski, K.; Panas, P. Single-and Double-Comb Tilted Fibre Bragg Grating Refractive Index Demodulation Methods with Fourier Transform Pre-Processing. Sensors 2022, 22, 2344. [Google Scholar] [CrossRef]
- Piretzidis, D.; Sideris, M.G. Expressions for the calculation of isotropic Gaussian filter kernels in the spherical harmonic domain. Stud. Geophys. Geod. 2022, 66, 1–22. [Google Scholar] [CrossRef]
- Lia, N. Estimasi Model Regresi Nonparametrik Menggunakan Estimator Nadaraya-Watson Dengan Fungsi Kernel Epanechnikov. Ph.D. Thesis, Universitas Hasanuddin, Makassar, Indonesia, 2022. [Google Scholar]
- Dai, Y.; Wang, Y.; Leng, M.; Yang, X.; Zhou, Q. LOWESS smoothing and Random Forest based GRU model: A short-term photovoltaic power generation forecasting method. Energy 2022, 256, 124661. [Google Scholar] [CrossRef]
- Schmid, M.; Rath, D.; Diebold, U. Why and How Savitzky–Golay Filters Should Be Replaced. ACS Meas. Sci. Au 2022, 2, 185–196. [Google Scholar] [CrossRef]
- Pouyani, M.F.; Vali, M.; Ghasemi, M.A. Lung sound signal denoising using discrete wavelet transform and artificial neural network. Biomed. Signal Process. Control 2022, 72, 103329. [Google Scholar] [CrossRef]
- Kose, M.R.; Ahirwal, M.K.; Atulkar, M. A Review on Biomedical Signals with Fundamentals of Digital Signal Processing. In Artificial Intelligence Applications for Health Care; CRC Press: Boca Raton, FL, USA, 2022; pp. 23–48. [Google Scholar]
- Talevich, E.; Shain, A.H.; Botton, T.; Bastian, B.C. CNVkit: Genome-wide copy number detection and visualization from targeted DNA sequencing. PLoS Comput. Biol. 2016, 12, e1004873. [Google Scholar] [CrossRef] [PubMed]
- Boeva, V.; Popova, T.; Bleakley, K.; Chiche, P.; Cappo, J.; Schleiermacher, G.; Janoueix-Lerosey, I.; Delattre, O.; Barillot, E. Control-FREEC: A tool for assessing copy number and allelic content using next-generation sequencing data. Bioinformatics 2012, 28, 423–425. [Google Scholar] [CrossRef] [PubMed]
- Dharanipragada, P.; Vogeti, S.; Parekh, N. iCopyDAV: Integrated platform for copy number variations—Detection, annotation and visualization. PLoS ONE 2018, 13, e0195334. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, Y.; Liu, R.; Lai, X.; Liu, Y.; Wang, S.; Zhang, X.; Wang, J. PEcnv: Accurate and efficient detection of copy number variations of various lengths. Briefings Bioinform. 2022, 23, bbac375. [Google Scholar] [CrossRef]
- Yuan, X.; Yu, J.; Xi, J.; Yang, L.; Shang, J.; Li, Z.; Duan, J. CNV_IFTV: An isolation forest and total variation-based detection of CNVs from short-read sequencing data. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 18, 539–549. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, H.; Yuan, X.; Gao, K.; Duan, J. Comparative study of whole exome sequencing-based copy number variation detection tools. BMC Bioinform. 2020, 21, 97. [Google Scholar] [CrossRef]
- Pei, Z.; Lee, D.S.; Card, D.; Weber, A. Local polynomial order in regression discontinuity designs. J. Bus. Econ. Stat. 2022, 40, 1259–1267. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.; Tu, X.; Qu, F.; Zhao, H. Recursive least squares-algorithm-based normalized adaptive minimum symbol error rate equalizer. IEEE Commun. Lett. 2022, 27, 317–321. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Dombi, J.; Dineva, A. Adaptive Savitzky-Golay filtering and its applications. Int. J. Adv. Intell. Paradig. 2020, 16, 145–156. [Google Scholar] [CrossRef]
- Mathai, A.M.; Provost, S.B.; Haubold, H.J. The Multivariate Gaussian and Related Distributions. In Multivariate Statistical Analysis in the Real and Complex Domains; Springer: Berlin/Heidelberg, Germany, 2022; pp. 129–215. [Google Scholar]
- Sun, Y.; Xin, J. Lorentzian peak sharpening and sparse blind source separation for NMR spectroscopy. Signal Image Video Process. 2022, 16, 633–641. [Google Scholar] [CrossRef]
- Yuan, X.; Miller, D.J.; Zhang, J.; Herrington, D.; Wang, Y. An overview of population genetic data simulation. J. Comput. Biol. 2012, 19, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Wahab, M.F.; Gritti, F.; O’Haver, T.C. Discrete Fourier transform techniques for noise reduction and digital enhancement of analytical signals. TrAC Trends Anal. Chem. 2021, 143, 116354. [Google Scholar] [CrossRef]
- Kus, V.; Jaruskova, K. Divergence decision tree classification with Kolmogorov kernel smoothing in high energy physics. J. Phys. Conf. Ser. IOP Publ. 2021, 1730, 012060. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.C. Kernel smoothing, mean shift, and their learning theory with directional data. J. Mach. Learn. Res. 2021, 22. [Google Scholar]
- Niedźwiecki, M.J.; Ciołek, M.; Gańcza, A.; Kaczmarek, P. Application of regularized Savitzky–Golay filters to identification of time-varying systems. Automatica 2021, 133, 109865. [Google Scholar] [CrossRef]
- Yang, H.; Cheng, Y.; Li, G. A denoising method for ship radiated noise based on Spearman variational mode decomposition, spatial-dependence recurrence sample entropy, improved wavelet threshold denoising, and Savitzky-Golay filter. Alex. Eng. J. 2021, 60, 3379–3400. [Google Scholar] [CrossRef]


| Peak | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.050 | 11 | 0.00010 | 21 | 0.00006 | 31 | 0.00005 | 41 | 0.00003 | |
| 1.000 | 33 | 0.00551 | 63 | 0.00326 | 93 | 0.00216 | 123 | 0.00116 | |
| 0.050 | 11 | 0.00008 | 21 | 0.00007 | 31 | 0.00006 | 41 | 0.00004 | |
| 1.000 | 33 | 0.00672 | 63 | 0.00421 | 93 | 0.00321 | 123 | 0.00213 | |
| 0.050 | 11 | 0.00009 | 21 | 0.00008 | 31 | 0.00007 | 41 | 0.00001 | |
| 1.000 | 33 | 0.00841 | 63 | 0.00554 | 93 | 0.00414 | 123 | 0.00394 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochieng, P.J.; Maróti, Z.; Dombi, J.; Krész, M.; Békési, J.; Kalmár, T. Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data. Information 2023, 14, 128. https://doi.org/10.3390/info14020128
Ochieng PJ, Maróti Z, Dombi J, Krész M, Békési J, Kalmár T. Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data. Information. 2023; 14(2):128. https://doi.org/10.3390/info14020128
Chicago/Turabian StyleOchieng, Peter Juma, Zoltán Maróti, József Dombi, Miklós Krész, József Békési, and Tibor Kalmár. 2023. "Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data" Information 14, no. 2: 128. https://doi.org/10.3390/info14020128
APA StyleOchieng, P. J., Maróti, Z., Dombi, J., Krész, M., Békési, J., & Kalmár, T. (2023). Adaptive Savitzky–Golay Filters for Analysis of Copy Number Variation Peaks from Whole-Exome Sequencing Data. Information, 14(2), 128. https://doi.org/10.3390/info14020128






