Evaluating Methods for Efficient Community Detection in Social Networks

Abstract

Exploring a community is an important aspect of social network analysis because it can be seen as a crucial way to decompose specific graphs into smaller graphs based on interactions between users. The process of discovering common features between groups of users, entitled “community detection”, is a fundamental feature for social network analysis, wherein the vertices represent the users and the edges their relationships. Our study focuses on identifying such phenomena on the Twitter graph of posts and on determining communities, which contain users with similar features. This paper presents the evaluation of six established community-discovery algorithms, namely Breadth-First Search, CNM, Louvain, MaxToMin, Newman–Girvan and Propinquity Dynamics, in terms of four widely used graphs and a collection of data fetched from Twitter about man-made and physical data. Furthermore, the size of each community, expressed as a percentage of the total number of vertices, is identified for the six particular algorithms, and corresponding results are extracted. In terms of user-based evaluation, we indicated to some students the communities that were extracted by every algorithm, with a corresponding user and their tweets in the grouping and considered three different alternatives for the extracted communities: “dense community”, “sparse community” and “in-between”. Our findings suggest that the community-detection algorithms can assist in identifying dense group of users.

1. Introduction

Social networks are a newly introduced concept of interconnected media for everyday interaction. As an integral part of modern digital lives, they generate, through popular social platforms (i.e., Facebook, Twitter etc.), a wealth of data and subsequently knowledge, which may provide useful information, through topics concerning broadly social life, or about a particular topic (i.e., politics). Its mesh-like structure reflects the interconnected associations and relationships between the interacting actors in a network, as it interacts across the world wide web. These are based on standards and technologies, enabling processes of shaping and sharing information through a framework within which they are supported by virtual communities and networks. This framework allows users to communicate and share information, ideas, interests and aspects of their daily lives in a dynamic and responsive way. It is worth mentioning that, given the potential of social networks, information management can be specialised by domain of interest, such as in culture, through the existing dissemination capabilities. Social networks have provided new fields for analysis of unique data types, which depicts structures of the relations between the given entities, also known as a graph. In light of the above, the analytics of graphs appears to address a multitude of practical applications.

The network, as a system with a complex structure, consists of interconnected sets of objects operating under given objectives. To date, various types of networks have developed, usually reflecting social trends, namely social networks, and the widespread adoption of web applications determines their absorptive capacity when they are created and their further adoption by society [1]. In this context, the development of methods to identify social trends from social media is of particular research interest. The present article focuses on network entities and the relationships between them resulting from user interaction. For instance, community detection can be used to support various other tasks by aligning social networks and big data in everyday life. Moreover, the importance of leveraging graphs, i.e., analyzing unique data structure types that represent the relationships between entities [2], has been highlighted while introducing graph analytics as a tool for this purpose [3].

Through their daily use of social networks, users produce and share digital content and can also share opinions and keep up to date on issues that are relevant to them. With the increasing diversity of social networks over the past decade, and thus their users, scientists are challenged to produce high quality services for users. Through user clustering, new patterns of interaction are emerging to identify commonalities between people in real-world interactions. Moreover, social networks typically comprise individuals who communicate with one another and belong to linked communities, and their analysis is a fundamental task for a task called “social network analysis” [4]. Because those networks have a complex and dynamic structure, these communities cannot be easily identified, leading to the conclusion that this is an open and often difficult issue that can be characterized as an optimization constraint. Thus, identifying node groups with more interfaces is an important research goal that can equally work in identifying fewer interconnections between them. Consequently, as a non-deterministic polynomial-time (NP-Hard) topic, community detection has in recent years allowed evolutionary algorithms to develop a new field of research [5,6].

Nowadays, a wider range of social media has been developed, including Twitter, an online social media service that allows users to manage profiles, which are made up of larger interacting communities in the sense of achieving individual or group goals. In particular, the popularity of online social networking among millions of people allows service beneficiaries to stay connected to their immediate social circle. Furthermore, Twitter offers the possibility of exchanging short messages (“tweets”), while contributing to the enrichment of data mining methods thanks to its available API, which allows data to be collected with minimal human input [7].

It is undoubted that a wealth of data is generated daily by user groups that require new analysis methods to efficiently process with high frequency the diversity, complexity, and characteristics that distinguish big data. Considering the above, social networks are regarded as an integral part of modern life, as they typically express by graphs consisting of tens of thousands of vertices and edges. More specifically, and in the context of the interactive function of the media, we consider vertices as the operators and edges as the interrelation between them. The process of discovering common features between groups of users, called “community detection”, is a fundamental feature for social networks analysis [8].

A network, i.e., every intricately interacting and interlinked group, serves a specific purpose, and is based on the notion that the allocation of a clustering factor obeys the rule of strength within social networking, hence decreasing as the degree of nodes grows. In this context, grouping procedures are also distinguished, the most basic of which is the clustering coefficient, as it constitutes a key factor in calculating the propensity of the nodes to be clustered with each other. This feature suggests that interconnected communities form social networks, presupposing their discovery for the purpose of further understanding the network architecture. In this, a community is thus considered to be a set of nodes having multiple ties to each other, while fewer external connections further their kind.

Cultural heritage management through social media engagement [9,10] can contribute to the development of numerical graph segmentation and automatic topic detection algorithms. In addition, they allow researchers to shed light on members’ personal preferences on specific topics of interest related to culture in general. Based on the above, we examine the evolution of graphs over time, by detecting the source nodes that initiated the evolution on a purely site-specific (topological) basis. In addition, we examine whether it is achievable to categorize nodes based on their age with no metrics. Social network analysis aims to improve the comprehension of the concepts of connectivity, centrality, and relevance of users in a social network. Other tasks that can be successfully implemented are predictive analysis for link formation, evaluation of betweenness centrality, visual representation, etc.

Online social networking is a new paradigm within the framework of big data analysis, where large volumes of data about heterogeneous social events and interactions are stored, with a very high degree of variability. The present research work was motivated by the important problems that arise, such as diffusion and influence maximization, community detection, and user recommendation, which require the intervention of skilled users with multidisciplinary backgrounds, making the current research activity quite challenging. Furthermore, social network constructs are distinct among other communication system configurations (natural, transit, and telecommunication) because of the occurrence of positive grade correlations called assortativity [11].

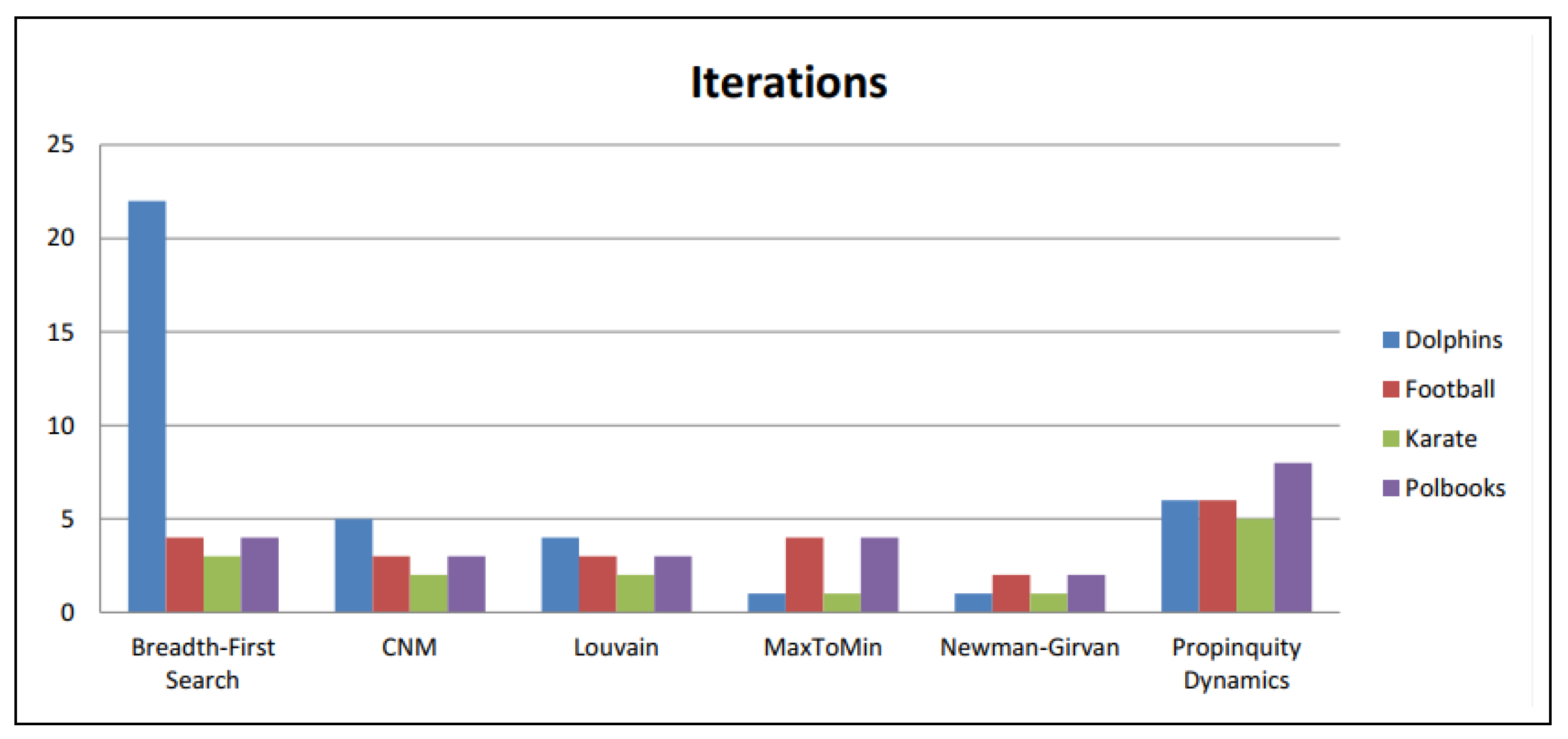
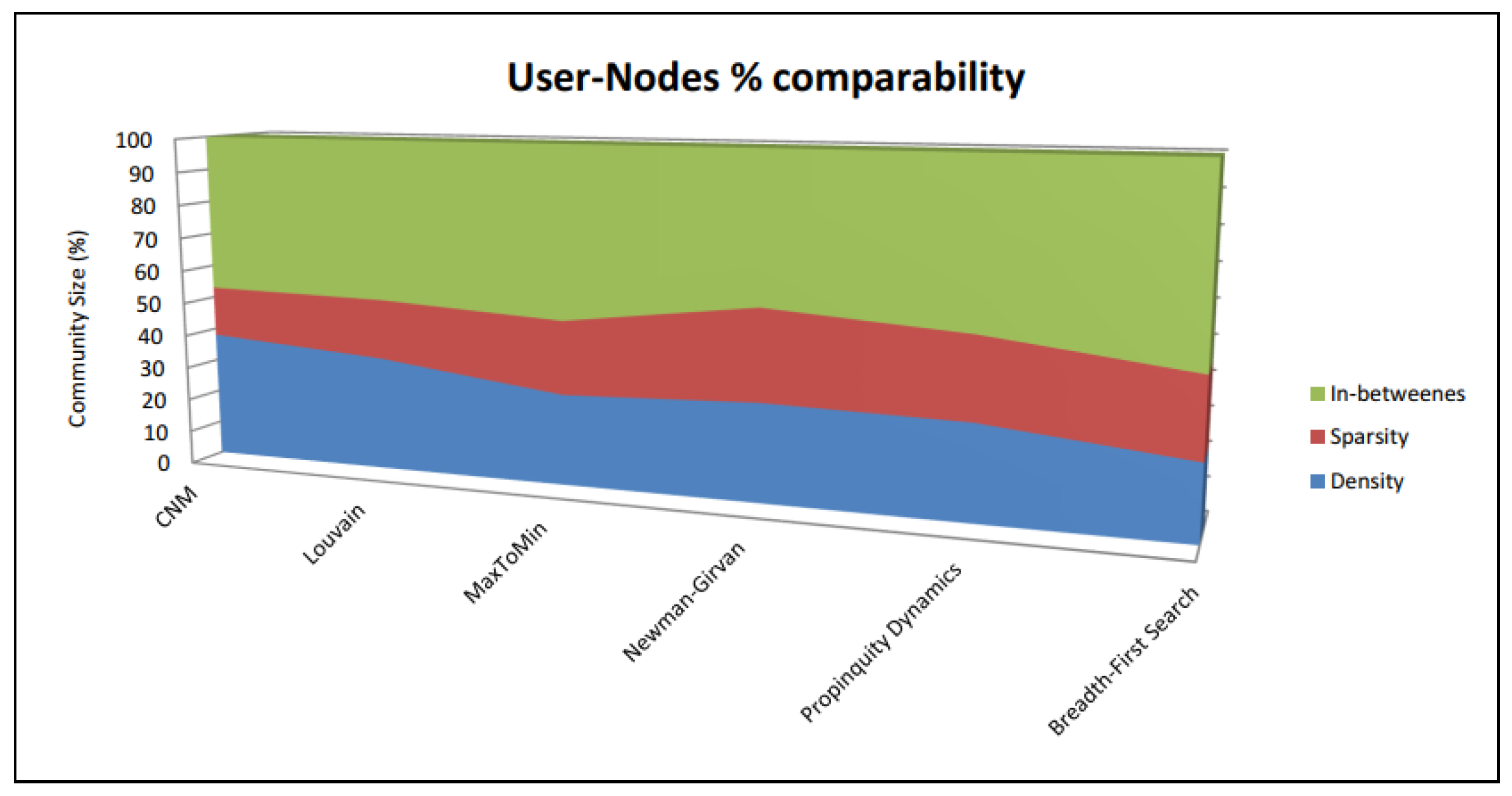
Herein, we aim to evaluate different community discovery algorithms for effective community discovery in social networks. Initially, six popular community detection paradigms, i.e., Breadth-First Search, CNM, Louvain, MaxToMin, Newman–Girvan and Propinquity Dynamics, are evaluated on four extensively exploited datasets based on normalized mutual information (NMI), number of iterations as well as the modularity metric. Moreover, we determined how large individual community sizes, expressed as a proportion of the overall pool of vertices, are for the six specific algorithms. As a next step, we used a set of data extracted from Twitter on cultural and natural heritage information in the Greek domain, which is related to several heritage sites, certain tourist sites and activities. Users evaluated the downloaded the Twitter dataset by selecting whether every extracted community had users with comparable characteristics. Three different options were considered for the exported communities, i.e., “dense community”, “sparse community” and “in-between” [12]. We proved that the application of each algorithm is directly proportional to its implementation domain as well as by the fundamental principles that characterize the network under study.

The remainder of the paper is structured as follows: Section 2 presents the related work regarding the community discovery algorithms, and Section 3 analyzes network centralities, such as centrality measures and modularity metric, and network indices. Section 4 presents the algorithms implemented in our paper along with their major characteristics. Furthermore, in Section 5, the implementation details, the four graphs and the derived Twitter dataset are highlighted, whereas Section 6 presents the evaluation experiments conducted and the results gathered. Ultimately, Section 7 presents conclusions and draws directions for future work.

2. Related Work

User relevance assessment appeared much earlier than the advent of social networks, as social ties were discovered before the web and online communities. Betweenness-type centrality is described in work specialised in centrality measures [13,14]. Instead, today’s multitude of different types of networks pose many computational issues. As previously mentioned, social network analytics is closely associated with graph clustering, whereas predictive text extraction or text analytics incorporates natural language processing (NLP) for thematic analysis. This section presents our brief overview of the work on community detection and topic-modeling techniques, focusing on social networks, especially Twitter. Recent studies have demonstrated that analytic sequences, through their integration into malleable information, aid researchers in harnessing and integrating user behavioral concepts into synthetic graphs with the ultimate goal of automatic topic detection.

Authors in [15] introduce an actual task of developing methods for determining information support of the web community-members’ personal data verification system. The level of information support of web community member personal data verification system allows evaluating the effectiveness of verification system in web-community management. Also, for identifying possible threats reflected by the user’s behavior towards a specific event, an approach for estimating aggression shown by different users in different Facebook groups or community pages, is presented in [16]. The experimental evaluation was conducted on a set of real data to prove that the method is efficient in extracting the intensity of the aggression shown by the users.

In their work, the authors in [16] addressed community discovery for topic modeling through a data store by employing a data analytics engine (i.e., Apache Spark) based on a database structure (a NoSQL-type such as MongoDB). The solution is implemented by using PSCAN [12,17], in tandem with LDA [18]. The latter topic modelling is of individuals in exported groupings. The latter operates on topic modelling of users in the extracted communities, which has an important role in their platform. For their research needs, they have employed a Twitter dataset, accounting solely for users with followers to guarantee that the respective graph for community detection is associated.

Subsequently, the social network analysis is inextricably linked to graph clustering algorithms and web search algorithms [8,19,20,21]. In particular, high density of network nodes has the characteristics of a community, which refers to several clusters of separate nodes in a graph with shared attributes in the operation of a system. The domain is associated with HITS [22], and web link analytics with the milestone of analyzing important web pages exploiting PageRank [23] reporting measure, and countless other variations suggested in [24]. On the other hand, HITS has two metrics, for use with a website as the information authority and with a node. Also, the aforementioned algorithm, i.e., PageRank, exploits one metric that relies on the level of importance of inbound links.

As previously mentioned, we refer to a community as a set of nodes in a communication system with strong ties between them [25], where various techniques have been introduced to detect the complex structures of the corresponding communities with application to social networks [8,20,21]. Some of the existing approaches for data clustering (segmental, spectral and hierarchical clustering) are commonly adapted for clustering of graphs [1,20,26,27]. Authors in [28] chose to use feature selection methods as a common approach to identify communities on Twitter. The PSCAN algorithm is usually implemented in the context of a Hadoop cloud, as a parallel scheme for the MapReduce model in extended applications (e.g., Twitter) [17]. Also, the superimposed topics can be identified; the identification of the desired topics is implemented via a generative statistical model (Latent Dirichlet allocation (LDA)) [29].

A plethora of automata have been reported in the context of community detection in the bibliography [1,20,26,30]. In particular, the HITS-type algorithm can be exploited in community computation when employed for the examination of non-major latent vectors. In the literature, we have also encountered the graph-partitioning problem related to communities, based on algorithms dealing primarily with spectral distribution approaches for partitioning objects via matrix eigenvectors [31,32]. At this point, it is worth noting that spectral partitioning was proposed in [27,33]. However, the study in [34] highlights the use of hierarchical clustering for graph partitioning.

Furthermore, Hong et al. proposed the use of various performance metrics for topic modelling under an empirical study [7]. More to this point, authors in [35] addressed the issue of topic modeling through LDA, which is a widely used probabilistic method. In particular, this is a standard tool and in this context, several extensions are proposed to address its limitations, especially in the field of social networks. Addressing the inadequacy of LDA in the sparseness of short documents in the tweet, several types of aggregation techniques were proposed in [36]. Consequently, it was demonstrated that clustering of similar tweets in individual documents significantly increases thematic coherence. Alvarez et al. [37] introduced the concept of aggregation techniques in thematic modeling by aggregating tweets from conversations.

Moreover, in the context of community detection, authors in [38] proposed the concept of modularity, which, alongside the divisive method, represents an initiative for further research. In addition, some works [39,40,41] lie in the context of exploiting a partitioning algorithm that can maximize modularity. In particular, the algorithm applies it as a quality indicator of the segmentation based on the modularity criterion, and by extension it is distinguished as an essential tool for locating community structures, as it quantifies the perceived community quality. It is noteworthy that dense internal connections and the small number of inter-connections are identified as the main criteria for the separation of communities. Moreover, existing research [42,43,44,45] has considered different algorithms under the notion of modularity; for example, intricate network structures determine the degree of performance of these algorithms, in contrast to other cases where network state is a necessary condition.

It is worth noting that through the works [44,46,47], it becomes clear that the significance and notion of leverage beyond the user perspective to the communication system perspective, as well as personality is the main criterion for the identification of influential communication systems. This results in the creation of such communities within the graphs of Twitter, using a grouping detection strategy based on modularity, which takes into consideration the individual personality traits of users. In addition, graph vertices derived from the above personality-based algorithms are discarded by introducing pre-processing sequences. Additionally, the user behaviour is highlighted on an emotional dimension, as it is reinforced by the introduction of a novel methodology, which effectively helps to identify communities [48,49,50].

Similarly, the existence of a multitude of methods for evaluating the quality of clustering, i.e., the coherence of the community [51], is apparent. Nevertheless, the majority of current cohesion metrics remain prohibitively expensive (i.e., peak distance among vertices) or susceptible to value extremes, such as metrics based on the graph diameter [52,53]. Finally, the works of [54,55] describe some of the realizations derived from standard community discovery, and researchers focus mainly on the graph partitioning resulting from this type of algorithm and how it maps to Twitter operational field rather than to other structural criteria more broadly. The aforementioned problematic is related to dedicated analytical methods such as CNM, Louvain, Walktrap, and Newman–Girvan’s Neo4j, and Edge Betweeness, in order to effectively evaluate their use in the field.

In addition, there are a number of studies which aim at improving suggestion-mining results; one of them considered the word-embedding approach and the XGBoost classifier in order to capture context and similarity with other words [56]. Authors contribute by improving the classifier performance through the XGBoost classifier, as compared with Naive Bayes and Random Forest.

3. Preliminaries

3.1. Analysis of Network Centrality

The network power based on the relationship between each node can be measured by network centrality, which shows independence, autonomy, dominance, and influence in a network. The network centrality is measured by several different metrics, i.e., degree centrality, closeness centrality, and betweenness centrality, among others [12,57].

Degree centrality denotes the degree to which a node is connected, and betweenness centrality denotes the extent to to which a node can easily reach out to other nodes [58]. There is therefore a need for efficient annotation of the measurements obtained from each node, an effect that follows from degree centrality [59]. It has been observed that a network is most affected among nodes, by positioning them in a state of interconnection with each other. On the other hand, betweenness centrality points as a mediating factor of the network across nodes. In particular, a node is considered to be in an optimal situation only if it is on the most direct route among a couple of nodes in the network. Similarly, the degree centrality, i.e., a node having the greatest betweenness centrality, has the real power to influence other nodes.

3.1.1. Centrality Measures

Centrality measures are one of the commonly exploited indicators in relation to network data analysis. They indicate the need for certain variables to be to parameterised, such as status, visibility, structural strength or prestige, through the dominance of the unit as a determinant in centrality analysis [60]. The measures on which the analysis is based can be categorised as listed below:

• The number of directly interlinked nodes is expressed by degree centrality of a node v formed as

  $$C_{\mathrm{D}}\left(v\right)=deg\left(v\right).$$

  (1)
• The closeness centrality describes the adjacency of a vertex v, which then highlights the proximity of a node in relation the existing set of nodes in the group. It is defined as

  $$C_C\left(u\right)=\sum _{v\in V}d(u,v).$$

  (2)
  This is referred to as the geodetic distance, in the case of $d(u,v)$, which describes the total vertices along the faster route that links the vertices u and v.
• To calculate the shortcut paths between random pairs of nodes in a graph containing the target node v, we need to know whether a vector lies between them. This is implemented by betweenness centrality and is defined as

  $$C_{\mathrm{B}}\left(v\right)=\sum _{y\ne z\in N}\frac{p_{st}\left(v\right)}{p_{st}}$$

  (3)

  where $p_{st}\left(v\right)$ stands for the total number of shortest paths containing v from s to t, and $p_{st}$ represents the sum of the number of different shortcuts across s and t within the underlying communication system.

3.1.2. Modularity

This captures the network structure, exploiting the dynamics of the partition of a communication system into communities [61], which is captured as follows:

$$Q\left(V\right)=\frac{1}{2M}\sum _{v_i,v_j\in V}\left(A_{i,j}-\frac{deg\left(v_i\right)deg\left(v_j\right)}{2M}\right){\delta }_{c_i,c_j}.$$

(4)

The matrix of adjacency of the given graph can be observed above, which displays values equal to 0 and 1; $A_{ij}=1$ in the case where two nodes are linked by an edge with $e_{ij}inE$. Note that the matrix is denoted by $M=\frac{1}{2}su{m}_{i}deg\left(v_i\right)$ and $\mathit{A}=\left[A_{ij}\right]\in {\mathbb{N}}^N\times N$. Furthermore, the set of expected edges between nodes $v_i$ and $v_j$ is captured via $\frac{deg\left(v_i\right)deg\left(v_j\right)}{2M}$, especially in the case where the aforementioned edges exhibit randomness in the distribution. The quality optimization of community-detection methods is underlined by high modularity values. This can be illustrated by the case where $c_i=c_j$ and ${\delta }_{c_i,c_j}=1$, or if $c_i\ne c_j$ and ${\delta }_{c_i,c_j}=0$, where $c_i$ indicates the fact $v_i$ is a part of the community c.

Notably, this type of method is limited by the inability to identify small-scale communities. Consequently, the identification of communities in networks, via the Louvain algorithm, cannot optimize articulation at a lower scale.

3.2. Network Indices

In principle, the Laplace matrix sets out the fundamental elements for understanding the proposed framework for defining network indices

$$L=D-A$$

(5)

where L is the Laplace matrix, D refers to the transverse rank matrix, and A refers to the contiguity matrix. Note that $a_{ij}=1$ if there is a link $i-j$ and 0 in the opposite case.

In addition, the eigenvector displays standardization for each component of the component being examined through

$$v_i=|\frac{v_i}{max\left(v_i\right)}|.$$

(6)

The number of nodes corresponds to N and, consequently, i ranges from 1 to N.

Furthermore, at a particular eigenvalue, the temporal context of the associated eigenvector is the mean relative weight of all nodes in the vector, which is weighted by the corresponding components of the eigenvector. This occurs because network eigenvectors do not grow exponentially. Instead, the corresponding eigenvalue increases accordingly.

In a given graph, the contained eigenvalues are decomposed by the following computation:

$$A\left(t_i\right)=V\left(t_i\right)\Lambda \left(t_i\right)V{\left(t_i\right)}^{\prime }.$$

(7)

In the above formula, the eigenvector matrix is expressed via V, while $V^{\prime }$ shows its transformation respectively. The above are determined in terms of time by $t_i$.

Also, eigenvalues are important in the reaction between eigenvectors, because, for the interval between $t_i$ and $t_{i+1}$, the latter remain constant during the change in the trace. This is where the subgraph centrality [38] comes in, it is a variable that each node i can contribute accordingly to the function

$$S{C}_i=\sum _j{(v_j^i)}^2{e}^{{\lambda }_j}.$$

(8)

It is worth noting the importance of the i-th dimension of the eigenvector $v_j$, which is expressed by means of ${\lambda }_j={\lambda }_j(t_i+1)$ and $v_j^i$.

It is also emphasized that the parameter $S{C}_i$ is tightly associated with the metric of communicability index [62], which may be evaluated as follows:

$$ECI=e^A.$$

(9)

A probabilistic interpretation is that $S{C}_i$ is commensurate with the likelihood of a random walker crossing near node i.

In the above formula, the equality $i=j$ determines the diagonal entries of the ECI table that refer to the data points $S{C}_i$. Also, where $i\ne j$, the communicability of the i and j nodes is indicated. Moreover, $EC{I}_i$ is proportionally related to node i, i.e., the age of the latter is influenced by the size of the former. This is probably explained in the fact that $S{C}_i$ is directly analogous to the likelihood of a casual walker approaching node i.

Subsequently, to assess the efficiency of the algorithm by using a commonly available global index averaged over the number of nodes [38,63], a rough calculation has been proposed:

$$EIN=\frac{1}{N}\sum _i{e}^{{\lambda }_i}.$$

(10)

The eigenvalues of each node are represented by $\lambda$.

In this respect, it is worth noting the possibility that the eigenvalues are the algebraic equivalent of the attributes given by the geodesic graph. Considering that EIN is a benchmark for the overall connectivity of the graph that impacts the communicability, the eigenvalues should indicate the efficiency of the algorithm. Therefore, it is evident that a high value of EIN is potentially correlated with sound performance of this algorithm.

3.3. Community Facility

In general, an undirected graph $G=(V,E)$ contains vertices ($V=\left\{v_i\right|i\in [1,2,\dots ,N]\}$) and edges ($E=\left\{e_{ij}\right|i,j\in [1,2,\dots ,N]\}$). The v ranges according to $deg\left(v\right)$ in a graph G, where in fact it can be considered as a network.

4. Algorithms for Community Detection

This section takes a look at five common community-detection techniques. Note that these algorithms are based on higher-order information that is discovered in the form of graph constructs. The latter is denoted as the count of vertices or edges that the graph computational function needs to address or cross, respectively. Standard applications involve the dimension or the actual amount of traces linking two specified vertices. This is justified, still partially, to the inherent need for link graphs for balancing local and global information. Graph-processing systems will therefore need to have comparable qualities if relevant information is to be derived.

A highest-class manifestation of the graph-community detection task is given by the fact that the smallest grouping is a triangular formation. From a vertex point of view, it can be considered as a tertiary level of quantity ordering. Furthermore, if a triangular formation is surrounded, that is also a tertiary quantity. This follows from the point that a simple association between subjects (an edge on a social graph) does not qualify as a community. Therefore, within a group, there must a minimum of one shared knowledge that connects the persons belonging to that team. Therefore, the above is mirrored in the conception that succeeding community-detection methodology is based directly or indirectly on higher-order measures. Graph-aggregation or spectral graph-separation algorithms, for example, use high-order constructs like principal eigenvectors or graph adjacency matrices [64].

4.1. Clauset–Newman–Moore Analysis

Clauset Newman Moore’s proposed algorithm (CNM) suggests a methodology for partitioning vertices, each of which is distinguished as a separate community. Sequentially, the algorithm allows analysis from “local” to “international” level up to the point of being constrained by the criterion a. That is, at a single vertex $v_i$, $a_i$ neighboring communities can be incrementally fused into larger communities via

$$a_i=\frac{degree\left(v_i\right)}{2\left|E\right|}.$$

(11)

Next, in the case of two adjacent peaks, $\Delta a_{i,j}$ is as follows:

$$\Delta a_{i,j}=\frac{1}{2\left|E\right|}-\frac{degree\left(v_i\right)degree\left(v_j\right)}{{4\left|E\right|}^2}.$$

(12)

The above shows a null value for non-adjacent vertices. That is, where $\Delta a_{i,j}$ we see the dimensional change that arises from introducing $(i,j)$ into the community. The introduction of a sparse matrix allows tracking of $\Delta a_{i,j}$, alongside the import of the communities in a binary tree, where each leaf is implicit in each vertex respectively. It is a given that in such a relationship it is necessary to determine the parent of the tree, which is the arising community in each individual case where two communities merge with each other. In addition, the two matching columns of the sparse matrix $\Delta a_{i,j}$ are fused and their data are updated.

4.2. Louvain Algorithm

The Louvain algorithm or multilevel [39] algorithm is a hypervisor-based grouping analysis that works on weighted graphs. At first, every vertex is a community. Hereafter, according to the change in local edge density, the community gradually merges with its neighbors. The goal is to create neighborhoods with high fringe density, whereas in the inter-community the concentration is still limited.

Louvain’s type analysis represents the perceptual notion of edge density in terms of modularity and the scale m from $-1$ to $+1$ is set as follows:

$$m=\left\{\begin{array}{cc}\frac{1}{2\left|E\right|}\sum _{(i,j)}(w_{i,j}-\frac{degree\left(v_i\right)degree\left(v_j\right)}{2\left|E\right|}),\hfill & v_i\in c_i\wedge v_j\in c_j\hfill \\ 0,\hfill & v_i,v_j\in c_i\hfill \end{array}\right..$$

(13)

In (13), $c_i$ and $c_j$ represent the community to which $v_i$ and $v_j$ belong, and $w_{i,j}$ is the weight of $(i,j)$. Although Louvain’s type of analysis applies to non-weighted graphs, the outcome is invariably a weighted graph, in which the weights are dependent on the local densities of the edges. Non-weighted graphs are considered graphs with original weight of 1.

The maximisation of modularity is implemented through a set of two distinct stages. During the initial stage, every $v_i$ is joined with each one of its adjacents in a grouping C, and the change in the modularity $\Delta m$ is computed as the change of the new type minus the old. Eventually, $v_i$ is delegated to $c_j$, resulting in a larger $\Delta m$. Note that in the second stage, we build a new graph which merges the vertices that belong to the common grouping to one vertex. Moreover, all vertices linking both groupings together create an vertex of which the weight is the total of the many.

4.3. Max-Min Analysis

First, the MaxToMin method is proposed; however, the Propinquity Dynamics (PD) and Breadth-First Search (BFS) algorithms could potentially be applied in this analysis. The latter aims to identify communities, while the former acts by constructing a graph topology with multiple communities. Note that BFS is also limited to finding nodes that do not exist exclusively in a community.

Therefore, the size of the neighbourhood is considered as the edge with the highest weight, as the “powerful” edge in the graph is associated with the random node where the analysis starts. Then, the MaxToMin algorithm tries to connect a community to the nodes that hold the strongest neighboring edges.

This technique allows the algorithm to move along the length of the graph. In effect, it goes from the edges of the strongest to the least strong, but it cannot do the reverse. The repetition of the process succeeds in discovering the community and the algorithm stops only in the case where no other weak edges related to the graph access are computed. Also, if a node is reachable by the algorithm execution of L-independent, it is assigned to its respective community L, which in turn is considered as overlapping with these communities.

4.4. NG Algorithm

The Newman–Girvan (NG) or edge betweeness algorithm [38] relies on betweenness centrality, an edge centrality measure that computes the fraction of the number of shortest paths connecting two vertices $v_i$ and $v_j$, given an edge $e_k$ is a part, denoted by ${\zeta }_{i,j}^k$, and the total number of shortest paths connecting $v_i$ and $v_j$, denoted by ${\zeta }_{i,j}$. Then the betweenness centrality of $e_k$, denoted by $B_k$, is calculated by averaging each vertex pair:

$$B_k=\left\{\begin{array}{cc}\frac{1}{\left(\genfrac{}{}{0pt}{}{\left|V\right|}{2}\right)}\sum _{(v_i,v_j)\in V\times V}\frac{{\zeta }_{i,j}^k}{{\zeta }_{i,j}},\hfill & v_i\ne v_j\hfill \\ 1,\hfill & v_i=v_j\hfill \end{array}\right..$$

(14)

In [38], the process of computing $B_k$ for each $e_k$ thereby similar to breadth-first search is described. The logic lies in the fact that vertices that belong to linking groupings should be based on the vertices that connect the groupings to exchange data, without the opposite to be always a valid scenario. Moreover, based on the topology of the graph, certain grouping-linked extremes might not score high on betweenness centrality, because other extremes might be preferred. Hence, the $e^{*}$ edge of the highest rate of betweenness centrality should be subtracted, and subsequently the procedure must be reapplied to the newly created graph. Ultimately, the edges joining the communities will be traced. In the case that the graph is disconnected, the repetition of the aforementioned the process for each connected component is required.

4.5. PD Algorithm

The name of the PD algorithm is derived from the sociological term “propinquity”, which refers to the proximity between individuals, either physiological or emotional. Its application in community-detection methodology is by determining the likelihood between two vertices to be part of a coherent community. Note that the PD algorithm accepts similarity information from the graph topology via a spontaneous procedure [65], without presupposing any information about the layout of a community.

The performance of the algorithm is based on incremental proximity computation, as community constructs are formed through reciprocal reinforcement of the concepts of proximity and topology. It is worth noting that the nodes of multiple communities can be later identified (e.g., in case of overlap).

The PD algorithm can effectively discern communities from euphonious graph data and its computational sophistication is equivalent to $O\left(k\right|V\left|\right)$ in dilute plots, with V and k being the total node number in the graph and the number of iterations, respectively. Yet this algorithm has another benefit in that it puts the focus on scalability while maintaining the quality of the community.

Coherent Neighborhood Propinquity: This similarity only considers local 2-hop neighbourhoods, supposing that the dimension in the consistent graph is not greater than 2, also presuming that the ensuing community is consistent. Given this, the amount of mutual neighbors of a junction pair is an essential criterion for determining its adjacencies. Thus, when evaluating a neighbourhood, the overall network connectedness of the overall vicinity should be taken into account.

Propinquity Calculation: Similarity calculation can be achieved by finding the intersection of their neighbours for each pair of nodes and thereafter calculates the edges connecting its mutual adjacents. The sophistication of this computation is about $O\left(\right(\left|V\right|+\left|E\right|\left)\right|E\left|\right)$, with E the number of the extremes.

5. Implementation

In this study, we analyzed degree and betweenness centrality measures of a co-occurrence network to examine how a node is related to the overall network and to investigate the node’s position. Additionally, we also analyzed the network position, and we used degree and betweenness centrality measures. The hub position means highly connected with others and is important in connecting others. The core position is highly connected with others but relatively less important in interconnecting.

The Estrada communicability and sub-graph centrality indices consider not only the direct impacts of the nearest possible nodes, as well as the long-term impacts propagated through a node’s participation in all sub-graphs traversing across the entire collection of routes [66,67].

5.1. Graph Development

To begin with, we selected the four most popular graphs to exploit for our pilot evaluation, i.e., Zachary Karate Club, Dolphin Network, Polbooks and American College Football [68,69]. A summary of those networks is shown in

Table 1. Summary of Graphs.

Title	Description	Number of Vertices	Number of Edges
Dolphins	Dolphin Social Network	62	159
Football	American College Football	115	613
Karate	Zachary’s Karate Club	34	78
Polbooks	Books about US Politics	105	441

in increasing sequence by the count of their vertices.

Initially, the Dolphin Network is an unguided network of frequent social interactions among 62 dolphins in a colony living off Doubtful Sound (NZ). The dataset consisting of American College Football is viewed as a set of American-type football matches among divisional colleges across the 2000 standard fall season. It consists of 115 teams divided into 12 categories, where each category comprises 8 to 12 teams. In addition, the Zachary Karate Club considers a social friendship based network among 34 members of a karate club at a 1970s North American university. A dispute between the president and instructor led to a split of the club into two associations of roughly the same caliber. Lastly, the Polbooks dataset is composed of a 2005 guided network of hyperlinks across political blogs in the US. Moreover, this grid is segmented by the political focus of the blogs, i.e., either conservative or liberal.

5.2. Twitter Dataset

Moreover, we have downloaded a corresponding dataset with the use of Twitter4j (http://twitter4j.org/en/index.html, accessed on 15 March 2022), a Java based platform utilized for interacting with the Twitter API. The Twitter subgraph was collected in a time interval of two months, that is 01/07/2021–30/09/2021. A topic-based sampling approach was used where tweets are collected via a keyword search query. More specifically, we have downloaded keywords which have relevance with cultural and natural heritage in the domain of Greece; these keywords are related to different heritages, specific tourist destinations and activities.

The properties of the dataset are presented in

Table 2. Subgraph Properties.

Property	Value	Property	Value
Vertices	8205	Retweets	98,565
Edges	33,125	Avg. Following	$4.55$
Hashtags	15	Avg. Followers	$6.33$
Tweets	21,315	Avg. Tweets	$80.25$

. The first column has fundamental graph structure properties such as the number of vertices and edges, whereas the second column has Twitter specific properties such as the average tweet length and the average number of followers. Note that the vertices are accounts and the directed edges represent “following” relationships.

Numerous pre-processing techniques were implemented during the mining strategy [70,71]. These steps include the utilization of regular expressions to remove, for example, unnecessary URLs or the representation of emoticons with their equivalent form, e.g., “lol” as “laugh out loud”. The removal of punctuation marks and stop-words is another important step. Also, the lemmatization and tokenization processes were employed for removing complex suffixes and retrieving the lexical form of each individual term.

6. Assessment

This section is dedicated to evaluating the results of the five community detection methods (as well as the well-known Breadth-First Search) on the same four graphs and on the Twitter dataset.

6.1. Graph Analytics

In the following

Table 3. Normalized Mutual Information.

Graph	Breadth-First Search	CNM	Louvain	MaxToMin	Newman-Girvan	Propinquity Dynamics
Dolphins	0.468	0.675	0.632	0.598	0.910	0.942
Football	0.909	0.903	0.911	0.926	0.915	0.926
Karate	0.309	0.624	0.699	0.924	0.885	0.924
Polbooks	0.494	0.544	0.553	0.577	0.865	0.638

, the results of the tested algorithms in respect to the NMI metric for the four distinct datasets are given. Newman–Girvan and Propinquity Dynamics achieve the best performance in almost all datasets whereas Breadth-First Search and CNM have the lower values. Concretely, regarding the dolphins dataset, Propinquity Dynamics and Newman–Girvan have the higher values and MaxToMin with Breadth-First Search have the lower ones. In terms of the football dataset, all the algorithms have almost the same performance with values ranging from $0.903$ to $0.926$. In the karate dataset, MaxToMin along with Propinquity Dynamics and Newman–Girvan perform equally well, and Breadth-First Search has the worst value, e.g., $0.309$. Finally, in Polbooks dataset, the six algorithms have the lowest values in contrast to the other three datasets, with Newman–Girvan having the best value. These results are also illustrated in Figure 1.

Table 4. Number of Iterations.

Graph	Breadth-First Search	CNM	Louvain	MaxToMin	Newman-Girvan	Propinquity Dynamics
Dolphins	22	5	4	1	1	6
Football	4	3	3	4	2	6
Karate	3	2	2	1	1	5
Polbooks	4	3	3	4	2	8

and Figure 2 present the performance of the examined algorithms in terms of the number of iterations for the four different graphs. The highest number of iterations in the dolphins dataset is achieved by the Breadth-First Search while the lowest number, equal to 1, is by MaxToMin. Regarding the football and karate graphs, the number of iterations is relatively low for all algorithms, whereas in Polbooks, Propinquity Dynamics needs 8 iterations for completing the community detection. It has to be noted that Newman–Girvan seems to perform equally well in all datasets as the number of iterations is extremely small, i.e., 1 and 2.

Table 5. Modularity.

Graph	Breadth-First Search	CNM	Louvain	MaxToMin	Newman-Girvan	Propinquity Dynamics
Dolphins	0.415	0.538	0.517	0.515	0.655	0.514
Football	0.422	0.626	0.581	0.539	0.635	0.601
Karate	0.343	0.425	0.402	0.395	0.611	0.371
Polbooks	0.419	0.563	0.522	0.487	0.586	0.512

contains the derived analysis related to the modularity metric, which are derived from the six algorithms mentioned above. The Newman–Girvan algorithm outperforms all other algorithms in all the datasets, with values ranging from $0.586$ to $0.655$. On the other hand, Breadth-First Search and MaxToMin perform poorly in contrast to the other three community-detection algorithms. It is worth mentioning that higher values of modularity are in the football and dolphins datasets, followed by Polbooks and, lastly, the karate graph. The modularity metric results are also depicted in Figure 3.

6.2. Twitter Graph Analysis

Table 6. Community range (%) of Twitter Graph.

ID	Breadth-First Search	CNM	Louvain	MaxToMin	Newman-Girvan	Propinquity Dynamics
1	20.2	21.4	13.8	12.3	15.7	12.5
2	14.7	17.2	13.4	11.7	13.4	11.5
3	13.2	13.4	12.4	11.2	12.9	11.1
4	11.6	11.5	12.1	10.6	12.2	10.5
5	10.1	10.5	11.3	10.1	11.2	10.1
6	5.2	9.8	7.9	8.1	9.5	8.4
7	4.6	8.1	6.7	7.3	6.1	7.2
8	4.2	5.2	6.4	7.1	5.2	7.1
9	3.9	2.9	6.3	6.5	4.4	6.3
10	3.7	-	5.1	5.2	3.3	5.4
11	3.3	-	4.6	4.1	2.6	4.3
12	2.9	-	-	3.5	2.4	3.5
13	2.4	-	-	2.3	1.1	2.1

depicts the extent of every individual community, expressed as a proportion of the sum of all vertices, as derived from the six specific algorithms. The CNM and Louvain algorithms yield fewer communities than the other four algorithms. Another observation is that in Breadth-First Search and CNM, bigger communities tend have a large fraction of the overall number of vertices, as opposed to other algorithms that generally lean toward being grouped by size.

The aforementioned results from Table 6 can also be illustrated in Figure 4. The findings are analytically shown with use of the corresponding figure as the larger communities, i.e., the first ones with the lower community ID, seem to constitute a high portion of the total number of vertices, especially in Breadth-First Search and CNM algorithms.

6.3. User Evaluation

Aiming at getting users to assess the Twitter dataset, we conducted web-based research and asked students of the Ionian University to rate the communities derived from each of our proposed algorithms.

In particular, we indicated to users the communities that were extracted by every algorithm, with a corresponding user and their tweets in the grouping. Following navigation of the set of data employed, people had to decide if each grouping contained users with comparable characteristics. They then considered three different alternatives for the extracted communities: “dense community”, “sparse community” and “in-between” [12], based on their own convictions.

Table 7. Communities % with comparable Users-Nodes.

Analysis	Density	Sparsity	In-Betweenes
CNM	38	15	47
Louvain	34	18	48
MaxToMin	27	22	51
Newman-Girvan	29	27	44
Propinquity Dynamics	28	24	48
Breadth-First Search	22	23	55

and Figure 5 indicate the community percentages, in which users rate the communities found by the six algorithms. Similarly to the previous experiment used for Twitter graph community sizes, the CNM and Louvain algorithms yield fewer communities and therefore produce the highest community density. As a result, the six algorithms all perform almost identically in the amount of sparse groupings, where prices range from 15 to 24, except for Newman–Girvan which has a rate equal to 27. At this point, we emphasize that we take into account the fact that finer attributes can enhance the efficiency of the community detection process further, except the nodal properties, in addition to key properties like the amount of followers or even the total tweets per individual.

6.4. Discussion

Due to degree centrality’s simplicity, sometimes it is helpful to consider in-degree and out-degree metrics differently, for instance when looking at transaction data or account activity.

In addition, betweenness centrality is valuable for the analysis of the interaction potential. Specifically, the high number of this measure might suggest a person who has dominance in different clusters in a communtication group or indicate that he or she is at the circumference of either cluster.

Closeness centrality can help in identifying effective “broadcasters” as long as we are dealing with a common network. However, assuming a highly connected network, then all nodes will often achieve a similar score. Another remark is that it will be useful to utilize this metric in order to extract influencers within a single cluster.

Eigenvector centrality constitutes an effective social networks analysis score, which can be ideal for gaining an insight into man-made social networks, but also for learning about such communication groups as the spread of malicious software. In addition, it is therefore a possibility to calculate the eigencentricity of each vertex by converging to a latent vector by the method of power iteration.

In our study, we consider community detection has been implemented into the network analysis on the assumption that edges are pre-identified as a feature class that allows grouping algorithms to distinguish peripheral nodes. Despite this particular niche and its applicability on a case-by-case basis, community detection techniques are applicable to specific network analysis issues over clustering methods, in that the latter are optimized on a set of specific features. It is pointed out that this paper provides a proof of concept as the applicability of each algorithm is directly proportional to its implementation domain (cf. Figure 5) as well as by the fundamental principles that characterize the network under study.

Subsequently, it is shown from our work that Newman–Girvan and Propinquity Dynamics methods are verified and proven to produce optimal performance on almost all datasets. Furthermore, the Breadth-First Search and CNM methods show the lowest values. Note that in the case of the dolphins graph, Propinquity Dynamics and Newman–Girvan have the highest values and MaxToMin with Breadth-First Search have the lowest values respectively.

7. Conclusions and Future Work

It becomes apparent that the successful detection of communities in social networks is the result of evaluation processes of different types of algorithms. In this context, six mainstream community-detection methodologies, namely Breadth-First Search, CNM, Louvain, MaxToMin, Newman–Girvan and Propinquity Dynamics, were evaluated against four most prevalent graphs based on the normalized mutual information (NMI), the number of iterations as well as the modularity metric. Experiments showed that for the NMI metric, Newman–Girvan and Propinquity Dynamics achieve the best performance in almost all graphs, whereas for the modularity metric, the Newman–Girvan algorithm outperforms all other algorithms in all graphs.

Additionally, this paper contributes to the use of contextual knowledge obtained from Twitter, including the evaluation of some popular community-detection algorithms that identify groups of people with comparable attitudes and characteristics with respect to this dataset. Another stage of this study is to suggest to some students the groupings elicited by each algorithm and in accordance with their own convictions, they considered making three different choices for the elicited communities: “dense community”, “sparse community” and “in-between”. Consequently, it turns out that the algorithms with the fewest communities are CNM and Louvain. They therefore tend to get the largest number of dense communities, and all six alternatives have approximately the same number of sparse groupings.

In future work, it is of strong motivation for us to explore the scaling problems addressed by more comprehensive graphs.More specifically, we plan to perform an extensive set of further experiments with other conditions (thematics) in order to determine the factors that affect the results of the paradigms at a more detailed level of detail. The adaptation of efficient heuristics to time-varying graphs is highly prospective and, hence, applicable to our suggested project. Experimental, analytical from the theory of dynamic systems or even different analytical algorithmic tools can be embedded into our further research.