5G-IPAKA: An Improved Primary Authentication and Key Agreement Protocol for 5G Networks

Abstract

The 3rd generation partnership project (3GPP) has been enhancing the security of the 5G AKA (authentication and key agreement) protocol. However, there may still be some shortcomings in the latest version of the 5G AKA protocol. According to the analysis of the latest version of the 5G AKA protocol, this paper points out seven of its shortcomings. To overcome these shortcomings, an improved primary authentication and key agreement protocol for 5G networks is proposed, which is named 5G-IPAKA. Compared with the latest version of the 5G AKA protocol, the main improvements include that the pre-shared key between the user equipment (UE) and the home network (HN) is replaced with a derivation key as the pre-shared key, the challenge-–response mechanism for the serving network (SN) is added, the mutual authentication and key confirmation occurs between the UE and the SN, and the message authentication code (MAC) failure procedure is replaced with a timeout mechanism on the HN. Then, the 5G-IPAKA protocol is proven secure in the mixed strand space model for mixed protocols. Further discussion and comparative analysis show that the 5G-IPAKA protocol can overcome the above shortcomings of the latest version of the 5G AKA protocol, and is better than the recently improved 5G AKA protocols. Additionally, the 5G-IPAKA protocol is efficient and backward-compatible.

1. Introduction

With the continuous popularization of 5G communication technology, in the near future, the 5G network, as an important communication infrastructure, will penetrate into diverse vertical fields, such as in transportation, medical treatment, and industry, and will also support various information interactions between people, people and things, and things and things [1]. In the 5G network, three different primary authentication and key agreement protocols are defined in the related 3rd generation partnership project (3GPP) specifications [2,3,4], including the 5G AKA (authentication and key agreement) protocol, the EAP-AKA’ protocol, and the 5G EAP-TLS protocol. The first two protocols are based on the shared key cryptography, while the last one is based on the public key cryptography. These protocols all aim to provide mutual authentication of subscribers and networks. Currently, they are in the process of standardization.

The 5G AKA protocol [2,3,4] was developed directly from the evolution packet system (EPS)-AKA protocol of the long-term evolution (LTE)/4G network [3], so it inherited certain security vulnerabilities from the EPS-AKA protocol, such as impersonation attacks, man-in-the-middle attacks (MitM), and denial of service (DoS) attacks [5,6,7,8,9,10,11]. In [12], the authors analyzed the 5G AKA protocol of TS 33.501 v0.7.0. They discovered a protocol vulnerability that would enable an attacker to impersonate another user in a serving network (SN). Based on the Tamarin model checker [13], Basin et al. [14] investigated the security properties of the 5G AKA protocol of TS 33.501 v15.1.0, and several major issues were revealed, which were related to user localization, the leakage of activity, the impact of active attackers, and the presence of malicious SN while roaming. In [15], the authors pointed out that the 5G AKA protocol suffers from link ability attacks, and proposed a new authentication scheme by making use of the Diffie–Hellman key exchange algorithm to generate the session key. This scheme was successful in preventing link ability attacks along with an MitM attack.

For the more recently 5G AKA protocol, the authors in [16] found a new attack type. They claimed that the protection mechanism of the sequence number (SQN) can be defeated under specific replay attacks due to its use of exclusive-OR (XOR) and a lack of randomness. In [17], the authors modeled all key components of the 5G AKA protocol (i.e., the user equipment, the serving network, and the home network) according to the definition in the 3GPP specification document. They discovered an attack that exploits a potential race condition and additionally showed that solving the race condition for the honest case does not necessarily prevent the attack. In [18], the authors investigated the privacy properties of the 5G AKA protocol using the Bana–Comon logic [19,20]. They discovered a novel de-synchronization attack and proved that their proposed protocol guarantees the privacy properties. In [21], the authors proposed a novel version of the 5G AKA protocol to prevent active attacks and gain resistance against malignant serving networks. Unfortunately, there is a possibility of an SN impersonation, so this scheme does not eliminate the vulnerability towards the MitM attack. Further, Gharsallah et al. in [22] also attempted to launch a revised version of the 5G AKA protocol. However, their proposed protocol suffers from privacy preservation, as the device identities are clearly transmitted in the air, which leads to numerous security attacks.

As time goes on, more attacks on the 5G AKA protocol were found due to the insecure channel between different network domains in the legacy mobile network. In [23], the authors discovered an attack exploiting subscription concealed identifier (SUCI) to track a subscriber in the 5G network, which is directly caused by the insecure air channel. To cover this issue, they proposed a secure authentication scheme by utilizing the existing public key infrastructure (PKI) mechanism. Further, they found a location sniffing attack, which can be implemented by an attacker through inexpensive devices [24]. Similarly, they proposed a fix scheme based on the existing PKI mechanism. In [25], the authors modeled the 5G AKA protocol with symbolic modeling using ProVerif based on three and four entities models, and then proposed their security consideration. Further, Mariya et al. [26] proposed an enhanced version of the authentication and key agreement protocol for 5G system that surmounts the limitations existing in the 5G AKA protocol. Parne et al. [27] introduced a protocol that preserves the privacy of the user identity and overcomes the identified problems of the 5G AKA protocol. Similarly, 3GPP has also been used to enhance the security of the 5G AKA protocol [2,3,4].

However, there may still be some shortcomings in the latest version of the 5G AKA protocol. To solve this problem, we first point out these possible shortcomings. Then, we propose an improved primary authentication and key agreement protocol for 5G networks, named 5G-IPAKA. Finally, we prove that the 5G-IPAKA protocol is secure and that it is efficient and backward-compatible.

The main contributions of this paper are as follows:

• By analyzing the latest version of the 5G AKA protocol, we point out that the protocol still has seven shortcomings;
• We propose a new 5G-IPAKA protocol by improving the latest version of the 5G AKA protocol from four aspects;
• We formally analyze the security of the 5G-IPAKA protocol in the mixed strand space model for mixed protocols [28]. As a result, the 5G-IPAKA protocol is secure in the mixed strand space model;
• Through discussion and analysis, we are able to overcome the above shortcomings of the latest version of the 5G AKA protocol;
• Through discussion and a comparative analysis, we show that the new 5G-IPAKA protocol is better than the recently improved 5G AKA protocols in overcoming the various shortcomings, and is efficient and backward-compatible.

The rest of this paper is organized as follows. Section 2 provides an overview of the latest version of the 5G AKA protocol. In Section 3, we point out seven shortcomings of the latest version of the 5G AKA protocol. Section 4 describes our proposed 5G-IPAKA protocol. Section 5 provides a formal verification of the 5G-IPAKA protocol in the mixed strand space model. In Section 6, we present the discussion and analysis, and conclude the paper in Section 7.

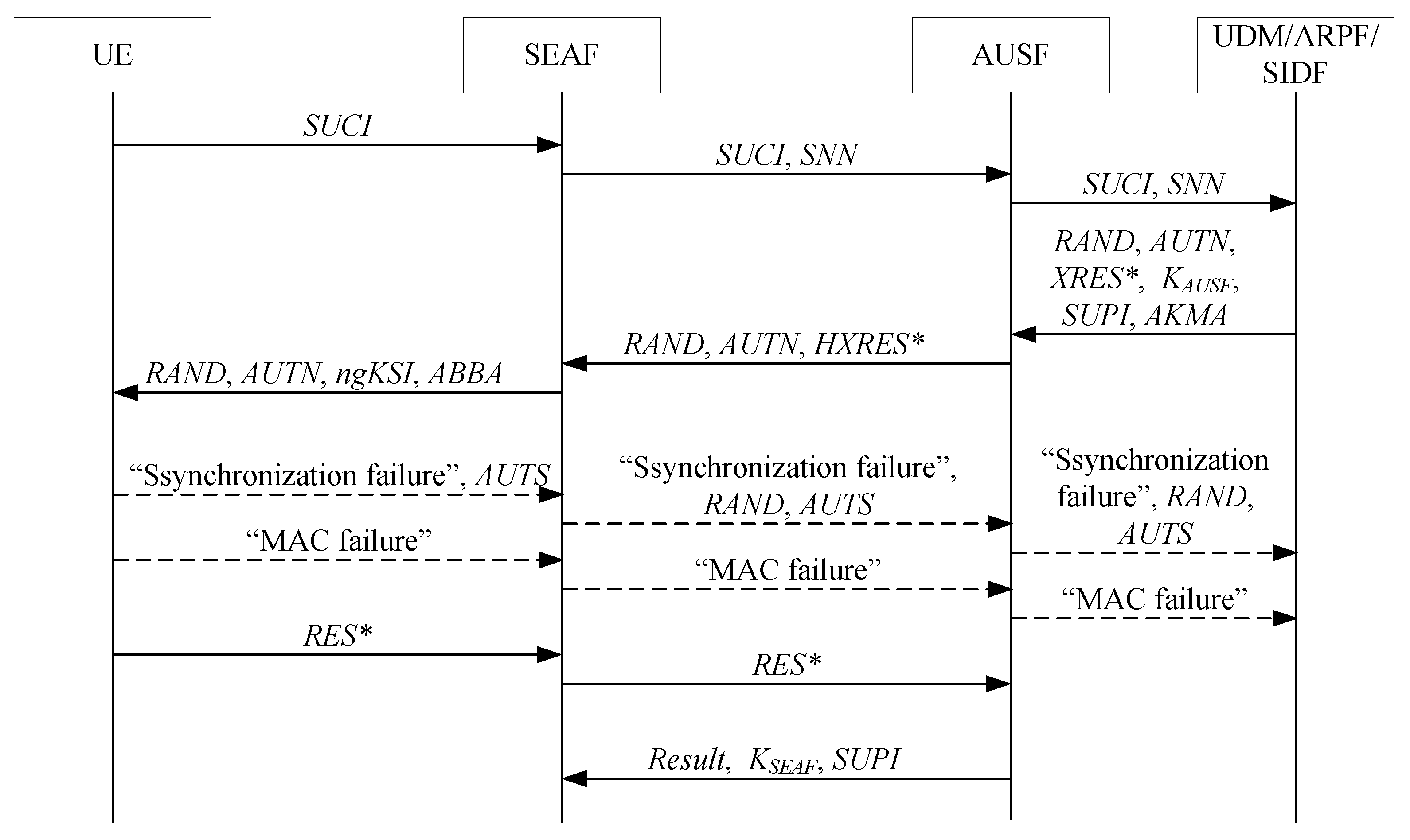
2. Overview of the 5G AKA Protocol

According to [2,3,4], the steps of the latest version of the 5G AKA protocol in the 3GPP standard version v17.4.0 of TS 33.501 are illustrated in Figure 1.

In Figure 1, the universal subscriber identity module (USIM) and the mobile equipment (ME) are located in the user equipment (UE), and the security anchor function (SEAF) is located in the SN. The authentication server function (AUSF), the unified data management (UDM), the authentication credential repository and processing function (ARPE), and the subscriber identity de-concealing function (SIDF) are located in the home network (HN). The messages between the SN and the HN are usually protected. The detailed steps of the latest version of the 5G AKA protocol are as follows:

• When the SEAF initiates an authentication with the UE, the UE sends $SUCI$ to the SEAF, where the UE includes the ME and the USIM. $SUCI$ denotes a SUCI of the UE and $SUCI=x\cdot G\left|\right|{\left\{SUPI\right\}}_{EK}\left|\right|MA{C}_{UE}$, where $SUPI$ denotes the subscription permanent identifier (SUPI) of the UE, $x\cdot G$ and $x$ are an ephemeral public–private key pair of the UE for Diffie–Hellman exchange, $y\cdot G$ and $y$ are the ephemeral public–private key pair of the HN for Diffie–Hellman exchange, $EK\left|\right|ICB\left|\right|MK=KDF(x\cdot y\cdot G)$ and $MA{C}_{UE}=HMAC(MK,{\left\{SUPI\right\}}_{EK})$, $EK$ is an encryption key, $ICB$ is an initial counter block (ICB), $MK$ is a message authentication code (MAC) key, $MA{C}_{UE}$ is a MAC of the UE, $KDF()$ is a key derivation function, and $HMAC()$ is a hash function for computing MAC;
• Upon receiving $SUCI$, the SEAF sends $SUCI$ and $SNN$ to the AUSF. $SNN$ denotes the serving network name (SNN) of the SN;
• If the SEAF is entitled to use $SNN$, then the AUSF stores the receiving $SNN$ and sends $SUCI$ and $SNN$ to the UDM;
• The UDM invokes the SIDF regardless of whether $SUCI$ is received. Then, the SIDF de-conceals $SUCI$ to gain $SUPI$ before the UDM can process the request. Based on $SUPI$, the UDM/ARPF chooses the authentication method;
• When 5G AKA is selected, the UDM/ARPF generates $RAND$, calculates $AUTN$ and $XRES*$, and derives $K_{AUSF}$, and then creates a 5G home environment authentication vector (5G HE AV) from $RAND$, $AUTN$, $XRES*$, and $K_{AUSF}$. $RAND$ is an unpredictable challenge of the HN. $AUTN$ is an authentication token of the HN and $AUTN=SQN\oplus AK\left|\right|AMF\left|\right|MAC$, where $SQN$ is a fresh sequence number generated by the HN, $AK$ is an anonymity key and $AK=f_5(K,RAND)$, $AMF$ is the authentication management field (AMF) and the separation bit of the AMF is set 1, $MAC$ is a MAC of the HN and $MAC=f_1(K,SQN|\left|RAND\right||AMF)$, $K$ is a long-term key between the UE and the HN, $f_1()$ is a message authentication function, and $f_5()$ is a key-generating function. Here, $XRES*=KDF(CK||IK,SNN$ $\left|\right|RAND\left|\right|XRES)$, where $CK$ is a cipher key and $CK=f_3(K,RAND)$, $IK$ is an integrity key and $IK=f_4(K,RAND)$, $XRES$ is an expected response and $XRES=f_2(K,RAND)$, $f_2()$ is a message authentication function, and $f_3()$ and $f_4()$ are two key-generating functions. $K_{AUSF}$ is a key derived from $CK$ and $IK$, and $K_{AUSF}=KDF(CK||IK,SNN||SQN\oplus AK)$;
• The UDM sends the 5G HE AV to the AUSF together with $SUPI$. When an authentication and key management for applications (AKMA) subscription is used, the UDM also sends $AKMA$ to the AUSF. $AKMA$ denotes the AKMA indication and routing indicator;
• The AUSF stores the $XRES*$ temporarily together with the received $SUPI$;
• The AUSF generates a 5G AV from the 5G HE AV received from the UDM/ARPF by computing $HXRES*$ from $XRES*$, computing $K_{SEAF}$ from $K_{AUSF}$, replacing $XRES*$ with $HXRES*$, and replacing $K_{AUSF}$ with $K_{SEAF}$ in the 5G HE AV, where $HXRES*=SHA256(RAND||XRES*)$, $K_{SEAF}=KDF(K_{AUSF},SNN)$, and $SHA256()$ is a hash function;
• The ASUF creates a 5G serving environment authentication vector (5G SE AV) by removing $K_{SEAF}$ from the 5G AV, then sends the 5G SE AV (i.e., $RAND$, $AUTN$, and $HXRES*$) to the SEAF;
• The SEAF stores $HXRES*$, and then sends $RAND$, $AUTN$, $ngKSI$, and $ABBA$ to the UE. Here, $ngKSI$ is used by the UE and the access and mobility management function (AMF) to identify the $K_{AMF}$ and the partial native security context that is created if the authentication is successful. $ABBA$ denotes the anti-bidding down between architectures (ABBA) parameter;
• In the UE, the ME forwards $RAND$ and $AUTN$ to the USIM. Upon receipt of $RAND$ and $AUTN$, the USIM first computes the anonymity key $AK$ and retrieves the sequence number $SQN=(SQN\oplus AK)\oplus AK$. Next, the USIM computes $XMAC=f_1(K,SQN|\left|RAND\right||AMF)$ and compares this with $MAC$, which is included in $AUTN$. Then, the USIM verifies that the received $SQN$ is in the correct range. If $XMAC$ is the same as $MAC$ and $SQN$ is in the correct range, then the USIM computes a response $RES=f_2(K,RAND)$, $CK$, and $IK$, and then returns $RES$, $CK$, and $IK$ to the ME. The ME then computes $RES*=KDF(CK||IK,SNN|\left|RAND\right||RES)$, $K_{AUSF}$, and $K_{SEAF}$;
• The UE sends $RES*$ to the SEAF;
• The SEAF computes $HRES*=SHA256(RAND||RES*)$ and compares this with $HXRES*$. If they coincide, then the SEAF considers the authentication successful from the serving network point of view; if not, then the SEAF considers the authentication unsuccessful;
• The SEAF sends the received $RES*$ to the AUSF;
• The AUSF compares the received $RES*$ with the stored $XRES*$. If $RES*$ and $XRES*$ are equal, then the AUSF considers the authentication successful from the home network point of view. Then, the AUSF informs the UDM about the authentication result;
• The AUSF indicates to the SEAF whether the authentication was successful or not from the home network point of view (i.e., $Result$). If the authentication was successful, then the ASUF also sends $K_{SEAF}$ and $SUPI$ to the SEAF.

In step 11, if $XMAC$ and $MAC$ are different, then the USIM indicates to the ME an MAC failure of $AUTN$. Then, the UE sends a “MAC failure” indication to the SEAF. Further, the SEAF sends the “MAC failure” indication to the AUSF. Finally, the ASUF sends the “MAC failure” indication to the UDM/ARPF.

In step 11, if $SQN$ is not in the correct range, then the USIM computes $AUTS=SQ{N}_{UE}\oplus A{K}^{\ast }\left|\right|MAC-S$, and then sends $AUTS$ with a “synchronization failure” indication to the ME, where $SQ{N}_{UE}$ denotes the highest sequence number the USIM has accepted, $A{K}^{\ast }=f_5^{\ast }(K,RAND)$, $MAC-S=f_1^{\ast }(K,SQ{N}_{UE}|\left|RAND\right||AM{F}_0)$, $AM{F}_0$ is a dummy value of all zeros, $f_1^{\ast }()$ is a message authentication function, and $f_5^{\ast }()$ is a key-generating function. Then, the UE sends $AUTS$ with a “synchronization failure” indication to the SEAF. Further, the SEAF sends $RAND$ and $AUTS$ with a “synchronization failure” indication to the AUSF. Finally, the ASUF sends $RAND$ and $AUTS$ with a “synchronization failure” indication to the UDM/ARPF.

3. Shortcomings of the 5G AKA Protocol

According to the analysis of the above 5G AKA protocol, there are still some shortcomings in the latest version of the 5G AKA protocol, as follows:

• $SUCI$can be replayed without being found. The HN cannot find out whether $SUCI$ is a replayed message because $SUCI$ does not contain the challenge of the HN. Similarly, the UE cannot find out whether $SUCI$ is a replayed message because $AUTN$ does not contain the challenge of the UE (i.e., $x$), which is included in $SUCI$ generated by the UE;
• Mutual authentication between the UE and the SN cannot be established. The UE cannot authenticate the SN because $AUTN$ does not contain $SNN$. Similarly, the SN cannot authenticate the UE for the following three reasons. Firstly, the SN does not verify $SUCI$, $AUTN$, $HXRES*$, $RES*$, and $AUTS$. Secondly, the second received message of the SN does not contain $SUPI$ to match with $SUCI$ in the first received message of the SN. Finally, the last received message of the SN does not contain $RAND$, meaning that $SUPI$ in the last received message of the SN cannot match with the UE identity in $AUTN$ and $HXRES*$, which are included in the second received message of the SN;
• $K_{SEAF}$ cannot reach an agreement. The last received message of the SN does not contain $RAND$, so this message can be a replayed message, meaning that $K_{SEAF}$ on the SN is not equal to $K_{SEAF}$ on the HN. As a result, $K_{SEAF}$ on the SN is not equal to $K_{SEAF}$ on the UE;
• The location privacy of the UE can be compromised. Because $AUTN$ does not contain the challenge of the UE (i.e., $x$), the first received message of the UE can be a replayed message. If $SQN\subset AUTN$ is in the correct range, then the location of the UE can be compromised by reidentifying $RES*$. If $SQN\subset AUTN$ is not in the correct range, then the location privacy of the UE can be compromised by identifying the “synchronization failure” indication; that is to say, when the first received message of the UE is replayed, the legitimate UE response is $RES*$ or a “synchronization failure” indication, but any other UE response is a “MAC failure” indication. As a result, the location privacy of the legitimate UE can be compromised;
• DoS attacks against the SN can be formed. Because the received messages of the SN does not contain the challenge of the SN, these messages can be replayed messages. As a result, the penetrator can impersonate the UE and the HN to complete the entire 5G AKA protocol with the SN, forming DoS attacks against the SN;
• Attacks based on MAC failure can be performed. Firstly, the penetrator can forge or tamper with the first received message of the UE to make the UE respond to a “MAC failure” indication, resulting in authentication failure. Secondly, the penetrator can directly send a “MAC failure” indication to the SN to cause authentication failure. Finally, the penetrator can also replay a “MAC failure” indication between the SN and the HN to cause authentication failure;
• Perfect forward secrecy cannot be provided. In the latest version of the 5G AKA protocol, if $K$ is leaked, then the penetrator can calculate $K_{AUSF}$ and $K_{SEAF}$ based on those messages transmitted in the past run of the protocol. As a result, the penetrator can decrypt those encrypted communication messages transmitted in the past run of the protocol. Therefore, the latest version of the 5G AKA protocol cannot provide perfect forward secrecy.

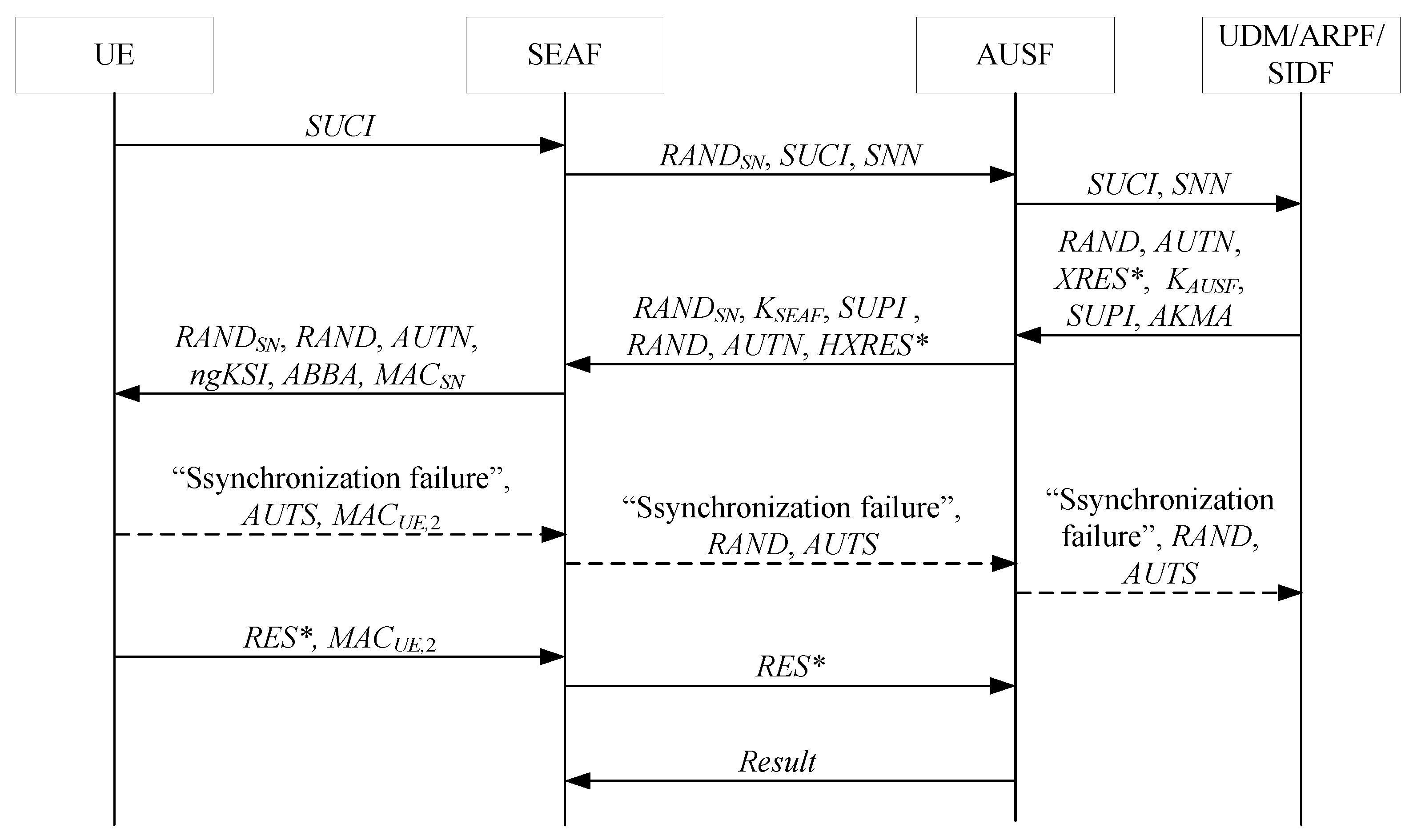
4. Our Proposed 5G-IPAKA Protocol

In order to overcome the above shortcomings of the latest version of the 5G AKA protocol, we propose the 5G-IPAKA protocol, which is illustrated in Figure 2.

In Figure 2, the detail steps of the 5G-IPAKA protocol are shown, as follows:

• When the SEAF initiates an authentication with the UE, the UE sends $SUCI$ to the SEAF;
• Upon receiving $SUCI$, the SEAF generates $RAN{D}_{SN}$ and then sends $RAN{D}_{SN}$, $SUCI$, and $SNN$ to the AUSF, where $RAN{D}_{SN}$ is an unpredictable challenge of the SEAF;
• If the SEAF is entitled to use $SNN$, then the AUSF stores the receiving $SNN$ and sends $SUCI$ and $SNN$ to the UDM;
• The UDM invokes the SIDF whether $SUCI$ is received or not. Then, the SIDF de-conceals $SUCI$ to gain $SUPI$ before the UDM can process the request. Based on $SUPI$, the UDM/ARPF chooses the authentication method;
• When 5G-IPAKA is selected, the UDM/ARPF generates $RAND$, calculates $AUTN$ and $XRES*$, and derives $K_{AUSF}$, and then creates a 5G HE AV from $RAND$, $AUTN$, $XRES*$, and $K_{AUSF}$, where $AUTN=SQN\oplus AK\left|\right|AMF\left|\right|MAC$, $AK=f_5(BK,RAND)$, $MAC=f_1(BK,SQN|\left|RAND\right||AMF)$, $CK=f_3(BK,RAND)$, $IK=f_4(BK,RAND)$, $XRES=f_2(BK,RAND)$, $XRES*=KDF(CK||IK,SNN$ $\left|\right|RAND\left|\right|XRES)$, $K_{AUSF}=KDF(CK||IK,SNN||SQN\oplus AK)$, and $BK=KDF(K,$ $x\cdot y\cdot G\left|\right|SNN)$;
• The UDM sends the 5G HE AV to the AUSF together with $SUPI$. When an AKMA subscription is used, the UDM also sends $AKMA$ to the AUSF;
• The AUSF stores the $XRES*$ temporarily together with the received $SUPI$;
• The AUSF generates a 5G AV from the 5G HE AV received from the UDM/ARPF by computing $HXRES*$ from $XRES*$, computing $K_{SEAF}$ from $K_{AUSF}$, replacing $XRES*$ with $HXRES*$, and replacing $K_{AUSF}$ with $K_{SEAF}$ in the 5G HE AV;
• The ASUF creates a 5G SE AV by adding $SUPI$ to the 5G AV, then sends the 5G SE AV (i.e., $RAND$, $AUTN$, $HXRES*$, $K_{SEAF}$, and $SUPI$) together with $RAN{D}_{SN}$ to the SEAF;
• The SEAF stores $HXRES*$, computes $MA{C}_{SN}$, and then sends $RAN{D}_{SN}$, $RAND$, $AUTN$, $ngKSI$, $ABBA$, and $MA{C}_{SN}$ to the UE, where $MA{C}_{SN}$ is a MAC of the SEAF and $MA{C}_{SN}=HMAC(K_{SEAF},RAN{D}_{SN}|\left|RAND\right|\left|AUTN\right|\left|ngKSI\right||ABBA)$;
• In the UE, the ME forwards $RAND$ and $AUTN$ to the USIM. Upon receipt of $RAND$ and $AUTN$, the USIM first computes $BK=KDF(K,x\cdot y\cdot G||SNN)$ and the anonymity key $AK=f_5(BK,RAND)$ and retrieves the sequence number $SQN=(SQN\oplus AK)\oplus AK$. Next, the USIM computes $XMAC=f_1(BK,SQN$ $\left|\right|RAND\left|\right|AMF)$ and compares this with $MAC$ which is included in $AUTN$. Then, the USIM verifies that the received $SQN$ is in the correct range. If $XMAC$ is the same as $MAC$ and $SQN$ is in the correct range, then the USIM computes a response $RES=f_2(BK,RAND)$, $CK=f_3(BK,RAND)$, and $IK=f_4(BK,RAND)$, and then returns $RES$, $CK$, and $IK$ to the ME. The ME then computes $RES*=KDF(CK||IK,SNN|\left|RAND\right||RES)$, $K_{AUSF}$, and $K_{SEAF}$. Finally, the ME verifies $MA{C}_{SN}$ using $K_{SEAF}$. If the verification fails, then the ME aborts;
• The UE computes $MA{C}_{UE,2}$, and then sends $RES*$ and $MA{C}_{UE,2}$ to the SEAF, where $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}||RES*)$ is another MAC of the UE;
• The SEAF verifies $MA{C}_{UE,2}$. If the verification fails, then the SEAF aborts. Otherwise, the SEAF computes $HRES*=SHA256(RAND||RES*)$ and compares this with $HXRES*$. If they coincide, then the SEAF considers the authentication as successful from the serving network point of view. If not, then the SEAF considers the authentication as unsuccessful;
• The SEAF sends the received $RES*$ to the AUSF;
• The AUSF compares the received $RES*$ with the stored $XRES*$. If $RES*$ and $XRES*$ are equal, then the AUSF considers the authentication as successful from the home network point of view. Then, the AUSF informs the UDM about the authentication result;
• The AUSF indicates to the SEAF whether the authentication was successful or not from the home network point of view (i.e., $Result$).

In step 11, if $XMAC$ and $MAC$ are different, then the UE directly discards the first received message of the UE without responding to a “MAC failure” indication, so the HN will initiate a new authentication procedure towards the UE when the HN does not receive an authentication response message or a synchronization failure message within a certain period of time.

In step 11, if $SQN$ is not in the correct range, then the USIM computes $AUTS=SQ{N}_{UE}\oplus A{K}^{\ast }\left|\right|MAC-S$, and then sends $AUTS$ with a “synchronization failure” indication to the ME, where $A{K}^{\ast }=f_5^{\ast }(BK,RAND)$ and $MAC-S=f_1^{\ast }(BK,$ $SQ{N}_{UE}\left|\right|RAND\left|\right|AM{F}_0)$. Then, the ME computes $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}$ $\left|\right|Syncf\left|\right|AUTS)$, and then sends $AUTS$ and $MA{C}_{UE,2}$ with a “synchronization failure” indication to the SEAF, where $Syncf=“\mathrm{Synchronization} \mathrm{failure}”$. Further, the SEAF verifies $MA{C}_{UE,2}$; if the verification fails then the SEAF aborts, otherwise the SEAF sends $RAND$ and $AUTS$ with a “synchronization failure” indication to the AUSF. Finally, the ASUF sends $RAND$ and $AUTS$ with a “synchronization failure” indication to the UDM/ARPF;

Note that the fields not specifically explained in the above steps are the same as Figure 1. Compared with the latest version of the 5G AKA protocol, the main improvements of our proposed 5G-IPAKA protocol are as follows:

• Replace the pre-shared key between the UE and the HN with a derivation key of the pre-shared key. In detail, $K$ is replaced with $BK=KDF(K,x\cdot y\cdot G||SNN)$ on the UE and the HN;
• Add the challenge-response mechanism for the SN. Firstly, $RAN{D}_{SN}$ is added to the first send message of the SEAF as a challenge and is added to the second received message of the SEAF as a response. Then, $RAN{D}_{SN}$ is added to the second send message of the SEAF as a challenge and is added to the third received message of the SEAF as a response (i.e., $RAN{D}_{SN}$ in $MA{C}_{UE,2}$);
• Add the mutual authentication and key confirmation between the UE and the SN. Firstly, $K_{SEAF}$ and $SUPI$ are moved to the second sent message of the AUSF from the last sent message of the AUSF. Then, the UE and the SN perform a mutual authentication and key confirmation process based on $MA{C}_{SN}$ and $MA{C}_{UE,2}$, which are generated by using $K_{SEAF}$;
• Replace the MAC failure procedure with the timeout mechanism on the HN. If $XMAC$ in the received $AUTN$ and $MAC$ calculated locally by the UE are different, then the UE directly discards the first received message of the UE without responding to a “MAC failure” indication, so the HN will initiate a new authentication procedure towards the UE when the HN does not receive an authentication response message or a synchronization failure message within a certain period of time.

5. Formal Verification of the 5G-IPAKA Protocol

To simplify the formal verification of the 5G-IPAKA protocol, we assume the following:

Assumption 1.

The parties of the 5G-IPAKA protocol shown in Figure 2 are simplified as the UE, the SN, and the HN;

Assumption 2.

There is a session key between the SN and the HN, and it is secure;

Assumption 3.

Here, $ngKSI$ and $ABBA$ do not affect the security of the 5G AKA protocol, so they are ignored.

According to these assumptions, the 5G-IPAKA protocol shown in Figure 2 can be summarized into two cases as follows:

Case I: The verification of $AUTN$ succeeds and the authentication is successful. The steps of this case are as follows:

• $UE\to SN$: $SUCI$;
• $SN\to HN$: ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}$;
• $HN\to SN$: ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right|\left|AUTN\right||HXRES*\}}_{K_{SN,HN}}$;
• $SN\to UE$: $RAN{D}_{SN}\left|\right|RAND\left|\right|AUTN\left|\right|MA{C}_{SN}$;
• $UE\to SN$: $RES*\left|\right|MA{C}_{UE,2}$;
• $SN\to HN$: ${\{RES*\}}_{K_{SN,HN}}$;
• $HN\to SN$: ${\left\{Result\right\}}_{K_{SN,HN}}$.

Case II: The verification of $AUTN$ fails and it is a synchronization failure. The steps of this case are as follows:

• $UE\to SN$: $SUCI$;
• $SN\to HN$: ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}$;
• $HN\to SN$: ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right|\left|AUTN\right||HXRES*\}}_{K_{SN,HN}}$;
• $SN\to UE$: $RAN{D}_{SN}\left|\right|RAND\left|\right|AUTN\left|\right|MA{C}_{SN}$;
• $UE\to SN$: $Syncf\left|\right|AUTS\left|\right|MA{C}_{UE,2}$;
• $SN\to HN$: ${\left\{Syncf\right|\left|RAND\right|\left|AUTS\right\}}_{K_{SN,HN}}$.

In the above cases, $K$ on the UE and the HN is replaced with $BK$, where $BK=KDF(K,x\cdot y\cdot G||SNN)$. $K_{SN,HN}$ denotes the session key between the SN and the HN.

The strand space model [28,29,30] is a well-studied formal analysis method for security protocols. In [28], the authors studied the case of mixed protocols, where principals use secret material in more than one protocol. In such cases, the two protocols can potentially interact, forming vulnerabilities that are not present in either protocol alone.

As mentioned above, there are two cases in the 5G-IPAKA protocol, so there may be interactions between these cases, forming vulnerabilities that do not exist in any single case. Therefore, we use the mixed strand space model [28] to analyze the security of our proposed 5G-IPAKA protocol as follows.

Definition 1.

A regular strand space ${\sum }_{\mathrm{I}}$ is a space for case I of the 5G-IPAKA protocol if ${\sum }_{\mathrm{I}}$ is the union of three kinds of strands: (1) Initiator strands $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $RES*]$ with trace: $<+SUCI$, $-RAN{D}_{SN}\left|\right|RAND\left|\right|AUTN$ $\left|\right|MA{C}_{SN}$, $+RES*\left|\right|MA{C}_{UE,2}>$. The principal associated with this strand is $UE$. $XMAC$ computed locally is equal to $MAC\subset AUTN$ and $SQN\subset AUTN$ is in the correct range (i.e., $SQ{N}_{UE}<SQN$). (2) Responder strands $r\in {\mathrm{Resp}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $H_1$, $H_2$, $H_3$, $Result$, $K_{SEAF}$, $SUPI]$ with trace: $<-SUCI$, $+{\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}$, $-{\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right|\left|H_1\right|\left|H_2\right\}}_{K_{SN,HN}}$, $+RAN{D}_{SN}\left|\right|RAND\left|\right|H_1\left|\right|MA{C}_{SN}$, $-H_3\left|\right|MA{C}_{UE,2}$, $+{\left\{H_3\right\}}_{K_{SN,HN}}$, $-{\left\{Result\right\}}_{K_{SN,HN}}>$. The principal associated with this strand is $SN$. $H_1$, $H_2$ and $H_3$ are three messages that are not inspected by $SN$, where $H_2=SHA256(RAND||H_3)$. (3) Server strands $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$ with trace: $<-{\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}$, $+\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right||SUPI$ $\left|\right|RAND\left|\right|AUTN\left|\right|HXRES*{\}}_{K_{SN,HN}}$, $-{\{RES*\}}_{K_{SN,HN}}$, $+{\left\{Result\right\}}_{K_{SN,HN}}>$. The principal associated with this strand is $HN$.

Definition 2.

A regular strand space ${\sum }_{\mathrm{II}}$ is a space for case II of the 5G-IPAKA protocol if ${\sum }_{\mathrm{II}}$ is the union of three kinds of strands: (1) Initiator strands $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $Syncf$, $AUTS]$ with trace: $<+SUCI$, $-RAN{D}_{SN}\left|\right|RAND$ $\left|\right|AUTN\left|\right|MA{C}_{SN}$, $+Syncf\left|\right|AUTS\left|\right|MA{C}_{UE,2}>$. The principal associated with this strand is $UE$. $XMAC$ computed locally is equal to $MAC\subset AUTN$, but $SQN\subset AUTN$ is not in the correct range (i.e., $SQ{N}_{UE}\ge SQN$). (2) Responder strands $r\in {\mathrm{Resp}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $H_1$, $H_2$, $Syncf$, $H_4]$ with trace: $<-SUCI$, $+{\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}$, $-\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right||H_1$ $\left|\right|H_2{\}}_{K_{SN,HN}}$, $+RAN{D}_{SN}\left|\right|RAND\left|\right|H_1\left|\right|MA{C}_{SN}$, $-Syncf\left|\right|H_4\left|\right|MA{C}_{UE,2}$, $+\{Syncf$ $\left|\right|RAND\left|\right|H_4{\}}_{K_{SN,HN}}>$. The principal associated with this strand is $SN$. $H_1$, $H_2$, and $H_4$ are three messages that are not inspected by $SN$. (3) Server strands $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$ with trace: $<-\{RAN{D}_{SN}$ $\left|\right|SUCI\left|\right|SNN{\}}_{K_{SN,HN}}$, $+\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right||RAND$ $\left|\right|AUTN\left|\right|HXRES*{\}}_{K_{SN,HN}}$, $-\left\{Syncf\right||RAND$ $\left|\right|AUTS{\}}_{K_{SN,HN}}>$. The principal associated with this strand is $HN$.

Definition 3.

An infiltrated strand space Σ,$\mathcal{P}$ is a space for the 5G-IPAKA protocol if Σ = Σ_I ∪ Σ_II ∪ $\mathcal{P}$, where penetrator strands p ∈ $\mathcal{P}$ [28,29,30].

Theorem 1.

Suppose (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing an initiator strand $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $RES*]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique server strand $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$ and a unique responder strand $r\in {\mathrm{Resp}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$.

Proof of Theorem 1.

Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2. Because $MAC=f_1(BK,SQN|\left|RAND\right||AMF)$ and $RAND$ uniquely originate in $\sum$, $MAC\subset AUTN\subset term(<s,2>)$ must uniquely originate on a server strand $t$ according to Definitions 1 to 3. If $t$ is a server strand of Definition 1, then $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D^{\prime }}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{SN}=HMAC(K_{SEAF},RAN{D}_{SN}||RAND$ $\left|\right|AUTN)$, $MA{C}_{SN}\subset term(<s,2>)$ must originate on a responder strand $r$. According to Assumption 2, ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUP{I}^{″}\right|\left|RAND\right|\left|AUTN\right|\left|{H^{″}}_2\right\}}_{K_{SN,HN}}=term(<r,3>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $RAN{D^{\prime }}_{SN}=RAN{D}_{SN}$. According to Assumption 2, ${\{RES*\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{I}}[U{E}^{‴}$, $SN$, $HN$, $SUC{I}^{‴}$, $SNN$, $RAN{D^{‴}}_{SN}$, $RAND$, ${H^{‴}}_1$, $HXRES*$, $RES*$, $Result$, ${K^{‴}}_{SEAF}$, $SUP{I}^{‴}]$, where $SUP{I}^{‴}\subset SUC{I}^{‴}$. Similarly, ${\left\{RAN{D^{‴}}_{SN}\right|\left|{K^{‴}}_{SEAF}\left|\right|SUP{I}^{‴}\right|\left|RAND\right|\left|{H^{‴}}_1\right||HXRES*\}}_{K_{SN,HN}}$ $=term(<r^{\prime },3>)$ must originate on a server strand $t^{″}$. Since $RAND$ uniquely originates in $\sum$, $t^{″}=t$, so $RAN{D^{‴}}_{SN}=RAN{D}_{SN}$, ${K^{‴}}_{SEAF}=K_{SEAF}$, ${H^{‴}}_1=AUTN$, $SUP{I}^{‴}=SUPI$ and $U{E}^{‴}=UE$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}=term(<t,1>)$ must originate on a responder strand $r^{″}$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{″}=r^{\prime }=r$, then $SUC{I}^{‴}=SUCI$.

If $t$ is a server strand of Definition 2, then $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D^{\prime }}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUT{S}^{\prime }]$, where $SQ{N^{\prime }}_{UE}\subset AUT{S}^{\prime }$. Since $BK\notin {\mathcal{K}}_P$, $MAC-S^{\prime }=f_1^{\ast }(BK,SQ{N^{\prime }}_{UE}|\left|RAND\right||AM{F}_0)$ $\subset AUT{S}^{\prime }\subset term(<t,3>)$ must originate on an initiator strand $s^{\prime }\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D^{″}}_{SN}$, $RAND$, $AUT{N}^{″}$, $Syncf$, $AUT{S}^{\prime }]$, so $x$ originates on $term(<s^{\prime },1>)$. According to Assumption 1, $x$ originates on $term(<s,1>)$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$. However, $s^{\prime }\in {\mathrm{Init}}_{\mathrm{II}}$ and $s\in {\mathrm{Init}}_{\mathrm{I}}$, $s^{\prime }\ne s$. Hence, $t$ is not a server strand of Definition 2. □

Theorem 2.

Suppose (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing an initiator strand $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $Syncf$, $AUTS]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique server strand $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$ and a unique responder strand $r\in {\mathrm{Resp}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$.

Proof of Theorem 2.

Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2. Because $MAC=f_1(BK,SQN|\left|RAND\right||AMF)$ and $RAND$ uniquely originate in $\sum$, $MAC\subset AUTN\subset term(<s,2>)$ must uniquely originate on a server strand $t$ according to Definitions 1–3.

If $t$ is a server strand of Definition 1, then $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D^{\prime }}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$. Since $BK\notin {\mathcal{K}}_P$, $CK=f_3(BK,RAND)\notin {\mathcal{K}}_P$ and $IK=f_4(BK,RAND)\notin {\mathcal{K}}_P$, so $CK\left|\right|IK\notin {\mathcal{K}}_P$. Hence, $RES*\subset term(<t,3>)$ must originate on an initiator strand $s^{\prime }\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUT{N}^{″}$, $RES*]$, so $x$ originates on $term(<s^{\prime },1>)$. According to Assumption 1, $x$ originates on $term(<s,1>)$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$. However, $s^{\prime }\in {\mathrm{Init}}_{\mathrm{I}}$ and $s\in {\mathrm{Init}}_{\mathrm{II}}$, $s^{\prime }\ne s$. Hence, $t$ is not a server strand of Definition 1.

If $t$ is a server strand of Definition 2, then $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D^{\prime }}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUT{S}^{\prime }]$, where $SQ{N^{\prime }}_{UE}\subset AUT{S}^{\prime }$. Since $BK\notin {\mathcal{K}}_P$, $MAC-S^{\prime }=f_1^{\ast }(BK,SQ{N^{\prime }}_{UE}|\left|RAND\right||AM{F}_0)$ $\subset AUT{S}^{\prime }\subset term(<t,3>)$ must originate on an initiator strand $s^{\prime }$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$, so $SQ{N^{\prime }}_{UE}=SQ{N}_{UE}$ and $AUT{S}^{\prime }=AUTS$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{SN}=HMAC(K_{SEAF},RAN{D}_{SN}||RAND$ $\left|\right|AUTN)$, $MA{C}_{SN}\subset term(<s,2>)$ must originate on a responder strand $r$. According to Assumption 2, ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUP{I}^{″}\right|\left|RAND\right|\left|AUTN\right|\left|{H^{″}}_2\right\}}_{K_{SN,HN}}=term(<r,3>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $RAN{D^{\prime }}_{SN}=RAN{D}_{SN}$. According to Assumption 2, ${\left\{Syncf\right|\left|RAND\right|\left|AUTS\right\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{II}}[U{E}^{‴}$, $SN$, $HN$, $SUP{I}^{‴}$, $SUC{I}^{‴}$, $SNN$, $RAN{D^{‴}}_{SN}$, ${K^{‴}}_{SEAF}$, $RAND$, ${H^{‴}}_1$, ${H^{‴}}_2$, $Syncf$, $AUTS]$, where $SUP{I}^{‴}\subset SUC{I}^{‴}$. Similarly, ${\left\{RAN{D^{‴}}_{SN}\right|\left|{K^{‴}}_{SEAF}\left|\right|SUP{I}^{‴}\right|\left|RAND\right|\left|{H^{‴}}_1\right|\left|{H^{‴}}_2\right\}}_{K_{SN,HN}}$ $=term(<r^{\prime },3>)$ must originate on a server strand $t^{″}$. Since $RAND$ uniquely originates in $\sum$, $t^{″}=t$, so $RAN{D^{‴}}_{SN}=RAN{D}_{SN}$, ${K^{‴}}_{SEAF}=K_{SEAF}$, ${H^{‴}}_1=AUTN$, ${H^{‴}}_2=HXRES*$, $SUP{I}^{‴}=SUPI$ and $U{E}^{‴}=UE$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}=term(<t,1>)$ must originate on a responder strand $r^{″}$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{″}=r^{\prime }=r$, so $SUC{I}^{‴}=SUCI$. □

According to Theorems 1 and 2, $UE$ successfully authenticates $HN$ and $SN$, and injection agreement [28,29,30] can be established.

Theorem 3.

Suppose (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing a server strand $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $RES*]$ and a unique responder strand $r\in {\mathrm{Resp}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$.

Proof of Theorem 3.

Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2. Because $CK=f_3(BK,RAND)$ and $IK=f_4(BK,RAND)$, $CK\notin {\mathcal{K}}_P$, and $IK\notin {\mathcal{K}}_P$, so $CK\left|\right|IK\notin {\mathcal{K}}_P$. Hence, $RES*=KDF(CK||IK,SNN|\left|RAND\right||RES)\subset term(<t,3>)$ must originate on an unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D^{\prime }}_{SN}$, $RAND$, $AUT{N}^{\prime }$, $RES*]$ according to Assumption 3, where $SQ{N}^{\prime }\subset AUT{N}^{\prime }$. Similarly, $MA{C}^{\prime }\subset AUT{N}^{\prime }\subset term(<s,2>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $SQ{N}^{\prime }=SQN$ and $AUT{N}^{\prime }=AUTN$. According to Assumption 2, ${\{RES*\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r\in {\mathrm{Resp}}_{\mathrm{I}}[U{E}^{″}$, $SN$, $HN$, $SUC{I}^{″}$, $SNN$, $RAN{D^{″}}_{SN}$, $RAND$, ${H^{″}}_1$, $HXRES*$, $RES*$, $Result$, ${K^{″}}_{SEAF}$, $SUP{I}^{″}]$, where $SUP{I}^{″}\subset SUC{I}^{″}$. Similarly, ${\left\{RAN{D^{″}}_{SN}\right|\left|{K^{″}}_{SEAF}\left|\right|SUP{I}^{″}\right|\left|RAND\right|\left|{H^{″}}_1\right||HXRES*\}}_{K_{SN,HN}}$ $=term(<r,3>)$ must originate on a server strand $t^{″}$. Since $RAND$ uniquely originates in $\sum$, $t^{″}=t$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$, ${K^{″}}_{SEAF}=K_{SEAF}$, ${H^{″}}_1=AUTN$, $SUP{I}^{″}=SUPI$ and $U{E}^{″}=UE$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}=term(<t,1>)$ must originate on a responder strand $r^{\prime }$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$, so $SUC{I}^{″}=SUCI$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}||RES*)$, $MA{C}_{UE,2}\subset term(<r,5>)$ must originate on an initiator strand $s^{\prime }$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$, so $RAN{D^{\prime }}_{SN}=RAN{D}_{SN}$. □

Theorem 4.

Suppose (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing a server strand $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $Syncf$, $AUTS]$ and a unique responder strand $r\in {\mathrm{Resp}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$.

Proof of Theorem 4.

Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2, so $MAC-S=f_1^{\ast }(BK,SQ{N}_{UE}|\left|RAND\right||AM{F}_0)\subset AUTS\subset term(<t,3>)$ must originate on a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D^{\prime }}_{SN}$, $RAND$, $AUT{N}^{\prime }$, $Syncf$, $AUTS]$ according to Assumption 3, where $SQ{N}^{\prime }\subset AUT{N}^{\prime }$. Similarly, $MA{C}^{\prime }\subset AUT{N}^{\prime }\subset term(<s,2>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $SQ{N}^{\prime }=SQN$ and $AUT{N}^{\prime }=AUTN$. According to Assumption 2, ${\left\{Syncf\right|\left|RAND\right|\left|AUTS\right\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r\in {\mathrm{Resp}}_{\mathrm{II}}[U{E}^{″}$, $SN$, $HN$, $SUP{I}^{″}$, $SUC{I}^{″}$, $SNN$, $RAN{D^{″}}_{SN}$, ${K^{″}}_{SEAF}$, $RAND$, ${H^{″}}_1$, ${H^{″}}_2$, $Syncf$, $AUTS]$, where $SUP{I}^{″}\subset SUC{I}^{″}$. Similarly, ${\left\{RAN{D^{″}}_{SN}\right|\left|{K^{″}}_{SEAF}\right|\left|SUP{I}^{″}\right|\left|RAND\right|\left|{H^{″}}_1\right|\left|{H^{″}}_2\right\}}_{K_{SN,HN}}=term(<r,3>)$ must originate on a server strand $t^{″}$. Since $RAND$ uniquely originates in $\sum$, $t^{″}=t$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$, ${K^{″}}_{SEAF}=K_{SEAF}$, $SUP{I}^{″}=SUPI$, $U{E}^{″}=UE$, ${H^{″}}_1=AUTN$ and ${H^{″}}_2=HXRES*$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUCI\right|\left|SNN\right\}}_{K_{SN,HN}}=term(<t,1>)$ must originate on a responder strand $r^{\prime }$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$, so $SUC{I}^{″}=SUCI$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}|\left|Syncf\right||AUTS)$, $MA{C}_{UE,2}\subset term(<r,5>)$ must originate on an initiator strand $s^{\prime }$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$, so $RAN{D^{\prime }}_{SN}=RAN{D}_{SN}$. □

According to Theorems 3 and 4, $HN$ successfully authenticates $UE$ and $SN$, and the injection agreement [28,29,30] can be established.

Theorem 5.

Suppose (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing a response strand $r\in {\mathrm{Resp}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $H_1$, $H_2$, $H_3$, $Result$, $K_{SEAF}$, $SUPI]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique server strand $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $HXRES*$, $RES*$, $Result$, $K_{SEAF}$, $SUPI]$, and a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $RES*]$.

Proof of Theorem 5.

Through Assumptions 2 and 3, $K_{SN,HN}\notin {\mathcal{K}}_P$ and $RAND$ uniquely originates in $\sum$, so ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right|\left|H_1\right|\left|H_2\right\}}_{K_{SN,HN}}=term(<r,3>)$ must uniquely originate on a server strand $t$ according to Definitions 1 to 3.

If $t$ is a server strand of Definition 1, then $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUC{I}^{\prime }$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUT{N}^{\prime }$, $(HXRES*{)}^{\prime }$, $(RES*{)}^{\prime }$, $Result$, $K_{SEAF}$, $SUPI]$, where $SUPI\subset SUC{I}^{\prime }$, $x^{\prime }\subset AUT{N}^{\prime }$, $x^{\prime }\subset (HXRES*{)}^{\prime }$, $x^{\prime }\subset (RES*{)}^{\prime }$ and $K_{SEAF}$ is generated for $SUPI$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUC{I}^{\prime }\right|\left|SNN\right\}}_{K_{SN,HN}}$ $=term(<t,1>)$ must originate on a responder strand $r^{\prime }$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$, so $SUC{I}^{\prime }=SUCI$ and $x^{\prime }=x$ according to Assumption 1. Hence, $AUT{N}^{\prime }=AUTN$, $(HXRES*{)}^{\prime }=HXRES*$ and $(RES*{)}^{\prime }=RES*$. Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2. Because $CK=f_3(BK,RAND)$ and $IK=f_4(BK,RAND)$, $CK\notin {\mathcal{K}}_P$ and $IK\notin {\mathcal{K}}_P$, so $CK\left|\right|IK\notin {\mathcal{K}}_P$. Hence, $RES*=KDF(CK||IK,SNN$ $\left|\right|RAND\left|\right|RES)\subset term(<t,3>)$ must originate on a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D^{″}}_{SN}$, $RAND$, $AUT{N}^{″}$, $RES*]$ according to Assumption 3, where $SQ{N}^{″}\subset AUT{N}^{″}$. Similarly, $MA{C}^{″}\subset AUT{N}^{″}\subset term(<s,2>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $SQ{N}^{″}=SQN$ and $AUT{N}^{″}=AUTN$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}||RES*)$, $MA{C}_{UE,2}\subset term(<r,5>)$ must originate on an initiator strand $s^{\prime }$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$.

If $t$ is a server strand of Definition 2, then $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUC{I}^{\prime }$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUT{N}^{\prime }$, $(HXRES*{)}^{\prime }$, $Syncf$, $AUT{S}^{\prime }]$, where $SUPI\subset SUC{I}^{\prime }$, $x^{\prime }\subset AUT{N}^{\prime }$, $x^{\prime }\subset (HXRES*{)}^{\prime }$ and $x^{\prime }\subset AUT{S}^{\prime }$. Similarly, ${\left\{Syncf\right|\left|RAND\right|\left|AUT{S}^{\prime }\right\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{II}}[U{E}^{″}$, $SN$, $HN$, $SUP{I}^{″}$, $SUC{I}^{″}$, $SNN$, $RAN{D^{″}}_{SN}$, ${K^{″}}_{SEAF}$, $RAND$, ${H^{″}}_1$, ${H^{″}}_2$, $Syncf$, $AUT{S}^{\prime }]$. Similarly, ${\left\{RAN{D^{″}}_{SN}\right|\left|{K^{″}}_{SEAF}\left|\right|SUP{I}^{″}\right|\left|RAND\right|\left|{H^{″}}_1\right|\left|{H^{″}}_2\right\}}_{K_{SN,HN}}$ $=term(<r^{\prime },3>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$ and $RAN{D}_{SN}$ originates on $term(<r^{\prime },2>)$. According to Assumptions 1 and 3, $RAN{D}_{SN}$ originates on $term(<r,2>)$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$. However, $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{II}}$ and $r\in {\mathrm{Resp}}_{\mathrm{I}}$, $r^{\prime }\ne r$. Hence, $t$ is not a server strand of Definition 2. □

Theorem 6.

Suppose: (1) $\sum$ is a space for the 5G-IPAKA protocol, and $\mathcal{C}$ is a bundle containing a response strand $r\in {\mathrm{Resp}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $H_1$, $H_2$, $Syncf$, $H_4]$; (2) $K\notin {\mathcal{K}}_P$ and $K_{SN,HN}\notin {\mathcal{K}}_P$; (3) $x$, $RAND$, $RAN{D}_{SN}$ uniquely originates in $\sum$. Then, $\mathcal{C}$ contains a unique server strand $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUCI$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUTN$, $HXRES*$, $Syncf$, $AUTS]$ and a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D}_{SN}$, $RAND$, $AUTN$, $Syncf$, $AUTS]$.

Proof of Theorem 6.

According to Assumptions 2 and 3, $K_{SN,HN}\notin {\mathcal{K}}_P$ and $RAND$ uniquely originate in $\sum$, so ${\left\{RAN{D}_{SN}\right|\left|K_{SEAF}\right|\left|SUPI\right|\left|RAND\right|\left|H_1\right|\left|H_2\right\}}_{K_{SN,HN}}=term(<r,3>)$ must uniquely originate on a server strand $t$ according to Definitions 5–7.

If $t$ is a server strand of Definition 1, then $t\in {\mathrm{Serv}}_{\mathrm{I}}[UE$, $SN$, $HN$, $SUC{I}^{\prime }$, $SNN$, $RAN{D}_{SN}$, $RAND$, $AUT{N}^{\prime }$, $(HXRES*{)}^{\prime }$, $(RES*{)}^{\prime }$, $Result$, $K_{SEAF}$, $SUPI]$, where $SUPI\subset SUC{I}^{\prime }$, $x^{\prime }\subset AUT{N}^{\prime }$, $x^{\prime }\subset (HXRES*{)}^{\prime }$, $x^{\prime }\subset (RES*{)}^{\prime }$, and $K_{SEAF}$ is generated for $SUPI$. Similarly, ${\{(RES*{)}^{\prime }\}}_{K_{SN,HN}}=term(<t,3>)$ must originate on a responder strand $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{I}}[U{E}^{″}$, $SN$, $HN$, $SUC{I}^{″}$, $SNN$, $RAN{D^{″}}_{SN}$, $RAND$, ${H^{″}}_1$, $(HXRES*{)}^{\prime }$, $(RES*{)}^{\prime }$, $Result$, ${K^{″}}_{SEAF}$, $SUP{I}^{″}]$. Similarly, ${\left\{RAN{D^{″}}_{SN}\right|\left|{K^{″}}_{SEAF}\left|\right|SUP{I}^{″}\right|\left|RAND\right|\left|{H^{″}}_1\right||(HXRES*{)}^{\prime }\}}_{K_{SN,HN}}$ $=term(<r^{\prime },3>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$ and $RAN{D}_{SN}$ originate on $term(<r^{\prime },2>)$. Through Assumptions 1 and 3, $RAN{D}_{SN}$ originates on $term(<r,2>)$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$. However, $r^{\prime }\in {\mathrm{Resp}}_{\mathrm{I}}$ and $r\in {\mathrm{Resp}}_{\mathrm{II}}$, $r^{\prime }\ne r$. Hence, $t$ is not a server strand of Definition 1.

If $t$ is a server strand of Definition 2, then $t\in {\mathrm{Serv}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUPI$, $SUC{I}^{\prime }$, $SNN$, $RAN{D}_{SN}$, $K_{SEAF}$, $RAND$, $AUT{N}^{\prime }$, $(HXRES*{)}^{\prime }$, $Syncf$, $AUT{S}^{\prime }]$, where $SUPI\subset SUC{I}^{\prime }$, $x^{\prime }\subset AUT{N}^{\prime }$, $x^{\prime }\subset (HXRES*{)}^{\prime }$ and $x^{\prime }\subset AUT{S}^{\prime }$. Similarly, ${\left\{RAN{D}_{SN}\right|\left|SUC{I}^{\prime }\right|\left|SNN\right\}}_{K_{SN,HN}}$ $=term(<t,1>)$ must originate on a responder strand $r^{\prime }$. Since $RAN{D}_{SN}$ uniquely originates in $\sum$, $r^{\prime }=r$, so $SUC{I}^{\prime }=SUCI$ and $x^{\prime }=x$ according to Assumption 1. Hence, $AUT{N}^{\prime }=AUTN$, $(HXRES*{)}^{\prime }=HXRES*$ and $AUT{S}^{\prime }=AUTS$. Since $BK=KDF(K,x\cdot y\cdot G||SNN)$, $BK\notin {\mathcal{K}}_P$ according to Assumption 2, $MAC-S=f_1^{\ast }(BK,SQ{N}_{UE}|\left|RAND\right||AM{F}_0)\subset AUTS\subset term(<t,3>)$ must originate on a unique initiator strand $s\in {\mathrm{Init}}_{\mathrm{II}}[UE$, $SN$, $HN$, $SUCI$, $RAN{D^{″}}_{SN}$, $RAND$, $AUT{N}^{″}$, $Syncf$, $AUTS]$ according to Assumption 3, where $SQ{N}^{″}\subset AUT{N}^{″}$. Similarly, $MA{C}^{″}\subset AUT{N}^{″}\subset term(<s,2>)$ must originate on a server strand $t^{\prime }$. Since $RAND$ uniquely originates in $\sum$, $t^{\prime }=t$, so $SQ{N}^{″}=SQN$ and $AUT{N}^{″}=AUTN$. According to $t$, $K_{SEAF}$ is encrypted by $K_{SN,HN}$. According to Assumption 2, $K_{SEAF}\notin {\mathcal{K}}_P$. Because $MA{C}_{UE,2}=HMAC(K_{SEAF},RAN{D}_{SN}|\left|Syncf\right||AUTS)$, $MA{C}_{UE,2}\subset term(<r,5>)$ must originate on an initiator strand $s^{\prime }$. Since $x$ uniquely originates in $\sum$, $s^{\prime }=s$, so $RAN{D^{″}}_{SN}=RAN{D}_{SN}$. □

According to Theorems 5 and 6, $SN$ successfully authenticates $UE$ and $HN$, and the injection agreement [28,29,30] can be established.

6. Discussion

6.1. Security of the 5G-IPAKA Protocol

According to the above formal verification of the 5G-IPAKA protocol, mutual authentication between the UE and the SN, mutual authentication between the UE and the SN, and mutual authentication between the SN and the HN are established. Additionally, an injection agreement [28,29,30] among the UE, the SN, and the HN is established. Therefore, the 5G-IPAKA protocol is secure in the mixed strand space model.

Because $K$ is replaced with $BK=KDF(K,x\cdot y\cdot G||SNN)$ on the UE and the HN, $AUTN$ must contain the challenge of the UE (i.e., $x$), which is included in $SUCI$ generated by the UE. Hence, the UE can find out whether $SUCI$ is a replayed message.

According to the above formal verification of the 5G-IPAKA protocol, mutual authentication between the UE and the SN is established. In addition, an injection agreement [28,29,30] among the UE, the SN, and the HN is established, so $K_{SEAF}$ can reach an agreement among the UE, the SN, and the HN.

Because $AUTN$ contains the challenge of the UE (i.e., $x$), the first received message of the UE (including $AUTN$) cannot be a replayed message, preventing the location privacy of the UE from being compromised.

Since the received messages of the SN contain the challenge of the SN (i.e., $RAN{D}_{SN}$), these messages cannot be some replayed messages, preventing DoS attacks against the SN. In addition, the UE directly discards the first received message without responding to a “MAC failure” indication when $XMAC$ messages in the received $AUTN$ and $MAC$ calculated locally by the UE are different, defending against attacks based on MAC failure.

Because $K$ is replaced with $BK=KDF(K,x\cdot y\cdot G||SNN)$, and both $K_{AUSF}$ and $K_{SEAF}$ are generated based on $BK$, this provides perfect forward secrecy (PFS) based on the Diffie–Hellman exchange.

Hence, our proposed 5G-IPAKA protocol can overcome the above shortcomings in the latest version of the 5G AKA protocol.

A comparative analysis between the 5G-IPAKA protocol and the recently improved 5G AKA protocols [23,24,26,27] regarding the shortcomings of the latest version of the 5G AKA protocol is shown in

Table 1. Comparative analysis between the 5G-IPAKA protocol and the recently improved 5G AKA protocols [23,24,26,27] regarding the shortcomings of the latest version of the 5G AKA protocol.

Shortcomings	5G AKA	[23]	[24]	[26]	[27]	5G-IPAKA
$SUCI$ can be replayed without being found	Yes	No	Yes	No	No	No
Mutual authentication between the UE and the SN cannot be established	Yes	Yes	Yes	Yes	Yes	No
$K_{SEAF}$ cannot reach an agreement	Yes	Yes	Yes	Yes	Yes	No
The location privacy of the UE can be compromised	Yes	No	No	No	No	No
DoS attacks against the SN can be formed	Yes	Yes	Yes	Yes	Yes	No
Attacks based on MAC failure can be performed	Yes	Yes	No	No	No	No
Perfect forward secrecy cannot be provided	Yes	Yes	Yes	Yes	Yes	No

.

From Table 1, the recently improved 5G AKA protocols still have some of the shortcomings of the latest version of the 5G AKA protocol, but our proposed 5G-IPAKA overcomes all the shortcomings of the latest version of the 5G AKA protocol.

In [23], the Eph private key and Eph public key of the UE (i.e., $x$ and $x\cdot G$), the public–private key pair of the SN, and the public–private key pair of the HN are used to ensure the security of the channel between the UE and the SN, the security of channel between the UE and the HN, and the security of the channel between the SN and the HN. Since the first received message of the UE is encrypted by the Eph public key of the UE, this means that the message can only be decrypted by the Eph private key of the UE, so it cannot be a replayed message, preventing the location privacy of the UE being compromised. In addition, the UE can find out whether $SUCI$ is a replayed message. However, the other parts fully inherit the 5G AKA protocol, so the other shortcomings of the 5G AKA protocol still exist in the protocol [23].

In [24], both the synchronization failure and the MAC failure are constructed as the format of $RES*$, making it impossible to distinguish them so as to prevent the location privacy of the UE being compromised and prevent attacks based on MAC failure. However, the other parts fully inherit the 5G AKA protocol, so the other shortcomings of the 5G AKA protocol still exist in the protocol of [24].

In [26], $SUCI$ is included in $AUT{H}_{SEAF}$ in the second received message of the UE, so the UE can find out whether $SUCI$ is a replayed message, where $AUT{H}_{SEAF}$ is an authentication token of the SEAF. Additionally, the protocol from [26] removes the synchronization failure procedure and the MAC failure procedure, preventing the location privacy of the UE from being compromised and defending against attacks based on MAC failure. Similarly, $MA{C}_{ARPF}$ is also included in $AUT{H}_{SEAF}$ from the second received message of the UE, but it does not contain $SEA{F}_{ID}$, where $MA{C}_{ARPF}$ is a MAC of the ARPF and $SEA{F}_{ID}$ is the identity of the SEAF (i.e., $SNN$ mentioned above). This means that the UE cannot authenticate the SN being authenticated by the HN, meaning that mutual authentication between the UE and the SN cannot be established and $K_{SEAF}$ cannot reach an agreement. In addition, $RAN{D}_{SEAF}$ is included in the $RAN{D^{\prime }}_{UE}$ of the second received message of the SEAF, $HXRES*$ of the third received message of the SEAF, and $RES*$ of the fourth received message of the SEAF, although the SEAF does not verify these fields, so DoS attacks against the SN can be formed, where $RAN{D^{\prime }}_{UE}$ is calculated based on $RAN{D}_{UE}$ and $RAN{D}_{SEAF}$ (i.e., the challenges of the UE and the SEAF, respectively). Because $K_{AUSF}$ and $K_{SEAF}$ can be calculated when $K$ is leaked, PFS cannot be provided.

In [27], the time synchronization among the UE, the SN, and the HN is maintained. $T_{UE}$ is included in $SUCI$, so $SUCI$ cannot be a replayed message, where $T_{UE}$ is a timestamp of the UE. Additionally, the protocol of [27] also removes the synchronization failure procedure and the MAC failure procedure, preventing the location privacy of the UE from being compromised and defending against attacks based on MAC failure. $MA{C}_{SN}$ is included in the first received message of the UE, but it does not contain $SNN$. This means that the UE cannot authenticate the SN being authenticated by the HN, meaning that mutual authentication between the UE and the SN cannot be established and $K_{SEAF}$ cannot reach an agreement. For the received messages, the SN does not verify $T_{UE}$ and $T_{HN}$ (i.e., a timestamp of the HN), but only verifies whether $RES$ is equal to $XRES$ in phase 1 of the protocol from [27], meaning that DoS attacks against the SN can be formed. Similar to [26], PFS cannot be provided.

Therefore, our proposed 5G-IPAKA protocol is better than these recently improved 5G AKA protocols in overcoming the shortcomings of the latest version of the 5G AKA protocol.

6.2. Performance of the 5G-IPAKA Protocol

A comparative analysis between the 5G-IPAKA protocol and the recently improved 5G AKA protocols [23,24,26,27] regarding the number of messages, the amount of calculation, and backward compatibility is shown in

Table 2. A comparative analysis between the 5G-IPAKA protocol and the recently improved 5G AKA protocols [23,24,26,27] regarding the number of messages, the amount of calculation, and backward compatibility.

Protocols	The Number of Messages	The Amount of Calculation	Backward Compatibility
5G AKA	11	1ECDH+1ED+12F+2XOR	-
[23]	11	4PED+1ED+10F+2XOR	No
[24]	11	2PED+1ECDH+1ED+13F+1XOR	No
[26]	9	1ECDH+1ED+12F	No
[27]	7	1ED+15F+1LRCS+6XOR	No
5G-IPAKA	9	1ECDH+1ED+16F+2XOR	Yes

.

In Table 2, the number of messages represents the number of messages among the UE, the SN, and the HN. ECDH denotes the generation and verification of an elliptic curve Diffie–Hellman (ECDH) exchange. PED denotes the generation and verification of a public key encryption and decryption process. ED denotes the generation and verification of a symmetric key encryption and decryption process. F denotes the generation and verification of a key function, key derivation function, MAC function, or a hash function, which are grouped into one category because they require the same amount of calculation [27]. LRCS denotes the left circular shift and the right circular shift. XOR denotes the generation and verification of an XOR value.

From Table 2, the number of messages in the 5G-IPAKA protocol is less than the 5G AKA protocol, although the amount of calculation is slightly higher than the 5G AKA protocol. The number of messages in the 5G-IPAKA protocol is less than the protocols in [23,24], and the amount of calculation is also lower than the protocols in [23,24] because they introduce multiple public key encryption and decryption processes. The number of messages in the 5G-IPAKA protocol is the same as the protocol in [26], although the amount of calculation is slightly higher than the protocol in [26]. The number of messages in the 5G-IPAKA protocol is more than in the protocol in [27], and the amount of calculation is also higher than the protocol in [27]. However, the protocol in [27] introduces a timestamp mechanism and must maintain the time synchronization among the UE, the SN, and the HN, which is difficult. Hence, our proposed 5G-IPAKA protocol is efficient.

Additionally, the protocols in [23,24,26,27] destroy the structure of the messages instead of adding fields to the messages or extending fields in the messages, so they are not backward-compatible. Our proposed 5G-IPAKA protocol only extends $K$ and adds some fields to the messages among the UE, the SN, and the HN, so it is forward compatible.

7. Conclusions

In this paper, according to the analysis of the latest version of the 5G AKA protocol, we point out seven shortcomings of this protocol, including that $SUCI$ can be replayed without being found, mutual authentication between the UE and the SN cannot be established, $K_{SEAF}$ cannot reach an agreement, the location privacy of the UE can be compromised, DoS attacks against the SN can be formed, attacks based on MAC failure can be performed, and PFS cannot be provided.

To overcome these shortcomings, we propose a 5G-IPAKA protocol. Compared with the latest version of the 5G AKA protocol, the main improvements of the 5G-IPAKA protocol include that the pre-shared key between the UE and the HN is replaced with a derivation key of the pre-shared key, the challenge-response mechanism for the SN is added, the mutual authentication and key confirmation between the UE and the SN is added, and the MAC failure procedure is replaced with a timeout mechanism on the HN.

Accordingly, we summarize the 5G-IPAKA protocol into two cases, and then use the mixed strand space model for mixed protocols to formally analyze the security of the 5G-IPAKA protocol. As a result, mutual authentication and injection among the UE, the SN, and the HN are established. Therefore, the 5G-IPAKA protocol is secure in the mixed strand space model.

Based on the further discussion and comparative analysis, the 5G-IPAKA protocol can overcome the above shortcomings of the latest version of the 5G AKA protocol, and is better than the recently improved 5G AKA protocols in overcoming these shortcomings. In addition, the 5G-IPAKA protocol is efficient and backward-compatible.

Recently, some authors also point out that the protection mechanism of SQN can be defeated due to its use of XOR in the 5G AKA protocol. This paper does not consider this security problem, and we will further study this security problem in the future.