Abstract
In recent years, skin cancer diagnosis has been aided by the most sophisticated and advanced machine learning algorithms, primarily implemented in the spatial domain. In this research work, we concentrated on two crucial phases of a computer-aided diagnosis system: (i) image enhancement through enhanced median filtering algorithms based on the range method, fuzzy relational method, and similarity coefficient, and (ii) wavelet decomposition using DB4, Symlet, RBIO, and extracting seven unique entropy features and eight statistical features from the segmented image. The extracted features were then normalized and provided for classification based on supervised and deep-learning algorithms. The proposed system is comprised of enhanced filtering algorithms, Normalized Otsu’s Segmentation, and wavelet-based entropy. Statistical feature extraction led to a classification accuracy of 93.6%, 0.71% higher than the spatial domain-based classification. With better classification accuracy, the proposed system will assist clinicians and dermatology specialists in identifying skin cancer early in its stages.
1. Introduction
Recent statistics on melanoma skin cancer show that “In the year 2016, it was estimated that 76,380 new cases of melanoma will be found in the United States and at the death rate of 10,130 from the disease” [1]. It comprises 2% of all other skin cancer cases, and 25% of its occurrence is in persons of age group below 45. Its incident rate doubled since 1973 and became stable in 2000. Hence, to reduce the mortality rate caused by melanoma, much research has been carried out on both clinical images and Dermoscopic images. Images of the skin lesions can be captured using digital cameras, and after biopsies, the layers of skin lesions are investigated through a microscope. Clinical images are the images captured using digital cameras and microscopes. Images captured using dermatoscopy are called dermoscopic images. Many researchers tried to diagnose skin cancer using prominent techniques such as image processing, soft computing, and data mining, etc. They have designed a Computer-Aided Diagnosis (CAD) system which acquires the image and predicts whether the lesion is benign or malignant. Generally, a computer-aided diagnosis system involves (i) image acquisition, (ii) preprocessing, (iii) segmentation, (iv) feature extraction or selection, (v) classification, and (vi) prediction. Novel algorithms are proposed and implemented in each phase to achieve higher accuracy that helps to prevent human lives from deadly cancer. These CAD systems assist dermatologists in verifying their predictions and help them to start with the treatment process as soon as possible. The workflow of the CAD system is shown in Figure 1.
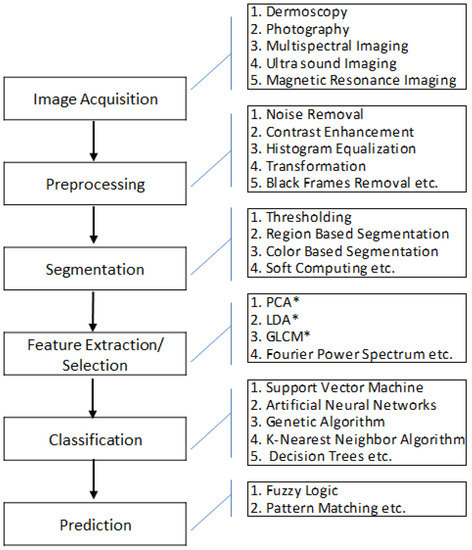
Figure 1.
Workflow of the CAD system. * is to highlight the techniques.
2. Related Works
Many researchers developed computer-aided diagnosis systems using advanced computing techniques [2,3]. A few interesting techniques that came out of various studies are given as follows: In this article [4] researchers tried to classify the melanoma and non-melanoma images using a support vector machine. Before the classification step, the melanoma images were cleansed, and the affected skin lesion was segmented using active contours. From the segmented images, color, shape, and texture features were extracted and fed as input to the SVM classifier. In this work [5], authors proposed a feature-selection framework for melanoma skin lesions which comprised of lesion localization using RCNN, deep feature extraction, and feature selection using iteration-controlled Newton–Raphson’s method. In work [6] attempted to implement transfer and deep-learning algorithms in IoT systems that can assist doctors in diagnosing the different types of skin lesions such as typical nevi and melanoma. They have tried convolutional neural networks (CNN) models such as VGG, Resnet, Inception, Inception-Resnet, and Nanette for melanoma and non-melanoma classification. For injuries, machine learning algorithms such as random forests, SVM, and multilayer perceptron were used for classification. The concept [7] presented an automated segmentation algorithm for skin lesion segmentation and support vector machine (SVM) based classification of melanoma and benign lesions. Developed an application called Dermo Deep [8], which classifies melanoma and nevus lesions with the help of multiple visual features and a deep neural network approach. They implemented the application with a massive number of segmented skin lesion images to train the network. Premaladha et al., 2016 developed a CAD system with classification techniques such as ANN, SVM, ANFIS, Hybrid AdaBoost algorithms, and Deep Learning-based Neural Networks (DLNN) [9]. We implemented all the classification techniques in the features extracted from the images in the spatial domain. In this research work, the frequency domain features were more focused, and the classification techniques were applied to those features. Kruk et al., 2015 used the color image for diagnosis using classifiers such as SVM, random forest, and extended descriptors such as K–S (Kolmogorov–Smirnov), descriptors “reflecting the change distribution of the intensity of pixels placed in the orbits of the increasing geometrical distances from the central point”, maximum sub-region descriptors, and percolation descriptor, etc. [10]. Researchers carried out a pilot study on representing the skin lesion images as a phylogenetic tree. Further classification was carried out with the rank values derived from the tree representation [11,12]. In addition to two novel methodologies of Scan-line method and the Fuzzy Relational method, to quantify the asymmetricity of the melanoma, skin lesions were proposed [13]. Asymmetricity is one of the essential features in the diagnosis of melanoma. In the proposed a system that does border extraction and segmentation followed by extraction of shape, texture, and color features [14]. The extracted features were then classified using their proposed ensemble approach that addresses the class imbalances in training data and achieves better classification accuracy. This research article [15] proposed a computer-aided system that does asymmetry analysis of shape, color, and texture features. In their proposal, asymmetry was quantified using Global Point Signatures (GPSs), and the features were classified using an SVM with 10-fold cross-validation.
2.1. Need for the Study
From the broad literature survey conducted, it is observed that most of the research works concentrate on spatial-domain features for classification using machine learning. Pretrained deep-learning models [16] extracted the candidate features in the spatial domain. In addition to the spatial domain features, the extracted features from the image in the frequency domain can contribute significantly to the classification.
2.2. Contribution of the Research Article
To develop a computer-aided diagnosis system without the manual interpretation of the clinical expert’s opinion for the classification [17] of skin lesion images, the workflow of the proposed model is described as follows.
- (i)
- A novel pre-processing method was used as a basis for median filtering. The traditional median filter was hybridized with the Range method (Algorithm 1), Fuzzy Relational method (Algorithm 2), and Similarity coefficient method (Algorithm 3);
- (ii)
- Segmentation was imparted using Normalized Otsu’s segmentation [18];
- (iii)
- Feature extraction was performed with Wavelet coefficients (DB4, Symlets, RBIO);
- (iv)
- Classification was performed using ANN, SVM, and ANFIS. The proposed algorithms were implemented with melanoma skin lesion images and enhanced for further processing. The quality factor of the enhanced image was then measured with statistical measures such as Peak Signal to Noise Ratio (PSNR) and Mean Square Error (MSE).
This paper is organized as follows: Section 3 provides the proposed methodologies, Section 4 deals with the experimental results, Section 4.2 is comprised of discussions, and finally, Section 5 relates the conclusion.
3. Proposed Methodology
3.1. Image Enhancement through an Enhanced Median Filter
The process of manipulating an image is performed such that “the resulted image is more suitable than the source image for a specific application” [19]. Images are processed to improve their visual interpretation or visual quality as required for a specific application. Filtering is one of the prominent enhancement techniques for removing noise from the image. This research work made use of an enhanced median filter to improve the quality of the skin lesion images.
Enhanced Median Filter work on the enhancement of the median filter was obtained by the three following proposed add-on techniques, which were applied to the original raw image before the median filter. These proposed methods enhanced the performance of the median filter. The pseudo-code representation for the proposed methodologies is given below.
3.1.1. Algorithm for Range Method
The first proposed algorithm is the range method. Initially, the color image was converted into a grayscale image, and then it was used to alter the intensity value of every pixel of the given grayscale image. It starts from the top-left 3 × 3 blocks, and then it is followed by the raster scan method. The algorithm for the proposed range method is given below in Algorithm 1:
| Algorithm 1: Range Method. |
| Input: Gray scale image of melanoma/benign skin lesion Output: Enhanced image
|
From the experiment, we found that if the image has more noise, then the mean value is not required, and hence, the min_diff and max_diff will be added and subtracted for those intensity values 0 or 255, respectively.
3.1.2. Algorithm for Fuzzy Relational Method
Fuzzy relational method is shown in Algorithm 2.
| Algorithm 2: Fuzzy Relational Method. |
| Input: Gray scale image of melanoma/benign skin lesion Output: Enhanced image
|
3.1.3. Algorithm for Similarity Coefficient Method
The third proposed method is the similarity coefficient method. Initially, the color image is turned into a grayscale image, which is then used to alter the intensity value of every pixel of the given grayscale image. It starts from the top left 3 × 3 blocks, and then it is followed by the raster scan method for moving every 3 × 3 blocks.
To find the similarity coefficient, the intensity value was converted into a binary value and each bit was considered for finding the similarity. Four parameters a, b, c and d were taken, where a represents the number of (1,1) pairs, b represents the number of (1,0) pairs, c represents the number of (0,1) pairs, and d represents the number of (0,0) pairs. The existing methods used to identify similarity coefficient, such as the Jaccardian method, mostly use only three parameters, and they omit the (0,0). Here, it was included to improve the precision of the enhancement. The algorithm for the proposed similarity coefficient method is given below (refer Algorithm 3):
| Algorithm 3: Similarity Coefficient Method. |
| Input: Grayscale image of melanoma/benign skin lesion Output: Enhanced image
|
The abovementioned proposed methodologies were implemented with 992 melanoma and nevus samples, which were sourced from the authorized databases [20].
3.2. Segmentation
Segmentation is the practice of separating the affected skin region from the normal skin. Normalized Otsu’s segmentation [21] was used in this paper to distinguish diseased skin from lively healthy skin. The traditional Otsu’s segmentation algorithm was enhanced with normalization using local-global block analysis, eliminating the variable illumination problem.
The significant features required to classify a skin lesion as malignant or benign are derived from the segmented region of the skin lesion image. As mentioned in Section 1, mostly geometrical features, texture features, and color features, etc. are used for classification purposes. Only few studies have contributed a computerized classification using frequency domain features. Some significant contributions are listed as follows: in the classification analysis presented in the early diagnosis of melanoma (Pigmented and melanocytic lesions), symbolic machine learning methods were tested using geometric features and wavelet features [22,23]. Maximum energy ratio and fractional energy ratio were the two features derived from the wavelet coefficients. In article [24] they proposed a methodology for melanoma diagnosis using the features extracted from the wavelet coefficients. They used different wavelet functions such as Daubechies 2, Daubechies 6, Symlet, Coiflet, and Biorsplines with three levels of decompositions. The mean and variance of the wavelet coefficients are the features extracted from the melanoma images. This study [25] presented a feature vector which comprised features extracted from a second-order histogram, Gray Level Co-occurrence Matrix (energy, contrast, correlation, and homogeneity), and high-frequency and low-frequency wavelet coefficients (Mean and Variance). The computerized diagnosis system proposed in [26] which used a combination of the spatial domain, frequency domain features, and geometry-based features for classification purposes. They also proposed the extracted texture-based features. Energy, mean, standard deviation, skewness, kurtosis, norm, entropy, and average energy were the features extracted from wavelets and used for classification using Random Forests (RF), Hidden Naive Bayes, and Support Vector Machines (SVM).
In this research work, we defined a new feature vector which includes novel entropy-based features and some statistical features. The segmented image was decomposed using wavelet functions such as Daubechies4, Symlet8, and RBIO6.8. From each image, four wavelet decompositions were acquired. The low-frequency components general render characteristics such as background details of a skin lesion image and the high-frequency components provide textural edge information. Hence, the set of entropy and statistical features given in Table 1 are derived from the low-frequency components of the segmented image.

Table 1.
Proposed feature vectors.
A total of 15 features were extracted for 992 benign and malignant lesions, and each wavelet provides a feature vector of 2550 features. Derived features were then given to the feature extraction phase to remove the redundant and less contributing features.
3.2.1. Entropy Features
Entropy is the measure of average information contained in a signal. It may also provide the measure of the impurity of a signal. Different variants of entropy were derived from the skin lesion image to classify whether the given lesion is benign or malignant.
3.2.2. Approximate Entropy (ApEn)
The statistical property was used to quantify the rate of complexity or the irregularity measures of a signal. Additionally, it explains the rate of producing new information. A finite sequence formulation of randomness is provided via proximity to maximal irregularity. ApEn is defined as in the Equation (1).
where m = embedding information, r = tolerance window, and N = number of points. The algorithm for deriving ApEn was explained in [27], and it has been used for EEG (Electroencephalogram) signals in the study [28,29]. ApEn was used for physiological time series analysis in article [30]. Here, ApEn provided the irregularity of the image signals under study.
3.2.3. Sample Entropy (SamEn)
Sample Entropy is the measure of information carried by a signal and it is an extension of ApEn. For m, which is the embedded dimension given for the tolerance r and no. of data points N, SamEn is a negative log of the probability such that if two sets of contemporaneous data points of length m have a distance greater than r, then two sets of concurrent data points of length m + 1 also greater than r.
Let be the set of data points with constant time intervals, the template vector of the m length is defined such that and distance can be of any distance function, no. of vector pairs in the template of length m and m + 1 with a distance greater than r is counted in A and B, respectively. With A and B, sample entropy is given as in Equation (2).
where A is the no. of template vectors of the m length with and B is the no. of template vectors of the m + 1 length with [31].
3.2.4. Shannon Entropy (ShEn)
Shannon Entropy was introduced in information theory to measure the impurity of the signal and characterizes the PDF of the signal for the continuous signal as presented in the Equation (3).
where i is the range over all the amplitudes of the signal and pi is the probability of the signal having ‘ai’ amplitude. It is the measure of the degree of uncertainty that exists in a system [32]. This measure has been used in waveform analysis for the best basis selection [33]. ShEn is also used in EEG signal analysis [34] and physiological time series analysis.
3.2.5. Log Energy Entropy (LogEn)
Log Energy Entropy is a simpler version of entropy (SamEn), which is defined as in Equation (4).
where i = index of the discrete states. Aydın et al. presented a log energy-based EEG signal classification using multilayer neural networks [35].
3.2.6. Threshold Entropy (ThEn)
Threshold Entropy provides a measure of entropy based on a fixed threshold value. It is denoted by . E(s) gives the number of instances (N) where the signal exceeds the threshold p.
3.2.7. Sure Entropy (SrEn)
Sure Entropy is an ideal tool for quantifying and ordering non-stationary signals, defined as in Equation (5).
where a positive threshold value is greater than 2, s denotes the terminus node signal and i denote the waveform of s [36,37].
3.2.8. Norm Entropy (NmEn)
Norm Entropy is denoted by where s is the terminus node signals, i is the waveform of terminus node signals, and p is the power between 1 and 2.
3.3. Statistical Features
To follow are the statistical features derived from the wavelet functions.
- where i = matrix of low/high-frequency components, = matrix element, M × N is the size of the coefficient matrix.
- if the vector has an odd number of values. , where m, n = two mid values if the vector has an even number of values. The median of the matrix gives the central tendency of the matrix.
- Standard deviation , where m n = Window size, represent the Input of r rows and c columns.
- The median absolute deviation is the measure of average absolute deviations from a central point with respect to the median. It is defined as the where m(X) = median of the values in a matrix or dataset, = element of a matrix, and mn = total number of elements.
- Mean absolute deviation also provides the average absolute deviations from a central point with respect to the mean value of the matrix. It is defined as where m(X) = mean, = element of a matrix, mn = total number of elements.
- Mathematically, the Norm is the total length of all the vectors in a vector space or matrices. The higher the norm value, the bigger the matrix is. Here, L1 norm and L2 norm were derived for the wavelet coefficients.
- L1 norm is also called Sum Absolute Difference, and it is the difference between two vectors which can be defined as where x = elements of the vector and i = index value.
- L2 norm is generally called the Euclidean norm, and it gives the vector difference. It is a sum of squared difference denoted by x = elements of the vector, and i = index value. The range is the takeaway between the maximum and minimum value of the vector space, and it is defined by .
Feature Selection
The features derived from the images were fed into the next phase, called feature selection. In this phase, the features that do not improve the classification accuracy were removed using the well-known kernel technique called Principal Component Analysis (PCA). It follows the statistical procedure of orthogonal transformation to transform a set of possibly correlated variables into a set of linearly uncorrelated variables called principal components.
The principal derived components are less than or equal to the original dataset. In this research work, the derived features were unique, and there was no redundancy. Hence, the feature vector was passed to the next phase, namely, a classification which utilizes entropy that deals with uncertainty.
3.4. Classification
The last phase of the CAD system is classification [38]. The dataset acquired from the feature extraction phase is classified using machine learning algorithms such as DLNN, Real, Modest, Gentle and hybrid AdaBoost algorithms, as discussed in [39]. Classification is also carried out using Adaptive Neuro-Fuzzy Inference System (ANFIS) and Support Vector Machine (SVM) classifiers as given below:
ANFIS
A Mamdani-rooted ANFIS was constructed with fifteen inputs and two outputs. Fifteen features in every image acquired from three different wavelet functions were given as the input, and then the output was speculated. The input and output variables both had a triangular membership function that was utilized to settle with the range of three lingual levels, namely, l, medium, and high, and, as a result, 315 rules for each wavelet function and some sample rules were found and are given below:
If (ApEn is medium) and (SamEn is medium) and (ShEn is medium) and (LogEn is low) and (ThEn is low) and (SrNm is low) and (NmEn is low) and (mean is medium) and (median is low) and (Std_dev is medium) and (Med_Abs_dev is low) and (Mean_Abs_dev is low) and (L1_Norm is low) and (L2_Norm is low) and (Range is medium) then the prediction is made clearly, i.e., it is (benign_initial).
If (ApEn is high) and (SamEn is medium) and (ShEn is low) and (LogEn is low) and (ThEn is high) and (SrNm is medium) and (NmEn is low) and (mean is medium) and (median is high) and (Std_dev is low) and (Med_Abs_dev is high) and (Mean_Abs_dev is medium) and (L1_Norm is low) and (L2_Norm is high) and (Range is medium) then the prediction is made clearly, i.e., it is (malignant_initial).
3.5. SVM
The SVM is one of the supervised learning algorithms that can solve problems in the classification of different experimental class domains. This can also be employed for regression problems where the frontier can handle the challenges. It is, notably, a model-free and data-driven model that fits the absolute for datasets with higher dimensionality such as our proposed problem. Experimental validation is the process of testing with the trained set of images to know how well the model is trained for the given training set. Each data item was plotted the form of dots in the n-dimensional area of the graphical format.
Here, SVM was implemented with the polynomial kernel with the input features of 15 numbers and 2 output features. Though there are different techniques to choose the viable hyper parameters for SVM, in this work, authors adopted a manual search and it could be inferred that is the polynomial kernel considered in this study with and being any two observations, followed by the coefficient of the polynomial with value as one, and the dimension with value 2. Further, the penalty parameter was set to unity; based on these parameter settings, the SVM classifier was used on the dataset and a reasonable performance could be obtained. The features of three wavelet functions are given separately for classification.
The classification of the feature vector derived from all three functions using SVM is given in Figure 2. It depicts the comparative analysis of the different function for the same feature vectors incorporated with the kernel’s polynomial of the SVM, which supports the higher dimensions.
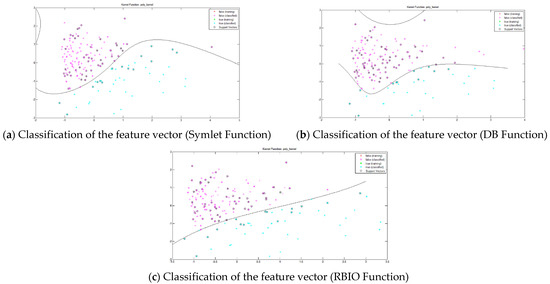
Figure 2.
The classification of the feature vectors of the three different functions. (a) Classification of the feature vector (Symlet Function) (b) Classification of the feature vector (DB Function) (c) Classification of the feature vector (RBIO Function).
4. Experimentation Results
The proposed system for skin cancer detection was implemented with the skin lesion images acquired from a publicly available dataset [40]. The results of each phase of the proposed approach are presented with a detailed discussion in this section.
The quality of the input skin lesion images was enhanced using the enhanced median filter approach. Experimentation results of the proposed algorithms are given in Figure 3. The resultant images of the proposed methods seem to be similar, but differed in their quality metrics, namely, Peak Signal to Noise Ratio (PSNR) and Mean Squared Error (MSE). If the calculated PSNR value was higher, then it was inferred that the quality of the image was improvised, and the degraded image was reconstructed to match the original image. MSE calculation helps to compare the true pixels of the original image to the degraded image. The result is the squares of the error between the original and the degraded image. Hence, a lower MSE value showed the better quality of the enhanced image. The proposed median filter was assessed with the quality metrics such as Peak Signal to Noise Ratio (PSNR) and Mean Square Error. Increased PSNR values and lowered values of MSE resulted in higher image quality. All the samples of the dataset were pre-processed with the proposed methodologies and Table 1 presents the metrics calculated for the ten sample images.
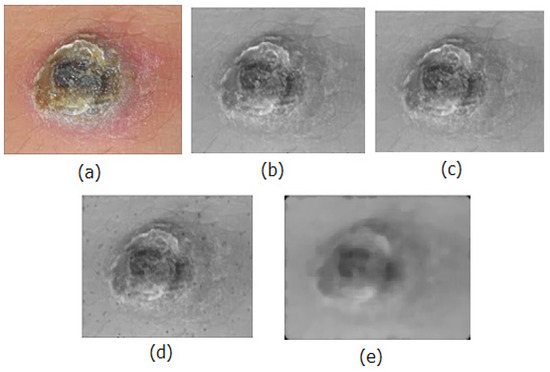
Figure 3.
Results of sample image-1: (a) original image, (b) traditional median filter, (c) proposed range method, (d) proposed Fuzzy Relational method, (e) proposed Similarity Coefficient method.
Hence, the output from the range method was taken for the segmentation phase. From Table 2 and Figure 4, it is inferred that the median filtering enhanced with the range method yields a better-quality image than the other two methods.

Table 2.
Statistical analysis of the images with respect to their PSNR and MSE values.
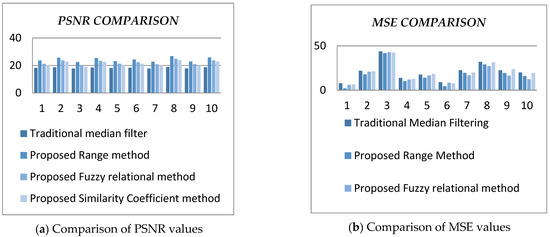
Figure 4.
Comparative analysis of PSNR and MSE values. (a) Comparison of PSNR values (b) Comparison of MSE values.
4.1. Normalized Otsu’s Segmentation
The output image given in Figure 5 was used to derive the feature vector from the different frequency levels using wavelet functions.

Figure 5.
Normalized Otsu’s Segmentation output with the pre-processing step. (a) Input Image (b) Preprocessed image (c) Segmented image.
Wavelet coefficients were derived from the segmented images, and the entropy-based and statistical features were extracted from the coefficients. Entropy-based and statistical features comprise the feature vector for classification. The results of the classification are given in Table 3.

Table 3.
Performance analysis and comparison chart between the classification techniques.
4.2. Discussion
The proposed computerized system for the diagnosis of melanoma uses hybrid median filtering for pre-processing, Normalized Otsu Segmentation, and Machine Learning (ML) algorithms such as ANN, ANFIS, and SVM for classification. All the ML algorithms were tested with the proposed feature vector of fifteen input features and two output features for the samples under study. In literature, only a few researchers used the frequency domain features for classification purposes, and the accuracy achieved by using the state-of-the-art literature is given in Table 3. Table 2 shows that
- The classification accuracy obtained from DLNN through the Symlet function was higher than all other machine learning algorithms for the used dataset.
- Clearly, selecting entropy-based features yielded higher classification accuracy than selecting the mean and variance of the wavelet coefficients.
- We obtained a subtle difference (0.07%) between the spatial and frequency domain classification accuracy.
During the implementation of the proposed system, we found that adding more samples for testing and training was not easy because of the enormous feature set. It indirectly increases the computational complexity, which is a drawback to estimating the classification accuracy in the frequency domain. In the present work, only 15 input features were derived from the low-frequency coefficients. If derived from the other three coefficients, the data size would be 44,640 features for 992 samples collected from a public data source and dermatological centers for detailed analysis/testing of the developed model. By applying Cronbach’s measure, the consistency of the dataset was determined to be 0.77, allowing to authors to proceed with the implementation of the proposed and extant models. The efficiency of our proposed work was tested for the most predominant datasets where it can be applied and experimented with for different medical images [45,46]. The dataset’s size will increase exponentially; hence, the space O(N) and computational complexity O() will also increase exponentially. The limitation of the proposed work was in terms of the execution of the proposed model, as the images had artefacts and therefore more complexity, which will be sorted out even more efficiently in the extended version of this research work.
4.3. Limitations
In the proposed work, the computer-aided diagnosis of melanoma used the hybrid median filter for pre-processing and Normalized Otsu segmentation and machine learning algorithms for the classification. By several ablation trials, we found the classification was interrupted due to the overwhelming artefacts on the images from the datasets with the hairy samples and Ruler markers.
Due to the presence of hair lines and the ruler markers in the image, the features were randomly scattered. Hair lines influenced artefact samples to show less classification accuracy in the average true negatives and false positives between sample images, as shown in Figure 6.
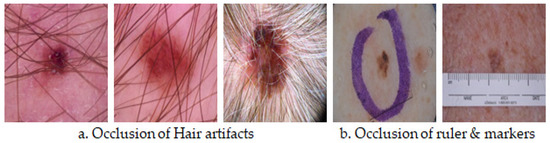
Figure 6.
Artefact occlusion samples from the dataset are misclassified. (a) Occlusion of hair artifacts and (b) Occlusion of ruler & markers.
5. Conclusions and Future Work
Finally, it is concluded that the feature vector derived from the Symlet provides higher classification accuracy when compared with the other wavelet functions. DLNN outperformed the other machine learning algorithms among the various classifiers. The techniques can be applied in various medical image segmentations such as breast cancer, lung cancer diagnosis etc. Though there is a subtle difference (0.07%) between the classification accuracy of the spatial and frequency domain, an overhead of high computational complexity exists in the frequency domain. Bio-inspired algorithms with the development of melanoma diagnosis applications using the concepts of exploration and exploitation in the classifiers will be designed for the extended version of our work.
Author Contributions
The contributions for this research article is done as follows: Conceptualization, K.S.R.; P.J. and N.V.; methodology, P.J. and N.V.; software, P.J. and N.V.; validation, P.R., A.M. and F.C.; formal analysis, R.K.; investigation, K.S.R.; resources, and data curation, P.J.; writing—original draft preparation, N.V.; writing—review and editing, P.J. and N.V.; visualization, R.K.; supervision, P.J.; project administration, F.C.; funding acquisition, P.J. All authors have read and agreed to the published version of the manuscript.
Funding
The authors have not disclosed any funding.
Informed Consent Statement
This article does not contain any studies with human participants or animals performed by any of the authors.
Data Availability Statement
Skin lesion images used to support the findings of this study have been acquired from the repositories mentioned in [47].
Acknowledgments
We: the authors, would like to thank the Department of Science and Technology, India, for their financial support through the Fund for Improvement of S&T Infrastructure (FIST) program (SR/FST/ETI-349/2013). We sincerely thank the SASTRA Deemed-to-be University for providing an excellent infrastructure to carry out the research work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Available online: http://www.cancer.org/cancer/skincancer-melanoma/detailedguide/melanoma-skin-cancer-key-statistics (accessed on 10 September 2021).
- Chatterjee, I. Artificial Intelligence and Patentability: Review and Discussions. Int. J. Mod. Res. 2021, 1, 15–21. [Google Scholar]
- Gupta, V.K.; Shukla, S.K.; Rawat, R.S. Crime tracking system and people’s safety in India using machine learning approaches. Int. J. Mod. Res. 2022, 2, 1–7. [Google Scholar]
- Gulati, S.; Bhogal, R.K. Classification of Melanoma from Dermoscopic Images Using Machine Learning. In Smart Intelligent Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 345–354. [Google Scholar]
- Khan, M.A.; Sharif, M.; Akram, T.; Bukhari, S.A.; Nayak, R.S. Developed Newton-Raphson based deep features selection framework for skin lesion recognition. Pattern Recognit. Lett. 2020, 129, 293–303. [Google Scholar] [CrossRef]
- Rodrigues, D.D.; Ivo, R.F.; Satapathy, S.C.; Wang, S.; Hemanth, J.; Rebouças Filho, P.P. A new approach for classification skin lesion based on transfer learning, deep learning, and IoT system. Pattern Recognit. Lett. 2020, 136, 8–15. [Google Scholar] [CrossRef]
- Seeja, R.D.; Suresh, A. Deep Learning Based Skin Lesion Segmentation and Classification of Melanoma Using Support Vector Machine (SVM). Asian Pac. J. Cancer Prev. 2019, 20, 1555–1561. [Google Scholar]
- Abbas, Q.; Celebi, M.E. DermoDeep-A classification of melanoma-nevus skin lesions using multi-feature fusion of visual features and deep neural network. Multimed. Tools Appl. 2019, 78, 23559–23580. [Google Scholar] [CrossRef]
- Premaladha, J.; Ravichandran, K.S. Novel Approaches for Diagnosing Melanoma Skin Lesions through Supervised and Deep Learning Algorithms. J. Med. Syst. 2016, 40, 1–12. [Google Scholar] [CrossRef]
- Kruk, M.; Swiderski, B.; Osowski, S.; Kurek, J.; Słowińska, M.; Walecka, I. Melanoma recognition using extended set of descriptors and classifiers. EURASIP J. Image Video Process. 2015, 1, 1–10. [Google Scholar] [CrossRef]
- Premaladha, J.; Ravichandran, K.S. Detection of Melanoma Skin Lesions Using Phylogeny. Natl. Acad. Sci. Lett. 2015, 38, 333–338. [Google Scholar] [CrossRef]
- Alrashed, F.A.; Alsubiheen, A.M.; Alshammari, H.; Mazi, S.I.; Al-Saud, S.A.; Alayoubi, S.; Kachanathu, S.J.; Albarrati, A.; Aldaihan, M.M.; Ahmad, T.; et al. Stress, Anxiety, and Depression in Pre-Clinical Medical Students: Prevalence and Association with Sleep Disorders. Sustainability 2022, 14, 11320. [Google Scholar] [CrossRef]
- Premaladha, J.; Ravichandran, K.S. Quantification of Fuzzy Borders and Fuzzy Asymmetry of Malignant Melanomas. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2015, 85, 303–314. [Google Scholar]
- Schaefer, G.; Krawczyk, B.; Celebi, M.E.; Iyatomi, H. An ensemble classification approach for melanoma diagnosis. Memetic Comput. 2014, 6, 233–240. [Google Scholar]
- Liu, Z.; Sun, J.; Smith, L.; Smith, M.; Warr, R. Distribution quantification on dermoscopy images for computer-assisted diagnosis of cutaneous melanomas. Med. Biol. Eng. Comput. 2012, 50, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.K.; Gupta, V.K.; Joshi, K.; Gupta, A.; Singh, M.K. Self-aware Execution Environment Model (SAE2) for the Performance Improvement of Multicore Systems. Int. J. Mod. Res. 2022, 2, 17–27. [Google Scholar]
- Sharma, T.; Nair, R.; Gomathi, S. Breast Cancer Image Classification using Transfer Learning and Convolutional Neural Network. Int. J. Mod. Res. 2022, 2, 8–16. [Google Scholar]
- Premaladha, J.; Priya, M.L.; Sujitha, S.; Ravichandran, K.S. Normalised Otsu’s Segmentation Algorithm for Melanoma Diagnosis. Indian J. Sci. Technol. 2015, 8, 1. [Google Scholar] [CrossRef]
- Janani, P.; Premaladha, J.; Ravichandran, K.S. Image Enhancement Techniques: A Study. Indian J. Sci. Technol. 2015, 8, 1–12. [Google Scholar] [CrossRef]
- Giotis, I.; Molders, N.; Land, S.; Biehl, M.; Jonkman, M.F.; Petkov, N. MED-NODE: A computer-assisted melanoma diagnosis system using non-dermoscopic images. Expert Syst. Appl. 2015, 42, 6578–6585. [Google Scholar]
- Yuan, X.; Martínez, J.-F.; Eckert, M.; López-Santidrián, L. An Improved Otsu Threshold Segmentation Method for Underwater Simultaneous Localization and Mapping-Based Navigation. Sensors 2016, 16, 1148. [Google Scholar] [CrossRef]
- Surowka, G. Symbolic learning supporting early diagnosis of melanoma. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; Volume 31, pp. 4104–4107. [Google Scholar]
- Surowka, G. Supervised learning of melanocytic skin lesion images. In Proceedings of the IEEE Conference on Human System Interactions, Kraków, Poland, 25–27 May 2008; pp. 121–125. [Google Scholar]
- Fassihi, N.; Shanbehzadeh, J.; Sarafzadeh, A.; Ghasemi, E. Melanoma diagnosis by the use of wavelet analysis based on morphological operators. In Proceedings of the International Multiconference of Engineers and Computer Scientists, Hong Kong, China, 16–18 March 2011; pp. 16–18. [Google Scholar]
- D’Alessandro, B.; Dhawan, A.P.; Mullani, N. Computer aided analysis of epi-illumination and transillumination images of skin lesions for diagnosis of skin cancers. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 3434–3438. [Google Scholar]
- Garnavi, R.; Aldeen, M.; Bailey, J. Computer-aided diagnosis of melanoma using border-and wavelet-based texture analysis. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1239–1252. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Bruhn, J.; Ropcke, H.; Hoeft, A. Approximate entropy as an electroencephalographic measure of anesthetic drug effect during desflurane anesthesia. Anesthesiology 2001, 92, 715–726. [Google Scholar]
- Attallah, O.; Sharkas, M.A.; Gadelkarim, H. Deep Learning Techniques for Automatic Detection of Embryonic Neurodevelopmental Disorders. Diagnostics 2020, 10, 27. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Machine Learning-Enriched Lamb Wave Approaches for Automated Damage Detection. Sensors 2020, 20, 1790. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1964; pp. 1–117. [Google Scholar] [CrossRef]
- Coifman, R.R.; Wickerhauser, M.V. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Sabeti, M.; Katebi, S.; Boostani, R. Entropy and complexity measures for EEG signal classification of schizophrenic and control participants. Artif. Intell. Med. 2009, 47, 263–274. [Google Scholar] [CrossRef]
- Aydın, S.; Saraoglu, H.M.; Kara, S. Log energy entropy-based EEG classification with multilayer neural networks in seizure. Ann. Biomed. Eng. 2009, 37, 2626–2630. [Google Scholar]
- Avci, D. An expert system for speaker identification using adaptive wavelet sure entropy. Expert Syst. Appl. 2009, 36, 6295–6300. [Google Scholar]
- Turkoglu, I.; Arslan, A.; Ilkay, E. An Intelligent system for diagnosis of the heart valve diseases with wavelet packet natural Networks. Comput. Biol. Med. 2003, 33, 319–331. [Google Scholar] [CrossRef]
- Duda, R.; Hart, P.; Stork, D. Pattern Classification, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2006; ISBN 978-0-471-05669-0. [Google Scholar]
- Premaladha, J.; Surendra Reddy, M.; Hemanth Kumar Reddy, T.; Sri Sai Charan, Y.; Nirmala, V. Recognition of Facial Expression Using Haar Cascade Classifier and Deep Learning. In Inventive Communication and Computational Technologies; Ranganathan, G., Fernando, X., Shi, F., Eds.; Lecture Notes in Networks and Systems; Springer: Singapore, 2022; Volume 311. [Google Scholar] [CrossRef]
- Codella, N.; Rotemberg, V.; Tschandl, P.; Celebi, M.E.; Dusza, S.; Gutman, D.; Helba, B.; Kalloo, A.; Liopyris, K.; Marchetti, M.; et al. Skin lesion analysis toward melanoma detection 2018: A challenge hosted by the international skin imaging collaboration (ISIC). arXiv 2019, arXiv:1902.03368. [Google Scholar]
- Mustafa, S.; Dauda, A.B.; Dauda, M. Image processing and SVM classification for melanoma detection. In Proceedings of the 2017 International Conference on Computing Networking and Informatics (ICCNI), Ota, Nigeria, 29–31 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Kaur, R.; GholamHosseini, H.; Sinha, R.; Lindén, M. Melanoma Classification Using a Novel Deep Convolutional Neural Network with Dermoscopic Images. Sensors 2022, 22, 1134. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, I.; Younus, M.; Walayat, K.; Kakar, M.U.; Ma, J. Automated multi-class classification of skin lesions through deep convolutional neural network with dermoscopic images. Comput. Med. Imaging Graph. 2021, 88, 101843. [Google Scholar] [CrossRef] [PubMed]
- Shukla, P.; Verma, A.; Abhishek Verma, S.; Kumar, M. Interpreting SVM for medical images using Quadtree. Multimed. Tools Appl. 2020, 79, 29353–29373. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, F.; Shahid, M.; Alam, M.; Ashraf, Z.; Sajid, M.; Kotecha, K.; Dhiman, G. Levelized Multiple Workflow Allocation Strategy under Precedence Constraints with Task Merging in IaaS Cloud Environment. IEEE Access 2022, 10, 92809–92827. [Google Scholar] [CrossRef]
- Kumar, R.; Dhiman, G. A Comparative Study of Fuzzy Optimization through Fuzzy Number. Int. J. Mod. Res. 2021, 1, 1–14. [Google Scholar]
- Hosny, K.M.; Kassem, M.A.; Foaud, M.M. Classification of skin lesions using transfer learning and augmentation with Alex-net. PLoS ONE 2019, 14, e0217293. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).