On the Reality of Signaling in Auctions
Abstract
1. Introduction
2. Related Work
3. Model
4. Preliminaries
4.1. The Rational Agents Case
4.2. Humans and Bounded Rationality
4.3. Changes and Necessary Adjustments
5. Empirical Study
5.1. Experimental Environment
5.1.1. Scoring System
5.1.2. Game Flow
5.2. Experimental Design
- Auction Setting (). Each auction setting includes the following parameters: (1) —the number of bidders who take part in the auction; (2) —the number of possible world states; (3) —the number of possible bidder’s types; and (4) —the valuation matrix that holds each bidder’s type valuation for each possible world state. All numerical values are expressed in terms of game points. Figure 2 depicts a screenshot of our experiment, demonstrating the settings that are introduced to the users. As part of our attempt to create an impartial decision-making process, we chose to eliminate any externalities that might distract the users and influence their decision-making process. Thus, we used uniform distribution for describing both each world state’s probability of being the actual one and each bidder’s type probability of being the actual bidder’s type, i.e., , and . With 5 options for the number of bidders, 2 options for the possible world states, and 2 options for the bidder types, we end up with core cases, each of which includes a specific combination of parameters (1), (2), and (3). Parameter (4) will be discussed by the end of the next stage.
- Information Cost (). As explained in Section 4, a rational information buyer will be willing to purchase the information only if its cost is lower than its value, i.e., the value of the information is the maximal amount a rational information buyer will agree to pay in exchange for the information. Therefore, a strategic expert will set the information cost to be equal to the exact value of the information. This, however, might not be the case when facing a human information buyer. We denote the value of the information using (), where is the auction setting and is the information to be disclosed by the expert (see Equation (3) for a complete calculation of ). To examine the effect that the extent of the difference between the value of information and its cost has on people and on their decision-making process, we set a range of possible information costs that can be used. For each core case defined, , given a specific piece of information the expert is interested in selling, , we first calculate the numeric value of (). Then, we extend each core case into 4 cases differing from one another only in the cost of the information. In two of the cases, the cost is lower than the actual value of the information, i.e., the costs are equal to and . In the other two cases, the cost is higher than the actual value of the information, i.e., the costs are equal to and . This results in an overall of 80 core cases to be examined for which 50% of the information should be purchased and 50% of it should not. Finally, we generate 25 random bidders’ valuation matrices for each core case, creating 2000 cases to be tested by human users. Each value of the bidders’ valuation was drawn from the range of . All values chosen were integers.
- Expert’s Strategy (s). We executed the basic version of The Mysterious Auction Game as presented in the previous subsection in three alternative, extended versions. The first version is the No-Signals (NS) version, in which no signals are used, and thus no free information is disclosed to the user before they are required to decide regarding acquisition of the information. The second version is the Random-Signals (RS) version in which signals are used, but the identity of the world states to be eliminated is decided randomly. The last version is the Greedy-Signals (GS) version in which signals are used and the identity of the world states to be eliminated is decided greedily, i.e., the expert chooses to eliminate the values that will lead to a maximal for the set of remaining values.
- 4
- User Awareness (Aw). For the cases where signals are used, i.e., RS and GS, we considered two awareness alternatives:
- Aware (A)—The user was informed that there is an additional player in the game, who gains from selling information. This was reflected both in the instructions provided to the users in the beginning of the game and through the user interface, so that for each round, the player’s own accumulated score is displayed together with the expert’s accumulated profit.
- Unaware (U)—The user was told that the “system” is interested in assisting him by eliminating several untrue world states. No changes were made in either the instructions or the user interface.
5.2.1. Recruitment of Participants
5.2.2. Participants’ Compensation
5.2.3. Participants’ Guidance
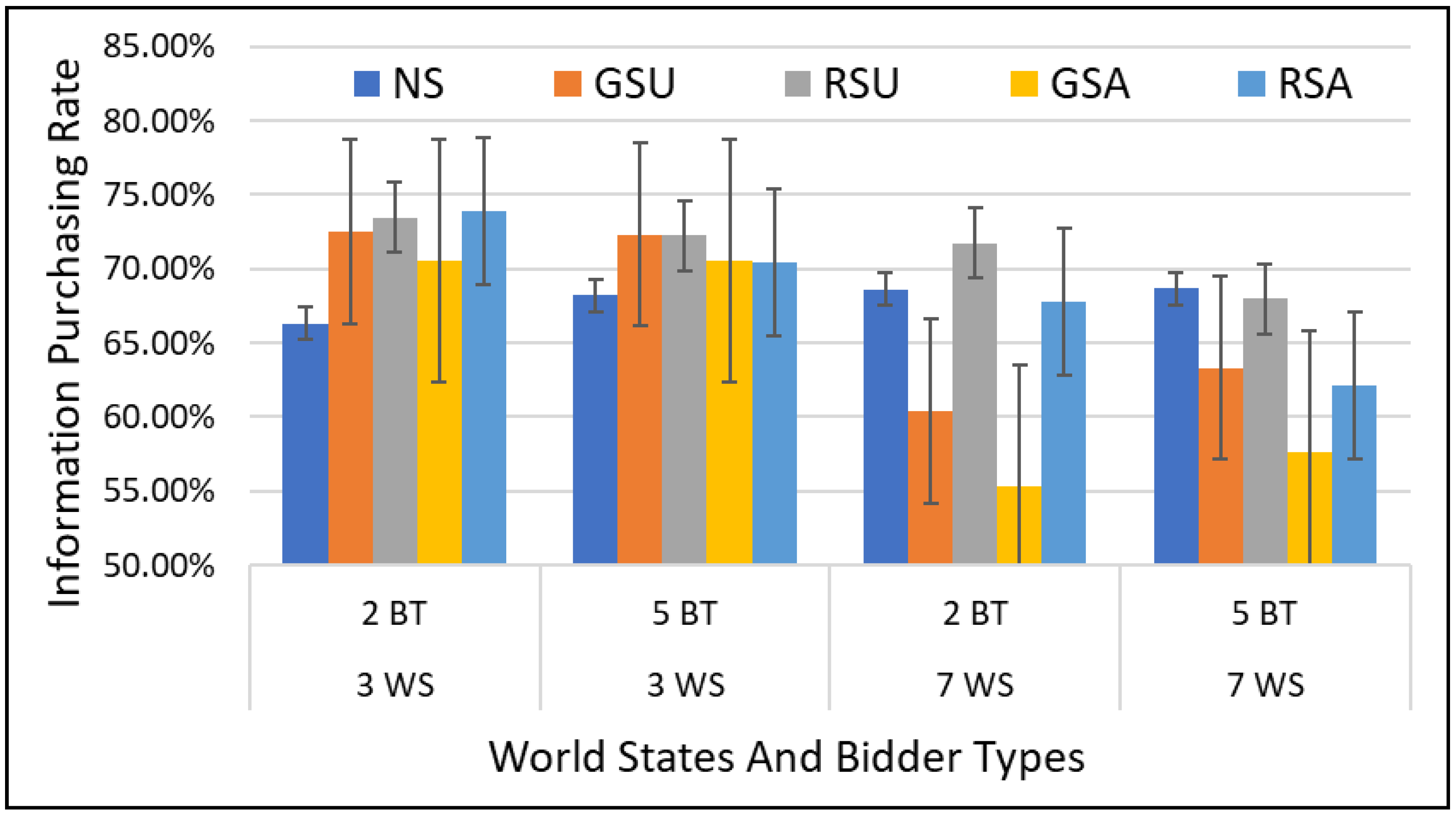
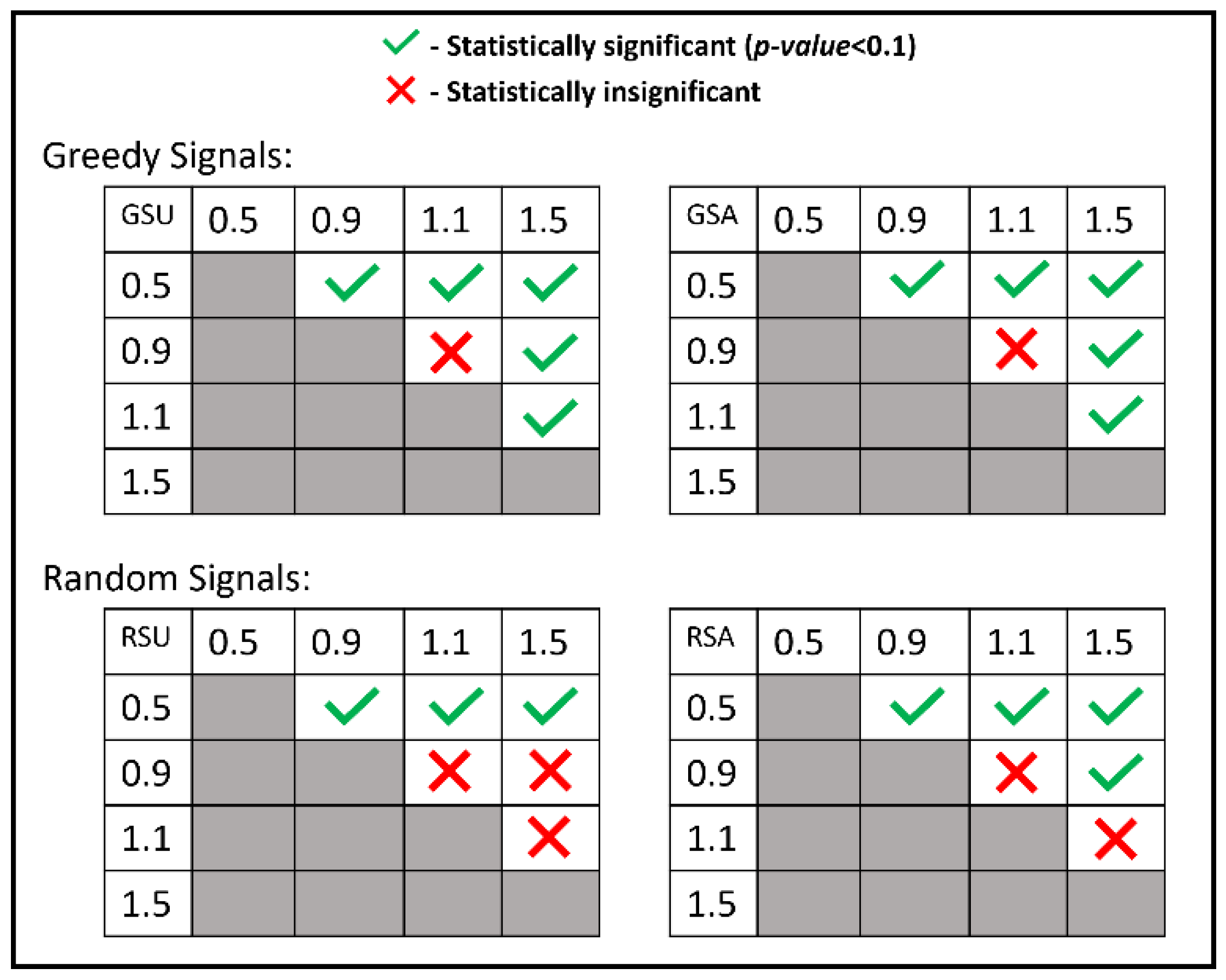
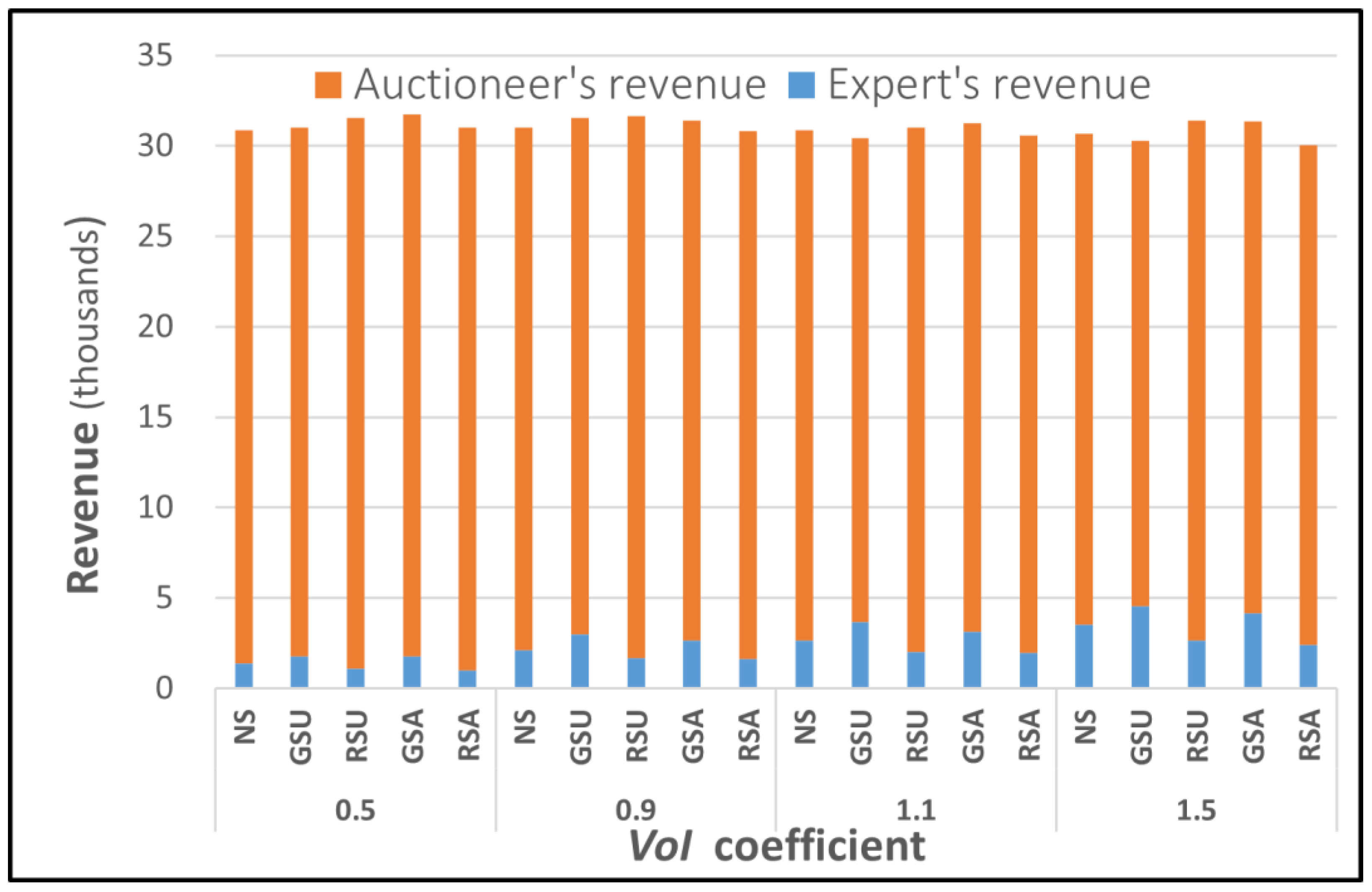
5.3. Results
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, X.; Jingti, H. Auction-based cloud service pricing and penalty with availability on demand. Information 2018, 9, 87. [Google Scholar] [CrossRef]
- Teytelboym, A.; Li, S.; Kominers, S.D.; Akbarpour, M.; Dworczak, P. Discovering auctions: Contributions of Paul Milgrom and Robert Wilson. Scand. J. Econ. 2021, 123, 709–750. [Google Scholar] [CrossRef]
- Eckbo, B.E.; Malenko, A.; Thorburn, K.S. Strategic decisions in takeover auctions: Recent developments. Annu. Rev. Financ. Econ. 2020, 12, 237–276. [Google Scholar] [CrossRef]
- Elshaar, S.; Sadaoui, S. Semi-supervised classification of fraud data in commercial auctions. Appl. Artif. Intell. 2020, 34, 47–63. [Google Scholar] [CrossRef]
- Curry, M.J.; Lyi, U.; Goldstein, T.; Dickerson, J.P. Learning Revenue-Maximizing Auctions with Differentiable Matching. In Proceedings of the 25th International Conference on Artificial Intelligence and Statistics, Valencia, Spain, 28–30 March 2022; pp. 6062–6073. [Google Scholar]
- Alkoby, S.; Sarne, D.; Das, S. Strategic Free Information Disclosure for Search-Based Information Platforms. In Proceedings of the 2015 International Conference on Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015. [Google Scholar]
- Alkoby, S.; Sarne, D.; Milchtaich, I. Strategic Signaling and Free Information Disclosure in Auctions. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 319–327. [Google Scholar] [CrossRef]
- Fishman, M.J. A theory of preemptive takeover bidding. RAND J. Econ. 1988, 19, 88–101. [Google Scholar] [CrossRef]
- Daniel, K.D.; Hirshleifer, D. A theory of costly sequential bidding. Rev. Financ. 2018, 22, 1631–1665. [Google Scholar] [CrossRef]
- Dodonova, A. Preemptive bidding and Pareto efficiency in takeover auctions. Econ. Lett. 2017, 159, 214–216. [Google Scholar] [CrossRef]
- Dodonova, A.; Khoroshilov, Y. Can preemptive bidding in takeover auctions be socially optimal? Yes it can. N. Am. J. Econ. Financ. 2014, 27, 34–47. [Google Scholar] [CrossRef]
- Li, Z.; Das, S. Revenue Enhancement Via Asymmetric Signaling in Interdependent-Value Auctions. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 2093–2100. [Google Scholar]
- Sarne, D.; Alkoby, S.; David, E. On the choice of obtaining and disclosing the common value in auctions. Artif. Intell. 2014, 215, 24–54. [Google Scholar] [CrossRef]
- Xu, H.; Cavallo, R. The Strange Role of Information Asymmetry in Auctions—Does More Accurate Value Estimation Benefit a Bidder? In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual Conference, 22 February–1 March 2022; pp. 5236–5243. [Google Scholar] [CrossRef]
- Milgrom, P.R.; Weber, R.J. A theory of auctions and competitive bidding. Econometrica 1982, 50, 1089–1122. [Google Scholar] [CrossRef]
- Bergemann, D.; Pesendorfer, M. Information structures in optimal auctions. J. Econ. Theory 2007, 137, 580–609. [Google Scholar] [CrossRef]
- Board, S. Revealing information in auctions: The allocation effect. Econ. Theory 2009, 38, 125–135. [Google Scholar] [CrossRef]
- Li, H.; Shi, X. Discriminatory information disclosure. Am. Econ. Rev. 2017, 107, 3363–3385. [Google Scholar] [CrossRef]
- Myerson, R.B. Optimal auction design. Math. Oper. Res. 1981, 6, 58–73. [Google Scholar] [CrossRef]
- Riley, J.G.; Samuelson, W.F. Optimal auctions. Am. Econ. Rev. 1981, 71, 381–392. [Google Scholar]
- Giovannoni, F.; Makris, M. Reputational bidding. Int. Econ. Rev. 2014, 55, 693–710. [Google Scholar] [CrossRef]
- Emek, Y.; Feldman, M.; Gamzu, I.; Paes Leme, R.; Tennenholtz, M. Signaling schemes for revenue maximization. ACM Trans. Econ. Comput. 2014, 2, 1–19. [Google Scholar] [CrossRef]
- Badanidiyuru, A.B.; Bhawalkar, K.; Xu, H. Targeting and signaling in ad auctions. In Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–10 January 2018; pp. 2545–2563. [Google Scholar] [CrossRef]
- Castiglioni, M.; Romano, G.; Marchesi, A.; Gatti, N. Signaling in Posted Price Auctions. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, Virtual Conference, 22 February–1 March 2022; pp. 4941–4948. [Google Scholar] [CrossRef]
- Ganuza, J.J.; Penalva, J.S. Signal orderings based on dispersion and the supply of private information in auctions. Econometrica 2010, 78, 1007–1030. [Google Scholar]
- Arefeva, A.; Meng, D. Revealing information in auctions: The optimal auction versus the second-price auction. Econ. Lett. 2021, 204, 109895. [Google Scholar] [CrossRef]
- Goeree, J.K. Bidding for the future: Signaling in auctions with an aftermarket. J. Econ. Theory 2003, 108, 345–364. [Google Scholar] [CrossRef]
- Molnar, J.; Virág, G. Revenue maximizing auctions with market interaction and signaling. Econ. Lett. 2008, 99, 360–363. [Google Scholar] [CrossRef]
- Rhodes-Kropf, M.; Katzman, E.B. The consequences of information revealed in auctions. Appl. Eco. Res. Bull. 2008, 2, 53–87. [Google Scholar] [CrossRef]
- Arefeva, A.; Meng, D. Information disclosure in housing auctions. SSRN 2021, 26. [Google Scholar] [CrossRef]
- Bergemann, D.; Heumann, T.; Morris, S.; Sorokin, C.; Winter, E. Optimal Information Disclosure in Auctions. SSRN 2022, DP16858, 25. [Google Scholar]
- Avinadav, T.; Chernonog, T.; Khmelnitsky, E. Revenue-sharing between developers of virtual products and platform distributors. Eur. J. Oper. Res. 2021, 290, 927–945. [Google Scholar] [CrossRef]
- Myers, E.; Puller, S.L.; West, J. Mandatory energy efficiency disclosure in housing markets. Am. Econ. J. Econ. Policy. 2020, 14, 453–487. [Google Scholar] [CrossRef]
- Lumsden, K.; Mirzabeiki, V. Determining the value of information for different partners in the supply chain. Int. J. Phys. Distrib. Logist. Manag. 2008, 38, 659–673. [Google Scholar] [CrossRef]
- Jonsson, P.; Myrelid, P. Supply chain information utilisation: Conceptualisation and antecedents. Int. J. Oper. Prod. Manag. 2016, 36, 1769–1799. [Google Scholar] [CrossRef]
- Keisler, J.M.; Collier, Z.A.; Chu, E.; Sinatra, N.; Linkov, I. Value of information analysis: The state of application. Environ. Syst. Decis. 2014, 34, 3–23. [Google Scholar] [CrossRef]
- Heath, A.; Manolopoulou, I.; Baio, G. A review of methods for analysis of the expected value of information. Med. Decis. Mak. 2017, 37, 747–758. [Google Scholar] [CrossRef]
- Quoc Viet, N.; Behdani, B.; Bloemhof, J. The value of information in supply chain decisions: A review of the literature and research agenda. Comput. Ind. Eng. 2018, 120, 68–82. [Google Scholar] [CrossRef]
- Daradkeh, M.; Gawanmeh, A.; Mansoor, W. Information adoption patterns and online knowledge payment behavior: The moderating role of product type. Information 2022, 13, 414. [Google Scholar] [CrossRef]
- Eidsvik, J.; Mukerji, T.; Bhattacharjya, D. Value of Information in the Earth Sciences: Integrating Spatial Modeling and Decision Analysis; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Kim, K.; Koh, Y. Auctions with flexible information acquisition. Games Econ. Behav. 2022, 133, 256–281. [Google Scholar] [CrossRef]
- Li, Y.; Huang, Z. Security-bid auctions with information acquisition. SSRN 2021, 3850243. [Google Scholar] [CrossRef]
- Board, S.; Lu, J. Competitive information disclosure in search markets. J. Political Econ. 2018, 126, 1965–2010. [Google Scholar] [CrossRef]
- Clark, D.J.; Kundu, T. Partial information disclosure in a contest. Econ. Lett. 2021, 204, 109915. [Google Scholar] [CrossRef]
- Gershkov, A. Optimal auctions and information disclosure. Rev. Econ. Des. 2009, 13, 335–344. [Google Scholar] [CrossRef]
- Bergemann, D.; Wambach, A. Sequential information disclosure in auctions. J. Econ. Theory 2015, 159, 1074–1095. [Google Scholar] [CrossRef]
- Evans, B.P.; Prokopenko, M. Bounded rationality for relaxing best response and mutual consistency: The Quantal Hierarchy model of decision-making. arXiv 2021, arXiv:2106.15844. [Google Scholar] [CrossRef]
- Xu, D.S.; Wei, C.; Wei, G.W. TODIM method for single-valued neutrosophic multiple attribute decision making. Information 2017, 8, 125. [Google Scholar] [CrossRef]
- Cohen, S.L.; Bingham, C.B.; Hallen, B.L. The role of accelerator designs in mitigating bounded rationality in new ventures. Adm. Sci. Q. 2019, 64, 810–854. [Google Scholar] [CrossRef]
- Nishimura, T. An experimental study of Crémer–McLean auctions. SSRN 2022, 4111200, 31. [Google Scholar] [CrossRef]
- Cooper, D.J.; Fang, H. Understanding overbidding in second price auctions: An experimental study. Econ. J. 2008, 118, 1572–1595. [Google Scholar] [CrossRef]
- Andreoni, J.; Che, Y.K.; Kim, J. Asymmetric information about rivals’ types in standard auctions: An experiment. Games Econ. Behav. 2007, 59, 240–259. [Google Scholar] [CrossRef]
- Alkoby, S.; Sarne, D. The Benefit in Free Information Disclosure When Selling Information to People. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 985–992. [Google Scholar] [CrossRef]
- Vickrey, W. Counterspeculation, auctions, and competitive sealed tenders. J. Financ. 1961, 16, 8–37. [Google Scholar] [CrossRef]
- Simon, A., II. Theories of bounded rationality, decision and organization. In Decision and Organization; McGuire, C.B., Radner, R., Eds.; Elsevier: Amsterdam, The Netherlands, 1972; pp. 161–176. [Google Scholar]
- Levy, P.; Sarne, D. Intelligent Advice Provisioning for Repeated Interaction. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 842–849. [Google Scholar] [CrossRef]
- Kahneman, D. A psychological point of view: Violations of rational rules as a diagnostic of mental processes. Behav. Brain Sci. 2000, 23, 681–683. [Google Scholar] [CrossRef]
- Hajaj, C.; Hazon, N.; Sarne, D. Improving comparison shopping agents’ competence through selective price disclosure. Electron. Commer. Res. Appl. 2015, 14, 563–581. [Google Scholar] [CrossRef]
- Kraus, S. Human-agent decision-making: Combining theory and practice. arXiv 2016, arXiv:1606.07514. [Google Scholar] [CrossRef][Green Version]
- Arnott, D.; Gao, S. Behavioral economics in information systems research: Critical analysis and research strategies. J. Inf. Technol. 2021, 37, 80–117. [Google Scholar] [CrossRef]
- Dawnay, E.; Shah, H. Behavioural Economics: Seven Principles for Policy-Makers; New Economics Foundation: London, UK, 2005. [Google Scholar]
- Caspi, C.E.; Canterbury, M.; Carlson, S.; Bain, J.; Bohen, L.; Grannon, K.; Peterson, H.; Kottke, T. A behavioural economics approach to improving healthy food selection among food pantry clients. Public Health Nutr. 2019, 22, 2030–2313. [Google Scholar] [CrossRef]
- Porto, R.B.; Foxall, G.R. The marketing-finance interface and national well-being: An operant behavioral economics analysis. Manag. Decis. Econ. 2022, 43, 2941–2954. [Google Scholar] [CrossRef]
- Alcaraz, G.G.; Massuet i Ardil, M.; Orts Sánchez, L.; Sánchez Buixeda, H. Behavioral Economics: Implications of Irrational Behavior in Marketing Practices. Bachelor’s Thesis, Pompeu Fabra University, Barcelona, Spain, 2021. [Google Scholar]
- Costa, D.F.; Carvalho, F.d.M.; Moreira, B.C.d.M. Behavioral economics and behavioral finance: A bibliometric analysis of the scientific fields. J. Econ. Surv. 2019, 33, 3–24. [Google Scholar] [CrossRef]
- Khan, W.U.; Shachak, A.; Seto, E. Understanding decision-making in the adoption of digital health technology: The role of behavioral economics’ prospect theory. J. Med. Internet Res. 2022, 24, e32714. [Google Scholar] [CrossRef]
- Alkoby, S.; Sarne, D.; Milchtaich, I. Strategic Signaling for Selling Information Goods. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 25–31. [Google Scholar] [CrossRef][Green Version]
- Paolacci, G.; Chandler, J.; Ipeirotis, P.G. Running experiments on Amazon Mechanical Turk. Judgm. Decis. Mak. 2010, 5, 411–419. [Google Scholar]
- Klos, A.; Weber, E.U.; Weber, M. Investment decisions and time horizon: Risk perception and risk behavior in repeated gambles. Manag. Sci. 2005, 51, 1777–1790. [Google Scholar] [CrossRef]
- Keren, G. Facing uncertainty in the game of bridge: A calibration study. Organ. Behav. Hum. Decis. Process. 1987, 39, 98–114. [Google Scholar] [CrossRef]
- Barron, B. When smart groups fail. J. Learn. Sci. 2003, 12, 307–359. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levi, A.; Alkoby, S. On the Reality of Signaling in Auctions. Information 2022, 13, 549. https://doi.org/10.3390/info13110549
Levi A, Alkoby S. On the Reality of Signaling in Auctions. Information. 2022; 13(11):549. https://doi.org/10.3390/info13110549
Chicago/Turabian StyleLevi, Aviad, and Shani Alkoby. 2022. "On the Reality of Signaling in Auctions" Information 13, no. 11: 549. https://doi.org/10.3390/info13110549
APA StyleLevi, A., & Alkoby, S. (2022). On the Reality of Signaling in Auctions. Information, 13(11), 549. https://doi.org/10.3390/info13110549








